A&A 484, 293-297 (2008)
DOI: 10.1051/0004-6361:20079210
An analysis of the durations of Swift gamma-ray bursts
Z.-B. Zhang1,2 -
C.-S. Choi1
1 - International Center for Astrophysics, Korea
Astronomy and Space Science Institute, 36-1 Hwaam, Yusong, Daejon
305-348, South Korea
2 -
Yunnan Observatory, National Astronomical Observatories, Chinese Academy of
Sciences,
PO Box 110, Kunming 650011, PR China
Received 7 December 2007 / Accepted 5 March 2008
Abstract
Context. Swift detectors are found to be more sensitive to long-soft bursts than pre-Swift missions. This may largely bias the distribution of durations and thus classification of gamma-ray bursts.
Aims. We systematically investigate the duration distribution of gamma-ray bursts in the Swift era vs. that of pre-Swift bursts.
Methods. For the purpose of this study, statistical methods such as the K-S test and linear/non-linear fitting analysis have been used to examine the duration properties of Swift bursts in both observer and source frames.
Results. For 95 GRBs with known redshift, we show that two log-normal distributions of duration are clearly divided at
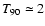 s. The intrinsic durations also show a bimodal distribution but shift systematically toward the smaller value and the distribution exhibits a narrower width than the observed one. Swift long bursts exhibit a wider duration dynamic range in both observer and source frames in comparison to pre-Swift long bursts.
s. The intrinsic durations also show a bimodal distribution but shift systematically toward the smaller value and the distribution exhibits a narrower width than the observed one. Swift long bursts exhibit a wider duration dynamic range in both observer and source frames in comparison to pre-Swift long bursts.
Conclusions. We find that Swift bursts and pre-Swift ones can share the same criterion of classification in terms of duration at 2 s, although both monitors have large differences with respect to sensitivity of a given energy band.
Key words: gamma rays: bursts - gamma rays: theory
Cosmic gamma-ray bursts (GRBs) are the most violent explosions
occurring at cosmological distances in the universe. When a GRB
takes place, satellites can monitor its temporal variability in the
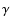 -ray energy band. The duration of the burst, T90, is
defined as the time interval in which the integrated photon counts
increase from 5% to 95% of the total counts. Based on an analysis
of durations using initial BASTE data, Kouveliotou et al. (1993)
divided GRBs into two classes, i.e., long GRBs (LGRBs) with
T90
> 2 s and short GRBs (SGRBs) with T90<2 s. The dichotomy has
been justified by subsequent investigations (e.g., Mao et al. 1994; Katz & Canel 1996; Meegan et al. 1996; Paciesas et al.
1999; Fishman 1999). The best parameters of a two-component
log-normal fit to the distribution data were first obtained by
McBreen et al. (1994). This fit is supported by the current BATSE
data with peak flux information (Horváth 2002;
Nakar 2007).
-ray energy band. The duration of the burst, T90, is
defined as the time interval in which the integrated photon counts
increase from 5% to 95% of the total counts. Based on an analysis
of durations using initial BASTE data, Kouveliotou et al. (1993)
divided GRBs into two classes, i.e., long GRBs (LGRBs) with
T90
> 2 s and short GRBs (SGRBs) with T90<2 s. The dichotomy has
been justified by subsequent investigations (e.g., Mao et al. 1994; Katz & Canel 1996; Meegan et al. 1996; Paciesas et al.
1999; Fishman 1999). The best parameters of a two-component
log-normal fit to the distribution data were first obtained by
McBreen et al. (1994). This fit is supported by the current BATSE
data with peak flux information (Horváth 2002;
Nakar 2007).
So far, much evidence showing the difference between two classes has
been discovered and presented (see Zhang 2006, for review). For
example, the spectra of LGRBs are softer than that of SGRBs in
general. Also, the pulse profiles of SGRBs are on average more
symmetric than those of LGRBs (Zhang & Xie 2007). The current Swift
observations show that LGRBs have their median cosmological redshift
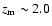 higher than that of SGRBs
higher than that of SGRBs
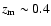 .
All these
differences suggest that both LGRBs and SGRBs are distinct physical
phenomena and are produced by model-independent emission engines
(e.g., Balázs et al. 2003). However, it is not clear what causes
these differences, especially in the origin of the bimodal T90distribution.
.
All these
differences suggest that both LGRBs and SGRBs are distinct physical
phenomena and are produced by model-independent emission engines
(e.g., Balázs et al. 2003). However, it is not clear what causes
these differences, especially in the origin of the bimodal T90distribution.
Koshut et al. (1996) pointed out that the observed duration
distribution may vary with instrument. It is therefore necessary to
investigate if a new GRB class exists and/or what physical factors
produce such properties (Gehrels et al. 2004). We focus our study on
the related issues of GRB classification using the updated Swift
data![[*]](/icons/foot_motif.gif) ,
,![[*]](/icons/foot_motif.gif) ,
,![[*]](/icons/foot_motif.gif) .
.
The higher sensitivity and angular resolution of Swift make it
superior to previous space telescopes (e.g. BATSE, BeppoSAX and
HETE-2). Accurate follow-up observations have further added to its
advantages (Gehrels et al. 2004). It can detect on an average about
2 GRBs per week within a 2 sr field of view, which is about two
times more than that of pre-Swift missions (Mészáros 2006).
However, the detection rate of SGRBs to total GRBs is much lower
(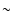
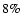 )
than the rate by BATSE (
)
than the rate by BATSE (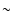
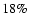 ), which is
attributed to both their different energy responses and the
relatively high spectral hardness of SGRBs (e.g., Band 2006a,b;
Gehrels et al. 2007). On the other hand, the lower sensitivity to
short duration bursts of Swift, relative to BATSE, makes it
accumulate relatively lower counts, comparable with the number of
background counts (Band 2006a). The effect of the instrument may
cause the detection rate of SGRBs to be somewhat underestimated.
), which is
attributed to both their different energy responses and the
relatively high spectral hardness of SGRBs (e.g., Band 2006a,b;
Gehrels et al. 2007). On the other hand, the lower sensitivity to
short duration bursts of Swift, relative to BATSE, makes it
accumulate relatively lower counts, comparable with the number of
background counts (Band 2006a). The effect of the instrument may
cause the detection rate of SGRBs to be somewhat underestimated.
In order to study the intrinsic properties of GRBs, we selected six
data sets, namely s1-s6, as listed in Table 1. As of 2007 July 1,
Swift has detected 75 LGRBs (s1) and 20 SGRBs (s2) with known
duration and redshift. The 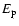 in the observed
in the observed
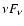 energy spectra are chosen to characterize the spectral hardness
relations with duration. Here, 44 GRBs from s1 also have available
energy spectra are chosen to characterize the spectral hardness
relations with duration. Here, 44 GRBs from s1 also have available 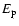 values and constitute our sample s3. In s2, only 11 sources
have a measured
values and constitute our sample s3. In s2, only 11 sources
have a measured 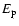 and these are employed to build the sample s4.
Unfortunately, the remaining 9 bursts in s2 (i.e., GRB 050202,
GRB 050906, GRB 050925, GRB 051105A, GRB 051210, GRB 060313, GRB 070209, GRB 070406 and GRB 070429B) do not have
the measured redshifts. For these we assigned a redshift value of
z=0.5 to the 9 bursts, approaching the median redshift of z=0.4,
as assumed by Norris & Bonnell (2006). These sources were included
in the present study to improve the statistics. However, we found
that the choice between z=0.5 and z=0.4 contributes only a small
relative error of
and these are employed to build the sample s4.
Unfortunately, the remaining 9 bursts in s2 (i.e., GRB 050202,
GRB 050906, GRB 050925, GRB 051105A, GRB 051210, GRB 060313, GRB 070209, GRB 070406 and GRB 070429B) do not have
the measured redshifts. For these we assigned a redshift value of
z=0.5 to the 9 bursts, approaching the median redshift of z=0.4,
as assumed by Norris & Bonnell (2006). These sources were included
in the present study to improve the statistics. However, we found
that the choice between z=0.5 and z=0.4 contributes only a small
relative error of 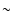 0.07, implying that the final results are
not sensitive to the above assumed redshift values. In our fifth
sample set, s5, we include 48 pre-Swift LGRBs whose z and T90are already measured, in which 18 sources, less than half (
0.07, implying that the final results are
not sensitive to the above assumed redshift values. In our fifth
sample set, s5, we include 48 pre-Swift LGRBs whose z and T90are already measured, in which 18 sources, less than half (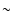 38%) of the
48 pre-Swift bursts, are detected by the BATSE mission
and constitute our sample s6.
38%) of the
48 pre-Swift bursts, are detected by the BATSE mission
and constitute our sample s6.
Table 1:
GRB samples of known durations (T90),
redshifts (z) and/or peak energies (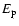 ).
).
To check whether the distributions of T90 are significantly
different, indicative of a dependence on the on-board instruments,
we first obtained the distributions of Swift bursts in both observer
and source frames. Then, we compare the durations of LGRBs between
Swift and pre-Swift/BATSE missions.
The accuracy of T90 measurements is in principle affected by
several factors including the identification of the time interval of
a burst, the sensitivity of instrument, background modeling, the
time resolution of the data, and the detailed shape of the burst
time profile, etc. Fig. 1 shows the T90 distribution for the
95 Swift GRBs, which include s1 and s2 samples (see Table 1). The
best fit with a two-lognormal function gives the center values
(
T90, p1=0.28-0.09+0.14 s and
T90,
p2=42.83-4.45+4.60 s) and the widths
(
w1=19.05-11.11+24.60 s and
w2=18.20-3.41+4.19 s) with the reduced Chi-square
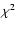 /d.o.f. = 0.67, which are roughly consistent with those
calculated from the BATSE data (McBreen et al. 1994; Meegan et al.
1996; Paciesas et al. 1999; Horváth 2002;
Nakar 2007). Note that
the number of objects classified as belonging to the two log-normals
to itself has been allowed to be a free parameter. The superposed
function has a minimum around 2 s as found by Kouveliotou et al.
(1993), indicating that the Swift sources are also divided into two
classes, SGRBs and LGRBs, although the Swift is more sensitive to
long soft bursts than the BATSE (Band 2006a,b; Gehrels et al. 2007).
This is an interesting result since the different detectors with
different bandwidth sensitivity do not affect the classification of
GRBs in terms of duration.
/d.o.f. = 0.67, which are roughly consistent with those
calculated from the BATSE data (McBreen et al. 1994; Meegan et al.
1996; Paciesas et al. 1999; Horváth 2002;
Nakar 2007). Note that
the number of objects classified as belonging to the two log-normals
to itself has been allowed to be a free parameter. The superposed
function has a minimum around 2 s as found by Kouveliotou et al.
(1993), indicating that the Swift sources are also divided into two
classes, SGRBs and LGRBs, although the Swift is more sensitive to
long soft bursts than the BATSE (Band 2006a,b; Gehrels et al. 2007).
This is an interesting result since the different detectors with
different bandwidth sensitivity do not affect the classification of
GRBs in terms of duration.
![\begin{figure}
\par\includegraphics[width=8cm]{9210fig1.eps}
\end{figure}](/articles/aa/full/2008/23/aa9210-07/Timg21.gif) |
Figure 1:
Bimodal distribution of durations for the 95 GRBs (s1 and s2; histogram)
and two-component log-normal fit to the data (solid line). The GRBs
are divided into two classes at
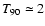 s (vertical line):
LGRBs (dotted line) and SGRBs (dashed line). s (vertical line):
LGRBs (dotted line) and SGRBs (dashed line). |
| Open with DEXTER |
One of the great progresses made by Swift is the increase in number
of higher redshift sources. It is known that the median redshift of
Swift LGRBs,
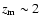 ,
is roughly two times larger than that of
pre-Swift. As pointed out by previous authors (Bagoly et al. 2006;
Jakobsson et al. 2006), the difference of redshift distributions
between the two samples is statistically significant. This may lead
to an evident discrepancy between the two intrinsic T90distributions. We therefore utilize the Swift sources to explore
this possibility.
,
is roughly two times larger than that of
pre-Swift. As pointed out by previous authors (Bagoly et al. 2006;
Jakobsson et al. 2006), the difference of redshift distributions
between the two samples is statistically significant. This may lead
to an evident discrepancy between the two intrinsic T90distributions. We therefore utilize the Swift sources to explore
this possibility.
The potential spectrum evolution, as a result of cosmological
redshift, can usually cause high energy 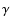 photons to shift
into or out of the finitely sensitive bandwidth of a given detector.
Note that here we had neglected the effect of a burst's spectrum
itself softening with time (Ford et al. 1995). In this case, the
transformation of T90 from observer frame to source frame is
generally expressed as
photons to shift
into or out of the finitely sensitive bandwidth of a given detector.
Note that here we had neglected the effect of a burst's spectrum
itself softening with time (Ford et al. 1995). In this case, the
transformation of T90 from observer frame to source frame is
generally expressed as
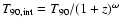 ,
in
which
,
in
which
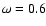 or 1, corresponding to energy stretching or not
(Fenimore & Bloom 1995; Mészáros & Mészáros 1995;
Mészáros & Mészáros 1996;
Horváth et al. 1996;
Balázs et al. 2003).
We consider a simple case of
or 1, corresponding to energy stretching or not
(Fenimore & Bloom 1995; Mészáros & Mészáros 1995;
Mészáros & Mészáros 1996;
Horváth et al. 1996;
Balázs et al. 2003).
We consider a simple case of 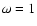 throughout this work, in
which the intrinsic duration is given by
throughout this work, in
which the intrinsic duration is given by
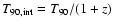 .
We calculate the intrinsic duration (
.
We calculate the intrinsic duration (
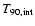 )
distribution for the 95 GRBs and compare it with the observed
one. As shown in Fig. 2, the
)
distribution for the 95 GRBs and compare it with the observed
one. As shown in Fig. 2, the
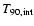 has a bimodal
distribution and is significantly shifted toward shorter durations
than the observed one. The best fit with a two-lognormal function
gives two centers (
T90, p1=0.13-0.05+0.12 s,
T90,
p2=12.30-1.83+2.15 s) and two widths
(
w1=10.96-8.14+31.69 s and
w2=17.38-5.63+8.32 s) with
has a bimodal
distribution and is significantly shifted toward shorter durations
than the observed one. The best fit with a two-lognormal function
gives two centers (
T90, p1=0.13-0.05+0.12 s,
T90,
p2=12.30-1.83+2.15 s) and two widths
(
w1=10.96-8.14+31.69 s and
w2=17.38-5.63+8.32 s) with 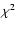 /d.o.f. = 0.92,
indicating that the distribution of
/d.o.f. = 0.92,
indicating that the distribution of
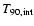 is indeed bimodal
but systematically narrower and shifted towards low values of
duration in comparison to the observed one. A Kolmogorov-Smirnov
(K-S) test returns the statistic D=0.27 with a probability of
P=0.001, suggesting the intrinsic and observed duration
distributions are drawn from different parent populations. This
result is consistent with the theoretical prediction by Bromm &
Loeb (2002), where they assumed that the formation of all GRBs
tightly follows the cosmic star formation history. However, some
instrument-dependent factors such as selection effects and
discrepancy between different detectors can distort the resulting
parent distribution of
is indeed bimodal
but systematically narrower and shifted towards low values of
duration in comparison to the observed one. A Kolmogorov-Smirnov
(K-S) test returns the statistic D=0.27 with a probability of
P=0.001, suggesting the intrinsic and observed duration
distributions are drawn from different parent populations. This
result is consistent with the theoretical prediction by Bromm &
Loeb (2002), where they assumed that the formation of all GRBs
tightly follows the cosmic star formation history. However, some
instrument-dependent factors such as selection effects and
discrepancy between different detectors can distort the resulting
parent distribution of
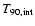 .
Once the disturbances are
removed from the observed distribution, the remainder is the true
parent distribution correlated with some physical predictions. In
this case, our current result can offer some corroborative
statistical evidence that the rate of GRBs may really trace the star
formation history, partly because the redshifts of SGRBs had not
been measured before Swift.
.
Once the disturbances are
removed from the observed distribution, the remainder is the true
parent distribution correlated with some physical predictions. In
this case, our current result can offer some corroborative
statistical evidence that the rate of GRBs may really trace the star
formation history, partly because the redshifts of SGRBs had not
been measured before Swift.
![\begin{figure}
\par\includegraphics[width=8cm]{9210fig2.eps}
\end{figure}](/articles/aa/full/2008/23/aa9210-07/Timg29.gif) |
Figure 2:
Comparison between the observed (solid line the same as Fig. 1) and the
intrinsic (dashed-dotted line) T90 distributions. |
| Open with DEXTER |
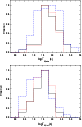 |
Figure 3:
The normalized duration distributions for the Swift (s1;
dashed line), pre-Swift (s5; solid line) and BATSE (s6; dotted line)
LGRBs in the observer (upper panel) and the source
(lower panel) frames. |
| Open with DEXTER |
T90 may be wrongly estimated because of the factors pointed out
in Sect. 3.1.1. In particular, the measured duration has been
found to be instrument-dependent (e.g., Koshut et al. 1996). We
examined the dependence of T90 on the instruments by comparing
the normalized distributions of different detectors in Fig. 3. For
this comparison, three samples including s1, s5, and s6 are used.
A log-normal fit to the six distributions gives the parameters
listed in Table 2. We find that the Swift sample has a wider
duration distribution than the pre-Swift and BATSE did in both
observer and source frames, while the widths of pre-Swift and BATSE
distributions of duration are equal. This implies that Swift can
detect GRBs over a wider dynamic range of T90, i.e., the
fraction of longer and shorter Swift LGRBs is significantly higher
than that of pre-Swift/BATSE LGRBs, except for the increased
detection rate of LGRBs due to the higher sensitivity to long soft
bursts of BAT loaded on Swift (Band 2006a,b). Considering the fact
that Swift bursts can still be separated at T90=2 s, we predict
that the width of the T90 distribution of Swift SGRBs could be
equally wider as pre-Swift detectors. Furthermore, we see from
Table 2 that the distribution centers of
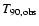 are very close to
each other, while for the
are very close to
each other, while for the
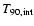 distribution, the centers of
the pre-Swift and BATSE bursts are much closer but significantly
larger than that of Swift bursts. The K-S test of the pre-Swift and
BATSE bursts provides the very large probability of
distribution, the centers of
the pre-Swift and BATSE bursts are much closer but significantly
larger than that of Swift bursts. The K-S test of the pre-Swift and
BATSE bursts provides the very large probability of 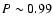 in
both observer and source frames showing that the s5 and s6 samples
are consistent with being drawn from the same parent distribution.
For the Swift
in
both observer and source frames showing that the s5 and s6 samples
are consistent with being drawn from the same parent distribution.
For the Swift
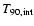 distribution, the obvious decrease of
the center value is attributable to the relative increase of the
fraction of high redshift sources, which could be caused by the
ubiquitous threshold effect of different instruments (e.g., Bromm &
Loeb 2002; Band 2006a,b).
distribution, the obvious decrease of
the center value is attributable to the relative increase of the
fraction of high redshift sources, which could be caused by the
ubiquitous threshold effect of different instruments (e.g., Bromm &
Loeb 2002; Band 2006a,b).
Table 2:
The best-fit parameters to the three data sets.
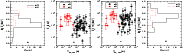 |
Figure 4:
Relations of T90 with 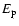 (panel b)) and
(panel b)) and
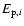 (panel c)). Panels a) and d) show
the distributions of the
(panel c)). Panels a) and d) show
the distributions of the 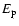 and
and
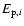 in logarithmic
timescale, respectively.
in logarithmic
timescale, respectively. |
| Open with DEXTER |
In theory, the peak energy 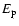 can be used to reflect the photon
components, similar to the hardness ratio between different energy
channels. The intrinsic peak energy (
can be used to reflect the photon
components, similar to the hardness ratio between different energy
channels. The intrinsic peak energy (
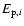 )
in the source frame
is related to the
)
in the source frame
is related to the 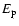 in the observer frame by
in the observer frame by
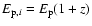 .
To verify the relation of spectral hardness to duration, we
drew plots of peak energy versus
.
To verify the relation of spectral hardness to duration, we
drew plots of peak energy versus
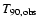 for the samples s3
and s4 as shown in Figs. 4b and c.
A linear correlation analysis gives the coefficient of r=-0.27with probability P=0.07 for Fig. 4b and r=0.004 with
P=0.98 for Fig. 4c, indicating that the tendency
towards SGRBs relatively harder than LGRBs exists in the observer
frame and almost disappears in the source frame. The former accords
with previous findings, for example, using the BATSE data (e.g.,
Kouveliotou et al. 1993) or the Swift data (e.g., Band 2006a).
for the samples s3
and s4 as shown in Figs. 4b and c.
A linear correlation analysis gives the coefficient of r=-0.27with probability P=0.07 for Fig. 4b and r=0.004 with
P=0.98 for Fig. 4c, indicating that the tendency
towards SGRBs relatively harder than LGRBs exists in the observer
frame and almost disappears in the source frame. The former accords
with previous findings, for example, using the BATSE data (e.g.,
Kouveliotou et al. 1993) or the Swift data (e.g., Band 2006a).
We also compare the peak energy of LGRBs and SGRBs in both observer
(Fig. 4a) and source frames (Fig. 4d). More
cosmological redshift correction is required for LGRBs when we
convert the physical variables from the observer frame to the source
frame. As a result, the trend of the relative spectral softness of
LGRBs (or the relative hardness of SGRBs) weakens. For our samples,
the long and short bursts have the median values of
74+120-45 keV and
398+493-220 keV, respectively, in
the observer frame, and
302+631-202 keV and
617+896-365 keV in the source frame. A K-S test returns the
different probabilities of P=0.01 for Fig. 4a and
P=0.15 for Fig. 4d, which suggests that the
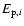 of long and short bursts may be drawn from the same parent
population.
of long and short bursts may be drawn from the same parent
population.
The duration distribution from the third BATSE catalog is suggested
to have a three-component log-normal form (Horváth 1998;
Mukherjee 1998; Hakkila et al. 2000). Similarly, the duration
distribution of the current 4B
catalog![[*]](/icons/foot_motif.gif) shows the possible existence of an intermediate group.
Further studies show that the third group is either the excess of
SGRBs with low fluence (Hakkila et al. 2003) or the softest LGRBs
(Horváth et al. 2006). It is still controversial whether the
third class exists or not, due to the lack of a physical explanation
(Horváth et al. 2006; see however, Chattopadhyay et al. 2007).
The third group might be caused by an instrumental bias that reduces
the durations of faint LGRBs (e.g., Hakkila et al. 2000; Hakkila
et al. 2003), suggesting that their presence is not physical but
phenomenological. Therefore, the bimodality of the duration
distribution is widely accepted today.
shows the possible existence of an intermediate group.
Further studies show that the third group is either the excess of
SGRBs with low fluence (Hakkila et al. 2003) or the softest LGRBs
(Horváth et al. 2006). It is still controversial whether the
third class exists or not, due to the lack of a physical explanation
(Horváth et al. 2006; see however, Chattopadhyay et al. 2007).
The third group might be caused by an instrumental bias that reduces
the durations of faint LGRBs (e.g., Hakkila et al. 2000; Hakkila
et al. 2003), suggesting that their presence is not physical but
phenomenological. Therefore, the bimodality of the duration
distribution is widely accepted today.
What causes the bimodality is an interesting but unsolved problem
owing to the absence of direct observational evidence, although
several works have tried to explain the bimodality within different
scenarios. It was suggested that the different spin axes of
millisecond pulsars can explain the two GRB classes (Usov 1992; Yi
& Blackman 1998). Subsequently, Huang et al. (2003) studied the
neutron star kick model (Dar & Plaga 1999) in detail and proved
that this model can successfully account for the two log-normal
distributions if the central engine has a neutron star of a high
kick velocity greater than 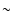 1000 km s-1. Yamazaki et al. (2004) put forward the so-called unified model consisting
of multiple subjets within an inhomogeneous main jet. Using this
model, Toma et al. (2005) explained that the
bimodality originates from discrete emitters in the main jet. They
also predicted that the two kinds of bursts should have the same
origin, i.e., supernovae, instead of the leading models, which
predict that the LGRBs and SGRBs are produced due to the core
collapse of a massive star and the merger of double compact objects,
respectively (see e.g., Cheng & Lu 2001; Zhang & Mészáros
2004; Piran 2005; Mészáros 2006; and Lee & Ramirez-Ruiz 2007,
for reviews). However, further investigations to the unified model
showed that the bimodal distribution could be reproduced only for
some special parameters (Janiuk et al. 2006).
1000 km s-1. Yamazaki et al. (2004) put forward the so-called unified model consisting
of multiple subjets within an inhomogeneous main jet. Using this
model, Toma et al. (2005) explained that the
bimodality originates from discrete emitters in the main jet. They
also predicted that the two kinds of bursts should have the same
origin, i.e., supernovae, instead of the leading models, which
predict that the LGRBs and SGRBs are produced due to the core
collapse of a massive star and the merger of double compact objects,
respectively (see e.g., Cheng & Lu 2001; Zhang & Mészáros
2004; Piran 2005; Mészáros 2006; and Lee & Ramirez-Ruiz 2007,
for reviews). However, further investigations to the unified model
showed that the bimodal distribution could be reproduced only for
some special parameters (Janiuk et al. 2006).
Recently, from an independent analysis of distinct timescales, Zhang
et al. (2007) suggested that LGRBs occur at greater distances from
the central engine while SGRBs at smaller distances, i.e., two
distinct 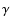 -ray emission regions may result in two different
properties of GRBs, including the varieties of pulse profiles, as
mentioned above. They also pointed out the fact that LGRBs usually
have a long positive spectral lag (e.g., Norris et al.
2000; Daigne & Mochkovitch 2003; Chen et al. 2005) and SGRBs have
negligible lag (Norris & Bonnell 2006; Zhang et al. 2006). This can
be explained under the assumption that the curvature effect is a
main contributor to the spectral lag (Ryde 2005; Shen et al.
2005). The predication of distinct emission regions for different
GRB classes and/or the nature of the bimodality still needs to be
clarified with more accurate observations in the future.
-ray emission regions may result in two different
properties of GRBs, including the varieties of pulse profiles, as
mentioned above. They also pointed out the fact that LGRBs usually
have a long positive spectral lag (e.g., Norris et al.
2000; Daigne & Mochkovitch 2003; Chen et al. 2005) and SGRBs have
negligible lag (Norris & Bonnell 2006; Zhang et al. 2006). This can
be explained under the assumption that the curvature effect is a
main contributor to the spectral lag (Ryde 2005; Shen et al.
2005). The predication of distinct emission regions for different
GRB classes and/or the nature of the bimodality still needs to be
clarified with more accurate observations in the future.
- We find that the observed
durations of Swift GRBs have two-lognormal distributions divided
clearly at
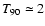 s. This implies that the classification
in terms of duration is unchanged from pre-Swift to the Swift era.
s. This implies that the classification
in terms of duration is unchanged from pre-Swift to the Swift era.
- The intrinsic durations also show a bimodal distribution but
shifted systematically toward the smaller value and the distribution
exhibits a narrower width relative to the observed distribution.
- The
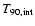 distributions of Swift and pre-Swift/BATSE
LGRBs are significantly different in the width and center values.
distributions of Swift and pre-Swift/BATSE
LGRBs are significantly different in the width and center values.
- Swift bursts have a wider duration dynamic range than
pre-Swift and BATSE bursts.
- The spectra of the SGRBs are predominantly harder than the
LGRBs, confirming the previous results from the BATSE bursts.
However, the trend of LGRBs with a relatively softer spectrum
largely weakens in the source frame.
Acknowledgements
We thank David L. Band and Attila Mészáros for their helpful
comments and suggestions. The authors thank the anonymous referee
for a thorough and constructive report which led to a substantial
improvement of the paper. We thank Istvan Horváth for good
communication and G. Maheswar for critical reading of the
manuscript. Z.B.Z. wishes to acknowledge the postdoctoral
fellowship from the Korea Astronomy and Space Science Institute
(KASI).
- Band, D. L. 2006a,
ApJ, 644, 378 [NASA ADS] [CrossRef]
- Band, D. L. 2006b,
AIPC, 836, 704 [NASA ADS]
(In the text)
- Balázs, L. G.,
Bagoly, Z., Horváth, I., Mészáros, A., &
Mészáros, P. 2003, A&A, 401, 129 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bagoly, Z.,
Mészáros, A., Balázs, L. G., et al. 2006, A&A,
453, 797 [NASA ADS] [CrossRef] [EDP Sciences]
- Bromm, V., &
Loeb, A. 2002, ApJ, 575, 111 [NASA ADS] [CrossRef]
- Butler, N. R.,
Kocevski, D. B., Joshua, S., et al. 2007, ApJ, 671, 656 [NASA ADS] [CrossRef]
-
Chattopadhyay, T., Misra, R., Chattopadhyay, A. K., & Naskar,
M. 2007, ApJ, 667, 1017 [NASA ADS] [CrossRef]
- Chen, L., Lou, Y.-Q.,
Wu, M., et al. 2005, ApJ, 619, 983 [NASA ADS] [CrossRef]
- Cheng, K. S., &
Lu, T. 2001, ChJAA, 1, 1 [NASA ADS]
- Daigne, F., &
Mochkovitch, R. 2003, MNRAS, 342, 587 [NASA ADS] [CrossRef]
- Dar, A., & Plaga, R.
1999, A&A, 349, 259 [NASA ADS]
(In the text)
- Fenimore, E.
E., & Bloom, J. S. 1995, ApJ, 453, 16 [NASA ADS] [CrossRef]
(In the text)
- Fishman, G. J.
1999, A&AS, 138, 395 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Ford, L. A., Band, D.
L., Matteson, J. L., et al. 1995, ApJ, 439, 307 [NASA ADS] [CrossRef]
(In the text)
- Friedman, A. S.,
& Bloom, J. S. 2005, ApJ, 627, 1 [NASA ADS] [CrossRef]
- Gehrels, N.,
Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef]
(In the text)
- Gehrels, N.,
Cannizzo, J. K., & Norris, J. P. 2007, NJPh, 9, 37 [NASA ADS] [CrossRef]
(In the text)
- Ghirlanda,
G., Ghisellini, G., & Lazzati, D. 2004, ApJ, 616, 331 [NASA ADS] [CrossRef]
- Hakkila, J.,
Haglin, D. J., Pendleton, G. N., et al. 2000, ApJ, 538, 165 [NASA ADS] [CrossRef]
(In the text)
- Hakkila, J.,
Giblin, T. W., Roiger, R. J., et al. 2003, ApJ, 582, 320 [NASA ADS] [CrossRef]
- Horváth, I.
1998, ApJ, 508, 757 [NASA ADS] [CrossRef]
(In the text)
- Horváth, I.
2002, A&A, 392, 791 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Horváth, I.,
Mészáros, P., & Mészáros, A. 1996, ApJ,
470, 56 [NASA ADS] [CrossRef]
(In the text)
- Horváth, I.,
Bala'zs, L. G., Bagoly, Z., et al. 2006, A&A, 447, 23 [NASA ADS] [CrossRef] [EDP Sciences]
- Huang, Y. F., Dai, Z.
G., Lu, T., Cheng, K. S., & Wu, X. F. 2003, ApJ, 594, 919 [NASA ADS] [CrossRef]
(In the text)
- Jakobsson,
P., Levan, A., Fynbo, J. P. U., et al. 2006, AIPC, 836, 552 [NASA ADS]
- Janiuk, A., Czerny,
B., Moderski, R., et al. 2006, MNRAS, 365, 874 [NASA ADS] [CrossRef]
- Katz, J. I., & Canel,
L. M. 1996, ApJ, 471, 915 [NASA ADS] [CrossRef]
- Kawai, N., et al.
2005 [arXiv:astro-ph/0512052]
-
Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ,
413, L101 [NASA ADS] [CrossRef]
(In the text)
- Koshut, T. M.,
Paciesas, W. S., Kouveliotou, C., et al. 1996, ApJ, 463, 570 [NASA ADS] [CrossRef]
(In the text)
- Lee, W. H., &
Ramirez-Ruiz, E. 2007, NJPh, 9, 17 [NASA ADS] [CrossRef]
- Mao, S., Narayan, R.,
& Piran, T. 1994, ApJ, 420, 171 [NASA ADS] [CrossRef]
(In the text)
- McBreen, B.,
Hurley, K. J., Long, R., et al. 1994, MNRAS, 271, 662 [NASA ADS]
(In the text)
- Meegan, C. A.,
Pendleton, G. N., Briggs, M. S., et al. 1996, ApJS, 106, 65 [NASA ADS] [CrossRef]
(In the text)
-
Mészáros, A., & Mészáros, P. 1996, ApJ,
466, 29 [NASA ADS] [CrossRef]
(In the text)
-
Mészáros, P. 2006, RPPh, 69, 2259 [NASA ADS]
(In the text)
-
Mészáros, P., & Mészáros, A. 1995, ApJ,
449, 9 [NASA ADS] [CrossRef]
(In the text)
- Mukherjee,
S., Feigelson, E. D., Jogesh, B. G., et al. 1998, ApJ, 508,
314 [NASA ADS] [CrossRef]
(In the text)
- Nakar, E. 2007, PhR,
442, 166 [NASA ADS]
(In the text)
- Norris, J. P.,
& Bonnell, J. T. 2006, ApJ, 643, 266 [NASA ADS] [CrossRef]
(In the text)
- Paciesas, W.,
Meegan, C., Pendleton, G., et al. 1999, ApJS, 122, 465 [NASA ADS] [CrossRef]
(In the text)
- Piran, T. 2005, Rvmp,
76, 1143 [NASA ADS] [CrossRef]
- Ryde, F. 2005, ApJ,
429, 869 [NASA ADS]
- Shen, R. F., Song, L.
M., & Li, Z. 2005, MNRAS, 362, 59 [NASA ADS] [CrossRef]
- Toma, K., Yamazaki, R.,
& Nakamura, T. 2005, ApJ, 620, 835 [NASA ADS] [CrossRef]
- Usov, V. V. 1992,
Nature, 357, 472 [NASA ADS] [CrossRef]
(In the text)
- Yamazaki, R.,
Ioka, K., & Nakamura, T. 2004, ApJ, 607, L103 [NASA ADS] [CrossRef]
- Yi, I., & Blackman, E.
G. 1998, ApJ, 494, L163 [NASA ADS] [CrossRef]
(In the text)
- Zhang, B. 2006,
Nature, 444, 1010 [NASA ADS] [CrossRef]
(In the text)
- Zhang, B., &
Mészáros, P. 2004, IJMPA, 19, 2385 [NASA ADS] [CrossRef]
- Zhang, Z. B., &
Xie, G. Z. 2007, Ap&SS, 310, 19 [NASA ADS] [CrossRef]
- Zhang, Z. B., Xie,
G. Z., Deng, J. G., et al. 2006, MNRAS, 373, 729 [NASA ADS] [CrossRef]
- Zhang, Z. B., Xie, G.
Z., Deng, J. G., et al. 2007, AN, 328, 99 [NASA ADS]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=8cm]{9210fig1.eps}
\end{figure}](/articles/aa/full/2008/23/aa9210-07/Timg21.gif)
![\begin{figure}
\par\includegraphics[width=8cm]{9210fig2.eps}
\end{figure}](/articles/aa/full/2008/23/aa9210-07/Timg29.gif)

