A&A 484, 251-265 (2008)
DOI: 10.1051/0004-6361:20078675

Structural signatures of medium-range order in annealed laboratory silicates

S. P. Thompson

Diamond Light Source, Diamond House, Harwell Science and Innovation Campus, Didcot, Oxfordshire OX11 0DE, GB

Received 14 September 2007 / Accepted 18 March 2008

Abstract
Context. Silicate dust grains exist in a wide range of astronomical environments and understanding the effect of these on grain structure is of great interest, particularly the effect of thermal annealing on amorphous silicates as a possible route to the formation of crystalline grains. Although laboratory simulations have largely focussed on IR-spectroscopic measurements, since these relate directly to observational data, laboratory synchrotron techniques such as X-ray absorption spectroscopy (XAS) and X-ray scattering are becoming increasingly routine in the analysis of recovered materials. With the increasing prospect of performing astronomical XAS observations, there is much to be gained from applying these techniques to laboratory analogues.
Aims. Diagnostic markers for medium-range order and the effect of thermal annealing on these in amorphous silicates of differing Mg content are characterised using synchrotron X-ray methods.
Methods. Three synthetic amorphous silicates with high, medium and low Mg:Si ratios were annealed at varying temperatures up to 1300 K. X-ray Absorption Near Edge Structure (XANES) spectra at the Si and Mg K-shell absorption edges and X-ray scattering patterns for low values of the X-ray scattering wavevector were recorded for these along with comparative data for commercially produced amorphous SiO2 and mineral samples of forsterite, enstatite and quartz.
Results. XANES features due to short- and medium-range structure are identified at both Mg and Si edges and a new temperature dependent behaviour observed in the medium-range structure surrounding Mg and Si. Based on changes to the morphological details of the XANES spectra, the medium-range structure changes between an enstatite-like and forsterite-like coordination with increasing temperature and appears to correlate directly with Mg content. Low wavevector X-ray scattering features were also found to be diagnostic of the type of medium-range structural ordering. However, these features depend on whether the relative arrangement of clusters of medium-range structure exhibit semi-periodic ordering over the longer-range, which can vary with annealing.

Key words: methods: laboratory - X-rays: ISM - ISM: dust, extinction - stars: circumstellar matter - comets: general

1 Introduction

Ever since the Infrared Space Observatory (ISO) revealed the presence of crystalline silicate dust in a wide range of astronomical settings (e.g. Waters et al. 1996; Tielens et al. 1998) there has been much interest in the thermal processing of amorphous silicate grains as a possible route to their formation. Prior to ISO, silicates were believed to form as disordered, or amorphous, grains in the outflows of O-rich stars at various stages of their evolution (e.g. Dorschner 1993). As such, crystalline silicates pose significant problems. For example, crystalline silicate features in stars with high mass-loss rates challenge our understanding of the nucleation and subsequent evolution of circumstellar matter (Kemper et al. 2001), while similar features in the spectra of certain comets (Bregman et al. 1987; Campins & Ryan 1989; Crovisier et al. 1996; Russell & Lynch 1996; Hayward & Hanner 1997), young pre-main sequence stars (Waelkens et al. 1996) and debris disk systems (Knacke et al. 1993; Fajardo-Acosta & Knacke 1995) similarly challenge our understanding of the prevailing conditions and processes that occur during the formation of planetary systems.

To place physical constraints on both models and observations it is necessary to investigate the behaviour of silicate analogue materials through laboratory investigation. Early efforts were primarily aimed at reproducing astronomical observations, particularly in the region near 10 and 20 $\mu$m where silicates exhibit strong absorption resonances. However, it was quickly realised that IR spectroscopy in isolation can not reveal the full story underlying grain properties as the limited structural information returned does not allow for unique solutions or constraints to be found (see review by Colangeli et al. 2003; or discussion by Nuth et al. 2002). Secondary characterisation by laboratory techniques such as EDX, diffraction, SEM, TEM etc. of properties not directly observable by astronomers have thus been required in order to constrain the spectroscopic measurements, but do not always easily translate into observational predictions. Comparative measurements using secondary techniques on cosmic grains from meteorites and collected interplanetary dust particles (IDPs) has offered a useful channel for validating results from analogue materials, though in both instances some degree of selection via secondary processing/alteration of pristine grains within parent bodies is likely to have occurred with only the most refractory components surviving through to the meteorite and IDP populations. The recent successful return of what are likely to be pristine grains by STARDUST (Brownlee et al. 2006; Ishii et al. 2008) along with the development of micro-handling and characterising techniques now offers a direct route to ground-truth validation of measurements made on laboratory analogues using techniques other than IR spectroscopy. Indeed, IR techniques are likely to be less prominent in the analysis of STARDUST samples due to the potentially small particle sizes ($\sim$5 $\mu$m) and the aerogel environment they are embedded in. IR microspectrometry over the 2.5-20 $\mu$m region where silicates show their strongest absorption features is likely to be complicated by the strong response of aerogel in this region due to its SiO2 content, though Keller & Flynn (2003) have obtained some mineralogical information from measurements made beyond 20 $\mu$m on aerogel embedded particles. Raman microspectroscopy may also be similarly limited by strong aerogel fluorescence, though again the technique has successfully been used on larger grains (Burchell et al. 2004).

X-ray scattering and X-ray absorption spectroscopy (XAS) are two non-destructive laboratory techniques for probing and characterising material structure which, following the development of high intensity tuneable synchrotron sources, have become routinely available in materials based disciplines. While X-ray scattering has often been used to determine whether astrophysical analogues are amorphous or crystalline, the use of X-ray absorption spectroscopy has so far been limited (Colangeli et al. 2003). XAS involves measuring the small oscillations in the X-ray absorption coefficient near the absorption edge of a given atomic element that arise from the scattering of the ejected photoelectron by surrounding atoms and provides information about their localised arrangement. The post-edge XAS spectrum is typically divided into two main regions with respect to the ejected photoelectron momentum, $k_{\rm e}$: the low-energy region ( $k_{\rm e}<\sim4$ Å-1), which produces the X-ray absorption near edge structure (XANES) and the high-energy region ( $k_{\rm e}>\sim4$ Å-1), which produces extended X-ray absorption fine structure (EXAFS). The latter high-energy region is dominated by single scattering events from immediate neighbouring atoms, whereas the low-energy region is dominated by multiple scattering involving more distant neighbours.

With the development of micro-focussing and sample scanning technologies at synchrotron sources, XAS has been applied to individual IDPs (e.g. Flynn et al. 2003, 2004; Brennan et al. 2005) and to cosmic grains embedded in meteorites (Bernhard et al. 2006). Indeed, X-ray techniques in general are likely to be important in the future analysis of STARDUST and similarly recovered samples since aerogel is highly transparent to X-rays, due to its low density resulting in long penetration depths (Bish et al. 2001). Preliminary investigations in this direction are already being reported (Flynn et al. 2006; Gainsforth et al. 2007; Grossemy et al. 2007a,b; Matrajt et al. 2007). Meanwhile, speculation on the possibility of performing astronomical XAS observations for condensed matter along the lines of sight to suitable X-ray sources has had a long history (Martin 1970; Evans 1986; Woo 1995; Woo et al. 1997; Forrey et al. 1998; Lee & Ravel 2005). Although the earliest detection of X-ray absorption features associated with the ISM were made by Schattenberg & Canizares (1986), it was not until the launch of the CHANDRA X-ray observatory that these speculations became a realistic possibility (Woo 1995; Woo et al. 1997; Forrey et al. 1998). Although most discussions on astronomical XAS have largely concentrated on the EXAFS region where calculations using model compounds are relatively straight forward, the low energy XANES region represents a better observational prospect since certain features in this region tend to be stronger. The amplitude of EXAFS oscillations both decrease in inverse proportion to the photoelectron momentum, $k_{\rm e}$, and are simultaneously damped by the action of a term involving the finite lifetime of the photoelectron such that at increasingly higher $k_{\rm e}$ its mean free path shortens and it travels shorter distances before being reabsorbed. These effects combine to make the XANES signal for most materials more pronounced than the EXAFS one. However, only limited observational results have so far been obtained. Lee et al. (2001, 2002) claimed to have observed strong modulations near the Si K-edge along lines of sight to several black hole systems, though poor statistics and the possibility of the modulations being instrumental in origin make the identification with dust grains questionable. Petric et al. (2005) identified oscillations in the spectrum of the microquasar source GRS 1915+105 also near the absorption edge energy of Si, while Ueda et al. (2005) reported observations of fine structure near the Si K-edge attributed by them to silicate dust in the galactic ISM along lines of sight to three highly absorbed X-ray binaries. These first steps towards realising astronomical XAS, along with the possibility of collecting laboratory data from recovered grains now mean that XAS is set to become a primary channel for gathering information about the nature of cosmic dust. Laboratory simulation is likely to play as pivotal a role here as it has in the IR, for although XAS is well understood from a theoretical point of view, calculations from first principles, particularly in the low energy XANES region, are very detailed, involve a large number of variable parameters, are computer intensive and highly model dependent with the consequence that much XANES work is still empirically driven.

XANES features in silicates originate from structural arrangements extending out to radial distances of $\sim$10 Å (Wu et al. 1998; Mottana et al. 1999) and are therefore of particular relevance to the study of astrophysical silicates since it is the vibrations of functional units on this scale of tetrahedral and inter-tetrahedral bonding that give rise to much of their characteristic IR spectral features (Hofmiester 1997; Jäger et al. 1998). Indeed, the optical properties of amorphous silicates in both the UV/VIS and IR regions arise from the presence of different structures, each with varying optical constants, that are themselves determined by short- and medium-range order (Jäger et al. 2003).

In this paper the evolution, with annealing temperature, of medium-range structure is investigated using synchrotron X-rays. The local environments surrounding Mg and Si are investigated via XANES measurements at the Mg and Si K-edges and features attributable to short- and medium-range ordering are identified. A new thermal behaviour is observed, relating to changes in the medium-range structure characterised by the XANES signal morphology. The results of X-ray scattering measurements, conducted using low values of the X-ray scattering wavevector are also presented. Under this condition, features in the scattering patterns are identified with the pseudo-periodic arrangement of different types of medium-range structural clusters and the evolution of these arrangements with temperature is investigated.

2 Theory

2.1 Ordering in the solid phase

Unlike crystalline materials, where structure is characterized by long-range periodic order (i.e. by correlations between the positions of atoms situated as far away as possible from each other), amorphous or non-crystalline materials were historically classified by the absence of long-range order. However, once the requirement for long-range order is removed what remains is not a total disorder, but a certain limited order termed short-range order, defined by the interatomic correlations in the first coordination spheres surrounding an arbitrary atom (i.e. up to the maximum distance over which atomic forces can act). However, many non-crystalline materials were found to exhibit a degree of structural order that extended over much larger distances and, on this basis, a new concept of medium-range (or intermediate-range) order was introduced (Philips 1979; Lucovski & Galeener 1980). Order on this scale derives from structural correlations typically in the range of $\sim$5 to 20 Å and is in excess of what would be expected for an ideal continuous random network characterized by a random dihedral angle distribution.

The forces linking atoms are the same in both crystalline and non-crystalline solids and, differences in formation conditions aside, the extended three dimensional structures of non-crystalline solids are produced in much the same way as those in crystalline materials, but without the requirements of periodicity and symmetry that characterize the crystalline state. Non-crystalline materials are thus by definition disordered in some respect of their structure. Unfortunately, order/disorder can not be precisely defined for non-crystalline materials and usually rests on determining what degree of order can be identified experimentally at different length scales. Four generic scales can be identified (Wright 1994):

1.
the basic repeating structural unit;
2.
the interconnection of these to form a network;
3.
the network topology;
4.
long-range density fluctuations.
The first two represent short-range structure, while the third and fourth describe medium- and long-range structure respectively.

Short-range structure encompasses the interatomic region of nearest neighbours and first coordination shells, generally represented by a structural building block with a radial distance typically out to $\sim$2 Å. In silicates this unit is the Si-O tetrahedron and is ubiquitous, varying little from one silicate to another (crystalline or otherwise). Consequently, at this level silicates are highly ordered. However, the parameters governing the way these units link together are highly variable (Mozzi & Warren 1969) and it is with the interconnection of tetrahedra, at the boundary between the short- and medium-range, that disorder can begin. Medium-range order generally extends from $\sim$2 Å out to a radial distance of $\sim$10-20 Å (Wright 1990). Structural features such as rings or chains occur over this range. Long-range order comprises larger periodic and symmetric groupings of these clustering elements over lengths greater than $\sim$10-20 Å and ordering at this level equates to crystallinity.

Although medium-range order is believed to play an important role in determining many of the physical-mechanical properties of solid disordered materials (Elliot 1983), both its physical nature and influence on such properties is still however poorly understood. Indeed, the relationship between short- and medium-range order varies between material systems. For example in covalent systems where the short-range order is well defined and is strictly dependent on the constraints of chemical bonding, ordering over the medium-range arises as a direct consequence of short-range order. However, in certain metallic systems (e.g. amorphous transition metal-metalloid alloy systems) where non-directional bonding prevails, the existence of short-range order is believed to be a direct consequence of the existence of a well defined medium-range order (Ossi 2003).

2.2 X-ray absorption near edge structure (XANES)

XAS is an element-specific technique sensitive to short- and medium-range structure. Light elements (e.g. Si, Mg or O), with K (or L) absorption edges in the 1-2 keV range require measurement in high vacuum (see Wong et al. 1994; de Groot 2001). XAS spectra (e.g. Fig. 8) generally contain four distinct regions (see review by Stern 1978; or Agarwal 1991):

-
the absorption edge step;
-
a large intense feature (termed the white line), sometimes present at the absorption edge peak;
-
a post-edge XANES region extending from $\sim$10 eV up to 40 or 50 eV beyond the absorption edge;
-
a post-edge EXAFS region extending from the XANES region out to a $\sim$few $\times$ 100 eV.
Fine structure in the XANES/EXAFS regions arises from transitions of the ejected inner-shell photoelectron from bound to unbound continuum states, with the difference between the incident X-ray energy and the electron's binding energy being conserved as kinetic energy. The photoelectron undergoes elastic and inelastic scattering from the surrounding electron density associated with neighbouring atoms, causing interference effects in its wavefunction. For N0 absorbing atoms per unit volume, irradiated by X-rays of circular frequency $\omega$, the absorption coefficient, $\mu$, can be described by the dipole approximation,

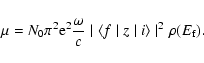\begin{displaymath}\mu=N_{0}\pi^{2}{\rm e}^{2}\frac{\omega}{c}\mid\langle f\mid z\mid i\rangle \mid^{2}\rho(E_{\rm f}). \end{displaymath} (1)

Here z is a scalar potential proportional to distance and  $\rho(E_{\rm f})$ is the density of final states for the unbound photoelectron. The electron's initial bound state is $\mid$$i\rangle$ and its final state $\mid$$f\rangle$, the latter being the sum of a spherical outgoing wave plus a back scattered wave due to surrounding atoms. These combine constructively and destructively so that $\mu$ does not vary smoothly with energy, but displays complex oscillatory fine structure.

When the excess photoelectron energy is below $\sim$10 eV, inelastic scattering from valence electrons at binding energies less than 10 eV is significant and the mean free path shortens ($\sim$few Å), scattering is then from nearest neighbour atoms only. However, elastic scattering mainly occurs from electrons with much greater binding energies (which do not normally participate in chemical bonding) and beyond 10 eV past the edge the photoelectron mean free path becomes long and scattering from distant neighbours is strong, with multiple scattering events for small and large bond angle configurations making significant contributions to the underlying scattering from pairs of atoms. Consequently, the XANES region is sensitive to the structural symmetry of the local environment and hence the bonding state of the absorber as well as pair correlations. In one-electron multiple scattering theory (Lee & Pendry 1975; Natoli et al. 1980; Natoli & Benfatto 1986; Natoli et al. 1990) XANES peak profiles and intensities are related to the number of possible scattering pathways accessible for a given photoelectron energy. Hence XANES are affected by site symmetry, number of nearest neighbour atoms, bond angles and distances (Bianconi et al. 1982), while peak energies are related to interatomic distances and hence bond properties.

XANES end when the photoelectron mean free path again decreases and multiple scattering events become weak. This happens when the de Broglie wavelength of the photoelectron, $\lambda_{\rm e}=hp^{-1}$ (which decreases with increasing excess kinetic energy), becomes comparable to the nearest neighbour distance. The XAS signal is then dominated by the single scattering events of the EXAFS region.

2.3 X-ray scattering and the low-k regime

Away from any absorption edges, the scattered X-ray intensity I(k), in electron units, from a material with N atoms is described by (Elliot 1983)

$\displaystyle I(k) = B(k) + N\langle f^{2}\rangle + N\langle f\rangle^{2}\int_{0}^{\infty}4\pi r^{2}[\rho(r)-\rho_{0}]\frac{\sin kr}{kr}{\rm d}r$     (2)

where the magnitude (i.e. wavenumber), k, of the scattering X-ray wavevector k for a beam of wavelength $\lambda$ incident at the sample at angle $\theta$ is given by

\begin{displaymath}k=4\pi\lambda^{-1}\sin\theta. \end{displaymath} (3)

The X-ray scattering wavevector is the difference between the incoming and scattered X-ray beams and defines a wavelength-independent reciprocal measurement space. B(k) is a background term accounting for air scatter and diffuse incoherent scattering and f is the atomic contribution to I(k), which in polyatomic systems is a weighted sum of contributions from each element, such that

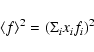\begin{displaymath}\langle f\rangle^{2} =(\Sigma_{i}x_{i}f_{i})^{2} \end{displaymath} (4)

and

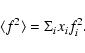\begin{displaymath}\langle f^{2}\rangle =\Sigma_{i}x_{i}f_{i}^{2}. \end{displaymath} (5)

The quantity within the integral in Eq. (2) is the contribution from the real-space variation (due to the molecular arrangement) of electron density, $\rho(r)$, relative to the average macroscopic bulk density, $\rho_{0}$. After correcting for background scatter, the atomic contribution to the measured intensity can be subtracted out to give the so called structure factor, S(k),

\begin{displaymath}S(k) = k\Big [ \frac{I(k)N^{-1}-\langle f^{2}\rangle}{\langle f\rangle^{2}}\Big ] \end{displaymath} (6)

which contains only the contribution from the molecular arrangement, i.e.

\begin{displaymath}S(k)= \int_{0}^{\infty}4\pi r[\rho(r)-\rho_{0}]\sin kr {\rm d}r. \end{displaymath} (7)

At low values of k many non-crystalline materials, particularly network formers such as silicates, exhibit a sharp peak in S(k). This feature, referred to as the first sharp diffraction peak (FSDP), or pre-peak, has long been recognised as a signature of medium-range order (Elliot 1991) since it does not correlate with features in the atomic radial distribution function (Greaves et al. 1979). Although no universal theory describing FSDP features in different materials exists (Ossi 2003), it is known that they are related to the relative arrangement of regions that are themselves ordered over the medium range. In this sense, the relationship between the FSDP and medium-range structure is well established (Gaskell 2001).

The range in k over which FSDP features are observed can be approximated by rewriting the non-background part of Eq. (2) in the Debye form, which describes the scattering contribution from a random arrangement,

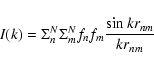\begin{displaymath}I(k)=\Sigma_{n}^{N}\Sigma_{m}^{N}f_{n}f_{m}\frac{\sin kr_{nm}}{kr_{nm}} \end{displaymath} (8)

where fn and fm are the atomic scattering contributions from atoms n and m and rnm is their separation distance. The term $\sin kr/kr$ has its first kr>0 maximum at $kr\simeq7.725$ and thus the limiting magnitude of the scattering vector, $k_{\rm c}=7.725/r$, is determined by the short-range order bond length. In silicates the Si-O bond length is typically $r_{\rm Si-O}\sim 1.6$ Å and we could in the case of a fully connected SiO2 network, for example, define a single medium-range order generating element to be a cluster of three tetrahedra sharing a common O atom at one vertex. This arrangement can be represented by a sphere centred on one Si atom, whose surface touches the centres of the other two tetrahedra. Thus, $r\simeq2r_{\rm Si-O}$ and features in the scattering pattern at values of $k\leq k_{\rm c}(=7.725/2r_{\rm Si-O})$ can be attributed to medium-range order. Tetrahedral clustering should thus be visible for values of k below $\sim$2.5 Å-1 (e.g. see Fig. 18). This limit, which defines the low-k regime, is however only approximate since it is for the limiting case of a completely random assemblage.

A well documented property of systems showing single FSDP features (Wright et al. 1985, 1991; Elliot 1992; Ossi 2003) is that when plotted as a function of the reduced parameter kr, the FSDP peak value is located at

\begin{displaymath}kr\simeq2.5, \end{displaymath} (9)

which allows the short-range bond length of the medium-range order generating cluster to be determined from the measured data.

An additional length can also be determined by analogy with crystalline Bragg diffraction, where peak position is characteristic of the distance between lattice planes. The position of the FSDP can be related to a real-space distance, D, by

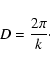\begin{displaymath}D=\frac{2\pi}{k}\cdot \end{displaymath} (10)

Which can be interpreted as the semi-ordered inter-cluster distance (see discussion in Sect. 4.3).

3 Experimental details

3.1 Sample manufacture

Cosmic silicate analogues have been manufactured by a variety of methods (see review by Colangeli et al. 2003; and discussion by Nuth et al. 2002). Most have focussed on producing amorphous particles and only a few (e.g. Hallenbeck et al. 1998; Nuth et al. 2002) attempt to simulate, to any degree, the astrophysical conditions of grain formation. For the present work amorphous silicates were manufactured using three variations of a sol-gel process due to Sabatier (1950) and Day (1974), which has been described in detail elsewhere (Thompson et al. 2007). Three silicates (hereafter, following Day 1976, denoted Product I, II and III respectively) were produced according to:
Product I:

$\displaystyle \mbox{Na}_{2}\mbox{SiO}_{3} + \mbox{MgCl}_{2} + \mbox{H}_{2}\mbox{O} \rightarrow \mbox{MgSiO}_{3} +2\mbox{NaCl} + \mbox{H}_{2}\mbox{O}.$     (11)

Product II:
$\displaystyle \mbox{Na}_{4}\mbox{SiO}_{4} + 2\mbox{MgCl}_{2} + \mbox{H}_{2}\mbo... ...iO}_{3} + 4\mbox{NaCl} + \mbox{Mg(OH)}_{2} +\mbox{NaOH} + \mbox{H}_{2}\mbox{O}.$     (12)

Product III:
$\displaystyle \mbox{Na}_{4}\mbox{SiO}_{4} + 2\mbox{MgCl}_{2} \rightarrow \mbox{Mg}_{2}\mbox{SiO}_{4} + 4\mbox{NaCl} + \mbox{H}_{2}\mbox{O}.$     (13)

In reaction (12) NaOH maintains the sodium orthosilicate solubility while inhibiting the precipitation of brucite (Mg(OH)2). Once produced, the silicates were ground by hand to produce fine-grained powders.


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f1.ps} \end{figure} Figure 1: Wide angle X-ray diffraction patterns showing development of crystallinity in annealed Product I silicate. Patterns in this and subsequent figures have been offset in the y-axis direction for clarity.
Open with DEXTER

Batches of each ground product were then placed in a Pt-coated Mo crucible and annealed under vacuum in a RF induction furnace (Tang et al. 1998) for $\sim$16 h, at the following temperatures: 900 K, 1000 K, 1200 K, 1300 K. At the end of each run the furnace power was switched off and the sample allowed to cool. Since the furnace body and RF coil are water cooled, the rate of temperature decrease is of the order of $\sim$300  $\hbox{$^\circ$ }$C per minute from high temperature and effectively quenches the structure. The long-range structure (amorphous v. crystalline) of each annealed sample was then characterised using wide angle X-ray synchrotron diffraction (station 2.3, Daresbury Laboratory Synchrotron Radiation Source (SRS)). At 1000 K (Fig. 1) Product I crystallizes into a well formed phase identified as forsterite (Thompson & Tang 2001). At 1300 K additional diffraction features attributable to crystalline enstatite have also been found to form (Thompson et al. 2007). Figure 2 shows powder diffraction patterns for Products II and III, both of which remain amorphous throughout the entire annealing range, although product II does show a change in the morphology of its powder pattern when annealed.


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f2.ps} \end{figure} Figure 2: Wide angle X-ray diffraction patterns for annealed samples of the Product II and III silicates. The absence of sharp diffraction peaks indicates an absence of long-range crystalline structure.
Open with DEXTER

While it is recognised that the method of production does not attempt to simulate the formation mechanism of silicates in space it does offer certain advantages. In particular, the production process is easily scalable and can yield large quantities of material allowing multiple multi-technique experiments to be performed. Making comparisons between published measurements of analogue samples produced by different methods has been a long-standing issue (Jäger et al. 1994, 2003; Nuth et al. 2002). The results presented here however have a high degree of parity with previously reported investigations (Thompson et al. 1996, 2002a,b, 2003, 2007; Thompson & Tang 2001). Sol-gel based silicates have also been used as analogues for circumstellar silicates in AGB stars by Jäger et al. (2003) who found the gel method produces hydrogenated materials with chemical properties similar to those expected of cosmic silicates. The hydrogenation of the samples used in the current work has been discussed previously (Thompson et al. 2003).

Average Mg:Si and Si:O ratios for the three silicates are given in Table 1, based on previous EDX analysis (Thompson et al. 2007) and are consistent, for example, with estimates of Mg:Si ratios for Comet Halley dust (Jessberger et al. 1988; Lawler et al. 1989). The average Mg:Si ratios for Products I and II are generally consistent with the enstatite end-product predicted by reactions (11) and (12). However reaction (13) has failed to produce the expected stoichimoetry and a silicate with a very low Mg content has resulted. Nevertheless, along with the crystalline forsterite, enstatite and quartz minerals and commercial amorphous silica also used in this study, the three silicates form part of a series of silicates with decreasing Mg:Si content.

Table 1: Average elemental ratios for Product I, II and III silicates determined from EDX measurements (Thompson et al. 2007).

3.2 Measurement

3.2.1 XANES

XANES spectra were collected at the Daresbury Laboratory SRS using station 3.4 (MacDowell et al. 1988; Roper et al. 1992), which is a XAS station covering the range 0.8 to 3.5 keV. At these energies absorption by air is strong and measurements are performed in high vacuum (typically $1.7 \times 10^{-7}$ Torr). Each sample powder was mixed with a small amount of high purity graphite powder and mounted on flat-faced aluminium holders to which double-sided conducting tape had been applied. The taped holder was pressed into the sample/graphite mix and any non-adhering powder removed by gentle tapping. The holders were then mounted in a spring-loaded conducting rack within the vacuum chamber, such that the angle of incidence of the synchrotron beam was $\sim$45 $\hbox{$^\circ$ }$ in the direction of the X-ray beam and perpendicular to it in the vertical direction. Sample preparation and mounting were performed under clean room conditions to avoid contamination (particularly from NaCl in human sweat since Na EXAFS oscillations could overlap the Mg XANES). During loading the sample chamber was purged with N2 gas. The energy ranges covering the Si and Mg K-shell absorption edges were scanned using the beamline's high vacuum water-cooled double-crystal monochromator located up-stream of the sample chamber. In this configuration a constant position monochromatic beam was achieved at each energy step by rotating the top crystal and both rotating and translating the bottom one, ensuring the number of absorbers in the beam for each spectrum remained constant. Spectra were recorded by total electron yield (Kordesch & Hoffman 1984), measured directly from the sample holder/rack assembly via a Kiethley 427 current amplifier. Incident beam intensity was monitored via a post-monochromator fine-gauge tungsten mesh and was used to normalise the spectra to the time decay of the synchrotron beam.

3.2.2 low-k scattering

Scattering measurements were performed using Station 2.3 at the SRS. Located 15 m from a 1.2 T dipole bending magnet, the 2.3 instrument is a concentric two-circle ($\theta$-2$\theta$) high-resolution angle-scanning device (Cernik et al. 1990; Collins et al. 1992), based on a parallel-beam optics design (Parrish et al. 1986). It receives X-rays in the range 0.5-2.5 Å, with monochromatic beam being selected via a water cooled double-bounce Si(111) channel-cut single crystal. This delivers a high-intensity parallel beam to the sample stage located at the centre of the instrument's two circles. Automatic wavelength calibration (Laundy et al. 2003) was performed using a high purity Si powder standard (National Institute of Standards and Technology NBS SRM640c). The powdered silicate samples were mounted in flat-plate mode on a single crystal Si wafer cut along a forbidden crystallographic direction to suppress diffraction contributions from the wafer itself. For the present work, the scattered beam was passed through an evacuated parallel-foils collimating assembly (Roberts & Tang 1998) mounted on the 2$\theta$-circle arm and detected using an enhanced dynamic range scintillation counter. The detector acceptance angle using this arrangement is 0.065$^{\circ}$ 2$\theta$, while the 2$\theta$-circle motor stepping resolution was set to 0.01$^{\circ}$. An X-ray wavelength of 1.499795 Å (calibrated) was selected, to give good resolution of the low-k features with a reasonably high X-ray photon flux to minimise data collection times. Individual atomic scattering factors, fi were calculated by the procedure described by Waasmaier & Kirfel (1995) and the weightings, xi were based on Table 1. The background contribution due to Compton scattering was calculated using the procedure of Smith et al. (1975) to which a relativistic correction was applied (Korsounski et al. 2003). Air scatter was assumed negligible due to the very short sample-to-foils distance.


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f3.ps} \end{figure} Figure 3: Measured Mg K-edge XANES spectra for forsterite and enstatite mineral samples, with the main features labelled A to F.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f4.ps} \end{figure} Figure 4: Measured Mg K-edge XANES spectra for unprocessed samples of the high-, medium- and low-Mg Product I, II and III silicates. Feature labels as per Fig. 3.
Open with DEXTER

4 Results

4.1 Mg K-edge XANES

Figure 3 shows Mg K-edge XANES spectra measured for crystalline mineral samples of enstatite and forsterite, with the main features labelled A to F. While most features are present in both spectra, in the forsterite spectrum the intensities of features B-F relative to A are weaker and the ABC complex appears more asymmetric. Since peak intensity is related to the number of available multiple scattering pathways involving the absorbing atom and its first- and higher-order neighbours, the reduced intensities in forsterite immediately suggest the sites occupied by Mg are less structured than those of enstatite.

Comparing spectra for the three unprocessed amorphous silicates (Fig. 4), the same A-F features can be identified in each spectrum, with Products I and II exhibiting morphologies similar to enstatite, albeit with weakened intensities. Of the two, Product I's features are the weakest. Surprisingly perhaps, given its low Mg:Si content, the morphology of Product III's spectrum is better matched by forsterite, where feature C appears only as a very weak shoulder and features D, E and F are also weak. Feature A in all three amorphous samples is less pronounced than in either of the crystalline spectra. Overall the environment occupied by Mg in the amorphous samples appears similar to the crystalline environments but with reduced structural order, as evidenced by the reduction in peak intensities.


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f5.ps} \end{figure} Figure 5: Thermal evolution of the measured Mg K-edge XANES spectra for annealed samples of the high-Mg content Product I silicate. Feature labels as per Fig. 3.
Open with DEXTER

Considering now the annealed spectra for Product I (Fig. 5), although in its unprocessed state the Mg environment resembles crystalline enstatite, annealing at 900 K produces a spectrum better matched by forsterite. Feature D has reduced in intensity, A has become stronger and better defined, while C has become a broad weak shoulder to an asymmetric ABC complex. The 1000 K spectrum also exhibits a similar forsterite morphology. However, at 1200 K this trend appears to reverse and the XANES once more begin to resemble enstatite, with feature's C and D increasing in strength. At 1300 K, the symmetric ABC complex of enstatite is clearly visible (note: for this particular sample only a small quantity of material survived the annealing and preparation stage, as evidenced by the small pre- to post-edge step, which exaggerates the strength of features A, B and C relative to the post-edge region).


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f6.ps} \end{figure} Figure 6: Thermal evolution of measured Mg K-edge XANES spectra for annealed samples of the medium Mg-content Product II silicate. Feature labels as per Fig. 3.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f7.ps} \end{figure} Figure 7: Thermal evolution of measured Mg K-edge XANES for annealed samples of the low Mg-content Product III silicate. Feature labels as per Fig. 3.
Open with DEXTER

The XANES spectra for Product I clearly exhibit an evolution in the local structural environment surrounding Mg from enstatite-like to forsterite-like and back to an enstatite-like with increasing temperature.

Product II exhibits a similar evolution (Fig. 6). Feature A becomes more defined, while C to F become progressively weaker and the ABC complex becomes increasingly asymmetric. However unlike Product I which has the highest Mg:Si ratio and changed to a forsterite-like spectrum at 900 K, the Product II spectrum assumes a more forsterite-like morphology at the higher temperature of 1000 K. Furthermore, for the temperatures studied, Product II does not revert back to an enstatite-like morphology. At 1300 K features C and D do show signs of increasing intensity and may be suggestive of a reversal at higher temperature.

For the silicate with the lowest Mg:Si ratio, Product III (Fig. 7), the initial morphology appears forsterite-like and although some minor changes occur with temperature (notably a strengthening of A, weakening of D and an increase in the ABC asymmetry), the Mg environment remains essentially forsterite-like over the entire annealing range.

All three silicates show Mg K-edge XANES morphologies that correspond well with those of crystalline enstatite and forsterite and in turn match closely other published spectra for these two minerals (Wu et al. 1996; Mottana et al. 1999; Cabaret et al. 1998). In addition, these morphologies correspond closely to those of other materials where Mg is known to be in 6-fold octahedral coordination with either O or OH, e.g. talc and brucite (Wong et al. 1994); Ca-pyroxenes, (Mottana et al. 1999) and various olivines (Mottana et al. 1996). The number of features (which reflects the number of scattering pathways) is less than the number measured for periclase (MgO) which is widely acknowledged as a model compound where Mg is in regular octahedral coordination (Rowen et al. 1993; Wong et al. 1994; Ildefonse et al. 1995; Wu et al. 1996). In particular the ABC triplet feature, with varying relative intensities, near the absorption edge is a common feature. Differences in the relative intensities of A, B and C were attributed by Wong et al. (1994) to variations in the number of coordinating OH ligands in various materials. In brucite (Mg(OH)2) for example, where Mg2+ is octahedrally coordinated by OH groups, octahedra share adjacent edges to form layer structures, giving a XANES spectrum (Yoshida et al. 1995; Aritani et al. 2000) very similar to enstatite. Although silicates also contain Si-O tetrahedra with H, O or OH at their vertices the similarity of the XANES for brucite and enstatite suggests silicate Mg K-edge XANES features are due to the existence of a larger structure containing ordered octahedral Mg extending well beyond the first coordination shell.

Model calculations for Ca-bearing crystalline pyroxene using atomic clusters of increasing size built around a central Mg atom show the Mg K-edge XANES to contain both short- and medium-range contributions (Mottana et al. 1999). Typically, a 2 Å radius cluster (7-atoms, 1 Mg and 6 O) gives a spectrum principally consisting of a strong un-split feature, intermediate of A and B in Fig. 3. Progressively increasing the cluster radius to 4.97 Å (50 atoms) produces a large feature with the A, B & C fine structure seen in Figs. 3 to 7. The C feature, that differentiates between crystalline enstatite and forsterite only appears in calculated spectra when the cluster radius is greater than $\sim$5-6 Å. Due to the close similarity between enstatite and brucite XANES it seems reasonable to associate the C peak with the presence of large ordered structures involving Mg octahedra, suggesting therefore that the observed change in morphology from enstatite to forsterite and back to enstatite observed for Product I (Fig. 5) and in part for Product II are the result of changes in the ordering of Mg-O octahedra over medium-range distances within large clusters, most likely due to the mobility of Mg during annealing. Since the three silicates contain progressively less Mg the Mg in product III, unlike Products I & II, is sufficiently dilute such that large ordered structures involving occupied Mg-O octahedra do not form within the temperatures and timescales used.

To test the dependence of XANES on medium-range ordering, theoretical Mg K-edge XANES were calculated for clusters based on ideal forsterite, rhombohedral enstatite and monoclinic enstatite structures (i.e. without static or thermal disorder) using the FDMNES code (Joly 2001). These calculations reproduce only $\mu$ and do not contain the pre- and post-edge background signals, nor the step function across the edge. Figure 8 shows calculated spectra for a 2 Å radius cluster, while Fig. 9 shows spectra for 5 Å clusters. From these it is clear that a single feature devoid of fine structure located just past the absorption edge arises from the interaction of the ejected Mg photoelectron with the six nearest O atoms and relates to the ordering of the first short-range co-ordination shell of O around Mg, while the development of features A, B & C in the larger cluster are due to interactions of the photoelectron at larger distances and mark the presence of medium-range structural ordering extending beyond the first short-range order shell. Differences in the relative intensities of the fine structure features for the different silicates at different stages of annealing are thus due to differences in their medium-range ordering rather than short-range coordination. Similarly, the unprocessed (i.e. as manufactured) Products I and II exhibit more structured medium-range Mg environments than Product III.

The position of the first strong post-edge feature in the annealed silicates however also exhibits some temperature dependency. For enstatite and forsterite its peak (feature B) is located at very similar energies, but in Products II and III shows a shift to lower energy with annealing temperature. Product I shows an initial shift to higher energy at 900 K, but then follows the same trend towards lower energy. The average Mg-O distance for forsterite ($\sim$2.1098 Å) is slightly smaller than for orthorhombic enstatite ($\sim$2.1782 Å) and these shifts may be attributable to a shortening of the average Mg-O distance, since the energies of post-edge features, $\Delta E$, when measured relative to the energy of the absorption edge, scale with inter-atomic distance, r, according to $\Delta E=\mbox{const.} \times r^{-2}$ (Natoli 1983).


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f8.ps} \end{figure} Figure 8: Calculated Mg K-edge XANES for clusters of radius of 2 Å centred on an Mg atom and based on crystalline Clino-Enstatite, Orthorhombic Enstatite and Forsterite structures, showing contribution of short-range order to XANES morphology.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f9.ps} \end{figure} Figure 9: Calculated Mg K-edge XANES for 5 Å radius clusters centred on an Mg atom for crystalline Clino-Enstatite, Orthorhombic Enstatite and Forsterite structures showing effect of increasing ordered cluster size on XANES morphology. Ordered medium-range structure results in formation of fine structure features.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f10.ps} \end{figure} Figure 10: Si K-edge XANES spectra measured for amorphous and crystalline (Quartz) SiO2, with the main features labelled G to K.
Open with DEXTER

4.2 Si K-edge XANES

Figures 10-12 show measured Si K-edge XANES for amorphous and crystalline SiO2 (quartz), forsterite and enstatite mineral samples and the three unprocessed silicates respectively. Clear differences exist between crystalline and amorphous SiO2 and again can be used to describe the morphologies of the other silicate spectra. Crystalline SiO2 exhibits five main features labelled G-K, plus a possible shoulder on the high energy side of feature K. Amorphous SiO2 shows only four of these: G, K, plus weak H and very weak I features. Crystalline enstatite shows strong G, I and K features plus a very weak J feature, while forsterite shows strong G and K features plus very weak H and I features. The unprocessed Product I and II silicates also show strong G and K features, plus intermediate H and I features. In Product III the intermediate features are extremely weak. The morphologies of Products I and II appear to fall somewhere between the crystalline forsterite and enstatite spectra, while the morphology of Product III appears much closer to forsterite.


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f11.ps} \end{figure} Figure 11: Si K-edge XANES spectra measured for forsterite and enstatite mineral samples, with feature labels as per Fig. 10.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f12.ps} \end{figure} Figure 12: Meaured Si K-edge XANES spectra for unprocessed samples of the high-, medium- and low-Mg Products I, II and III. Feature labels as per Fig. 10.
Open with DEXTER

Considering now the Si K-edge spectra for the annealed Product I (Fig. 13), at 900 K features H and I have diminished, such that the spectrum now resembles forsterite. At 1000 K the intermediate features disappear. However at 1200 K feature I reappears as a strong feature similar to the enstatite pattern and remains so up to 1300 K. The behaviour of the Si K-edge XANES thus follow the Mg K-edge in changing from enstatite-like to forsterite-like and back to enstatite-like. However the presence of feature H as a weak shoulder suggests some Si remains in forsterite-like co-ordination. The Product II Si K-edge XANES (Fig. 14) show a similar evolution, G and K are present throughout, while H and I decrease with increasing temperature. As with the Mg K-edge XANES the Si K-edge XANES features do not recover at higher temperature. Finally, Product III (Fig. 15) again shows very little evolution with temperature, features H and I are absent in the annealed spectra leaving G and K as the only features present at each temperature. The morphology of the annealed Product III spectra show less structure than either forsterite or amorphous SiO2.


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f13.ps} \end{figure} Figure 13: Evolution of measured Si K-edge XANES spectra with annealing temperature for the high-Mg Product I silicate. Feature labels as per Fig. 10.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f14.ps} \end{figure} Figure 14: Evolution of measured Si K-edge XANES spectra with annealing temperature for samples of the medium-Mg Product II. Featurelabels as per Fig. 10.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f15.ps} \end{figure} Figure 15: Evolution of measured Si K-edge XANES spectra with annealing temperature for samples of the low-Mg Product III. Feature labels as per Fig. 10.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f16.ps} \end{figure} Figure 16: Calculated Si K-edge XANES for the first Si-O coordination shell for Clino-Enstatite, Orthorhombic Enstatite and Forsterite structures, showing contribution of short-range order to XANES morphology.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f17.ps} \end{figure} Figure 17: Calculated Si K-edge XANES for 5 Å Clino-Enstatite cluster, 5 Å Orthorhombic Enstatite cluster and 4.5 Å forsterite cluster each centred on a Si atom, showing effect of increasing ordered cluster size on XANES morphology. Ordered medium-range structure results in formation of fine structure features
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f18.ps} \end{figure} Figure 18: X-ray scattering feature measured at low values of the X-ray scattering wavevector for amorphous SiO2. X-axis units are Å-1. The single peak is located at 1.603 Å-1, corresponding to values of r=1.56 Å for the short-range order bond length and D=3.92 Å for the pseudo-ordered inter-cluster distance.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f19.ps} \end{figure} Figure 19: X-ray scattering features measured at low values of the X-ray scattering wavevector for samples of the high-Mg Product I silicate annealed below its crystallisation temperature. For the three features labelled (1) to (3) short-range order bond lengths, r, of 1.66(1), 1.31(2), 1.01(3) Å are obtained for the unprocessed sample and 1.66(1), 1.35(2), 1.01(3) Å for the 900 K sample. Pseudo-ordered inter-cluster distances, D, of 4.17(1), 3.30(2), 2.54(3) for the unprocessed sample and 4.16(1), 3.39(2), 2.54(1) for the 900 K sample are obtained.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f20.ps} \end{figure} Figure 20: X-ray scattering features measured at low values of the X-ray scattering wavevector for annealed samples of the medium-Mg Product II silicate. For the features labelled (1) to (3) short-range order bond lengths, r, of 1.73(1), 1.30(2), 1.01(3) Å are obtained for the unprocessed sample, 1.75(1), 1.30(2) Å for the 1000 K sample and 1.37(2), 1.03(3) Å for the 1300 K sample. Corresponding pseudo-ordered inter-cluster distances, D, of 4.34(1), 3.27(2), 2.53(3) are obtained for the unprocessed sample, 4.41(1), 3.27(2), for the 1000 K sample and 3.441(2), 2.59(3), for the 1300 K sample.
Open with DEXTER

The tetrahedral coordination of Si by four O atoms is a common feature of all silicates and as a consequence both crystalline and amorphous silicates exhibit very similar K-edge XANES (Li et al. 1993, 1995; Wu et al. 1998; Poe et al. 1997, 2004; Bender 2002; Henderson & Fleet 1997; Henderson 1995; Farges et al. 1999; Thompson et al. 1996; Gilbert et al. 2003). Typically, all show the strong white line feature G and a broad hump feature K seen in Fig. 10. Only the relative intensities of the intermediate H, I, & J features tend to show any variation with composition or state and are usually stronger in crystalline samples. On first inspection this could be taken to imply that the Si-O tetrahedra in amorphous samples are themselves disordered. However in crystalline configurations the tetrahedra are slightly distorted, while in amorphous configurations they tend to be more regular (Henderson 1995; Henderson et al. 1995). According to the molecular orbital model of Li et al. (1993), the intermediate features are due to spin-forbidden transitions of the Si 1s electrons to empty 3d states. The asymmetry caused by the slight distortion of the tetrahedra in the crystalline phase results in a mixing of unoccupied 3p like features into the 3d states to produce symmetry forbidden shape resonances. In amorphous configurations the reduction in tetrahedral distortion causes the photoelectron to sample a more symmetric environment, reducing the mixing of states and hence the intensities of the intermediate features. The absence of long-range order therefore improves the silicate's short-range order. The presence of the intermediate H-J features are thus clear indicators of structural order extending beyond the first Si-O co-ordination shell and is consistent with model calculations for $\alpha$-quartz (Wu et al. 1998) and amorphous SiO2 (Chaboy et al. 1995; Levelut et al. 2001). This is confirmed by model calculations for 1.6 and 5 Å cluster radii for forsterite and enstatite, as shown in Figs. 16 and 17.

4.3 low-k scattering


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f21.ps} \end{figure} Figure 21: X-ray scattering feature measured at low values of the X-ray scattering wavevector for annealed samples of the low-Mg Product III silicate. The single peak is located at 1.829, 1.749, 1.66 Å-1 for the unprocessed, 1000 K and 1300 K samples respectively, corresponding to short-range order bond length values, r, of 1.37, 1.43, 1.51 Å and pseudo-ordered inter-cluster distances, D, of 3.44, 3.59, 3.78 Å respectively.
Open with DEXTER

Figure 18 shows the low-k scattering pattern for amorphous SiO2 while Fig. 19 compares the low-k scattering for the unprocessed and 900 K Product I silicate (at higher annealing temperatures the Product I pattern showed crystalline Bragg diffraction features which either obscure or destroy the FSDP signal). The Product I patterns differ markedly from amorphous SiO2 in that multiple features occur (labelled (1) to (3) in the figure). A clear variation with temperature of features (1) and (2) is also visible. The low-k patterns for Product II (Fig. 20) show a similar multiple feature morphology and again exhibit a clear evolution with annealing temperature. However in this silicate the three features are clearly visible in the initial unprocessed sample, but with annealing, feature (1) decreases to a weak shoulder at 1000 K and is not visible at 1300 K; while feature (3), although initially strong, is barely discernable at 1000 K and remains only as a much narrower and very weak feature at 1300 K. The low-k patterns for Product III on the other hand (Fig. 21) resemble amorphous SiO2 (Fig. 18) in exhibiting only a single broad peak located near the feature (2) position in the other two silicates. However, there is a clear shift in peak position with annealing temperature for this feature. Table 2 gives the measured k-space positions of the features in Figs. 18 to 21 and corresponding values of r and D (Eqs. (9) and (10)).

The r value of 1.56 Å for amorphous SiO2, corresponds well to the shorter Si-O bond length in crystalline quartz of 1.598 Å, while feature (1) in Product I in both unprocessed and annealed samples gives a r value of 1.66 Å, matching the Si-O bond length ranges in forsterite (1.6-1.65 Å), monoclinic enstatite (1.56-1.68 Å) and multiply-linked orthorhombic enstatite (1.51-1.82 Å). For Product II, the r values of 1.72 and 1.75 Å for feature (1) for the unprocessed and 1000 K samples appear better matched by the single-linked orthorhombic enstatite Si-O bond lengths of 1.75 to 1.82 Å.

Features (2) and (3) in Products I and II give r values of $\sim$1.3 and 1.01 Å that are unrealistically short for Si-O bonding. To interpret these we make use of the observation (Ossi 2003) that the position of FSDP features in many glass systems lies almost coincident with the first, often most intense, diffraction peak in their corresponding crystal phases. The lattice d-spaces of the strongest crystalline diffraction peaks for quartz, forsterite and various enstatites, drawn from published crystallographic data are listed in Table 3. The D-values from Table 2 for feature (2) for both the unprocessed and annealed samples of Product I and II are variously 3.30, 3.39, 3.27, 3.27 and 3.44 Å, which by comparison with Table 3 suggests a clear association with the SiO2 quartz structure, whose strongest crystalline diffraction peak has a d-space of $\sim$3.34 Å. Similarly, the feature (3) D-values of 2.477, 2.472, 2.479 and 2.426 Å are suggestive of either forsterite or single-linked orthorhombic enstatite (d-space $\sim$2.46 and 2.43 Å respectively). Ossi (2003) attributed the correspondence between FSDP D-values and the equivalent crystalline d-spaces to pseudo-ordering of the relative inter-cluster arrangement. In this scheme, the relative arrangement over larger distances of clusters that are themselves ordered over the medium-range exhibits certain scattering characteristics that are similar to those of ordered lattice planes in crystalline materials. For example, in SiO2 the interconnection of tetrahedra leads to the formation of medium-range order in the form of rings. In crystalline SiO2 the ring statistics are highly constrained, but in the amorphous case are relatively unconstrained and no long-range periodic ordering of the clusters occurs. However their aperiodic arrangement does result in a quasi-regular, large scale variation in atomic (i.e. electron) density, which gives rise to Bragg-like diffraction at low-k. Since features (1) and (2) diminish with annealing, this suggests that any such quasi-periodic long-range variation in atomic density associated with the relative arrangement of forsterite/enstatite-like clusters initially present in these samples relaxes during annealing. In this respect the behaviour of features (1) and (2) with temperature does not correspond directly to the changes in the local environments surrounding Mg or Si seen using XANES since X-ray scattering probes only the longer-range density variations produced by the relative arrangement of these medium-range structures, not their internal structure.

In light of the above, interpreting the Product III feature appears difficult: initially, in the unprocessed sample its D-value of 3.44 Å corresponds well to the d-space of quartz, but its r-value of 1.37 Å gives a short-range bond length that is too low, while annealing at 1300 K gives an r-value of 1.51 Å, which is close to the quartz Si-O bond length, but its D-value of 3.78 Å lies between quartz and cristobalite, while at the intermediate annealing temperature of 1000 K, neither D or r correspond to either crystalline structure. Since the large scale structure of silicates is dominated by the arrangement of tetrahedral Si-O units, the absence of any low-k features in Product III associated with forsterite/enstatite clustering is clearly due to its low Mg:Si content, i.e. forsterite/enstatite clusters are sufficiently dilute that they do not significantly contribute to any long-range quasi Bragg-like density variation. The single feature in Product III thus arises from an averaged sampling of a distribution of arrangements of medium-range SiO2 clusters. This large scale variation initially bears some resemblance to the long-range structure of quartz, but as the sample is annealed the large scale variation in atomic density adopts a different configuration, no longer resembling any crystalline counterpart. Indeed, the corroboration of this may be found in comparing the temperature sequence of the D- and r-values for Product III (D=3.44, 3.59, 3.78 Å; r=1.37, 1.43, 1.51 Å) with the a-SiO2 values (D=3.92 Å, r=1.56 Å). Both values in Product III appear to be tending towards those of amorphous SiO2, the long-range variation in atomic density of which, with reference to Table 3, does not resemble crystalline quartz. The as-manufactured samples appear to possess a degree of quasi long-range ordering which is removed or relaxed by annealing at temperatures below crystallisation.

5 Discussion

5.1 XAS as an astronomical tool

As a prospective astronomical tool the observation of XAS features from in situ dust grains has the potential to provide information about the structural state of the grain material. However, the work reported here shows isolated observations of the stronger XANES signal may be constrained. The similarity of the XANES morphologies in various silicates, particularly at the Si K-edge, will make definitive identification of the mineral species difficult, though data of sufficiently high resolution and quality may allow differences at the Mg K-edge to be identified. However, certain XANES features have been shown here to arise from the existence of ordered medium-range structure extending beyond the first short-range coordination shell. Unfortunately, as shown here, the presence of medium-range order is not diagnostic of crystalline structure.

Based on the limitations of current near-IR and UV observational technology, Li & Draine (2001) calculated that as much as $\sim$20$\%$ of the total interstellar Si may be carried by crystalline grains smaller than $\sim$7.5 Å in radius, which is close to the cluster sizes required to reproduce the medium-range fine-structure features in the model calculations. For example, at the Mg edge Mottana et al. required a $\sim$6.19 Å radius cluster to describe the Mg K-edge XANES spectrum of Ca-pyroxene; while Wu et al. required a $\sim$7.0 Å radius cluster to account for the Si K-edge in crystalline SiO2. Although rigorous size dependent calculations have not been performed as part of the present study, it appears (Figs. 9 and 17) that a limit close to $\sim$7 Å is also likely for Mg-silicates. Very small, but ordered, grains below this size will not contain enough atoms to produce the medium-range XANES features and will not be identifiable by this method.

Table 2: Low-k FSDP feature positions with corresponding real-space distances and short-range order bond length.

Table 3: d-spaces of strongest diffraction peaks for crystalline cristobalite, quartz and Mg-silicates, different entries for orthorhombic enstatite correspond to variations in the size of the unit cell due to multiply-linked chain structures.

Furthermore, astronomical XANES is also likely to be insensitive to those grains that are on or just above the size limit for producing medium-range XANES features due to the effect of inelastic losses on the photoelectron energy. These result in an energy-dependent broadening (and weakening) of features, which can result in an underestimation of size. This effect was ignored in the calculations for Figs. 8, 9, 16 and 17, but can be simulated by convoluting the calculated XANES spectra with a Lorentzian function containing an energy dependent width of the form (Muller et al. 1982)

\begin{displaymath}\Gamma(E)=\Gamma_{\rm C}+\Gamma (E). \end{displaymath} (14)

The constant part, $\Gamma_{\rm C}$ accounts for the life time of the core-hole left behind by the ejected photoelectron, while the energy dependent term, $\Gamma (E)$, represents all the inelastic processes that depend on the electron's mean free path. Figure 22 illustrates the result of energy dependent broadening on the spectrum of forsterite cluster of 5 Å radius. The effect is to washout the fine structure such that the spectrum appears similar to that of a much smaller ordered cluster size. Observations of astronomical XANES, therefore, may not be able to distinguish between small ordered grains and larger disordered grains.


  \begin{figure} \par\includegraphics[height=3.1in,width=3.1in]{8675_f22.ps} \end{figure} Figure 22: Effect of energy dependent broadening on Mg K-edge forsterite XANES. Bottom plot is the calculated spectrum for a cluster radius (C.R.) of 3.5 Å without energy dependent broadening; middle is for a 5 Å radius cluster without energy dependent broadening; top plot is for the same 5 Å cluster but including contributions from energy dependent broadening.
Open with DEXTER

6 Conclusions

Three annealed amorphous silicates with differing Mg content have been investigated using two synchrotron radiation techniques. Using XANES spectroscopy, features originating from the presence of short-range order and the growth of extended medium-range order have been identified and a new behaviour observed whereby the medium-range environment surrounding both Mg and Si atoms is seen to change between forsterite-like and enstatite-like structures as a function of annealing temperature and Mg content. X-ray scattering at low values of the X-ray scattering wavevector has been shown to provide a useful means of determining whether clusters of medium-range order exhibit some degree of longer-range ordering and in such circumstances can be used to distinguish between cluster types. Since X-ray techniques are becoming increasingly important in the analysis of recovered materials and in the case of XANES as a prospective observational tool, this and further studies on analogue materials will be essential for providing a direct means of interpreting measurements and subsequently processing histories in both recovered cosmic materials and potentially in situ grains.

From the present work, it does not seem unreasonable to speculate as to whether variations in the silicate bands at 10 and 20 $\mu$m (or components thereof) are not due to medium-range ordering effects. Although there have been many attempts in the laboratory to find a relationship between silicate composition and spectral response at 10 and 20 $\mu$m (e.g. Jäger et al. 2003), no general rule has emerged that allows unique identifications to be made from observational data. The situation is further complicated by the numerous laboratory studies showing shifts in the 10 $\mu$m peak position with even relatively minor thermal processing. The consensus conclusion is that the 10 $\mu$m band for (amorphous) silicates exhibits only a minor dependence on chemical composition (Molster & Waters 2003). However, in the silicates investigated here, the existence of medium-range structures attributable to distinct forsterite, enstatite and SiO2-like clustering was identified and annealing below the crystallisation threshold resulted in changes to their relative aperiodic arrangement. Ordering at this scale involves the very structural units that contribute to the fine structure within the 10 and 20 $\mu$m bands and it may well be that variations at 10 and 20 $\mu$m are more reflective of variations in medium-range order rather than direct differences in composition. Characterising medium-range order in laboratory silicates may therefore offer a new and potentially revealing line of enquiry with which to understand the relationship between grain state and spectral response.

Acknowledgements
The experimental XAS part of this work was supported through the provision of SRS beamtime award 42305.

References

 
Copyright ESO 2008