A&A 483, L25-L28 (2008)
DOI: 10.1051/0004-6361:200809417
LETTER TO THE EDITOR
Persistent circumpolar vortices on the extrasolar giant planet HD 37605 b
J. Langton1 - G. Laughlin2
1 - Department of Physics, University of California at Santa Cruz, Santa Cruz, CA 95064, USA
2 -
UCO/Lick Observatory, Department of Astronomy and Astrophysics, University of California at Santa Cruz, Santa Cruz, CA 95064, USA
Received 18 January 2008 / Accepted 25 March 2008
Abstract
Aims. We examine the atmospheric dynamics on the extrasolar gas giant HD 37605 b (P=54.2 d). As this planet's orbit is highly eccentric (e=0.737), the intensity of stellar heating varies by a factor of 40 over the course of an orbit. We also consider the effect of cloud formation on the dynamical flows and the temperature evolution resulting from this extremely variable forcing.
Methods. We employ a grid-based two-dimensional compressible hydrodynamics code to model the atmosphere of the extrasolar giant planet HD 37605 b. We use a resolution of 512 longitude gridpoints and 257 latitude gridpoints. The stellar heating is simulated using a one-layer, two-frequency, two-stream approximation to true radiative transfer.
Results. This time-dependent insolation causes the formation of circumpolar vortices near both poles. These vortices appear to be stable over many orbits, and sequester a large volume of cold air, effectively shielding their interiors from the full blast of irradiation at periastron. Evolution of tracers initially placed within these vortices shows the rate of exchange of material between the interior and exterior of these vortices is small: material initially inside the vortex can be expected to remain in the vortex for 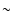 2 P. We note that this result is contingent upon a cloudless atmosphere; the formation of clouds potentially causes a large reduction in both temperature variation and wind speed.
2 P. We note that this result is contingent upon a cloudless atmosphere; the formation of clouds potentially causes a large reduction in both temperature variation and wind speed.
Key words: stars: planetary systems - hydrodynamics - turbulence
The discovery of over 200 planets (Udry et al. 2007; Butler et al. 2006) orbiting other stars over the past decade has opened new frontiers in both astronomical observations and theoretical analysis. Many of these planets occupy dynamical regimes not seen within our own solar system. The hot Jupiters, gas giants on circular orbits with semimajor axes a < 0.1 AU, have proven to be ubiquitous, and have commanded a great deal of attention from both observers (Charbonneau et al. 2005,2002; Deming et al. 2005; Harrington et al. 2007; Knutson et al. 2007; Deming et al. 2006) and modellers (Cooper & Showman 2005; Showman & Guillot 2002; Fortney et al. 2006; Dobbs-Dixon & Lin 2007; Burrows et al. 2006; Cho et al. 2007; Langton & Laughlin 2007; Iro et al. 2005; Cho et al. 2003). To date, less study has been devoted to Jovian-mass planets of somewhat longer period which travel on orbits with significant eccentricty. Preliminary theoretical models (Langton & Laughlin 2008) have shown that the dynamics on such planets are interesting, and in many cases, may have observational consequences. In this Letter, we examine the atmospheric behavior of the extrasolar giant planet HD 37605 b, an
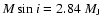 planet with e=0.737 and P=54.2 d.
planet with e=0.737 and P=54.2 d.
HD 37605 b was discovered in 2004, the first planet found by the Hobby-Eberly Telescope (Cochran et al. 2004). The planet is not known to transit its parent star, so its inclination remains unknown. Given a = 0.26 AU and a relatively cool K0 V primary, HD 37605 b likely occupies a significantly different atmospheric regime than the short-period planets that have been observed to date in the near-IR. Prior to the depletion of its cryogen in February 2009, the Spitzer Space Telescope has proven to be an invaluable tool in measuring the temperatures and temperature distributions on a number of exoplanets (Harrington et al. 2006; Knutson et al. 2007), and is expected to yield interesting measurements of the eccentric planets HAT-P-2 b and HD 80606 b. Unfortunately, it is unlikely to possess the short-wavelength sensitivity necessary to resolve the light curve of the much cooler HD 37605 b during its potential non-cryogenic mission. Direct observational characterization of planets such as HD 37605 b will likely have to wait for the launch of JWST.
We employ a grid-based two-dimensional hydrodynamic model with a resolution of 512 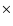 257 to simulate the upper atmosphere of HD 37605 b. For a full description of the model, we refer the reader to Langton & Laughlin (2008). Here, we simply summarize the most important features.
257 to simulate the upper atmosphere of HD 37605 b. For a full description of the model, we refer the reader to Langton & Laughlin (2008). Here, we simply summarize the most important features.
The hydrodynamics are obtained by numerical integration of the primitive equations as applied to the surface of an irradiated, rotating sphere:
where
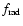 gives the thermal forcing,
gives the thermal forcing,
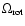 is the angular frequency of the planet's rotation,
is the angular frequency of the planet's rotation, 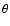 is the latitude, and
is the latitude, and 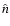 is a unit vector normal to the planet's surface.
is a unit vector normal to the planet's surface.
For a gas giant traveling on a relatively short period eccentric orbit, the rotation rate is not synchronized as would be expected for a planet on a circular orbit. The dominant tidal forces at periastron should ensure pseudo-synchronization of the rotation period (Hut 1981), however, which can be expressed
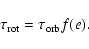 |
(4) |
In pseudo-synchronization, the planet rotates appproximately synchronously with the orbit
during the time immediately surrounding the periastron passage.
The precise functional form of f(e) is currently subject to some debate (see, e.g. Ivanov & Papaloizou 2007). Here we choose to adopt the Hut's expression for f(e), which yields a rotation
period of 6.77 d:
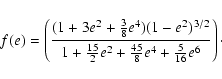 |
(5) |
We calculate
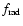 using a one-layer, two-frequency radiative transfer scheme. We take the mean opacity for incident stellar radiation to be k1, while the mean opacity for outgoing long-wave radiation is k2. In this simplified model, the thermal forcing can be expressed as
using a one-layer, two-frequency radiative transfer scheme. We take the mean opacity for incident stellar radiation to be k1, while the mean opacity for outgoing long-wave radiation is k2. In this simplified model, the thermal forcing can be expressed as
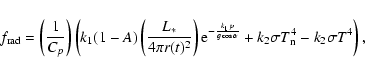 |
(6) |
where where A is the Bond Albedo, L* is the stellar luminosity, and r(t) is the time-dependant distance between the star and the planet. The night-side equilibrium temperature
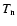 results from a combination of the intrinsic planetary flux due to tidal heating and the upwelling of thermal radiation emitted at high optical depth, and is calculated using a one-dimensional radiative transfer code.
results from a combination of the intrinsic planetary flux due to tidal heating and the upwelling of thermal radiation emitted at high optical depth, and is calculated using a one-dimensional radiative transfer code.
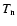 represents a characteristic equilibrium temperature of the atmosphere around optical depth unity in the absence of direct stellar irradiation. The strength of tidal heating depends strongly on the semi-major axis. In this case, since HD 37605 b's orbit is wider by a factor of
represents a characteristic equilibrium temperature of the atmosphere around optical depth unity in the absence of direct stellar irradiation. The strength of tidal heating depends strongly on the semi-major axis. In this case, since HD 37605 b's orbit is wider by a factor of 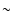 4 than that of a typical hot Jupiter, we do not believe that tidal heating contributes significantly to the energy budget in the upper atmosphere. In the absence of significant tidal heating, we find
4 than that of a typical hot Jupiter, we do not believe that tidal heating contributes significantly to the energy budget in the upper atmosphere. In the absence of significant tidal heating, we find
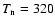 K on HD 37605 b.
The forcing that results from this scheme strongly depends on the choice of k1, k2, and p. Motivated by many-layer radiative models of HD 209458 b (Cooper & Showman 2005; Iro et al. 2005), we choose k1 = 2
K on HD 37605 b.
The forcing that results from this scheme strongly depends on the choice of k1, k2, and p. Motivated by many-layer radiative models of HD 209458 b (Cooper & Showman 2005; Iro et al. 2005), we choose k1 = 2 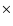 10-4 m2 kg-1, k2 = 4
10-4 m2 kg-1, k2 = 4 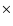 10-4 m2 kg-1, and
p = 250 (g/10 m s-2) mbar, where g is the acceleration due to gravity at the planet's surface. Our choices for k1 and k2 potentially can be tested via Sptizer observations of eccentric giant planets such as HD 80606 b (Naef et al. 2001) and HD 17156 b (Barbieri et al. 2007)
10-4 m2 kg-1, and
p = 250 (g/10 m s-2) mbar, where g is the acceleration due to gravity at the planet's surface. Our choices for k1 and k2 potentially can be tested via Sptizer observations of eccentric giant planets such as HD 80606 b (Naef et al. 2001) and HD 17156 b (Barbieri et al. 2007)
Our model is the first GCM for short-period extrasolar giant planets that admits strongly time-dependant irradiation conditions. It is nevertheless subject to several potentially significant sources of error. In our radiative formulation, we ignore the variation of opacities with temperature and pressure, which is known to be significant. We also do not consider the variation in opacity with wavelength within the infrared regime; this implies, for example, that the 24-micron photosphere and the 3-micron photosphere occur at the same pressure level. Both of these simplifications are likely to cause some discrepancy between our predictions and future observations. Furthermore, the opacities are based on model atmospheres of short period planets with
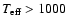 K; at HD 37605 b's lower temperature, the relevant atmospheric chemistry and condensation products are likely to be significantly different.
Nevertheless, we believe that the model provides the potential for a good first-order understanding of how the atmosphere of planets such as HD 37605 b respond to highly variable stellar heating.
K; at HD 37605 b's lower temperature, the relevant atmospheric chemistry and condensation products are likely to be significantly different.
Nevertheless, we believe that the model provides the potential for a good first-order understanding of how the atmosphere of planets such as HD 37605 b respond to highly variable stellar heating.
We adopt a low albedo A=0.1, based upon MOST observations of HD 209458 b (Rowe et al. 2007). We also note that a low albedo is consistent with the predictions of Sudarsky et al. (2005) in regards to an extrasolar giant planet with 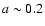 AU. This is tantamount to the assumption of a cloudless atmosphere. With the other parameters as above, our model yields a temperature range of 340 K to 690 K for HD 37605 b in the cloudless case. Interestingly, this range of temperatures straddles
AU. This is tantamount to the assumption of a cloudless atmosphere. With the other parameters as above, our model yields a temperature range of 340 K to 690 K for HD 37605 b in the cloudless case. Interestingly, this range of temperatures straddles
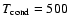 K, the temperature at which water clouds may be expected to form above the 8-micron photosphere. These highly reflective clouds dramatically change the energy input during the periastron passage. To examine this effect, we adopt a simple model where the planet is dark at temperatures too high for water clouds to form: A=0.1 for
K, the temperature at which water clouds may be expected to form above the 8-micron photosphere. These highly reflective clouds dramatically change the energy input during the periastron passage. To examine this effect, we adopt a simple model where the planet is dark at temperatures too high for water clouds to form: A=0.1 for
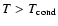 .
However, when
.
However, when
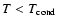 ,
we assume that cloud formation results in a much higher albedo A=0.8. In this case, the insolation absorbed during periastron is insufficient to burn off the water clouds and the planet remains cool and nearly isothermal (410 K < T < 420 K) throughout the orbit. The temperature gradient is too small to produce significant winds, and the atmosphere remains quiescent and essentially featureless.
,
we assume that cloud formation results in a much higher albedo A=0.8. In this case, the insolation absorbed during periastron is insufficient to burn off the water clouds and the planet remains cool and nearly isothermal (410 K < T < 420 K) throughout the orbit. The temperature gradient is too small to produce significant winds, and the atmosphere remains quiescent and essentially featureless.
In the cloudless model, however, the temperature contrast results in much richer dynamical behavior.
The temperature distribution, shown in Fig. 1, shows the turbulent nature of the atmospheric flow in the absence of significant cloud cover.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9417f1.eps}\end{figure}](/articles/aa/full/2008/21/aa09417-08/Timg21.gif) |
Figure 1:
The evolution of the temperature distribution of HD 37605 b over the course of an orbit, assuming a cloudless model. The top left panel shows the northern hemisphere P/4 prior to periastron; the top right is at periastron; the bottom left is P/4 after periastron; and the bottom right is at apastron (P/2 after periastron). |
| Open with DEXTER |
Particularly notable is a cold spot at high latitudes, which traverses through a chaotic orbit about the pole with a period of approximately P/3. The temperature in this region remains below  360 K even during the periastron passage, when the rest of the planet experiences dramatic heating.
360 K even during the periastron passage, when the rest of the planet experiences dramatic heating.
This cold region is produced by a stable vortex which traps cold air and shields its interior from the higher temperatures of the surrounding regions. (See Fig. 2.) In our simulation, this vortex develops after the first periastron passage and is stable for the duration of the simulation (5 P = 271 d). Like its associated cold spot, the vortex traces a chaotic trajectory about the pole, completing its circuit in  P/3. This phenomenon exists in both hemispheres; while Figs. 1 and 2 show only the northern hemisphere; the southern hemisphere is characterized by similar structure in both the temperature distribution and the vorticity.
P/3. This phenomenon exists in both hemispheres; while Figs. 1 and 2 show only the northern hemisphere; the southern hemisphere is characterized by similar structure in both the temperature distribution and the vorticity.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{9417f2.eps}\end{figure}](/articles/aa/full/2008/21/aa09417-08/Timg22.gif) |
Figure 2:
The evolution of the relative vorticity of atmospheric flow of HD 37605 b over the course of an orbit,assuming a cloudless model. The top left panel shows the northern hemisphere P/4 prior to periastron; the top right is at periastron; the bottom left is P/4 after periastron; and the bottom right is at apastron (P/2 after periastron). Relative vorticity measures the extent to which the flow is rotational; it corresponds to the angular frequency of a paddlewheel placed at a given point. The southern hemisphere is characterized by similar structure. |
| Open with DEXTER |
These circumpolar vortices prove to be quite efficient at preventing the exchange of material between the inside and the outside. To quantify this effect, we consider the evolution of a tracer initially placed inside the northern polar vortex. The tracer density obeys the continuity equation (Eq. (3)), but does not contribute to the dynamics of the rest of the atmosphere. The evolution of this tracer over two orbits, shown in Fig. 3, vividly demonstrates the sequestration capabilities of the vortex. We use the maximum tracer density, as seen in Fig. 4, as a somewhat heuristic, yet effective, measurement of the tracer concentration inside the vortex.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9417f3.eps}\end{figure}](/articles/aa/full/2008/21/aa09417-08/Timg23.gif) |
Figure 3:
The evolution of tracer density over two orbital periods, with the tracer initially placed inside the northern polar vortex. By t=2 P, the maximum tracer density has decreased significantly as the material trapped inside begins to escape. |
| Open with DEXTER |
The maximum tracer density shows that the tracer concentration remains high for an extended period - 1.7 P in this case. However, when the tracer begins to escape, it does so relatively rapidly, with the maximum density decreasing by 40% in just 0.3 P. The reason for this sudden dissolution is related to the chaotic motion of the vortex itself. At times, the vortex remains relatively stationary, while at other times, it can travel quite rapidly, outstripping the local wind speed. In such situations, the material inside the vortex cannot advect quickly enough to keep pace with the vortex, and a significant portion of the tracer is left behind.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{9417f4.eps}\end{figure}](/articles/aa/full/2008/21/aa09417-08/Timg24.gif) |
Figure 4:
Maximum tracer density as a function of time. This provides an effective, if somewhat heuristic, measurement of the coherence of the tracer as it moves under the influence of the polar vortex. Note that the vortex initially acts to concentrate the material inside, and that the tracer maintains its coherence until the sudden onset of dissolution at t=1.7 P. |
| Open with DEXTER |
In this Letter, we have simulated the dynamics of the upper atmosphere of the extrasolar giant planet HD 37605 b. As the planet's orbit is highly elliptical, the atmosphere's behavior is primarily governed by its response to the periastron passage, during which the insolation increases by a factor of 40. The flow is characterized by stable circumpolar vortical structures which persist over many orbits, chaotically orbiting the pole  3 times per orbital period. These vortices shield their interiors from the intense heating experienced by the rest of the planet during its periastron passage. Despite maximum temperatures climbing to 690 K, these cold spots maintain temperatures between 335 K and 370 K throughout the orbit.
3 times per orbital period. These vortices shield their interiors from the intense heating experienced by the rest of the planet during its periastron passage. Despite maximum temperatures climbing to 690 K, these cold spots maintain temperatures between 335 K and 370 K throughout the orbit.
Additionally, the vortices display considerable efficiency in retaining the material in its interior. A concentration of some tracer initially placed at the center of the vortex will remain inside the vortex for approximately two full orbits. However, the eventual diffusion of the tracer is quite rapid after the material begins to escape. Additionally, the chaotic nature of the vortices' motion about the pole makes consistent prediction of the tracer escape time difficult.
Planets such as HD 37605 b will be of considerable scientific significance because their orbit carries them in and out of of the stellar insolation regime where water clouds are expected to condense. If planetary climate evolution is driven towards either the extreme of a globally cloudy or a globally cloud-free state, there will be dramatic consequences for the planet's optical light curve. In favorable situations, the phase function of a high-albedo planet sheathed in water clouds will be detectable with space-based photometry. In our future work, we will provide a more detailed analysis of this issue as the computational model is improved.
Clearly, then, the dynamical situation on HD 37605 b raises numerous interesting possibilities. If there is any analogy with the atmospheres of the solar gas giants, we can expect HD 37605 b to be rich in a wide variety of organic compounds. In that context, the possible presence of large areas of the atmosphere which remain always in a temperature regime appropriate to liquid water, which are thermally isolated from and exchange material slowly with the rest of the atmosphere, provides much fodder for speculation, and a great deal of motivation for continued inquiry as atmospheric models become increasingly sophisticated.
Acknowledgements
The code used in this research employs the the spherical harmonic transforms included in the SPHEREPACK library, made available by UCAR. We acknowledge support from the United States NSF CAREER Grant AST-0449986, and from the NASA Planetary Geology and Geophysics Program through Grant NNG04GK19G.
- Burrows, A., Sudarsky,
D., & Hubeny, I. 2006, ApJ, 650, 1140 [NASA ADS] [CrossRef]
- Butler, R. P.,
Wright, J. T., Marcy, G. W., et al. 2006, ApJ, 646, 505 [NASA ADS] [CrossRef]
- Charbonneau, D., Brown,
T. M., Noyes, R. W., & Gilliland, R. L. 2002,
ApJ, 568, 377 [NASA ADS] [CrossRef]
- Charbonneau, D., Allen,
L. E., Megeath, S. T., et al. 2005, ApJ, 626, 523 [NASA ADS] [CrossRef]
- Cho, J. Y.-K.,
Menou, K., Hansen, B. M. S., & Seager, S. 2003, ApJ,
587, L117 [NASA ADS] [CrossRef]
- Cho, J. Y.-K.,
Menou, K., Hansen, B. M. S., & Seager, S. 2007
[arXiv:astro-ph/0607338v2]
- Cochran, W. D.,
Endl, M., McArthur, B., et al. 2004, ApJ, 611, L133 [NASA ADS] [CrossRef]
(In the text)
- Cooper, C. S., &
Showman, A. P. 2005, ApJ, 629, L45 [NASA ADS] [CrossRef]
- Deming, D., Seager, S.,
Richardson, L. J., et al. 2005, Nature, 434, 740 [NASA ADS] [CrossRef]
- Deming, D., Harrington,
J., Seager, S., et al. 2006, ApJ, 644, 560 [NASA ADS] [CrossRef]
- Dobbs-Dixon, I., &
Lin, D. N. C. 2007 [arXiv:0704.3269]
- Fortney, J. J.,
Cooper, C. S., Showman, A. P., Marley, M. S., &
Freedman, R. S. 2006, ApJ, 652, 746 [NASA ADS] [CrossRef]
- Harrington, J., Hansen,
B. M., Luszcz, S. H., et al. 2006, Science, 314,
623 [NASA ADS] [CrossRef]
- Harrington, J., Luszcz,
S., Seager, S., Deming, D., & Richardson, L. J. 2007,
Nature, 447, 691 [NASA ADS] [CrossRef]
- Ivanov, P. B., &
Papaloizou, J. C. B. 2007, MNRAS, 376, 682 [NASA ADS] [CrossRef]
- Knutson, H. A.,
Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447,
183 [NASA ADS] [CrossRef]
- Langton, J., &
Laughlin, G. 2007, ApJ, 657, L113 [NASA ADS] [CrossRef]
- Langton, J., &
Laughlin, G. 2008, ApJ, 674, 1106 [NASA ADS] [CrossRef]
(In the text)
- Hut, P. 1981, A&A,
99, 126 [NASA ADS]
(In the text)
- Iro, N., Be'zard, B.,
& Guillot, T. 2005, A&A, 436, 719 [NASA ADS] [CrossRef] [EDP Sciences]
- Rowe, J. F.,
et al. 2007 [arXiv:0711.4111]
(In the text)
- Showman, A. P., &
Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences]
- Sudarsky, D., Burrows,
A., Hubeny, I., & Li, A. 2005, ApJ, 627, 520 [NASA ADS] [CrossRef]
(In the text)
- Udry, S., Fischer, D.,
& Queloz, D. 2007, Protostars and Planets V, 685 [NASA ADS]
Copyright ESO 2008
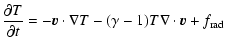
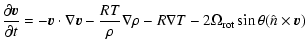
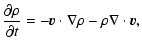
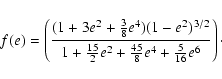
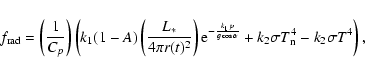
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9417f1.eps}\end{figure}](/articles/aa/full/2008/21/aa09417-08/Timg21.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{9417f2.eps}\end{figure}](/articles/aa/full/2008/21/aa09417-08/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9417f3.eps}\end{figure}](/articles/aa/full/2008/21/aa09417-08/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{9417f4.eps}\end{figure}](/articles/aa/full/2008/21/aa09417-08/Timg24.gif)