A&A 483, 461-469 (2008)
DOI: 10.1051/0004-6361:20078922
Gaussian decomposition of H I surveys
IV. Galactic intermediate- and high-velocity clouds
U. Haud
Tartu Observatory, 61602 Tõravere, Tartumaa, Estonia
Received 25 October 2007 / Accepted 22 January 2008
Abstract
Context. Traditionally intermediate- (IVC) and high-velocity hydrogen clouds (HVC) were defined to be concentrations of H I gas, with line-of-sight velocities that are inconsistent with data on the differential rotation of the Galaxy.
Aims. We attempt to demonstrate that IVCs and HVCs can be identified from density enhancements in parameter distributions of Galactic H I 21 cm radio lines.
Methods. To investigate the properties of the 21 cm radio lines, the profiles of ``The Leiden/Argentine/Bonn (LAB) Survey of Galactic H I'' are decomposed into Gaussian components using a fully automatic algorithm. We focus on some regions with an increased number of Gaussians in phase space, defined by the component central velocity (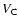 )
and the full width at the level of half maximum (FWHM). To separate the Gaussians responsible for the phase-space density enhancements, we model the width distributions of Gaussian components at equally-populated velocity intervals, using lognormal distributions.
)
and the full width at the level of half maximum (FWHM). To separate the Gaussians responsible for the phase-space density enhancements, we model the width distributions of Gaussian components at equally-populated velocity intervals, using lognormal distributions.
Results. We study the Gaussians, which parameters fall into the regions of the phase-space density enhancements at
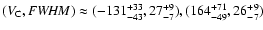 and
and
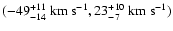 ,
where the indexes indicate the half widths at the level of half maximum (HWHM) of the enhancements. The sky distribution of the Gaussians, corresponding to the first two concentrations, very well represents the sky distribution of HVCs, as obtained on the basis of the traditional definition of these objects. The Gaussians of the last concentration correspond to IVCs. Based on this identification, the division line between IVCs and HVCs can be drawn at about
,
where the indexes indicate the half widths at the level of half maximum (HWHM) of the enhancements. The sky distribution of the Gaussians, corresponding to the first two concentrations, very well represents the sky distribution of HVCs, as obtained on the basis of the traditional definition of these objects. The Gaussians of the last concentration correspond to IVCs. Based on this identification, the division line between IVCs and HVCs can be drawn at about
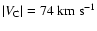 ,
and IVCs can be identified down to velocities of about
,
and IVCs can be identified down to velocities of about
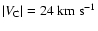 .
Traces of both IVCs and HVCs can also be seen in the sky distribution of Gaussians with
.
Traces of both IVCs and HVCs can also be seen in the sky distribution of Gaussians with
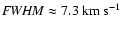 .
In HVCs, these cold cores have small angular dimensions and low observed brightness temperatures
.
In HVCs, these cold cores have small angular dimensions and low observed brightness temperatures 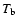 .
In IVCs, the cores are both larger and brighter.
.
In IVCs, the cores are both larger and brighter.
Conclusions. When neglecting the general decrease in the amount of gas at higher
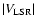 ,
the IVCs and HVCs are observed as distinctive maxima in the
,
the IVCs and HVCs are observed as distinctive maxima in the
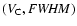 distribution of the Gaussians, representing the structure of the 21 cm radio lines of the Galactic H I. This definition is less dependant than the traditional one, on the differential rotation model of the Galaxy. The consideration of line-width information may enable IVCs and HVCs to be better distinguished from each other, and from the ordinary Galactic H I.
distribution of the Gaussians, representing the structure of the 21 cm radio lines of the Galactic H I. This definition is less dependant than the traditional one, on the differential rotation model of the Galaxy. The consideration of line-width information may enable IVCs and HVCs to be better distinguished from each other, and from the ordinary Galactic H I.
Key words: ISM: atoms - ISM: clouds - radio lines: ISM
In historical reviews, Wakker (2004) and Wakker et al.
(2004) state that early surveys of high-velocity
H I clouds (HVCs), completed in The Netherlands, were
concentrated at high Galactic latitudes, where normal disc gas has
a low velocity. Velocities were reported relative to the Local
Standard of Rest (LSR), using a limit of
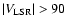 or
or
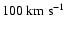 to define HVCs. During the course of
these surveys, gas at velocities between -50 and
to define HVCs. During the course of
these surveys, gas at velocities between -50 and
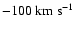 was also found in many different
directions. These objects were called intermediate-velocity clouds
(IVCs). In this situation, a division of tasks was decided upon:
astronomers of Leiden would analyse the high-velocity gas
(
was also found in many different
directions. These objects were called intermediate-velocity clouds
(IVCs). In this situation, a division of tasks was decided upon:
astronomers of Leiden would analyse the high-velocity gas
(
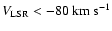 ), while those at
Groningen would concentrate on the IVCs.
), while those at
Groningen would concentrate on the IVCs.
As we can see, the velocity limits in these definitions are
arbitrary, uncertain and partly based on historical arguments. A
more physical approach to distinguishing of HVCs was introduced by
Wakker (1991), who defined the ``deviation velocity'',
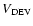 ,
to be the difference between the LSR velocity of
the cloud and the extreme velocity allowed by Galactic
differential rotation in a particular direction. However, de Heij
et al. (2002) presented a slightly different definition of
the deviation velocity, which allows for a Galactic Warp.
,
to be the difference between the LSR velocity of
the cloud and the extreme velocity allowed by Galactic
differential rotation in a particular direction. However, de Heij
et al. (2002) presented a slightly different definition of
the deviation velocity, which allows for a Galactic Warp.
The definition of IVCs has remained uncertain. Albert & Danly
(2004) state that IVCs are dynamically significant gas
with velocities outside the range of the sum of Galactic rotation
and Galactic velocity dispersion, but not as extreme as the
velocities of HVCs. Numerically, they propose the velocity range
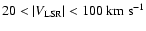 ,
but velocities
below
,
but velocities
below
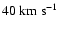 can often be caused by differential
Galactic rotation. Some authors have argued that the division
between HVCs and IVCs, based on the LSR velocity, may be
artificial. However, Wakker (2001) found that IVCs appear
to exist approximately
can often be caused by differential
Galactic rotation. Some authors have argued that the division
between HVCs and IVCs, based on the LSR velocity, may be
artificial. However, Wakker (2001) found that IVCs appear
to exist approximately
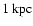 from the Galactic plane,
while HVCs with known distance limits lie at
from the Galactic plane,
while HVCs with known distance limits lie at
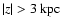 (Wakker 2004).
(Wakker 2004).
![\begin{figure}
\par\includegraphics[width=12cm,clip]{color/8922fig1.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg30.gif) |
Figure 1:
Distribution of Gaussian parameters in the
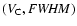 plane. The x-axis is linear
for the queue numbers of the Gaussians in the ascending
sequence of the component velocities. The corresponding
velocity scale is stretched around
plane. The x-axis is linear
for the queue numbers of the Gaussians in the ascending
sequence of the component velocities. The corresponding
velocity scale is stretched around
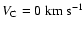 and compressed at higher velocities.
To illustrate this, the ticks on the x-axis are drawn at
-450, -184, -117, -94, -75, -63, -54, -47,
-41, -35, -30.1, -25.6, -21.8, -18.5, -15.6,
-13.3, -11.4, -9.9, -8.6, -7.6, -6.7, -5.8,
-5.0, -4.3, -3.6, -3.00, -2.38, -1.78, -1.18,
-0.57, 0.00, 0.56, 1.14, 1.71, 2.29, 2.89, 3.6, 4.3, 5.1,
5.9, 6.9, 7.9, 9.2, 10.7, 12.5, 14.9, 17.9, 21.9, 27.1, 34,
43, 54, 65, 79, 95, 121, 206 and
and compressed at higher velocities.
To illustrate this, the ticks on the x-axis are drawn at
-450, -184, -117, -94, -75, -63, -54, -47,
-41, -35, -30.1, -25.6, -21.8, -18.5, -15.6,
-13.3, -11.4, -9.9, -8.6, -7.6, -6.7, -5.8,
-5.0, -4.3, -3.6, -3.00, -2.38, -1.78, -1.18,
-0.57, 0.00, 0.56, 1.14, 1.71, 2.29, 2.89, 3.6, 4.3, 5.1,
5.9, 6.9, 7.9, 9.2, 10.7, 12.5, 14.9, 17.9, 21.9, 27.1, 34,
43, 54, 65, 79, 95, 121, 206 and
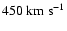 .
The y-axis is logarithmic in FWHM. The contour lines are
drawn at the levels of 1, 3, 7, 15, 35, 60, 90, 115, 145,
170, 195, 225, 250, 280, 315, 355, 395, and 445 Gaussians per
counting bin. The frequency enhancements, discussed in the
text, are marked with blue circles. .
The y-axis is logarithmic in FWHM. The contour lines are
drawn at the levels of 1, 3, 7, 15, 35, 60, 90, 115, 145,
170, 195, 225, 250, 280, 315, 355, 395, and 445 Gaussians per
counting bin. The frequency enhancements, discussed in the
text, are marked with blue circles. |
| Open with DEXTER |
The situation with HVCs and IVCs is further complicated by the
fact that the gas with a velocity, which is dynamically unusual or
significant in its local or Galactic frame, may appear close to
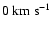 with respect to the LSR. Therefore, it may
be interesting to define these objects in way that is not based
only on models of Galactic differential rotation. In this paper we
try to identify both IVCs and HVCs using the frequency
distribution of the Gaussian component parameters, derived in the
decomposition of the Leiden/Argentine/Bonn (LAB) full sky database
of H I profiles (Kalberla et al. 2005).
with respect to the LSR. Therefore, it may
be interesting to define these objects in way that is not based
only on models of Galactic differential rotation. In this paper we
try to identify both IVCs and HVCs using the frequency
distribution of the Gaussian component parameters, derived in the
decomposition of the Leiden/Argentine/Bonn (LAB) full sky database
of H I profiles (Kalberla et al. 2005).
A detailed justification for the use of Gaussian decomposition, in
such a study, was provided by Haud & Kalberla (2007,
hereafter Paper III). The program that decomposes data from large
21 cm H I line surveys into Gaussian components, was
described in the first paper of this series (Haud 2000,
hereafter Paper I). The observational data for decomposition are
from the LAB database of H I 21 cm line profiles, which
combines the new revision (LDS2, Kalberla et al. 2005) of
the Leiden/Dwingeloo Survey (LDS, Hartmann 1994), and a
similar Southern sky survey (IARS, Bajaja et al. 2005)
completed at the Instituto Argentino de Radioastronomia. The LAB
database is described in detail by Kalberla et al. (2005).
Our method of Gaussian decomposition generated 1 064 808
Gaussians for 138 830 profiles from LDS2, and 444 573 Gaussians
for 50 980 profiles from IARS.
In Paper II (Haud & Kalberla 2006), we analysed the
distributions of the parameters of the obtained Gaussians. We
focused mainly on the separation of the components describing
different artefacts of the observations (interferences), reduction
(baseline problems) and the decomposition (separation of signal
from noise) process. In Paper III, we introduced the study of the
width distributions of the Gaussian components at
equally-populated velocity intervals, and demonstrated that for
Gaussians with relatively small LSR velocities (
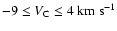 )
it is possible to
distinguish three or four groups of preferred line widths. The
mean widths of these groups are
)
it is possible to
distinguish three or four groups of preferred line widths. The
mean widths of these groups are
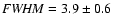 ,
,
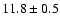 ,
,
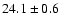 ,
and
,
and
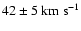 .
In the present paper, we continue the
analysis of the distribution of the Gaussian parameters, but focus
on the components with the central LSR velocities
.
In the present paper, we continue the
analysis of the distribution of the Gaussian parameters, but focus
on the components with the central LSR velocities
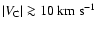 .
We demonstrate that some frequency
enhancements in this region define two classes of objects whose
general properties are similar to those of the IVCs and HVCs,
defined by more traditional velocity criteria.
.
We demonstrate that some frequency
enhancements in this region define two classes of objects whose
general properties are similar to those of the IVCs and HVCs,
defined by more traditional velocity criteria.
In Paper III, we introduced the diagram (Fig. 2. of Paper III) of
the frequency distributions of Gaussian component widths at
equally-populated velocity intervals. We define the Gaussians by
the standard formula
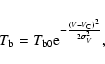 |
(1) |
where 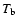 is the brightness temperature, and V is the
velocity of the gas relative to the Local Standard of Rest.
is the brightness temperature, and V is the
velocity of the gas relative to the Local Standard of Rest.
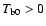 is the height of the Gaussian at its central
velocity
is the height of the Gaussian at its central
velocity 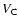 .
We characterise the widths of the
components by their full width at the level of half maximum
(FWHM), which is related to the velocity dispersion
.
We characterise the widths of the
components by their full width at the level of half maximum
(FWHM), which is related to the velocity dispersion 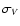 ,
obtained from our decomposition program, by a simple scaling
relation
,
obtained from our decomposition program, by a simple scaling
relation
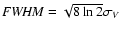 .
.
Because the Gaussian functions fitted to the complex H I profiles, close to the Galactic plane, cannot be directly
interpreted in terms of the properties of gas clouds, in Paper III
we focused on the higher Galactic latitudes, and stressed the
differences in the
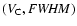 frequency
distribution of Gaussians at different latitudes. In this paper,
we concentrate on higher velocities, where differences in the
distributions for different latitude ranges are smaller, and
therefore present, in Fig. 1, the distribution of
Gaussians for all Galactic latitudes. To construct this figure, we
arranged all Gaussians with central velocities in the
decomposition range (
frequency
distribution of Gaussians at different latitudes. In this paper,
we concentrate on higher velocities, where differences in the
distributions for different latitude ranges are smaller, and
therefore present, in Fig. 1, the distribution of
Gaussians for all Galactic latitudes. To construct this figure, we
arranged all Gaussians with central velocities in the
decomposition range (
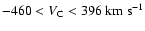 in the LDS2 and
in the LDS2 and
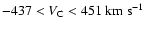 in the IARS; for details see Papers I and II), in ascending order of their
in the IARS; for details see Papers I and II), in ascending order of their 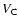 .
We then grouped
the sequence into 129 bins of an equal number of Gaussians,
rejecting some Gaussians with the most extreme velocities. We
binned the line widths in equal steps of
.
We then grouped
the sequence into 129 bins of an equal number of Gaussians,
rejecting some Gaussians with the most extreme velocities. We
binned the line widths in equal steps of
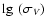 of 0.025.
The isolines in Fig. 1 provide the number of Gaussians
at each of such two-dimensional parameter interval.
of 0.025.
The isolines in Fig. 1 provide the number of Gaussians
at each of such two-dimensional parameter interval.
In Fig. 1, the region most densely populated by
Gaussians, lies in the lower part of the figure at relatively
small LSR velocities. In Paper III, we demonstrated that most of
these Gaussians represent the cold neutral medium of the Galactic
disc. In the present figure, this low-velocity region is also
seriously contaminated by Gaussians from the strongest H I profiles, close to the Galactic plane, parameters of which are not
directly related to the properties of the real gas. At somewhat
higher negative velocities (from
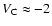 to
to
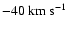 )
and larger line widths (from
)
and larger line widths (from
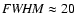 to
to
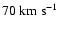 ), we can
see an elongated region of high Gaussian density. We will not
discuss this feature in the present paper. At even higher negative
velocities in Fig. 1, we can see two high-density
regions centred at
), we can
see an elongated region of high Gaussian density. We will not
discuss this feature in the present paper. At even higher negative
velocities in Fig. 1, we can see two high-density
regions centred at
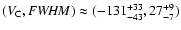 and
and
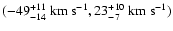 (the largest blue circles in
Fig. 1). Here the indexes of the values of the
velocities and line widths provide estimates of the half widths of
the corresponding distributions at the level of half maximum. At
positive velocities, only one such frequency enhancement is
clearly visible about
(the largest blue circles in
Fig. 1). Here the indexes of the values of the
velocities and line widths provide estimates of the half widths of
the corresponding distributions at the level of half maximum. At
positive velocities, only one such frequency enhancement is
clearly visible about
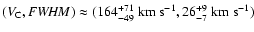 .
These enhancements contain the
Gaussians of our main interest in the present paper. At even
higher negative and positive velocities, two concentrations of
narrow Gaussians are clearly visible (at the bottom corners of the
figure). These are generated by the presence of spurious
Gaussians, as discussed in Paper II.
.
These enhancements contain the
Gaussians of our main interest in the present paper. At even
higher negative and positive velocities, two concentrations of
narrow Gaussians are clearly visible (at the bottom corners of the
figure). These are generated by the presence of spurious
Gaussians, as discussed in Paper II.
In Paper III, we demonstrated that, for Gaussians with relatively
small LSR velocities, it is possible to distinguish three or four
groups of preferred line widths. Similar line-width groups appear
to exist at higher velocities, but their mean widths depend on the
velocity of the selected Gaussians, and only in relatively small
velocity intervals, we can consider the line-width distributions
to be nearly independent of the central velocity of the Gaussians.
Therefore, we must require a separate model of the width
distribution, for each equally-populated velocity interval. Only
this would make it possible to distinguish between components,
belonging to different line-width groups.
As in the case of lower velocities, we model all the width
distributions with a sum of lognormal functions defined by
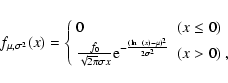 |
(2) |
where f0, 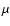 and
and 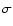 may be considered as free
parameters for fitting the model distribution to the observed one.
As in Paper III, we used, in most cases, four lognormal functions
for each modelled velocity interval. Only at the highest positive
and negative velocities, we introduced an additional lognormal to
reject the spurious Gaussians, causing the enhancements at the
lower corners of Fig. 1.
may be considered as free
parameters for fitting the model distribution to the observed one.
As in Paper III, we used, in most cases, four lognormal functions
for each modelled velocity interval. Only at the highest positive
and negative velocities, we introduced an additional lognormal to
reject the spurious Gaussians, causing the enhancements at the
lower corners of Fig. 1.
Many different density functions are available that can model the
distributions of Gaussian widths, which are defined to be
positive. We chose to use the lognormal function because its usage
is technically convenient: if a parameter is distributed according
to the lognormal law, the distribution of the logarithms of the
parameter is described by a Gaussian. Mebold (1972) also
argued that his narrow and shallow components could be identified
most easily, when the line-width distribution is studied in a
logarithmic scale. Moreover, from all tested density functions,
the lognormal provided the best fits.
The described modelling was relatively easy for the negative
velocity part of the distribution in Fig. 1, but more
ambiguous for positive velocities, as there the number of
Gaussians is smaller, equally-populated velocity intervals are
wider, and the density maxima are less obvious. At the same time,
it can be seen from Fig. 1 that the general structure of
the distribution is similar for negative and positive velocities.
The enhancements are weaker at positive velocities, but we may
find that these weaker maxima are at approximately the same
positions as for negative velocities: a strong enhancement at
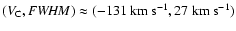 corresponds to a weaker one at
corresponds to a weaker one at
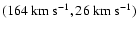 ,
and a weaker
enhancement at
,
and a weaker
enhancement at
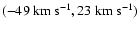 corresponds to an even weaker one at about
corresponds to an even weaker one at about
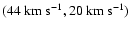 .
Therefore, to
consider the positive velocity information, we decided to average
the positive and negative velocity sides of the distribution
(Fig. 2a), and to construct the same model for the
positive and negative velocities (Fig. 2b).
.
Therefore, to
consider the positive velocity information, we decided to average
the positive and negative velocity sides of the distribution
(Fig. 2a), and to construct the same model for the
positive and negative velocities (Fig. 2b).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig2.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg59.gif) |
Figure 2:
Symmetrised distribution of Gaussian parameters in the
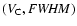 plane a) and the
corresponding model distribution b). The contour lines are
obtained in the same way as in Fig. 1. The ticks
on the x-axis are drawn at 0.00,
plane a) and the
corresponding model distribution b). The contour lines are
obtained in the same way as in Fig. 1. The ticks
on the x-axis are drawn at 0.00,  0.54, 0.54,  1.10, 1.10,
 1.66, 1.66,  2.22, 2.22,  2.79, 2.79,  3.4, 3.4,  4.1, 4.1,
 4.7, 4.7,  5.5, 5.5,  6.3, 6.3,  7.2, 7.2,  8.2, 8.2,  9.3, 9.3,  10.8, 10.8,  12.4, 12.4,  14.5, 14.5,  17.1, 17.1,  20.3, 20.3,  24.2, 24.2,  28.9, 28.9,  35, 35,  41, 41,  49, 49,
 57, 57,  67, 67,  80, 80,  98, 98,  122, 122,  203 and 203 and 
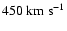 .
The vertical blue lines
indicate the range of modelling .
The vertical blue lines
indicate the range of modelling
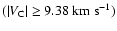 ,
the thick black lines mark the
run of the peaks of the two line-width groups and the dashed
lines on both sides of the thick lines give the extent of
the regions, where the Gaussians belong respectively to
group 1 or 2 with the probability higher than 75%. ,
the thick black lines mark the
run of the peaks of the two line-width groups and the dashed
lines on both sides of the thick lines give the extent of
the regions, where the Gaussians belong respectively to
group 1 or 2 with the probability higher than 75%. |
| Open with DEXTER |
During the modelling, we encountered one additional problem. When
the values of f0 and 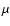 for lognormal distributions were
well determined, the values of
for lognormal distributions were
well determined, the values of 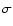 of different lognormal
functions were often strongly correlated with each other. This
occasionally meant that the
of different lognormal
functions were often strongly correlated with each other. This
occasionally meant that the 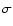 of the same line-width
component, had very different values for neighbouring velocity
intervals. Numerically, when the mean uncertainties in fitting
f0 and
of the same line-width
component, had very different values for neighbouring velocity
intervals. Numerically, when the mean uncertainties in fitting
f0 and 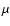 were 8.6% and 2.5%, respectively, the
corresponding uncertainty in the values of
were 8.6% and 2.5%, respectively, the
corresponding uncertainty in the values of 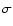 was about
38%. To overcome this problem, we first fitted all width
distributions, considering f0,
was about
38%. To overcome this problem, we first fitted all width
distributions, considering f0, 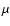 and
and 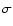 of all
lognormal functions as free parameters. We then analysed the
of all
lognormal functions as free parameters. We then analysed the
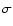 of each line-width component, as a function of the number
of the velocity interval, and applied natural smoothing splines.
In the second run of fitting of the sums of lognormal functions to
the width distributions of Gaussians in different
equally-populated velocity intervals, we replaced the values of
of each line-width component, as a function of the number
of the velocity interval, and applied natural smoothing splines.
In the second run of fitting of the sums of lognormal functions to
the width distributions of Gaussians in different
equally-populated velocity intervals, we replaced the values of
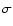 ,
obtained in the first fitting, with the results of the
smoothing, and kept the values of
,
obtained in the first fitting, with the results of the
smoothing, and kept the values of 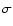 fixed while iterating
f0 and
fixed while iterating
f0 and 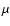 .
The resulting model distribution is provided in
Fig. 2b. We are not interested in velocities close to
zero, which were discussed in Paper III. The modelling was
performed only for
.
The resulting model distribution is provided in
Fig. 2b. We are not interested in velocities close to
zero, which were discussed in Paper III. The modelling was
performed only for
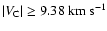 ,
indicated in Fig. 2b with blue vertical lines.
,
indicated in Fig. 2b with blue vertical lines.
After defining line-width groups of Gaussians using different
lognormal functions, it is interesting to find out how these
groups are related to actual gas within and about the Galaxy. To
study this question, we need to determine which Gaussian belongs
to which line-width group. The frequency distributions of
Gaussians of different groups, however, overlap considerably and
we are unable to identify with full confidence the Gaussians
belonging to any particular group. However, using our model
distribution, we can estimate for every Gaussian the probability
of belonging to some particular line-width group.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig3.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg64.gif) |
Figure 3:
Sky distribution in Galactic coordinates of the
Gaussians, belonging to the second line-width group at
velocities
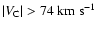 a) and
the brightness of the high-velocity hydrogen clouds from the
Hulsbosch & Wakker (1988) and Morras et al.
(2000) surveys b). The labels with capital letters
indicate the larger HVC complexes according to Wakker
(2004). In the upper panel the colours encode the
values of
a) and
the brightness of the high-velocity hydrogen clouds from the
Hulsbosch & Wakker (1988) and Morras et al.
(2000) surveys b). The labels with capital letters
indicate the larger HVC complexes according to Wakker
(2004). In the upper panel the colours encode the
values of
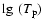 .
In the lower panel the same colour
scale corresponds to the logarithms of the brightness
temperatures of the HVC detections. In both panels near the
Galactic plane the strongest Gaussians with .
In the lower panel the same colour
scale corresponds to the logarithms of the brightness
temperatures of the HVC detections. In both panels near the
Galactic plane the strongest Gaussians with 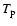 or
or
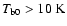 are not plotted.
are not plotted. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig4.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg65.gif) |
Figure 4:
Same as Fig. 3, but the colours represent
the LSR velocities of the gas. |
| Open with DEXTER |
So, let us define the probability that a Gaussian belongs to the
line-width group i as
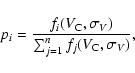 |
(3) |
where fi is the density function of the lognormal distribution,
as defined by Eq. (2), corresponding to the ith
line-width group, 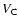 is the central velocity, and
is the central velocity, and
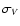 the width of the particular Gaussian and n = 4 or 5,
depending on the velocity interval under consideration. To study
the sky distribution of the Gaussians from the selected line-width
group i, we can then plot
the width of the particular Gaussian and n = 4 or 5,
depending on the velocity interval under consideration. To study
the sky distribution of the Gaussians from the selected line-width
group i, we can then plot
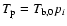 ,
the
heights of Gaussians
,
the
heights of Gaussians
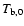 ,
multiplied by the
probability that the Gaussian belongs to this line-width group
pi. In this way, all the Gaussians from our decomposition will
be presented on each plot. However, the brightness of the
Gaussians, for which the probability of belonging to a particular
line-width group is low, is suppressed considerably by these small
probabilities. To enhance the contrast in plots even more, and
because the noise level of the LAB Survey is about
,
multiplied by the
probability that the Gaussian belongs to this line-width group
pi. In this way, all the Gaussians from our decomposition will
be presented on each plot. However, the brightness of the
Gaussians, for which the probability of belonging to a particular
line-width group is low, is suppressed considerably by these small
probabilities. To enhance the contrast in plots even more, and
because the noise level of the LAB Survey is about
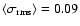 K (see Paper II), we also do
not plot Gaussians for which
K (see Paper II), we also do
not plot Gaussians for which
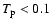 K. In this way we
exclude, from the sky plots, most of the weak Gaussians, which
represent the survey baseline problems. Stronger spurious
Gaussians are excluded, according to the criteria described in
Paper II.
K. In this way we
exclude, from the sky plots, most of the weak Gaussians, which
represent the survey baseline problems. Stronger spurious
Gaussians are excluded, according to the criteria described in
Paper II.
As stated in the previous section, we are mostly interested in
frequency enhancements in Fig. 1, which are centred at
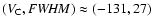 ,
(-49, 23),
(44, 20) and
,
(-49, 23),
(44, 20) and
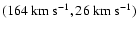 .
In our model, these enhancements
correspond to the line-width group 2 as labelled in
Fig. 2b. As can be seen from Fig. 1, at
negative velocities this line-width group clearly forms two
frequency enhancements in different velocity regions. These
frequency enhancements are separated by the region, more dominated
by Gaussians of other line-width groups, and the second group has
a frequency minimum at about
.
In our model, these enhancements
correspond to the line-width group 2 as labelled in
Fig. 2b. As can be seen from Fig. 1, at
negative velocities this line-width group clearly forms two
frequency enhancements in different velocity regions. These
frequency enhancements are separated by the region, more dominated
by Gaussians of other line-width groups, and the second group has
a frequency minimum at about
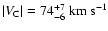 .
The same appears to be true for
positive velocities, but there the picture is considerably less
clear.
.
The same appears to be true for
positive velocities, but there the picture is considerably less
clear.
We concentrate first on Gaussians of the second line-width group
with
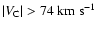 .
Figure 3a
illustrates the sky distribution of brightness temperatures of
these components, and Fig. 4a provides the distribution
of LSR velocities for the same Gaussians. In Fig. 3b, we
present the sky distribution of brightness temperatures of HVCs
with
.
Figure 3a
illustrates the sky distribution of brightness temperatures of
these components, and Fig. 4a provides the distribution
of LSR velocities for the same Gaussians. In Fig. 3b, we
present the sky distribution of brightness temperatures of HVCs
with
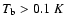 as compiled from Hulsbosch & Wakker
(1988) and Morras et al. (2000) catalogues, and
Fig. 4b provides their velocity distribution. Comparing
the panels of these figures, a surprising similarity is visible
between the distributions for the objects, selected from different
observational data by different procedures.
as compiled from Hulsbosch & Wakker
(1988) and Morras et al. (2000) catalogues, and
Fig. 4b provides their velocity distribution. Comparing
the panels of these figures, a surprising similarity is visible
between the distributions for the objects, selected from different
observational data by different procedures.
The HVC catalogues by Hulsbosch & Wakker (1988) and
Morras et al. (2000) are based on H I profiles with
a velocity resolution of about
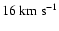 and a
noise level of about
and a
noise level of about
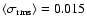 K. All the observed profiles were scanned visually for the
presence of components at high velocities, using two selection
criteria: the component should have a brightness temperature
K. All the observed profiles were scanned visually for the
presence of components at high velocities, using two selection
criteria: the component should have a brightness temperature
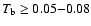 K and should have
K and should have
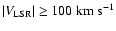 or
or
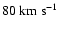 .
Figures 3a and 4a are based on the LAB Survey,
which has a velocity resolution of about
.
Figures 3a and 4a are based on the LAB Survey,
which has a velocity resolution of about
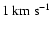 ,
and a noise level of about 0.09 K. Both figures were made without
any visual inspection of the profiles, using statistical data for
Gaussians (mostly
,
and a noise level of about 0.09 K. Both figures were made without
any visual inspection of the profiles, using statistical data for
Gaussians (mostly
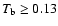 K) obtained in a fully
automatic decomposition of the survey profiles. In our study the
first selection criterion was the line width, which was not
directly used by Hulsbosch & Wakker (1988) and Morras et al. (2000). Nevertheless, all well-known HVC complexes are
clearly visible in both figures.
K) obtained in a fully
automatic decomposition of the survey profiles. In our study the
first selection criterion was the line width, which was not
directly used by Hulsbosch & Wakker (1988) and Morras et al. (2000). Nevertheless, all well-known HVC complexes are
clearly visible in both figures.
Besides the differences, described above, there is a selection
criterion almost in common for panels a and b of Figs. 3
and 4 - the velocity range. For panels a of these
figures, we have used Gaussians with
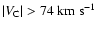 .
Figures 3b and 4b
represent the gas with
.
Figures 3b and 4b
represent the gas with
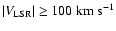 or
or
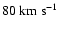 .
It is
possible that the similarity of these velocity limits is the main
factor that determines the similarity of the sky distributions.
However, in this case, Figs. 3a and 4a must
remain unchanged if we keep the velocity limits, defined above,
but instead of Gaussians from line-width group 2, use those from
some other group (number 1, for example). The actual results do
not confirm this expectation. The sky distribution of the
Gaussians of the first line-width group (Fig. 5a) is
different from that of the second line-width group
(Fig. 3a). The well-populated HVC complexes are no
longer visible. In Fig. 5a, only small concentrations of
weak dots are observed in the regions, which in Fig. 3a
are populated by the largest HVC complexes.
.
It is
possible that the similarity of these velocity limits is the main
factor that determines the similarity of the sky distributions.
However, in this case, Figs. 3a and 4a must
remain unchanged if we keep the velocity limits, defined above,
but instead of Gaussians from line-width group 2, use those from
some other group (number 1, for example). The actual results do
not confirm this expectation. The sky distribution of the
Gaussians of the first line-width group (Fig. 5a) is
different from that of the second line-width group
(Fig. 3a). The well-populated HVC complexes are no
longer visible. In Fig. 5a, only small concentrations of
weak dots are observed in the regions, which in Fig. 3a
are populated by the largest HVC complexes.
This result becomes understandable in the light of the discussion
by Kalberla & Haud (2006): most of the high-velocity
clouds have a well-defined two-component structure, where the cold
HVC phase has a typical line-width of about
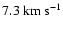 ,
and exists only within more extended
broad-line regions, typically with
,
and exists only within more extended
broad-line regions, typically with
 .
Therefore, we may state that the
modelling of the line-width distribution of Gaussians permits us
to separate the warm and cold gas phases in HVCs, as it was also
possible for the local H I gas. However, for the local gas
the corresponding line widths were
.
Therefore, we may state that the
modelling of the line-width distribution of Gaussians permits us
to separate the warm and cold gas phases in HVCs, as it was also
possible for the local H I gas. However, for the local gas
the corresponding line widths were
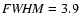 and
and
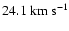 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig5.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg85.gif) |
Figure 5:
Same as Fig. 3a, but for the line-width
group 1 a) and for all Gaussians, except those belonging to
the line-width groups 1 and 2 b). |
| Open with DEXTER |
There are still Gaussians belonging neither to line-width
component 1 nor to component 2. Their sky distribution is given in
Fig. 5b. This figure shares the same velocity limit as
Figs. 3a and 5a, but here we can see only
rather weak traces of all HVC structures. Of course, it would be
nice, if in this figure there were no traces of HVCs at all, but
we must remember that the separation of the Gaussians into
different line-width groups is only statistical and the
probabilities are determined from the smoothed model. It seems
that this model has worked most badly for some parts of the
Magellanic Stream.
Besides the similarities between Figs. 3a and b, there are also considerable differences. The most
obvious one is the presence in Fig. 3a of a large number
of strong Gaussians, close to the Galactic plane and in the region
of the Magellanic Clouds. However, close to the Galactic plane the
Gaussians are obtained from the decomposition of very complex
H I profiles of the Galactic disc, in which the real gas
structures are heavily blended with each other; these Gaussians
should therefore not be considered as directly representing the
properties of the ISM. The same regions are heavily populated in
both panels of Fig. 5. In these regions, the
decomposition provides the Gaussians of all possible parameters,
and without any concentration of these parameter values in any
region of parameter space. In Fig. 1, these Gaussians
form the general background against which we may distinguish the
features, more directly representing the properties of Galactic
H I. The same holds also for the main bodies of the
Magellanic Clouds.
As we can estimate from the comparison of different sky
distribution figures, close to the Galactic plane, the region of
``confusion'' lies generally at
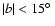 .
Above this
latitude limit, the distribution of Gaussians appears to be
representative of the properties of HVCs. This is of particular
importance for the Outer Arm Cloud (OAC). In early studies (Habing
1966; Hulsbosch & Wakker 1988), this complex was
considered to be an HVC. Verschuur (1975) and Haud
(1992) have modelled the complex as part of the outer disc
of the Milky Way. Based on the deviation velocity, a recent review
(Wakker 2004) considers the OAC to be an
intermediate-velocity cloud. From a statistical analysis of the
Gaussian parameters, we are unable to conclude much about the OAC
close to the Galactic plane. In the parts most distant from the
galactic plane however, the gas properties appear to agree with
the gas properties in HVCs.
.
Above this
latitude limit, the distribution of Gaussians appears to be
representative of the properties of HVCs. This is of particular
importance for the Outer Arm Cloud (OAC). In early studies (Habing
1966; Hulsbosch & Wakker 1988), this complex was
considered to be an HVC. Verschuur (1975) and Haud
(1992) have modelled the complex as part of the outer disc
of the Milky Way. Based on the deviation velocity, a recent review
(Wakker 2004) considers the OAC to be an
intermediate-velocity cloud. From a statistical analysis of the
Gaussian parameters, we are unable to conclude much about the OAC
close to the Galactic plane. In the parts most distant from the
galactic plane however, the gas properties appear to agree with
the gas properties in HVCs.
In conclusion, we note that two different approaches to
identifying high-velocity H I gas at high Galactic
latitudes (
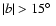 ), have produced remarkably similar
results. We cannot, of course, consider these methods to be
completely independent ones. The classical definition of HVCs is
fully based on their LSR velocities, and the model of differential
rotation of the Galactic disc. The horizontal structure of
Fig. 1 is largely determined by the Galactic
differential rotation as well, but a comparison of
Figs. 3a, 5a and 5b demonstrates
that velocity is not the only factor that defines HVCs. Moreover,
when using the statistical distribution of Gaussian parameters, we
can estimate the extent of the velocity and line-width intervals
populated by the components, which most likely represent HVCs.
Unfortunately, the analysis becomes complicated and unreliable,
when approaching the Galactic plane, where the classic definition
of HVCs also has the greatest trouble.
), have produced remarkably similar
results. We cannot, of course, consider these methods to be
completely independent ones. The classical definition of HVCs is
fully based on their LSR velocities, and the model of differential
rotation of the Galactic disc. The horizontal structure of
Fig. 1 is largely determined by the Galactic
differential rotation as well, but a comparison of
Figs. 3a, 5a and 5b demonstrates
that velocity is not the only factor that defines HVCs. Moreover,
when using the statistical distribution of Gaussian parameters, we
can estimate the extent of the velocity and line-width intervals
populated by the components, which most likely represent HVCs.
Unfortunately, the analysis becomes complicated and unreliable,
when approaching the Galactic plane, where the classic definition
of HVCs also has the greatest trouble.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig6.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg89.gif) |
Figure 6:
Same as Figs. 3a, 5a and 5b, but for the velocity interval
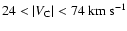 .
a) The sky
distribution of the Gaussians, belonging to the second
line-width group. The solid contour and the labels indicate
the region of major intermediate-velocity gas features
according to Kuntz & Danly (1996) and Wakker
(2001). b) The sky distribution of the Gaussians
belonging to the first line-width group. The circles
indicate the locations of the intermediate-velocity gas
clumps from the catalogue by Kuntz & Danly (1996).
c) The sky distribution of all Gaussians, except the ones
corresponding to the first and second line-width group. .
a) The sky
distribution of the Gaussians, belonging to the second
line-width group. The solid contour and the labels indicate
the region of major intermediate-velocity gas features
according to Kuntz & Danly (1996) and Wakker
(2001). b) The sky distribution of the Gaussians
belonging to the first line-width group. The circles
indicate the locations of the intermediate-velocity gas
clumps from the catalogue by Kuntz & Danly (1996).
c) The sky distribution of all Gaussians, except the ones
corresponding to the first and second line-width group. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig7.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg90.gif) |
Figure 7:
Same as Fig. 6a, but the colours represent
the LSR velocities of the gas. |
| Open with DEXTER |
We have so far considered line-width groups only for velocities
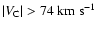 .
There is however,
another maximum at lower velocities, which peaks at
.
There is however,
another maximum at lower velocities, which peaks at
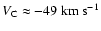 .
The lower velocity limit of this
frequency enhancement is questionable. The concentration about
.
The lower velocity limit of this
frequency enhancement is questionable. The concentration about
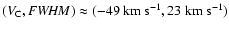 ,
in Fig. 1, reaches its HWHM at
,
in Fig. 1, reaches its HWHM at
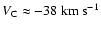 .
The relative
frequency of group-2 Gaussians drops to the level of the minimum
between two peaks in Fig. 2b at about
.
The relative
frequency of group-2 Gaussians drops to the level of the minimum
between two peaks in Fig. 2b at about
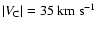 ,
but even after this, group 2 can still
modelled until about
,
but even after this, group 2 can still
modelled until about
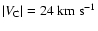 .
At
even lower velocities, the determined parameters of the second
line-width group became rather uncertain, the corresponding
Gaussians are relatively few in number, and we do not discuss
these velocities.
.
At
even lower velocities, the determined parameters of the second
line-width group became rather uncertain, the corresponding
Gaussians are relatively few in number, and we do not discuss
these velocities.
The sky distribution of the Gaussians of the second line-width
group in the intermediate velocity range
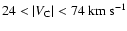 is shown in Fig. 6a. Their
velocity distribution is provided in Fig. 7. In
Fig. 6a, we mark with a thick solid line, the
is shown in Fig. 6a. Their
velocity distribution is provided in Fig. 7. In
Fig. 6a, we mark with a thick solid line, the
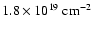 surface density contour of the
intermediate-velocity hydrogen clouds, as published in Fig. 8 of
Kuntz & Danly (1996). Some additional IVC complexes,
identified by Wakker (2001), are also labelled. We see
that, as in the case of HVCs at higher velocities, in the
intermediate velocity range the distribution of Gaussians, from
the second line-width group, closely follows the main features of
the distribution of the IVCs. This indicates that both HVCs and
IVCs appear to represent related features in different velocity
ranges.
surface density contour of the
intermediate-velocity hydrogen clouds, as published in Fig. 8 of
Kuntz & Danly (1996). Some additional IVC complexes,
identified by Wakker (2001), are also labelled. We see
that, as in the case of HVCs at higher velocities, in the
intermediate velocity range the distribution of Gaussians, from
the second line-width group, closely follows the main features of
the distribution of the IVCs. This indicates that both HVCs and
IVCs appear to represent related features in different velocity
ranges.
As for HVCs, in the intermediate velocity range, many Gaussians of
the first line-width group are concentrated in sky regions
populated by IVC gas, of the second line-width group
(Fig. 6b). Among these are Gaussians, for which the
probabilities of belonging to the first or second line-width group
are nearly equal to each other. These Gaussians are plotted both
in Figs. 6a and b. A more detailed
examination of the situation however, indicates that this is not
the only effect. In many sky positions in the region covered by IV
Arches and Spur, the decomposed hydrogen profiles contain
Gaussians from both line-width groups. Altogether the profiles for
36 375 sky positions at
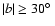 contain Gaussians,
which can be classified with at least 50% confidence to belong to
the first or second line-width group, and of these sky positions,
9015 profiles, or nearly 25%, contain both the Gaussians of the
first and the second line-width group.
contain Gaussians,
which can be classified with at least 50% confidence to belong to
the first or second line-width group, and of these sky positions,
9015 profiles, or nearly 25%, contain both the Gaussians of the
first and the second line-width group.
The comparison of Figs. 6a and b reveals
differences in the properties of the IVC components, corresponding
to the two different line-width groups. When the clouds
corresponding to the first line-width group appear to be brighter
and clumpier, those corresponding to the second line-width group
cover the sky in the regions of IV Arches and Spur more uniformly,
but with smaller average brightness. A similar behaviour by the
intermediate-velocity gas was noted by Kuntz & Danly
(1996), who stated that the bulk of the
intermediate-velocity gas is primarily composed of clumps, which
appear to be surrounded by a lower column density envelope.
In their Table 1, Kuntz & Danly (1996) published the
catalogue of denser clumps, which we have presented in
Fig. 6b as circles centred at the positions of the peak
column densities of the clumps. Unfortunately, the above-mentioned
Table 1 does not contain much information about the shapes and
sizes of the clumps. We therefore plot these objects in
Fig. 6b, as circles of radii proportional to the clump
peak intensities, which are provided by Kuntz & Danly
(1996). As can be seen, the brighter clumps from the
catalogue coincide with the concentrations of Gaussians in our
figure. The correspondence is more problematic for the weakest
clumps (for which the circles have been reduced in size to dots),
but here we must consider that the paper by Kuntz & Danly
(1996) was based on the Bell Laboratories H I survey described by Stark et al. (1992). The rms noise
per channel for this survey was 0.017 K, a value more than 5 times lower than for LDS, such that many of the weakest clumps
detected in these data may not be detected by us. Moreover, the
sampling grid of the Bell Laboratories survey was
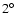 in
declination and about
in
declination and about
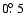 in right ascension, which was
rebinned by Kuntz & Danly (1996) into a regular grid,
comparable to the beam size of about
in right ascension, which was
rebinned by Kuntz & Danly (1996) into a regular grid,
comparable to the beam size of about
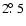 ,
of the horn
reflector used. As a result, the locations of the circles in
Fig. 6b should not be considered to be accurate.
,
of the horn
reflector used. As a result, the locations of the circles in
Fig. 6b should not be considered to be accurate.
Our results appear to confirm that the IVCs have a two-component
structure: brighter clumps, whose emission lines correspond to the
first line-width group; and lower column density envelopes, whose
emission can be described by Gaussians of the second line-width
group. A similar two-component structure is found for HVCs, for
which the velocity profiles are often composed of a broad
(
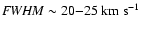 ), and a narrow
(
), and a narrow
(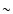
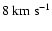 )
component (Wakker & Woerden
1997; mean
)
component (Wakker & Woerden
1997; mean
 and
and
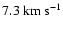 according
to Kalberla & Haud 2006). The corresponding mean line
widths for IVCs, are
according
to Kalberla & Haud 2006). The corresponding mean line
widths for IVCs, are
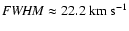 and
and
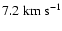 ,
respectively.
,
respectively.
Figure 6c corresponds to Fig. 5b for the high
velocity region and demonstrates that in the sky distribution of
the Gaussians, not belonging to line-width groups 1 or 2, we can
see only weak traces of the IVCs. These traces once again, are
mostly caused by difficult-to-classify, relatively bright
Gaussians, which appear both in Figs. 6a or 6b
and Fig. 6c. Moreover, the visibility of these traces is
enhanced in Fig. 6c, because we do not plot in any sky
distribution, the Gaussians, which are considered to be spurious,
according to the selection criteria described in Paper II. By
adding these components, Fig. 6c would be more
homogeneously filled with random dots. Only the Galactic plane
would remain visible, as a region of slightly enhanced
concentration of the Gaussians. Close to the Galactic plane,
however, the Gaussian decomposition itself is badly determined,
and Gaussians of all possible parameters are found. This region is
therefore, filled by dots in all sky distribution figures.
Finally, according to our knowledge, so far there have not been
any systematic searches of IVCs in the southern sky (the blank
region in Fig. 3 of Wakker 2004). As LAB includes both the
northern and the southern data, our Fig. 6 also contains
information on the southern IVCs. However, as we can see, in this
figure the regions, observable only from the southern hemisphere
of the Earth, are almost empty, and the only possible new IVC
complexes are the concentrations of dots in the region
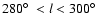 ,
,
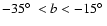 .
In this region, we can
see 2-3 ``clouds'' with typical IVCs properties: relatively small
and bright concentrations of the group-1 Gaussians, surrounded by
wider envelopes of the weaker group-2 Gaussians.
.
In this region, we can
see 2-3 ``clouds'' with typical IVCs properties: relatively small
and bright concentrations of the group-1 Gaussians, surrounded by
wider envelopes of the weaker group-2 Gaussians.
We have demonstrated that both the HVCs and IVCs could be
identified as concentrations of Gaussians in
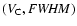 frequency plots. For both cloud types, we have
identified a two-phase structure, where the cold phase,
corresponding in Gaussian width distribution to group 1, exists
within more extended broad-line (line-width group 2) regions. In
this respect, both HVCs and IVCs appear to represent related
dynamical features, in different velocity ranges. However, besides
similarities, there are differences between the cloud types. The
first difference can be seen in Fig. 1: at both negative
and positive velocities the concentrations of Gaussians,
corresponding to the envelopes of the IVCs, are located at lower
line-widths than those corresponding to HVCs.
frequency plots. For both cloud types, we have
identified a two-phase structure, where the cold phase,
corresponding in Gaussian width distribution to group 1, exists
within more extended broad-line (line-width group 2) regions. In
this respect, both HVCs and IVCs appear to represent related
dynamical features, in different velocity ranges. However, besides
similarities, there are differences between the cloud types. The
first difference can be seen in Fig. 1: at both negative
and positive velocities the concentrations of Gaussians,
corresponding to the envelopes of the IVCs, are located at lower
line-widths than those corresponding to HVCs.
We have noted differences in the relative intensities of the cores
and envelopes of HVCs and IVCs. In HVCs, the components obtained
from LAB, and corresponding to the cold cores, are relatively
weak, and the angular dimensions of the cores found are relatively
small. The cores in IVCs appear to be larger, with more intense
radiation. This could imply that both the linear dimensions and
gas content, of the cores of HVCs and IVCs, are similar, but IVCs
are closer to us, on average, than the HVCs. The cores of the more
distant HVCs would then have smaller angular sizes, and fill the
aperture of a
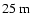 telescope to a lesser extent than
the more nearby cores of IVCs. As a result, they are detected more
weakly. This interpretation is supported by Schwarz & Wakker
(2004), who state that intermediate (10
telescope to a lesser extent than
the more nearby cores of IVCs. As a result, they are detected more
weakly. This interpretation is supported by Schwarz & Wakker
(2004), who state that intermediate (10 )
resolution
observations of HVCs imply smaller core angular dimensions, and
higher core brightnesses than measured at lower resolution. The
explanation is also in agreement with distance estimates of HVCs
and IVCs (Wakker 2004).
)
resolution
observations of HVCs imply smaller core angular dimensions, and
higher core brightnesses than measured at lower resolution. The
explanation is also in agreement with distance estimates of HVCs
and IVCs (Wakker 2004).
These differences in the apparent importance of the cold cores in
HVCs and IVCs, may help to distinguish between HVCs and IVCs. For
example, Fig. 6 illustrates the sky distribution of
Gaussians with intermediate velocities. In Fig. 6a, we
observe a concentration of points at
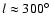 ,
,
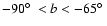 .
In Fig. 6b, we only see small
concentrations of weak Gaussians in this region. This is typical
of HVCs, and we know that the discussed concentration of
relatively low velocity is a part of the Magellanic Stream. In
general, the velocities in the Magellanic Stream are high, but
Fig. 6 presents only a small part of the full stream. In
this part the velocity is relatively low, due to projection
effects.
.
In Fig. 6b, we only see small
concentrations of weak Gaussians in this region. This is typical
of HVCs, and we know that the discussed concentration of
relatively low velocity is a part of the Magellanic Stream. In
general, the velocities in the Magellanic Stream are high, but
Fig. 6 presents only a small part of the full stream. In
this part the velocity is relatively low, due to projection
effects.
A more interesting example is found in Figs. 3a and 5a. In Fig. 3a (line-width group 2), we find
two weak concentrations of dots at
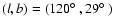 and
and
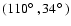 .
In Fig. 5a (line-width group 1), these clouds are considerably brighter, which is a
characteristic of IVCs. The mean LSR velocities of the objects are
-80.9 and
.
In Fig. 5a (line-width group 1), these clouds are considerably brighter, which is a
characteristic of IVCs. The mean LSR velocities of the objects are
-80.9 and
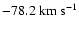 ,
respectively. These
velocities are slightly above the limit
,
respectively. These
velocities are slightly above the limit
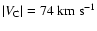 ,
which we use to separate IVCs from HVCs.
There is usually, however, no sharp separation between statistical
distributions. The velocity distributions of HVCs and IVCs
probably partially overlap, as do the line-width distributions of
Gaussians from the first and second line-width groups. Based on
their core-envelope structure, we expect that the two clouds are,
in fact, intermediate-velocity clouds with velocities that are
characteristic of HVCs. The same is possibly true for the cloud
around
,
which we use to separate IVCs from HVCs.
There is usually, however, no sharp separation between statistical
distributions. The velocity distributions of HVCs and IVCs
probably partially overlap, as do the line-width distributions of
Gaussians from the first and second line-width groups. Based on
their core-envelope structure, we expect that the two clouds are,
in fact, intermediate-velocity clouds with velocities that are
characteristic of HVCs. The same is possibly true for the cloud
around
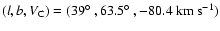 ,
in Figs. 3a and 5a. The Magellanic Stream, however, is classified as an
HVC, even though, in one part its velocities are more
characteristic of IVCs.
,
in Figs. 3a and 5a. The Magellanic Stream, however, is classified as an
HVC, even though, in one part its velocities are more
characteristic of IVCs.
In this context, it is interesting to consider the Outer Arm
Cloud. From the comparison of our sky distribution images, it
appears in most parts that the properties of the gas in the OAC
correspond to those of the HVC. In two regions only, this large
HVC complex could be overlaid with a considerable amount of IVC
gas. One of these regions is located at about
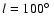 ,
and
the corresponding IVC gas appears to form an extension of the high
latitude IV Arch, to close to zero latitude. Another region with a
large number of intermediate-velocity cores, located at
,
and
the corresponding IVC gas appears to form an extension of the high
latitude IV Arch, to close to zero latitude. Another region with a
large number of intermediate-velocity cores, located at
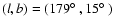 ,
may for example be the northern extension of
the AC Shell. In any case, the gas properties of the OAC appear to
be different from those of normal gas in the Galactic disc.
,
may for example be the northern extension of
the AC Shell. In any case, the gas properties of the OAC appear to
be different from those of normal gas in the Galactic disc.
Kalberla & Haud (2006) found that the cold cores of HVC
complexes have a random velocity distribution, with a typical
dispersion of
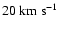 .
Kuntz & Danly
(1996) found evidence that the infall velocity of IVCs
reaches a maximum at positions of highest column density. Similar
results can be seen in our Fig. 1: at negative
velocities the line-width group-1 Gaussians, in the intermediate
velocity range, reach a maximum in their frequency distribution at
.
Kuntz & Danly
(1996) found evidence that the infall velocity of IVCs
reaches a maximum at positions of highest column density. Similar
results can be seen in our Fig. 1: at negative
velocities the line-width group-1 Gaussians, in the intermediate
velocity range, reach a maximum in their frequency distribution at
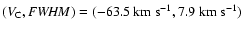 ,
whereas the components of line-width
group 2 have a corresponding maximum at
,
whereas the components of line-width
group 2 have a corresponding maximum at
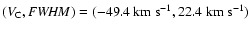 ,
i.e., the cold cores often have larger
infall velocities than their warmer envelopes.
,
i.e., the cold cores often have larger
infall velocities than their warmer envelopes.
In Fig. 1, the distribution of group-1 Gaussians is
contaminated by spurious components from profiles close to the
Galactic plane. To consider this further, we made similar figures
for the regions
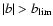 ,
with different
,
with different
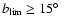 .
In these figures, the frequency
maximum of group-1 Gaussians, in the intermediate velocity range,
is shifted to lower velocities, in most cases close to
.
In these figures, the frequency
maximum of group-1 Gaussians, in the intermediate velocity range,
is shifted to lower velocities, in most cases close to
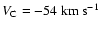 .
The location of the
frequency maxima of group-2 Gaussians remains practically
unchanged. This indicates that the velocity differences are only
partly explained by the contamination.
.
The location of the
frequency maxima of group-2 Gaussians remains practically
unchanged. This indicates that the velocity differences are only
partly explained by the contamination.
At positive velocities, it is difficult to draw a similar
conclusion. From symmetry considerations however, it is
interesting to mention that there is a weak density enhancement at
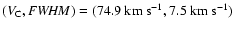 ,
but for higher values of
,
but for higher values of
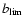 ,
it disappears completely from the plots. At the
same time, the density enhancement, corresponding to the envelopes
of the positive velocity IVCs, becomes much more prominent in
higher latitude plots, than in Fig. 1.
,
it disappears completely from the plots. At the
same time, the density enhancement, corresponding to the envelopes
of the positive velocity IVCs, becomes much more prominent in
higher latitude plots, than in Fig. 1.
Different and almost arbitrary definitions of the IVCs and HVCs
exist so far, and the main HVC catalogues (Hulsbosch & Wakker
1988; Morras et al. 2000) have been compiled by
visual inspection of the observed profiles for the presence of
components at high velocities. In this paper, we have tried an
automated approach by decomposing all profiles into Gaussian
components and studying the frequency distributions of the
parameters of the obtained Gaussians. Our approach identifies most
well-known HVC and IVC complexes on the basis of remarkable
density enhancements in particular regions of the (
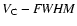 )
frequency diagram of the Gaussian parameters. The
general properties of objects, separated in this way are almost
identical to the properties of IVCs and HVCs, defined in the
traditional way:
)
frequency diagram of the Gaussian parameters. The
general properties of objects, separated in this way are almost
identical to the properties of IVCs and HVCs, defined in the
traditional way:
- the sky distributions of
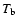 and
and
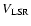 of statistically-identified IVCs and HVCs,
are similar to those of the classical complexes;
of statistically-identified IVCs and HVCs,
are similar to those of the classical complexes;
- the division line between HVCs and IVCs most likely lies
at about
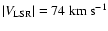 ;
;
- both HVCs and IVCs have a two-component core-envelope
structure;
- the cold cores of HVCs and IVCs have almost the same
mean line-widths:
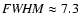 and
and
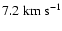 ,
respectively;
,
respectively;
- when the mean line-width of the envelopes of HVCs
is
 ,
the
corresponding value for IVCs is only
,
the
corresponding value for IVCs is only
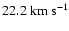 ;
;
- the angular dimensions and the brightnesses of HVC
cores, derived using the LAB, are smaller than the
corresponding values for the cores of IVCs.
- the infall velocities of the cores of IVCs often
appear to be higher than the infall velocities of the
corresponding envelopes.
The differences in the core-envelope structure of the HVCs and
IVCs can provide additional information to help distinguish
between the two cloud types.
Considering the frequency distribution, presented in
Fig. 1, and other properties of IVCs and HVCs discussed
in this paper, the suggestion by Kuntz & Danly (1996; see
also Kerp et al. 1996a,b) that IVCs were once
HVCs that have decelerated on approach to the disc, appears
plausible. In Fig. 1, a deep minimum is present between
maxima, which correspond to negative-velocity IVCs and HVCs. This
minimum could indicate that most observable intermediate-velocity
clouds are the results of a large accretion event, or that the
lifetime of IVCs and HVCs, is much longer than the interaction
phase (deceleration time) between high-velocity clouds and the
Galactic disc, or halo gas.
At the same time, it is commonly believed that the metallicities
of HVCs are lower than those of IVCs (Wakker 2001), which
makes the possibility of a relationship between high- and
intermediate-velocity cloud complexes controversial. This
metallicity difference could apparently be explained if IVCs were
HVCs at later stages of the HVC - disc collision. The clouds
would then have accreted a large amount of Galactic matter. From
numerical simulations, however, remains unclear the extent to
which such gas-mixing in cloud cores can occur (e.g.
Santillán et al. 1999, but see also Vieser 2001).
A more detailed discussion of the properties of IVCs and HVCs,
would require not only knowledge of the probability with which a
particular Gaussian belongs to a intermediate- or high-velocity
gas cloud, but a full identification of structures in position -
position - velocity - line width space.
Acknowledgements
The author would like to thank W. B. Burton for providing the
preliminary data from the LDS for program testing prior the
publication of the survey. A considerable part of the work on
creating the decomposition program was done during the stay of
U. Haud at the Radioastronomical Institute of Bonn University (now
Argelander-Institut für Astronomie). The hospitality of the
staff members of the Institute is greatly appreciated. We thank
the anonymous referee and the A&A editor M. Walmsley for fruitful
discussions and considerable help. The project was supported by
the Estonian Science Foundation grant No. 6106.
- Albert, C. E., &
Danly, L. 2004, Intermediate-Velocity Clouds, In High-Velocity
Clouds, ed. H. van Woerden, B. P. Wakker, U. J. Schwarz, & K.
de Boer (Astrophysics and Space Science Library), 312, 73
(In the text)
- Bajaja, E., Arnal, E. M.,
Larrarte, J. J., et al. 2005, A&A, 440, 767 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- de Heij, V., Braun, B.,
& Burton, W. B. 2002, A&A, 391, 159 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Habing, H. J. 1966, Bull.
Astron. Inst. Netherlands, 18, 323 [NASA ADS]
(In the text)
- Hartmann, L. 1994, The
Leiden/Dwingeloo Survey of Galactic Neutral Hydrogen, Ph.D. Thesis,
Leiden Univ.
(In the text)
- Haud, U. 1992, MNRAS,
257, 707 [NASA ADS]
(In the text)
- Haud, U. 2000, A&A,
364, 83 [NASA ADS] (Paper I)
(In the text)
- Haud, U., & Kalberla,
P. M. W. 2006, Balt. Astron., 15, 413 [NASA ADS] (Paper II)
(In the text)
- Haud, U., & Kalberla,
P. M. W. 2007, A&A, 466, 555 [NASA ADS] [CrossRef] [EDP Sciences] (Paper III)
(In the text)
- Hulsbosch, A. N. M.,
& Wakker, B. P. 1988, A&AS, 75, 191 [NASA ADS]
(In the text)
- Kalberla, P. M. W., &
Haud, U. 2006, A&A, 455, 481 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kalberla, P. M. W.,
Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [CrossRef] [EDP Sciences]
(In the text)
- Kerp, J., Mack, K.-H.,
Egger, R., et al. 1996a, A&A, 312, 67 [NASA ADS]
(In the text)
- Kerp, J., Burton, W. B.,
Egger, R., et al. 1996b, A&A, 342, 213 [NASA ADS]
- Kuntz, K. D., &
Danly, L. 1996, ApJ, 457, 703 [NASA ADS] [CrossRef]
(In the text)
- Mebold, U. 1972, A&A,
19, 13 [NASA ADS]
(In the text)
- Morras, R., Bajaja, E.,
Arnal, E. M., & Pöppel, W. G. L. 2000, A&AS, 142,
25 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Santillán, A.,
Franco, J., Martos, M., & Kim, J. 1999, ApJ, 515, 657 [NASA ADS] [CrossRef]
(In the text)
- Schwarz, U. J., &
Wakker, B. P. 2004, The Large- and Small-Scale Structure of HVCs,
In High-Velocity Clouds, ed. H. van Woerden, B. P. Wakker, U. J.
Schwarz, & K. de Boer (Astrophysics and Space Science Library),
312, 145
(In the text)
- Stark, A. A., Gammie, C.
F., Wilson, R. W., et al. 1992, ApJS, 79, 77 [NASA ADS] [CrossRef]
(In the text)
- Verschuur, G. L. 1975,
ARA&A, 13, 257 [NASA ADS] [CrossRef]
(In the text)
- Vieser, W. 2001, Ph.D.
Thesis, Universität Kiel
(In the text)
- Wakker, B. P. 1991,
A&A, 250, 499 [NASA ADS]
(In the text)
- Wakker, B. P. 2001, ApJS,
136, 463 [NASA ADS] [CrossRef]
(In the text)
- Wakker, B. P. 2004,
HVC/IVC Maps and HVC Distribution Function, In High-Velocity
Clouds, ed. H. van Woerden, B. P. Wakker, U. J. Schwarz, & K.
de Boer (Astrophysics and Space Science Library), 312, 25
(In the text)
- Wakker, B. P., & van
Woerden, H. 1997, ARA&A, 35 [CrossRef] 217
(In the text)
- Wakker, B. P., de Boer,
K. S., & van Woerden, H. 2004, History of HVC Research - An
Overview, In High-Velocity Clouds, ed. H. van Woerden, B. P.
Wakker, U. J. Schwarz, & K. de Boer (Astrophysics and Space
Science Library), 312, 1
(In the text)
- Westphalen, G. 1997,
Ph.D. Thesis, Bonn Univ.
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=12cm,clip]{color/8922fig1.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg30.gif)
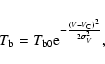
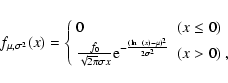
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig2.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig3.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig4.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg65.gif)
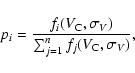
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig5.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig6.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{color/8922fig7.eps} \end{figure}](/articles/aa/full/2008/20/aa8922-07/Timg90.gif)