A&A 483, 425-435 (2008)
DOI: 10.1051/0004-6361:20078691

Large-scale variations of the cosmic X-ray background and the X-ray emissivity of the local Universe

M. Revnivtsev1,2 - S. Molkov2,1,3 - S. Sazonov1,2


1 - Max-Planck-Institute für Astrophysik, Karl-Schwarzschild-Str. 1, 85740 Garching bei München, Germany
2 - Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32, 117997 Moscow, Russia
3 - Centre d'Étude Spatiale des Rayonnements, 31028 Toulouse, France

Received 17 September 2007 / Accepted 19 March 2008

Abstract
We study the cosmic X-ray background (CXB) intensity variations on large angular scales using the slew data from the RXTE observatory. We detect intensity variations up to $\sim $$2\%$ on angular scales of 20-40$^\circ $. These variations are partly correlated with the local large-scale structure, which allowed us to estimate the emissivity of the local Universe in the energy band 2-10 keV at $(8\pm4)$ $\times $ 1038 h75 erg s-1 Mpc-3. The spectral energy distribution of the large-angular-scale variations is hard and is compatible with that of the CXB, which implies that normal galaxies and clusters of galaxies, whose spectra are typically much softer, do not contribute more than 15% to the total X-ray emissivity of the local Universe. Most of the observed CXB anisotropy (after exclusion of point sources with fluxes $\ga$10-11 erg s-1 cm-2) can be attributed to low-luminosity AGNs.

Key words: galaxies: active - galaxies: Seyfert - galaxies: statistics - X-rays: galaxies - X-rays: general

1 Introduction

The Universe is a bright source of X-ray emission. The first discovery in X-ray astronomy was that of the brightest source in the X-ray sky - the accreting neutron star Sco X-1 - along with an isotropic cosmic X-ray background (Giacconi et al. 1962), which was later shown to be composed of emission from a large number of discrete extragalactic sources (Giacconi et al. 1979).

Virtually all astrophysical objects produce X-ray emission: starting from numerous ordinary stars, with typical X-ray (2-10 keV) luminosities $L_{\rm x}\sim 10^{27}$-1030 erg s-1, through accreting white dwarfs ( $L_{\rm x}\sim10^{30}{-}10^{34}$ erg s-1), neutron stars and black holes ( $L_{\rm x}\sim10^{35}{-}10^{38}$ erg s-1), to active galactic nuclei (AGNs) and quasars ( $L_{\rm x}\sim 10^{40}$-1046 erg s-1).

The bulk of the cosmic X-ray background (CXB) is created by AGNs with luminosities $\sim $1042-1045 erg s-1 (e.g. Ueda et al. 2003), but a non-negligible contribution to the CXB must be provided by low-luminosity ( $L_{\rm x}\sim 10^{40}$-1042 erg s-1) AGNs, which constitute the majority of active supermassive black holes in the local Universe (see e.g. Ho et al. 1997; Elvis et al. 1984), as well as by ordinary galaxies, due to their populations of X-ray binaries and stars. Unfortunately, it is difficult to estimate the cumulative luminosities of these faint extragalactic sources simply by counting them, as is usually done for powerful AGNs. Indeed, a normal galaxy or a low-luminosity AGN with an X-ray luminosity $\sim $1040 erg s-1 located at a redshift typical of CXB sources ($z\sim$ 1-2) will produce an X-ray flux less than 10-17 erg s-1 cm-2, which cannot be detected by existing X-ray telescopes. However, the cumulative emissivity of all weak sources can in principle be estimated using measurements of the CXB (e.g. Boldt 1992).

It has long been understood that the properties of CXB sources are not constant but have evolved with cosmic time (e.g. Silk 1968; Longair 1966; Schmidt 1968; Maccacaro et al. 1991,1983). In particular, the cumulative X-ray volume emissivity of AGNs was much higher at redshifts of $z\sim$ 1-2 than it is at the present time (e.g. Barger et al. 2005; Maccacaro et al. 1983), the star-formation rate (and the associated rate of X-ray production) was similarly higher (Madau et al. 1996), and so on. It is therefore clear that the integrated X-ray emissivity of a unit volume or of a unit mass of Universe has evolved with time, so knowing its local (z=0) value is essential for understanding the evolution of different populations of X-ray sources, in particular supermassive black holes in the centers of galaxies.

Even the latest all-sky surveys conducted at energies above 2 keV (Krivonos et al. 2007b; Revnivtsev et al. 2004; Markwardt et al. 2005), with their sensitivity $\sim $ 10-11-11.5 erg s-1 cm-2, can detect sources with luminosities $\la$1041 erg s-1 only at distances smaller than 10 Mpc, which is not enough to obtain a representative sample of such objects and to estimate their cumulative luminosity. Stacking of individually undetectable fluxes from nearby low-luminosity X-ray sources can hardly help, because the number density of such sources increases with decreasing luminosity not fast enough ( $L{\rm d}~N/{\rm d}\!\log L\propto L^{-(\la 1)}$, see e.g. Persic et al. 1989; Elvis et al. 1984) to compensate for the rapidly declining signal-to-noise ratio.

However, it has been realized that the CXB can help in estimating the total X-ray emissivity of the local Universe (e.g. Carrera et al. 1995; Scharf et al. 2000; Shafer & Fabian 1983; Warwick et al. 1980; Miyaji et al. 1994; Jahoda et al. 1991; Schwartz 1980). The idea is quite simple - the Universe has large-scale structure characterized at zero redshift by a factor of a few or larger density contrast on scales of tens of Mpc. Since X-ray sources are expected to trace the overall matter distribution, they should exhibit a similar space density contrast. When observed in an X-ray survey, the cumulative emission of all individually undetectable sources located in an overdense region of the local Universe will create an area of enhanced sky surface brightness on top of the nearly isotropic X-ray background emission created at larger distances. The amplitude of this large angular scale enhancement of the CXB intensity can be converted into a value of the cumulative volume emissivity of faint X-ray sources, provided that one knows the distribution of matter density in that local region of the Universe and the so-called bias factor of X-ray sources (i.e. the ratio of fractional X-ray source number density fluctuations to fractional matter density fluctuations).

Recent advances in the understaning of the bias factor of AGNs indicate that in the nearby Universe ($z\sim0$) it is close to unity (see e.g. Tegmark & Peebles 1998; Boughn & Crittenden 2004). Arguably the most direct determination of the bias factor (specifically, a measurement of the ratio of fractional number density variations of X-ray sources to fractional number density variations of IRAS infrared-selected galaxies) was recently made using the INTEGRAL all-sky hard X-ray survey (Krivonos et al. 2007b), and the AGN bias factor was confirmed to be close to unity. This implies that to convert CXB intensity variations into an X-ray emissivity of the local Universe we can use any good tracer of mass density in the local volume, for instance infrared galaxies (see e.g. Basilakos & Plionis 2006). Supporting evidence that AGNs closely trace the distribution of galaxies was recently presented by Li et al. (2006) based on an optically selected sample of narrow-line AGNs from the Sloan Digital Sky Survey.

According to the current knowledge of the distribution of matter in the local Universe, even its largest angular scale anisotropy - the dipole component - continues to grow to distances $\ga$100-200 Mpc (e.g. Basilakos & Plionis 2006; Kocevski et al. 2004; Rowan-Robinson et al. 1990), where the distribution of matter is not yet well known. Nonetheless, there are distinct density patterns in the nearest ($\la$30-70 Mpc) Universe that should be imprinted into the CXB intensity distribution and could be studied with the available X-ray data.

In this paper we essentially repeat the analysis of large-scale anisotropies of the CXB that was previousely performed based on HEAO1/A2 data (e.g. Boughn et al. 2002; Shafer & Fabian 1983; Scharf et al. 2000; Miyaji et al. 1994; Jahoda et al. 1991), using a newly available dataset from the PCA instrument aboard RXTE and redetermine the X-ray emissivity of the local (z=0) Universe utilizing the advantages of the higher collective area of RXTE/PCA and its smaller field of view (and consequently the reduced confusion noise).

Thoughout the paper we adopt a Hubble constant H0=75 h75 km s-1 Mpc-1 and recalculate all relevant quantities from cited papers to this reference value.

   
2 Data analysis

   
2.1 Systematic limitations

The high level of isotropy of the cosmic X-ray background was noticed already shortly after its discovery (e.g. Schwartz 1970). In order to detect and accurately measure the anisotropy of the CXB caused either by our motion with respect to the outer Universe where the bulk of the CXB is created (the so-called Compton-Getting, or CG effect, Compton & Getting 1935) or by the large-scale structure of the Universe at zero redshift, one should reach an accuracy of measuring the CXB intensity of 0.1-0.5% of its average level.

Indeed, the relative dipole-like ( $\delta I/I\propto 1+\Delta \cos \theta$) variations of the CXB intensity due to our motion with respect to the outer Universe radiation field (the cosmic microwave background, CMB) are expected to be (see e.g. Scharf et al. 2000) on the order of

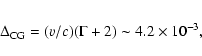
\begin{eqnarray*}\Delta_{\rm CG}=(v/c)(\Gamma+2)\sim 4.2\times10^{-3}, \end{eqnarray*}


where $\Gamma\approx1.4$ is the photon index of the CXB in the RXTE/PCA effective energy band 3-20 keV.

The X-ray dipole due to large-scale structure in the local Universe, produced by inhomogeneities in the matter density distribution at distances $D_{\rm LSS}\la$ 50-100 Mpc, is expected to be

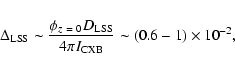
\begin{eqnarray*}\Delta_{\rm LSS}\sim {\phi_{z~=~0} D_{\rm LSS} \over{4\pi I_{\rm CXB}}} \sim (0.6-1) \times 10^{-2}, \end{eqnarray*}


where $\phi_{z~=~0} \sim 10^{39}$ erg s-1 Mpc-3 is the average volume emissivity of the local Universe and $I_{\rm CXB}\sim 7$ $\times $ 10-8 erg s-1 cm-2 sr-1 is the average CXB intensity in the 2-10 keV energy band.

Such accuracy presents a challenge for a vast majority of X-ray instruments. One of the best instruments suitable for measuring the tiny large-scale CXB anisotropies was the A2 experiment aboard the HEAO1 observatory (Rothschild et al. 1979). It had a special design of detectors that made it possible to subtract the internal background of the detectors with almost absolute accuracy. However, its detectors had relatively large fields of view ($1.5^\circ$ $\times $ $3^\circ$, $3^\circ$ $\times $ $3^\circ$and $3^\circ$ $\times $ $6^\circ$) and therefore seriously suffered from the confusion noise produced by sources with flux below the detection threshold.

The field of view of the RXTE/PCA spectrometer is significantly smaller ($\sim $0.974 sq deg), while its effective area is significantly larger ($\sim $6400 cm2 of all the detectors combined, or $\sim $1300 cm2 of a single detector), and the model of the PCA detector background developed by the PCA team allows one to subtract it with an accuracy of at least 2-3% of the CXB intensity (Jahoda et al. 2006). Therefore, RXTE/PCA is currently the best instrument for studying large-scale anisotropies of the CXB.

The noise created by point sources with flux just below the detection threshold is still an issue for RXTE/PCA. Its influence can be estimated as follows (see e.g. Warwick et al. 1980). Suppose that the differential number-flux function of point sources  ${\rm d}N(S)$ is isotropic over the sky and can be described by a power law with a slope of -5/2:

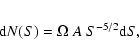
\begin{eqnarray*}{\rm d}N(S)=\Omega ~ A~ S^{-5/2} {\rm d}S, \end{eqnarray*}


where S is the source flux, A is a normalization constant and $\Omega$ is the solid angle subtended by the survey. In reality the number-flux function of extragalactic sources flattens below 10-14 erg s-1 cm-2 (e.g. Vikhlinin et al. 1995; Hasinger et al. 1993), but this does not strongly change the following estimates.

The number of sources in any infinitely small flux bin is subject to Poisson statistics, hence we can write for the dispersion of the integrated signal:

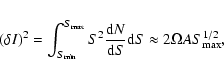
\begin{eqnarray*}(\delta I)^2 = \int_{S_{\rm min}}^{S_{\rm max}}{S^2 {{\rm d}N\over{{\rm d}S}} {\rm d}S} \approx 2\Omega A S_{\rm max}^{1/2}, \end{eqnarray*}


where $S_{\rm max}$ is the maximal flux of undetected sources.

The relative uncertainty in the flux from the solid angle $\Omega$will be $\delta I/I \propto S^{1/4}_{\rm max}/\Omega^{1/2}$. For the real number-flux function of extragalactic sources in the energy band 2-10 keV ( $A\approx 0.015~{\rm deg}^{-2}~(10^{-11}~{\rm erg}~{\rm s}^{-1}~{\rm cm}^{-2})^{3/2}$, see e.g. Revnivtsev et al. 2004), this will be

 \begin{displaymath}% \left({\delta I\over{I}} \right)_{\Omega}\approx 8.7\times 10^{-2} {S_{\rm max,11}^{1/4} \Omega_{\rm deg} ^{-1/2}}. \end{displaymath} (1)

Here $S_{\rm max,11}$ is the maximal flux of sources in units of 10-11 erg s-1 cm-2, and $\Omega_{\rm deg}$ is the solid angle of the survey in degrees. We adopted the CXB intensity in the 2-10 keV to be equal to 1.95 $\times $ 10-11 erg s-1 cm-2 deg-2 (Revnivtsev et al. 2003,2005, see also more on this below).

From the above estimates it is clear that in order to reach the required accuracy of (1-5) $\times $ 10-3 of the CXB intensity one needs to exclude sources with fluxes down to $\sim $10-11 erg s-1 cm-2 and average CXB intensity measurements over areas of $\sim $1000 deg2.

The sensitivity of the RXTE Slew Survey varies across the sky due to the non-uniform exposure map. Therefore, strictly speaking the limiting flux for source detection is not the same in different parts of the sky. However, more than 60% of the sky is covered with sensitivity better than 10-11 erg s-1 cm-2 and nearly all of the remaining sky is covered down to 2.5 $\times $ 10-11 erg s-1 cm-2 (2-10 keV).

Given the sensitivity map of the survey, we can estimate variations in the X-ray flux that can be resolved into point sources in a given region of the sky if we assume an isotropic distribution of sources over the sky with the number flux function described above:

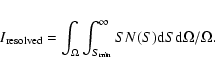
\begin{eqnarray*}I_{\rm resolved}=\int_{\Omega} \int_{S_{\rm min}}^{\infty}S N(S) {\rm d}S {\rm d}\Omega / \Omega. \end{eqnarray*}


The resulting distribution of $I_{\rm resolved}$ values averaged over cones with 25$^\circ $ half-open angle (solid angle 1932 sq deg) is roughly Gaussian and has a width (1$\sigma$) $\sim $0.5% of the mean CXB intensity.

Therefore, despite the non-uniform coverage of the sky with RXTE/PCA slews, the adopted method of data reduction allows for secure sky cleaning, which should not create any significant artificial structures on the map of the CXB intensity measured over large solid angles.

2.2 RXTE/PCA slew data

Over its lifetime (Dec. 1995-present), the spectrometer PCA on the RXTE observatory has collected a lot of data during slews between pointed observations. The high collective area of the PCA detectors ($\sim $1300 cm2 of each of the five) makes it possible to detect sources down to fluxes $\sim $5 $\times $ 1012 erg s-1 cm-2 and this detection limit is determined solely by the confusion noise (Revnivtsev et al. 2004; Markwardt & Swank 2004).

For our analysis we used all publicly available data of RXTE/PCA scans and slews from February, 1996 till February 8, 2007. During a significant period of RXTE operations only some of the five PCA detectors were switched on (this mode of operations became dominant after the end of Epoch3 of the PCA voltage, i.e. since March 1999), therefore not all of the PCA detectors have collected sufficient exposure time and sky coverage for our purposes. For this reason, in our analysis we used only detector #2, which collected $\sim $6-6.5 Ms of data between February, 1996 and February 8, 2007 (we consider here only regions away from the Galactic plane, $\vert b\vert>14^\circ$, and >$3^\circ$ away from the detected point sources reported in Revnivtsev et al. 2004).

We analyzed the data of the first layer (which typically enables the highest signal-to-noise ratio for weak X-ray sources) of the PCU2 in two energy bands, 3-8 and 8-20 keV, which were converted into instrumental channels using response matrices (constructed with the HEASOFT 6.0 package) appropriate for each observation. We similarly analyzed observations of the Crab nebula, 6 background pointings (see Jahoda et al. 2006) and ``dark'' Earth[*].

Flux measurements by RXTE/PCA are subject to systematic uncertainties. Absolute flux measurements (in particular those of the CXB) depend on how well the effective area of the detector is known, the knowledge of the effective solid angle of the collimator and so on. In our analysis we relied on an absolute X-ray flux calibrator - the Crab nebula. Specifically, our results are obtained under the assumption that the Crab spectrum is ${\rm d}N/{\rm d}E=10 E^{-2.05}$ (which implies a flux in the 2-10 keV energy band $F_{\rm Crab}=2.39$ $\times $ 10-8 erg s-1 cm-2).

As we are interested in low X-ray intensity variations over the sky we should take into account all systematic uncertainties that could affect our measurements at the level of a per cent or so.

Our data analysis consists of the following steps:

Below we describe these steps in more detail.

2.3 Background subtraction

One of the main systematic uncertainties of relative flux measurement is the accuracy of the PCA background subtraction. The currently standard approach to this consists of modeling the background with the highest possible accuracy using a number of tracers recorded onboard on the 16-s time scale and verifying that ``empty'' sky regions have zero intensity after background subtraction. Although the CXB contribution to the flux measured by RXTE/PCA is eliminated by this procedure, it can be recovered by observations of dark Earth (see e.g. Revnivtsev et al. 2003).

The current version of RXTE/PCA software (LHEASOFT 6.0) provides an outstandingly accurate model of the instrumental background (L_7_240CM version of the background), which allows for an accuracy of background subtraction of a few per cent, i.e. the root-mean-square amplitude of the unmodeled deviations is $\sim $0.02-0.03 cnts/s/PCU/beam in the 3-8 keV energy band, which corresponds to $\sim $3 $\times $ 10-13 erg s-1 cm-2 deg-2 for a Crab-like spectrum (e.g. Markwardt et al. 2002; Jahoda et al. 2006, see also Fig. 1), or $\sim $2-3% of the average CXB intensity.

However, as our aim is to measure the CXB intensity with an accuracy of 0.1-0.5%, we made special corrections to take into account the unmodeled part of the RXTE/PCA background, taking advantage of the observational fact that this part appears to be an additive component to all measured count rates irrespective of the pointing of a given PCA observation. As an example of such a behavior, we show in Fig. 1 background subtracted, 4-month-binned count rates averaged over the whole sky, over the cone of $25^\circ $ half-opening angle around $(l,b)=(130^\circ ,40^\circ )$ and over the 6 RXTE/PCA pointings that were used to calibrate the PCA background model. The similarity of the patterns of the unmodeled parts of the background in these three cases is apparent.

If we assume that the true intensity averaged over the whole sky is zero at relatively high Galactic latitudes $\vert b\vert > 25^\circ $ (to eliminate the contribution from the Galactic ridge X-ray emission, see Sect. 2.6) and also excluding $3^\circ$ regions around detected point sources, the 4-month-averaged measurements of sky intensity provide us an estimate of the unmodeled part of the RXTE/PCA background, which we add to the model-predicted rates of the PCA background.

In our subsequent analysis we only used data obtained later than 108 RXTE seconds (i.e. after March 3rd, 1997), because only during this period more than 3 background poinings were used to calibrate the PCA background model, which apparently has an effect on the accuracy of the background subtraction (see Fig. 1).

The effect of the additional background subtraction is demonstrated in the lower panel of Fig. 1. We see that the two-step background subtracted sky intensity from some sky region is much more stable than that obtained after just the first (standard) step and that the variations of the inferred intensity are almost compatible with the statistical uncertainties of the measurements.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{8691fig1.ps}\end{figure} Figure 1: Upper panel: background subracted intensities of sky, averaged over 4-month intervals. Crosses denote all-sky averaged values, open circles the intensity integrated over a $25^\circ $-radius circle around $(l,b)=(130^\circ ,40^\circ )$ and the solid line the intensity averaged over the 6 RXTE/PCA background pointings. It can be seen that all three curves demonstrate similar variations with time, which we consider the unmodeled part of the RXTE/PCA instrumental background. Lower panel: background subtracted intensity from $(l,b)=(130^\circ ,40^\circ )$ with the all-sky-averaged value subtracted. The unmodeled intensity variations have become much lower and are almost compatible with the statistical uncertainties.
Open with DEXTER

2.4 Drift in the detector parameters

Another important issue in X-ray flux measurement is the parameters of the detector. The efficiency of the PCA detectors slightly changed during the large time span considered here (1996-2007) for different reasons, including slow drift of the energy scale of the detectors and a slight change of the gas purity or pressure within the signal volumes (see e.g. Jahoda et al. 2006).

This small ($\sim $5%) drift of the detector effective area manifests itself in the measured count rates from the Crab, a constant X-ray source which has been regularly observed by RXTE (see Fig. 2). We made a special correction for this effect, modeling it by a piecewise function.

In order to check the stability of the corrected count rates we studied the detector count rate during dark-Earth observations. By construction, the PCA background model eliminates the count rate during off-bright-source observations, automatically subtracting the average CXB flux contribution. Observations of dark Earth therefore allow one to see this oversubtracted part of the PCA background, which is essentially the all-sky average CXB flux (see Revnivtsev et al. 2003). The count rates measured during dark-Earth observations, corrected for all the above effects, are shown in Fig. 2. We see that the resulting dark-Earth count rate (=-CXB flux) is stable to within $\sim $0.5-1%.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{8691fig2.ps}\end{figure} Figure 2: Upper panel: background subtracted count rate of the Crab nebula measured in the energy band 3-8 keV with RXTE/PCA over its lifetime. The count rate is not corrected for the deatime fraction which is typically $\sim $4% higher during Crab observations than during off-source observations. Lower panel: background subtracted count rate of dark Earth corrected for the ``unmodeled'' background and for the drift of the detector parameters.
Open with DEXTER

Similar corrections were done in the energy channel 8-20 keV.

After all the corrections, the CXB intensity measured within relatively large sky areas (so that the Poisson variance of the number of unresolved sources within a given area does not influence the result) exhibits definite variations over the sky. We studied the time dependence of these variations to check for any remaining systematic effects in our data. The difference in the CXB intensity between various sky regions revealed no systematic variations ( $\sigma_{\rm systematic}<0.01$ cnts/s/PCU, see Fig. 3).

2.5 CXB intensity

As a byproduct of the analysis described above we have estimated the CXB intensity in two broad energy channels (= $- {\rm dark~Earth~flux}$). The averaged CXB fluxes measured by PCA in the bands 3-8 keV and 8-20 keV are 0.847 $\pm$ 0.008 mCrab/beam and 1.43 $\pm$ 0.05 mCrab/beam, respectively. Note that in making these estimates we adopted that the average deadtime fraction during Crab observations is $\sim $4% higher than that during empty sky/dark Earth observations (see e.g. Jahoda et al. 2006).

For a power-law spectral shape of the CXB with a photon index $\Gamma=1.4$ the flux measured by PCA in the energy band 3-8 keV corresponds to a flux at 2-10 keV of $(1.95\pm0.02)$ $\times $ 10-11 erg s-1 cm-2 beam-1. Taking into account that the effective solid angle of the PCA spectrometer is $\sim $0.974 sq deg, we find that the average CXB intensity $I_{\rm CXB,~2-10~keV}=(2.00\pm0.02)$ $\times $ 10-11 erg s-1 cm-2 deg-2.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{8691fig3.ps}\end{figure} Figure 3: Differences of the count rates integrated over a $25^\circ $-radius circle around different (l,b) positions at various epochs (approximately 4-month averaged): between $(120^\circ ,40^\circ )$ and $(320^\circ ,40^\circ )$ - crosses, and between $(100^\circ ,40^\circ )$ and $(120^\circ ,40^\circ )$ - open circles. It can be seen that these differences are quite stable with time and apparently not strongly affected by systematic effects. The uncertainty caused by the Poisson variations of the number of unresolved point sources within the considered regions (see Eq. (1)) is $\sim $1.5 $\times $ 10-3 cnts/s/PCU.
Open with DEXTER

   
2.6 Contribution of the Galaxy

Our Galaxy is a bright emitter in soft (e.g. McCammon & Sanders 1990), standard (e.g. Revnivtsev et al. 2006; Worrall et al. 1982) and hard X-rays (e.g. Krivonos et al. 2007a). Due to the large angular scale of this emission, it can contribute to the large-scale anisotropy of the CXB and therefore this contribution should be estimated and subtracted or masked.

The operating energy band of RXTE/PCA (3-20 keV) precludes a detection of the soft X-ray background of the Galaxy, hence only the Galactic ridge X-ray emission (GRXE) is important for our study.

It was recently shown that most likely the GRXE is a superposition of weak Galactic sources, namely cataclysmic variables and coronally active stars, and that its surface brightness closely follows the near-infrared (NIR) surface brightness of the Galaxy (Revnivtsev et al. 2006). Therefore, one can estimate the ridge X-ray intensity in a given direction by rescaling the NIR map of the Galaxy.

However, due to the discrete nature of the GRXE one should not expect to see this emission in regions of extremely low surface number density of stellar objects, such as the Galactic poles. Indeed, if we assume the volume emissivity distribution of Galactic X-ray emission to be $\phi(z)={\rm d}L_{\rm x}/{\rm d}V\sim 1.5$ $\times $ $10^{26} \exp~(-z/z_0)$ erg s-1 pc-3 with the exponential scale hight $z_0\sim130$ pc (Revnivtsev et al. 2006), the flux from a solid angle $\Omega$ in the direction of the Galactic poles ( $\vert b\vert=90^\circ$) will be

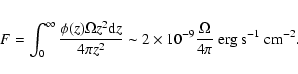
\begin{eqnarray*}F=\int^{\infty}_{0}{ {{\phi(z)\Omega z^2 {\rm d}z}\over{4\pi z^... ...\sim2\times10^{-9} {\Omega\over{4\pi}}~{\rm erg~s^{-1}~cm^{-2}}. \end{eqnarray*}


For a 1 sq deg solid angle, the flux will be $\sim $5 $\times $ 10-14 erg s-1 cm-2, i.e. $\sim $0.25% of the CXB flux. Some addition from the stellar population of the bulge of our Galaxy (Bahcall 1986) can be anticipated, however it will not be larger than that of the disk.

However, in reality the GRXE flux from these directions should be even lower because sources creating the GRXE are expected to be quite rare there. Indeed, in the direction of the Galactic poles the mass of stars in the solid angle $\Omega$ is (here we assume for simplicity an exponential distribution of stellar density in the Galactic disk, $\rho(z)=\rho_0 \exp~(-z/z_0)$, the stellar density in the Solar vicinity being $\rho_0=0.04~M_\odot$/pc3, Robin et al. 2003)

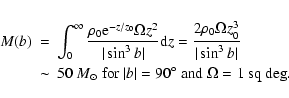
\begin{eqnarray*}M(b) &=& \int_{0}^{\infty}{{\rho_0 {\rm e}^{-z/z_0} \Omega z^2\... ...{\rm for}~\vert b\vert=90^\circ~{\rm and}~\Omega=1~{\rm sq~deg}. \end{eqnarray*}


Such a small stellar population will simply not contain any X-ray sources, such as cataclysmic variables, which create the bulk of the GRXE at energies 3-20 keV. Indeed, more than 50% of the GRXE is created by sources with luminosities >1030 erg s-1 (Sazonov et al. 2006; Revnivtsev et al. 2007), whose density is smaller than $10^{-3}~M_\odot^{-1}$. Therefore, more than $M_{\rm lim} >10^{3}~M_\odot$ of stars are needed to create significant X-ray flux from the studied direction. Such a mass in a $\Omega\approx1$ sq deg solid angle will be present if $\vert\sin^3(b)\vert\la 2\Omega \rho_0 z_0^3/M_{\rm lim}$, i.e. for $\vert b\vert\la 20^\circ$. Nonetheless, for rough estimates of the GRXE contribution one can use the scaled (as shown in Revnivtsev et al. 2006) brightness of the Galaxy at 3.5 $\mu$m (see Fig. 4).

After all the filterings we constructed an X-ray intensity profile of the sky along the Galactic latitude, by averaging measured intensities over $\vert l\vert<40^\circ $ (Fig. 4). At latitudes $\vert b\vert > 25^\circ $ no dependence of the sky surface brightness on latitude exceeding the involved uncertainties is seen, hence we mask the wide $\vert b\vert<25^\circ $ region from our subsequent analysis.


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{8691fig4.ps}\end{figure} Figure 4: Upper panel: latitudinal (at $\vert l\vert<40^\circ $) profile of X-ray (3-8 keV) surface brightness of the Galaxy, obtained by rescaling the NIR map of the sky (Revnivtsev et al. 2006), presented in units of the average CXB intensity in the 3-8 keV energy band. The value of the NIR sky brightness at the Galactic poles has been subtracted. The small variations of the NIR intensity at $\vert b\vert>50^\circ $ are due to weak point sources present in the studied areas. It can be seen that at $\vert b\vert > 25^\circ $, the contamination of the CXB by the Galaxy is smaller than $\sim $1%. In reality it should drop much faster at $\vert b\vert>20^\circ $ due to the discrete nature of the GRXE (see text). Lower panel: the same profile is shown in linear scale along with real measurements of the X-ray (3-8 keV) intensity at $\vert l\vert<40^\circ $. All the flux measurements were corrected following the prescriptions described in Sect. 2. The dashed lines denote the area ( $\vert b\vert<25^\circ $) that was excluded from the subsequent analysis of the CXB maps due to the apparent non-negligible contrbution of Galactic X-ray emission.
Open with DEXTER

We note that the signal previously seen at $25^\circ<\vert b\vert<60^\circ$ by HEAO1/A2 (Iwan et al. 1982) may be created by unresolved Galactic and extragalactic sources for which the HEAO1/A2 instrument was less sensitive than PCA due to the wider field of view of the former and consequently higher confusion noise. This is supported by the fact that Iwan et al. (1982) claimed the Galactic background emission to be present at $\vert l\vert>90^\circ$ at a level comparable to that at $\vert l\vert<90^\circ$, while the latest studies show that there is virtually no GRXE emission from the Galactic anticenter region (Revnivtsev et al. 2006).

3 Results

3.1 Large-scale structure of the local Universe

The Universe is highly homogeneous on large scales ($\gg$100-200 Mpc, e.g. Wu et al. 1999). Due to this uniformity and because most of the CXB originates at relatively large distances from us (at redshifts $z\sim$ 1-2, e.g. Hasinger et al. 2005; Ueda et al. 2003), the CXB is very isotropic. However, at smaller distances the Universe becomes inhomogeneous and this should cause some anisotropies of the CXB intensity. Since the CXB is composed of discrete sources, these anisotropies should be studied on angular scales sufficiently large that the Poisson variations of the number of sources within the area of study are unimportant, as described by Eq. (1).

The dipole component of the CXB intensity caused by the local large-scale structure saturates at distances $D\la200$-300 Mpc (e.g. Scharf et al. 2000; Kocevski et al. 2004). However, higher order harmonics might be created by more distant structures. This fact can significantly complicate the comparison of the CXB anisotropies with the structures in the nearby Universe known from sky surveys (e.g. the well-known IRAS PSCz survey in the infrared band, Saunders et al. 2000), because typically such structures are well probed only out to distances $\sim $100-200 Mpc.

In order to study the amplitude of CXB anisotropies that may be created by more distant structures we analyzed the distribution of galaxies resulting in the semi-analytic modeling of formation of galaxies in the Millennium simulation (De Lucia & Blaizot 2007). It was shown (e.g. Wang et al. 2007) that the distribution of $z\approx0$ galaxies in this simulation has statistical properties that resemble those of the real populations of galaxies in the local Universe. Our examination of the distribution of simulated galaxies showed that the matter density structures at distances >100-200 Mpc create fluctuations of the CXB intensity comparable in amplitude with those created by the more nearby mass concentrations. Therefore, one should anticipate only a partial correlation of the CXB intensity map with that of the nearest mass concentrations.

3.2 CXB intensity maps and dipole component

After implementing all the masks and corrections (see the previous section), we constructed maps of sky intensity (with the average CXB intensity subtracted as a consequence of the PCA background subtraction) in the energy bands 3-8 keV (Fig. 5) and 8-20 keV.

The simplest all-sky anisotropy that can be studied using these maps is the CXB dipole component.

A simple determination of the dipole component of the CXB angular distribution - its approximation by the function $I/I_0=1+\Delta \cos\theta$ (where $\theta$ is the angle between a given direction and the direction of the dipole) - yields the amplitude $\Delta$. The obtained parameters of the CXB dipole in the 3-8 keV energy band are presented in Table 1.

Several effects can produce a dipole component of the cosmic X-ray background. First, it may arise from some primordial anisotropy of the Universe at high redshifts.

Second, the observed CXB dipole must contain a contribution from the Doppler effect associated with our motion with respect to the reference frame in which the bulk of the CXB emission is produced ($z\sim1$-2).


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{8691fig5.ps}\end{figure} Figure 5: Adaptively smoothed map of the CXB intensity in the 3-8 keV energy band, in Galactic coordinates. Plotted is the X-ray intensity averaged over cones with half opening angles 20-40$^\circ $, excluding areas around point sources and a band around the Galactic plane ( $\vert b\vert<25^\circ $). The contours represent the levels of deviations of the CXB intensity from its average value by -1%, -0.5%, 0%, 0.5% and 1%.
Open with DEXTER

Finally, relatively nearby (z<0.1-0.5) mass concentrations can impose their imprints on the CXB map and, in particular, create a non-negligible dipole component. According to our current understanding of the distribution of matter density in the nearby Universe, it indeed contains a dipole component that causes a bulk motion of the local group of galaxies, which in turn can be seen via measurements of the dipole component in the map of the cosmic microwave background (see e.g. Rowan-Robinson et al. 1990).

As dipole anisotropy is a very wide feature on the sky, it is very hard to disentangle in the CXB intensity map the different components of the total dipole signal described above.

One promising approach would be to study the dependence of the amplitude of CXB intensity variations on energy. Indeed, as was already mentioned in Sect. 2.1, the amplitude of the Compton-Getting dipole component (caused by our motion with respect to the CXB reference frame) has a strong dependence on the slope of the CXB spectrum in the considered energy band: $\delta I/I\propto \Gamma(E)+2$, where $\Gamma(E)$ is the characteristic power-law photon index of the spectrum at energy E. This means that in hard X-rays (50-200 keV), where the CXB spectrum has a much steeper slope $\Gamma\sim2.2$-2.6 than at energies below $\sim $20 keV ( $\Gamma\sim1.4$), the amplitude of the CG effect must be considerably higher and have a specific energy dependence. On the other hand, the spectrum of the CXB dipole component created by large-scale structures in the nearby Universe is expected to be similar to that of the cumulative emission spectrum of local X-ray sources (mainly AGNs), which resembles the CXB spectrum blueshifted by a factor of $\sim $2.5(Sazonov et al. 2008). Therefore, the relative amplitude of this dipole component must also be approximately constant below $\sim $20 keV and growing at higher energies, but the energy dependence is expected to be different from that of the CG dipole.

Unfortunately, within the RXTE energy band we cannot distinguish the CG dipole from the large-scale structure one. Therefore, in our analysis we estimated the CG dipole based on the known parameters of our motion with respect to the cosmic microwave background (Lineweaver et al. 1996).

In Table 1 we present the measured CXB dipole in the energy band 3-8 keV and its value after subtraction of the CG component. We note that the obtained dipole amplitude and orientation are in good agreement with the values determined from the analysis of HEAO1/A2 data (Scharf et al. 2000).

Table 1: Parameters of the CXB dipole component in the energy band 3-8 keV determined from RXTE/PCA data.

3.3 X-ray emissivity of the local Universe

In order to compare the CXB intensity variations with the expected variations due to the nearby mass concentrations, we made use of the IRAS PSCz survey of galaxies (Saunders et al. 2000). The underlying assumption of our analysis below is that X-ray emitting AGNs trace the underlying mass distribution approximately as well as IRAS galaxies, i.e. the relative bias factor between the two classes of objects is close to unity. As discussed in the Introduction, this has been shown to be the case at least on large distance scales.

The difference in the distribution of nearby (<100-200 Mpc) galaxies in a pair of directions will cause a difference in the CXB intensities in these directions. Suppose that the X-ray emissivity per unit number density of galaxies is constant ( $\psi={\rm d}L/{\rm d}N={\rm const.}$), whereas the space density of galaxies ( $\rho={\rm d}N/{\rm d}V$) varies with direction and with distance from us (R). Let the density of galaxies in one direction be $\rho_1(R)$and in another $\rho_2(R)$. Then the difference of the CXB fluxes $\Delta F$ created by the density variations, measured within a solid angle $\Omega$ in these directions will be

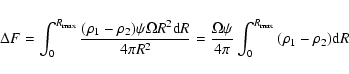
\begin{eqnarray*}\Delta F = \int_{0}^{R_{\rm max}}{{(\rho_1-\rho_2) \psi \Omega ... ...si \over{4\pi}} \int_{0}^{R_{\rm max}}{(\rho_1-\rho_2) {\rm d}R} \end{eqnarray*}


or

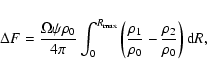
\begin{eqnarray*}\Delta F = {\Omega \psi \rho_0 \over{4\pi}} \int_{0}^{R_{\rm ma... ...ft({\rho_1\over{\rho_0}}-{\rho_2\over{\rho_0}}\right) {\rm d}R}, \end{eqnarray*}


where $\rho_0$ is the space density of galaxies averaged over a large volume. The value $\psi \rho_0=\phi$ is the X-ray volume emissivity of the local Universe in units of erg s-1 Mpc-3. Substituting in the above formula the average density $\rho_0$ for $\rho_2(R)$, we can construct a map of predicted relative deviations of the CXB intensity from its average level, generated by local ($\la$150 Mpc) inhomogeneities.

We estimated the space density of IRAS galaxies with luminosities > $10^{8}~L_\odot$ from the PSCz catalog by taking into account the dependence of the minimum detectable galaxy luminosity on distance and the finite sky coverage of the survey.

In doing that we assumed that the density of galaxies averaged over the entire sky does not depend on distance from us. As we are interested in relative galaxy densities  $\rho/\rho_0$, we have made the most straightforward correction for the distance dependence of the minimum detectable galaxy luminosity: compared the number of detected galaxies within a given solid angle $\Omega$ at given distance R with that averaged over the whole sky:

\begin{eqnarray*}{\rho\over{\rho_0}}\left(R,\Omega\right)\equiv {N([R,R+{\rm d}R], \Omega) \over{N([R,R+{\rm d}R],{\rm All~sky})}}\cdot \end{eqnarray*}


An account for the finite sky coverage of the survey was made with the help of a mask, created from the PSCz catalog data.

We only considered density variations out to a radius of $\sim $ 150 h75-1 Mpc.


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{8691fig6.ps}\end{figure} Figure 6: Space density of IRAS galaxies calculated in two directions of the sky within cones with a half-opening angle of 25$^\circ $ ( upper panel) and the radially integrated difference of these densities ( lower panel).
Open with DEXTER

Figure 6 shows the radially integrated difference $\int(\rho_1-\rho_2)/\rho_0 {\rm d}R$ between the IRAS galaxy number densities in two particular directions, determined within cones with a half-opening angle of 25$^\circ $. Figure 7 shows an all-sky map of relative galaxy number density variations $R^*=\int(\rho-\rho_0)/\rho_0 {\rm d}R$, calculated in similar $25^\circ $ cones. It can be seen that mass concentrations in the nearby Universe create a clear excess in the upper-right part of the map, which resembles the pecularity on the CXB intensity map (Fig. 5). Due to the much smaller contrast of R* values in the southern Galactic hemisphere, its correlation with the CXB intensity map provides very little information in addition to the northern hemisphere. Therefore, in studing the infrared-X-ray correlation we only considered the northern hemisphere.


  \begin{figure} \par\includegraphics[width=8cm,clip]{8691fig7.ps}\end{figure} Figure 7: Radially integrated relative space density of galaxies ( $R^*=\int{(\rho_1-\rho_0})/\rho_0{\rm d}R$), measured in cones with a half-opening angle of $25^\circ $.
Open with DEXTER

In Fig. 8 we show a scatter plot of relative variations of the CXB intensity (3-8 keV) with respect to relative number density variations of nearby galaxies across the sky. There is marginal evidence of a correlation between these two quantities.

Since we have filtered out sources with X-ray flux larger than $F_{\rm lim}$ from the all-sky map, the linear part of this correlation provides us an estimate of the cumulative emissivity of sources with luminosities $L<L_{\rm lim}=4\pi F_{\rm lim} \langle D\rangle ^2$, where $F_{\rm lim}$ is the typical sensitivity of the survey, and $\langle D\rangle$ is the characteristic distance at which inhomogeneities in the galaxy distribution are probed (see e.g. Fig. 6). We note that after we added new RXTE data, the typical sensitivity  $F_{\rm lim}$ of our survey has slightly improved with respect to the value reported by Revnivtsev et al. (2004) and is now $\sim $10-11 erg s-1 cm-2 for Crab-like spectra in the energy band 2-10 keV. This translates into a limiting luminosity $L_{\rm lim}\sim$ 1-3 $\times $ 1042 erg s-1 for $\langle D\rangle=30$-50 Mpc, the distances at which most of the local anisotropy is created (see Fig. 6).

Thus we find from the linear part of the correlation shown in Fig. 8 that the cumulative emissivity of local sources with $L<L_{\rm lim}$ is $(4.4\pm3.9)$ $\times $ 1038 h75 erg s-1 Mpc-3 in the energy band 2-10 keV.

On the other hand, the cumulative X-ray emissivity of nearby AGNs with higher luminosities ( $L\ga 10^{42}$ erg s-1) has been measured fairly accurately by directly counting sources (e.g. Sazonov & Revnivtsev 2004; Piccinotti et al. 1982; Ueda et al. 2003). Taking into account that in the 3-20 keV band the cumulative emission of such AGNs is characterized by a spectral slope similar to that of the CXB, i.e. $\Gamma\sim1.4$ (Sazonov et al. 2008), we can convert the emissivity in the 3-20 keV band reported by Sazonov & Revnivtsev (2004) to 2-10 keV[*]: ${\rm d}L/{\rm d}V(\log L>42)=(4.5\pm 0.9)$ $\times $  1038 h75 erg s-1 Mpc-3.

Adding up the contributions of sources with luminosities below $\sim $1042 erg s-1 and AGNs with luminosities over $\sim $1042 erg s-1, estimated above, we find that the total X-ray emissivity of the local Universe in the energy band 2-10 keV is $(9\pm4)$ $\times $  1038 h75 erg s-1 Mpc-3.

In reality, the liming luminosity depends on the distance to sources and also on the direction in the sky (due to the non-uniform exposure map of the RXTE Slew Survey). Therefore, to do a more accurate estimate of the X-ray volume emissivity of the nearby Universe, ideally it would be better not to exclude bright sources from the analysis and correlate total (due to both weak and bright sources) flux variations with the integrated density contrast of galaxies. However, bright sources in the real sky would introduce strong Poisson-like noise in the sought correlation. To circumvent this problem and in an attempt to obtain a more accurate estimate of the total local X-ray emissivity, we evaluated the contribution of bright sources (which are luminous AGNs with $L_{\rm x}\ga 10^{42}$ erg s-1) by integrating their known luminosity function rather then by summing up the observed fluxes of really detected sources.

To this end, we adopted the shape of the luminosity function of bright ( $L_{\rm x}\ga 10^{42}$ erg s-1) AGNs as we have measured it using the RXTE Slew Survey (Sazonov & Revnivtsev 2004), whereas the normalization of the luminosity function was taken to be proportional to the matter density as traced by IRAS galaxies, with the constraint that the total emissivity in the 2-10 keV energy band averaged over the local Universe is ${\rm d}L/{\rm d}V(\log L_{\rm x}>42)=(4.5\pm 0.9)$ $\times $ 1038 h75 erg s-1 Mpc-3.

Thus, we calculated the contribution of bright sources according to the formula:

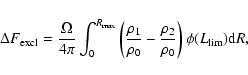
\begin{eqnarray*}{\Delta F_{\rm excl}}= {\Omega \over{4\pi}} \int_{0}^{R_{\rm ma... ...o_0}} -{\rho_2\over{\rho_0}}\right) \phi(L_{\rm lim}) {\rm d}R}, \end{eqnarray*}


where $\phi(L_{\rm lim}) = \int_{L_{\rm lim}}^{\infty}{ L {\rm d}N}$ is the cumulative emissivity of sources with luminosities $L>L_{\rm lim}=4\pi R^2 f_{\rm lim}$. The resulting correlation of the predicted flux variations due to bright AGNs with the integrated density contrast of galaxies R* is shown in Fig. 8 by the red area. The linear part of the correlation of total flux variations (the sum of the linear parts of the correlations for bright and faint sources) gives us an estimate of the total X-ray volume emissivity of the local Universe: ${\rm d}L/{\rm d}V=(8\pm4)$ $\times $ 1038 h75 erg s-1 Mpc-3, which is in good agreement with the more simple estimate obtained above.


  \begin{figure} \par\includegraphics[angle=-90,width=8cm,clip]{8691fig8.ps}\end{figure} Figure 8: Distribution of CXB variations measured by RXTE/PCA in the energy band 3-8 keV in beams of size 1932 sq deg (cones with a $25^\circ $ half-open angle), as a function of radially integrated relative number densities of IRAS galaxies ( $R^*=\int(\rho-\rho_0)/\rho_0 {\rm d}R$) calculated in the same beams. The dashed line shows the best-fit linear correlation between these two quantities: I/(cnts/s/PCU/beam) = ${\rm const.}+ (7.7\pm 7.0)$ $\times $ 10-5 R*/Mpc. The red area shows the correlation between R* and the flux variations produced by the bright sources excluded from our analysis, expected based on the AGN luminosity function measured with RXTE (Sazonov & Revnivtsev 2004).
Open with DEXTER

Here we would like to mention one more time that the exact values of X-ray emissivity of the local Universe obtained here are affected by the variability of our sensitivity for point sources removal over the sky (see e.g. Sect. 2.1). However, even adopting the most conservative flux limit for point sources removal we obtain the value of the local Universe X-ray emissivity within the quoted 1$\sigma$ confidence interval.

3.4 Spectrum of variations

The simple estimates presented in Sect. 2.1 suggest that, due to the descrete nature of the CXB, variations of the CXB flux on different angular scales should have different energy spectra. Indeed, on small angular scales (e.g. 1 sq deg), Poisson variations of the number of unresolved sources (with flux below the detection threshold) dominate and one should expect that a few sources within the field of view of the detector will provide a dominant contribution to such variations. Therefore, the count rate variations will have spectral hardness typical of such ( $f\sim10^{-12-12.5}$ erg s-1 cm-2) sources and will have the amplitude give by Eq. (1).

After filtering our bright sources and averaging the resulting count rates over areas of the sky $\gg$1 sq deg, one should expect that the spectrum of the variations will have a shape typical for the total emissivity of the local Universe (Sazonov et al. 2008), since the majority of the CXB flux variations on such angular scales are produced by large-scale mass structures in the nearby Universe (note that we have subtracted the estimated contributiuon of the CG dipole).

As we show in Fig. 9, the slope of the scatter plot of flux variations (with respect to the average CXB intensity) measured in PCA (1 sq deg) beams in the 3-8 and 8-20 keV energy bands is 0.31 $\pm$ 0.02, which corresponds to the hardness ratio of a power-law spectrum with a photon index $\Gamma=1.8$ $\pm$ 0.1. For comparison, the slope of the scatter plot of flux variations measured over larger solid angles ($\sim $2000 sq deg) is 0.42 $\pm$ 0.07, which corresponds to the hardness ratio of a power law with a photon index $\Gamma=1.4$ $\pm$ 0.2. Therefore, we do find an indication that unresolved sources with flux below the RXTE detection threshold have softer spectra than the CXB (see a similar result obtained using GINGA data in Butcher et al. 1997).


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{8691fig9.ps}\end{figure} Figure 9: Scatter plot of count rates in the energy bands 3-8 and 8-20 keV measured within the field of view of RXTE/PCA during its observations of the 6 background pointings at different times ( upper plot), and of fluxes averaged over different wide ($25^\circ $half-opening angle) cones after application of all the data filterings. The solid lines show the corresponding best-fit linear correlations. The average CXB flux has been subtracted from the count rates in both energy channels.
Open with DEXTER

Another important conclusion that can be drawn from this RXTE/PCA measurement of the spectrum of large-angular-scale variations is that the total X-ray emission of the local Universe is characterized by spectral hardness similar to that of the CXB. This in particular implies that emission from non-active galaxies and clusters of galaxies, which is typically much softer than the CXB, does not significantly contribute to the total X-ray emissivity of the local Universe. Assuming that the cumulative spectral energy distribution of non-active galaxies and low-luminosity ( $L_{\rm x}<10^{42}$ erg s-1) clusters of galaxies is characterized by a hardness ratio (8-20 keV over 3-8 keV) that coresponds to a power law with a photon index $\Gamma>2.5$ in the energy band 3-20 keV, we can estimate that such objects contribute less than 15% of the total emissivity of the local Universe. This is consistent with our estimates presented below that are based on the statistics of local non-active galaxies and clusters of galaxies.

3.5 Low-luminosity objects in the local Universe

As we summarize in Table 2 and detail below, it seems possible to explain the total emissivity of sources with luminosities $\log L_{\rm 2-10~keV}<42$, estimated above from the correlation of the CXB anisotropies with the local large-scale structure, as a superposition of contributions from known types of sources: low-luminosity AGNs, clusters of galaxies, normal and starforming galaxies.

3.5.1 Low-luminosity AGN

AGNs with X-ray luminosities below 1042 erg s-1, which we refer to below as low-luminosity AGNs (LLAGNs) are known to be abundant in the local Universe (e.g. Ho et al. 1997). Elvis et al. (1984) used a sample of optically selected LLAGNs to estimate the X-ray luminosity function of such objects by converting their measured H$_\alpha$ luminosities to X-ray luminosities under the assumption of linear correlation between these two quantities. These authors concluded that the cumulative emissivity of LLAGNs is $\sim $3 $\times $ 1038 h75 erg s-1 Mpc-3, i.e. comparable to that of AGNs with higher luminosities.

3.5.2 Clusters of galaxies

The X-ray emission from clusters of galaxies is typically fairly soft, especially from low-luminosity (low-mass) clusters. Therefore, the cumulative emissivity of clusters of galaxies must strongly depend on the energy band of the study. We consider here the standard X-ray energy band 2-10 keV, where the cumulative emissivity of clusters of galaxies can be estimated from their soft X-ray luminosity function (e.g. Mullis et al. 2004; Böhringer et al. 2002) using the well-known intracluster gas temperature-luminosity relation (e.g. Markevitch 1998). We find that clusters with luminosities below 1042 erg s-1 in the energy band 2-10 keV contribute together $\la$ 1037 h75 erg s-1 Mpc-3 to the local X-ray emissivity.

3.5.3 Normal and starforming galaxies

The contribution of normal and starforming galaxies to the X-ray emissivity in the energy band 2-10 keV mainly comes from low-mass and high-mass X-ray binaries (LMXBs and HXMBs), respectively. The shape of the luminosity function of LMXBs is approximately constant while its normalization is proportional to the galaxy mass (e.g. Gilfanov 2004; Fabbiano 1986). Therefore, the cumulative emissivity of normal galaxies can be estimated from the known value of integrated stellar mass density ( $\Omega_*h\sim (1.6{-}3.5)$ $\times $ 103, i.e. $\rho_*=(2.4{-}5.2)$ $\times $ $10^{8}~h^3_{75}~M_\odot$ Mpc-3) in the low-redshift Universe (Cole et al. 2001; Kochanek et al. 2001). This gives a value of (2-4) $\times $  1037 h75 erg s-1 Mpc-3.

The emissivity of starforming galaxies in the energy band 2-10 keV (due to HMXBs) can be estimated either via the luminosity function of nearby starforming galaxies (e.g. Ranalli et al. 2005), or by converting the average star formation rate in the local Universe (e.g. Gallego et al. 1995) to an X-ray volume emissivity using known statistical properties of HMXBs in starforming galaxies (e.g. Gilfanov et al. 2004). Both types of estimate suggest that the emissivity is approximately (3-4) $\times $  1037 h75 erg s-1 Mpc-3.

Table 2: Emissivities (2-10 keV) of different types of low-luminosity objects ( $L_{\rm 2-10~keV}<10^{42}$ erg s-1) in the local Universe in units of 1038 h75 erg s-1 Mpc-3.

4 Summary

Using data collected by the PCA instrument during slews of the RXTE observatory between its pointed observations in 1996-2007 we have obtained an all-sky map of the cosmic X-ray background intensity. Through a careful data analysis we measured the CXB intensity variations with an accuracy $\sim $0.5%.

On small angular scales we detected variations with $\sim $7% FWHM, which are most likely caused by Poisson variations of the number of weak sources below the detection threshold in the field of view of the detector.

Upon application of different filters, we detected statistically significant variations of the CXB intensity on the 20-40$^\circ $ angular scales with an amplitude $\sim $2%. Part of these variations is correlated with mass concentrations in the nearby (D<150 Mpc) Universe, which allowed us to make an estimate of the total emissivity of low-luminosity ( $\log L_{\rm 2-10~keV}\la42$) sources. The obtained value is in agreement with those determined previously based on HEAO1/A2 data (Miyaji et al. 1994; Jahoda et al. 1991). We note that these authors studied correlations on smaller angular scales and had to deal with complications due to the strong influence of Poisson statistics and clustering of sources.

The spectral hardness ratio of large-angular-scale variations of the CXB intensity is compatible with that of the average CXB spectrum. This allowed us to put an upper limit on the combined contribution of soft X-ray sources (normal and starforming galaxies, and low-mass clusters of galaxies) to the total emissivity of the local Universe in the energy band 2-10 keV: <15%. Most of the observed CXB anisotropy can be attributed to low-luminosity AGNs.

Acknowledgements
M.R. thank Gerard Lemson for assistance in the usage of the results of the Millennium simulations. This research made use of data obtained from the High Energy Astrophysics Science Archive Research Center Online Service, provided by the NASA/Goddard Space Flight Center. This work was supported by DFG-Schwerpunktprogramme SPP 1177.

References

 
Copyright ESO 2008