A&A 483, 661-672 (2008)
DOI: 10.1051/0004-6361:20078468

Optical properties of silicon carbide for astrophysical applications

I. New laboratory infrared reflectance spectra and optical constants[*]

K. M. Pitman1,2 - A. M. Hofmeister2 - A. B. Corman3 - A. K. Speck3


1 - Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
2 - Department of Earth and Planetary Sciences, Washington University, St. Louis, MO 63130, USA
3 - Department of Physics and Astronomy, University of Missouri-Columbia, Columbia, MO 65211, USA

Received 10 August 2007 / Accepted 1 March 2008

Abstract
Aims. The SiC optical constants are fundamental inputs for radiative transfer (RT) models of astrophysical dust environments. However, previously published values contain errors and do not adequately represent the bulk physical properties of the cubic ($\beta $) SiC polytype usually found around carbon stars. We provide new, uncompromised optical constants for $\beta $- and $\alpha $-SiC derived from single-crystal reflectance spectra and investigate quantitatively (i) whether there is any difference between $\alpha $- and $\beta $-SiC that can be seen in infrared (IR) spectra and optical functions and (ii) whether weak features from $\lambda \sim 12.5{-}13.0~\mu$m need to be fitted.
Methods. We measured mid- and far-IR reflectance spectra for two samples of 3C ($\beta $-)SiC and four samples of 6H ($\alpha $-)SiC. For the latter group, we acquired polarized data ($E \bot c$, $E \Vert c$ orientations). We calculated the real and imaginary parts of the complex refractive index ( $n(\lambda) + {\rm i}k(\lambda)$) and the ideal absorption coefficients via classical dispersion fits to our reflectance spectra.
Results. We find that $\beta $-SiC and $\vec{E} \bot \vec{c}$ $\alpha $-SiC have almost identical optical functions but that $n(\lambda)$ and $k(\lambda)$ for $\vec{E} \Vert \vec{c}$ $\alpha $-SiC are shifted to lower frequency. Peak positions determined for both 3C ($\beta $-) and 6H ($\alpha $-)SiC polytypes agree with Raman measurements and show that a systematic error of 4 cm-1 exists in previously published IR analyses, attributable to inadequate resolution of older instruments for the steep, sharp modes of SiC. Weak modes are present for samples with impurities. Our calculated absorption coefficients are much higher than laboratory measurements. Whereas astrophysical dust grain sizes remain fairly unconstrained, SiC grains larger than about 1 $\mu $m in diameter will be opaque at frequencies near the peak center.
Conclusions. Previous optical constants for SiC do not reflect the true bulk properties, and they are only valid for a narrow grain size range. The new optical constants presented here will allow narrow constraints to be placed on the grain size and shape distribution that dominate in astrophysical environments.

Key words: methods: laboratory - stars: carbon - stars: circumstellar matter - ISM: dust, extinction

1 Introduction

Dust grains play an essential role in star formation, contribute to interstellar processes, and are important to radiatively-driven mass loss from evolved stars. Thus, a detailed understanding of cosmic dust is necessary to determine its role in many astrophysical environments. Laboratory studies of space-borne dust have furthered our understanding of the physical properties (e.g., composition, size, shape, crystal structure, and porosity) and, in turn, the origin of these grains. Silicon carbide (SiC) were the first presolar dust grains found (Bernatowicz et al. 1987) and are thus extremely important. It is inferred that $\sim $99% of meteoritic SiC grains were formed around carbon (C-)stars for which the carbon to oxygen ratio (C/O) is greater than unity (e.g., Bernatowicz et al. 2006). These pristine samples of stardust have provided details of the grain size and crystal structure of circumstellar dust. The most significant result from presolar SiC grain studies is that nearly all ($\sim $80%) are of the $\beta $-polytype (i.e., have a cubic crystal structure; see Sect. 2) and the 6H-$\alpha $-polytype is never found. The formation of SiC in C-rich environments was predicted nearly 40 years ago via equilibrium condensation models (Friedemann 1969; Gilman 1969). Subsequently, a broad feature located at $\sim $11 $\mu $m similar to that found in laboratory infrared (IR) spectra of SiC grains was discovered in the spectra of C-stars (Hackwell 1972; Treffers & Cohen 1974). The $\sim $11 $\mu $m spectral feature is almost ubiquitous amongst observed spectra of C-stars, although its precise position, strength, and shape varies from star to star. Whereas amorphous or graphitic carbon grains dominate the circumstellar shells of C-stars, these species do not have diagnostic IR features and merely contribute to the dust continuum. Consequently, the $\sim $11 $\mu $m SiC feature has been used extensively to infer physical properties of and processes occurring within these circumstellar shells. In addition, the lack of observational evidence for the $\sim $11 $\mu $m feature in spectral studies of the interstellar medium (ISM) has placed an upper limit on the interstellar SiC abundance.

Studies that attempt to quantify the abundance of SiC from the strength of its $\sim $11 $\mu $m feature require laboratory data in two forms: IR absorption measurements for direct comparison to observational spectra; and complex refractive indices derived from reflectance measurements and supplied to radiative transfer (RT) codes to assess the relative contributions of different minerals to a given observed spectrum (cf. Thompson et al. 2006). The complex refractive indices of SiC used in astronomical studies derive primarily from three sources: Bohren & Huffman (1983), Pégourié (1988), and Laor & Draine (1993). However, there are several problems with these datasets.

1.
Most complex refractive indices (optical functions, or ``constants,'' $n(\lambda)$ and $k(\lambda)$) were calculated from reflectivity measurements of $\alpha $-SiC, rather than the dominant $\beta $-SiC. In addition, the existing $\alpha $-SiC laboratory reflectance data were gathered at resolutions lower by at least a factor of two than can be attained with modern instrumentation.

2.
Published works on SiC (e.g., Dorschner et al. 1977; Friedemann et al. 1981; Borghesi et al. 1985; Orofino et al. 1991; Papoular et al. 1998; Mutschke et al. 1999; Andersen et al. 1999b, and references therein) are predominantly laboratory absorbance studies of powder, not bulk, samples. Thin films created from powders are imperfect and dispersions of powders tend to clump such that grains cluster, causing strong differences in the optical properties of the sample (cf., Huffman 1988). The matrix in which the powder is dispersed influences the shape and profile of the bands; therefore, measurements made using this technique are not quantitative (Mutschke et al. 1999). Measuring reflectances at different angles or a combination of reflectance and transmission of a single-crystal is optimal for calculating optical constants.

3.
Whereas samples from laser pyrolysis methods are considered to produce SiC particles most closely resembling those found in stellar environments (cf. Willacy & Cherchneff 1998; Mutschke et al. 1999), such samples are not appropriate for determining bulk (grain size independent) optical constants. This is because laser pyrolysis methods do not produce crystals sufficiently large for the collection of polarized IR reflectivity data (of the order of several mm in diameter, cf. Hofmeister et al. 2003).

4.
The KBr matrix correction (cf. Friedemann et al. 1981) has been applied to some laboratory spectra of sub-micron diameter SiC grains dispersed in single-crystal matrices. Studies of thin films and isolated nanoparticles of $\beta $-SiC have shown that this wavelength shift is unnecessary when measurements are made carefully (Speck et al. 1999; Clément et al. 2003). Use of the KBr matrix correction caused a discrepancy between the IR spectra of SiC polytypes found in meteorites and around C-stars, which has since been resolved (see Speck et al. 1999). However, the most widely used SiC optical constant datasets predate this discovery and thus the KBr matrix correction was adopted by Bohren & Huffman (1983, p. 342) for spherical grains and Pégourié (1988) and is indirectly included in the Laor & Draine (1993) dataset, which used both the Pégourié (1988) and Bohren & Huffman (1983) data.

5.
In addition, the most widely used SiC optical constants have been calculated from compiled laboratory spectra which originated from different samples (cf., corundum; Speck et al. 2000). For $\beta $-SiC, refractive indices have been compiled from various sources by Adachi (1999) from 0.13 $\mu $m  $\leq \lambda \leq$ 124 $\mu $m, but modelers must extrapolate for the complex index of refraction in subregions along that interval (e.g., 0.5 $\mu $m  $\leq \lambda \leq 0.65$ $\mu $m; see Jiang et al. 2005).

6.
The shortcomings of these datasets compromise the results of RT studies. Martin & Rogers (1987), Lorenz-Martins & Lefevre (1993, 1994), Lorenz-Martins et al. (2001), Groenewegen (1995), Groenewegen et al. (1998), Griffin (1990, 1993), Bagnulo et al. (1995, 1997, 1998) and others have used these optical constants in RT models of C-stars in order to place limits on the SiC abundance. Given the problems described above, the abundances derived in those studies are probably incorrect. These optical constants have also been used in modeling environments that might include SiC (e.g., LMC stars, Speck et al. 2006; PPNe, Clube & Gledhill 2004; PNe, Hoare 1990). The veracity of those results is now suspect. Moreover, the existing SiC optical constants are valid only for a limited grain size distribution. The Borghesi et al. (1985) laboratory data, used by Pégourié (1988) and consequently Laor & Draine (1993), are based on a narrow grain size distribution (a-2.1, with typical size of a = 0.04 $\mu $m), which is narrower than the modeled grain size distributions assumed by Laor & Draine (1993); thus, these data are inappropriate for analysing grain size effects (e.g., Bagnulo et al. 1995; see Speck et al. 2005). Furthermore, these optical constants have been used to determine the maximum abundance of SiC grains in 21 $\mu $m PPNe (Jiang et al. 2005). These derived upper limits cannot be trusted.

7.
Optical properties of SiC are also used in studies of dust formation (e.g., Kozasa et al. 1996), hydrodynamics of circumstellar shells (e.g., Windsteig et al. 1997; Steffen et al. 1997) and mean opacities (Ferguson et al. 2005; Alexander & Ferguson 1994). Such studies are compromised.

8.
The different datasets of SiC optical constants produce different results. For example, using a band strength based on the data presented by Bohren & Huffman (1983) and Borghesi et al. (1985), Whittet et al. (1990) determined an upper limit for the abundance of SiC in the ISM such that less than 5% of the available Si atoms could reside in SiC grains. A similar study used data from Borghesi et al. (1985) to constrain further the SiC abundance to less than 4% of the available Si atoms that could reside in SiC grains (Chiar & Tielens 2006). However, Min et al. (2007) used the optical constants derived by Laor & Draine (1993) and found that 3% of the interstellar grains are SiC, implying that 9-12% of the available Si atoms are bound in SiC grains. Clearly the precise choice of optical constants and IR laboratory data has important consequences for quantitative analyses of the impact of SiC grains on astrophysical environments.

Given these issues, there is a need for new, more robust optical constants. We address these problems by providing new n and k values obtained from high-resolution laboratory reflectance measurements of both $\alpha $- and $\beta $-SiC single-crystals samples. In Sects. 2-4, we present and interpret measurements of mid- and far-IR room temperature reflectance spectra for several polytypes and orientations ( $\vec{E} \bot c$, $\vec{E} \Vert c$) of commercially manufactured SiC: semiconductor grade purity 3C ($\beta $-)SiC and various samples of 6H ($\alpha $-)SiC synthesised for use as diamond replacements. Though $\beta $-SiC powder and thin film samples have been measured in the laboratory previously (see review by Andersen et al. 1999b), this study is the first to our knowledge to measure single-crystal (bulk) $\beta $-SiC samples in reflectance. We extracted the real and imaginary parts of the complex refractive index ( $n(\lambda) + {\rm i}k(\lambda)$) from these data using classical dispersion analyses (Spitzer et al. 1962). The data presented in this work have direct application to carbon-rich AGB stellar outflows, novae, supernovae, and proto-planetary nebulae. Given recent Spitzer Space Telescope results for AGB stars and PNe in the LMC and SMC (e.g., Speck et al. 2006; Lagadec et al. 2007; Zijlstra et al. 2006; Stanghellini et al. 2007), new SiC laboratory data are essential to understanding the effect of metallicity on dust formation and may also improve our understanding of SiC content of the ISM.

2 Symmetry analyses of silicon carbide

Analysing IR data from different variants of SiC requires an understanding of the relationship between the vibrational modes and structure. All varieties of SiC involve tetrahedral linkage of Si and C atoms (Taylor & Jones 1960). Two minerals having the same chemical composition but different crystal structures are called polymorphs; when structural differences are due to the stacking of sheets, this is referred to as polytypism. About 200 different SiC polytypes exist (Mitra et al. 1969; Liu et al. 2004); it is debated which form most closely fits the observed feature near 11 $\mu $m in C-stars (see review by Speck et al. 1999). Layers of Si and C atoms can stack into a fcc cubic crystal (3C, or $\beta $ polytype, SiC; Bechstedt et al. 1997), into hexagonal layers, or into a combination of both cubic and hexagonal shapes ($\alpha $ polytypes). Schematic diagrams of layering in SiC are given in the literature (e.g., Käckell et al. 1994; Mutschke et al. 1999; Bernatowicz et al. 2006). The 6H form of $\alpha $-SiC is available in large sizes commercially and, thus, is most commonly measured in the laboratory. Which polytype of SiC forms in space strongly depends on the temperature and gas pressure within the dust forming region. The 6H form is stable at temperatures up to $\sim $3000 K. At lower temperatures, different polytypes will form, including 4H $\alpha $, 3C $\beta $ and 2H $\alpha $ (in order of decreasing formation temperature; Bernatowicz et al. 2006). As long as T<2400 K, $\beta $-SiC formation is favoured when condensation takes place in a vacuum. $\beta $-SiC will transform into 6H $\alpha $-SiC at temperatures above $\sim $2400 K, but it is thermodynamically unlikely that this process will work in reverse; at best, a few percent 6H $\alpha $-SiC will transform into $\beta $-SiC (I. P. Parkin; private communication). Presolar SiC grains contain 3C $\beta $-SiC (80%), 2H $\alpha $-SiC (3%), and intergrowths of these two forms (17%) (Daulton et al. 2003).

Structural differences between the polytypes affect their interaction with light in two ways. First, light passing through $\beta $-SiC lacks a preferred direction, whereas the layers in $\alpha $-SiC cause the interaction of light with Si-C dipoles to differ when the electric field vector ($\vec{E}$) travels either perpendicular to the crystal's $\vec{c}$ axis (ordinary ray) or parallel to $\vec{c}$ (extraordinary ray). Second, different numbers of vibrational modes are expected for SiC polytypes on the basis of symmetry (Patrick 1968; Feldman et al. 1968). Because the polytypes are related to one another through different stackings of layers, one can infer the number, type, and frequency of vibrational modes of any given polytype from the increase in size of the crystal's unit cell over that of $\beta $-SiC (i.e., from folding the dispersion relations in the first Brillouin zone; see Burns 1990). Folding the Brillouin zone of the 3C ($\beta $-)SiC once results in 2H SiC; folding it three times in succession results in the 6H polymorph. Phonon dispersion curves of $\beta $-SiC have been determined using symmetry analysis and Raman spectroscopic measurements of various polytypes (Nakashima & Harima 1997). In Raman measurements, the transverse optic (TO) component of each IR mode, or minimum in $\epsilon_{2}$, manifests as a peak that is distinct from the longitudinal optic (LO) component, or maximum in Im(1/$\epsilon$). However, IR activity is complicated by several factors. (1) Energy in an IR experiment is absorbed at all frequencies between the TO and LO components. (2) Si-C pairs that produce LO activity when $\vec{E} \bot \vec{c}$ are the same pairs that produce TO activity when $\vec{E} \Vert \vec{c}$. (3) Some modes are strong, and some are weak. Although symmetry considerations do not predict intensities, the main Si-C stretch in $\beta $-SiC should dominate the IR spectra of the various hexagonal and rhombohedral polymorphs. (4) Stacking disorder may contribute additional modes expected for other polymorphs (e.g., 15R modes may occur in 6H crystals). (5) Acoustic overtones and accidental degeneracies are always possible in IR spectra. Therefore, Raman frequencies and dispersion curves (Nakashima & Harima 1997; Feldman et al. 1968) serve as a useful cross-check for the peak wavelengths of our SiC laboratory IR reflectance spectra. Our results for 3C- and 6H-SiC peak positions, summarized in Table 1, are within 1-3 cm-1 of previous determinations of the TO and LO modes of SiC (see, e.g., the compilation by Mutschke et al. 1999, and references therein). Comparison to previous $n(\nu)$, $k(\nu)$ studies is presented in Sect. 5.1.

Table 1: IR peak positions of SiC: Raman measurements vs. this study.

3 Experimental methods

3.1 Sample characteristics

Grain properties and manufacturers' information for the SiC samples studied here are presented in Table 2. We verified sample polytype by optical microscopy and by the spectroscopic results below. Some samples were highly pure (Table 2). Though we cannot rule out small departures from non-stoichiometry (e.g., Kimura et al. 2006), impurities at the few per cent level would be required to affect band positions in the mid- to far-IR. The colours of the $\alpha $-SiC samples are associated with impurities which should not affect the main spectral band. Under magnification of $\times$50, the samples are homogeneous in colour and, thus, in estimated impurities. The samples lack inclusions but present crystal growth sectors (i.e., planes parallel to $\vec{c}$).

Hexagonal polymorphs of SiC grow as plates perpendicular to the crystal plane (001). This orientation was confirmed using sample morphology and optical microscopy. For $\alpha $-SiC, we created $\vec{a}{-}\vec{a}$ plates and $\vec{a}{-}\vec{c}$ plates by grinding and polishing parallel or perpendicular to the large faces of our samples, respectively. Because SiC is an extremely hard mineral (9.1-9.5 on the Mohs scale at $20~^{\circ}$C) with layering and growth sectors, mirror surfaces were difficult to attain. Thus, the measured reflectance will be lower than the true, absolute reflectance.

Table 2: Experimental samples: manufacturer information and references.

3.2 Laboratory IR spectroscopic measurements

Room temperature (18-19$^{\circ}$C) IR specular reflectance spectra were acquired at near-normal incidence (i.e., the beam passes through the microscope at an angle of = $~90 \pm 10^{\circ}$) using a Spectra-Tech Fourier transform infrared (FT-IR) spectrometer[*] microscope in an evacuated Bomem DA 3.02 Fourier transform spectrometer[*]. Resolutions of 1 cm-1 (mostly for the mid-IR) or 2 cm-1 resolution (far-IR) suffice to separate peaks for solid samples at room temperature. Instrumental accuracy is $\sim $0.01 cm-1. For the $\vec{E} \Vert \vec{c}$ polarization of 6H only, we used a specular reflection device instead of the microscope, wherein the incident beam strikes the centre of the sample at 30$^{\circ}$ to the normal. We used the ``S'' polarization, where the direction of the electric field is parallel to the line defined by the two mirror planes. The beam size was 600 $\mu $m in the microscope and $\sim $1 mm in the specular reflectance device. A Si-bolometer and a coated mylar beamsplitter were used for the far-IR, $\sim $50 to 650 cm-1 ($\sim $200-15.0 $\mu $m). A KBr beamsplitter and a liquid-nitrogen-cooled HgCdTe detector were used for the mid-IR, 450-4000 cm-1 ($\sim $22-2.5 $\mu $m). A gold mirror (100% reflection assumed; 98% average reflection measured) was used as the reference. 2000 scans yielded a reasonable noise level.

The laboratory reflectance spectra in Figs. 1 and 2 have been merged, corrected for artifacts and rescaled from the raw spectra. Where reflectance spectra were available for both wavelength regions, mid- and far-IR reflectance intensities were scaled to match in the region of overlap and merged. Because back reflections (e.g., from growth sectors, Hofmeister et al. 2003) increase apparent reflectance, the segment with the lowest reflectance above 1000 cm-1 was presumed to be correct. For the $\vec{a}{-}\vec{a}$ sections, we collected spectra from several areas and present the spectrum with the highest reflectance at the peak center (i.e., best polished surface). For our $\alpha $-SiC, the maximum absolute reflectance measured is low (R = 0.72) due to surface imperfections. We estimate the effect of errors in R on our data analysis and compare peak shapes by scaling all reflectance spectra to 92-99% maximum reflectance (cf. Spitzer et al. 1959b; Il'in et al. 1972; Zorba et al. 1996; Goncharenko et al. 1996). Our (blue-gray) $\alpha $-SiC hopper crystal sample was large enough to provide good data from the $\vec{a}{-}\vec{c}$ section, but its structure of intergrown, stacked crystals caused artifacts in the reflectance spectrum. The $\vec{a}{-}\vec{a}$ plates we studied were too thin to allow us to collect data from the $\vec{a}{-}\vec{c}$ edges. The size of our mossanite sample was marginally large enough for a $\vec{a}{-}\vec{c}$ sample but is comparable in size to the beam diameter and thus our apparatus may not have sampled the same areas from the reference mirror and the moissanite sample.

3.3 IR data analysis

To avoid presenting results that are affected by back reflections, we compared reflectance $R_{\nu}$ in the limit that $k \rightarrow 0$ at visible wavelengths,

 \begin{displaymath}R_{\nu} \approx \frac{(n_{\nu} - 1)^{2}}{(n_{\nu} + 1)^{2}} \end{displaymath} (1)

with literature values of the index of refraction determined through microscopy in white or yellow light ($\lambda$ = 467 nm or $\nu $ = 22 000 cm-1, respectively, Table 2). If the reflectance at $\nu $ = 4000 cm-1 was less than $R_{\rm white}$ by a few percent, then back reflections did not affect the data.

We used Kramers-Kronig analyses (Fahrenfort 1961; Roessler 1965) to determine starting estimates of peak positions and widths and followed up with classical dispersion analyses to provide robust $n(\nu)$ and $k(\nu)$ values. $\beta $-SiC has poorly resolved peaks; this is problematic for a Kramers-Kronig calculation, but not for classical dispersion analysis (e.g., Giesting & Hofmeister 2002). Values of n and k from our best fits are presented in Figs. 3b-7b and online at the CDS (Tables 3-7).

3.3.1 Classical dispersion analysis

Reflection and transmission by bulk media can be described using the complex refractive index ( $n - {\rm i}k$) which in turn is related to the complex dielectric function ( $\epsilon_{1} + {\rm i}\epsilon_{2}$).

 \begin{displaymath}n = \left( \frac{1}{2} \left( ( \epsilon_{1}^{2} + \epsilon_{2}^{2} )^{1/2} + \epsilon_{1} \right) \right)^{1/2} \end{displaymath} (2)


 \begin{displaymath}k = \left( \frac{1}{2} \left( ( \epsilon_{1}^{2} + \epsilon_{2}^{2} )^{1/2} - \epsilon_{1} \right) \right)^{1/2} \end{displaymath} (3)


 \begin{displaymath}\epsilon_{1} = n^{2} - k^{2} \end{displaymath} (4)


 \begin{displaymath}\epsilon_{2} = 2nk. \end{displaymath} (5)

These quantities may be obtained by fitting the laboratory reflectance spectra using classical dispersion analysis (e.g., Spitzer et al. 1962). This method treats the vibrations produced by the interaction of light with the sample as damped harmonic oscillators (i.e., the peaks in $\epsilon_{2}$ and Im(1/$\epsilon$) have Lorentzian shapes, cf. Wooten 1972).
  \begin{figure} \par\includegraphics[width=7cm,clip]{8468f1.eps} \end{figure} Figure 1: Mid- and mid+far-IR laboratory specular reflectance as a function of wavenumber (wavelength) for $\vec{E} \Vert \vec{c}$ faces of $\alpha $-SiC: moissanite (dash-dot line) and gray 6H (dashed line). Laboratory values scaled to 95% maximum reflectance from 35% (moissanite) and 45% (gray 6H).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{8468f2.eps} \end{figure} Figure 2: Mid- and mid+far-IR laboratory specular reflectance for $\vec{E} \bot \vec{c}$ faces of $\beta $-SiC (thick solid line) and four $\alpha $-SiC samples (as labeled). A mode occurs at $\sim $965 cm-1; polish effects account for the differences in shape of the main peak. Values scaled from 72% ($\beta $-SiC), 95% (moissanite), 84% (gray 6H), 76% (green 6H) and 84% (yellow 6H) to 98% maximum reflectance.
Open with DEXTER

We constructed synthetic reflectance spectra from three parameters: (1) the TO peak positions ($\nu_{i}$) determined from the maxima in $\epsilon_{2}(\nu)$, the full width at half-maximum (FWHMi) of each peak in $\epsilon_{2}(\nu)$, and the oscillator strength fi =2 FWHM $_{i} \sigma_{\rm max} / \nu_{i}^{2}$, where the conductivity $\sigma(\nu) = \nu \epsilon_{2}(\nu)/2$. The light angle of incidence $\Phi$ is accounted for after Jackson (1975):

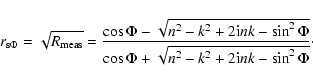\begin{displaymath}r_{\rm s\Phi} = \sqrt{R_{\rm meas}} = \frac{ \cos\Phi - \sqrt... ...\Phi + \sqrt{n^{2} - k^{2} + 2{\rm i}nk - \sin^{2}\Phi} }\cdot \end{displaymath} (6)

The equations for the components of the dielectric function for m oscillators using the damping coefficient $\Gamma_{i} = 2\pi{\it FWHM}_{i}$ are


 \begin{displaymath}\epsilon_{1} = \epsilon_{\infty} + \sum_{j=1}^{\rm m} \frac{ ... ...2} ) }{( \nu_{j}^{2} - \nu^{2})^{2} + \Gamma_{j}^{2}\nu^{2} }, \end{displaymath} (7)

where $\epsilon_{\infty}$ is n2 in the visible, and

 \begin{displaymath}\epsilon_{2} = \sum_{j=1}^{m} \frac{f_{j} \nu_{j}^{2} \Gamma_... ...u }{(\nu_{j}^{2} - \nu^{2})^{2} + \Gamma_{j}^{2}\nu^{2} }\cdot \end{displaymath} (8)

The absorption coefficient A is calculated from

 \begin{displaymath}A(\nu) = \frac{2\pi\nu\epsilon_{2}(\nu)}{n(\nu)} = 4 \pi \nu k(\nu). \end{displaymath} (9)

We note that Mutschke et al. (1999) have calculated spectral absorption and emission cross-sections for different particle shapes using ad hoc damping coefficients $\gamma$ for 6H-SiC. Mutschke et al. (1999) provide a simplified version of Eq. (7) that is appropriate for spectra arising from one oscillator (their Eq. (1)) and further relate the strength of a single oscillator to $\nu_{\rm LO}^{2} - \nu_{\rm TO}^{2}$ (their Eq. (2)). Because multiple oscillators occur for certain polarizations of SiC and are seen in all of our samples, we instead use Eqs. (7)-(9) to constrain peak widths and oscillator strengths.


  \begin{figure} \par\includegraphics[width=7cm,clip]{8468f3a.eps}\par\vspace*{2mm} \includegraphics[width=7cm,clip]{8468f3b.eps} \end{figure} Figure 3: Reflectivity at near-normal incidence of 6H gray $\alpha $-SiC ( $\vec{E} \Vert \vec{c}$ orientation) and derived functions from classical dispersion analysis. a) Laboratory reflectivity spectrum (solid line, scaled to 95% maximum reflectance), calculated reflectivity fitted by 1 oscillator ($\nu _{1}$ = 787.5 cm-1, FWHM1 = 5.50 cm-1, oscillator strength f1 = 4.45) (dashed line), and fitted by 4 oscillators ($\nu _{1}$ =787.5 cm-1, FWHM1 = 6.60 cm-1, f1 = 3.57; $\nu _{2}$ = 825.0 cm-1, FWHM2 = 20.0 cm-1, f2 = 0.3; $\nu _{3}$ = 883.7 cm-1, FWHM3 = 2.5 cm-1, f3 = 0.00475; $\nu _{4}$ = 888.5 cm-1, FWHM4 = 3.3 cm-1, f4 = 0.00425) (dot-dashed line). b) Real and imaginary parts of the complex index of refraction for the 1 oscillator fit: n (dashed line) and k (dot-dashed line).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{8468f4a.eps}\par\vspace*{2mm} \includegraphics[width=7cm,clip]{8468f4b.eps} \end{figure} Figure 4: Reflectivity at near-normal incidence of 6H gray $\alpha $-SiC ( $\vec{E} \bot \vec{c}$ orientation) and derived n and k. a) Laboratory reflectivity spectrum (solid line, scaled to 97% maximum reflectance), calculated reflectivity fitted by 1 oscillator ($\nu $ = 797.5 cm-1, FWHM = 5.30 cm-1, f = 3.33)(long dashed line), and by 2 oscillators ($\nu _{1}$ = 797.5 cm-1, FWHM1 = 5.20 cm-1, f1 = 3.32; $\nu _{2}$ = 928.0 cm-1, FWHM2 = 65.0 cm-1, f2 = 0.013) (dot-dashed line). b) n (dashed line) and k (dot-dashed line) for the 2 oscillator fit.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{8468f5a.eps}\par\vspace*{2mm} \includegraphics[width=7cm,clip]{8468f5b.eps} \end{figure} Figure 5: Reflectivity at near-normal incidence of moissanite ($\alpha $-SiC, $\vec{E} \Vert \vec{c}$ orientation) and derived n and k fitted by 1 oscillator ($\nu $ = 802.0 cm-1, FWHM = 4.0 cm-1, f = 3.4). a) Laboratory reflectivity spectrum (solid line, scaled to 97% maximum reflectance) and calculated reflectivity (dashed line). b) n (dashed line) and k (dot-dashed line).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{8468f6a.eps}\par\vspace*{2mm} \includegraphics[width=7cm,clip]{8468f6b.eps} \end{figure} Figure 6: Reflectivity at near-normal incidence of moissanite ($\alpha $-SiC, $\vec{E} \bot \vec{c}$ orientation) and derived n and k. a) Laboratory reflectivity spectrum (solid line, scaled to 97% maximum reflectance), calculated reflectivity fitted by 1 oscillator ($\nu $ = 799.0 cm-1, FWHM = 4.0 cm-1, f = 3.4) (dashed line), and by 4 oscillators ($\nu _{1}$ = 797.5 cm-1, FWHM1 = 1.75 cm-1, f1 = 2.04; $\nu _{2}$ = 799.0 cm-1, FWHM2 = 7.0 cm-1, f2 = 1.10; $\nu _{3}$ = 808.0 cm-1, FWHM3 = 14.0 cm-1, f3 = 0.28; $\nu _{4}$ = 970.0 cm-1, FWHM4 = 12.5 cm-1, f4 = 0.0010) (dot-dashed line). b) n (dashed line) and k (dot-dashed line) for the 1 oscillator fit.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{8468f7a.eps}\par\vspace*{2mm} \includegraphics[width=7cm,clip]{8468f7b.eps} \end{figure} Figure 7: Reflectivity at near-normal incidence of $\beta $-SiC and derived n, k. a) Laboratory reflectivity spectrum (solid line, scaled to 98% maximum reflectance), calculated reflectivity for 1 oscillator (dashed line: $\nu $ = 797.5 cm-1, FWHM = 6.0 cm-1, f = 3.5) and 3 oscillators (dot-dashed line: nu1 = 797.5 cm-1, FWHM1 = 2.66 cm-1, f1 = 2.7, nu2 = 802 cm-1, FWHM2 = 7.0 cm-1, f2 = 0.68, nu3 = 875 cm-1, FWHM3 = 7.0 cm-1, f3 = 0.03). An LO mode occurs at $\nu $ = 975 cm-1. b) n (dashed line) and k (dot-dashed line) for the 1 oscillator fit.
Open with DEXTER

4 Results

4.1 Laboratory reflectance spectra

Laboratory reflectance spectra of $\alpha $- and $\beta $-SiC are presented in Figs. 1, 2; peak positions are given in cm-1 wavenumber, or 104/($\lambda$ in $\mu $m). Reflectance spectra of $\beta $-SiC show a large, broad feature extending from the TO position near 797.5 cm-1 to a LO mode near 973 cm-1, consistent with Raman frequencies measured by Feldman et al. (1968). Because the sum of transverse and longitudinal acoustic modes at $\nu_{\rm TA} + \nu_{\rm LA} = 876$ cm-1 falls between the LO and TO modes of $\beta $-SiC, a resonance is possible near that position. For $\alpha $-SiC, from zone folding and Raman measurements of the dispersion, IR modes for $\vec{E} \Vert \vec{c}$ could also occur at 965, 940, 889, and 836 cm-1 and in $\vec{E} \bot \vec{c}$ at 797, 789, 772, and 767 cm-1. As in $\beta $-SiC, the strong TO mode in $\alpha $-SiC occurs near 797 cm-1 in $\vec{E} \bot \vec{c}$ and at $\sim $789 cm-1 for $\vec{E} \Vert \vec{c}$ in $\alpha $-SiC. Modes at lower frequencies are not apparent, i.e., these are too weak for resolution in reflectivity data, if they exist.

We fitted the laboratory reflectance spectra via classical dispersion analysis to characterize the position, FWHM, and oscillator strength parameters of the main peak and also to resolve the structure near the TO and LO positions in both SiC polytypes. This structure does not occur near the expected peak positions and appears to be due to physical optics effects, as discussed in Sect. 4.2. The suspect features may be described as a divot in the reflectance spectrum near the TO mode for both polarizations of the $\alpha $-SiC (moissanite and 6H gray) samples, in $\vec{E} \bot \vec{c}$ polarization only for the yellow $\alpha $-SiC sample, and also in the $\beta $-SiC wafer sample. In $\vec{E} \bot \vec{c}$ for the 6H gray and, to some extent, the green $\alpha $-SiC reflectance spectra, the slope near the LO mode is more shallow than that of the yellow $\alpha $-SiC and moissanite reflectance spectra and may also be a spectral artifact.

4.2 Optical constants: n$(\nu )$, k$(\nu )$

We fitted our laboratory reflectance data to various numbers of oscillators via classical dispersion analysis to determine if the derived optical constants and absorption coefficients are strongly affected by both weak features predicted from symmetry analyses and by spectral artifacts induced by layering or small sample size. Figures 3-7 show the resulting optical functions and the corresponding fitting parameters. By comparing and contrasting these fits, we determine whether multiple oscillators or a single oscillator best represents the behaviour of $\alpha $- and $\beta $-SiC. The n and k values obtained from single-crystal spectra samples are not dependent on grain size.

For $\beta $-SiC, a classical dispersion analysis fit using one oscillator matches the peak sites and the sloping top of the main reflectance peak well, but to fit the corner dip and the slight sway on the top of the peak, three oscillators are required (Figs. 7, 10a). The LO mode is at $\nu = 973$ cm-1. The large breadth and the position of the 875 cm-1 feature is consistent with assignment as an acoustic overtone. Its presence is within the uncertainty of the measurements. From Fig. 10a, n and k are slightly affected by the number of oscillators used. Using three oscillators instead of one makes the peak in k more narrow and causes the maximum k value to increase by 25%. The total area under the peak for k is not affected by the number of oscillators. Similarly, n differs little when the number of oscillators is varied. Because no extra oscillators are expected at 802 cm-1 for $\beta $-SiC, we suspect the appearance of a peak at that location is associated with back reflections for this very thin wafer. For the purpose of modelling the spectrum, the single oscillator fit ( $\nu = 797.5$ cm-1, FWHM = 6.0 cm-1, and f = 3.5 with $\nu_{\rm LO}$ = 975 cm-1) suffices and agrees with symmetry analysis.

Fitting the moissanite $\vec{E} \bot \vec{c}$ reflectance spectrum with one oscillator shows that there is structure on the main band near both 800 and 950 cm-1 (Fig. 6). Also, the divot makes it difficult to constrain the TO position. A one oscillator fit with peak wavenumber at 797.5 cm-1, FWHM = 4.5 cm-1, and f = 3.45 is equally good (not shown). Two additional oscillators are needed to characterize the structure near 800 cm-1, and one additional oscillator is needed to account for the structure near 970 cm-1 (Fig. 6). The best fit for two oscillators is $\nu _{1}$ = 797.5 cm-1, FWHM1 = 4.1 cm-1, f1 = 3.45 and $\nu _{2}$ = 970.0 cm-1, FWHM2 = 11.0 cm-1, and f2 = 0.0010. The presence of a peak at 970 cm-1 is in agreement with zone folding and Raman data. Addition of the 970 cm-1 makes very little difference to n and k (Fig. 10).

For the 6H gray $\alpha $-SiC sample ( $\vec{E} \bot \vec{c}$), a one oscillator fit does not match the slope at high frequency (Fig. 4). n and k differ very little between the fits, though multiple oscillators appear to make k more narrow and peak at a higher value (Fig. 10). The main peak parameters differ very little among various fits to different numbers of oscillators for this reflectance spectrum. The green and yellow $\alpha $-SiC samples ( $\vec{E} \bot \vec{c}$) were fitted with a single oscillator (not shown). For the green $\alpha $-SiC, the best fitting parameters are a peak position of 797.5 cm-1, FWHM = 6.0 cm-1 and f = 3.3; n.b., this does not fit the slope at high frequency well. For the yellow $\alpha $-SiC, the best fitting parameters are a peak position at 798.0 cm-1, FWHM = 5.5 cm-1 and f = 3.5. This TO position is not well constrained due to the presence of the divot.

Regarding possible spectral artifacts, Spitzer et al. (1959b) also observed a divot in their reflectance spectrum for a polished SiC surface and a slope for an oxidized surface; they obtained their best data for a grown surface. Data on $\alpha $-SiC, $\vec{E} \bot \vec{c}$ from Fig. 9.6 in Bohren & Huffman (1983) resemble the results of Spitzer et al. (1959b) for the grown surface. No divot exists, but the slope is greater than we observed for moissanite. We note that the green and 6H gray $\alpha $-SiC samples both have thin layers perpendicular to $\vec{c}$ and high slopes at high $\nu $. The 6H gray $\alpha $-SiC sample has a slightly stronger slope, but not much (Fig. 2). The yellow $\alpha $-SiC and moissanite samples lack the slope but have the divot at low $\nu $. These samples are single crystals; however, the yellow $\alpha $-SiC is the thinnest sample and its spectrum has the deepest divot. The moissanite is not thin but has growth sectors (on the order of 0.5 mm thick). We conclude that the divot is connected with back reflections, not surface polish, because the green and yellow $\alpha $-SiC and moissanite samples are all polished by the manufacturers and have smooth surfaces. Given how difficult this divot was to fit via classical dispersion analysis, it cannot be a vibrational mode and is probably associated with a physical optics effect and the high reflectivity of the sample. We also conclude that the slope at high frequency is associated with the thin layers and is also a problem of physical optics. Neither the slope nor the divot are intrinsic to the samples. Samples larger than 5 mm in diameter without growth sectors are needed to provide the best possible data for SiC.

For moissanite ( $\vec{E} \Vert \vec{c}$), the main reflectance peak has a very large divot, which is an artifact, as in the $\vec{E} \bot \vec{c}$ polarization (Fig. 5). Because of the divot, the TO peak position is difficult to constrain. The best classical dispersion fit provides a high value of $\nu $ (802 cm-1) that is uncertain. The data do not reveal the presence of any of the folded modes or of acoustic overtone/combination bands. The 6H gray ( $\vec{E} \Vert \vec{c}$) sample can be fitted with one oscillator at $\nu $ = 787.8 cm-1 with a FWHM = 5.5 cm-1 and f = 4.45 (Fig. 3). The peak position is hard to constrain, but clearly it is lower than the TO peak for $\vec{E} \bot \vec{c}$. The corresponding LO position is at $\nu_{\rm LO}$ = 966.9 cm-1. The divot at low frequency is different, being composed of one broad mode near 830 cm-1 and having reduced intensity near the TO position, like the other samples (Fig. 1). The latter fact should not impact the TO position of the main peak. We attempted fits with various numbers of peaks. The 4 oscillator fit in Fig. 3 confirms the low frequency TO position near 787 cm-1 for 6H gray $\alpha $-SiC ( $\vec{E} \Vert \vec{c}$). The presence of two modes near 888 cm-1 are consistent with zone folding and possible involvement of resonance with the acoustic modes. However, the narrow widths for these bands indicate that these are fundamentals, not overtones. The broad feature near 835 cm-1 appears to be a folded mode; its position is consistent with Raman spectra, although its breadth suggests it is an overtone/combination band. In contrast, the reduced intensity near the TO position was difficult to fit, which is the hallmark of a spectral artifact and consistent with the problems incurred in the other samples. The strong layering in the 6H gray $\alpha $-SiC sample could contribute to the artifacts. The fit parameters that should represent the intrinsic behaviour of this particular sample are $\nu $ = 787.8 cm-1 (FWHM = 5.5 cm-1, f = 4.35), 836.0 cm-1 (FWHM = 30.0 cm-1, f = 0.10), 883.7 cm-1 (FWHM = 2.5 cm-1, f = 0.0041) and 888.5 cm-1 (FWHM = 3.3 cm-1, f = 0.0033). The intense LO mode occurs at 968.9 cm-1, consistent with Raman measurements. We suggest that the sample has impurities connected with the strength of the folded modes. These weak modes add structure to the n and k spectra but do not change the peak maximum.


  \begin{figure} \par\includegraphics[width=6.8cm,clip]{8468f8.eps} \end{figure} Figure 8: Laboratory thin film absorbances (Speck et al. 1999; Speck et al. 2005) divided by estimated sample thicknesses ( $d \sim 0.5~\mu$m) compared to calculated classical dispersion analysis absorbance coefficients for $\alpha $-SiC. Calculated absorbance coefficients for the remaining $\alpha $-SiC samples are indistinguishable.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.8cm,clip]{8468f9.eps} \end{figure} Figure 9: Laboratory thin film absorbances (Speck et al. 1999, 2005) divided by estimated sample thicknesses (d $\sim $ 0.15 $\mu $m for $\beta $-SiC, 0.5 $\mu $m for nano samples) compared to calculated classical dispersion analysis absorbance coefficients for a 1 oscillator fit to $\beta $-SiC (Fig. 7). Given the uncertainty in estimated sample thicknesses, laboratory values can be scaled by factors of 3-5.
Open with DEXTER

4.3 Calculated absorbance

Absorbances calculated via classical dispersion analyses are cross-checked through comparison with measured absorbance of the $\alpha $- and $\beta $-SiC samples (Figs. 8, 9). In contrast to the calculated $A(\nu)$, laboratory absorbances ( $a_{\rm SCM}$) are dependent on grain size via

 \begin{displaymath}a_{\rm SCM} = \frac{A(\nu)d}{2.3026} - 2\log_{10}~(1 - R). \end{displaymath} (10)

$a_{\rm SCM}$ is converted for direct comparison to $A(\nu)$ in the figures. For $\alpha $-SiC, a weighted average,

 \begin{displaymath}a_{avg} = (2a_{\bot} + a_{\Vert})/3, \end{displaymath} (11)

is used in the comparison of Fig. 8. Averaging provides one main peak and a shoulder for $\alpha $-SiC. The position of the main peak matches that of $\beta $-SiC (Fig. 9), but the shoulder is at lower frequency. Real, measured spectra have strongly rounded peaks due to light leakage between cracks in thin-film samples or around the particulates in dispersions. In measured spectra, the $\alpha $-SiC peak occurs at a lower frequency than for $\beta $-SiC, consistent with our calculations. Because of the light leakage, the two peaks for $\alpha $-SiC are blended into one band. In Fig. 8, the measured spectrum of $\alpha $-SiC fits into the envelope. Some of the differences between the calculated and measured absorbances are due to reflectivity not being subtracted from the raw data; in these diamond anvil cell measurements, the spectral baseline involves both the reflectivity of the diamonds and of the sample, and it is not clear how best to proceed with the subtraction. In dispersions, the spectral baselines are uncontrolled, consisting of sample and medium properties. For $\beta $-SiC, the measured peaks are much more rounded than in the calculations and more rounded than the peaks measured for $\alpha $-SiC (cf. Figs. 8, 9). Because the $\beta $-SiC chips are harder, it is more difficult to make a thin film; this results in a more rounded profile. The nano-$\beta $-SiC samples are softer and form a better thin film, producing a peak very close to the ideal and also a large shoulder at the LO position. The prominence of the LO mode is expected for the $\beta $-SiC absorbance spectrum which consists of a doubly degenerate TO mode and a single LO mode. Hence absorbance peaks round and shift to high frequency in measurements as compared to classical dispersion analysis calculations (Fig. 9). For the hexagonal samples, symmetry suggests something much different: a degenerate planar optic mode near the cubic TO position and 1 axial optic mode near the LO position. That is, the TO and LO modes that are strongly coupled in the cubic structure are decoupled in the hexagonal structure. For $\vec{E} \bot \vec{c}$ in $\alpha $-SiC, the TO and LO modes are like those in $\beta $-SiC. The behaviour of the absorbance spectrum for $\alpha $-SiC ( $\vec{E} \Vert \vec{c}$) is confusing because several criteria must be met that seem to be contradictory. One is that the TO mode must be lower in frequency than the LO mode, despite the fact that symmetry suggests a main mode occurs near $\nu $ = 970 cm-1 for the axial configuration. Another is that the same dipoles exist, so the stretching frequency cannot be much different. The end result is that the LO position is preserved and the TO position is derived from a zone-folded mode. It seems that more strength is shifted to the TO  position in the process. But it is also expected that the hexagonal particles are preferentially oriented and that the measured absorption is skewed to the TO position. These effects combined indicate that less energy goes toward the LO position in $\alpha $-SiC than in $\beta $-SiC, consistent with the rounding of the peaks and the lower frequency of the $\alpha $-SiC peak maximum.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{8468f10.eps} \end{figure} Figure 10: Comparison of n and k values calculated via classical dispersion for single and multiple oscillator fits: a) $\beta $-SiC (Fig. 7, Sect. 4.2), and  b) $\alpha $-SiC (moissanite $\vec{E} \bot \vec{c}$, Fig. 6). In a), peak heights for n and k increase if more oscillators are used in the fit. In  b), adding oscillators to account for structure at $\nu $ $\sim $ 800, 970 cm-1 improves the fit to the laboratory reflectance spectrum, but the difference to n and k is small.
Open with DEXTER

5 Discussion

Past studies are divided on whether the crystal structure of SiC can be determined from IR spectra (in favor: Borghesi et al. 1985; Speck et al. 1999; opposed: Spitzer et al. 1959a,b; Papoular et al. 1998; Andersen et al. 1999a,b; Mutschke et al. 1999). Section 4 shows that spectroscopic differences exist between certain orientations of $\alpha $- and $\beta $-SiC. This section compares $\beta $-SiC to $\alpha $-SiC from the laboratory perspective and discusses implications for astronomers.

5.1 Comparisons to previous works

Spitzer et al. (1959a) obtained reflectivity data from a thin (0.06 $\mu $m) film of $\beta $-SiC that was vapour-deposited on a Si surface ( $\nu_{\rm TO} =$ 793.6 cm-1, $\Gamma =8.4$ cm-1, f = 3.30). The film was slightly irregular in appearance and thin enough to transmit light at all frequencies (their Fig. 3). Because the TO mode dominates those spectra, the TO peak position should be as accurate as their spectrometer could provide. However, the width of 8.5 cm-1 is large compared to that from 6H crystals, which probably stems from the LO mode being disproportionately large in the thin-film spectra. This effect occurs commonly due to non-normal beam incidence, wedging of the film, or irregular film thickness (Berreman 1963). The LO value obtained from the parameters of Spitzer et al. (1959a) will be influenced by the large $\Gamma$ value.

The $\alpha $-SiC $\vec{E} \bot \vec{c}$ data shown in Fig. 9.6 of Bohren & Huffman (1983) is historically important because it was used in the widely cited work by Laor & Draine (1993). Because Bohren & Huffman (1983) only provide reflectance data for $\vec{E} \bot \vec{c}$ and did not provide experimental details, such as which type of $\alpha $-SiC was used, direct comparison between our 6H-SiC data and past studies is weighted more heavily toward results of the Spitzer et al. (1959b) study, which provides data for both polarizations of 6H single-crystals.

Our results suggest that the $n(\lambda)$ and $k(\lambda)$ for $\nu $ = 797.5 cm-1, FWHM = 4.0-6.0 cm-1 and f = 3.3-3.45 best represent $\alpha $-SiC $\vec{E} \bot \vec{c}$. These values are quite similar to the $\vec{E} \bot \vec{c}$ results of Spitzer et al. (1959b) for 6H-SiC ( $\nu_{\rm TO}$ = 793.9 cm-1, FWHM = 4.8 cm-1, f = 3.30) and Bohren & Huffman (1983) for $\alpha $-SiC ( $\nu_{\rm LO} = 969.2$ cm-1, $\nu_{\rm TO} = 793$ cm-1, $\Gamma = 4.7$ cm-1). Thus, we confirm past findings that f is high and that the FWHM of the main SiC peak is of the order of 5 cm-1. For dispersive instruments such as the ones used by Spitzer et al. (1959b) and presumably Bohren & Huffman (1983), resolutions depend on the slits used and vary with wavelength. Low resolution is suggested by the spacing of data points in previous figures by these authors. High resolution is needed to properly depict profiles of sharp, steeply rising peaks (cf. Bowey et al. 2001), such as the reflectance peaks for SiC. The few cm-1 difference for the reported TO positions may either be due to resolution difference or to older, dispersive instruments lacking internal calibration that exists in modern FT-IR spectrometers. Peak positions obtained from our high resolution reflectance measurements agree closely with Raman studies (Table 1); because Raman peaks are narrower than IR reflectance or absorbance peaks and have FWHM values similar to those of the TO modes in the dielectric functions, the TO values presented in this study can be considered more accurate than the lower values previously reported. Spectral artifacts observed by Spitzer et al. (1959b) exist for our samples as well and are consistent with the presence of back reflections from internal surfaces. This deduction is based on the different thicknesses of the internal reflection surfaces in our various samples. In contrast to the Bohren & Huffman (1983) $\alpha $-SiC data and Spitzer et al. (1959b) data for the 6H-SiC grown surface, we see a new divot in our 6H-SiC spectra. The slope of the spectral profiles in past studies is greater than what we observed for moissanite. The weak oscillator seen in our 6H-SiC data at $\nu $ = 970 cm-1, FWHM = 11.0 cm-1 and f = 0.001 is real, but its presence barely alters n and k and will not affect RT models.

For $\vec{E} \Vert \vec{c}$, Spitzer et al. (1959b) observed one weak band near 883 cm-1. We observed a doublet due to use of higher resolution. Their peak parameters of $\nu $ = 785.9 cm-1, FWHM = 5.5 cm-1, and f = 3.3 for a single oscillator fit (with a LO mode at 966.9 cm-1) are quite similar to ours and within the experimental uncertainty, given the results for various samples. Their TO positions for both polarizations are low, consistent with the resolution or calibration. We conclude that the best representation of $\vec{E} \Vert \vec{c}$ for essentially pure $\alpha $-SiC is the 1 oscillator fit for our 6H gray sample.

There exists precedent in the SiC literature to average spectral parameters from many laboratory studies to obtain TO frequency positions, LO frequency positions or oscillator strengths, and FWHM values for SiC. For example, Mutschke et al. (1999) give the following frequencies, averaged from experimental studies from the 1960's to 1990's (their Table 1): (for 3C-SiC) $E_{\rm 1T} = A_{\rm 1T} = 795.9$ cm-1, $E_{\rm 1L} = A_{\rm 1L} = 972.3$ cm-1, and (for 6H-SiC) $E_{\rm 1T} = 797.0$ cm-1, $A_{\rm 1T} = 788.1$ cm-1, $E_{\rm 1L} = 969.9$ cm-1, $A_{\rm 1L} = 965.3$ cm-1. The frequency positions presented in our paper seem at first glance to be farther from values based on Raman measurements (from Hofmann et al. 1994, 3C-SiC: $E_{\rm 1T} = A_{\rm 1T} = 795.7$ cm-1, $E_{\rm 1L} = A_{\rm 1L} = 979.0$ cm-1; 6H-SiC: $E_{\rm 1T} = 797.0$ cm-1, $A_{\rm 1T} = 788.1$ cm-1, $E_{\rm 1L} = 969.9$ cm-1, $A_{\rm 1L} = 965.3$ cm-1); however, if the data by Spitzer et al. (1959a,b) had been included in the averages, the mean values reported by Mutschke et al. (1999) would be shifted by an amount up to 0.4 cm-1.

We have discussed our data in context with some of the major past laboratory studies and compilations of experimental data on SiC. To determine which spectral parameters are most representative of SiC, we strongly encourage readers to assess individual datasets on a case-by-case basis. This is because a single set of extremely precise data may be as accurate or more so than values obtained by averaging several sets of moderately precise data (McKenna & Hodges 1988; Kohn & Spear 1991). Averaging datasets also presumes that all errors in each dataset are random. If, instead, systematic errors arise either in data collection or analysis, then averaging will not provide the true values (e.g., Bevington 1969). Systematic errors exist in previously published SiC reflectance data, e.g., the differences between the instrumental resolutions of dispersive and FT-IR spectrometers can contribute up to factors of a few cm-1 difference in the reported positions of peaks. For these reasons, we discourage readers from directly combining our (or any FT-IR) SiC data with older results.

5.2 Differences between $\beta $- and $\alpha $-SiC; implications for 2H

By obtaining reflectivity spectra from different samples and polytypes, we have constrained the peak parameters of the main SiC features and the optical functions below UV frequencies where metal-anion charge transfer exists. Peak parameters for $\beta $ and $\vec{E} \bot \vec{c}$ of 6H $\alpha $ SiC were virtually indistinguishable ($\nu $ = 797.5 cm-1, FWHM = 5-6 cm-1, f $\sim $ 3.5). The parameters for $\vec{E} \Vert \vec{c}$ of 6H $\alpha $-SiC were also similar but the peaks occurred at slightly lower frequencies. This behaviour is consistent with symmetry analysis and Raman data (Table 1), indicating that peak positions from past IR studies err by several cm-1. Additional weak modes exist (acoustic for $\beta $-SiC, zone-folded for 6H $\alpha $-SiC), but most of these are too weak and broad to affect $n(\lambda)$ and $k(\lambda)$. For samples with impurities (excess C), zone-folded modes near 880 cm-1 are relatively strong and sharp. The presence of these modes in $\vec{E} \Vert \vec{c}$ alters $n(\lambda)$ and $k(\lambda)$ in a minor way by shifting the main peak $\nu $ down by < 2 cm-1. Thus, we believe that the 1 oscillator fit should be used for $\beta $-SiC or for ``pure'' SiC. The doublet in $\alpha $-SiC ( $\vec{E} \Vert \vec{c}$) is real and should be accounted for; we recommend use of a 3 oscillator fit for that or for SiC with carbon excess or stacking anomalies.

The peak parameters for 6H $\alpha $-SiC can also be used for 2H $\alpha $-SiC. The symmetry analysis and Raman data (Sect. 2) indicate that the IR peak parameters for $\vec{E} \bot \vec{c}$ of 2H should be similar to those for 6H, i.e., our data on moissanite represent 2H for $\vec{E} \Vert \vec{c}$. For $\vec{E} \Vert \vec{c}$ of 2H $\alpha $-SiC, a weak mode should occur near 838 cm-1 and the strong mode is downshifted in frequency to about 965 cm-1. Although folded modes are not expected near 888 cm-1, a broad feature is seen in this region for 3C SiC. We suggest that 2H $\alpha $-SiC ( $\vec{E} \Vert \vec{c}$) is represented by the parameters found for the main peak and 838 cm-1 mode of 6H SiC, with the broad oscillator near 881 cm-1 from $\beta $-SiC.

5.3 Recommendations for radiative transfer modelers

The purpose of this paper is to provide accurate optical data for the polytype of SiC most commonly found in astronomical environments ($\beta $-SiC) and the most commonly manufactured SiC polytype ($\alpha $-SiC), so that we and others may construct improved radiative transfer (RT) models. The advantages to modelers in using this dataset are that (1) we measured $\beta $-SiC and $\alpha $-SiC in all orientations in the same laboratory, (2) we have used the full classical dispersion equations to arrive at $n(\lambda)$ and $k(\lambda)$, and (3) our n and k data are not dependent on grain size. The electronic files for n and k (Tables 3-7, available at the CDS, where Col. 1 is $\lambda$ in $\mu $m, Col. 2 is n, and Col. 3 is k) have been prepared assuming that these will be inputs to the RT code DUSTY (Nenkova et al. 2000). The original n and k data files we generated contained over 4000 points; we have regridded these data to a smaller number of points as required for DUSTY, maintaining high $\lambda$ resolution where needed (i.e., where the slope of the data is steep) and using low $\lambda$ resolution where the slope is shallow or flat. We provide the regridded n and k data electronically; readers may contact the authors for the 4000 point high resolution files. If using DUSTY, the default wavelength grid is too coarse and must be altered to provide sufficient spectral resolution at 10-13 $\mu $m where SiC has its strong resonance feature. The spectral resolution in this region is 0.005 $\mu $m. DUSTY and many other RT models invoke Mie theory to calculate absorption and scattering cross-sections when a user supplies n and k. This implicitly assumes spherical grains. As discussed below, spherical grains are probably inappropriate in most astrophysical environments. Thus, we recommend supplying absorption and scattering coefficients for non-spherical grains calculated from our n and k instead of directly supplying n and k to DUSTY.

The intrinsic shape for circumstellar SiC grains remains unknown. Some recent works have modelled SiC grains as spheres (cf., Gauba & Parthasarathy 2004; Thompson et al. 2006; Lunttila & Juvela 2007). Jiang et al. (2005) argue that spheres are adequate for $\mu $m- or sub-$\mu $m-sized SiC grains at $\lambda > 11$ $\mu $m because the broadening of the 11.3 and 21 $\mu $m features (expected if one assumes that the grains are a continuous distribution of ellipsoids) is not likely to differ in the Rayleigh regime. Rayleigh scattering suffices when particles are small. However, the strength of the absorption as well as particle size is required to ascertain which scattering regime pertains (Lynch & Mazuk 1999). Because SiC has high absorption and nearly perfect reflection at peak center and the SiC particle sizes expected in astronomical environments are close to the sizes where Rayleigh scattering no longer applies, other shapes should be considered. It is clear that distributions of more complex shapes (e.g., Continuous Distribution of Ellipsoids, CDE, Bohren & Huffman 1983; Distribution of Hollow Spheres, Min et al. 2003; aggregates, Andersen et al. 2006, and references therein) should be used in rigorous parameter space explorations of SiC grains. Most of the standard non-spherical grain shape distributions give rise to a feature at the relevant wavelength and with the broader observed feature width.

There is no clear consensus on what the grain size distribution for SiC grains should be (see review by Speck et al. 2008, submitted). SiC grains should deviate from the MRN grain size distribution (i.e., $m_{\rm d}(a) \propto a^{-q}$, where $m_{\rm d}$ is the number of grains in the size interval ( $a, a + {\rm d}a$) and q = 3.5, $a_{\rm min}$ = 0.005 $\mu $m and $a_{\rm max}$ = 0.25 $\mu $m; Mathis et al. 1977), used in works cited in Sect. 1 and the default grain size distribution in DUSTY. The MRN distribution is based on UV and visible data and gives no information for IR wavelengths. In addition, SiC dust is generally found in circumstellar, not interstellar, dust; circumstellar dust is known not to be MRN in size or composition. Some previously published n and k data are based on specific samples and are only relevant to the grain sizes used in the lab experiments which provided the raw data. In both Pégourié (1988) and Laor & Draine (1993), the data originates from SiC-600 (ground and sedimented) sample from Borghesi et al. (1985). The Borghesi et al. (1985) sample is 99.3% pure 6H $\alpha $-SiC, with a typical grain size of 0.04 $\mu $m and a large grain size tail which goes as $\propto$ a-2.1 ( $a_{\rm max} \sim 0.5$ $\mu $m). From the IR spectrum, one infers that the grains are ellipsoidal rather than spherical or irregular (even though the unground grains are clearly irregular in morphology). n and k derived from the Borghesi et al. (1985) data should thus only be applied to the grains in a similar grain size/shape regime. The n and k values presented here offer an advantage over past datasets in that the new values may be used for extended grain size distributions such as MRN or KMH (Kim et al. 1994).

Several recent papers have discussed the occurrence of a mid-IR absorption feature in the spectra of a few carbon stars (e.g., Clément et al. 2003, 2005; Speck et al. 2005, 2006, 2008, submitted; Pitman et al. 2006). Whilst this feature has been attributed to SiC, it tends to occur at a shorter wavelength. Investigating grain size and shape effects with the new optical constants may allow us not only to fit this mid-IR feature, but also to determine what physical parameters differ in the stars that exhibit this absorption feature. In addition, past studies of grain size and shape based on the optical constants of Pégourié (1988) and Laor & Draine (1993) should be revisited.

6 Conclusions

1.
Previously reported laboratory reflectivity data are for $\alpha $-SiC, whereas SiC dust surrounding astronomical objects is $\beta $-SiC; the optical functions $n(\lambda)$ and $k(\lambda)$ for these differ slightly. We have provided electronic table values for optical functions $n(\lambda)$ and $k(\lambda)$ at $\lambda = 0.05{-}2000$ $\mu $m derived via classical dispersion analysis from room temperature, near-normal incidence laboratory specular reflectance spectra of several samples of both 3C ($\beta $-) and 6H ($\alpha $-) SiC. These n and k values are independent of grain size, do not change with scaling of the raw reflectance spectra, and may be used when modelling optically thin conditions.

2.
We have investigated whether fitting SiC IR spectra with one or more oscillators makes a difference to n and k. We suggest that a one oscillator fit best represents pure SiC. A three oscillator fit best represents impure SiC (due to carbon excess or layer stacking). $\beta $-SiC and $\alpha $-SiC $\vec{E} \bot \vec{c}$ are best fitted using one oscillator with peak parameters $\nu $ = 797.5 cm-1, FWHM = 4.0-6.0 cm-1, and f = 3.5. Adding a peak at $\nu = 970$ cm-1 makes little difference to n and k. For pure $\alpha $-SiC $\vec{E} \Vert \vec{c}$, 1 oscillator works well; as impurities increase, 3 oscillators are needed. Strong layering of the sample contributes spectral artifacts to the reflectance spectra of $\alpha $-SiC when $\vec{E} \Vert \vec{c}$; thus, the fit parameters for that orientation carry more uncertainty. The main difference between n and k for the different orientations of 6H $\alpha $-SiC is that the TO peak position for $\vec{E} \Vert \vec{c}$ is lower than that of $\vec{E} \bot \vec{c}$. Because the fit parameters for 6H $\alpha $-SiC ( $\vec{E} \bot \vec{c}$) are similar to those of $\beta $-SiC, this is also the main difference between $\alpha $-SiC and $\beta $-SiC. Peak parameters for the moissanite sample may also be used for meteoritic 2H $\alpha $-SiC.

3.
Peak positions in our SiC reflectance spectra are in agreement with Raman determinations of peak positions for SiC, which should be highly accurate due to the narrow widths, instrument calibrations, and large number of measurements made. Our calculated peak widths and strengths for 6H-SiC are in agreement with published Raman and reflectance studies. Past data for $\beta $-SiC were collected from a thin film and give information on the TO mode, but the presence of the LO mode may affect those results. Differences in peak positions between this and past works are due to calibration, instrumental resolution, or a combination of both effects. Apart from the fact that past n and k datasets were compiled from several studies, older n and k values are not appropriate for dust that is optically thin at all frequencies, nor are these values appropriate for all grain sizes; thus, n and k data from past studies should be used carefully. Comparing and contrasting results of more sophisticated radiative transfer models that use these new n and k values as inputs will allow the community to test competing hypotheses on grain size and shape effects in astronomical environments in future work.

Acknowledgements
This work was supported by NASA APRA04-000-0041, NSF-AST 0607341, and NSF-AST 0607418 and partly performed at the Jet Propulsion Laboratory, California Institute of Technology, under contract to the National Aeronautics and Space Administration. K.M.P. is supported by an appointment to the NASA Postdoctoral Program, administered by Oak Ridge Associated Universities. The authors thank M. Meixner, I. Parkin, G. C. Clayton, C. Dijkstra, and A. Koziol for their help and H. Mutschke for careful reviews of our manuscript leading to improvements in the presentation of these results.

References

 
Copyright ESO 2008