A&A 483, 301-309 (2008)
DOI: 10.1051/0004-6361:20079128
Radiative damping of standing acoustic waves in solar coronal loops
S. J. Bradshaw1 - R. Erdélyi2
1 - Space and Atmospheric Physics, Blackett Laboratory, Imperial College London, Prince
Consort Road, SW7 2BZ London, UK
2 - Solar Physics and Space Plasma Research Centre (SP2RC), Department
of Applied Mathematics, University of Sheffield, Hicks Building, Hounsfield Road, S3 7RH Sheffield, UK
Received 23 November 2007 / Accepted 12 March 2008
Abstract
Context. A detailed understanding of the physical processes that determine the damping timescales of magneto-acoustic waves is essential to interpret diagnostic results from the application of solar magneto-seismology.
Aims. The influence of the transition region and the importance of radiative emission, arising from equilibrium and non-equilibrium ionisation balances, for the damping timescale of the fundamental mode standing acoustic wave is investigated.
Methods. An extensive numerical study, in the framework of the field-aligned hydrodynamic approximation, is carried out of the damping of the fundamental mode standing wave in a solar coronal loop, for a wide range of loop lengths and apex temperatures.
Results. It was found that the radiative emission arising from a non-equilibrium ionisation balance will always act to reduce the damping timescale (in comparison to the equilibrium case) and may do so by up to 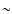 10%. The physics of the transition region is most crucial in determining the magnitude of the reduction of the damping timescale when a non-equilibrium ionisation balance is properly accounted for.
10%. The physics of the transition region is most crucial in determining the magnitude of the reduction of the damping timescale when a non-equilibrium ionisation balance is properly accounted for.
Conclusions. The methods of solar magneto-seismology, in particular the tools of coronal seismology, may be used to estimate loop lengths to a reasonable degree of accuracy, although estimates of the apex temperature are significantly less reliable, and one should use alternative (e.g. spectroscopic) diagnostics instead.
Key words: Sun: transition region - Sun: corona - Sun: UV radiation - atomic processes - hydrodynamics
1 Introduction
The magnetically complex solar corona supports a zoo of
magnetohydrodynamic (MHD) waves. These MHD waves were theoretically
predicted more than a full solar cycle ago, however, their existence
in the solar corona was uniquely observed only after the launch of
high-resolution space missions such as SOHO (SOlar and Heliospheric
Observatory), TRACE (Transition Region And Coronal Explorer) and
Hinode. The presence of a wide range of MHD waves allows several
observationally relevant questions to be addressed. What is the
relationship between the observed energy budget of the waves in
comparison to the energy needed to maintain the observed unique
temperature profile from the photosphere into the corona? What is
their contribution to the acceleration of the solar wind? What is
their role in carrying convective energy from sub-photospheric
regions into the higher atmosphere? What is their role in the
coupling of the various regions of the Sun? The observed properties
of these waves (e.g. amplitudes, periods and damping timescales)
can be used to deduce values for physical properties of the solar
corona, as suggested by Roberts et al. (1984) in the context of
coronal seismology. However, obtaining reliable diagnostic
values requires a detailed understanding of the physical processes
governing the behaviour of the wave modes used in the analysis.
The method of coronal seismology was also applied to the
lower solar atmosphere (Erdélyi 2006a,b), and the term solar atmospheric magnetoseismology was proposed (e.g.
Banerjee et al. 2007). For recent reviews on
magnetoseismology of the solar corona see Nakariakov & Verwichte (2005),
Banerjee et al. (2007) and references therein. In the present work,
acoustic (longitudinal slow-mode) waves will be of primary interest.
In particular, the efficient damping of these waves by radiation
processes in both equilibrium and non-equilibrium ionisation will be
considered in detail.
Direct observations of spatially and temporally resolved
magneto-acoustic waves (MAWs), propagating along coronal
loops, were made available by the EIT instrument on board the SoHO
satellite and have been discussed by Berghmans & Clette (1999).
Propagating MAWs were later identified in TRACE observations by
De Moortel et al. (2000, 2002a-c).
Robbrecht et al. (2001) carried out a multi-instrument study of
propagating MAWs using EIT and TRACE observations. The sources of
these waves were identified by the authors as small-scale
brightenings at one of the loop foot-points. Perhaps the most likely
of the many possible explanations for the presence of these waves is
the direct leakage of photospheric motions into the corona along
tilted magnetic field lines (De Pontieu et al. 2003a,b, 2004, and
2005). However, none of these
explanations have really addressed damping of the observed
longitudinal MAWs and the potential importance of radiative emission
from the plasma itself.
Conversely, oscillations that have been interpreted as standing MAWs have been observed in significantly hotter
(T > 6 MK) coronal loops by the SUMER instrument on board SoHO
(Kliem et al. 2002; Wang et al. 2002, 2003a,b).
Recently Taroyan et al. (2007b) have carried out forward modelling of
these particular SUMER observations and described the observed
oscillations, including their spectral signatures, from excitation
to damping. Although the spectral signatures were recovered with
considerable accuracy, questions remained open regarding an
efficient damping mechanism for the waves observed by SUMER, despite
taking into account the complex radiative properties of the coronal
plasma. The period of a standing MAW in a coronal loop can be
expressed in terms of the sound speed and the loop length
(Roberts et al. 1984), and standing and propagating MAWs
can be differentiated from one another by examining the phase
relationship between velocity and the intensity of optically thin
emission lines. The phase difference is 1/4 of a period for standing
waves and zero for propagating waves. The SUMER data show clearly that
the phase speeds derived from the observed periods and loop lengths are
in good agreement with the sound speed, and that the intensity fluctuations
lag the Doppler shifts by 1/4 of a period.
The physical mechanism by which standing MAWs can be excited in
coronal loops is not as clear as in the propagating case, due to a
lack of observational clues. Numerical models have demonstrated the
ready excitation of the second harmonic of a standing acoustic wave
by impulsive coronal heating (Bradshaw & Mason 2003b; Bradshaw et al. 2004; Nakariakov et al. 2004; Tsiklauri et al. 2004), however, the waves observed by
SUMER have periods corresponding to the fundamental mode.
Taroyan et al. (2007a) has proposed a novel diagnostic
tool how to identify the various harmonics through Doppler-shift
studies of power spectra of oscillations in randomly (or otherwise)
heated coronal loops. Through a model of spatio-temporal random
energy releases concentrated near the footpoints of a coronal loop,
proposed by Mendoza-Briceño et al. (2002, 2005),
Mendoza-Briceño & Erdélyi (2006) studied the
oscillatory response of coronal loops to random energy injections.
Both standing and propagating longitudinal (i.e. acoustic) waves
were found in the simulations. In particular, periodic features,
such as wave packets, with periods of 150-220 s, 500-600 s and
800-1000 s were found. It was also shown that the periods increase
with the loop length and decrease with the scale-length of the
heating pulses.
Wang et al. (2003a, 2005) have also suggested that the
fundamental mode standing acoustic wave could be excited by the
injection of hot plasma at a loop transition region or chromospheric
foot-point, driven by the reconnection of the existing magnetic
field with emerging flux. Taroyan et al. (2005) provided numerical
confirmation of this idea by showing that the fundamental mode
standing acoustic wave can indeed be excited in a coronal loop by
impulsive heating at a chromospheric foot-point, provided the
duration of the pulse matches the period of the fundamental mode.
More details on advances in forward modelling can be found in
Taroyan et al. (2007b) using SUMER observations and in
Taroyan & Bradshaw (2008) using Hinode EIS imaging and spectroscopic
responses.
The damping of magneto-acoustic waves has also attracted a
large amount of attention in recent years, since the damping
timescale can reveal the dominant physical processes that control
the energy balance of the coronal loops in which the waves are
observed. The effect of thermal conduction on wave damping was
investigated by Porter et al. (1994), Nakariakov et al. (2000),
Ofman & Wang (2002), De Moortel et al. (2002c) and Mendoza-Briceño et al. (2004).
The influence of compressive viscosity was studied by Porter et al. (1994),
Nakariakov et al. (2000), Ofman et al. (2000) and Ofman & Wang (2002).
Nakariakov et al. (2000) and Mendoza-Briceño et al. (2004) also included
gravitational stratification, and McEwan et al. (2006) examined
thermal stratification. In general, thermal conduction was found to
be the dominant damping mechanism, although it was also found that
the occurence of steeper velocity gradients under the influence of
gravity could enhance the damping due to compressive viscosity,
particularly in the hotter loops observed by SUMER
(Mendoza-Briceño et al. 2004).
Radiation has been overlooked as a damping mechanism, largely
because the coronal radiative energy losses are indeed small when
compared with thermal conduction for the cases considered in
previous works. However, when one considers the influence of a
self-consistent transition region in the models, the roles of the
various physical processes in the energy balance become less clear
(Mendoza-Briceño et al. 2004). The transition region is
considerably denser than the corona and also contains some of the
most strongly emitting ions. Therefore, since the radiative energy
loss is proportional to
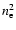 (where
(where 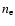 is the electron number
density), one might expect a significant amount of the wave's energy
to be lost from the transition region as it is transported to/from
the corona during the lifetime of the wave (e.g. before its
amplitude is damped by a factor of 1/e). Furthermore, previous
work has shown that the radiative emission curve can be strongly
modified in the presence of a non-equilibrium ionisation balance
(Spadaro et al. 1990; Hansteen 1993; Sarro et al. 1999; Teriaca et al. 1999; Bradshaw & Mason 2003a,b; Müller et al. 2003; Bradshaw et al. 2004;
Müller et al. 2004). Hence, the purpose of the current
work is to consider the influence of the transition region and the
effect on the damping timescale of a standing acoustic wave due to
the radiative energy losses that arise from equilibrium and
non-equilibrium ionisation balances.
is the electron number
density), one might expect a significant amount of the wave's energy
to be lost from the transition region as it is transported to/from
the corona during the lifetime of the wave (e.g. before its
amplitude is damped by a factor of 1/e). Furthermore, previous
work has shown that the radiative emission curve can be strongly
modified in the presence of a non-equilibrium ionisation balance
(Spadaro et al. 1990; Hansteen 1993; Sarro et al. 1999; Teriaca et al. 1999; Bradshaw & Mason 2003a,b; Müller et al. 2003; Bradshaw et al. 2004;
Müller et al. 2004). Hence, the purpose of the current
work is to consider the influence of the transition region and the
effect on the damping timescale of a standing acoustic wave due to
the radiative energy losses that arise from equilibrium and
non-equilibrium ionisation balances.
The paper is structured as follows: in Sect. 2 the
numerical model is described; the results are presented and
discussed in Sect. 3; and a summary of the work, the
conclusions reached and ideas for future studies are given in
Sect. 4.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9128fig1.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg17.gif) |
Figure 1:
Upper panel: number density (solid line) and temperature (triple-dash dot line) profiles for a hydrostatic loop of length L = 8  109 cm and apex temperature
109 cm and apex temperature
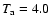 MK, with a uniform volumetric heating rate of MK, with a uniform volumetric heating rate of
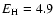  10-3 erg cm-3 s-1 required to maintain equilibrium. Lower panel: standing fundamental mode acoustic wave, with v0=107 cm s-1.
10-3 erg cm-3 s-1 required to maintain equilibrium. Lower panel: standing fundamental mode acoustic wave, with v0=107 cm s-1. |
| Open with DEXTER |
2 Numerical model
The damping of a standing acoustic wave is studied by superimposing
the velocity profile of the fundamental mode on an initially
hydrostatic coronal loop in a one-dimensional geometry
(Fig. 1, upper panel) and following the subsequent
thermodynamic evolution of the plasma in time (t). The hydrostatic
initial conditions describe a loop structured with a cool, dense
chromosphere at each foot-point, self-consistent chromosphere-corona
transition regions, and an overlying hot, tenuous corona. The
spatial profile of the velocity wave is given by
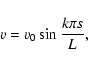 |
(1) |
where k is the mode number (k=1 for the fundamental mode), s is the spatial coordinate along the magnetic field and L is the total length (foot-point to foot-point) of the loop
(Fig. 1, lower panel). The hydrodynamic equations
describing the thermodynamic evolution of the plasma are given by
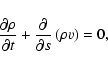 |
(2) |
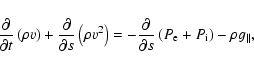 |
(3) |
and
The plasma is considered to be composed of electrons and ions
(mostly protons in the form of ionised hydrogen). In these equations
a subscript e (i) denotes a property of the electron (ion) fluid.
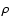 ,
n and T are the mass density, number density and
temperature, respectively. The closure conditions for
Eqs. (2) to (5) give the energy densities,
,
n and T are the mass density, number density and
temperature, respectively. The closure conditions for
Eqs. (2) to (5) give the energy densities,
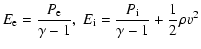 |
|
|
(6) |
(the electron kinetic energy is a factor
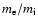 of the ion kinetic energy and
is thus neglected) and pressures,
of the ion kinetic energy and
is thus neglected) and pressures,
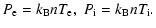 |
|
|
(7) |
The first term on the right-hand side of Eqs. (4)
and (5) represents the thermally conducted flux carried by each particle species. The Spitzer coefficient for the electron thermal
conduction is
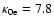
 10-7 erg cm-1 s-1 K-7/2and it is assumed that protons dominate the ion thermal conduction, giving
10-7 erg cm-1 s-1 K-7/2and it is assumed that protons dominate the ion thermal conduction, giving
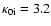
 10-8 erg cm-1 s-1 K-7/2.
The second term on the right-hand side of Eqs. (4)
and (5), the flux of the electron pressure,
10-8 erg cm-1 s-1 K-7/2.
The second term on the right-hand side of Eqs. (4)
and (5), the flux of the electron pressure,  ,
represents
the work done by/on the particles due to the weak electric fields
that arise from quasi-neutral conditions. The third term represents
thermal equilibration between the particle species via collisions. The
Coulomb collision frequency is given by
,
represents
the work done by/on the particles due to the weak electric fields
that arise from quasi-neutral conditions. The third term represents
thermal equilibration between the particle species via collisions. The
Coulomb collision frequency is given by
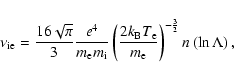 |
(8) |
where
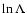 is the Coulomb logarithm. Gravitational effects,
where g|| is the component of gravity parallel to the magnetic
field, have been included for the ion fluid and neglected for the
electron fluid.
is the Coulomb logarithm. Gravitational effects,
where g|| is the component of gravity parallel to the magnetic
field, have been included for the ion fluid and neglected for the
electron fluid. 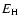 is the volumetric heating rate and its value
in the current work is exactly that required to maintain the initial
atmosphere in hydrostatic equilibrium.
is the volumetric heating rate and its value
in the current work is exactly that required to maintain the initial
atmosphere in hydrostatic equilibrium. 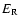 is the volumetric rate
of energy loss due to optically-thin radiative emission, which
includes contributions from the emission lines of the most abundant
elements found in the solar atmosphere and thermal bremsstrahlung.
In the current work the radiative energy losses are calculated for
both equilibrium and non-equilibrium ionisation balances in order to
determine the relative importance of non-equilibrium radiative
effects in the damping of standing acoustic waves. The ionisation
balance (the relative abundance of the ions of a particular element)
is given by
is the volumetric rate
of energy loss due to optically-thin radiative emission, which
includes contributions from the emission lines of the most abundant
elements found in the solar atmosphere and thermal bremsstrahlung.
In the current work the radiative energy losses are calculated for
both equilibrium and non-equilibrium ionisation balances in order to
determine the relative importance of non-equilibrium radiative
effects in the damping of standing acoustic waves. The ionisation
balance (the relative abundance of the ions of a particular element)
is given by
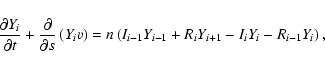 |
(9) |
where Y denotes the element (e.g. H, He, C, etc.) and i the
ionisation stage. For example, Yi=1 denotes neutral Y (or
Y I in spectroscopic notation) and Yi=2 denotes the first
ionisation stage of Y (Y II), etc. Values of
Yi=1=0.25 and
Yi=2=0.75, for example, would show that 25% of element Y is
present in the form of neutral Y and 75% is present in the form
of singly-ionised Y. I and R are temperature dependent
ionisation and recombination rates, respectively. The rates of
Mazzotta et al. (1998) are used here. In equilibrium the
time-dependent and velocity-dependent terms of Eq. (9)
are neglected and the ionisation balance is a function of
temperature only. Away from equilibrium, the ionisation balance
exhibits a complicated dependence upon the local rate of
ionisation/recombination and the transport of ions into/out of
the emitting volume. The emissivity for a single element of atomic
number Z is given by
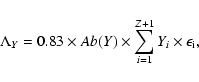 |
(10) |
where 0.83 is the proton:electron ratio, Ab(Y) is the abundance of
element Y relative to hydrogen and
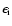 is the emissivity of
ionisation stage i. The summation is over all ionisation stages
(neutral to fully ionised). The ion emissivities used here are
obtained from the Chianti database (Dere et al. 1997; Landi et al. 2006).
is the emissivity of
ionisation stage i. The summation is over all ionisation stages
(neutral to fully ionised). The ion emissivities used here are
obtained from the Chianti database (Dere et al. 1997; Landi et al. 2006).
Finally, the volumetric rate of energy loss due to optically-thin
radiative emission in Eq. (4)
is given by
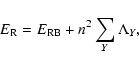 |
(11) |
where
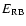 is thermal bremsstrahlung and the summation is over
all of the elements with emission lines that make a significant
contribution to the radiative energy loss. The fifteen most abundant
elements in the set determined by Feldman (1992) are included
in the radiation calculation (H, He, C, N, O, Ne, Na, Mg, Al, Si, S,
Ar, Ca, Fe and Ni). Thus, as one can see, the non-equilibrium ionisation
balance is coupled via Eqs. (9)-(11) to
the hydrodynamic equation for the electron energy, Eq. (4).
is thermal bremsstrahlung and the summation is over
all of the elements with emission lines that make a significant
contribution to the radiative energy loss. The fifteen most abundant
elements in the set determined by Feldman (1992) are included
in the radiation calculation (H, He, C, N, O, Ne, Na, Mg, Al, Si, S,
Ar, Ca, Fe and Ni). Thus, as one can see, the non-equilibrium ionisation
balance is coupled via Eqs. (9)-(11) to
the hydrodynamic equation for the electron energy, Eq. (4).
Table 1:
The uniform heating rates for the hydrostatic initial conditions.
Table 1 shows the uniform heating rate (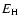 )
required
to maintain equilibrium for each of the hydrostatic initial
conditions, characterised by the loop length (L) and the apex
temperature (
)
required
to maintain equilibrium for each of the hydrostatic initial
conditions, characterised by the loop length (L) and the apex
temperature (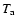 ), that were used in the current work. The
fundamental mode of a standing acoustic wave, with a maximum
velocity amplitude v0=107 cm s-1, was superimposed on each
of these initial conditions. The numerical code HYDRAD was then used
to solve the coupled system of partial differential equations
represented by Eqs. (2) to (7) and
Eq. (9) to find the damping timescales of the
fundamental mode for each set of initial conditions, both for
equilibrium and non-equilibrium treatments of the ionisation balance
and the associated radiative energy losses. Thus, a total of 32 numerical experiments were carried out. For details of the HYDRAD code and recent published results see: Bradshaw & Mason (2003b);
Bradshaw et al. (2004); Bradshaw & Cargill (2006); Taroyan et al. (2007a);
Taroyan et al. (2007b); and Taroyan & Bradshaw (2008).
), that were used in the current work. The
fundamental mode of a standing acoustic wave, with a maximum
velocity amplitude v0=107 cm s-1, was superimposed on each
of these initial conditions. The numerical code HYDRAD was then used
to solve the coupled system of partial differential equations
represented by Eqs. (2) to (7) and
Eq. (9) to find the damping timescales of the
fundamental mode for each set of initial conditions, both for
equilibrium and non-equilibrium treatments of the ionisation balance
and the associated radiative energy losses. Thus, a total of 32 numerical experiments were carried out. For details of the HYDRAD code and recent published results see: Bradshaw & Mason (2003b);
Bradshaw et al. (2004); Bradshaw & Cargill (2006); Taroyan et al. (2007a);
Taroyan et al. (2007b); and Taroyan & Bradshaw (2008).
The missing values in Table 1 indicate the region of the
parameter space in which it was not feasible to carry out the
numerical experiments due to computational constraints; these arose
due to the small time steps associated with the electron thermal
conduction term of Eq. (4)
that were required to
maintain numerical stability in short, hot loops. The numerical
experiments for which the ionisation balance was treated in
equilibrium in this region of the parameter space could be carried
out fairly quickly, however, the run-times required by the
experiments using the non-equilibrium treatment (a vastly more
demanding problem) were considered impractical. In an effort to
reduce the computational time for the
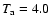 MK and
MK and
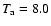 MK experiments, only the most abundant elements (H, He, C,
O and Fe) were included in the non-equilibrium ionisation balance
and radiative energy loss calculations. The remaining ten elements
were treated in equilibrium. All fifteen elements were included in
the non-equilibrium ionisation balance and radiative energy loss
calculations for the
MK experiments, only the most abundant elements (H, He, C,
O and Fe) were included in the non-equilibrium ionisation balance
and radiative energy loss calculations. The remaining ten elements
were treated in equilibrium. All fifteen elements were included in
the non-equilibrium ionisation balance and radiative energy loss
calculations for the
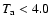 MK experiments.
MK experiments.
Since the influence of the transition region on the damping
timescales is of considerable interest in the current work it is
necessary to ensure that adequate resolution is achieved. The vast
range of spatial scales that exist in the solar atmosphere can make
this a significant difficulty for numerical work. To solve this
problem HYDRAD employs an adaptive grid, which has proven extremely
effective at resolving the smallest scale features and tracking them
as they propagate. In the current work the smallest grid cell is
104 cm (100 m).
3 Discussion of results
Table 2:
Damping timescales of the fundamental mode standing wave for an equilibrium ionisation balance. The associated percentage errors are quoted in brackets.
Table 3:
Damping timescales of the fundamental mode standing wave for a non-equilibrium ionisation balance. The associated percentage errors are quoted in brackets.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9128figb.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg64.gif) |
Figure 2:
The absolute, normalised average velocity,
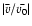 ,
during the decay phase of the fundamental mode standing wave, for ,
during the decay phase of the fundamental mode standing wave, for 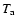 = 0.5 MK, 2 = 0.5 MK, 2 
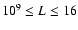  109 cm and an equilibrium ionisation balance.
109 cm and an equilibrium ionisation balance. |
| Open with DEXTER |
Figure 2 shows the profile of the absolute, normalised average velocity,
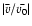 ,
during the decay of a fundamental mode standing wave. The plotted example is for
,
during the decay of a fundamental mode standing wave. The plotted example is for
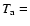 0.5 MK, 2
0.5 MK, 2 
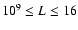
 109 cm and
an equilibrium ionisation balance. The average velocity is defined by
109 cm and
an equilibrium ionisation balance. The average velocity is defined by
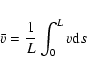 |
(12) |
and 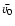 is the average velocity at t=0 s.
is the average velocity at t=0 s.
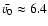
 106 cm s-1 for the velocity
profile given in the lower panel of Fig. 1. Equation (12) was
considered to provide a more suitable measure of the decay of the
wave than choosing, for example, to plot the velocity at the apex of
the loop as a function of time, because it characterises the decay
of the wave along the entire length of the loop.
106 cm s-1 for the velocity
profile given in the lower panel of Fig. 1. Equation (12) was
considered to provide a more suitable measure of the decay of the
wave than choosing, for example, to plot the velocity at the apex of
the loop as a function of time, because it characterises the decay
of the wave along the entire length of the loop.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9128fig2.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg69.gif) |
Figure 3:
Exponentially decaying curve fits to the peaks in
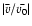 ,
along loops with 2 ,
along loops with 2 
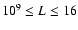  109 cm, during the decay phase of the fundamental mode standing wave. The curve fits correspond to the mode decay for an equilibrium (+ symbol, solid line) and a non-equilibrium (* symbol, triple-dash dot line) ionisation balance. The apex temperature,
109 cm, during the decay phase of the fundamental mode standing wave. The curve fits correspond to the mode decay for an equilibrium (+ symbol, solid line) and a non-equilibrium (* symbol, triple-dash dot line) ionisation balance. The apex temperature, 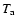 ,
of the initial hydrostatic equilibrium is 0.5 MK. ,
of the initial hydrostatic equilibrium is 0.5 MK. |
| Open with DEXTER |
Figures 3 to 7 show the locations of the peaks in
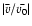 as the standing
mode decays during each of the numerical experiments carried out in
the present study. For example, the locations of the peaks in Fig. 2 are
marked by the + symbols in the corresponding plots in Fig. 3. Figures 3 to 7 also show exponential curve fits to the locations of the peaks.
The curve fits have the form
as the standing
mode decays during each of the numerical experiments carried out in
the present study. For example, the locations of the peaks in Fig. 2 are
marked by the + symbols in the corresponding plots in Fig. 3. Figures 3 to 7 also show exponential curve fits to the locations of the peaks.
The curve fits have the form
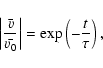 |
(13) |
from which the damping timescales, 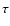 ,
can be estimated. These
are given in Tables 2 and 3, which show the damping timescales of the fundamental mode standing wave in a loop of length (L) and apex temperature (
,
can be estimated. These
are given in Tables 2 and 3, which show the damping timescales of the fundamental mode standing wave in a loop of length (L) and apex temperature (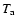 )
for
equilibrium and non-equilibrium ionisation balances. The nature of the damping is not exactly exponential; the wave decays initially somewhat more rapidly than at later times and so the given damping timescales may be regarded as averages over the decay phase. The percentage errors associated with the damping timescales
give the root-mean-square deviation of the quoted value from the damping timescale at any particular time during the decay phase. Thus, the errors are correlated in the sense that whenever the average damping timescale is an underestimate (overestimate)
during a numerical experiment for an equilibrium ionisation balances then it is an underestimate (overestimate) in the corresponding experiment for a non-equilibrium ionisation balance.
)
for
equilibrium and non-equilibrium ionisation balances. The nature of the damping is not exactly exponential; the wave decays initially somewhat more rapidly than at later times and so the given damping timescales may be regarded as averages over the decay phase. The percentage errors associated with the damping timescales
give the root-mean-square deviation of the quoted value from the damping timescale at any particular time during the decay phase. Thus, the errors are correlated in the sense that whenever the average damping timescale is an underestimate (overestimate)
during a numerical experiment for an equilibrium ionisation balances then it is an underestimate (overestimate) in the corresponding experiment for a non-equilibrium ionisation balance.
Though such a simple description as an exponential decay would, of course, not be expected for such a complex process in which several physical mechanisms operate, it is an adequate characterisation to provide an intuitive indication of the relative magnitude of the radiative contribution to the damping timescale, for equilibrium and non-equilibrium ionisation balances.
Table 4:
The percentage difference between the damping timescales
in Tables 2 and 3.
As expected, the shorter or hotter the loop the smaller the damping
timescale of the fundamental mode standing wave and it is also
clear that radiation due to a non-equilibrium ionisation balance leads to consistently
smaller estimates for the damping timescale in comparison with the corresponding equilibrium case.
The percentage differences between the damping timescales for the equilibrium and non-equilibrium
cases in Tables 2 and 3 are given in Table 4, which shows
that the damping timescale can be reduced by up to 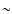 10%.
There is no clear tendency to indicate exactly how significant the effect of a
non-equilibrium ionisation balance on the damping timescale will be for
a loop of given length, although it is generally the case that the
magnitude of the effect is reduced for hotter loops. The densities in
high temperature, near-hydrostatic loops are greater than in cooler,
near-hydrostatic loops, thus collisional timescales are reduced and the
ionisation balance will be closer to equilibrium.
10%.
There is no clear tendency to indicate exactly how significant the effect of a
non-equilibrium ionisation balance on the damping timescale will be for
a loop of given length, although it is generally the case that the
magnitude of the effect is reduced for hotter loops. The densities in
high temperature, near-hydrostatic loops are greater than in cooler,
near-hydrostatic loops, thus collisional timescales are reduced and the
ionisation balance will be closer to equilibrium.
One might be tempted to generalise and suggest that the ionisation
balance is likely to be close to equilibrium in all loops with
densities above a certain threshold. However, to do so would be to
miss several extremely important and more subtle aspects of the
behaviour of the ionisation balance. In the present work the
ionisation balance is driven away from equilibrium by the
interaction between the bulk flow and the temperature gradient, and
it is driven towards equilibrium by ionisation/recombination at a
rate dependent upon the density. The ionisation balance will be
driven further from equilibrium by stronger flows and steeper
temperature gradients, and closer to equilibrium by higher
densities. Understanding the interplay between these processes is
crucially important to understanding the behaviour of the ionisation
balance and determining its effect upon the damping timescale.
Figures 6 and 7 show that the damping timescales
for the loops with
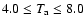 MK are very similar for
each corresponding equilibrium and non-equilibrium case, and so the
ionisation balance must always remain close to equilibrium. The
loops in these two figures are hot and dense, but also relatively
long (8
MK are very similar for
each corresponding equilibrium and non-equilibrium case, and so the
ionisation balance must always remain close to equilibrium. The
loops in these two figures are hot and dense, but also relatively
long (8 
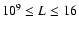
 109 cm) and so the
temperature gradient is comparatively shallow relative to the bulk
flow velocity. A significantly stronger bulk flow would be required
to transport ions across the temperature gradient before they could
equilibrate with their surroundings, and drive the ionisation
balance sufficiently far from equilibrium that it may have an effect
upon the damping timescale. One might expect that the ionisation
balance in loops with
109 cm) and so the
temperature gradient is comparatively shallow relative to the bulk
flow velocity. A significantly stronger bulk flow would be required
to transport ions across the temperature gradient before they could
equilibrate with their surroundings, and drive the ionisation
balance sufficiently far from equilibrium that it may have an effect
upon the damping timescale. One might expect that the ionisation
balance in loops with
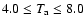 MK and L < 8
MK and L < 8  109 cm would be driven further from equilibrium than in the cases
with
109 cm would be driven further from equilibrium than in the cases
with 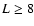
 109 cm, due to the steeper temperature
gradients that would be present in the hydrostatic initial conditions.
However, a steeper temperature
gradient implies an enhanced heat flux from the corona and in order
to drive the necessary heat flux it follows that the radiative
energy loss from the transition region must increase. Since
109 cm, due to the steeper temperature
gradients that would be present in the hydrostatic initial conditions.
However, a steeper temperature
gradient implies an enhanced heat flux from the corona and in order
to drive the necessary heat flux it follows that the radiative
energy loss from the transition region must increase. Since
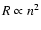 the density must also increase and the ionisation
balance may then be driven towards equilibrium. The density may also be
increased due to chromospheric evaporation driven by the heat flux.
It is worth bearing in mind that the non-equilibrium ionisation balance was calculated
for a reduced set of elements in these cases in order to speed up
the calculations and the effect of a non-equilibrium ionisation
balance may consequently be somewhat underestimated. However, the
chosen elements are the most abundant and radiate the most strongly,
and the addition of elements to the non-equilibrium
ionisation balance calculations is not expected to alter these
results significantly.
the density must also increase and the ionisation
balance may then be driven towards equilibrium. The density may also be
increased due to chromospheric evaporation driven by the heat flux.
It is worth bearing in mind that the non-equilibrium ionisation balance was calculated
for a reduced set of elements in these cases in order to speed up
the calculations and the effect of a non-equilibrium ionisation
balance may consequently be somewhat underestimated. However, the
chosen elements are the most abundant and radiate the most strongly,
and the addition of elements to the non-equilibrium
ionisation balance calculations is not expected to alter these
results significantly.
Figures 3 to 5 show some evidence for the effect of
the interplay between the processes described above on the
ionisation balance and the effect on the damping timescale.
Consider Fig. 3 in which the temperature gradient is
relatively shallow for all L since
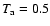 MK. The decay
profiles for the equilibrium and non-equilibrium ionisation balances
are almost identical for the L=2
MK. The decay
profiles for the equilibrium and non-equilibrium ionisation balances
are almost identical for the L=2  109 cm case, despite the
shift in the locations of the peaks (the + and * symbols are not
temporally coincident). This suggests that the effect of the
temporal offset of the peaks in the non-equilibrium case coupled
with the slightly smaller amplitude of each peak compared with the
corresponding peak in the equilibrium case cancel, resulting in the
same damping timescale for each case. The decay profiles differ
between the equilibrium and non-equilibrium cases for the loops with
L=4
109 cm case, despite the
shift in the locations of the peaks (the + and * symbols are not
temporally coincident). This suggests that the effect of the
temporal offset of the peaks in the non-equilibrium case coupled
with the slightly smaller amplitude of each peak compared with the
corresponding peak in the equilibrium case cancel, resulting in the
same damping timescale for each case. The decay profiles differ
between the equilibrium and non-equilibrium cases for the loops with
L=4  109 and L=8
109 and L=8  109 cm, with the damping
timescales reduced in the non-equilibrium cases. Due to the low
densities in these cases, the collisional timescales are not small
enough for the ionisation balance to equilibrate as ions are
transported across the temperature gradient, even though it is
relatively shallow. The decay curve is only fitted to two peaks for
the loop with L=16
109 cm, with the damping
timescales reduced in the non-equilibrium cases. Due to the low
densities in these cases, the collisional timescales are not small
enough for the ionisation balance to equilibrate as ions are
transported across the temperature gradient, even though it is
relatively shallow. The decay curve is only fitted to two peaks for
the loop with L=16  10 9 cm (at t=0 and
10 9 cm (at t=0 and
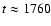 s), though it is evident that the second peaks are more or
less temporally coincident with very similar values for the relative
velocities. This suggests that although the densities are the lowest
encountered in any of the numerical experiments, the temperature
gradient is sufficiently shallow that there is time for the
ionisation balance to be collisionally equilibrated as ions are
transported by the bulk flow.
s), though it is evident that the second peaks are more or
less temporally coincident with very similar values for the relative
velocities. This suggests that although the densities are the lowest
encountered in any of the numerical experiments, the temperature
gradient is sufficiently shallow that there is time for the
ionisation balance to be collisionally equilibrated as ions are
transported by the bulk flow.
The decay profiles of the
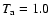 MK loops in Fig. 4 all
exhibit differences between the equilibrium and non-equilibrium
cases, with the damping timescales reduced in the non-equilibrium
cases. Despite the higher densities and smaller collisional
equilibration timescales in these hotter loops, compared with the
corresponding
MK loops in Fig. 4 all
exhibit differences between the equilibrium and non-equilibrium
cases, with the damping timescales reduced in the non-equilibrium
cases. Despite the higher densities and smaller collisional
equilibration timescales in these hotter loops, compared with the
corresponding
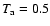 MK loops in Fig. 3, the
non-equilibrium nature of the ionisation balances suggests a
significant sensitivity to the temperature gradients, which are
steeper in Fig. 4 than in Fig. 3. The temperature
gradients of the
MK loops in Fig. 3, the
non-equilibrium nature of the ionisation balances suggests a
significant sensitivity to the temperature gradients, which are
steeper in Fig. 4 than in Fig. 3. The temperature
gradients of the
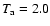 MK loops in Fig. 5 are steeper
than in the previous two figures, but their densities are also
greater and collisional equilibration is better able to mitigate the
sensitivity of the ionisation balance to the temperature gradient.
The
MK loops in Fig. 5 are steeper
than in the previous two figures, but their densities are also
greater and collisional equilibration is better able to mitigate the
sensitivity of the ionisation balance to the temperature gradient.
The
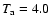 and
and
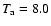 MK loops in Figs. 6 and 7 continue this trend, as already discussed.
MK loops in Figs. 6 and 7 continue this trend, as already discussed.
Overall, these results indicate the existence of regimes, dependent
upon the densities and the strength of the bulk flow relative to the
temperature gradient, within which the ionisation balance may have a
significant effect in reducing the damping timescale of the
fundamental mode standing wave. However, this may not be the full
picture since one must also consider the atomic properties of the
particular population of emitting ions. For example, as discussed,
one might expect the ionisation balance to be closest to equilibrium
in the hottest and most dense loops, but it is also true that the
ionisation potentials for the correspondingly more highly charged
population of ions are greater, which makes them more difficult to
ionise as they are transported across a steep, positive temperature
gradient and drives the ionisation balance away from equilibrium.
Furthermore, highly charged ions generally radiate more weakly than
lower charge states and a non-equilibrium population of ions, formed
at a lower temperature than the local temperature of the plasma,
would tend to radiate more strongly under these conditions, thus
increasing the rate of energy loss from the loop and reducing the
damping timescales accordingly. Therefore, when one considers the
effects of a non-equilibrium ionisation balance one must appreciate
the interaction between the physical and dynamical properties of the
plasma and the atomic properties of the ion population. This adds a
substantial layer of complexity to the problem.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{9128fig7.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg81.gif) |
Figure 8:
The non-equilibrium ionisation balance (solid line) of He, C, O and Fe for the case L=8  109 cm and
109 cm and
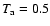 MK at MK at 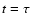 (966 s in Table 3). The equilibrium ionisaton balance (dotted line) is plotted for comparison.
(966 s in Table 3). The equilibrium ionisaton balance (dotted line) is plotted for comparison. |
| Open with DEXTER |
Figures 8 to 12 show the ionisation balances of the
elements He, C, O and a selection of Fe ions (these are among the
most strongly radiating elements in the solar atmosphere) in the
left-hand leg of the loop (s < L/2) for the cases L=8  109 cm and
109 cm and
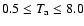 MK. The non-equilibrium
ionisation balance is taken at
MK. The non-equilibrium
ionisation balance is taken at 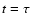 ,
when the amplitude of the
fundamental mode standing wave has decayed by a factor 1/e, and
plotted with the corresponding equilibrium ionisation balances for
comparison. In Figs. 8 and 9 it is clear that the
ionisation balances have essentially shifted to higher temperatures
(via transport across the temperature gradient) and, as mentioned
above, ions will generally radiate more strongly at temperatures
that are higher than their equilibrium formation temperatures. Thus,
shifting the ionisation balances to higher temperatures will result
in a greater rate of energy loss from the loop and hence more
efficient damping, as observed from the numerical experiments.
Generally, the ionisation balances oscillate between higher and
lower temperatures as the wave decays (the velocity amplitude
changes sign and ions are transported in the opposite direction), as
can be seen in Figs. 10 and 11 where the ionisation
balance has shifted to lower temperatures. When the ions are
transported to higher temperatures they encounter lower densities
and so their non-equilibrium states persist. Conversely, when the
ions are transported to lower temperatures they encounter higher
densities and equilibrate more rapidly. The effect on the
non-equilibrium ionisation balance is a larger population of lower
charge states than would be found in equilibrium and, since lower
charge states generally radiate more strongly than higher charge
states, correspondingly greater radiative losses and reduced damping
timescales in the non-equilibrium cases. The ionisation balances
are very close to equilibrium in Fig. 12.
,
when the amplitude of the
fundamental mode standing wave has decayed by a factor 1/e, and
plotted with the corresponding equilibrium ionisation balances for
comparison. In Figs. 8 and 9 it is clear that the
ionisation balances have essentially shifted to higher temperatures
(via transport across the temperature gradient) and, as mentioned
above, ions will generally radiate more strongly at temperatures
that are higher than their equilibrium formation temperatures. Thus,
shifting the ionisation balances to higher temperatures will result
in a greater rate of energy loss from the loop and hence more
efficient damping, as observed from the numerical experiments.
Generally, the ionisation balances oscillate between higher and
lower temperatures as the wave decays (the velocity amplitude
changes sign and ions are transported in the opposite direction), as
can be seen in Figs. 10 and 11 where the ionisation
balance has shifted to lower temperatures. When the ions are
transported to higher temperatures they encounter lower densities
and so their non-equilibrium states persist. Conversely, when the
ions are transported to lower temperatures they encounter higher
densities and equilibrate more rapidly. The effect on the
non-equilibrium ionisation balance is a larger population of lower
charge states than would be found in equilibrium and, since lower
charge states generally radiate more strongly than higher charge
states, correspondingly greater radiative losses and reduced damping
timescales in the non-equilibrium cases. The ionisation balances
are very close to equilibrium in Fig. 12.
A common feature of the ionisation balances in all of
Figs. 8 to 12 is that the populations of ions
formed at lower (transition region) temperatures exhibit far
stronger departures from equilibrium with the thermal properties of
the plasma, despite the fact that the strongest flows are found at
higher (coronal) temperatures (since the anti-node of the
fundamental mode standing wave is located at the loop apex). This
emphasises the sensitivity of the ionisation balance to the
transition region temperature gradient and shows that it is the
physics of the transition region that is responsible for the reduced
damping timescales when non-equilibrium processes on the ionisation
balance are properly accounted for. Therefore, as also shown by
Bradshaw & Cargill (2005), the transition region can be very important in
governing the dynamical behaviour of the entire loop. The
populations of the more highly charged ions found at coronal
temperatures remain closer to equilibrium due to the much shallower
temperature gradients. Clearly, the non-equilibrium ionisation
balances induced by the decay of the fundamental mode standing wave
will affect the properties of the transition region emission lines
that may be used for spectroscopic diagnostic purposes, but the
results discussed here also show that diagnostics with coronal
emission lines should be reliable for use in coronal seismology
applications.
As an example, consider a set of observations of the decay of a
fundamental mode standing wave in a coronal loop from which
spectroscopically derived measurements of 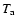 (from line ratios)
and v (from Doppler shifts) can be obtained. The damping
timescale,
(from line ratios)
and v (from Doppler shifts) can be obtained. The damping
timescale, 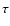 ,
can be calculated from the Doppler shifts. These
results can then be used to determine L, a traditionally difficult
measurement to make due to projection and line-of-sight effects. The
question to be addressed is what effect does the non-equilibrium
ionisation balance that may be induced in the transition region have
on the reliability of the measurement of L?
,
can be calculated from the Doppler shifts. These
results can then be used to determine L, a traditionally difficult
measurement to make due to projection and line-of-sight effects. The
question to be addressed is what effect does the non-equilibrium
ionisation balance that may be induced in the transition region have
on the reliability of the measurement of L?
If it is assumed that the damping timescale varies as some power of
the length or temperature of the loop, e.g.
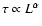 or
or
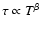 ,
then the values of the power-law indices
,
then the values of the power-law indices 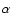 and
and 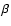 can be estimated for constant length or
temperature from the damping timescales in Tables 2 and 3.
can be estimated for constant length or
temperature from the damping timescales in Tables 2 and 3.
Table 5:
Values of 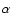 calculated from the damping timescales in Tables 2 and 3.
calculated from the damping timescales in Tables 2 and 3.
Table 6:
Values of 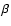 calculated from the damping timescales in Tables 2 and 3.
calculated from the damping timescales in Tables 2 and 3.
Tables 5 and 6 show the values of 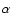 and
and
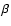 calculated using a least-squares fit, and the corresponding
coefficient of determination (R2), for constant values of
calculated using a least-squares fit, and the corresponding
coefficient of determination (R2), for constant values of 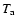 and L. Table 5 shows that the dependence of the damping
timescale on L is approximately linear for both equilibrium and
non-equilibrium ionisation balances. Table 6 shows that
the damping timescale exhibits a gradually weakening dependence on
and L. Table 5 shows that the dependence of the damping
timescale on L is approximately linear for both equilibrium and
non-equilibrium ionisation balances. Table 6 shows that
the damping timescale exhibits a gradually weakening dependence on
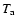 with increasing L. The power-law fits for L=16
with increasing L. The power-law fits for L=16  109 cm are relatively poor due to the lack of peak locations in
Figs. 3 to 7 from which to calculate the decay
timescales. For example, in Fig. 3 there are only two
peaks in the profile of
109 cm are relatively poor due to the lack of peak locations in
Figs. 3 to 7 from which to calculate the decay
timescales. For example, in Fig. 3 there are only two
peaks in the profile of 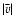 for L=16
for L=16  109 cm; one at
t=0 and another at
109 cm; one at
t=0 and another at
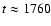 s. However, the general trend
is indicative and shows that for the longest loops the damping
timescale of the fundamental mode standing wave is only weakly
dependent upon
s. However, the general trend
is indicative and shows that for the longest loops the damping
timescale of the fundamental mode standing wave is only weakly
dependent upon 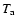 .
.
The values of 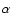 for the equilibrium and non-equilibrium cases
in Table 5 are essentially identical, with values of
R2 very close to 1.0. Therefore, given the values of
for the equilibrium and non-equilibrium cases
in Table 5 are essentially identical, with values of
R2 very close to 1.0. Therefore, given the values of 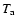 (as
obtained from line ratios) to select an appropriate value of
(as
obtained from line ratios) to select an appropriate value of
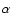 and
and 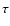 (as obtained from Doppler shifts), one may
determine L and be confident that a non-equilibrium ionisation
balance induced in the transition region should not have a
significant effect on the result. Conversely, Table 6
shows that
(as obtained from Doppler shifts), one may
determine L and be confident that a non-equilibrium ionisation
balance induced in the transition region should not have a
significant effect on the result. Conversely, Table 6
shows that 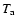 could be obtained from measurements of L with
considerably less accuracy for shorter loops and not at all for
longer loops.
could be obtained from measurements of L with
considerably less accuracy for shorter loops and not at all for
longer loops.
4 Summary, conclusions and future work
A detailed understanding of the physical processes that determine
the damping timescales of MAWs is essential to the interpretation
of diagnostic results obtained from the application of
magneto-seismology. An extensive numerical study
of the damping of the fundamental mode standing wave in a solar
coronal loop, for a wide range of loop lengths and apex
temperatures, has been carried out in order to assess the influence
of the transition region and the importance of radiative energy losses,
arising from equilibrium and non-equilibrium ionisation balances,
on the damping timescale.
It has been found that the radiative emission arising from a non-equilibrium
ionisation balance will always act to reduce the damping timescale (in
comparison to the equilibrium case) and may do so by up to  10%.
Mendoza-Briceño et al. (2004) found a similar order of reduction in
the damping timescale when they included gravitational stratification.
A non-equilibrium ionisation balance acts to reduce the damping timescale due
to a bias towards the existence of lower charge states, which gives rise to
greater radiative energy losses because lower charge states tend to radiate
more strongly than higher charge states.
10%.
Mendoza-Briceño et al. (2004) found a similar order of reduction in
the damping timescale when they included gravitational stratification.
A non-equilibrium ionisation balance acts to reduce the damping timescale due
to a bias towards the existence of lower charge states, which gives rise to
greater radiative energy losses because lower charge states tend to radiate
more strongly than higher charge states.
The population of ions formed at transition region temperatures exhibit the
strongest departures from equilibrium, which emphasises the sensitivity of
the ionisation balance to the transition region temperature gradient and shows
that the physics of the transition region is most crucial in determining
the magnitude of the reduction of the damping timescale when a non-equilibrium
ionisation balance is properly accounted for.
Overall, these results indicate the existence of regimes, dependent upon a coupling
between the density, the strength of the bulk flow relative to the temperature gradient
and the atomic properties of the emitting ions, within which the ionisation balance
may have a significant (of order 10%) effect in reducing the damping timescale
of the fundamental mode standing wave.
The ionisation balance induced in the transition region by the decay of the
fundamental mode standing wave may also affect the properties of the emission
lines used for spectroscopic diagnostics. However, due to the shallower temperature
gradients, diagnostics with coronal emission lines should be reliable.
Finally, as an application of coronal seismology, it has been found that given a reliable
determination of the apex temperature and the damping timescale using spectroscopic
diagnostic methods, one may estimate the loop length to a reasonable degree of accuracy
and be confident that a non-equilibrium ionisation balance in the transition region
should not introduce any significant ambiguity to the result. Conversely, it has been shown
that one should not attempt to estimate the apex temperature from measurements of the loop
length and the damping timescale.
There are a number of avenues along which the current work might profitably be extended.
A regime of substantially stronger bulk flows would provide more strongly
non-equilibrium ionisation balances and may affect the conclusion regarding the reliability
of a determination of the loop length, L, from 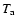 and
and 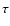 .
However, in the lower
temperature and lower density range of the parameter space, the chosen maximum bulk flow
velocity of 107 cm s-1 has a relatively large Mach number, and so this effect has been
accounted for to some extent. However, it would be interesting to study a regime
of constant Mach number with varying L and
.
However, in the lower
temperature and lower density range of the parameter space, the chosen maximum bulk flow
velocity of 107 cm s-1 has a relatively large Mach number, and so this effect has been
accounted for to some extent. However, it would be interesting to study a regime
of constant Mach number with varying L and 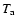 .
At the higher densities implied by higher
temperatures, one may expect the correspondingly greater rates of ionisation and recombination
to drive the ionisation balance towards equilibrium, although, as discussed in the text, the
atomic properties of the ions may also have an important effect.
.
At the higher densities implied by higher
temperatures, one may expect the correspondingly greater rates of ionisation and recombination
to drive the ionisation balance towards equilibrium, although, as discussed in the text, the
atomic properties of the ions may also have an important effect.
One important extension of the present investigation would be the self-consistent generation of a
fundamental mode standing wave (as in Taroyan et al. 2005) rather than imposing a
fundamental mode velocity profile on a hydrostatic solution, and following its subsequent decay.
As shown by De Moortel & Bradshaw (2008), the physical properties of coronal perturbations can be
very difficult to recover from observational data alone and one must look to forward-modeling
in order to guide the interpretation of observational results. Therefore, an important
extension of the present work would be the generation of synthetic observations, using
forward-modeling techniques, in order to identify spectral signatures of the damping of
fundamental mode standing waves and to assess their reliability in terms of recovering the
underlying physics of this process.
Acknowledgements
S.B. is grateful to the STFC for their support through the award of a
Post-Doctoral Fellowship. R.E. acknowledges M. Kéray for patient
encouragement and is also grateful to the NSF, Hungary (OTKA, Ref. No. K67746)
for the financial support received.
- Banerjee,
D., Erdélyi, R., Oliver, R., & O'Shea, E. 2007,
Sol. Phys., 136
(In the text)
-
Berghmans, D., & Clette, F. 1999, Sol. Phys., 186,
207 [NASA ADS] [CrossRef]
(In the text)
-
Bradshaw, S. J., & Mason, H. E. 2003a, A&A, 401,
699 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Bradshaw, S. J., & Mason, H. E. 2003b, A&A, 407,
1127 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bradshaw,
S. J., & Cargill, P. J. 2005, A&A, 437, 311 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bradshaw,
S. J., & Cargill, P. J. 2006, A&A, 458, 987 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bradshaw,
S. J., Del Zanna, G., & Mason, H. E. 2004, A&A,
425, 287 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- De
Moortel, I., & Bradshaw, S. J. 2008, Sol. Phys.,
submitted
(In the text)
- De
Moortel, I., Ireland, J., & Walsh, R. W. 2000, A&A,
355, L23 [NASA ADS]
(In the text)
- De
Moortel, I., Hood, A. W., Ireland, J., & Walsh, R. W.
2002a, Sol. Phys., 209, 89 [NASA ADS] [CrossRef]
(In the text)
- De
Moortel, I., Ireland, J., Hood, A. W., & Walsh, R. W.
2002b, A&A, 387, L13 [NASA ADS] [CrossRef] [EDP Sciences]
- De
Moortel, I., Ireland, J., Walsh, R. W., & Hood, A. W.
2002c, Sol. Phys., 209, 61 [NASA ADS] [CrossRef]
(In the text)
- De
Pontieu, B., Erdélyi, R., & de Wijn, A. G. 2003a,
ApJ, 595, L63 [NASA ADS] [CrossRef]
(In the text)
- De
Pontieu, B., Tarbell, T., & Erdélyi, R. 2003b, ApJ, 590,
502 [NASA ADS] [CrossRef]
- De
Pontieu, B., Erdélyi, R., & James, S. P. 2004,
Nature, 430, 536 [NASA ADS] [CrossRef]
(In the text)
- De
Pontieu, B., Erdélyi, R., & De Moortel, I. 2005, ApJ, 624,
L61 [NASA ADS] [CrossRef]
(In the text)
- Dere, K. P.,
Landi, E., Mason, H. E., Monsignori Fossi, B. C., &
Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Erdélyi, R. 2006a, Royal Soc. London Philos. Trans. Ser. A,
364, 351 [NASA ADS] [CrossRef]
(In the text)
-
Erdélyi, R. 2006b, in ESA Special Publication, 624,
Proceedings of SOHO 18/GONG 2006/HELAS I, Beyond the spherical
Sun
- Feldman, U.
1992, Phys. Scri., 46, 202 [NASA ADS] [CrossRef]
(In the text)
- Hansteen,
V. 1993, ApJ, 402, 741 [NASA ADS] [CrossRef]
(In the text)
- Kliem, B.,
Dammasch, I. E., Curdt, W., & Wilhelm, K. 2002, ApJ, 568,
L61 [NASA ADS] [CrossRef]
(In the text)
- Landi, E., Del
Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef]
(In the text)
- Mazzotta,
P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998,
A&AS, 133, 403 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- McEwan,
M. P., Donnelly, G. R., Díaz, A. J., &
Roberts, B. 2006, A&A, 460, 893 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Mendoza-Briceño, C. A.,
& Erdélyi, R. 2006, ApJ, 648, 722 [NASA ADS] [CrossRef]
(In the text)
- Mendoza-Briceño, C. A.,
Erdélyi, R., & Di G. Sigalotti, L. 2002, ApJ, 579,
L49 [NASA ADS] [CrossRef]
(In the text)
- Mendoza-Briceño, C. A.,
Erdélyi, R., & Sigalotti, L. D. G. 2004, ApJ,
605, 493 [NASA ADS] [CrossRef]
(In the text)
- Mendoza-Briceño, C. A.,
Sigalotti, L. D. G., & Erdélyi, R. 2005, ApJ,
624, 1080 [NASA ADS] [CrossRef]
(In the text)
-
Müller, D. A. N., Hansteen, V. H., & Peter,
H. 2003, A&A, 411, 605 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Müller, D. A. N., Peter, H., & Hansteen,
V. H. 2004, A&A, 424, 289 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Nakariakov, V. M., & Verwichte, E. 2005, Living Rev. Sol.
Phys., 2, 3 [NASA ADS]
(In the text)
-
Nakariakov, V. M., Verwichte, E., Berghmans, D., &
Robbrecht, E. 2000, A&A, 362, 1151 [NASA ADS]
(In the text)
-
Nakariakov, V. M., Tsiklauri, D., Kelly, A., Arber,
T. D., & Aschwanden, M. J. 2004, A&A, 414,
L25 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Ofman, L.,
& Wang, T. 2002, ApJ, 580, L85 [NASA ADS] [CrossRef]
(In the text)
- Ofman, L.,
Nakariakov, V. M., & Sehgal, N. 2000, ApJ, 533, 1071 [NASA ADS] [CrossRef]
(In the text)
- Porter,
L. J., Klimchuk, J. A., & Sturrock, P. A. 1994,
ApJ, 435, 502 [NASA ADS] [CrossRef]
(In the text)
-
Robbrecht, E., Verwichte, E., Berghmans, D., et al. 2001,
A&A, 370, 591 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Roberts,
B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279,
857 [NASA ADS] [CrossRef]
(In the text)
- Sarro,
L. M., Erdélyi, R., Doyle, J. G., & Pérez,
M. E. 1999, A&A, 351, 721 [NASA ADS]
(In the text)
- Spadaro,
D., Zappala, R. A., Antiochos, S. K., Lanzafame, G.,
& Noci, G. 1990, ApJ, 362, 370 [NASA ADS] [CrossRef]
(In the text)
- Taroyan,
Y., & Bradshaw, S. J. 2008, A&A, submitted
(In the text)
- Taroyan,
Y., Erdélyi, R., Doyle, J. G., & Bradshaw, S. J.
2005, A&A, 438, 713 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Taroyan,
Y., Erdélyi, R., Doyle, J. G., & Bradshaw, S. J.
2007a, A&A, 462, 331 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Taroyan,
Y., Erdélyi, R., Wang, T. J., & Bradshaw, S. J.
2007b, ApJ, 659, L173 [NASA ADS] [CrossRef]
(In the text)
- Teriaca,
L., Doyle, J. G., Erdélyi, R., & Sarro, L. M.
1999, A&A, 352, L99 [NASA ADS]
(In the text)
-
Tsiklauri, D., Nakariakov, V. M., Arber, T. D., &
Aschwanden, M. J. 2004, A&A, 422, 351 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Wang, T.,
Solanki, S. K., Curdt, W., Innes, D. E., & Dammasch,
I. E. 2002, ApJ, 574, L101 [NASA ADS] [CrossRef]
(In the text)
- Wang,
T. J., Solanki, S. K., Curdt, W., et al. 2003a,
A&A, 406, 1105 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Wang,
T. J., Solanki, S. K., Innes, D. E., Curdt, W.,
& Marsch, E. 2003b, A&A, 402, L17 [NASA ADS] [CrossRef] [EDP Sciences]
- Wang, T. J.,
Solanki, S. K., Innes, D. E., & Curdt, W. 2005,
A&A, 435, 753 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9128fig1.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg17.gif)
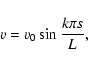
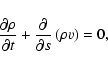
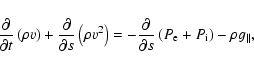
![$\displaystyle %
\frac{\partial E_{\rm e}}{\partial t} +
\frac{\partial}{\partial s}\left[\left(E_{\rm e} + P_{\rm e}\right)v\right]$](/articles/aa/full/2008/19/aa9128-07/img21.gif)
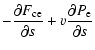
![$\displaystyle %
\frac{\partial E_{\rm i}}{\partial t} +
\frac{\partial}{\partial s}\left[\left(E_{\rm i} + P_{\rm i}\right)v\right]$](/articles/aa/full/2008/19/aa9128-07/img24.gif)
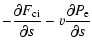
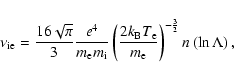
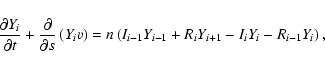
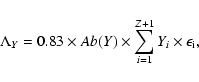
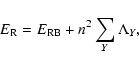
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9128figb.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg64.gif)
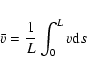
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9128fig2.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9128fig3.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{9128fig4.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg71.gif)
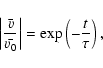
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{9128fig7.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg81.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{9128fig8.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg82.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{9128fig9.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg83.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{9128figc.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg84.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{9128figd.ps}\end{figure}](/articles/aa/full/2008/19/aa9128-07/Timg85.gif)