A&A 483, 1-5 (2008)
DOI: 10.1051/0004-6361:20079074
M. Persic1 - A. De Angelis2,3
1 - INAF and INFN, via G.B.Tiepolo 11, 34143 Trieste, Italy
2 -
Università di Udine and INFN, via delle Scienze 208, 33100 Udine, Italy
3 -
Instituto Superior Técnico, Lisboa, Portugal
Received 15 November 2007 / Accepted 29 January 2008
Abstract
The distribution of TeV spectral slopes versus redshift for currently known
TeV blazars (16 sources with z ![]() 0.21, and one with z > 0.25) is essentially a
scatter plot with hardly any hint of a global trend. We suggest that this is the outcome
of two combined effects of intergalactic
0.21, and one with z > 0.25) is essentially a
scatter plot with hardly any hint of a global trend. We suggest that this is the outcome
of two combined effects of intergalactic
![]() absorption, plus an inherent
feature of the SSC (synchro-self-Compton) process of blazar emission. First, flux dimming
introduces a bias that favors detection of progressively more flaring sources at higher
redshifts. According to mainstream SSC models, more flaring source states imply sources
with flatter TeV slopes. This results in a structured relation between intrinsic TeV slope
and redshift. The second effect, spectral steepening by intergalactic absorption, affects
sources progressively with distance and effectively wipes out the intrinsic slope-redshift
correlation.
absorption, plus an inherent
feature of the SSC (synchro-self-Compton) process of blazar emission. First, flux dimming
introduces a bias that favors detection of progressively more flaring sources at higher
redshifts. According to mainstream SSC models, more flaring source states imply sources
with flatter TeV slopes. This results in a structured relation between intrinsic TeV slope
and redshift. The second effect, spectral steepening by intergalactic absorption, affects
sources progressively with distance and effectively wipes out the intrinsic slope-redshift
correlation.
Key words: galaxies: BL Lacertae objects: general - gamma rays: observations - cosmology: diffuse radiation
With the increasing number of very high energy (VHE) ![]() -ray detection of blazars, a broad correlation between observed slope and redshift was generally expected, in the sense that higher redshift sources would tend to show systematically steeper spectra.
-ray detection of blazars, a broad correlation between observed slope and redshift was generally expected, in the sense that higher redshift sources would tend to show systematically steeper spectra.
The reason for this is absorption of the emitted VHE emission by the intergalactic background
light (IBL), i.e. the integrated optical/IR emission from the evolving stellar populations in galaxies (e.g., Hauser & Dwek 2001). In fact, pair creation due to the interaction of a hard photon (with energy E) with a soft photon (with energy ![]() )
is expected provided that
)
is expected provided that
![]() >
>
![]() .
The cross section of the
.
The cross section of the
![]()
![]()
![]() interaction,
interaction,
![]() (Heitler 1960) is maximized when
(Heitler 1960) is maximized when ![]()
![]()
![]() .
Then, if E
.
Then, if E ![]() 1 TeV, pair creation
will be most likely for
1 TeV, pair creation
will be most likely for ![]()
![]()
![]() eV, which corresponds to a 2
eV, which corresponds to a 2 ![]() m (K-band) photon. The formalism required to evaluate this effect has been largely developed by Stecker and collaborators (e.g., Stecker 1971; Stecker et al. 1992, 2006).
m (K-band) photon. The formalism required to evaluate this effect has been largely developed by Stecker and collaborators (e.g., Stecker 1971; Stecker et al. 1992, 2006).
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{slope_z.ps}\end{figure}](/articles/aa/full/2008/19/aa9074-07/Timg15.gif) |
Figure 1: Observed TeV slope vs. redshift for known TeV blazars. Bars denote statistical uncertainties as quoted in the original papers. |
| Open with DEXTER | |
However, when we plot the currently known observed TeV slopes against redshift (Fig. 1),
we see a scatter plot with hardly any sign of a global correlation: neglecting slope
uncertainties, a global linear correlation is suggested only marginally (![]() 2
2![]() )
by the whole data sample (r = 0.52, N=18). Even so, most of the suggestion's strength
comes from only the two points at z > 0: for the bulk of the distribution, which provides
a fair sampling of the redshift interval z
)
by the whole data sample (r = 0.52, N=18). Even so, most of the suggestion's strength
comes from only the two points at z > 0: for the bulk of the distribution, which provides
a fair sampling of the redshift interval z ![]() 0.2, there is no correlation (r = 0.22,
N=16). In this note we propose an interpretation of Fig. 1.
0.2, there is no correlation (r = 0.22,
N=16). In this note we propose an interpretation of Fig. 1.
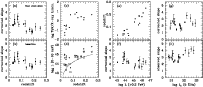 |
Figure 2:
Parameter trends for the TeV blazars in Table 1.
(i) IBL-corrected VHE slope vs. redshift. The spectral slopes have been corrected for IBL absorption according to the ``fast evolution'' a) and ``baseline'' b) IBL models of
Stecker et al. (2006) as parameterized by Stecker & Scully (2006).
(ii) VHE to 2-10 keV luminosity ratio versus redshift c), and 2-10 keV luminosity
versus redshift d). Given the modest redshifts encompassed by the current sample of TeV blazars, distances have been computed according to D(z) = cz/H0 (with H0 = 72 km s-1 Mpc-1), and luminosities have not been k-corrected. The VHE luminosities are
IBL-corrected using the baseline model of Stecker & Scully (2006). In panel d), the filled dots represent X-ray data taken simultaneously with the TeV measurements, whereas the empty squares represent historical low flux states; the thin dotted curve represents the ``visibility function'' for a 2-10 keV instrumental sensitivity of 7 |
| Open with DEXTER | |
Table 1: TeV blazar data.
The cross section for the reaction
![]()
![]()
![]() is
(Heitler 1960),
is
(Heitler 1960),
| (1) |
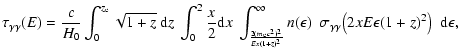 |
(2) |
Along the same path, but using recent data on galaxy luminosity functions and redshift evolution,
Stecker et al. (2006, 2007a,b) made a detailed evaluation of the IBL density as a function of both energy and redshift for 0.003 eV ![]()
![]()
![]() 13.6 eV and 0 < z < 6 in the
13.6 eV and 0 < z < 6 in the ![]() CDM universe with
CDM universe with
![]() = 0.7 and
= 0.7 and
![]() = 0.3. Using their calculated IBL photon densities, they
calculated
= 0.3. Using their calculated IBL photon densities, they
calculated
![]() for
for ![]() -rays with energies 0.004
-rays with energies 0.004 ![]() (E/TeV)
(E/TeV) ![]() 100 emitted by sources at redshift 0 < z < 5.
100 emitted by sources at redshift 0 < z < 5.
Stecker & Scully (2006) fitted such
![]() to
a form that was assumed to be logarithmic in E in the energy range 0.2 TeV
to
a form that was assumed to be logarithmic in E in the energy range 0.2 TeV ![]() E
E ![]() 2 TeV and linear in z for 0.05
2 TeV and linear in z for 0.05 ![]() z < 0.4, i.e.,
z < 0.4, i.e.,
![]() = (A+Bz) +
= (A+Bz) +
![]() .
Consequently, if the intrinsic source spectrum can be described as a power law,
.
Consequently, if the intrinsic source spectrum can be described as a power law,
![]() =
=
![]() ,
in the band between 0.2 TeV and 2 TeV, the observed emission can be approximated as
,
in the band between 0.2 TeV and 2 TeV, the observed emission can be approximated as
![]() =
=
![]()
![]() ,
i.e., the spectrum will be attenuated by a factor
,
i.e., the spectrum will be attenuated by a factor
![]() and steepened by
and steepened by
![]() = C+Dz. The numerical values given by Stecker & Scully (2006) are A = -0.346 (-0.475), B=16.3 (21.6), C = -0.0675 (-0.0972), and D= 7.99 (10.6) in the Stecker et al. (2006) baseline (fast) evolution model.
= C+Dz. The numerical values given by Stecker & Scully (2006) are A = -0.346 (-0.475), B=16.3 (21.6), C = -0.0675 (-0.0972), and D= 7.99 (10.6) in the Stecker et al. (2006) baseline (fast) evolution model.
In Figs. 2a,b we plot the IBL-corrected slopes versus redshift, using the fast (Fig. 2a) and baseline (Fig. 2b) evolution models of Stecker & Scully (2006)![]() . A loose trend of flatter slopes at higher redshift is apparent now: from Table 1 we derive
. A loose trend of flatter slopes at higher redshift is apparent now: from Table 1 we derive ![]()
![]()
![]() = 2.62
= 2.62 ![]() 0.16 for z < 0.1 and
0.16 for z < 0.1 and ![]()
![]()
![]() = 1.97
= 1.97 ![]() 0.15 for z > 0.1 (using the baseline correction; the fast-evolution correction only
enhances the effect). In this paper we suggest that the trend of intrinsic slope with redshift is
induced by a luminosity effect - the latter, in turn, resulting from a selection effect. A
possible correlation of spectral flatness and luminosity with redshift was also pointed out by
Stecker et al. (2007a,b).
0.15 for z > 0.1 (using the baseline correction; the fast-evolution correction only
enhances the effect). In this paper we suggest that the trend of intrinsic slope with redshift is
induced by a luminosity effect - the latter, in turn, resulting from a selection effect. A
possible correlation of spectral flatness and luminosity with redshift was also pointed out by
Stecker et al. (2007a,b).
Let us consider which emission conditions in blazars can lead to flatter TeV slopes. The standard synchrotron-Compton emission model of blazars (e.g., Jones et al. 1974; Maraschi et al. 1992; Mastikiadis & Kirk 1997) gives us a clue on the link between active phase and TeV spectral shape in blazars. Its basic feature is that, if the distribution function of the emitting electrons changes at the highest energies, correlated flaring at X-ray and TeV energies are produced, with the highest energy electrons producing X-rays via snchrotron and the TeV radiation via IC scattering.
A well-known example of this correlation is provided by Mrk 501 (Pian et al. 1998): during the giant flare of April 1997, its (apparent) bolometric luminosity increased by a factor of ![]() 20, its
synchrotron and IC peaks shifted to higher energies by, respectively, a factor
20, its
synchrotron and IC peaks shifted to higher energies by, respectively, a factor ![]() 100 (into the
hard X-ray range,
100 (into the
hard X-ray range, ![]() 50-100 keV) and a factor
50-100 keV) and a factor ![]() 10 (Klein-Nishina limited, into
the sub-TeV range), and
10 (Klein-Nishina limited, into
the sub-TeV range), and
![]() increased by a factor of
increased by a factor of ![]() 3. As the shift of the
synchrotron peak by
3. As the shift of the
synchrotron peak by ![]() 2 orders of magnitude could not be due to variations of the magnetic field and/or the Doppler factor because enormous variations would have been demanded on either quantity that would have revealed themselves by affecting other parts of the spectrum (which was not observed), the luminosity and spectral variation could be explained by invoking an injection, continuous throughout the duration of the burst, of energetic electrons that became superposed to the baseline distribution of emitting electrons responsible for the quiescent emission of Mrk 501. The former had a spectrum that
was flatter than the latter, and extended to higher (by a factor
2 orders of magnitude could not be due to variations of the magnetic field and/or the Doppler factor because enormous variations would have been demanded on either quantity that would have revealed themselves by affecting other parts of the spectrum (which was not observed), the luminosity and spectral variation could be explained by invoking an injection, continuous throughout the duration of the burst, of energetic electrons that became superposed to the baseline distribution of emitting electrons responsible for the quiescent emission of Mrk 501. The former had a spectrum that
was flatter than the latter, and extended to higher (by a factor ![]() 10-30) energies (see Pian et al. 1998). The resulting spectral energy distribution (SED) involved, w.r.t. the baseline case, a higher power output, a higher Compton/synchrotron power ratio, and both the synchrotron and Compton
peaks located at higher energies: that meant a harder TeV slope and enhanced 2-10 keV and TeV fluxes. The hardening and increase of the TeV emission, simultaneously with an increase of the 2-10 keV emission, has been observed also in other blazars, down to very short (e.g., hours and minutes) time scales (e.g., see Mrk 421 and Mrk 501 in Table 1 and references cited therein).
10-30) energies (see Pian et al. 1998). The resulting spectral energy distribution (SED) involved, w.r.t. the baseline case, a higher power output, a higher Compton/synchrotron power ratio, and both the synchrotron and Compton
peaks located at higher energies: that meant a harder TeV slope and enhanced 2-10 keV and TeV fluxes. The hardening and increase of the TeV emission, simultaneously with an increase of the 2-10 keV emission, has been observed also in other blazars, down to very short (e.g., hours and minutes) time scales (e.g., see Mrk 421 and Mrk 501 in Table 1 and references cited therein).
Because all the known TeV blazars, including Mrk 501, are of the HBL type (with one LBL exception, BL Lacertae), whose SEDs are well reproduced by the SSC model (Ghisellini et al. 1998), we expect that the basic features of Pian et al.'s (1998) model of the 1997 burst of Mrk 501 apply to TeV blazar in general. Hence, we do expect a correlation between harder TeV spectral shapes and more active emission states in (HBL) blazars. We then have to examine whether more distant sources are found, on the average, in more active states.
Within the theoretical SSC framework outlined above, two indicators of enhanced emission activity are (i) the TeV/X-ray luminosity ratio, and (ii) the X-ray enhancement. The former quantity,
based on simultaneous data, represents the Compton/synchrotron power ratio. The latter quantity is
defined as the ratio of the 2-10 keV power, measured simultaneously with the TeV observations, to its lowest historical level: it measures the increase of the synchrotron power, i.e. the strength of the activity.
(i) In Fig. 2c we plot the ratio of intrinsic TeV to X-ray luminosity versus redshift. In both bands, the luminosities are computed from the observed fluxes and redshifts (k-corrections do not significantly alter the results![]() ), whereas
the TeV luminosities are IBL-corrected using the baseline model of Stecker & Scully (2006). Even though the fields of view (FoVs) of the different X-ray and Cherenkov detectors are different, since the measured blazar fluxes do originate from (effectively) point-like sources and no other (known) X-ray or TeV sources lie in the detectors' FoVs, in Fig. 2c there is no need to account for the different FoVs. Furthermore,
in the SSC framework the synchrotron and Compton emissions are essentially cospatial and hence are affected by the same beaming-related boost factor. Indeed there is a sharp correlation, suggesting an increasing importance of the Compton hump for more distant sources.
), whereas
the TeV luminosities are IBL-corrected using the baseline model of Stecker & Scully (2006). Even though the fields of view (FoVs) of the different X-ray and Cherenkov detectors are different, since the measured blazar fluxes do originate from (effectively) point-like sources and no other (known) X-ray or TeV sources lie in the detectors' FoVs, in Fig. 2c there is no need to account for the different FoVs. Furthermore,
in the SSC framework the synchrotron and Compton emissions are essentially cospatial and hence are affected by the same beaming-related boost factor. Indeed there is a sharp correlation, suggesting an increasing importance of the Compton hump for more distant sources.
(ii) In Fig. 2d we plot the X-ray luminosities of our TeV blazars versus redshift (filled dots: fluxes measured simultaneously with the TeV measurements; open squares: faintest historical fluxes). The lower limit to the allowed
![]() distribution in Fig. 2d is dictated by a combination of X-ray telescope sensitivities, exposure times, and source spectral shape: for sake of
illustration, in Fig. 2d we plot an effective limiting sensitivity of
distribution in Fig. 2d is dictated by a combination of X-ray telescope sensitivities, exposure times, and source spectral shape: for sake of
illustration, in Fig. 2d we plot an effective limiting sensitivity of ![]() = 0.7
= 0.7 ![]() 10-11 erg cm-2 s-1. A trend is apparent in the data. Whereas the ground-state emissions (open squares) tend to be found close to the limiting curve, the TeV-selected X-ray emissions tend to lie significantly above it. The strongest enhancements, as defined here, occur for the nearest sources (z < 0.1): this however stems from a selection effect, as fainter fluxes can be detected from more
nearby, but otherwise similar, sources. For more substantial redshifts (z > 0.1), we notice that the X-ray emissions tend to be more enhanced w.r.t. their ground states with increasing z: although noisy, there appears to be a link between such enhancements and redshift.
10-11 erg cm-2 s-1. A trend is apparent in the data. Whereas the ground-state emissions (open squares) tend to be found close to the limiting curve, the TeV-selected X-ray emissions tend to lie significantly above it. The strongest enhancements, as defined here, occur for the nearest sources (z < 0.1): this however stems from a selection effect, as fainter fluxes can be detected from more
nearby, but otherwise similar, sources. For more substantial redshifts (z > 0.1), we notice that the X-ray emissions tend to be more enhanced w.r.t. their ground states with increasing z: although noisy, there appears to be a link between such enhancements and redshift.
Thus, both our activity indicators suggest that TeV sources further away tend to be observed during more active phases. Why? Our tentative answer - a selection effect - is based on the following argument. Moving to higher redshifts, X-ray and TeV measurements are both affected by geometrical flux dilution (![]() z-2), but the latter are also affected by IBL aborption (
z-2), but the latter are also affected by IBL aborption (![]()
![]() ). This implies that, in order for sources to be detected at both keV and TeV energies with a given pair of X-ray and Cherenkov detectors, the ratio of intrinsic TeV to 2-10 keV luminosities must increase with redshift starting from a threshold redshift that depends on the sensitivity of the two instruments. Recalling the behavior of the SSC model for Mrk 501's giant 1997 flare by Pian et al. (1998), this means observing sources that are in increasingly higher states of emission.
). This implies that, in order for sources to be detected at both keV and TeV energies with a given pair of X-ray and Cherenkov detectors, the ratio of intrinsic TeV to 2-10 keV luminosities must increase with redshift starting from a threshold redshift that depends on the sensitivity of the two instruments. Recalling the behavior of the SSC model for Mrk 501's giant 1997 flare by Pian et al. (1998), this means observing sources that are in increasingly higher states of emission.
This argument entails a testable prediction. If distant TeV blazars are observed during strong flares, then, because of the high electron energies involved, the electrons' scattering cross-section is reduced by the Klein-Nishina effect, which will cause the Compton peak to shift to higher energies more slowly than the synchrotron peak (which depends on the square of the electron energy). We then expect the TeV spectral shape to change quite little at the highest redshifts (z > 0.1) - or equivalently, through the
![]() relation (see Fig. 2e), at the highest
luminosities (
relation (see Fig. 2e), at the highest
luminosities (
![]() > 1045 erg cm-2 s-1). Conversely, for less luminous sources (i.e., sources caught in less active states) the energetics suggests a still largely Compton regime of the upscattered photons, which allows the Compton peak to shift to higher energies at the same rate as the synchrotron peak: hence a spectral flattening is expected with increasing luminosity for the more
nearby sources. The data seem to conform to this prediction (see Fig. 2f), with the weaker sources showing a steeper intrinsic value (
> 1045 erg cm-2 s-1). Conversely, for less luminous sources (i.e., sources caught in less active states) the energetics suggests a still largely Compton regime of the upscattered photons, which allows the Compton peak to shift to higher energies at the same rate as the synchrotron peak: hence a spectral flattening is expected with increasing luminosity for the more
nearby sources. The data seem to conform to this prediction (see Fig. 2f), with the weaker sources showing a steeper intrinsic value (
![]()
![]() 3) and the more powerful ones being spectrally
revealed in the vicinity of the Compton peak (
3) and the more powerful ones being spectrally
revealed in the vicinity of the Compton peak (
![]()
![]() 2).
2).
The radio emission, on the other hand, is largely decoupled from the X-ray and TeV emissions. In the ``canonical'' model of blazar emission the high-energy (X-ray and ![]() -ray) emission, though constituting most of the output, is produced in a region of the blazar's jet that has to be compact in order to account for the short-time variability shown by the blazars. This makes the radio emission from such region strongly self-absorbed, so that the observed radio emission must originate in a much larger volume. Therefore the
link between the radio emission and the X-/
-ray) emission, though constituting most of the output, is produced in a region of the blazar's jet that has to be compact in order to account for the short-time variability shown by the blazars. This makes the radio emission from such region strongly self-absorbed, so that the observed radio emission must originate in a much larger volume. Therefore the
link between the radio emission and the X-/![]() -ray region may be much more subtle and less direct than suggested by a simple application of the SSC model (e.g., Costamante & Ghisellini 2002). As a consequence,
the above arguments linking TeV slope and X-/
-ray region may be much more subtle and less direct than suggested by a simple application of the SSC model (e.g., Costamante & Ghisellini 2002). As a consequence,
the above arguments linking TeV slope and X-/![]() -ray luminosity do not apply in the radio case: indeed, there is no correlation between intrinsic TeV slopes and radio luminosities (Fig. 2g). There is, however, an
overall trend of steeper observed slopes with increasing luminosities (Fig. 2h), a consequence of more luminous objects being typically more distant and hence more IBL-affected at TeV energies, coupled with the essentially flat distribution of
-ray luminosity do not apply in the radio case: indeed, there is no correlation between intrinsic TeV slopes and radio luminosities (Fig. 2g). There is, however, an
overall trend of steeper observed slopes with increasing luminosities (Fig. 2h), a consequence of more luminous objects being typically more distant and hence more IBL-affected at TeV energies, coupled with the essentially flat distribution of
![]() .
.
Within the quite modest statistics and redshift range spanned by known TeV blazars, we find - contrary to some early expectations - no obvious dependence of the observed TeV slopes on redshift. However we find that, once the TeV slopes and luminosities are corrected for intergalactic absorption, flatter slopes tend to
be found in more distant, more luminous blazars. (A correlation of flatness and luminosity with redshift has been suggested also by Stecker et al. 2007a,b.) We argue that this latter correlation descends from a selection effect: use of X-ray data, both simultaneous with TeV data and archival (when available), suggest that, for
z ![]() 0.1, more distant TeV blazars are in more active states (at the epoch of their observation); and more active states mean - given the link between blazar activity and spectral shape observed in nearby objects (e.g., Mrk 501) - harder TeV spectra. This activity-distance link, in turn, results from the selective effect
of IBL absorption (that affects TeV, not keV, photons), which forces more distant objects to have higher intrinsic TeV/X-ray ratios in order to be detectable. In sum, the IBL appears to affect the blazars' TeV slope versus redshift distribution in two ways: first, by causing only objects in progressively more active states, hence with
flatter intrinsic slopes, to be detected at higher redshifts; and then, by making the observed slopes steeper to the observer, more so for higher redshifts. The result of this twofold action of the IBL is - within the relatively small redshift range probed, z
0.1, more distant TeV blazars are in more active states (at the epoch of their observation); and more active states mean - given the link between blazar activity and spectral shape observed in nearby objects (e.g., Mrk 501) - harder TeV spectra. This activity-distance link, in turn, results from the selective effect
of IBL absorption (that affects TeV, not keV, photons), which forces more distant objects to have higher intrinsic TeV/X-ray ratios in order to be detectable. In sum, the IBL appears to affect the blazars' TeV slope versus redshift distribution in two ways: first, by causing only objects in progressively more active states, hence with
flatter intrinsic slopes, to be detected at higher redshifts; and then, by making the observed slopes steeper to the observer, more so for higher redshifts. The result of this twofold action of the IBL is - within the relatively small redshift range probed, z ![]() 0.25 - a substantial lack of correlation between measured TeV slopes and redshift.
0.25 - a substantial lack of correlation between measured TeV slopes and redshift.
It is clear, however, that if higher-luminosity/activity sources are detected at higher redshifts, the underlying Klein-Nishima regime will imply a substantially flat slope,
![]()
![]() 2, over a large luminosity range - hence over a relatively large redshift interval. Due to the redshift dependence
of the IBL opacity, this entails a sharp correlation between observed spectral slope and redshift. We then predict that IACT observations of z
2, over a large luminosity range - hence over a relatively large redshift interval. Due to the redshift dependence
of the IBL opacity, this entails a sharp correlation between observed spectral slope and redshift. We then predict that IACT observations of z ![]() 0.2 blazars will observe progressively higher
0.2 blazars will observe progressively higher
![]() 's with increasing redshift.
's with increasing redshift.
Of course, the above considerations are only as good as the adopted IBL model (Stecker et al. 2006) is. For a different IBL redshift dependence, the resulting distribution of points in Figs. 2a,b would also be different.
More exotic interpretations of the intergalactic extinction, e.g., in the framework of the mixing between photons and a very light axion-like particle (De Angelis et al. 2007), would predict more moderate flux dimming
and spectral distortion than entailed by most IBL schemes (e.g., Kneiske 2004; Mazin & Raue 2007). Reversing the arguments, if the maximum allowed hardness of TeV blazar spectra is known, the observed spectrum of a source with known distance in principle allows one to deduce an upper limit to the IBL. Aharonian et al. (2006b), using the HESS observation of 1ES 1101-032 and arguing that
![]()
![]() 1.5, place
an upper limit to the IBL at 1.5
1.5, place
an upper limit to the IBL at 1.5 ![]() m that is close to its lower limit (i.e., the integration of galaxy counts), hence suggesting a ``low'' IBL. Stecker et al. (2007a,b) however, argue that
m that is close to its lower limit (i.e., the integration of galaxy counts), hence suggesting a ``low'' IBL. Stecker et al. (2007a,b) however, argue that
![]() < 1.5 can be produced if particles in blazar jets are accelerated at relativistic shocks, and hence loosen
Aharonian et al.'s (2006b) upper limit, so permitting a higher IBL density field. Finally, if both the intrinsic blazar spectrum and the IBL are assumed, the observed TeV spectrum can be used to estimate the distance to the source (e.g., Mazin & Goebel 2007).
< 1.5 can be produced if particles in blazar jets are accelerated at relativistic shocks, and hence loosen
Aharonian et al.'s (2006b) upper limit, so permitting a higher IBL density field. Finally, if both the intrinsic blazar spectrum and the IBL are assumed, the observed TeV spectrum can be used to estimate the distance to the source (e.g., Mazin & Goebel 2007).
It will be important to increase the statics in order to clarify the situation. This can be achieved both by probing larger redshifts with deeper Cherenkov observations and by measuring TeV fluxes and spectra of nearby (z < 0.1) blazars in different states of activity. The latter point, in particular, will enhance the statistics
of the low-z portion of Figs. 1, 2a,b,f by adding crucial information on the quiet states of (nearby) blazars.
As for the former point, the newly operating VERITAS telescope and the upcoming enhanced MAGIC and HESS telescopes should improve the sensitivity of ground-based observations considerably, so adding to the number of known z > 0.2 TeV blazars with spectral information above ![]() 0.1 TeV. The impending GLAST satellite, too, will have an importat role in such expansion: its (largely IBL-unaffected) operational band,
0.1 TeV. The impending GLAST satellite, too, will have an importat role in such expansion: its (largely IBL-unaffected) operational band, ![]() 0.01-100 GeV (with a sensitivity higher, by a factor of
0.01-100 GeV (with a sensitivity higher, by a factor of ![]() 50, than its predecessor EGRET), will
sample the blazar SED around the Compton peak, so in principle allowing the solution of the SSC model and hence the knowledge of the intrinsic slope above
50, than its predecessor EGRET), will
sample the blazar SED around the Compton peak, so in principle allowing the solution of the SSC model and hence the knowledge of the intrinsic slope above ![]() 0.1 TeV.
0.1 TeV.
Finally, we emphasize the need for future TeV blazar discoveries to be immediately followed-up in X-rays, that will help to validate or invalidate the main argument made in this paper, i.e. that more flaring sources are detected at higher redshifts. This, if confirmed, would lend further support for the SSC process in blazar emission.
Acknowledgements
We thank Elena Pian, Daniel Mazin, and an anonymous referee for useful comments and suggestions. We acknowledge the MAGIC collaboration for providing a stimulating, friendly, and effective work environment.
Note added in proof
Subsequent to the acceptance of this paper, newly published data for the HBL blazar RGB J0152+017 was added. This is reflected in the figures and text (and Table 1). The results and conclusions of the paper are not affected in any major way by the inclusion of the new data.