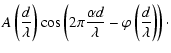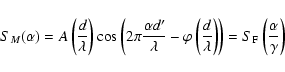A&A 483, 361-364 (2008)
DOI: 10.1051/0004-6361:20078659
Imaging with hypertelescopes: a simple modal approach
C. Aime
Université de Nice Sophia Antipolis, Centre National de la Recherche Scientifique, UMR 6525 H. Fizeau, Observatoire de la Côte d'Azur, Campus
Valrose, 06108 Nice Cedex 2, France
Received 12 September 2007 / Accepted 18 February 2008
Abstract
Aims. We give a simple analysis of imaging with hypertelescopes, a technique proposed by Labeyrie to produce snapshot images using arrays of telescopes. The approach is modal: we describe the transformations induced by the densification onto a sinusoidal decomposition of the focal image instead of the usual point spread function approach.
Methods. We first express the image formed at the focus of a diluted array of apertures as the product
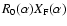 of the diffraction pattern of the elementary apertures
of the diffraction pattern of the elementary apertures
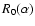 by the object-dependent interference term
by the object-dependent interference term
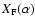 between all apertures. The interference term, which can be written in the form of a Fourier Series for an extremely diluted array, produces replications of the object, which makes observing the image difficult. We express the focal image after the densification using the approach of Tallon and Tallon-Bosc.
between all apertures. The interference term, which can be written in the form of a Fourier Series for an extremely diluted array, produces replications of the object, which makes observing the image difficult. We express the focal image after the densification using the approach of Tallon and Tallon-Bosc.
Results. The result is very simple for an extremely diluted array. We show that the focal image in a periscopic densification of the array can be written as
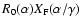 ,
where
,
where 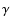 is the factor of densification. There is a dilatation of the interference term while the diffraction term is unchanged. After de-zooming, the image can be written as
is the factor of densification. There is a dilatation of the interference term while the diffraction term is unchanged. After de-zooming, the image can be written as
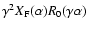 ,
an expression which clearly indicates that the final image corresponds to the center of the Fizeau image intensified by
,
an expression which clearly indicates that the final image corresponds to the center of the Fizeau image intensified by
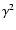 .
The imaging limitations of hypertelescopes are therefore those of the original configuration. The effect of the suppression of image replications is illustrated in a numerical simulation for a fully redundant configuration and a non-redundant one.
.
The imaging limitations of hypertelescopes are therefore those of the original configuration. The effect of the suppression of image replications is illustrated in a numerical simulation for a fully redundant configuration and a non-redundant one.
Key words: instrumentation: interferometers - instrumentation: high angular resolution -
telescopes
Labeyrie (1996) proposed to obtain snapshot
images from a diluted array of telescopes by rearranging the
output pupil using the periscopic principle of Michelson. The
technique, called hypertelescope or densified aperture, is
restricted to conformal transformations in which the pattern of
sub-pupil centers is identical in the entrance and exit pupils.
One of the particularities of the technique is that the point
spread function is no longer space invariant, because the
interference and diffraction patterns of the telescopes move at
different velocities according to the position of the point source
on the sky. This makes it difficult to derive the final image.
Several recent publications were made on this subject, especially
concerning the field of view, as discussed by Lardière et al.
(2007) and Patru et al. (2007).
The analysis presented here is modal. It does not use the
space-varying point spread function, but analyzes the
transformations produced by a hypertelescope on the angular
frequencies transmitted by the array. For that we use the
results of Tallon & Tallon-Bosc (1992), who compared
Fizeau and Michelson interferometers. We will give a simple
formulation for the case, already considered by Labeyrie
(1996), of an highly diluted array and a very small object.
For the usual mode of operation of telescopes, the image 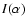 in the focal plane is given by the convolution relation:
in the focal plane is given by the convolution relation:
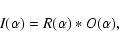 |
(1) |
where * denotes the 2D convolution on components (
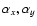 )
of
)
of 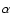 ,
the angular coordinates on the sky.
,
the angular coordinates on the sky. 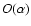 is the geometrical image of the object in the
focal plane, and
is the geometrical image of the object in the
focal plane, and 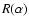 is the Point Spread Function (PSF),
given by:
is the Point Spread Function (PSF),
given by:
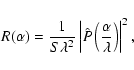 |
(2) |
where  is the light wavelength and S is the
area of the telescope aperture of transmission P(r), with r=(x,
y). In the Fourier plane, the object image relationship appears
as a linear filtering:
is the light wavelength and S is the
area of the telescope aperture of transmission P(r), with r=(x,
y). In the Fourier plane, the object image relationship appears
as a linear filtering:
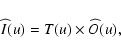 |
(3) |
where u denotes 2D angular frequencies (ux, uy),
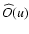 is the image transform, and T(u) is the Optical Transfer Function (OTF), a complex function that
describes the transmission in amplitude and phase of the angular
frequencies. Taking the Fourier transform of Eq. (2),
the OTF can be written as the aperture autocorrelation function:
is the image transform, and T(u) is the Optical Transfer Function (OTF), a complex function that
describes the transmission in amplitude and phase of the angular
frequencies. Taking the Fourier transform of Eq. (2),
the OTF can be written as the aperture autocorrelation function:
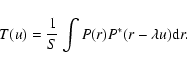 |
(4) |
These relations are valid regardless of the fact that
P(r) is a monolithic aperture or a collection of diluted
apertures. For K (non-overlapping) identical apertures of
transmissions P0(r), centered at 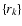 ,
the
transmission P(r) can be written as:
,
the
transmission P(r) can be written as:
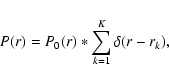 |
(5) |
and the corresponding PSF takes the form:
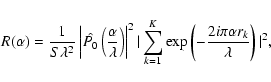 |
(6) |
where
S= K S0, S0 being the area of an
elementary aperture. The corresponding OTF can be written as:
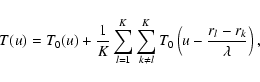 |
(7) |
which acts as a multiple band-pass linear filter that
transmits the angular frequencies in discrete zones of the
frequency plane.
The imaging of stellar or planetary surfaces will require
resolutions corresponding to arrays spreading over tens of
kilometers. The resulting array will be extremely diluted and the
surface S of each individual telescope will be negligible
compared to the dimensions of the array. Each individual
telescope will not resolve the object and therefore there will be
no measurable variation of
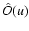 over T0(u). We can then
use the simplified expression:
over T0(u). We can then
use the simplified expression:
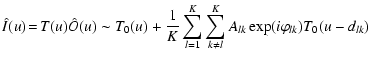 |
|
|
(8) |
where
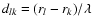 ,
and Alkand
,
and Alkand
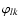 are the amplitude and phase of
are the amplitude and phase of
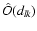 .
The focal plane image can be written:
.
The focal plane image can be written:
where
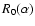 is the envelop of the diffraction
pattern of the elementary apertures and
is the envelop of the diffraction
pattern of the elementary apertures and
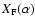 is the
interference term of the form a Fourier Series whose coefficients
depend on the object.
is the
interference term of the form a Fourier Series whose coefficients
depend on the object.
The principle of hypertelescopes is described in Labeyrie
(1996). The array densification may be obtained
extending to many sub-apertures the periscopic arrangement of
Michelson's 20-feet interferometer. Alternatively it is possible
to use inverted Galilean telescopes to increase the diameter of
the elementary apertures (Labeyrie 2002). The two
techniques may be used simultaneously and Labeyrie
(1996) defines a pupil concentration coefficient 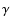 that takes into account the two aspects. The result will be the same regardless of the technique used, but the mathematical
formalism to describe the densification operation in terms of
imaging is different in the intermediate results. For example the
use of Galilean telescopes imposes a reduction of the wave
amplitude to keep the energy constant, which is not the case for
the Michelson periscopic arrangement we consider here. In
accordance with Labeyrie's convention,
that takes into account the two aspects. The result will be the same regardless of the technique used, but the mathematical
formalism to describe the densification operation in terms of
imaging is different in the intermediate results. For example the
use of Galilean telescopes imposes a reduction of the wave
amplitude to keep the energy constant, which is not the case for
the Michelson periscopic arrangement we consider here. In
accordance with Labeyrie's convention, 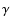 is the
densification parameter (greater than 1) equal to the ratio of
telescope center separations before and after the densifying
operation.
is the
densification parameter (greater than 1) equal to the ratio of
telescope center separations before and after the densifying
operation.
The mathematical formalism necessary to describe hypertelescopes was given four years before Labeyrie (1996)'s paper by Tallon & Tallon-Bosc (1992). They showed that the Michelson periscopic
system performs a change of angular frequencies in the image. The
part of the Fourier plane transmitted by a pair of telescopes
around the frequency
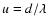 is shifted as a whole to a
lower frequency
is shifted as a whole to a
lower frequency
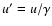 ,
without any modification
of the frequency transmission in modulus and phase. This result was obtained using subtle
manipulations of Fourier optics. Because of these frequency
translations, the system is no longer a linear system and there
is no reason to look for a relation of convolution in the usual
sense of the term. On the contrary, a space-varying point spread
response is required to perform the frequency shifting.
,
without any modification
of the frequency transmission in modulus and phase. This result was obtained using subtle
manipulations of Fourier optics. Because of these frequency
translations, the system is no longer a linear system and there
is no reason to look for a relation of convolution in the usual
sense of the term. On the contrary, a space-varying point spread
response is required to perform the frequency shifting.
For extremely diluted arrays, the individual apertures can only sample the
angular frequency plane in a collection of point-like regions.
Then the translation operation merges with a simple homothetic
transformation of a factor 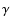 .
In that case, it is possible
to give a very simple demonstration of Tallon and Tallon-Bosc
result, as we show in the Appendix.
.
In that case, it is possible
to give a very simple demonstration of Tallon and Tallon-Bosc
result, as we show in the Appendix.
Applying Tallon and Tallon-Bosc's result to the case of the
extremely diluted array corresponds to substitute
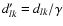 to dlk in Eq. (9).
Denoting
to dlk in Eq. (9).
Denoting
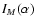 the observed focal plane image after
densification, we can write:
the observed focal plane image after
densification, we can write:
The interferometric term
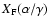 is dilated by the
factor
is dilated by the
factor 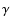 ,
while the diffraction term is unchanged. In a
heuristic manner, the result can be described as follows: we
observe in the focal plane the interferometric object-dependent
image
,
while the diffraction term is unchanged. In a
heuristic manner, the result can be described as follows: we
observe in the focal plane the interferometric object-dependent
image
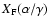 through a fixed window
through a fixed window
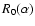 .
As the rate of densification
.
As the rate of densification 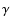 is increased,
the interferometric pattern is zoomed while the observed region
remains unchanged. In the limiting case, only the central part of
the image is left, therefore corresponding to a snapshot usable
picture, as explained by Labeyrie (1996). In Eq. (10) there is no explicit amplification of the image
intensity, and just a dilatation of its size by a factor
is increased,
the interferometric pattern is zoomed while the observed region
remains unchanged. In the limiting case, only the central part of
the image is left, therefore corresponding to a snapshot usable
picture, as explained by Labeyrie (1996). In Eq. (10) there is no explicit amplification of the image
intensity, and just a dilatation of its size by a factor 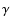 .
The two effects are however equivalent. The amplification appears
if we keep the image size unchanged on the sky by de-zooming the
whole picture of the factor
.
The two effects are however equivalent. The amplification appears
if we keep the image size unchanged on the sky by de-zooming the
whole picture of the factor 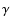 .
The flux is unchanged, and we have:
.
The flux is unchanged, and we have:
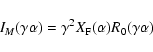 |
(11) |
which shows that the resulting image corresponds to the
Fizeau image limited to its center and intensified by the term
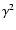 .
In the limiting case,
.
In the limiting case,
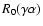 restricts the image to a single object,
without replications. The gain
restricts the image to a single object,
without replications. The gain
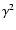 corresponds to the
number of object replications in the Fizeau image that are summed
in the densified image. The hypertelescope works as an optical
device that performs an analog addition of all individual images
replicated by the Fizeau array. Equation (11) also shows that
the conditions of the field of view are the same in a
hypertelescope as the original array in the Fizeau configuration.
That conclusion was already indicated, but not really
demonstrated, in several papers (Lardiere 2007; Patru 2007).
corresponds to the
number of object replications in the Fizeau image that are summed
in the densified image. The hypertelescope works as an optical
device that performs an analog addition of all individual images
replicated by the Fizeau array. Equation (11) also shows that
the conditions of the field of view are the same in a
hypertelescope as the original array in the Fizeau configuration.
That conclusion was already indicated, but not really
demonstrated, in several papers (Lardiere 2007; Patru 2007).
Note that Eqs. (10) and (11) are consistent
with Labeyrie (1996)'s results. In Eq. (3) of this
paper, the intensity in the image is first written as a Fredholm
equation (called a pseudo-convolution). An approximate expression
is derived for
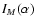 .
It is denoted B(x,y) in Eq. (4). It can be rewritten as:
.
It is denoted B(x,y) in Eq. (4). It can be rewritten as:
![\begin{displaymath}%
I_{M}(\alpha)\approx \frac{1}{\gamma^{2}}
R_0( \alpha)\lef...
...t(\frac{\alpha}{\gamma}\right)\otimes {\rm Int}(\alpha)\right]
\end{displaymath}](/articles/aa/full/2008/19/aa8659-07/img42.gif) |
(12) |
where
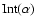 corresponds to the interference
function of the densified array (called I(x,y) in Labeyrie's
paper). In this form the interest of hypertelescopes is not
obvious, especially for the term
corresponds to the interference
function of the densified array (called I(x,y) in Labeyrie's
paper). In this form the interest of hypertelescopes is not
obvious, especially for the term
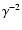 that seems to
reduce the image intensity. However, if we apply the same
de-zooming procedure as discussed above, Eq. (12)
becomes:
that seems to
reduce the image intensity. However, if we apply the same
de-zooming procedure as discussed above, Eq. (12)
becomes:
![\begin{displaymath}%
I_{M}(\gamma \alpha)\approx \gamma^{2}R_0(\gamma \alpha)[O(\alpha)\otimes {\rm Int}(\gamma \alpha)]
\end{displaymath}](/articles/aa/full/2008/19/aa8659-07/img45.gif) |
(13) |
where we have made use of the fact that for a
two-dimensional convolution, if
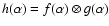 ,
then
,
then
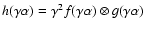 .
This formulation shows that the
present formal approach is fully compatible with Labeyrie's
more intuitive results.
.
This formulation shows that the
present formal approach is fully compatible with Labeyrie's
more intuitive results.
A numerical illustration is given in the next section for a better
understanding of the densified aperture technique.
The shape of
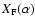 strongly depends on the array
configuration. Its expression is not simple, in general. It takes
a convenient form for a redundant array of telescopes equally
spaced by a distance d on a regular square grid at
strongly depends on the array
configuration. Its expression is not simple, in general. It takes
a convenient form for a redundant array of telescopes equally
spaced by a distance d on a regular square grid at
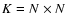 positions. The OTF covers
(2N-1)2 regions of the frequency
plane on a regular grid, of the form:
positions. The OTF covers
(2N-1)2 regions of the frequency
plane on a regular grid, of the form:
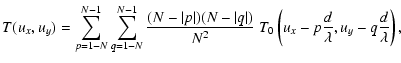 |
|
|
(14) |
and the PSF simplifies to:
 = =  |
(15) |
These expressions are those of a two-dimensional
grating. The PSF presents peaks of width
 ,
each
,
each
 .
The overall spatial extension is given by the
diffraction pattern of the elementary apertures. For circular
apertures of diameter D, the number of peaks is of the order of (d/D)2. The convolution between the object and the PSF produces replications. To avoid overlapping of the images, the
object extent cannot be larger than
.
The overall spatial extension is given by the
diffraction pattern of the elementary apertures. For circular
apertures of diameter D, the number of peaks is of the order of (d/D)2. The convolution between the object and the PSF produces replications. To avoid overlapping of the images, the
object extent cannot be larger than
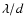 .
.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{8659fig1.eps}\end{figure}](/articles/aa/full/2008/19/aa8659-07/Timg54.gif) |
Figure 1:
Numerical illustrations. Left three figures: Fizeau imaging. Top: the array of
7  7 square apertures (side length 3 units, separation between aperture
centers of 20 units); below: the object angular frequencies in the
Fourier (modulus in a log scale); bottom: the direct image showing the object replication.
Center three figures, from top to bottom: densified aperture for a separation reduced to
5 units, the Fourier plane showing the non-overlapping densified OTF (only the central non-zero part is shown) and the focal image. Right three figures: same as center for a full densification. The focal plane images are drawn at the same scale, and the zooming effect of Eq. (10) appears clearly.
7 square apertures (side length 3 units, separation between aperture
centers of 20 units); below: the object angular frequencies in the
Fourier (modulus in a log scale); bottom: the direct image showing the object replication.
Center three figures, from top to bottom: densified aperture for a separation reduced to
5 units, the Fourier plane showing the non-overlapping densified OTF (only the central non-zero part is shown) and the focal image. Right three figures: same as center for a full densification. The focal plane images are drawn at the same scale, and the zooming effect of Eq. (10) appears clearly. |
| Open with DEXTER |
We give in Fig. 1 an illustration of the effect of aperture densification for the
observation of a Saturn like exoplanet using a fully redundant
array of 49 apertures set on a square grid (7  7). The
elementary apertures are squares of side length 3 units and the distances between
telescopes centers are 20 units (arbitrary units). The figure shows the results for three operating modes, the direct Fizeau configuration and two rates of
densification. One rate corresponds to the complete aperture
densification where the images of the elementary apertures are
brought close-by to form a monolithic aperture, as in the
original Labeyrie (1996) proposal. In the other
rate of densification, that we may call OTF densification, a
distance is left between apertures so that there is no overlapping
of individual autocorrelation functions of elementary telescopes
and no overlapping of frequencies in the Fourier plane.
7). The
elementary apertures are squares of side length 3 units and the distances between
telescopes centers are 20 units (arbitrary units). The figure shows the results for three operating modes, the direct Fizeau configuration and two rates of
densification. One rate corresponds to the complete aperture
densification where the images of the elementary apertures are
brought close-by to form a monolithic aperture, as in the
original Labeyrie (1996) proposal. In the other
rate of densification, that we may call OTF densification, a
distance is left between apertures so that there is no overlapping
of individual autocorrelation functions of elementary telescopes
and no overlapping of frequencies in the Fourier plane.
For the numerical computation, we have used the complete Tallon
& Tallon-Bosc (1992) model to synthesize the
resulting image, without any approximation. The operation is
performed in the Fourier plane. The array of N  N apertures, with N=7, gives the object's spectrum for
(2N-1)2=169 regions of the Fourier plane, as shown in
Fig. 1 for the modulus of the image transform. The first
step in the procedure leading to the densified image consists of
translating the high frequency parts towards the lower
frequencies, each of the 168 external regions being moved towards
the low frequencies. The result for the OTF densification is a
low frequency padding of the Fourier plane, without any frequency
overlapping, while the complete aperture densification induces a
marginal frequency overlapping. At least for the object we have
chosen, it seems that this frequency overlap will not produce
visible modification in the final image.
N apertures, with N=7, gives the object's spectrum for
(2N-1)2=169 regions of the Fourier plane, as shown in
Fig. 1 for the modulus of the image transform. The first
step in the procedure leading to the densified image consists of
translating the high frequency parts towards the lower
frequencies, each of the 168 external regions being moved towards
the low frequencies. The result for the OTF densification is a
low frequency padding of the Fourier plane, without any frequency
overlapping, while the complete aperture densification induces a
marginal frequency overlapping. At least for the object we have
chosen, it seems that this frequency overlap will not produce
visible modification in the final image.
Final focal plane images are obtained by a Fourier transform of
the densified Fourier plane. The approach is modal in the sense
that we have considered only angular frequencies in the Fourier
plane. There is no need in this approach to compute the space
varying response for each point source to obtain the final image.
The resulting image is obtained exactly and very quickly, without
the need to integrate the Fredholm relation. The resulting images
of this exact simulation are in good agreement with the
approximated expression of Eq. (10). The zooming effect
on the object is clearly visible.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{8659fig2.eps}\end{figure}](/articles/aa/full/2008/19/aa8659-07/Timg55.gif) |
Figure 2:
Same array as in Fig. 1, but for a distance between apertures
enlarged to 35. Left: Fizeau imaging showing the object replications.
Center: densified apertures corresponding to a distance of 5 between apertures. Right: close-by densification 3. The overlapping of images is present in the
Fizeau configuration and the image cannot be recovered. |
| Open with DEXTER |
In the illustration of Fig. 1, the distances between telescope
centers were chosen so as to correctly sample
the object's Fourier transform. We illustrate in Fig. 2
what happens with the same array if separations between apertures
are increased to be too large to correctly sample the object's
Fourier transform. This undersampling in the frequency plane
produces an aliasing in the direct plane.
The object images overlap and the observation becomes useless.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{8659fig3.eps}\end{figure}](/articles/aa/full/2008/19/aa8659-07/Timg56.gif) |
Figure 3:
Example of the result that can be obtained with a fully non-redundant
array of 22 square apertures (side length 3 units, minimum distance between aperture
centers 10 units). Left: Fizeau imaging. Right: hypertelescope configuration.
From top to bottom: aperture, Fourier and focal plane. |
| Open with DEXTER |
This simulation illustrates the fact that the image properties
are fully defined by the geometry of the original array, and do
not depend on the mode of configuration of the exit aperture. A
very important point is that the object's Fourier plane must be
correctly sampled by the array configuration. Obtaining resolved
information within each individual region
T0(u-dlk) is
useless in terms of the Shannon theorem.
A fully redundant two-dimensional apertures is certainly not the
best solution. In terms of frequency coverage, non redundant
configurations are more efficient. We give in Fig. 3 an
example of what could be obtained for an array of 22 non-redundant
apertures giving the object's spectrum for 463 regions of the
Fourier plane. In that simulation, that uses the same elementary
square apertures as before, the minimum distance between apertures
is 10 units. The maximum densification is obtained when the
closest apertures are joined. This effect is clearly visible for
the three elementary apertures in the upper left part of the array
(Fig. 3 top-right). However the densified non-redundant
aperture remains rather sparse, and is no longer similar to a
monolithic aperture. What is densified is the OTF, at least for
its central part there. Note that the configuration shown here is
for illustration only. Finding the optimal configuration for a
given number of apertures is not treated here. The images shown
here are raw results, with no attempt to improve the resolution by
any image processing. In that respect, there is probably much more
to expect from the data processing of non-redundant arrays,
especially if a technique can be used to fill in the frequency
gaps left by these configurations.
Acknowledgements
The author would like to thank the referee Isabelle Tallon-Bosc
for very constructive comments.
The approach developed by Tallon & Tallon-Bosc (1992) is complete, and there is no need to further develop their computation. However, for a
better understanding of the technique, we present a simplified
heuristic presentation in the case of extremely diluted arrays.
We describe it for a system of two telescopes. A point source of
the object at the angular position 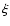 produces on the aperture
plane a wavefront tilted by the angle
produces on the aperture
plane a wavefront tilted by the angle 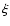 .
The path
difference between the two aperture is
.
The path
difference between the two aperture is 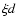 .
Orientating the
axis in the focal plane as on the sky, it produces a fringe
pattern of the form
.
Orientating the
axis in the focal plane as on the sky, it produces a fringe
pattern of the form
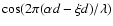 for the oscillatory term.
Now let us consider the object as a sum of sinusoidal terms such as
for the oscillatory term.
Now let us consider the object as a sum of sinusoidal terms such as
 .
Summing the point responses for all
positions
.
Summing the point responses for all
positions 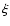 ,
we reach the well known result:
,
we reach the well known result:
When the exit aperture is densified from d to d', the fringe
pattern in the focal plane has a frequency
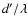 .
The path
difference between apertures remains
.
The path
difference between apertures remains 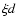 ,
and the telescope
response to a point source in the direction
,
and the telescope
response to a point source in the direction 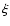 becomes
becomes
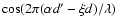 .
Substituting this quantity to
.
Substituting this quantity to
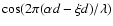 in the above equation, we directly obtain the result:
in the above equation, we directly obtain the result:
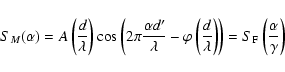 |
(A.2) |
which demonstrates the rule used to derive Eq. (10).
- Labeyrie,
A. 1996, A&A, 118, 517 [NASA ADS] [CrossRef]
(In the text)
- Labeyrie,
A. 2002, EAS Pub. Ser., 8, 327
(In the text)
- Lardière, O.,
Martinache, F., & Patru, F. 2007, MNRAS, 375, 977 [NASA ADS] [CrossRef]
(In the text)
- Patru, F., Mourard, D.,
Lardière, O., & Lagarde, S. 2007, MNRAS, 376, 1047 [NASA ADS] [CrossRef]
(In the text)
- Tallon, M., &
Tallon-Bosc, I. 1992, A&A, 253, 641 [NASA ADS]
(In the text)
Copyright ESO 2008
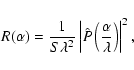
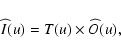
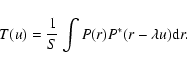
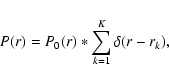
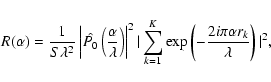
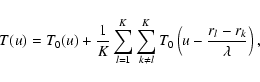
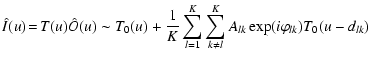
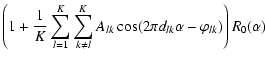
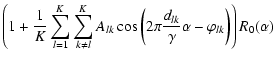
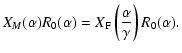
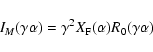
![\begin{displaymath}%
I_{M}(\alpha)\approx \frac{1}{\gamma^{2}}
R_0( \alpha)\lef...
...t(\frac{\alpha}{\gamma}\right)\otimes {\rm Int}(\alpha)\right]
\end{displaymath}](/articles/aa/full/2008/19/aa8659-07/img42.gif)
![\begin{displaymath}%
I_{M}(\gamma \alpha)\approx \gamma^{2}R_0(\gamma \alpha)[O(\alpha)\otimes {\rm Int}(\gamma \alpha)]
\end{displaymath}](/articles/aa/full/2008/19/aa8659-07/img45.gif)
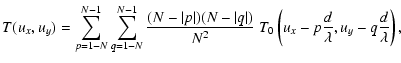
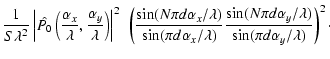
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{8659fig1.eps}\end{figure}](/articles/aa/full/2008/19/aa8659-07/Timg54.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{8659fig2.eps}\end{figure}](/articles/aa/full/2008/19/aa8659-07/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{8659fig3.eps}\end{figure}](/articles/aa/full/2008/19/aa8659-07/Timg56.gif)