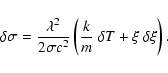A&A 483, 271-283 (2008)
DOI: 10.1051/0004-6361:20077903
Solar off-limb line widths: Alfvén waves, ion-cyclotron waves, and preferential heating
L. Dolla1 - J. Solomon1,2
1 - Institut d'Astrophysique Spatiale, UMR8617, Université Paris-Sud, 91405 Orsay, France
2 - CNRS, Orsay 91405, France
Received 16 May 2007 / Accepted 18 January 2008
Abstract
Context. Alfvén waves and ion-cyclotron absorption of high-frequency waves are frequently brought into models devoted to coronal heating and fast solar-wind acceleration. Signatures of ion-cyclotron resonance have already been observed in situ in the solar wind (HELIOS spacecrafts) and, recently, in the upper corona (UVCS/SOHO remote-sensing results).
Aims. We propose a method to constrain both the Alfvén wave amplitude and the preferential heating induced by ion-cyclotron resonance, above a partially developed polar coronal hole observed with the SUMER/SOHO spectrometer.
Methods. The instrumental stray light contribution is first substracted from the spectra. By supposing that the non-thermal velocity is related to the Alfvén wave amplitude, it is constrained through a density diagnostic and the gradient of the width of the Mg x 625 Å line. The temperatures of several coronal ions, as functions of the distance above the limb, are then determined by substracting the non-thermal component to the observed line widths.
Results. The effect of stray light explains the apparent decrease with height in the width of several spectral lines, this decrease usually starting about 0.1-0.2  above the limb. This result rules out any direct evidence of damping of the Alfvén waves, often suggested by other authors. We also find that the ions with the smallest charge-to-mass ratios are the hottest ones at a fixed altitude and that they are subject to a stronger heating, as compared to the others, between 57
above the limb. This result rules out any direct evidence of damping of the Alfvén waves, often suggested by other authors. We also find that the ions with the smallest charge-to-mass ratios are the hottest ones at a fixed altitude and that they are subject to a stronger heating, as compared to the others, between 57
 and 102
and 102
 above the limb. This constitutes a serious clue to ion-cyclotron preferential heating.
above the limb. This constitutes a serious clue to ion-cyclotron preferential heating.
Key words: Sun: corona - Sun: UV radiation - line: profiles
1 Introduction
Ion-cyclotron resonance is often suggested as one of the possible processes that accelerate the fast solar wind and heat the corona.
Different modelling approaches are used, like hybrid simulations (e.g. Liewer et al. 1999; Ofman 2004), kinetic models (Isenberg 2001; Isenberg et al. 2001; Vocks & Marsch 2002; Marsch & Tu 2001), or fluid models. In this last category Cranmer et al. (1999a) for example, include several ion species and show that it is necessary to regenerate the cyclotron waves through the wind to provide enough energy to the wind. This may be done, for example, by including an Alfvén wave turbulent cascade, as in Tu & Marsch (1997) (two fluids) or Hu et al. (2000) (four fluids), while Markovskii (2001) and Markovskii & Hollweg (2002) study the direct generation of cyclotron waves via plasma instabilities.
In the models that use turbulent cascade, the Alfvén wave power is distributed into a power law spectrum, with ion-cyclotron waves being its high frequency limit. On the one hand, these waves are gradually absorbed by the particles as the different local ion gyrofrequencies decrease with altitude and match the wave frequency, taking into account the Doppler effect due to the particle velocity (for the theoretical aspects of the cyclotron absorption, see e.g. Hollweg & Isenberg 2002). On the other hand, they replenish through the energy cascade process from low to high frequencies.
The large decrease in the magnetic field intensity because of the rapid expansion of the flux tubes can favour the resonance occurring at a relatively low altitude above the solar surface, as in the so-called ``funnels'' (e.g. Li 2002; Hackenberg et al. 2000). In this respect, the superradial expansion of the flux tubes in coronal holes (Kopp & Holzer 1976), which are thought to be the source of the fast solar wind, is also important.
In some models, Alfvén waves are directly dissipated to provide energy to the wind.
According to Parker (1991), though, this dissipation is not significant below 5  ,
so that it is more likely that Alfvén waves stay undamped in the low corona.
,
so that it is more likely that Alfvén waves stay undamped in the low corona.
Several signatures of wave-particle interaction, which can be attributed to the ion-cyclotron resonance, have already been observed in the solar wind. The in situ observations of the Helios spacecrafts, for example, showed differential speed of minor heavy ions, anisotropies of temperatures (
 ), and preferential heating of some ion species (Schwenn & Marsch 1991). In the upper corona, the UVCS spectro-coronometer on board SOHO made it possible to observe the same kinds of signatures from 2.5 to more than 5
), and preferential heating of some ion species (Schwenn & Marsch 1991). In the upper corona, the UVCS spectro-coronometer on board SOHO made it possible to observe the same kinds of signatures from 2.5 to more than 5 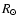 from disc centre, through spectroscopic studies coupled to some modelling (Kohl et al. 1998; Li et al. 1998; Esser et al. 1999; Cranmer et al. 1999b).
In the lower corona, in contrast, there is lack of conclusive studies,
and yet it is particularly important to verify whether any process that accelerates the fast solar wind starts acting in the lower corona. Observing this region is also important for constraining the energy actually dissipated by the cyclotron resonance and for differentiating the different theories that have been proposed.
from disc centre, through spectroscopic studies coupled to some modelling (Kohl et al. 1998; Li et al. 1998; Esser et al. 1999; Cranmer et al. 1999b).
In the lower corona, in contrast, there is lack of conclusive studies,
and yet it is particularly important to verify whether any process that accelerates the fast solar wind starts acting in the lower corona. Observing this region is also important for constraining the energy actually dissipated by the cyclotron resonance and for differentiating the different theories that have been proposed.
In this article, we concentrate on the possibility of revealing the preferential heating of the ion species having the lowest charge-to-mass ratios (q/m).
Retrieving the temperature of different ion species can be made via the analysis of the widths of emission lines. It is worthwhile noting that the temperature diagnostics based on line ratios are sensitive to the electron temperature and cannot help in measuring the ion one.
Our paper is organised as follows. In Sect. 2, we present the usual interpretation of the coronal line widths and of their variations above the limb, as well as solutions proposed in the literature for distinguishing the thermal and the non-thermal components.
In Sect. 3, we present the observations and the associated data processing, with emphasis on the correction for the stray light contribution in the spectra. In Sect. 4, we explain the method we used to separate thermal and non-thermal Doppler effects in the measured line widths. The results are presented in Sect. 5, while Sect. 6 gives the conclusions.
2 Retrieving the information contained in coronal line widths
The plasma observed above the limb is optically thin for most of the transition region and coronal lines in the VUV range observed by instruments like SUMER (Chae et al. 1998; Dere & Mason 1993; Lee et al. 2000). The two main contributions to the line width then come from thermal and non-thermal Doppler effects.
The non-thermal velocity, also known as ``unresolved'' velocity,  was originally introduced to interpret the width of the transition region and coronal lines observed on the disc. In fact, there is an excess broadening as compared to the thermal component due to the formation temperature
was originally introduced to interpret the width of the transition region and coronal lines observed on the disc. In fact, there is an excess broadening as compared to the thermal component due to the formation temperature 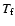 of these lines.
This additional contribution was first attributed to velocity fluctuations induced by acoustic waves (Boland et al. 1973), before MHD waves or fluid turbulence were considered (e.g. Harrison et al. 2002; Hassler et al. 1990; Boland et al. 1975; Doyle et al. 1999). The term ``unresolved velocity'' in fact refers to motions on scales smaller than the resolution scale. One should also take into account the motions integrated on the depth of the line of sight (LOS), and on scales smaller than the temporal resolution of the instrument. If both thermal and non-thermal contributions are Gaussian (Tu et al. 1998), the half-width
of these lines.
This additional contribution was first attributed to velocity fluctuations induced by acoustic waves (Boland et al. 1973), before MHD waves or fluid turbulence were considered (e.g. Harrison et al. 2002; Hassler et al. 1990; Boland et al. 1975; Doyle et al. 1999). The term ``unresolved velocity'' in fact refers to motions on scales smaller than the resolution scale. One should also take into account the motions integrated on the depth of the line of sight (LOS), and on scales smaller than the temporal resolution of the instrument. If both thermal and non-thermal contributions are Gaussian (Tu et al. 1998), the half-width 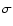 at
at
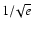 follows the formula given by Dere & Mason (1993):
follows the formula given by Dere & Mason (1993):
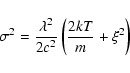 |
(1) |
where 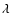 is the wavelength, c the speed of light, k the Boltzmann constant.
The non-thermal velocity
is the wavelength, c the speed of light, k the Boltzmann constant.
The non-thermal velocity  is proportional to the mean velocity fluctuations integrated on the observed solid angle and the exposure time,
is proportional to the mean velocity fluctuations integrated on the observed solid angle and the exposure time,
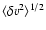 .
The coefficient of proportionality, relatively close to 1, depends on the degrees of freedom of the fluid motion (e.g. Tu et al. 1998).
.
The coefficient of proportionality, relatively close to 1, depends on the degrees of freedom of the fluid motion (e.g. Tu et al. 1998).
Variations in the non-thermal velocity have been investigated by several authors: (i) centre-to-limb variations by Mariska et al. (1978), Chae et al. (1998), Lee et al. (2000), Doyle et al. (2000), see also Erdelyi et al. (1998) for the interpretation in terms of MHD modes; (ii) variation depending on the nature of the observed region (coronal holes, ``quiet Sun'', active region); and (iii) radial variation out of the limb, which is of interest for this article and which we will present in the next section. Depending on all these different conditions, the value of  varies roughly from 10 to
varies roughly from 10 to
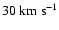 .
.
From on-disc observations, we retain the results of Chae et al. (1998), which assumed that the temperature of each ion species that they observed was the corresponding formation temperature (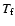 ). They consequently deduced the non-thermal velocity from the line widths, and plotted it as a function of
). They consequently deduced the non-thermal velocity from the line widths, and plotted it as a function of 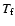 .
The same kind of analysis was also performed by, e.g., Boland et al. (1975) and Dere & Mason (1993). The curve of Chae et al. (1998) increases from
.
The same kind of analysis was also performed by, e.g., Boland et al. (1975) and Dere & Mason (1993). The curve of Chae et al. (1998) increases from 
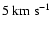 at
at
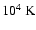 up to
up to 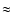
 around 3
around 3 
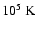 (O VI), then decreases to
(O VI), then decreases to 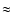
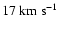 at
at
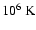 (Fe XII). One can roughly interpret this curve in terms of LOS integration: different
(Fe XII). One can roughly interpret this curve in terms of LOS integration: different 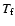 of ions observed at the same pointing on the disc can be associated to different altitudes above the solar surface. The curve then traces the value of the non-thermal velocity through the different temperature layers of the solar atmosphere (Mariska et al. 1978).
of ions observed at the same pointing on the disc can be associated to different altitudes above the solar surface. The curve then traces the value of the non-thermal velocity through the different temperature layers of the solar atmosphere (Mariska et al. 1978).
2.2 Past observations of line widths above the solar limb
Most authors who have observed above the limb, in coronal holes, report that the line widths first increase with the altitude before presenting a plateau or, sometimes, starting to decrease at 1.1 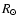 from disc centre: e.g. Hassler et al. (1990), with the Mg X 609 and 625 Å lines up to 1.2
from disc centre: e.g. Hassler et al. (1990), with the Mg X 609 and 625 Å lines up to 1.2 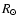 ,
or Banerjee et al. (1998), with SUMER/SOHO observing the Si VIII 1445 Å line. These authors interpreted this behaviour as caused by Alfvén waves, with the increase due to flux conservation and decrease due to damping.
Using CDS/SOHO, O'Shea et al. (2003) observed the width of the Mg X 625 Å line starting to decrease around 1.06
,
or Banerjee et al. (1998), with SUMER/SOHO observing the Si VIII 1445 Å line. These authors interpreted this behaviour as caused by Alfvén waves, with the increase due to flux conservation and decrease due to damping.
Using CDS/SOHO, O'Shea et al. (2003) observed the width of the Mg X 625 Å line starting to decrease around 1.06 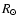 ,
the exact position varying with the data sets, but always for the same value of the line widths.
But O'Shea et al. (2004), when observing the Si XII 520 Å line in addition to the two Mg X 609 and 625 Å lines, found a discrepancy between both species and concluded that the behaviour of the Mg X lines results from photoexcitation growing as the altitude increases.
Still above a coronal hole, using SUMER, Lee et al. (2000) found a link between the altitude where the line widths change their behaviour and the intensity scale height. Nevertheless, they used a lot of particularly cold lines, which they could not observe more than 20
,
the exact position varying with the data sets, but always for the same value of the line widths.
But O'Shea et al. (2004), when observing the Si XII 520 Å line in addition to the two Mg X 609 and 625 Å lines, found a discrepancy between both species and concluded that the behaviour of the Mg X lines results from photoexcitation growing as the altitude increases.
Still above a coronal hole, using SUMER, Lee et al. (2000) found a link between the altitude where the line widths change their behaviour and the intensity scale height. Nevertheless, they used a lot of particularly cold lines, which they could not observe more than 20
 above the limb. They also found a curve
above the limb. They also found a curve
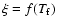 as did Chae et al. (1998).
as did Chae et al. (1998).
Above a quiet Sun region at the equator, Harrison et al. (2002) observed a decrease in the line width of the Mg X 625 Å line, with CDS, starting at about 1.04 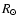 ,
the width being narrower than above coronal holes. They linked this behaviour to the damping of Alfvén waves in close field loops. Wilhelm et al. (2004), using SUMER still at the equator but at a different date, did not find the same behaviour. The results of both instruments were reconciled after joint observations (Wilhelm et al. 2005) that revealed no decrease, but a slight plateau. Besides, Peter & Vocks (2003) observed a local maximum of the widths of transition region lines (O V and S VI), less than 10
,
the width being narrower than above coronal holes. They linked this behaviour to the damping of Alfvén waves in close field loops. Wilhelm et al. (2004), using SUMER still at the equator but at a different date, did not find the same behaviour. The results of both instruments were reconciled after joint observations (Wilhelm et al. 2005) that revealed no decrease, but a slight plateau. Besides, Peter & Vocks (2003) observed a local maximum of the widths of transition region lines (O V and S VI), less than 10
 (
(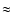
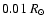 )
above the limb, which they attribute to the dissipation of ion-cyclotron waves, the decrease at higher altitudes being due to collisional cooling when the ion-cyclotron dissipation vanishes.
)
above the limb, which they attribute to the dissipation of ion-cyclotron waves, the decrease at higher altitudes being due to collisional cooling when the ion-cyclotron dissipation vanishes.
Singh et al. (2003b,a) analysed ground-based observations of Fe X, Fe XIII, and Fe XIV lines (visible and infrared), up to 140
 in streamers. On average, the Fe X 6374 Å line width increases with altitude, those of the Fe XIII 10 747 and 10 798 Å lines increase sligthly less, whereas that of the Fe XIV 5303 Å line decreases slightly. Concluding that the line-width behaviour depends on the formation temperature,
they reject the interpretation in terms of variation of Alfvén wave amplitude and prefer to explain it by an LOS effect in a thermally stratified corona.
Still from the ground, Contesse et al. (2004) observe no clear decrease in the width of the Fe XIV 5303 Å line, but instead a plateau up to 1.5
in streamers. On average, the Fe X 6374 Å line width increases with altitude, those of the Fe XIII 10 747 and 10 798 Å lines increase sligthly less, whereas that of the Fe XIV 5303 Å line decreases slightly. Concluding that the line-width behaviour depends on the formation temperature,
they reject the interpretation in terms of variation of Alfvén wave amplitude and prefer to explain it by an LOS effect in a thermally stratified corona.
Still from the ground, Contesse et al. (2004) observe no clear decrease in the width of the Fe XIV 5303 Å line, but instead a plateau up to 1.5 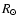 at the equator (east and west) and up to 1.2
at the equator (east and west) and up to 1.2 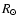 above both poles, the observed line widths being larger above the poles than above the equatorial regions.
above both poles, the observed line widths being larger above the poles than above the equatorial regions.
Using UVCS/SOHO, it is possible to observe several solar radii above the solar limb, essentially the H I Ly 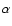 and the O VI lines at 1032 and 1037 Å. The observations showed that widths generally increase more with the altitude in the upper part of the corona, i.e. above 2
and the O VI lines at 1032 and 1037 Å. The observations showed that widths generally increase more with the altitude in the upper part of the corona, i.e. above 2 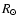 from disc centre, than in the lower one (Morgan & Habbal 2004; Frazin et al. 1999; Li et al. 1998; Kohl et al. 1998; Cranmer et al. 1999b; Esser et al. 1999; Doyle et al. 1999).
from disc centre, than in the lower one (Morgan & Habbal 2004; Frazin et al. 1999; Li et al. 1998; Kohl et al. 1998; Cranmer et al. 1999b; Esser et al. 1999; Doyle et al. 1999).
2.3 Distinguishing thermal and non-thermal Doppler effects
The line width contains information about the result of potential heatings (the temperature 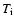 of the different ions species) and about the possible source of heating, that is to say, the Alfvén wave amplitude via direct dissipation or via ion-cyclotron resonance after a turbulent cascade. All difficulties come from these two pieces of information merged in only one observable. Most methods used in the literature consist in making an assumption about one of the above quantities, depending on the purpose of the authors, i.e. constraining the Alfvén wave amplitude or revealing any preferential heating.
of the different ions species) and about the possible source of heating, that is to say, the Alfvén wave amplitude via direct dissipation or via ion-cyclotron resonance after a turbulent cascade. All difficulties come from these two pieces of information merged in only one observable. Most methods used in the literature consist in making an assumption about one of the above quantities, depending on the purpose of the authors, i.e. constraining the Alfvén wave amplitude or revealing any preferential heating.
One can find mostly two kinds of hypotheses on the ion temperature: the isothermal or the formation temperature hypotheses. One example of isothermal hypothesis can be found in Feldman et al. (2000) or Doschek et al. (2001). They determine the electron temperature through the emission measure and assume that all species are in thermal equilibrium. Then, they find different values of  for the different ion species and discuss about possible errors to explain why they do not obtain a unique value for
for the different ion species and discuss about possible errors to explain why they do not obtain a unique value for  .
In fact, Moran (2003) shows for a coronal hole that it is not possible for all ion species to have the same temperature and the same non-thermal velocity at the same time.
.
In fact, Moran (2003) shows for a coronal hole that it is not possible for all ion species to have the same temperature and the same non-thermal velocity at the same time.
Numerous authors prefer to assume that the temperature 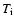 of each ion is the formation temperature of the line (e.g. Hassler et al. 1990; Contesse et al. 2004). But this supposes ionization equilibrium, while several authors think that the plasma above coronal holes is weakly collisional (Banerjee et al. 1998; Tu et al. 1998). When a preferential heating process, like ion-cyclotron resonance, is at work on time scales smaller than the collisional cooling (cf. Table 1), the assumption
of each ion is the formation temperature of the line (e.g. Hassler et al. 1990; Contesse et al. 2004). But this supposes ionization equilibrium, while several authors think that the plasma above coronal holes is weakly collisional (Banerjee et al. 1998; Tu et al. 1998). When a preferential heating process, like ion-cyclotron resonance, is at work on time scales smaller than the collisional cooling (cf. Table 1), the assumption
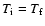 no longer makes sense.
no longer makes sense.
Doyle et al. (1999), for a coronal hole, use a more elaborated hypothesis for the temperature. They suppose that the electron temperature 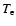 is equal to the formation temperature of the observed Si VIII line and deduce the proton temperature
is equal to the formation temperature of the observed Si VIII line and deduce the proton temperature 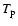 from hydrostatic equilibrium, constrained by a density diagnostic. Then, they suppose that
from hydrostatic equilibrium, constrained by a density diagnostic. Then, they suppose that
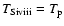 (and
(and
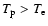 )
before they deduce
)
before they deduce  from the Si VIII line width.
from the Si VIII line width.
The first hypothesis about the non-thermal velocity  that can be made is that all ion species have the same
that can be made is that all ion species have the same  .
This is reasonable if this velocity comes from fluid motions, i.e.
regardless of the species; this may be false if some species have high differential speeds (Hollweg & Isenberg 2002), which should not be the case in the lower corona. The problem is then to determine the value of
.
This is reasonable if this velocity comes from fluid motions, i.e.
regardless of the species; this may be false if some species have high differential speeds (Hollweg & Isenberg 2002), which should not be the case in the lower corona. The problem is then to determine the value of  .
Seely et al. (1997) adjust
.
Seely et al. (1997) adjust  so that the temperature of the Fe ion species, i.e. the heaviest element they observe, is similar to that of ion species of neighbouring
so that the temperature of the Fe ion species, i.e. the heaviest element they observe, is similar to that of ion species of neighbouring 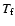 ,
as they suppose that all ion species that have a common
,
as they suppose that all ion species that have a common 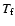 are in thermal equilibrium.
They then deduce the temperature of all the other ion species, which appear to be larger than their own formation temperature; the lower the formation temperature, the larger the difference. These authors conclude that this situation may come from out-of-equilibrium processes (heating or cooling phase) or from preferential heating. They also conclude that the underestimation of the ion temperatures led Hassler et al. (1990) to overestimate
are in thermal equilibrium.
They then deduce the temperature of all the other ion species, which appear to be larger than their own formation temperature; the lower the formation temperature, the larger the difference. These authors conclude that this situation may come from out-of-equilibrium processes (heating or cooling phase) or from preferential heating. They also conclude that the underestimation of the ion temperatures led Hassler et al. (1990) to overestimate  at altitudes of
at altitudes of
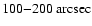 .
.
When looking for the signature of preferential heating in coronal holes, Tu et al. (1998) cautiously give an upper and a lower limit to  .
The lower one being 0, they set the upper one by setting to zero the thermal width of the lines from the heaviest ion having the smallest Doppler width (Fe XII) in their data set. Then, they constrain the temperature of all ion species, and note a stronger heating of ions having the smallest q/m between about 1.04 and 1.18
.
The lower one being 0, they set the upper one by setting to zero the thermal width of the lines from the heaviest ion having the smallest Doppler width (Fe XII) in their data set. Then, they constrain the temperature of all ion species, and note a stronger heating of ions having the smallest q/m between about 1.04 and 1.18 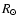 .
.
One possibility for better constraining  is to suppose that the non-thermal velocity is solely due to undamped Alfvén waves. To conserve the wave energy in an expanding flux tube, while the mass density
is to suppose that the non-thermal velocity is solely due to undamped Alfvén waves. To conserve the wave energy in an expanding flux tube, while the mass density 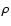 decreases, the wave amplitude must increase so that (e.g. Moran 2001)
decreases, the wave amplitude must increase so that (e.g. Moran 2001)
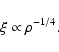 |
(2) |
The line-width variation with the altitude has been analysed with respect to this effect in Hassler et al. (1990) for Mg X and Banerjee et al. (1998) and Pekünlü et al. (2002) for Si VIII.
Conclusions that can be drawn from the study of VUV solar line widths appear to strongly depend on the method used to separate the thermal from the non-thermal contribution. Two points emerge from past studies: (i) the probable existence of a non-thermal velocity whose radial behaviour above the limb mimics that of undamped Alfvén wave amplitude. The question of whether these waves begin to damp at a certain point above the solar surface does not seem to have been solved. (ii) Another process may be at work that affects different lines in different ways. A q/m dependence is suspected that could be associated to ion-cyclotron resonance.
The purpose of this article is to verify and constrain both of these two points without using hypotheses that a priori preclude one of them. We will focus on observations of a polar coronal hole, below 1.2  .
To avoid bias resulting from the line formation (e.g. photoexcitation) and from unknown line blendings, it seems useful to observe as many lines as possible. A wide range of masses and q/m of the ion species also favour the distinction between the relative contribution of thermal and non-thermal velocity in the observed line widths.
.
To avoid bias resulting from the line formation (e.g. photoexcitation) and from unknown line blendings, it seems useful to observe as many lines as possible. A wide range of masses and q/m of the ion species also favour the distinction between the relative contribution of thermal and non-thermal velocity in the observed line widths.
Table 1:
Comparison of the characteristic cyclotron time of some species with their heat exchange time with protons, in the lower corona.
3 Observations and data processing
The VUV Spectrometer SUMER on board the SOHO spacecraft is described in Wilhelm et al. (1995), Wilhelm et al. (1997), and Lemaire et al. (1997).
Table 2 briefly presents all data sets used in this article. The main one, called set 1, consists of ten spectral ranges, observed using detector A on 30 May 2002 during MEDOC Campaign #9. The lines of interest are listed in Table 3. The complete observation was about 13 h long. The centre of the slit was pointed at
 ,
,
 (i.e. at the North Pole). The
(i.e. at the North Pole). The
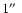
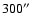 slit was used, oriented in the north-south direction, covering a wide range of altitudes at the same time (from about 50
slit was used, oriented in the north-south direction, covering a wide range of altitudes at the same time (from about 50
 to 350
to 350
 above the solar limb, with an apparent solar radius of 956
above the solar limb, with an apparent solar radius of 956
 ). The width of 1
). The width of 1
 reaches a compromise between the photon statistics and the instrumental width.
reaches a compromise between the photon statistics and the instrumental width.
Table 2:
Description of data sets.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{7903fi01}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg55.gif) |
Figure 1:
EIT/SOHO context image for data set 1 (195 Å channel). The spatial coverage of the SUMER slit is shown. |
| Open with DEXTER |
The EIT/SOHO images on that day (Fig. 1) show that the coronal hole appearing on the solar disc at the North Pole is not developed well. Inspection of EIT movies of the preceding and following solar rotations reveals that the coronal hole is far from being symmetric, and highly elongated along one particular direction towards the equator. Nonetheless, it appears that some part of the coronal hole is lying right under the position we are pointing at in the plane of the sky, and LASCO images show no streamer on the north-south axis. However, we cannot dismiss the possibility of a contamination of the LOS by any plasma belonging to non-hole (i.e. ``Quiet Sun'', QS) part of the corona. To gain more confidence, we compared the behaviour of the width of the Mg X 625 Å line (observed at 1249.88 Å in second order) in three other data sets.
Data set 2 corresponds to the south pole observed two days before data set 1 (same altitude range); the EIT survey shows that there is no coronal hole at the south pole at this period. Data sets 3 and 4 correspond to other polar coronal holes (CH). Figure 2 shows that the behaviour of the line width in set 1 compares well to those in sets 3 and 4, because it keeps increasing at low altitudes and then decreases at the highest altitudes.
In contrast, data set 2 displays a different behaviour, with a large plateau starting from 60
 ,
and it will be analysed more thoroughly in a future paper.
According to Wilhelm et al. (2004), the Mg X 609 and 625 Å line widths are larger in coronal holes than in the Quiet corona (by more than 30% at 100
,
and it will be analysed more thoroughly in a future paper.
According to Wilhelm et al. (2004), the Mg X 609 and 625 Å line widths are larger in coronal holes than in the Quiet corona (by more than 30% at 100
 ). Data sets 1 to 4 do not show such large differences. The maximum one is between sets 1 and 2, and the Mg X line width in set 1 is only larger than that of set 2 by
). Data sets 1 to 4 do not show such large differences. The maximum one is between sets 1 and 2, and the Mg X line width in set 1 is only larger than that of set 2 by 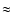
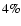 at 100
at 100
 .
In fact, from 60
.
In fact, from 60
 to 100
to 100
 ,
our values are higher than those of Wilhelm et al. (2004) in the Quiet corona by about 15% and lower than those in coronal holes by about 15%. Nevertheless, they are closer to what was observed by Doschek et al. (2001) in coronal holes, although a contamination by non-hole material cannot be dismissed, especially because the magnetic topology is far from being as simple as during solar minima. The density, discussed in Sect. 4.1, is similar to what has been previously measured in coronal holes.
,
our values are higher than those of Wilhelm et al. (2004) in the Quiet corona by about 15% and lower than those in coronal holes by about 15%. Nevertheless, they are closer to what was observed by Doschek et al. (2001) in coronal holes, although a contamination by non-hole material cannot be dismissed, especially because the magnetic topology is far from being as simple as during solar minima. The density, discussed in Sect. 4.1, is similar to what has been previously measured in coronal holes.
![\begin{figure}
\par\hspace*{-3mm}\includegraphics[width=7.5cm,clip]{7903fi02}\vspace*{5mm}
\includegraphics[width=7.2cm,clip]{7903fi03}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg57.gif) |
Figure 2:
Comparison of the line width ( top panel) and the total counts per second ( bottom panel) measured for the Mg X 625 Å line (observed in second order; the measured width is then twice as large as the width that would be measured in first order), for the four data sets acquired above the solar poles (Table 2). The error bars are only plotted for both extremities in the abscissas, for better visibility. The stray light contribution has not been removed yet. The total counts in the line are discussed in Sect. 5.1. |
| Open with DEXTER |
A density diagnostic has been made using additional data acquired on 30 May 2002.
The lines of Si VIII at 1440 and 1445 Å were observed by SUMER, covering the same field of view as data set 1, with a
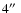
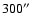 slit. This wider slit thus provides better photon statistics for the line ratio, at the expense of an optimal instrumental width. The total exposure time was about 2 h and 50 min.
slit. This wider slit thus provides better photon statistics for the line ratio, at the expense of an optimal instrumental width. The total exposure time was about 2 h and 50 min.
Raw data were corrected using the standard SUMER procedures provided by Solar Software (flatfield and geometric distorsion of the detector). Note that the observation of faint lines with long exposure times is only possible because the detector noise is low,  3
3 
 (Wilhelm et al. 1997), which makes
(Wilhelm et al. 1997), which makes 
 for a 1-h exposure time. The final spectra were obtained through the addition of consecutive 300 s exposures, after visual inspection of each exposure. The complete detector image was recovered (1024
for a 1-h exposure time. The final spectra were obtained through the addition of consecutive 300 s exposures, after visual inspection of each exposure. The complete detector image was recovered (1024  360 pixels, wavelength
360 pixels, wavelength  spatial dimension Y). The instrument is stigmatic in the spatial dimension Y, with a theoretical spatial resolution around 1
spatial dimension Y). The instrument is stigmatic in the spatial dimension Y, with a theoretical spatial resolution around 1
 .
For better statistics, several spatial pixels were added before analysing the spectral profiles. These intervals appeared to be narrow enough to avoid any significant artificial broadening of the lines owing to the residual distortion of the detector. A rough estimate of the altitude corresponding to each spectrum was provided through the pointing coordinates of the instrument.
.
For better statistics, several spatial pixels were added before analysing the spectral profiles. These intervals appeared to be narrow enough to avoid any significant artificial broadening of the lines owing to the residual distortion of the detector. A rough estimate of the altitude corresponding to each spectrum was provided through the pointing coordinates of the instrument.
3.1 Correction from the instrumental stray light
As SUMER is not a coronagraph (no occultor is included), the solar disc produces stray light during off-limb observations, essentially via the point-spread function properties induced by defects in the reflective surfaces, of spatial sizes of the same order of magnitude as the observed wavelength. Note that, whatever the pointing is, the complete image of the Sun is permanently formed by the main parabola.
This instrumental stray light is negligible for on-disc observations, but the contamination increases as the altitude of observation above the limb increases, until it is responsible for the quasi-complete photon rate detected above 1.6 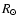 (Feldman et al. 1999). This problem is even more critical in coronal holes than above the ``quiet'' corona, as the emissivity is lower.
Consequently, each off-limb spectrum is the sum of the real spectrum emitted by the corona and of the stray-light spectrum. At each point of the image of the Sun produced by the mirror, the intensity of the stray light results from contributions convolved over the entire source (disc plus corona seen above the limb). But the main contribution comes from the disc, where the different regions (active regions, coronal holes, and ``Quiet Sun'') emit different spectra. This results in a stray-light spectrum that varies with the position and date of observations.
(Feldman et al. 1999). This problem is even more critical in coronal holes than above the ``quiet'' corona, as the emissivity is lower.
Consequently, each off-limb spectrum is the sum of the real spectrum emitted by the corona and of the stray-light spectrum. At each point of the image of the Sun produced by the mirror, the intensity of the stray light results from contributions convolved over the entire source (disc plus corona seen above the limb). But the main contribution comes from the disc, where the different regions (active regions, coronal holes, and ``Quiet Sun'') emit different spectra. This results in a stray-light spectrum that varies with the position and date of observations.
Every line that can be observed on the disc contributes to the stray-light spectrum observed above the limb, so that coronal lines (Mg X 625 Å, Fe XII 1242 Å, etc.) are not only blended with their own stray light, but they can also be blended with colder lines of neighbouring wavelengths. This last effect is usually underestimated.
To correct for the instrumental stray light, we used a method already described in Dolla et al. (2003), Dolla et al. (2004), and Dolla (2006), which enabled us to predict the stray-light spectrum contaminating the coronal spectrum observed at any altitude. This predicted spectrum is then substracted from the off-limb spectrum (see also Singh et al. 2003b; Banerjee et al. 2000; Singh et al. 2003a).
For the observed spectral ranges, a reference spectrum was taken well above the limb, so that the spectrum can be considered as purely due to stray light. All reference spectra were acquired with a long exposure (several hours), usually pointing at (
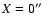 ,
,
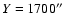 ). The same slit was used as for the off-limb spectra.
The stray-light spectrum is then predicted at any lower altitude by determining the factor that makes the total counts in a reference cold line coincide in both the observed off-limb spectrum and the predicted stray-light spectrum. If no line offers sufficient statistics, one can use the continuum, such as for the Fe X/Fe XI spectral range, near 1465 Å.
Some examples of stray light prediction are shown in Fig. 3 (see also Dolla 2006; Dolla et al. 2004,2003).
). The same slit was used as for the off-limb spectra.
The stray-light spectrum is then predicted at any lower altitude by determining the factor that makes the total counts in a reference cold line coincide in both the observed off-limb spectrum and the predicted stray-light spectrum. If no line offers sufficient statistics, one can use the continuum, such as for the Fe X/Fe XI spectral range, near 1465 Å.
Some examples of stray light prediction are shown in Fig. 3 (see also Dolla 2006; Dolla et al. 2004,2003).
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{7903fi04}\vspace*{3mm}
\in...
...{7903fi05}\vspace*{3mm}
\includegraphics[width=7.3cm,clip]{7903fi06}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg62.gif) |
Figure 3:
Examples of stray-light spectrum predictions for a spectral range covering 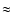 40 Å around the Si VIII line at 944 Å (data set 2). Each observed off-limb spectrum (in grey) is the sum of an instrumental stray-light spectrum (predicted in black) and of the real coronal spectrum. As the altitude increases (here, from 60 to 134 and 253 arcsec above the limb), several cold lines become more prominent in the off-limb spectrum (like H I and S VI lines, here). Meanwhile, some coronal lines become more and more contaminated by the blending with neighbouring cold lines (like Si VIII blended with S VI); blending can also be caused by the same coronal line when this one is prominent in on-disc spectra (e.g., for Mg X around 1250 Å in second order). In these figures, spectra are in counts per wavelength pixels (with integration over wider spatial ranges for increasing altitude). 40 Å around the Si VIII line at 944 Å (data set 2). Each observed off-limb spectrum (in grey) is the sum of an instrumental stray-light spectrum (predicted in black) and of the real coronal spectrum. As the altitude increases (here, from 60 to 134 and 253 arcsec above the limb), several cold lines become more prominent in the off-limb spectrum (like H I and S VI lines, here). Meanwhile, some coronal lines become more and more contaminated by the blending with neighbouring cold lines (like Si VIII blended with S VI); blending can also be caused by the same coronal line when this one is prominent in on-disc spectra (e.g., for Mg X around 1250 Å in second order). In these figures, spectra are in counts per wavelength pixels (with integration over wider spatial ranges for increasing altitude). |
| Open with DEXTER |
We showed in Dolla et al. (2003) that reference spectra taken directly on the disc pointing at a ``quiet Sun'' region, and averaged over all the spatial pixels observed by the slit, do not allow a precise prediction of the stray-light spectrum, because these spectra do not take every kind of region on the disc into account.
With high-altitude spectra, on the contrary, the convolution on the entire disc has already been performed. This also avoids modeling it like in Gabriel et al. (2003). Of course, the extrapolation of the high-altitude spectrum as a stray-light reference at any altitude is not totally correct, as the different contributions from the different areas of the disc are modified. This affects the ratios between the predicted lines, but the relative error on this ratio becomes more negligible as the altitude increases (cf. Feldman et al. 1999; Doschek & Feldman 2000), precisely as the absolute correction increases.
During the observations, a high-altitude reference spectrum for the stray light was not taken for every spectral range observed at lower altitudes in the corona. In particular, judging from previous SUMER data and from spectral lines atlases, we thought that this was not necessary for the Si VIII 1440 and 1445 Å lines. Nevertheless, Fig. 4 shows a bump in the blue wing, growing as the altitude
increases. The same bump can be found in different data sets, so that statistical error is excluded. A possible stray light contamination, also noticed by Banerjee et al. (1998), may explain it. We suspect that another bump is present on the red wing. In fact, these bumps do not appear when using the 4
 slit, probably because the wider instrumental profile smoothes the emission profiles.
slit, probably because the wider instrumental profile smoothes the emission profiles.
According to Ekberg & Feldman (2003), the Si XI 604.15 Å line is blended with an Fe VII line. The blending line is a cold one (class ``b'', following the designation of Feldman et al. 1997), so that any direct blending is probably negligible above the limb. A stray light contamination is likely, but has been underestimated at the time of the data acquisition, and no high-altitude spectrum is available for the stray light determination.
The half-width at
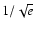 is provided through a least-square Gaussian fit including a second-order polynomial. The spectrum corrected for the stray light is in counts px-1, so as to use statistical errors as weights. The width in pixels is turned into angstroms by using the known dispersion of the spectrometer. The equivalent size of a pixel ranges from 42 to 45 mÅ in first order, depending on the observed wavelength. No precise calibration of the line wavelength is necessary, and we used the values given by Feldman et al. (1997). The fitting procedure provides a 1-sigma error on the width, which we set to 0.1 pixel as a minimum. When the counts at line maximum were below 150 or so, the fitting procedure became unstable, so that we only show results of lines presenting more than 150 counts at their maximum.
is provided through a least-square Gaussian fit including a second-order polynomial. The spectrum corrected for the stray light is in counts px-1, so as to use statistical errors as weights. The width in pixels is turned into angstroms by using the known dispersion of the spectrometer. The equivalent size of a pixel ranges from 42 to 45 mÅ in first order, depending on the observed wavelength. No precise calibration of the line wavelength is necessary, and we used the values given by Feldman et al. (1997). The fitting procedure provides a 1-sigma error on the width, which we set to 0.1 pixel as a minimum. When the counts at line maximum were below 150 or so, the fitting procedure became unstable, so that we only show results of lines presenting more than 150 counts at their maximum.
The spectrum observed on the detector corresponds to the convolution of the spectrum arriving at the aperture of the spectrometer with the instrumental profile. This profile mainly comes from the finite width of the slit.
Both off-limb and stray-light reference spectra are acquired with the same slit width, therefore the corrected spectrum is still convolved with the same instrumental profile (Dolla 2006).
The instrumental width, for detector A, does not depend on the wavelength. The procedure con_width_funct_3 in Solar Software![[*]](/icons/foot_motif.gif) , updated following a study made by Chae et al. (1998), remove it through a deconvolution process, which proves to be equivalent to removing (quadratically) a Gaussian contribution of 42 mÅ (99 mÅ in FWHM).
, updated following a study made by Chae et al. (1998), remove it through a deconvolution process, which proves to be equivalent to removing (quadratically) a Gaussian contribution of 42 mÅ (99 mÅ in FWHM).
![\begin{figure}
\par\includegraphics[width=7.15cm,clip]{7903fi07}\hspace*{4mm}
\includegraphics[width=7cm,clip]{7903fi08}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg64.gif) |
Figure 4:
Si VIII line profiles (1445 Å) at 58
 and 178
and 178
 above a coronal hole (data set 1). No correction of the stray light has been applied, because no high-altitude reference spectrum was taken for that. The ``bumps'' marked by the arrows, getting larger with the altitude and present on other data sets, suggest that this line is slightly contaminated by one cold line or more, appearing as instrumental stray light.
above a coronal hole (data set 1). No correction of the stray light has been applied, because no high-altitude reference spectrum was taken for that. The ``bumps'' marked by the arrows, getting larger with the altitude and present on other data sets, suggest that this line is slightly contaminated by one cold line or more, appearing as instrumental stray light. |
| Open with DEXTER |
4 Method of separating the two contributions in the coronal line widths
As shown in Dolla et al. (2004), that the non-thermal velocity is not well-constrained prevents direct conclusion about the preferential heating, by plotting either the temperature at a given altitude or the difference in temperature between two altitudes, as a function of q/m. In effect, owing to the small number of available lines, the ion species that are more likely to take advantage of cyclotron heating, i.e. having low q/m ratios, are also those with low 1/m ratios, that is to say, those whose width is more sensitive to the value of  (cf. Eq. (1)).
(cf. Eq. (1)).
Instead of making an assumption on the value of  ,
we preferred to make an assumption on its nature. If we suppose that Alfvén waves are responsible for the non-thermal velocity, then its radial variation can be constrained using Eq. (2) and a density diagnostic. We also consider that the Mg X species, having the highest q/m ratio in our data set, is less likely to be heated through the cyclotron resonance, and we suppose that its line width will only increase because of an increase in the non-thermal velocity. This hypothesis will then be verified a posteriori on a given interval.
,
we preferred to make an assumption on its nature. If we suppose that Alfvén waves are responsible for the non-thermal velocity, then its radial variation can be constrained using Eq. (2) and a density diagnostic. We also consider that the Mg X species, having the highest q/m ratio in our data set, is less likely to be heated through the cyclotron resonance, and we suppose that its line width will only increase because of an increase in the non-thermal velocity. This hypothesis will then be verified a posteriori on a given interval.
4.1 Density diagnostic
The Si VIII spectra are produced by a running sum over 40 pixels in the spatial direction of the detector. The total counts in the spectral ranges corresponding to both Si VIII lines (1440 and 1445 Å) are integrated. The continuum contribution is then substracted.
The mass density 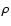 can be obtained through the electron density
can be obtained through the electron density 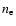 ,
which is derived in Fig. 5 from the theoretical curve linking the line ratio (1445/1440) to the electron density (Doschek et al. 1997, their Fig. 1).
,
which is derived in Fig. 5 from the theoretical curve linking the line ratio (1445/1440) to the electron density (Doschek et al. 1997, their Fig. 1).
Above 270
 ,
the measured line ratio becomes lower than 1, so that no solution is given by the diagnostic. The Si VIII line ratio becomes far less sensitive at electron densities below
,
the measured line ratio becomes lower than 1, so that no solution is given by the diagnostic. The Si VIII line ratio becomes far less sensitive at electron densities below
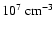 and the 1445 Å line suffer from the stray light mentioned above. For all these reasons, we have less confidence in the results above 180
and the 1445 Å line suffer from the stray light mentioned above. For all these reasons, we have less confidence in the results above 180
 .
.
These density values are similar to those of Doschek et al. (1997) measured in a polar coronal hole and at the same altitude range. They nevertheless decrease more rapidly with the altitude.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{7903fi09}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg66.gif) |
Figure 5:
Electron density  with increasing altitude above the Northpolar coronal hole (data set 1). The dotted lines denote the error bars.
with increasing altitude above the Northpolar coronal hole (data set 1). The dotted lines denote the error bars. |
| Open with DEXTER |
Equation (1) can be rewritten as the quadratic sum of thermal and non-thermal velocity:
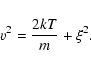 |
(3) |
By using the assumption that the Mg X 625 Å line-width variation is solely due to a variation in  between positions r0 and r (i.e.
between positions r0 and r (i.e.
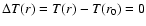 ,
with r0 the lowest position in data set 1 i.e. at the bottom of the slit), we can write
,
with r0 the lowest position in data set 1 i.e. at the bottom of the slit), we can write
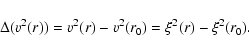 |
(4) |
The flux conservation of the Alfvén waves yields
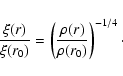 |
(5) |
From Eqs. (4) anf (5), we get
![\begin{displaymath}%
\xi(r_0) = \left[ \frac{\Delta (v^2 (r))}{ \left( \frac{\rho(r)}{\rho(r_0)} \right)^{-1/2} - 1} \right]^{1/2}\cdot
\end{displaymath}](/articles/aa/full/2008/19/aa7903-07/img71.gif) |
(6) |
Thus, 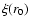 can be determined for any r where the hypothesis
can be determined for any r where the hypothesis
 is true and where
is true and where 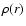 and v(r) can be measured.
and v(r) can be measured.
Figure 6 shows that the value of 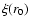 is relatively constant for r in the range [70; 150] arcsec, which tends to prove that the
is relatively constant for r in the range [70; 150] arcsec, which tends to prove that the
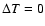 hypothesis is valid on that interval. As the error on
hypothesis is valid on that interval. As the error on 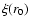 increases when the values of v2(r) and
increases when the values of v2(r) and 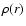 are close to that at r0, the lowest altitudes are associated with particularly large error bars. To get a higher precision, we made a weighted average of
are close to that at r0, the lowest altitudes are associated with particularly large error bars. To get a higher precision, we made a weighted average of 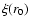 over the [90; 150] interval, reduced not to unnecessarily broaden the error bars. We got
over the [90; 150] interval, reduced not to unnecessarily broaden the error bars. We got
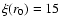
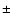
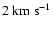 .
.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{7903fi10} \end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg78.gif) |
Figure 6:
Value of the non-thermal velocity 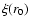 calculated at the lowest
altitude observed in
data set 1 (i.e.
calculated at the lowest
altitude observed in
data set 1 (i.e.
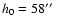 above the limb)
for increasing altitude
above the limb)
for increasing altitude
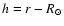 (see Eq. (6)). We used the difference in width between r and r0,
for the Mg X 625 Å line. The dotted lines denote the error bars.
(see Eq. (6)). We used the difference in width between r and r0,
for the Mg X 625 Å line. The dotted lines denote the error bars. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7903fi11}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg79.gif) |
Figure 7:
Non-thermal velocity  with increasing altitude above the North polar coronal hole (data set 1), derived by using the flux conservation of Alfvén waves (Eq. (5)). The dotted lines denote the error bars.
with increasing altitude above the North polar coronal hole (data set 1), derived by using the flux conservation of Alfvén waves (Eq. (5)). The dotted lines denote the error bars. |
| Open with DEXTER |
Once we have 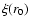 ,
,
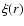 comes from Eq. (5) (Fig. 7), every where we know
comes from Eq. (5) (Fig. 7), every where we know 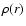 .
The Mg X 625 Å line width and the
.
The Mg X 625 Å line width and the
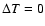 hypothesis were only used to determine the constant
hypothesis were only used to determine the constant 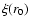 .
The determination of
.
The determination of 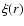 now only requires the density diagnostic. Nevertheless, Eq. (5) is only valid if we assume that Alfvén waves undergo no damping between r0 and r and, of course, if Alfvén waves are entirely responsible for the appearance of the non-thermal velocity.
now only requires the density diagnostic. Nevertheless, Eq. (5) is only valid if we assume that Alfvén waves undergo no damping between r0 and r and, of course, if Alfvén waves are entirely responsible for the appearance of the non-thermal velocity.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7903fi12}\hspace*{5mm}
\includegraphics[width=7cm,clip]{7903fi13}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg81.gif) |
Figure 8:
Line-width variation above the limb for some ions in data set 1. Spectra are created by a running sum over 40 spatial pixels. In grey, the value when the stray light is not corrected; the value after correction (in black) is not available for every ion (e.g. Si VIII). The appearance of a decrease when some particular altitude is reached is explained by the stray light contamination (first panel, e.g. Fe X blended with O I, or Mg X, blended with the same line as stray light). The second panel shows some lines that start to decrease (or stay constant) from the lowest altitude that we observed (with or without correction), which apparently contradicts the behaviour of the other lines. For better visibility, the errors bars are only shown on both extremities of the curves, and the width of Fe X is shifted by -0.03 Å (first panel), while that of S X is shifted by -0.02 Å (second panel). |
| Open with DEXTER |
Above 150
 ,
the slope of the density curve changes.
This may be due to the presence of a different structure on the plane of the sky, e.g. a difference between plume and interplume.
If so, one would expect that the flux conservation is no longer valid above 150
,
the slope of the density curve changes.
This may be due to the presence of a different structure on the plane of the sky, e.g. a difference between plume and interplume.
If so, one would expect that the flux conservation is no longer valid above 150
 ,
as the necessary continuity of the flux tubes is compromised. We nevertheless derived
,
as the necessary continuity of the flux tubes is compromised. We nevertheless derived  up to 270
up to 270
 ,
keeping in mind that the results are less reliable above 150
,
keeping in mind that the results are less reliable above 150
 .
.
Temperature for each ion species can now be determined from the observed linewiths (shown in Fig. 8) by using Eq. (1). The altitude range is nonetheless restricted to positions where the non-thermal velocity is determined, i.e. below about 270
 .
To produce each spectrum, we performed a running sum over 40 spatial pixels.
The results are shown in Fig. 9 and discussed below.
.
To produce each spectrum, we performed a running sum over 40 spatial pixels.
The results are shown in Fig. 9 and discussed below.
5 Results and discussion
5.1 No evidence of Alfvén wave damping
Before analysing more deeply the coronal line widths in terms of temperature and non-thermal velocity, we will discuss the radial variation of the width as a whole.
This is an important issue because, in past studies, the fact that the widths of coronal lines were decreasing above some given altitude was sometimes interpreted as the signature of the damping of Alfvén waves. In fact, it appears that this decrease is essentially an effect of the instrumental stray light.
Figure 8 shows some examples of the width of different lines, with increasing altitude above the limb. The Mg X 625 Å and Si VIII 1445 Å lines, in particular, have been widely analysed in the literature. When no stray light correction is made, the Mg X 625 Å line presents the same behaviour as observed by previous authors: first, the line width increases, then reaches a maximum around 200
 (
(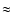
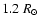 from disc centre), and starts to decrease. We find the same kind of behaviour for the Fe X 1028 Å or Fe XII 1242 Å lines. There are not enough statistics for the Si VIII 1445 Å line to extend the curve above 140
from disc centre), and starts to decrease. We find the same kind of behaviour for the Fe X 1028 Å or Fe XII 1242 Å lines. There are not enough statistics for the Si VIII 1445 Å line to extend the curve above 140
 .
When we correct spectra from the stray light contribution in the case of the Mg X line, it is no longer possible to see any decrease, but maybe a flattening trend. For the Fe X and Fe XII lines, the stray light becomes so strong that there are not enough statistics to follow them as high as in the case with no correction; nevertheless, it appears an increasing trend for both lines.
.
When we correct spectra from the stray light contribution in the case of the Mg X line, it is no longer possible to see any decrease, but maybe a flattening trend. For the Fe X and Fe XII lines, the stray light becomes so strong that there are not enough statistics to follow them as high as in the case with no correction; nevertheless, it appears an increasing trend for both lines.
That the stray light contamination is responsible for reducing the coronal line widths observed above the limb is well known, but appears to be underestimated in most studies with SUMER, as we find that the effect is already noticeable well below 200
 .
One should question in particular any study that does not directly predicts the stray-light spectra.
.
One should question in particular any study that does not directly predicts the stray-light spectra.
The explanation of this effect is rather simple: lines are always narrower in stray-light spectra than in off-limb spectra; therefore, when the stray light contamination grows as the altitude increases, the observed line width is reduced. It is worthwhile recalling that a stray-light spectrum is similar to any typical spectrum that could be observed on the disc in the same wavelength range. Therefore two cases are possible: either the stray-light blending is caused by the same coronal or transition region line, when it is particularly prominent on the disc (e.g. for Mg X 625 Å or Fe XII 1242 Å and 1349 Å), or it is due to another line of neighbouring wavelength (e.g. Fe X lines that are blended with O I near 1028 Å or with C I near 1463.5 Å). In this case, the blending line is usually a colder and narrower one, dominant on the disc, while the hotter one is dominant above the limb.
When no stray light correction is made, the observation of either a plateau or a decrease after the initial increase with the altitude, and the altitude where this is observed, is then simply determined by the way the ratio of stray light to coronal emission evolves with the altitude.
In general, lines having a lower formation temperature than the others present a radiance that decreases more rapidly with the altitude, and are consequently subject to more contamination.
Thus, in Fig. 8, the uncorrected Fe X line width starts to decrease at a lower altitude (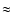
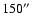 )
than that of Mg X (
)
than that of Mg X (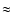
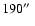 ), which also starts to decrease at a lower altitude than that of Fe XII (
), which also starts to decrease at a lower altitude than that of Fe XII (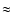
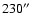 ;
cf. Fig. 10 for the formation temperatures of these ions).
But from one data set to another, the same line can also present different behaviours. One can notice in Fig. 2 (upper panel) that the Mg X 625 Å line width presents a plateau from 60
;
cf. Fig. 10 for the formation temperatures of these ions).
But from one data set to another, the same line can also present different behaviours. One can notice in Fig. 2 (upper panel) that the Mg X 625 Å line width presents a plateau from 60
 to 180
to 180
 ,
while it reaches a maximum at three different altitudes in data sets 1, 3, and 4.
For these sets, the difference in altitude of the maximum present some correlation with the observed radiance (bottom panel). Note that if the observed radiance consists of the addition of the intrinsic and of the stray light radiance, the last one is negligible at low altitude, so that the curves give a good idea of the intrinsic radiance there.
Thus, the curve starts to decrease before all the others in set 3 (
,
while it reaches a maximum at three different altitudes in data sets 1, 3, and 4.
For these sets, the difference in altitude of the maximum present some correlation with the observed radiance (bottom panel). Note that if the observed radiance consists of the addition of the intrinsic and of the stray light radiance, the last one is negligible at low altitude, so that the curves give a good idea of the intrinsic radiance there.
Thus, the curve starts to decrease before all the others in set 3 (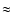
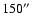 )
and reaches a plateau in set 4 (still around 150
)
and reaches a plateau in set 4 (still around 150
 )
before the maximum seen in set 1 (
)
before the maximum seen in set 1 (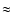
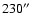 ). This fact can be explained by an almost identical stray light contribution in all data sets, dominating more rapidly in data sets where the intrinsic emission is smaller.
). This fact can be explained by an almost identical stray light contribution in all data sets, dominating more rapidly in data sets where the intrinsic emission is smaller.
![\begin{figure}
\par\hspace*{-1mm}\includegraphics[width=6.95cm,clip]{7903fi14}\v...
...7903fi15}\vspace*{3mm}
\includegraphics[width=6.85cm,clip]{7903fi16}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg86.gif) |
Figure 9:
Temperature with increasing altitude above the limb (data set 1; spectra are produced by a running sum over 40 spatial pixels). |
| Open with DEXTER |
There is, however, one reservation concerning the interpretation of the decrease in the line width in terms of stray light contamination: even after correction, there is still a decrease, or an almost constant value, for some lines in data set 1: both O VI, the Si XI 580.91 Å, and the S X 1196.20 Å lines (Fig. 8, right panel). For these lines, there is no increase phase, as this decreasing trend begins at 57
 .
Once the non-thermal velocity is removed, the derived temperatures decrease with increasing altitude (Fig. 9, third panel). We have no explanation for this behaviour, as these lines are not intense enough on-disc to be subject to photoexcitation, except for O VI. It is possible that these lines are affected by some blends.
.
Once the non-thermal velocity is removed, the derived temperatures decrease with increasing altitude (Fig. 9, third panel). We have no explanation for this behaviour, as these lines are not intense enough on-disc to be subject to photoexcitation, except for O VI. It is possible that these lines are affected by some blends.
5.2 Signatures of preferential heating
The ion temperatures in Fig. 9 are of the same order of magnitude as what is found in previous studies (e.g. Tu et al. 1998; Patsourakos et al. 2002); they all exceed 2 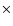
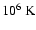 at 57
at 57
 .
They exhibit a wide range of values, which makes the isothermal hypothesis unlikely. The temperature of the three iron lines, for example, are arranged in the opposite order to their corresponding ionization temperature (Fig. 10). Then the LOS effect associated to the stratification in temperature of the corona also appears unlikely.
The temperature increases with the altitude for most of the lines, except in the bottom frame of Fig. 9 corresponding to the exceptions mentioned above. This implies some heating mechanism. The relative discrepancy between both temperatures yielded by the Fe XII lines at 1242 and 1349 Å, below 130
.
They exhibit a wide range of values, which makes the isothermal hypothesis unlikely. The temperature of the three iron lines, for example, are arranged in the opposite order to their corresponding ionization temperature (Fig. 10). Then the LOS effect associated to the stratification in temperature of the corona also appears unlikely.
The temperature increases with the altitude for most of the lines, except in the bottom frame of Fig. 9 corresponding to the exceptions mentioned above. This implies some heating mechanism. The relative discrepancy between both temperatures yielded by the Fe XII lines at 1242 and 1349 Å, below 130
 ,
may be explained by the blending of the 1242 Å line with an Si X line (cf. Table 1 in Feldman et al. 1997), as well as by the error bars. The temperature of Fe X is very high, but it is confirmed at low altitude by a second Fe X line, at 1463 Å (see Fig. 12).
,
may be explained by the blending of the 1242 Å line with an Si X line (cf. Table 1 in Feldman et al. 1997), as well as by the error bars. The temperature of Fe X is very high, but it is confirmed at low altitude by a second Fe X line, at 1463 Å (see Fig. 12).
![\begin{figure}
\par\includegraphics[width=7.05cm,clip]{7903fi17}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg87.gif) |
Figure 10:
Measured ion temperatures (data set 1, 57
 above the limb) as functions of the maximum ionization temperatures (taken from Arnaud & Rothenflug 1985). They are well above the corresponding ionization temperature (dotted line).
above the limb) as functions of the maximum ionization temperatures (taken from Arnaud & Rothenflug 1985). They are well above the corresponding ionization temperature (dotted line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{7903fi18}\hspace*{4mm}
\includegraphics[width=6.9cm,clip]{7903fi19}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg88.gif) |
Figure 11:
Difference in temperature between 57
 and 102
and 102
 ,
once the non-thermal contribution is removed ( left panel). The right panel corresponds to the case where we suppose that there is no variation in non-thermal velocity, only a temperature one. This case is equivalent to the case ,
once the non-thermal contribution is removed ( left panel). The right panel corresponds to the case where we suppose that there is no variation in non-thermal velocity, only a temperature one. This case is equivalent to the case 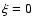 ,
i.e. when no non-thermal velocity is considered at all.
The fitting functions are discussed in Sect. 5.2. The slopes of the linear fits are ,
i.e. when no non-thermal velocity is considered at all.
The fitting functions are discussed in Sect. 5.2. The slopes of the linear fits are
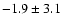 and
and
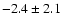 ,
respectively, in the left and the right panels (in ,
respectively, in the left and the right panels (in
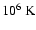 per unit of normalized q/m).
per unit of normalized q/m). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{7903fi20}\hspace*{7mm}
\includegraphics[width=6.8cm,clip]{7903fi21}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg89.gif) |
Figure 12:
Temperatures as functions of the charge-to-mass ratio q/m, 57
 ( left panel) and 102
( left panel) and 102
 ( right panel) above a polar coronal hole (data set 1; the non-thermal velocity has been removed from the line widths). The interest of making a linear fit is discussed in Sect. 5.2.
( right panel) above a polar coronal hole (data set 1; the non-thermal velocity has been removed from the line widths). The interest of making a linear fit is discussed in Sect. 5.2. |
| Open with DEXTER |
To reveal a preferential heating, we plot in Fig. 11 the difference in temperature as a function of the q/m ratio between 57
 and 102
and 102
 ,
for as many lines as possible in data set 1. The line widths and temperatures measured at these altitudes are presented in Table 3.
It is important to note that, for lines seen in second order, the widths are twice as large as what would be measured in first order. This is taken into account when using Eq. (1) and the derived ones. We average over 30 pixels at 57
,
for as many lines as possible in data set 1. The line widths and temperatures measured at these altitudes are presented in Table 3.
It is important to note that, for lines seen in second order, the widths are twice as large as what would be measured in first order. This is taken into account when using Eq. (1) and the derived ones. We average over 30 pixels at 57
 and 60 pixels at 102
and 60 pixels at 102
 ,
to exploit some very faint lines. There were not enough statistics at 102
,
to exploit some very faint lines. There were not enough statistics at 102
 to analyse the Fe X line at 1463 Å, so that we only keep the one at 1028 Å. In the left panel, the non-thermal velocity has been taken into account, using results in Fig. 7: 15 and
to analyse the Fe X line at 1463 Å, so that we only keep the one at 1028 Å. In the left panel, the non-thermal velocity has been taken into account, using results in Fig. 7: 15 and
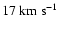 at 57
at 57
 and 102
and 102
 ,
respectively. The right panel corresponds to the case where no variation in non-thermal velocity is considered between 57
,
respectively. The right panel corresponds to the case where no variation in non-thermal velocity is considered between 57
 and 102
and 102
 ,
which is discussed in Sect. 5.3.
The large error bars are due to the errors propagated from both the observed and the stray-light spectra to the line width (Gaussian-fit procedure) and the error on the determination of the non-thermal velocity. The weighted power law and linear fits show a trend for the ion species having the lowest q/m ratios to experience more heating than the others, which is compatible with ion-cyclotron preferential heating. Both kinds of fit curves are not very different from each other. We do not intend to fit the data with any particular theoretical model. However, the power law tends to 0 for high q/m, while the linear fit, with a slope of -1.9
,
which is discussed in Sect. 5.3.
The large error bars are due to the errors propagated from both the observed and the stray-light spectra to the line width (Gaussian-fit procedure) and the error on the determination of the non-thermal velocity. The weighted power law and linear fits show a trend for the ion species having the lowest q/m ratios to experience more heating than the others, which is compatible with ion-cyclotron preferential heating. Both kinds of fit curves are not very different from each other. We do not intend to fit the data with any particular theoretical model. However, the power law tends to 0 for high q/m, while the linear fit, with a slope of -1.9 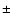 3.1 (in
3.1 (in
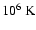 per unit of normalized q/m), plummets towards
per unit of normalized q/m), plummets towards
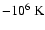 for q/m = 1 (protons). Therefore, a power law seems to better represent a preferential heating of low q/m species, although the correct function is probably much more complicated.
One can notice that the different line width behaviours observed by Singh et al. (2003b,a), which they link to the formation temperature (LOS effect), are also compatible with ion-cyclotron heating. It is worthwhile noting that they correct for the instrumental stray light with the same method as we do. The case of Fe XIV, in their study, the line width of which decreases with the altitude, is nevertheless disturbing. But this is somehow similar to the behaviour of some lines in our data set 1 (Fig. 9, bottom panel). If it is a real variation in temperature, this apparent ``cooling'' process should be explained. We notice, though, that all these lines are associated to the highest q/m, meaning that they are less likely to be concerned by ion-cyclotron heating. Therefore, it is possible that all other ions experience the same kind of cooling, or a decrease in non-thermal velocity, but that this effect is counterbalanced by the preferential heating for the ions having the lowest q/m.
for q/m = 1 (protons). Therefore, a power law seems to better represent a preferential heating of low q/m species, although the correct function is probably much more complicated.
One can notice that the different line width behaviours observed by Singh et al. (2003b,a), which they link to the formation temperature (LOS effect), are also compatible with ion-cyclotron heating. It is worthwhile noting that they correct for the instrumental stray light with the same method as we do. The case of Fe XIV, in their study, the line width of which decreases with the altitude, is nevertheless disturbing. But this is somehow similar to the behaviour of some lines in our data set 1 (Fig. 9, bottom panel). If it is a real variation in temperature, this apparent ``cooling'' process should be explained. We notice, though, that all these lines are associated to the highest q/m, meaning that they are less likely to be concerned by ion-cyclotron heating. Therefore, it is possible that all other ions experience the same kind of cooling, or a decrease in non-thermal velocity, but that this effect is counterbalanced by the preferential heating for the ions having the lowest q/m.
A second kind of analysis consists in plotting the ion temperatures as functions of q/m, at a given altitude (Fig. 12). It shows that the ion species having the lowest q/m have a higher temperature than the others. The trend is emphasised more at 102
 than at 57
than at 57
 ,
which is consistent with the previous analysis. The particularly high temperature of Fe X tends to compress the graph, but the trend does not rely on this ion alone. To show that, we use a weighted linear fit including the Fe X data or not. Even if a straight line is obviously not the proper function to fit the data, it makes the comparison simpler, while no theoretical function is available. At 57
,
which is consistent with the previous analysis. The particularly high temperature of Fe X tends to compress the graph, but the trend does not rely on this ion alone. To show that, we use a weighted linear fit including the Fe X data or not. Even if a straight line is obviously not the proper function to fit the data, it makes the comparison simpler, while no theoretical function is available. At 57
 ,
the slope is equal to -2.2
,
the slope is equal to -2.2 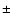 1.2 with Fe X and -0.9
1.2 with Fe X and -0.9 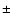 1.3 without it, still in
1.3 without it, still in
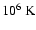 per unit of normalized q/m. At 102
per unit of normalized q/m. At 102
 ,
it gives -4.7
,
it gives -4.7 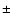 1.7 with Fe X and -2.7
1.7 with Fe X and -2.7 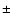 1.8 without it.
1.8 without it.
Table 3:
Line widths measured in data set 1 (coronal hole) at two positions above the solar limb, and the associated ion temperatures.
To interpret these curves, some points must be emphasised. First, the protons can be considered as a cooling source for all minor ion species that could be subject to any preferential heating. They compose the largest part of the coronal plasma so that collisions of one given minor ion are much more frequent with protons than with other species. As the q/m ratio of the protons, equal to 1 with our normalization, is higher than those of all the minor ions, they are also least likely to experience cyclotron heating. Consequently, their temperature must be lower than or equal to that of the ions having the highest q/m ratios, and the temperature of all other species is the result of a competition between preferential heating and cooling with the protons. By measuring differences in temperature, one only has access to the net heating.
Second, most of the ion-cyclotron numerical simulations show that the species having the lowest q/m absorb most of the wave power available, to the detriment of the others that cannot resonate efficiently yet (e.g. Vocks & Marsch 2002; Cranmer 2000). This could explain the high temperature of Fe X as compared to the other species.
That low q/m ions are already hotter than the others at 57
 suggests that ion-cyclotron resonance has already taken place at lower altitudes. Such a preferential heating is still at work between 57
suggests that ion-cyclotron resonance has already taken place at lower altitudes. Such a preferential heating is still at work between 57
 and 102
and 102
 (cf. Fig. 11).
If the net heating experienced by the lowest q/m ion species, as well as their temperatures, appear high, one should keep in mind, though, that these are minor ions. Therefore, this heating does not require much energy, nothing comparable to what is needed to appreciably heat the protons.
And yet, even if we have no direct measurement of the proton temperature here, one can speculate that it is not very different from those of the ions species having the higher q/m ratios.
One can firmly suppose from the discussion in the previous paragraph, indeed, that the potential cyclotron heating for the high q/m species is low. Then, it is not likely that large temperature differences with the protons can be maintained against collisions.
If the proton temperature is as high as those of the colder ion species observed, this is far more than the electron temperature usually observed in coronal holes (
(cf. Fig. 11).
If the net heating experienced by the lowest q/m ion species, as well as their temperatures, appear high, one should keep in mind, though, that these are minor ions. Therefore, this heating does not require much energy, nothing comparable to what is needed to appreciably heat the protons.
And yet, even if we have no direct measurement of the proton temperature here, one can speculate that it is not very different from those of the ions species having the higher q/m ratios.
One can firmly suppose from the discussion in the previous paragraph, indeed, that the potential cyclotron heating for the high q/m species is low. Then, it is not likely that large temperature differences with the protons can be maintained against collisions.
If the proton temperature is as high as those of the colder ion species observed, this is far more than the electron temperature usually observed in coronal holes (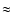 8
8 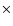 105 K, Wilhelm et al. 1998; Habbal et al. 1993; David et al. 1998).
Then, one has to consider that the protons may have been heated in comparison with the electrons, again at altitudes below 57
105 K, Wilhelm et al. 1998; Habbal et al. 1993; David et al. 1998).
Then, one has to consider that the protons may have been heated in comparison with the electrons, again at altitudes below 57
 .
Investigating the helium or hydrogen temperatures and their variations with the altitude would be a big help for getting more information in the q/m analysis, but the associated lines in the SUMER spectrum suffer from a strong stray-light blending.
.
Investigating the helium or hydrogen temperatures and their variations with the altitude would be a big help for getting more information in the q/m analysis, but the associated lines in the SUMER spectrum suffer from a strong stray-light blending.
5.3 Derived non-thermal velocity and its effect on the signature
The signatures of preferential heating are sensitive to the derived non-thermal velocity. In particular, any variation in width is distributed among variations in temperature and in non-thermal velocity:
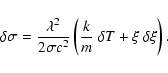 |
(7) |
Even if there is little variation in  between 57
between 57
 and 102
and 102
 (2
(2
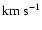 ), the actual value of
), the actual value of  has a strong effect on the interpretation of the line-width variation. The value of
has a strong effect on the interpretation of the line-width variation. The value of 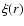 was derived under flux conservation condition, with no damping occurring for the Alfvén waves. We have already said that it was not possible to verify this assumption, because the Mg X 625 Å line width keeps increasing, so a possible decrease in
was derived under flux conservation condition, with no damping occurring for the Alfvén waves. We have already said that it was not possible to verify this assumption, because the Mg X 625 Å line width keeps increasing, so a possible decrease in  may be hidden by an increase in temperature. If
may be hidden by an increase in temperature. If
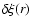 starts to decrease, in reality, above some position r or even becomes negative, i.e. the damping is greater than the amplitude increase due to the flux conservation, then the line-width growth only has to be attributed to a growth of temperature. But this situation may only amplify the preferential heating trend, both in absolute temperatures and in differences in temperature, as shown in the right panel of Fig. 11. Note that the case
starts to decrease, in reality, above some position r or even becomes negative, i.e. the damping is greater than the amplitude increase due to the flux conservation, then the line-width growth only has to be attributed to a growth of temperature. But this situation may only amplify the preferential heating trend, both in absolute temperatures and in differences in temperature, as shown in the right panel of Fig. 11. Note that the case
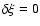 is equivalent to the case
is equivalent to the case
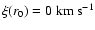 (cf. Eq. (7)).
In contrast, if
(cf. Eq. (7)).
In contrast, if 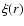 is larger than what we find, considering for example that Alfvén waves are not responsible for the apparent non-thermal velocity, hence that
is larger than what we find, considering for example that Alfvén waves are not responsible for the apparent non-thermal velocity, hence that  is not constrained by the flux conservation, then the preferential heating trends are weakened.
is not constrained by the flux conservation, then the preferential heating trends are weakened.
The non-thermal velocities that we got at low altitude in the coronal hole are within the lower limit of previously published results. However, most of those results were obtained by using the formation temperature hypothesis, which underestimates the ion temperatures.
A value of 25 or 30
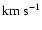 for the alfvénic fluctuations is typically used as a boundary condition at the coronal base in numerical simulations of heating and acceleration of the fast solar wind (see references in Sect. 1). However, this value is only
encountered above 200
for the alfvénic fluctuations is typically used as a boundary condition at the coronal base in numerical simulations of heating and acceleration of the fast solar wind (see references in Sect. 1). However, this value is only
encountered above 200
 in our results. There is then a lack of energy at the coronal base to reproduce the speed and temperature of the fast solar wind by using these models.
in our results. There is then a lack of energy at the coronal base to reproduce the speed and temperature of the fast solar wind by using these models.
6 Conclusions
Alfvén waves and ion-cyclotron resonance, i.e. absorption of the high frequencies, are commonly used in theoretical models to provide the corona with heating and/or the fast solar wind with acceleration. Signatures of ion-cyclotron heating have been reported in the upper corona (>
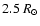 )
and in the solar wind. It appears important, then, to investigate ion-cyclotron resonance closer to the Sun, where the coronal line widths offer the opportunity to study both the temperature of different ion species and the amplitude of possible Alfvén waves. This is of course a challenging task as these quantities are merged into one observable, the line width. Most of the time, methods were used that excluded a priori the possibility of analysing both contributions simultaneously. Our analysis, on the contrary, achieves a synthesis of different approaches that can be found separately in the literature, to both test and constrain the presence of Alfvén waves and the preferential heating. We constrained the former by the gradient of the Mg X 625 Å line width, while the latter appears from the gradient of ion temperatures and from the distinct ion temperatures measured at a given altitude.
)
and in the solar wind. It appears important, then, to investigate ion-cyclotron resonance closer to the Sun, where the coronal line widths offer the opportunity to study both the temperature of different ion species and the amplitude of possible Alfvén waves. This is of course a challenging task as these quantities are merged into one observable, the line width. Most of the time, methods were used that excluded a priori the possibility of analysing both contributions simultaneously. Our analysis, on the contrary, achieves a synthesis of different approaches that can be found separately in the literature, to both test and constrain the presence of Alfvén waves and the preferential heating. We constrained the former by the gradient of the Mg X 625 Å line width, while the latter appears from the gradient of ion temperatures and from the distinct ion temperatures measured at a given altitude.
Our analysis rests on the following hypotheses: i) the coronal lines broadening is solely due to the thermal and non-thermal Doppler effects through Gaussian contributions. ii) The non-thermal velocity  comes from the integration of fluid motions of the coronal plasma on both the observed solid angle and the exposure time, and is identical for all ion species at a given altitude. iii) These motions are due to the presence of Alfvén waves; if there is no damping, their amplitude increases with the altitude to conserve the energy flux in a density-stratified corona. iv) The increase in width of the Mg X 625 Å line (the highest q/m), at low altitude, results only from undamped Alfvén waves, i.e.
comes from the integration of fluid motions of the coronal plasma on both the observed solid angle and the exposure time, and is identical for all ion species at a given altitude. iii) These motions are due to the presence of Alfvén waves; if there is no damping, their amplitude increases with the altitude to conserve the energy flux in a density-stratified corona. iv) The increase in width of the Mg X 625 Å line (the highest q/m), at low altitude, results only from undamped Alfvén waves, i.e.
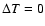 ,
so that a boundary constraint can be set for
,
so that a boundary constraint can be set for  using a density diagnostic (Si VIII line ratio) and the energy flux conservation. v) The Alfvén waves stay undamped on the entire observed spatial range, so that
using a density diagnostic (Si VIII line ratio) and the energy flux conservation. v) The Alfvén waves stay undamped on the entire observed spatial range, so that 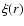 can be derived.
can be derived.
Several results must be emphasised. The decrease in the coronal line widths, occurring around 1.2 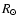 for Mg X for example, is essentially an effect of the instrumental stray light contamination that disappear when we remove the predicted stray-light spectrum.
We cannot rule out, though, the existence of a plateau at higher altitudes than we observed. This result is in accordance with some theoretical ones that find it difficult to damp the Alfvén waves in the lower corona (Parker 1991).
for Mg X for example, is essentially an effect of the instrumental stray light contamination that disappear when we remove the predicted stray-light spectrum.
We cannot rule out, though, the existence of a plateau at higher altitudes than we observed. This result is in accordance with some theoretical ones that find it difficult to damp the Alfvén waves in the lower corona (Parker 1991).
The derived non-thermal velocity is about
 at 60
at 60
 ,
while a value of
,
while a value of
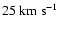 is only reached at 200
is only reached at 200
 above the limb. This means a widely lower wave energy than that commonly used in numerical simulations of heating and acceleration of the fast solar wind. Consequently, one has to find another form of energy, or of dissipation process, to replace or at least complement the processes usually presented in models based on alfvénic fluctuations.
above the limb. This means a widely lower wave energy than that commonly used in numerical simulations of heating and acceleration of the fast solar wind. Consequently, one has to find another form of energy, or of dissipation process, to replace or at least complement the processes usually presented in models based on alfvénic fluctuations.
Two kinds of signatures of preferential heating are found: ion species having the lowest q/m ratios are the hottest ones at a given altitude and experience more heating as the altitude increases from 57
 to 102
to 102
 .
If some damping of the Alfvén waves occurred, i.e. if hypothesis v) was wrong, then these trends would be stronger. Yet, this is neither a proof by itself of cyclotron resonance occurring in the corona, nor does it imply that this is a dominant energy source for acceleration of the fast solar wind or the heating of the corona: the energetics have to be analysed in more depth. Minor ions can only help to trace the cyclotron resonance that may also concern the protons.
The ion temperatures and probably the proton one are higher than the electron temperature usually measured in coronal holes, which imply some preferential heating that must have taken place below the lowest altitude where we observed, i.e. 57
.
If some damping of the Alfvén waves occurred, i.e. if hypothesis v) was wrong, then these trends would be stronger. Yet, this is neither a proof by itself of cyclotron resonance occurring in the corona, nor does it imply that this is a dominant energy source for acceleration of the fast solar wind or the heating of the corona: the energetics have to be analysed in more depth. Minor ions can only help to trace the cyclotron resonance that may also concern the protons.
The ion temperatures and probably the proton one are higher than the electron temperature usually measured in coronal holes, which imply some preferential heating that must have taken place below the lowest altitude where we observed, i.e. 57
 .
.
Some facts may possibly weaken our analysis. First, the width of some lines starts to decrease at the lowest altitude we observed. This contradicts our interpretation in terms of a common increase in the wave amplitude, but this can be due to another contribution in the line width, influencing these lines more. Second, the lines associated with the lowest q/m ratios (Fe X and Fe XI, particularly) are highly contaminated with stray light, so that it is difficult to follow their behaviour at higher altitudes. We are also aware of the large error bars in our derived quantities. Therefore, our results have to be confirmed by additional observations and further analyses.
This work also emphasises some needs for future instrumentation, especially in terms of spectrometers. The study of line widths emitted in the low corona requires a small instrumental width as compared to the intrinsic width.
It is important to develop a better rejection of the light coming from the solar disc, for off-limb observations. Furthermore, a solar probe could achieve important in situ observations to complement the remote-sensing observations, and even calibrate their interpretation.
Acknowledgements
We wish to thank P. Lemaire, A. Gabriel, J. C. Vial, G. Nigro and L. Teriaca for useful discussions, and K. Bocchialini for organising the MEDOC Campaigns at IAS (http://www.medoc-ias.u-psud.fr), which made this work possible. We also want to thanks the anonymous referee who made valuable suggestions to improve the quality of this article. The density diagnostic was made by using data from JOP 158. SOHO is a mission of international cooperation between ESA and
NASA. The SUMER project is financially supported by DLR, CNES, NASA,
and ESA PRODEX Programme (Swiss contribution).
- Arnaud, M., &
Rothenflug, R. 1985, A&AS, 60, 425 [NASA ADS]
(In the text)
- Banerjee, D.,
Teriaca, L., Doyle, J. G., & Wilhelm, K. 1998, A&A,
339, 208 [NASA ADS]
(In the text)
- Banerjee, D.,
Teriaca, L., Doyle, J. G., & Lemaire, P. 2000,
Sol. Phys., 194, 43 [NASA ADS] [CrossRef]
- Boland, B. C.,
Engstrom, S. F. T., Jones, B. B., & Wilson, R.
1973, A&A, 22, 161 [NASA ADS]
(In the text)
- Boland, B. C.,
Dyer, E. P., Firth, J. G., et al. 1975, MNRAS, 171,
697 [NASA ADS]
- Chae, J., Schühle,
U., & Lemaire, P. 1998, ApJ, 505, 957 [NASA ADS] [CrossRef]
- Contesse, L.,
Koutchmy, S., & Viladrich, C. 2004, Ann. Geophys., 22,
3055 [NASA ADS]
(In the text)
- Cranmer,
S. R. 2000, ApJ, 532, 1197 [NASA ADS] [CrossRef]
- Cranmer,
S. R., Field, G. B., & Kohl, J. L. 1999a, ApJ,
518, 937 [NASA ADS] [CrossRef]
(In the text)
- Cranmer,
S. R., Kohl, J. L., Noci, G., et al. 1999b, ApJ,
511, 481 [NASA ADS] [CrossRef]
- David, C., Gabriel,
A. H., Bely-Dubau, F., et al. 1998, A&A, 336,
L90 [NASA ADS]
- Dere, K. P., &
Mason, H. E. 1993, Sol. Phys., 144, 217 [NASA ADS] [CrossRef]
- Dolla, L. 2006,
Ph.D. Thesis, Université Paris-Sud
(In the text)
- Dolla, L., Lemaire,
P., Solomon, J., & Vial, J.-C. 2003, in Solar Wind Ten, AIP
Conf. Proc., 679, 351
(In the text)
- Dolla, L., Solomon,
J., & Lemaire, P. 2004, in SOHO 13 Waves, Oscillations and
Small-Scale Transients Events in the Solar Atmosphere: Joint View
from SOHO and TRACE, ESA SP-547, 391
(In the text)
- Doschek,
G. A., & Feldman, U. 2000, ApJ, 529, 599 [NASA ADS] [CrossRef]
- Doschek,
G. A., Warren, H. P., Laming, J. M., et al.
1997, ApJ, 482, L109 [NASA ADS] [CrossRef]
(In the text)
- Doschek,
G. A., Feldman, U., Laming, J. M., Schühle, U.,
& Wilhelm, K. 2001, ApJ, 546, 559 [NASA ADS] [CrossRef]
(In the text)
- Doyle, J. G.,
Teriaca, L., & Banerjee, D. 1999, A&A, 349, 956 [NASA ADS]
- Doyle, J. G.,
Teriaca, L., & Banerjee, D. 2000, A&A, 356, 335 [NASA ADS]
(In the text)
- Ekberg, J. O.,
& Feldman, U. 2003, ApJS, 148, 567 [NASA ADS] [CrossRef]
(In the text)
- Erdelyi, R.,
Doyle, J. G., Perez, M. E., & Wilhelm, K. 1998,
A&A, 337, 287 [NASA ADS]
(In the text)
- Esser, R., Fineschi,
S., Dobrzycka, D., et al. 1999, ApJ, 510, L63 [NASA ADS] [CrossRef]
- Feldman, U.,
Behring, W. E., Curdt, W., et al. 1997, ApJS, 113,
195 [NASA ADS] [CrossRef]
(In the text)
- Feldman, U.,
Doschek, G. A., Schühle, U., & Wilhelm, K. 1999, ApJ,
518, 500 [NASA ADS] [CrossRef]
(In the text)
- Feldman, U.,
Curdt, W., Landi, E., & Wilhelm, K. 2000, ApJ, 544, 508 [NASA ADS] [CrossRef]
(In the text)
- Frazin, R. A.,
Modigliani, A., Ciaravella, A., et al. 1999, in AIP Conf.
Ser., 235
- Gabriel,
A. H., Bely-Dubau, F., & Lemaire, P. 2003, ApJ, 589,
623 [NASA ADS] [CrossRef]
(In the text)
- Habbal, S. R.,
Esser, R., & Arndt, M. B. 1993, ApJ, 413, 435 [NASA ADS] [CrossRef]
- Hackenberg,
P., Marsch, E., & Mann, G. 2000, A&A, 360, 1139 [NASA ADS]
- Harrison,
R. A., Hood, A. W., & Pike, C. D. 2002, A&A,
392, 319 [NASA ADS] [CrossRef] [EDP Sciences]
- Hassler,
D. M., Rottman, G. J., Shoub, E. C., & Holzer,
T. E. 1990, ApJ, 348, L77 [NASA ADS] [CrossRef]
- Hollweg,
J. V., & Isenberg, P. A. 2002, J. Geophys. Res.,
12
(In the text)
- Hu, Y. Q., Esser, R.,
& Habbal, S. R. 2000, J. Geophys. Res., 105,
5093 [NASA ADS] [CrossRef]
(In the text)
- Isenberg,
P. A. 2001, J. Geophys. Res., 29249 [NASA ADS] [CrossRef]
- Isenberg,
P. A., Lee, M. A., & Hollweg, J. V. 2001,
J. Geophys. Res., 5649 [NASA ADS] [CrossRef]
- Kohl, J. L., Noci,
G., Antonucci, E., et al. 1998, ApJ, 501, L127 [NASA ADS] [CrossRef]
- Kopp, R. A., &
Holzer, T. E. 1976, Sol. Phys., 49, 43 [NASA ADS] [CrossRef]
(In the text)
- Lee, H., Yun, H. S.,
& Chae, J. 2000, J. Korean Astron. Soc., 33, 57 [NASA ADS]
- Lemaire, P.,
Wilhelm, K., Curdt, W., et al. 1997, Sol. Phys., 170,
105 [NASA ADS] [CrossRef]
(In the text)
- Li, X. 2002, ApJ, 571,
L67 [NASA ADS] [CrossRef]
- Li, X., Habbal, S. R.,
Kohl, J., & Noci, G. 1998, ApJ, 501, L133 [NASA ADS] [CrossRef]
- Liewer, P., Velli,
M., & Goldstein, B. 1999, Space Sci. Rev., 87, 257 [NASA ADS] [CrossRef]
- Mariska,
J. T., Feldman, U., & Doschek, G. A. 1978, ApJ, 226,
698 [NASA ADS] [CrossRef]
(In the text)
- Markovskii,
S. A. 2001, ApJ, 557, 337 [NASA ADS] [CrossRef]
(In the text)
- Markovskii,
S. A., & Hollweg, J. V. 2002,
Geophys. Res. Lett., 29, 24 [NASA ADS] [CrossRef]
(In the text)
- Marsch, E., &
Tu, C.-Y. 2001, J. Geophys. Res., 106, 227 [NASA ADS] [CrossRef]
- Moran, T. G.
2001, A&A, 374, L9 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Moran, T. G.
2003, ApJ, 598, 657 [NASA ADS] [CrossRef]
(In the text)
- Morgan, H., &
Habbal, S. R. 2004, in BAAS, 36, 695
- Ofman, L. 2004, in
SOHO 13 Waves, Oscillations and Small-Scale Transients Events in
the Solar Atmosphere: Joint View from SOHO and TRACE, ESA SP-547,
345
- O'Shea, E.,
Banerjee, D., & Poedts, S. 2003, A&A, 400, 1065 [NASA ADS] [CrossRef] [EDP Sciences]
- O'Shea, E.,
Banerjee, D., & Doyle, G. 2004, in SOHO 15 Coronal Heating, ESA
SP-575, 142
- Parker, E. N.
1991, ApJ, 372, 719 [NASA ADS] [CrossRef]
(In the text)
-
Patsourakos, S., Habbal, S. R., & Hu, Y. Q. 2002,
ApJ, 581, L125 [NASA ADS] [CrossRef]
-
Pekünlü, E. R., Bozkurt, Z., Afsar, M., Soydugan,
E., & Soydugan, F. 2002, MNRAS, 336, 1195 [NASA ADS] [CrossRef]
(In the text)
- Peter, H., &
Vocks, C. 2003, A&A, 411, L481 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Schwenn, R.,
& Marsch, E. 1991, Physics of the Inner Heliosphere II,
Particules, Waves and Turbulence (Springer-Verlag)
(In the text)
- Seely, J. F.,
Feldman, U., Schuehle, U., et al. 1997, ApJ, 484, L87 [NASA ADS] [CrossRef]
(In the text)
- Singh, J., Ichimoto,
K., Sakurai, T., & Muneer, S. 2003a, ApJ, 585, 516 [NASA ADS] [CrossRef]
- Singh, J., Sakurai,
T., Ichimoto, K., & Muneer, S. 2003b, Sol. Phys., 212,
343 [NASA ADS] [CrossRef]
- Tu, C. Y., &
Marsch, E. 1997, Sol. Phys., 171, 363 [NASA ADS] [CrossRef]
(In the text)
- Tu, C.-Y., Marsch, E.,
Wilhelm, K., & Curdt, W. 1998, ApJ, 503, 475 [NASA ADS] [CrossRef]
(In the text)
- Vocks, C., &
Marsch, E. 2002, ApJ, 568, 1030 [NASA ADS] [CrossRef]
- Wesson, J. A.
2004, Tokamaks, third edition (Oxford Science Pub.)
- Wilhelm, K.,
Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162,
189 [NASA ADS] [CrossRef]
(In the text)
- Wilhelm, K.,
Lemaire, P., Curdt, W., et al. 1997, Sol. Phys., 170,
75 [NASA ADS] [CrossRef]
(In the text)
- Wilhelm, K.,
Marsch, E., Dwivedi, B. N., et al. 1998, ApJ, 500,
1023 [NASA ADS] [CrossRef]
- Wilhelm, K.,
Dwivedi, B. N., & Teriaca, L. 2004, A&A, 415,
1133 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Wilhelm, K.,
Fludra, A., Teriaca, L., et al. 2005, A&A, 435, 733 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
Copyright ESO 2008
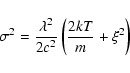
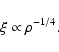
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{7903fi01}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg55.gif)
![\begin{figure}
\par\hspace*{-3mm}\includegraphics[width=7.5cm,clip]{7903fi02}\vspace*{5mm}
\includegraphics[width=7.2cm,clip]{7903fi03}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg57.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{7903fi04}\vspace*{3mm}
\in...
...{7903fi05}\vspace*{3mm}
\includegraphics[width=7.3cm,clip]{7903fi06}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg62.gif)
![\begin{figure}
\par\includegraphics[width=7.15cm,clip]{7903fi07}\hspace*{4mm}
\includegraphics[width=7cm,clip]{7903fi08}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{7903fi09}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg66.gif)
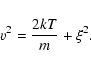
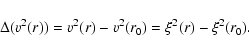
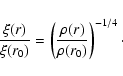
![\begin{displaymath}%
\xi(r_0) = \left[ \frac{\Delta (v^2 (r))}{ \left( \frac{\rho(r)}{\rho(r_0)} \right)^{-1/2} - 1} \right]^{1/2}\cdot
\end{displaymath}](/articles/aa/full/2008/19/aa7903-07/img71.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{7903fi10} \end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg78.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7903fi11}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg79.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7903fi12}\hspace*{5mm}
\includegraphics[width=7cm,clip]{7903fi13}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg81.gif)
![\begin{figure}
\par\hspace*{-1mm}\includegraphics[width=6.95cm,clip]{7903fi14}\v...
...7903fi15}\vspace*{3mm}
\includegraphics[width=6.85cm,clip]{7903fi16}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=7.05cm,clip]{7903fi17}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{7903fi18}\hspace*{4mm}
\includegraphics[width=6.9cm,clip]{7903fi19}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{7903fi20}\hspace*{7mm}
\includegraphics[width=6.8cm,clip]{7903fi21}\end{figure}](/articles/aa/full/2008/19/aa7903-07/Timg89.gif)