A&A 482, 981-987 (2008)
DOI: 10.1051/0004-6361:20079202
In situ spectroscopy of the solar sorona
H. Morgan1,2 - S. Fineschi3,4 - S. R. Habbal2 - B. Li1
1 - Institute for Maths. and Phys. Sciences, Prifysgol Aberystwyth, Ceredigion, Cymru SY23 3BZ, UK
2 -
Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
3 -
INAF - Osservatorio Astronomico di Torino, via Osservatorio 20, 10025 Pino Torinese (TO), Italy
4 -
Smithsonian Astrophysical Observatory, 60 Garden St., 02138 Cambridge, MA, USA
Received 5 December 2007 / Accepted 21 February 2008
Abstract
Context. Future spacecraft missions, such as the proposed Solar Probe mission, will venture close to the Sun, allowing spectrometers measuring emission from heavy ions or neutrals in the solar wind to have radial lines of sight (LOS) pointing away from the Sun, or indeed in any direction other than sunwards.
Aims. We show that a radial LOS gives excellent solar wind diagnostics, with tight constraints on ion density, outflow velocity, and effective temperature parallel to the coronal magnetic field. In addition, we present the concept that a spectrometer onboard a spacecraft reaching the solar corona can yield measurements somewhat similar to an in situ sampling instrument, in that the 3D velocity distribution and density of the emitting ions can be measured.
Methods. The well-studied O VI doublet at 1031.96 and 1037.6 Å and the H Ly- line at 1215.67 Å are chosen as examples. Solar wind parameters obtained from a 2D three-fluid magnetohydrodynamic (MHD) model, and formulations for collisional and radiative emission along a radial LOS, are used to calculate spectral line profiles for these lines at various heights within a streamer and coronal hole.
line at 1215.67 Å are chosen as examples. Solar wind parameters obtained from a 2D three-fluid magnetohydrodynamic (MHD) model, and formulations for collisional and radiative emission along a radial LOS, are used to calculate spectral line profiles for these lines at various heights within a streamer and coronal hole.
Results. For O VI, the collisional line profiles directly measure the ion velocity distribution in the radial direction, with the general Doppler shift of the profiles related to the bulk ion outflow velocity and the width of the line related to the effective ion temperature parallel to the magnetic field. An obvious skew in the collisional profiles is seen in regions with a high gradient in outflow velocity and/or temperature. The resonant (or radiative) line profiles behave very differently from those currently observed in 90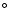 scattering. They are more closely related to the profile and distribution of the exciting chromospheric spectrum: the lines are narrow and are centered at wavelengths mirrored around the rest wavelength of the ion emission, allowing easy separation of the collisional and radiative components. Despite the Ly-
scattering. They are more closely related to the profile and distribution of the exciting chromospheric spectrum: the lines are narrow and are centered at wavelengths mirrored around the rest wavelength of the ion emission, allowing easy separation of the collisional and radiative components. Despite the Ly- line being much more intense than the O VI lines, the large width and high intensity of the Ly-
line being much more intense than the O VI lines, the large width and high intensity of the Ly- radiative component in comparison to the collisional component is such that these two components cannot be separated. The Ly-
radiative component in comparison to the collisional component is such that these two components cannot be separated. The Ly- line is therefore less suitable for solar wind diagnostics.
line is therefore less suitable for solar wind diagnostics.
Conclusions. The prospect of coronal in situ spectral observations, combined with simultaneous in situ sampling measurements of the solar wind and magnetic field will give unsurpassed constraints on models of solar wind heating and acceleration.
Key words: Sun: corona - Sun: particle emission - Sun: solar wind
1 Introduction
In the next few decades of solar system exploration it is likely that spacecraft missions will venture far closer to the Sun than has been previously attempted. The proposed Solar Probe mission (McComas et al. 2007) will attempt passes close to the Sun at different phases of the activity cycle, possibly flying to heights as low as 4  .
This mission will give invaluable in situ measurements of the inner corona. This article models and discusses the expected spectral profiles from a UV spectrometer aboard such a spacecraft. Inspired by rocket experiment observations of Ly-
.
This mission will give invaluable in situ measurements of the inner corona. This article models and discusses the expected spectral profiles from a UV spectrometer aboard such a spacecraft. Inspired by rocket experiment observations of Ly- during the total solar eclipse of 1970 (Gabriel 1971), and the extended emission of the line to large heights in the corona due to radiative scattering (Beckers & Chipman 1974), Kohl (1978) gave a comprehensive description of a spectrometer that could observe from within the inner corona aboard a Solar Probe spacecraft, with extensive descriptions and discussions of observing the H Ly-
during the total solar eclipse of 1970 (Gabriel 1971), and the extended emission of the line to large heights in the corona due to radiative scattering (Beckers & Chipman 1974), Kohl (1978) gave a comprehensive description of a spectrometer that could observe from within the inner corona aboard a Solar Probe spacecraft, with extensive descriptions and discussions of observing the H Ly- line along a radial line of sight (LOS), and LOS at other viewing angles. This work extends on the ideas of Kohl (1978) by including the O VI doublet at 1031.96 and 1037.6 Å, as well as the Ly-
line along a radial line of sight (LOS), and LOS at other viewing angles. This work extends on the ideas of Kohl (1978) by including the O VI doublet at 1031.96 and 1037.6 Å, as well as the Ly- line at 1215.67 Å.
line at 1215.67 Å.
The current Solar and Heliospheric Observatory (SOHO) spacecraft orbits the L1 Lagrangian point between the Earth and the Sun. Due to the large distance between SOHO and the Sun, the UltraViolet Coronagraph Spectrometer (UVCS) instrument aboard SOHO (Kohl et al. 1995) can only view the 90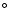 scattering of UV coronal emission. An UV spectrometer placed in the inner corona can measure along a radial LOS. This LOS would necessarily point away from the Sun due to the high intensity of the disk emission, therefore will give 180
scattering of UV coronal emission. An UV spectrometer placed in the inner corona can measure along a radial LOS. This LOS would necessarily point away from the Sun due to the high intensity of the disk emission, therefore will give 180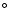 scattering. It would be simple to incorporate a mechanism within the spectrometer to measure in directions other than radial, so, in principle, the local 90
scattering. It would be simple to incorporate a mechanism within the spectrometer to measure in directions other than radial, so, in principle, the local 90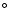 scattering can also be measured. We concentrate on the radial LOS in this work, this being a more novel observation.
scattering can also be measured. We concentrate on the radial LOS in this work, this being a more novel observation.
Section 2 presents the geometry and analytical equations suitable for calculating collisional and radiative intensity along a radial LOS. Section 3 describes the parameters obtained from a global, two-dimensional, magnetohydrodynamic (MHD) three-fluid model for both coronal hole and streamer solar wind regions, and shows O VI line profiles computed along a radial LOS using the model parameters. Section 4 follows the same approach for H Ly- .
Section 5 briefly discusses the locality of the emission measured along a radial LOS. Section 6 gives a basic outline of the instrumental characteristics for a spectrometer suitable for Solar Probe. A discussion of the results and conclusions are given in Sect. 7.
.
Section 5 briefly discusses the locality of the emission measured along a radial LOS. Section 6 gives a basic outline of the instrumental characteristics for a spectrometer suitable for Solar Probe. A discussion of the results and conclusions are given in Sect. 7.
2 A radial line of sight
Withbroe et al. (1982) and Noci & Maccari (1999) (and references within) give detailed general formulations on radiative and collisional emission in the solar corona. The geometry and resulting radiative and collisional equations for a radial LOS are somewhat simpler than those for 90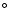 scattering. The radial LOS geometry is shown in Fig. 1. The observer is at point I, looking away from the Sun along the radial x-axis. Point P is an emitting point along the x-axis. The origin is at Sun center, O, and E is a point on the Sun's disk.
scattering. The radial LOS geometry is shown in Fig. 1. The observer is at point I, looking away from the Sun along the radial x-axis. Point P is an emitting point along the x-axis. The origin is at Sun center, O, and E is a point on the Sun's disk. 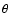 is the angle OPE between the radial and the direction of the incident radiation.
is the angle OPE between the radial and the direction of the incident radiation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig1.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg18.gif) |
Figure 1:
Radial LOS geometry. Point O is the Sun center, E is a point on the disk emitting the exciting radiation, P is a point along the radial direction in the corona and I is the position of the observer. The x-axis points along the radial direction with the origin at Sun center. 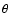 is the angle OPE.
is the angle OPE. |
| Open with DEXTER |
For collisional emission, we need only consider the velocity distribution of emitters along the radial x-axis, which we assume to be Maxwellian:
![\begin{displaymath}
f(v_x) = \left(\frac{1}{\pi\alpha_x}\right)^{1/2} \exp\left[ -\frac{1}{\alpha_x} (v_x - u_x)^{2} \right],
\end{displaymath}](/articles/aa/full/2008/18/aa9202-07/img19.gif) |
(1) |
where
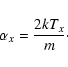 |
(2) |
The effective temperature is Tx (which includes wave and turbulent motions), vx is the particle velocity and ux is the outflow speed, all parallel to the solar radial direction. The ion mass is m and k is Boltzmann's constant.
At wavelength 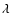 ,
the collisional intensity of a spectral line with a center rest wavelength of
,
the collisional intensity of a spectral line with a center rest wavelength of 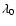 viewed by an observer positioned a distance xI from the Sun center along the radial x-axis can be written as
viewed by an observer positioned a distance xI from the Sun center along the radial x-axis can be written as
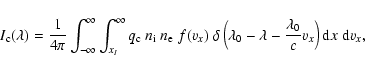 |
(3) |
where 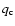 is the collisional excitation rate coefficient of the atomic transition. The delta function in the integral over the velocity distribution selects only those ions at the correct velocity to emit at the observed wavelength,
is the collisional excitation rate coefficient of the atomic transition. The delta function in the integral over the velocity distribution selects only those ions at the correct velocity to emit at the observed wavelength,
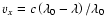 .
Substituting for vx in Eq. (1) gives an analytical form of Eq. (3) that can be integrated over x to give the collisional intensity at wavelength
.
Substituting for vx in Eq. (1) gives an analytical form of Eq. (3) that can be integrated over x to give the collisional intensity at wavelength 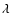
![$\displaystyle I_{\rm c}(\lambda) = \frac{1}{4\pi}\left(\frac{1}{\pi\alpha_x}\ri...
..._{0}} \left( \lambda_{0} - \lambda \right) - u_x\right]^{2} \right) \;{\rm d}x.$](/articles/aa/full/2008/18/aa9202-07/img26.gif) |
|
|
(4) |
A rigorous treatment of the radial LOS radiative component demands the inclusion of the velocity distribution perpendicular to the LOS. This would be redundant if the Sun was approximated by a point source. A bi-Maxwellian velocity distribution which is symmetric around the x-axis is assumed:
![\begin{displaymath}
f(v_x,v_y) = \left(\frac{1}{\pi\alpha_x}\right)^{1/2} \left(...
...}{\alpha_x} (v_x - u_x)^{2} -\frac{v_y^{2}}{\alpha_y} \right],
\end{displaymath}](/articles/aa/full/2008/18/aa9202-07/img27.gif) |
(5) |
where
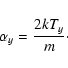 |
(6) |
Ty is the effective temperature and vy is the particle velocity, both perpendicular to the solar radial direction.
The radiative intensity for a radial LOS with a disk emission
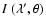 symmetric around the disk center is given by
symmetric around the disk center is given by
where B12 is the Einstein coefficient and
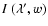 is the incident chromospheric radiation at wavelength
is the incident chromospheric radiation at wavelength
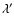 .
.
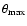 is the maximum angle subtended by the Sun's disk at P, the position of the emission volume. The scattering profile is
is the maximum angle subtended by the Sun's disk at P, the position of the emission volume. The scattering profile is
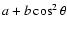 .
For O VI 1032, a is 7/8 and b is 3/8; for O VI 1037 there is no preference for scattering direction therefore a is 1 and b is 0 (Noci et al. 1987). For Ly-
.
For O VI 1032, a is 7/8 and b is 3/8; for O VI 1037 there is no preference for scattering direction therefore a is 1 and b is 0 (Noci et al. 1987). For Ly- ,
a is 11/12 and b is 3/12. Li et al. (1998) give a generic form of Eq. (7).
,
a is 11/12 and b is 3/12. Li et al. (1998) give a generic form of Eq. (7).
In the integral over the velocity distribution, the first delta function selects only those ions which have the correct velocity to be in resonance with the incident wavelength,
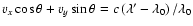 .
The second delta function selects only those ions emitting at wavelength
.
The second delta function selects only those ions emitting at wavelength 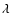 as seen by the observer,
as seen by the observer,
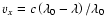 .
Substituting for vx and vy in Eq. (5) gives an analytical form for Eq. (7) that can be integrated over x,
.
Substituting for vx and vy in Eq. (5) gives an analytical form for Eq. (7) that can be integrated over x, 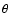 and
and
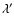 to give the radiative intensity at wavelength
to give the radiative intensity at wavelength 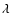 :
:
The y component is included in this formulation but in practice could be considered negligible in most cases, particularly at larger heights.
3 Modelled O VI profiles
O VI profiles are calculated using Eqs. (4) and (8) for coronal hole and streamer solar wind conditions, for two different temperature anisotropies and for many different heights. For this purpose, we use solar wind parameters obtained from a global two-dimensional magnetohydrodynamic (MHD) three fluid model which consists of electrons, protons and O5+ ions and extends from the coronal base out to 1 AU (Li et al. 2006,2004). The electrons are heated by thermal conduction and Coulomb collisions and the ion species are heated by an empirical energy flux. An ad hoc field-aligned momentum addition is applied to O5+ to help accelerate them so that the speed profile is constrained by UVCS observations. The model is further constrained by in situ measurements of the fast and slow solar wind close to Earth. The 2D model corresponds to a solar minimum scenario, with fast wind from a large super-radial diverging polar coronal hole and slow wind from an equatorial streamer. Two radial paths are taken through the 2D grid of model results, one at position angle  directly above the polar coronal hole and another at
directly above the polar coronal hole and another at  centered on the equatorial streamer. Plasma conditions from 4 to 30
centered on the equatorial streamer. Plasma conditions from 4 to 30  along these two radial paths are shown in Fig. 2.
along these two radial paths are shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig2.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg47.gif) |
Figure 2:
Plasma conditions obtained from the MHD 3-fluid model from 4 to 30  for the equatorial streamer ( left column) and the polar coronal hole ( right column). The top row shows electron (
for the equatorial streamer ( left column) and the polar coronal hole ( right column). The top row shows electron (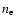 )
and O5+ ( )
and O5+ (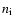 )
density, the middle shows electron ( )
density, the middle shows electron (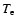 )
and O5+ ( )
and O5+ (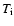 )
temperature and the bottom shows O5+ outflow velocity ( )
temperature and the bottom shows O5+ outflow velocity (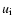 ). ). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig3.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg53.gif) |
Figure 3:
Modelled O VI profiles for an equatorial streamer and a high 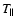 (
(
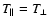 ,
isotropic). The left column is for O VI 1032 and the right for O VI 1037. From top to bottom, each row shows calculations for an observer at height 4, 6, 8, 10 and 15 ,
isotropic). The left column is for O VI 1032 and the right for O VI 1037. From top to bottom, each row shows calculations for an observer at height 4, 6, 8, 10 and 15  .
The solid line gives the collisional component and the dashed is the radiative component. The x axis shows wavelength in .
The solid line gives the collisional component and the dashed is the radiative component. The x axis shows wavelength in 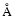 ,
and the y axis shows intensity in units of 106 photons s ,
and the y axis shows intensity in units of 106 photons s
 cm cm
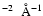 ,
where ,
where 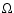 is the solid angle.
is the solid angle. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig4.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg55.gif) |
Figure 4:
Same as Fig. 3 for a polar coronal hole and a low 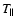 (
(
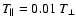 ,
anisotropic). The radiative components are absent at all heights in this case (due to the high outflow velocity and low temperature along the radial). The y axis shows intensity in units of 104 photons s ,
anisotropic). The radiative components are absent at all heights in this case (due to the high outflow velocity and low temperature along the radial). The y axis shows intensity in units of 104 photons s
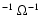 cm cm
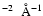 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig5.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg56.gif) |
Figure 5:
Same as Fig. 3 for a polar coronal hole and a high 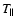 (
(
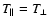 ,
isotropic). The y axis shows intensity in units of 104 photons s ,
isotropic). The y axis shows intensity in units of 104 photons s
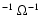 cm cm
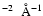 .
The resonance component is apparent in these figures due to the broad velocity distribution of the ions in the solar radial direction (large .
The resonance component is apparent in these figures due to the broad velocity distribution of the ions in the solar radial direction (large 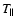 ). ). |
| Open with DEXTER |
Figures 3 to 5 show O VI 1031.96 and 1037.6 Å collisional and radiative profiles calculated for radial lines of sight. The profiles of Fig. 3 are calculated for the equatorial streamer, Figs. 4 and 5 for the polar coronal hole. The calculations are repeated for profiles observed at five heights - 4, 6, 8, 10, and 15  .
Figure 4 is calculated with a narrow radial velocity distribution (anisotropic case), with ion temperature parallel to the radial (
.
Figure 4 is calculated with a narrow radial velocity distribution (anisotropic case), with ion temperature parallel to the radial (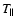 )
set at 1% of the ion temperature profiles shown in Fig. 2, but without dropping below the electron temperature,
)
set at 1% of the ion temperature profiles shown in Fig. 2, but without dropping below the electron temperature, 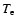 ,
also shown in Fig. 2. Figures 3 and 5 are calculated for a wide radial velocity distribution, with
,
also shown in Fig. 2. Figures 3 and 5 are calculated for a wide radial velocity distribution, with 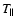 equal to the ion temperature profiles shown in Fig. 2. We have not shown results for a streamer with an anisotropic temperature distribution, since they are very similar to the isotropic case (restraining
equal to the ion temperature profiles shown in Fig. 2. We have not shown results for a streamer with an anisotropic temperature distribution, since they are very similar to the isotropic case (restraining 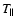 to a minimum of
to a minimum of 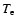 prevents the ion velocity distribution from becoming very anisotropic within the streamer).
prevents the ion velocity distribution from becoming very anisotropic within the streamer).
In all cases, the collisional profiles show the velocity distribution of the emitters along the LOS in a simple intuitive manner. The outflow velocity ux results in a simple bulk Doppler shift of the collisional spectral profile to wavelength
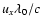 (redshift). The width of the collisional profile gives a direct measurement of the effective ion temperature (including thermal and wave motions) along the LOS, or parallel to the magnetic field. The solar wind heating and/or acceleration, if present (an increasing
(redshift). The width of the collisional profile gives a direct measurement of the effective ion temperature (including thermal and wave motions) along the LOS, or parallel to the magnetic field. The solar wind heating and/or acceleration, if present (an increasing 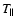 and/or ux along the LOS) leads to a skewness of the profile, with a wider wing at longer wavelengths.
and/or ux along the LOS) leads to a skewness of the profile, with a wider wing at longer wavelengths.
At low 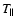 ,
the 1032 radiative profiles dim sharply with increasing velocity. Indeed, the radiative component in the coronal hole with low
,
the 1032 radiative profiles dim sharply with increasing velocity. Indeed, the radiative component in the coronal hole with low 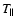 is so low as to be undetectable at all heights (Fig. 4), and is not visible in the figure. The high velocities and low
is so low as to be undetectable at all heights (Fig. 4), and is not visible in the figure. The high velocities and low 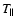 do not allow any resonance between the chromospheric 1032 line and the coronal ions. With a higher
do not allow any resonance between the chromospheric 1032 line and the coronal ions. With a higher 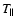 (Fig. 5), the coronal velocity distribution is broad enough to allow some coronal ions to resonate.
(Fig. 5), the coronal velocity distribution is broad enough to allow some coronal ions to resonate.
The 1037 radiative profiles are very interesting. Taking the streamer profiles as an example (Fig. 3), one can see the primary resonance peak at 1037.6 Å, which dims with increasing outflow velocity and height in a predictable and similar way to the 1032 resonance line. There is a secondary peak at 1038.3 Å which increases in resonance with increasing outflow. At a height of 15  ,
a third resonance peak has just begun to develop at 1038.8 Å. With increasing outflow velocity, the coronal resonance component peaks at wavelengths which are a mirror image of the chromospheric peaks (mirrored around the central rest wavelength of the line - 1037.6 Å in this case). Therefore, the resonance (or Doppler pumping) of the coronal 1037.6 Å line at 1038.3 and 1038.8 Å is due to the CII lines at 1037.0 and 1036.3 Å.
,
a third resonance peak has just begun to develop at 1038.8 Å. With increasing outflow velocity, the coronal resonance component peaks at wavelengths which are a mirror image of the chromospheric peaks (mirrored around the central rest wavelength of the line - 1037.6 Å in this case). Therefore, the resonance (or Doppler pumping) of the coronal 1037.6 Å line at 1038.3 and 1038.8 Å is due to the CII lines at 1037.0 and 1036.3 Å.
An insight into the basic behavior of Eq. (7) under conditions of 180 scattering can be found by approximating the Sun to a point source, so that
scattering can be found by approximating the Sun to a point source, so that 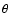 is zero and vy is redundant. In this case, the delta functions of Eq. (7) are only non-zero when
is zero and vy is redundant. In this case, the delta functions of Eq. (7) are only non-zero when
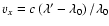 and
and
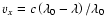 .
Equating vx gives the simple relationship
.
Equating vx gives the simple relationship
Thus the intensity of the radiative component at an observed wavelength
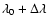 is related to the exciting chromospheric intensity at wavelength
is related to the exciting chromospheric intensity at wavelength
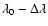 .
If a volume of emitters in the corona had a uniform and wide distribution of velocities (rather than a peaked Maxwellian distribution), their observed emission would be a scaled copy of the chromospheric spectrum, but mirrored around
.
If a volume of emitters in the corona had a uniform and wide distribution of velocities (rather than a peaked Maxwellian distribution), their observed emission would be a scaled copy of the chromospheric spectrum, but mirrored around 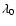 .
.
4 Modelled Ly- profiles
profiles
The Ly- line at 1215.67 Å has been systematically observed by the UVCS instrument. Viewing Ly-
line at 1215.67 Å has been systematically observed by the UVCS instrument. Viewing Ly- from a Solar Probe spacecraft has been discussed in detail by Kohl (1978). At lower heights in the corona, the neutral hydrogen is strongly coupled to the protons (Allen et al. 2000). Measurements of Ly-
from a Solar Probe spacecraft has been discussed in detail by Kohl (1978). At lower heights in the corona, the neutral hydrogen is strongly coupled to the protons (Allen et al. 2000). Measurements of Ly- can therefore give indirect information on protons, although measurements of coronal neutral species are also of direct interest. Figure 6 shows various model parameters used to create Ly-
can therefore give indirect information on protons, although measurements of coronal neutral species are also of direct interest. Figure 6 shows various model parameters used to create Ly- line profiles for a radial LOS. The protons in the 2D MHD model are used as a direct proxy for neutral hydrogen. The ratio of neutral hydrogen particle density relative to the protons is simply
line profiles for a radial LOS. The protons in the 2D MHD model are used as a direct proxy for neutral hydrogen. The ratio of neutral hydrogen particle density relative to the protons is simply
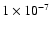 ,
as given by Allen et al. (1998). The chromospheric disk emission of Ly-
,
as given by Allen et al. (1998). The chromospheric disk emission of Ly- used to calculate the radiative component is also shown in Fig. 6. Note the strong self-reversal at the line center.
used to calculate the radiative component is also shown in Fig. 6. Note the strong self-reversal at the line center.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9202fig6.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg63.gif) |
Figure 6:
Electron and proton/neutral hydrogen density (top left), electron and proton temperature (top right) and proton outflow velocity (bottom left) obtained from the 2D MHD model for an equatorial streamer. Bottom right shows the model chromospheric line profile for Ly- ,
with the y axis in units of 1015 photons s ,
with the y axis in units of 1015 photons s
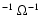 cm cm
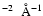 .
This profile is obtained from the Solar Ultraviolet Measurements of Emitted Radiation (SUMER)/SOHO solar atlas of Curdt et al. (2001), for quiet Sun region observations. .
This profile is obtained from the Solar Ultraviolet Measurements of Emitted Radiation (SUMER)/SOHO solar atlas of Curdt et al. (2001), for quiet Sun region observations. |
| Open with DEXTER |
Figure 7 shows collisional and radiative line profiles for Ly- calculated for the streamer at heights of 4 and 5
calculated for the streamer at heights of 4 and 5  .
The important feature for Ly-
.
The important feature for Ly- is the strength of the radiative component in comparison to the collisional one. The chromospheric Ly-
is the strength of the radiative component in comparison to the collisional one. The chromospheric Ly- line is so intense that the coronal radiative component is over three orders of magnitude stronger than the collisional Ly-
line is so intense that the coronal radiative component is over three orders of magnitude stronger than the collisional Ly- component. In addition, the radiative component is rather wide (in comparison for example with the radiative component of O VI in Fig. 5). It would be difficult if not impossible therefore to separate the two components. This leaves the radiative component as the only useable observable. As with O VI, the radiative component of Ly-
component. In addition, the radiative component is rather wide (in comparison for example with the radiative component of O VI in Fig. 5). It would be difficult if not impossible therefore to separate the two components. This leaves the radiative component as the only useable observable. As with O VI, the radiative component of Ly- is close to the chromospheric profile. At 4
is close to the chromospheric profile. At 4  ,
the two peaks surrounding the central trough are seen, but, since there is a significant outflow velocity of coronal hydrogen, the peak at the longer wavelength has a higher intensity. This effect becomes stronger with increasing outflow velocity, as can be seen at 5
,
the two peaks surrounding the central trough are seen, but, since there is a significant outflow velocity of coronal hydrogen, the peak at the longer wavelength has a higher intensity. This effect becomes stronger with increasing outflow velocity, as can be seen at 5  .
This effect is sensitive to the temperature of hydrogen along the LOS as well as the outflow velocity. Therefore it is not a useful diagnostic without additional measurements.
.
This effect is sensitive to the temperature of hydrogen along the LOS as well as the outflow velocity. Therefore it is not a useful diagnostic without additional measurements.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig7.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg64.gif) |
Figure 7:
Modelled Ly- profiles for an equatorial streamer with an isotropic temperature distribution, at an observing height of 4
profiles for an equatorial streamer with an isotropic temperature distribution, at an observing height of 4  ( top row) and 5
( top row) and 5  ( bottom row). The left column shows the collisional component and the right shows the radiative. The x axis shows wavelength in
( bottom row). The left column shows the collisional component and the right shows the radiative. The x axis shows wavelength in 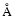 ,
and the y axis shows intensity in units of 105 photons s ,
and the y axis shows intensity in units of 105 photons s
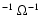 cm cm
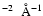 for the collisional and 109 photons s
for the collisional and 109 photons s
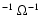 cm cm
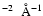 for the radiative.
for the radiative. |
| Open with DEXTER |
5 Locality of the emission
Here we consider the emission contribution along a radial LOS to the measured intensity. Consider, for example, a spherically symmetric corona with a r-2 decrease in density and, for simplicity, a constant outflow velocity at all heights. For this simple case Fig. 8 shows how the collisional and radiative emission decreases along the LOS. The proposed instrument lies in the corona and the main contribution to the observed line intensities comes from the highest density of ions in the locality of the instrument itself. For an observation at 4  ,
the radiative emission drops to 5% of the local emission by a height of
,
the radiative emission drops to 5% of the local emission by a height of 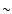 11
11  .
The collisional emission drops to 5% at a height of
.
The collisional emission drops to 5% at a height of 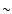 8.5
8.5  .
The instrument is therefore measuring far more extended regions of the corona than an in situ particle instrument, but more localized compared to the
.
The instrument is therefore measuring far more extended regions of the corona than an in situ particle instrument, but more localized compared to the  scattering LOS measured by the current UVCS/SOHO instrument (due primarily to the drop in density along the LOS, which is generally steepest along the radial direction).
scattering LOS measured by the current UVCS/SOHO instrument (due primarily to the drop in density along the LOS, which is generally steepest along the radial direction).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9202fig8.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg65.gif) |
Figure 8:
The drop in emission along a radial LOS shown as a fraction of the emission at the point of observation. This is shown as a function of the height of observation and the height above that observation. The top plot is calculated for collisional emission, and the bottom for radiative. The calculations were made assuming a constant outflow velocity and a r-2 decrease of density with height. |
| Open with DEXTER |
6 Instrumental considerations
This section discusses some basic instrumental considerations for an UV spectrometer suitable for a Solar Probe-type mission. The instrument concept consists of an off-axis parabolic telescope mirror feeding a spectrograph with a toric varied line-space (TVLS) grating. Unlike toric uniform line-space gratings with 1:1 magnification, TVLS gratings allow for the instrument magnification to be built into the spectrograph. This results in a more compact design. For instance, the conceptual instrument adopted for deriving the observational examples illustrated in the following, can be made as compact as
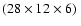 cm3. The instrumental assumptions are summarized in Table 1.
cm3. The instrumental assumptions are summarized in Table 1.
Table 1:
Instrument characteristics.
Figure 9 shows estimated dwell times for the O VI doublet lines and the Ly- line. The dwell time is defined here as the time necessary to accumulate 103 and 104 counts in the line profiles of the O VI doublet and the Ly-
line. The dwell time is defined here as the time necessary to accumulate 103 and 104 counts in the line profiles of the O VI doublet and the Ly- line respectively. Also shown in figure 9 is the time the spacecraft is expected to take to change height by 1
line respectively. Also shown in figure 9 is the time the spacecraft is expected to take to change height by 1  .
Figure 9 can be used to calculate the cumulative field-of-view of the spectrometer. For instance, when the Probe is at 6
.
Figure 9 can be used to calculate the cumulative field-of-view of the spectrometer. For instance, when the Probe is at 6  ,
a 10 min dwell time is sufficient for accumulating 103 and 104 counts in the line profiles of the O VI doublet and the Ly-
,
a 10 min dwell time is sufficient for accumulating 103 and 104 counts in the line profiles of the O VI doublet and the Ly- line respectively. At this height, the spacecraft rate of fall is
line respectively. At this height, the spacecraft rate of fall is 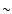 1
1  per 100 min. Therefore, in 10 min it travels by 0.1
per 100 min. Therefore, in 10 min it travels by 0.1  .
The angle swept by the instantaneous FOV defined by the slit width (0.7 arcmin) results in a cumulative FOV of
.
The angle swept by the instantaneous FOV defined by the slit width (0.7 arcmin) results in a cumulative FOV of 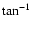 (0.1
(0.1  /6
/6 
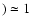
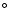 .
.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{9202fig9.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg72.gif) |
Figure 9:
The dwell times necessary to accumulate 103 counts in the O VI doublet and 104 counts in the Ly- line, is compared to the time-scale that the Probe spacecraft takes to change its heliocentric distance by 1
line, is compared to the time-scale that the Probe spacecraft takes to change its heliocentric distance by 1  .
Within 20 .
Within 20  ,
this time-scale is ,
this time-scale is 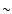 80 min. 80 min. |
| Open with DEXTER |
A basic technical advantage of an in situ spectrometer would be the absence of contamination by stray light from the Sun's disk, which can be a problem with some lower-signal observations made by the current UVCS. An in situ spectrometer which only observes in anti-sunward directions would not need the coronagraphic abilities of the current UVCS. A potential problem is the galactic O VI background, with measured intensities of 1800 to 9100 photons s
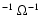 cm-2 (Dixon et al. 2006). This is comparable to the intensity of the O VI coronal lines in coronal holes at heights above 6
cm-2 (Dixon et al. 2006). This is comparable to the intensity of the O VI coronal lines in coronal holes at heights above 6  ,
as can be seen in Figs. 4 and 5. However, in the coronal hole at this height the collisional component is Doppler-shifted to wavelengths longer than that of the galactic O VI, which should ensure little contamination.
,
as can be seen in Figs. 4 and 5. However, in the coronal hole at this height the collisional component is Doppler-shifted to wavelengths longer than that of the galactic O VI, which should ensure little contamination.
7 Discussion and conclusion
As shown in Sect. 4 for the case of Ly- ,
the separation of collisional and radiative components is not possible due to the overwhelming intensity and large width of the radiative component. This does not rule out measuring other neutral species, or other lines of hydrogen. However, for the remainder of this section, we limit the discussion to O VI.
,
the separation of collisional and radiative components is not possible due to the overwhelming intensity and large width of the radiative component. This does not rule out measuring other neutral species, or other lines of hydrogen. However, for the remainder of this section, we limit the discussion to O VI.
In the case of O VI, one of the main benefits of a radial LOS is the ease of separation of the collisional and radiative components, which is not a trivial matter with  scattering. In general, the resonance peaks, if present, are distinct from the collisional ones, at least in one of the two O VI lines. In cases where it is only possible to separate the collisional from the radiative in one line of the doublet, this allows the exact subtraction of the collisional component in the other line, since we know that the intensity ratio of the collisional components is always 2. The collisional component of either line gives a tight constraint on the velocity distribution (including bulk outflow velocity) of the ions along the line of sight. A skewness in the line will be measured in regions of high velocity and/or temperature gradient. The most extreme example is seen in Fig. 4 at a height of 4
scattering. In general, the resonance peaks, if present, are distinct from the collisional ones, at least in one of the two O VI lines. In cases where it is only possible to separate the collisional from the radiative in one line of the doublet, this allows the exact subtraction of the collisional component in the other line, since we know that the intensity ratio of the collisional components is always 2. The collisional component of either line gives a tight constraint on the velocity distribution (including bulk outflow velocity) of the ions along the line of sight. A skewness in the line will be measured in regions of high velocity and/or temperature gradient. The most extreme example is seen in Fig. 4 at a height of 4  .
Regions of high heating can then be readily identified directly in the observations, and an estimate of the temperature or velocity gradient can be made.
.
Regions of high heating can then be readily identified directly in the observations, and an estimate of the temperature or velocity gradient can be made.
Any spacecraft carrying a spectrometer close to the Sun will be equipped with in situ sampling instruments. These will give electron and proton density and velocity distribution measurements. It can be seen therefore, from Eq. (3), that given this independent in situ measurement of electron density and temperature, and the direct measurement of the ion velocity distribution given by the collisional component, that the ion density may be constrained directly from the intensity of the measured collisional component. This then allows us to easily calculate the ion abundance relative to the electrons or protons. It is likely that abundance enhancements of O5+ may be seen in some streamers (see Habbal et al. 2007, and references within), with implications for models of energy deposition in streamers.
From a practical point of view, the isolated resonance component gives an excellent wavelength calibration, since the profiles and central wavelengths of the chromospheric spectral lines are well known (Curdt et al. 2001). From Eq. (7), since all ion parameters are well constrained by the measured collisional component, the chromospheric disk intensity may be calculated for the O VI doublet, and, given a high enough outflow velocity, for the C II doublet. This would be a useful measurement since the chromospheric spectrum of O VI varies enormously from coronal hole/quiet Sun regions and sunspot regions (see Morgan et al. 2006, and references within). As well as being of general interest in the context of chromospheric densities and temperatures, quantifying this variation will enable a more accurate interpretation of the ten years of existing UVCS data.
The width of the collisional profile gives a direct measurement of the temperature along the radial direction, 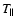 ,
a value which at present is only weakly constrained by the semi-empirical modelling of UVCS/SOHO observations. It would be a relatively simple matter to assemble a simple mechanism at the front end of the proposed spectrometer which would allow observations along directions other than the radial LOS (for example, perpendicular to the radial). This would give a 3D ion velocity distribution, a measurement usually associated with in situ sampling instruments.
,
a value which at present is only weakly constrained by the semi-empirical modelling of UVCS/SOHO observations. It would be a relatively simple matter to assemble a simple mechanism at the front end of the proposed spectrometer which would allow observations along directions other than the radial LOS (for example, perpendicular to the radial). This would give a 3D ion velocity distribution, a measurement usually associated with in situ sampling instruments.
An important question is what does an in situ spectrometer offer that a particle experiment does not? While it is true that a particle experiment can directly measure densities and velocity distributions with more accuracy than spectrometer measurements of light emission from those particles, a spectrometer offers the following main advantages (or enhancements) to particle experiments:
- Measurements of extended coronal regions. This will help characterize structures which the spacecraft will traverse such as plumes, jets, current sheets, coronal hole-streamer boundaries etc. The spectrometer would be able to establish whether the varying signals measured by the particle experiments are due to turbulence or due to static structures.
- Coronal Mass Ejection (CME) observations. Particle experiments will only measure the CMEs as they pass the spacecraft whilst the spectrometer will continue to measure CMEs as they travel along the LOS. From Fig. 8, for observations at a height of 4
 ,
the signal of a CME will drop to 5% at a height of
,
the signal of a CME will drop to 5% at a height of 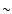 9
9  (this is different for the radiative and collisional components). For a CME travelling at 1000 km s-1, this is an hour of observation where the spectrometer can continue to measure the evolution of the CME (of course, the 5% level we have chosen here is arbitrary, and probably on the conservative side for a CME observation at 4
(this is different for the radiative and collisional components). For a CME travelling at 1000 km s-1, this is an hour of observation where the spectrometer can continue to measure the evolution of the CME (of course, the 5% level we have chosen here is arbitrary, and probably on the conservative side for a CME observation at 4  ).
).
- Evolution of the solar wind. As described above, bulk accelerations or temperature gradients lead to a skewness in the measured line profiles. This measurement of the solar wind evolution along the LOS will greatly enhance the detailed particle instrument measurements at the position of the spacecraft.
- Wave propagation. Density waves have been shown to exist in the extended corona, and have been measured in white light (Ofman et al. 2000,1997) and in the intensity of the Ly-
 line by UVCS (Morgan et al. 2004). A spectrometer would allow the measurement of the propagation and lifetime of these waves.
line by UVCS (Morgan et al. 2004). A spectrometer would allow the measurement of the propagation and lifetime of these waves.
- Correction for particle measurements. The particle measurements are influenced by the Solar Probe heat shield, since the instrument necessarily lies in the lee of the shield. This means that some particles within the coronal velocity distribution cannot be measured reliably. A spectrometer will be a straightforward method of identifying and correcting these inaccuracies.
The prospect of a new UV spectrometer aboard near-Sun missions is very exciting. The UV spectral observations, combined with in situ sampling measurements of electrons, protons and the coronal magnetic field will give unsurpassed constraints on models of solar wind heating and acceleration.
Acknowledgements
We extend our gratitude to Dr. John C. Raymond (CfA), whose useful suggestions and insights greatly improved this work. This work was supported by NASA grant NNX07AH90G to the Institute for Astronomy and PPARC grant (B. Li) to Aberystwyth University. The UVCS/SOHO instrument is a collaborative effort between NASA, the Agenzia Spaziale Italiana and a Swiss participation. SOHO is a mission of international cooperation between ESA and NASA.
- Allen,
L. A., Habbal, S. R., & Hu, Y. Q. 1998,
J. Geophys. Res., 103, 6551 [NASA ADS] [CrossRef]
(In the text)
- Allen,
L. A., Habbal, S. R., & Li, X. 2000,
J. Geophys. Res., 105, 23123 [NASA ADS] [CrossRef]
(In the text)
- Beckers,
J. M., & Chipman, E. 1974, Sol. Phys., 34, 151 [NASA ADS] [CrossRef]
(In the text)
- Curdt, W.,
Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Dixon,
W. V. D., Sankrit, R., & Otte, B. 2006, ApJ, 647,
328 [NASA ADS] [CrossRef]
(In the text)
- Gabriel,
A. H. 1971, Sol. Phys., 21, 392 [NASA ADS] [CrossRef]
(In the text)
- Habbal,
S. R., Morgan, H., Johnson, J., et al. 2007, ApJ, 663,
598 [NASA ADS] [CrossRef]
(In the text)
- Kohl, J. L.
1978, in A Close-up of the Sun, ed. M. Neugebauer, &
R. W. Davies, 354
(In the text)
- Kohl, J. L.,
Esser, R., Gardner, L. D., et al. 1995, Sol. Phys.,
162, 313 [NASA ADS] [CrossRef]
(In the text)
- Li, B., Li, X., Hu,
Y.-Q., & Habbal, S. R. 2004, J. Geophys. Res., Space
Phys., 109, 7103
- Li, B., Li, X.,
& Labrosse, N. 2006, J. Geophys. Res., Space Phys., 111,
8106
- Li, X., Habbal,
S. R., Kohl, J., & Noci, G. 1998, ApJ, 501, L133 [NASA ADS] [CrossRef]
(In the text)
- McComas, D.,
Velli, M., Lewis, W., & Acton, L. 2007, Rev. Geophys., 45,
RG1004
(In the text)
- Morgan, H.,
Habbal, S. R., & Li, X. 2004, ApJ, 605, 521 [NASA ADS] [CrossRef]
(In the text)
- Morgan, H.,
Habbal, S. R., & Woo, R. 2006, Sol. Phys., 236,
263 [NASA ADS] [CrossRef]
(In the text)
- Noci, G., Kohl,
J. L., & Withbroe, G. L. 1987, ApJ, 315, 706 [NASA ADS] [CrossRef]
(In the text)
- Noci, G., &
Maccari, L. 1999, A&A, 341, 275 [NASA ADS]
(In the text)
- Ofman, L.,
Romoli, M., Poletto, G., Noci, G., & Kohl, J. L. 1997,
ApJ, 491, L111 [NASA ADS] [CrossRef]
- Ofman, L.,
Romoli, M., Poletto, G., Noci, G., & Kohl, J. L. 2000,
ApJ, 529, 592 [NASA ADS] [CrossRef]
- Withbroe,
G. L., Kohl, J. L., Weiser, H., & Munro, R. H.
1982, Space Sci. Rev., 33, 17 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
![\begin{displaymath}
f(v_x) = \left(\frac{1}{\pi\alpha_x}\right)^{1/2} \exp\left[ -\frac{1}{\alpha_x} (v_x - u_x)^{2} \right],
\end{displaymath}](/articles/aa/full/2008/18/aa9202-07/img19.gif)
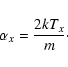
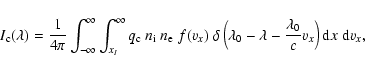
![$\displaystyle I_{\rm c}(\lambda) = \frac{1}{4\pi}\left(\frac{1}{\pi\alpha_x}\ri...
..._{0}} \left( \lambda_{0} - \lambda \right) - u_x\right]^{2} \right) \;{\rm d}x.$](/articles/aa/full/2008/18/aa9202-07/img26.gif)
![\begin{displaymath}
f(v_x,v_y) = \left(\frac{1}{\pi\alpha_x}\right)^{1/2} \left(...
...}{\alpha_x} (v_x - u_x)^{2} -\frac{v_y^{2}}{\alpha_y} \right],
\end{displaymath}](/articles/aa/full/2008/18/aa9202-07/img27.gif)
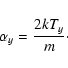
![$\displaystyle \frac{hB_{12}}{4\pi\lambda_0}
\int^{\infty}_{-\infty}\int^{\infty...
..._{\rm max}}_{0}\; n_{\rm i}\; 2\pi \sin\theta \left[ a + b \cos^2\theta \right]$](/articles/aa/full/2008/18/aa9202-07/img31.gif)
![$\displaystyle \frac{hB_{12}}{2\lambda_0}
\int^{\infty}_{x_I} \int^{\infty}_{-\i...
...\theta_{\rm max}}_{0}
n_{\rm i} \; \sin\theta \left[ a + b \cos^2\theta \right]$](/articles/aa/full/2008/18/aa9202-07/img41.gif)
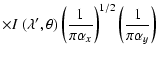
![$\displaystyle \times ~ \exp \Big[ -\frac{1}{\alpha_x} \left( \frac{c}{\lambda_0} [\lambda_0 - \lambda] -u_x \right)^2$](/articles/aa/full/2008/18/aa9202-07/img43.gif)
![$\displaystyle - \frac{c^2}{\alpha_y~\lambda_0^2\sin^2\theta}
\left( \lambda^\pr...
...lambda\right] \right)^2 \Big]
{\rm d}\theta ~{\rm d}\lambda ^\prime ~{\rm d}x .$](/articles/aa/full/2008/18/aa9202-07/img44.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig2.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg47.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig3.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg53.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig4.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig5.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9202fig6.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9202fig7.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9202fig8.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{9202fig9.eps}\end{figure}](/articles/aa/full/2008/18/aa9202-07/Timg72.gif)