A&A 482, 973-979 (2008)
DOI: 10.1051/0004-6361:20079069
Are there Kronian electrons in the inner heliosphere?
D. Lange - H. Fichtner
Institut für Theoretische Physik IV, Weltraum- und Astrophysik Ruhr-Universität Bochum, Germany
Received 14 November 2007 / Accepted 8 February 2008
Abstract
Context. As the largest in our solar system the Jovian magnetosphere is treated in the literature as the dominant source of a few-MeV electrons, which have been measured by various spacecraft. In particular, observations obtained with Ulysses have significantly broadened the available data base.
Aims. We simulated the transports of MeV electrons in the heliosphere on the basis of a time-dependent, three-dimensional modulation model. For this purpose the cosmic rays, the Jovian and the Saturnian electron sources have been, for the first time, considered together in the simulation of electron fluxes. The simulated electron intensities are discussed along the Ulysses and Cassini trajectories. The Ulysses spacecraft already passed by the planet Jupiter twice (1992, 2004), and Cassini passed by Jupiter in 2001 and reached Saturn in the year 2004. The strength of the electron source at Jupiter is relatively well known and well modelled. To determine the source strength of Saturn in comparison to that of Jupiter, we compared all available spacecraft measurements at Jupiter/Saturn in the overlapping energy range. We study the general distribution of Kronian electrons by successively using three different strengths of the Saturn source in our simulations. In addition, the effects of the solar activity are taken into account by varying the velocity field of the solar wind and the anisotropic diffusion tensor.
Methods. Studying the particle diffusion is particularly relevant, because the really unknown function in the used transport equation is the diffusion tensor. The Jovian and/or Kronian electrons are suitable for studying the transport of energetic particles because the source locations are well known.
Results. At 1 MeV the intensities along the Ulysses and the Cassini trajectories are clearly influenced by the presence of Kronian electrons.
Conclusions. Our results reveal that the electrons from the Kronian magnetosphere, as the second largest, cannot be neglected in the very-low MeV energy range.
Key words: diffusion - convection - methods: numerical
The first fly-by of a spacecraft at Jupiter, by Pioneer 10 in 1973, showed that the Jovian magnetosphere is a relatively strong electron source in the inner heliosphere with energies up to 30 MeV (Simpson et al. 1974). Later Pioneer 11 (1974) and the Voyager spacecraft (1979) supported this observation (Simpson et al. 1975; Zwickl et al. 1981).
In 1990, the Ulysses spacecraft was launched and Ulysses again orbits the Sun for the third time after it passed by Jupiter in 1992 and 2004 (Balogh et al. 2001). The Cassini spacecraft was launched in 1997 and, after three swing-by manoeuvres at Venus (1998, 1999) and Earth (1999), it passed Jupiter on the way to Saturn in 2001 (Krupp et al. 2004). In 2004, Cassini was injected into orbit around Saturn. Figure 1 shows the Ulysses (first orbit) and Cassini trajectories. In our simulations we consider the electron intensities along the Ulysses and Cassini trajectories, because the Jovian and/or Kronian electrons are suitable for studying the transport of energetic particles.
The time-dependent, three-dimensional modulation of the electron flux in the heliosphere is based in our model on a momentum integration of the Parker transport equation (Parker 1965), in which we use the following definition of the electron pressure (Kissmann et al. 2003; Lange et al. 2006; Fichtner et al. 1996):
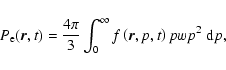 |
(1) |
where w is the particle speed. Parker's transport equation then takes the form
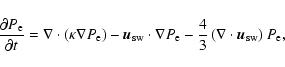 |
(2) |
where
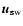 is the solar wind velocity and
is the solar wind velocity and
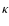 has to be understood as the momentum-averaged diffusion tensor; that is,
has to be understood as the momentum-averaged diffusion tensor; that is,
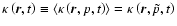 ,
with a suitable
,
with a suitable
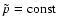 .
In the following the diffusion tensor is evaluated at a momentum
.
In the following the diffusion tensor is evaluated at a momentum 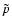 corresponding to an energy of 1 MeV. The resulting
corresponding to an energy of 1 MeV. The resulting 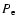 exhibits very similar space and time variations as the phase space distribution
exhibits very similar space and time variations as the phase space distribution
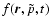 in the (original) Parker equation. The four-dimensional integrated Parker transport Eq. (2) is the basis for our electron flux simulations in the heliosphere.
Consequently, the two contributing functions are the diffusion tensor
in the (original) Parker equation. The four-dimensional integrated Parker transport Eq. (2) is the basis for our electron flux simulations in the heliosphere.
Consequently, the two contributing functions are the diffusion tensor
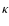 and solar wind velocity
and solar wind velocity
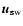 for the particle transport.
for the particle transport.
The measurements of SWOOPS (Solar Wind Observations Over the Poles of the Sun) onboard Ulysses give a detailed picture of the latitudinal structure of the solar wind velocity field. The model for the solar wind velocity field used in the simulations is based upon SWOOPS observations. It is assumed that
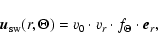 |
(3) |
where r is the radial distance, 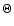 the polar angle, and
the polar angle, and
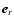 the unit vector in the radial direction. Any non-radial propagation is neglected. These
the unit vector in the radial direction. Any non-radial propagation is neglected. These 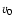 denotes the slow wind of 400 km s-1. The radial dependence
vr(r) is given as (Ferreira 2002):
denotes the slow wind of 400 km s-1. The radial dependence
vr(r) is given as (Ferreira 2002):
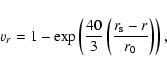 |
(4) |
with r and 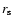 (radius of the Sun), given in AU, with
(radius of the Sun), given in AU, with
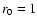 AU. From this form it follows that the solar wind is accelerated close to the Sun and reaches a constant speed at a heliocentric distance of 0.3 AU. For the latitudinal dependence
AU. From this form it follows that the solar wind is accelerated close to the Sun and reaches a constant speed at a heliocentric distance of 0.3 AU. For the latitudinal dependence
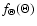 during solar minimum conditions, we use the form (Ferreira 2002):
during solar minimum conditions, we use the form (Ferreira 2002):
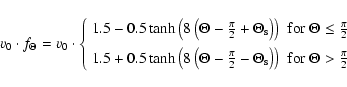 |
(5) |
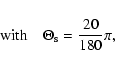 |
(6) |
where
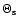 is the angle that characterises the transition from low to high speed solar wind and thus specifies the inclination of the so-called streamer belt (region of slow solar wind with speeds lower than 400 km s-1) with respect to the solar equator. This angle is taken as 20
is the angle that characterises the transition from low to high speed solar wind and thus specifies the inclination of the so-called streamer belt (region of slow solar wind with speeds lower than 400 km s-1) with respect to the solar equator. This angle is taken as 20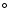 in the following. Figure 2 shows the function
in the following. Figure 2 shows the function
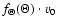 ,
which is symmetric to the heliographic equator. It should be pointed out that this structure only occurs at solar minimum conditions. At solar maximum, fast solar wind is absent, and a highly variable slow wind exends over all latitudes with an average speed of 400 km s-1 such as was also observed by SWOOPS. The SWOOPS observations are described in McComas et al. (2003). A model for the latitudinal variation of the solar velocity field with solar activity is discussed in Lange et al. (2006) and used for the simulations.
,
which is symmetric to the heliographic equator. It should be pointed out that this structure only occurs at solar minimum conditions. At solar maximum, fast solar wind is absent, and a highly variable slow wind exends over all latitudes with an average speed of 400 km s-1 such as was also observed by SWOOPS. The SWOOPS observations are described in McComas et al. (2003). A model for the latitudinal variation of the solar velocity field with solar activity is discussed in Lange et al. (2006) and used for the simulations.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{9069fig3.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg35.gif) |
Figure 2:
The latitudinal structure of the solar wind velocity
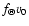 ,
see Eq. (5) for solar minimum conditions. ,
see Eq. (5) for solar minimum conditions. |
| Open with DEXTER |
The diffusion tensor used in the Parker Eq. (1) is given in spherical coordinates as
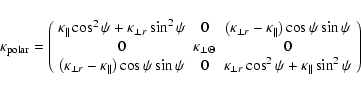 |
(7) |
and consists of a parallel diffusion coefficient
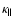 and two perpendicular coefficients, namely
and two perpendicular coefficients, namely
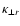 in the radial direction and
in the radial direction and
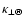 in the polar direction. The spiral angle
in the polar direction. The spiral angle 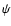 is defined as the angle between the radial direction and the average heliospheric magnetic field (HMF) at a certain position,
is defined as the angle between the radial direction and the average heliospheric magnetic field (HMF) at a certain position,
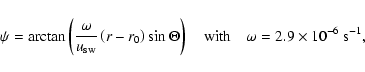 |
(8) |
where 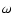 is the angular velocity of the Sun,
is the angular velocity of the Sun,
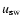 the solar wind speed,
the solar wind speed,
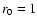 AU, and
AU, and 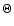 is the polar angle. For the parallel diffusion coefficient
is the polar angle. For the parallel diffusion coefficient
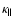 ,
the following general form is assumed:
,
the following general form is assumed:
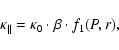 |
(9) |
where 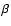 is the ratio of the speed of the electrons, v, to the speed of light, c, and
is the ratio of the speed of the electrons, v, to the speed of light, c, and
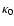 is a constant given as 4.5
is a constant given as 4.5 
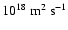 .
Also
.
Also 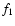 is a function of the radial distance and the rigidity P (or energy) for which we use the same functional dependence as given in Ferreira et al. (2001b,a).
is a function of the radial distance and the rigidity P (or energy) for which we use the same functional dependence as given in Ferreira et al. (2001b,a).
![\begin{figure}
\par\includegraphics[width=15.7cm,clip]{9069fig4.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg52.gif) |
Figure 3:
Measurements of the differential electron intensity around 1 MeV from the 4 spacecraft Voyager (1 and 2), Pioneer 11, and Cassini. For comparison, measurements of Pioneer 10 and Cassini at Jupiter are shown. Open symbols stand for measurements at Saturn and filled symbols for those at Jupiter. The first two panels refer to inbound measurements of the Kronian magnetosphere at a distance of about 5 and 11  .
The right panel is for a distance of approximately 20 .
The right panel is for a distance of approximately 20  ,
which for Voyager 2 and Pioneer 11 corresponds to their crossing distance of the Kronian magnetopause. The Voyager 1 and Cassini data points are measurements inside the Kronian magnetosphere. Pioneer 10 measurements refer to a distance of about 3 ,
which for Voyager 2 and Pioneer 11 corresponds to their crossing distance of the Kronian magnetopause. The Voyager 1 and Cassini data points are measurements inside the Kronian magnetosphere. Pioneer 10 measurements refer to a distance of about 3 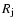 ,
which is inside the Jovian magnetosphere. The upper Cassini data point in the right panel determines the location where Cassini entered the Jovian magnetosphere, which was at a distance of about 200 ,
which is inside the Jovian magnetosphere. The upper Cassini data point in the right panel determines the location where Cassini entered the Jovian magnetosphere, which was at a distance of about 200 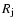 ,
whereas the lower data point is equivalent to the spacecraft's closest approach to Jupiter of about 140 ,
whereas the lower data point is equivalent to the spacecraft's closest approach to Jupiter of about 140 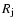 .
( .
(
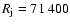 km, km,
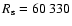 km). km). |
| Open with DEXTER |
It has become standard practice to scale the perpendicular diffusion coefficients as the parallel coefficient. Recent developments of nonlinear (as opposed to quasilinear) theories of diffusion perpendicular to the HMF (see Minnie et al. 2007; Shalchi & Kourakis 2007) have not yet matured enough so that their use for a detailed comparison of observational data and model results is not feasible, so far. Here the perpendicular coefficients
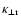 and
and
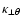 are assumed to have the following form (see Ferreira et al. 2001b,a):
are assumed to have the following form (see Ferreira et al. 2001b,a):
| |
|
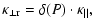 |
(10) |
| |
|
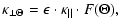 |
(11) |
where
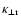 has an additional dependence on rigidity P:
has an additional dependence on rigidity P:
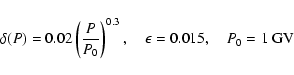 |
(12) |
and
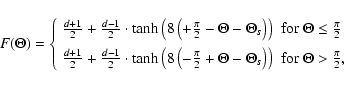 |
(13) |
where
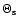 is once again the angle, which characterises the inclination of the streamer belt. Function
is once again the angle, which characterises the inclination of the streamer belt. Function 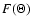 increases from unity in the ecliptic plane (90
increases from unity in the ecliptic plane (90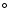 ), which gives no enhancement, towards the poles depending on the value of d. The form of the latitudinal structure of
), which gives no enhancement, towards the poles depending on the value of d. The form of the latitudinal structure of 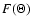 is analogous to the latitudinal structure of the solar wind, given by Eq. (5). In Lange et al. (2006), it is shown that in the phase of solar minimum, an enhanced latitudinal transport corresponding to d=6 is necessary and in the solar maximum, by analogy to the variation of the latitudinal structure of the solar wind, that the factor d=1 applies to all latitudes. A model for variation with the solar cycle is also discussed in Lange et al. (2006).
is analogous to the latitudinal structure of the solar wind, given by Eq. (5). In Lange et al. (2006), it is shown that in the phase of solar minimum, an enhanced latitudinal transport corresponding to d=6 is necessary and in the solar maximum, by analogy to the variation of the latitudinal structure of the solar wind, that the factor d=1 applies to all latitudes. A model for variation with the solar cycle is also discussed in Lange et al. (2006).
The magnetosphere of Jupiter has been already investigated by six fly-by missions of the Pioneer (10 and 11), Voyager (1 and 2), Ulysses, and Cassini spacecraft. In contrast, the magnetosphere of Saturn was only passed by Pioneer 11 and Voyager (1 and 2). Cassini was injected into an orbit around Saturn on July 1, 2004. The sizes and dynamics of the two largest magnetospheres in the solar system are quite different. The distances in sunward direction for Jupiter is around 82 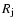 and for Saturn around 24
and for Saturn around 24  (Krupp 2005) (1
(Krupp 2005) (1
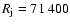 km, 1
km, 1
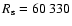 km). In contrast to the Jovian magnetosphere, the distribution of energetic particles in the Kronian magnetosphere is massively affected by the planetary rings and moons of Saturn (Frank et al. 1980; Krimigis et al. 2005). The (sunward) distance of the magnetopause varies and is typically in the range 17 to 32
km). In contrast to the Jovian magnetosphere, the distribution of energetic particles in the Kronian magnetosphere is massively affected by the planetary rings and moons of Saturn (Frank et al. 1980; Krimigis et al. 2005). The (sunward) distance of the magnetopause varies and is typically in the range 17 to 32  .
Our aim is now to determine the source function of Kronian electrons to use it simultaneously with that of Jovian electrons in the simulations. The source function at Jupiter is well known and tested and is constructed to be compatible with Pioneer 10 and ISEE 3 data (see next chapter for details). Because of that and the apparently similar slopes of the magnetospheric energy spectra (see below), we use a similar function for Saturn in the simulations, by multiplying with a factor
.
Our aim is now to determine the source function of Kronian electrons to use it simultaneously with that of Jovian electrons in the simulations. The source function at Jupiter is well known and tested and is constructed to be compatible with Pioneer 10 and ISEE 3 data (see next chapter for details). Because of that and the apparently similar slopes of the magnetospheric energy spectra (see below), we use a similar function for Saturn in the simulations, by multiplying with a factor 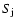 .
Thus, the factor
.
Thus, the factor 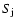 represents the ratio of the electron source strength of Saturn to Jupiter.
represents the ratio of the electron source strength of Saturn to Jupiter.
To find or estimate 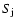 ,
we consider now all available measurements of spacecraft in energy ranges of overlap. It should be pointed out that spacecraft measurements, especially the fly-by missions, only provide snapshots of a state of the magnetosphere at given times and points in the magnetosphere. During the fly-by of Pioneer 11 a large solar particle event hit the magnetosphere and extremely compressed it, wherefore Pioneer 11 crossed the magnetopause already at about 17
,
we consider now all available measurements of spacecraft in energy ranges of overlap. It should be pointed out that spacecraft measurements, especially the fly-by missions, only provide snapshots of a state of the magnetosphere at given times and points in the magnetosphere. During the fly-by of Pioneer 11 a large solar particle event hit the magnetosphere and extremely compressed it, wherefore Pioneer 11 crossed the magnetopause already at about 17  (Maurice et al. 1996b; Krupp et al. 2005). The Voyager 1 and 2 encounters with the magnetopause did occur at 23 and 19
(Maurice et al. 1996b; Krupp et al. 2005). The Voyager 1 and 2 encounters with the magnetopause did occur at 23 and 19  ,
respectively, because the magnetosphere was more quiescent there and then (Krimigis et al. 1983).
,
respectively, because the magnetosphere was more quiescent there and then (Krimigis et al. 1983).
Figure 3 shows measurements of the differential electron intensity around 1 MeV from the 4 spacecraft Voyager (1 and 2), Pioneer 11, and Cassini at Saturn. For comparison, measurements of Pioneer 10 and Cassini at Jupiter are shown (filled symbols). Ulysses measurements of electron intensities are only available in the energy range of >3 MeV. The first two panels in Fig. 3 refer to different measurements inside the Kronian magnetosphere with a distance of about 5 and 11  .
The right panel stands for a distance of approximately 20
.
The right panel stands for a distance of approximately 20  ,
which determines the crossing point of the Kronian magnetopause for some pictured spacecraft measurements.
,
which determines the crossing point of the Kronian magnetopause for some pictured spacecraft measurements.
It is obvious that with increasing energy and distance, the intensity decreases with all spacecraft measurements, as expected. At distances of about 5  the intensities measured at Saturn are about one to two orders of magnitude higher than measured by Pioneer 10 at Jupiter. The Voyager 2 measurements in this panel correspond to a distance of about 4.3
the intensities measured at Saturn are about one to two orders of magnitude higher than measured by Pioneer 10 at Jupiter. The Voyager 2 measurements in this panel correspond to a distance of about 4.3  ,
Pioneer 11 data to 5.7
,
Pioneer 11 data to 5.7  (Krimigis et al. 1983) and the Cassini data to 5
(Krimigis et al. 1983) and the Cassini data to 5  (Krimigis et al. 2005). Note that Pioneer 10 was much deeper in the Jovian than the other spacecraft in the Kronian magnetosphere, because the measurements shown correspond to a distance of about 3
(Krimigis et al. 2005). Note that Pioneer 10 was much deeper in the Jovian than the other spacecraft in the Kronian magnetosphere, because the measurements shown correspond to a distance of about 3 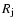 (Ferreira 2002). The ratio of distance to size of the magnetosphere is 3/82 = 0.037 for Pioneer 10 at Jupiter and approximately 5/24 = 0.208 for the spacecraft Voyager 2 and Pioneer 11 and Cassini at Saturn. The Saturn measurements at distances of about 11
(Ferreira 2002). The ratio of distance to size of the magnetosphere is 3/82 = 0.037 for Pioneer 10 at Jupiter and approximately 5/24 = 0.208 for the spacecraft Voyager 2 and Pioneer 11 and Cassini at Saturn. The Saturn measurements at distances of about 11  revealed intensities that are about an order of magnitude lower than at 5
revealed intensities that are about an order of magnitude lower than at 5  so that the Pioneer 10 measurements at Jupiter (same as in the left panel) now agree relatively well with the Saturn measurements. The two lower data points measured by Voyager 2 correspond to a distance of about 13
so that the Pioneer 10 measurements at Jupiter (same as in the left panel) now agree relatively well with the Saturn measurements. The two lower data points measured by Voyager 2 correspond to a distance of about 13  (Krimigis et al. 1983), whereas the two upper ones correspond to 11
(Krimigis et al. 1983), whereas the two upper ones correspond to 11  (Maurice et al. 1996a). The other data points of the Voyager 1, Cassini, and Pioneer 11 spacecraft are located in the range of 11
(Maurice et al. 1996a). The other data points of the Voyager 1, Cassini, and Pioneer 11 spacecraft are located in the range of 11  (Krimigis et al. 2005; Trainor et al. 1980; Krupp et al. 2005; Krimigis et al. 1983). At about 20
(Krimigis et al. 2005; Trainor et al. 1980; Krupp et al. 2005; Krimigis et al. 1983). At about 20  ,
the Cassini measurements at Jupiter and Saturn are shown here in direct comparison. The displayed Cassini measurements at 1 MeV were obtained with the LEMMS instrument(Low Energy Magnetospheric Measurement System), which observes electrons at energies >905 keV.
The upper data point was measured when Cassini crossed the magnetopause of Jupiter, which was at a distance of about 200
,
the Cassini measurements at Jupiter and Saturn are shown here in direct comparison. The displayed Cassini measurements at 1 MeV were obtained with the LEMMS instrument(Low Energy Magnetospheric Measurement System), which observes electrons at energies >905 keV.
The upper data point was measured when Cassini crossed the magnetopause of Jupiter, which was at a distance of about 200 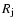 (Krupp et al. 2004). The lower data point corresponds to a distance of about 140
(Krupp et al. 2004). The lower data point corresponds to a distance of about 140 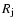 ,
which is equivalent to the spacecraft´s closest approach to Jupiter. The measurements of Cassini at Saturn at about 20
,
which is equivalent to the spacecraft´s closest approach to Jupiter. The measurements of Cassini at Saturn at about 20  are inside the Kronian magnetosphere (Krimigis et al. 2005; Krupp et al. 2005). The shown Pioneer 11 measurements also correspond to the crossing of the magnetopause, which occurred at a distance of about 18
are inside the Kronian magnetosphere (Krimigis et al. 2005; Krupp et al. 2005). The shown Pioneer 11 measurements also correspond to the crossing of the magnetopause, which occurred at a distance of about 18  (Trainor et al. 1980) as mentioned above. Voyager 1 and 2 data points are measured at a distance of 19
(Trainor et al. 1980) as mentioned above. Voyager 1 and 2 data points are measured at a distance of 19  (Krimigis et al. 1983), which was for Voyager 2 the crossing point of the magnetopause, whereas for Voyager 1 it was already 23
(Krimigis et al. 1983), which was for Voyager 2 the crossing point of the magnetopause, whereas for Voyager 1 it was already 23  ,
so that the Voyager 2 measurement were made just inside the inner Kronian magnetosphere. It should be clearly pointed out that the direct comparison and interpretation of the displayed spacecraft measurements in Fig. 3 have to be treated with some care. The different spacecraft arrived at Jupiter/Saturn in different states of their magnetospheres and the observations were made in different energy channels. The LEMMS observations at 1 MeV correspond to electrons with energies >905 keV, so that electrons with higher energies are also included.
Because of that, Fig. 3 provides only a rough picture of the comparison of the magnetospheres of Jupiter and Saturn. The main and obvious effect is, however, that electrons accelerated in the Kronian magnetosphere should not be expected to be negligible in comparison to Jovian electrons. This fact motivated us to consider Jovian and Kronian electrons together in the simulation of electron transport in the heliosphere. On the basis of the 1 MeV data in the last panel, we used a factor of
,
so that the Voyager 2 measurement were made just inside the inner Kronian magnetosphere. It should be clearly pointed out that the direct comparison and interpretation of the displayed spacecraft measurements in Fig. 3 have to be treated with some care. The different spacecraft arrived at Jupiter/Saturn in different states of their magnetospheres and the observations were made in different energy channels. The LEMMS observations at 1 MeV correspond to electrons with energies >905 keV, so that electrons with higher energies are also included.
Because of that, Fig. 3 provides only a rough picture of the comparison of the magnetospheres of Jupiter and Saturn. The main and obvious effect is, however, that electrons accelerated in the Kronian magnetosphere should not be expected to be negligible in comparison to Jovian electrons. This fact motivated us to consider Jovian and Kronian electrons together in the simulation of electron transport in the heliosphere. On the basis of the 1 MeV data in the last panel, we used a factor of
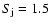 in our simulations, which is in good agreement with the shown measurements. A factor of
in our simulations, which is in good agreement with the shown measurements. A factor of
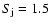 represents a 1.5 times stronger source function than used for Jupiter. To study the general behaviour and distribution of Kronian electrons in the heliosphere we considered in addition two more ratios of the source strength. We also set
represents a 1.5 times stronger source function than used for Jupiter. To study the general behaviour and distribution of Kronian electrons in the heliosphere we considered in addition two more ratios of the source strength. We also set 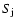 to 7.5 and 0.3, which represents a five times higher and five times lower source strength, respectively, compared to
to 7.5 and 0.3, which represents a five times higher and five times lower source strength, respectively, compared to
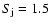 .
Note that also these two alternative factors are still in approximately good agreement with the range of 1 MeV measurements.
.
Note that also these two alternative factors are still in approximately good agreement with the range of 1 MeV measurements.
The diffusion tensor, the latitudinal solar wind structure, and the source of Jovian and Kronian electrons are incorporated into the Parker equation and the three different source strength ratios 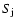 were tested in the numerical simulations. The simulated electron intensities are then discussed along the Ulysses and Cassini trajectories subsequently. To solve the Parker Eq. (2), we used the VLUGR3 code developed by Blom & Verwer (1994b,a) as in Lange et al. (2006).
were tested in the numerical simulations. The simulated electron intensities are then discussed along the Ulysses and Cassini trajectories subsequently. To solve the Parker Eq. (2), we used the VLUGR3 code developed by Blom & Verwer (1994b,a) as in Lange et al. (2006).
The outer boundary of the simulated heliosphere was set to 120 AU, where the electron spectrum determined by Langner et al. (2001) was used as the local interstellar spectrum for galactic electrons. The source function 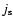 for electrons produced at Jupiter is given by Ferreira et al. (2001a) as
for electrons produced at Jupiter is given by Ferreira et al. (2001a) as
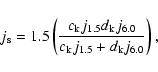 |
(14) |
with
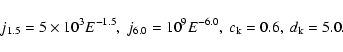 |
(15) |
This function, with differential intensities 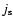 ,
given in units of
,
given in units of
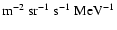 and kinetic energy in units of GeV, is a combination of
and kinetic energy in units of GeV, is a combination of
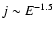 and
and
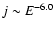 spectra and is constructed to be compatible with ISEE 3 spectra and Pioneer 10 data. The source function is implemented in the numerical model as a ``point'' source by specifying
spectra and is constructed to be compatible with ISEE 3 spectra and Pioneer 10 data. The source function is implemented in the numerical model as a ``point'' source by specifying 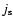 at a single grid point with an extent of
at a single grid point with an extent of  0.15 AU in the radial direction. For the source function
0.15 AU in the radial direction. For the source function 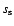 of electrons produced at Saturn, we used the function (14) as well, but multiplied by the factor
of electrons produced at Saturn, we used the function (14) as well, but multiplied by the factor 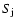 ,
so that
,
so that 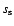 is given as
is given as
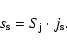 |
(16) |
The source is also implemented in the numerical model as a point source by specifying 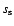 at a single grid point, but in contrast to
at a single grid point, but in contrast to 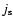 with no extension in radial direction to take into account that the size of Kronian magnetosphere is much smaller than the Jovian magnetosphere.
with no extension in radial direction to take into account that the size of Kronian magnetosphere is much smaller than the Jovian magnetosphere.
First of all, we present a simulation with only two electron sources, namely the galactic and the Jovian electrons. The diffusion tensor
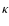 and the solar wind speed
and the solar wind speed
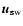 are time-independent, so that the latitudinal structure of the solar wind (see Fig. 2) is kept at the conditions valid for solar minimum. The minimum solar wind velocity, which occurs at the latitudes of the streamer belt, is set to 400 km s-1 and the maximum speed to 750 km s-1 at high latitudes (see Fig. 2). The computed 1 MeV intensities (normalized to the galactic source) along the Ulysses and Cassini trajectories are shown in Fig. 4. The radial and latitudinal coordinates of the Ulysses and Cassini trajectories are shown in the top panel.
In February 1992, the first Jupiter fly-by of the Ulysses spacecraft is evident by the high intensities then. Since this fly-by, Ulysses is travelling in an elliptical, Sun-focused orbit inclined by 80 degrees with respect to the solar equator.
In the beginning of the years 1995, 1998, and 2001, ecliptic passages took place, but the passage in 1998 was not identifiable in intensity. This is because, at this time Jupiter was behind the Sun, as seen from Ulysses, and in additon Ulysses reached aphelion (see Fig. 1), so that the connection to the Jovian source was very weak, in the radial, as well as in longitudinal, direction. In the beginning of 2004, 12 years after the first encounter with Jupiter, the second fly-by of the Ulysses spacecraft occurred. However, the distance of closest approach was seven times more than the first one, which is reflected by the lower intensity at that time. The first peak in the intensity along the Cassini trajectory corresponds to the first swing-by manoeuvre at Venus, and the second wider peak in 1999 designates together the second and third swing-by manoeuvre at Venus and shortly there after at Earth. The peaks were caused by slight oscillations around the ecliptic plane of 6 degrees in latitude during this phase.
After these manoeuvres in the very inner heliosphere, the spacecraft set off to its final destination, Saturn, and passed Jupiter on its way in the end of year 2000: the Jupiter fly-by is clearly visible. Thereafter the intensity decreases, because there is no Saturn source in this simulation, as mentioned above. In July 2004, Cassini was injected into an orbit around Saturn.
Also, the Cassini electron intensities in the inner heliosphere (around 1 AU, 1998 to 2000) are higher than or equal to those at Ulysses at larger radial distances (around 5 AU) in this period. This can be understood as result of the increase in the diffusion coefficients with heliocentric distance. Because of that, more electrons subside in the inner than in the ``outer'' heliosphere. This also explains the relatively low intensities after Cassini passed Jupiter on the way to Saturn. The Jupiter peak from Cassini is narrower in comparison to the peaks of the Ulysses intensities. This is because that Cassini always remained near the ecliptic plane, whereas Ulysses is coming from high latitudes, except for the first approach, where the spacecraft was also coming from near the ecliptic plane and was not injected to higher latitudes until after the swing-by manoeuvre (see Fig. 1). Thus, the left side of the first Ulysses Jupiter peak is comparable to that of Cassini. The wider peak of the second Jupiter fly-by of Ulysses is the result of the more effective electron transport in a latitudinal direction as in the radial direction. The study of the particle diffusion is very relevant, because the really unknown function in the Parker Eq. (2) is the diffusion tensor, so if Ulysses and Cassini observations were available in an energy range of overlap, the radial and latitudinal diffusion could be investigated in detail by two spacecraft at different positions in the radial and latitudinal directions.
are time-independent, so that the latitudinal structure of the solar wind (see Fig. 2) is kept at the conditions valid for solar minimum. The minimum solar wind velocity, which occurs at the latitudes of the streamer belt, is set to 400 km s-1 and the maximum speed to 750 km s-1 at high latitudes (see Fig. 2). The computed 1 MeV intensities (normalized to the galactic source) along the Ulysses and Cassini trajectories are shown in Fig. 4. The radial and latitudinal coordinates of the Ulysses and Cassini trajectories are shown in the top panel.
In February 1992, the first Jupiter fly-by of the Ulysses spacecraft is evident by the high intensities then. Since this fly-by, Ulysses is travelling in an elliptical, Sun-focused orbit inclined by 80 degrees with respect to the solar equator.
In the beginning of the years 1995, 1998, and 2001, ecliptic passages took place, but the passage in 1998 was not identifiable in intensity. This is because, at this time Jupiter was behind the Sun, as seen from Ulysses, and in additon Ulysses reached aphelion (see Fig. 1), so that the connection to the Jovian source was very weak, in the radial, as well as in longitudinal, direction. In the beginning of 2004, 12 years after the first encounter with Jupiter, the second fly-by of the Ulysses spacecraft occurred. However, the distance of closest approach was seven times more than the first one, which is reflected by the lower intensity at that time. The first peak in the intensity along the Cassini trajectory corresponds to the first swing-by manoeuvre at Venus, and the second wider peak in 1999 designates together the second and third swing-by manoeuvre at Venus and shortly there after at Earth. The peaks were caused by slight oscillations around the ecliptic plane of 6 degrees in latitude during this phase.
After these manoeuvres in the very inner heliosphere, the spacecraft set off to its final destination, Saturn, and passed Jupiter on its way in the end of year 2000: the Jupiter fly-by is clearly visible. Thereafter the intensity decreases, because there is no Saturn source in this simulation, as mentioned above. In July 2004, Cassini was injected into an orbit around Saturn.
Also, the Cassini electron intensities in the inner heliosphere (around 1 AU, 1998 to 2000) are higher than or equal to those at Ulysses at larger radial distances (around 5 AU) in this period. This can be understood as result of the increase in the diffusion coefficients with heliocentric distance. Because of that, more electrons subside in the inner than in the ``outer'' heliosphere. This also explains the relatively low intensities after Cassini passed Jupiter on the way to Saturn. The Jupiter peak from Cassini is narrower in comparison to the peaks of the Ulysses intensities. This is because that Cassini always remained near the ecliptic plane, whereas Ulysses is coming from high latitudes, except for the first approach, where the spacecraft was also coming from near the ecliptic plane and was not injected to higher latitudes until after the swing-by manoeuvre (see Fig. 1). Thus, the left side of the first Ulysses Jupiter peak is comparable to that of Cassini. The wider peak of the second Jupiter fly-by of Ulysses is the result of the more effective electron transport in a latitudinal direction as in the radial direction. The study of the particle diffusion is very relevant, because the really unknown function in the Parker Eq. (2) is the diffusion tensor, so if Ulysses and Cassini observations were available in an energy range of overlap, the radial and latitudinal diffusion could be investigated in detail by two spacecraft at different positions in the radial and latitudinal directions.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9069fig5.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg69.gif) |
Figure 4:
The computed electron intensities (normalized to the galactic source) along the Cassini (solid line) and Ulysses (dashed line) trajectories at an energy of 1 MeV. This simulation was performed only with the galactic and the Jovian electron source. The heliocentric distance and heliographic latitude of the Ulysses and Cassini trajectories are shown in the top panel. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9069fig6.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg70.gif) |
Figure 5:
The computed electron intensities along the Cassini (solid line) and Ulysses (dashed line) trajectories at an energy of 1 MeV. This simulation was performed with the galactic, the Jovian, and the Kronian electron sources. We set
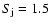 ,
so that the Saturn source is 1.5 times stronger than the source at Jupiter. The heliocentric distance and heliographic latitude of the Ulysses and Cassini trajectories are shown in the top panel. ,
so that the Saturn source is 1.5 times stronger than the source at Jupiter. The heliocentric distance and heliographic latitude of the Ulysses and Cassini trajectories are shown in the top panel. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{9069fig7.eps}\vspace*{2mm}
\includegraphics[width=5.8cm,clip]{9069fig8.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg71.gif) |
Figure 6:
Contour plot of the 1 MeV electron intensity in the ecliptic plane at 1998.0 inside 10 AU: the top panel is related to the situation in Fig. 4 (no Saturn source) and the bottom panel to Fig. 5 (with Saturn source,
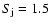 ). The position of Ulysses is marked as the filled triangle and Cassini as the filled circle. The Parker spiral and the extensions of the Jupiter and Saturn source are clearly visible at about 5 AU and 9 AU. ). The position of Ulysses is marked as the filled triangle and Cassini as the filled circle. The Parker spiral and the extensions of the Jupiter and Saturn source are clearly visible at about 5 AU and 9 AU. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9069fig9.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg72.gif) |
Figure 7:
The computed electron intensities along the Ulysses trajectory at an energy of 1 MeV. Displayed are simulations with three factors of 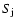 ,
0.3, 1.5, and 7.5 (dashed lines), together with the simulation without the Saturn source ( ,
0.3, 1.5, and 7.5 (dashed lines), together with the simulation without the Saturn source (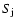 = 0, solid line). The diffusion tensor = 0, solid line). The diffusion tensor
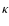 and the solar wind speed
and the solar wind speed
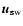 are time-independent, so that the latitudinal structure of the solar wind (see Fig. 2) is kept at the conditions valid for the solar minimum. The minimum and maximum value of the solar wind velocity are set to
are time-independent, so that the latitudinal structure of the solar wind (see Fig. 2) is kept at the conditions valid for the solar minimum. The minimum and maximum value of the solar wind velocity are set to
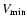 = 400 km s-1 and = 400 km s-1 and
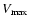 = 750 km s-1. The heliocentric distance and heliographic latitude of the Ulysses trajectory are shown in the top panel. = 750 km s-1. The heliocentric distance and heliographic latitude of the Ulysses trajectory are shown in the top panel. |
| Open with DEXTER |
In the following simulations we have, in addition, implemented the Kronian electron source. We set
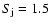 ,
so that the Saturn source is 1.5 times stronger than the source at Jupiter. Otherwise we used the same parameters as in the simulation without the Kronian electrons in Fig. 4. The results for this simulation are shown in Fig. 5. In general, the intensities are higher in comparison to Fig. 4.
The Ulysses fly-bys at Jupiter are unaltered in intensities, which is expected. But the period between the fly-bys shows clearly higher intensities with a maximum at the ecliptic passage at 1998.0. The two first peaks and the Jupiter fly-by of the Cassini spacecraft are also unaltered. Cassini´s approach to Saturn after the Jupiter fly-by in 2001 is explicitly visible in the increasing intensities in contrast to Fig. 4. The intensity when Cassini arrived at Saturn in the middle of 2004 is less than the Jupiter peaks, although the Saturn source is 1.5 times stronger than the Jupiter source. This is an effect of the increased diffusion coefficients with distance, so that the intensity at Saturn is in situ not as prominent as in situ at Jupiter. This is confirmed by the fact that the peak is not very sharp and that the intensity maximum is already reached half a year before Cassini finally reached Saturn. Cassini reached up to 9 AU on the way to Saturn, after the Jupiter fly-by in 2001. The occurrence of the maximum during the Ulysses ecliptic passage at 1998.0 is an interesting finding, because this passage is not visible in the simulation without the Saturn source in Fig. 4, as mentioned above. Note that Ulysses´ farthest heliocentric distance is about 5.4 AU, which is equivalent to Jupiters´ heliocentric distance. Figure 6 displays a contour plot of the ecliptic plane at 1998.0 inside 10 AU, where the upper panel is related to the situation in Fig. 4 (no Saturn source) and the right panel to Fig. 5 (with Saturn source). As mentioned, Ulysses was in the ecliptic plane at about 5 AU in the beginning of 1998, whereas Cassini was just launched at 1 AU. The Parker spiral and the extensions of the Jupiter and Saturn source are clearly visible at about 5 AU and 9 AU. The Saturn source is spread more in longitude there, as a result of the 1.5 times stronger source and the increased diffusion at greater distances. It is observable in the lower panel that the Jupiter and Saturn sources are connected by intensity contour lines there. This explains the Ulysses maximum in 1998.0 in Fig. 5, because on these lines Saturn injects electrons into the inner heliosphere.
,
so that the Saturn source is 1.5 times stronger than the source at Jupiter. Otherwise we used the same parameters as in the simulation without the Kronian electrons in Fig. 4. The results for this simulation are shown in Fig. 5. In general, the intensities are higher in comparison to Fig. 4.
The Ulysses fly-bys at Jupiter are unaltered in intensities, which is expected. But the period between the fly-bys shows clearly higher intensities with a maximum at the ecliptic passage at 1998.0. The two first peaks and the Jupiter fly-by of the Cassini spacecraft are also unaltered. Cassini´s approach to Saturn after the Jupiter fly-by in 2001 is explicitly visible in the increasing intensities in contrast to Fig. 4. The intensity when Cassini arrived at Saturn in the middle of 2004 is less than the Jupiter peaks, although the Saturn source is 1.5 times stronger than the Jupiter source. This is an effect of the increased diffusion coefficients with distance, so that the intensity at Saturn is in situ not as prominent as in situ at Jupiter. This is confirmed by the fact that the peak is not very sharp and that the intensity maximum is already reached half a year before Cassini finally reached Saturn. Cassini reached up to 9 AU on the way to Saturn, after the Jupiter fly-by in 2001. The occurrence of the maximum during the Ulysses ecliptic passage at 1998.0 is an interesting finding, because this passage is not visible in the simulation without the Saturn source in Fig. 4, as mentioned above. Note that Ulysses´ farthest heliocentric distance is about 5.4 AU, which is equivalent to Jupiters´ heliocentric distance. Figure 6 displays a contour plot of the ecliptic plane at 1998.0 inside 10 AU, where the upper panel is related to the situation in Fig. 4 (no Saturn source) and the right panel to Fig. 5 (with Saturn source). As mentioned, Ulysses was in the ecliptic plane at about 5 AU in the beginning of 1998, whereas Cassini was just launched at 1 AU. The Parker spiral and the extensions of the Jupiter and Saturn source are clearly visible at about 5 AU and 9 AU. The Saturn source is spread more in longitude there, as a result of the 1.5 times stronger source and the increased diffusion at greater distances. It is observable in the lower panel that the Jupiter and Saturn sources are connected by intensity contour lines there. This explains the Ulysses maximum in 1998.0 in Fig. 5, because on these lines Saturn injects electrons into the inner heliosphere.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{9069fig10.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg73.gif) |
Figure 8:
The computed electron intensities along the Cassini trajectory at an energy of 1 MeV. Displayed are simulations with three factors of 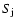 ,
0.3, 1.5 and 7.5 (dashed lines), together with the simulation without the Saturn source ( ,
0.3, 1.5 and 7.5 (dashed lines), together with the simulation without the Saturn source (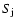 = 0, solid line). The diffusion tensor = 0, solid line). The diffusion tensor
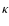 and the solar wind speed
and the solar wind speed
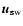 are time-independent, so that the latitudinal structure of the solar wind (see Fig. 2) is kept at the conditions valid for the solar minimum. The minimum and maximum value of the solar wind velocity are set to
are time-independent, so that the latitudinal structure of the solar wind (see Fig. 2) is kept at the conditions valid for the solar minimum. The minimum and maximum value of the solar wind velocity are set to
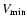 = 400 km s-1 and = 400 km s-1 and
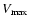 = 750 km s-1. The heliocentric distance and heliographic latitude of the Cassini trajectory are shown in the top panel. = 750 km s-1. The heliocentric distance and heliographic latitude of the Cassini trajectory are shown in the top panel. |
| Open with DEXTER |
To study the general behaviour of Kronian electrons along the Ulysses and Cassini trajectories, we now consider two other ratios of the source strength 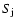 .
We set
.
We set 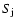 to 7.5 and 0.3. These two factors agree in part with the 1 MeV spacecraft measurements at Jupiter and Saturn shown in Fig. 3. Figures 7 and 8 display the simulations with the three factors of
to 7.5 and 0.3. These two factors agree in part with the 1 MeV spacecraft measurements at Jupiter and Saturn shown in Fig. 3. Figures 7 and 8 display the simulations with the three factors of 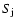 ,
0.3,1.5, and 7.5, together with the simulations without the Saturn source (
,
0.3,1.5, and 7.5, together with the simulations without the Saturn source (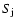 = 0) for the Ulysses and the Cassini trajectories, respectively. It is clearly visible in Fig. 7 that the Kronian electrons produce a maximum in 1998.0 along the Ulysses trajectory, even when the Saturn source strength is relative weak with
= 0) for the Ulysses and the Cassini trajectories, respectively. It is clearly visible in Fig. 7 that the Kronian electrons produce a maximum in 1998.0 along the Ulysses trajectory, even when the Saturn source strength is relative weak with
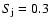 .
Along the Cassini trajectory (Fig. 8), the Kronian electrons have hardly any effect until the Jupiter fly-by 2001, except when
.
Along the Cassini trajectory (Fig. 8), the Kronian electrons have hardly any effect until the Jupiter fly-by 2001, except when
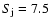 .
The very inner heliosphere is then filled with Kronian electrons even at low latitudes.
.
The very inner heliosphere is then filled with Kronian electrons even at low latitudes.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{9069fig11.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg76.gif) |
Figure 9:
The computed electron intensities along the Ulysses trajectory at an energy of 1 MeV, where
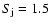 .
A time-dependent model (Lange et al. 2006) and parameters for the solar activity are used here (solid line). The beginning of the solar maximum phase is set to 1995.8, the transition period for the solar wind field to two months, and four months for the latitudinal diffusion coefficient. In comparison, the dashed lines display the result without the solar activity variation (as in Fig. 5). The heliocentric distance and heliographic latitude of the Ulysses trajectory are shown in the top panel. .
A time-dependent model (Lange et al. 2006) and parameters for the solar activity are used here (solid line). The beginning of the solar maximum phase is set to 1995.8, the transition period for the solar wind field to two months, and four months for the latitudinal diffusion coefficient. In comparison, the dashed lines display the result without the solar activity variation (as in Fig. 5). The heliocentric distance and heliographic latitude of the Ulysses trajectory are shown in the top panel. |
| Open with DEXTER |
The distribution and transport of electrons in the heliosphere also depends on the solar activity. The SWOOPS instrument has observed a variable solar wind velocity field at high (beyond the streamer belt) latitudes during the solar maximum phase (see chapter 2.1.). A time-dependent model for the latitudinal variation of the solar velocity field with solar activity is discussed in detail in Lange et al. (2006). In this model the high solar wind speed beyond the streamer belt (800 km s-1) is decreased during the increase in solar activity between 1996 and 2005. The structure of the latitudinal diffusion coefficient is treated analogously. In Lange et al. (2006), the beginning of the solar activity and the transition period, where the conditions of solar minimum change into those of solar maximum, were determined in the simulations to produce a best fit to the Ulysses/KET data (KET observes electrons in the energy range between 3 and 10 MeV). It was found that the activity increased from about 1995.8 onwards and that the transition periods for the solar wind velocity field and for the latitudinal diffusion coefficient were two and four months, respectively. This time-dependent model and parameters were used in the simulation shown in Fig. 9 for the Ulysses and in Fig. 10 for the Cassini trajectory, where
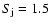 .
In comparison the result without the solar activity variation (same as in Fig. 5). Until 1995.8, the solar minimum phase is present and the two curves are equal in Fig. 9. During solar maximum conditions from 1996 onwards, the intensities in Figs. 9 and 10 are higher than in the simulation without any solar activity, caused by the reduced solar wind velocity and latitudinal diffusion. The convection speed has decreased to half of the solar minimum value, so that the energetic electrons are no longer strongly transported outwards. The latitudinal diffusion at high latitudes is reduced to the value of the streamer belt, so that the Jovian and Kronian electrons can propagate more homogeneously to all heliographic latitudes. This can be seen especially by the wide peak at the second Jupiter fly-by of Ulysses in 2004 (Fig. 9), where Ulysses comes from high latitudes.
.
In comparison the result without the solar activity variation (same as in Fig. 5). Until 1995.8, the solar minimum phase is present and the two curves are equal in Fig. 9. During solar maximum conditions from 1996 onwards, the intensities in Figs. 9 and 10 are higher than in the simulation without any solar activity, caused by the reduced solar wind velocity and latitudinal diffusion. The convection speed has decreased to half of the solar minimum value, so that the energetic electrons are no longer strongly transported outwards. The latitudinal diffusion at high latitudes is reduced to the value of the streamer belt, so that the Jovian and Kronian electrons can propagate more homogeneously to all heliographic latitudes. This can be seen especially by the wide peak at the second Jupiter fly-by of Ulysses in 2004 (Fig. 9), where Ulysses comes from high latitudes.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{9069fig12.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg77.gif) |
Figure 10:
The computed electron intensities along the Cassini trajectory at an energy of 1 MeV, where
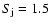 .
A time-dependent model (Lange et al. 2006) and parameters for the solar activity are used here (solid line). The beginning of the solar maximum phase is set to 1995.8, the transition period for the solar wind field to two months and four months for the latitudinal diffusion coefficient. In comparison, the dashed lines display the result without the solar activity variation (as in Fig. 5). The heliocentric distance and heliographic latitude of the Cassini trajectory are shown in the top panel. .
A time-dependent model (Lange et al. 2006) and parameters for the solar activity are used here (solid line). The beginning of the solar maximum phase is set to 1995.8, the transition period for the solar wind field to two months and four months for the latitudinal diffusion coefficient. In comparison, the dashed lines display the result without the solar activity variation (as in Fig. 5). The heliocentric distance and heliographic latitude of the Cassini trajectory are shown in the top panel. |
| Open with DEXTER |
We performed simulations with a time-dependent 3D-model for 1 MeV electron fluxes in the heliosphere, by using three different electron sources: the galactic, the Jovian, and the Kronian. The source strength of Saturn in comparison to Jupiter, 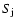 ,
could be determined to be around 1.5 under consideration of all available spacecraft measurements at Saturn and Jupiter in the low-energy range of a few MeV. The simulated electron intensities were discussed along the Ulysses and Cassini trajectories, and it clearly turns out that the electrons from the Kronian magnetosphere cannot be neglected. Even in the extreme case where the source strength is relatively weak with
,
could be determined to be around 1.5 under consideration of all available spacecraft measurements at Saturn and Jupiter in the low-energy range of a few MeV. The simulated electron intensities were discussed along the Ulysses and Cassini trajectories, and it clearly turns out that the electrons from the Kronian magnetosphere cannot be neglected. Even in the extreme case where the source strength is relatively weak with
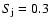 ,
the effect of Kronian electrons is visible along both the Ulysses and Cassini trajectories. The increased diffusion at greater heliocentric distance fostered the distribution of Kronian electrons in the inner heliosphere in comparison to the Jovian electrons. In Lange et al. (2006), we performed simulations only with the Jovian source at an energy of 7 MeV in comparison with Ulysses/KET data, where a considerable lower computed intensity (as compared to observed) was found at around 1999. This deficiency was compensated with a variation of the Jovian source caused by the solar activity around 1998/99. An increasing factor of the Jovian source strength of 8 was suggested there. This high factor is in critical discussion (Morioka et al. 1999) and with the additional Kronian source, it is possible to reduce or even compensate this factor at low energies, as clearly shown in Fig. 7.
,
the effect of Kronian electrons is visible along both the Ulysses and Cassini trajectories. The increased diffusion at greater heliocentric distance fostered the distribution of Kronian electrons in the inner heliosphere in comparison to the Jovian electrons. In Lange et al. (2006), we performed simulations only with the Jovian source at an energy of 7 MeV in comparison with Ulysses/KET data, where a considerable lower computed intensity (as compared to observed) was found at around 1999. This deficiency was compensated with a variation of the Jovian source caused by the solar activity around 1998/99. An increasing factor of the Jovian source strength of 8 was suggested there. This high factor is in critical discussion (Morioka et al. 1999) and with the additional Kronian source, it is possible to reduce or even compensate this factor at low energies, as clearly shown in Fig. 7.
Obviously, while the existence of a non-negligible Kronian electron source complicates the fluxes at low energies, at the same time it adds a valuable constraint to diffusion models of energetic particles. Unfortunately, apart from Ulysses, no measured data in this high-energy range of 7 MeV are available to determine the Jovain/Kronian source strength ratio 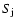 as in Fig. 3. The real distribution of electrons in the inner heliosphere and the actual source strength of Saturn in comparison to Jupiter,
as in Fig. 3. The real distribution of electrons in the inner heliosphere and the actual source strength of Saturn in comparison to Jupiter, 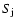 ,
can only be answered with data calibration. To date, no LEMMS data are available along the Cassini trajectory.
,
can only be answered with data calibration. To date, no LEMMS data are available along the Cassini trajectory.
Acknowledgements
We thank Bernd Heber for providing the trajectory data for Ulysses and critical comments and the referee for a constructive and, thus, helpful report.
- Balogh, A., Marsden, R.,
& Smith, E. 2001, The Heliosphere near Solar Minimum, The
Ulysses perspective (Springer-Verlag)
(In the text)
- Blom, J., & Verwer,
J. 1994a, Report NM-R9404, CWI, Amsterdam
- Blom, J., & Verwer,
J. 1994b, Report NM-R9405, CWI, Amsterdam
- Ferreira, S. 2002, Ph.D.
Thesis
(In the text)
- Ferreira, S.,
Potgieter, M., Burger, R., Heber, B., & Fichtner, H. 2001a, J.
Geophys. Res., 106, 24979 [NASA ADS] [CrossRef]
- Ferreira, S.,
Potgieter, M., Burger, R., et al. 2001b, J. Geophys. Res.,
106, 29313 [NASA ADS] [CrossRef]
- Fichtner, H.,
Sreenivasan, S., & Fahr, H. 1996, A&A, 308, 248 [NASA ADS]
- Frank, L., Burek, B.,
Ackerson, K., Wolfe, J., & Mihalov, J. 1980, J. Geophys. Res.,
85, 5695 [NASA ADS] [CrossRef]
- Kissmann, R., Fichtner,
H., Heber, B., Ferreira, S., & Potgieter, M. 2003, Adv. Space
Res., 32, 681 [NASA ADS] [CrossRef]
- Krimigis, S., Carbary,
J., Keath, E., et al. 1983, J. Geophys. Res., 88, 8871 [NASA ADS] [CrossRef]
(In the text)
- Krimigis, S., Mitchell,
D., Hamilton, D., et al. 2005, Science, 307, 1270 [NASA ADS] [CrossRef]
- Krupp, N. 2005, Space
Sci. Rev., 166, 345 [NASA ADS] [CrossRef]
(In the text)
- Krupp, N., Woch, J.,
Lagg, A., et al. 2004, J. Geophys. Res. (Space Phys.), 109
A18, 9
(In the text)
- Krupp, N., Lagg, A.,
Woch, J., et al. 2005, Geophys. Res. Lett., 32, 20 [CrossRef]
- Lange, D., Fichtner, H.,
& Kissmann, R. 2006, A&A, 449, 401 [NASA ADS] [CrossRef] [EDP Sciences]
- Langner, U., de Jager,
O., & Potgieter, M. 2001, Adv. Space Res., 27, 517 [NASA ADS] [CrossRef]
(In the text)
- Maurice, S., Sittler,
E., Cooper, J., et al. 1996a, J. Geophys. Res., 101,
15211 [NASA ADS] [CrossRef]
(In the text)
- Maurice, S., Engle, I.,
Blanc, M., & Skubis, M. 1996b, J. Geophys. Res., 101,
27053 [NASA ADS] [CrossRef]
- McComas, D., Elliott, H.,
& Schwadron, N. 2003, J. Geophys. Res., 30, 1517
(In the text)
- Minnie, J., Bieber, J.,
& Matthaeus, W. 2007, ApJ, 663, 1049 [NASA ADS] [CrossRef]
- Morioka, A., Tsuchiya,
F., & Misawa, H. 1999, Earth Planets Space, 51, 987 [NASA ADS]
(In the text)
- Parker, E. 1965,
Planetary and Space Science, 13, 9 [NASA ADS] [CrossRef]
(In the text)
- Shalchi, A., &
Kourakis, I. 2007, A&A, 470, 405 [NASA ADS] [CrossRef] [EDP Sciences]
- Simpson, J., Hamilton,
D., Lentz, G., et al. 1974, Science, 183, 306 [NASA ADS] [CrossRef]
(In the text)
- Simpson, J., Hamilton,
D., Lentz, G., et al. 1975, Science, 188, 455 [NASA ADS] [CrossRef]
- Trainor, J., McDonald,
F., & Schardt, A. 1980, Science, 207, 421 [NASA ADS] [CrossRef]
- Zwickl, R., Krimigis, S.,
Carbary, J., et al. 1981, J. Geophys. Res., 86, 8125 [NASA ADS] [CrossRef]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{9069fig1.eps}\par\includegraphics[width=6.7cm,clip]{9069fig2.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg12.gif)
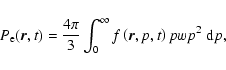
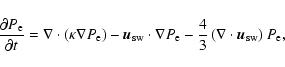
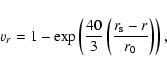
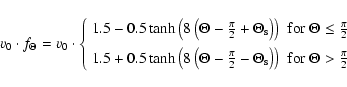
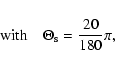
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{9069fig3.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg35.gif)
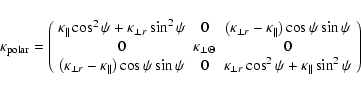
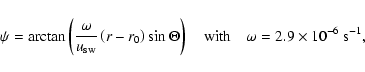
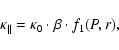
![\begin{figure}
\par\includegraphics[width=15.7cm,clip]{9069fig4.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg52.gif)
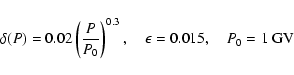
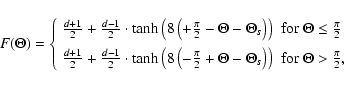
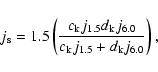
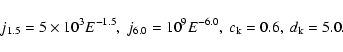
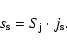
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9069fig5.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9069fig6.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{9069fig7.eps}\vspace*{2mm}
\includegraphics[width=5.8cm,clip]{9069fig8.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9069fig9.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg72.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{9069fig10.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg73.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{9069fig11.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{9069fig12.eps}\end{figure}](/articles/aa/full/2008/18/aa9069-07/Timg77.gif)