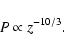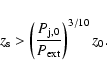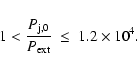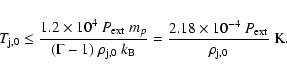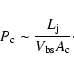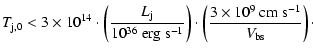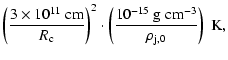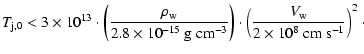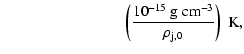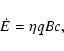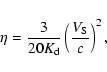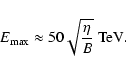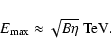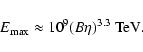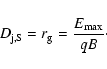A&A 482, 917-927 (2008)
DOI: 10.1051/0004-6361:20078929
On the interaction of microquasar jets with
stellar winds
M. Perucho1 - V. Bosch-Ramon2
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, Bonn 53121, Germany
2 -
Max Planck Institut für Kernphysik, Saupfercheckweg 1,
Heidelberg 69117, Germany
Received 26 October 2007 / Accepted 6 February 2008
Abstract
Context. Strong interactions between jets and stellar winds at binary-system, spatial-scales could occur in high-mass microquasars.
Aims. We study here, mainly from a dynamical but also a radiative point of view, the collision between a dense stellar wind and a mildly relativistic hydrodynamical jet of supersonic nature.
Methods. We have performed numerical two-dimensional simulations of jets, with cylindrical and planar (slab) symmetry, crossing the stellar-wind material. From the results of the simulations, we derive estimates of the particle acceleration efficiency, using first-order, Fermi-acceleration theory, and provide insight into the possible radiative outcomes.
Results. We find that, during jet launching, the jet head generates a strong shock in the wind. During and after this process, strong recollimation shocks can occur due to the initial overpressure of the jet with its environment. The conditions in all these shocks are convenient to accelerate particles up to  TeV energies, which can lead to leptonic (synchrotron and inverse Compton) and hadronic (proton-proton) radiation. In principle, the cylindrical jet simulations show that the jet is stable, and can escape from the system even at relatively low power. However, when accounting for the wind ram pressure, the jet can be bent and disrupted for power
TeV energies, which can lead to leptonic (synchrotron and inverse Compton) and hadronic (proton-proton) radiation. In principle, the cylindrical jet simulations show that the jet is stable, and can escape from the system even at relatively low power. However, when accounting for the wind ram pressure, the jet can be bent and disrupted for power
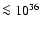 erg s-1.
erg s-1.
Key words: X-rays: binaries - stars: individual: LS 5039 -
radiation mechanisms: non-thermal
1 Introduction
Strong shocks can take place in very different astrophysical scenarios, for example, due to the formation of structures in extragalactic galaxy clusters (e.g. Kang, et al. 1996), active galactic
nuclei (AGN) jets (e.g. Begelman et al. 1984), supernova
remnants (e.g. van der Laan 1962), star-forming regions
(e.g. Bykov & Fleishman 1992), pulsar winds (e.g. Rees
& Gunn 1974), galactic, relativistic jets (e.g. Zealey,
et al. 1980), or jets in young stars (e.g. Araudo et al.
2007 and references therein).
In the case of AGNs, the interaction of jets with their environment allows the
study of jet properties, such as matter content and energy budget,
in the case of both Fanaroff-Riley II (FRII; e.g. Scheck et al. 2002; Krause
2005) and Fanaroff-Riley I (FRI; e.g. Perucho & Martí 2007)
sources. The simulation of extragalactic jets, and their interaction with the
environment have been addressed by a number of authors during the past decades
(e.g., Martí et al. 1997; Komissarov & Falle 1998; Aloy
et al. 1999; Rosen et al. 1999; Scheck et al. 2002;
Leismann et al. 2005; Perucho et al. 2005,2006; and Mizuno et al. 2007). In particular, the evolution of jets in homogeneous and
inhomogeneous ambient media, the influence of internal energy on the
structure of the jets, the mass load of external material, the evolution of FRI
and FRII sources, and the growth of the Kelvin-Helmholtz instability in
relativistic flows, have all been thoroughly studied.
In the case of microquasars, X-ray binary systems with relativistic jets (e.g. Mirabel & Rodríguez 1999; Ribó 2005), there have not been many studies of the consequences of the interaction between the jet and the surrounding medium (e.g. Velázquez & Raga 2000).
A common approach has been to compare with extragalactic jets to point out similarities between the two types of sources (e.g., Gómez
2001; Hardee & Hughes 2003). It appears clear that these galactic outflows should generate some kind of structure
in their termination region, although the characteristics of this region from the radiative and dynamical point of view are unclear (e.g.
Aharonian & Atoyan 1998; Heinz 2002; Heinz & Sunyaev 2002; Bosch-Ramon et al. 2005; Bordas et al., in preparation), and only a
handful of sources show hints or evidences of jet/medium interaction (e.g. SS 433, Zealey et al. 1980; XTE J1550-564, Corbel et al. 2002; Cygnus X-3, Heindl et al. 2003; Cygnus X-1, Martí et al. 1996; Gallo et al. 2005; H1743-322, Corbel et al. 2005; Circinus X-1, Tudose et al. 2006; LS I +61 303, Paredes et al. 2007).
A microquasar jet can interact strongly not only with the interstellar medium.
In high-mass microquasars (HMMQ), the massive and hot primary star suffers
severe mass loss in the form of a supersonic wind that can embed the
jet![[*]](/icons/foot_motif.gif) .
This wind can have a strong
impact on the jet dynamics on binary-system, spatial-scales. The jet
may be destroyed by the wind, preventing jet detection. In such a scenario, shocks
are likely to occur, leading to efficient particle acceleration and the
production of multiwavelength radiation. This illustrates the importance of
studying the interaction between the jet and the stellar wind, using
hydrodynamics. Previous works treated the jet/stellar wind interaction using a
more phenomenological approach, and focused on possible radiative outcomes (e.g.
Romero et al. 2003; Romero et al. 2005; Aharonian et al.
2006a). Regarding the production of non-thermal particles in the
present context, diffusive shock (first-order Fermi) acceleration is a plausible
mechanism (e.g. Drury 1983). Other mechanisms of particle acceleration
may be operating as well, such as second-order Fermi acceleration (Fermi
1949), shear acceleration (e.g. Rieger & Duffy 2004), or
the so-called converter mechanism (e.g. Derishev et al. 2003).
.
This wind can have a strong
impact on the jet dynamics on binary-system, spatial-scales. The jet
may be destroyed by the wind, preventing jet detection. In such a scenario, shocks
are likely to occur, leading to efficient particle acceleration and the
production of multiwavelength radiation. This illustrates the importance of
studying the interaction between the jet and the stellar wind, using
hydrodynamics. Previous works treated the jet/stellar wind interaction using a
more phenomenological approach, and focused on possible radiative outcomes (e.g.
Romero et al. 2003; Romero et al. 2005; Aharonian et al.
2006a). Regarding the production of non-thermal particles in the
present context, diffusive shock (first-order Fermi) acceleration is a plausible
mechanism (e.g. Drury 1983). Other mechanisms of particle acceleration
may be operating as well, such as second-order Fermi acceleration (Fermi
1949), shear acceleration (e.g. Rieger & Duffy 2004), or
the so-called converter mechanism (e.g. Derishev et al. 2003).
In this work, we present the results from two-dimensional relativistic
hydrodynamical simulations, with cylindrical and slab symmetry, in a simplified
scenario of the jet/stellar wind interaction in an HMMQ. Our principal goal is to provide
first-order estimates of the dynamical impact of the wind on the jet. In
addition to this, we provide semi-analytical estimates on the radiative
outcome of the simulation results.
In the next section, we briefly describe the main features of the scenario
considered and present the physical parameters of the simulations; in
Sect. 3, we characterize the setup of the simulations and explain their
technical aspects; in Sect. 4, we present the results obtained, which
are discussed in Sect. 5, together with the consequences derived from
the simulations, from the point of view of radiation or jet stability. We
summarize results and conclusions in Sect. 6.
2 Physical scenario
The physical scenario adopted here corresponds to an HMMQ with physical parameters similar to those of
Cygnus X-1 or LS 5039, two close high-mass X-ray binaries with jets and with moderate-to-strong stellar-mass
loss from a primary O star, in the form of a fast and supersonic wind. The distance between the jet base and
the primary star is fixed to
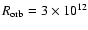 cm. This distance is similar to those
in LS 5039 (Casares et al. 2005) and Cygnus X-1 (Gies & Bolton 1986).
Typical luminosities and photon energies for O stars are
cm. This distance is similar to those
in LS 5039 (Casares et al. 2005) and Cygnus X-1 (Gies & Bolton 1986).
Typical luminosities and photon energies for O stars are
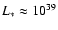 erg s-1 and
erg s-1 and
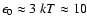 eV, respectively; the stellar wind present speeds
eV, respectively; the stellar wind present speeds
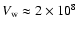 cm s-1, mass loss rates
cm s-1, mass loss rates
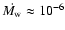
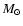 yr-1, and temperatures
yr-1, and temperatures
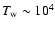 K.
K.
For the jet, we adopt a hydrodynamical supersonic outflow, ejected
perpendicular to the orbital plane, at mildly relativistic
velocities,
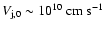 ,
and
temperature
,
and
temperature
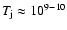 K
K
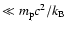 ,
where
,
where 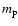 is the proton mass, c is the speed of
light and
is the proton mass, c is the speed of
light and 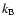 is the Boltzmann constant. The choice of
temperature is arbitrary because we only assume that the
jet is supersonic. Nevertheless, the temperature plays a role and
its relevance is discussed in Sect. 5. In this work,
we focus on jets formed by protons and electrons, as expected in
cases where the jet is fed with particles from the accretion disk. Given
the adopted temperatures and jet speeds, the most reasonable
choice of adiabatic exponent is
is the Boltzmann constant. The choice of
temperature is arbitrary because we only assume that the
jet is supersonic. Nevertheless, the temperature plays a role and
its relevance is discussed in Sect. 5. In this work,
we focus on jets formed by protons and electrons, as expected in
cases where the jet is fed with particles from the accretion disk. Given
the adopted temperatures and jet speeds, the most reasonable
choice of adiabatic exponent is
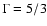 .
.
If we consider a leptonic jet, the adopted temperatures would imply an
important increase in the internal energy of the particles.
This would significantly reduce the Mach number, affecting the
assumption of a supersonic flow used here. Scheck et al. (2002) have shown that a supersonic leptonic jet with the same
energy flux than a hadronic jet, develops in a very similar way.
Therefore, large differences are not expected if the kinetic
luminosity of the jet remains constant, regardless of its
composition.
Regarding the geometry adopted for the simulation, a cylindrical symmetry can suffice to study the jet head
shock formation in the wind. Since the jet speed
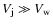 ,
the wind speed (which breaks the
cylindrical symmetry) is neglected. As it will be seen in the slab simulations, this assumption is
reasonable for powerful jets, but not in the case of weaker ones. At the present stage, slab symmetry
simulations are sufficient to show the importance of the stellar wind ram pressure on the jet, because the
timescales on which the wind surrounds the jet (
,
the wind speed (which breaks the
cylindrical symmetry) is neglected. As it will be seen in the slab simulations, this assumption is
reasonable for powerful jets, but not in the case of weaker ones. At the present stage, slab symmetry
simulations are sufficient to show the importance of the stellar wind ram pressure on the jet, because the
timescales on which the wind surrounds the jet (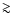
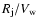 ;
where
;
where 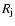 is the jet
radius) are longer than the simulation timescales. Also, the adopted configuration of the stellar wind,
emanating from one side of the jet, is consistent with an orbital timescale much longer than the simulation
timescales. These simplifications are reasonable in our case, because we plan to highlight remarkable features and not to obtain accurate quantitative predictions.
is the jet
radius) are longer than the simulation timescales. Also, the adopted configuration of the stellar wind,
emanating from one side of the jet, is consistent with an orbital timescale much longer than the simulation
timescales. These simplifications are reasonable in our case, because we plan to highlight remarkable features and not to obtain accurate quantitative predictions.
We note that the wind structure is an important point in our simulations. It has been proposed that massive
stellar winds may be porous (e.g. Owocki & Cohen 2006). In addition, mass-loss rates of OB stars may be
smaller up to a factor of several, due to wind clumping, as shown, e.g., in Puls et al. (2006), where estimates
for the real mass-loss rates of several O stars, after wind clumpiness correction, are provided. For extremely
porous winds, the collision of the jet with small and dense clumps (i.e. the dynamically-relevant part
of the wind) would be rare, although these interactions could have interesting radiative outcomes (e.g.
Aharonian & Atoyan 1996; Romero et al. 2007a). Smaller mass-loss rates would in addition weaken the jet kinetic luminosity constraints derived in this work.
In our simulations, the jet starts at a distance
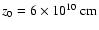 from the compact object,
where it should be still little affected dynamically by the environment. The initial half-opening angle
of the jet is taken to be 0.1 radians, which is given by the relation between the advance and expansion
velocities
from the compact object,
where it should be still little affected dynamically by the environment. The initial half-opening angle
of the jet is taken to be 0.1 radians, which is given by the relation between the advance and expansion
velocities![[*]](/icons/foot_motif.gif) . The jet then propagates through the system, sweeping up stellar-wind material. Two shocks are eventually generated, one in the stellar wind (i.e. a forward or bow shock), and another in the jet itself (i.e. a backwards or reverse shock). The shocked material is referred to as shell for the wind (i.e. a bow shock downstream), and cocoon for the jet (i.e. a reverse shock downstream). The jet continues to advance but slows down due to kinetic-energy exchange with swept-up wind
material. It can eventually be bent, and even destroyed, by the stellar-wind ram pressure. The pressure of the wind, or cocoon, as compared to the lateral pressure of the jet, can give rise to strong recollimation shocks. Recollimation shocks can destroy the jet, via deceleration and loss of collimation of the fluid downstream of the shocks (Perucho & Martí 2007).
. The jet then propagates through the system, sweeping up stellar-wind material. Two shocks are eventually generated, one in the stellar wind (i.e. a forward or bow shock), and another in the jet itself (i.e. a backwards or reverse shock). The shocked material is referred to as shell for the wind (i.e. a bow shock downstream), and cocoon for the jet (i.e. a reverse shock downstream). The jet continues to advance but slows down due to kinetic-energy exchange with swept-up wind
material. It can eventually be bent, and even destroyed, by the stellar-wind ram pressure. The pressure of the wind, or cocoon, as compared to the lateral pressure of the jet, can give rise to strong recollimation shocks. Recollimation shocks can destroy the jet, via deceleration and loss of collimation of the fluid downstream of the shocks (Perucho & Martí 2007).
3 Jet/wind interaction simulations
We performed five numerical simulations, three with cylindrical
symmetry and two with slab symmetry, in order to study the evolution
of HMMQ jets with different injection powers.
The simulations were performed using a two-dimensional finite-difference code based on a high-resolution
shock-capturing scheme, which solves the equations of relativistic hydrodynamics written in conservation
form. This code is an upgrade of the code described in Martí et al. (1997) (e.g. see Perucho et al. 2005). Simulations were performed in two dual-core processors in the Max-Planck-Institut für
Radioastronomie.
The numerical grid of the cylindrical-geometry simulations is formed by 320 cells in the radial direction and 2400 cells in the axial direction in a uniform region, with physical dimensions of
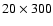
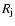 .
An expanded grid with 160 cells in the transversal direction, brings the boundary from
.
An expanded grid with 160 cells in the transversal direction, brings the boundary from
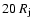 to
to
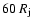 ,
whereas an extended grid in the axial direction, consisting of 480 extra
cells, spans the grid axially from
,
whereas an extended grid in the axial direction, consisting of 480 extra
cells, spans the grid axially from
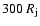 to
to
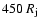 .
The enlargement of the grid is necessary to ensure that
the boundary conditions are sufficiently far from the region of interest, and to avoid numerical reflection of waves in the boundaries affecting our results. The numerical resolution in the uniform grid is thus of 16 cells/
.
The enlargement of the grid is necessary to ensure that
the boundary conditions are sufficiently far from the region of interest, and to avoid numerical reflection of waves in the boundaries affecting our results. The numerical resolution in the uniform grid is thus of 16 cells/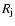 in the radial direction and 8 cells/
in the radial direction and 8 cells/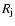 in the axial direction. Outflow boundary
conditions are used on the outer boundaries of the grid, inflow at injection, and reflection at the jet axis
in the cylindrical case. In the simulations, all the physical variables are scaled to the units of the
code, which are the jet radius
in the axial direction. Outflow boundary
conditions are used on the outer boundaries of the grid, inflow at injection, and reflection at the jet axis
in the cylindrical case. In the simulations, all the physical variables are scaled to the units of the
code, which are the jet radius 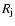 ,
the rest-mass density of the ambient medium
,
the rest-mass density of the ambient medium
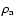 ,
and the speed of light c.
,
and the speed of light c.
The jet is injected in the grid at a distance of
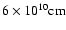 from the compact object, and its initial radius is taken to be
from the compact object, and its initial radius is taken to be
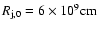 .
The time unit of the code is thus equivalent to 0.2 s, derived using the radius of the jet at injection and the speed of light (
.
The time unit of the code is thus equivalent to 0.2 s, derived using the radius of the jet at injection and the speed of light (
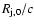 ). The grid covers the distance between
). The grid covers the distance between
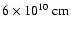 and
and
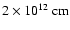 ,
i.e., 60% of
,
i.e., 60% of
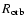 .
The ambient medium, i.e. the stellar wind, is composed of
a gas with thermodynamical properties derived from Sect. 2 (see Table 1). Both the jet and
the ambient medium are considered to be formed by a non-relativistic gas with adiabatic exponent
.
The ambient medium, i.e. the stellar wind, is composed of
a gas with thermodynamical properties derived from Sect. 2 (see Table 1). Both the jet and
the ambient medium are considered to be formed by a non-relativistic gas with adiabatic exponent
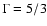 .
.
Table 1:
Parameters of the wind.
Table 2:
Parameters of the jets.
In the simulations, the jets are injected with different
properties. The physical parameters that characterize the three simulations,
are listed in Table 2. The main difference between simulations is the kinetic
luminosity (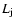 ): for a weak jet (case I) this is
): for a weak jet (case I) this is
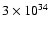 erg s-1;
for a mild jet (case II), it is 1036 erg s-1; and for a powerful jet (case III),
erg s-1;
for a mild jet (case II), it is 1036 erg s-1; and for a powerful jet (case III),
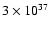 erg s-1. The selection of the jet
power is addressed to show some illustrative cases: the lowest
value, that of case I, is similar to the minimum power required to
power radio emission under reasonable assumptions of the radio
emitter (e.g. for Cygnus X-1, see Heinz 2006); that of
case II is a bit smaller than the power estimates found for
Cygnus X-1 (Gallo et al. 2005), and similar to the
erg s-1. The selection of the jet
power is addressed to show some illustrative cases: the lowest
value, that of case I, is similar to the minimum power required to
power radio emission under reasonable assumptions of the radio
emitter (e.g. for Cygnus X-1, see Heinz 2006); that of
case II is a bit smaller than the power estimates found for
Cygnus X-1 (Gallo et al. 2005), and similar to the
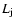 inferred for LS 5039 (Paredes et
al. 2006), and the maximum value, that of case III, is
between the upper limit for the Cygnus X-1
inferred for LS 5039 (Paredes et
al. 2006), and the maximum value, that of case III, is
between the upper limit for the Cygnus X-1 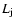 and the
and the
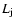 of SS 433 (e.g. Gallo et al. 2005; Marshall
et al. 2002). These jets are evolved until they
have reached distances similar to the binary system size.
of SS 433 (e.g. Gallo et al. 2005; Marshall
et al. 2002). These jets are evolved until they
have reached distances similar to the binary system size.
The velocities of the jets were selected as those of mildly
relativistic flows, with Lorentz factors
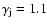 for
case I, and
for
case I, and
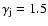 for cases II and III. The jet Mach
numbers are similar in cases I (47.02) and II (51.05), whereas it
is much smaller in case III (9.35). In the latter, the increase in
the jet power is due to an increase in the internal energy of the
jet, keeping the same jet speed as in case II. The jet
temperatures also show this fact, because the jet in case III has a
temperature larger than that of case II by a factor 30. This
allows us to see the influence of changes of the velocity and the
internal energy on the jet evolution.
for cases II and III. The jet Mach
numbers are similar in cases I (47.02) and II (51.05), whereas it
is much smaller in case III (9.35). In the latter, the increase in
the jet power is due to an increase in the internal energy of the
jet, keeping the same jet speed as in case II. The jet
temperatures also show this fact, because the jet in case III has a
temperature larger than that of case II by a factor 30. This
allows us to see the influence of changes of the velocity and the
internal energy on the jet evolution.
In the case of the slab geometry simulations, the grid size is shortened to
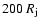 along the jet
axis, and it is doubled in the direction transversal to the jet axis (it extends from
along the jet
axis, and it is doubled in the direction transversal to the jet axis (it extends from
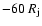 to
to
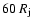 ). The numerical resolution is identical to that used in the cylindrical simulations. The jet
is injected into an ambient medium that mimics the presence of a spherical wind, centered on a star at a
distance
). The numerical resolution is identical to that used in the cylindrical simulations. The jet
is injected into an ambient medium that mimics the presence of a spherical wind, centered on a star at a
distance
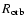 from the compact object, in the orbital plane, with the properties mentioned in
Sect. 2. In this case, the boundary conditions are injection on the side from which the wind is
assumed to originate and on the base of the jet, and outflow in the outer boundaries, on the opposite side of the
grid and at the end of the grid in the axial direction. This kind of simulations was completed for cases I and
II
from the compact object, in the orbital plane, with the properties mentioned in
Sect. 2. In this case, the boundary conditions are injection on the side from which the wind is
assumed to originate and on the base of the jet, and outflow in the outer boundaries, on the opposite side of the
grid and at the end of the grid in the axial direction. This kind of simulations was completed for cases I and
II![[*]](/icons/foot_motif.gif) , since the interaction with the wind was expected to be
relevant to the jet dynamics.
, since the interaction with the wind was expected to be
relevant to the jet dynamics.
 |
Figure 1:
Maps of axial velocity (cm s-1), rest mass density (g cm-3) and pressure (dyn) at the end of the simulation (
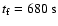 )
of a weak jet in slab geometry, case I. The horizontal and vertical coordinates indicate distances (cm) to the injection point in the numerical grid and the jet axis, respectively. The stellar wind is centered on the position of the primary star, at )
of a weak jet in slab geometry, case I. The horizontal and vertical coordinates indicate distances (cm) to the injection point in the numerical grid and the jet axis, respectively. The stellar wind is centered on the position of the primary star, at
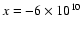 cm and cm and
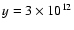 cm in the figure. cm in the figure. |
| Open with DEXTER |
 |
Figure 2:
Maps of rest mass density (g cm-3) and pressure
(dyn) at the end of the simulation (
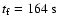 )
of
the mild jet (case II) in cylindric geometry. The horizontal and
vertical coordinates, and the star location, are like in Fig. 1. )
of
the mild jet (case II) in cylindric geometry. The horizontal and
vertical coordinates, and the star location, are like in Fig. 1. |
| Open with DEXTER |
4 Results
Cylindrical jet
The jet in case I, travels the distance between the injection and outer boundary of the numerical grid, in a time of
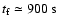 .
The bow shock generated by the injection of the jet in the ambient
medium, moves at a mean speed of
.
The bow shock generated by the injection of the jet in the ambient
medium, moves at a mean speed of
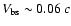 .
The jet generates a high-pressure cocoon that keeps it collimated (see the discussion in the next section). No additional shocks or significant jet perturbations are generated, and the jet propagates well collimated through the wind. We note that the speed of the unshocked jet does not change significantly along the axis. We do not show any image of this simulation due to the lack of remarkable features like shocks. A similar result was obtained in case II. We thus refer the reader to Fig. 2 (see Sect. 4.2).
.
The jet generates a high-pressure cocoon that keeps it collimated (see the discussion in the next section). No additional shocks or significant jet perturbations are generated, and the jet propagates well collimated through the wind. We note that the speed of the unshocked jet does not change significantly along the axis. We do not show any image of this simulation due to the lack of remarkable features like shocks. A similar result was obtained in case II. We thus refer the reader to Fig. 2 (see Sect. 4.2).
Our approximation of a static wind is reviewed critically after results of the slab-jet simulation are presented below. In this simulation, the wind has the appropriate velocity.
Slab jet
A similar simulation was completed in planar coordinates, including the wind motion. The wind emanates from
a point source, at the location of the primary star. Figure 1 shows panels of
axial velocity, rest-mass density and pressure, at the moment that the jet head leaves the grid. The
impact of the wind on the evolution of weak jets is clear from the plots. The bow shock generated by the jet
moves at a speed of 0.05 c, and is deformed by the wind and asymmetry in pressure on each side of the jet. The
wind pushes the jet sideways, and two diagonal shocks, at
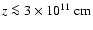 ,
are formed due
to the interaction with the environment, which is in overpressure with respect to the jet flow. After the
first shock, the jet widens and recollimates, starting a new process of expansion after
,
are formed due
to the interaction with the environment, which is in overpressure with respect to the jet flow. After the
first shock, the jet widens and recollimates, starting a new process of expansion after
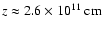 .
The jet is finally disrupted due to the action of the wind, after the jet has lost some
of its initial inertia due to the previous internal shocks. A strong shock is generated at the disruption
point at
.
The jet is finally disrupted due to the action of the wind, after the jet has lost some
of its initial inertia due to the previous internal shocks. A strong shock is generated at the disruption
point at
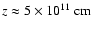 .
Beyond this point, the jet is diverted significantly, and some of the fast material, in the remaining outflow, leaves the regular numerical grid sideways at
.
Beyond this point, the jet is diverted significantly, and some of the fast material, in the remaining outflow, leaves the regular numerical grid sideways at
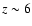 -
-
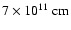 .
This simulation illustrates the case of a frustrated jet that has become a decollimated, slow outflow due to the effect of the wind.
.
This simulation illustrates the case of a frustrated jet that has become a decollimated, slow outflow due to the effect of the wind.
Cylindrical jet
The simulation of case II in cylindrical coordinates is similar to that of case I. Figure 2
shows the rest-mass density and pressure of the jet, as its head reaches the end of the grid.
Some internal shocks are produced by the slight overpressure of the jet, with respect to the cocoon at
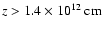 :
this is responsible for the main differences between the results for this case and of case I. Before
:
this is responsible for the main differences between the results for this case and of case I. Before
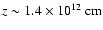 ,
the
jet is collimated efficiently by the high-pressure cocoon. The bow-shock propagates at
,
the
jet is collimated efficiently by the high-pressure cocoon. The bow-shock propagates at
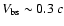 ,
and is therefore significantly faster than in the previous case. The bow-shock introduces a jump in
pressure of 108 with respect to the cold wind. The internal, conical shocks observed in the jet itself,
show jumps in pressure of 102-104, although there are no strong changes of axial velocity with respect
to the unshocked jet material. This implies that not much kinetic energy could be transferred to non-thermal particles via these shocks.
,
and is therefore significantly faster than in the previous case. The bow-shock introduces a jump in
pressure of 108 with respect to the cold wind. The internal, conical shocks observed in the jet itself,
show jumps in pressure of 102-104, although there are no strong changes of axial velocity with respect
to the unshocked jet material. This implies that not much kinetic energy could be transferred to non-thermal particles via these shocks.
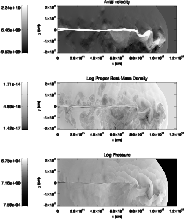 |
Figure 3:
Maps of axial velocity (cm s-1), rest mass density
(g cm-3) and pressure (dyn) at the end of the simulation
(
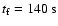 )
of a mild jet in slab geometry, case II.
The horizontal and
vertical coordinates, and the star location, are like in Fig. 1. )
of a mild jet in slab geometry, case II.
The horizontal and
vertical coordinates, and the star location, are like in Fig. 1. |
| Open with DEXTER |
Slab jet
In case II, a slab simulation was performed, accounting for the velocity of the stellar wind from the
primary star. Figure 3 shows several maps of physical magnitudes from the simulation. The
bow-shock is faster than for the slab case I (
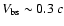 ). Several diagonal shocks are
formed due to interaction with the wind, in the direction of the jet trajectory.
The jet is in under pressure with respect to the ambient medium, which generates an initial collimation. The pinching triggered by the first collimation shock and the subsequent expansion of the jet, and the thrust exerted by the wind on the jet, together, generate nonlinear structures on the jet. In this case, the jet is finally disrupted at
). Several diagonal shocks are
formed due to interaction with the wind, in the direction of the jet trajectory.
The jet is in under pressure with respect to the ambient medium, which generates an initial collimation. The pinching triggered by the first collimation shock and the subsequent expansion of the jet, and the thrust exerted by the wind on the jet, together, generate nonlinear structures on the jet. In this case, the jet is finally disrupted at
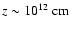 (see Fig. 3). The pattern of shocks at the disruption region is similar to that observed in Fig. 1. These results show that the jet can be disrupted by the stellar-wind ram pressure even for intermediate kinetic luminosities.
(see Fig. 3). The pattern of shocks at the disruption region is similar to that observed in Fig. 1. These results show that the jet can be disrupted by the stellar-wind ram pressure even for intermediate kinetic luminosities.
The simulation of a powerful jet (
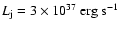 )
produces results that are significantly different from those of the previous cylindrical simulations. Figure 4 displays maps of rest-mass density, pressure and axial velocity, as the bow-shock reaches the limit of the regular grid. The bow-shock propagates at
)
produces results that are significantly different from those of the previous cylindrical simulations. Figure 4 displays maps of rest-mass density, pressure and axial velocity, as the bow-shock reaches the limit of the regular grid. The bow-shock propagates at
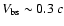 .
This
.
This
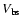 is the same as in case II because part of the larger initial thrust of case III jet is invested in lateral expansion and
heating. The latter happens due to, in contrast to
the previous cases, a strong recollimation shock formed at
is the same as in case II because part of the larger initial thrust of case III jet is invested in lateral expansion and
heating. The latter happens due to, in contrast to
the previous cases, a strong recollimation shock formed at
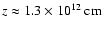 .
This
shock is formed due to the initial overpressure of the jet with respect to the cocoon.
.
This
shock is formed due to the initial overpressure of the jet with respect to the cocoon.
The formation of such shocks is dependent on the relation between pressures in the cocoon and jet.
The jump in pressure generated on the jet axis is of the order of 104. In a second stage of
jet evolution, when the bow-shock is away from the studied region and the cocoon is substituted by the
stellar wind, recollimation shocks can change their position and properties. However, as is shown in the next
section, these shocks may still be present. Such shocks, if sufficiently strong, can trigger pinching of the jet, as
observed in Fig. 4, which, in turn, can lead to mass load of ambient gas and jet disruption
(Perucho & Martí 2007). This explains the importance of such recollimation shocks, not only in terms of particle acceleration and subsequent radiation, but also jet dynamics.
 |
Figure 4:
Maps of axial velocity (cm/s), rest mass density
(g cm-3) and pressure (dyn) at the end of the simulation
(
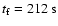 ), for a powerful jet (case III). The horizontal and
vertical coordinates, and the star location, are like in Fig. 1. ), for a powerful jet (case III). The horizontal and
vertical coordinates, and the star location, are like in Fig. 1. |
| Open with DEXTER |
5 Discussion
5.1 On the formation of shocks in the studied region
We see that two different types of shock may form: reverse/bow shocks, which cross the region of constant density (within 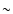
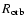 )
at a fraction of c on timescales
)
at a fraction of c on timescales
 ;
and recollimation shocks, generated by the
interaction of the jet with its environment, the cocoon or the stellar wind itself. Unlike the reverse/bow
shock, which appears naturally as shown by the simulations, the formation of recollimation shocks
depends on the complex jet/medium pressure balance, and deserves further analysis. The possibility that they
arise is discussed in this section in terms of the jet properties and their environments.
;
and recollimation shocks, generated by the
interaction of the jet with its environment, the cocoon or the stellar wind itself. Unlike the reverse/bow
shock, which appears naturally as shown by the simulations, the formation of recollimation shocks
depends on the complex jet/medium pressure balance, and deserves further analysis. The possibility that they
arise is discussed in this section in terms of the jet properties and their environments.
Recollimation shocks form when an initially-overpressured jet expands and reaches a lower pressure than that
of its environment. In order to know whether a jet generates such a shock, and at which distance, the change
of jet pressure with distance is needed to be compared with that of the ambient medium. In an adiabatic
expansion, the condition
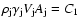 holds, where C1 is a
constant and
holds, where C1 is a
constant and 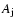 is the jet cross section. In our simulations, the jet velocity and Lorentz factor
are basically constant, implying
is the jet cross section. In our simulations, the jet velocity and Lorentz factor
are basically constant, implying
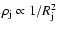 ,
which, for a conical jet, transforms
into
,
which, for a conical jet, transforms
into
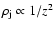 ,
i.e., the density of the jet decreases as the square of the distance to
the source. It is also known that the jet pressure (
,
i.e., the density of the jet decreases as the square of the distance to
the source. It is also known that the jet pressure (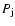 )
and density satisfy the relation
)
and density satisfy the relation
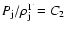 ,
where
,
where 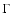 is the adiabatic exponent and C2 a constant. Thus,
is the adiabatic exponent and C2 a constant. Thus,
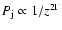 ,
which implies (
,
which implies (
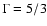 ):
):
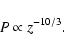 |
(1) |
A minimum distance for the position of a recollimation shock can be given as the place where the pressure in
the jet is the same as the pressure of the ambient medium (
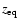 )
)![[*]](/icons/foot_motif.gif) . We can express this distance in terms of the pressure of the jet, at a reference position z0 (
. We can express this distance in terms of the pressure of the jet, at a reference position z0 (
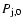 ), which will be taken to be the injection point in the grid, and the pressure of the ambient medium (
), which will be taken to be the injection point in the grid, and the pressure of the ambient medium (
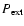 ). From Eq. (1):
). From Eq. (1):
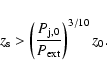 |
(2) |
Using these results, we can determine limits on the pressure (and temperature) of the jets, which are suitable to develop recollimation shocks. We fix the right-hand side of the inequality in Eq. (2) to be 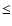
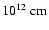 ,
a safe estimate for
,
a safe estimate for
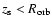 ,
because we require maximal wind/jet interaction. We can then estimate the initial overpressure of the jet that results in a recollimation shock, inside a distance
,
because we require maximal wind/jet interaction. We can then estimate the initial overpressure of the jet that results in a recollimation shock, inside a distance
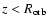 .
If z0 is
taken as the injection point, i.e.,
.
If z0 is
taken as the injection point, i.e.,
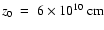 ,
we obtain:
,
we obtain:
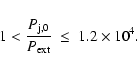 |
(3) |
Equation (3) can be written in terms of the jet temperature (
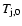 )
and the jet density (
)
and the jet density (
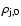 )
at the injection point:
)
at the injection point:
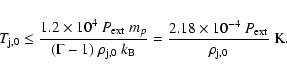 |
(4) |
Both cylindrical and slab simulations show that, initially, the jets are embedded in their cocoons. However,
as shown by the slab-jet simulations, the stellar wind quickly starts to affect dynamically the bow-shock
and the jet itself. As soon as the jet head has left the binary system, shocked wind will substitute cocoon
material. We note that the wind properties change via shocking with the jet. In this case, the
relative pressure of the jet with respectto the ambient would also change, at least on the side where the
wind impacts. This asymmetry in the ambient medium can give rise to asymmetric shocks, generated on one side
of the jet and propagating diagonally through it, as observed in the slab simulations (Figs. 1
and 3). In short, these two different scenarios, i.e. interaction with the cocoon and the wind, have to be taken into account.
When the pressure of the ambient medium corresponds to that of the
cocoon, the following equation (Begelman & Cioffi 1989) estimates the pressure of the latter (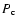 )
as a function of the jet kinetic power, advance speed of the bow shock, and the surface of interaction between the bow shock and the ambient medium (
)
as a function of the jet kinetic power, advance speed of the bow shock, and the surface of interaction between the bow shock and the ambient medium (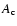 ):
):
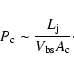 |
(5) |
When the external pressure is exerted by the wind on the jet, it
can be computed by assuming that the density of the shocked wind
is four times the original density of the wind, based on the
Rankine-Hugoniot jump conditions, and that most of the kinetic
energy of the wind is thermalized and, thus, its internal energy
is similar to the original kinetic one.
Jet/Cocoon interaction
For a typical jet with kinetic power
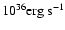 ,
bow-shock advance speed 0.1 c, and bow-shock radius of about
,
bow-shock advance speed 0.1 c, and bow-shock radius of about
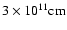 ,
the cocoon pressure is
,
the cocoon pressure is
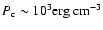 .
Then, if the density in the jet at
injection (
.
Then, if the density in the jet at
injection (
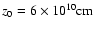 )
is
)
is
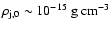 ,
the temperature must be:
,
the temperature must be:
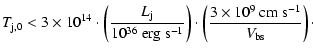 |
|
|
|
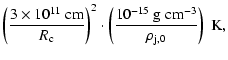 |
|
|
(6) |
which is fulfilled accounting for the fact that the jet must be supersonic (i.e.
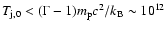 K).
K).
The pressure at z0 can be set to be larger than that of the ambient medium in order to allow for the initial expansion of the jet (see Eq. (3)). A lower limit on the temperature of the jet
can be fixed:
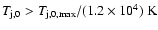 .
In the cylindrical simulations of cases I and II,
the temperatures of the jets are below this limit (see
Table 2), so that they do not generate recollimation shocks
(see Fig. 2). The location of the injection point in the numerical grid, z0, is, however, arbitrary. At some point closer to the compact object, the pressure inside the jet will become larger than inside the cocoon. This is implied by the fact that the jet pressure increases towards the compact object such as
.
In the cylindrical simulations of cases I and II,
the temperatures of the jets are below this limit (see
Table 2), so that they do not generate recollimation shocks
(see Fig. 2). The location of the injection point in the numerical grid, z0, is, however, arbitrary. At some point closer to the compact object, the pressure inside the jet will become larger than inside the cocoon. This is implied by the fact that the jet pressure increases towards the compact object such as
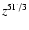 .
The conditions for the generation of a recollimation shock in the simulations, would then exist.
.
The conditions for the generation of a recollimation shock in the simulations, would then exist.
Jet/wind interaction
In the case of a jet interacting with the stellar wind, the
pressure is derived as explained above to obtain
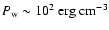 .
Using the jet density given above for
the jet,
.
Using the jet density given above for
the jet,
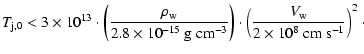 |
|
|
|
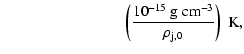 |
|
|
(7) |
which is achieved by taking into account that the jet must be supersonic.
We conclude that the presence of standing shocks within the binary
system, is probable within our prediction limits.
As discussed above, strong shocks take place in the jet head, i.e. the bow/reverse shocks, and in the
jet/cocoon contact surface, i.e. the recollimation shocks. In practice, the capability of the jet head structures to
produce non-thermal emission, is linked to the time that they remain within the system,
because the shock-energy transfer diminishes further out, as the wind density rapidly decreases.
In addition, quasi-permanent recollimation shocks between the jet and the stellar wind can also occur, as noted in Sect. 5.1. Since all these shocks are strong, and we know approximately the speed of the shocks from the simulations, we can estimate the particle-acceleration efficiency. In the following, we compute the maximum energy, and the emission spectral-energy-distribution of particles accelerated under shock conditions, similar to those shown by the simulations.
Particle acceleration
As a first order approach, and provided that the shock Lorentz
factors are 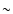 1, we compute the particle acceleration rate in
the context of the non-relativistic (first-order Fermi) diffusive shock acceleration
mechanism, in the tes-particle approximation,
one-dimensional case, and with a dynamically negligible magnetic field.
This mechanism typically predicts, for strong shocks, a power-law particle
distribution of index -2 (e.g. Drury 1983). The
acceleration rate in cgs units can be computed using:
1, we compute the particle acceleration rate in
the context of the non-relativistic (first-order Fermi) diffusive shock acceleration
mechanism, in the tes-particle approximation,
one-dimensional case, and with a dynamically negligible magnetic field.
This mechanism typically predicts, for strong shocks, a power-law particle
distribution of index -2 (e.g. Drury 1983). The
acceleration rate in cgs units can be computed using:
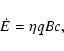 |
(8) |
where 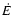 is the particle energy gain per time unit, q the
particle charge, B the magnetic field in the accelerator, and
is the particle energy gain per time unit, q the
particle charge, B the magnetic field in the accelerator, and
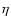 the acceleration efficiency coefficient, which can be
calculated using the formula (e.g. Protheroe 1999):
the acceleration efficiency coefficient, which can be
calculated using the formula (e.g. Protheroe 1999):
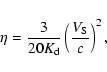 |
(9) |
for a parallel magnetic field, where 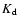 is proportional
to the diffusion coefficient (
is proportional
to the diffusion coefficient (
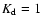 corresponds to the
Bohm regime), and
corresponds to the
Bohm regime), and 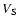 is the speed of the shock in the
upstream reference-frame. The value of the second parameter can be
determined using the results of the simulations, allowing
is the speed of the shock in the
upstream reference-frame. The value of the second parameter can be
determined using the results of the simulations, allowing 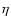 to be estimated. For
the reverse and forward shocks, we assume velocities that are typical for when the jet
head is within the binary system, which implies a value
to be estimated. For
the reverse and forward shocks, we assume velocities that are typical for when the jet
head is within the binary system, which implies a value
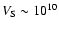 cm s-1.
In case of recollimation
shocks, as shown in Fig. 4, velocity jumps could reach
similar values. In the Bohm diffusion case,
cm s-1.
In case of recollimation
shocks, as shown in Fig. 4, velocity jumps could reach
similar values. In the Bohm diffusion case,
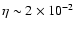 .
We recall that the recollimation shock shown in Fig. 4
is related to the cocoon, although such structure could also be produced by
interaction of the jet lateral surface with the stellar wind.
.
We recall that the recollimation shock shown in Fig. 4
is related to the cocoon, although such structure could also be produced by
interaction of the jet lateral surface with the stellar wind.
Concerning the B-strength, the hydrodynamical assumption
imposes an energy-density for the adopted magnetic field
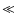 the (internal plus kinetic) matter energy-density.
Thus, the value assumed for the B-field must be well below that required for equipartition with jet matter. B should be
the (internal plus kinetic) matter energy-density.
Thus, the value assumed for the B-field must be well below that required for equipartition with jet matter. B should be 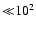 -104 G, depending on the jet power and shock properties. This values stand for those of the (internal plus kinetic) matter energy-density in shocked material, as provided by simulations, which ranges in value between
-104 G, depending on the jet power and shock properties. This values stand for those of the (internal plus kinetic) matter energy-density in shocked material, as provided by simulations, which ranges in value between
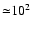 -106 erg cm-3.
-106 erg cm-3.
We can compute the maximum energy of the particles equating Eq. (8) to the particle energy losses.
In the case of electrons, when the synchrotron energy-losses are dominant, the maximum particle energy can be derived using the equation:
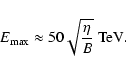 |
(10) |
For inverse Compton (IC) losses in the Thomson regime (
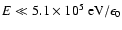 ;
;
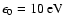 ), the maximum particle energy, after taking account of stellar radiation density in the jet,
), the maximum particle energy, after taking account of stellar radiation density in the jet,
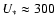 erg cm-3, can be estimated using the expression:
erg cm-3, can be estimated using the expression:
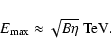 |
(11) |
In the Klein-Nishina (KN) regime (
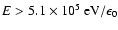 )
(Khangulyan, et al. 2008), this expression is replaced by the following expression,
)
(Khangulyan, et al. 2008), this expression is replaced by the following expression,
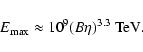 |
(12) |
 is taken to be the lowest value of all shown
is taken to be the lowest value of all shown
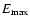 .
For
.
For
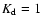 ,
,
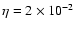 ,
synchrotron energy losses are dominant for
,
synchrotron energy losses are dominant for 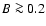 G.
G.
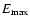 can reach 1 TeV for
B=50 G, and 10 TeV for B=0.4 G.
can reach 1 TeV for
B=50 G, and 10 TeV for B=0.4 G.
In the case of inefficient energy losses, as it commonly happens for protons, the size
of the accelerator, approximated to be the diameter of the jet
at the shock location (
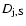 ), provides an upper-limit
to the maximum particle energy, when equated to the particle mean-free-path (in our case, the gyroradius):
), provides an upper-limit
to the maximum particle energy, when equated to the particle mean-free-path (in our case, the gyroradius):
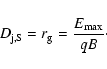 |
(13) |
Higher energy particles escape the accelerator because they cannot
be confined by the magnetic field. For
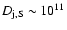 cm,
cm,
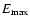 may reach
may reach 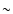 103 TeV.
103 TeV.
Characterizing the particle energy distribution
As soon as electrons are injected into the emitter, they lose energy via synchrotron and IC processes.
Relativistic Bremsstrahlung, and ionization losses of electrons, are negligible due respectively to the long timescales, and the high ionization degree of the shocked material. Protons lose energy mainly via
proton-proton collisions, although in general, the efficiency of this process is small. All particles are convected, on timescales that are
shorter than the radiation timescale for the electrons with the higher energies, and
protons of any energy. The convection timescale can be estimated using
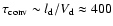 s, where
s, where
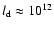 cm and
cm and
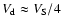 (from the strong shock-jump conditions), are the length of the downstream region and the convection velocity, respectively (as derived from the simulations).
(from the strong shock-jump conditions), are the length of the downstream region and the convection velocity, respectively (as derived from the simulations).
To respect the restriction of both a cold jet and test particle shocks, we
assume that the non-thermal particle energy-density is smaller than the
thermal energy-density, and fix the ratio between these energy-densities
to be 0.1 close to the shock surface. Taking into account the above
assumption, and the fact that downstream, thermal particles carry a power
similar to that of the jet, the injected luminosity in the form of non-thermal
particles is 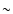
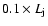 .
.
5.2.2 Radiation
Leptonic emission
We compute the SED of the synchrotron and IC components, adopting a homogeneous model for the emitting region. Because we are unable to determine the magnetic field, two B-values, rendering different but representative situations, have been adopted: B=0.4 and 50 G. The first value yields a dominant, high-energy IC component, reaching energies well above 1 TeV. The second value corresponds to a high magnetic field, in the limits of the hydrodynamical
approximation. This latter case implies dominant synchrotron radiation.
To compute the impact of synchrotron self-absorption,
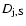 ,
has been adopted as the
width of the emitting region.
,
has been adopted as the
width of the emitting region.
For B=50 G,
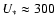 erg cm-3, and
erg cm-3, and
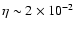 ,
synchrotron energy losses limit
,
synchrotron energy losses limit
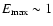 TeV, and the energy in non-thermal particles are radiated with similar luminosities via synchrotron and IC channels due to comparable timescales. Above the injection energy, the (cooled) particle spectrum follows a power-law of exponent -2 up to the energy at which convection and radiative timescales become equal, around 1 GeV.
In the one-zone approximation, electrons below 1 GeV escape the emitter before cooling
completely, although they could still produce radiation outside the binary system.
Above this energy, the particle spectrum becomes radiatively cooled
with index -3.
TeV, and the energy in non-thermal particles are radiated with similar luminosities via synchrotron and IC channels due to comparable timescales. Above the injection energy, the (cooled) particle spectrum follows a power-law of exponent -2 up to the energy at which convection and radiative timescales become equal, around 1 GeV.
In the one-zone approximation, electrons below 1 GeV escape the emitter before cooling
completely, although they could still produce radiation outside the binary system.
Above this energy, the particle spectrum becomes radiatively cooled
with index -3.
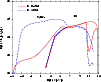 |
Figure 5:
Typical
computed SED of the synchrotron and IC emission produced in a
shock region. We adopt B=0.4 (solid line) and 50 G (long-dashed
line). The production (thin line) and the photon-photon absorbed (thick line)
SED cases are presented. |
| Open with DEXTER |
We have also explored the case of B=0.4 G, for which the maximum energy reaches around 10 TeV. In this case, low magnetic fields render a synchrotron component with luminosities well below the IC ones and a hard particle spectrum at the highest energies due to the impact of KN IC losses, which harden the particle energy distribution when dominant. In contrast, synchrotron and Thomson IC losses, steepen the spectrum; see Khangulyan et al. (2008) for a thorough discussion). In Fig. 5 we show the corresponding SED for these two cases. The total radiated luminosity is 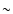 1035 erg s-1, which is shared between the synchrotron and IC components, with the relation proportions depending on B. We note that the age of the source producing the SED, presented in Fig. 5, was fixed to be the typical lifetime of the shocks (
1035 erg s-1, which is shared between the synchrotron and IC components, with the relation proportions depending on B. We note that the age of the source producing the SED, presented in Fig. 5, was fixed to be the typical lifetime of the shocks (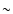
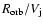 ).
).
We note that for B=50 G, when synchrotron emission is high, the synchrotron self-absorption frequency is 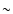 60 GHz when assuming a low energy cutoff at
60 GHz when assuming a low energy cutoff at 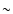
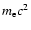 ,
effectively yielding little
radiation in the radio band. If the cutoff were at higher energies, electrons would radiate with a
monoenergetic particle distribution in the radio band for a such magnetic field, rendering a hard
SED (of exponent 4/3) and little radiation in the radio band. In this scenario, it is unclear whether radio emission from the accelerator/emitter would be detectable. Electron cooling, and transport within the flow bulk, can yield extended synchrotron radiation in the radio band, in cases where radio-emitting electrons are carried to (farther) regions of appropriate B.
,
effectively yielding little
radiation in the radio band. If the cutoff were at higher energies, electrons would radiate with a
monoenergetic particle distribution in the radio band for a such magnetic field, rendering a hard
SED (of exponent 4/3) and little radiation in the radio band. In this scenario, it is unclear whether radio emission from the accelerator/emitter would be detectable. Electron cooling, and transport within the flow bulk, can yield extended synchrotron radiation in the radio band, in cases where radio-emitting electrons are carried to (farther) regions of appropriate B.
IC scattering and photon-photon absorption in the stellar radiation field have been considered
using angular-averaged cross-sections. Since we do not apply this model to any specific object at present,
we do not account for the geometry of these interactions. Accounting for the geometry of photon-photon absorption, the latter can have less impact for certain accelerator/emitter located locations (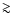 1012 cm) and orbital phases. This would improve the probability of detection for this kind of sources in the TeV range. We refer to Khangulyan et al. (2008) for an exhaustive discussion of IC and photon-photon absorption angular effects. Secondary pairs produced in the system may also be relevant from the radiative point of view (see Khangulyan et al. 2008; Bosch-Ramon, et al. 2008).
1012 cm) and orbital phases. This would improve the probability of detection for this kind of sources in the TeV range. We refer to Khangulyan et al. (2008) for an exhaustive discussion of IC and photon-photon absorption angular effects. Secondary pairs produced in the system may also be relevant from the radiative point of view (see Khangulyan et al. 2008; Bosch-Ramon, et al. 2008).
Hadronic emission
In the case of protons, the densities in the jet are, in general, low and proton-proton energy losses![[*]](/icons/foot_motif.gif) are not important,
yielding a small amount of
are not important,
yielding a small amount of 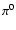 -decay gamma-rays. The most suitable case occurs when the proton escape velocity is low and density high in the region. This can occur in the
shell region. Recollimation shocks can lead to jet-density enhancement and low-convection velocities. The mixing of jet and stellar-wind material can also lead
to high-density regions that suffer the impact of relativistic protons.
-decay gamma-rays. The most suitable case occurs when the proton escape velocity is low and density high in the region. This can occur in the
shell region. Recollimation shocks can lead to jet-density enhancement and low-convection velocities. The mixing of jet and stellar-wind material can also lead
to high-density regions that suffer the impact of relativistic protons.
In our context, gamma-ray fluxes
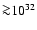 erg s-1 would be expected from proton-proton interactions if
erg s-1 would be expected from proton-proton interactions if
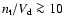 (i.e.
(i.e.
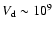 cm s-1 implies
cm s-1 implies
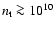 cm-3) for
cm-3) for
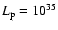 erg s-1, where
erg s-1, where 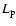 and
and 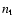 are the relativistic proton
luminosity and the target density, respectively. Although the efficiency of hadronic processes is relatively low for the production of gamma-rays, the interaction of
powerful jets and dense winds could indeed lead to the generation of detectable TeV emission. In these proton-proton interactions, neutrinos (e.g. Romero et al.
2005; Aharonian et al. 2006a; Christiansen, et al. 2006) and secondary electron-positron pairs would also be
produced, with luminosities similar to the gamma-ray ones. The radiation of secondary pairs would be relevant mainly at low energies (e.g. Orellana et al. 2007).
are the relativistic proton
luminosity and the target density, respectively. Although the efficiency of hadronic processes is relatively low for the production of gamma-rays, the interaction of
powerful jets and dense winds could indeed lead to the generation of detectable TeV emission. In these proton-proton interactions, neutrinos (e.g. Romero et al.
2005; Aharonian et al. 2006a; Christiansen, et al. 2006) and secondary electron-positron pairs would also be
produced, with luminosities similar to the gamma-ray ones. The radiation of secondary pairs would be relevant mainly at low energies (e.g. Orellana et al. 2007).
Variability
Initially, the forward
and reverse shocks can produce non-thermal radiating particles as long as the jet ttavels through the system, with timescales 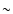
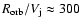 s. In the case where recollimation shocks in the jet, due to cocoon material pressure, form, particle acceleration lasts as long as the cocoon pressure is higher than the pressure of the jet.
s. In the case where recollimation shocks in the jet, due to cocoon material pressure, form, particle acceleration lasts as long as the cocoon pressure is higher than the pressure of the jet.
Because the cocoon pressure is roughly proportional to 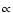 1/t2, as soon as the jet head is outside the binary system, cocoon recollimation-shocks, inside the system region, should not last much longer than
1/t2, as soon as the jet head is outside the binary system, cocoon recollimation-shocks, inside the system region, should not last much longer than 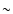
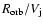 .
All such events should appear as short bursts of X-rays, and possibly also GeV-TeV and radio band emission.
.
All such events should appear as short bursts of X-rays, and possibly also GeV-TeV and radio band emission.
Irregular jet-ejection on timescales longer than
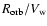 (the wind replenishment timescale), in a massive system, could lead to high-energy, recurrent flares, as observed for Cygnus X-1 (Albert et al. 2007), and in some orbital phases of LS 5039 (Aharonian et al. 2006b), and LS I +61 303 (Rico 2007). The observed hour timescale variability associated with these flares, could be explained by a new ejection
facing stellar-wind, replenished during a previous jet inactivity period of similar or longer duration. Eventual recollimation shocks due to wind ram pressure, instead of cocoon
pressure, could stand as long as the jet injection lasts and the wind properties are relatively smooth. The variability of emission in this phase would be likely dominated by
jet injection fluctuations or wind inhomogeneities, with associated timescales
(the wind replenishment timescale), in a massive system, could lead to high-energy, recurrent flares, as observed for Cygnus X-1 (Albert et al. 2007), and in some orbital phases of LS 5039 (Aharonian et al. 2006b), and LS I +61 303 (Rico 2007). The observed hour timescale variability associated with these flares, could be explained by a new ejection
facing stellar-wind, replenished during a previous jet inactivity period of similar or longer duration. Eventual recollimation shocks due to wind ram pressure, instead of cocoon
pressure, could stand as long as the jet injection lasts and the wind properties are relatively smooth. The variability of emission in this phase would be likely dominated by
jet injection fluctuations or wind inhomogeneities, with associated timescales 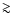
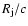 .
.
As a test for jet bending, numerical simulations in slab geometry have been performed. It has been shown that the wind can efficiently transport shell and cocoon
material sidewards. In the same way, the wind can significantly deflect the supersonic jet itself via transferring of enough lateral momentum. We have shown that even
in the case of a jet with kinetic power
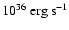 ,
the wind appears to be able to disrupt the flow. Such a disrupted jet can look like a radio structure
changing its morphology along the orbit, such as that found by Dhawan et al. (2006) in LS I +61 303, and interpreted by these authors as the collision between the
star and pulsar winds. This interpretation would be challenged by the morphologies obtained from hydrodynamical simulations by Romero et al. (2007b) and Bogovalov et al. (2007).
,
the wind appears to be able to disrupt the flow. Such a disrupted jet can look like a radio structure
changing its morphology along the orbit, such as that found by Dhawan et al. (2006) in LS I +61 303, and interpreted by these authors as the collision between the
star and pulsar winds. This interpretation would be challenged by the morphologies obtained from hydrodynamical simulations by Romero et al. (2007b) and Bogovalov et al. (2007).
The simulations and calculations presented here show that the recollimation shocks can, on the one hand, develop easily inside the binary-system region and, on the other
hand, influence significantly the evolution of the jet.
As already stated, these shocks can both generate radiation efficiently and favor jet mass-loading and deceleration via pinching, which makes wind-deflection easier. These shocks have already been reported in a work by Peter & Eichler (1995), which studied the collimation of jets by the inertia of the ambient medium. In the maps shown in that work, shocks similar to those observed in Fig. 4, were detected.
The jet parameters that we have adopted produce small growth-rates of Kelvin-Helmholtz instability, mainly in the cases II and III. Therefore, disruption due to the growth of such an instability, inside the region of interaction with the wind, is not expected. Otherwise, our simulations show that the jets develop non-linear
structures due to their initial overpressure, thus the growth of linear instabilities is not expected either. In short, the stability of the jet depends mainly on its inertia, in contrast to the inertia of the wind, and on the strength of the recollimation shocks (Perucho et al. 2005,2007).
6 Summary
The crossing of a hydrodynamical supersonic jet, through the inner
parts of an HMMQ, renders strong forward/reverse and
recollimation shocks. These shocks produce strong pressure and
density enhancements, and some jet deceleration. The impact of
the wind ram pressure on weak jets can prevent the formation of
larger scale jets because of strong bending and jet disruption. We
estimate that this occurs for jet kinetic luminosities below
1036 erg s-1 for the strong winds of O-type stars.
If efficient leptonic and/or hadronic particle acceleration takes place, the
presence of photon, matter and magnetic fields, will yield significant amounts of
radiation from radio to very high energies.
On the one hand, leptons would radiate mainly via synchrotron and IC
processes. On the other hand, protons could interact with shell
nuclei producing gamma-rays via neutral pion decay, and
electron-positron pairs and neutrinos via decay of charged pions.
Secondary pairs may also yield some amount of low-energy
radiation. In addition, the complexity of the wind/jet
interactions leads to a plethora of variability timescales of the
emission that could be more relevant than any intrinsic jet
fluctuation.
Further three-dimensional numerical simulations including more
realistic implementations of the problem, magnetic fields, and
radiative processes, should improve our understanding of the
physics of jets in microquasars.
Acknowledgements
The authors benefited from valuable discussions with D.
Khangulyan. The authors thank G. E. Romero for a thorough reading of the manuscript.
V.B-R. acknowledges support
by DGI of MEC under grant AYA2007-68034-C03-01 and FEDER funds.
V.B-R. gratefully acknowledges support from the Alexander von
Humboldt Foundation. This work was supported in part by the
Spanish Dirección General de Enseñanza Superior under
grant AYA2004-08067-C03-01. M.P. acknowledges support from a
postdoctoral fellowship of the Generalitat Valenciana
(Beca Postdoctoral d'Excel lència).
lència).
- Aharonian, F.
A., & Atoyan, A. M. 1996, SSRv, 75, 357 [NASA ADS]
(In the text)
- Aharonian, F.
A., & Atoyan, A. M. 1996, NewAR, 42, 579 [NASA ADS] [CrossRef]
(In the text)
- Aharonian,
F. A., Anchordoqui, L. A., Khangulyan, D., & Montaruli, T.
2006a, J. Phys. Conf. Ser., 39, 408 [NASA ADS] [CrossRef]
(In the text)
- Aharonian,
F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006b, A&A,
460, 743 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Albert, J., Aliu,
E., Anderhub, H., et al. 2007, ApJ, 665, L51 [NASA ADS] [CrossRef]
(In the text)
- Aloy, M. A.,
Ibáñez, J. M., Martí, J. M., Gómez, J. L.,
& Müller, E. 1999, ApJ, 523, L125 [NASA ADS] [CrossRef]
(In the text)
- Araudo, A. T.,
Romero, G. E., Bosch-Ramon, V., & Paredes, J. M. 2007, A&A,
476, 1289 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Begelman, M. C., &
Cioffi, D. F. 1989, ApJ, 345, L21 [NASA ADS] [CrossRef]
(In the text)
- Begelman, M. C.,
Blandford, M. D., & Rees, M. J. 1984, RvMP, 56, 225 [NASA ADS]
(In the text)
- Bell, A. R. 1978 MNRAS,
182, 443
- Bogovalov, S.
V., Khangulyan, D., Koldoba, A. V., Ustyugova, G. V., &
Aharonian F. A. 2007, MNRAS, submitted
[arXiv:astro-ph/0710.1961]
(In the text)
- Bosch-Ramon, V.,
Aharonian, F. A., & Paredes, J. M. 2005, A&A, 432, 609 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bosch-Ramon, V.,
khnagulyan, D., & Aharonian, F. A. 2008, A&A, 482, 397 [CrossRef] [EDP Sciences]
(In the text)
- Bykov, A. M., &
Fleishman, G. D. 1992, MNRAS, 255, 269 [NASA ADS]
(In the text)
- Casares, J., Ribó,
M., Ribas, I., Paredes, J. M., Martí, J., & Herrero, A.
2005, MNRAS, 364, 899 [NASA ADS] [CrossRef]
(In the text)
- Corbel, S., Fender,
R. P., & Tzioumis, A. K., et al. 2002, Science, 298, 196 [NASA ADS] [CrossRef]
(In the text)
- Corbel, S., Kaaret,
P., & Fender, R. P. 2005, et al. ApJ, 632, 504
(In the text)
-
Christiansen, H. R., Orellana, M., & Romero, G. E. 2006, Phys.
Rev. D, 73, 3012 [CrossRef]
(In the text)
- Derishev, E.
V., Aharonian, F. A., Kocharovsky, V. V., & Kocharovsky, Vl. V.
2003, Phys. Rev. D, 68, 3003 [NASA ADS] [CrossRef]
(In the text)
- Dhawan, V.,
Mioduszewski, A., & Rupen, M. 2006, in Proc. of the VI
Microquasar Workshop, Como-2006
(In the text)
- Drury, L. 1983, RPPh,
46, 973 [NASA ADS]
(In the text)
- Fermi, E. 1949, Phys.
Rev., 75, 1169 [NASA ADS] [CrossRef]
(In the text)
- Gabici, S., &
Blasi, P. 2004, APh, 20, 579 [NASA ADS]
- Gallo, E., Fender,
R., & Kaiser, C., et al. 2005, Nature, 436, 819 [NASA ADS] [CrossRef]
(In the text)
- Gies, D. R. & Bolton,
C. T. 1986, ApJ, 304, 371 [NASA ADS] [CrossRef]
(In the text)
- Gómez, J. L.
2001, Ap&SS, 276, 281 [CrossRef]
(In the text)
- Hardee, P. E.,
& Hughes, P. A. 2003, ApJ, 583, 116 [NASA ADS] [CrossRef]
(In the text)
- Heindl, W. A.,
Tomsick, J. A., Wijnands, R., & Smith, D. M. 2003, ApJ, 588,
L97 [NASA ADS] [CrossRef]
(In the text)
- Heinz, S. 2002,
A&A, 388, L40 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Heinz, S. 2006, ApJ,
636, 316 [NASA ADS] [CrossRef]
(In the text)
- Heinz, S., &
Sunyaev, R. 2002, A&A, 390, 751 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kang, H., Ryu, D.,
& Jones, T. W. 1996, ApJ, 56, 422 [NASA ADS] [CrossRef]
(In the text)
- Khangulyan,
D., Aharonian, F. A., & Bosch-Ramon, V. 2008, MNRAS, 383,
467 [NASA ADS]
(In the text)
- Komissarov, S. S.,
& Falle, S. A. E. G. 1998, MNRAS, 297, 1087 [NASA ADS] [CrossRef]
(In the text)
- Krause, M. 2005, A&A,
431, 45 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- van der Laan, H. 1962,
MNRAS, 124, 179 [NASA ADS]
(In the text)
- Leahy, J. P. 1991, in
Beams and Jets in Astrophysics, ed. P. A. Hughe (Cambridge:
Astrophysics Series), 100
- Leismann, T.,
Antón, L., Aloy, M. A., et al. 2005, A&A, 436, 503 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Marshall, H.
L., Canizares, C. R., & Schulz, N. S. 2002, ApJ, 564, 941 [NASA ADS] [CrossRef]
(In the text)
- Martí, J.,
Rodriguez, L. F., Mirabel, I. F., & Paredes, J. M. 1996,
A&A, 306, 449 [NASA ADS]
(In the text)
- Martí, J. M.,
Müller, E., Font, J. A., Ibáñez, J. M., &
Marquina, A. 1997, ApJ, 479, 151 [NASA ADS] [CrossRef]
(In the text)
- Mirabel, I. F.,
& Rodríguez, L. F. 1999, AR&A, 37, 409 [NASA ADS] [CrossRef]
(In the text)
- Mizuno, Y., Hardee, P.
E., & Nishikawa, K.-I. 2007, ApJ, 662, 835 [NASA ADS] [CrossRef]
(In the text)
- Orellana, M.,
Bordas, P., Bosch-Ramon, V., Romero, G. E., & Paredes, J. M.
2007, A&A, 476, 9 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Owocki, S., &
Cohen, D. 2006, ApJ, 648, 565 [NASA ADS] [CrossRef]
- Paredes, J. M.,
Bosch-Ramon, V., & Romero, E. 2006, A&A, 451, 259 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Paredes, J. M.,
Ribó, M., & Bosch-Ramon, V., et al. 2007, ApJ, 664,
L39 [NASA ADS] [CrossRef]
(In the text)
- Perucho, M., Martí, J. M.,
& Hanasz, M. 2005, A&A, 443, 863 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Perucho, M., Lobanov, A. P.,
Martí, J. M., & Hardee, P. E. 2006, A&A, 456, 493 [NASA ADS] [CrossRef] [EDP Sciences]
- Perucho, M. &
Martí, J. M. 2007, MNRAS, in press,
[arXiv:0709.1784]
(In the text)
- Peter, W., & Eichler,
D. 1995, ApJ, 438, 244 [NASA ADS] [CrossRef]
(In the text)
- Protheroe, R.
J. 1999, ADP-AT-98-9 [astro-ph/9812055]
(In the text)
- Puls, J., Markova, N.,
Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences]
- Rees, M. J., &
Gunn, J. E. 1974, MNRAS, 167, 1 [NASA ADS]
(In the text)
- Ribó, M. 2005,
ASPC, 340, 269 [NASA ADS]
(In the text)
- Rico, J., for the MAGIC
collaboration, talk presented in the conference: High energy
processes in relativistic jets, Dublin, Ireland
(In the text)
- Rieger, F. M.,
& Duffy, P. 2004, ApJ 617, 155 [NASA ADS] [CrossRef]
(In the text)
- Romero, G. E.,
Torres, D. F., Kaufman Bernadó, M. M., & Mirabel, I. F.
2003, A&A, 410, L1 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Romero, G. E.,
& Orellana, M. 2005, A&A, 439, 237 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Romero, G. E., Owocki
S. P., Araudo, A. T., Townsend, R., & Benaglia P. 2007a,
workshop proceedings, Clumping in Hot Star Winds
[arXiv:astro-ph/0708.1525]
(In the text)
- Romero, G. E.,
Okazaki, A. T., Orellana, M., & Owocki, S. P. 2007b, A&A,
474, 15 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Rosen, A., Hughes, P.A.,
Duncan, G.C., & Hardee, P.E. 1999, ApJ, 516, 729 [NASA ADS] [CrossRef]
(In the text)
- Scheck, L., Aloy, M.A.,
Martí, J. M., Gómez, J.L., & Müller, E. 2002,
MNRAS, 331, 615 [NASA ADS] [CrossRef]
(In the text)
- Tsinganos, K., Vlahakis,
N., Bogovalov, S. V., Sauty, C., & Trussoni, E. 2004,
Ap&SS, 293, 55 [NASA ADS] [CrossRef]
- Tudose, V., Fender,
R. P., & Kaiser, C. R., et al. 2006, MNRAS, 372, 417 [NASA ADS] [CrossRef]
(In the text)
-
Velázquez, P. F., & Raga, A. C. 2000, A&A, 362,
780 [NASA ADS]
(In the text)
- Zealey, W. J.,
Dopita, M. A., & Malin, D. F. 1980, MNRAS, 192, 731 [NASA ADS]
(In the text)
Copyright ESO 2008