A&A 482, 639-651 (2008)
DOI: 10.1051/0004-6361:20078848
Abundance variations and first ionization potential trends during large stellar flares
R. Nordon1 - E. Behar2,1
1 - Department of Physics, Technion, Haifa 32000, Israel
2 - Senior NPP Fellow, Code 662, NASA/Goddard Space Flight Center, Greenbelt, MD 20771, USA
Received 14 October 2007 / Accepted 22 January 2008
Abstract
Context. In the solar corona, elements of low first ionization potential (FIP 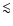 10 eV) are enriched relative to their abundances in the photosphere, while high-FIP abundances remain unchanged. This was labeled as the Solar FIP effect. High-resolution X-ray spectroscopy has revealed that active stellar coronae show an opposite effect, which was labeled the inverse-FIP (IFIP) effect. The correlation found between coronal activity and the FIP/IFIP bias suggests that flaring activity is involved in switching from FIP to IFIP.
10 eV) are enriched relative to their abundances in the photosphere, while high-FIP abundances remain unchanged. This was labeled as the Solar FIP effect. High-resolution X-ray spectroscopy has revealed that active stellar coronae show an opposite effect, which was labeled the inverse-FIP (IFIP) effect. The correlation found between coronal activity and the FIP/IFIP bias suggests that flaring activity is involved in switching from FIP to IFIP.
Aims. This work aims at a more systematic understanding of the FIP trends during stellar flares and complements an earlier study based on Chandra alone.
Methods. The eight brightest X-ray flares observed with XMM-Newton are analyzed and compared with their respective quiescence states. Together with six previous flares observed with Chandra, this establishes the best currently available sample of flares. We look for abundance variations during the flare and their correlation with FIP. For that purpose, we define a new FIP bias measure.
Results. A trend is found where coronae that are IFIP-biased in quiescence, show a FIP bias during flares relative to their quiescence composition. This effect is reversed for coronae that are FIP-biased in quiescence. The observed trend is thus consistent with chromospheric evaporation rather than with a FIP mechanism operating during flares. It also suggests that the quiescent IFIP bias is real and that the large flares are not the direct cause of the IFIP effect in stellar coronae.
Key words: stars: activity - stars: coronae - stars: flare - stars: abundances - X-rays: stars
The study of stellar coronae was given a significant boost by the launch of XMM-Newton and Chandra by allowing high-resolution X-ray spectroscopy.
Observations have revealed that the familiar solar first ionization potential (FIP) effect, in which the abundance of low-FIP elements is enhanced in the corona compared with high-FIP elements (Laming et al. 1995; Feldman 1992), also observed on other stars (example: Drake et al. 1997), does not exist in all stellar corona. Some cases show no FIP bias (Raassen et al. 2002; Drake et al. 1995), while others show a clear inverse effect (IFIP), in which the high-FIP elements are enriched over the low-FIP ones (Brinkman et al. 2001). Some examples show more complex patterns that could indicate that more parameters, other than FIP, may have an effect (Huenemoerder et al. 2003; Ball et al. 2005).
Table 1:
XMM-Newton observations used in this work.
Later studies indicated a correlation between coronal activity and the FIP effect. Audard et al. (2003) find that highly active RS CVn binaries, as indicated by their effective coronal temperatures, show an IFIP effect while less active (cooler) coronae show either no effect or a solar FIP effect. Telleschi et al. (2005) find a related result in a sample of solar like stars, where abundances change from IFIP to FIP with the age (and decreasing activity) of the star. On the other hand, Wood & Linsky (2006) compared the abundances of two K type dwarf binaries of similar basic properties (age, spectral type, rotation period, activity level). They report different abundance effects ranging from solar-like FIP to a weak IFIP effect, or none, in spite of the similar activity levels.
Since high coronal activity and temperatures are manifested in frequent flares, the correlation between activity and abundances suggests that flares may affect the FIP pattern in some way. However, in analyzing individual stellar flares, mixed results are obtained differing from target to target: Güdel et al. (1999), Audard et al. (2001), and Raassen et al. (2003) have found an increase in low-FIP abundances during flares on UX Ari, HR 1099, and dwarf binary AT Mic, respectively. In some other cases, the variations in abundances were not FIP-related (Osten et al. 2003; Güdel et al. 2004), or not detected at all (Raassen et al. 2007). Nordon & Behar (2007) have analyzed six large flares on different stars observed with Chandra and find an increase in low-FIP abundances during five of the flares and no effect in one case. These results indicate that if abundance variations were observed during flares, they tended toward the solar-like FIP bias of the flare abundances relative to quiescence (i.e., when measured in quiescence abundance units). This is the opposite of what one might expect from the activity-abundance relations reported by Audard et al. (2003) and Telleschi et al. (2005). Caution should be applied regarding this last statement, as the sample in Nordon & Behar (2007) is biased to only include the largest flares.
The definitions of flare and quiescence states are themselves somewhat ambiguous. There is growing evidence that the perceived quiescence state is a superposition of many small (micro) flares. From the statistics of large-to-medium flares, the distribution of the number of flares per unit time as a function of energy released behaves like a power law:
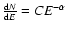 with typical values
with typical values
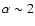 (Hudson 1991; Güdel et al. 2003; Audard et al. 2000; Caramazza et al. 2007; Kashyap et al. 2002). Audard & Güdel (1999) used the Extreme Ultraviolet Explorer (EUVE) to investigate two of the targets also used in this work (47 Cas & EK Dra) and find a flare statistical distribution with
(Hudson 1991; Güdel et al. 2003; Audard et al. 2000; Caramazza et al. 2007; Kashyap et al. 2002). Audard & Güdel (1999) used the Extreme Ultraviolet Explorer (EUVE) to investigate two of the targets also used in this work (47 Cas & EK Dra) and find a flare statistical distribution with
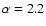
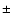 0.2.
If this statistical law holds down to low energies, it means a large number of flares per typical flare cooling time, which in turn would resemble a continuous emission. It is also important to note that
0.2.
If this statistical law holds down to low energies, it means a large number of flares per typical flare cooling time, which in turn would resemble a continuous emission. It is also important to note that
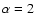 is a critical value above which the total power released by low-energy flares depends on (and requires) a low-energy cut-off. Values of
is a critical value above which the total power released by low-energy flares depends on (and requires) a low-energy cut-off. Values of 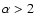 can potentially explain all quiescent coronal emission as the result of micro-flaring activity.
can potentially explain all quiescent coronal emission as the result of micro-flaring activity.
Stellar photospheric abundances are not well-determined and solar-like abundances are usually assumed. Even in the solar case, photospheric abundances have been revised significantly in the past 20 years from the often used Anders & Grevesse (1989). Most of the variation is in the absolute abundances (measured relative to H) and less in relative abundances of the common heavy elements. The abundance of Ne is notoriously difficult to determine, and a significant revision of it has been suggested (Drake & Testa 2005). The photospheric abundance of Ne is especially important for the coronal FIP effect in stars, as the two dominant high-FIP elements observed in X-ray are Ne and O. The uncertainties in assumed photospheric abundances are a constant source of doubt about the reality of the IFIP effect (Sanz-Forcada et al. 2004).
In this work we continue the work of Nordon & Behar (2007), which we refer to as Paper I. Here, we analyze the spectra of eight flares obtained from the XMM-Newton archive. We selected the brightest flares, in terms of number of counts, that allow for accurate line flux measurements. We then compare the thermal and chemical structure between the flaring and quiescence states seeking abundance variation and FIP trends. Together with the Chandra flares, we now have a sample of 14 flares, analyzed with similar methods.
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{8848fig1.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg11.gif) |
Figure 1:
Light curves of the flares extracted from EPIC-pn, except for 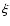 Boo flare that was extracted from EPIC-MOS. Time segments used for flare and quiescence spectra extraction are marked by F and Q respectively. CC Eri and Boo flare that was extracted from EPIC-MOS. Time segments used for flare and quiescence spectra extraction are marked by F and Q respectively. CC Eri and 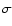 Gem show no clear quiescence during the observation and therefore a different observation was used as quiescence reference. See text for details. Gem show no clear quiescence during the observation and therefore a different observation was used as quiescence reference. See text for details. |
| Open with DEXTER |
The XMM-Newton public archive was searched for observations of stars of spectral types A to M that include large flares. Light curves were extracted and examined. The criteria for large is that enough photons were collected during the flare to allow detailed spectral analysis.
In this work, we required at least a total of 3000 first-order photon counts, between 6-20 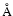 ,
in the RGS instruments combined.
Many flares were found, but we retained only those that could provide statistically meaningful measurements. The sample is therefore likely to be biased toward the larger flares occurring perhaps on the more active stars, but these are our current limitations.
,
in the RGS instruments combined.
Many flares were found, but we retained only those that could provide statistically meaningful measurements. The sample is therefore likely to be biased toward the larger flares occurring perhaps on the more active stars, but these are our current limitations.
The targets and details of the observations are presented in Table 1. Some of these observations have been analyzed before. See Testa et al. (2007), Crespo-Chacón et al. (2007), Schmitt et al. (2003), Güdel et al. (2002a), and Reale et al. (2004) for works related to some of the flares analyzed here. The light curves of the selected observations are presented in Fig. 1. The time segments used for flare and quiescence extraction of the spectra are marked on the plots. In the XMM-Newton observations of CC Eri and 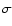 Gem, not enough photons were detected in quiescence, and quiescence spectra from Chandra HETGS observations were used. For CC Eri, the quiescence data from Paper I, and for
Gem, not enough photons were detected in quiescence, and quiescence spectra from Chandra HETGS observations were used. For CC Eri, the quiescence data from Paper I, and for 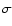 Gem a 120 ks archival observation (Obs. ID 5422, 6282).
Gem a 120 ks archival observation (Obs. ID 5422, 6282).
The present analysis methods are similar to those used in Paper I. We briefly summarize them and emphasize the differences due to the use of XMM-Newton instruments instead of Chandra. The goal is to reconstruct the thermal structure of the plasma and measure the abundances during flaring and quiescence states. The method relies on line-flux analysis, which is much more sensitive to temperatures and abundances than the continuum.
To investigate FIP biased abundance variations, we are interested in relative, more than absolute, abundances. Therefore, the continuum that is dominated by H and is typically used to measure the absolute abundances is less important. Instead, we measure the abundances relative to Fe, which emits lines from a wide range of plasma temperatures.
Due to the high resolution of the grating instruments, the lines have a very high equivalent width and local continuum uncertainties have a relatively weak effect on the measured fluxes. Line fluxes measured from the CCD instruments (lower resolution) are prone to the larger systematic errors caused by uncertainties in the continuum determination and increased difficulty in resolving line blends. This should be kept in mind when reviewing the results based solely on the latter.
We define the emission measure distribution (EMD) as:
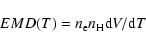 |
(1) |
where
 are the averaged e- and H number densities in the plasma at the temperature interval [T,
are the averaged e- and H number densities in the plasma at the temperature interval [T,
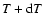 ]. Since hydrogen does not emit lines at coronal temperatures, its emission contribution is confined to the continuum. We are interested in abundance and thermal structure variations, so the more useful quantity for our purpose is the iron emission measure distribution (FeEMD):
]. Since hydrogen does not emit lines at coronal temperatures, its emission contribution is confined to the continuum. We are interested in abundance and thermal structure variations, so the more useful quantity for our purpose is the iron emission measure distribution (FeEMD):
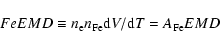 |
(2) |
where
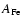 is the iron abundance relative to H.
is the iron abundance relative to H.
XMM-Newton comprises several different instruments. The longer wavelengths (6-38 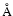 )
are covered by the two high-resolution reflection-grating spectrometers (RGS) that resolve the emission lines. The high-energy end up to 15 keV is covered by the two EPIC-MOS and single EPIC-pn CCDs, which offer lower spectral resolution. Since the present targets are all X-ray-bright point sources, EPIC-MOS often piled up. This is a much lesser problem in EPIC-pn, so we use only this instrument for the high energies, except in the case of
)
are covered by the two high-resolution reflection-grating spectrometers (RGS) that resolve the emission lines. The high-energy end up to 15 keV is covered by the two EPIC-MOS and single EPIC-pn CCDs, which offer lower spectral resolution. Since the present targets are all X-ray-bright point sources, EPIC-MOS often piled up. This is a much lesser problem in EPIC-pn, so we use only this instrument for the high energies, except in the case of 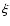 Boo where EPIC-pn data were not available.
This reduces the accuracy of the line fluxes measured at wavelengths shorter than 6
Boo where EPIC-pn data were not available.
This reduces the accuracy of the line fluxes measured at wavelengths shorter than 6 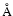 .
The K-shell lines of S, Ar, and Ca can thus be measured only at CCD resolution. The Si-K lines are just at the end of the RGS band, and the signal was good enough in a few cases to allow high-resolution constraints on these lines.
.
The K-shell lines of S, Ar, and Ca can thus be measured only at CCD resolution. The Si-K lines are just at the end of the RGS band, and the signal was good enough in a few cases to allow high-resolution constraints on these lines.
The observed spectrum is fitted by sets of complete individual-ion spectra simultaneously (Behar et al. 2001), together with a bremsstrahlung continuum, composed of several discrete-temperature components, as explained in Paper I. We emphasize again that the fitted continuum only serves here the line-flux measurements and is used neither in the EMD nor in the abundance analysis. The extracted line fluxes are listed in Tables A.1-A.8 in the Appendix.
Once a list of line fluxes is compiled, we use the same methods as in Paper I to measure the FeEMD and the abundances. In short, the set of equations to be solved for the measured line flux
FZqj i from ion q, of element Z, due to the transition
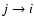 is:
is:
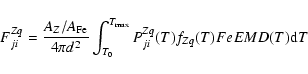 |
(3) |
where d is the distance to the target,
PZqji the line emission rate coefficient per unit electron density, fZq(T) the ionic fraction, and
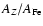 is the abundance relative to Fe. Rate coefficients are calculated using HULLAC (Bar-Shalom et al. 2001). Ionic fractions for Fe, Ar, S, Si, and Mg are from Gu (2003), while Mazzotta et al. (1998) is used for the other elements.
A parametrized FeEMD is fitted to reproduce the measured flux of a selected set of strong and weakly blended Fe lines. For non-Fe elements, we use pairs of lines from different ionization degrees, in which case their flux ratio is fitted.
In practice, with the RGS, the lowest temperature constraint is obtained from the ratio of the two K-shell charge states of oxygen.
The emission from O VII drops significantly below kT= 0.1 keV, giving us no constraints on the EMD at lower temperatures. Therefore 0.1 keV is chosen as the lower limit for the EMD analysis. Once the FeEMD is determined, it is used to calculate the abundances
is the abundance relative to Fe. Rate coefficients are calculated using HULLAC (Bar-Shalom et al. 2001). Ionic fractions for Fe, Ar, S, Si, and Mg are from Gu (2003), while Mazzotta et al. (1998) is used for the other elements.
A parametrized FeEMD is fitted to reproduce the measured flux of a selected set of strong and weakly blended Fe lines. For non-Fe elements, we use pairs of lines from different ionization degrees, in which case their flux ratio is fitted.
In practice, with the RGS, the lowest temperature constraint is obtained from the ratio of the two K-shell charge states of oxygen.
The emission from O VII drops significantly below kT= 0.1 keV, giving us no constraints on the EMD at lower temperatures. Therefore 0.1 keV is chosen as the lower limit for the EMD analysis. Once the FeEMD is determined, it is used to calculate the abundances
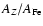 by plugging it back into Eq. (3). Elements for which only one ionization degree is detected in a specific observation (i.e. one of the lines is consistent with zero, see line-flux tables in the supplement) are not used for FeEMD constraints, but are used for measuring abundances.
by plugging it back into Eq. (3). Elements for which only one ionization degree is detected in a specific observation (i.e. one of the lines is consistent with zero, see line-flux tables in the supplement) are not used for FeEMD constraints, but are used for measuring abundances.
The FeEMD is described by a staircase function where FeEMD in a bin represents the averaged FeEMD over the bin temperature range. The calculated errors on the FeEMD also include uncertainties caused by cross-talk between neighboring bins. Increasing the temperature resolution by using narrower FeEMD bins results in larger uncertainties in individual bins. For this reason, we also calculate the useful quantity of the Fe integrated emission measure:
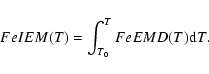 |
(4) |
Integrating the FeEMD over T, while accounting for the correlations between bins reduces the uncertainties and provides a clearer picture of the temperatures of excess flare emission, as demonstrated in Paper I and in the following. To check that the results depend only weakly on the binning and on the functional form of the FeEMD, similar to what was done in Paper I, we also fit an FeEMD parametrized as an exponent of a polynomial:
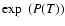 .
Evidently, the FeIEM and the abundances calculated using this solution agree extremely well with those obtained from the staircase FeEMD. An important advantage of the latter is that it enables the computation of local FeEMD uncertainties, not available with globally parametrized functions.
.
Evidently, the FeIEM and the abundances calculated using this solution agree extremely well with those obtained from the staircase FeEMD. An important advantage of the latter is that it enables the computation of local FeEMD uncertainties, not available with globally parametrized functions.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{8848fig2.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg23.gif) |
Figure 2:
FeEMD solutions for the flare (orange) and quiescence (blue).
Errors are 1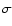 and include uncertainties due to correlation between the bins.
Dashed lines represent the polynomial parameterized solutions.
and include uncertainties due to correlation between the bins.
Dashed lines represent the polynomial parameterized solutions. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{8848fig3.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg24.gif) |
Figure 3:
FeIEM results for flare (orange) and quiescent (blue) states, namely the progressive integral over the FeEMD of Fig. 2. Plotted errors account for uncertainties due to correlations between bins during integration.
Dotted lines show the results of the integration over the polynomial parameterized FeEMD (see Fig. 2). |
| Open with DEXTER |
Figure 2 shows the fitted FeEMD for each target, in flare and in quiescence states. The errors on the bin-form FeEMD are 1-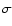 and include uncertainties due to both line fluxes and correlations between bins. The most notable flare FeEMD excess is observed for CC Eri,
and include uncertainties due to both line fluxes and correlations between bins. The most notable flare FeEMD excess is observed for CC Eri, 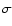 Gem, and Proxima Cen. The other flares only become more obvious upon integration (FeIEM).
The polynomial FeEMDs give somewhat similar patterns to the bin-form FeEMDs.
At high temperatures, typically 5-8 keV, the polynomial model tends to fit a spike,
since the constraints in this temperature region are dominated by the Fe XXIV and Fe XXV ratio and a single-T component is enough to fix it. Fe XXVI is just beginning to form and has a weak signal in most flares. Line emissivities of other elements are very low in this temperature range, because they are mostly in bare ion form.
Gem, and Proxima Cen. The other flares only become more obvious upon integration (FeIEM).
The polynomial FeEMDs give somewhat similar patterns to the bin-form FeEMDs.
At high temperatures, typically 5-8 keV, the polynomial model tends to fit a spike,
since the constraints in this temperature region are dominated by the Fe XXIV and Fe XXV ratio and a single-T component is enough to fix it. Fe XXVI is just beginning to form and has a weak signal in most flares. Line emissivities of other elements are very low in this temperature range, because they are mostly in bare ion form.
Table 2:
Abundances measured relative to Fe during flare, quiescence1, and the flare to quiescence ratio.
Figure 3 shows the cumulative distribution (iron integrated emission measure, FeIEM) from 0.1-10 keV. Errors are calculated including correlations between bins, so they largely cancel out with integration. This considerably reduces the relative errors and thus provides a useful physical comparison between flare and non-flare. The polynomial parametrized FeIEM are seen to match well with the integrated bin-form FeIEM results, within the errors. In poorly constrained FeEMD temperature regions, the bin-form and polynomial FeIEM curves may diverge slightly, only to re-converge once integrated over the less certain range.
This is clearly demonstrated in the high-T range, where the polynomial model has a distinct spike, but results in the same FeIEM after integration. The two models always agree particularly well on the total EM, represented by the last point in the FeIEM plots of Fig. 3.
This demonstrates that the errors in the FeEMD are clearly dominated by the degeneracy of the FeEMD solution and that the chosen parametrization has very little effect.
From Figs. 2 and 3, we see that most of the excess emission during the flare originates from temperatures above kT = 1 keV. In most cases, the time-averaged emission measure, under 1 keV, during the flare is not significantly different from the quiescence emission measure. Only CC Eri, 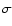 Gem, and Prox Cen have significant EM excess up to 1 keV as is evident in Fig. 3. If we think of the flare in terms of impulsive heating and gradual radiative/conductive cooling, then the time-averaged EMD excess is due to plasma cooling through a given temperature. Flares that exhibit high total EM excess, but little low-T excess, raise the intriguing question of how the EM is lost, without leaving a trace of cooling.
A low EMD in a given temperature range, as observed in the time-averaged data, could result from very rapid cooling through that temperature range. A significant increase in conductive cooling at low temperatures could potentially provide this rapid cooling mechanism, although a special geometry would need to be invoked to make conduction more efficient at low-T than at high-T.
Especially in the cases of the flares on HR1099, 47 Cas, EK Dra, and
Gem, and Prox Cen have significant EM excess up to 1 keV as is evident in Fig. 3. If we think of the flare in terms of impulsive heating and gradual radiative/conductive cooling, then the time-averaged EMD excess is due to plasma cooling through a given temperature. Flares that exhibit high total EM excess, but little low-T excess, raise the intriguing question of how the EM is lost, without leaving a trace of cooling.
A low EMD in a given temperature range, as observed in the time-averaged data, could result from very rapid cooling through that temperature range. A significant increase in conductive cooling at low temperatures could potentially provide this rapid cooling mechanism, although a special geometry would need to be invoked to make conduction more efficient at low-T than at high-T.
Especially in the cases of the flares on HR1099, 47 Cas, EK Dra, and 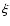 Boo, EM loss other than rapid cooling through X-ray sensitive temperatures may be required. Possibilities include rotation of the flare region beyond the limb, or a rapid decrease in density due to expansion.
In the case of Algol, this could be caused by the eclipse hiding the decay phase (see Fig. 1).
Boo, EM loss other than rapid cooling through X-ray sensitive temperatures may be required. Possibilities include rotation of the flare region beyond the limb, or a rapid decrease in density due to expansion.
In the case of Algol, this could be caused by the eclipse hiding the decay phase (see Fig. 1).
The measured abundances relative to Fe, obtained from the binned FeEMD, are described in Table 2. They are measured relative to Fe using only emission lines and not relative to hydrogen. Note that the abundances are the actual abundances and not relative to solar. The errors on the abundances include both statistical errors on the measured line fluxes and errors due to FeEMD solution uncertainties. One must keep in mind that some of the lines are measured using the EPIC instruments which may add systematic errors. This is especially true for the abundances of S, Ar, and Ca.
Another source of systematic errors is our inability to resolve the EMD below  0.1 keV. The lines of N and C, which form largely at these low temperatures, might thus suffer from additional uncertainties. We therefore concentrate on the more reliable abundances of O, Ne, Mg, Si, and Fe as reference. Note that abundances obtained from bright X-ray emission lines are constrained even better than the solar photospheric abundance measurements. The abundances obtained from the polynomial FeEMD are identical to those obtained from the binned FeEMD, largely within a fraction of a standard deviation. Due to the similarity of the results, the tables only specify the abundances obtained from the binned parametrization, for which we can include FeEMD-induced uncertainties.
0.1 keV. The lines of N and C, which form largely at these low temperatures, might thus suffer from additional uncertainties. We therefore concentrate on the more reliable abundances of O, Ne, Mg, Si, and Fe as reference. Note that abundances obtained from bright X-ray emission lines are constrained even better than the solar photospheric abundance measurements. The abundances obtained from the polynomial FeEMD are identical to those obtained from the binned FeEMD, largely within a fraction of a standard deviation. Due to the similarity of the results, the tables only specify the abundances obtained from the binned parametrization, for which we can include FeEMD-induced uncertainties.
Figure 4 shows the abundance ratios of flare and quiescence states as a function of FIP. These ratios were derived directly from the X-ray data and require no knowledge of photospheric abundances. Consequently, they provide a clean measure of abundance variations during and due to the flare. It should be emphasized that what are defined as ``flare'' abundances are an EMD-weighted average of the flaring region and the background quiescence abundances.
In Fig. 4, the abundances based on RGS data are considered the most reliable. Abundances determined from EPIC data are less certain, as is that of Ni which is based on weak and somewhat blended lines. The abundances of C and N may be influenced by emission from unresolved low temperatures that could systematically affect their measurement.
As seen in Fig. 4, flares on different stars show different FIP trends ranging from solar FIP to inverse FIP and including no FIP effect at all. Although at first sight this may seem like arbitrary abundance behavior during flares, in the following section we argue that in fact a clear FIP-bias pattern emerges from these plots.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{8848fig4.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg27.gif) |
Figure 4:
Flare abundances relative to quiescence, as a function of FIP. Elements observed with the RGS (O, Ne, Mg, Si) are considered the most reliable and are marked in red. Those observed only with the low-resolution EPIC instruments are marked black. Elements whose abundance determination depends on the EMD below temperatures of kT=0.1 keV, for which we did not solve, may suffer from systematic errors and are plotted in gray. The vertical dotted line mark the FIP of of the reference element Fe. |
| Open with DEXTER |
We can differentiate between three cases: relative FIP, relative IFIP and no effect. CC Eri and 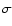 Gem show a change in the abundances during the flare that resembles the solar FIP effect. i.e. low FIP elements are enriched relative to the high FIP elements. These results are similar to what was found in Paper I for five out of the six flares observed with Chandra, including a different flare on CC Eri. A similar result for
Gem show a change in the abundances during the flare that resembles the solar FIP effect. i.e. low FIP elements are enriched relative to the high FIP elements. These results are similar to what was found in Paper I for five out of the six flares observed with Chandra, including a different flare on CC Eri. A similar result for 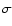 Gem for the same flare, but using a different quiescence reference, was reported by Nordon et al. (2006). The flare on Proxima Cen, on the other hand, shows an inverse-FIP like effect, where it is the high FIP elements that are enriched over the low FIP ones. This result confirms the pattern reported by Güdel et al. (2004). The other five flares show no clear pattern and are consistent within the errors with no abundance variation.
Gem for the same flare, but using a different quiescence reference, was reported by Nordon et al. (2006). The flare on Proxima Cen, on the other hand, shows an inverse-FIP like effect, where it is the high FIP elements that are enriched over the low FIP ones. This result confirms the pattern reported by Güdel et al. (2004). The other five flares show no clear pattern and are consistent within the errors with no abundance variation.
A measure for the FIP bias is required to better quantify the abundance variations. Let us define an FIP-bias measure as:
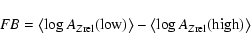 |
(5) |
where
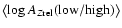 is the mean abundance (in log) of the low/high FIP elements measured relative to a set of reference abundances. The averaging of the log abundances is a Gaussian mean, and uncertainties are propagated accordingly.
We use the traditional solar distinction between low (FIP < 10 eV) and high (FIP > 10 eV) FIP elements. A positive FB value indicates a solar-like FIP bias, while a negative FB value indicates an IFIP bias. The FB defined above can be applied either to flare abundances with reference to quiescence (
is the mean abundance (in log) of the low/high FIP elements measured relative to a set of reference abundances. The averaging of the log abundances is a Gaussian mean, and uncertainties are propagated accordingly.
We use the traditional solar distinction between low (FIP < 10 eV) and high (FIP > 10 eV) FIP elements. A positive FB value indicates a solar-like FIP bias, while a negative FB value indicates an IFIP bias. The FB defined above can be applied either to flare abundances with reference to quiescence (
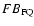 )
or to quiescence abundances with reference to photospheric (e.g., solar;
)
or to quiescence abundances with reference to photospheric (e.g., solar;
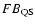 ). In the present analysis, to minimize systematic errors in the calculation of the FB, we use only O and Ne as the high-FIP elements and Si, Mg, and Fe (implicitly) as the low-FIP elements, thus leaving out the other, less well-constrained abundances.
). In the present analysis, to minimize systematic errors in the calculation of the FB, we use only O and Ne as the high-FIP elements and Si, Mg, and Fe (implicitly) as the low-FIP elements, thus leaving out the other, less well-constrained abundances.
We calculate
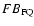 and
and
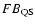 for each flare and assume the solar abundances of Asplund et al. (2005) as photospheric abundances.
Figure 5 shows a plot of
for each flare and assume the solar abundances of Asplund et al. (2005) as photospheric abundances.
Figure 5 shows a plot of
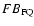 as a function of
as a function of
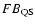 for all XMM-Newton flares analyzed in this paper and also for the six flares from Paper I observed with Chandra. Most stellar flares in the sample tend to exhibit a positive
for all XMM-Newton flares analyzed in this paper and also for the six flares from Paper I observed with Chandra. Most stellar flares in the sample tend to exhibit a positive
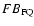 .
In other words, low-FIP abundances increase relative to high-FIP abundances during the flare. Only two flares show a statistically significant negative
.
In other words, low-FIP abundances increase relative to high-FIP abundances during the flare. Only two flares show a statistically significant negative
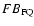 :
Proxima Cen and
:
Proxima Cen and 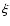 Boo. Five flares are consistent with
Boo. Five flares are consistent with
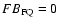 to within a standard deviation. The errors plotted in Fig. 5 reflect the statistical uncertainties of the line fluxes and also include the EMD-induced uncertainties. It is important to emphasize that the calculation of
to within a standard deviation. The errors plotted in Fig. 5 reflect the statistical uncertainties of the line fluxes and also include the EMD-induced uncertainties. It is important to emphasize that the calculation of
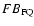 suffers from very little systematic errors, since it does not require any knowledge of the photospheric abundances. Furthermore, it results from a systematic abundance study in both the present work and Paper I that uses the same methods and the same atomic data for all flare and quiescence abundances.
suffers from very little systematic errors, since it does not require any knowledge of the photospheric abundances. Furthermore, it results from a systematic abundance study in both the present work and Paper I that uses the same methods and the same atomic data for all flare and quiescence abundances.
The calculated
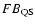 values (the x axis in Fig. 5) do depend on the set of photospheric abundances selected. We adopt the solar abundances of Asplund et al. (2005), as well as their errors, which are included in (and can dominate) the
values (the x axis in Fig. 5) do depend on the set of photospheric abundances selected. We adopt the solar abundances of Asplund et al. (2005), as well as their errors, which are included in (and can dominate) the
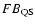 errors plotted in Fig. 5. For the sake of discussion, we assume that the stellar photospheres are similar in composition to the Sun. Deviation of the actual photospheric abundances from solar would affect the horizontal position of the data points in Fig. 5, but not their vertical position. Not surprisingly, the flare targets tend to be of the
errors plotted in Fig. 5. For the sake of discussion, we assume that the stellar photospheres are similar in composition to the Sun. Deviation of the actual photospheric abundances from solar would affect the horizontal position of the data points in Fig. 5, but not their vertical position. Not surprisingly, the flare targets tend to be of the
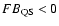 type, i.e., IFIP coronae, since large flares are more commonly observed on active coronae, which are IFIP-biased (Audard et al. 2003; Brinkman et al. 2001; Telleschi et al. 2005).
Note that the two flares observed to have
type, i.e., IFIP coronae, since large flares are more commonly observed on active coronae, which are IFIP-biased (Audard et al. 2003; Brinkman et al. 2001; Telleschi et al. 2005).
Note that the two flares observed to have
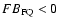 are also those that erupt on the stars with the highest
are also those that erupt on the stars with the highest
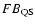 values.
values.
Since X-ray observations of coronal flares on
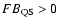 (solar FIP biased, less active) stars are rare for the reasons described above, we look to expand our sample for Fig. 5 to solar flares. A few solar flares have been analyzed for abundances that included both high and low FIP elements: Feldman & Widing (1990) analyzed a flare observed with Skylab and found significant abundance variations during the flare. In fact, the flare abundances were close to solar photospheric values.
The elements used are O and Ne (high-FIP), and Mg and Ca (low-FIP). Schmelz (1993) analyzed two flares observed by the Solar Maximum Mission (SMM), and Fludra & Schmelz (1995) measured the abundances in these two flares again using a different method. In these flares, the elements observed were Ne and O (high-FIP) and Fe, Ca, Si, and Mg (low-FIP).
Since quiescent abundances from the active regions were not directly measured by these authors, we use
(solar FIP biased, less active) stars are rare for the reasons described above, we look to expand our sample for Fig. 5 to solar flares. A few solar flares have been analyzed for abundances that included both high and low FIP elements: Feldman & Widing (1990) analyzed a flare observed with Skylab and found significant abundance variations during the flare. In fact, the flare abundances were close to solar photospheric values.
The elements used are O and Ne (high-FIP), and Mg and Ca (low-FIP). Schmelz (1993) analyzed two flares observed by the Solar Maximum Mission (SMM), and Fludra & Schmelz (1995) measured the abundances in these two flares again using a different method. In these flares, the elements observed were Ne and O (high-FIP) and Fe, Ca, Si, and Mg (low-FIP).
Since quiescent abundances from the active regions were not directly measured by these authors, we use
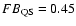
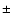 0.15 for the quiescent solar corona representing roughly the typical enrichment by a factor of 2-4 of low-FIP elements in solar active regions (Feldman 1992). It can be seen in Fig. 5 that the solar flares continue the trend of
0.15 for the quiescent solar corona representing roughly the typical enrichment by a factor of 2-4 of low-FIP elements in solar active regions (Feldman 1992). It can be seen in Fig. 5 that the solar flares continue the trend of
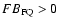 shifting to
shifting to
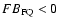 as
as
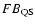 increases. In other words, low-FIP enriched coronae, such as the Sun, feature a relative enrichment of high-FIP elements during flares.
increases. In other words, low-FIP enriched coronae, such as the Sun, feature a relative enrichment of high-FIP elements during flares.
Why is the abundance variation not observed in all flares? That there is none is certainly a possibility, but a better explanation is that our ability to detect variations is limited. Detection of abundance variation depends strongly on the excess of EM during the flare, at temperatures that produce significant line emission. The emissivities of lines of O, Ne, and Mg peak at temperatures below kT = 1 keV. The Si ion emissivities peaks at slightly higher temperatures of kT 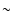 1.2 keV. At higher temperatures, these elements become fully ionized and emit no lines. Therefore, one needs a significant EM excess at temperatures of
1.2 keV. At higher temperatures, these elements become fully ionized and emit no lines. Therefore, one needs a significant EM excess at temperatures of 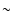 1 keV to observe abundance variations. Looking at Fig. 3, we see that most of the EM excess during the flares appears at temperatures of kT> 2 keV. Some of the flares show very little EM excess below 1 keV. For these, we expect to have difficulty detecting abundance variations,
given the seemingly steady quiescence (background) emission.
Figure 6 demonstrates this effect. It shows the
1 keV to observe abundance variations. Looking at Fig. 3, we see that most of the EM excess during the flares appears at temperatures of kT> 2 keV. Some of the flares show very little EM excess below 1 keV. For these, we expect to have difficulty detecting abundance variations,
given the seemingly steady quiescence (background) emission.
Figure 6 demonstrates this effect. It shows the
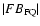 value vs. the flare to quiescence ratio of the FeIEM at 1 keV, which represents the EM excess during the flare from the relevant low-T (kT < 1 keV) plasma. The figure shows very clearly that all of the flares in which no abundance variation was detected during the flare (FB
value vs. the flare to quiescence ratio of the FeIEM at 1 keV, which represents the EM excess during the flare from the relevant low-T (kT < 1 keV) plasma. The figure shows very clearly that all of the flares in which no abundance variation was detected during the flare (FB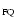 consistent with zero) ``suffer'' from little to no low-T EM excess. When the EM excess is large, we are always able to detect variations. We conclude that the abundance change during the flare is set by the coronal and photospheric composition, but the actually measured value of
consistent with zero) ``suffer'' from little to no low-T EM excess. When the EM excess is large, we are always able to detect variations. We conclude that the abundance change during the flare is set by the coronal and photospheric composition, but the actually measured value of
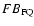 and our ability to detect the changes depend on the EM excess at line-emitting temperatures and thus on the details of the flare evolution.
and our ability to detect the changes depend on the EM excess at line-emitting temperatures and thus on the details of the flare evolution.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8848fig5.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg40.gif) |
Figure 5:
The FIP bias measure FB, defined in Eq. (5), of the flare plasma relative to quiescence as a function of the FB of the corona in quiescence, relative to Solar (photospheric). Black circles are from XMM-Newton observations, blue squares are from Chandra (Paper I) violet diamonds are for solar flares. |
| Open with DEXTER |
In some flares we therefore clearly detect a different composition from that of the quiescent corona (Fig. 4). Chromospheric evaporation has been suggested as an explanation for varying abundances observed during flares, e.g., Ottmann & Schmitt (1996). In this scenario, accelerated fast particles from the reconnection region spiral down the magnetic loop and are stopped in the denser chromosphere, releasing their energy. This heats chromospheric material to coronal temperatures and causes expansion, observed on the Sun in the form of blue-shifted lines during the initial phase of the flare (Milligan et al. 2006). During the decay phase, evaporation probably driven by heat conduction has been reported (Berlicki et al. 2005; Zarro & Lemen 1988; Schmieder et al. 1987).
If indeed chromospheric evaporation is responsible for the excess emission of the flare, then the composition of the flaring plasma is expected to resemble photospheric composition. For a corona with a quiescent IFIP bias, evaporated chromospheric plasma would appear to be FIP-biased when compared with quiescence composition, while for a FIP-biased corona, the evaporated chromospheric plasma would produce an IFIP effect. Indeed, this is what is observed in Fig. 5.
In two of the flares, namely those on 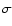 Gem (Güdel et al. 2002a) and on Proxima Cen (Güdel et al. 2002b), a Neupert effect (Neupert 1968) has been observed.
The Neupert effect is perceived as direct evidence for chromospheric evaporation. The flare on
Gem (Güdel et al. 2002a) and on Proxima Cen (Güdel et al. 2002b), a Neupert effect (Neupert 1968) has been observed.
The Neupert effect is perceived as direct evidence for chromospheric evaporation. The flare on 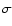 Gem, one of the most active RSCVn's with a strong quiescence IFIP bias
Gem, one of the most active RSCVn's with a strong quiescence IFIP bias
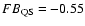
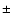 0.08, shows a clear relative enhancement of low-FIP abundances, reflected in a flare to quiescence FIP-bias
0.08, shows a clear relative enhancement of low-FIP abundances, reflected in a flare to quiescence FIP-bias
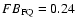
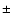 0.04, (see also Nordon et al. 2006). Conversely, Proxima Cen, a close X-ray faint M dwarf with a small quiescent FIP bias of
0.04, (see also Nordon et al. 2006). Conversely, Proxima Cen, a close X-ray faint M dwarf with a small quiescent FIP bias of
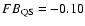
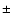 0.09, if any, shows the most distinct IFIP effect during the flare with
0.09, if any, shows the most distinct IFIP effect during the flare with
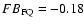
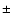 0.06. The overall picture emerging from Fig. 5 is that flares bring up chromospheric material, which manifests the photospheric composition. If the coronal composition is different from that of the photosphere, the flare can produce a notable abundance effect, best observed by means of the X-ray emission lines.
Moreover, this result supports the viability of the quiescent IFIP effect, since it is those stars that also show a relative FIP bias during the flare. If the excess flare emission in these stars is due to evaporated chromospheric plasma and its composition reflects that of their chromosphere, it proves that indeed the coronal composition is different from the photosphere composition and that the inverse-FIP effect in these coronae is indeed genuine (and not just an artifact of using inappropriate photospheric abundances).
0.06. The overall picture emerging from Fig. 5 is that flares bring up chromospheric material, which manifests the photospheric composition. If the coronal composition is different from that of the photosphere, the flare can produce a notable abundance effect, best observed by means of the X-ray emission lines.
Moreover, this result supports the viability of the quiescent IFIP effect, since it is those stars that also show a relative FIP bias during the flare. If the excess flare emission in these stars is due to evaporated chromospheric plasma and its composition reflects that of their chromosphere, it proves that indeed the coronal composition is different from the photosphere composition and that the inverse-FIP effect in these coronae is indeed genuine (and not just an artifact of using inappropriate photospheric abundances).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8848fig6.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg45.gif) |
Figure 6:
Absolute value of FIP bias measure FB as a function of the ratio of integrated EM from 0.1 to 1 keV in the flare relative to quiescence. A low-T EM excess is required in order to enable the detection of abundance variations of the key elements O, Ne, Mg and Si. |
| Open with DEXTER |
It still remains unclear how evaporation affects the observed abundances in the case of a micro-flaring quiescence. If the quiescence state is in itself a superposition of small flares, continuously evaporating material with photospheric composition, it should drive the mean coronal abundances toward photospheric.
Accommodating the mean quiescent FIP bias with FIP variation during large flares requires that chemical mixing during micro-flares is insignificant, unlike the effect observed here in some of the large flares. Possible reasons for this include either (i) less energetic electrons not penetrating deep enough into the chromosphere and heating material of coronal composition; or (ii) less efficient heat conduction at the foot print, reducing conductive induced evaporation. There is also the possibility that typical micro-flares are fundamentally different from the large flares. On the Sun we observe a wide variety of flares in their geometries and behavior (e.g. single loop vs. two ribbon, gradual vs. impulsive). It is therefore quite possible that the common micro-flare is not simply a scaled-down version of the very large flares discussed in this work.
Variation in observed abundances during stellar flares does not necessarily require evaporation of plasma with different chemical compositions. The solar corona is not uniform and abundances vary from one coronal structure to another. The FIP bias is also known to develop on a time scale of days, reaching the typical coronal values within 2-3 days and increasing more thereafter (Widing & Feldman 2001). If we assume stellar coronae are similar, the measured quiescent abundances are an EM-weighted average of all coronal structures. In a flaring state, the flare dominates the emission, and the measured mean abundance will tend toward that of the flaring structure.
In order to explain Fig. 5, with similar solar-like coronal structures that develop a solar-like FIP effect with time, the flaring structures in the active coronae (those with lowest
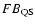 values) would have to be older than average, while in the less active coronae (highest
values) would have to be older than average, while in the less active coronae (highest
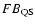 ), they would have to be younger than average. However, it is not clear why this would be the case. On the other hand, the apparent correlation in Fig. 5 between quiescent FIP bias and flare FIP bias, with no clear-cut counter examples of low-
), they would have to be younger than average. However, it is not clear why this would be the case. On the other hand, the apparent correlation in Fig. 5 between quiescent FIP bias and flare FIP bias, with no clear-cut counter examples of low-
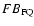 -low-
-low-
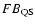 or high-
or high-
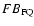 -high-
-high-
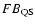 data points, makes us deem the local abundance explanation fairly unlikely. Nonetheless, magnetic structure variations accompanied by an FIP/IFIP effect that changes with time may have some effect on the measured
data points, makes us deem the local abundance explanation fairly unlikely. Nonetheless, magnetic structure variations accompanied by an FIP/IFIP effect that changes with time may have some effect on the measured
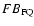 values, causing it to vary from flare to flare (in addition to the other factors).
values, causing it to vary from flare to flare (in addition to the other factors).
Eight large stellar flares, observed with XMM-Newton, were analyzed for their thermal and chemical structure. With the six large flares observed with Chandra and analyzed using similar methods (Paper I), we present a sample of fourteen large flares with good photon statistics, observed in the X-ray at high spectral resolution. To identify and quantify abundance variations during the flares, which may be FIP related, we defined an FIP-bias measure (FB).
In seven out of the fourteen cases, we found an enrichment of low-FIP elements compared to high-FIP elements during the flares (i.e., a solar-type FIP bias
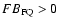 ), while five cases are consistent with no FIP-related bias and two show preferential enrichment of high-FIP elements over the low-FIP ones (i.e., IFIP,
), while five cases are consistent with no FIP-related bias and two show preferential enrichment of high-FIP elements over the low-FIP ones (i.e., IFIP,
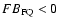 ). Since the abundance variation that we measure is between flaring and quiescent states of the coronae in the X-rays, no knowledge of photospheric abundances is required to determine
). Since the abundance variation that we measure is between flaring and quiescent states of the coronae in the X-rays, no knowledge of photospheric abundances is required to determine
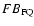 .
The FIP effect during the flare (the sign of FB
.
The FIP effect during the flare (the sign of FB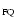 )
seems to correlate with the quiescent FIP bias of the corona, so that strong quiescent IFIP coronae tend to have
)
seems to correlate with the quiescent FIP bias of the corona, so that strong quiescent IFIP coronae tend to have
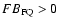 ,
while coronae with lower values of
,
while coronae with lower values of
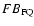 show the opposite effect. Solar flares also support this trend.
show the opposite effect. Solar flares also support this trend.
The most likely explanation for this effect is that of chromospheric evaporation during flares, where a significant amount of the excess EM during the flare is due to heated chromospheric material. For an FIP-biased corona, chromospheric composition is relatively IFIP-biased and vice versa: For IFIP quiescent coronae, chromospheric composition is relatively FIP-biased. This effect suggests that the observed inverse-FIP effect in the more active stellar coronae is indeed real and not an effect caused by photospheric abundances different from solar. Also, as flares seem to simply raise chromospheric material into the corona, the flares themselves cannot be the direct cause for the IFIP effect - at least not the large flares observed here - as continuous strong flaring would tend to lower the absolute FB towards zero, but could not reverse the effect from FIP to IFIP or vice versa.
Acknowledgements
This research was supported by ISF grant 28/03 and by a grant from the Asher Space Institute at the Technion.
Fluxes of H-like ion lines include both transitions of the unresolved Ly-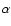 doublet.
Fluxes of He-like ion lines include only the resonant transition.
Fluxes of L-shell Fe ion lines include all transitions within
doublet.
Fluxes of He-like ion lines include only the resonant transition.
Fluxes of L-shell Fe ion lines include all transitions within  0.03 Å of the specified wavelength.
0.03 Å of the specified wavelength.
Table A.1:
Measured line fluxes in 10-4 photons s-1 cm-2 of CC Eri.
Table A.2:
Measured line fluxes in 10-4 photons s-1 cm-2 of Algol.
Table A.3:
Measured line fluxes in 10-4 photons s-1 cm-2 of 47 Cas.
Table A.4:
Measured line fluxes in 10-4 photons s-1 cm-2 of EK Dra.
Table A.5:
Measured line fluxes in 10-4 photons s-1 cm-2 of HR1099.
Table A.6:
Measured line fluxes in 10-4 photons s-1 cm-2 of Proxima Cen.
Table A.7:
Measured line fluxes in 10-4 photons s-1 cm-2 of  Gem.
Gem.
Table A.8:
Measured line fluxes in 10-4 photons s-1 cm-2 of 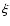 Boo.
Boo.
- Anders, E., & Grevesse,
N. 1989, Geochimica et Cosmochimica Acta, 53, 197 [NASA ADS] [CrossRef]
(In the text)
-
Antiochos, S. K. 1980, ApJ, 241, 385 [NASA ADS] [CrossRef]
- Asplund, M.,
Grevesse, N., & Sauval, A. J. 2005, Cosmic Abundances
Records of Stellar Evolution and Nucleosynthesis in honor of David
L. Lambert, ed. F. N. Bash, & T. G. Barnes, ASP
Conf. Ser., 336, 25
(In the text)
- Audard, M.,
& Güdel, M. 1999, ApJ, 513, 53 [NASA ADS] [CrossRef]
(In the text)
- Audard, M.,
Güdel, M., Drake, J. J., & Kashyap, V. L. 2000,
ApJ, 541, 396 [NASA ADS] [CrossRef]
- Audard, M.,
Güdel, M., & Mewe, R. 2001, A&A, 365, 318 [NASA ADS] [CrossRef]
(In the text)
- Audard, M.,
Güdel, M., Sres, A., Raassen, A. J. J., & Mewe, R. 2003,
A&A, 398, 1137 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Ball, B., Drake, J.
J., Lin, L., et al. 2005, ApJ, 634, 1336 [NASA ADS] [CrossRef]
- Bar-Shalom, A.,
Klapisch, M., & Oreg, J. 2001, J. Quant. Spectr. Radiat.
Transfer, 71, 169 [NASA ADS] [CrossRef]
(In the text)
- Behar, E.,
Cottam, J., & Kahn, S. M. 2001, ApJ, 548, 966 [NASA ADS] [CrossRef]
(In the text)
- Berlicki,
A., Heinzel, P., Schmieder, B., Mein, P., & Mein, N. 2005,
A&A, 430, 679 [NASA ADS] [CrossRef] [EDP Sciences]
- Brinkman,
A. C., Behar, E., Güdel, M., et al. 2001, A&A, 365,
324 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Budding, E.,
Erdem, A., Cicek, C., et al. 2004, A&A, 417, 263 [NASA ADS] [CrossRef] [EDP Sciences]
-
Caramazza, M., Flaccomio, E., Micela, G., et al. 2007,
A&A, 471, 645 [NASA ADS] [CrossRef] [EDP Sciences]
-
Crespo-Chacón, I., Micela, G., Reale, F., et al. 2007,
A&A, 471, 929 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Drake, J., &
Testa, P. 2005, Nature, 436, 525 [NASA ADS] [CrossRef]
(In the text)
- Drake, J. J.,
Laming, J. M., & Widing, K. G. 1995, ApJ, 443, 393 [NASA ADS] [CrossRef]
- Drake, J. J.,
Laming, J. M., & Widing, K. G. 1997, ApJ, 478, 403 [NASA ADS] [CrossRef]
(In the text)
- Duemmler,
R., Ilyin, I. V., & Tuominen, I. 1997, 123, 209
- Feldman, U.
1992, Phys. Scr., 46, 202 [NASA ADS] [CrossRef]
- Feldman, U.,
& Widing, K. G. 1990, ApJ, 363, 292 [NASA ADS] [CrossRef]
(In the text)
- Fludra, A.,
& Schmelz, J. T. 1995, ApJ, 447, 936 [NASA ADS] [CrossRef]
(In the text)
- Gu, M. F. 2003, ApJ,
590, 1131 [NASA ADS] [CrossRef] and Private communication
(In the text)
- Güdel, M.,
Guinan, E. F., & Skinner, S. L. 1998, The 10th Cambridge
Workshop on Cool Stars, Stellar Systems and the Sun,
ed. R. A. Donahue, & J. A. Bookbinder
(San Fransisco: ASP), ASP Conf. Ser., 154, 1041
- Güdel, M.,
Linsky, J. L., Brown, A., & Nagase, F. 1999, ApJ, 511, 405 [NASA ADS] [CrossRef]
(In the text)
- Güdel,
M., Audard, M., Smith, K. W., et al. 2002a, ApJ, 577, 371 [NASA ADS] [CrossRef]
(In the text)
- Güdel,
M., Audard, M., & Skinner, S. L. 2002b, ApJ, 580, L73 [NASA ADS] [CrossRef]
(In the text)
- Güdel, M.,
Audard, M., Kashyap, V. L., Drake, J., & Guinan, E. F.
2003, ApJ, 582, 423 [NASA ADS] [CrossRef]
- Güdel, M.,
Audard, M., Reale, F., Skinner, S. L., & Linsky,
J. L. 2004, A&A, 416, 713 [NASA ADS] [CrossRef] [EDP Sciences]
- Hudson, H. S.
1991, Solar Phys., 133, 357 [NASA ADS] [CrossRef]
-
Huenemoerder, D. P., Canizares, C. R., Drake, J. J., &
Sanz-Forcada, J. 2003, ApJ, 595, 1131 [NASA ADS] [CrossRef]
- Kashyap, V.
L., Drake, J. J., Güdel, M., & Audard, M. 2002, ApJ, 580,
1118 [NASA ADS] [CrossRef]
- Laming, J. M.,
Drake, J. J., & Widing, K. G. 1995, ApJ, 443, 416 [NASA ADS] [CrossRef]
- Perryman, M. A.
C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323,
L49 [NASA ADS]
- Maggio, A.,
Flaccomio, E., Favata, F., et al. 2007, ApJ, 660, 1462 [NASA ADS] [CrossRef]
- Mazzotta,
P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998,
A&AS, 133, 403 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Milligan,
R. O., Gallagher, P. T., Mathioudakis, M., & Keenan, F. P.
2006, ApJ, 642, 169 [NASA ADS] [CrossRef]
(In the text)
- Neupert, W.
M. 1968, ApJ, 153, L59 [NASA ADS] [CrossRef]
(In the text)
- Nordon, R.,
& Behar, E. 2007, A&A, 464, 309 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Nordon, R.,
Behar, E., & Güdel, M. 2006, A&A, 446, 621 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Osten, R. A.,
Ayres, T. R., Brown, A., Linsky, J. L., & Krishnamurthi, A.
2003, ApJ, 582, 1073 [NASA ADS] [CrossRef]
- Ottmann, R.,
& Schmitt, J. H. M. M. 1996, A&A, 307,
813 [NASA ADS]
(In the text)
- Raassen, A.
J. J., Mewe, R., Audard, M., et al. 2002, A&A, 389,
228 [NASA ADS] [CrossRef] [EDP Sciences]
- Raassen, A.
J. J., Mewe, R., Audard, M., & Güdel, M. 2003, 411,
509
(In the text)
- Raassen, A.
J. J., Mitra-Kraev, U., & Güdel, M. 2007, MNRAS, 379,
1075 [NASA ADS] [CrossRef]
(In the text)
-
Schmieder, B., Forbes, T. G., Malherbe, J. M., & Machado,
M. E. 1987, ApJ, 317, 956 [NASA ADS] [CrossRef]
- Reale, F.,
Güdel, M., Peres, G., & Audard, M. 2004, A&A, 416,
733 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Sanz-Forcada, J.,
Favata, F., & Micela, G. 2004, A&A, 416, 281 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Schmitt, J.
H. M. M., Ness, J. U., & Franco, G. 2003, A&A, 412,
849 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Schmelz, J.
T. 1993, ApJ, 408, 373 [NASA ADS] [CrossRef]
(In the text)
-
Segransan, D., Kervella, P., Forveille, T., & Queloz, D. 2003,
A&A, 397, L5 [NASA ADS] [CrossRef] [EDP Sciences]
-
Strassmeier, K. G., Hall, D. S., Fekel, F. C., & Scheck, M.
1993, A&AS, 100, 173 [NASA ADS]
- Tellesci,
A., Güdel, M., Briggs, K., et al. 2005, ApJ, 622,
653 [NASA ADS] [CrossRef]
(In the text)
- Testa, P., Reale,
F., Garcia-Alvarez, D., & Huenemoerder, D. P. 2007, ApJ,
663, 1232 [NASA ADS] [CrossRef]
(In the text)
- Widing, K. G.,
& Feldman, U. 2001, ApJ, 555, 426 [NASA ADS] [CrossRef]
(In the text)
- Widing, K. G.,
Landi, E., & Feldman, U. 2005, ApJ, 622, 1215 [NASA ADS] [CrossRef]
- Wood, B. E., &
Linsky, J. L. 2006, ApJ, 643, 444 [NASA ADS] [CrossRef]
(In the text)
- Zarro, D. M.,
& Lemen, J. R. 1988, ApJ, 329, 456 [NASA ADS] [CrossRef]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{8848fig1.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg11.gif)
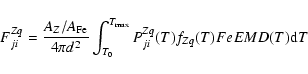
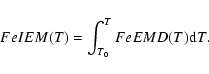
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{8848fig2.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=17.6cm,clip]{8848fig3.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg24.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{8848fig4.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg27.gif)
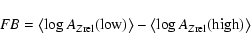
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8848fig5.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg40.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8848fig6.eps}\end{figure}](/articles/aa/full/2008/17/aa8848-07/Timg45.gif)