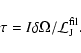A&A 482, 597-605 (2008)
DOI: 10.1051/0004-6361:20078620
Angular momentum transport by internal gravity waves
IV. Wave generation by surface convection zone, from the pre-main sequence
to the early-AGB in intermediate mass stars
S. Talon1 - C. Charbonnel2,3
1 - Département de Physique, Université de Montréal, Montréal PQ H3C 3J7, Canada
2 - Geneva Observatory, University of Geneva, ch. des Maillettes 51, 1290 Sauverny, Switzerland
3 - Laboratoire d'Astrophysique de Toulouse et Tarbes, CNRS UMR 5572, OMP, Université Paul
Sabatier 3, 14 Av. E. Belin, 31400 Toulouse, France
Received 5 September 2007 / Accepted 26 December 2007
Abstract
Context. This is the fourth in a series of papers that deal with angular momentum transport by internal gravity waves in stellar interiors.
Aims. Here, we want to examine the potential role of waves in other evolutionary phases than the main sequence.
Methods. We study the evolution of a 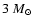 Population I model from the pre-main sequence to the early-AGB phase and examine whether waves can lead to angular momentum redistribution and/or element diffusion at the external convection zone boundary.
Population I model from the pre-main sequence to the early-AGB phase and examine whether waves can lead to angular momentum redistribution and/or element diffusion at the external convection zone boundary.
Results. We find that, although waves produced by the surface convection zone can be ignored safely for such a star during the main sequence, it is not the case for later evolutionary stages. In particular, angular momentum transport by internal waves could be quite important at the end of the sub-giant branch and during the early-AGB phase. Wave-induced mixing of chemicals is expected during the early-AGB phase.
Key words: hydrodynamics - turbulence - waves -
methods: numerical - stars: interiors - stars: rotation
In recent years, several authors studied the impact of internal gravity waves (IGWs)
in a variety of main sequence stars. These waves were initially invoked as a source
of mixing in stellar interiors in low-mass stars with
an extended surface convection
zone (Press 1981; García López & Spruit 1991;
Schatzman 1993; Montalbán 1994) and also as an efficient process in the synchronization
of massive binary stars (Goldreich & Nicholson 1989). More recently, it was suggested that
IGWs may play a role in braking the solar core
(Schatzman 1993; Zahn et al. 1997;
Kumar & Quataert 1997). This idea was confirmed first in static models
(Talon et al. 2002) and recently in the complete evolution of solar-mass models,
evolved all the way from the pre-main sequence to 4.6 Gy (Charbonnel & Talon 2005).
All these authors find that IGWs are easily excited,
and a similar conclusion is reached by
studies of convection on top of a stably stratified layer in 2D and 3D hydrodynamic
numerical simulations (e.g. Hurlburt et al. 1986, 1994;
Andersen 1994; Nordlund et al. 1996; Kiraga et al. 2003; Dintrans et al. 2005; Rogers &
Glatzmeier 2005a,b). These waves have a strong impact on stellar evolution,
especially through their effect on the rotation profile.
Through differential filtering, IGWs indeed play a major role in the redistribution
of angular momentum in stars, which determines the extent and magnitude of
rotation-induced mixing (Talon & Charbonnel 2005, hereafter TC05).
In the spirit of applying a unique set of physical
principles to stellar evolution, one needs to assess the impact of such waves on stars of
all masses and at various evolutionary stages.
It is our purpose in this series of papers to consistently examine the full
Hertzsprung-Russel diagram (HRD) for determining when such waves are efficiently emitted and
how they can affect stars when their complete rotational history is being
considered.
In Talon & Charbonnel (2003, hereafter Paper I; see also
Talon & Charbonnel 1998),
we showed how the appearance of IGWs in
solar-metallicity main sequence stars with an effective temperature
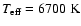 (i.e., when the surface convection zone becomes
substantial) can explain the existence of the
lithium dip
(i.e., when the surface convection zone becomes
substantial) can explain the existence of the
lithium dip![[*]](/icons/foot_motif.gif) in stars undergoing rotational mixing.
in stars undergoing rotational mixing.
In Talon & Charbonnel (2004, hereafter Paper II), we examined the
IGW generation in Population II main sequence stars.
We showed that, along the lithium plateau![[*]](/icons/foot_motif.gif) ,
the net angular momentum luminosity of IGWs is constant
and high enough to enforce quasi solid-body rotation similar to that
of the Sun in these stars.
We proposed that this behavior could play a major role in explaining
the constancy of the lithium abundance in the oldest
dwarf stars of our Galaxy (see also a discussion in
Charbonnel & Primas 2005).
,
the net angular momentum luminosity of IGWs is constant
and high enough to enforce quasi solid-body rotation similar to that
of the Sun in these stars.
We proposed that this behavior could play a major role in explaining
the constancy of the lithium abundance in the oldest
dwarf stars of our Galaxy (see also a discussion in
Charbonnel & Primas 2005).
Here, we wish to look at other evolutionary stages, especially the pre-main sequence
(PMS) and the more advanced stages for intermediate-mass stars.
We focus in particular on stars in which IGWs generation
by the surface convection zone is limited on the
main sequence, i.e., Pop I star originating from the left side of the Li dip.
To do so, we follow the evolution of a 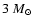 ,
Z=0.02 star
from the PMS up to the early asymptotic giant branch (early-AGB)
,
Z=0.02 star
from the PMS up to the early asymptotic giant branch (early-AGB)![[*]](/icons/foot_motif.gif) .
We estimate at which stages waves are efficiently generated in the outer convection zone.
This is a prerequisite for evaluating
their impact on the rotation profile of the corresponding stellar models.
We also look at the existence of a shear layer oscillation (or SLO) as a direct
source of turbulence and mixing at the convective boundary.
.
We estimate at which stages waves are efficiently generated in the outer convection zone.
This is a prerequisite for evaluating
their impact on the rotation profile of the corresponding stellar models.
We also look at the existence of a shear layer oscillation (or SLO) as a direct
source of turbulence and mixing at the convective boundary.
We begin in Sect. 2 with a description of
the evolution of relevant characteristics for
our 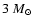 ,
Z=0.02 star.
In Sect. 3, we recall the main aspects
of the formalism
we used to evaluate the impact of IGWs on stellar evolution.
The following sections are devoted
to discussing the pre-main sequence (Sect. 4), the main sequence and
the sub-giant branch (Sect. 5), the red-giant branch
(Sect. 6), and
the clump and the early-AGB (Sect. 7).
,
Z=0.02 star.
In Sect. 3, we recall the main aspects
of the formalism
we used to evaluate the impact of IGWs on stellar evolution.
The following sections are devoted
to discussing the pre-main sequence (Sect. 4), the main sequence and
the sub-giant branch (Sect. 5), the red-giant branch
(Sect. 6), and
the clump and the early-AGB (Sect. 7).
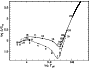 |
Figure 1:
Evolution of our 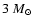 Pop I model in the HR diagram,
from the PMS to the early-AGB. Numbers correspond to
selected evolutionary points that are listed in
Table 1. For clarity, the PMS is drawn with a dashed line, and
the corresponding models are identified by squares, while the star symbol corresponds to
the appearance of the convective core.
The circles correspond to evolutionary points on the main sequence, sub-giant, and first
ascent giant branches, while triangles refer to evolutionary points on the clump and
on the early-AGB.
Pop I model in the HR diagram,
from the PMS to the early-AGB. Numbers correspond to
selected evolutionary points that are listed in
Table 1. For clarity, the PMS is drawn with a dashed line, and
the corresponding models are identified by squares, while the star symbol corresponds to
the appearance of the convective core.
The circles correspond to evolutionary points on the main sequence, sub-giant, and first
ascent giant branches, while triangles refer to evolutionary points on the clump and
on the early-AGB. |
| Open with DEXTER |
2 Evolution of relevant characteristics
In this paper we focus on a 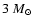 with a metallicity Z=0.02 computed with the
stellar evolution code STAREVOL (V2.30; Siess et al. 2000).
Details regarding the code and the input physics may be found in TC05
and Palacios et al. (2006).
The model was computed with classical assumptions, i.e., with neither atomic
diffusion nor rotation.
Convection is treated using the standard mixing length theory with
with a metallicity Z=0.02 computed with the
stellar evolution code STAREVOL (V2.30; Siess et al. 2000).
Details regarding the code and the input physics may be found in TC05
and Palacios et al. (2006).
The model was computed with classical assumptions, i.e., with neither atomic
diffusion nor rotation.
Convection is treated using the standard mixing length theory with
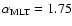 .
The treatment of convection has an impact on the excited wave spectrum
(see Sect. 3.1).
.
The treatment of convection has an impact on the excited wave spectrum
(see Sect. 3.1).
When a star evolves, the characteristics that are relevant to wave excitation
and to momentum extraction by IGWs change.
We thus chose a series of models (i.e., evolutionary points) to correctly represent
the evolution of the stellar structure in terms of convection zone properties,
therefore in terms of IGW characteristics.
The position of the selected points along the evolutionary track in the HR diagram
for the 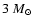 Pop I star is shown in Fig. 1.
Pop I star is shown in Fig. 1.
Figure 2 shows the
temperature at the boundary of both central and external convection zones at the selected
evolutionary points,
which is a way to characterize the depth and extension of these regions as
the surface and central temperatures (also shown in the figure) of the star evolve.
In such an intermediate-mass star, both central hydrogen- and helium-burning occur
in a convective core. Wave excitation by core convection on the main sequence
is discussed elsewhere (Pantillon et al. 2007, Paper III).
Here we only focus on wave excitation by the surface convection zone.
Figures 3 and 4 illustrate the evolution of the main
properties that are required to understand the behavior of IGWs in the
framework described in Sect. 3.
Wave excitation is stronger when the convective scale
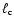 is larger. However, when the turn-over timescale
is larger. However, when the turn-over timescale
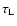 becomes too large,
this efficiency diminishes.
As we shall see in Sect. 3 and subsequent sections, the combination of these
two factors produces large differences in the overall efficiency of wave generation
as the stellar structure evolves.
Another important property for wave-induced transport is the thermal diffusivity
becomes too large,
this efficiency diminishes.
As we shall see in Sect. 3 and subsequent sections, the combination of these
two factors produces large differences in the overall efficiency of wave generation
as the stellar structure evolves.
Another important property for wave-induced transport is the thermal diffusivity
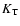 at the top of the radiative region.
On the main sequence for the star we focus on,
at the top of the radiative region.
On the main sequence for the star we focus on, 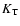 is so large that all
the low frequency waves
(here, we mean waves with
is so large that all
the low frequency waves
(here, we mean waves with
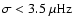 )
are dissipated as soon as they are
formed, hence the absence of a filtered flux in the corresponding models (see
Sect. 5).
)
are dissipated as soon as they are
formed, hence the absence of a filtered flux in the corresponding models (see
Sect. 5).
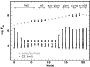 |
Figure 2:
Evolution of the temperature at the boundaries of convection zones for
the evolutionary points selected for the 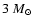 Pop I star and given
in Table 1. Core and surface (i.e.,
Pop I star and given
in Table 1. Core and surface (i.e.,
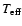 )
temperatures are also shown.
The evolutionary phases are indicated. )
temperatures are also shown.
The evolutionary phases are indicated. |
| Open with DEXTER |
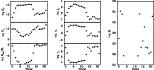 |
Figure 3:
Evolution of the surface convection zone properties for the
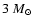 Pop I
evolutionary points from Table 1. It shows the thermal conductivity
Pop I
evolutionary points from Table 1. It shows the thermal conductivity
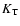 (in
(in
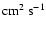 )
at the convective boundary,
the convective flux )
at the convective boundary,
the convective flux
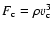 (in
(in
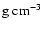 )
taken )
taken
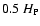 into the convection zone, the mass of the convection zone,
the spherical harmonic degree corresponding to the convective scale
into the convection zone, the mass of the convection zone,
the spherical harmonic degree corresponding to the convective scale
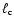 ,
the convective frequency ,
the convective frequency
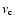 (in
(in 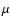 Hz), the typical convective timescale Hz), the typical convective timescale
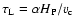 ,
as well as the total energy
luminosity (in ,
as well as the total energy
luminosity (in
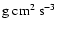 )
prior to any damping in waves
(this is for waves with )
prior to any damping in waves
(this is for waves with
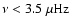 and
and
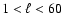 ). ). |
| Open with DEXTER |
Finally, damping also depends strongly on the Brunt-Väisälä frequency
(Eq. (7)), whose thermal part is given by
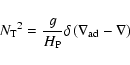 |
(2) |
with
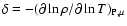 ,
and other
symbols have their usual meaning. From Fig. 4 we see that
during the PMS, the star's contraction leads to an increase in gravity and a
reduction of the pressure scale height, which produce a large increase in
,
and other
symbols have their usual meaning. From Fig. 4 we see that
during the PMS, the star's contraction leads to an increase in gravity and a
reduction of the pressure scale height, which produce a large increase in
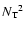 when combined. Later, during the giant phase, the expansion
of the outer layers produces a
large decrease in
when combined. Later, during the giant phase, the expansion
of the outer layers produces a
large decrease in
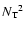 outside the hydrogen-burning shell. More important, core
contraction produces a major increase inside this shell; in fact,
outside the hydrogen-burning shell. More important, core
contraction produces a major increase inside this shell; in fact,
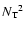 becomes so
large there that (low-frequency) waves will be unable to cross that boundary.
A large angular momentum deposition is expected there, provided there is differential
rotation above to produce a bias in the local wave flux.
becomes so
large there that (low-frequency) waves will be unable to cross that boundary.
A large angular momentum deposition is expected there, provided there is differential
rotation above to produce a bias in the local wave flux.
 |
Figure 4:
Evolution of the (thermal part of the) Brunt-Väisälä frequency vs. mass
for our 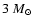 Pop I star.
( Top) The dashed lines correspond to PMS models and
the continuous lines,
to MS models. In PMS models,
Pop I star.
( Top) The dashed lines correspond to PMS models and
the continuous lines,
to MS models. In PMS models,
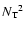 increases with evolution, while it decreases
in MS models. The shade of gray becomes lighter for more evolved models.
The dashed arrow corresponds to the evolution during the PMS and the continuous one
to the evolution during the MS.
( Bottom) The continuous lines correspond
to sub-giants and giants, the short-dashed lines to
the clump, and the long-dashed lines to early-AGB models.
In the outer layers,
increases with evolution, while it decreases
in MS models. The shade of gray becomes lighter for more evolved models.
The dashed arrow corresponds to the evolution during the PMS and the continuous one
to the evolution during the MS.
( Bottom) The continuous lines correspond
to sub-giants and giants, the short-dashed lines to
the clump, and the long-dashed lines to early-AGB models.
In the outer layers,
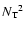 diminishes
with time while it is the opposite in the core.
The arrows indicate time evolution.
diminishes
with time while it is the opposite in the core.
The arrows indicate time evolution. |
| Open with DEXTER |
3 Formalism
The formalism we use to describe IGW properties is extensively described elsewhere
(Papers I and II, and TC05).
Here, we only recall the main features of our model and discuss the
critical physical principles.
3.1 Wave spectrum
In terms of angular momentum evolution, the relevant parameter is the filtered
angular momentum luminosity slightly below the convection envelope
(hereafter CE).
To get that luminosity, we first need to obtain the spectrum of excited waves.
As we did in previous studies, we apply
the Goldreich et al. (1994) formalism to IGWs to calculate this spectrum.
The energy flux per unit frequency
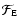 is then
is then
 |
Figure 5:
Evolution of the spectrum of angular momentum luminosity
integrated over
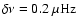 (in (in
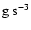 prior to any damping of IGWs
on the PMS (upper row)
and from the giant branch to the early AGB in the
prior to any damping of IGWs
on the PMS (upper row)
and from the giant branch to the early AGB in the 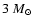 Pop I star.
Models 4 to 11 have no waves with
Pop I star.
Models 4 to 11 have no waves with
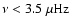 and are thus not shown here.
and are thus not shown here. |
| Open with DEXTER |
![$\displaystyle {\cal F}_{\rm E} \left(\ell, \omega \right)= \frac{\omega^2}{4\pi...
...(\ell+1)/2r^2\right] \frac{v_{\rm c}^3 L^4 }{1
+ (\omega \tau_{\rm L})^{15/2}},$](/articles/aa/full/2008/17/aa8620-07/img53.gif) |
|
|
(3) |
where
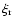 and
and
![$[\ell(\ell+1)]^{1/2}\xi_{\rm h}$](/articles/aa/full/2008/17/aa8620-07/img55.gif) are the radial and horizontal
displacement wave functions, which are normalized to unit energy flux just
below the convection zone,
are the radial and horizontal
displacement wave functions, which are normalized to unit energy flux just
below the convection zone, 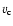 is the convective velocity,
is the convective velocity,
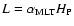 the radial
size of an energy bearing turbulent eddy,
the radial
size of an energy bearing turbulent eddy,
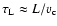 the
characteristic convective time, and
the
characteristic convective time, and 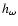 is the
radial size of the largest eddy at depth r with characteristic frequency
of
is the
radial size of the largest eddy at depth r with characteristic frequency
of 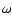 or higher (
or higher (
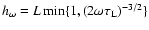 ).
The radial wave number
).
The radial wave number 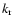 is related to the horizontal wave number
is related to the horizontal wave number 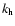 by
by
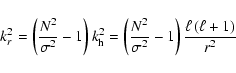 |
(4) |
where N2 is the Brunt-Väisälä frequency. In the convection zone, the mode is
evanescent and the penetration depth varies as
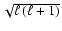 .
The momentum flux per unit frequency
.
The momentum flux per unit frequency
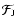 is then related to the
kinetic energy flux by
is then related to the
kinetic energy flux by
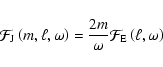 |
(5) |
(Goldreich & Nicholson 1989; Zahn et al. 1997).
We integrate this quantity horizontally to get an angular momentum
luminosity
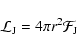 |
(6) |
which, in the absence of dissipation, has the advantage of being a conserved quantity
(Bretherton 1969; Zahn et al. 1997).
This angular momentum luminosity, integrated over
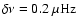 ,
is illustrated in Fig. 5 for our selected evolutionary
points, that have low frequency waves with
,
is illustrated in Fig. 5 for our selected evolutionary
points, that have low frequency waves with
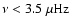 .
.
Each wave then travels inward and is damped by thermal diffusivity and by viscosity.
The local momentum luminosity of waves is given by
![\begin{displaymath}{\cal L}_{\rm J}(r) = \sum_{\sigma, \ell, m} {{\cal L}_{\rm J...
...ft(r_{\rm cz} \right)\exp \left[-\tau(r, \sigma, \ell) \right]
\end{displaymath}](/articles/aa/full/2008/17/aa8620-07/img69.gif) |
(7) |
where ``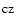 '' refers to the base of the convection zone.
'' refers to the base of the convection zone.
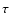 corresponds to the integration of the local damping rate and takes into account
the mean molecular weight stratification
corresponds to the integration of the local damping rate and takes into account
the mean molecular weight stratification
![\begin{displaymath}\tau(r, \sigma, \ell) = \left[\ell(\ell+1) \right]^{3\over2} ...
... \over N^2 - \sigma^2}\right)^{1 \over 2} {{\rm d}r
\over r^3}
\end{displaymath}](/articles/aa/full/2008/17/aa8620-07/img72.gif) |
(8) |
(Zahn et al. 1997).
In this expression,
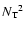 is the thermal part of the Brunt-Väisälä
frequency (see Eq. (1)),
is the thermal part of the Brunt-Väisälä
frequency (see Eq. (1)),
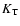 the thermal diffusivity, and
the thermal diffusivity, and
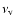 the (vertical) turbulent viscosity.
Finally
the (vertical) turbulent viscosity.
Finally 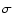 is the local, Doppler-shifted frequency
is the local, Doppler-shifted frequency
![\begin{displaymath}\sigma(r) = \omega - m
\left[\Omega(r)-\Omega _{\rm cz} \right]
\end{displaymath}](/articles/aa/full/2008/17/aa8620-07/img75.gif) |
(9) |
and 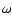 is the wave frequency in the reference frame of the convection
zone.
Let us mention that only the radial velocity gradients are taken into account
in this expression for damping. This is because angular momentum transport
is dominated by the low-frequency waves (
is the wave frequency in the reference frame of the convection
zone.
Let us mention that only the radial velocity gradients are taken into account
in this expression for damping. This is because angular momentum transport
is dominated by the low-frequency waves (
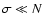 ), which implies
that horizontal gradients are much smaller than vertical ones (cf. Eq. (3)).
), which implies
that horizontal gradients are much smaller than vertical ones (cf. Eq. (3)).
When meridional circulation, turbulence, and waves are all taken into account,
the evolution of angular momentum follows
![$\displaystyle \rho \frac{{\rm d}}{{\rm d}t} \left[r^2 {\Omega} \right]=
\frac{1...
...- \frac{3}{8\pi} \frac{1}{r^2} \frac{\partial}{\partial r}{{\cal L}_{\rm J}(r)}$](/articles/aa/full/2008/17/aa8620-07/img77.gif) |
|
|
(10) |
(Talon & Zahn 1998),
where U is the radial meridional circulation velocity.
Horizontal averaging was performed for this equation, and meridional circulation was
considered only at first order. In this paper, this equation is used only to calculate the
fast SLO's dynamics (see Sect. 3.2) and thus, U is neglected. The
complete equation is used when longer timescales are involved as discussed e.g. in
Charbonnel & Talon (2005).
In this work, we neglect any contribution from convective overshoot due to the lack
of a usable prescription (although work is underway to
include this effect, Belkacem et al., in preparation).
We expect this contribution to be more efficient for low-frequency, low-degree
waves, and as such, it would have an impact mostly on the timescale for
angular momentum extraction in the core (see Sect. 3.3).
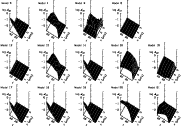 |
Figure 6:
Differential wave amplitude variation
over a depth of 0.05 R* (see text). |
| Open with DEXTER |
3.2 Shear layer oscillation (SLO)
One key feature when looking at the wave-mean flow interaction is that the dissipation of
IGWs produces an increase in the local differential rotation, which is caused by the
increased dissipation of waves that travel in the direction of the shear (see
Eqs. (7) and (8)). In conjunction with
viscosity, this leads to the formation of an oscillating doubled-peak shear layer that
oscillates on a short timescale (Gough & McIntyre 1998;
Ringot 1998; Kumar et al. 1999).
This shear layer oscillation (hereafter SLO) occurs if the deposition of angular
momentum by IGWs is large enough when compared with viscosity![[*]](/icons/foot_motif.gif) (Kim & MacGregor 2001;
see also a discussion in TC05, Sect. 3.1).
(Kim & MacGregor 2001;
see also a discussion in TC05, Sect. 3.1).
To calculate the turbulence associated with this oscillation, we relied on
a standard prescription for shear turbulence away from regions
with mean molecular weight gradients
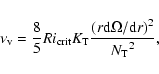 |
(11) |
which takes radiative losses into account (Townsend In the text
1958;
Maeder 1995). This coefficient is time-averaged over a complete
oscillation cycle (for details, see TC05, Sect. 3.1).
The first feature we are interested in is whether or not the formation of
such an SLO is possible at various evolutionary stages, since the associated turbulence
could produce mixing in a small region below the surface convection zone.
Figure 6 shows the differential wave amplitude
variation in the region of SLO formation. The plotted quantity corresponds to
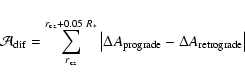 |
(12) |
where 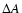 corresponds to the local amplitude variation,
caused by radiative damping (see Eq. (7))
for the
corresponds to the local amplitude variation,
caused by radiative damping (see Eq. (7))
for the  wave and for a local gradient of
wave and for a local gradient of
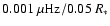 .
This choice of differential rotation is quite arbitrary, but TC05 (see their Sect. 3.2)
show that, as long as
differential rotation is not too strong (that is, it remains below about
.
This choice of differential rotation is quite arbitrary, but TC05 (see their Sect. 3.2)
show that, as long as
differential rotation is not too strong (that is, it remains below about
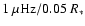 ), differential damping is linear. The value
of 0.05 R* is typical of the thickness of the SLO (TC05).
), differential damping is linear. The value
of 0.05 R* is typical of the thickness of the SLO (TC05).
When
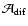 is large, prograde and retrograde waves
are deposited at different locations in the region of SLO formation and thus
contribute to the potential generation of an SLO. As the wave frequency rises,
the Doppler shift is felt less by the star and
is large, prograde and retrograde waves
are deposited at different locations in the region of SLO formation and thus
contribute to the potential generation of an SLO. As the wave frequency rises,
the Doppler shift is felt less by the star and
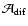 remains small.
For frequencies that are too low, the
waves can be damped even before the Doppler shift may take place (see e.g.
Model 1).
remains small.
For frequencies that are too low, the
waves can be damped even before the Doppler shift may take place (see e.g.
Model 1).
To discuss the formation of the SLO,
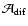 should be
multiplied by the angular momentum luminosity of waves, which is shown in
Fig. 5 for the GMK model.
This was done for example for models 13 and 15 in Fig. 7.
For these two models, the waves that would give rise to the appearance of an SLO are
quite similar, as the differential amplitude figure shows (Fig. 6).
However, there is an SLO only in model 13, because in model 15, the wave angular momentum
luminosity corresponding to such waves is simply too small.
We note that, for any other
excitation model, an SLO would be obtained for an angular momentum luminosity on the order of
1033-1034 (or more) in the region with
should be
multiplied by the angular momentum luminosity of waves, which is shown in
Fig. 5 for the GMK model.
This was done for example for models 13 and 15 in Fig. 7.
For these two models, the waves that would give rise to the appearance of an SLO are
quite similar, as the differential amplitude figure shows (Fig. 6).
However, there is an SLO only in model 13, because in model 15, the wave angular momentum
luminosity corresponding to such waves is simply too small.
We note that, for any other
excitation model, an SLO would be obtained for an angular momentum luminosity on the order of
1033-1034 (or more) in the region with
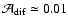 to 0.1.
Therefore, for any excitation model we can rapidly evaluate whether an SLO should
develop from our Fig. 6.
to 0.1.
Therefore, for any excitation model we can rapidly evaluate whether an SLO should
develop from our Fig. 6.
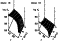 |
Figure 7:
Differential wave angular momentum luminosity variation
over a depth of 0.05 R* for models 13 and 15. |
| Open with DEXTER |
 |
Figure 8:
Net wave amplitude beyond a depth of 0.05 R* (see text). |
| Open with DEXTER |
The existence of such an SLO has been challenged by
Rogers & Glatzmeier (2006, hereafter RG06).
In 2D numerical simulations of penetrative convection in the Sun, they
find that IGWs are efficiently excited by convection, as did the other authors who studied
this (Hurlburt et al. 1986, 1994;
Andersen 1994; Nordlund et al. 1996;
Kiraga et al. 2003; Dintrans et al. 2005;
Rogers & Glatzmeier 2005a,b).
In these simulations, wave spectra are much broader than the ones
predicted in theoretical models based on Reynolds stresses (Kumar et al. 1999,
hereafter KTZ99).
However, contrary to the expectations of other authors (see in particular the
discussion by Kiraga et al. 2003), RG06
obtain an energy flux![[*]](/icons/foot_motif.gif) that is smaller
in the low-frequency regime
than the one calculated
by KTZ99, and that, even though one expects the excitation by convective plumes that has been
ignored by KTZ99 to yield a large contribution to wave generation.
that is smaller
in the low-frequency regime
than the one calculated
by KTZ99, and that, even though one expects the excitation by convective plumes that has been
ignored by KTZ99 to yield a large contribution to wave generation.
In their simulations, RG06 thus have a much weaker wave flux
in the low-frequency regime than what
is required to generate an SLO (see the above discussion in
Fig. 7),
although the one for the high frequency waves is much larger.
It may thus not be surprising that RG06 do not find such an SLO in their simulation.
Furthermore, the size of the SLO being smaller (in KTZ99) than the difference between the
rotation rate at the base of the convection zone (at the equator) and the base of the
tachocline, an SLO would not appear as a shear reversal in their simulation.
Last, the RG06 simulation is simply not long enough to show the SLO.
As pointed out by
the authors, in their numerical simulation there is differential rotation in the tachocline
driven by convective plumes. But the total duration of the simulation being only one year, it
would be impossible to see a superposed SLO since its timescale is expected to
be of about a few years, according to the KTZ99 calculations.
Furthermore, since RG06 have a reduced wave flux compared to KTZ99, this timescale
would be even longer, and thus clearly beyond the possibilities of the RG06 simulation.
![\begin{figure}
\par\includegraphics[origin=rb,angle=-90,width=11cm,clip]{8620fig9.ps}
\end{figure}](/articles/aa/full/2008/17/aa8620-07/Timg93.gif) |
Figure 9:
Shear layer oscillation in
the
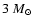 Pop I model at the evolutionary points where
this feature appears.
For each evolutionary point, successive profiles are separated by
Pop I model at the evolutionary points where
this feature appears.
For each evolutionary point, successive profiles are separated by
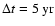 . . |
| Open with DEXTER |
Table 1:
Selected models along the evolutionary track of a 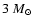 Pop I star.
The filtered angular momentum luminosity
Pop I star.
The filtered angular momentum luminosity
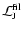 is taken as
0.05 R below the CZ (or at
is taken as
0.05 R below the CZ (or at
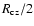 if it is larger)
for a differential rotation of
if it is larger)
for a differential rotation of
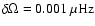 .
Also provided are the star's moment of inertia of the radiative
zone
.
Also provided are the star's moment of inertia of the radiative
zone 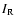 and the resulting timescale
and the resulting timescale
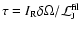 for IGWs.
The last column gives the time
for IGWs.
The last column gives the time 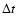 between consecutive models (with the convention
between consecutive models (with the convention
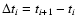 ).
No waves are generated in models 4 to 11.
).
No waves are generated in models 4 to 11.
3.3 Filtered angular momentum luminosity
We must also look at the secular effect of IGWs in the deep interior
(see TC05 for details).
In the presence of differential rotation, the dissipation of prograde and retrograde waves
in the SLO is
not symmetric, and this leads to a finite amount of angular momentum being deposited in the
interior beyond the SLO.
Figure 8 shows the net amplitude of waves
at a depth of 0.05 R*, defined by
 |
(14) |
for a local gradient of
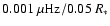 .
Multiplied
by the angular momentum luminosity of waves, this
is the filtered angular momentum luminosity
.
Multiplied
by the angular momentum luminosity of waves, this
is the filtered angular momentum luminosity
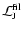 given
in Table 1 for our selected evolutionary points.
Let us mention that, in fact, the existence of an SLO is not even required
to obtain this differential damping between prograde and retrograde waves, so
as long as differential rotation exists at the base of the convection zone, waves will
have a net impact on the rotation rate of the interior.
The timescale required to delete the imposed differential rotation is
of the order of
given
in Table 1 for our selected evolutionary points.
Let us mention that, in fact, the existence of an SLO is not even required
to obtain this differential damping between prograde and retrograde waves, so
as long as differential rotation exists at the base of the convection zone, waves will
have a net impact on the rotation rate of the interior.
The timescale required to delete the imposed differential rotation is
of the order of
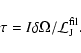 |
(15) |
The SLO's dynamics is studied by solving Eq. (9) with small timesteps
and using the whole wave spectrum, while for the secular evolution of the star,
one has to instead use the filtered angular momentum luminosity
(see TC05 for details).
All the relevant quantities are given
in Table 1 for our selected evolutionary points.
Let us also mention here that differential damping is required both for the SLO and for the
filtered angular momentum luminosity.
Since this relies on the Doppler shift of the frequency (see Eqs. (7)
and (8)), angular momentum redistribution will be dominated by
the low-frequency waves, which experience a larger Doppler shift, but that
is not so low that they will be immediately damped. Numerical
tests indicate that this occurs around (
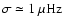 ).
).
4 Pre-main sequence
We start with a fully convective contracting star.
As it descends along the Hayashi track, a radiative core appears (Fig. 1).
In mass coordinates, the top of this radiative region migrates towards the surface until
the star reaches the main sequence. This is accompanied by a growth of the characteristic
convective length scale at the bottom of the convection zone
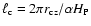 (see Fig. 3), which
temporarily favors the generation of waves (see models 0 to 2).
(see Fig. 3), which
temporarily favors the generation of waves (see models 0 to 2).
However, with further retraction of the envelope, the thermal diffusivity 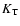 at the convective boundary increases,
which favors the disappearance of low-frequency and/or large degree waves
(see Fig. 5 and Eq. (7)).
This explains the reduction of the total energy flux
at the end of the PMS (models 3 to 6) and on the MS.
at the convective boundary increases,
which favors the disappearance of low-frequency and/or large degree waves
(see Fig. 5 and Eq. (7)).
This explains the reduction of the total energy flux
at the end of the PMS (models 3 to 6) and on the MS.
During the pre-main sequence, an SLO exists only for a very short period of time.
The evolution of the SLO for models 1 and 2 is shown in Fig. 9,
where the successive profiles are separated by 5 years.
The larger amplitude in model 1 compared to model 2 can be understood in terms
of thermal diffusivity: since 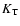 increases with radius, as the top of the radiative
zone migrates outwards with evolution, waves are dissipated more efficiently in
model 2 than in model 1. In model 3, damping is so large that the formation of
a SLO is no longer possible, and all low-frequency waves are dissipated in model 4.
The turbulent diffusion coefficient associated with this SLO, D (see Eq. (10)
and the discussion around it), is shown
in Fig. 10 as a function of reduced radius.
While the shear is much stronger in model 1 than in model 2, the magnitude
of D and width
of the turbulent regions are quite similar. This is because the reduced shear
is compensated for by the larger thermal diffusivity in model 2 (cf. Eq. (10)).
In both models,
D is relatively high just below the convective envelope, and it drops rapidly
with depth. It is negligible in the region with a temperature
(i.e.
increases with radius, as the top of the radiative
zone migrates outwards with evolution, waves are dissipated more efficiently in
model 2 than in model 1. In model 3, damping is so large that the formation of
a SLO is no longer possible, and all low-frequency waves are dissipated in model 4.
The turbulent diffusion coefficient associated with this SLO, D (see Eq. (10)
and the discussion around it), is shown
in Fig. 10 as a function of reduced radius.
While the shear is much stronger in model 1 than in model 2, the magnitude
of D and width
of the turbulent regions are quite similar. This is because the reduced shear
is compensated for by the larger thermal diffusivity in model 2 (cf. Eq. (10)).
In both models,
D is relatively high just below the convective envelope, and it drops rapidly
with depth. It is negligible in the region with a temperature
(i.e.
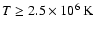 )
high enough for efficient lithium burning.
This temperature is attained at reduced radii of
)
high enough for efficient lithium burning.
This temperature is attained at reduced radii of
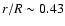 and 0.41
in models 1 and 2 respectively.
This implies that, for this mass, the transport of elements through wave-induced turbulence
has no impact on the pre-main sequence evolution of the surface abundance
of the light elements
such as lithium, beryllium, or boron (the latest two elements burning at an even
higher temperature)
and 0.41
in models 1 and 2 respectively.
This implies that, for this mass, the transport of elements through wave-induced turbulence
has no impact on the pre-main sequence evolution of the surface abundance
of the light elements
such as lithium, beryllium, or boron (the latest two elements burning at an even
higher temperature)![[*]](/icons/foot_motif.gif) .
.
The role of IGWs is more uncertain for the rotation profile.
In the case of rapid rotation (
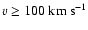 ), the initial
rotation profile is deleted by meridional circulation in a fraction of the main-sequence
lifetime. In a slow rotator, however, this is not the case, and the memory
of angular momentum transport by IGWs will influence
mixing
), the initial
rotation profile is deleted by meridional circulation in a fraction of the main-sequence
lifetime. In a slow rotator, however, this is not the case, and the memory
of angular momentum transport by IGWs will influence
mixing![[*]](/icons/foot_motif.gif) . Detailed evolutionary calculations of angular momentum
in the presence of internal waves should thus take this evolutionary phase into account
especially in the case of slow rotators (Charbonnel & Talon, in preparation).
. Detailed evolutionary calculations of angular momentum
in the presence of internal waves should thus take this evolutionary phase into account
especially in the case of slow rotators (Charbonnel & Talon, in preparation).
 |
Figure 10:
Turbulent wave-induced diffusion coefficient at the convection zone boundary
on the pre-main sequence in the 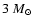 Pop I star.
Pop I star. |
| Open with DEXTER |
5 Main sequence and sub-giant branch
On the main sequence (models 7 to 9) and early on the sub-giant branch (models 10 and 11),
the surface convection zone of the star remains quite
shallow and contains no more than 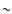
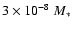 .
In the bottom part of
the convection zone, which is the main driver of IGWs, the mean convective
flux is too small (
.
In the bottom part of
the convection zone, which is the main driver of IGWs, the mean convective
flux is too small (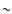
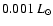 )
to excite IGWs efficiently
(see Fig. 3).
Furthermore, the thermal diffusivity below the convection zone is quite large,
and perturbations traveling into the radiative zone
are rapidly damped instead of becoming waves. This is the case in particular
for all the low-frequency waves that are needed for driving an SLO
)
to excite IGWs efficiently
(see Fig. 3).
Furthermore, the thermal diffusivity below the convection zone is quite large,
and perturbations traveling into the radiative zone
are rapidly damped instead of becoming waves. This is the case in particular
for all the low-frequency waves that are needed for driving an SLO![[*]](/icons/foot_motif.gif) (for waves with a frequency
(for waves with a frequency
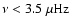 ,
,
 ).
There is thus no SLO or any secular effect on the rotation profile from this
exterior convection zone, both on the MS and at the beginning of the sub-giant branch
in such an intermediate-mass star.
).
There is thus no SLO or any secular effect on the rotation profile from this
exterior convection zone, both on the MS and at the beginning of the sub-giant branch
in such an intermediate-mass star.
This result agrees with the conclusions of Paper I, i.e.,
the total momentum luminosity in waves drops dramatically in main sequence
Pop I stars with initial masses higher than 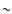
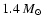 ,
i.e. stars originating from the left side of the Li dip, compared to stars
with lower initial mass.
,
i.e. stars originating from the left side of the Li dip, compared to stars
with lower initial mass.
Angular momentum transport by IGWs becomes important as the star moves farther along
the sub-giant branch.
Indeed the retraction of the convective envelope is accompanied by a diminution
of the thermal diffusivity and an increase in the convective flux.
To properly assess the importance of waves in the star's rotation, we should
compare the timescale 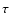 (Eq. (14)) with the lifetime of various evolutionary stages;
both quantities are given in Table 1.
Model 13 is of special interest here because it lies at the end of the sub-giant branch
(see Fig. 1) and supports a particularly large wave flux,
due to a unique combination
of many factors (including the convective time- and length-scales, see Fig. 3).
This implies that possible differential rotation, which could be a relic of the star's
main sequence history and subsequent contraction, will be strongly reduced by IGWs
when the star leaves the Hertzsprung gap. This will have a profound impact on the
subsequent evolution.
Let us also mention that, close to the core, waves could actually create a large differential
rotation. This was observed in the numerical simulation by RG06 and is
also visible when one looks at the Fig. 3 of
Talon et al. (2002), where, close to the core, strong
shears appear in the early stages of the simulation. Detailed calculations, including
meridional circulation, shear turbulence, and wave induced angular momentum transport, are
required to come to any conclusion other than that the wave will have a strong impact at
this stage.
(Eq. (14)) with the lifetime of various evolutionary stages;
both quantities are given in Table 1.
Model 13 is of special interest here because it lies at the end of the sub-giant branch
(see Fig. 1) and supports a particularly large wave flux,
due to a unique combination
of many factors (including the convective time- and length-scales, see Fig. 3).
This implies that possible differential rotation, which could be a relic of the star's
main sequence history and subsequent contraction, will be strongly reduced by IGWs
when the star leaves the Hertzsprung gap. This will have a profound impact on the
subsequent evolution.
Let us also mention that, close to the core, waves could actually create a large differential
rotation. This was observed in the numerical simulation by RG06 and is
also visible when one looks at the Fig. 3 of
Talon et al. (2002), where, close to the core, strong
shears appear in the early stages of the simulation. Detailed calculations, including
meridional circulation, shear turbulence, and wave induced angular momentum transport, are
required to come to any conclusion other than that the wave will have a strong impact at
this stage.
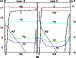 |
Figure 11:
Turbulent wave-induced diffusion coefficient at the convection zone boundary
in the 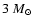 Pop I star ( left) on the red giant branch
and ( right) on the early-AGB
(wide continuous curve, left scale).
Superimposed is the logarithm of the mass fraction of H, 4He, 12C,
13C and 14N (right scale).
The abscissa is the scaled mass coordinate
Pop I star ( left) on the red giant branch
and ( right) on the early-AGB
(wide continuous curve, left scale).
Superimposed is the logarithm of the mass fraction of H, 4He, 12C,
13C and 14N (right scale).
The abscissa is the scaled mass coordinate 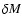 which equals 0 at the base of the hydrogen-burning shell and 1 at the base of the CE
(see text). Also shown is the Brunt-Väisälä frequency (wide dashed curve, right scale).
which equals 0 at the base of the hydrogen-burning shell and 1 at the base of the CE
(see text). Also shown is the Brunt-Väisälä frequency (wide dashed curve, right scale). |
| Open with DEXTER |
6 Red giant branch
As the star evolves to the red giant branch, the surface convection zone deepens,
and the thermal conductivity below the convection envelope is reduced
with the photon mean free path (models 12 to 16, see Fig. 3).
Wave excitation during this phase is quite similar to what has been
observed in PMS stars.
A SLO appears at the tip of the RGB (Model 16).
The corresponding diffusion coefficient is shown in Fig. 11,
together with the abundance profile of the lightest elements that are affected by shell
hydrogen-burning. These quantities are plotted against 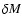 ,
which is a relative mass coordinate allowing for a blow-up of the
radiative region above the hydrogen-burning shell (hereafter HBS)
and is defined as
,
which is a relative mass coordinate allowing for a blow-up of the
radiative region above the hydrogen-burning shell (hereafter HBS)
and is defined as
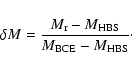 |
(16) |
Here 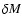 is equal to 1 at the base of the convective envelope and 0 at
the base of the HBS (where
X = 10-7).
The abundance profiles at that phase have been modified by dilution
during the first dredge-up episode and are being reconstructed by shell hydrogen-burning.
We see that D drops very rapidly just below the CE. Additionally,
the star leaves that phase very rapidly. As a consequence,
wave-induced turbulence is not expected to modify the surface abundances
on the RGB for such an intermediate-mass Pop I star.
is equal to 1 at the base of the convective envelope and 0 at
the base of the HBS (where
X = 10-7).
The abundance profiles at that phase have been modified by dilution
during the first dredge-up episode and are being reconstructed by shell hydrogen-burning.
We see that D drops very rapidly just below the CE. Additionally,
the star leaves that phase very rapidly. As a consequence,
wave-induced turbulence is not expected to modify the surface abundances
on the RGB for such an intermediate-mass Pop I star.
The rotation profile should hardly be influenced by IGWs for that star
on the RGB, in view of the timescale 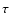 (Eq. (14)) which
is now almost two orders of magnitude higher than the lifetime at that
stage (see Table 1).
(Eq. (14)) which
is now almost two orders of magnitude higher than the lifetime at that
stage (see Table 1).
7 Clump and early-AGB
Model 16 marks the ignition of central He-burning in the non-degenerate core,
and model 17 corresponds to the arrival of the star in the so-called clump
in the HR diagram.
At that moment the convective envelope strongly retreats in mass,
before deepening again slowly until the central exhaustion of helium,
which occurs for model 18![[*]](/icons/foot_motif.gif) .
Then the star moves to the early-AGB.
During that period, the total energy flux in waves remains relatively modest
and there is no SLO.
.
Then the star moves to the early-AGB.
During that period, the total energy flux in waves remains relatively modest
and there is no SLO.
The situation changes drastically in model 21 however.
At that point, the convective envelope has reached its maximum depth,
which stays almost constant until the first thermal pulse occurs
(at
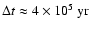 after model 21).
During that second dredge-up, the convective envelope has engulfed most (but not all)
of the more external step of the 14N profile left behind by the CN-cycle, which explains
the steep gradients in the abundance profiles of that element and of the carbon isotopes
just below the convective envelope. In this region, D is relatively high, and
we expect that the associated mixing leads to an additional slight variation in the surface
abundance of 12C and 13C (but not of the carbon isotopic ratio since CN is
at the equilibrium), and of 14N with respect to standard second dredge-up.
after model 21).
During that second dredge-up, the convective envelope has engulfed most (but not all)
of the more external step of the 14N profile left behind by the CN-cycle, which explains
the steep gradients in the abundance profiles of that element and of the carbon isotopes
just below the convective envelope. In this region, D is relatively high, and
we expect that the associated mixing leads to an additional slight variation in the surface
abundance of 12C and 13C (but not of the carbon isotopic ratio since CN is
at the equilibrium), and of 14N with respect to standard second dredge-up.
For the transport of angular momentum, the rapid increase in the Brunt-Väisälä
frequency in the HBS could produce strong shears that, in complete calculations taking
rotational mixing into account, would be an important source of mixing during the early-AGB.
This would modify the composition close to the core and would strongly modify
the subsequent evolution.
In this paper, we examined when and how internal gravity waves
generated by surface convection zones are expected to have
an impact on stellar models that only have shallow surface convection zones
during the main sequence. We find that several evolutionary stages can
experience angular momentum redistribution by IGWs:
- During the pre-main sequence, just as the star leaves the Hayashi track,
waves are efficiently excited and filtered. While this has no impact on
light element abundances and only has a limited effect on fast rotators (see
Sect. 4), it could strongly modify the main-sequence rotation profile
of slow rotators.
- At the end of the sub-giant branch (i.e., at the boundary of the
Hayashi track), angular momentum redistribution is oncemore quite efficient and
could totally change the angular momentum profile that has been established during
the main sequence and the sub-giant phase contraction.
- During the early-AGB, IGW generation again becomes substantial: mixing can be
expected to occur both at the convective boundary, due to the presence of an SLO and at the
hydrogen-burning-shell boundary, due to the enhanced damping of waves caused by the
increase in the Brunt-Väisälä frequency.
Stellar models including meridional circulation, shear turbulence, and wave-induced
mixing are underway to quantify this impact (Charbonnel & Talon, in preparation).
Acknowledgements
We thank the referee for her/his comments that helped us improve the
manuscript. C.C. is supported by the Swiss National Science Foundation (FNS).
We acknowledge the financial support of the Programme National de
Physique Stellaire (PNPS) of CNRS/INSU, France.
Computational resources were provided by the Réseau québécois de
calcul de haute performance (RQCHP).
- Andersen, B. N.
1994, Sol. Phys., 152, 241 [NASA ADS] [CrossRef]
(In the text)
-
Balachandran, S. 1995, ApJ, 446, 203 [NASA ADS] [CrossRef]
- Boesgaard, A.
M., & Tripicco, M. J. 1986, ApJ, 302, L49 [NASA ADS] [CrossRef]
- Bretherton,
F. P. 1969, Quart. J. R. Met. Soc., 95, 213 [NASA ADS] [CrossRef]
(In the text)
- Charbonnel,
C., & Primas, F. 2005, A&A, 442, 961 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [NASA ADS] [CrossRef]
- Dintrans, B.,
Brandenburg, A., Nordlund, Å, & Stein, R. F. 2005,
A&A, 438, 365 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
García López, R. J., & Spruit, H. C. 1991, ApJ, 377,
268 [NASA ADS] [CrossRef]
(In the text)
- Goldreich,
P., & Nicholson, P. D. 1989, ApJ, 342, 1079 [NASA ADS] [CrossRef]
(In the text)
- Goldreich,
P., Murray, N., & Kumar, P. 1994, ApJ, 424, 466 [NASA ADS] [CrossRef]
- Gough, D. O., &
McIntyre, M. E. 1998, Nature, 394, 755 [NASA ADS] [CrossRef]
(In the text)
- Kim Eun-jin,
& MacGregor, K. B. 2001, ApJ, 556, L117 [NASA ADS] [CrossRef]
- Kiraga, M., Jahn,
K., Stepien, K., & Zahn, J.-P. 2003, Acta Astron., 53, 321 [NASA ADS]
(In the text)
- Kumar, P., &
Quataert, E. J. 1997, ApJ, 475, L143 [NASA ADS] [CrossRef]
(In the text)
- Kumar, P., Talon, S.,
& Zahn, J.-P. 1999, ApJ, 520, 859 [NASA ADS] [CrossRef]
(In the text)
- Hurlburt, N.
E., Toomre, J., & Massaguer, J. M. 1986, ApJ, 311, 563 [NASA ADS] [CrossRef]
(In the text)
- Hurlburt, N.
E., Toomre, J., Massaguer, J. M., & Zahn, J.-P. 1994, ApJ, 421,
245 [NASA ADS] [CrossRef]
- Maeder, A. 1995,
A&A, 299, 84 [NASA ADS]
(In the text)
-
Montalbán, J. 1994, A&A, 281, 421 [NASA ADS]
(In the text)
- Nordlund, A.,
Stein, R. F., & Brandenburg, A. 1996, Bull. Astron. Soc. of
India, 24, 261 [NASA ADS]
(In the text)
- Palacios, A.,
Charbonnel, C., Talon, S., & Siess, L. 2006, A&A, 453,
261 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Pantillon, F.
P., Talon, S., & Charbonnel, C. 2007, A&A, 474, 155 [NASA ADS] [CrossRef] [EDP Sciences] (Paper
III)
(In the text)
- Press, W. H. 1981,
ApJ, 245, 286 [NASA ADS] [CrossRef]
(In the text)
- Ringot, O. 1998,
A&A, 335, 89 [NASA ADS]
(In the text)
- Rogers, T. M.,
& Glatzmeier, G. A. 2005a, ApJ, 620, 432 [NASA ADS] [CrossRef]
(In the text)
- Rogers, T. M.,
& Glatzmeier, G. A. 2005b, MNRAS, 364, 1135 [NASA ADS] [CrossRef]
- Rogers, T. M.,
& Glatzmeier, G. A. 2006, ApJ, 653, 765 [NASA ADS] [CrossRef] (RG06)
- Schatzman, E.
1993, A&A, 279, 431 [NASA ADS]
(In the text)
- Siess, L., Dufour,
E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS]
(In the text)
- Spite, M., &
Spite, F. 1982, Nature, 297, 483 [NASA ADS] [CrossRef]
- Talon, S., &
Charbonnel, C. 1998, A&A, 335, 959 [NASA ADS]
(In the text)
- Talon, S., &
Charbonnel, C. 2003, A&A, 405, 1025 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I)
(In the text)
- Talon, S., &
Charbonnel, C. 2004, A&A, 418, 1051 [NASA ADS] [CrossRef] [EDP Sciences] (Paper II)
(In the text)
- Talon, S., &
Charbonnel, C. 2005, A&A, 440, 981 [NASA ADS] [CrossRef] [EDP Sciences], TC05
(In the text)
- Talon, S., &
Kumar, P., & Zahn, J.-P. 2002, ApJ, 574, L175 [NASA ADS] [CrossRef]
(In the text)
- Talon, S., &
Richard, O., & Michaud, G. 2006, ApJ, 645, 634 [NASA ADS] [CrossRef]
- Talon, S., &
Zahn, J.-P. 1998, A&A, 329, 315 [NASA ADS]
- Townsend, A. A.
1958, J. Fluid Mech., 4, 361 [NASA ADS] [CrossRef]
(In the text)
-
Wallerstein, G., Herbig, G. H., & Conti, P. S. 1965, ApJ, 141,
610 [NASA ADS] [CrossRef]
- Zahn, J.-P., Talon, S.,
& Matias, J. 1997, A&A, 322, 320 [NASA ADS]
(In the text)
Copyright ESO 2008



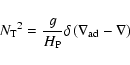


![$\displaystyle {\cal F}_{\rm E} \left(\ell, \omega \right)= \frac{\omega^2}{4\pi...
...(\ell+1)/2r^2\right] \frac{v_{\rm c}^3 L^4 }{1
+ (\omega \tau_{\rm L})^{15/2}},$](/articles/aa/full/2008/17/aa8620-07/img53.gif)
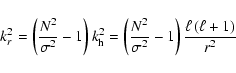
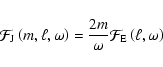
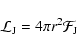
![\begin{displaymath}{\cal L}_{\rm J}(r) = \sum_{\sigma, \ell, m} {{\cal L}_{\rm J...
...ft(r_{\rm cz} \right)\exp \left[-\tau(r, \sigma, \ell) \right]
\end{displaymath}](/articles/aa/full/2008/17/aa8620-07/img69.gif)
![\begin{displaymath}\tau(r, \sigma, \ell) = \left[\ell(\ell+1) \right]^{3\over2} ...
... \over N^2 - \sigma^2}\right)^{1 \over 2} {{\rm d}r
\over r^3}
\end{displaymath}](/articles/aa/full/2008/17/aa8620-07/img72.gif)
![$\displaystyle \rho \frac{{\rm d}}{{\rm d}t} \left[r^2 {\Omega} \right]=
\frac{1...
...- \frac{3}{8\pi} \frac{1}{r^2} \frac{\partial}{\partial r}{{\cal L}_{\rm J}(r)}$](/articles/aa/full/2008/17/aa8620-07/img77.gif)

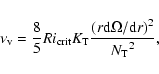
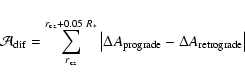

![\begin{figure}
\par\includegraphics[origin=rb,angle=-90,width=11cm,clip]{8620fig9.ps}
\end{figure}](/articles/aa/full/2008/17/aa8620-07/Timg93.gif)