A&A 482, 179-196 (2008)
DOI: 10.1051/0004-6361:20079203
A. Belloche1 - K. M. Menten1 - C. Comito1 - H. S. P. Müller1,2 - P. Schilke1 - J. Ott3,4,5 - S. Thorwirth1 - C. Hieret1
1 - Max-Planck Institut für Radioastronomie, Auf dem Hügel 69,
53121 Bonn, Germany
2 -
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77, 50937 Köln, Germany
3 -
National Radio Astronomy Observatory, 520 Edgemont Road,
Charlottesville, VA 22903-2475, USA
4 -
California Institute of Technology, 1200 E. California Blvd., Caltech Astronomy, 105-24, Pasadena, CA 91125-2400, USA
5 -
CSIRO Australia Telescope National Facility, Cnr Vimiera &
Pembroke Roads, Marsfield NSW 2122, Australia
Received 6 December 2007 / Accepted 16 January 2008
Abstract
Context. Amino acids are building blocks of proteins and therefore key ingredients for the origin of life. The simplest amino acid, glycine (NH2CH2COOH), has long been searched for in the interstellar medium but has not been unambiguously detected so far. At the same time, more and more complex molecules have been newly found toward the prolific Galactic center source Sagittarius B2.
Aims. Since the search for glycine has turned out to be extremely difficult, we aimed at detecting a chemically related species (possibly a direct precursor), amino acetonitrile (NH2CH2CN).
Methods. With the IRAM 30 m telescope we carried out a complete line survey of the hot core regions Sgr B2(N) and (M) in the 3 mm range, plus partial surveys at 2 and 1.3 mm. We analyzed our 30 m line survey in the LTE approximation and modeled the emission of all known molecules simultaneously. We identified spectral features at the frequencies predicted for amino acetonitrile lines having intensities compatible with a unique rotation temperature. We also used the Very Large Array to look for cold, extended emission from amino acetonitrile.
Results. We detected amino acetonitrile in Sgr B2(N) in our 30 m telescope line survey and conducted confirmatory observations of selected lines with the IRAM Plateau de Bure and the Australia Telescope Compact Array interferometers. The emission arises from a known hot core, the Large Molecule Heimat, and is compact with a source diameter of 2
![]() (0.08 pc). We derived a column density of 2.8
(0.08 pc). We derived a column density of 2.8 ![]() 1016 cm-2, a temperature of 100 K, and a linewidth of 7 km s-1. Based on the simultaneously observed continuum emission, we calculated a density of 1.7
1016 cm-2, a temperature of 100 K, and a linewidth of 7 km s-1. Based on the simultaneously observed continuum emission, we calculated a density of 1.7 ![]() 108 cm-3, a mass of 2340
108 cm-3, a mass of 2340 ![]() ,
and an amino acetonitrile fractional abundance of 2.2
,
and an amino acetonitrile fractional abundance of 2.2 ![]() 10-9. The high abundance and temperature may indicate that amino acetonitrile is formed by grain surface chemistry. We did not detect any hot, compact amino acetonitrile emission toward Sgr B2(M) or any cold, extended emission toward Sgr B2, with column-density upper limits of 6
10-9. The high abundance and temperature may indicate that amino acetonitrile is formed by grain surface chemistry. We did not detect any hot, compact amino acetonitrile emission toward Sgr B2(M) or any cold, extended emission toward Sgr B2, with column-density upper limits of 6 ![]() 1015 and 3
1015 and 3 ![]() 1012-14 cm-2, respectively.
1012-14 cm-2, respectively.
Conclusions. Based on our amino acetonitrile detection toward Sgr B2(N) and a comparison to the pair methylcyanide/acetic acid both detected in this source, we suggest that the column density of both glycine conformers in Sgr B2(N) is well below the best upper limits published recently by other authors, and probably below the confusion limit in the 1-3 mm range.
Key words: astrobiology - astrochemistry - line: identification - stars: formation - ISM: individual objects: Sagittarius B2 - ISM: molecules
Among the still growing list of complex molecules found in the interstellar medium, so-called ``bio''molecules garner special attention. In particular, the quest for interstellar amino acids, building blocks of proteins, has engaged radio and millimeter wavelength astronomers for a long time. Numerous published and unpublished searches have been made for interstellar glycine, the simplest amino acid (Ceccarelli et al. 2000; Jones et al. 2007; Combes et al. 1996; Hollis et al. 2003,1980; Brown et al. 1979; Berulis et al. 1985; Cunningham et al. 2007). Its recent ``detection'' claimed by Kuan et al. (2003) has been persuasively rebutted by Snyder et al. (2005). Since the early days of molecular radio astronomy, Sagittarius B2 has been a favorite target in searches for complex molecules in space.
Sagittarius B2 (hereafter Sgr B2 for short) is a very massive
(several million solar masses) and extremely active region of high-mass star formation at a
projected distance of ![]() 100 pc from the Galactic center. Its distance
from the Sun is assumed to be the same as the Galactic center distance, R0.
Reid (1993), reviewing various methods to determine R0, arrived at a
``best estimate'' of 8.0
100 pc from the Galactic center. Its distance
from the Sun is assumed to be the same as the Galactic center distance, R0.
Reid (1993), reviewing various methods to determine R0, arrived at a
``best estimate'' of 8.0 ![]() 0.5 kpc, a value that we adopt in this article.
It is supported by recent modeling of trajectories of stars orbiting the
central black hole, which yields 7.94
0.5 kpc, a value that we adopt in this article.
It is supported by recent modeling of trajectories of stars orbiting the
central black hole, which yields 7.94 ![]() 0.42 kpc (Eisenhauer et al. 2003).
0.42 kpc (Eisenhauer et al. 2003).
There are two major centers of activity, Sgr B2(M) and
Sgr B2(N) separated by
![]() 2 pc. In each of them, recent star formation manifests itself in a
multitude of H II regions of many sizes, from hypercompact to compact
(Gaume et al. 1995), and there is abundant material to form
new stars evident by massive sources of molecular line emission and submillimeter
continuum emission from dust (Lis et al. 1991,1993).
2 pc. In each of them, recent star formation manifests itself in a
multitude of H II regions of many sizes, from hypercompact to compact
(Gaume et al. 1995), and there is abundant material to form
new stars evident by massive sources of molecular line emission and submillimeter
continuum emission from dust (Lis et al. 1991,1993).
Some of the first detections of interstellar organic molecules (at cm-wavelengths!) were made toward Sgr B2 (see Menten 2004, for a historical perspective). The low intrinsic line strengths make these cm lines unlikely candidates for detection. However, the situation is helped, first, by the fact that many of the transitions in question may have inverted levels (Menten 2004) and amplify background radio continuum emission which is very intense at cm wavelengths (Hollis et al. 2007). Second, the spatial distributions of many species are characterized by spatially extended emission covering areas beyond Sgr B2 itself, filling single dish telescope beams, thus producing appreciable intensity even when observed with low spatial resolution (Jones et al. 2008; Cummins et al. 1986). This emission is characterized by low rotation temperatures, favoring lower frequency lines. Recent identifications of ``new'' species include glycolaldehyde CH2OHCHO (Hollis et al. 2001,2000), ethylene glycol HOCH2CH2OH (Hollis et al. 2002), and vinyl alcohol CH2CHOH (Turner & Apponi 2001).
Sgr B2 and its surroundings are part of the Central Molecular Zone (CMZ) of
our Galaxy, a ![]()
![]() latitude wide band stretching around the
Galactic center from longitude
latitude wide band stretching around the
Galactic center from longitude
![]() to
to
![]() (see, e.g., Morris & Serabyn 1996). The CMZ contains spatially extended emission
of many complex organic molecules
(Dahmen et al. 1997; Menten 2004; Requena-Torres et al. 2006; Minh et al. 1992).
(see, e.g., Morris & Serabyn 1996). The CMZ contains spatially extended emission
of many complex organic molecules
(Dahmen et al. 1997; Menten 2004; Requena-Torres et al. 2006; Minh et al. 1992).
Near Sgr B2(N), there is a hot, dense compact source that has a mm-wavelength line density second to no other known object. This source, for which Snyder et al. (1994) coined the name ``Large Molecule Heimat'' (LMH), is characterized by very high densities (>107 cm-3) and gas temperatures (>100 K). In recent years arcsecond resolution interferometry with the BIMA array has resulted in the detection and imaging of increasingly complex organic species toward the LMH, such as vinyl cyanide CH2CHCN, methyl formate HCOOCH3, and ethyl cyanide CH3CH2CN (Miao et al. 1995; Miao & Snyder 1997), formamide NH2CHO, isocyanic acid HNCO, and methyl formate HCOOCH3 (Kuan & Snyder 1996), acetic acid CH3COOH (Mehringer et al. 1997; Remijan et al. 2002), formic acid HCOOH (Liu et al. 2001), and acetone (CH3)2CO (Snyder et al. 2002). All the interferometric observations are consistent with a compact (<few arcsec diameter) source that had already been identified as the source of high-density-tracing non-metastable ammonia line emission by Vogel et al. (1987) and thermal methanol emission by Mehringer & Menten (1997, their source ``i''). The LMH also hosts a powerful H2O maser region (Reid et al. 1988), which provides evidence that it is very young (see Sect. 4.1).
Complex molecules in general have large partition functions, in particular for the elevated temperatures (>100 K) in molecular hot cores, dense and compact cloud condensations internally heated by a deeply embedded, young high-mass (proto)stellar object. Therefore, most individual spectral lines are weak and might easily get hidden in the ``line forest'' found toward these frequently extremely line-rich sources. To a large part, this forest consists of rotational lines, many of them presently unidentifiable, from within relatively low-lying vibrational states of molecules. Most of the candidate molecules from which these lines originate are known to exist in these sources, but laboratory spectroscopy is presently lacking for lines from the states in question. At this point in the game, unequivocally identifying a species in a spectrum of a hot core covering a wide spectral range requires the following steps: as described in detail in Sect. 3.2, assuming Local Thermodynamic Equilibrium (LTE) (which applies at the high densities in hot cores) a model spectrum is calculated for an assumed rotation temperature, column density, line width and other parameters. This predicts lines of a given intensity at all the known frequencies. Then at least two conditions have to be fulfilled: (i) all predicted lines should have a counterpart in the observed spectrum with the right intensity and width - no single line should be missing; (ii) follow-up observations with interferometers have to prove whether all lines from the candidate species are emitted from the same spot. Given the chemical variety in hot core regions, this is a powerful constraint. Moreover, interferometer images tend to have less line confusion, since many lines that are blended in larger beam single-dish spectra arise from different locations or are emitted by an extended region that is spatially filtered out. Using an interferometer for aiding molecule identifications was pioneered by Snyder and collaborators who (mostly) used the Berkeley-Illinois-Maryland-Array (BIMA) to clearly identify a number of species in the Sgr B2(N) Large Molecule Heimat (see Sect. 1.1.2).
We carried out a complete line survey of the hot core regions Sgr B2(N) and (M) with the IRAM 30 m telescope at 3 mm, along with partial surveys at 2 and 1.3 mm. One of the overall goals of our survey was to better characterize the molecular content of both regions. It also allows searches for ``new'' species once we have identified the lines emitted by known molecules (including vibrationally and torsionally excited states). In particular, many complex molecules have enough lines in the covered frequency ranges to apply criterion (i) above. Once a species fulfils this criterion, interferometer measurements of selected lines can be made to check criterion (ii).
One of our target molecules was amino acetonitrile (NH2CH2CN), a molecule chemically related to glycine. Whether it is a precursor to the latter is under debate (see Sect. 4.3). Not many astronomical searches for amino acetonitrile have been reported in the literature. In his dissertation, Storey (1976) reported searches for the JKa,Kc = 211-212 and 101-000 transitions at 1350.5 and 9071.7 MHz, respectively with the Parkes 64 m telescope. On afterthought, the only chance of success for their observations would have been if amino acetonitrile existed on large spatial scales, similar to the molecules described in Sect. 1.1.1 (see Sect. 3.7 for further limits on extended amino acetonitrile emission). Recently, Wirström et al. (2007) reported unsuccessful searches of a number of mm-wavelength transitions of amino acetonitrile toward a number of hot cores.
Here, we report our detection of warm compact emission from amino acetonitrile in Sgr B2(N) with the IRAM 30 m telescope, the Plateau de Bure Interferometer (PdBI) and the Australia Telescope Compact Array (ATCA), and upper limits on cold, spatially extended emission from amino acetonitrile that we obtained with the NRAO Very Large Array (VLA). Section 2 summarizes the observational details. We present our results in Sect. 3. Implications in terms of interstellar chemistry are discussed in Sect. 4. Our conclusions are summarized in Sect. 5.
We carried out millimeter line observations with the IRAM 30 m telescope on
Pico Veleta, Spain, in January 2004, September 2004 and January 2005. We used
four SIS heterodyne receivers simultaneously, two in the 3 mm window connected
to the autocorrelation spectrometer VESPA and two in the 1.3 mm window with
filter banks as backends. A few selected frequency ranges were also observed
with one SIS receiver at 2 mm in January 2004. The channel spacing and
bandwidth were 0.313 and 420 MHz for each receiver at 3 and 2 mm,
and 1 and 512 MHz for each receiver at 1.3 mm, respectively. The
observations were done in single-sideband mode with sideband rejections of
![]() 1-3
1-3![]() at 3 mm,
at 3 mm, ![]() 5-7
5-7![]() at 2 mm, and
at 2 mm, and ![]() 5-8
5-8![]() at 1.3 mm. The half-power beamwidths can be computed with the equation HPBW
(
at 1.3 mm. The half-power beamwidths can be computed with the equation HPBW
(
![]() ) =
) =
![]() .
The forward efficiencies
.
The forward efficiencies
![]() were 0.95 at 3 mm, 0.93 at 2 mm, and 0.91 at 1.3 mm,
respectively. The main-beam efficiencies were computed using the Ruze function
were 0.95 at 3 mm, 0.93 at 2 mm, and 0.91 at 1.3 mm,
respectively. The main-beam efficiencies were computed using the Ruze function
![]() ,
with
,
with
![]() ,
,
![]() ,
and
,
and ![]() the wavelength in mm (see
the IRAM 30 m telescope system summary on http://www.iram.es).
The system temperatures ranged from 96 to 600 K at 3 mm, from 220 to 720 K at
2 mm (except at 176 GHz where they ranged from 2400 to 3000 K), and from 280
to 1200 K at 1.3 mm. The telescope pointing was checked
every
the wavelength in mm (see
the IRAM 30 m telescope system summary on http://www.iram.es).
The system temperatures ranged from 96 to 600 K at 3 mm, from 220 to 720 K at
2 mm (except at 176 GHz where they ranged from 2400 to 3000 K), and from 280
to 1200 K at 1.3 mm. The telescope pointing was checked
every ![]() 1.5 h on Mercury, Mars, 1757-240 or G10.62, and found to be
accurate to 2-3
1.5 h on Mercury, Mars, 1757-240 or G10.62, and found to be
accurate to 2-3
![]() (rms). The telescope focus was optimized on Mercury,
Jupiter, Mars or G34.3+0.2 every
(rms). The telescope focus was optimized on Mercury,
Jupiter, Mars or G34.3+0.2 every ![]() 1.5-3 h.
The observations were performed toward both sources
Sgr B2(N) (
1.5-3 h.
The observations were performed toward both sources
Sgr B2(N) (
![]() = 17
= 17![]() 47
47![]() 20
20
![]() 0,
0,
![]() =
= ![]() 22
22
![]() 19.0
19.0
![]() ,
,
![]() = 64 km s-1) and Sgr B2(M)
(
= 64 km s-1) and Sgr B2(M)
(
![]() = 17
= 17![]() 47
47![]() 20
20
![]() 4,
4,
![]() =
= ![]() 23
23
![]() 07.0
07.0
![]() ,
,
![]() = 62 km s-1) in
position-switching mode with a reference position offset by
(
= 62 km s-1) in
position-switching mode with a reference position offset by
(
![]() ,
,
![]() ) = (
) = (
![]() ,
,
![]() )
with respect
to the former. The emission toward this reference position was found to be
weak:
)
with respect
to the former. The emission toward this reference position was found to be
weak:
![]() (12CO 1-0)
(12CO 1-0) ![]() 2 K,
2 K,
![]() (CS 2-1)
(CS 2-1) ![]() 0.05 K,
0.05 K,
![]() (12CO 2-1)
(12CO 2-1) ![]() 1.5 K,
1.5 K,
![]() (13CO 2-1)
(13CO 2-1) ![]() 0.1 K,
and it is negligible for higher excitation lines and/or complex species.
0.1 K,
and it is negligible for higher excitation lines and/or complex species.
We observed the full 3 mm window between 80 and 116 GHz toward both sources.
The step between two adjacent tuning frequencies
was 395 MHz, which yielded an overlap of 50 MHz.
The autocorrelator VESPA produces artificial spikes with a width of 3-5 channels at the junction between subbands (typically 2 or 3 spikes per
spectrum). To get rid of these artefacts, half of the integration time at each
tuning frequency was spent with the backend shifted by 50 MHz, so that we
could, without any loss of information, systematically remove
in each spectrum 5 channels at each of the 6 junctions between subbands that
were possibly affected by this phenomenon. At 2 mm, we observed at only 8 selected frequencies, and removed the artificial spikes in the same way as at
3 mm. At 1 mm, we covered the frequency ranges 201.8 to 204.6 GHz and 205.0
to 217.7 GHz, plus a number of selected spots at higher frequency. For
each individual
spectrum, we removed a 0
![]() -order (constant) baseline by selecting
a group of channels which seemed to be free of emission or absorption. However,
many spectra are full of lines, especially at 1.3 mm where we reached the
confusion limit, and we may have overestimated the level of the baseline for
some of them.
-order (constant) baseline by selecting
a group of channels which seemed to be free of emission or absorption. However,
many spectra are full of lines, especially at 1.3 mm where we reached the
confusion limit, and we may have overestimated the level of the baseline for
some of them.
In
![]() scale, the rms noise level achieved towards
Sgr B2(N) is about 15-20 mK below 100 GHz, 20-30 mK between 100 and 114.5 GHz, and about 50 mK between 114.5 and 116 GHz. At 1.3 mm, we reached the
confusion limit for most of the spectra. The data were reduced with the
CLASS software, which is part of the GILDAS software package
(see http://www.iram.fr/IRAMFR/GILDAS).
scale, the rms noise level achieved towards
Sgr B2(N) is about 15-20 mK below 100 GHz, 20-30 mK between 100 and 114.5 GHz, and about 50 mK between 114.5 and 116 GHz. At 1.3 mm, we reached the
confusion limit for most of the spectra. The data were reduced with the
CLASS software, which is part of the GILDAS software package
(see http://www.iram.fr/IRAMFR/GILDAS).
We observed Sgr B2(N) with the PdBI for 4.7 h on February 7
![]() ,
2006 with 6 antennas in the high-resolution A configuration (E24E68E04N46W27N29). The coordinates of the phase center were
,
2006 with 6 antennas in the high-resolution A configuration (E24E68E04N46W27N29). The coordinates of the phase center were
![]() ,
,
![]() .
The 3 and 1.2 mm
receivers were tuned to 81.982 and 245.380 GHz, respectively, in single side
band mode. At 3 mm, there were two spectral windows centered at 81.736 and
82.228 GHz with a bandwidth of 80 MHz and a channel separation of 0.313 MHz,
and two continuum windows of 320 MHz bandwidth centered at 81.852 and
82.112 GHz. The atmospheric phase stability was good for the 3 mm band but
bad for the 1.2 mm band. Therefore we do not analyze the 1.2 mm data. The
system temperatures were typically 150-220 K at 3 mm in the lower sideband.
The (naturally-weighted) synthesized half-power beam width was
.
The 3 and 1.2 mm
receivers were tuned to 81.982 and 245.380 GHz, respectively, in single side
band mode. At 3 mm, there were two spectral windows centered at 81.736 and
82.228 GHz with a bandwidth of 80 MHz and a channel separation of 0.313 MHz,
and two continuum windows of 320 MHz bandwidth centered at 81.852 and
82.112 GHz. The atmospheric phase stability was good for the 3 mm band but
bad for the 1.2 mm band. Therefore we do not analyze the 1.2 mm data. The
system temperatures were typically 150-220 K at 3 mm in the lower sideband.
The (naturally-weighted) synthesized half-power beam width was
![]()
![]()
![]() with PA 10
with PA 10![]() ,
and the primary beam was
,
and the primary beam was
![]()
![]() FWHM. The correlator bandpass was calibrated on the quasar
3C 273. Phase calibration was determined on the nearby sources NRAO 530
and 1622-297. The time-dependent amplitude calibration was done on
1622-297, NRAO 530, 1334-127, and 1749+096,
while the absolute flux density scale was derived from MWC 349. The absolute
calibration uncertainty is estimated to be
FWHM. The correlator bandpass was calibrated on the quasar
3C 273. Phase calibration was determined on the nearby sources NRAO 530
and 1622-297. The time-dependent amplitude calibration was done on
1622-297, NRAO 530, 1334-127, and 1749+096,
while the absolute flux density scale was derived from MWC 349. The absolute
calibration uncertainty is estimated to be ![]() 15
15![]() .
The data were
calibrated and imaged using the GILDAS software. The continuum emission was
estimated on line-free portions of the bands and removed in the uv plane. The deconvolution was performed with the CLEAN method (Clark 1980).
.
The data were
calibrated and imaged using the GILDAS software. The continuum emission was
estimated on line-free portions of the bands and removed in the uv plane. The deconvolution was performed with the CLEAN method (Clark 1980).
We observed Sgr B2(N) with the ATCA on May 17
![]() ,
2006 in the
hybrid H 214 configuration for 6 h, for 7 h on July 30
,
2006 in the
hybrid H 214 configuration for 6 h, for 7 h on July 30
![]() ,
2006 in the H 168 configuration, and for 6 hours in the
compact H 75 configuration on September 25
,
2006 in the H 168 configuration, and for 6 hours in the
compact H 75 configuration on September 25
![]() ,
2006.
The coordinates of the phase center were
,
2006.
The coordinates of the phase center were
![]() ,
,
![]() .
The 3 mm receiver was alternately tuned to three frequency pairs of 90.550 and 93.200 GHz,
90.779 and 93.200 GHz, and 99.978 and 97.378 GHz in single side band mode,
where only the first frequency of each pair was in spectral line mode with
32 MHz bandwidth and 128 channels. The second frequency of each pair was
configured for continuum observations with 128 MHz bandwidth
each. The system temperatures were typically 60 K. The
(naturally-weighted) synthesized half-power beam width was
.
The 3 mm receiver was alternately tuned to three frequency pairs of 90.550 and 93.200 GHz,
90.779 and 93.200 GHz, and 99.978 and 97.378 GHz in single side band mode,
where only the first frequency of each pair was in spectral line mode with
32 MHz bandwidth and 128 channels. The second frequency of each pair was
configured for continuum observations with 128 MHz bandwidth
each. The system temperatures were typically 60 K. The
(naturally-weighted) synthesized half-power beam width was
![]()
![]()
![]() with PA
with PA ![]() for H 214,
for H 214,
![]()
![]()
![]() with PA
with PA ![]() for H 168, and
for H 168, and
![]()
![]()
![]() with PA
with PA ![]() for H 75. The
combination of H 214 and H 168 yields a synthesized half-power beam width of
for H 75. The
combination of H 214 and H 168 yields a synthesized half-power beam width of
![]()
![]()
![]() with PA
with PA ![]() ,
and the combination of
all three configurations a synthesized half-power beam width of
,
and the combination of
all three configurations a synthesized half-power beam width of
![]()
![]()
![]() with PA
with PA ![]() .
The primary beam was
.
The primary beam was ![]()
![]() FWHM. The correlator bandpass was
calibrated on PKS 1253-055. The phase and gain calibration was
determined on the nearby source PKS 1759-39. The absolute flux
density scale was derived from Uranus. The absolute calibration
uncertainty is estimated to be
FWHM. The correlator bandpass was
calibrated on PKS 1253-055. The phase and gain calibration was
determined on the nearby source PKS 1759-39. The absolute flux
density scale was derived from Uranus. The absolute calibration
uncertainty is estimated to be ![]() 20
20![]() .
The data were
calibrated, continuum subtracted, imaged, and deconvolved using the
software package MIRIAD (Sault et al. 1995).
.
The data were
calibrated, continuum subtracted, imaged, and deconvolved using the
software package MIRIAD (Sault et al. 1995).
Our ATCA data are affected by two problems. First, the tuning frequency used
in May was not updated for the new observatory velocity in July and September.
As a result, the observed bands were shifted by +12 and +16 MHz in rest
frequency in the H 168 and H 75 configurations with respect to the H 214 configuration. Second, we suspect a technical problem with the tuning at 99 GHz
in May and July because we do not detect any line in the H 214 and H 168 configurations while we easily detect two lines in the H 75 configuration:
one unidentified line and one line from CH3CH3CO,
![]() according to our line survey with the IRAM 30 m telescope. Comparing this band
to the two other bands where we detect every line in each configuration
(albeit with different intensities due to variable spatial filtering), we
consider it to be very unlikely that the two lines detected at 99 GHz in the H 75 configuration are completely filtered out in the H 214 and H 168 configurations. Since the
amino acetonitrile transition is shifted out of the H 75 band at 99 GHz (due
to the variation of the observatory velocity), we do not analyze this dataset
in the present article.
according to our line survey with the IRAM 30 m telescope. Comparing this band
to the two other bands where we detect every line in each configuration
(albeit with different intensities due to variable spatial filtering), we
consider it to be very unlikely that the two lines detected at 99 GHz in the H 75 configuration are completely filtered out in the H 214 and H 168 configurations. Since the
amino acetonitrile transition is shifted out of the H 75 band at 99 GHz (due
to the variation of the observatory velocity), we do not analyze this dataset
in the present article.
We used the NRAO Very Large Array to search for the
101-000 multiplet
of amino acetonitrile at 9071.208 MHz and examine the possibility of cold
extended emission from this molecule. The VLA data were taken over a 1.5 h
interval on February 13
![]() ,
2003 when the array was in its lowest-resolution
(D) configuration. Three
,
2003 when the array was in its lowest-resolution
(D) configuration. Three ![]() 20 min long scans of the following
position in Sgr B2 were alternated with scans of the phase calibrator
NRAO 530. For absolute flux density calibration, 3C 286 was observed. Our phase
center in Sgr B2 was at
20 min long scans of the following
position in Sgr B2 were alternated with scans of the phase calibrator
NRAO 530. For absolute flux density calibration, 3C 286 was observed. Our phase
center in Sgr B2 was at
![]() = 17
= 17![]() 47
47![]() 20
20
![]() 00,
00,
![]() =
= ![]() 22
22
![]() 51.0
51.0
![]() .
This is
.
This is
![]() South and
South and
![]() North of our 30 m telescope pointing
positions for Sgr B2(N) and (M), respectively.
North of our 30 m telescope pointing
positions for Sgr B2(N) and (M), respectively.
Our observations were done in spectral line mode with one intermediate
frequency (IF) band split into 32 channels, each of which had a width of
0.1953 MHz, corresponding to 6.46 km s-1. The usable central 72![]() frequency range of the IF bandwidth, 4.49 MHz, covered all the multiplet's 7 hyperfine structure (hfs) components
frequency range of the IF bandwidth, 4.49 MHz, covered all the multiplet's 7 hyperfine structure (hfs) components![]() . This frequency range corresponds to a total velocity coverage of
148 km s-1. The center velocity was set to
. This frequency range corresponds to a total velocity coverage of
148 km s-1. The center velocity was set to
![]() = 65 km s-1. A 4.49 MHz bandwidth ``pseudo continuum'' database (the so-called
``channel 0'') was created by averaging the central 23 channels. The uv-data
were calibrated using the NRAO's Astronomical Imaging Processing System
(AIPS). Several iterations of self calibration delivered a high quality continuum image. Using
UVLIN, the average of selected regions of the line uv-database were
subtracted channel by channel from the latter to remove the continuum level.
To calibrate the spectral line data, the phase and amplitude corrections
determined by the initial calibration, as well as by the self calibration were
transferred to the line database and applied to them successively, producing a
23 channel database which was imaged channel by channel using natural
weighting. The synthesized beam width of the images is
= 65 km s-1. A 4.49 MHz bandwidth ``pseudo continuum'' database (the so-called
``channel 0'') was created by averaging the central 23 channels. The uv-data
were calibrated using the NRAO's Astronomical Imaging Processing System
(AIPS). Several iterations of self calibration delivered a high quality continuum image. Using
UVLIN, the average of selected regions of the line uv-database were
subtracted channel by channel from the latter to remove the continuum level.
To calibrate the spectral line data, the phase and amplitude corrections
determined by the initial calibration, as well as by the self calibration were
transferred to the line database and applied to them successively, producing a
23 channel database which was imaged channel by channel using natural
weighting. The synthesized beam width of the images is
![]()
![]()
![]() FWHM with a position angle of
FWHM with a position angle of
![]() East of North.
East of North.
In the course of the present investigation an amino acetonitrile entry (tag: 56507) has been prepared for the catalog of the Cologne Database for Molecular Spectroscopy (CDMS, see Müller et al. 2005,2001). The laboratory transition frequencies were summarized by Bogey et al. (1990). Their work included microwave transitions reported without 14N quadrupole splitting by MacDonald & Tyler (1972), Pickett (1973), as well as microwave transitions reported with quadrupole splitting by Brown et al. (1977); the latter data were used with the reported splitting. Line fitting and prediction of transition frequencies was done with the SPFIT/SPCAT suite of programs (Pickett 1991) using a Watson type Hamiltonian in the S reduction in the representation Ir (see, e.g., Gordy & Cook 1984).
The set of spectroscopic parameters reported by Bogey et al. (1990)
included terms of up to decic order (SK), rather unusual for an apparently
rigid and fairly heavy molecule, and we found the higher order parameters to
be surprisingly large. Moreover, the off-diagonal sextic distortion parameter h3 was larger in magnitude than h2, and h1 was not even used in the
fit; the importance of these parameters is reversed to what is more commonly
found. Therefore, we performed a trial fit with the octic and decic
parameters as well as h2 and h3 omitted and the sextic term HK fixed
to a value that was estimated from
![]() .
Subsequently, we found that inclusion of h1 improved the quality of the
fit. All transitions but five having
.
Subsequently, we found that inclusion of h1 improved the quality of the
fit. All transitions but five having
![]() and
and
![]() could be reproduced well. Two of these had
Ka = 3-2 and deviated
could be reproduced well. Two of these had
Ka = 3-2 and deviated
![]() 3.5 MHz from the predicted frequencies which was only twice the
predicted uncertainty. The inclusion of these transitions in the fit caused
relatively small changes in A and DK; changes in the remaining parameters
were within the uncertainties. Therefore, it is likely that the assignments of
these two transitions are correct. Effects on the predicted
3.5 MHz from the predicted frequencies which was only twice the
predicted uncertainty. The inclusion of these transitions in the fit caused
relatively small changes in A and DK; changes in the remaining parameters
were within the uncertainties. Therefore, it is likely that the assignments of
these two transitions are correct. Effects on the predicted
![]() transition frequencies are negligible. The remaining three transitions are
considered to be mis-assignments as their inclusion would require many more
higher order distortion parameters with apparently unphysical values and a
poorer quality of the fit. Hence, those transitions were omitted from our fit.
The resulting spectroscopic parameters are given in
Table 1. The rotational partition function at 75 and 150 K
is 4403 and 12 460, respectively.
transition frequencies are negligible. The remaining three transitions are
considered to be mis-assignments as their inclusion would require many more
higher order distortion parameters with apparently unphysical values and a
poorer quality of the fit. Hence, those transitions were omitted from our fit.
The resulting spectroscopic parameters are given in
Table 1. The rotational partition function at 75 and 150 K
is 4403 and 12 460, respectively.

(b) Assumed value (see Sect. 3.1). |
The average line density above 3![]() in our 30 m survey is about 100 and 25 features per GHz for Sgr B2(N) and (M), respectively, translating into about
3700 and 950 lines over the whole 80-116 GHz band. To identify a new molecule
in such a line forest and reduce the risk of mis-assignments, it is essential
to model first the emission of all known molecules, including vibrationally
and torsionally excited states, and their isotopologues. We used the
XCLASS software (see Comito et al. 2005, and references therein)
to model the emission and absorption lines in the LTE approximation. These
calculations take into account the beam dilution, the line opacity, and the
line blending. The molecular spectroscopic parameters are taken from our line
catalog which contains all entries from the CDMS catalog
(Müller et al. 2005,2001) and from the molecular
spectroscopic database of the Jet Propulsion Laboratory
(JPL, see Pickett et al. 1998), plus additional ``private'' entries.
in our 30 m survey is about 100 and 25 features per GHz for Sgr B2(N) and (M), respectively, translating into about
3700 and 950 lines over the whole 80-116 GHz band. To identify a new molecule
in such a line forest and reduce the risk of mis-assignments, it is essential
to model first the emission of all known molecules, including vibrationally
and torsionally excited states, and their isotopologues. We used the
XCLASS software (see Comito et al. 2005, and references therein)
to model the emission and absorption lines in the LTE approximation. These
calculations take into account the beam dilution, the line opacity, and the
line blending. The molecular spectroscopic parameters are taken from our line
catalog which contains all entries from the CDMS catalog
(Müller et al. 2005,2001) and from the molecular
spectroscopic database of the Jet Propulsion Laboratory
(JPL, see Pickett et al. 1998), plus additional ``private'' entries.
Each molecule is modeled separately with the following set of input parameters: source size, rotational temperature, column density, velocity linewidth, velocity offset with respect to the systemic velocity of the source, and a flag indicating if it is an emission or absorption component. For some of the molecules, it was necessary to include several velocity components to reproduce the observed spectra. The velocity components in emission are supposed to be non-interacting, i.e. the intensities add up linearly. The radiative transfer is computed in the following way: first the emission line spectrum is calculated, and then the absorption lines, using the full (lines + continuum) emission spectrum as background to absorb against. The vibrationally and/or torsionally excited states of some molecules were modeled separately from the ground state. The input parameters were varied until a good fit to the data was obtained for each molecule. The whole spectrum including all the identified molecules was then computed at once, and the parameters for each molecule were adjusted again when necessary. The quality of the fit was checked by eye over the whole frequency coverage of the line survey. We favored our eye-checking method against an automated fitting because the high occurence of line blending and the uncertainty in the baseline removal would in many cases make an automated fitting procedure fail.
The detailed results of this modeling will be published in a forthcoming
article describing the complete survey (Belloche et al., in prep.). So
far, we have identified 51 different molecules, 60 isotopologues, and 41 vibrationally/torsionally excited states in Sgr B2(N), which represent about 60![]() of the lines detected above
the 3
of the lines detected above
the 3![]() level. In Sgr B2(M), the corresponding numbers are 41, 50, 20,
and 50
level. In Sgr B2(M), the corresponding numbers are 41, 50, 20,
and 50![]() ,
respectively.
,
respectively.
| Na | Transition | Frequency | Unc.b |
|
Fe |
|
|
|
Comments | |||
| (MHz) | (kHz) | (K) | (D2) | (mK) | (K km s-1) | (K km s-1) | (K km s-1) | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) |
| 1 | 9 0, 9-8 0, 8 | 80 947.479 | 7 | 16 | 60 | 33 | 1 | 0.13 | 0.65(16) | 0.38 | 0.42 | no blend |
| 3 | 9 5, 5-8 5, 4 | 81 700.966 | 6 | 47 | 41 | 13 | 2 | 0.16 | 0.92(07) | 0.67 | 0.75 | partial blend with U-line |
| 4 | 9 5, 4-8 5, 3 | 81 700.967 | 6 | 47 | 41 | 13 | 2 | - | - | - | - | - |
| 5 | 9 6, 3-8 6, 2 | 81 702.498 | 5 | 60 | 33 | 13 | 2 | - | - | - | - | - |
| 6 | 9 6, 4-8 6, 3 | 81 702.498 | 5 | 60 | 33 | 13 | 2 | - | - | - | - | - |
| 7 | 9 4, 6-8 4, 5 | 81 709.838 | 6 | 35 | 48 | 13 | 3 | 0.23 | 0.39(06) | 0.66 | 0.73 | no blend |
| 8 | 9 7, 2-8 7, 1 | 81 709.848 | 6 | 76 | 24 | 13 | 3 | - | - | - | - | - |
| 9 | 9 7, 3-8 7, 2 | 81 709.848 | 6 | 76 | 24 | 13 | 3 | - | - | - | - | - |
| 10 | 9 4, 5-8 4, 4 | 81 710.098 | 6 | 35 | 48 | 13 | 3 | - | - | - | - | - |
| 11 | 9 3, 7-8 3, 6 | 81 733.892 | 6 | 27 | 53 | 13 | 4 | 0.11 | 0.50(06) | 0.32 | 1.46 | blend with CH3OCH3 and |
| HCC13CN, v6 = 1 | ||||||||||||
| 12 | 9 3, 6-8 3, 5 | 81 756.174 | 6 | 27 | 53 | 13 | 5 | 0.11 | 0.39(06) | 0.32 | 0.32 | blend with U-line |
| 13 | 9 2, 7-8 2, 6 | 82 224.644 | 7 | 21 | 57 | 19 | 6 | 0.12 | 0.19(08) | 0.36 | 0.35 | uncertain baseline |
| 17 | 10 2, 9-9 2, 8 | 90 561.332 | 6 | 25 | 64 | 20 | 7 | 0.14 | 0.64(09) | 0.52 | 1.01 | blend with weak |
| C2H5CN, v13 = 1/v21 = 1 | ||||||||||||
| 18 | 10 6, 4-9 6, 3 | 90 783.538 | 6 | 64 | 43 | 14 | 8 | 0.28 | 1.54(06) | 1.05 | 1.40 | partial blend with CH2(OH)CHO and |
| U-line | ||||||||||||
| 19 | 10 6, 5-9 6, 4 | 90 783.538 | 6 | 64 | 43 | 14 | 8 | - | - | - | - | - |
| 20 | 10 5, 6-9 5, 5 | 90 784.281 | 6 | 50 | 50 | 14 | 8 | - | - | - | - | - |
| 21 | 10 5, 5-9 5, 4 | 90 784.285 | 6 | 50 | 50 | 14 | 8 | - | - | - | - | - |
| 22 | 10 7, 3-9 7, 2 | 90 790.259 | 6 | 80 | 34 | 14 | 9 | 0.09 | 0.51(06) | 0.33 | 0.56 | blend with U-line |
| 23 | 10 7, 4-9 7, 3 | 90 790.259 | 6 | 80 | 34 | 14 | 9 | - | - | - | - | - |
| 24 | 10 4, 7-9 4, 6 | 90 798.685 | 6 | 39 | 56 | 14 | 10 | 0.21 | 1.42(06) | 0.81 | 0.95 | blend with U-line |
| 25 | 10 4, 6-9 4, 5 | 90 799.249 | 6 | 39 | 56 | 14 | 10 | - | - | - | - | - |
| 28 | 10 3, 8-9 3, 7 | 90 829.945 | 6 | 31 | 60 | 14 | 11 | 0.13 | 0.84(06) | 0.47 | 0.51 | blend with U-line also in M? |
| 29 | 10 3, 7-9 3, 6 | 90 868.038 | 6 | 31 | 60 | 14 | 12 | 0.13 | 0.49(06) | 0.47 | 0.57 | partial blend with U-line |
| 30 | 10 2, 8-9 2, 7 | 91 496.108 | 8 | 25 | 64 | 24 | 13 | 0.15 | 0.86(11) | 0.53 | 0.71 | partial blend with CH3CN, v4 = 1 and |
| U-line | ||||||||||||
| 32 | 11 1,11-10 1,10 | 97 015.224 | 8 | 25 | 72 | 21 | 14 | 0.18 | 2.05(09) | 0.71 | 1.78 | partial blend with C2H5OH and |
| CH3OCHO | ||||||||||||
| 47 | 11 3, 9-10 3, 8 | 99 928.886 | 6 | 35 | 68 | 14 | 15 | 0.15 | 1.31(06) | 0.66 | 1.24 | partial blend with NH2CN and U-line |
| 48 | 11 3, 8-10 3, 7 | 99 990.567 | 7 | 35 | 68 | 14 | 16 | 0.15 | 0.80(06) | 0.66 | 0.74 | no blend |
| 49 | 11 2, 9-10 2, 8 | 100 800.876 | 8 | 29 | 71 | 20 | 17 | 0.17 | 1.38(08) | 0.75 | 1.25 | partial blend with CH3CH3CO, v= 0 |
| and U-line | ||||||||||||
| 50 | 11 1,10-10 1, 9 | 101 899.795 | 8 | 26 | 72 | 34 | 18 | 0.18 | 0.56(14) | 0.81 | 0.88 | uncertain baseline |
| 51 | 12 1,12-11 1,11 | 105 777.991 | 8 | 29 | 79 | 43 | 19 | 0.20 | 1.98(18) | 0.95 | 2.88 | blend with c-C2H4O and |
| C2H5CN, v= 0 | ||||||||||||
| 52 | 12 0,12-11 0,11 | 107 283.142 | 8 | 29 | 80 | 24 | 20 | 0.21 | 2.67(10) | 1.00 | 2.01 | blend with C2H5OH and U-line |
| 53 | 12 2,11-11 2,10 | 108 581.408 | 7 | 34 | 77 | 20 | 21 | 0.19 | 1.49(08) | 0.97 | 1.94 | weak blend with C2H5OH |
| 58 | 12 5, 8-11 5, 7 | 108 956.206 | 6 | 60 | 66 | 29 | 22 | 0.26 | 2.19(11) | 1.34 | 3.44 | blend with C2H5OH |
| 59 | 12 5, 7-11 5, 6 | 108 956.229 | 6 | 60 | 66 | 29 | 22 | - | - | - | - | - |
| 68 | 12 3,10-11 3, 9 | 109 030.225 | 6 | 40 | 75 | 29 | 23 | 0.18 | 1.67(11) | 0.89 | 1.24 | partial blend with HC3N, v4 = 1, |
| C2H5OH, and U-line | ||||||||||||
| 71 | 12 1,11-11 1,10 | 111 076.901 | 8 | 31 | 79 | 25 | 24 | 0.21 | 1.16(10) | 1.08 | 1.39 | slightly shifted? |
| 72 | 13 1,13-12 1,12 | 114 528.654 | 8 | 34 | 86 | 37 | 25 | 0.23 | 2.49(15) | 1.23 | 1.42 | partial blend with U-line |
| 84 | 1510, 5-1410, 4 | 136 248.969 | 10 | 169 | 55 | 28 | 26 | 0.09 | 2.10(10) | 0.72 | 1.03 | blend with U-line |
| 85 | 1510, 6-1410, 5 | 136 248.969 | 10 | 169 | 55 | 28 | 26 | - | - | - | - | - |
| 89 | 15 4,11-14 4,10 | 136 303.599 | 6 | 65 | 93 | 28 | 27 | 0.21 | 3.99(09) | 1.62 | 4.02 | blend with a(CH2OH)2 and CH3C3N |
| 92 | 15 3,13-14 3,12 | 136 341.155 | 6 | 57 | 96 | 28 | 28 | 0.24 | 2.92(10) | 1.81 | 2.22 | partial blend with U-line also in M |
| 103 | 16 5,12-15 5,11 | 145 325.871 | 30 | 83 | 96 | 25 | 29 | 0.39 | 2.89(08) | 3.30 | 4.80 | uncertain baseline, partial blend |
| with C2H5CN, v13 = 1/v21 = 1 | ||||||||||||
| 104 | 16 5,11-15 5,10 | 145 326.209 | 30 | 83 | 96 | 25 | 29 | - | - | - | - | - |
| 105 | 1610, 6-1510, 5 | 145 330.985 | 40 | 175 | 65 | 25 | 30 | 0.11 | 0.97(07) | 0.92 | 1.02 | uncertain baseline |
| 106 | 1610, 7-1510, 6 | 145 330.985 | 40 | 175 | 65 | 25 | 30 | - | - | - | - | - |
| 115 | 16 3,14-15 3,13 | 145 443.850 | 30 | 63 | 103 | 25 | 31 | 0.25 | 4.33(08) | 2.18 | 4.68 | blend with C2H5CN, v= 0 and |
| U-line | ||||||||||||
| 118 | 16 1,15-15 1,14 | 147 495.789 | 6 | 55 | 106 | 31 | 32 | 0.29 | 3.27(11) | 2.54 | 11.47 | partial blend with H3C13CN, v8 = 1 |
| 139 | 17 4,13-16 4,12 | 154 542.406 | 5 | 79 | 107 | 112 | 33 | 0.44 | 13.25(42) | 4.63 | 5.52 | blend with U-line |
| 140 | 17 3,15-16 3,14 | 154 544.046 | 5 | 70 | 109 | 112 | 33 | - | - | - | - | - |
| 145 | 18 7,12-17 7,11 | 163 454.794 | 5 | 127 | 101 | 38 | 34 | 0.49 | 10.38(13) | 5.32 | 16.48 | partial blend with HC13CCN, |
| v6 = 1 and HCC13CN, v6 = 1 | ||||||||||||
| 146 | 18 7,11-17 7,10 | 163 454.794 | 5 | 127 | 101 | 38 | 34 | - | - | - | - | - |
| 147 | 18 8,10-17 8, 9 | 163 456.136 | 6 | 146 | 96 | 38 | 34 | - | - | - | - | - |
| 148 | 18 8,11-17 8,10 | 163 456.136 | 6 | 146 | 96 | 38 | 34 | - | - | - | - | - |
| 149 | 18 9, 9-17 9, 8 | 163 470.472 | 8 | 166 | 90 | 38 | 35 | 0.41 | 15.17(14) | 5.57 | 21.97 | partial blend with HCC13CN,v7 = 1 |
| 150 | 18 9,10-17 9, 9 | 163 470.472 | 8 | 166 | 90 | 38 | 35 | - | - | - | - | - |
| 151 | 18 6,13-17 6,12 | 163 473.305 | 5 | 111 | 106 | 38 | 35 | - | - | - | - | - |
| 152 | 18 6,12-17 6,11 | 163 473.321 | 5 | 111 | 106 | 38 | 35 | - | - | - | - | - |
| 155 | 1811, 7-1711, 6 | 163 525.533 | 11 | 216 | 75 | 38 | 36 | 0.49 | 10.26(13) | 5.27 | 17.96 | blend with HC3N, v4 = 1 |
| 156 | 1811, 8-1711, 7 | 163 525.533 | 11 | 216 | 75 | 38 | 36 | - | - | - | - | - |
| 157 | 18 5,14-17 5,13 | 163 526.183 | 4 | 97 | 110 | 38 | 36 | - | - | - | - | - |
| 158 | 18 5,13-17 5,12 | 163 527.171 | 4 | 97 | 110 | 38 | 36 | - | - | - | - | - |
| 163 | 18 4,15-17 4,14 | 163 635.326 | 5 | 86 | 114 | 38 | 37 | 0.25 | 4.08(11) | 2.82 | 5.01 | partial blend with C3H7CN |
| 164 | 18 3,16-17 3,15 | 163 640.468 | 5 | 78 | 116 | 38 | 38 | 0.28 | 4.65(11) | 2.99 | 6.77 | partial blend with C3H7CN |
| 177 | 19 6,14-18 6,13 | 172 566.092 | 50 | 119 | 114 | 44 | 39 | 0.38 | 10.01(14) | 4.39 | 6.43 | partial blend with U-line and |
| HCC13CN, v7 = 1 | ||||||||||||
| 178 | 19 6,13-18 6,12 | 172 566.092 | 50 | 119 | 114 | 44 | 39 | - | - | - | - | - |
| 227 | 23 4,20-22 4,19 | 209 272.189 | 6 | 130 | 148 | 58 | 40 | 0.26 | 7.29(29) | 4.62 | 14.85 | blend CH3CH3CO, v= 0 |
| 237 | 23 1,22-22 1,21 | 209 629.913 | 9 | 113 | 152 | 45 | 41 | 0.32 | 9.03(24) | 5.54 | 30.88 | blend with HC13CCN, v7 = 2 and |
| HCC13CN, v7 = 2 | ||||||||||||
| 247 | 25 9,16-24 9,15 | 227 040.487 | 50 | 230 | 145 | 96 | 42 | 0.29 | 9.58(55) | 9.45 | 35.33 | partial blend with CN absorption |
| and CH3CH3CO,
|
||||||||||||
| 248 | 25 9,17-24 9,16 | 227 040.487 | 50 | 230 | 145 | 96 | 42 | - | - | - | - | - |
| 249 | 25 8,18-24 8,17 | 227 045.287 | 50 | 210 | 149 | 96 | 42 | - | - | - | - | - |
| 250 | 25 8,17-24 8,16 | 227 045.287 | 50 | 210 | 149 | 96 | 42 | - | - | - | - | - |
| 251 | 2510,15-2410,14 | 227 055.944 | 50 | 254 | 139 | 96 | 43 | 0.15 | -0.64(44) | 3.29 | 3.62 | partial blend with CN absorption |
| 252 | 2510,16-2410,15 | 227 055.944 | 50 | 254 | 139 | 96 | 43 | - | - | - | - | - |
| 253 | 25 7,19-24 7,18 | 227 079.847 | 50 | 191 | 153 | 96 | 44 | 0.32 | 10.94(44) | 7.16 | 57.69 | blend with CH2CH13CN and |
| CH3OH, v= 0 | ||||||||||||
| 254 | 25 7,18-24 7,17 | 227 079.847 | 50 | 191 | 153 | 96 | 44 | - | - | - | - | - |
| 273 | 25 2,23-24 2,22 | 231 485.527 | 50 | 138 | 165 | 40 | 45 | 0.30 | 12.73(19) | 6.27 | 6.60 | blend with U-line? |
| 292 | 26 6,21-25 6,20 | 236 269.491 | 60 | 186 | 163 | 37 | 46 | 0.36 | 15.53(18) | 8.02 | 14.17 | partial blend with t-C2H5OCHO |
| and U-line | ||||||||||||
| 293 | 26 6,20-25 6,19 | 236 270.459 | 60 | 186 | 163 | 37 | 46 | - | - | - | - | - |
| 306 | 28 0,28-27 0,27 | 244 765.968 | 21 | 160 | 186 | 39 | 47 | 0.28 | 9.56(19) | 6.62 | 10.35 | blend with CH313CH2CN, v= 0 |
| and U-line | ||||||||||||
| 322 | 27 6,22-26 6,21 | 245 378.722 | 10 | 197 | 170 | 72 | 48 | 0.35 | 16.69(36) | 8.29 | 22.21 | blend with 13CH3CH2CN, v= 0? |
| 323 | 27 6,21-26 6,20 | 245 380.146 | 10 | 197 | 170 | 72 | 48 | - | - | - | - | - |
| 368 | 29 9,20-28 9,19 | 263 364.923 | 22 | 277 | 174 | 74 | 49 | 0.26 | 6.72(37) | 8.51 | 9.17 | baseline problem?, blend with |
| U-line | ||||||||||||
| 369 | 29 9,21-28 9,20 | 263 364.923 | 22 | 277 | 174 | 74 | 49 | - | - | - | - | - |
| 370 | 2910,19-2810,18 | 263 368.355 | 26 | 300 | 170 | 74 | 49 | - | - | - | - | - |
| 371 | 2910,20-2810,19 | 263 368.355 | 26 | 300 | 170 | 74 | 49 | - | - | - | - | - |
| 384 | 29 6,24-28 6,23 | 263 604.573 | 12 | 221 | 184 | 74 | 50 | 0.28 | 10.29(36) | 8.81 | 14.22 | baseline problem?, partial blend |
| with CH3CH3CO,
|
||||||||||||
| CH3OCH3 | ||||||||||||
| 385 | 29 6,23-28 6,22 | 263 607.689 | 12 | 221 | 184 | 74 | 50 | - | - | - | - | - |
| 398 | 29 4,26-28 4,25 | 264 055.836 | 13 | 197 | 189 | 108 | 51 | 0.22 | 18.36(49) | 5.92 | 14.22 | partial blend with C2H5CN, v= 0 |
| and CH3CH3CO, v= 0 |
|
Notes:
a Numbering of the observed transitions with |
We consider it essential for claiming a detection of a new molecule that all
lines of this molecule in our observed bands are consistent with this claim,
i.e. are either detected or blended with lines of other species. Therefore, in
the following, we inspect all transitions of amino acetonitrile in our
frequency range. Our line survey at 3, 2, and 1.3 mm covers 596 transitions of our
amino acetonitrile catalog (v= 0 only). Our LTE modeling shows, however, that
the transitions with the line strength times the appropriate (a- or
b-type) dipole moment squared, ![]() ,
smaller than 20 D2 are much too
weak to be detectable with the sensitivity we achieved.
Therefore, we list in Table 2 (online material) only
the 398 transitions above this threshold. To save some space, when two
transitions have a frequency difference smaller than 0.1 MHz which cannot be
resolved, we list only the first one. We number the transitions in Col. 1 and
give their quantum numbers in Col. 2. The frequencies, the frequency
uncertainties, the energies of the lower levels in temperature units, and the
,
smaller than 20 D2 are much too
weak to be detectable with the sensitivity we achieved.
Therefore, we list in Table 2 (online material) only
the 398 transitions above this threshold. To save some space, when two
transitions have a frequency difference smaller than 0.1 MHz which cannot be
resolved, we list only the first one. We number the transitions in Col. 1 and
give their quantum numbers in Col. 2. The frequencies, the frequency
uncertainties, the energies of the lower levels in temperature units, and the
![]() values are listed in Cols. 3-6, respectively.
Since the spectra are in most cases close to the line confusion limit and it
is difficult to measure the noise level, we give in Col. 7 the rms sensitivity
computed from the system temperature and the integration time:
values are listed in Cols. 3-6, respectively.
Since the spectra are in most cases close to the line confusion limit and it
is difficult to measure the noise level, we give in Col. 7 the rms sensitivity
computed from the system temperature and the integration time:
![]() ,
with
,
with
![]() and
and
![]() the forward and beam efficiencies,
the forward and beam efficiencies,
![]() the
system temperature,
the
system temperature, ![]() the spectral resolution, and t the total
integration time (on-source plus off-source).
the spectral resolution, and t the total
integration time (on-source plus off-source).
We list in Col. 8 of Table 2 comments about the blends affecting the amino acetonitrile transitions. As can be seen in this table, most of the amino acetonitrile lines covered by our survey of Sgr B2(N) are heavily blended with lines of other molecules and therefore cannot be identified in this source. Only 88 of the 398 transitions are relatively free of contamination from other molecules, known or still unidentified according to our modeling. They are marked ``Detected'' or ``Group detected'' in Col. 8 of Table 2, and are listed with more information in Table 3. They correspond to 51 observed features which are shown in Fig. 1 (online material) and labeled in Col. 8 of Table 3. For reference, we show the spectrum observed toward Sgr B2(M) in this figure also. We identified the amino acetonitrile lines and the blends affecting them with the LTE model of this molecule and the LTE model including all molecules (see Sect. 3.2). The parameters of our best-fit LTE model of amino acetonitrile are listed in Table 4, and the model is overlaid in red on the spectrum observed toward Sgr B2(N) in Fig. 1. The best-fit LTE model including all molecules is shown in green in the same figure. The source size we used to model the amino acetonitrile emission was derived from our interferometric measurements (see Sect. 3.4 below).
For the frequency range corresponding to each observed amino acetonitrile
feature, we list in Table 3 the integrated intensities of
the observed spectrum (Col. 10), of the best-fit model of amino acetonitrile (Col. 11), and of the
best-fit model including all molecules (Col. 12). In these columns, the dash
symbol indicates transitions belonging to the same feature. Columns 1 to 7 are
the same as in Table 2. The ![]() uncertainty given in Col. 10
was computed using the estimated noise level of Col. 7. These measurements are
plotted in the form of a population diagram in Fig. 2, which
plots upper level column density divided by statistical weight,
uncertainty given in Col. 10
was computed using the estimated noise level of Col. 7. These measurements are
plotted in the form of a population diagram in Fig. 2, which
plots upper level column density divided by statistical weight,
![]() ,
versus the upper level energy in Kelvins (see Goldsmith & Langer 1999).
The data are shown in black and our best-fit model of amino acetonitrile in
red. Out of 21 features encompassing several transitions,
10 contain transitions with different energy levels and were ignored in the
population diagram (features 2, 3, 8, 33, 34, 35, 36, 42, and 49).
We used Eq. (A5) of Snyder et al. (2005) to compute the ordinate values. This
equation assumes optically thin emission. To estimate by how much
line opacities affect this diagram, we applied the opacity correction factor
,
versus the upper level energy in Kelvins (see Goldsmith & Langer 1999).
The data are shown in black and our best-fit model of amino acetonitrile in
red. Out of 21 features encompassing several transitions,
10 contain transitions with different energy levels and were ignored in the
population diagram (features 2, 3, 8, 33, 34, 35, 36, 42, and 49).
We used Eq. (A5) of Snyder et al. (2005) to compute the ordinate values. This
equation assumes optically thin emission. To estimate by how much
line opacities affect this diagram, we applied the opacity correction factor
![]() (see Snyder et al. 2005; Goldsmith & Langer 1999) to the
modeled intensities, using the opacities from our radiative transfer
calculations (Col. 9 of Table 3); the result is shown in
green in Fig. 2. The population diagram derived from the modeled spectrum
is slightly shifted upwards but its shape, in particular its slope (the
inverse of which approximately determines the rotation temperature),
is not significantly changed, since
(see Snyder et al. 2005; Goldsmith & Langer 1999) to the
modeled intensities, using the opacities from our radiative transfer
calculations (Col. 9 of Table 3); the result is shown in
green in Fig. 2. The population diagram derived from the modeled spectrum
is slightly shifted upwards but its shape, in particular its slope (the
inverse of which approximately determines the rotation temperature),
is not significantly changed, since
![]() does not vary much (from
0.04 to 0.24). The populations derived from the observed
spectrum in the optically thin approximation are therefore not significantly
affected by the optical depth of the amino acetonitrile
transitions
does not vary much (from
0.04 to 0.24). The populations derived from the observed
spectrum in the optically thin approximation are therefore not significantly
affected by the optical depth of the amino acetonitrile
transitions![]() .
The scatter of the black crosses in Fig. 2 is therefore
dominated by the blends with other molecules and uncertainties in the baseline
removal (indicated by the downwards and upwards blue arrows, respectively).
From this analysis, we conclude that our best-fit model for amino acetonitrile
is fully consistent with our 30 m data of Sgr B2(N).
.
The scatter of the black crosses in Fig. 2 is therefore
dominated by the blends with other molecules and uncertainties in the baseline
removal (indicated by the downwards and upwards blue arrows, respectively).
From this analysis, we conclude that our best-fit model for amino acetonitrile
is fully consistent with our 30 m data of Sgr B2(N).
Finally, as mentioned above, the 310 transitions of Table 2 not shown in Fig. 1 are all but one heavily blended with transitions of other molecules and cannot be clearly identified in Sgr B2(N). The single exception is amino acetonitrile transition 192 shown in Fig. 3. There are too many blended lines in this frequency range to properly remove the baseline. It is very uncertain and the true baseline is most likely at a lower level than computed here. The presence of several H13CN 2-1 velocity components in absorption also complicates the analysis. Therefore it is very likely that the (single) apparent disagreement concerning transition 192 between our best-fit model and the 30 m spectrum observed toward Sgr B2(N) is not real and does not invalidate our claim of detection of amino acetonitrile.
![\begin{figure}
\par\includegraphics[angle=270,width=9cm,clip]{9203f3.eps}\end{figure}](/articles/aa/full/2008/16/aa9203-07/Timg89.gif) |
Figure 3: Spectrum obtained toward Sgr B2(N) ( bottom) and Sgr B2(M) ( top) with the IRAM 30 m telescope at the frequency of amino acetonitrile (AAN) transition 192 (see caption of Fig. 1 for more details about the color coding). There are too many blended lines in the spectrum of Sgr B2(N) to properly remove the baseline, which is very uncertain and most likely at a lower level than could be computed here. This is the only discrepancy concerning the amino acetonitrile lines in the whole survey. The absorption lines, particularly strong in the spectrum of Sgr B2(M), are velocity components of H13CN 2-1. |
The two 3 mm spectral windows of the PdBI were chosen to cover the five amino acetonitrile features F2 to F6. The spectra toward Sgr B2(N) are shown for both windows toward 3 positions P1, P2, and P3 in Figs. 4a to f. Many lines are detected, the strongest one being a line from within the vibrationally excited state v7 = 1 of cyanoacetylene (HC3N) at 82.2 GHz. We also easily detect lines from within its vibrationally excited state v4 = 1, from its isotopologues HC13CCN and HCC13CN in the v7 = 1 state, from ethyl cyanide (C2H5CN), as well as two unidentified lines at 82.213 and 82.262 GHz. At a lower level, we find emission for all the amino acetonitrile features F2 to F6, and we also detect methylformate (CH3OCHO).
| Sizea |
|
|
FWHM |
|
| ('') | (K) | (cm-2) | (km s-1) | (km s-1) |
| (1) | (2) | (3) | (4) | (5) |
| 2.0 | 100 |
|
7.0 | 0.0 |
|
a Source diameter (FWHM). b Column density of amino acetonitrile. c Velocity offset with respect to the systemic velocity of Sgr B2(N) |
| Molecule | Fa |
|
|
|
|
|
|
|
PAd |
|
|
|
| (MHz)) | (MHz) | (Jy/beam km s-1) | ('') | ('') | ('') | ('') | ( |
(Jy km s-1) | (Jy km s-1) | |||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) |
| AAN | F2 | 81 700.21 | 81 703.33 | 0.09 | 0.68 | -1.60 |
0.30 |
3.9 |
2.00 |
20.5 |
1.76 | 2.89 |
| AAN | F3 | 81 708.02 | 81 712.08 | 0.10 | 0.68 | -1.25 |
0.02 |
3.8 |
1.39 |
10.1 |
1.24 | 1.75 |
| AAN | F4 | 81 732.71 | 81 734.90 | 0.06 | 0.44 | -1.70 |
0.35 |
3.6 |
1.54 |
14.0 |
0.86 | 0.98 |
| AAN | F5 | 81 754.90 | 81 757.40 | 0.06 | 0.24 | -1.52 |
0.03 |
3.2 |
1.20 |
12.5 |
0.30 | 1.15 |
| AAN | F6 | 82 223.46 | 82 226.27 | 0.06 | 0.43 | -1.43 |
0.28 |
3.5 |
1.54 |
6.0 |
0.79 | 0.97 |
| Reference | 81 704.27 | 81 707.08 | 0.07 | ... | ... | ... | ... | ... | ... | ... | ... | |
| C2H5CN | HV | 81 741.77 | 81 744.90 | 0.11 | 2.05 | -1.64 |
5.58 |
3.8 |
1.50 |
5.7 |
4.07 | 6.38 |
| C2H5CN | LV | 81 745.21 | 81 749.27 | 0.15 | 2.82 | -1.74 |
0.46 |
3.8 |
2.87 |
13.7 |
10.43 | 12.94 |
| HC13CCN v7=1 | 81 726.15 | 81 728.96 | 0.09 | 2.20 | -1.35 |
0.60 |
3.7 |
1.68 |
12.6 |
4.98 | 4.81 | |
| HC3N v4=1 | 81 767.71 | 81 771.15 | 0.10 | 2.14 | -1.43 |
0.28 |
3.6 |
1.35 |
9.9 |
3.78 | 3.85 | |
| HC3N v7=1g | HV | 82 196.27 | 82 198.77 | 0.25 | 6.17 | -2.16 |
0.69 |
4.0 |
1.84 |
16.2 |
16.05 | 23.88 |
| 3.36 | -1.50 |
5.25 |
4.0 |
1.36 |
5.5 |
5.35 | ... | |||||
| HC3N v7=1 | LV | 82 199.40 | 82 201.58 | 0.36 | 9.06 | -1.67 |
0.42 |
3.7 |
2.50 |
10.2 |
31.04 | 33.48 |
| HC3N v7=1 | BW | 82 202.52 | 82 203.77 | 0.12 | 3.37 | -0.71 |
0.24 |
3.1 |
2.77 |
45.0 |
11.75 | 12.39 |
| CH3OCHO | 82 242.21 | 82 245.33 | 0.10 | 0.67 | -2.83 |
1.23 |
4.8 |
2.58 |
9.5 |
2.83 | 6.62 | |
|
a Feature numbered like in Col. 8 of Table 3 for amino acetonitrile (AAN). HV and LV mean ``high'' and ``low'' velocity components, respectively, and BW means blueshifted linewing. b Frequency range over which the intensity was integrated. c Noise level in the integrated intensity map shown in Fig. 5. d Peak flux, offsets in right ascension and declination with respect to the reference position of Fig. 5, major and minor diameters (FWHM), and position angle (East from North) derived by fitting an elliptical 2D Gaussian to the integrated intensity map shown in Fig. 5. The uncertainty in Col. 11 is the formal uncertainty given by the fitting routine GAUSS_2D, while the uncertainties correspond to the beam size divided by two times the signal-to-noise ratio in Cols. 7 and 8 and by the signal-to-noise ratio in Cols. 9 and 10. e Flux spatially integrated over the region showing emission in the integrated intensity map of Fig. 5. f Integrated flux of the 30 m spectrum computed over the frequency range given in Cols. 3 and 4. g The two emission peaks of Fig. 5k were fitted separately. |
The integrated intensity maps of the amino acetonitrile features F2 to F6 are presented in Figs. 5a to e, along with two maps of ethyl cyanide (Figs. 5g and h), four maps of cyanoacetylene in the vibrationally excited states v4 = 1 and v7 = 1 (Figs. 5j to m), one map of its isotopologue HC13CCN in the state v7 = 1 (Fig. 5i), one map of methylformate (Fig. 5n), and a reference map computed on the PdBI line-free frequency range between F2 and F3 (Fig. 5f). The frequency intervals used to compute the integrated intensities are given in Cols. 3 and 4 of Table 5 and shown with dotted lines in Fig. 4. We used the fitting routine GAUSS_2D of the GILDAS software to measure the position, size, and peak flux of each integrated emission. The results are listed in Cols. 6 to 11 in Table 5. We label P1 the mean peak position of features F2 to F6, P2 the northern peak position of ethyl cyanide, and P3 the peak position of methylformate (see Table 6 and the plus symbols in Fig. 5). Finally, the PdBI velocity-integrated flux spatially integrated over the emitting region is listed in Col. 12 and the 30 m velocity-integrated intensity is given in Col. 13.
![\begin{figure}
\par\includegraphics[angle=270,width=8.9cm,clip]{9203f4.eps}\end{figure}](/articles/aa/full/2008/16/aa9203-07/Timg103.gif) |
Figure 4: Spectra obtained with the Plateau de Bure interferometer (a) to f)) and the 30 m telescope (g) and h)) toward Sgr B2(N) (in black). The dotted lines show the frequency ranges listed in Table 5. The offset position with respect to the reference position of Fig. 5 is given in each panel, along with a label (P1 to P3, see their definition in Table 6). The lines identified in our 30 m survey are labeled in blue. The red spectra show our best-fit model for amino acetonitrile (AAN) while the green spectrum corresponds to the 30 m model including all molecules. The observed lines which have no counterpart in the green spectrum are still unidentified. |
We present in Fig. 5o the map of continuum emission at
82.0 GHz, integrated over line-free frequency ranges. The continuum emission
has a complex structure. The main region peaks at
![]() ,
,
![]() ,
i.e.
within 0.1
,
i.e.
within 0.1
![]() of the position of the ultracompact H II region K2.
It also shows hints of emission at the position of the ultracompact H II regions K1 and K3, although the spatial resolution is too poor to resolve them
(see, e.g., Gaume et al. 1995). There are other secondary peaks. One of them
coincides with the peak of the shell-like H II region K6 while another
one is located close (<
of the position of the ultracompact H II region K2.
It also shows hints of emission at the position of the ultracompact H II regions K1 and K3, although the spatial resolution is too poor to resolve them
(see, e.g., Gaume et al. 1995). There are other secondary peaks. One of them
coincides with the peak of the shell-like H II region K6 while another
one is located close (<
![]() )
to the peak of the shell-like H II region K5 and traces most likely the same shell. On the other hand, we detect
no 3.7 mm emission at the position of the weak ultracompact H II region K9.69 (Gaume et al. 1995).
)
to the peak of the shell-like H II region K5 and traces most likely the same shell. On the other hand, we detect
no 3.7 mm emission at the position of the weak ultracompact H II region K9.69 (Gaume et al. 1995).
![\begin{figure}
\par\includegraphics[height=18.4cm,angle=-90,clip]{NEWFIG5/9203f5.eps}\end{figure}](/articles/aa/full/2008/16/aa9203-07/Timg107.gif) |
Figure 5:
Integrated intensity maps (panels a) to n)) and
continuum map (panel o)) obtained toward Sgr B2(N) with the Plateau
de Bure interferometer at 82 GHz. Panels a) to e) show
the amino acetonitrile (AAN) features F2 to F6 (see Fig. 4 and
Table 3). Panel f) is a reference map integrated
on the emission-free frequency range between F2 and F3. Panels g)
to n) show the other molecules listed in Table 5. The
lowest contour (positive in black solid line and negative in blue dotted line)
and the contour step are
2 |
The strong lines detected with the PdBI (Figs. 5g to n) allow us
to gain insight into the distribution of molecular line emission in Sgr B2(N).
The double-peaked profile of ethyl cyanide seen with the 30 m telescope (see
Fig. 4g) is resolved with the PdBI into two sources P1 and P2
separated by about 5.3
![]() (see Figs. 4a, c, g, h, and Table 6). P1 and P2 are spatially and kinematically
coincident with the quasi-thermal methanol emission cores ``i'' and ``h''
within
(see Figs. 4a, c, g, h, and Table 6). P1 and P2 are spatially and kinematically
coincident with the quasi-thermal methanol emission cores ``i'' and ``h''
within
![]() and
and
![]() ,
respectively (Mehringer & Menten 1997).
Cores ``i'' and ``h'' were both previously detected in ethyl cyanide (Jones et al. 2007; Liu & Snyder 1999; Hollis et al. 2003). Many
molecules (but not amino acetonitrile within the limits of our sensitivity)
actually show this double-peaked profile in our 30 m survey of Sgr B2(N) and
are most likely emitted by these two sources.
P1 and P2 are also detected in our PdBI data in the vibrationally excited
state v7 = 1 of cyanoacetylene (see Figs. 4b, d, and 5k, l), and there is a hint of emission toward P2
in the isotopologue HC13CCN while P1 is easily detected (see
Figs. 4c and a). In addition, the wings of the main component of
cyanoacetylene v7 = 1 are spatially shifted: the redshifted wing peaks about
,
respectively (Mehringer & Menten 1997).
Cores ``i'' and ``h'' were both previously detected in ethyl cyanide (Jones et al. 2007; Liu & Snyder 1999; Hollis et al. 2003). Many
molecules (but not amino acetonitrile within the limits of our sensitivity)
actually show this double-peaked profile in our 30 m survey of Sgr B2(N) and
are most likely emitted by these two sources.
P1 and P2 are also detected in our PdBI data in the vibrationally excited
state v7 = 1 of cyanoacetylene (see Figs. 4b, d, and 5k, l), and there is a hint of emission toward P2
in the isotopologue HC13CCN while P1 is easily detected (see
Figs. 4c and a). In addition, the wings of the main component of
cyanoacetylene v7 = 1 are spatially shifted: the redshifted wing peaks about
![]() North-West of P1 while the blueshifted wing peaks
about
North-West of P1 while the blueshifted wing peaks
about
![]() East of P1 (Figs. 5k and m). This
East-West velocity gradient was previously reported by several authors
(e.g. de Vicente et al. 2000; Hollis et al. 2003; Lis et al. 1993). Although it could result from
cloud rotation, it is most likely a sign of outflow activity
(see, e.g., Liu & Snyder 1999).
The transition with highest energy in our PdBI sample is a
transition of cyanoacetylene in the vibrationally excited state v4 = 1
(
East of P1 (Figs. 5k and m). This
East-West velocity gradient was previously reported by several authors
(e.g. de Vicente et al. 2000; Hollis et al. 2003; Lis et al. 1993). Although it could result from
cloud rotation, it is most likely a sign of outflow activity
(see, e.g., Liu & Snyder 1999).
The transition with highest energy in our PdBI sample is a
transition of cyanoacetylene in the vibrationally excited state v4 = 1
(
![]() K). Within the limits of our sensitivity, we detect emission
only toward P1 in this highly excited transition (Fig. 5j).
Finally, methylformate peaks at a position significantly offset from P1, at
K). Within the limits of our sensitivity, we detect emission
only toward P1 in this highly excited transition (Fig. 5j).
Finally, methylformate peaks at a position significantly offset from P1, at
![]() to the
North-West (Fig. 5n). It has no counterpart in the continuum map
of Fig. 5o. To sum up, our PdBI data reveal three main positions
of molecular line emission (P1 and P2 corresponding to the methanol cores ``i'' and ``h'', and P3 the peak position of methylformate), and an East-West
velocity gradient around P1.
to the
North-West (Fig. 5n). It has no counterpart in the continuum map
of Fig. 5o. To sum up, our PdBI data reveal three main positions
of molecular line emission (P1 and P2 corresponding to the methanol cores ``i'' and ``h'', and P3 the peak position of methylformate), and an East-West
velocity gradient around P1.
Within the limits of our sensitivity, the amino acetonitrile features F2 to F6
detected with the PdBI show only one peak, and they all peak at the same
position (Figs. 5a to e). We are confident that the emission detected in
features F2 to F6 is not contaminated by the continuum since no significant
signal is detected in the reference map (Fig. 5f).
Their weighted-mean peak position was labeled P1 above
(offset -1.5 ![]()
![]() ,
0.2
,
0.2 ![]()
![]() ,
see
Table 6). The fact that all features are detected at the same position is
consistent with their assignment to the same molecule (see above the shifted
position of methylformate for instance). The deconvolved major and
minor axes of the emission detected in features F2 to F6 are in
the range 0-2.2
,
see
Table 6). The fact that all features are detected at the same position is
consistent with their assignment to the same molecule (see above the shifted
position of methylformate for instance). The deconvolved major and
minor axes of the emission detected in features F2 to F6 are in
the range 0-2.2
![]() and 1.0-1.9
and 1.0-1.9
![]() ,
respectively. The
amino acetonitrile emission is therefore slightly resolved and has a size of
roughly 2
,
respectively. The
amino acetonitrile emission is therefore slightly resolved and has a size of
roughly 2
![]() FWHM, which we used for the LTE modeling.
The spatially integrated fluxes of F4 and F6
agree within 20
FWHM, which we used for the LTE modeling.
The spatially integrated fluxes of F4 and F6
agree within 20![]() with the fluxes measured with the 30 m telescope (see
Cols. 12 and 13 of Table 5). The emission detected with the
30 m telescope in these two features of amino acetonitrile is therefore compact
(2
with the fluxes measured with the 30 m telescope (see
Cols. 12 and 13 of Table 5). The emission detected with the
30 m telescope in these two features of amino acetonitrile is therefore compact
(2
![]() )
and was not filtered out by the interferometer. The other
features F2, F3, and F5 have 30 m fluxes 1.6, 1.4, and 3.8 times larger than the PdBI fluxes, respectively: the emission filtered out by the interferometer
most likely corresponds to the unidentified transitions blended with
these amino acetonitrile features (see Fig. 4a). In addition,
the low signal-to-noise ratio of feature F5 detected with the PdBI may
significantly affect the flux measurement.
)
and was not filtered out by the interferometer. The other
features F2, F3, and F5 have 30 m fluxes 1.6, 1.4, and 3.8 times larger than the PdBI fluxes, respectively: the emission filtered out by the interferometer
most likely corresponds to the unidentified transitions blended with
these amino acetonitrile features (see Fig. 4a). In addition,
the low signal-to-noise ratio of feature F5 detected with the PdBI may
significantly affect the flux measurement.
We used the parameters of the 30 m model (see Table 4) to compute a model spectrum of amino acetonitrile with the spatial resolution of the PdBI (using the geometrical mean of the elliptical beam). The agreement with the peak spectrum is good, within a factor of 2 (see Figs. 4a and b). The small discrepancy may come from the somewhat uncertain source size and from our approximate modeling of the interferometric beam pattern: spherical beam and full uv coverage for the model versus elliptical beam and partially sampled uv coverage for the observations. Overall, our LTE model of amino acetonitrile is therefore well consistent with the compact emission detected with the PdBI.
| RA (J2000) | Dec (J2000) | Comments | |
|
|
|
||
| PdBI | |||
| 82 |
|
|
continuum 82.0 GHz |
| P1 |
|
|
mean AANa F2 to F6 |
| P2 |
|
|
mean HC3N v7=1, C2H5CN |
| P3 |
|
|
peak CH3OCHO |
| ATCA | |||
| 95 |
|
|
mean continuum |
| 93.2 and 97.4 GHz | |||
| P4 |
|
|
mean AAN F7 to F10 |
| P5 |
|
|
mean HC13CCN v7=1, |
| CH3OH
|
|||
a AAN stands for amino acetonitrile.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9203f6.eps}\end{figure}](/articles/aa/full/2008/16/aa9203-07/Timg129.gif) |
Figure 6: Spectra obtained with the Australia Telescope Compact Array (a) to j)) and the 30 m telescope (k) and l)) toward Sgr B2(N) (black histogram). The dotted lines show the frequency ranges listed in Table 7. The offset position with respect to the reference position of Fig. 7 is given in each panel. The lines identified in our 30 m survey are labeled in blue. The red spectrum shows our best-fit model for amino acetonitrile (AAN) while the green spectrum corresponds to the 30 m model including all molecules. The observed lines which have no counterpart in the green spectrum are still unidentified. a) and b) show the extended configuration H 214, c) and d) the intermediate configuration H 168, e) and f) the compact configuration H 75, g) and h) the combination of H 214 and H 168, and i) and j) the combination of all three configurations. The spectral coverage is not the same for all configurations because the sky tuning frequency for H 168 and H 75 was not corrected for the observatory velocity variations. The clean beam size ( HPBW) is given in each panel. |
The two 3 mm spectral windows of the ATCA were chosen to cover the four
amino acetonitrile features F7 to F10. The spectra toward position P4 of
Sgr B2(N) (offset
![]() , 0.1
, 0.1
![]() )
are presented for both windows in
Fig. 6. Since the spectral windows were not exactly the same in
each configuration (see Sect. 2.3), we show the spectra for each
configuration (Figs. 6a to f), plus the combination of the two
broadest ones (Figs. 6g and h), and the combination of all
three configurations (Figs. 6i and j). Nearly all the lines seen
with the 30 m telescope are detected with the ATCA toward P4. In the 90.6 GHz
band, we detect the blue wing of an SO2 transition (Fig. 6a), the
red wing of an HC13CCN ground-state transition (Fig. 6e),
an unidentified line, and feature F7. In the 90.8 GHz band, we detect the
low-velocity component of a
)
are presented for both windows in
Fig. 6. Since the spectral windows were not exactly the same in
each configuration (see Sect. 2.3), we show the spectra for each
configuration (Figs. 6a to f), plus the combination of the two
broadest ones (Figs. 6g and h), and the combination of all
three configurations (Figs. 6i and j). Nearly all the lines seen
with the 30 m telescope are detected with the ATCA toward P4. In the 90.6 GHz
band, we detect the blue wing of an SO2 transition (Fig. 6a), the
red wing of an HC13CCN ground-state transition (Fig. 6e),
an unidentified line, and feature F7. In the 90.8 GHz band, we detect the
low-velocity component of a
![]() = 1 transition of methanol, the
low-velocity component of a v7 = 1 transition of HC13CCN
(Figs. 6d and f), and the three amino acetonitrile features F8,
F9, and F10. Toward the northern position P5, we detect a second velocity
component of methanol
= 1 transition of methanol, the
low-velocity component of a v7 = 1 transition of HC13CCN
(Figs. 6d and f), and the three amino acetonitrile features F8,
F9, and F10. Toward the northern position P5, we detect a second velocity
component of methanol
![]() and HC13CCN v7=1 (not shown
in Fig. 6, see below).
and HC13CCN v7=1 (not shown
in Fig. 6, see below).
The integrated intensity maps of the amino acetonitrile features F7 to F10 in
the different configurations are presented in Figs. 7a to p,
along with maps of the excited states of methanol and HC13CCN
(Figs. 7q to v). The frequency intervals used to compute the
integrated intensities are given in Cols. 3 and 4 of Table 7 and
drawn in dotted lines in Fig. 6. We used the fitting routine
GAUSS_2D of the GILDAS software to measure the position, size, and peak
flux of each integrated emission. The results are listed in Cols. 6 to 11 of
Table 7. We label P4 the weighted-mean peak position of features F7 to F10, computed using the combined configuration H 214 + H 168 (only
H 214 for F8), and P5 the average northern peak position of methanol and
HC13CCN. The mean peak position P4 is at the
offset (-2.0 ![]()
![]() ,
0.1
,
0.1 ![]()
![]() ), and the average position P5 is at (-1.9
), and the average position P5 is at (-1.9 ![]()
![]() ,
5.2
,
5.2 ![]()
![]() )
(see coordinates in
Table 6 and positions in Fig. 7x).
Finally, the ATCA velocity-integrated flux spatially integrated over the
emitting region is listed in Col. 12 of Table 7 and the 30 m
velocity-integrated intensity is given in Col. 13.
)
(see coordinates in
Table 6 and positions in Fig. 7x).
Finally, the ATCA velocity-integrated flux spatially integrated over the
emitting region is listed in Col. 12 of Table 7 and the 30 m
velocity-integrated intensity is given in Col. 13.
| Moleculea | Conf.b |
|
|
|
|
|
|
|
PAe |
|
|
|
| (MHz)) | (MHz) | (Jy/beam km s-1) | ('') | ('') | ('') | ('') | ( |
(Jy km s-1) | (Jy km s-1) | |||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) |
| AAN F7 | E | 90 558.99 | 90 563.99 | 0.12 | 0.87 | -2.32 |
-0.22 |
2.9 |
2.2 |
29.2 |
1.12 | 3.06 |
| AAN F7 | I | 90 559.05 | 90 564.05 | 0.15 | 1.47 | -1.94 |
0.58 |
3.6 |
2.7 |
-79.8 |
1.73 | 3.06 |
| AAN F7 | C | 90 561.48 | 90 564.23 | 0.10 | 1.53 | -0.96 |
0.71 |
7.0 |
4.8 |
-80.3 |
1.37 | 1.79 |
| AAN F7 | M | 90 559.13 | 90 563.96 | 0.12 | 1.19 | -2.10 |
0.25 |
3.1 |
2.7 |
83.5 |
1.71 | 2.96 |
| AAN F7 | A | 90 562.03 | 90 563.96 | 0.06 | 0.61 | -1.23 |
0.26 |
5.3 |
3.3 |
87.1 |
1.37 | 1.00 |
| AAN F8 | E | 90 781.27 | 90 786.77 | 0.21 | 1.22 | -1.94 |
-0.18 |
3.8 |
2.1 |
45.0 |
1.70 | 7.23 |
| AAN F9 | E | 90 788.02 | 90 792.02 | 0.09 | 0.45 | -1.70 |
-0.06 |
3.4 |
1.9 |
45.0 |
0.49 | 2.14 |
| AAN F9 | I | 90 788.11 | 90 792.11 | 0.13 | 0.97 | -1.77 |
0.23 |
3.6 |
2.2 |
-84.0 |
1.01 | 2.14 |
| AAN F9 | C | 90 790.54 | 90 792.04 | 0.10 | 2.00 | -1.25 |
0.49 |
6.1 |
5.8 |
-45.0 |
1.86 | 1.59 |
| AAN F9 | M | 90 788.04 | 90 792.16 | 0.10 | 0.85 | -1.67 |
0.02 |
3.1 |
2.4 |
75.9 |
1.07 | 2.14 |
| AAN F9 | A | 90 790.95 | 90 792.16 | 0.05 | 0.63 | -1.26 |
0.23 |
4.8 |
3.9 |
84.5 |
1.51 | 1.31 |
| AAN F10 | E | 90 796.52 | 90 800.77 | 0.16 | 1.17 | -2.51 |
0.02 |
2.7 |
2.2 |
-81.2 |
1.38 | 6.48 |
| AAN F10 | I | 90 796.61 | 90 800.86 | 0.10 | 0.93 | -1.81 |
0.20 |
3.3 |
2.0 |
82.3 |
0.79 | 6.19 |
| AAN F10 | C | 90 796.54 | 90 800.79 | 0.15 | 3.36 | -1.08 |
0.28 |
6.6 |
4.9 |
-77.7 |
2.78 | 6.48 |
| AAN F10 | M | 90 796.52 | 90 800.88 | 0.13 | 1.32 | -2.28 |
0.03 |
2.9 |
2.2 |
83.7 |
1.42 | 6.48 |
| AAN F10 | A | 90 796.52 | 90 800.88 | 0.13 | 1.82 | -1.66 |
0.12 |
4.5 |
3.1 |
-89.3 |
3.24 | 6.48 |
| HC13CCN v7=1 HV | I | 90 804.36 | 90 805.36 | 0.05 | 0.49 | -1.94 |
5.16 |
3.0 |
2.0 |
84.4 |
0.41 | 2.39 |
| HC13CCN v7=1 LV | I | 90 806.11 | 90 809.36 | 0.14 | 2.74 | -1.56 |
0.55 |
3.7 |
2.1 |
83.6 |
2.69 | 10.30 |
| HC13CCN v7=1 LV | C | 90 806.04 | 90 809.29 | 0.15 | 4.98 | -1.71 |
0.25 |
7.1 |
4.4 |
-83.8 |
4.12 | 10.30 |
| CH3OH
|
I | 90 809.61 | 90 811.11 | 0.09 | 1.52 | -1.85 |
5.23 |
3.7 |
2.1 |
-85.7 |
1.54 | 6.55 |
| CH3OH
|
I | 90 812.36 | 90 814.11 | 0.11 | 1.60 | -1.84 |
0.44 |
3.8 |
3.6 |
23.7 |
2.72 | 10.40 |
| CH3OH
|
C | 90 812.29 | 90 814.29 | 0.12 | 5.22 | -1.86 |
-0.03 |
7.1 |
4.5 |
-77.9 |
4.29 | 10.40 |
|
a For amino acetonitrile (AAN), we give the feature number like in Col. 8 of Table 3. For the other molecules, HV and LV mean high and low velocity component, respectively. b Interferometer configuration: E: extended (H 214), I: intermediate (H 168), C: compact (H 75), M: mixed (H 214 + H 168), A: all (H 214 + H 168 + H 75). c Frequency range over which the intensity was integrated. d Noise level in the integrated intensity map shown in Fig. 7. e Peak flux, offsets in right ascension and declination with respect to the reference position of Fig. 7, major and minor diameters (FWHM), and position angle (East from North) derived by fitting an elliptical 2D Gaussian to the integrated intensity map shown in Fig. 7. The uncertainty in Col. 11 is the formal uncertainty given by the fitting routine GAUSS_2D, while the uncertainties correspond to the beam size divided by two times the signal-to-noise ratio in Cols. 7 and 8 and by the signal-to-noise ratio in Cols. 9 and 10. f Flux spatially integrated over the region showing emission in the integrated intensity map of Fig. 7. g Integrated flux of the 30 m spectrum computed over the frequency range given in Cols. 3 and 4. |
![\begin{figure}
\par\includegraphics[angle=270,width=18cm,clip]{9203f7.eps}\end{figure}](/articles/aa/full/2008/16/aa9203-07/Timg135.gif) |
Figure 7:
Integrated intensity maps (panels a) to v)) and
continuum map (panel w)) obtained toward Sgr B2(N) with the Australia
Telescope Compact Array at 3 mm. Panels a) to p)
show the amino acetonitrile features F7 to F10 in the different
configurations (see Fig. 6).
Panels q) to v) show the other molecules listed in
Table 7. The lower contour (positive in black solid line
and negative in blue dotted line) and the contour step are
3 |
Since the line-free frequency ranges in the two spectral windows are too
small to compute a reliable continuum map, we present in Fig. 7w
a map combining the emission obtained at 93.2 and 97.4 GHz in the continuum
mode. The contaminating lines were avoided in the integration. The continuum
emission detected with the ATCA has properties very similar to the emission
detected with the PdBI (see Sect. 3.4). The emission peaks at
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
i.e.
within 0.3
,
i.e.
within 0.3
![]() of the ultracompact H II region K2
(Gaume et al. 1995). The continuum emission is somewhat extended around the
main peak: it extends toward the other ultracompact H II regions K1, K3,
and the shell-like H II region K5, but these features are not resolved
with the ATCA. We also detect a shell-like emission close to K6, but its
signal-to-noise ratio is lower than in the PdBI data. We do not detect any
emission toward the weak ultracompact H II region K9.69
(Gaume et al. 1995).
of the ultracompact H II region K2
(Gaume et al. 1995). The continuum emission is somewhat extended around the
main peak: it extends toward the other ultracompact H II regions K1, K3,
and the shell-like H II region K5, but these features are not resolved
with the ATCA. We also detect a shell-like emission close to K6, but its
signal-to-noise ratio is lower than in the PdBI data. We do not detect any
emission toward the weak ultracompact H II region K9.69
(Gaume et al. 1995).
The strong methanol
![]() and HC13CCN v7=1 lines show the
same structure as the strong lines detected with the PdBI, namely emission from
two different positions separated by about 5.1
and HC13CCN v7=1 lines show the
same structure as the strong lines detected with the PdBI, namely emission from
two different positions separated by about 5.1
![]() in declination, each
with a distinct velocity (Figs. 7q, r, t, and u). These two
positions P4 and P5 coincide with the PdBI positions P1 and P2, respectively,
within 0.5
in declination, each
with a distinct velocity (Figs. 7q, r, t, and u). These two
positions P4 and P5 coincide with the PdBI positions P1 and P2, respectively,
within 0.5
![]() which is about one fifth of the ATCA synthesized beam (see
Fig. 7x for a visual comparison). Therefore we are very
confident that they correspond to the same regions. The third position P3
detected with the PdBI in methylformate is not detected in the small number of
transitions observed with the ATCA.
which is about one fifth of the ATCA synthesized beam (see
Fig. 7x for a visual comparison). Therefore we are very
confident that they correspond to the same regions. The third position P3
detected with the PdBI in methylformate is not detected in the small number of
transitions observed with the ATCA.
Within the limits of our sensitivity, the amino acetonitrile features F7 to F10
show only one peak, and they all peak at the same position P4 coincident with
the PdBI position P1. Therefore, all amino acetonitrile features
detected with both the ATCA and the PdBI peak at the same position, which is
consistent with their assignment to the same molecule.
The emission detected in features F7 to F10 is barely resolved with the ATCA.
Given the uncertainties, it is consistent with the source size of 2
![]() suggested by our measurements with the PdBI. The ATCA spatially integrated
flux of feature F7 in the mixed configuration H 214 + H168 agrees with the
30 m telescope flux within 40
suggested by our measurements with the PdBI. The ATCA spatially integrated
flux of feature F7 in the mixed configuration H 214 + H168 agrees with the
30 m telescope flux within 40![]() .
Given the calibration uncertainties of
both instruments, and the somewhat larger noise in the 30 m spectrum, most of
the flux of feature F7 is recovered with the ATCA. On the other hand, the ATCA
spatially integrated fluxes of features F8 to F10 are significantly weaker
than the 30 m telescope fluxes. The main reason for this disagreement may be
the contamination of the 30 m spectrum by emission from transitions of
other molecules which are still unidentified in our survey (see
Fig. 6l). This contaminating emission is missed by the
interferometer either because it peaks at an offset position or because it is
extended and filtered out.
.
Given the calibration uncertainties of
both instruments, and the somewhat larger noise in the 30 m spectrum, most of
the flux of feature F7 is recovered with the ATCA. On the other hand, the ATCA
spatially integrated fluxes of features F8 to F10 are significantly weaker
than the 30 m telescope fluxes. The main reason for this disagreement may be
the contamination of the 30 m spectrum by emission from transitions of
other molecules which are still unidentified in our survey (see
Fig. 6l). This contaminating emission is missed by the
interferometer either because it peaks at an offset position or because it is
extended and filtered out.
The model spectrum of amino acetonitrile computed with the same parameters as the 30 m model (see Table 4) but with the spatial resolution of the ATCA is shown in red in Figs. 6a to j. The agreement with the spectra obtained with the ATCA is good, within a factor of 2 (see comment about the interferometric modeling in Sect. 3.4). Overall, our LTE model of amino acetonitrile is therefore well consistent with the compact emission detected with the ATCA.
The continuum emission detected with the PdBI (see Fig. 5o) has
a peak intensity of 0.459 ![]() 0.009 Jy/
0.009 Jy/
![]()
![]()
![]() -beam.
In the 2''-diameter region convolved with the PdBI beam centered on the AAN peak
position P1 (convolved FWHM:
-beam.
In the 2''-diameter region convolved with the PdBI beam centered on the AAN peak
position P1 (convolved FWHM:
![]()
![]()
![]() ), we measure a
mean intensity of 0.257 Jy/beam and a flux of 0.556 Jy. The continuum emission
from Sgr B2(N) at 3.7 mm is dominated by thermal dust emission, at most
30
), we measure a
mean intensity of 0.257 Jy/beam and a flux of 0.556 Jy. The continuum emission
from Sgr B2(N) at 3.7 mm is dominated by thermal dust emission, at most
30![]() come from free-free emission (Kuan et al. 1996), probably even less
toward the ultracompact H II region K2 since its flux is only 20 and
60 mJy at 2 and 1.3 cm, respectively (Gaume & Claussen 1990; Gaume et al. 1995). In
addition, the thermal dust emission is optically thin (Carlstrom & Vogel 1989),
so we can estimate the H2 column density using the equation:
come from free-free emission (Kuan et al. 1996), probably even less
toward the ultracompact H II region K2 since its flux is only 20 and
60 mJy at 2 and 1.3 cm, respectively (Gaume & Claussen 1990; Gaume et al. 1995). In
addition, the thermal dust emission is optically thin (Carlstrom & Vogel 1989),
so we can estimate the H2 column density using the equation:
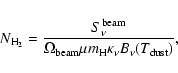 |
(1) |
Using the column density derived from our modeling (see
Table 4), we find an amino acetonitrile abundance relative to
H2 of about 2.2 ![]() 10-9 in the inner region of deconvolved
FWHM diameter 2
10-9 in the inner region of deconvolved
FWHM diameter 2
![]() ,
with an uncertainty on the abundance of at least a
factor of 2 given the uncertainties on the dust mass opacity and the dust
emissivity exponent.
,
with an uncertainty on the abundance of at least a
factor of 2 given the uncertainties on the dust mass opacity and the dust
emissivity exponent.
The continuum emission detected with the ATCA at a mean frequency of 95.3 GHz
has a peak intensity of 1.00 Jy/
![]()
![]()
![]() -beam. This
intensity is 1.8 times larger than the PdBI continuum flux measured over an
area
-beam. This
intensity is 1.8 times larger than the PdBI continuum flux measured over an
area
![]()
![]()
![]() (see above). If this flux difference comes
from the frequency dependence of the continuum emission, then we derive a
frequency exponent of 3.9 which is, within the calibration uncertainties,
consistent with the exponent of 3.5 expected for thermal dust emission with a
dust emissivity exponent
(see above). If this flux difference comes
from the frequency dependence of the continuum emission, then we derive a
frequency exponent of 3.9 which is, within the calibration uncertainties,
consistent with the exponent of 3.5 expected for thermal dust emission with a
dust emissivity exponent
![]() assumed above. We are therefore
confident that the continuum emission detected toward K2 with the PdBI and the
ATCA is largely dominated by thermal dust emission.
assumed above. We are therefore
confident that the continuum emission detected toward K2 with the PdBI and the
ATCA is largely dominated by thermal dust emission.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{9203f8.eps}\end{figure}](/articles/aa/full/2008/16/aa9203-07/Timg155.gif) |
Figure 8:
Continuum image of the Sgr B2 region obtained with the Very Large
Array at 9.1 GHz . The lowest contour
level is 4 times the rms noise level of 8 mJy beam-1 and contours double
in value until they reach 512 times that level. The dotted circle represents
the FWHM of the VLA antennas' primary beam at 9.1 GHz. The image is not
corrected for attenuation due to the primary beam's response. Note that it is
produced from data taken over only a 1 h period and has limited dynamic
range and sensitivity. It is, however, consistent with the higher
sensitivity three-pointing-mosaic 4.8 GHz image presented by
Mehringer et al. (1995), which has a similar resolution. The synthesized beam is
represented in the lower left corner. The upper and lower shaded circles are
centered at the Sgr B2(N) and (M) pointing positions of our 30 m telescope
spectral line survey, respectively. Their size corresponds to the
|
Figure 8 shows the continuum image of the Sgr B2 region we
obtained at 9.1 GHz with the VLA. At this frequency, the primary beam has a
FWHM of ![]()
![]() .
Our uv-data should adequately sample structures
with sizes of up to
.
Our uv-data should adequately sample structures
with sizes of up to
![]() .
There are two major
continuum sources, Sgr B2(N) and (M), whose emission is
a blend of the contributions of many separate sources that are resolved in
higher resolution images (e.g., Gaume et al. 1995). A number of secondary
sources are evident. The peak brightness,
.
There are two major
continuum sources, Sgr B2(N) and (M), whose emission is
a blend of the contributions of many separate sources that are resolved in
higher resolution images (e.g., Gaume et al. 1995). A number of secondary
sources are evident. The peak brightness, ![]() ,
toward Sgr B2(N) is
2.85 Jy beam-1. Toward Sgr B2(M) we measure
,
toward Sgr B2(N) is
2.85 Jy beam-1. Toward Sgr B2(M) we measure
![]() Jy beam-1. The image has a relatively high 1
Jy beam-1. The image has a relatively high 1![]() rms noise level of
8.4 mJy beam-1 that is determined by dynamic range limitations. Nowhere
in the whole line datacube do we find any significant line emission or
absorption above 3.4 mJy beam-1 (5 times the 1
rms noise level of
8.4 mJy beam-1 that is determined by dynamic range limitations. Nowhere
in the whole line datacube do we find any significant line emission or
absorption above 3.4 mJy beam-1 (5 times the 1![]() rms noise level in
the images of the spectral line emission). This
corresponds to a brightness temperature upper limit of 0.35 K. With this, and
assuming a width of 30 km s-1, similar to other lines with extended
emission (e.g., Hollis et al. 2004; Hunt et al. 1999) we can use the standard relation to
calculate an upper limit to the column densities of the upper
levels of the strongest of the
JKa,Kc = 101-000 hfs components
of
rms noise level in
the images of the spectral line emission). This
corresponds to a brightness temperature upper limit of 0.35 K. With this, and
assuming a width of 30 km s-1, similar to other lines with extended
emission (e.g., Hollis et al. 2004; Hunt et al. 1999) we can use the standard relation to
calculate an upper limit to the column densities of the upper
levels of the strongest of the
JKa,Kc = 101-000 hfs components
of ![]() 8
8 ![]() 1012 cm-2. Hollis et al. (2004) use a two temperature
component picture to explain their multitransition glycolaldehyde study,
invoking components with temperatures of T = 8 and 50 K. For 8 K, our limit
on the total column density of extended amino acetonitrile would be
1012 cm-2. Hollis et al. (2004) use a two temperature
component picture to explain their multitransition glycolaldehyde study,
invoking components with temperatures of T = 8 and 50 K. For 8 K, our limit
on the total column density of extended amino acetonitrile would be
![]() 3
3 ![]() 1014 cm-2 and for 50 K it would be
1014 cm-2 and for 50 K it would be
![]() 3
3 ![]() 1016 cm-2. The low-T value is on the same order as
the total column density of glycolaldehyde that Hollis et al. (2004) calculate for
this temperature.
1016 cm-2. The low-T value is on the same order as
the total column density of glycolaldehyde that Hollis et al. (2004) calculate for
this temperature.
Using the ATCA, Hunt et al. (1999) imaged Sgr B2 in the J=1-0 line of HC3N
at a frequency near 9.1 GHz, very close to our amino acetonitrile frequency.
In their
![]()
![]()
![]() resolution images they found the spatial
distribution of the line emission to resemble that of the continuum emission
very closely. Assuming that possible extended amino acetonitrile had a similar
distribution, the high continuum flux densities allow us to determine very
sensitive limits on possible absorption (or weakly inverted emission)
toward the continuum emission. We calculate very low
resolution images they found the spatial
distribution of the line emission to resemble that of the continuum emission
very closely. Assuming that possible extended amino acetonitrile had a similar
distribution, the high continuum flux densities allow us to determine very
sensitive limits on possible absorption (or weakly inverted emission)
toward the continuum emission. We calculate very low
![]() limits on the absolute value of the optical depth of
8.3
limits on the absolute value of the optical depth of
8.3 ![]() 10-4 and 1.2
10-4 and 1.2 ![]() 10-3 toward Sgr B2(N) and (M). This
implies
10-3 toward Sgr B2(N) and (M). This
implies ![]() 125 and 20 times lower column density limits for T = 8 and
50 K, respectively, compared to limits on possible thermal emission quoted above.
125 and 20 times lower column density limits for T = 8 and
50 K, respectively, compared to limits on possible thermal emission quoted above.
We detected compact emission from amino acetonitrile in Sgr B2(N)
with a source size of 2
![]() FWHM, a column density of
2.8
FWHM, a column density of
2.8 ![]() 1016 cm-2, an excitation temperature of 100 K, a
linewidth of 7 km s-1, and a centroid velocity of 64 km s-1 (see
Table 4). We estimated the abundance of amino acetonitrile
to be 2.2
1016 cm-2, an excitation temperature of 100 K, a
linewidth of 7 km s-1, and a centroid velocity of 64 km s-1 (see
Table 4). We estimated the abundance of amino acetonitrile
to be 2.2 ![]() 10-9 in this compact region. We found no evidence for
a possible colder, more extended emission. The compact emission peaks at
position P1 (see Sect. 3.4 and Table 6), which is
located 0.4
10-9 in this compact region. We found no evidence for
a possible colder, more extended emission. The compact emission peaks at
position P1 (see Sect. 3.4 and Table 6), which is
located 0.4
![]() South of the ultracompact H II region K2 where the
3.7 mm thermal dust continuum emission detected with the PdBI also peaks.
This angular separation is at a level of 2
South of the ultracompact H II region K2 where the
3.7 mm thermal dust continuum emission detected with the PdBI also peaks.
This angular separation is at a level of 2![]() only, so it may not be
significant. Our PdBI and ATCA data show that ethyl cyanide C2H5CN,
cyanoacetylene HC3N in its excited states v7 = 1 and v4 = 1,
HC13CCN in its excited state v7 = 1, and methanol CH3OH in its
excited state
only, so it may not be
significant. Our PdBI and ATCA data show that ethyl cyanide C2H5CN,
cyanoacetylene HC3N in its excited states v7 = 1 and v4 = 1,
HC13CCN in its excited state v7 = 1, and methanol CH3OH in its
excited state
![]() also peak at this position P1. The amino acetonitrile
emission arises therefore from the hot core region called the
``Large Molecule Heimat'' (see Sect. 1.1.2).
Our PdBI continuum data show that this compact region is extremely
dense (1.7
also peak at this position P1. The amino acetonitrile
emission arises therefore from the hot core region called the
``Large Molecule Heimat'' (see Sect. 1.1.2).
Our PdBI continuum data show that this compact region is extremely
dense (1.7 ![]() 108 cm-3) and massive (2340
108 cm-3) and massive (2340 ![]() ). The
ultracompact H II region K2 is most likely still embedded in the dense, hot core traced by the thermal dust emission and seems therefore to be the youngest source among the numerous
ultracompact H II regions populating the Sgr B2 molecular cloud.
In addition, the LMH hosts the powerful Sgr B2(N) H2O maser region. The
distribution of the maser emission over
). The
ultracompact H II region K2 is most likely still embedded in the dense, hot core traced by the thermal dust emission and seems therefore to be the youngest source among the numerous
ultracompact H II regions populating the Sgr B2 molecular cloud.
In addition, the LMH hosts the powerful Sgr B2(N) H2O maser region. The
distribution of the maser emission over
![]()
![]()
![]() was mapped
using Very Long Baseline Interferometry by Reid et al. (1988), who also fitted a
kinematical model invoking expansion and rotation. The best fit center of
expansion is displaced from our interferometric position P1 by
(
was mapped
using Very Long Baseline Interferometry by Reid et al. (1988), who also fitted a
kinematical model invoking expansion and rotation. The best fit center of
expansion is displaced from our interferometric position P1 by
(
![]() ) = (
) = (
![]() ), which is
less than the combined positional uncertainty of the VLBI and PdBI data. The
best fit radial component of the expansion velocity, 63
), which is
less than the combined positional uncertainty of the VLBI and PdBI data. The
best fit radial component of the expansion velocity, 63 ![]() 3 km s-1,
is also in excellent agreement with the 64 km s-1 that we obtain for the
LMH (see Table 4). H2O masers are associated with young
stellar objects in their earliest stages when they drive powerful outflows,
such as the one found in Sgr B2(N) which has a total velocity extent of
3 km s-1,
is also in excellent agreement with the 64 km s-1 that we obtain for the
LMH (see Table 4). H2O masers are associated with young
stellar objects in their earliest stages when they drive powerful outflows,
such as the one found in Sgr B2(N) which has a total velocity extent of
![]()
![]() km s-1 (see, e.g., Reid et al. 1988). Thus, the
water vapor maser provides evidence for the youth of the LMH, the very compact
region where the amino acetonitrile emission originates from.
km s-1 (see, e.g., Reid et al. 1988). Thus, the
water vapor maser provides evidence for the youth of the LMH, the very compact
region where the amino acetonitrile emission originates from.
Bisschop et al. (2007) measured the abundances of various complex molecules in massive hot core regions and classified these molecules as ``cold'' (<100 K) or ``hot'' (>100 K). Based on the high abundances, the similar high rotation temperatures, and the relative constant abundance ratios of the oxygen-bearing species and two nitrogen-bearing species, they concluded that the ``hot'' molecules share a common solid state formation scheme. From an analysis of the emission of complex organic molecules in molecular clouds in the Galactic center region and a comparison to results previously obtained in hot cores, Requena-Torres et al. (2006) support also the scenario in which complex organic molecules are formed on the grain surfaces. The high temperature and abundance we measured for amino acetonitrile suggest it shares the same properties as the ``hot'' molecules found by Bisschop et al. (2007), which favors its formation on the grain surfaces, although its detection in other hot cores to check if it follows the abundance correlations found by Bisschop et al. (2007) and Requena-Torres et al. (2006) is needed to prove this conclusion.
Wirström et al. (2007) failed to detect amino acetonitrile in the hot cores
Orion KL, W51 e1/e2, S140, and W3(OH)
with the Onsala 20 m telescope. They
found beam-averaged column density upper limits of
1.1-3.5 ![]() 1013 cm-2 for amino acetonitrile, while they detected
vinylcyanide C2H3CN with a column density of
1013 cm-2 for amino acetonitrile, while they detected
vinylcyanide C2H3CN with a column density of ![]() 2
2 ![]() 1014 cm-2 in the first two sources. Our 30 m observations of Sgr B2(N) imply a
column density of 8
1014 cm-2 in the first two sources. Our 30 m observations of Sgr B2(N) imply a
column density of 8 ![]() 1017 cm-2 for vinylcyanide with a source
size of 2.3
1017 cm-2 for vinylcyanide with a source
size of 2.3
![]() (Belloche et al., in prep.), i.e. about 30 times
our amino acetonitrile column density. If the column density ratio of these
two species in Sgr B2(N) holds for other hot cores, then the observations of
Wirström et al. (2007) were not sensitive enough to detect amino acetonitrile in
their sources.
(Belloche et al., in prep.), i.e. about 30 times
our amino acetonitrile column density. If the column density ratio of these
two species in Sgr B2(N) holds for other hot cores, then the observations of
Wirström et al. (2007) were not sensitive enough to detect amino acetonitrile in
their sources.
Our PdBI and ATCA data show that the double peak structure seen in many
transitions detected with the 30 m telescope are produced by two sources
separated by about 5.3
![]() in the North-South direction (positions P1 and
P2, see Sect. 3.4). The centroid velocity difference between these
two positions is about 9 km s-1. The northern and more redshifted source (P2) is about twice weaker in the molecular emission detected in our 30 m data
(Belloche et al., in prep.). These two sources were already detected
in ethylcyanide with high-resolution observations
(see, e.g., Jones et al. 2007; Liu & Snyder 1999; Hollis et al. 2003). Our interferometric data
show that cyanoacetylene HC3N and its isotopologue HC13CCN in their
excited state v7 = 1, and methanol in its excited state
in the North-South direction (positions P1 and
P2, see Sect. 3.4). The centroid velocity difference between these
two positions is about 9 km s-1. The northern and more redshifted source (P2) is about twice weaker in the molecular emission detected in our 30 m data
(Belloche et al., in prep.). These two sources were already detected
in ethylcyanide with high-resolution observations
(see, e.g., Jones et al. 2007; Liu & Snyder 1999; Hollis et al. 2003). Our interferometric data
show that cyanoacetylene HC3N and its isotopologue HC13CCN in their
excited state v7 = 1, and methanol in its excited state
![]() are also
detected toward both sources. In the PdBI spectra shown in
Figs. 4c and d, we do not find a clear evidence for
amino acetonitrile at a velocity of
are also
detected toward both sources. In the PdBI spectra shown in
Figs. 4c and d, we do not find a clear evidence for
amino acetonitrile at a velocity of ![]() 73 km s-1. There may be a hint
of emission at a level about a factor of 2 lower than the emission toward P1
(see also Feature F3 in the 30 m spectrum in Fig. 4g), but it is
below our 3
73 km s-1. There may be a hint
of emission at a level about a factor of 2 lower than the emission toward P1
(see also Feature F3 in the 30 m spectrum in Fig. 4g), but it is
below our 3![]() detection limit. Therefore we cannot rule out
that amino acetonitrile shares the same property as, e.g., ethylcyanide,
cyanoacetylene, and methanol and is also present in the northern source P2 at
a level about twice lower than in P1.
detection limit. Therefore we cannot rule out
that amino acetonitrile shares the same property as, e.g., ethylcyanide,
cyanoacetylene, and methanol and is also present in the northern source P2 at
a level about twice lower than in P1.
The molecular source P2 is not detected at a 3![]() level of
26 mJy/
level of
26 mJy/
![]()
![]()
![]() -beam in the continuum map we obtained
with the PdBI at 82.0 GHz (see Fig. 5o). On the other hand, we
detect some emission with an intensity of
280 mJy/
-beam in the continuum map we obtained
with the PdBI at 82.0 GHz (see Fig. 5o). On the other hand, we
detect some emission with an intensity of
280 mJy/
![]()
![]()
![]() -beam
in the continuum map obtained with the ATCA at a mean frequency of 95.3 GHz
(see Fig. 7w). If this
emission is more extended than the PdBI beam, then the PdBI upper limit
translates into 79 mJy in the ATCA beam, which yields an unphysical frequency
exponent of
-beam
in the continuum map obtained with the ATCA at a mean frequency of 95.3 GHz
(see Fig. 7w). If this
emission is more extended than the PdBI beam, then the PdBI upper limit
translates into 79 mJy in the ATCA beam, which yields an unphysical frequency
exponent of ![]() 8 for the continuum emission toward P2 (see
Sect. 3.6). We suspect that the ATCA continuum toward P2 is
contaminated by a low-level line emission. In any case, since
the continuum emission toward P2 is much weaker than toward P1 at 3 mm, P2
must be less dense and/or less hot than the hot core P1. P2 coincides with
a weak blob of emission in the 1.3 cm VLA map of Gaume et al. (1995) (see their
Figs. 6 and 7). However, this blob is located within the shell-like, weak,
extended emission associated with K5 and it is difficult to know if it is
compact or not from the 1.3 cm map published by these authors. Therefore the
hot core P2 traced by the molecular emission may also be associated with an
ultracompact H II region, weaker than K2.
Alternatively, if it is not directely associated with a compact source of
free-free emission, it may have been formed by the interaction of the
shell-like structure K5 with the ambient medium, and could be in an earlier
stage of evolution than the hot core P1 (LMH) associated with the ultracompact
H II region K2.
8 for the continuum emission toward P2 (see
Sect. 3.6). We suspect that the ATCA continuum toward P2 is
contaminated by a low-level line emission. In any case, since
the continuum emission toward P2 is much weaker than toward P1 at 3 mm, P2
must be less dense and/or less hot than the hot core P1. P2 coincides with
a weak blob of emission in the 1.3 cm VLA map of Gaume et al. (1995) (see their
Figs. 6 and 7). However, this blob is located within the shell-like, weak,
extended emission associated with K5 and it is difficult to know if it is
compact or not from the 1.3 cm map published by these authors. Therefore the
hot core P2 traced by the molecular emission may also be associated with an
ultracompact H II region, weaker than K2.
Alternatively, if it is not directely associated with a compact source of
free-free emission, it may have been formed by the interaction of the
shell-like structure K5 with the ambient medium, and could be in an earlier
stage of evolution than the hot core P1 (LMH) associated with the ultracompact
H II region K2.
We do not detect amino acetonitrile in our 30 m survey toward Sgr B2(M). Using
the same parameters as for Sgr B2(N) (100 K and a FWHM source size of
![]() ), we find a
), we find a ![]()
![]() column density upper limit of
6
column density upper limit of
6 ![]() 1015 cm-2 in the LTE approximation. The column density of
amino acetonitrile is thus at least a factor
1015 cm-2 in the LTE approximation. The column density of
amino acetonitrile is thus at least a factor ![]() 5 weaker toward Sgr B2(M)
than toward Sgr B2(N). This is not surprising since, e.g., Nummelin et al. (2000)
found that hot-core-type molecules are more abundant in Sgr B2(N) by factors 3-8 as compared to Sgr B2(M).
5 weaker toward Sgr B2(M)
than toward Sgr B2(N). This is not surprising since, e.g., Nummelin et al. (2000)
found that hot-core-type molecules are more abundant in Sgr B2(N) by factors 3-8 as compared to Sgr B2(M).
Amino acids, building blocks of proteins and therefore key ingredients to explain the origin of life, have been found in meteorites on Earth. Their deuterium isotopic composition suggests that they, or at least their direct precursors, were formed in the cold interstellar medium (e.g. Pizzarello & Huang 2005). Looking for amino acids in the interstellar medium is therefore appealing. However, the simplest amino acid glycine has been intensively searched for in the past 30 years, but has unfortunately not been discovered yet (e.g. Snyder et al. 2005; Brown et al. 1979; Cunningham et al. 2007).
Amino acetonitrile was proposed early on as a possible direct precursor of glycine in the interstellar medium (e.g. Brown et al. 1977). The formation of glycine via a Strecker-cyanohydrin synthesis has long been favored (Peltzer et al. 1984; Ehrenfreund et al. 2001; Bernstein et al. 2004). This pathway involves a carbonyl compound (such as an aldehyde or a ketone), hydrogen cyanide, and ammonia, and produces the amino nitrile which, after hydrolysis, yields the amino acid. However, the Strecker synthesis cannot explain the higher deuterium fractionation of amino acids compared to hydroxy acids which was measured in meteorites (see Elsila et al. 2007, and references therein).
Amino acids were successfully produced in the laboratory by UV-photolysis of ice mixtures mimicking the mantles of insterstellar grains (Bernstein et al. 2002; Muñoz Caro et al. 2002). For an ice mixture composed of H2O, CH3OH, NH3, and HCN, Woon (2002) proposed theoretically a pathway of radical-radical reactions involving the radicals t-HOCO and CH2NH2 produced by UV irradiation. This hypothesis was tested and verified experimentally by Holtom et al. (2005) with an ice mixture of CH3NH2 and CO2 bombarded by energetic electrons mimicking the impact of cosmic rays in the interstellar medium. This pathway leading to glycine does not involve the formation of amino acetonitrile. On the other hand, Elsila et al. (2007) experimented the UV-photolysis of an ice mixture of H2O, CH3OH, HCN, and NH3, and found with isotopic labeling techniques multiple pathways leading to the formation of amino acids. The main pathway involves the formation of the amino nitrile and they proposed ``a modified radical-radical mechanism that takes into account the formation of nitriles as amino acid precursor molecules''. They also noticed that a Strecker-type synthesis may be at most a minor contributor to the formation of glycine.
The formation of glycine in the gas phase was also investigated. Blagojevic et al. (2003) synthesized ionized glycine via the reaction of the hydroxylamine ion NH2OH+ with acetic acid CH3COOH. They proposed the formation of the precursor hydroxylamine NH2OH in the grain mantles and the formation of acetic acid via ion-molecule reactions in the gas phase. Based on quantum chemical calculations, Maeda & Ohno (2006) found another pathway to form glycine in the gas phase involving barrierless reactions between closed-shell species. Their pathway starts from CO2, NH3, and CH2, and leads to glycine via the reaction of CO2 with the closed-shell molecule CH2NH3, a higher energy isomer of methylamine CH3NH2. However, they mentioned that CH2NH3 should be efficiently destroyed by H2O, so this pathway may be unlikely in the interstellar gas phase where water can be very abundant. Both gas phase formation routes do not involve amino acetonitrile as a direct precursor of glycine.
This brief overview of the experimental and theoretical work on the formation of amino acids in the interstellar medium shows that there is no consensus about the chemical precursors of amino acids. It is however important to note that the amino acids produced in the ice experiments mentioned above (except Holtom et al. 2005) are found experimentally after the hydrolysis of the ice residues. It is possible that only their precursors (e.g. amino nitriles) are synthesized by the ice photochemistry, and that the amino acids are formed only later, e.g. on the comet/asteroids surfaces, by hydrolysis (Elsila et al. 2007). Therefore amino acetonitrile may well be a direct precursor of glycine.
The formation of amino acetonitrile itself was also investigated theoretically
by Koch et al. (2008). They found that water can efficiently catalyze a reaction
between methylenimine CH2NH and hydrogen isocyanide HNC to form
amino acetonitrile in the grain mantles at a temperature of 50 K.
Methylenimine was detected in the gas phase toward Sgr B2(N) by, e.g., Nummelin et al. (2000).
They found evidence for both hot, compact and cold, extended components and
derived a column density of 3.3 ![]() 1017 cm-2 for the compact
component, with a source size of 2.7
1017 cm-2 for the compact
component, with a source size of 2.7
![]() and a temperature of
210+400-80 K, which is consistent with our own analysis
(Belloche et al., in prep.). This
column density is an order of magnitude larger than
the column density we derived for amino acetonitrile, which does not rule out
methylenimine as a precursor of amino acetonitrile.
and a temperature of
210+400-80 K, which is consistent with our own analysis
(Belloche et al., in prep.). This
column density is an order of magnitude larger than
the column density we derived for amino acetonitrile, which does not rule out
methylenimine as a precursor of amino acetonitrile.
The frequency coverage of our 30 m survey of Sgr B2(N) includes many transitions
of glycine as listed in the CDMS catalog (entries 75 511 and 75 512), but we do
not detect this molecule within the limits of our LTE analysis. Using the same parameters as for amino acetonitrile (100 K and a source size of 2
![]() ,
see Table 4), we derive a column density upper limit of 2.0
,
see Table 4), we derive a column density upper limit of 2.0 ![]() 1017 cm-2 for conformer I and
5.0
1017 cm-2 for conformer I and
5.0 ![]() 1015 cm-2 for conformer II. Alternatively, the upper
limit on emission from glycine more extended than the 30 m beam at 3 mm
(
1015 cm-2 for conformer II. Alternatively, the upper
limit on emission from glycine more extended than the 30 m beam at 3 mm
(![]()
![]() )
is 1.2
)
is 1.2 ![]() 1015 cm-2 for conformer I and
3.0
1015 cm-2 for conformer I and
3.0 ![]() 1013 cm-2 for conformer II. For a temperature of 75 K,
we find column density upper limits for conformer I of 1.5
1013 cm-2 for conformer II. For a temperature of 75 K,
we find column density upper limits for conformer I of 1.5 ![]() 1017 cm-2 for a source size of 2
1017 cm-2 for a source size of 2
![]() and 8.9
and 8.9 ![]() 1014 cm-2for emission more extended than the 30 m beam, and for conformer II
3.7
1014 cm-2for emission more extended than the 30 m beam, and for conformer II
3.7 ![]() 1015 cm-2 and 2.2
1015 cm-2 and 2.2 ![]() 1013 cm-2,
respectively.
1013 cm-2,
respectively.
Jones et al. (2007) did not detect glycine conformer I in Sgr B2(N) with the ATCA
and derived a 3![]() upper limit of 1.4
upper limit of 1.4 ![]() 1015 cm-2 for the
beam-averaged column density at 75 K, which translates into an upper
limit of 2.0
1015 cm-2 for the
beam-averaged column density at 75 K, which translates into an upper
limit of 2.0 ![]() 1016 cm-2 for a source size of 2
1016 cm-2 for a source size of 2
![]() after
correction for beam dilution (
after
correction for beam dilution (
![]()
![]()
![]() ). This upper
limit on any compact emission from glycine is at a level 8 times lower than
the one we derive with the 30 m telescope. As Jones et al. (2007) mentioned, the
tentative detection of Kuan et al. (2003) is inconsistent with this upper
limit in the case of compact emission.
On the other hand, the ATCA non-detection does not exclude extended emission
at the level found by Kuan et al. (2003) who reported a beam-averaged column
density of 4.2
). This upper
limit on any compact emission from glycine is at a level 8 times lower than
the one we derive with the 30 m telescope. As Jones et al. (2007) mentioned, the
tentative detection of Kuan et al. (2003) is inconsistent with this upper
limit in the case of compact emission.
On the other hand, the ATCA non-detection does not exclude extended emission
at the level found by Kuan et al. (2003) who reported a beam-averaged column
density of 4.2 ![]() 1014 cm-2 with the NRAO 12 m telescope and
a rotational temperature of 75 K. However Cunningham et al. (2007) did not detect
glycine conformer I in Sgr B2(N) with the 22 m Mopra telescope
and derived a 3
1014 cm-2 with the NRAO 12 m telescope and
a rotational temperature of 75 K. However Cunningham et al. (2007) did not detect
glycine conformer I in Sgr B2(N) with the 22 m Mopra telescope
and derived a 3![]() upper limit of 3.7
upper limit of 3.7 ![]() 1014 cm-2 for the
beam-averaged column density at 75 K. This upper limit is at a level
2.4 times lower than our beam-averaged upper limit. However, their upper
limit was derived for a position offset by 26
1014 cm-2 for the
beam-averaged column density at 75 K. This upper limit is at a level
2.4 times lower than our beam-averaged upper limit. However, their upper
limit was derived for a position offset by 26
![]() from the hot core
position, so it only rules out emission from Sgr B2(N) more extended than
from the hot core
position, so it only rules out emission from Sgr B2(N) more extended than
![]()
![]() in diameter. If glycine's emission were centered on the hot
core position with a diameter of
in diameter. If glycine's emission were centered on the hot
core position with a diameter of ![]()
![]() ,
Mopra would have missed
,
Mopra would have missed
![]()
![]() of the flux, and their upper limit would be 1.9
of the flux, and their upper limit would be 1.9 ![]() 1015 cm-2. In that case, our upper limit is more significant, but not low enough to rule out the
tentative detection reported by Kuan et al. (2003) if glycine is confined to a
source size of
1015 cm-2. In that case, our upper limit is more significant, but not low enough to rule out the
tentative detection reported by Kuan et al. (2003) if glycine is confined to a
source size of ![]()
![]() .
However, the arguments presented by
Snyder et al. (2005) do rule out this case. As a conclusion, the upper limits of
Cunningham et al. (2007), Jones et al. (2007), and Snyder et al. (2005) rule out emission
of glycine conformer I at the level reported by Kuan et al. (2003) in Sgr B2(N)
for any source size.
.
However, the arguments presented by
Snyder et al. (2005) do rule out this case. As a conclusion, the upper limits of
Cunningham et al. (2007), Jones et al. (2007), and Snyder et al. (2005) rule out emission
of glycine conformer I at the level reported by Kuan et al. (2003) in Sgr B2(N)
for any source size.
Cunningham et al. (2007) found an upper limit of 7.7 ![]() 1012 cm-2for the beam-averaged column density of glycine conformer II with Mopra toward
the central position of Sgr B2(N). This upper limit is nearly a factor of 3 lower than the upper limit we derived above with the 30 m telescope for
extended emission. With the ATCA, Jones et al. (2007) found an upper limit of
8.6
1012 cm-2for the beam-averaged column density of glycine conformer II with Mopra toward
the central position of Sgr B2(N). This upper limit is nearly a factor of 3 lower than the upper limit we derived above with the 30 m telescope for
extended emission. With the ATCA, Jones et al. (2007) found an upper limit of
8.6 ![]() 1013 cm-2 for the beam-averaged column density, which
translates into 1.2
1013 cm-2 for the beam-averaged column density, which
translates into 1.2 ![]() 1015 cm-2 for a source size of
2
1015 cm-2 for a source size of
2
![]() .
This upper limit is again a factor of 3 lower than the upper limit
we derived above with the 30 m telescope for compact emission.
.
This upper limit is again a factor of 3 lower than the upper limit
we derived above with the 30 m telescope for compact emission.
Bernstein et al. (2004) found experimentally that organic acids are less stable
than organic nitriles against UV photodestruction but they concluded that
in dense molecular clouds, the ratio nitrile to acid should
be affected by less than a factor of 2 over the lifetime of the cloud.
Therefore it could be instructive to compare the pairs
methylcyanide/acetic acid (CH3CN/CH3COOH) and
amino acetonitrile/glycine (NH2CH2CN/NH2CH2COOH). In our 30 m line
survey (Belloche et al., in prep.), we derive a column density ratio
on the order of 200 for CH3CN/CH3COOH toward Sgr B2(N). If the two pairs
are produced by similar chemical pathways yielding similar column density
ratios, then we expect the glycine column density to be two orders of
magnitude smaller than the amino acetonitrile column density, i.e. about
2 ![]() 1014 cm-2 for a compact source of 2
1014 cm-2 for a compact source of 2
![]() diameter, which
is nearly two orders of magnitude smaller than the upper limit derived above
for glycine conformer I from the ATCA measurements of Jones et al. (2007), and a
factor 5 smaller for conformer II. Therefore glycine emission may be well
below the confusion limit in Sgr B2(N).
diameter, which
is nearly two orders of magnitude smaller than the upper limit derived above
for glycine conformer I from the ATCA measurements of Jones et al. (2007), and a
factor 5 smaller for conformer II. Therefore glycine emission may be well
below the confusion limit in Sgr B2(N).
We used the complete 3 mm and partial 2 and 1.3 mm line surveys obtained with the IRAM 30 m telescope toward the hot cores Sgr B2(N) and (M) to search for emission from the complex molecule amino acetonitrile. We carried out follow-up observations with the IRAM Plateau de Bure and ATCA interferometers at selected frequencies. We also looked for extended emission from cold amino acetonitrile with the VLA. We report the detection of amino acetonitrile toward the hot core Sgr B2(N)-LMH, which is the first detection of this molecule in the interstellar medium. Our main results and conclusions are the following:
Acknowledgements
We thank the IRAM staff in Grenoble for observing at the PdBI and for their help with the data reduction, the IRAM staff in Granada for service observing in January 2005, and Sergio Martin for providing the reference (off) position for our 30 m observations. We thank John Pearson for his predictions of the first excited state of ethylcyanide, Claus Nielsen for providing transition frequencies of formamide isotopologues, Isabelle Kleiner, Vadim Ilyushin, and Frank Lovas for acetic acid frequencies, and Brian Drouin for his predictions of acetone. H.S.P.M. and the CDMS had been supported initially through the Deutsche Forschungsgemeinschaft (DFG) via the collaborative research grant SFB 494. Recent support is provided by the Bundesministerium für Bildung und Forschung administered through Deutsches Zentrum für Luft- und Raumfahrt (DLR; the German space agency). J.O. is a Jansky Fellow of the National Radio Astronomy Observatory. C.H. is a fellow of the Studienstiftung des deutschen Volkes and member of the International Max-Planck Research School for Radio and Infrared Astronomy.
| Na | Transitionb | Frequency | Unc.c | Comments | |||
| (MHz) | (kHz) | (K) | (D2) | (mK) | |||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
| 1 | 9 0, 9-8 0, 8 | 80 947.479 | 7 | 16 | 60 | 33 | Detected |
| 2 | 9 2, 8-8 2, 7 | 81 535.184 | 6 | 21 | 57 | 18 | Strong HC13CCN, v= 0 |
| 3 | 9 5, 5-8 5, 4 |
81 700.966 | 6 | 47 | 41 | 13 | Group detected, partial blend with U-line |
| 5 | 9 6, 3-8 6, 2 |
81 702.498 | 5 | 60 | 33 | 13 | Group detected, partial blend with U-line |
| 7 | 9 4, 6-8 4, 5 |
81 709.838 | 6 | 35 | 48 | 13 | Group detected |
| 9 | 9 7, 3-8 7, 2 | 81 709.848 | 6 | 76 | 24 | 13 | Group detected |
| 10 | 9 4, 5-8 4, 4 | 81 710.098 | 6 | 35 | 48 | 13 | Group detected |
| 11 | 9 3, 7-8 3, 6 | 81 733.892 | 6 | 27 | 53 | 13 | Detected, blend with CH3OCH3 and HCC13CN, v6 = 1 |
| 12 | 9 3, 6-8 3, 5 | 81 756.174 | 6 | 27 | 53 | 13 | Detected, blend with U-line |
| 13 | 9 2, 7-8 2, 6 | 82 224.644 | 7 | 21 | 57 | 19 | Detected, uncertain baseline |
| 14 | 9 1, 8-8 1, 7 | 83 480.894 | 8 | 17 | 59 | 17 | Blend with C2H3CN, v= 0 |
| 15 | 10 1,10-9 1, 9 | 88 240.541 | 8 | 20 | 66 | 19 | Strong HNCO, v= 0 and HN13CO, v= 0 |
| 16 | 10 0,10-9 0, 9 | 89 770.285 | 7 | 19 | 66 | 18 | Blend with U-line |
| 17 | 10 2, 9-9 2, 8 | 90 561.332 | 6 | 25 | 64 | 20 | Detected, blend with weak C2H5CN, v13 = 1/v21 = 1 |
| 18 | 10 6, 4-9 6, 3 |
90 783.538 | 6 | 64 | 43 | 14 | Group detected, partial blend with CH2(OH)CHO and U-line |
| 20 | 10 5, 6-9 5, 5 |
90 784.281 | 6 | 50 | 50 | 14 | Group detected, partial blend with CH2(OH)CHO and U-line |
| 22 | 10 7, 3-9 7, 2 |
90 790.259 | 6 | 80 | 34 | 14 | Group detected, blend with U-line |
| 24 | 10 4, 7-9 4, 6 | 90 798.685 | 6 | 39 | 56 | 14 | Group detected, blend with U-line |
| 25 | 10 4, 6-9 4, 5 | 90 799.249 | 6 | 39 | 56 | 14 | Group detected, blend with U-line |
| 26 | 10 8, 2-9 8, 1 |
90 801.896 | 7 | 98 | 24 | 14 | Blend with U-line and HC13CCN, v7 = 1 |
| 28 | 10 3, 8-9 3, 7 | 90 829.945 | 6 | 31 | 60 | 14 | Detected, blend with U-line also in M? |
| 29 | 10 3, 7-9 3, 6 | 90 868.038 | 6 | 31 | 60 | 14 | Detected, partial blend with U-line |
| 30 | 10 2, 8-9 2, 7 | 91 496.108 | 8 | 25 | 64 | 24 | Detected, partial blend with CH3CN, v4 = 1 and U-line |
| 31 | 10 1, 9-9 1, 8 | 92 700.172 | 8 | 21 | 66 | 28 | Blend with U-line and CH3OCH3 |
| 32 | 11 1,11-10 1,10 | 97 015.224 | 8 | 25 | 72 | 21 | Detected, partial blend with C2H5OH and CH3OCHO |
| 33 | 11 0,11-10 0,10 | 98 548.363 | 8 | 24 | 73 | 18 | Blend with C2H5CN, v= 0 |
| 34 | 11 2,10-10 2, 9 | 99 577.063 | 7 | 29 | 71 | 19 | Blend with CH3OCHO,
|
| 35 | 11 6, 6-10 6, 5 |
99 865.516 | 6 | 68 | 51 | 14 | Strong blend with C2H5OH, CCS |
| 37 | 11 5, 7-10 5, 6 |
99 869.306 | 6 | 55 | 58 | 14 | Strong CH3OCHO,
|
| 39 | 11 7, 4-10 7, 3 |
99 871.151 | 6 | 84 | 43 | 14 | Strong CH3OCHO,
|
| 41 | 11 8, 3-10 8, 2 |
99 882.826 | 7 | 103 | 34 | 14 | Strong blend with C2H5CN, v13 = 1/v21 = 1 |
| 43 | 11 4, 8-10 4, 7 | 99 890.599 | 6 | 44 | 63 | 14 | Strong blend with HC13CCN, v7 = 1 and HC13CCN, v6 = 1 |
| 44 | 11 4, 7-10 4, 6 | 99 891.725 | 6 | 44 | 63 | 14 | Strong blend with HC13CCN, v6 = 1 and NH2CN |
| 45 | 11 9, 2-10 9, 1 |
99 898.969 | 8 | 124 | 24 | 14 | Strong HCC13CN, v6 = 1 |
| 47 | 11 3, 9-10 3, 8 | 99 928.886 | 6 | 35 | 68 | 14 | Detected, partial blend with NH2CN and U-line |
| 48 | 11 3, 8-10 3, 7 | 99 990.567 | 7 | 35 | 68 | 14 | Detected |
| 49 | 11 2, 9-10 2, 8 | 100 800.876 | 8 | 29 | 71 | 20 | Detected, partial blend with CH3CH3CO, v= 0 and U-line |
| 50 | 11 1,10-10 1, 9 | 101 899.795 | 8 | 26 | 72 | 34 | Detected, uncertain baseline |
| 51 | 12 1,12-11 1,11 | 105 777.991 | 8 | 29 | 79 | 43 | Detected, blend with c-C2H4O and C2H5CN, v= 0 |
| 52 | 12 0,12-11 0,11 | 107 283.142 | 8 | 29 | 80 | 24 | Detected, blend with C2H5OH and U-line |
| 53 | 12 2,11-11 2,10 | 108 581.408 | 7 | 34 | 77 | 20 | Detected, weak blend with C2H5OH |
| 54 | 12 6, 7-11 6, 6 |
108 948.523 | 6 | 73 | 60 | 29 | Blend with C2H5CN, v= 0 and C2H5OH |
| 56 | 12 7, 5-11 7, 4 |
108 952.574 | 6 | 89 | 53 | 29 | Blend with C2H5OH |
| 58 | 12 5, 8-11 5, 7 |
108 956.206 | 6 | 60 | 66 | 29 | Group detected, blend with C2H5OH |
| 60 | 12 8, 4-11 8, 3 |
108 963.964 | 7 | 108 | 44 | 29 | Strong blend with HC13CCN, v7 = 1 |
| 62 | 12 9, 3-11 9, 2 |
108 980.660 | 8 | 128 | 35 | 29 | Strong blend with HCC13CN, v6 = 1 |
| 64 | 12 4, 9-11 4, 8 | 108 985.821 | 6 | 48 | 71 | 29 | Blend with HCC13CN, v7 = 1 |
| 65 | 12 4, 8-11 4, 7 | 108 987.928 | 6 | 48 | 71 | 29 | Blend with HCC13CN, v7 = 1 |
| 66 | 1210, 2-1110, 1 |
109 001.603 | 10 | 152 | 24 | 29 | Weak |
| 68 | 12 3,10-11 3, 9 | 109 030.225 | 6 | 40 | 75 | 29 | Detected, partial blend with HC3N, v4 = 1, C2H5OH, and U-line |
| 69 | 12 3, 9-11 3, 8 | 109 125.734 | 7 | 40 | 75 | 29 | Strong HC13CCN, v7 = 1 |
| 70 | 12 2,10-11 2, 9 | 110 136.314 | 8 | 34 | 77 | 24 | Blend with 13CH3OH, v= 0 |
| 71 | 12 1,11-11 1,10 | 111 076.901 | 8 | 31 | 79 | 25 | Detected, slightly shifted? |
| 72 | 13 1,13-12 1,12 | 114 528.654 | 8 | 34 | 86 | 37 | Detected, partial blend with U-line |
| 73 | 13 0,13-12 0,12 | 115 977.853 | 50 | 34 | 86 | 79 | Blend with CH313CH2CN, v= 0, CH3CH3CO, and C2H5CN, v= 0 |
| 74 | 15 7, 9-14 7, 8 |
136 200.478 | 6 | 106 | 78 | 28 | Strong HC13CCN, v7 = 1 |
| 76 | 15 6,10-14 6, 9 |
136 204.641 | 5 | 90 | 84 | 28 | Strong HC13CCN, v7 = 1 |
| 78 | 15 8, 7-14 8, 6 |
136 208.805 | 7 | 125 | 71 | 28 | Strong HC13CCN, v7 = 1 and HC13CCN, v6 = 1 |
| 80 | 15 9, 6-14 9, 5 |
136 225.653 | 8 | 145 | 64 | 28 | Strong HCC13CN, v6 = 1 and HCC13CN, v7 = 1 |
| 82 | 15 5,11-14 5,10 | 136 229.823 | 5 | 77 | 89 | 28 | Blend with HCC13CN, v7 = 1 |
| 83 | 15 5,10-14 5, 9 | 136 230.008 | 5 | 77 | 89 | 28 | Blend with HCC13CN, v7 = 1 |
| 84 | 1510, 5-1410, 4 |
136 248.969 | 10 | 169 | 55 | 28 | Group detected, blend with U-line |
| 86 | 1511, 4-1411, 3 |
136 277.600 | 13 | 195 | 46 | 28 | Strong HC3N, v4 = 1 and CH3OCHO |
| 88 | 15 4,12-14 4,11 | 136 293.271 | 6 | 65 | 93 | 28 | Strong CH313CH2CN |
| 89 | 15 4,11-14 4,10 | 136 303.599 | 6 | 65 | 93 | 28 | Detected, blend with a(CH2OH)2 and CH3C3N |
| 90 | 1512, 3-1412, 2 |
136 310.849 | 16 | 223 | 36 | 28 | Weak, blend with CH3C3N |
| 92 | 15 3,13-14 3,12 | 136 341.155 | 6 | 57 | 96 | 28 | Detected, partial blend with U-line also in M |
| 93 | 1513, 2-1413, 1 |
136 348.271 | 21 | 253 | 25 | 28 | Weak, blend with U-line |
| 95 | 16 7, 9-15 7, 8 |
145 284.487 | 30 | 113 | 86 | 25 | Strong HC13CCN, v7 = 1 |
| 97 | 16 8, 8-15 8, 7 |
145 290.958 | 30 | 131 | 80 | 25 | Blend with HC13CCN, v6 = 1 |
| 99 | 16 6,11-15 6,10 |
145 292.688 | 30 | 97 | 91 | 25 | Blend with HC13CCN, v6 = 1 |
| 101 | 16 9, 7-15 9, 6 |
145 307.254 | 30 | 152 | 73 | 25 | Strong C2H5CN, v13 = 1/v21 = 1, HCC13CN, v7 = 1, C2H3CN, v15 = 1 |
| 103 | 16 5,12-15 5,11 | 145 325.871 | 30 | 83 | 96 | 25 | Group detected, uncertain baseline, partial blend with |
| C2H5CN, v13 = 1/v21 = 1 | |||||||
| 104 | 16 5,11-15 5,10 | 145 326.209 | 30 | 83 | 96 | 25 | Group detected, uncertain baseline, partial blend with |
| C2H5CN, v13 = 1/v21 = 1 | |||||||
| 105 | 1610, 6-1510, 5 |
145 330.985 | 40 | 175 | 65 | 25 | Group detected, uncertain baseline |
| 107 | 1611, 5-1511, 4 |
145 360.684 | 30 | 201 | 56 | 25 | Strong HC3N, v4 = 1 |
| 109 | 1612, 4-1512, 3 |
145 395.485 | 60 | 229 | 46 | 25 | Blend with C3H7CN |
| 111 | 16 4,13-15 4,12 | 145 403.421 | 30 | 72 | 100 | 25 | Blend with U-line or wing of C2H5CN, v= 0 |
| 112 | 16 4,12-15 4,11 | 145 419.704 | 30 | 72 | 100 | 25 | Strong C2H5CN, v= 0 |
| 113 | 1613, 3-1513, 2 |
145 434.928 | 60 | 260 | 36 | 25 | Weak, blend with U-line |
| 115 | 16 3,14-15 3,13 | 145 443.850 | 30 | 63 | 103 | 25 | Detected, blend with C2H5CN, v= 0 and U-line |
| 116 | 1614, 2-1514, 1 |
145 478.462 | 60 | 293 | 25 | 25 | Weak, strong O13CS |
| 118 | 16 1,15-15 1,14 | 147 495.789 | 6 | 55 | 106 | 31 | Detected, partial blend with H3C13CN, v8 = 1 |
| 119 | 16 2,14-15 2,13 | 147 675.839 | 30 | 58 | 105 | 31 | Blend with H3C13CN, v8 = 1, U-line, and CH3OCHO |
| 120 | 17 7,10-16 7, 9 |
154 369.232 | 40 | 120 | 94 | 112 | Strong HC13CCN, v7 = 1 and HC13CCN, v6 = 1 |
| 122 | 17 8, 9-16 8, 8 |
154 373.384 | 40 | 138 | 88 | 112 | Strong HC13CCN, v6 = 1 |
| 124 | 17 6,12-16 6,11 |
154 382.222 | 40 | 104 | 99 | 112 | Strong HCC13CN, v6 = 1 and HCC13CN, v7 = 1 |
| 126 | 17 9, 8-16 9, 7 |
154 388.904 | 40 | 159 | 81 | 112 | Strong HCC13CN, v7 = 1 |
| 128 | 1710, 7-1610, 6 |
154 412.758 | 50 | 182 | 74 | 112 | Strong HNCO, v= 0 |
| 130 | 17 5,13-16 5,12 | 154 424.604 | 40 | 90 | 103 | 112 | Strong CH3OH, v= 0 |
| 131 | 17 5,12-16 5,11 | 154 425.216 | 40 | 90 | 103 | 112 | Strong CH3OH, v= 0 |
| 132 | 1711, 6-1611, 5 |
154 443.330 | 60 | 208 | 66 | 112 | Strong HC3N, v4 = 1 and CH313CH2CN |
| 134 | 1712, 5-1612, 4 |
154 479.566 | 15 | 236 | 57 | 112 | Strong C2H5CN, v= 0 |
| 136 | 17 4,14-16 4,13 | 154 517.470 | 5 | 79 | 107 | 112 | Blend with C2H5CN, v13 = 1/v21 = 1 |
| 137 | 1713, 4-1613, 3 |
154 520.861 | 19 | 267 | 47 | 112 | Blend with C2H5CN, v13 = 1/v21 = 1 |
| 139 | 17 4,13-16 4,12 | 154 542.406 | 5 | 79 | 107 | 112 | Group detected, blend with U-line |
| 140 | 17 3,15-16 3,14 | 154 544.046 | 5 | 70 | 109 | 112 | Group detected, blend with U-line |
| 141 | 1714, 3-1614, 2 |
154 566.773 | 25 | 300 | 36 | 112 | Weak, strong U-line |
| 143 | 1715, 2-1615, 1 |
154 617.004 | 33 | 335 | 25 | 112 | Weak, strong U-line and C2H5CN, v13 = 1/v21 = 1 |
| 145 | 18 7,12-17 7,11 |
163 454.794 | 5 | 127 | 101 | 38 | Group detected, partial blend with HC13CCN, v6 = 1 |
| and HCC13CN, v6 = 1 | |||||||
| 147 | 18 8,10-17 8, 9 |
163 456.136 | 6 | 146 | 96 | 38 | Group detected, partial blend with HC13CCN, v6 = 1 |
| and HCC13CN, v6 = 1 | |||||||
| 149 | 18 9, 9-17 9, 8 |
163 470.472 | 8 | 166 | 90 | 38 | Group detected, partial blend with HCC13CN,v7 = 1 |
| 151 | 18 6,13-17 6,12 |
163 473.305 | 5 | 111 | 106 | 38 | Group detected, partial blend with HCC13CN,v7 = 1 |
| 153 | 1810, 8-1710, 7 |
163 494.265 | 9 | 190 | 83 | 38 | Strong CH313CH2CN |
| 155 | 1811, 7-1711, 6 |
163 525.533 | 11 | 216 | 75 | 38 | Group detected, blend with HC3N, v4 = 1 |
| 157 | 18 5,14-17 5,13 | 163 526.183 | 4 | 97 | 110 | 38 | Group detected, blend with HC3N, v4 = 1 |
| 158 | 18 5,13-17 5,12 | 163 527.171 | 4 | 97 | 110 | 38 | Group detected, blend with HC3N, v4 = 1 |
| 159 | 1812, 6-1712, 5 |
163 563.084 | 14 | 244 | 66 | 38 | Blend with C2H3CN, v15 = 2 and SO2, v= 0 |
| 161 | 1813, 5-1713, 4 |
163 606.161 | 18 | 274 | 57 | 38 | Strong SO2, v= 0 |
| 163 | 18 4,15-17 4,14 | 163 635.326 | 5 | 86 | 114 | 38 | Detected, partial blend with C3H7CN |
| 164 | 18 3,16-17 3,15 | 163 640.468 | 5 | 78 | 116 | 38 | Detected, partial blend with C3H7CN |
| 165 | 1814, 4-1714, 3 |
163 654.261 | 24 | 307 | 47 | 38 | Weak, blend with H13CONH2, v= 0 |
| 167 | 18 4,14-17 4,13 | 163 672.524 | 5 | 86 | 114 | 38 | Strong C2H5CN, v13 = 1/v21 = 1 |
| 168 | 1815, 3-1715, 2 |
163 707.031 | 32 | 343 | 37 | 38 | Weak, blend with CH2(OH)CHO |
| 170 | 18 2,16-17 2,15 | 166 463.884 | 30 | 72 | 118 | 66 | Blend with 13CH2CHCN |
| 171 | 19 8,12-18 8,11 |
172 539.195 | 40 | 153 | 104 | 44 | Strong HCC13CN, v6 = 1 |
| 173 | 19 7,13-18 7,12 |
172 541.207 | 40 | 135 | 109 | 44 | Strong HCC13CN, v6 = 1 |
| 175 | 19 9,10-18 9, 9 |
172 552.010 | 40 | 174 | 98 | 44 | Strong HCC13CN, v7 = 1 |
| 177 | 19 6,14-18 6,13 |
172 566.092 | 50 | 119 | 114 | 44 | Group detected, partial blend with U-line and HCC13CN, v7 = 1 |
| 179 | 1910, 9-1810, 8 |
172 575.485 | 50 | 198 | 91 | 44 | Strong U-line |
| 181 | 1911, 8-1811, 7 |
172 607.260 | 60 | 223 | 84 | 44 | Strong HC3N, v4 = 1 |
| 183 | 19 5,15-18 5,14 | 172 630.750 | 30 | 105 | 117 | 44 | Strong U-line and t-HCOOH |
| 184 | 19 5,14-18 5,13 | 172 632.382 | 30 | 105 | 117 | 44 | Strong U-line and t-HCOOH |
| 185 | 1912, 7-1812, 6 |
172 645.994 | 13 | 252 | 76 | 44 | Blend with t-HCOOH, H13CN, and U-line |
| 187 | 1913, 6-1813, 5 |
172 690.745 | 17 | 282 | 67 | 44 | Strong H13CN and CH3OCHO |
| 189 | 19 3,17-18 3,16 | 172 731.699 | 30 | 86 | 123 | 44 | Blend with U-line and C2H3CN, v= 0 |
| 190 | 1914, 5-1814, 4 |
172 740.945 | 23 | 315 | 58 | 44 | Strong C2H3CN, v= 0 |
| 192 | 19 4,16-18 4,15 | 172 756.821 | 30 | 94 | 121 | 44 | Baseline problem? |
| 193 | 1915, 4-1815, 3 |
172 796.183 | 30 | 351 | 48 | 44 | Weak, strong HCC13CN, v7 = 1 |
| 195 | 19 4,15-18 4,14 | 172 811.041 | 30 | 94 | 121 | 44 | Strong C2H5CN, v= 0 |
| 196 | 1916, 3-1816, 2 |
172 856.161 | 40 | 388 | 37 | 44 | Weak, strong HC3N, v= 0 and HC3N, v5 = 1/v7 = 3 |
| 198 | 20 0,20-19 0,19 | 176 174.096 | 30 | 81 | 132 | 365 | Noisy, partial blend with HNCO, v5 = 1 and U-line |
| 199 | 23 0,23-22 0,22 | 201 875.876 | 10 | 108 | 152 | 138 | Strong 13CH3CH2CN, v= 0 |
| 200 | 22 2,20-21 2,19 | 203 812.341 | 10 | 107 | 145 | 364 | Strong C2H3CN, v= 0 |
| 201 | 23 2,22-22 2,21 | 206 652.454 | 9 | 115 | 151 | 106 | Blend with C2H5CN, v= 0 |
| 202 | 23 8,16-22 8,15 |
208 875.040 | 8 | 189 | 134 | 160 | Blend with HCC13CN, v7 = 1, CH3CH3CO,
|
| 204 | 23 9,14-22 9,13 |
208 877.860 | 9 | 210 | 129 | 160 | Blend with HCC13CN, v7 = 1, CH3CH3CO,
|
| 206 | 23 7,17-22 7,16 |
208 896.163 | 7 | 171 | 139 | 160 | Strong C2H3CN, v= 0 |
| 208 | 2310,13-2210,12 |
208 897.241 | 10 | 233 | 124 | 160 | Strong C2H3CN, v= 0 |
| 210 | 2311,12-2211,11 |
208 929.064 | 10 | 259 | 118 | 160 | Strong C2H3CN, v= 0 |
| 212 | 23 6,18-22 6,17 | 208 955.555 | 6 | 155 | 142 | 160 | Blend with C2H3CN, v= 0 and U-line |
| 213 | 23 6,17-22 6,16 | 208 955.797 | 6 | 155 | 142 | 160 | Blend with C2H3CN, v= 0 and U-line |
| 214 | 2312,11-2212,10 |
208 970.868 | 11 | 287 | 111 | 160 | Strong C2H3CN, v= 0 |
| 216 | 23 3,21-22 3,20 | 209 015.508 | 7 | 121 | 150 | 160 | Strong C2H5CN, v= 0 and C2H3CN, v= 0 |
| 217 | 2313,10-2213, 9 |
209 021.101 | 13 | 318 | 104 | 160 | Strong C2H3CN, v= 0 |
| 219 | 2314, 9-2214, 8 |
209 078.736 | 16 | 351 | 96 | 160 | Strong C2H3CN, v= 0 |
| 221 | 23 5,19-22 5,18 | 209 081.032 | 6 | 141 | 146 | 160 | Strong C2H3CN, v= 0 |
| 222 | 23 5,18-22 5,17 | 209 090.124 | 6 | 141 | 146 | 160 | Strong C2H3CN, v= 0 |
| 223 | 2315, 8-2215, 7 |
209 143.066 | 23 | 386 | 88 | 160 | Weak, strong HC13CCN, v7 = 1 |
| 225 | 2316, 7-2216, 6 |
209 213.584 | 33 | 424 | 79 | 58 | Weak, strong H2CS and C2H3CN, v15 = 1 |
| 227 | 23 4,20-22 4,19 | 209 272.189 | 6 | 130 | 148 | 58 | Detected, blend CH3CH3CO, v= 0 |
| 228 | 2317, 6-2217, 5 |
209 289.914 | 46 | 464 | 69 | 58 | Weak, blend with C2H5CN, v13 = 1/v21 = 1 and C2H3CN, v15 = 1 |
| 230 | 2318, 5-2218, 4 |
209 371.766 | 64 | 507 | 59 | 58 | Weak, blend with C2H5OH |
| 232 | 2319, 4-2219, 3 |
209 458.910 | 86 | 552 | 49 | 58 | Weak, strong C2H3CN, v15 = 2 and C2H5CN, v= 0 |
| 234 | 23 4,19-22 4,18 | 209 473.790 | 7 | 130 | 148 | 58 | Strong C2H3CN, v15 = 2 and CH3OCHO |
| 235 | 2320, 3-2220, 2 |
209 551.156 | 114 | 599 | 37 | 58 | Weak, strong C2H3CN, v11 = 1 |
| 237 | 23 1,22-22 1,21 | 209 629.913 | 9 | 113 | 152 | 45 | Detected, blend with HC13CCN, v7 = 2 and HCC13CN, v7 = 2 |
| 238 | 2321, 2-2221, 1 |
209 648.342 | 146 | 649 | 25 | 45 | Weak, blend with U-line and C2H3CN, v11 = 1 |
| 240 | 24 1,24-23 1,23 | 210 072.793 | 12 | 118 | 159 | 45 | Blend with C2H5CN, v13 = 1/v21 = 1 and 13CH3CH2CN, v= 0 |
| 241 | 24 0,24-23 0,23 | 210 448.044 | 12 | 118 | 159 | 64 | Strong CH3OCHO |
| 242 | 23 3,20-22 3,19 | 211 099.150 | 12 | 122 | 150 | 33 | Blend with U-lines |
| 243 | 23 2,21-22 2,20 | 213 074.653 | 70 | 117 | 152 | 48 | Strong SO2, v= 0 |
| 244 | 24 2,23-23 2,22 | 215 466.138 | 10 | 124 | 158 | 74 | Strong C2H5CN, v13 = 1/v21 = 1 |
| 245 | 24 3,21-23 3,20 | 220 537.064 | 14 | 132 | 157 | 98 | Strong CH3CN, v8 = 0 |
| 246 | 25 1,24-24 1,23 | 226 957.428 | 40 | 134 | 165 | 96 | Strong CN absorption |
| 247 | 25 9,16-24 9,15 |
227 040.487 | 50 | 230 | 145 | 96 | Group detected, partial blend with CN absorption and |
| CH3CH3CO,
|
|||||||
| 249 | 25 8,18-24 8,17 |
227 045.287 | 50 | 210 | 149 | 96 | Group detected, partial blend with CN absorption and |
| CH3CH3CO,
|
|||||||
| 251 | 2510,15-2410,14 |
227 055.944 | 50 | 254 | 139 | 96 | Group detected, partial blend with CN absorption |
| 253 | 25 7,19-24 7,18 |
227 079.847 | 50 | 191 | 153 | 96 | Group detected, blend with CH2CH13CN and CH3OH, v= 0 |
| 255 | 2511,14-2411,13 |
227 086.424 | 50 | 280 | 134 | 96 | Blend with CH2CH13CN and CH3OH, v= 0 |
| 257 | 25 3,23-24 3,22 | 227 088.938 | 40 | 142 | 164 | 96 | Blend with CH2CH13CN and CH3OH, v= 0 |
| 258 | 2512,13-2412,12 |
227 128.728 | 60 | 308 | 128 | 96 | Blend with C2H5CN, v= 0 and C2H3CN, v= 0 |
| 260 | 2517, 8-2417, 7 |
227 467.235 | 45 | 485 | 89 | 85 | Weak, blend with CH2(OH)CHO, CH2CH13CN and |
| t-C2H5OCHO | |||||||
| 262 | 25 4,22-24 4,21 | 227 539.318 | 40 | 151 | 162 | 85 | Strong HCONH2, v12 = 1 and C2H5CN, v= 0 |
| 263 | 2518, 7-2418, 6 |
227 555.295 | 63 | 528 | 80 | 85 | Weak, strong CH3OCHO |
| 265 | 26 0,26-25 0,25 | 227 601.595 | 16 | 138 | 172 | 85 | Strong HCONH2, v= 0 |
| 266 | 2519, 6-2419, 5 |
227 649.239 | 85 | 572 | 70 | 85 | Weak, blend with CH3OCH3 |
| 268 | 2520, 5-2420, 4 |
227 748.834 | 113 | 620 | 60 | 85 | Weak, blend with 13CH3CH2CN, v= 0 |
| 270 | 2521, 4-2421, 3 |
227 853.885 | 147 | 669 | 49 | 85 | Weak, strong HC13CCN, v7 = 2 and HCC13CN, v7 = 2 |
| 272 | 25 4,21-24 4,20 | 227 892.614 | 60 | 151 | 162 | 85 | Strong HCC13CN, v7 = 2, C2H5OH, and HC13CCN, v7 = 2 |
| 273 | 25 2,23-24 2,22 | 231 485.527 | 50 | 138 | 165 | 40 | Detected, blend with U-line? |
| 274 | 26 1,25-25 1,24 | 235 562.532 | 50 | 145 | 172 | 131 | Strong C2H3CN, v= 0 |
| 275 | 27 1,27-26 1,26 | 235 964.814 | 19 | 149 | 179 | 131 | Strong 13CH3OH, v= 0 |
| 276 | 26 3,24-25 3,23 | 236 103.949 | 40 | 153 | 170 | 37 | Blend with HCC13CN, v7 = 1 and C2H5CN, v13 = 1/v21 = 1 |
| 277 | 26 9,17-25 9,16 |
236 121.689 | 50 | 241 | 152 | 37 | Blend with 13CH3CH2CN |
| 279 | 26 8,19-25 8,18 |
236 131.044 | 50 | 220 | 156 | 37 | Blend with CH213CHCN |
| 281 | 2610,16-2510,15 |
236 134.730 | 50 | 265 | 147 | 37 | Blend with CH213CHCN |
| 283 | 2611,15-2511,14 |
236 164.129 | 60 | 291 | 142 | 37 | Strong C2H3CN, v11 = 1 and 13CH3CH2CN, v= 0 |
| 285 | 26 7,20-25 7,19 |
236 173.437 | 60 | 202 | 160 | 37 | Blend with C2H3CN, v11 = 1, CH213CHCN, and |
| 13CH3CH2CN, v= 0 | |||||||
| 287 | 27 0,27-26 0,26 | 236 182.602 | 18 | 149 | 179 | 37 | Blend with CH213CHCN, 13CH3CH2CN, v= 0, and HC3N, v4 = 1 |
| 288 | 2612,14-2512,13 |
236 206.427 | 19 | 319 | 136 | 37 | Strong SO2, v= 0 |
| 290 | 2613,13-2513,12 |
236 259.339 | 21 | 349 | 130 | 37 | Blend with C2H5CN, v13 = 1/v21 = 1 and t-C2H5OCHO |
| 292 | 26 6,21-25 6,20 | 236 269.491 | 60 | 186 | 163 | 37 | Group detected, partial blend with t-C2H5OCHO and U-line |
| 293 | 26 6,20-25 6,19 | 236 270.459 | 60 | 186 | 163 | 37 | Group detected, partial blend with t-C2H5OCHO and U-line |
| 294 | 2614,12-2514,11 |
236 321.411 | 23 | 382 | 123 | 37 | Weak, blend with C2H5OH and CH313CH2CN, v= 0 |
| 296 | 2615,11-2515,10 |
236 391.638 | 27 | 418 | 115 | 37 | Weak, blend with CH213CHCN |
| 298 | 26 5,22-25 5,21 | 236 454.502 | 40 | 173 | 166 | 37 | Blend with SO, v= 0 and 13CH3CH2CN, v= 0, baseline problem? |
| 299 | 2616,10-2516, 9 |
236 469.303 | 35 | 456 | 107 | 37 | Weak, blend with CH2CH13CN |
| 301 | 26 5,21-25 5,20 | 236 481.643 | 40 | 173 | 166 | 37 | Blend with CH213CHCN |
| 302 | 2617, 9-2517, 8 |
236 553.897 | 80 | 496 | 99 | 37 | Weak, blend with t-C2H5OCHO, 13CH3CH2CN, v= 0, and |
| CH3COOH,
|
|||||||
| 304 | 27 1,26-26 1,25 | 244 135.969 | 14 | 156 | 178 | 46 | Blend with C2H5CN, v13 = 1/v21 = 1 |
| 305 | 28 1,28-27 1,27 | 244 585.841 | 21 | 161 | 186 | 39 | Strong CH3OCHO and HCC13CN, v= 0 |
| 306 | 28 0,28-27 0,27 | 244 765.968 | 21 | 160 | 186 | 39 | Detected, blend with CH313CH2CN, v= 0 and U-line |
| 307 | 27 3,25-26 3,24 | 245 102.984 | 11 | 164 | 177 | 72 | Blend with 13CH3CH2CN, v= 0 |
| 308 | 27 9,18-26 9,17 |
245 202.855 | 16 | 253 | 159 | 72 | Blend with 13CH3CH2CN, v= 0 and U-line? |
| 310 | 2710,17-2610,16 |
245 213.055 | 19 | 276 | 155 | 72 | Strong CH3OH, v= 0 |
| 312 | 27 8,20-26 8,19 |
245 217.230 | 13 | 232 | 164 | 72 | Strong CH3OH, v= 0 |
| 314 | 2711,16-2611,15 |
245 241.163 | 21 | 302 | 150 | 72 | Blend with C2H513CN, v= 0 and C2H3CN, v15 = 1 |
| 316 | 27 7,21-26 7,20 |
245 268.168 | 11 | 213 | 167 | 72 | Blend with HC3N, v4 = 1 |
| 318 | 2712,15-2612,14 |
245 283.214 | 24 | 330 | 144 | 72 | Blend with C2H513CN, v= 0 |
| 320 | 2713,14-2613,13 |
245 336.715 | 26 | 361 | 138 | 72 | Strong SO2, v= 0 |
| 322 | 27 6,22-26 6,21 | 245 378.722 | 10 | 197 | 170 | 72 | Group detected, blend with 13CH3CH2CN, v= 0? |
| 323 | 27 6,21-26 6,20 | 245 380.146 | 10 | 197 | 170 | 72 | Group detected, blend with 13CH3CH2CN, v= 0? |
| 324 | 2714,13-2614,12 |
245 400.026 | 29 | 394 | 131 | 72 | Blend with U-line, CH3CH3CO, v= 0 and 13CH3CH2CN, v= 0? |
| 326 | 2715,12-2615,11 |
245 472.024 | 33 | 429 | 124 | 72 | Weak, strong C2H5CN, v13 = 1/v21 = 1 and C2H3CN, v11 = 1 |
| 328 | 2716,11-2616,10 |
245 551.911 | 40 | 467 | 116 | 53 | Weak, blend with SO2, v= 0 |
| 330 | 27 5,23-26 5,22 | 245 585.766 | 10 | 184 | 173 | 53 | Strong CH213CHCN and HC3N, v= 0 |
| 331 | 27 5,22-26 5,21 | 245 623.711 | 10 | 184 | 173 | 53 | Strong HC3N, v5 = 1/v7 = 3 and CH213CHCN |
| 332 | 2717,10-2617, 9 |
245 639.099 | 51 | 507 | 108 | 53 | Weak, blend with C2H3CN, v15 = 2 |
| 334 | 2718, 9-2618, 8 |
245 733.144 | 67 | 550 | 100 | 53 | Weak, strong HNCO, v5 = 1 |
| 336 | 27 4,24-26 4,23 | 245 803.548 | 10 | 173 | 175 | 53 | Blend with CH2CH13CN |
| 337 | 2719, 8-2619, 7 |
245 833.697 | 88 | 595 | 91 | 53 | Weak, strong U-line, partial blend with CH2CH13CN and |
| C2H3CN, v11 = 1/v15 = 1 | |||||||
| 339 | 2720, 7-2620, 6 |
245 940.476 | 116 | 642 | 81 | 53 | Weak, strong U-line and CH3OCHO,
|
| 341 | 2721, 6-2621, 5 |
246 053.247 | 150 | 692 | 71 | 53 | Weak, strong CH3OCHO |
| 343 | 28 3,26-27 3,25 | 254 085.051 | 12 | 176 | 184 | 32 | Blend with CH3CH3CO, v= 0 and C2H5CN, v= 0 |
| 344 | 28 9,19-27 9,18 |
254 283.930 | 19 | 264 | 167 | 32 | Strong SO2, v= 0 and 13CH3OH, v= 0 |
| 346 | 2810,18-2710,17 |
254 290.939 | 22 | 288 | 162 | 32 | Strong SO2, v= 0, 13CH3OH, v= 0, 13CH2CHCN, |
| 13CH3CH2CN, v= 0, and H13CONH2, v12 = 1 | |||||||
| 348 | 28 8,21-27 8,20 |
254 303.873 | 15 | 244 | 171 | 32 | Blend with 13CH3CH2CN, v= 0 and C2H5CN, v= 0 |
| 350 | 2811,17-2711,16 |
254 317.460 | 26 | 314 | 157 | 32 | Strong C2H5CN, v= 0 and 13CH3OH, v= 0 |
| 352 | 2812,16-2712,15 |
254 359.074 | 29 | 342 | 152 | 32 | Blend with H13CONH2, v= 0 |
| 354 | 28 7,22-27 7,21 |
254 364.160 | 12 | 225 | 174 | 32 | Blend with H13CONH2, v= 0 |
| 356 | 2813,15-2713,14 |
254 413.004 | 32 | 372 | 146 | 32 | Strong C2H5CN, v= 0, H13CONH2, v= 0, and CH3OH, v= 0 |
| 358 | 2822, 6-2722, 5 |
255 273.081 | 196 | 755 | 71 | 217 | Weak, strong 13CH3OH, v= 0 and CH2CH13CN |
| 360 | 2823, 5-2723, 4 |
255 401.564 | 245 | 809 | 60 | 217 | Weak, blend with CH3CH3CO,
|
| 362 | 2824, 4-2724, 3 |
255 535.733 | 304 | 866 | 49 | 217 | Weak, blend with SO2, v= 0 and U-line? |
| 364 | 28 4,24-27 4,23 | 255 674.369 | 18 | 185 | 182 | 217 | Strong HC3N, v7 = 1 |
| 365 | 2825, 3-2725, 2 |
255 675.432 | 372 | 925 | 38 | 217 | Strong HC3N, v7 = 1 |
| 367 | 28 2,26-27 2,25 | 258 775.885 | 19 | 172 | 185 | 1609 | Weak, blend with CH3OH, v= 0 |
| 368 | 29 9,20-28 9,19 |
263 364.923 | 22 | 277 | 174 | 74 | Group detected, baseline problem?, blend with U-line |
| 370 | 2910,19-2810,18 |
263 368.355 | 26 | 300 | 170 | 74 | Group detected, baseline problem?, blend with U-line |
| 372 | 29 8,22-28 8,21 |
263 390.982 | 17 | 256 | 178 | 74 | Blend with HNCO, v4 = 1 and CH3OCH3 |
| 374 | 2911,18-2811,17 |
263 393.008 | 31 | 326 | 165 | 74 | Blend with HNCO, v4 = 1 and CH3OCH3 |
| 376 | 2912,17-2812,16 |
263 433.971 | 35 | 354 | 160 | 74 | Strong HC3N, v4 = 1, HNCO, v5 = 1, and HNCO, v= 0 |
| 378 | 29 7,23-28 7,22 |
263 461.436 | 14 | 237 | 181 | 74 | Blend with HNCO, v= 0, CH3CH3CO, v= 0 and C2H5OH |
| 380 | 2913,16-2813,15 |
263 488.164 | 40 | 385 | 154 | 74 | Blend with C2H513CN, v= 0 |
| 382 | 2914,15-2814,14 |
263 553.566 | 44 | 418 | 148 | 74 | Strong SO2, v= 0, HCONH2, v12 = 1, and CH2(OH)CHO |
| 384 | 29 6,24-28 6,23 | 263 604.573 | 12 | 221 | 184 | 74 | Group detected, baseline problem?, partial blend with |
| CH3CH3CO,
|
|||||||
| 385 | 29 6,23-28 6,22 | 263 607.689 | 12 | 221 | 184 | 74 | Group detected, baseline problem?, partial blend with |
| CH3CH3CO,
|
|||||||
| 386 | 2915,14-2815,13 |
263 628.792 | 50 | 453 | 141 | 74 | Strong CH3OCH3 |
| 388 | 2916,13-2816,12 |
263 712.865 | 57 | 491 | 134 | 108 | Weak, strong HCC13CN, v7 = 1 and HNCO, v6 = 1 |
| 390 | 2917,12-2817,11 |
263 805.068 | 67 | 531 | 126 | 108 | Weak, strong HC3N, v5 = 1/v7 = 3 and C2H5CN, v= 0 |
| 392 | 29 5,25-28 5,24 | 263 857.842 | 12 | 208 | 187 | 108 | Blend with HCONH2, v= 0 and C2H513CN, v= 0 |
| 393 | 2918,11-2818,10 |
263 904.858 | 81 | 574 | 118 | 108 | Weak, blend with SO2, v= 0, C2H5CN, v13 = 1/v21 = 1, and U-line? |
| 395 | 29 5,24-28 5,23 | 263 928.994 | 13 | 208 | 187 | 108 | Blend with C2H5CN, v13 = 1/v21 = 1 and C2H5CN, v= 0 |
| 396 | 2919,10-2819, 9 |
264 011.816 | 101 | 619 | 110 | 108 | Weak, strong CH313CH2CN, v= 0 |
| 398 | 29 4,26-28 4,25 | 264 055.836 | 13 | 197 | 189 | 108 | Detected, partial blend with C2H5CN, v= 0 and |
| CH3CH3CO, v= 0 |
|
a Numbering of the observed transitions with b Transitions marked with a c Frequency uncertainty. d Lower energy level in temperature units ( e Calculated rms noise level in |
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{9203f101.ps}\hsp...
...ce*{0.5cm}
\includegraphics[angle=270,width=7.3cm,clip]{9203f108.ps}\end{figure}](/articles/aa/full/2008/16/aa9203-07/Timg178.gif) |
Figure 1:
Transitions of amino acetonitrile (AAN) detected with the IRAM 30 m telescope.
Each panel consists of two plots and is labeled in black in the upper right corner.
The lower plot shows in black the spectrum obtained toward Sgr B2(N) in main-beam temperature scale (K), while the upper plot shows the spectrum toward Sgr B2(M). The rest frequency axis is labeled in GHz. The systemic velocities assumed for Sgr B2(N) and (M) are 64 and 62 km s-1, respectively. The lines identified in the Sgr B2(N) spectrum are labeled in blue. The top red label indicates the AAN transition centered in each plot (numbered like in Col. 1 of Table 3), along with the energy of its lower level in K (
|