A&A 482, 229-236 (2008)
DOI: 10.1051/0004-6361:20078896
Near-infrared reddening of extra-galactic giant molecular clouds in a face-on geometry
J. Kainulainen1,2 - M. Juvela2 - J. Alves3
1 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
2 - Observatory, PO Box 14, 00014 University of Helsinki, Finland
3 - Calar Alto Observatory, Centro Astronómico Hispano, Alemán, C/q Jesús Durbán Remón 2-2, 04004 Almeria, Spain
Received 22 October 2007 / Accepted 8 February 2008
Abstract
Aims. We describe the near-infrared reddening signature of giant molecular clouds (GMCs) in external galaxies. In particular, we examine the EJ-H and EH-K color excesses and the effective extinction law observed in discrete GMC regions. We also study the effect of the relative scale height of the GMC distribution to the color excesses, and to the observed mass function of GMCs when the masses are derived using color excess as a linear estimator of mass.
Methods. We performed Monte Carlo radiative transfer simulations with 3D models of stellar radiation and clumpy dust distributions, resembling a face-on geometry. The scattered light is included in the models, and near-infrared color maps were calculated from the simulated data. We performed the simulations with different scale heights of GMCs and compared the color excesses and attenuation of light in different geometries. We extracted GMCs from the simulated color maps and compared the mass functions to the input mass functions.
Results. The effective near-infrared reddening law, i.e. the ratio
EJ-H/EH-K, has a value close to unity in GMC regions. The ratio depends significantly on the relative scale height of GMCs,  ,
and for
,
and for  values
values
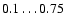 ,
we find the typical ratios of
,
we find the typical ratios of
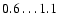 .
The effective extinction law turns out to be very flat in GMC regions. We find the ratios of apparent extinctions of
.
The effective extinction law turns out to be very flat in GMC regions. We find the ratios of apparent extinctions of
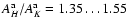 and
and
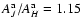 .
The effect of the scattered flux on the effective reddening law, as well as on the effective extinction law, is significant. Regarding the GMC mass function, we find no correlation between the input and observed slopes of the mass functions. Instead, the observed slope reflects the parameter
.
The effect of the scattered flux on the effective reddening law, as well as on the effective extinction law, is significant. Regarding the GMC mass function, we find no correlation between the input and observed slopes of the mass functions. Instead, the observed slope reflects the parameter  and the dynamical range of the mass function. As the observed slope depends on the geometric parameters, which are not known, it is not possible to constrain the slope of the mass function using this technique. We estimate that only a fraction of
and the dynamical range of the mass function. As the observed slope depends on the geometric parameters, which are not known, it is not possible to constrain the slope of the mass function using this technique. We estimate that only a fraction of
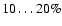 of the total mass of GMCs is recovered, if the observed color excess values are transformed to masses using the Galactic reddening law. In the case of individual clouds, the fraction can vary between
of the total mass of GMCs is recovered, if the observed color excess values are transformed to masses using the Galactic reddening law. In the case of individual clouds, the fraction can vary between 
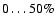 .
.
Key words: radiative transfer - scattering - ISM: clouds - galaxies: ISM - ISM: dust, extinction
The dust content of galaxies has an enormous effect on their observed properties in both local and high-redshift universes, as it is responsible for the thermal emission at infrared wavelengths, it attenuates the stellar radiation from near-infrared to optical, and it efficiently blocks radiation at ultraviolet wavelengths. The realistic description of the effects of dust is thus crucial for numerous applications ranging from describing galaxy evolution to estimating the amount of dark matter. Albeit important, estimating the impact of dust is, in most of the cases, all but a trivial task, because the effects caused by dust depend drastically, not only on the amount of it, but also on the exact spatial distribution and the physical composition of it.
Perhaps the most obvious manifestation of dust in galaxies outside the Milky Way are the lanes of dark clouds seen in the nearby spiral galaxies. In face-on spirals, the distribution of these dusty giant molecular clouds (GMCs) follows the stellar spiral arms qualitatively. In edge-on spirals, the GMCs are seen as an optically thick layer, concentrated heavily on the midplane of the galaxy. At the distance of nearby galaxies, the sizes of GMCs correspond to angular diameters of a few arcseconds. This basically rules out the possibility of studying them in detail using single-dish observations at the frequencies of common tracers of molecular gas, such as CO. Interferometric observations can achieve the required resolution, but mapping large areas is overwhelmingly time-consuming and sensitivity is rather poor.
Direct imaging of galaxies from optical to near-infared offers a high-resolution view of the distribution of GMCs inside them. At these wavelengths, an arcsecond-scale resolution is easily achieved with standard imaging observations. Qualitatively, the presence and distribution of GMCs can be established by color maps made from observations in two broadband filters, e.g. B-V or J-K. This approach has been used, often accompanied with image-processing techniques such as unsharp masking, to disentangle the GMCs from the color maps (e.g. Regan 1995, 2000; Howk & Savage 1997, 1999, 2000; Trewhella 1998; Elmegreen 1998; Thompson et al. 2004). The studies are typically performed in optical wavelengths due to the higher contrast towards the dust features, and until this past decade, due to the lack of large near-infrared array cameras.
Interpretating the observed color map data is severely hampered by the unknown relative geometry of dust and stars in the galaxy. The flux emitted by stars between a dust feature and the observer, as well as the star light that enters a cloud from all directions and scatters towards the observer, both reduce the reddening signature of dust clouds. Thus, describing reddening effects requires radiative transfer calculations. As the basic problem of the radiative transfer in a dusty medium is important for several fields, dusty systems have been studied in the past by numerous authors and from several points of view. In the context of embedded, galaxy-like dust distributions, a lot of emphasis has been placed on describing the obscuration by inhomogenous dust that has a low volume-filling factor and in which high density contrasts are present (e.g. Witt et al. 1992, 1996, 2000; Pierini et al. 2004). This set-up resembles the geometry of mixed GMCs and stellar distribution, with low column-density lines of sight dominating the light escaping from the system (i.e. the observed flux). It is particularly tailored to interpreting observations of the central regions of starburst galaxies or of the high-redshift, star-forming galaxies. It is a common result of these studies that color excesses can be highly nonlinear functions of optical depth, and they saturate at relatively low values. The small-scale structure, i.e. the clumpiness, significantly lowers the observed reddening compared to what is caused by a homogenous dust distribution, and the effect of scattering is not neglible at most of the wavelengths.
In this paper we examine the obscuration effects observed in the regions of particularly high column density, i.e. in the GMCs. The configuration chosen in our simulations differs from the studies quoted above, because the dust structures in our models experience strong illumination from an extended distribution of stellar light surrounding the dust. The dust clouds are small compared to the extent of the stellar light distribution, and therefore the flux observed in on-cloud pixels is likely to be dominated by the emission of the stars completely in front of all the dust. This paper is second in a series where we study the near-infrared reddening properties of GMCs, which are embedded inside a disk-like stellar radiation field. In the first paper we showed that the slope of the observed GMC mass function, derived from the NIR color excess data using foreground screen approximation, can significantly differ from the true mass function (Kainulainen et al. 2007, Paper I hereafter). In this paper we expand the results of Paper I and describe the near-infrared reddening and attenuation occurring in the GMC regions in detail. We examine the effective reddening and extinction laws in our models, with emphasis on how the relative scale height of the GMC distribution,  ,
affects their values. We also examine the shape of the observed mass function as a function of the parameter
,
affects their values. We also examine the shape of the observed mass function as a function of the parameter  to find out if the slope of the mass function can be constrained when some geometric parameters are known. In Sect. 2 the radiative transfer method and cloud models are presented. The results are presented and discussed in Sects. 3 and 4. In Sect. 5 we give our conclusions.
to find out if the slope of the mass function can be constrained when some geometric parameters are known. In Sect. 2 the radiative transfer method and cloud models are presented. The results are presented and discussed in Sects. 3 and 4. In Sect. 5 we give our conclusions.
The radiative transfer method, the basic geometry of the models, and the cloud extraction have all been described in Paper I. In short, the models consist of an exponential distribution of discrete clouds, which are embedded in an exponential distribution of stellar light. The left panel of Fig. 1 shows an example of input density distribution projected on a plane. The distributions of clouds and stars are characterized by their scale heights, 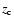 and
and 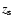 ,
respectively. The ratio of the scale heights,
,
respectively. The ratio of the scale heights,
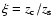 ,
is the main parameter describing the model geometry. The models are viewed from a face-on angle, i.e. the inclination angle of zero. The dust properties in the simulations are based on those of Draine (2003), and we used the tabulated values for Milky Way and
,
is the main parameter describing the model geometry. The models are viewed from a face-on angle, i.e. the inclination angle of zero. The dust properties in the simulations are based on those of Draine (2003), and we used the tabulated values for Milky Way and
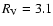 ,
which are available on the web
,
which are available on the web![[*]](/icons/foot_motif.gif) .
We generated 36 models, which result from choosing four different values for
.
We generated 36 models, which result from choosing four different values for  ,
three values for the slope of the input mass function
,
three values for the slope of the input mass function
 ,
and three values for the low-mass cut-off of the mass function,
,
and three values for the low-mass cut-off of the mass function,
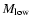 .
The models and corresponding input parameters are listed in Table 1. In addition to the three parameters above, Table 1 gives the volume-filling factor, and the surface-density filling factor in each model. The filling factor is defined as the number of cells with non-zero density divided by the total number of cells. The surface-density filling factor is defined in a similar way, but it is calculated after projecting the model on a two-dimensional plane.
.
The models and corresponding input parameters are listed in Table 1. In addition to the three parameters above, Table 1 gives the volume-filling factor, and the surface-density filling factor in each model. The filling factor is defined as the number of cells with non-zero density divided by the total number of cells. The surface-density filling factor is defined in a similar way, but it is calculated after projecting the model on a two-dimensional plane.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{8896fig0.eps} \end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg25.gif) |
Figure 1:
An example of one realization of a model used in the simulations (model #14). Left: column density. Right: corresponding simulated H-K color map. |
| Open with DEXTER |
The radiative transfer calculations are performed in JHK bands, and the resulting fluxes are used to construct simulated surface brightness maps. The surface brightness maps are further combined to color maps, namely H-K and J-H. The right panel of Fig. 1 shows an example of the H-K color map resulting from one realization of model #14. The color maps are further combined to 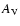 extinction maps using the NICER method (Lombardi & Alves 2001), applied to the surface brightess data. In the NICER method, the estimate of
extinction maps using the NICER method (Lombardi & Alves 2001), applied to the surface brightess data. In the NICER method, the estimate of 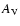 results from comparing the colors of on-cloud pixels to the colors of nearby off-cloud pixels.
results from comparing the colors of on-cloud pixels to the colors of nearby off-cloud pixels.
Table 1:
The input parameters and observed properties of the models.
In our models the colors of off-cloud regions are constant, so we selected one off-cloud region per model from which the off-cloud colors were calculated. In the selection we used the empty regions of J-H color maps. The individual clouds were identified from the extinction maps using the clumpfind routine ``clfind2d'' (Williams et al. 1994). The masses of identified clouds were calculated by summing up the extinction of all the on-cloud pixels, assuming the foreground screen geometry, and using the Milky Way ratio of
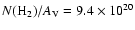 cm-2 mag-1 (Bohlin et al. 1978). Thus, the masses we refer to in the paper represent the gaseous masses of the clouds, and we express it in the units of solar masses
cm-2 mag-1 (Bohlin et al. 1978). Thus, the masses we refer to in the paper represent the gaseous masses of the clouds, and we express it in the units of solar masses 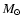 .
The masses are then used to construct the observed mass functions presented in Sect. 3. It is noteworthy that practically all the clouds that were embedded in the models (
.
The masses are then used to construct the observed mass functions presented in Sect. 3. It is noteworthy that practically all the clouds that were embedded in the models (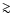 95%) were dense enough to be detected, if they were located completely in front of the stellar light distribution. This means that there is no incompleteness in the observed mass function due to the family of clouds that intrinsically cannot be detected.
95%) were dense enough to be detected, if they were located completely in front of the stellar light distribution. This means that there is no incompleteness in the observed mass function due to the family of clouds that intrinsically cannot be detected.
The same procedure of cloud extraction was used to construct the true cloud mass functions from the inital density distributions that were projected on a two-dimensional plane. The power-law model was fitted to the data to extract the slope of the true mass function
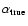 .
We note that this is not exactly the same as
.
We note that this is not exactly the same as
 ,
which was defined as the slope of the distribution from which the masses of input clouds were determined. In other words, the true mass functions presented in Sect. 3 are not composed of the initial input masses of the clouds, but rather of their masses after 2D projection and the clumpfind treatment. This was done to make sure that the cloud extraction procedure itself does not affect the slope of the observed mass function. The results of the power-law fits show that the slopes of the true mass functions are in good agreement with the initial ones, deviating 0.2 from the value of them at most (the slopes are given in Cols. 2 and 7 of Table 1).
,
which was defined as the slope of the distribution from which the masses of input clouds were determined. In other words, the true mass functions presented in Sect. 3 are not composed of the initial input masses of the clouds, but rather of their masses after 2D projection and the clumpfind treatment. This was done to make sure that the cloud extraction procedure itself does not affect the slope of the observed mass function. The results of the power-law fits show that the slopes of the true mass functions are in good agreement with the initial ones, deviating 0.2 from the value of them at most (the slopes are given in Cols. 2 and 7 of Table 1).
The results of the radiative transfer simulations, which are the main results of this paper, are summarized in Table 1. The first five columns of Table 1 give the input parameters for each model. The definitions of these parameters have been given in Sect. 2. The following columns show the output properties of the models. Both
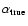 and
and
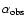 ,
given in Cols. 6 and 7, are the exponents of the power-law fits to the true and observed mass functions. The 8th column gives the fraction of the detected clouds, i.e. the number of clouds extracted from the NICER extinction map divided by the number of input clouds. Column 9 shows the total observed mass divided by the the total input mass. Columns 10 and 11 show the slope of the fit made to the frequency distribution of color excess pixel values (see Sect. 3.1.1).
,
given in Cols. 6 and 7, are the exponents of the power-law fits to the true and observed mass functions. The 8th column gives the fraction of the detected clouds, i.e. the number of clouds extracted from the NICER extinction map divided by the number of input clouds. Column 9 shows the total observed mass divided by the the total input mass. Columns 10 and 11 show the slope of the fit made to the frequency distribution of color excess pixel values (see Sect. 3.1.1).
In the following we describe the observable characteristics of a typical series of simulations and the dependency of the observables on the model parameters. We use the models 5-8 as examples in most of the figures, as they represent an average set of input parameters.
Figure 2 shows the normalized frequency distributions of EH-K and EJ-H values in models 5-8, with  values 0.1, 0.27, 0.5, and 0.75. Below
values 0.1, 0.27, 0.5, and 0.75. Below 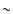 0.1 the distributions are dominated by the pixel noise. At higher color excesses the histograms follow an exponential distribution roughly, with the slope obviously depending on the value of
0.1 the distributions are dominated by the pixel noise. At higher color excesses the histograms follow an exponential distribution roughly, with the slope obviously depending on the value of  .
The exponential decay of the color excess values is interesting, as the initial distribution of cell densities, and thus the optical dephts of pixels, was a power law. We fit a model
.
The exponential decay of the color excess values is interesting, as the initial distribution of cell densities, and thus the optical dephts of pixels, was a power law. We fit a model
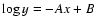 to the color excess values higher than 0.2. We note that the change in the number of clouds per unit volume, i.e. the change in surface density, only shifts the distribution in vertical direction, but does not affect the parameter A of the fit. The top panel of Fig. 2 also shows the fits on top of the pixel histograms. The A parameters resulting from the fit are given in Table 1 and summarized in the lower panel of Fig. 2. The A parameters depend strongly on
to the color excess values higher than 0.2. We note that the change in the number of clouds per unit volume, i.e. the change in surface density, only shifts the distribution in vertical direction, but does not affect the parameter A of the fit. The top panel of Fig. 2 also shows the fits on top of the pixel histograms. The A parameters resulting from the fit are given in Table 1 and summarized in the lower panel of Fig. 2. The A parameters depend strongly on  ,
being about 10 for models with
,
being about 10 for models with 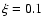 ,
and becoming shallower with increasing values of
,
and becoming shallower with increasing values of  .
In the models with
.
In the models with 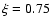 the average value is
the average value is 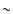 4.
4.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{8896fig1.eps}\par\vspace*{2mm}
\includegraphics[width=7.8cm,clip]{8896fig2.eps}
\end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg39.gif) |
Figure 2:
Top: normalized histograms of EH-K and EJ-H values in the models 5-8 (dotted, dashed, dash-dotted, and solid lines, respectively). The solid lines are fits of the equation
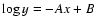 to the data with E>0.2. Bottom: summary of the fitted A parameters for all the models of the study. The blue asterisks correspond to EH-K values and the red diamonds to EJ-H values. The error bars represent the 1
to the data with E>0.2. Bottom: summary of the fitted A parameters for all the models of the study. The blue asterisks correspond to EH-K values and the red diamonds to EJ-H values. The error bars represent the 1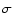 error of the fits. The horizontal lines give the error-weighted average of the data points. The average values are also printed in the frames.
error of the fits. The horizontal lines give the error-weighted average of the data points. The average values are also printed in the frames. |
| Open with DEXTER |
The ratio of the two color excesses,
EJ-H / EH-K, is especially interesting, as it describes the effective reddening law in the particular geometry. We fitted a linear model to all
(EH-K,EJ-H) pixel values of a model, and the resulting slope was 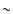 1 in practically all models. This is, as expected for embedded dust distribution, much flatter than the reddening laws for Galactic dust and foreground screen geometry (in our models:
EJ-H / EH-K=1.5, Draine 2003).
1 in practically all models. This is, as expected for embedded dust distribution, much flatter than the reddening laws for Galactic dust and foreground screen geometry (in our models:
EJ-H / EH-K=1.5, Draine 2003).
The ratio of color excesses can be determined individually in each of the clouds. We perform this by taking the average value of
EH-K / EJ-H ratios for ten pixels with highest EH-K to represent the ratio in that cloud. Figure 3 shows the histograms of the resulting ratios in models 5-8. Even though the distributions are wide, reflecting the large scatter in the
EJ-H / EH-K values of pixels due to photometric errors, they are clearly distinct. The peak of the distribution moves towards higher values for higher values of  ,
which is expected as the fraction of foreground light gets smaller on average. This behavior remains hidden in the average relation, where the distribution is dominated by the pixels with relatively low optical depths. However, it becomes detectable when determined separately for individual clouds.
,
which is expected as the fraction of foreground light gets smaller on average. This behavior remains hidden in the average relation, where the distribution is dominated by the pixels with relatively low optical depths. However, it becomes detectable when determined separately for individual clouds.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8896fig3.eps} \end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg40.gif) |
Figure 3:
The histograms of the
EJ-H / EH-K ratios of all detected GMCs in the models 5-8. The ratio is measured at the point of maximum EH-K in each cloud. The approximate peak values corresponding the  values of 0.1, 0.27, 0.5, and 0.75 are 0.5, 0.6, 0.9, and 1.1. The number of the model and the corresponding
values of 0.1, 0.27, 0.5, and 0.75 are 0.5, 0.6, 0.9, and 1.1. The number of the model and the corresponding  value are marked in the frames. The dotted lines show the ratio if the scattered flux is neglected (see Sect. 3.3).
value are marked in the frames. The dotted lines show the ratio if the scattered flux is neglected (see Sect. 3.3). |
| Open with DEXTER |
The masses of detected clouds were used to construct the observed mass functions, and a power-law model, described by the parameter
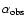 ,
is fitted to data. For the binning we used the equation
,
is fitted to data. For the binning we used the equation
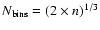 where n is the number of clouds in the histogram. The lowest mass bin that is taken into the fit is selected individually by eye for each model. The slopes of both true and observed mass functions are listed in Cols. 6 and 7 of Table 1.
The appearance of the mass functions is similar to those already described in Paper I (Fig. 2). The dynamical range of the observed mass function is approximately two decades, starting from
where n is the number of clouds in the histogram. The lowest mass bin that is taken into the fit is selected individually by eye for each model. The slopes of both true and observed mass functions are listed in Cols. 6 and 7 of Table 1.
The appearance of the mass functions is similar to those already described in Paper I (Fig. 2). The dynamical range of the observed mass function is approximately two decades, starting from 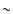
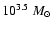 and terminating at
and terminating at
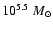 .
In some models, the power law does not represent the observed mass function well over the whole observed dynamical scale. Instead, the mass function has a breaking point at
.
In some models, the power law does not represent the observed mass function well over the whole observed dynamical scale. Instead, the mass function has a breaking point at
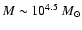 ,
below which the mass function flattens, or is completely flat. This happens typically in the models where both
,
below which the mass function flattens, or is completely flat. This happens typically in the models where both  and the low-mass cut-off of the mass function,
and the low-mass cut-off of the mass function,
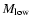 ,
are high.
,
are high.
Figure 4 shows the relation between the true and observed slopes in all the models. The observed slopes vary between 1.8 and 2.9, and there is no correlation between the true and observed slopes. The models with flat input slopes are observed to have similar range of slopes as the models with steep input slopes. In some particular parameter settings, such as models marked with purple diamonds (models 27-28, 31-32, and 35-36), the observed slopes follow the true slopes loosely if  is high. In these models the
is high. In these models the
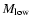 parameter is
parameter is
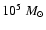 .
The observed slopes correlate slightly with the parameter
.
The observed slopes correlate slightly with the parameter  ,
as on average, the models with low
,
as on average, the models with low  values tend to show steeper slopes (
values tend to show steeper slopes (
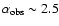 )
than the models with high
)
than the models with high  values (
values (
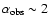 ). As the correlation between
). As the correlation between
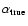 and
and
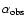 is very poor, it is not possible to estimate
is very poor, it is not possible to estimate
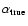 by using simply a measurement of
by using simply a measurement of
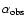 .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8896fig4.eps} \end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg48.gif) |
Figure 4:
The slope of the observed mass function as a function of the slope of the true mass function in all models of the study. The different panels correspond to different values of  parameter. The red plus signs correspond to
parameter. The red plus signs correspond to
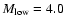 (models 1-12), blue asterisks to
(models 1-12), blue asterisks to
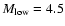 (models 13-24), and purple diamonds to
(models 13-24), and purple diamonds to
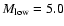 (models 25-36).
(models 25-36). |
| Open with DEXTER |
The sizes of the detected clouds, i.e. the number of on-cloud pixels, were compared to the sizes of the corresponding input clouds. The observed sizes are smaller than input sizes with an average factor of 0.85. The ratio remains remarkably constant, as 90% of all clouds in all the models have ratios between
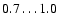 .
Thus, if the cloud is detected using near-infrared excesses, it is likely to be detected close to its full extent, and only the most diffuse outer edges remain undetected.
.
Thus, if the cloud is detected using near-infrared excesses, it is likely to be detected close to its full extent, and only the most diffuse outer edges remain undetected.
As the absolute value of background flux in our models is known (the background flux is constant and the positions with zero optical depth are known), we can examine the apparent extinction in the models. The apparent extinction is defined as
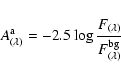 |
(1) |
where
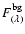 is the unattenuated background flux. The values of apparent extinction are typically a few tenths of a magnitude in our models. We estimate the wavelength dependency of the apparent extinction by calculating the ratios
is the unattenuated background flux. The values of apparent extinction are typically a few tenths of a magnitude in our models. We estimate the wavelength dependency of the apparent extinction by calculating the ratios
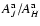 and
and
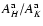 at the positions of each extracted cloud. These ratios describe how the extinction depends on wavelength in the particular geometry, and thus the curve defined by them is often called an effective extinction law. We calculate the ratios in each cloud by taking the average of ten pixels where the EH-K is highest. The resulting histograms are shown in Fig. 5. The distributions of
at the positions of each extracted cloud. These ratios describe how the extinction depends on wavelength in the particular geometry, and thus the curve defined by them is often called an effective extinction law. We calculate the ratios in each cloud by taking the average of ten pixels where the EH-K is highest. The resulting histograms are shown in Fig. 5. The distributions of
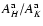 values have maxima between
values have maxima between 
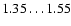 ,
depending slightly on the value of
,
depending slightly on the value of  .
The distributions of
.
The distributions of
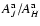 have their maxima only slightly above unity, typically at
have their maxima only slightly above unity, typically at  1.1. The ratios are clearly lower than in the case of foreground screen extinction (in our models:
1.1. The ratios are clearly lower than in the case of foreground screen extinction (in our models:
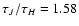 and
and
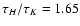 ,
Draine 2003).
,
Draine 2003).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{8896fig5.eps}\par\vspace*{2mm}
\includegraphics[width=8.2cm,clip]{8896fig6.eps}\par\end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg55.gif) |
Figure 5:
Top: the histogram of the ratio of apparent extinction,
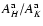 ,
evaluated in each on-cloud region. The apparent extinction is as defined by Eq. (1). The data are for models 5-8, with the model number and the corresponding ,
evaluated in each on-cloud region. The apparent extinction is as defined by Eq. (1). The data are for models 5-8, with the model number and the corresponding  values marked in the frames. The dotted lines show the corresponding histograms if the scattered light is neglected. (See Sect. 3.3) Bottom: the same for
values marked in the frames. The dotted lines show the corresponding histograms if the scattered light is neglected. (See Sect. 3.3) Bottom: the same for
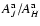 . . |
| Open with DEXTER |
As already found in Paper I, the masses of the clouds that are detected can be drastically lower than their true masses. As an example, Fig. 6 shows the comparison of the true and observed masses of clouds in model 8. The scatter in the relation is very high. Essentially, a cloud can be observed with any mass lower than its true mass with a significant probability, down to the detection limit. In addition to the mass that is missed due to underesting the masses of detected clouds, a fraction of the clouds always remain completely undetected. This is mainly due to the population that is located on the farther side of the galaxy. As the flux of the on-cloud pixels is completely dominated by the foreground flux, these clouds do not produce significant reddening features to the color maps. We calculated the total amount of undetected mass by summing up the observed extinction maps and comparing them to the total sum of input column density maps. The resulting ratios, reported in Col. 10 of Table 1, are obviously very dependent on the dynamical range of input masses. Thus, the given ratios should only be taken as order-of-magnitude estimates for undetected mass.
![\begin{figure}
\par\hspace*{3.5mm} \includegraphics[width=7.7cm,clip]{8896fig7.eps}\par\vspace*{2mm}
\includegraphics[width=7.7cm,clip]{8896fig8.eps} \end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg56.gif) |
Figure 6:
Top: the observed masses of clouds as a function of the true mass of clouds in model 8. The observed masses are calculated from the EH-K values by assuming the foreground screen geometry and Galactic gas-to-dust ratio. The dotted line shows the one-to-one ratio. Bottom: the fraction of detected clouds, i.e. the completeness function, in models 5-8 (dotted, dashed, dash-dotted, and solid lines). The masses are given in solar masses. |
| Open with DEXTER |
Following the treatment in Paper I, we also calculated the fraction of detected clouds as a function of true mass by comparing the positions of clouds detected from input column density maps to the positions of clouds detected from the EJ-H color excess maps. The behavior of the resulting completeness function was described in Paper I. The larger set of models in this paper allows the examination of the  dependence of the completeness function. Figure 6 shows an example of the
dependence of the completeness function. Figure 6 shows an example of the  dependence in models 5-8. The decrease in the completeness below
dependence in models 5-8. The decrease in the completeness below
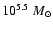 is greater for lower values of
is greater for lower values of  .
In the models with
.
In the models with 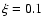 basically no clouds with
basically no clouds with
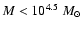 are detected. In the models with
are detected. In the models with 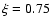 clouds with
clouds with
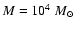 still have a probability of a few percent of being detected. Above
still have a probability of a few percent of being detected. Above
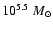 the detection probability is slightly higher for the models with lower
the detection probability is slightly higher for the models with lower  .
This is simply because the amount of clouds for which the fraction of foreground flux is high is larger in models with high
.
This is simply because the amount of clouds for which the fraction of foreground flux is high is larger in models with high  .
The color of foreground light dominates the colors observed on these clouds over the small fraction of reddened background light.
.
The color of foreground light dominates the colors observed on these clouds over the small fraction of reddened background light.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8896fig9.eps} \end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg59.gif) |
Figure 7:
The density contours of the fraction of scattered light in model 5 at Top: J, Middle: H, and Bottom: K bands. The fraction refers to the scattered flux in the pixel divided by the total flux in that pixel (i.e. not by the total unattenuated flux). The solid lines show the median value of the relation for different 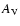 values in model 5 (
values in model 5 (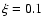 ). For comparison, the dashed line shows the median ratio for model 8 ( ). For comparison, the dashed line shows the median ratio for model 8 (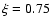 ). ). |
| Open with DEXTER |
3.3 The significance of the scattered light
During the simulations the scattered and emitted fluxes were registered separately, so we can explore the role of the scattering in the effective reddening and attenuation laws by using only the emitted fluxes. Figures 3 and 5 show the corresponding reddening and attenuation laws, and as the scattered light is not present the dispersion in histograms is much smaller. The peaks are clearly shifted towards higher ratios in both reddening and attenuation data. Thus, the scattered flux has a significant effect on both values.
The level of the scattered flux with respect to the total observed flux is shown in Fig. 7. To better visualize the data, the figure shows the probability density of data points smoothed with a Gaussian kernel. The data is shown for the model 5, and the overplotted lines show the median value of the relation in models 5 and 8.
The increase in the fraction of the scattered flux is close to linear up to
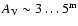 .
At higher optical depths the fraction saturates quickly, reaching its maximum at
.
At higher optical depths the fraction saturates quickly, reaching its maximum at
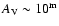 in J and H bands. In K band the fraction continues to increase slowly until
in J and H bands. In K band the fraction continues to increase slowly until
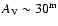 .
The value of
.
The value of  has a relatively weak, yet detectable, effect on the median value of the relation. The median value decreases slightly with increasing
has a relatively weak, yet detectable, effect on the median value of the relation. The median value decreases slightly with increasing  ,
which results from the average radiation field experienced by a cloud being stronger when the
,
which results from the average radiation field experienced by a cloud being stronger when the  value is low.
value is low.
In some studies an estimation of the optical depths along the line of sight has been attempted by using measurements of apparent extinction at two or more wavelengths (e.g. Howk & Savage 1997, 2000). In this approach the scattered flux is neglected, and the resulting equations for radiative transfer can be solved. We applied this method to our models, but the equations failed to converge for most of the clouds. This failure was clearly due to the scattered flux, as the same procedure using only emitted fluxes indeed yielded improved estimates of optical depths. We also made an effort to use the data presented in Fig. 7 to numerically solve the actual optical depth. Typically, this operation multiplied cloud masses with a factor varying from 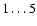 .
Even though on average the cloud masses were thus improved, the effect was highly variable, and the form of the mass function was completely destroyed in every model. Considering that the uncertainty caused by unknown background flux is neglible in our models, we conclude that this correction is not feasible for gaining an improved estimate of the mass function.
.
Even though on average the cloud masses were thus improved, the effect was highly variable, and the form of the mass function was completely destroyed in every model. Considering that the uncertainty caused by unknown background flux is neglible in our models, we conclude that this correction is not feasible for gaining an improved estimate of the mass function.
4 Discussion
As has been well-established in the previous studies of this subject, the large scatter and strong saturation of colors as a function of the total optical depth are dominating the simulations. These effects, originating from the varying relative geometry and inhomogeneity of dust distribution, affect both the level of extinction and its wavelength dependency (i.e. the effective extinction law). The knowledge of the realistic effective extinction law is crucial for numerous applications, where the observed signal from an object or region of interest needs to be corrected for the effects of dust. For example, for this purpose Calzetti et al. (1997, 2000, 2001) have derived an empirical attenuation law for central regions of starburst galaxies. Likewise, theoretical attenuation curves have been calculated for several geometries of inhomogenous dust and stars (e.g. Pierini et al. 2004, and references therein). In this paper we particularly examine the on-cloud pixels rather than the integrated light over a region covered with a mixture of GMCs and low column-density lines of sight. We emphasize how the reddening properties of discrete cloud regions can vary, even in the fixed face-on geometry, when embedded GMCs are considered.
As we are considering only the on-cloud pixels, the effects of the scattered flux undoubtedly increase. In the most massive clouds, which are the ones most likely to be detected in extinction maps, the fraction of the scattered flux to the total flux of a pixel can go up to several tens of percent (Fig. 7). The scattered flux has a significant effect on the scale of color excesses, dampening the overall color excess level with a factor of
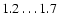 .
.
Our simulations predict the effective reddening law, constructed from the values of the on-cloud pixels of detected clouds, to be close to unity. This result is only valid for the selected geometry, i.e. for a face-on galaxy. Even though the same average relation was found in all the models, we showed that, when each cloud is examined separately, a  dependence can be found (Fig. 2). This demonstrates how a relatively straightforwardly measured observable reflects the geometry of the observed region despite the complicating effect of the scattered flux. In practice determining
EJ-H/EH-K ratio for a single cloud is rather uncertain due to the photometric accuracy and generally low values of EJ-H and EH-K, and thus a sample of hundreds of clouds is likely to be needed to get an estimate of the
dependence can be found (Fig. 2). This demonstrates how a relatively straightforwardly measured observable reflects the geometry of the observed region despite the complicating effect of the scattered flux. In practice determining
EJ-H/EH-K ratio for a single cloud is rather uncertain due to the photometric accuracy and generally low values of EJ-H and EH-K, and thus a sample of hundreds of clouds is likely to be needed to get an estimate of the  value of a face-on galaxy. It is interesting that even in the models with lowest average foreground emission, i.e. models with
value of a face-on galaxy. It is interesting that even in the models with lowest average foreground emission, i.e. models with 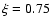 ,
the effective reddening law remained very flat. Thus, if the overall conditions do not differ significantly from the simulations, high
EJ-H/EH-K ratios should not be observed unless the foreground emission in the observed region really is neglible. This means that, if a cloud region is observed to have a high
EJ-H/EH-K ratio, it can be argued that the foreground screen approximation is valid for it.
,
the effective reddening law remained very flat. Thus, if the overall conditions do not differ significantly from the simulations, high
EJ-H/EH-K ratios should not be observed unless the foreground emission in the observed region really is neglible. This means that, if a cloud region is observed to have a high
EJ-H/EH-K ratio, it can be argued that the foreground screen approximation is valid for it.
In the case of an embedded cloud, the effective reddening law does not relate the observed color excesses directly to apparent extinction (as would in the case of a foreground cloud). Thus, the effective extinction law cannot be inferred from those data alone. We evaluated the effective extinction law by determining the apparent extinction of on-cloud pixels, which is trivial in our models. We do note that this is not typically the case with spiral galaxies, as the knowledge of absolute background flux to a good precision would require a detailed model for the distribution of stellar light. The typical ratios of
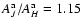 and
and
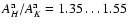 were found (Fig. 2). These ratios are similar to the values derived in a pair of occulting galaxies by Berlind et al. (1997). We find this similarity convincing, as the regions sampled in Berlind et al. are relatively small, not much larger than individual GMCs. Thus, the study might represent the conditions described by our simulations relatively well.
were found (Fig. 2). These ratios are similar to the values derived in a pair of occulting galaxies by Berlind et al. (1997). We find this similarity convincing, as the regions sampled in Berlind et al. are relatively small, not much larger than individual GMCs. Thus, the study might represent the conditions described by our simulations relatively well.
In addition to described reddening effects, we examined the mass functions derived from the color excess data, and thus expanded the work in Paper I by increasing the number of models. The main emphasis regarding the mass functions is to examine the observed slope at different values of  .
In the context of cloud mass functions, the direct consequence of the saturation of color excesses is that the observed mass function is confined to a narrow dynamical range compared to the original mass function. A comparison of models that are otherwise similar, but have different
.
In the context of cloud mass functions, the direct consequence of the saturation of color excesses is that the observed mass function is confined to a narrow dynamical range compared to the original mass function. A comparison of models that are otherwise similar, but have different  values, shows that the confinement depends slightly on
values, shows that the confinement depends slightly on  .
The difference in the high-mass end between the models with
.
The difference in the high-mass end between the models with 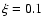 and
and 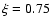 is typically
is typically
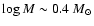 ,
while the low-mass end is at
,
while the low-mass end is at
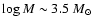 in all the models.
in all the models.
In most of our models, the observed slope of the mass function differs at least 0.3 from the slope of the true mass function. As shown in Fig. 4, there is practically no correlation between the true and observed slopes. The observed slope obviously depends on the parameter  ,
because the slopes are generally
,
because the slopes are generally 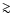 2.5 in the models with
2.5 in the models with 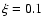 ,
and in the models with
,
and in the models with 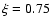 they are closer to 2. However,
they are closer to 2. However,  clearly is not the only parameter affecting the slope. While the models with
clearly is not the only parameter affecting the slope. While the models with
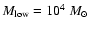 show practically constant observed slopes for all true slopes (red plus signs in Fig. 4), the slopes in the models with
show practically constant observed slopes for all true slopes (red plus signs in Fig. 4), the slopes in the models with
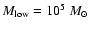 do increase with the input slope in those cases where
do increase with the input slope in those cases where  is large (purple diamonds). The reason for this is most likely that the dispersion between the true and observed masses of low-mass clouds is higher than in high-mass clouds. Furthermore, when the
is large (purple diamonds). The reason for this is most likely that the dispersion between the true and observed masses of low-mass clouds is higher than in high-mass clouds. Furthermore, when the  value is high, the reddening signatures are stronger and the cloud definition better. When both
value is high, the reddening signatures are stronger and the cloud definition better. When both  and
and
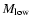 are high, the relation between the true and observed masses is significantly better than for low
are high, the relation between the true and observed masses is significantly better than for low  and
and
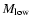 .
Thus, if there is no reason to assume a truncation on the low-mass side of the mass function, the presence of the lowest mass clouds makes the slope of the observed mass function quite insensitive to the true slope. However, if the truncation occurs at masses significantly lower than
.
Thus, if there is no reason to assume a truncation on the low-mass side of the mass function, the presence of the lowest mass clouds makes the slope of the observed mass function quite insensitive to the true slope. However, if the truncation occurs at masses significantly lower than
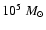 ,
only a relatively small number of detected clouds will be affected by it, and thus the cut-off should be meaningless regarding the observed mass function.
,
only a relatively small number of detected clouds will be affected by it, and thus the cut-off should be meaningless regarding the observed mass function.
The near-infrared color excess values, used in conjunction with the simple foreground screen approximation, do not provide a feasible method of determining the mass function of extra-galactic GMCs. However, the information carried by color excess data regarding the geometric parameters remains interesting as such, and its sensitivity to dust features makes it a powerful tracer of GMCs despite the poor correspondence to real mass. Also, the results of this study are restricted to a face-on geometry where the most important factor, the fraction of foreground flux, is high and more importantly unknown. Several situations can be imagined, where the distribution of GMCs with respect to the main illumination source is much better constrained (e.g. nuclear-centered rings, dust structures in highly inclined systems, etc.). The use of NIR color excess as a mass tracer in these cases may prove to be feasible, but that remains to be confirmed with simulations specific for the geometry in question.
We examined the near-infrared reddening properties of extra-galactic GMCs with Monte Carlo radiative transfer models. Our models resemble the face-on geometry and correspond to the dimensions of the most nearby spiral galaxies. We have investigated the effect of the relative scale height of GMCs,  ,
to the observed color excesses and the mass spectrum of GMCs. We also derived the values of effective reddening law,
EJ-H/EH-K, and the effective extinction law for our models. The main conclusions of our simulations are as follows.
,
to the observed color excesses and the mass spectrum of GMCs. We also derived the values of effective reddening law,
EJ-H/EH-K, and the effective extinction law for our models. The main conclusions of our simulations are as follows.
- 1.
- The effective NIR reddening law of GMCs in a face-on geometry is predicted to have an average slope close to unity. The observed
EJ-H/EH-K ratios of on-cloud regions depend heavily on the exact geometry of the system, which in the context of a face-on galaxy is reflected by the value of
 .
From the simulations we find the average ratios of
EJ-H/EH-K=0.6, 0.7, 0.9, and 1.1 for the
.
From the simulations we find the average ratios of
EJ-H/EH-K=0.6, 0.7, 0.9, and 1.1 for the  values of 0.1, 0.27, 0.5, and 0.75, respectively. The ratios towards spatially separate GMCs should be distinguishable within the typical photometric errors, and thus the value can be used as an indicator of line-of-sight geometry.
values of 0.1, 0.27, 0.5, and 0.75, respectively. The ratios towards spatially separate GMCs should be distinguishable within the typical photometric errors, and thus the value can be used as an indicator of line-of-sight geometry.
- 2.
- The apparent extinction of GMC regions shows very flat wavelength dependency in J, H, and K bands. We find that typically
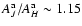 and
and
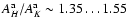 ,
the latter depending slightly on
,
the latter depending slightly on  .
.
- 3.
- The comparisons of the models with and without scattering suggest that the scattered flux has a non-neglible effect on the color excesses and the apparent extinction of GMC regions.
- 4.
- We extend the results of Paper I, confirming that near-infrared color excess is an unrelieable measure of the column density of GMCs. If EH-K values are transformed to masses assuming the Galactic reddening law, on average a fraction on the order of 10-20% of the total mass is recovered. In the case of individual GMCs, the percentage can vary alot, being basically anything between
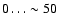 %.
%.
- 5.
- The mass function constructed by using the color excesses and the Galactic reddening law is sensitive to the parameter
 .
The models with lower
.
The models with lower  values tend to have steeper (
values tend to have steeper (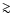 2.5) slopes than models with high
2.5) slopes than models with high  values (
values (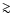 2.0). The dynamical range of the underlying mass function also modifies the observed slope. There is a strong degeneracy in the observed slope with respect to the parameters
2.0). The dynamical range of the underlying mass function also modifies the observed slope. There is a strong degeneracy in the observed slope with respect to the parameters
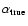 ,
,
 ,
and
,
and
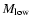 .
As none of these parameters is observationally well constrained, it is not possible to determine
.
As none of these parameters is observationally well constrained, it is not possible to determine
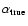 based only on measuring
based only on measuring
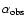 .
.
Acknowledgements
We thank the referee, S. Bianchi, whose comments improved the paper considerably.
- Berlind, A. A.,
Quillen, A. C., Pogge, R. W., & Sellgren, K. 1997, AJ, 114,
107 [NASA ADS] [CrossRef]
(In the text)
- Bohlin, R. C.,
Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef]
(In the text)
- Calzetti, D.
1997, AJ, 113, 162 [NASA ADS] [CrossRef]
(In the text)
- Calzetti, D.
2001, PASP, 113, 1449 [NASA ADS] [CrossRef]
(In the text)
- Calzetti, D.,
Armus, L., Bohlin, et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef]
(In the text)
- Draine, B. T. 2003,
ApJ, 598, 1017 [NASA ADS] [CrossRef]
(In the text)
- Elmegreen, D.
M., Chromey, F. R., & Warren, A. R. 1998, AJ, 116, 2834 [NASA ADS] [CrossRef]
(In the text)
- Howk, J. C., &
Savage, B. D. 1997, AJ, 114, 2463 [NASA ADS] [CrossRef]
(In the text)
- Howk, J. C., &
Savage, B. D. 1999, AJ, 117, 2077 [NASA ADS] [CrossRef]
(In the text)
- Howk, J. C., &
Savage, B. D. 2000, AJ, 119, 644 [NASA ADS] [CrossRef]
(In the text)
-
Kainulainen, J., Juvela, M., & Alves J. 2007, A&A, 468, 581 [NASA ADS] [CrossRef] [EDP Sciences]
(Paper I)
(In the text)
- Lombardi, M.,
& Alves, J. 2001, A&A, 377, 1023 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Pierini, D.,
Gordon, K. D., Witt, A. N., & Madsen, G. J. 2004, ApJ, 617,
1022 [NASA ADS] [CrossRef]
(In the text)
- Regan, M. W. 2000,
ApJ, 541, 142 [NASA ADS] [CrossRef]
(In the text)
- Regan, M. W., Vogel,
S. N., & Teuben, P. J. 1995, ApJ, 449, 576 [NASA ADS] [CrossRef]
(In the text)
- Rieke, G. H., &
Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef]
- Thompson, T. W.
J., Howk, J. C., & Savage, B. D. 2004, AJ, 128, 662 [NASA ADS] [CrossRef]
(In the text)
- Trewhella, M.
1998, MNRAS, 297, 807 [NASA ADS] [CrossRef]
(In the text)
- Williams, J.
P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef]
(In the text)
- Witt, A. N., &
Gordon, K. D. 1996, ApJ, 463, 681 [NASA ADS] [CrossRef]
(In the text)
- Witt, A. N., &
Gordon, K. D. 2000, ApJ, 528, 799 [NASA ADS] [CrossRef]
(In the text)
- Witt, A. N., Thronson,
H. A., & Capuano, J. M. 1992, ApJ, 393, 611 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{8896fig1.eps}\par\vspace*{2mm}
\includegraphics[width=7.8cm,clip]{8896fig2.eps}
\end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8896fig3.eps} \end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg40.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8896fig4.eps} \end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg48.gif)
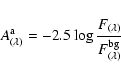
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{8896fig5.eps}\par\vspace*{2mm}
\includegraphics[width=8.2cm,clip]{8896fig6.eps}\par\end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg55.gif)
![\begin{figure}
\par\hspace*{3.5mm} \includegraphics[width=7.7cm,clip]{8896fig7.eps}\par\vspace*{2mm}
\includegraphics[width=7.7cm,clip]{8896fig8.eps} \end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8896fig9.eps} \end{figure}](/articles/aa/full/2008/16/aa8896-07/Timg59.gif)