A&A 482, 133-150 (2008)
DOI: 10.1051/0004-6361:20078874
L. K. Hunt1 - F. Combes2 - S. García-Burillo3 - E. Schinnerer4 - M. Krips5 - A. J. Baker6 - F. Boone2 - A. Eckart7 - S. Léon8 - R. Neri9 - L. J. Tacconi10
1 - INAF-Istituto di Radioastronomia/Sez. Firenze, Largo Enrico Fermi 5, 50125 Firenze, Italy
2 - Observatoire de Paris, LERMA, 61 Av. de l'Observatoire, 75014 Paris, France
3 - Observatorio Astronómico Nacional (OAN) - Observatorio de Madrid,
C/ Alfonso XII, 3, 28014 Madrid, Spain
4 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
5 - Harvard-Smithsonian Center for Astrophysics, SMA, 645 N. A'ohoku Pl., Hilo, HI 96720, USA
6 - Department of Physics and Astronomy, Rutgers, State University of New Jersey, 136 Frelinghuysen Road, Piscataway, NJ 08854, USA
7 - I. Physikalisches Institut, Universität zu Köln, Zülpicherstrasse 77,
50937 Köln, Germany
8 - IRAM-Pico Veleta Observatory, Avenida Divina Pastora 7, Local 20, 18012 Granada, Spain
9 - IRAM-Institut de Radio Astronomie Millimétrique, 300 Rue de la Piscine,
38406 St.Mt.d`Hères, France
10 - Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
Received 16 October 2007 / Accepted 7 February 2008
Abstract
We present CO(1-0) and CO(2-1) maps of the starburst/Seyfert 1 galaxy NGC 2782 obtained with the IRAM interferometer, at 2
![]() 1
1![]() 1
1
![]() 5
and 0
5
and 0
![]() 7
7![]() 0
0
![]() 6 resolution
respectively. The CO emission is aligned along the stellar nuclear bar
of radius
6 resolution
respectively. The CO emission is aligned along the stellar nuclear bar
of radius ![]() 1 kpc, configured in an elongated structure with two spiral arms
at high pitch angle
1 kpc, configured in an elongated structure with two spiral arms
at high pitch angle
![]() .
At the extremity of the nuclear bar, the CO changes direction to
trace two more extended spiral features at a lower pitch angle.
These are the beginning of two straight dust lanes, which are aligned
parallel to an oval distortion, reminiscent of a primary bar,
almost perpendicular to the nuclear one.
The two embedded bars appear in Spitzer IRAC near-infrared images,
and HST color images, although highly obscured by dust in the latter.
We compute the torques exerted by the stellar bars on the gas,
and find systematically negative average torques down to the resolution limit of the images,
providing evidence of gas inflow tantalizingly close to the nucleus of NGC 2782.
We propose a dynamical scenario based on numerical simulations
to interpret coherently the radio, optical,
and molecular gas features in the center of the galaxy.
Star formation is occurring in a partial ring
at
.
At the extremity of the nuclear bar, the CO changes direction to
trace two more extended spiral features at a lower pitch angle.
These are the beginning of two straight dust lanes, which are aligned
parallel to an oval distortion, reminiscent of a primary bar,
almost perpendicular to the nuclear one.
The two embedded bars appear in Spitzer IRAC near-infrared images,
and HST color images, although highly obscured by dust in the latter.
We compute the torques exerted by the stellar bars on the gas,
and find systematically negative average torques down to the resolution limit of the images,
providing evidence of gas inflow tantalizingly close to the nucleus of NGC 2782.
We propose a dynamical scenario based on numerical simulations
to interpret coherently the radio, optical,
and molecular gas features in the center of the galaxy.
Star formation is occurring in a partial ring
at ![]() 1.3 kpc radius corresponding to the Inner Lindblad Resonance (ILR)
of the primary bar;
this ring-like structure encircles the nuclear bar, and is studded with
H
1.3 kpc radius corresponding to the Inner Lindblad Resonance (ILR)
of the primary bar;
this ring-like structure encircles the nuclear bar, and is studded with
H![]() emission.
The gas traced by CO emission is driven inward
by the gravity torques of the decoupled nuclear bar, since most of it is inside
its corotation.
N-body simulations, including gas dissipation, predict the secondary bar decoupling,
the formation of the elongated ring at the
emission.
The gas traced by CO emission is driven inward
by the gravity torques of the decoupled nuclear bar, since most of it is inside
its corotation.
N-body simulations, including gas dissipation, predict the secondary bar decoupling,
the formation of the elongated ring at the ![]() 1 kpc-radius ILR of the primary bar,
and the gas inflow to the ILR of the nuclear bar at a radius of
1 kpc-radius ILR of the primary bar,
and the gas inflow to the ILR of the nuclear bar at a radius of ![]() 200-300 pc.
The presence of molecular gas inside the ILR of the primary bar,
transported by a second nuclear bar, is a potential ``smoking gun'';
the gas there is certainly fueling the central starburst,
and in a second step could fuel directly the AGN.
200-300 pc.
The presence of molecular gas inside the ILR of the primary bar,
transported by a second nuclear bar, is a potential ``smoking gun'';
the gas there is certainly fueling the central starburst,
and in a second step could fuel directly the AGN.
Key words: galaxies: individual NGC 2782 - galaxies: starburst - galaxies: spiral - galaxies: kinematics and dynamics - galaxies: ISM
Molecular gas is the dominant gas component in the inner regions of spiral galaxies, making CO lines unique tracers of nuclear gas dynamics. As such, they are also a powerful diagnostic for identifying how active nuclei (AGN) are fueled. To feed an AGN through accretion, there must be an adequate supply of gas whose angular momentum has been sufficiently reduced to enable inflow within the small spatial scales surrounding the black hole. Although there is rarely a lack of circumnuclear fuel, it is not yet clear how angular momentum is removed to enable nuclear accretion.
To better understand how AGN are fed and maintained,
we have been conducting for several years now a high-resolution high-sensitivity
CO survey (NUGA, García-Burillo et al. 2003) of galaxies
at the IRAM Plateau de Bure Interferometer (PdBI).
Altogether we have observed 12 galaxies in two CO transitions
with up to four configurations of the array, so as to achieve the most sensitive
(typically ![]() -4 mJy beam-1 in 10 km s-1 channels) and
the highest resolution (1-2
-4 mJy beam-1 in 10 km s-1 channels) and
the highest resolution (1-2
![]() )
survey currently available.
The results of the NUGA survey so far have been surprising: there is no single
unambiguous circumnuclear molecular gas feature connected with the nuclear activity.
One- and two-armed instabilities (García-Burillo et al. 2003),
well-ordered rings and nuclear spirals (Combes et al. 2004),
circumnuclear asymmetries (Krips et al. 2005),
and large-scale bars (Boone et al. 2007) are among
the variety of molecular gas morphologies revealed by our survey.
Moreover, an analysis of the torques exerted by the
stellar gravitational potential on the molecular gas in four galaxies suggests
that the gas tends to be driven away from the
the AGN (
)
survey currently available.
The results of the NUGA survey so far have been surprising: there is no single
unambiguous circumnuclear molecular gas feature connected with the nuclear activity.
One- and two-armed instabilities (García-Burillo et al. 2003),
well-ordered rings and nuclear spirals (Combes et al. 2004),
circumnuclear asymmetries (Krips et al. 2005),
and large-scale bars (Boone et al. 2007) are among
the variety of molecular gas morphologies revealed by our survey.
Moreover, an analysis of the torques exerted by the
stellar gravitational potential on the molecular gas in four galaxies suggests
that the gas tends to be driven away from the
the AGN (![]() 50 pc), rather than toward it (García-Burillo et al. 2005).
Nevertheless, these dynamics do not correspond to the violent molecular outflows
and superwinds predicted in AGN feedback models (e.g., Hopkins & Hernquist 2006; Narayanan et al. 2006),
because the observed velocities are much too small.
50 pc), rather than toward it (García-Burillo et al. 2005).
Nevertheless, these dynamics do not correspond to the violent molecular outflows
and superwinds predicted in AGN feedback models (e.g., Hopkins & Hernquist 2006; Narayanan et al. 2006),
because the observed velocities are much too small.
Much of the explanation of this variety of morphologies appears to be related
to timescales (García-Burillo et al. 2005).
It is well established that large-scale bars transport gas
inward very efficiently (e.g., Combes & Gerin 1985; Sakamoto et al. 1999),
and there is very little doubt that bars can drive powerful starbursts
(Jogee et al. 2005; Knapen et al. 2002).
However, no clear correlation between bars and nuclear activity
has yet been found (e.g., Mulchaey & Regan 1997).
This may be because the timescales for bar-induced gas inflow
and AGN duty cycles are very different.
Bars drive inflow over timescales (![]() 300 Myr) that are
similar to the typical gas-consumption timescales of a few
times
300 Myr) that are
similar to the typical gas-consumption timescales of a few
times
![]() yr found in nuclear starbursts (e.g., Jogee et al. 2005).
But AGN accretion-rate duty cycles are much shorter than this
(
yr found in nuclear starbursts (e.g., Jogee et al. 2005).
But AGN accretion-rate duty cycles are much shorter than this
(![]() 1-10 Myr, King & Pringle 2007; Heckman et al. 2004; Hopkins & Hernquist 2006), and
there are several indications that active accretion
occurs only intermittently over the lifetime of a galaxy
(King & Pringle 2007; Ferrarese et al. 2001; Janiuk et al. 2004; Marecki et al. 2003; Hopkins & Hernquist 2006).
The resulting implication is that most AGN are probably between active
accretion episodes, and catching galaxies with nuclear accretion
``switched on'' may be difficult.
1-10 Myr, King & Pringle 2007; Heckman et al. 2004; Hopkins & Hernquist 2006), and
there are several indications that active accretion
occurs only intermittently over the lifetime of a galaxy
(King & Pringle 2007; Ferrarese et al. 2001; Janiuk et al. 2004; Marecki et al. 2003; Hopkins & Hernquist 2006).
The resulting implication is that most AGN are probably between active
accretion episodes, and catching galaxies with nuclear accretion
``switched on'' may be difficult.
In this paper, the ninth of the NUGA series,
we present observations that suggest that we have
found one of these potentially rare
AGN with possible gas inflow in the current epoch.
NGC 2782 is an early-type spiral galaxy [SABa(rs)] with peculiar morphology.
In addition to a pronounced stellar tail or sheet ![]() 20 kpc to the east, it shows
three optical ripples (e.g., Smith 1994) thought to be signatures of
tidal interactions (Schweizer & Seitzer 1988).
A massive H I plume extends
20 kpc to the east, it shows
three optical ripples (e.g., Smith 1994) thought to be signatures of
tidal interactions (Schweizer & Seitzer 1988).
A massive H I plume extends ![]() 54 kpc to the northwest,
and the neutral atomic gas in the inner disk is counterrotating
with respect to the gas motions in the outer regions (Smith 1991).
The central regions of NGC 2782 host a massive nuclear starburst, with a far-infrared
(FIR) luminosity of
54 kpc to the northwest,
and the neutral atomic gas in the inner disk is counterrotating
with respect to the gas motions in the outer regions (Smith 1991).
The central regions of NGC 2782 host a massive nuclear starburst, with a far-infrared
(FIR) luminosity of
![]()
![]() ,
comparable to that in M 82 (Devereux 1989).
Three-dimensional optical spectroscopy (Yoshida et al. 1999) shows evidence for a high-speed
ionized gas outflow, with the bipolar structure in the radio
continuum indicative of a confined superbubble (Jogee et al. 1998).
In the outflow, there are also high-excitation extranuclear emission lines
thought to be due to shock heating (Boer et al. 1992).
,
comparable to that in M 82 (Devereux 1989).
Three-dimensional optical spectroscopy (Yoshida et al. 1999) shows evidence for a high-speed
ionized gas outflow, with the bipolar structure in the radio
continuum indicative of a confined superbubble (Jogee et al. 1998).
In the outflow, there are also high-excitation extranuclear emission lines
thought to be due to shock heating (Boer et al. 1992).
Until recently, it was thought that the outflow and energetics in NGC 2782 were powered by
a starburst alone, but recent radio and X-ray observations reveal an optically-hidden AGN.
MERLIN and EVN/VLBI observations show a high-brightness-temperature
extremely compact (![]() 0
0
![]() 05) radio source, unambiguous
evidence of an AGN (Krips et al. 2007).
NGC 2782 is also a Compton-thick X-ray source
with a 6.4 keV iron feature coming from its innermost regions (Zhang et al. 2006).
There is a bright unresolved X-ray core
and extended emission roughly coincident with the radio morphology in the
high-resolution (
05) radio source, unambiguous
evidence of an AGN (Krips et al. 2007).
NGC 2782 is also a Compton-thick X-ray source
with a 6.4 keV iron feature coming from its innermost regions (Zhang et al. 2006).
There is a bright unresolved X-ray core
and extended emission roughly coincident with the radio morphology in the
high-resolution (![]() 1
1
![]() )
image by Saikia et al. (1994).
)
image by Saikia et al. (1994).
The nuclear region of NGC 2782 has been observed previously in the 12CO(1-0) line by Ishuzuki (1994) with the Nobeyama Millimeter Array and by Jogee et al. (1999) using the Owens Valley Radio Observatory. We reobserved NGC 2782 in 12CO(1-0) at PdBI with better spatial resolution and a sensitivity roughly five times that of previous observations, and for the first time in the 12CO(2-1) line. This enables a rigorous derivation of the torques acting on the molecular gas in NGC 2782, and a quantitative assessment of the infall of material to the nucleus. We first present our new observations in Sect. 2, together with our multiwavelength imaging dataset. The morphology and kinematics of the molecular gas are discussed in Sect. 3, and we describe the stellar structure in Sect. 4 and the starburst episode in Sect. 5. We then derive the gravitational potential from the infrared image, and infer the torques acting on the molecular gas in Sect. 6. Finally, we present numerical simulations which motivate our proposed scenario of decoupled double bars in this galaxy. The molecular gas in NGC 2782 is apparently being driven inward by the nuclear bar, decoupled from the primary bar, since we detect azimuthally averaged torques which are negative down to the resolution limit of our images.
We observed NGC 2782 with the IRAM PdBI in the ABCD configuration of the array
between December 2001 and February 2003 in the 12CO(1-0) (115 GHz) and the
12CO(2-1) (230 GHz) rotational transitions. The PdBI receiver characteristics,
the observing procedures, and the image reconstruction are the same as those
described in García-Burillo et al. (2003).
The quasar 3C273 was used for bandpass calibration and the
quasar 0923+392 was used to calibrate both the phase and the atmospheric variations.
We used uniform weighting to generate 2-1 maps with a
field of view of 21
![]() and natural weighting to produce the 1-0 maps
with a field of view of 42
and natural weighting to produce the 1-0 maps
with a field of view of 42
![]() .
Such a procedure maximizes the flux recovered in CO(1-0) and optimizes the
spatial resolution in CO(2-1).
.
Such a procedure maximizes the flux recovered in CO(1-0) and optimizes the
spatial resolution in CO(2-1).
The rms noise ![]() in
10 km s-1 wide velocity channels is 2.0 mJy beam-1 and
5.2 mJy beam-1, with beam sizes of 2
in
10 km s-1 wide velocity channels is 2.0 mJy beam-1 and
5.2 mJy beam-1, with beam sizes of 2
![]() 1
1![]() 1
1
![]() 5 and
0
5 and
0
![]() 7
7![]() 0
0
![]() 6 at 115 and 230 GHz, respectively. At a level
of
6 at 115 and 230 GHz, respectively. At a level
of
![]() ,
no 3 mm (1 mm) continuum is detected toward NGC 2782 to a
level of 1 mJy beam-1 (3 mJy beam-1). The conversion factors
between Jy beam-1 and K are 30 K Jy-1 beam at 115 GHz, and
58 K Jy-1 beam at 230 GHz. By default, all velocities are referred to
the heliocentric recession velocity v0=2545 km s-1 and
,
no 3 mm (1 mm) continuum is detected toward NGC 2782 to a
level of 1 mJy beam-1 (3 mJy beam-1). The conversion factors
between Jy beam-1 and K are 30 K Jy-1 beam at 115 GHz, and
58 K Jy-1 beam at 230 GHz. By default, all velocities are referred to
the heliocentric recession velocity v0=2545 km s-1 and
![]() offsets are relative to the phase tracking center of
the observations (RA2000, Dec2000)=(09
offsets are relative to the phase tracking center of
the observations (RA2000, Dec2000)=(09![]() 14
14![]() 05.08
05.08![]() ,
40
,
40![]() 06
06![]() 49.4
49.4![]() ).
The displayed maps are not corrected for primary beam attenuation.
).
The displayed maps are not corrected for primary beam attenuation.
We will assume a distance to NGC 2782 of D=35 Mpc, which is derived from the local velocity field model
given in Mould et al. (2000) and a Hubble constant H0=73 km s-1 Mpc-1.
At this distance 1
![]() corresponds to 171 pc.
corresponds to 171 pc.
We retrieved HST archival images of NGC 2782 with WFPC2 in
the F555W and F814W filters.
Cosmic rays were eliminated, and the images were calibrated
and converted to V and I as described in Holtzman et al. (1995).
We performed an astrometric calibration using stars
from the U.S. Naval Observatory Astrometric Catalog B1.0 (USNO-B1.0).
Five stars from this catalogue appear in the
![]() WFPC2
image of NGC 2782 and they were used to derive
the astrometric solution with imwcs in the WCSTools
package
WFPC2
image of NGC 2782 and they were used to derive
the astrometric solution with imwcs in the WCSTools
package![]() .
The solution has an rms uncertainty of 0
.
The solution has an rms uncertainty of 0
![]() 24, or 2.4 WFPC2 (mosaic) pixels,
and differs from the original HST one by
24, or 2.4 WFPC2 (mosaic) pixels,
and differs from the original HST one by ![]() 1
1
![]() .
We made V-I color images by
converting the flux units to magnitudes and subtracting the two magnitude images.
.
We made V-I color images by
converting the flux units to magnitudes and subtracting the two magnitude images.
IRAC images at 3.6 ![]() m
were retrieved from the Spitzer archive.
We started with the Basic Calibrated Data images,
and aligned and combined them with MOPEX (Makovoz & Marleau 2005) which accounts
for distortion and rotates to a fiducial coordinate system.
1
m
were retrieved from the Spitzer archive.
We started with the Basic Calibrated Data images,
and aligned and combined them with MOPEX (Makovoz & Marleau 2005) which accounts
for distortion and rotates to a fiducial coordinate system.
1
![]() 20 pixels were imposed for the final image,
roughly the same as the original IRAC detector.
Significant banding was present
from a bright star in the field,
and this was corrected for by
interpolation over the affected rows before combination with MOPEX.
Combination of these corrected images showed no discernible effect of
the original flaw.
20 pixels were imposed for the final image,
roughly the same as the original IRAC detector.
Significant banding was present
from a bright star in the field,
and this was corrected for by
interpolation over the affected rows before combination with MOPEX.
Combination of these corrected images showed no discernible effect of
the original flaw.
The infrared and optical images will be discussed in Sects. 4 and 5.
Figures 1 and 2 show the velocity-channel maps
of 12CO(1-0) and 12CO(2-1) emission in the central region of NGC 2782.
The kinematics show the typical signature of a rotating disk,
together with non-circular motions more prominent to the south.
The western (eastern) side of the CO bar is red- (blue-) shifted relative to
the systemic velocity
![]() ,
which is fitted to be at
,
which is fitted to be at
![]() km s-1.
This agrees very well with the H I heliocentric velocity of 2555 km s-1(Smith 1994).
km s-1.
This agrees very well with the H I heliocentric velocity of 2555 km s-1(Smith 1994).
![\begin{figure}
\par\includegraphics[width=18cm,clip]{8874fig1.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg48.gif) |
Figure 1:
12CO(1-0) velocity-channel maps observed with the
PdBI in the nucleus of NGC 2782 with a spatial resolution of
2.1
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{8874fig2.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg49.gif) |
Figure 2:
Same as Fig. 1 but for the 2-1 line of 12CO.
Spatial resolution reaches 0.7
|
| Open with DEXTER | |
The dynamical center was derived from the center of symmetry of the velocity field,
and chosen to maximize the velocity dispersion.
It is determined to lie at (
![]() ,
,
![]() ) =
(09
) =
(09![]() 14
14![]() 05.11
05.11![]() ,
40
,
40![]() 06
06![]() 49.24
49.24
![]() ),
not far from the phase-tracking center.
The position of the dynamical center coincides almost exactly with
the compact radio source discovered by Krips et al. (2007):
(
),
not far from the phase-tracking center.
The position of the dynamical center coincides almost exactly with
the compact radio source discovered by Krips et al. (2007):
(
![]() ,
,
![]() ) =
(09
) =
(09![]() 14
14![]() 05.11
05.11![]() ,
40
,
40![]() 06
06![]() 49.32
49.32
![]() ).
Both are also within the errors of the
position of the ``C'' component of the NGC 2782 nucleus
described by Saikia et al. (1994).
Therefore we ascribe the position of the AGN and the dynamical center
of NGC 2782 to the position derived here from the CO kinematics.
).
Both are also within the errors of the
position of the ``C'' component of the NGC 2782 nucleus
described by Saikia et al. (1994).
Therefore we ascribe the position of the AGN and the dynamical center
of NGC 2782 to the position derived here from the CO kinematics.
The overall distribution of the molecular gas is illustrated in
Figure 3 which shows the velocity-integrated CO intensity maps,
achieved by integrating channels from v=-230 to 230 km s-1.
The naturally weighted 12CO(1-0) map is shown in the top panel of Fig. 3,
and the uniform-weight 12CO(2-1) map in the bottom panel.
After correcting for primary beam attenuation and considering only measurements
with a signal-to-noise of ![]() or greater on the data cube,
our naturally weighted (1-0) observations in the central 42
or greater on the data cube,
our naturally weighted (1-0) observations in the central 42
![]() detect
an integrated CO flux of 150 Jy km s-1.
This corresponds to 65% of that in the
Five College Radio Astronomy Observatory single dish measurements
(within 45
detect
an integrated CO flux of 150 Jy km s-1.
This corresponds to 65% of that in the
Five College Radio Astronomy Observatory single dish measurements
(within 45
![]() :
230 Jy km s-1, Young et al. 1995),
and roughly 78% of the flux measured by Jogee et al. (1999, 195 Jy km s-1).
Our measurements are sensitive to small-scale structure but are missing some
fraction of the diffuse component.
We use the short-spacing single dish observations by Young et al. (1995)
to derive the gas mass for numerical simulations in Sect. 7.3.
:
230 Jy km s-1, Young et al. 1995),
and roughly 78% of the flux measured by Jogee et al. (1999, 195 Jy km s-1).
Our measurements are sensitive to small-scale structure but are missing some
fraction of the diffuse component.
We use the short-spacing single dish observations by Young et al. (1995)
to derive the gas mass for numerical simulations in Sect. 7.3.
The 12CO(1-0) emission is distributed in a nuclear elongated structure
already identified by Jogee et al. (1999).
Our observations clearly delineate the
diffuse spiral arms extending to the north and south.
The spirals are not symmetric, and there is substantially more emission to the
southeast than to the northwest.
The filaments at ![]() 10
10
![]() to the north and south in CO(1-0) correspond to
the spiral arms from the outer stellar oval (which we discuss in more detail
below).
Indeed, the CO ``spur'' labeled ``O2'' by Jogee et al. (1999) appears to be associated
with the extended southern spiral arm shown in our maps
(see Fig. 3).
to the north and south in CO(1-0) correspond to
the spiral arms from the outer stellar oval (which we discuss in more detail
below).
Indeed, the CO ``spur'' labeled ``O2'' by Jogee et al. (1999) appears to be associated
with the extended southern spiral arm shown in our maps
(see Fig. 3).
The central structure in the 12CO(2-1) map is clearly resolved;
the higher resolution afforded by our new observations
shows a clearly elongated structure with spiral arms commencing at the
ends of the elongation.
The gas in the inner spiral arms is aligned along the elongation with a pitch angle
of
![]() ,
which makes the feature resemble more a bar than an inclined or edge-on disk.
At the end of the feature, the gas changes direction to follow the outer spiral
arms, which are situated at a lower pitch angle.
Moreover, the molecular gas is clearly responding to the stellar
oval/bar which we will discuss in Sect. 4.
Hence, we will refer to the circumnuclear molecular structure as
the ``nuclear gas bar'', as distinct from the nuclear stellar bar (see below).
,
which makes the feature resemble more a bar than an inclined or edge-on disk.
At the end of the feature, the gas changes direction to follow the outer spiral
arms, which are situated at a lower pitch angle.
Moreover, the molecular gas is clearly responding to the stellar
oval/bar which we will discuss in Sect. 4.
Hence, we will refer to the circumnuclear molecular structure as
the ``nuclear gas bar'', as distinct from the nuclear stellar bar (see below).
The molecular gas mass within the 42
![]() PdB primary beam field is
PdB primary beam field is
![]()
![]() ,
assuming the CO-to-H2 conversion factor
,
assuming the CO-to-H2 conversion factor
![]() cm-2 (K km s-1)-1 given by Solomon & Barrett (1991).
Including the helium mass in the clouds (multiplying
cm-2 (K km s-1)-1 given by Solomon & Barrett (1991).
Including the helium mass in the clouds (multiplying
![]() )
gives
)
gives
![]()
![]() .
Most of the molecular gas mass in NGC 2782 is in the nuclear gas bar+spiral,
making it an extremely massive structure.
Indeed, the circumnuclear molecular gas component in NGC 2782 is particularly massive,
roughly 3 times more so than most of the NUGA galaxies studied so far
(NGC 4826: García-Burillo et al. 2003; NGC 7217: Combes et al. 2004; NGC 3718: Krips et al. 2005
NGC 4579: García-Burillo et al. 2005; NGC 6951:
García-Burillo et al. 2005, all have molecular masses on the order of
.
Most of the molecular gas mass in NGC 2782 is in the nuclear gas bar+spiral,
making it an extremely massive structure.
Indeed, the circumnuclear molecular gas component in NGC 2782 is particularly massive,
roughly 3 times more so than most of the NUGA galaxies studied so far
(NGC 4826: García-Burillo et al. 2003; NGC 7217: Combes et al. 2004; NGC 3718: Krips et al. 2005
NGC 4579: García-Burillo et al. 2005; NGC 6951:
García-Burillo et al. 2005, all have molecular masses on the order of
![]()
![]() ).
Only NGC 4569 (Boone et al. 2007), with
).
Only NGC 4569 (Boone et al. 2007), with
![]()
![]() ,
is
roughly comparable with NGC 2782.
,
is
roughly comparable with NGC 2782.
![\begin{figure}
\par\includegraphics[width=8.8cm]{8874fig3.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg60.gif) |
Figure 3: a) The natural-weight map in 12CO(1-0) shown in grey scale with contours ranging from 0.5 to 8.0 Jy km s-1 in 1 Jy km s-1 intervals. b) The uniform-weight map in 12CO(2-1) shown in grey scale with contours ranging from 1 to 7.0 Jy km s-1 in 1 Jy km s-1 intervals. |
| Open with DEXTER | |
Figure 4 shows the mean velocity field derived from
CO(1-0) (top panel) and CO(2-1) (bottom).
The star marks the position of the AGN (coincident with the dynamical
center).
The kinematic signature of a rotating disk is clearly seen in Fig. 4,
and in the body of the circumnuclear molecular spiral, there are
few non-circular motions.
However, the southern spiral arm in the CO(1-0) map (top panel of Fig. 4)
shows clear streaming motions, and
appears to be somewhat decoupled from the nuclear spiral because of
the velocity discontinuity toward the southeast.
In the bottom panel of Fig. 4,
systematic kinks appear in the CO(2-1) velocity field
near the position of the AGN (![]() 0
0
![]() 5, barely resolved) both to the north and the south.
5, barely resolved) both to the north and the south.
![\begin{figure}
\par\includegraphics[width=8.8cm]{8874fig4.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg61.gif) |
Figure 4: 12CO(1-0) a) and 12CO(2-1) b) isovelocities contoured over false-color velocity maps. The AGN (dynamical center) position is marked with a star. |
| Open with DEXTER | |
We derive a kinematic major axis of PA = (75 ![]() 5)
5)![]() ,
consistent with previous determinations (75
,
consistent with previous determinations (75![]() ,
Jogee et al. 1999).
We will assume that the inclination angle of the nuclear spiral in NGC 2782 is
,
Jogee et al. 1999).
We will assume that the inclination angle of the nuclear spiral in NGC 2782 is
![]() 30
30![]() (see also Jogee et al. 1999).
A smaller inclination would result in
(see also Jogee et al. 1999).
A smaller inclination would result in ![]() corrected velocities which would be
too large to be consistent with even the largest spiral galaxies and ellipticals.
A larger inclination seems equally unlikely because of the relatively straight
extended spiral arms (see discussion in Sect. 5);
if the inclination were
corrected velocities which would be
too large to be consistent with even the largest spiral galaxies and ellipticals.
A larger inclination seems equally unlikely because of the relatively straight
extended spiral arms (see discussion in Sect. 5);
if the inclination were ![]() 30
30![]() ,
the arms would be
apparently more compressed relative to the line of nodes.
That the galaxy disk is inclined at 30
,
the arms would be
apparently more compressed relative to the line of nodes.
That the galaxy disk is inclined at 30![]() is confirmed by the
two-dimensional bulge-disk decomposition and the elliptical isophote fitting
described in Sect. 4.
is confirmed by the
two-dimensional bulge-disk decomposition and the elliptical isophote fitting
described in Sect. 4.
![\begin{figure}
\par\includegraphics[width=8.8cm]{8874fig5.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg65.gif) |
Figure 5:
a) Position-velocity diagram of 12CO(1-0) along the kinematic major axis
of NGC 2782 (PA = 75 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{8874fig6.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg66.gif) |
Figure 6:
a) Position-velocity diagram of 12CO(1-0) along the kinematic minor axis
of NGC 2782 (PA = 165 |
| Open with DEXTER | |
Position-velocity (PV) diagrams along the major kinematic axis of NGC 2782 are shown in Fig. 5, and along the minor axis in Fig. 6.
In both figures, 12CO(1-0) is given in the top panel, and 12CO(2-1) in the bottom.
The top panel of Fig. 5 reveals regular circular rotation together
with mild streaming motions in the molecular gas.
However, the rough alignment of the molecular feature at PA ![]() 88
88![]() with the line-of-nodes of the galaxy (
with the line-of-nodes of the galaxy (
![]() -
-![]() ,
see Sect. 4)
inhibits a clear signature of non-circular streaming motions.
Consequently,
the major-axis PV diagram cannot provide
conclusive evidence for out-of-plane kinematics or for kinematic decoupling of the
nuclear structure from the larger-scale stellar disk.
The kinematics shown by the minor-axis PV in Fig. 6
are quite regular in the extended regions,
but show significant velocity dispersion close to the nucleus.
This could reflect an unresolved rotational velocity component,
suggesting a large central dynamical mass (see below).
Finally,
Fig. 6 shows no evidence for molecular gas outflow, as tentatively
suggested by Jogee et al. (1999).
,
see Sect. 4)
inhibits a clear signature of non-circular streaming motions.
Consequently,
the major-axis PV diagram cannot provide
conclusive evidence for out-of-plane kinematics or for kinematic decoupling of the
nuclear structure from the larger-scale stellar disk.
The kinematics shown by the minor-axis PV in Fig. 6
are quite regular in the extended regions,
but show significant velocity dispersion close to the nucleus.
This could reflect an unresolved rotational velocity component,
suggesting a large central dynamical mass (see below).
Finally,
Fig. 6 shows no evidence for molecular gas outflow, as tentatively
suggested by Jogee et al. (1999).
We have derived a rotation curve (RC) from the PV diagram taken along
the kinematic major axis of NGC 2782 at a PA = 75 ![]() .
The terminal velocities were derived by fitting multiple Gaussian
profiles to the spectra across the major axis.
The fitted velocity centroids, corrected for
.
The terminal velocities were derived by fitting multiple Gaussian
profiles to the spectra across the major axis.
The fitted velocity centroids, corrected for ![]() (
(
![]() ),
give
),
give
![]() for each galactocentric distance.
Although for both lines the RCs to the south
(negative velocities) are slightly steeper within the inner 300 pc than
those to the north (positive), we averaged together the two
curves derived from either side of the major axis.
Hence, the resulting
for each galactocentric distance.
Although for both lines the RCs to the south
(negative velocities) are slightly steeper within the inner 300 pc than
those to the north (positive), we averaged together the two
curves derived from either side of the major axis.
Hence, the resulting
![]() may be slightly shallower in the
inner regions than the true mass distribution would imply.
Because data for both lines were consistent, we combined both curves
into an average by spline interpolation.
The final RC is shown in Sect. 7.2 in the context of
our numerical simulations.
may be slightly shallower in the
inner regions than the true mass distribution would imply.
Because data for both lines were consistent, we combined both curves
into an average by spline interpolation.
The final RC is shown in Sect. 7.2 in the context of
our numerical simulations.
The peak velocity is
![]() km s-1, or
km s-1, or ![]() 340 km s-1 for
340 km s-1 for
![]() ,
obtained at a radius of 850 pc (5
,
obtained at a radius of 850 pc (5
![]() )
to the south,
but at
)
to the south,
but at ![]() 1 kpc (
1 kpc (![]() 6
6
![]() )
in the RC obtained from averaging
both lines and both sides of the major axis.
From the peak velocity, we can derive a rough estimate of the
dynamical mass:
)
in the RC obtained from averaging
both lines and both sides of the major axis.
From the peak velocity, we can derive a rough estimate of the
dynamical mass:
![]() where M(R) is in
where M(R) is in ![]() ,
R in kpc, and V in km s-1.
Assuming the most flattened disk-like distribution (i.e., including a multiplicative
constant of 0.6), at a radius of 1 kpc,
we would find
,
R in kpc, and V in km s-1.
Assuming the most flattened disk-like distribution (i.e., including a multiplicative
constant of 0.6), at a radius of 1 kpc,
we would find
![]()
![]() .
Within a 1.7 kpc radius, where virtually all of the observed molecular gas is located,
assuming a flat rotation curve (see Sect. 7.2), we would
infer
.
Within a 1.7 kpc radius, where virtually all of the observed molecular gas is located,
assuming a flat rotation curve (see Sect. 7.2), we would
infer
![]()
![]() .
Comparing with the mass in molecular gas including helium would give
a molecular mass fraction of
.
Comparing with the mass in molecular gas including helium would give
a molecular mass fraction of ![]() 7% in this region,
in agreement with Jogee et al. (1999).
7% in this region,
in agreement with Jogee et al. (1999).
Figure 7 shows the CO(1-0) and (2-1) total intensity
maps overlaid on the IRAC 3.6 ![]() m image described in Sect. 2.1.
This wavelength traces very well the massive component of the stellar
populations in galaxies, and has the added advantage of very low extinction
even compared to the K band.
Two main inner structures can be seen in Fig. 7:
an inner stellar bar/oval with
a
m image described in Sect. 2.1.
This wavelength traces very well the massive component of the stellar
populations in galaxies, and has the added advantage of very low extinction
even compared to the K band.
Two main inner structures can be seen in Fig. 7:
an inner stellar bar/oval with
a
![]() and diameter of
and diameter of ![]() 15
15
![]() ,
and an outer oval at
,
and an outer oval at
![]() and diameter of
and diameter of ![]() 30
30
![]()
![]() .
Previous K-band observations (Jogee et al. 1999) identified
similar features, but with slightly different PA's and
a larger radius for the outer oval than we find here
(25
.
Previous K-band observations (Jogee et al. 1999) identified
similar features, but with slightly different PA's and
a larger radius for the outer oval than we find here
(25
![]() vs.
vs. ![]() 15
15
![]() ).
Both structures are clearly present in NGC 2782,
and as we shall see in Sect. 6, contribute to the
dynamical perturbations in this galaxy.
).
Both structures are clearly present in NGC 2782,
and as we shall see in Sect. 6, contribute to the
dynamical perturbations in this galaxy.
![\begin{figure}
\par\includegraphics[width=8.8cm]{8874fig7.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg75.gif) |
Figure 7:
a) 12CO(1-0) total intensity contoured over a false-color
representation of the IRAC 3.6 |
| Open with DEXTER | |
A large-scale view of NGC 2782 at 3.6 ![]() m is illustrated in
(the left panel of) Fig. 8.
The detached stellar sheet or tail outside the main galaxy disk is evident
to the east, and the elongation or distortion of the disk to the west is clearly visible.
There are also stellar arcs or ``ripples'' (Jogee et al. 1999; Smith 1994) about 25
m is illustrated in
(the left panel of) Fig. 8.
The detached stellar sheet or tail outside the main galaxy disk is evident
to the east, and the elongation or distortion of the disk to the west is clearly visible.
There are also stellar arcs or ``ripples'' (Jogee et al. 1999; Smith 1994) about 25
![]() to the west of the nucleus. All these features are seen in optical images (Jogee et al. 1999; Smith 1994)
and in H I (Smith 1991). Moreover, in H I, there is a long (
to the west of the nucleus. All these features are seen in optical images (Jogee et al. 1999; Smith 1994)
and in H I (Smith 1991). Moreover, in H I, there is a long (![]() 54 kpc) plume or
tidal tail extending to the north,
with its origin at the westernmost edge of the distorted disk (Smith 1991).
54 kpc) plume or
tidal tail extending to the north,
with its origin at the westernmost edge of the distorted disk (Smith 1991).
To better understand the mass distribution and investigate the non-axisymmetric
structure in the stars,
we performed a two-dimensional bulge/disk decomposition on the IRAC 3.6 ![]() m image of NGC 2782 with galfit, the publicly available algorithm developed by
Peng et al. (2002).
The MOPEX point-response function was used for convolution with the image, and
the background sky level was fixed to the measured value rather than fit.
Initial parameters for bulge and disk were guessed by using the scaling relations
given by Moriondo et al. (1998) and Hunt et al. (2004).
The final best fit was achieved with a generalized exponential (Sersic) bulge,
an exponential disk, and a nuclear point source.
m image of NGC 2782 with galfit, the publicly available algorithm developed by
Peng et al. (2002).
The MOPEX point-response function was used for convolution with the image, and
the background sky level was fixed to the measured value rather than fit.
Initial parameters for bulge and disk were guessed by using the scaling relations
given by Moriondo et al. (1998) and Hunt et al. (2004).
The final best fit was achieved with a generalized exponential (Sersic) bulge,
an exponential disk, and a nuclear point source.
We ran several sets of fits, in order to experiment with masking the stellar
tails or sheets predominant to the east.
Fitting the whole image (![]() 3.4
3.4![]() diameter) results in a bulge with
shape index n = 3 (a de Vaucouleurs bulge has n = 4),
an effective radius of 1.1 kpc and an apparent inclination of 32
diameter) results in a bulge with
shape index n = 3 (a de Vaucouleurs bulge has n = 4),
an effective radius of 1.1 kpc and an apparent inclination of 32![]() .
This bulge contains about 60% of the total 3.6
.
This bulge contains about 60% of the total 3.6 ![]() m light.
The resulting disk, with a scalelength of 2.9 kpc and an inclination of 41
m light.
The resulting disk, with a scalelength of 2.9 kpc and an inclination of 41![]() ,
together with a nuclear point source
contribute about 33% and 7%, respectively, to the total luminosity.
The fitted aspect ratio of the disk is very close to that given for NGC 2782 in NED, which
corresponds to a system inclination of 42
,
together with a nuclear point source
contribute about 33% and 7%, respectively, to the total luminosity.
The fitted aspect ratio of the disk is very close to that given for NGC 2782 in NED, which
corresponds to a system inclination of 42![]() .
The bulge PA of 19
.
The bulge PA of 19![]() is ill-determined because of its low apparent flattening,
but the fitted orientation of the disk (
is ill-determined because of its low apparent flattening,
but the fitted orientation of the disk (
![]() )
is consistent with
the angle of the line-of-nodes estimated by Jogee et al. (1999)
and with the kinematical major axis found in Sect. 3.2.
)
is consistent with
the angle of the line-of-nodes estimated by Jogee et al. (1999)
and with the kinematical major axis found in Sect. 3.2.
Masking the stellar ``sheets'', and confining the fit to the undisturbed portion of the
outer regions (within a ![]() 2.4
2.4![]() diameter, 24 kpc) gives a slightly different,
probably more reliable, fit.
The bulge has a steeper shape index (n = 4), the nuclear point source is smaller,
and the disk is less inclined.
The fraction of bulge-to-total luminosity remains the same,
diameter, 24 kpc) gives a slightly different,
probably more reliable, fit.
The bulge has a steeper shape index (n = 4), the nuclear point source is smaller,
and the disk is less inclined.
The fraction of bulge-to-total luminosity remains the same, ![]() 60%.
The masked fits give a disk inclination of 33
60%.
The masked fits give a disk inclination of 33![]() ,
more similar to that of the bulge,
and more consistent with the visual aspect of the galaxy.
Indeed, inspection of Fig. 8 suggests a strikingly round
appearance, at least in the regular portion of the disk out to a radius of
,
more similar to that of the bulge,
and more consistent with the visual aspect of the galaxy.
Indeed, inspection of Fig. 8 suggests a strikingly round
appearance, at least in the regular portion of the disk out to a radius of ![]() 50
50
![]() (
(![]() 9 kpc).
This impression is confirmed by fitting the isophotes to ellipses
9 kpc).
This impression is confirmed by fitting the isophotes to ellipses![]() which
shows that at galactocentric distances as large as 12.5 kpc, the
fitted system ellipticity implies an inclination of
which
shows that at galactocentric distances as large as 12.5 kpc, the
fitted system ellipticity implies an inclination of
![]() at
at
![]() .
Hence, we confirm
.
Hence, we confirm ![]() 30
30![]() for the system inclination (as described in
Sect. 3.2), obtained with the masked bulge-disk decomposition.
for the system inclination (as described in
Sect. 3.2), obtained with the masked bulge-disk decomposition.
The fit provides a convenient axisymmetric model for unsharp masking.
The large-scale residuals from the fit described above are shown in the right panel of Fig. 8.
The correspondence with the features in the unsharp masked optical images (Smith 1994)
is excellent.
The stellar sheet to the east, and the ripples and distortion of the disk to the west,
are clearly revealed.
The small-scale residuals of the bulge/disk decomposition are shown in Fig. 9
with CO(1-0) (left panel) and CO(2-1) (right) overlaid in contours;
both the ``masked'' fits and the fits to the entire image give virtually
identical residuals in the circumnuclear region.
The large (1
![]() 2) pixels of the IRAC image impede detailed comparison, but
the residuals from the fit have an m=2 structure, and strongly resemble a
stellar bar.
Some small component of residuals could perhaps be hot dust rather than stars,
because of the red K-L color excess observed in the center of NGC 2782 (Hunt & Giovanardi 1992).
Nevertheless, dust cannot contribute significantly to the structure of the residuals
because the K-L color is redder outside the bar-like structure than within it.
In fact,
the position of the bar-like residuals coincides perfectly with the CO emission,
and provides a classic illustration of the theoretical behavior of the
spiral response of a gas component to bar forcing.
In this case, the gas is phase shifted in advance relative to the bar (leading),
as can be seen to the northeast and the southwest in the ``S'' shape of the spiral.
2) pixels of the IRAC image impede detailed comparison, but
the residuals from the fit have an m=2 structure, and strongly resemble a
stellar bar.
Some small component of residuals could perhaps be hot dust rather than stars,
because of the red K-L color excess observed in the center of NGC 2782 (Hunt & Giovanardi 1992).
Nevertheless, dust cannot contribute significantly to the structure of the residuals
because the K-L color is redder outside the bar-like structure than within it.
In fact,
the position of the bar-like residuals coincides perfectly with the CO emission,
and provides a classic illustration of the theoretical behavior of the
spiral response of a gas component to bar forcing.
In this case, the gas is phase shifted in advance relative to the bar (leading),
as can be seen to the northeast and the southwest in the ``S'' shape of the spiral.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=8.5cm,clip]{8874f8a.ps...
...e*{1mm}
\includegraphics[angle=-90,width=8.5cm,clip]{8874f8b.ps} }\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg79.gif) |
Figure 8:
a) IRAC 3.6 |
| Open with DEXTER | |
While stellar structure can be more readily inferred from near-infrared (NIR)
wavelengths, dust extinction and star formation are best investigated
in the optical.
Figure 10 shows the CO intensity maps overlaid on the HST/WFPC2
F814W image.
The F814W emission of the circumnuclear region shows a strong asymmetric excess to the
northwest of the AGN (hereafter called the ``NW excess''), roughly coincident with the
structure in the H![]() maps (Jogee et al. 1999).
This excess is contiguous with an entire arc of bright knots to the north running from east
to west, again reflecting the H
maps (Jogee et al. 1999).
This excess is contiguous with an entire arc of bright knots to the north running from east
to west, again reflecting the H![]() emission-line morphology.
Part of this arc lies within the 12CO(2-1) emission, while the excess to the
northwest is outside of it. There is also an extended F814W excess generally to the south,
leading to a lopsided appearance at this wavelength.
emission-line morphology.
Part of this arc lies within the 12CO(2-1) emission, while the excess to the
northwest is outside of it. There is also an extended F814W excess generally to the south,
leading to a lopsided appearance at this wavelength.
Figure 11 presents the CO intensity maps overlaid on the HST/WFPC2
V-I image described in Sect. 2.1.
The red V-I color delineating the spiral arm to the northwest is neatly traced
by the CO(1-0) emission.
This red arm connects to the CO spiral with a hook-like structure which winds
around the NW excess, following the CO emission to the nucleus.
The blue V-I colors of the F814W arc to the north of the AGN
suggest that it is tracing the same star-formation episode revealed by H![]() .
.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{8874fig9.ps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg80.gif) |
Figure 9:
a) Shows CO(1-0) total intensity contours overlaid on the
gray-scale residuals (in MJy/sr) of the bulge-disk decomposition performed on the 3.6 |
| Open with DEXTER | |
This northern arc of star formation was identified by Jogee et al. (1998) and Jogee et al. (1999),
and occurs roughly cospatially with an outflow thought to be driven by the starburst.
The outflow is seen at radio wavelengths and in optical emission lines
(Jogee et al. 1998; Boer et al. 1992; Saikia et al. 1994; Yoshida et al. 1999; Jogee et al. 1999).
It is relatively north-south symmetric in the 6 cm radio continuum (Saikia et al. 1994),
but has the form of a ``mushroom'' in the optical
(clearly illustrated by Fig. 8 in Jogee et al. 1999).
The arc defines the ``cap'' of the mushroom, and the slightly narrower
``stem'' extends southward, ending at the blue knot roughly ![]() 7
7
![]() south and 1
south and 1
![]() east of the nucleus.
This mushroom shape is not clearly seen in the V-I image.
The roughly normal V-I colors (
east of the nucleus.
This mushroom shape is not clearly seen in the V-I image.
The roughly normal V-I colors (![]() 0.8-1) to the south of the CO(2-1) emission
suggest that the unreddened stellar population of the bulge is obscuring
the star formation to the south,
a conclusion which we will motivate in the following.
0.8-1) to the south of the CO(2-1) emission
suggest that the unreddened stellar population of the bulge is obscuring
the star formation to the south,
a conclusion which we will motivate in the following.
The three-dimensional orientation of the galaxy disk can be inferred on the basis
of the red V-I colors in the extended spiral arm in the northwest.
The roughly symmetric spiral arm to the southeast is not reddened,
implying that the spiral structure to the northwest is being seen through an obscuring
dust lane, coplanar with the inclined stellar disk.
If this is true, then the north would be the near side of the disk, and the
south would be the far side.
This orientation would also mean that the spiral arms are trailing, which
is the most probable configuration.
The implication is that, toward the south, the stellar disk is seen through the
intervening bulge.
The relatively small bulge effective scalelength of 5
![]() -6
-6
![]() means that
means that
![]() 50% of the bulge light lies within the region of the CO emission.
To the south,
the bulge stars with normal V-I colors are overwhelming the young blue stars
in the star-formation event.
Hence, the southern part of the ``mushroom'' structure is not observed in V-I,
but in emission lines,
since the bulge is not expected to contain a significant amount of dust,
nor does it emit contaminating line emission.
To the south most of the bulge is in front of the intervening dust lane,
while to the north, dust obscures more of the bulge
because most of the bulge light is behind it.
This interpretation would also help explain the
F814W image with its apparent lopsidedness to the south.
In any case, the dust must be clumpy, and
inhomogeneities in the dust distribution
allow random regions behind the dust to shine through.
50% of the bulge light lies within the region of the CO emission.
To the south,
the bulge stars with normal V-I colors are overwhelming the young blue stars
in the star-formation event.
Hence, the southern part of the ``mushroom'' structure is not observed in V-I,
but in emission lines,
since the bulge is not expected to contain a significant amount of dust,
nor does it emit contaminating line emission.
To the south most of the bulge is in front of the intervening dust lane,
while to the north, dust obscures more of the bulge
because most of the bulge light is behind it.
This interpretation would also help explain the
F814W image with its apparent lopsidedness to the south.
In any case, the dust must be clumpy, and
inhomogeneities in the dust distribution
allow random regions behind the dust to shine through.
The AGN (dynamical center)
is located at the northwest border of a tiny red arc ![]() 80 pc to the southeast
(``parachute''-like, see Fig. 11).
In this region, there are broad H
80 pc to the southeast
(``parachute''-like, see Fig. 11).
In this region, there are broad H![]() lines which show considerable north-south asymmetry,
unlike the narrow component of the emission lines which is
relatively symmetric (Yoshida et al. 1999).
Interestingly, this red arc in the color map is at the same position as the
velocity discontinuities in the CO(2-1) spider diagrams (see Sect. 3.2).
Because of the feature's extremely small size, we can not make
any reliable statements, but speculate that it
could be the color (and kinematic) signature of a small-scale AGN outflow out of the
plane of the disk.
lines which show considerable north-south asymmetry,
unlike the narrow component of the emission lines which is
relatively symmetric (Yoshida et al. 1999).
Interestingly, this red arc in the color map is at the same position as the
velocity discontinuities in the CO(2-1) spider diagrams (see Sect. 3.2).
Because of the feature's extremely small size, we can not make
any reliable statements, but speculate that it
could be the color (and kinematic) signature of a small-scale AGN outflow out of the
plane of the disk.
![\begin{figure}
\par\includegraphics[width=8.8cm]{8874fig10.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg81.gif) |
Figure 10: a) 12CO(1-0) total intensity contoured over a false-color representation of the HST/WFPC2 F814W image of NGC 2782. b) The same for 12CO(2-1). In both panels, the AGN (dynamical center) position is marked with a star. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{8874fig11.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg82.gif) |
Figure 11: a) 12CO(1-0) total intensity contoured over a false-color representation of the HST/WFPC2 V-I image of NGC 2782. The spiral arm to the northwest is clearly traced by the CO(1-0) emission. b) The same for 12CO(2-1). In both panels, the AGN (dynamical center) position is marked with a star. |
| Open with DEXTER | |
Streaming motions along the bar led Jogee et al. (1999) to conclude that there could be
gas inflow feeding the starburst.
However, streaming motions by themselves do not imply any transfer of
angular momentum, nor can they be used to infer the direction of such transfer.
Hence,
we now examine the torques exerted by the stellar potential on the molecular gas
in NGC 2782, in order to assess whether the gas is, on average, flowing in or out.
Although our PdBI map recovers ![]() 65% of that from single-dish measurements,
in the following analysis what matters is the structured gas component.
The diffuse large-scale molecular gas contributes equal quantities of
positive and negative torques on the gas orbits; hence it does not
influence the net torque.
65% of that from single-dish measurements,
in the following analysis what matters is the structured gas component.
The diffuse large-scale molecular gas contributes equal quantities of
positive and negative torques on the gas orbits; hence it does not
influence the net torque.
There is no clear evidence for non-coplanarity of the CO nuclear bar+spiral and the
large-scale stellar disk.
The stellar bar is oriented at
![]() ,
and the kinematic major axis
at
,
and the kinematic major axis
at
![]() ,
somewhat hampering the identification of non-circular
motions.
Nevertheless, were the two structures to be non-coplanar,
we would expect to see some kinematic evidence which is not seen.
Hence, in disagreement with the schematic model presented by Yoshida et al. (1999),
in what follows, we
assume that all the flattened structures (nuclear CO spiral, nuclear stellar bar,
and outer stellar oval) lie within the same disk plane.
,
somewhat hampering the identification of non-circular
motions.
Nevertheless, were the two structures to be non-coplanar,
we would expect to see some kinematic evidence which is not seen.
Hence, in disagreement with the schematic model presented by Yoshida et al. (1999),
in what follows, we
assume that all the flattened structures (nuclear CO spiral, nuclear stellar bar,
and outer stellar oval) lie within the same disk plane.
To derive the torques exerted by the stars on the gas,
we adopt the method presented in García-Burillo et al. (2005) which relies on a stellar potential
![]() derived from a NIR image and on the gas response as inferred from the
CO maps.
We assume that the total mass is determined by the stars,
essentially invoking an extreme ``maximum disk'' solution (e.g., Kent 1987),
in which the gas self-gravity and the dark matter halo are neglected.
We further assume that the measured gas column density N(x,y) derived from the CO
total intensity maps is a reliable estimate of the probability of finding gas at (x,y)in the current epoch.
This is reasonable, namely that CO traces the total gas content,
since atomic gas in the nuclei
of galaxies is typically a very small fraction of the total gas mass.
derived from a NIR image and on the gas response as inferred from the
CO maps.
We assume that the total mass is determined by the stars,
essentially invoking an extreme ``maximum disk'' solution (e.g., Kent 1987),
in which the gas self-gravity and the dark matter halo are neglected.
We further assume that the measured gas column density N(x,y) derived from the CO
total intensity maps is a reliable estimate of the probability of finding gas at (x,y)in the current epoch.
This is reasonable, namely that CO traces the total gas content,
since atomic gas in the nuclei
of galaxies is typically a very small fraction of the total gas mass.
As emphasized in García-Burillo et al. (2005), a single key assumption underlies the validity of our estimate of angular momentum transfer in the gas: we implicitly assume that the gas response to the stellar potential is roughly stationary in the reference frame of the potential over a few rotation periods. This would not be the case in the presence of strong self-gravity in the gaseous components. However, otherwise, even in galaxies with several stellar pattern speeds at different radii in the disk, numerical simulations suggest that the gas response adjusts its response to the dominant stellar configuration at a given radius (see García-Burillo et al. 2005, and references therein).
The stellar potential in NGC 2782 was derived from the IRAC 3.6 ![]() m image by
first rebinning to 0
m image by
first rebinning to 0
![]() 15 pixels, then deprojecting with
a PA = 75
15 pixels, then deprojecting with
a PA = 75![]() and an inclination of 30
and an inclination of 30![]() .
To account for the vertical mass distribution,
the rebinned deprojected image was convolved with an isothermal plane
model of constant scale height
.
To account for the vertical mass distribution,
the rebinned deprojected image was convolved with an isothermal plane
model of constant scale height ![]() 1/12th of the radial disk scalelength
(e.g., Buta & Block 2001; Quillen et al. 1994).
Figure 12 shows the deprojected IRAC image,
with the 12CO(1-0) and 12CO(2-1) total intensity maps superimposed in
contours.
The orientations of the stellar outer oval and the nuclear oval/bar are clearly visible
even in the deprojected image and are marked with a solid line.
1/12th of the radial disk scalelength
(e.g., Buta & Block 2001; Quillen et al. 1994).
Figure 12 shows the deprojected IRAC image,
with the 12CO(1-0) and 12CO(2-1) total intensity maps superimposed in
contours.
The orientations of the stellar outer oval and the nuclear oval/bar are clearly visible
even in the deprojected image and are marked with a solid line.
![\begin{figure}
\par\includegraphics[width=9cm,angle=-90]{8874fig12.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg85.gif) |
Figure 12:
a) 12CO(1-0) total intensity contoured over a false-color
representation the IRAC 3.6 |
| Open with DEXTER | |
In the absence of extinction and stellar population gradients,
the mass-to-light ratio can be assumed to be constant across
this deprojected (face-on) galaxy image
(e.g., Freeman 1992; Persic et al. 1996);
the mass is therefore directly proportional to the 3.6 ![]() m
light distribution.
With this assumption, we derive the potential
m
light distribution.
With this assumption, we derive the potential ![]() by solving
the Poisson equation:
by solving
the Poisson equation:
![]() using a Fast Fourier Transform (FFT) technique on a
using a Fast Fourier Transform (FFT) technique on a
![]() Cartesian grid as in Combes et al. (1990).
Beyond a radius of 3.4 kpc,
Cartesian grid as in Combes et al. (1990).
Beyond a radius of 3.4 kpc, ![]() is set to 0, thus suppressing any
spurious m=4 terms in the derived potential.
This is adequate to compute
is set to 0, thus suppressing any
spurious m=4 terms in the derived potential.
This is adequate to compute ![]() in the central regions of the
galaxy sampled by the PdB CO(1-0) primary beam.
in the central regions of the
galaxy sampled by the PdB CO(1-0) primary beam.
Following Combes & Sanders (1981), we
then expand the potential ![]() in Fourier components:
in Fourier components:
![\begin{figure}
\par\includegraphics[width=6cm,angle=-90, bb=56 35 297 720]{8874fig13.ps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg95.gif) |
Figure 13:
a) The different normalised Fourier components Qm
(defined in Eq. (3), as the maximum tangential force, normalised to the
radial force), for the potential of NGC 2782, derived from the NIR image. The top solid
line is the total tangential force Qt,
the next solid line is Q2, the dashed line Q1, the dotted line Q3,
and the dotted-dashed one Q4.
b) The corresponding phases |
| Open with DEXTER | |
The angular derivative of the potential
![]() gives at each
location the torque field
per unit mass
gives at each
location the torque field
per unit mass
![]() ;
by definition
;
by definition ![]() is independent of
the gas distribution in the plane of the galaxy.
The azimuthal average of
is independent of
the gas distribution in the plane of the galaxy.
The azimuthal average of ![]() ,
using N(x,y) as the weighting function,
corresponds to the
global variation of the specific gas angular momentum transfer occurring at this
radius (
,
using N(x,y) as the weighting function,
corresponds to the
global variation of the specific gas angular momentum transfer occurring at this
radius (
![]() ).
The
).
The ![]() subscript indicates an azimuthal average, evaluated at a given
radius R(x,y).
For convenience of calculation on a pixelized image, we express the torques in
Cartesian coordinates.
subscript indicates an azimuthal average, evaluated at a given
radius R(x,y).
For convenience of calculation on a pixelized image, we express the torques in
Cartesian coordinates.
The rotation direction of the gas in the galaxy disk determines the sign of
![]() :
positive (negative) if the torque
drives the gas outward (inward) at (x,y).
To calculate the effective variations of angular momentum in the galaxy plane,
we then weight the torques by the gas column densities N(x,y) derived from the
12CO(1-0) and 2-1 lines:
:
positive (negative) if the torque
drives the gas outward (inward) at (x,y).
To calculate the effective variations of angular momentum in the galaxy plane,
we then weight the torques by the gas column densities N(x,y) derived from the
12CO(1-0) and 2-1 lines:
![]() .
Figure 14 shows the normalized version of these maps
.
Figure 14 shows the normalized version of these maps
![]() where we have divided
where we have divided
![]() by the azimuthal average of the gas density.
The
by the azimuthal average of the gas density.
The ![]() superscript indicates this normalized
superscript indicates this normalized ![]() ,
so that we can
use dimensionless quantities (both in Cartesian coordinates and below in polar ones).
Both panels in Fig. 14
show the typical ``butterfly'' diagram due to an m=2 perturbation
(e.g. Laurikainen & Salo 2002; Buta & Block 2001).
,
so that we can
use dimensionless quantities (both in Cartesian coordinates and below in polar ones).
Both panels in Fig. 14
show the typical ``butterfly'' diagram due to an m=2 perturbation
(e.g. Laurikainen & Salo 2002; Buta & Block 2001).
![\begin{figure}
\par\includegraphics[width=18cm]{8874fig14.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg103.gif) |
Figure 14:
a) 12CO(1-0) total intensity contoured over a false-color
representation of the torque maps |
| Open with DEXTER | |
The radial gas flow induced by the torques is estimated by azimuthally averaging the
effective variations of angular momentum density in the plane:
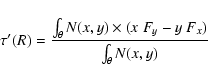 |
(3) |
![\begin{figure}
\par\includegraphics[width=8.8cm]{8874fig15.eps}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg113.gif) |
Figure 15:
a) The relative torque in dimensionless units
of
|
| Open with DEXTER | |
The other galaxies in the NUGA sample analyzed so far
(García-Burillo et al. 2005; Boone et al. 2007; García-Burillo et al. 2003; Combes et al. 2004) mainly show positive
torques near the nucleus, with negative torques at varying
amplitudes only for radii ![]() 500 pc.
Only in NGC 4579 are the average torques negative
down to 200 pc, but the spatial resolution of the torque map
for that galaxy is sufficiently good that
we can see that, inside that radius,
the gas is flowing away from the nucleus.
NGC 2782 is the first galaxy in our sample that shows systematically
negative torques down to the resolution limit imposed by
our torque image.
Moreover, in the entire region probed by our CO maps,
nowhere is the gas subjected to average positive torques.
The relatively poor resolution (1
500 pc.
Only in NGC 4579 are the average torques negative
down to 200 pc, but the spatial resolution of the torque map
for that galaxy is sufficiently good that
we can see that, inside that radius,
the gas is flowing away from the nucleus.
NGC 2782 is the first galaxy in our sample that shows systematically
negative torques down to the resolution limit imposed by
our torque image.
Moreover, in the entire region probed by our CO maps,
nowhere is the gas subjected to average positive torques.
The relatively poor resolution (1
![]() 2) of the potential map
(IRAC 3.6
2) of the potential map
(IRAC 3.6 ![]() m) makes it impossible to assess the torque amplitude
inside a radius of 200 pc
m) makes it impossible to assess the torque amplitude
inside a radius of 200 pc![]() .
Indeed, the slightly positive torques in Fig. 15
are unreliable, and may simply be an artefact of insufficient
spatial resolution.
Nevertheless, the systematically negative trend of the average torques
in NGC 2782 hints that gas is being transported tantalizingly close to the
AGN.
This gas is certainly fuelling the nuclear starburst, and may,
subsequently, be feeding the AGN.
In the following, we develop a dynamical scenario which will explain
why we think this occurs in NGC 2782.
.
Indeed, the slightly positive torques in Fig. 15
are unreliable, and may simply be an artefact of insufficient
spatial resolution.
Nevertheless, the systematically negative trend of the average torques
in NGC 2782 hints that gas is being transported tantalizingly close to the
AGN.
This gas is certainly fuelling the nuclear starburst, and may,
subsequently, be feeding the AGN.
In the following, we develop a dynamical scenario which will explain
why we think this occurs in NGC 2782.
Although the outer parts of NGC 2782 show
clear signs of a past interaction (tidal tails, distorted disk, stellar sheets),
the inner parts appear dynamically relaxed, not unexpectedly since
the dynamical timescale is shorter by one or two orders of magnitude at ![]() kpc,
than at
kpc,
than at ![]() kpc.
kpc.
The previous sections have shown that NGC 2782 contains
many features of a double-barred galaxy.
Although the nuclear bar is unfortunately almost aligned with the galaxy
line of nodes, the disk is nearly
face-on (30![]() ), which helps to distinguish the morphological
features.
In the near-infrared, there is
a nuclear stellar bar of radius
), which helps to distinguish the morphological
features.
In the near-infrared, there is
a nuclear stellar bar of radius ![]() 1 kpc,
embedded within an outer stellar oval of radius
1 kpc,
embedded within an outer stellar oval of radius ![]() 2.5 kpc.
This outer oval, which we will call the primary bar,
is oriented at
2.5 kpc.
This outer oval, which we will call the primary bar,
is oriented at
![]() ,
misaligned (and not quite perpendicular)
with the nuclear stellar bar at
,
misaligned (and not quite perpendicular)
with the nuclear stellar bar at
![]() .
The molecular gas distribution is mainly elongated along the nuclear bar,
and reveals two spiral features emerging from its ends,
aligned with the conspicuous dust lanes already noted by Jogee et al. (1998,1999).
These dust lanes are strikingly straight, reminiscent
of barred galaxies with dust lanes parallel to the bar,
but located on the bar's leading edge on either side of the nucleus.
We therefore interpret the large-scale CO(1-0) features corresponding to the
straight dust lanes as the gas response to the primary bar;
they have indeed a similar orientation.
The inner elongated molecular morphology, evident in both CO(1-0)
and CO(2-1), constitutes the gas response to the nuclear bar.
.
The molecular gas distribution is mainly elongated along the nuclear bar,
and reveals two spiral features emerging from its ends,
aligned with the conspicuous dust lanes already noted by Jogee et al. (1998,1999).
These dust lanes are strikingly straight, reminiscent
of barred galaxies with dust lanes parallel to the bar,
but located on the bar's leading edge on either side of the nucleus.
We therefore interpret the large-scale CO(1-0) features corresponding to the
straight dust lanes as the gas response to the primary bar;
they have indeed a similar orientation.
The inner elongated molecular morphology, evident in both CO(1-0)
and CO(2-1), constitutes the gas response to the nuclear bar.
The H![]() morphology is more puzzling, because of
a clumpy dust obscuration which masks part of it.
As noted by Jogee et al. (1998), there are two main features in H
morphology is more puzzling, because of
a clumpy dust obscuration which masks part of it.
As noted by Jogee et al. (1998), there are two main features in H![]() :
one is the outflow driven by the starburst, perpendicular to
the nuclear stellar bar, and aligned with the radio continuum outflow
(Saikia et al. 1994), and the other is the elongated ring,
of about 1 kpc in radius, encircling the nuclear bar. The ring
is particularly demarcated on the northern side, where it forms a
180
:
one is the outflow driven by the starburst, perpendicular to
the nuclear stellar bar, and aligned with the radio continuum outflow
(Saikia et al. 1994), and the other is the elongated ring,
of about 1 kpc in radius, encircling the nuclear bar. The ring
is particularly demarcated on the northern side, where it forms a
180![]() arc, making the structure resemble more a
half-ring or what we called the ``cap of the mushroom'' in Sect.
5. But there is also a southern equivalent (dubbed the
``mushroom stem''), largely obscured by dust.
Toward the west, there is a remarkable dust finger,
devouring the ring, which superposes quite well with the CO distribution
(see Fig. 11).
arc, making the structure resemble more a
half-ring or what we called the ``cap of the mushroom'' in Sect.
5. But there is also a southern equivalent (dubbed the
``mushroom stem''), largely obscured by dust.
Toward the west, there is a remarkable dust finger,
devouring the ring, which superposes quite well with the CO distribution
(see Fig. 11).
The two different H![]() components are well distinguished by
their different kinematics: large outflowing velocities in the
north-south component (bubble to the south in front of the dust lane, and
obscured flow in the north behind it),
and a normally rotating ring around the nuclear bar (Yoshida et al. 1999).
We interpret the low-velocity rotating component as
the nuclear ring, associated with the inner Lindblad resonance (ILR) of
the primary bar, and encircling the nuclear bar, i.e. close
to the corotation (CR) of the nuclear bar (more exactly at the UHR, or 4:1 resonance).
The dust features are more conspicuous toward
the north because the near side is the north side.
The bulge is more evident toward the south,
masking the dust obscuration from the disk's far side.
But this does not imply that there is no dust and gas
there, obscuring the southern half-ring in H
components are well distinguished by
their different kinematics: large outflowing velocities in the
north-south component (bubble to the south in front of the dust lane, and
obscured flow in the north behind it),
and a normally rotating ring around the nuclear bar (Yoshida et al. 1999).
We interpret the low-velocity rotating component as
the nuclear ring, associated with the inner Lindblad resonance (ILR) of
the primary bar, and encircling the nuclear bar, i.e. close
to the corotation (CR) of the nuclear bar (more exactly at the UHR, or 4:1 resonance).
The dust features are more conspicuous toward
the north because the near side is the north side.
The bulge is more evident toward the south,
masking the dust obscuration from the disk's far side.
But this does not imply that there is no dust and gas
there, obscuring the southern half-ring in H![]() :
on the contrary,
there is CO emission in this southern part, coinciding with
holes in the H
:
on the contrary,
there is CO emission in this southern part, coinciding with
holes in the H![]() distribution.
distribution.
The H![]() emission is the most intense in the partial ring, which lends support
to our ILR interpretation, since it is well-known
that resonances are locations where the gas is transiently stalled
due to the torques provided by the stellar bar. Thus, the gas has time to
form young stars, as typically revealed in many barred galaxies,
such as NGC 2997, NGC 4314, or NGC 4321 (Allard et al. 2006; Maoz et al. 1996; Benedict et al. 2002).
In the case of NGC 2782, because of the secondary bar,
gas is then driven further inward, as suggested by the CO
straight spiral arms (pitch angle close to 90
emission is the most intense in the partial ring, which lends support
to our ILR interpretation, since it is well-known
that resonances are locations where the gas is transiently stalled
due to the torques provided by the stellar bar. Thus, the gas has time to
form young stars, as typically revealed in many barred galaxies,
such as NGC 2997, NGC 4314, or NGC 4321 (Allard et al. 2006; Maoz et al. 1996; Benedict et al. 2002).
In the case of NGC 2782, because of the secondary bar,
gas is then driven further inward, as suggested by the CO
straight spiral arms (pitch angle close to 90![]() )
aligned
with the nuclear bar. This gas also forms stars, explaining the presence
of H
)
aligned
with the nuclear bar. This gas also forms stars, explaining the presence
of H![]() also in the nuclear disk.
also in the nuclear disk.
The dynamical scenario we propose to explain these main features is the following:
first a primary bar forms, most likely triggered by the interaction that gave rise
to the disturbed morphology in the outer parts of NGC 2782.
The gravity torques from this primary bar drive the gas inward, and
create a gaseous nuclear ring at its ILR. Intense star formation
gives rise to the H![]() nuclear ring, seen now as a sharp half-ring arc.
In the meantime, the gas inflow has weakened the primary bar
(e.g., Bournaud et al. 2005; Bournaud & Combes 2002),
and a nuclear bar has dynamically decoupled, rotating at a different pattern speed.
The two different pattern speeds are usually such that the corotation
of the nuclear bar corresponds to the ILR of the primary bar,
thus avoiding excessive chaos in the orbits (Friedli & Martinet 1993).
The nuclear bar then governs the gas inflow toward the center.
Instead of being stalled at the primary ILR, now the gas is subject
to the negative gravity torques of the secondary bar,
between its CR and its own ILR. This explains why we see
CO emission inside the ILR of the primary bar, and why the torques
computation reveals that gas is flowing inward toward the center.
nuclear ring, seen now as a sharp half-ring arc.
In the meantime, the gas inflow has weakened the primary bar
(e.g., Bournaud et al. 2005; Bournaud & Combes 2002),
and a nuclear bar has dynamically decoupled, rotating at a different pattern speed.
The two different pattern speeds are usually such that the corotation
of the nuclear bar corresponds to the ILR of the primary bar,
thus avoiding excessive chaos in the orbits (Friedli & Martinet 1993).
The nuclear bar then governs the gas inflow toward the center.
Instead of being stalled at the primary ILR, now the gas is subject
to the negative gravity torques of the secondary bar,
between its CR and its own ILR. This explains why we see
CO emission inside the ILR of the primary bar, and why the torques
computation reveals that gas is flowing inward toward the center.
This scenario is slightly different from one where the gas decouples from the stars to form a gaseous nuclear bar with a faster (Englmaier & Shlosman 2004) or slower (Heller et al. 2001) pattern speed than the primary bar. We propose here that the nuclear bar exists both in the stellar and gaseous components, and always with a higher pattern speed than the primary.
To better understand the physical mechanisms, and reproduce the observed morphology, we performed N-body simulations with stars and gas, including star formation. We believe that the nuclear bar decoupling is a disk phenomenon, occurring on short timescales, with little contribution of a slowly rotating spherical component, such as a bulge or dark matter halo, so we adopt the simplification of 2D simulations, with the spherical components added analytically. Self-gravity is included only for the disk (gas+stars).
The N-body simulations were carried out
using the FFT algorithm to solve the Poisson equation, with
two kinds of grids: Cartesian and polar,
the latter optimizing the spatial resolution toward the center.
The useful Cartesian grid was
![]() (or
(or
![]() in total
to avoid periodic images), with a total radius of 8 kpc. The cell size
is then 62 pc. The softening was taken as 250 pc, in order to roughly
reproduce the actual effective softening from the thickness of the disk.
The polar grid is composed of
in total
to avoid periodic images), with a total radius of 8 kpc. The cell size
is then 62 pc. The softening was taken as 250 pc, in order to roughly
reproduce the actual effective softening from the thickness of the disk.
The polar grid is composed of
![]() radial, and
radial, and
![]() azimuthal
separations. The radial spacing of the grid is exponential at large scales,
and linear at small scales, following the prescription by
Pfenniger & Friedli (1993).
The polar-grid cell size ranges from 10 pc at the center to
azimuthal
separations. The radial spacing of the grid is exponential at large scales,
and linear at small scales, following the prescription by
Pfenniger & Friedli (1993).
The polar-grid cell size ranges from 10 pc at the center to
![]() 1 kpc at the outskirts (at 22 kpc).
The minimum softening is also fixed
at 250 pc, and is larger in the outer regions.
The two different kinds of simulations, polar and Cartesian,
were performed separately, in order to gauge the effect of
different spatial resolution on the results;
both methods give similar outcomes.
1 kpc at the outskirts (at 22 kpc).
The minimum softening is also fixed
at 250 pc, and is larger in the outer regions.
The two different kinds of simulations, polar and Cartesian,
were performed separately, in order to gauge the effect of
different spatial resolution on the results;
both methods give similar outcomes.
The stellar component
is represented by 120 000 particles, and the gas component by 40 000.
Two rigid spherical potentials are added analytically, with a Plummer shape:
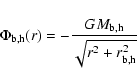
The stellar disk is initially a Kuzmin-Toomre disk of surface density:
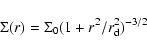
Table 1: Initial conditions parameters.
The gas is treated as a self-gravitating component in the N-body
simulation, and its dissipation is treated by a sticky particle code,
as in Combes & Gerin (1985). The initial gas-to-total mass ratio
(
![]() )
ranges between 5 and 10%.
Star formation is included, with a conventional Schmidt-law recipe,
although this will not be discussed here, since the timescales
are short enough that the gas depletion is not significant.
At the present time, the observed gas mass in NGC 2782 within a
)
ranges between 5 and 10%.
Star formation is included, with a conventional Schmidt-law recipe,
although this will not be discussed here, since the timescales
are short enough that the gas depletion is not significant.
At the present time, the observed gas mass in NGC 2782 within a ![]() 3 kpc
radius is about
3 kpc
radius is about
![]()
![]()
![]() .
The gas clouds are subject to inelastic collisions, with a collision
cell size of 67 pc for the Cartesian code,
and 117 pc for the polar code (region where particles are selected
to possibly collide). This corresponds to a lower limit for the average mean
free path of clouds between two collisions. The collisions are considered
every 2 Myr. In a collision, the sign of the relative
cloud velocities is reversed and the absolute values are reduced:
relative velocities after the collision are only 0.65 times their original value.
The dissipation rate is controlled by this factor.
All gas particles have the same mass.
.
The gas clouds are subject to inelastic collisions, with a collision
cell size of 67 pc for the Cartesian code,
and 117 pc for the polar code (region where particles are selected
to possibly collide). This corresponds to a lower limit for the average mean
free path of clouds between two collisions. The collisions are considered
every 2 Myr. In a collision, the sign of the relative
cloud velocities is reversed and the absolute values are reduced:
relative velocities after the collision are only 0.65 times their original value.
The dissipation rate is controlled by this factor.
All gas particles have the same mass.
The rotation curve corresponding to Run A
is plotted in comparison to the empirical RC (see Sect. 3.3)
in Fig. 16.
All other runs have similar rotation curves.
In the figure, we show the circular velocity
![]() deduced from the potential
(
deduced from the potential
(
![]() ).
In the range of 200-800 pc, there are non-circular
streaming motions (see Sect. 3.2)
which contribute to the derived empirical
).
In the range of 200-800 pc, there are non-circular
streaming motions (see Sect. 3.2)
which contribute to the derived empirical
![]() .
Indeed, we have calculated
.
Indeed, we have calculated
![]() of the gas from the model,
azimuthally averaged at a given radius, and find streaming motions of
amplitude similar to the observed discrepancies between the empirical RC as
traced by CO and the predicted
of the gas from the model,
azimuthally averaged at a given radius, and find streaming motions of
amplitude similar to the observed discrepancies between the empirical RC as
traced by CO and the predicted
![]()
![]() .
Given the uncertainties, and the asymmetry of the
two sides of the major axis (see Sect. 3.3),
all theoretical curves are compatible with the empirical ones.
The data points for the epicyclic frequency resonances, marked by
.
Given the uncertainties, and the asymmetry of the
two sides of the major axis (see Sect. 3.3),
all theoretical curves are compatible with the empirical ones.
The data points for the epicyclic frequency resonances, marked by ![]() and + in Fig. 16, are
calculated by numerically differentiating the smoothed empirical RC.
These data are also generally compatible
with the predictions of the numerical simulations.
and + in Fig. 16, are
calculated by numerically differentiating the smoothed empirical RC.
These data are also generally compatible
with the predictions of the numerical simulations.
![\begin{figure}
\par\includegraphics[width=8.8cm,bb=17 300 590 713]{8874fig16.ps}\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg133.gif) |
Figure 16:
Rotation and derived frequency curves |
| Open with DEXTER | |
Several runs have been carried out in order to test the various parameters, and evaluate the dependence of the results on the central mass concentration and on the initial gas mass fraction. These parameters are crucial for the nuclear bar decoupling. Only four of these models are displayed in Table 1.
We found that a high central mass concentration was
necessary to decouple the secondary bar, as already
shown by Friedli & Martinet (1993).
This can be understood because
the two pattern speeds are close to the precessing rates
of the supporting orbits, which are traced by the
![]() curve. A high mass concentration produces a marked maximum
of this curve in the center, with a large radial gradient
favorable to the decoupling.
Also, a high gas mass fraction of at least 5% of the total mass
is required for the decoupling. The nuclear bar is even
stronger with a gas fraction of 10%.
In Run B and D, with a scale-length of the bulge twice that
of Run A and C, the mass concentration was not enough to
produce the decoupling of the nuclear bar.
curve. A high mass concentration produces a marked maximum
of this curve in the center, with a large radial gradient
favorable to the decoupling.
Also, a high gas mass fraction of at least 5% of the total mass
is required for the decoupling. The nuclear bar is even
stronger with a gas fraction of 10%.
In Run B and D, with a scale-length of the bulge twice that
of Run A and C, the mass concentration was not enough to
produce the decoupling of the nuclear bar.
Run A, with a small bulge scalelength, and a high gas
mass fraction, provides the best fit for NGC 2782.
The stellar and gaseous morphologies are displayed in
Fig. 17 at three epochs, shortly after the second
bar decoupling.
As seen in Fig. 17,
between ![]() 700 and 750 Myr the gas is inflowing. Moreover,
the gas is always ``leading'' the stars, and thus is slowed down by
them.
700 and 750 Myr the gas is inflowing. Moreover,
the gas is always ``leading'' the stars, and thus is slowed down by
them.
![\begin{figure}
\par\rotatebox{0}{\includegraphics[angle=-90,width=18cm]{8874fig17.ps}}
\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg134.gif) |
Figure 17: Left panel: false-color plot of the stellar component distribution, in Run A (the intensity scale is linear and axes are in kpc). Middle: false-color plot of the corresponding gaseous component (the intensity scale is logarithmic). Right: same as the middle panel, but with an expanded spatial scale. It can be seen that the gas which was predominantly in the more external ring (ILR of the primary bar) at T = 690 Myr, is falling progressively inward, and is primarily inside the ILR at T=750 Myr. The gas infalling along the ``dust lanes'' is aligned along the nuclear bar, where the CO is observed in NGC 2782. |
| Open with DEXTER | |
The Fourier analysis of the gravitational potential
during the decoupling of the two bars clearly shows the development
of the two modes.
The Fourier analysis has been performed as a function of radius,
every 2 Myr, during 100 Myr in this period.
The Fourier transform of the results over
the time axis gives the pattern
speed as a function of radius, as shown in Fig. 18,
with a resolution in
![]() of 30 km s-1 kpc-1.
Of necessity, the temporal averaging must
be performed over the lifetime of the transient features;
this averaging ``thickens'' the value of
of 30 km s-1 kpc-1.
Of necessity, the temporal averaging must
be performed over the lifetime of the transient features;
this averaging ``thickens'' the value of
![]() in the plot
because of the time variation of the pattern speed of the nuclear bar.
in the plot
because of the time variation of the pattern speed of the nuclear bar.
![\begin{figure}
\par\rotatebox{-90}{\includegraphics[width=6.8cm]{8874fig18.ps}}\end{figure}](/articles/aa/full/2008/16/aa8874-07/Timg136.gif) |
Figure 18:
Left: intensity of the m=2 and m=4
Fourier components of the potential in Run A, during
the second bar decoupling.
Right: power spectrum of the m=2 Fourier component,
giving the pattern speed as a function of radius, during a
period of 100 Myr corresponding to the coexistence of the two bars.
Since the pattern speed of the nuclear bar varies with time
during this period, its
|
| Open with DEXTER | |
Figure 18 lets us unambiguously isolate two bars in the potential, dominated by the stellar component:
The previous simulations, adapted to the rotation curve
of NGC 2782, support the scenario proposed in Sect. 7.1.
A primary bar, perhaps triggered by the past interaction, has driven gas
toward its ILR, and while this bar was weakening, a secondary embedded bar
has decoupled,
prolonging the gas inflow inside the ILR ring, which is now
conspicuous in star formation and H![]() emission. The gas has
been driven into two spiral arms, aligned with the nuclear bar,
and is now winding up to the ILR of the nuclear bar, i.e. at
about 200-300 pc radius.
This scenario allows a coherent interpretation of the low-velocity H
emission. The gas has
been driven into two spiral arms, aligned with the nuclear bar,
and is now winding up to the ILR of the nuclear bar, i.e. at
about 200-300 pc radius.
This scenario allows a coherent interpretation of the low-velocity H![]() component and the entire CO morphology, as well as of our finding of
negative gravity torques.
In NGC 2782, there seems to be a ``smoking gun'', namely
the presence of molecular gas inside the ILR
of the primary bar, made possible by the decoupling of a secondary nuclear
bar from the primary one.
The gas there is certainly fueling
the central starburst, at the origin of the ionized gas bubble,
and in a second step should fuel directly the AGN.
The timescales in this central region are
quite short, about 6 Myr for the gas rotation period at 300 pc.
Dynamical friction and viscous torques can then relatively
quickly provide gas to fuel the AGN (García-Burillo et al. 2007,2005),
although the present simulations
do not have enough spatial resolution to simulate that realistically.
Alternatively, the ILR of the nuclear bar suggested by our models
could impede further gas inflow inside the resolution limit of our images.
component and the entire CO morphology, as well as of our finding of
negative gravity torques.
In NGC 2782, there seems to be a ``smoking gun'', namely
the presence of molecular gas inside the ILR
of the primary bar, made possible by the decoupling of a secondary nuclear
bar from the primary one.
The gas there is certainly fueling
the central starburst, at the origin of the ionized gas bubble,
and in a second step should fuel directly the AGN.
The timescales in this central region are
quite short, about 6 Myr for the gas rotation period at 300 pc.
Dynamical friction and viscous torques can then relatively
quickly provide gas to fuel the AGN (García-Burillo et al. 2007,2005),
although the present simulations
do not have enough spatial resolution to simulate that realistically.
Alternatively, the ILR of the nuclear bar suggested by our models
could impede further gas inflow inside the resolution limit of our images.
According to our simulations, there are two salient characteristics
of NGC 2782 which lead to the secondary bar decoupling,
and the ensuing negative torques.
The first is its conspicuous stellar bulge, as suggested by the bulge-disk
decomposition described in Sect. 4.1.
This is the biggest contributor to the central mass concentration,
and the likely cause of the resonances that give rise to the gas
buildup in the rings, with the subsequent decoupling of the secondary
nuclear bar.
The second feature is the particularly high gas mass fraction in NGC 2782.
As discussed in Sect. 3.1, the mass of the
molecular gas in NGC 2782 is the most extreme of all the NUGA galaxies
observed so far;
within a region ![]() 4 kpc in diameter, the molecular gas
comprises 7% of
4 kpc in diameter, the molecular gas
comprises 7% of
![]() .
This centrally concentrated molecular gas could be the result of
the interaction which NGC 2782 has undergone.
A high gas mass fraction is a necessary condition
for the decoupling of the secondary bar, and thus promotes infall.
Finally, we could be observing NGC 2782 in a particularly favorable
epoch for the fueling of its AGN.
Future work on our statistical sample will help understand duty cycles
and timescales for the creation and maintenance of active accretion
in galactic nuclei.
.
This centrally concentrated molecular gas could be the result of
the interaction which NGC 2782 has undergone.
A high gas mass fraction is a necessary condition
for the decoupling of the secondary bar, and thus promotes infall.
Finally, we could be observing NGC 2782 in a particularly favorable
epoch for the fueling of its AGN.
Future work on our statistical sample will help understand duty cycles
and timescales for the creation and maintenance of active accretion
in galactic nuclei.
We summarize our main results as follows:
Acknowledgements
L.K.H. sincerely thanks the LERMA-Observatoire de Paris for generous funding and kind hospitality during the writing of this paper. We would like to thank the anonymous referee for insightful questions which helped clarify the text. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.