A&A 482, 341-347 (2008)
DOI: 10.1051/0004-6361:20078833
A. S. Bonomo1,2 - A. F. Lanza2
1 - Dipartimento di Fisica e Astronomia, Sezione Astrofisica, Università degli Studi di Catania, Italy
2 -
INAF - Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
Received 11 October 2007 / Accepted 20 February 2008
Abstract
Aims. We present a comparison of two methods of fitting solar-like variability to increase the efficiency of the detection of Earth-like planetary transits across the disc of a Sun-like star. One of them is the harmonic fitting method that coupled with the Box fitting Least-Square (BLS) detection algorithm demonstrated the best performance during the first CoRoT blind test.
Methods. We apply a Monte Carlo approach by simulating a large number of light curves of duration 150 days for different values of planetary radius, orbital period, epoch of the first transit, and standard deviation of the photon shot noise. Stellar variability is assumed in all the cases to be given by the Total Solar Irradiance variations as observed close to the maximum of solar cycle 23. After fitting solar variability, transits are searched for by means of the BLS algorithm.
Results. We find that a model based on three point-like active regions reduces the impact of stellar microvariability more effectively than a best fit with a linear combination of 200 harmonic functions provided that the standard deviation of the noise is 2-4 times larger than the central depth of the transits. On the other hand, the 200-harmonic fit is better when the standard deviation of the noise is comparable to the transit depth.
Conclusions. Our results show the advantage of a model that includes a simple but physically motivated treatment of stellar microvariability for the detection of planetary transits, when the standard deviation of the photon shot noise is greater than the transit depth and stellar variability is analogous to solar irradiance variations.
Key words: planetary systems - methods: data analysis - techniques: photometric - stars: activity - stars: late-type
Since the pioneering work by Mayor & Queloz (1995), about 270 extrasolar planets
have been discovered, mostly through the periodic oscillations of the radial
velocity of their parent stars![]() . About 35
show transits across the disc of their stars allowing us to remove
degeneracy between orbital inclination and amplitude of the radial velocity curve,
thus providing information on planet's mass and radius. Transit searches from the ground are limited to giant planets because their photometric precision cannot be pushed beyond the millimagnitude limit due to the scintillation of the Earth's atmosphere.
This limitation can be overcome by space-borne telescopes. The space missions
CoRoT and Kepler have been specifically designed for searching planetary transits and
can reach the photometric precision to detect transits of terrestrial planets
in front of late-type main-sequence stars (Baglin 2003; Moutou et al. 2005; Borucki et al. 2004).
. About 35
show transits across the disc of their stars allowing us to remove
degeneracy between orbital inclination and amplitude of the radial velocity curve,
thus providing information on planet's mass and radius. Transit searches from the ground are limited to giant planets because their photometric precision cannot be pushed beyond the millimagnitude limit due to the scintillation of the Earth's atmosphere.
This limitation can be overcome by space-borne telescopes. The space missions
CoRoT and Kepler have been specifically designed for searching planetary transits and
can reach the photometric precision to detect transits of terrestrial planets
in front of late-type main-sequence stars (Baglin 2003; Moutou et al. 2005; Borucki et al. 2004).
The main source of noise in the detection of terrestrial planet transits at the level of precision of space-borne photometry is the intrinsic variability of the parent star. For late-type stars having an outer convection zone, magnetic activity is the main source of variability and can severely limit the capability of detecting transits even in relatively inactive stars. In the case of the Sun, the transit of a large sunspot group across the disc produces a dip of the solar irradiance of 2000-2500 parts per million (ppm), whereas the central transit of an earth-sized planet produces a flux decrease of only 84 ppm (Jenkins 2002). During phases of minimum activity, even when no sizeable spot group is detected, the solar flux is modulated by faculae, with amplitudes usually exceeding 100-200 ppm.
![\begin{figure}
\par\includegraphics[height=14.6cm,width=5.3cm,angle=90,clip]{8833f1.ps}\end{figure}](/articles/aa/full/2008/16/aa8833-07/Timg9.gif) |
Figure 1: The Total Solar Irradiance time series (level 2.0 data of the VIRGO experiment) used to simulate Sun-like microvariability in the present investigation. Small horizontal red dashes at the bottom of the plot mark gaps in the time series. |
| Open with DEXTER | |
In principle, the extraction of the transit signal from a light curve contaminated by stellar microvariability is possible thanks to the different timescales characterizing transit duration and stellar variability. Specifically, the former ranges from a few hours to about one day, in the case of terrestrial planets with orbital periods up to about one year around a solar-like star, while the latter is dominated by the rotational modulation of the largest active regions and their evolution, taking place on time scales from weeks to months in the case of the Sun (cf., e.g., Lanza et al. 2007; Jenkins 2002; Lanza et al. 2003, and references therein).
Several methods have been proposed to reduce the impact of solar-like variability on transit detection, starting from simple high-pass filters (Defaÿ et al. 2001) to optimal filters (Jenkins et al. 2002; Carpano et al. 2003). Those methods work well only for continuous, evenly sampled timeseries because gaps or irregular sampling introduce aliasing problems. Moreover, optimal filters need a sufficiently long timeseries to estimate the power spectrum of the intrinsic stellar variability from the data themselves to construct the filter. For a slowly rotating star such as the Sun, this implies a time series of at least two or three months, given that most of the variability is on rotational timescales. Recently Aigrain & Irwin (2004) have proposed methods to overcome the difficulties due to irregular sampling or gaps, based on a least-square fit of individual sine and cosine components or on the application of iterative non-linear filters.
The first CoRoT blind test (Moutou et al. 2005) represented a testbed for several different methods to treat solar-like variability and showed the potentiality of those methods in combination with suitable transit finding algorithms to detect transits in a set of one thousand simulated light curves also including gaps and instrumental effects. The best method to remove stellar microvariability proved to be a best fit based on the use of 200 sine and cosine harmonic functions coupled with the BLS transit finder algorithm (Kovács et al. 2002) proposed by the Geneva team.
In the present paper, we propose a different method to treat stellar variability, based on our model of the Total Solar Irradiance (TSI) variations (Lanza et al. 2007,2003). Previous models do not exploit knowledge of the cause of the variation, that is the intrinsic evolution and the rotational modulation of the visibility of active regions, while our model includes such effects. The residuals obtained after subtracting our model have a maximum amplitude of 100-150 ppm and an almost Gaussian distribution (cf. Lanza et al. 2003, and Sect. 3.1), suggesting us to apply algorithms developed for the detection of planetary transits in the presence of a Gaussian white noise. The performance of the proposed approach will be compared with that of the 200-harmonic best-fit algorithm of the CoRoT blind test to establish advantages and limitations of the new method. Moreover, other methods will be briefly discussed in Sect. 5, deferring a detailed comparison to successive papers.
To assess the performance of the proposed method, we shall analyse an extensive set of simulated light curves. Each light curve includes flux variations produced by Sun-like activity, planetary transits, and photon shot noise, respectively.
To simulate the effects of Sun-like activity, we choose a subset of the TSI variation of duration 170 days ranging from January 1![]() to June 19
to June 19![]() 2001 as observed by the radiometers of the VIRGO experiment on board of the SoHO satellite
(Fröhlich et al. 1997,1995, see Fig. 1). Specifically,
we use the 2.0-level TSI time series with a time sampling of one value per hour, accessible
from the VIRGO web site at the Physikalisch-Meteorologisches Observatorium
Davos - World Radiation Center
2001 as observed by the radiometers of the VIRGO experiment on board of the SoHO satellite
(Fröhlich et al. 1997,1995, see Fig. 1). Specifically,
we use the 2.0-level TSI time series with a time sampling of one value per hour, accessible
from the VIRGO web site at the Physikalisch-Meteorologisches Observatorium
Davos - World Radiation Center![]() . The standard deviation of the
hourly TSI data is 20 ppm. Short quasi-periodic gaps, not exceeding a few hours, are present in the TSI time series and are retained in our simulations as representative of the gaps expected for a space-borne photometric experiment. Their total duration is 36 h, i.e., 0.9 percent of the time series (see Fig. 1).
. The standard deviation of the
hourly TSI data is 20 ppm. Short quasi-periodic gaps, not exceeding a few hours, are present in the TSI time series and are retained in our simulations as representative of the gaps expected for a space-borne photometric experiment. Their total duration is 36 h, i.e., 0.9 percent of the time series (see Fig. 1).
The considered time series falls close to the maximum of activity cycle 23 and shows flux variations up to 2600 ppm due to the transits of large active regions across the solar disc. Therefore, this time series is well suited to study the impact of the largest Sun-like variability on planetary transit detection. Note that the level of activity of the Sun at the maximum of the 11-yr cycle is close to the median activity level of field dwarf stars of spectral types F and G, as found by Schmitt (1997) by comparing their coronal X-ray fluxes.
We prefer to use real solar irradiance data instead of simulating stellar microvariability with the approaches proposed by, e.g., Aigrain et al. (2004) or Lanza et al. (2006). Actually, those models are based on extrapolations of the solar variability characteristics to the case of more active stars and cannot be tested observationally yet.
To simulate stellar variability for intervals of 150 days, such as those of the long runs of the space experiment CoRoT, we extract 150-d sections of the above TSI time series choosing starting points at random between 0 and 20 days. In this way, we get different realisations of Sun-like activity, reducing possible systematic effects associated with the variations contained in a fixed TSI subset (cf. Sect. 3.1).
We computed light curves of planetary transits by means of the IDL procedure
Universal Transit Modeller (UTM) (Deeg 1999).
We consider circular planetary orbits with periods of 5, 10, 25, and 50 days, and an inclination of
![]() ,
i.e., the planet transits across the centre of the disc of the star.
The radius of the planet is varied between 1.0 and 2.0
,
i.e., the planet transits across the centre of the disc of the star.
The radius of the planet is varied between 1.0 and 2.0
![]() in steps of
in steps of
![]() .
A radius of 1
.
A radius of 1 ![]() and a mass of 1
and a mass of 1 ![]() are assumed for the star and
a quadratic limb-darkening law is adopted for the stellar photosphere.
Therefore, the duration of the transits ranges from 3.11 h for an orbital period of 5 days up to 6.67 h for a period of 50 days.
are assumed for the star and
a quadratic limb-darkening law is adopted for the stellar photosphere.
Therefore, the duration of the transits ranges from 3.11 h for an orbital period of 5 days up to 6.67 h for a period of 50 days.
In this way, we have simulated a total of 20 different transit light curves. Finally, we shift the initial transit to a random phase between 0.0 and 1.0, taken from a uniform distribution, and add stellar variability and photon shot noise, assuming that Poisson statistics can be well approximated by Gaussian statistics at the photon count levels characteristic of planetary transit searches. We consider four levels of noise, i.e., with standard deviations of 100, 200, 300, and 1000 ppm, which correspond approximately to the noise levels reached in one-hour integration time for G2V stars of magnitudes V = 12, 13, 14, and 16 as observed by CoRoT, respectively![]() .
One hundred independent white Gaussian noise realisations are computed
for each value of the standard deviation and added to each of the noiseless light curves giving a total of 8000 light curves with transits.
.
One hundred independent white Gaussian noise realisations are computed
for each value of the standard deviation and added to each of the noiseless light curves giving a total of 8000 light curves with transits.
In a search for planetary transits it is important to estimate the number of false alarms produced by those random combinations of the noise that may approximate a transit feature (see Doyle et al. 2000, and Sect. 4). We determine the frequency of false alarms by analysing transitless light curves obtained by combining solar irradiance variations with 100 random sequences for each of the above noise standard deviations, for a total of 400 light curves.
The simulated light curves are analysed in two steps. First, we fit stellar microvariability by applying our model based on three active regions (hereinafter 3-spot model; Lanza et al. 2003) and the model proposed by the Geneva team for the CoRoT blind test, based on a least-square fit with harmonic functions (hereinafter 200-harmonic fitting; Moutou et al. 2005). Next, we apply the Box-fitting Least Square algorithm (or BLS; Kovács et al. 2002) to search for transits in the time series of the residuals obtained with the two different variability models to see which one gives the best performance in terms of detected transits and reduced false alarms. The residuals of the transitless light curves are analysed in the same way to find the frequency of false alarms produced by noise.
The model is described by Lanza et al. (2003), and its performance is studied in detail by Lanza et al. (2007,2003) in the case of the Sun at different phases of the 11-yr cycle. Therefore, we limit ourselves to a brief introduction. The model makes use of three active regions, containing both cool spots and warm faculae, to fit the rotational modulation of the TSI, and a uniformly distributed background component to fit the variation of its mean level along the 11-yr cycle. The ratio of the area of the faculae to that of the sunspots in each active region is fixed.
The rotation period
![]() is assumed as a free parameter ranging from 23.0 to 33.5 days,
and its value is determined, together
with the other free parameters, by minimizing the
is assumed as a free parameter ranging from 23.0 to 33.5 days,
and its value is determined, together
with the other free parameters, by minimizing the ![]() (see Lanza et al. 2003).
The inclination of the rotation axis i is set at the solar value during the fitting
process. Considering also the mean flux level, the areas and the co-ordinates of the three active regions, the number of free parameters is eleven.
(see Lanza et al. 2003).
The inclination of the rotation axis i is set at the solar value during the fitting
process. Considering also the mean flux level, the areas and the co-ordinates of the three active regions, the number of free parameters is eleven.
The timescale of evolution of the active region pattern on the Sun is significantly
shorter than the rotation period. The longest time interval that can be modelled with three stable active regions is 14 days (cf. Lanza et al. 2003).
Hence, the time series is subdivided into subsets of
14 days, each of which is fitted with the model described above.
The duration of a transit is at least one
order of magnitude shorter than the timescale of variation of the active region
configuration, ensuring that the model is not significantly affected by transit dips.
Small discontinuities at the level of ![]() 30-50 ppm are sometimes present at the matching points between successive 14-d best fits. Their impact on our results is minimized by the random choice of the origin of the TSI time series used to simulate
stellar activity, ensuring that those features never fall at the same points of the solar variation series.
30-50 ppm are sometimes present at the matching points between successive 14-d best fits. Their impact on our results is minimized by the random choice of the origin of the TSI time series used to simulate
stellar activity, ensuring that those features never fall at the same points of the solar variation series.
In Fig. 2, we plot, with solid lines, the distributions of the residuals of the best fit to the TSI from 6 February 1996 to 6 February 2007, distinguishing three time intervals corresponding to the minimum, intermediate, and maximum levels of activity along solar cycle 23, respectively. The distributions are well approximated by Gaussians except in the tails that appear slightly higher than a normal distribution. Power spectra of the residuals are plotted in Fig. 3 (left panel), revealing a characteristic inverse dependence on frequency up to 0.25 h-1 (Jenkins 2002), and an almost white spectrum at higher frequencies. Note the high level of power during the intermediate phase of cycle 23 owing to the appearance of large sunspot groups in the decaying phase of the cycle.
![\begin{figure}
\par\includegraphics[height=9.6cm,width=7.4cm,clip]{8833f2.ps}\end{figure}](/articles/aa/full/2008/16/aa8833-07/Timg20.gif) |
Figure 2:
Distributions of the residuals of the TSI best fit along solar cycle 23 obtained with the 3-spot model (solid black histograms) and the 200-harmonic fitting (dashed green histograms) for the three labelled time intervals corresponding to the minimum ( top panel), intermediate ( middle panel) and maximum ( bottom panel) of activity. Solid-black lines and green-dashed lines are Gaussian best fits to the 3-spot and the 200-harmonic residual distributions, respectively. The standard deviations of the Gaussian best fits are
indicated in the panels with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=13cm,width=6.6cm,angle=90,clip]{8833f3.ps}\end{figure}](/articles/aa/full/2008/16/aa8833-07/Timg21.gif) |
Figure 3: Power spectra of the residuals of the TSI best fit obtained with the 3-spot model ( left panel) and the 200-harmonic fitting ( right panel). Different linestyles and colors indicate different levels of activity: black-solid line: maximum; green-dashed line: intermediate; and, red-dotted line: minimum. |
| Open with DEXTER | |
Stellar variability is modelled as a sum of harmonics of a fundamental frequency
![]() ,
where T is the whole duration of each time series, i.e.,
,
where T is the whole duration of each time series, i.e.,
![]() 150 days. The number of considered harmonics is fixed at
150 days. The number of considered harmonics is fixed at
![]() ,
so the highest
frequency in the model corresponds to a period of 1.5 days, well below the frequency range where most of the transit power is concentrated. Therefore, the fitting technique is not expected to greatly affect the transit signal. The model flux at time ti is given by:
,
so the highest
frequency in the model corresponds to a period of 1.5 days, well below the frequency range where most of the transit power is concentrated. Therefore, the fitting technique is not expected to greatly affect the transit signal. The model flux at time ti is given by:
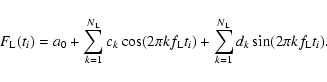 |
(1) |
The distributions of the residuals are well approximated by Gaussians except in the tails that appear slightly higher than a normal distribution (see Fig. 2, dashed green plots). Their standard deviations are smaller than those of the residuals obtained with the 3-spot model. Power spectra of the residuals are plotted in Fig. 3 (right panel), and are similar to those obtained with the 3-spot model, except for the cutoff at a frequency corresponding to the period of 1.5 days.
We analyse the time series of the residuals obtained by the above fitting approaches to detect
transits by means of the BLS algorithm. It assumes that transits are strictly periodic with a period P and that the noiseless time series assumes only two values, i.e., H outside of transits and L inside transits. In other words, each transit is assumed to have a simple box-shaped profile, that is enough for detection purposes.
The time spent in transit at the level L is qP, where the fractionary transit length q is a small number
![]() .
The time of the first transit in the time series is indicated by t0. In the presence of a white Gaussian noise with a constant standard deviation
.
The time of the first transit in the time series is indicated by t0. In the presence of a white Gaussian noise with a constant standard deviation ![]() ,
assuming that the average level of the time series is zero, the algorithm aims to find the
best model by an estimation of the four free parameters P, q,
,
assuming that the average level of the time series is zero, the algorithm aims to find the
best model by an estimation of the four free parameters P, q,
![]() ,
and t0 that minimize the
,
and t0 that minimize the ![]() between the model and the data.
We refer the reader to Kovács et al. (2002) for further details.
Here we note only that a useful measure of the signal-to-noise ratio of a transit detection is given by:
between the model and the data.
We refer the reader to Kovács et al. (2002) for further details.
Here we note only that a useful measure of the signal-to-noise ratio of a transit detection is given by:
The implementation of the BLS algorithm is performed by means of the Fortran subroutine accessible
at http://www.konkoly.hu/staff/kovacs.html. We modified it slightly to avoid negative values of ![]() that would correspond to periodic positive spikes, retaining only best fits with a positive value of
that would correspond to periodic positive spikes, retaining only best fits with a positive value of ![]() that correspond to transit dips. The parameter space is searched for transits with a period P between 1 and 150 days, with 30 000 values of
the frequency uniformly spaced between
that correspond to transit dips. The parameter space is searched for transits with a period P between 1 and 150 days, with 30 000 values of
the frequency uniformly spaced between
![]() and 1 day-1; the fractionary length of the transit q is varied between 0.002 and 0.08, assuming a number of 700 phase bins in the light curve folded at each trial period. Such a sampling of the parameter space ensures that none of the simulated transits will get lost because of
an inappropriate choice of the free parameters in our search
(for an optimal choice of the free parameter steps and ranges
see, e.g., Kovács et al. 2002; Jenkins et al. 2002; Doyle et al. 2000).
and 1 day-1; the fractionary length of the transit q is varied between 0.002 and 0.08, assuming a number of 700 phase bins in the light curve folded at each trial period. Such a sampling of the parameter space ensures that none of the simulated transits will get lost because of
an inappropriate choice of the free parameters in our search
(for an optimal choice of the free parameter steps and ranges
see, e.g., Kovács et al. 2002; Jenkins et al. 2002; Doyle et al. 2000).
We managed the large computational load of our experiment by running our analyses on
a large grid infrastructure consisting of three high-performance computing nodes
located in Catania, Palermo, and Messina. The total number of CPUs is 560, each one being
an AMD Opteron dual-core 64-bit processor with 1 or 2 GB of RAM (Becciani 2007).
The CPU time for fitting solar variability and performing transit search was on the average
![]() 11 min per light curve with the 3-spot method and
11 min per light curve with the 3-spot method and ![]() 4 min per light curve with the 200-harmonic method, while about 2.5 days of elapsed time were necessary to analyse our
complete set of 8000 light curves.
4 min per light curve with the 200-harmonic method, while about 2.5 days of elapsed time were necessary to analyse our
complete set of 8000 light curves.
A typical sample of our results is given in Fig. 4, where
the distributions of the values of ![]() are plotted for simulations with a planet of
are plotted for simulations with a planet of
![]() ,
the labelled values of the orbital period P, and a standard
deviation of the noise
,
the labelled values of the orbital period P, and a standard
deviation of the noise
![]() ppm. The vertical dash-dotted lines indicate the false-alarm thresholds for the 200-harmonic fitting
ppm. The vertical dash-dotted lines indicate the false-alarm thresholds for the 200-harmonic fitting
![]() and for the 3-spot model
and for the 3-spot model
![]() ,
respectively. They are derived from the analysis of the transitless
light curves under the requisite that the frequency of false alarms be
,
respectively. They are derived from the analysis of the transitless
light curves under the requisite that the frequency of false alarms be
![]() 0.01 (i.e, not exceeding one in a hundred).
0.01 (i.e, not exceeding one in a hundred).
The histograms in Fig. 4 show the distributions of ![]() for the cases where the orbital period of the planet was correctly identified or incorrectly identified, respectively. For a correct identification of the period, we require that
the orbital period given by the BLS routine is within
for the cases where the orbital period of the planet was correctly identified or incorrectly identified, respectively. For a correct identification of the period, we require that
the orbital period given by the BLS routine is within ![]() 0.1 days from the true period.
When the period is correctly identified and
0.1 days from the true period.
When the period is correctly identified and
![]() ,
we count the detection as a positive one. Note that very few cases with
,
we count the detection as a positive one. Note that very few cases with
![]() and P outside of the acceptable range are visible in the panels of
Fig. 4. These are not counted as positive detections.
and P outside of the acceptable range are visible in the panels of
Fig. 4. These are not counted as positive detections.
![\begin{figure}
\par\includegraphics[height=7.6cm,width=9.2cm,angle=90,clip]{8833f4.ps}\end{figure}](/articles/aa/full/2008/16/aa8833-07/Timg41.gif) |
Figure 4:
Distributions of the values of |
| Open with DEXTER | |
The frequencies of positive detections obtained for different values of planetary radius,
orbital period, and noise level are reported in Table 1, omitting records for values of ![]() giving no detections, except for the cases with the smallest orbital periods.
In the first column, we list the planetary radius R; in the second, the
standard deviation of the Gaussian photon shot noise
giving no detections, except for the cases with the smallest orbital periods.
In the first column, we list the planetary radius R; in the second, the
standard deviation of the Gaussian photon shot noise ![]() ;
in the third, the orbital period P; in the fourth, the frequency of positive detections with the 200-harmonic method
;
in the third, the orbital period P; in the fourth, the frequency of positive detections with the 200-harmonic method ![]() ;
and in the fifth, the frequency of positive detections with the 3-spot method
;
and in the fifth, the frequency of positive detections with the 3-spot method
![]() ,
respectively. We note that for a noise standard deviation of 100 ppm, the 200-harmonic
method is better than the 3-spot method, especially for planetary radii
,
respectively. We note that for a noise standard deviation of 100 ppm, the 200-harmonic
method is better than the 3-spot method, especially for planetary radii
![]() .
On the other hand, for higher noise levels (
.
On the other hand, for higher noise levels (
![]() ppm), the 3-spot method gives a better performance than the 200-harmonic
method, especially for planetary radii
ppm), the 3-spot method gives a better performance than the 200-harmonic
method, especially for planetary radii
![]() .
.
As an illustrative application of our results, let us
consider, e.g., a G2V star of V=12 observed in the CoRoT white-light exochannel with an
integration time of one hour. In this case,
![]() ppm and
planets with radii as small as
ppm and
planets with radii as small as
![]() and orbital period
and orbital period ![]() days should be detectable in more than
95 percent of the cases if stellar variability
and photon shot noise are the only effects limiting photometric precision. However, a proper assessment of the performance of a given space instrument should also consider other effects
(see Moutou et al. 2005; Bordé et al. 2003), which goes beyond the purpose of the present study aimed
at comparing different stellar activity fitting methods.
days should be detectable in more than
95 percent of the cases if stellar variability
and photon shot noise are the only effects limiting photometric precision. However, a proper assessment of the performance of a given space instrument should also consider other effects
(see Moutou et al. 2005; Bordé et al. 2003), which goes beyond the purpose of the present study aimed
at comparing different stellar activity fitting methods.
Table 1: Fraction of positive detections obtained in our experiment.
The results presented above prompted us to investigate the cause of the
different performance of the two methods at different levels of noise and
planetary radii. We found that the 200-harmonic method, having 401 degrees of freedom to fit the entire 150-d sequence, is better suited to reproduce the flux
perturbations due to magnetic activity and noise than the 3-spot method, which has only 11 free parameters for each 14-d best fit (cf. Figs. 2 and 3).
However, the use of a set of orthogonal functions to fit stellar variability
produces a significant distortion of the planetary transits in the residual
light curves. In particular, the depth of the transits is reduced, as it is clear by
considering the best fits obtained in the case of a light curve containing only transits
(cf. Fig. 5). This is a consequence of the well-known Gibbs phenomenon
(e.g., Morse & Feshbach 1954). Since the transit dip is mathematically
similar to a couple of close discontinuities of the first kind, the fitting function, which is
a truncated series of orthogonal trigonometric functions, overshoots the flux variation at the
ingress and at the bottom of the transit leading to a reduction of its
depth ![]() in the residual curve. Note that the problem is not alleviated by increasing
the order NL of the fitting functions because it is a consequence of the orthogonal nature of
the adopted set of fitting functions (cf. Morse & Feshbach 1954). When the standard deviation of the noise is small (
in the residual curve. Note that the problem is not alleviated by increasing
the order NL of the fitting functions because it is a consequence of the orthogonal nature of
the adopted set of fitting functions (cf. Morse & Feshbach 1954). When the standard deviation of the noise is small (
![]() ppm), the reduction of
ppm), the reduction of ![]() does not
greatly affect the detection efficiency because
does not
greatly affect the detection efficiency because ![]() ,
although reduced (cf. Eq. (2)), is still above the significance threshold.
Hence, the 200-harmonic method performs better than the 3-spot method since it fits the light variations better. On the other hand, when the noise level increases (
,
although reduced (cf. Eq. (2)), is still above the significance threshold.
Hence, the 200-harmonic method performs better than the 3-spot method since it fits the light variations better. On the other hand, when the noise level increases (
![]() ppm), the reduction of
ppm), the reduction of ![]() has a larger impact on the
has a larger impact on the ![]() -statistics, as more and more values of
-statistics, as more and more values of ![]() fall below the threshold, making the performance of the 200-harmonic method worse than that of the 3-spot method (see Fig. 6). Note that the 3-spot method
is based on the use of only three fitting functions that are not orthogonal, thus it is not affected by the Gibbs phenomenon. Moreover,
the reduction of the transit depth in the residual light curve is very small because the fitting
functions mainly follow the points outside transits, especially when the transit duration is
short and the orbital period is long with respect to the adopted 14-d time interval during which the parameters controlling the shape of the fitting functions are kept fixed.
fall below the threshold, making the performance of the 200-harmonic method worse than that of the 3-spot method (see Fig. 6). Note that the 3-spot method
is based on the use of only three fitting functions that are not orthogonal, thus it is not affected by the Gibbs phenomenon. Moreover,
the reduction of the transit depth in the residual light curve is very small because the fitting
functions mainly follow the points outside transits, especially when the transit duration is
short and the orbital period is long with respect to the adopted 14-d time interval during which the parameters controlling the shape of the fitting functions are kept fixed.
![\begin{figure}
\par\includegraphics[height=5.2cm,width=5cm,angle=90,clip]{8833f5.ps}\end{figure}](/articles/aa/full/2008/16/aa8833-07/Timg55.gif) |
Figure 5: Residuals obtained with the 200-harmonic method (red-dotted line) and the 3-spot method (blue-dashed line) for a noiseless light curve containing only transits; the black-solid line is the light variation during the transit. Note the Gibbs phenomenon affecting the residuals obtained with the 200-harmonic fit and the smaller distortion of the transit profile obtained with the 3-spot method. |
| Open with DEXTER | |
The Gibbs phenomenon also affects other filtering methods proposed to reduce the impact of stellar microvariability, such as, e.g., that of Carpano et al. (2003), or the Wiener-like discrete filters by Aigrain & Irwin (2004). Wavelet-based methods (e.g., Jenkins 2002) may be useful to overcome the problems related to Gibbs phenomenon, given the non-orthogonal nature of their basis functions, but they are negatively affected by gaps in the time series. On the other hand, the non-linear iterative filter proposed by Aigrain & Irwin (2004) is pratically insensitive to gaps or irregular sampling and does not make use of orthogonal functions. Therefore, it is worth a detailed comparison with our method and this will be the subject of a forthcoming work.
![\begin{figure}
\par\includegraphics[height=4.9cm,width=5cm,angle=90,clip]{8833f6.ps}\end{figure}](/articles/aa/full/2008/16/aa8833-07/Timg57.gif) |
Figure 6:
Signal-to-noise ratio
|
| Open with DEXTER | |
Note that the 3-spot method performs well in the presence of gaps (see Lanza et al. 2007,2003) because the model is naturally interpolated through them to follow the observations. The main limitations of the 3-spot model are the computing time and the necessity of adjusting some of the parameters if the star is not analogous to the Sun. The computation time is really not a problem when a parallel high-performance computing system is available, as we have demonstrated through the extensive use of a grid-based system to perform our calculations. As a matter of fact, the problem of analysing the large number of light curves coming from a space experiment is a fully-parallelizable problem and the elapsed time scales with the inverse of the number of available CPUs.
The problem of adjusting model parameters to analyse light curves of stars not strictly analogous to the Sun has been treated by Lanza et al. (2004,2007,2003), and will not be reconsidered here since we intend to discuss it systematically in a successive paper.
We have performed extensive numerical experiments to compare two different methods of fitting Sun-like variability for the detection of Earth-like planetary transits. Our results show that the 3-spot model performs better than the 200-harmonic fitting when the standard deviation of the photon shot noise is 2-4 times greater than the central depth of the transit. Conversely, the 200-harmonic fitting performs better when the noise standard deviation is comparable to the depth of the transit. This behaviour has been interpreted as a consequence of the Gibbs phenomenon and is expected to be common to all filtering and fitting methods based on sets of orthogonal functions. On the other hand, the assumption of some general and simple physical hypotheses about the origin of Sun-like variability allows the 3-spot method to reach a truly appealing performance, in spite of the fact that it has only eleven degrees of freedom.
Therefore, it is worthwhile to conduct further detailed comparisons, in particular with non-linear iterative filters, such as that proposed by Aigrain & Irwin (2004). We plan to perform such tests by simultaneously applying different methods to the same, large set of simulated light curves, thus extending the Monte Carlo approach of the present paper.
Acknowledgements
The authors are grateful to the Referee, Dr. S. Aigrain, for her comments on a previous version of the present paper that greatly helped to improve their work. They also gratefully acknowledge Drs. U. Becciani, A. Costa, A. Grillo, and the system managers of the Trigrid and Cometa Consortia for their technical advice and kind assistance during the implementation and running of the present numerical experiments on grid-based high performance computing systems. A.S.B. and A.F.L. are also grateful to Drs. R. Alonso, P. Barge, P. Bordé, R. Cautain, M. Deluil, A. Leger, C. Moutou, for useful discussions on several aspects of the present work. The availability of unpublished data of the VIRGO Experiment on the cooperative ESA/NASA Mission SoHO from the VIRGO Team through PMOD/WRC, Davos, Switzerland, is gratefully acknowledged. The authors gratefully acknowledge support from the Italian Space Agency (ASI) under contract ASI/INAF I/015/07/0, work package 3170. This research has made use of results produced by the PI2S2 Project managed by the Consorzio COMETA, a project co-funded by the Italian Ministry of University and Research (MUR) within the Piano Operativo Nazionale ``Ricerca Scientifica, Sviluppo Tecnologico, Alta Formazione'' (PON 2000-2006). More information is available at http://www.pi2s2.it and http://www.consorzio-cometa.it.
Active star research and exoplanetary studies at INAF-Catania Astrophysical Observatory and the Department of Physics and Astronomy of Catania University is funded by MUR (Ministero dell'Università e Ricerca), and by Regione Siciliana, whose financial support is gratefully acknowledged. This research has made use of the ADS-CDS databases, operated at the CDS, Strasbourg, France.