A&A 481, 279-294 (2008)
DOI: 10.1051/0004-6361:20067045
Cosmological models in scalar tensor theories of gravity and observations:
a class of general solutions
M. Demianski1,2 - E. Piedipalumbo3,4 -
C. Rubano3,4 - P. Scudellaro3,4
1 - Institute for Theoretical Physics, University of
Warsaw, Hoza 69, 00-681 Warsaw, Poland
2 -
Department of
Astronomy,
Williams College, Williamstown, MA 01267, USA
3 -
Dipartimento di
Scienze Fisiche, Università di Napoli Federico II, Compl.
Univ. Monte S. Angelo, 80126 Naples, Italy
4 -
Istituto Nazionale
di Fisica Nucleare, Sez. Napoli, Via Cinthia, Compl. Univ. Monte
S. Angelo, 80126 Naples, Italy
Received 29 December 2006 / Accepted 6 November 2007
Abstract
Aims. We study cosmological models in scalar tensor theories of gravity with power-law potentials as models of an accelerating universe.
Methods. We consider cosmological models in scalar tensor theories of gravity that describe an accelerating universe and study a family of inverse power-law potentials, for which exact solutions of the Einstein equations are known. We also compare theoretical predictions of our models with observations. For this we use the following data: the publicly available catalogs of type Ia supernovae and high redshift gamma ray bursts, the parameters of large-scale structure determined by the 2-degree Field Galaxy Redshift Survey (2dFGRS), and measurements of cosmological distances based on the Sunyaev-Zel'dovich effect, among others.
Results. We present a class of cosmological models that describe the evolution of a homogeneous and isotropic universe filled with dust-like matter and a scalar field that is non minimally-coupled to gravity. We show that this class of models depends on three parameters: V0 - the amplitude of the scalar field potential,
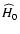 - the present value of the Hubble constant, and a real parameter s that determines the overall evolution of the universe. It turns out that these models have a very interesting feature naturally producing an epoch of accelerated expansion. We fix the values of these parameters by comparing predictions of our model with observational data. It turns out that our model is compatible with the presently available observational data.
- the present value of the Hubble constant, and a real parameter s that determines the overall evolution of the universe. It turns out that these models have a very interesting feature naturally producing an epoch of accelerated expansion. We fix the values of these parameters by comparing predictions of our model with observational data. It turns out that our model is compatible with the presently available observational data.
Key words: cosmology: theory -
cosmology: cosmological parameters - cosmology: observations
Recent observations of the type Ia supernovae and CMB anisotropy
indicate that the total matter-energy density of the universe is now
dominated by some kind of dark energy causing an accelerated
expansion of the Universe (Perlmutter 1997; Riess et al. 1998,2004; Spergel et al. 2006).
The origin and nature of this dark energy remains
unknown (Zeldovich 1967; Weinberg 1989).
Prompted by this discovery, a new class of cosmological models has
recently been proposed. In these models the standard cosmological constant 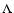 -term is
replaced by a dynamical, time-dependent component - quintessence or
dark energy - that is added to baryons, cold dark matter (CDM),
photons, and neutrinos. The equation of state of the dark energy is
assumed to be of a hydrodynamical type
-term is
replaced by a dynamical, time-dependent component - quintessence or
dark energy - that is added to baryons, cold dark matter (CDM),
photons, and neutrinos. The equation of state of the dark energy is
assumed to be of a hydrodynamical type
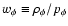 ,
where
,
where
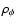 and
and 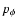 are, respectively,
the energy density and pressure, and
are, respectively,
the energy density and pressure, and
 ,
which
implies a negative contribution to the total pressure of the cosmic
fluid. When
,
which
implies a negative contribution to the total pressure of the cosmic
fluid. When
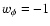 ,
we recover the standard cosmological
constant term. One of the possible physical realization of
quintessence is a cosmic scalar field (Caldwell et al. 1998), which
induces dynamically a repulsive gravitational force that is
responsible for the observed now accelerated expansion of the universe.
,
we recover the standard cosmological
constant term. One of the possible physical realization of
quintessence is a cosmic scalar field (Caldwell et al. 1998), which
induces dynamically a repulsive gravitational force that is
responsible for the observed now accelerated expansion of the universe.
The existence of dark energy, which now dominates the overall
energy density in the universe, is posing several theoretical
problems. First, it is natural to ask why we observe the
universe at exactly the time when the dark energy dominates matter (cosmic coincidence problem). The second
issue, a fine-tuning problem, arises from the fact that
if the dark energy is constant, such as in the standard
cosmological constant scenario, then at the beginning of the
radiation era its energy density should have been vanishingly
small in comparison with the radiation and matter component.
This poses a problem, since to explain the inflationary
behavior of the early universe and the late time dark energy
dominated regime, the dark energy should evolve and cannot
simply be a constant. All these circumstances
stimulated a renewed interest in the generalized gravity
theories, and prompted consideration of a variable 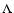 term in more general classes of theories, such as the
scalar tensor theories of gravity.
term in more general classes of theories, such as the
scalar tensor theories of gravity.
In our earlier paper (Demianski et al. 2006) we analyzed extended
quintessence models, for which exact solutions of the Einstein
equations are known, and discussed how in these models it is possible
to treat the fine tuning problem in an alternative way. We applied
our consideration to a special model, based on one of the most
commonly used quintessence potentials
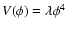 ,
corresponding to the coupling
,
corresponding to the coupling
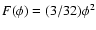 (so-called
induced gravity). We showed that this model corresponds to a
special, and physically significant, case that emerged by requiring
the existence of a Noether symmetry in the pointlike
Lagrangian. In this paper we analyze a new and wider class of
theories derived from the Noether symmetry requirement. One of the
main advantages of such models is that they exhibit power-law couplings and potentials and admit a tracker behavior.
In some sense we complete and generalize the analysis initiated in
Marino & de Ritis (2001) and de Ritis et al. (2000), where the attention was focused on the
mechanism of obtaining an effective cosmological constant through
the cosmological no-hair theorem, and the analysis of the
solution was restricted to the asymptotical
(so-called
induced gravity). We showed that this model corresponds to a
special, and physically significant, case that emerged by requiring
the existence of a Noether symmetry in the pointlike
Lagrangian. In this paper we analyze a new and wider class of
theories derived from the Noether symmetry requirement. One of the
main advantages of such models is that they exhibit power-law couplings and potentials and admit a tracker behavior.
In some sense we complete and generalize the analysis initiated in
Marino & de Ritis (2001) and de Ritis et al. (2000), where the attention was focused on the
mechanism of obtaining an effective cosmological constant through
the cosmological no-hair theorem, and the analysis of the
solution was restricted to the asymptotical
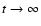 regime. Extending our analysis to the whole time evolution, we
are not only able to clarify the properties of such solutions, but
also to compare predictions of these models with observations. We
concentrate on the following data: the publicly available data on
type Ia supernovae and gamma ray bursts, the parameters of large
scale structure determined by the 2-degree Field Galaxy Redshift
Survey (2dFGRS), and the measurements of cosmological distance with
the Sunyaev-Zel'dovich effect.
regime. Extending our analysis to the whole time evolution, we
are not only able to clarify the properties of such solutions, but
also to compare predictions of these models with observations. We
concentrate on the following data: the publicly available data on
type Ia supernovae and gamma ray bursts, the parameters of large
scale structure determined by the 2-degree Field Galaxy Redshift
Survey (2dFGRS), and the measurements of cosmological distance with
the Sunyaev-Zel'dovich effect.
2.1 Specifying the model
Since the detailed properties of a quintessence model, whose
coupling and potential form are derived by requiring the existence of
a Noether symmetry, are extensively discussed in Demianski et al. (2006, Paper I), here we only summarize the basic results,
referring readers to our previous paper for details. Let us consider
the general action for a scalar field 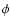 ,
non minimally-coupled
with gravity, but not coupled with matter; in this case, we have
,
non minimally-coupled
with gravity, but not coupled with matter; in this case, we have
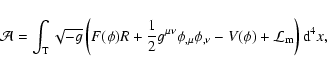 |
(1) |
where 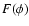 and
and 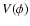 are two generic functions representing
the coupling of the scalar field with geometry and its potential
energy density respectively, R is the scalar curvature,
are two generic functions representing
the coupling of the scalar field with geometry and its potential
energy density respectively, R is the scalar curvature,
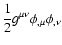 is the kinetic energy of the scalar field
is the kinetic energy of the scalar field 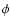 ,
and
,
and
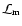 describes the standard matter content. In units such that
describes the standard matter content. In units such that
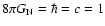 ,
where
,
where 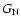 is the Newtonian constant, we
recover the standard gravity when F is equal to -1/2, while in
general the effective gravitational coupling is
is the Newtonian constant, we
recover the standard gravity when F is equal to -1/2, while in
general the effective gravitational coupling is
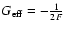 .
Here we would like to study the simple case of a
homogeneous and isotropic universe, which implies that the scalar
field
.
Here we would like to study the simple case of a
homogeneous and isotropic universe, which implies that the scalar
field 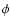 only depends on time. It turns out that for the flat
Friedman-Robertson-Walker universe filled with matter satisfying
the equation of state
only depends on time. It turns out that for the flat
Friedman-Robertson-Walker universe filled with matter satisfying
the equation of state
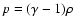 and the scalar field
and the scalar field
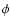 ,
the action in Eq. (1) reduces to the pointlike Lagrangian to
,
the action in Eq. (1) reduces to the pointlike Lagrangian to
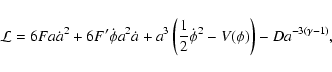 |
(2) |
where a is the scale factor and prime denotes derivative with
respect to 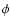 ,
while the dot denotes derivative with respect to
time. Moreover, the constant D> 0 is defined in such a way that
the matter density
,
while the dot denotes derivative with respect to
time. Moreover, the constant D> 0 is defined in such a way that
the matter density
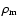 is expressed as
is expressed as
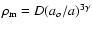 ,
where
,
where
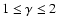 .
The effective
pressure and energy density of the
.
The effective
pressure and energy density of the 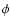 -field are given by
-field are given by
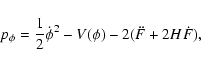 |
(3) |
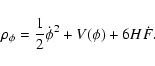 |
(4) |
These two expressions, even if not pertaining to a conserved
energy-momentum tensor, do define an effective equation of state
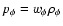 ,
which drives the late time behavior
of the model.
,
which drives the late time behavior
of the model.
From now on we restrict ourselves to a dust-filled universe with
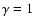 ,
and
,
and
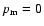 .
Using the point-like Lagrangian Eq. (2) in the action and varying it with respect to
.
Using the point-like Lagrangian Eq. (2) in the action and varying it with respect to 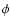 ,
we
obtain the Euler-Lagrange equations
,
we
obtain the Euler-Lagrange equations
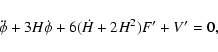 |
(5) |
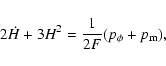 |
(6) |
together with the first integral
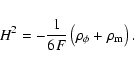 |
(7) |
Let us now introduce the concept of an effective cosmological
constant
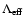 .
Using Eq. (7) it is natural to
define the effective cosmological constant as
.
Using Eq. (7) it is natural to
define the effective cosmological constant as
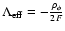 and the effective
gravitational constant as
and the effective
gravitational constant as
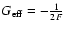 .
With these
definitions we can rewrite Eq. (7) as
.
With these
definitions we can rewrite Eq. (7) as
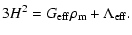 |
|
|
(8) |
Introducing the standard Omega parameters by
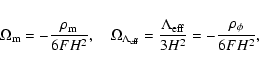 |
(9) |
we find as usual that
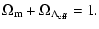 |
|
|
(10) |
Imposing the Noether symmetry in the quintessence
minisuperspace,
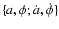 ,
where the
point-like Lagrangian is defined, it is possible to exactly
integrate the Einstein field equations Eqs. (7) and (6), as well as to find a form for the two unknown functions
,
where the
point-like Lagrangian is defined, it is possible to exactly
integrate the Einstein field equations Eqs. (7) and (6), as well as to find a form for the two unknown functions 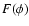 and
and 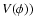 (for details see, Capozziello et al. 1996; Demianski et al. 1991). The
existence of this symmetry actually leads to the following relation
between the functions
(for details see, Capozziello et al. 1996; Demianski et al. 1991). The
existence of this symmetry actually leads to the following relation
between the functions 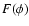 and
and 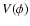 :
:
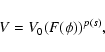 |
(11) |
where V0 is a constant, and
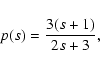 |
(12) |
with s a real number. Moreover, a possible simple choice for the
coupling is
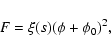 |
(13) |
where 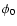 is a constant that does not affect our results
and, therefore, from now on we set it to zero, and
is a constant that does not affect our results
and, therefore, from now on we set it to zero, and
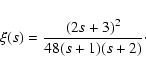 |
(14) |
Let us note that the form of the coupling given by (13) is
quite relevant from the point of view of fundamental physics. It
describes so-called induced gravity. The induced gravity model
was initially proposed by Zee in 1979, as a theory of
gravity incorporating the concept of spontaneous symmetry breaking.
It was based on the observation that in gauge theories the
dimensional coupling constants arising in a low-energy effective
theory can be expressed in terms of the vacuum expectation values of
scalar fields. In such a model the gravitational and cosmological
constants are not introduced by hand, but are generated in the
process of symmetry breaking of a scalar field non minimally-coupled
with the Ricci scalar in the Lagrangian describing the system.
Once the Noether symmetry is specified, it is possible to
find a corresponding conserved quantity and use it as a new
dynamical variable (for details see Capozziello et al. 1996; Demianski et al. 1991). One can then
solve the corresponding Lagrange equations, and finally after
returning to the original variables we obtain the sought-after a(t) and 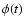 .
The final results can be written in the form
.
The final results can be written in the form
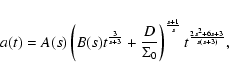 |
(15) |
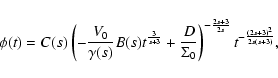 |
(16) |
where A(s), B(s), C(s), 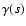 ,
and
,
and 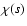 are given
by
are given
by
and
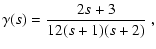 |
|
|
(20) |
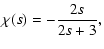 |
|
|
(21) |
where D is the matter density constant,
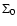 a constant
of integration resulting from the Noether symmetry, and V0the constant that determines the scale of the potential. Together
with the independent parameters, we then use these three constants
a constant
of integration resulting from the Noether symmetry, and V0the constant that determines the scale of the potential. Together
with the independent parameters, we then use these three constants
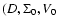 ), which however are not directly measurable,
but they do parametrize the possible solutions of the model. In the
next section we shall reduce their number by means of additional
assumptions along the lines of Paper I.
), which however are not directly measurable,
but they do parametrize the possible solutions of the model. In the
next section we shall reduce their number by means of additional
assumptions along the lines of Paper I.
As is apparent from Eqs. (15) and (16) there are two additional particular values
of s, namely s=0 and s=-3, which should be treated
independently.
When s= 0, a Noether symmetry exists if
- 1.
-
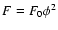 ,
and
,
and
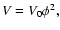
- 2.
-
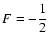 (minimal coupling), and
(minimal coupling), and
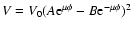 ,
with
,
with
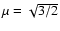 ,
and A, B being constants.
,
and A, B being constants.
The case of the minimal coupling has been thoroughly investigated in
Rubano & Scudellaro (2002), Rubano et al. (2003), and Demianski et al. (2005). If B=0 we obtain an exponential potential, which is a very
important model of quintessence with a standard scalar field.
When s=-3, we recover the case of the quartic potential treated in
the Paper I. We therefore concentrate on the other values of s. As we shall see in a moment, this will lead to a very
different class of potentials from those discussed in Paper I. In
fact we obtain inverse power-law type potentials, which are
interesting and recently widely used in the literature.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig1.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg103.gif) |
Figure 1:
Diagram of 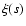 as function of s.
It turns out that an attractive gravity requires
as function of s.
It turns out that an attractive gravity requires
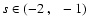 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{7045fig2.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg104.gif) |
Figure 2:
Behavior of the coupling factor 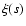 (red curve) and the
power-law exponent p(s) (blue curve). We see that with an appropriate
choice of s in the range
(-1.5 , -1) all the values for
the exponents are available.
(red curve) and the
power-law exponent p(s) (blue curve). We see that with an appropriate
choice of s in the range
(-1.5 , -1) all the values for
the exponents are available. |
| Open with DEXTER |
First of all, we have to find the physically acceptable range for s, and the most important requirement is, of course, that
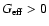 ,
i.e. F<0. This restricts s to (-2, -1) as shown
in Fig. 1. As mentioned above in the range
,
i.e. F<0. This restricts s to (-2, -1) as shown
in Fig. 1. As mentioned above in the range
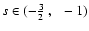 the potential
the potential 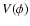 is of an inverse power-law type,
is of an inverse power-law type,
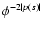 .
In this case our model naturally admits
cosmological scaling solutions, recently studied, for example by
Amendola (1999) and Uzan (1999) in the context of quintessence models. In
Fig. 2 we see that all the possible exponents for the
inverse power-law potential are available.
To determine the integration constants D and
.
In this case our model naturally admits
cosmological scaling solutions, recently studied, for example by
Amendola (1999) and Uzan (1999) in the context of quintessence models. In
Fig. 2 we see that all the possible exponents for the
inverse power-law potential are available.
To determine the integration constants D and  ,
we follow
the procedure used in Paper I, by using the age of the universe,
t0, as a unit of time. Because of our choice of time unit, the
expansion rate H(t) is dimensionless, so that our Hubble constant
is clearly of order 1 and not (numerically) the same as the H0that is usually measured in
,
we follow
the procedure used in Paper I, by using the age of the universe,
t0, as a unit of time. Because of our choice of time unit, the
expansion rate H(t) is dimensionless, so that our Hubble constant
is clearly of order 1 and not (numerically) the same as the H0that is usually measured in
 .
Setting
a0= a(t0)=1 and
.
Setting
a0= a(t0)=1 and
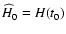 ,
we are able to express
,
we are able to express 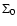 and D as functions of s and
and D as functions of s and
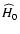 .
We
obtain
.
We
obtain
Therefore, our family of models, labeled by s, depends only on V0, and
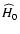 .
For both these parameters, we not
only have a thorough knowledge of their physical meaning, but for
.
For both these parameters, we not
only have a thorough knowledge of their physical meaning, but for
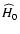 we can also strongly constrain its range of
variability. Actually, we may easily obtain the relation
we can also strongly constrain its range of
variability. Actually, we may easily obtain the relation
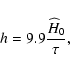 |
(24) |
where as usual
h=H0/100 and 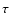 is the age of the universe
in Gy. We see that
is the age of the universe
in Gy. We see that
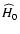 fixes only the product
fixes only the product 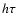 .
In particular, we know that
.
In particular, we know that
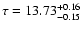 (see for instance Spergel et al. 2006), thus we get h< 0.76 for
(see for instance Spergel et al. 2006), thus we get h< 0.76 for
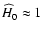 .
The actual value of h may be
obtained by some of the subsequent tests or in others it has to be
set as a prior condition - this will be specified in each case considered
below.
.
The actual value of h may be
obtained by some of the subsequent tests or in others it has to be
set as a prior condition - this will be specified in each case considered
below.
Using the available observational data, we can further constrain the
range of possible values of s. Actually requiring that today
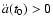 ,
as indicated by observations of supernovae Ia and
WMAP, we constrain the range of possible values of s to
,
as indicated by observations of supernovae Ia and
WMAP, we constrain the range of possible values of s to
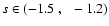 .
.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig3.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg123.gif) |
Figure 3:
Plot of
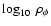 versus
versus
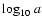 (solid black line).
The upper and lower dashed lines indicate the log-log plot of a-3 and a-4 versus a, respectively. It turns out that
(solid black line).
The upper and lower dashed lines indicate the log-log plot of a-3 and a-4 versus a, respectively. It turns out that 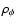 scales
as a-n, with 3<n<4. In this and subsequent plots, we use the mean
values for the parameters obtained through fits (see Table 2).
scales
as a-n, with 3<n<4. In this and subsequent plots, we use the mean
values for the parameters obtained through fits (see Table 2). |
| Open with DEXTER |
From Eqs. (15) and (16) it turns out
that for low values of t the scale factor and the scalar field
behave as
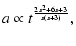 |
|
|
(25) |
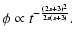 |
|
|
(26) |
Substituting these functions in 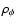 ,
as given by
the Eq. (4), we get that for low t the scalar
field density
,
as given by
the Eq. (4), we get that for low t the scalar
field density
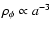 .
This is however true
only asymptotically for very small t. Exact computation as
shown in Fig. 3 gives
.
This is however true
only asymptotically for very small t. Exact computation as
shown in Fig. 3 gives
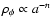 ,
with
,
with 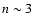 .
This justifies our assertion that our model
naturally admits scaling solutions. The situation changes
dramatically near the present time (see below).
For high values of t, the scale factor and the scalar field
behave as
.
This justifies our assertion that our model
naturally admits scaling solutions. The situation changes
dramatically near the present time (see below).
For high values of t, the scale factor and the scalar field
behave as
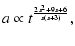 |
|
|
(27) |
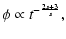 |
|
|
(28) |
respectively, as shown in Marino & de Ritis (2001), where this asymptotical
regime is discussed. It is interesting to note, as shown in
Paper I, that 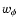 represents an equation of state,
in the usual sense, of the effective cosmological constant
represents an equation of state,
in the usual sense, of the effective cosmological constant
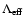 ,
and that
,
and that
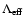 asymptotically behaves
as a true cosmological constant (
asymptotically behaves
as a true cosmological constant (
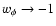 )
as
)
as
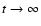 .
Since both
.
Since both
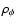 and
and 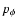 depend on
depend on 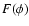 through its time
derivative (see Eqs. (4) and (3))
and asymptotically
through its time
derivative (see Eqs. (4) and (3))
and asymptotically
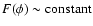 ,
we recover in this limit the minimally coupled theory. In Figs. 4 and 5 we show the evolution with the
redshift and the rate of evolution of
,
we recover in this limit the minimally coupled theory. In Figs. 4 and 5 we show the evolution with the
redshift and the rate of evolution of 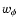 ,
where the fast
transition toward
,
where the fast
transition toward
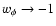 appears between z=3and z=0.5. Before reaching this asymptotic regime, the energy
density
appears between z=3and z=0.5. Before reaching this asymptotic regime, the energy
density
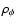 is dominated by the coupling term
is dominated by the coupling term
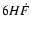 .
Concluding this section we present the traditional
plot
.
Concluding this section we present the traditional
plot
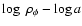 and compare it with the
evolution of matter density (see Fig. 6). It is
interesting to see that
and compare it with the
evolution of matter density (see Fig. 6). It is
interesting to see that
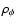 follows the matter
density during the matter-dominated era, and it becomes dominant
at a late time.
follows the matter
density during the matter-dominated era, and it becomes dominant
at a late time.
Recently, the cosmological relevance of extended
gravity theories as scalar tensor or higher order theories has been widely explored. However, in the weak field approximation,
all these classes of theories are expected to reproduce the
Einstein general relativity that, in any case, is experimentally
tested only in this limit. This fact is a matter of debate, since
several relativistic theories do not reproduce Einstein results at
the Newtonian approximation but, in some sense, generalize them,
giving rise, for example, to Yukawa-like corrections to the
Newtonian potential, which could have interesting physical
consequences. Moreover, in general, any relativistic theory of
gravitation can yield corrections to the Newton potential (see for
example, Will 1993), which in the post-Newtonian (PPN) formalism
could furnish tests for such theory, mainly based on the Solar
System experiments. In this section we want to discuss the
Newtonian limit of our class of scalar-tensor theories of
gravity, the induced gravity theories, and to study the
parametrized post Newtonian (PPN) behavior of these theories.
In particular, it turns out that the Newtonian limit depends on
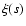 .
Furthermore, we find a quadratic correction to the
Newtonian potential strictly depending on the presence of the
scalar-field potential, which acts as a cosmological constant.
.
Furthermore, we find a quadratic correction to the
Newtonian potential strictly depending on the presence of the
scalar-field potential, which acts as a cosmological constant.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig4.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg136.gif) |
Figure 4:
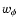 as a function of
as a function of
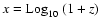 ,
for the averaged mean values provided by our
analysis, as shown in Table 2. We observe a transition from a small constant
value in the past, ,
for the averaged mean values provided by our
analysis, as shown in Table 2. We observe a transition from a small constant
value in the past,
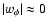 ,
to ,
to
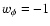 at present.
at present. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig5.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg138.gif) |
Figure 5:
Rate of change in the equation of state as measured by
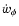 versus the
versus the 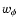 parameter. The values of the parameters
correspond to the average values provided by our
analysis and shown in Table 2.
parameter. The values of the parameters
correspond to the average values provided by our
analysis and shown in Table 2. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig6.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg140.gif) |
Figure 6:
Plot of
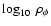 versus
versus
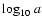 in the Jordan frame.
The vertical bar marks
in the Jordan frame.
The vertical bar marks
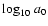 .
The solid red straight
line indicates the log-log plot of .
The solid red straight
line indicates the log-log plot of
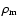 versus a. The matter dominated-era and the transition to the present dark-energy dominated regime are represented.
versus a. The matter dominated-era and the transition to the present dark-energy dominated regime are represented. |
| Open with DEXTER |
In order to recover the Newtonian limit of our theory described by the action
in Eq. (1), associated with the effective stress-energy
tensor
where
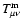 is the usual stress-energy tensor of matter
and
is the usual stress-energy tensor of matter
and  is the d'Alembert operator, we write the metric tensor
as
is the d'Alembert operator, we write the metric tensor
as
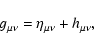 |
(30) |
where
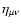 is the Minkowski metric and
is the Minkowski metric and
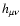 is a small correction. In the same way, we define the
scalar field
is a small correction. In the same way, we define the
scalar field 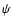 as a perturbation, of the same order as
as a perturbation, of the same order as
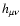 ,
of the original field
,
of the original field 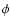 ,
that is
,
that is
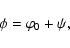 |
(31) |
where
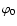 is a constant of order unity. It is clear that
for
is a constant of order unity. It is clear that
for
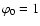 and
and 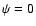 the standard Einstein general
relativity with
the standard Einstein general
relativity with  is recovered.
To write the Einstein tensor
is recovered.
To write the Einstein tensor
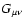 in an appropriate form, we
define the auxiliary fields
in an appropriate form, we
define the auxiliary fields
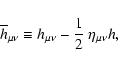 |
(32) |
and
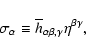 |
(33) |
where
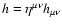 .
Given these definitions, to the first order in
.
Given these definitions, to the first order in
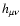 ,
we
obtain
,
we
obtain
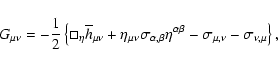 |
(34) |
where
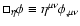 .
To
obtain the weak-field limit of the field equations we also have to
expand the effective stress-energy tensor. This means that it is
necessary to expand the coupling function and the self-interacting
potential. Specifically, it turns out that expanding the coupling
function
.
To
obtain the weak-field limit of the field equations we also have to
expand the effective stress-energy tensor. This means that it is
necessary to expand the coupling function and the self-interacting
potential. Specifically, it turns out that expanding the coupling
function 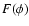 and the self-interacting potential
and the self-interacting potential 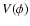 (by
using their explicit forms) up to the second order in
(by
using their explicit forms) up to the second order in 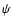 ,
we get
,
we get
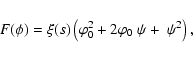 |
(35) |
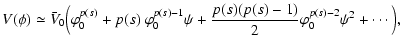 |
|
|
(36) |
where
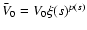 .
Then, to the first order,
the effective stress-energy tensor becomes
.
Then, to the first order,
the effective stress-energy tensor becomes
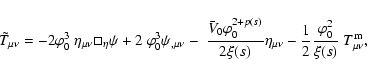 |
(37) |
and the field equations assume the form
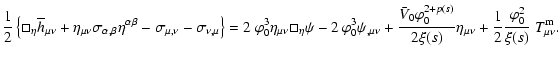 |
|
|
(38) |
When
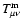 describes a point particle of mass M and
for
describes a point particle of mass M and
for
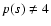 and
and
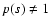 ,
we get
,
we get
where only terms linear in V0 are given and we omitted the
constant terms.
A satisfactory description of the PPN limit for scalar tensor
theories is developed in Esposito-Farese (2004) and Damour et al. (1993). In
these papers, this limit has been thoroughly discussed leading to
interesting results even in the case of strong gravitational sources
like pulsars and neutron stars where the deviations from general
relativity are considered in a non-perturbative regime
(Damour et al. 1993). The starting point for such an analysis is a
redefinition of the non minimally-coupled Lagrangian action in terms
of a minimally-coupled scalar field model via a conformal
transformation of the form
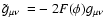 .
In fact, assuming the transformation rules
.
In fact, assuming the transformation rules
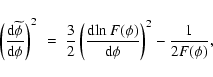 |
(41) |
and
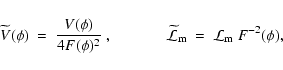 |
(42) |
one rewrites the action as
![\begin{displaymath}
\widetilde{{\cal A}}~=
~\int{\sqrt{-\widetilde{g}}\left[\wid...
...lde{\phi})+
\widetilde{{\cal L}}_{\rm m}\right]{\rm d}^{4}x} .
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img177.gif) |
(43) |
The first consequence of such a transformation is that the
non-minimal coupling is transferred to the ordinary matter sector,
introducing an interaction term between matter and the scalar field.
Actually, the Lagrangian
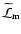 depends not only
on the conformally transformed metric
depends not only
on the conformally transformed metric
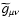 and
the matter fields, but it also depends on the coupling function. In
the same way, the field equations can be recast in the Einstein
frame. The energy-momentum tensor is defined as
and
the matter fields, but it also depends on the coupling function. In
the same way, the field equations can be recast in the Einstein
frame. The energy-momentum tensor is defined as
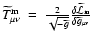 and is
related to the Jordan expression as
and is
related to the Jordan expression as
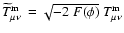 .
Possible deviations from the
standard general relativity can be tested through the Solar System
experiments (Will 1993) and binary pulsar observations, which give
an experimental estimate of the PPN parameters. The generalization
of these quantities to the scalar-tensor theories allows the
PPN-parameters to be expressed in terms of the non-minimal coupling
function
.
Possible deviations from the
standard general relativity can be tested through the Solar System
experiments (Will 1993) and binary pulsar observations, which give
an experimental estimate of the PPN parameters. The generalization
of these quantities to the scalar-tensor theories allows the
PPN-parameters to be expressed in terms of the non-minimal coupling
function 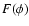 ,
and
in our case using
Eqs. (13) and (14), we obtain
,
and
in our case using
Eqs. (13) and (14), we obtain
![\begin{displaymath}
\gamma^{\rm PPN}-1~=~-\frac{F'(\phi)^2}{F(\phi)+2[F'(\phi)]^2}~=-~\frac{4\xi(s)}{1+8\xi(s)} ,
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img182.gif) |
(44) |
![\begin{displaymath}\beta^{\rm PPN}-1~=~\frac{F(\phi){\cdot}
F'(\phi)}{F(\phi)+3[F'(\phi)]^2}\frac{{\rm d}\gamma^{\rm PPN}}{{\rm d}\phi}~=0 .
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img183.gif) |
(45) |
The above definitions imply that the PPN-parameters in general
depend on the non-minimal coupling function 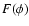 and its
derivatives. However in our model
and its
derivatives. However in our model
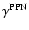 depends only on
s while
depends only on
s while
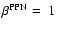 .
The PPN-parameters can be directly
constrained by the observational data. Actually, Solar System
experiments give accurate indications on the ranges of
.
The PPN-parameters can be directly
constrained by the observational data. Actually, Solar System
experiments give accurate indications on the ranges of![[*]](/icons/foot_motif.gif)
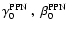 .
.
Table 1:
A brief summary of recent
constraints on the PPN-parameters.
We summarize the experimental results in Table 1. These
results have been used by Schimd et al. (2005) to set the following
constrains:
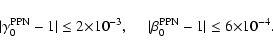 |
(46) |
It turns out that the limit for
 in the Eq. (46) is naturally verified, for each value of s, while
the constraint on
in the Eq. (46) is naturally verified, for each value of s, while
the constraint on
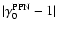 is satisfied only for
is satisfied only for
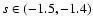 ,
as shown in Fig. 7.
,
as shown in Fig. 7.
For the sake of completeness, here we even take into account the
shift that the scalar-tensor gravity induces on the theoretical
predictions for the local value of the gravitational constant as
coming from the Cavendish-like experiments. This quantity
represents the gravitational coupling measured when the Newton
force arises between two masses:
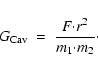 |
(47) |
In the case of scalar tensor gravity, the Cavendish coupling is
related to F and F' and is given by :
and in our models it depends only on s.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig7.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg198.gif) |
Figure 7:
Current limits on the PPN parameters restrict the range of the parameter s.
We see that the constraint on
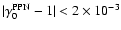 leads to
leads to
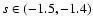 ,
as shown in the inner zoom. ,
as shown in the inner zoom. |
| Open with DEXTER |
Finally, in Fig. 8 we plot the Brans-Dicke
parameter
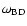 as a function of s: actually, for our
model
as a function of s: actually, for our
model
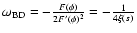 .
It turns out that just for
.
It turns out that just for
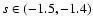 ,
,
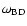 satisfies the limits coming both from the
Solar System experiments,
satisfies the limits coming both from the
Solar System experiments,
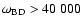 (Will 1993), and
current cosmological observations, including cosmic microwave
anisotropy data and the galaxy power spectrum data, give
(Will 1993), and
current cosmological observations, including cosmic microwave
anisotropy data and the galaxy power spectrum data, give
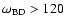 (Acquaviva et al. 2005)
(Acquaviva et al. 2005)![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig8.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg201.gif) |
Figure 8:
Behavior of the Brans-Dicke parameter
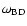 as a function of s. For
as a function of s. For
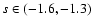 , ,
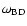 satisfies limits placed by the solar system experiments
( satisfies limits placed by the solar system experiments
(
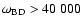 )
and by current cosmological observations
( )
and by current cosmological observations
(
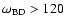 ). ).
|
| Open with DEXTER |
Conformal transformations are often used
to convert the non minimally-coupled scalar field models into the
minimally-coupled ones, to gain mathematical simplification. The
Jordan frame, in which the scalar field is non minimally-coupled to the Ricci curvature, is mapped into the Einstein
frame in which the transformed scalar field is minimally-coupled
but at a price of coupling matter to the scalar field. The two
frames are not physically equivalent, and some care has to be taken
in applying this technique (see for instance Faraoni 2000 for a
critical discussion of this point). In this section we study the
effect of conformal transformations on our models and show that, in
presence of matter, it can mimic a coupling between the quintessence
scalar field and dark matter. We discuss some implications of such a
fictitious interaction on the effective equation of state.
Actually it turns out that, since the interaction alters the
redshift dependence of the matter density, it is possible to obtain
an effective transformed dark-energy equation of state of
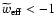 .
Let us start from the transformation
rules connected with the conformal transformation
.
Let us start from the transformation
rules connected with the conformal transformation
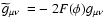 :
:
With these new variables the Lagrangian in the
Eq. (2) becomes
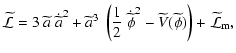 |
|
|
(53) |
where the dot now denotes derivative with respect to
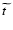 ,
and
,
and
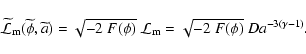 |
(54) |
An observer in the Einstein frame would infer that the scalar field
is coupled to the dark matter, and this interaction is
represented by the term
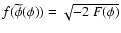 ,
as can be seen more clearly from the field equations:
,
as can be seen more clearly from the field equations:
where
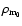 is the actual matter density (treated here as
dust),
is the actual matter density (treated here as
dust),
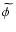 the value of
the value of
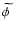 today,
and
today,
and
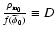 .
It turns out
that the density of dark matter does not evolve as
.
It turns out
that the density of dark matter does not evolve as
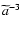 ,
but scales as
,
but scales as
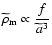 .
Also the Klein-Gordon
Eq. (55) differs from the standard one because of
the last term on the right hand side.
As shown in (Das et al. 2006) interaction between dark matter and dark
energy could result in an effective equation of state
.
Also the Klein-Gordon
Eq. (55) differs from the standard one because of
the last term on the right hand side.
As shown in (Das et al. 2006) interaction between dark matter and dark
energy could result in an effective equation of state
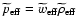 ,
mimicking the
,
mimicking the 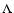 CDM
model. Actually
CDM
model. Actually
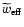 is defined by the matter
continuity equation
is defined by the matter
continuity equation
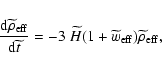 |
(57) |
where
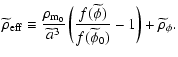 |
|
|
(58) |
It can be shown that
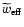 is simply related to
is simply related to
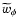
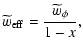 |
|
|
(59) |
where
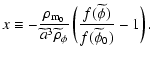 |
|
|
(60) |
Since x=0 today, one has
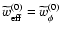 ,
which is greater than or
equal to -1. It turns out, however, that fincreases in time (Das et al. 2006), so that
,
which is greater than or
equal to -1. It turns out, however, that fincreases in time (Das et al. 2006), so that 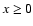 and it is possible to have
and it is possible to have
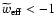 in the past. In such a way
interaction between dark matter and dark energy could
generate a superquintessence regime, provided that the
observer treats the dark matter as non-interacting, and ascribes
part of the dark matter density to the scalar field, as is shown
in Eq. (58). On the other hand an interacting dark
energy component could hide the effect of a non standard
gravity, in the Einstein frame, provided that it is considered
as the physical one.
in the past. In such a way
interaction between dark matter and dark energy could
generate a superquintessence regime, provided that the
observer treats the dark matter as non-interacting, and ascribes
part of the dark matter density to the scalar field, as is shown
in Eq. (58). On the other hand an interacting dark
energy component could hide the effect of a non standard
gravity, in the Einstein frame, provided that it is considered
as the physical one.
Let us consider our nonminimally coupled model characterized by the
functions
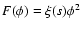 and
and
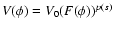 .
According to the rules in Eqs. (49)-(52) we obtain the following relations
between the transformed and original dynamical quantities:
.
According to the rules in Eqs. (49)-(52) we obtain the following relations
between the transformed and original dynamical quantities:
As we see from Eq. (62), the
cosmic evolution is mediated in the transformed frame by the presence of the scalar
field. The explicit form of Eq. (51), which connects the
cosmic time in both frames, can be written in analytical form, but
is indeed rather complicated, because actually it turns out that
From Eqs. (61)-(64) we can evaluate the
scalar field energy density and pressure, and the equation of state
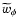 according to the usual definitions.
As in the Jordan frame, it turns out that also in the Einstein frame
according to the usual definitions.
As in the Jordan frame, it turns out that also in the Einstein frame
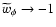 for
for
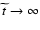 (see for instance Fig. 10).
(see for instance Fig. 10).
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig10.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg245.gif) |
Figure 10:
Evolution with the redshift of
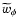 in
the Einstein frame.
in
the Einstein frame. |
| Open with DEXTER |
Concluding this section we present the traditional plot
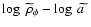 and compare
it with the
and compare
it with the
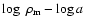 relation (see Fig. 11). Interestingly we see that, just because of the
interaction term,
relation (see Fig. 11). Interestingly we see that, just because of the
interaction term,
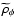 no longer tracks
the matter during the matter dominated era, as happens in the
Jordan frame (see Fig. 6), but becomes dominant at
earlier times.
It is interesting to write down the effective equation of
state
no longer tracks
the matter during the matter dominated era, as happens in the
Jordan frame (see Fig. 6), but becomes dominant at
earlier times.
It is interesting to write down the effective equation of
state
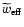 (see Eq. (57)), which
mimics a CDM model. Actually in our case,
(see Eq. (57)), which
mimics a CDM model. Actually in our case,
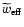 is
is
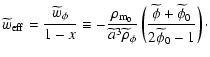 |
|
|
(65) |
It turns out that here
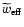 and
and
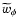 are practically indistinguishable,
since in our model the transformed scalar field
are practically indistinguishable,
since in our model the transformed scalar field
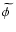 weakly evolves with time as shown in
Fig. 9.
weakly evolves with time as shown in
Fig. 9.
In this section we
briefly discuss how the scalar tensor theories of gravity could
be involved in a cosmological model with mass varying
neutrinos that mimic the dark energy, a quite different
theoretical scenario of evolution of the universe that recently
has been suggested by Fardon et al. (2004). Let us recall that the mass differences between neutrino mass eigenstates
(m1, m2, m3) have recently been measured in oscillation
experiments (Lesgourgues & Pastor 2006). Observations of atmospheric
neutrinos suggest a squared mass difference of
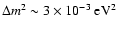 ,
while solar neutrino observations and
results from the KamLAND neutrino experiment point towards
,
while solar neutrino observations and
results from the KamLAND neutrino experiment point towards
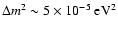 .
While only weak
constraints on the absolute mass scale (
.
While only weak
constraints on the absolute mass scale (
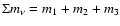 )
have been obtained from single
)
have been obtained from single 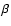 -decay
experiments, the double-beta decay searches from the
Heidelberg-Moscow experiment have reported a signal for a
neutrino mass at >
-decay
experiments, the double-beta decay searches from the
Heidelberg-Moscow experiment have reported a signal for a
neutrino mass at >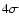 level (Klapdor-Kleingrothaus et al. 2004), recently
promoted to >
level (Klapdor-Kleingrothaus et al. 2004), recently
promoted to >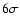 level (Klapdor-Kleingrothaus 2006). This last result
translates into a total neutrino mass of
level (Klapdor-Kleingrothaus 2006). This last result
translates into a total neutrino mass of
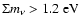 at
at 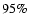 c.l., but this claim is still considered controversial (see Elliott & Engel 2004).
c.l., but this claim is still considered controversial (see Elliott & Engel 2004).
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig11.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg261.gif) |
Figure 11:
Plot of
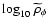 versus
versus
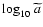 in the Einstein frame.
The vertical bar marks
in the Einstein frame.
The vertical bar marks
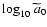 . .
|
| Open with DEXTER |
It is known in the literature
(Lesgourgues & Pastor 2006) that massive neutrinos can be extremely relevant
for cosmology as they leave key signatures in several
cosmological data sets. More specifically, massive neutrinos
suppress the growth of fluctuations on scales below the horizon
scale when they become non relativistic. Current cosmological
data have been able to indirectly constrain the absolute
neutrino mass to
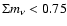 eV at
eV at 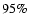 c.l.
(Spergel et al. 2006), and are challenging the Heidelberg-Moscow
claim. However, as first noticed by (Hannestad 2005), there is
some form of anticorrelation between the equation of state
parameter w and
c.l.
(Spergel et al. 2006), and are challenging the Heidelberg-Moscow
claim. However, as first noticed by (Hannestad 2005), there is
some form of anticorrelation between the equation of state
parameter w and
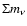 .
The cosmological bound on
neutrino masses can therefore be relaxed by considering a dark
energy component with a more negative value of
.
The cosmological bound on
neutrino masses can therefore be relaxed by considering a dark
energy component with a more negative value of
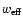 than a
cosmological constant. Actually it has been proved that the
Heidelberg-Moscow result is compatible with the cosmological
data only if the equation of state (with w being constant) is
than a
cosmological constant. Actually it has been proved that the
Heidelberg-Moscow result is compatible with the cosmological
data only if the equation of state (with w being constant) is
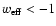 at
at 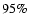 .
.
This result suggests an interesting
link between neutrinos and dark energy (see for instance
Brookfield et al. 2006b,a; Kaplan et al. 2004; Amendola 2004; Bi et al. 2004). According to
this scenario the late-time accelerated expansion of the
universe is driven by the coupling between the quintessential
scalar field and neutrinos. Because of this coupling the mass of
neutrinos becomes a function of this scalar field. Since the
scalar field evolves with time, the mass of neutrinos is not
constant (mass-varying neutrinos): the main theoretical
motivation for this connection relies on the fact that the
energy scale of the dark energy is close to the neutrinos
mass scale. Moreover, as discussed above, in interacting dark
energy models, the net effect of the interaction is to change
the apparent equation of state of the dark energy, allowing a so-called superquintessence regime, with
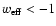 .
Interestingly enough, if the Heidelberg-Moscow results are
combined with the WMAP 3-years data and other
independent cosmological observations, such as the ones connected
with the large-scale structure - coming from galaxy redshift
surveys and Lyman-
.
Interestingly enough, if the Heidelberg-Moscow results are
combined with the WMAP 3-years data and other
independent cosmological observations, such as the ones connected
with the large-scale structure - coming from galaxy redshift
surveys and Lyman- forests - or with the SNIa surveys,
it is possible to constrain the equation of state to
forests - or with the SNIa surveys,
it is possible to constrain the equation of state to
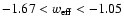 at
at 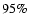 c.l., ruling out a cosmological
constant greater than
c.l., ruling out a cosmological
constant greater than 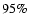 c.l. (see De La Macorra et al. 2007).
c.l. (see De La Macorra et al. 2007).
In the following we discuss the coupling between neutrinos
and dark energy from the point of view of the conformal
transformation, according to the arguments outlined in the
previous section; i.e. we show that the neutrino mass and
scalar field coupling can be interpreted as an effect of
conformal transformations from the Jordan to the Einstein frames,
as it happens for the coupling between the dark energy and
the dark matter. For our purpose the neutrinos can be either
Dirac or Majorana particles, the only necessary ingredient is
that, according to Fardon et al. (2004), the neutrino mass is a
function of the scalar field. In the cosmological context,
neutrinos should be treated as a gas (Brookfield et al. 2006b) and
described by the collisionless distribution function
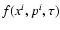 in the phase space (where
in the phase space (where 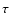 is the
conformal time) that satisfies the Boltzmann equation. When
neutrinos are collisionless, the distribution function f does
not depend explicitly on time. We can then solve the Boltzmann
equation and calculate the energy density stored in neutrinos
(f0 is the background neutrino distribution function):
is the
conformal time) that satisfies the Boltzmann equation. When
neutrinos are collisionless, the distribution function f does
not depend explicitly on time. We can then solve the Boltzmann
equation and calculate the energy density stored in neutrinos
(f0 is the background neutrino distribution function):
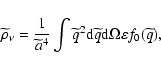 |
(66) |
with
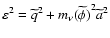 ,
,
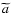 is the scale factor and
is the scale factor and
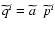 is the
comoving momentum. The pressure is
is the
comoving momentum. The pressure is
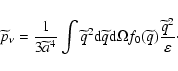 |
(67) |
From these equations, we derive that
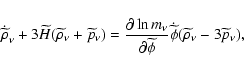 |
(68) |
(note that here the dot denotes the derivative with respect to
 ). The Klein Gordon equation for the scalar field reads
). The Klein Gordon equation for the scalar field reads
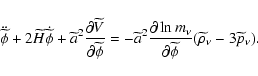 |
(69) |
We see that Eq. (69) is formally equivalent to Eq. (55), but now the term on the righthand side describes
coupling of the scalar field to the neutrino mass. As shown above,
the interaction between neutrinos and dark energy could result in an
effective equation of state
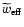 ,
defined in Eq. (57), while
,
defined in Eq. (57), while
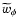 is defined in the
standard way by
is defined in the
standard way by
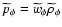 .
As
in the previous section, the
.
As
in the previous section, the
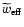 parameter is
related to
parameter is
related to
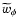 by
by
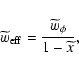 |
(70) |
with
![\begin{displaymath}\widetilde{x}=-\frac{\widetilde{\rho}_{\nu0}}{\widetilde{a}^3...
...m_\nu(\widetilde{\phi})}{m_\nu(\widetilde{\phi}_0)}-
1\right].
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img278.gif) |
(71) |
Also in this case
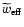 can be less than -1, as
was pointed out in the context of models with dark-matter/dark-energy interaction. This circumstance could lead to an
observational test to establish which of the frames, Jordan or
Einstein, is the physical one, since the coupling between the
quintessential scalar field is provided by the function
can be less than -1, as
was pointed out in the context of models with dark-matter/dark-energy interaction. This circumstance could lead to an
observational test to establish which of the frames, Jordan or
Einstein, is the physical one, since the coupling between the
quintessential scalar field is provided by the function 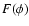 ,
which should drive not only the dark-matter evolution (see Eq. (55)), but also the neutrinos mass variation and the
evolution of the gravitational constant
,
which should drive not only the dark-matter evolution (see Eq. (55)), but also the neutrinos mass variation and the
evolution of the gravitational constant
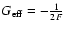 .
.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig12.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg279.gif) |
Figure 12:
Redshift dependence of the second derivative of the scale
factor. The transition from a decelerating to an
accelerating expansion occurs close to 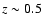 ,
as predicted by recent observations of SNIa ,
as predicted by recent observations of SNIa
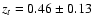 (Riess et al. 2004,
2007).
(Riess et al. 2004,
2007). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig13.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg280.gif) |
Figure 13:
Observational data of the SNIa sample compiled by Riess et al. (2007)
fitted to our model. The solid curve is the best fit curve, compared with a standard 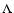 CDM model
with CDM model
with
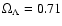 (red dashed line).
(red dashed line). |
| Open with DEXTER |
In this section we present results from fits of predictions of our
model to the best SNIa data sets presently available. As a starting
point we consider the sample of 182 SNIa compiled in Riess et al. (2007), which includes the 21 new type Ia supernovae
recently discovered with the Hubble Space Telescope (HST), and
combines previous SNIa data sets, namely the Gold Sample compiled in
Riess et al. (2004) supplemented by the SNLS data set (Astier et al. 2005).
Following the procedure described in Paper I, we perform a
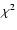 analysis comparing the redshift dependence of the
theoretical values to the observational estimates of the distance
modulus,
analysis comparing the redshift dependence of the
theoretical values to the observational estimates of the distance
modulus, 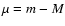 ,
which in scalar tensor theories of gravity takes
the form
,
which in scalar tensor theories of gravity takes
the form
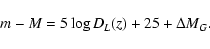 |
(72) |
Here the presence of the correction term
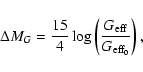 |
(73) |
describes the effect of the time variation of the effective
gravitational constant
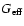 on the luminosity of high-redshift supernovae and allows one to test the scalar tensor
theories of gravity (Uzan 2003; Gaztañaga et al. 2001) using the SNIa data.
Moreover, the luminosity distance for a general flat and homogeneous cosmological model
can be expressed as an integral of the Hubble function as
on the luminosity of high-redshift supernovae and allows one to test the scalar tensor
theories of gravity (Uzan 2003; Gaztañaga et al. 2001) using the SNIa data.
Moreover, the luminosity distance for a general flat and homogeneous cosmological model
can be expressed as an integral of the Hubble function as
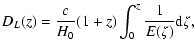 |
|
|
(74) |
where
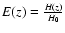 is related to the Hubble
function expressed in terms of
z=a0/a(t) - 1. Let us note that
the luminosity distance also depends on the Hubble distance
is related to the Hubble
function expressed in terms of
z=a0/a(t) - 1. Let us note that
the luminosity distance also depends on the Hubble distance
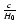 (which does not depend on the choice of the unit of
time). Such freedom allows us to fit h or the a priori unknown age of the universe
(which does not depend on the choice of the unit of
time). Such freedom allows us to fit h or the a priori unknown age of the universe 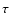 using the SNIa dataset.
We find that
using the SNIa dataset.
We find that
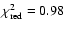 for 182 data points, and the best
fit values are
for 182 data points, and the best
fit values are
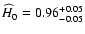 ,
s=-1.46+0.04-0.03, which corresponds to
,
s=-1.46+0.04-0.03, which corresponds to
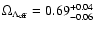 .
We also get
.
We also get
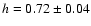 .
In Fig. 13 we compare the best-fit curve with the
observational data sets.
.
In Fig. 13 we compare the best-fit curve with the
observational data sets.
After having explored the Hubble diagram
of SNIa, let us now follow the more general approach, as suggested by
Daly & Djorgovski (2004) and already tested in Paper I.
Consider as a cosmological observable the dimensionless coordinate
distance defined as
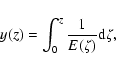 |
(75) |
noting that y(z) does not explicitly depend on h, so that
any choice for h does not alter the main result. Daly &
Djorgovski have determined y(z) for the SNIa in the Gold
Sample of Riess et al. (2004) which is the most
homogeneous SNIa sample available today. Since SNIa allows DL to be
estimated rather than y, a value of h has to be set.
Fitting the Hubble law to a large set of low redshift (z <
0.1) SNIa, Daly & Djorgovski (2004) have set
To enlarge the sample, Daly & Djorgovski added 20 points on the
y(z) diagram using a technique of distance determination based on
the angular dimension of radiogalaxies (Daly & Djorgovski 2004). This data set
has been recently supplemented by 71 new supernovae from the
Supernova Legacy Survey of Astier et al. (2005), which allowed
determination of dimensionless coordinate distances to these
supernovae. These were obtained using the values and uncertainties
of 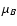 listed in Table 9 of Astier et al. (2005), with h = 0.7. This
extended sample that spans the redshift range
(0.1, 1.8) has been
suitably homogenized.
Using the following merit function
listed in Table 9 of Astier et al. (2005), with h = 0.7. This
extended sample that spans the redshift range
(0.1, 1.8) has been
suitably homogenized.
Using the following merit function
![\begin{displaymath}\chi^2(s, {\widehat H}_0) = \frac{1}{N - 3} \sum_{i = 1}^{N}{...
...(z_i; \alpha_1, {\widehat H}_0) - y_i}{\sigma_i} \right
]^2} ,
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img295.gif) |
(76) |
we find that
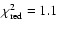 for 248 data points, and the
best-fit values are
for 248 data points, and the
best-fit values are
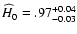 ,
s=-1.49+0.02-0.04. In Fig. 14 we compare the
best-fit curve with the observational data set, as in Paper I.
,
s=-1.49+0.02-0.04. In Fig. 14 we compare the
best-fit curve with the observational data set, as in Paper I.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig14.eps}\end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg297.gif) |
Figure 14:
Updated Daly & Djorgovski database (Daly & Djorgovski 2005)
fitted to our model. The solid curve is the best fit curve with
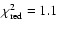 for 248 data points, and the best
fit values are
for 248 data points, and the best
fit values are
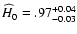 ,
s=-1.49+0.02-0.04. ,
s=-1.49+0.02-0.04. |
| Open with DEXTER |
In this section we discuss a possible observational determination of
H(z) based on the method developed by Jimenez et al. (2003), which
involves differential age measurements. We present some constraints
that can be placed on the evolution of our quintessence model by
this data. First, it is worth pointing out some aspects connected with
the sensitivity of the cosmology to the t(z) and
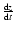 relations. Actually, it is well known that in scalar tensor theories
of gravity, as well as in general relativity, the expansion history
of the universe is determined by the function H(z). This implies
that observational quantities, such as the luminosity distance, the
angular diameter distance, and the lookback time, all depend on
H(z). It turns out that the most appropriate mathematical tool for
studing the sensitivity of the cosmological model to such observables
is the functional derivative of the corresponding relations with
respect to the cosmological parameters (see Saini et al. 2003, for a
discussion about this point in relation to distance measurements).
However, from an empirical point of view, it is also possible to
show that the lookback time is much more sensitive to the
cosmological model than other observables, such as the luminosity
distance and the distance modulus. This circumstance encourages us
to use, together with the other more standard techniques discussed
above, the age of cosmic clocks to test alternative
cosmological scenarios. Apart from the advantage of providing an
alternative investigation instrument, the age-based methods use
the higher sensitivity to the cosmological parameters of the
relations. Actually, it is well known that in scalar tensor theories
of gravity, as well as in general relativity, the expansion history
of the universe is determined by the function H(z). This implies
that observational quantities, such as the luminosity distance, the
angular diameter distance, and the lookback time, all depend on
H(z). It turns out that the most appropriate mathematical tool for
studing the sensitivity of the cosmological model to such observables
is the functional derivative of the corresponding relations with
respect to the cosmological parameters (see Saini et al. 2003, for a
discussion about this point in relation to distance measurements).
However, from an empirical point of view, it is also possible to
show that the lookback time is much more sensitive to the
cosmological model than other observables, such as the luminosity
distance and the distance modulus. This circumstance encourages us
to use, together with the other more standard techniques discussed
above, the age of cosmic clocks to test alternative
cosmological scenarios. Apart from the advantage of providing an
alternative investigation instrument, the age-based methods use
the higher sensitivity to the cosmological parameters of the
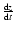 relation, as shown in Figs. 15 and 16. Moreover, as we discuss in the following,
such a method reveals its full strength when applied to old objects
at very high z. Actually it turns out that this kind of analysis
could remove, or at least reduce, the degeneracy that we observe at
lower redshifts, for example the one in the Hubble diagram for SNIa
observations, which can be fitted by different cosmological models
with a similar statistical significance.
Since the Hubble parameter can be related to the differential age of
the universe as a function of redshift by the equation
relation, as shown in Figs. 15 and 16. Moreover, as we discuss in the following,
such a method reveals its full strength when applied to old objects
at very high z. Actually it turns out that this kind of analysis
could remove, or at least reduce, the degeneracy that we observe at
lower redshifts, for example the one in the Hubble diagram for SNIa
observations, which can be fitted by different cosmological models
with a similar statistical significance.
Since the Hubble parameter can be related to the differential age of
the universe as a function of redshift by the equation
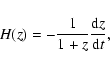 |
(77) |
a determination of dz/dt directly measures H(z).
Jimenez et al. (2003) demonstrated the feasibility of
this method by applying it to a  sample of galaxies.
With the availability of new galaxy surveys, it becomes possible to
determine H(z) at z > 0.
sample of galaxies.
With the availability of new galaxy surveys, it becomes possible to
determine H(z) at z > 0.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig15.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg300.gif) |
Figure 15:
The sensitivity of the
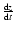 relation compared to the values of the parameters in our
model. The red line shows
relation compared to the values of the parameters in our
model. The red line shows
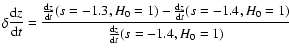 ,
and the blue line shows ,
and the blue line shows
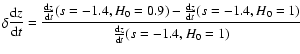 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig16.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg301.gif) |
Figure 16:
The sensitivity of the
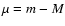 relation compared to the values of the parameters in our model
in. The red line shows
relation compared to the values of the parameters in our model
in. The red line shows
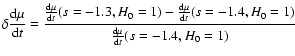 ,
and the
blue line shows ,
and the
blue line shows
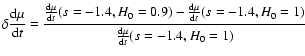 . .
|
| Open with DEXTER |
Here we use the dz/dt data from
(Simon et al. 2005) to determine H(z) in the redshift range
0.1 < z <
1.8. To follow the procedure described in Simon et al. (2005), first we
group all galaxies together that are within
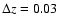 of each
other. This gives an estimate of the age of the universe at a given
redshift. We then compute age differences only for those bins in
redshift that are separated by more than
of each
other. This gives an estimate of the age of the universe at a given
redshift. We then compute age differences only for those bins in
redshift that are separated by more than
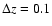 but less
than
but less
than
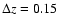 .
The first limit is imposed so that the age
evolution between the two bins is larger than the error in the age
determination. We note here that differential ages are less
sensitive to systematic errors than absolute ages (see Jimenez et al. 2003). The observational value of H(z) is then directly computed by
using Eq. (77), and after that the ages data have been
scaled according to our choice of the unit of time (the unknown
scaling factor has been provided by the
.
The first limit is imposed so that the age
evolution between the two bins is larger than the error in the age
determination. We note here that differential ages are less
sensitive to systematic errors than absolute ages (see Jimenez et al. 2003). The observational value of H(z) is then directly computed by
using Eq. (77), and after that the ages data have been
scaled according to our choice of the unit of time (the unknown
scaling factor has been provided by the 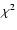 procedure). To
determine the best-fit parameters, we define the following merit
function:
procedure). To
determine the best-fit parameters, we define the following merit
function:
![\begin{displaymath}\chi^2(s, {\widehat H}_0) = \frac{1}{N - 3} \sum_{i = 1}^{N}{...
...ac{H(z_i; s, {\widehat H}_0) - H_i}{\sigma_i} \right ]^2}\cdot
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img305.gif) |
(78) |
We obtain
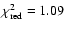 for 9 data points, and the
best-fit values are
for 9 data points, and the
best-fit values are
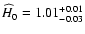 ,
s=-1.49+0.03-0.09. In Fig. 17 we compare
the best-fit curve with the observational data set. It is interesting to note that future
high redshift data could distinguish the degeneration among different models, since at high z the predicted H(z) more sensitively
depends on the values of the parameters.
,
s=-1.49+0.03-0.09. In Fig. 17 we compare
the best-fit curve with the observational data set. It is interesting to note that future
high redshift data could distinguish the degeneration among different models, since at high z the predicted H(z) more sensitively
depends on the values of the parameters.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig17.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg308.gif) |
Figure 17:
The best-fit curve of the measured values of H(z) corresponding to
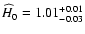 ,
s=-1.49+0.03-0.09. ,
s=-1.49+0.03-0.09. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig18.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg309.gif) |
Figure 18:
The best-fit curve to the H(z) data for our nmc model (dark blue line) and for the quintessence QCDM
fitted to the new released WMAP- three years + SNLS data
(WMAP New Three Year Results 2006)
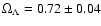 , ,
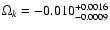 ,
w=-1.06+0.13-0.08 (blue line). ,
w=-1.06+0.13-0.08 (blue line). |
| Open with DEXTER |
In this section we discuss how the parameters of our model can be
constrained by the angular diameter distance 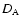 as measured using
the Sunyaev-Zeldovich effect (SZE) and the thermal bremsstrahlung
(X-ray brightness data) for galaxy clusters. The distance
measurements using Sunyaev-Zeldovich effect and X-ray emission from
the intracluster medium have to take into account that these
processes depend on different combinations of some of the parameters
of the clusters (see Birkinshaw 1999, and references therein). The SZE is
a result of the inverse Compton scattering of the CMB photons on hot
electrons of the intercluster gas, which preserves the number of
photons but allows photons to gain energy thereby generating a
decrement of the temperature in the Rayleigh-Jeans part of the
black-body spectrum while an increment appears in the Wien region.
We limit our analysis to the so-called thermal or static
SZE. The kinematic effect, present only in clusters with a
nonzero peculiar velocity with respect to the Hubble flow along the
line of sight, will be neglected since the thermal SZE is typically
an order of magnitude larger than the kinematic one. As in Paper I,
we introduce the so-called Compton parameter, y, defined as the
optical depth
as measured using
the Sunyaev-Zeldovich effect (SZE) and the thermal bremsstrahlung
(X-ray brightness data) for galaxy clusters. The distance
measurements using Sunyaev-Zeldovich effect and X-ray emission from
the intracluster medium have to take into account that these
processes depend on different combinations of some of the parameters
of the clusters (see Birkinshaw 1999, and references therein). The SZE is
a result of the inverse Compton scattering of the CMB photons on hot
electrons of the intercluster gas, which preserves the number of
photons but allows photons to gain energy thereby generating a
decrement of the temperature in the Rayleigh-Jeans part of the
black-body spectrum while an increment appears in the Wien region.
We limit our analysis to the so-called thermal or static
SZE. The kinematic effect, present only in clusters with a
nonzero peculiar velocity with respect to the Hubble flow along the
line of sight, will be neglected since the thermal SZE is typically
an order of magnitude larger than the kinematic one. As in Paper I,
we introduce the so-called Compton parameter, y, defined as the
optical depth
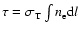 times the energy gain
per scattering:
times the energy gain
per scattering:
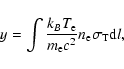 |
(79) |
where 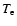 is the temperature of the electrons in the
intracluster gas,
is the temperature of the electrons in the
intracluster gas, 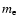 the electron mass,
the electron mass, 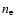 the number
density of the electrons, and
the number
density of the electrons, and
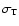 is the Thompson cross
section of electron scattering, and the integration is performed along the line of
sight. In the low-frequency regime of the
Rayleigh-Jeans approximation, the shift of temperature is
is the Thompson cross
section of electron scattering, and the integration is performed along the line of
sight. In the low-frequency regime of the
Rayleigh-Jeans approximation, the shift of temperature is
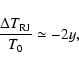 |
(80) |
where T0 is the unperturbed CMB temperature. The next step in
quantifing the SZE decrement is to specify the model for the
intracluster electron density and temperature distribution, which appropriately describes the observational properties of the gas.
Following Bonamente et al. (2005), we use a hydrostatic equilibrium double 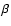 -model.
Actually, at the center of clusters the density may be high enough that the
radiative cooling time-scale is less than the cluster's age, leading
to a reduction in temperature and an increase in central density.
This can increase the central X-ray emissivity. At large radii, the density of the gas is
low enough that X-ray emission can be sustained for cosmological
periods without significant cooling. Therefore, cool core clusters effectively
exhibit two components: a centrally concentrated gas peak and a broad,
shallower distribution of the gas. This phenomenon motivated the
modeling of the gas density with a function of the form:
-model.
Actually, at the center of clusters the density may be high enough that the
radiative cooling time-scale is less than the cluster's age, leading
to a reduction in temperature and an increase in central density.
This can increase the central X-ray emissivity. At large radii, the density of the gas is
low enough that X-ray emission can be sustained for cosmological
periods without significant cooling. Therefore, cool core clusters effectively
exhibit two components: a centrally concentrated gas peak and a broad,
shallower distribution of the gas. This phenomenon motivated the
modeling of the gas density with a function of the form:
![\begin{displaymath}n_{\rm e}(r) = n_{\rm e0} \cdot
\left[f\left( 1+\frac{r^2}{r_...
...+\frac{r^2}{r_{\rm c2}^2} \right)^{-\frac{3\beta}{2}} \right].
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img318.gif) |
(81) |
The quantity
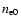 is the central density, f governs the
fractional contributions of the narrow and broad components
(
is the central density, f governs the
fractional contributions of the narrow and broad components
(
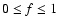 ),
),
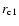 and
and
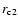 are the two core radii
that describe the shape of the inner and outer portions of the
density distribution, and
are the two core radii
that describe the shape of the inner and outer portions of the
density distribution, and 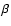 determines the slope at large
radii. The same
determines the slope at large
radii. The same 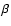 is used for both the central and outer
distribution in order to reduce the total number of degrees of
freedom
is used for both the central and outer
distribution in order to reduce the total number of degrees of
freedom![[*]](/icons/foot_motif.gif) . This shape generalizes the
single
. This shape generalizes the
single 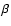 -model profile, introduced by Cavaliere &
Fusco-Femiano (1976) and commonly used to fit X-ray surface
brightness profiles, to a double
-model profile, introduced by Cavaliere &
Fusco-Femiano (1976) and commonly used to fit X-ray surface
brightness profiles, to a double 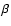 -model of the density
that has the freedom of following both the central spike in
density and the gentler outer distribution. A double
-model of the density
that has the freedom of following both the central spike in
density and the gentler outer distribution. A double
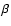 -model of the surface brightness was first used by Mohr
et al. (1999) to fit X-ray data of galaxy clusters, and the density
model of Eq. (81) was further developed by La Roque et al. (2006).
The X-ray surface brightness is related to the gas density as
-model of the surface brightness was first used by Mohr
et al. (1999) to fit X-ray data of galaxy clusters, and the density
model of Eq. (81) was further developed by La Roque et al. (2006).
The X-ray surface brightness is related to the gas density as
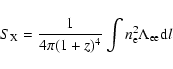 |
(82) |
where z is the cluster redshift,
 the X-ray
cooling function, and it is a function of plasma temperature and
energy in the rest frame of the cluster, including contributions
from relativistic electron-ion thermal bremsstrahlung,
electron-electron thermal bremsstrahlung, recombination, and two
photon processes. The cluster angular diameter distance
the X-ray
cooling function, and it is a function of plasma temperature and
energy in the rest frame of the cluster, including contributions
from relativistic electron-ion thermal bremsstrahlung,
electron-electron thermal bremsstrahlung, recombination, and two
photon processes. The cluster angular diameter distance
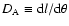 ,
where
,
where 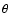 is the line-of-sight angular
size, can be inferred with a joint analysis of SZE, taking
advantage of the different density dependence of the X-ray
emission and SZE decrement:
is the line-of-sight angular
size, can be inferred with a joint analysis of SZE, taking
advantage of the different density dependence of the X-ray
emission and SZE decrement:
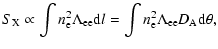 |
|
|
(83) |
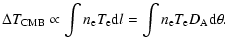 |
|
|
|
It turns out that
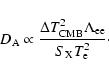 |
(84) |
Note that 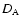 is
proportional to
is
proportional to
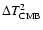 and
and
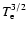 (since
(since
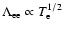 ), so the
distance determination is strongly dependent on the accuracy of the
SZE decrement and X-ray temperature measurements.
), so the
distance determination is strongly dependent on the accuracy of the
SZE decrement and X-ray temperature measurements.
Recently distances to 18 clusters with redshift ranging from
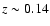 to
to
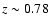 have been determined from a likelihood joint
analysis of SZE and X-ray observations (see Table 7 in
Reese et al. 2002). Our analysis used angular diameter
distance measurements for a sample of 83 clusters, containing the 18
above-mentioned clusters, another 24 known previously (see
Birkinshaw 1999), and a recently released sample with the measurement of
the angular diameter distances from the Chandra X-ray imaging
and Sunyaev-Zel'dovich effect mapping of 39 high-redshift clusters
of galaxies (
have been determined from a likelihood joint
analysis of SZE and X-ray observations (see Table 7 in
Reese et al. 2002). Our analysis used angular diameter
distance measurements for a sample of 83 clusters, containing the 18
above-mentioned clusters, another 24 known previously (see
Birkinshaw 1999), and a recently released sample with the measurement of
the angular diameter distances from the Chandra X-ray imaging
and Sunyaev-Zel'dovich effect mapping of 39 high-redshift clusters
of galaxies (
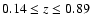 )
(Bonamente et al. 2005). The
unprecedented spatial resolution of Chandra, combined with
its simultaneous spectral resolution, allows a more accurate
determination of distances. Let us consider the merit function of
the form
)
(Bonamente et al. 2005). The
unprecedented spatial resolution of Chandra, combined with
its simultaneous spectral resolution, allows a more accurate
determination of distances. Let us consider the merit function of
the form
![$\displaystyle \chi^2(s, {\widehat H}_0) = \frac{1}{N - 3} \sum_{i =
1}^{N}\left[ \frac{(D_{\rm A}(z_i; s, {\widehat H}_0)-D_i) }{\sigma_i}
\right]^2\cdot$](/articles/aa/full/2008/14/aa7045-06/img336.gif) |
|
|
(85) |
Fitting the data we obtain
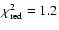 for 83 data points, and the best-fit values are
for 83 data points, and the best-fit values are
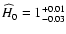 ,
s=-1.49+0.03-0.09 and
,
s=-1.49+0.03-0.09 and
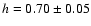 .
In Fig. 19 we compare the best-fit curve with the
observational SZE data.
.
In Fig. 19 we compare the best-fit curve with the
observational SZE data.
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{7045fig19.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg339.gif) |
Figure 19:
Observational SZE data fitted to our model with
the best-fit values
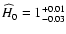 ,
s=-1.49+0.03-0.09, and ,
s=-1.49+0.03-0.09, and
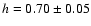 .
The empty boxes indicate distance
measurements for a sample of 44 mentioned clusters
(see Birkinshaw 1999; Reese et al. 2002),while the filled diamonds indicate the measurement
of the angular diameter distances from Chandra X-ray imaging
and Sunyaev-Zel'dovich effect mapping of 39 high-redshift clusters
(Bonamente et al. 2005). .
The empty boxes indicate distance
measurements for a sample of 44 mentioned clusters
(see Birkinshaw 1999; Reese et al. 2002),while the filled diamonds indicate the measurement
of the angular diameter distances from Chandra X-ray imaging
and Sunyaev-Zel'dovich effect mapping of 39 high-redshift clusters
(Bonamente et al. 2005). |
| Open with DEXTER |
Gamma-ray bursts (GRBs) are bright explosions visible across
most of the Universe, certainly out to redshifts of 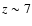 and likely out to
and likely out to 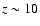 .
Recent studies have pointed out
that GRBs may be used as standard cosmological candles
(Friedman & Bloom 2005; Ghirlanda et al. 2004). It turns out that the energy
released during bursts spans nearly three orders of magnitude,
and the distribution of the opening angles of the emission, as
deduced from the timing of the achromatic steepening of the
afterglow emission, spans a similar wide range of values.
However, when the apparently isotropic energy release and the
conic opening of the emission are combined to infer the
intrinsic, true energy release, the resulting distribution does
not widen, as is expected for uncorrelated data, but shrinks to
a very well-determined value (Frail & Kulkarni 2003), with a remarkably
small (one-sided) scattering, corresponding to about a factor
of 2 in total energy. Similar studies in the X-ray band have
reproduced the same results. It is thus very tempting to study
to what extent this property of GRBs makes them suitable
cosmological standard candles. Schaefer (2003)
proposed to use the two well-known correlations of the GRBs
luminosity (with variability and with time delay), while others
have exploited the recently reported relationship between the
beaming-corrected
.
Recent studies have pointed out
that GRBs may be used as standard cosmological candles
(Friedman & Bloom 2005; Ghirlanda et al. 2004). It turns out that the energy
released during bursts spans nearly three orders of magnitude,
and the distribution of the opening angles of the emission, as
deduced from the timing of the achromatic steepening of the
afterglow emission, spans a similar wide range of values.
However, when the apparently isotropic energy release and the
conic opening of the emission are combined to infer the
intrinsic, true energy release, the resulting distribution does
not widen, as is expected for uncorrelated data, but shrinks to
a very well-determined value (Frail & Kulkarni 2003), with a remarkably
small (one-sided) scattering, corresponding to about a factor
of 2 in total energy. Similar studies in the X-ray band have
reproduced the same results. It is thus very tempting to study
to what extent this property of GRBs makes them suitable
cosmological standard candles. Schaefer (2003)
proposed to use the two well-known correlations of the GRBs
luminosity (with variability and with time delay), while others
have exploited the recently reported relationship between the
beaming-corrected 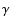 -ray energy and the locally observed
peak energy of GRBs (see for instance Dai et al. 2004). As for the
possible variation of ambient density from burst to burst, which
may widen the distribution of bursts energies, Frail & Kulkarni
(2003) note that this spread is already contained in
their data sample, and yet the distribution of energy released
is still very narrow. There are at least two reasons GRBs
are better than type Ia supernovae as cosmological candles. On
the one hand, GRBs are easy to find and locate: even 1980s
technology allowed BATSE to locate
-ray energy and the locally observed
peak energy of GRBs (see for instance Dai et al. 2004). As for the
possible variation of ambient density from burst to burst, which
may widen the distribution of bursts energies, Frail & Kulkarni
(2003) note that this spread is already contained in
their data sample, and yet the distribution of energy released
is still very narrow. There are at least two reasons GRBs
are better than type Ia supernovae as cosmological candles. On
the one hand, GRBs are easy to find and locate: even 1980s
technology allowed BATSE to locate 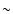 1 GRB per day, making
the build-up of a 300-object database a one-year enterprise.
The Swift satellite launched on 20 November 2004, detects
GRBs at about the same rate as BATSE, but with a nearly perfect
capacity for identifying their redshifts simultaneously with the
afterglow observations
1 GRB per day, making
the build-up of a 300-object database a one-year enterprise.
The Swift satellite launched on 20 November 2004, detects
GRBs at about the same rate as BATSE, but with a nearly perfect
capacity for identifying their redshifts simultaneously with the
afterglow observations![[*]](/icons/foot_motif.gif) .
Second, GRBs have been detected out to very high redshifts: even
the current sample contains several events with z> 3, with one
(GRB 000131) at z = 4.5 and another at z=6.3. This should be
contrasted with the difficulty of locating SN at z > 1 and
absence of any SN with z
> 2. On the other hand, the distribution of luminosities of SNIa is
narrower than the distribution of energy released by GRBs,
corresponding to a magnitude dispersion
.
Second, GRBs have been detected out to very high redshifts: even
the current sample contains several events with z> 3, with one
(GRB 000131) at z = 4.5 and another at z=6.3. This should be
contrasted with the difficulty of locating SN at z > 1 and
absence of any SN with z
> 2. On the other hand, the distribution of luminosities of SNIa is
narrower than the distribution of energy released by GRBs,
corresponding to a magnitude dispersion
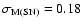 rather than
rather than
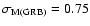 .
Therefore GRBs may provide a
complementary standard candle, out to distances that cannot be
probed by SNIa, their major limitation being the larger intrinsic
scatter of the energy released, as compared to the small scatter in
peak luminosities of SNIa. There currently exists enough information
to calibrate luminosity distances and independent redshifts for nine
bursts (Schaefer 2003). These bursts were all detected by BATSE
with redshifts measured from optical spectra of either the afterglow
or the host galaxy. The highly unusual GRB980425 (associated with
supernova SN1998bw) is not included because it is likely to be
qualitatively different from the classical GRBs. Bursts with red
shifts that were not recorded by BATSE still cannot have their
observed parameters converted to energies and fluxes that are
comparable with BATSE data. For the present analysis we use a
sample of GRBs that had their redshifts estimated (),
as represented in Fig. 20, with
the distance modulus
.
Therefore GRBs may provide a
complementary standard candle, out to distances that cannot be
probed by SNIa, their major limitation being the larger intrinsic
scatter of the energy released, as compared to the small scatter in
peak luminosities of SNIa. There currently exists enough information
to calibrate luminosity distances and independent redshifts for nine
bursts (Schaefer 2003). These bursts were all detected by BATSE
with redshifts measured from optical spectra of either the afterglow
or the host galaxy. The highly unusual GRB980425 (associated with
supernova SN1998bw) is not included because it is likely to be
qualitatively different from the classical GRBs. Bursts with red
shifts that were not recorded by BATSE still cannot have their
observed parameters converted to energies and fluxes that are
comparable with BATSE data. For the present analysis we use a
sample of GRBs that had their redshifts estimated (),
as represented in Fig. 20, with
the distance modulus 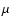 ,
given by Eq. (72).
,
given by Eq. (72).
To this aim, the only difference with respect to the SNIa is that
we slightly modify the correction term of Eq. (73) and take
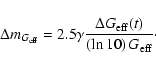 |
(86) |
We expect that 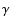 is of order unity, so that the
G-correction would be roughly half a magnitude. We obtain
is of order unity, so that the
G-correction would be roughly half a magnitude. We obtain
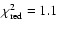 for 24 data points and the best-fit value
is
for 24 data points and the best-fit value
is
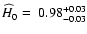 ,
s=-1.43+0.02-0.04, which are compatible with the SNIa
results. We also find that
,
s=-1.43+0.02-0.04, which are compatible with the SNIa
results. We also find that  ,
which appears in Eq. (86), is equal to 1.5. In Fig. 20
we compare the best-fit curve with both the GRBs and the SNIa
Gold Sample.
,
which appears in Eq. (86), is equal to 1.5. In Fig. 20
we compare the best-fit curve with both the GRBs and the SNIa
Gold Sample.
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{7045fig20.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg349.gif) |
Figure 20:
Observational Hubble diagram for the recent SNIa sample
compiled by Riess et al. (2006) (empty lozenges), and the GRBs
data by () (empty boxes) fitted to our model. The
solid curve is the best-fit curve with,
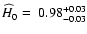 ,
s=-1.43+0.02-0.04. The
red dashed line corresponds to the standard ,
s=-1.43+0.02-0.04. The
red dashed line corresponds to the standard 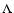 CDM model
with CDM model
with
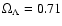 . . |
| Open with DEXTER |
Measurements of the gas mass fraction in galaxy clusters have been
proposed as a test of cosmological models (Allen et al. 2002). Both
theoretical arguments and numerical simulations predict that the
baryonic mass fraction in the largest relaxed galaxy clusters should
not depend on the redshift and should provide an estimate of the
cosmological baryonic density parameter
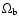 (Eke et al. 1998).
The baryonic content in galaxy clusters is dominated by the hot
X-ray emitting intra-cluster gas so that what is actually
measured is the gas mass fraction
(Eke et al. 1998).
The baryonic content in galaxy clusters is dominated by the hot
X-ray emitting intra-cluster gas so that what is actually
measured is the gas mass fraction
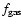 ,
and it is this quantity
that should not depend on the redshift. Moreover, it is expected
that the baryonic mass fraction in clusters is equal to the
universal ratio
,
and it is this quantity
that should not depend on the redshift. Moreover, it is expected
that the baryonic mass fraction in clusters is equal to the
universal ratio
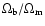 so that
so that
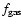 should indeed
be given by
should indeed
be given by
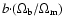 ,
where the
multiplicative factor b is motivated by simulations that suggest
that the gas fraction is lower than the universal ratio. Following
the procedure described in Allen et al. (2002, 2004), and already
used in Paper I we adopt the standard CDM model (i.e., a flat
universe with
,
where the
multiplicative factor b is motivated by simulations that suggest
that the gas fraction is lower than the universal ratio. Following
the procedure described in Allen et al. (2002, 2004), and already
used in Paper I we adopt the standard CDM model (i.e., a flat
universe with
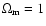 and h = 0.5) as a reference cosmology
in making the measurements, so that the theoretical expectation for
the apparent variation of
and h = 0.5) as a reference cosmology
in making the measurements, so that the theoretical expectation for
the apparent variation of
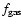 with the redshift is
with the redshift is
![\begin{displaymath}f_{\rm gas}(z) = \frac{b \Omega_b}{(1 + 0.19 \sqrt{h}) \Omega...
...{\rm A}^{\rm SCDM}(z)}{D_{\rm A}^{\rm mod}(z)} \right ]^{1.5},
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img354.gif) |
(87) |
where we substitute the appropriate expression of
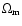 for
our model, and
for
our model, and
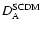 and
and
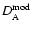 are the angular
diameter distance for the SCDM and our model respectively. Allen
et al. (2002) have extensively analyzed the set of
simulations in Eke et al. (1998) to get
are the angular
diameter distance for the SCDM and our model respectively. Allen
et al. (2002) have extensively analyzed the set of
simulations in Eke et al. (1998) to get
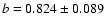 ,
so we set b = 0.824 in our analysis below. Actually, we checked that, for values in the
,
so we set b = 0.824 in our analysis below. Actually, we checked that, for values in the  range quoted above,
the main results do not depend on b. Moreover we defined
the following merit function:
range quoted above,
the main results do not depend on b. Moreover we defined
the following merit function:
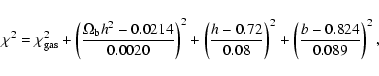 |
(88) |
where
![\begin{displaymath}\chi_{\rm gas}^2 = \sum_{i = 1}^{N_{\rm gas}}{\left [ \frac{f...
...0) - f_{\rm gas}^{\rm obs}(z_i)}{\sigma_{\rm gi}} \right
]^2}.
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img361.gif) |
(89) |
Here
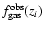 is the measured gas fraction in galaxy
clusters at redshift zi with an error
is the measured gas fraction in galaxy
clusters at redshift zi with an error
 ,
and the
sum is over the
,
and the
sum is over the
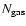 clusters considered. Let us note that
recently Allen et al. (2004) have released a catalog of
26 large relaxed clusters with a precise measurement of both the
gas mass fraction
clusters considered. Let us note that
recently Allen et al. (2004) have released a catalog of
26 large relaxed clusters with a precise measurement of both the
gas mass fraction
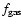 and the redshift z. We use these
data to perform our likelihood analysis, we get
and the redshift z. We use these
data to perform our likelihood analysis, we get
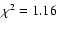 for 26 data points, and
s=-1.39+0.04-0.01,
for 26 data points, and
s=-1.39+0.04-0.01,
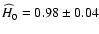 ,
,
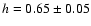 ,
and
,
and
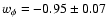 .
A brief comparison of our results with similar recent
results from Lima et al. (2003), where the equation of
state characterizing the dark energy component is constrained by
using galaxy clusters x-ray data and can still be done. Their
analysis, however, considers quintessence models in
the standard gravity theories, with a non evolving equation of
state, but they allow the so-called phantom dark energy with w
< -1, which violates the null-energy condition. As the best
fit value of w to the data of Allen et al. (2002) they obtain
w=-1.29-0.792+0.686. In order to directly compare this
result with our analysis, we first fit the model considered in
Lima et al. (2003) to the updated and wider data set of
Allen et al. (2004), used in our analysis. To this aim we also refer
to the model function
.
A brief comparison of our results with similar recent
results from Lima et al. (2003), where the equation of
state characterizing the dark energy component is constrained by
using galaxy clusters x-ray data and can still be done. Their
analysis, however, considers quintessence models in
the standard gravity theories, with a non evolving equation of
state, but they allow the so-called phantom dark energy with w
< -1, which violates the null-energy condition. As the best
fit value of w to the data of Allen et al. (2002) they obtain
w=-1.29-0.792+0.686. In order to directly compare this
result with our analysis, we first fit the model considered in
Lima et al. (2003) to the updated and wider data set of
Allen et al. (2004), used in our analysis. To this aim we also refer
to the model function
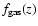 and the merit function
and the merit function
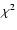 ,
defined in Eqs. (87) and (88), respectively. We get
,
defined in Eqs. (87) and (88), respectively. We get
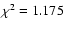 for 26 data
points, and
for 26 data
points, and
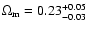 ,
h=0.76+0.04-0.09, and
,
h=0.76+0.04-0.09, and
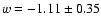 ,
so w<-1, which
corresponds to a phantom energy. Let us note that our model
instead gives
,
so w<-1, which
corresponds to a phantom energy. Let us note that our model
instead gives
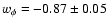 ,
what does not violate the
null energy condition. In Fig. 21 we compare
the best-fit curves for our and the Lima et al. model with the
observational data.
,
what does not violate the
null energy condition. In Fig. 21 we compare
the best-fit curves for our and the Lima et al. model with the
observational data.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig21.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg374.gif) |
Figure 21:
The best-fit curve to the
 data for our nmc model (red thick line) and for the quintessence model (black thick line)
considered in Lima et al. (2003). It is interesting to note that, as pointed out also for the model described in Demianski et al. (2006),
even if the statistical significance of the best-fit procedure for these two models is comparable, the best fit relative to our nmc model seems
to be dominated by smaller redshift data,
and the one relative to the Lima et al. model by higher redshift data.
data for our nmc model (red thick line) and for the quintessence model (black thick line)
considered in Lima et al. (2003). It is interesting to note that, as pointed out also for the model described in Demianski et al. (2006),
even if the statistical significance of the best-fit procedure for these two models is comparable, the best fit relative to our nmc model seems
to be dominated by smaller redshift data,
and the one relative to the Lima et al. model by higher redshift data. |
| Open with DEXTER |
In this section we consider the evolution of scalar density
perturbations in the longitudinal gauge d
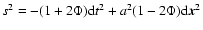 .
It is well-known that in the
framework of the minimally-coupled theory, where we have to deal
with a fully relativistic component, that becomes homogeneous on smaller
scales than the horizon, the standard quintessence
cannot cluster on such scales. In the non minimally-coupled
quintessence theories it is instead possible to separate a pure
gravitational term both in the stress-energy tensor
.
It is well-known that in the
framework of the minimally-coupled theory, where we have to deal
with a fully relativistic component, that becomes homogeneous on smaller
scales than the horizon, the standard quintessence
cannot cluster on such scales. In the non minimally-coupled
quintessence theories it is instead possible to separate a pure
gravitational term both in the stress-energy tensor
 and in the energy density
and in the energy density 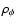 ,
so the situation changes, and
it is necessary to consider also fluctuations of the scalar field.
However, it turns out (Boisseau et al. 2000; Riazuelo & Uzan 2002) that the equation for
dust-like matter density perturbations inside the horizon can be
written as follows
,
so the situation changes, and
it is necessary to consider also fluctuations of the scalar field.
However, it turns out (Boisseau et al. 2000; Riazuelo & Uzan 2002) that the equation for
dust-like matter density perturbations inside the horizon can be
written as follows
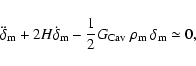 |
(90) |
where
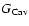 is the effective gravitational constant
defined by
is the effective gravitational constant
defined by
![\begin{displaymath}G_{\rm Cav}=
~-\frac{1}{2\xi(s)\phi^2}\left[\frac{1+16\xi(s)}{1+12\xi(s)}\right]\cdot
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img379.gif) |
(91) |
Equation (90) describes, in the non minimally coupled
models, the evolution of the CDM density contrast,
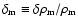 ,
for perturbations inside the horizon. In
our model Eq. (90) is rather complicated and takes the
form
,
for perturbations inside the horizon. In
our model Eq. (90) is rather complicated and takes the
form
Equation (92) does not admit exact solutions and can only be
solved numerically. However, since with our choice of
normalization the whole history of the Universe is confined to
the range ![$t\in[0,1]$](/articles/aa/full/2008/14/aa7045-06/img385.gif) ;
therefore, to study the behavior of
solutions for
;
therefore, to study the behavior of
solutions for 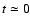 ,
we can always expand the functions in
Eq. (92) in series around t=0, in order to get
approximate solutions. Actually, we obtain an integrable Fuchsian
differential equation, which is a hypergeometric equation. We
then use such a solution to set the initial conditions at t=0to numerically integrate Eq. (92) in the whole range
[0,1]. We use the growing mode
,
we can always expand the functions in
Eq. (92) in series around t=0, in order to get
approximate solutions. Actually, we obtain an integrable Fuchsian
differential equation, which is a hypergeometric equation. We
then use such a solution to set the initial conditions at t=0to numerically integrate Eq. (92) in the whole range
[0,1]. We use the growing mode 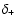 and define the
growth index f as
and define the
growth index f as
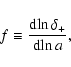 |
(93) |
where a is the scale factor.
Once we know how the growth index f evolves with redshift
and how it depends on our model parameters, we can use the
available observational data to estimate the values of these
parameters and the present value of
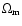 .
The
2dFGRS team has recently collected positions and redshifts of
about 220 000 galaxies and presented a detailed analysis of the
two-point correlation function. They measured the redshift
distortion parameter
.
The
2dFGRS team has recently collected positions and redshifts of
about 220 000 galaxies and presented a detailed analysis of the
two-point correlation function. They measured the redshift
distortion parameter
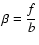 ,
where b is
the bias parameter describing the difference in the distribution
of galaxies and mass, and find that
,
where b is
the bias parameter describing the difference in the distribution
of galaxies and mass, and find that
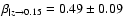 and
and
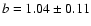 .
From the
observationally determined
.
From the
observationally determined  and b, it is now
straightforward to get the value of the growth index at z=0.15corresponding to the effective depth of the survey. Verde et al. (2001) used the bispectrum of 2dFGRS galaxies, and
Lahav et al. (2002) combined the 2dFGRS data with CMB
data, and they obtained
and b, it is now
straightforward to get the value of the growth index at z=0.15corresponding to the effective depth of the survey. Verde et al. (2001) used the bispectrum of 2dFGRS galaxies, and
Lahav et al. (2002) combined the 2dFGRS data with CMB
data, and they obtained
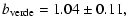 |
|
|
(94) |
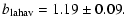 |
|
|
(95) |
Using these two values for b, we calculated the value of the
growth index f at z=0.15 to get, respectively,
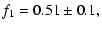 |
|
|
(96) |
 |
|
|
(97) |
To evaluate the growth index at z=0.15 we first have to invert the
z-t relation and find t(0.15): actually the z-t relation is
rather involved and cannot be analytically inverted, so we perform
this inversion numerically. Finally, we get
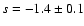
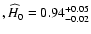 ,
,
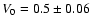 ,
which
corresponds to
,
which
corresponds to
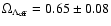 .
In Fig. 22 we show how the growth index is changing
with redshift in our non minimally-coupled model as compared with
the standard
.
In Fig. 22 we show how the growth index is changing
with redshift in our non minimally-coupled model as compared with
the standard  CDM model, with
CDM model, with
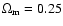 ,
and a
quintessence model, the minimally-coupled exponential model
described in Demianski et al. (2005). We note that at low redshift, theoretical
predictions of these different models are not distinguishable, so
independent measurements from large redshift surveys at different
depths could disentangle this degeneracy.
,
and a
quintessence model, the minimally-coupled exponential model
described in Demianski et al. (2005). We note that at low redshift, theoretical
predictions of these different models are not distinguishable, so
independent measurements from large redshift surveys at different
depths could disentangle this degeneracy.
In this paper we have extended the analysis that we performed in
Paper I (where we have analyzed a special extended quintessence model, based on one of the most
commonly used quintessence potentials
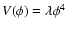 ,
corresponding to the coupling
,
corresponding to the coupling
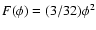 ), considering a new and wider class of
theories for which exact solutions of the Einstein
equations are known. We also discussed how it is possible in such models
to treat the fine-tuning problem in an alternative way. We have shown that an epoch of accelerated expansion appears
in a natural way in the family of such models
selected by requiring that their corresponding point like Lagrangian
admits a Noether symmetry. In the non minimally-coupled scalar tensor theory
of gravity, it is possible to perform an appropriate conformal
transformation and to move from the Jordan picture to the standard
Einstein one, but then matter becomes coupled to the scalar field. We
explored both descriptions and also considered the neutrino
mass varying model as a possible example of non minimally-coupled
scalar tensor theory.
), considering a new and wider class of
theories for which exact solutions of the Einstein
equations are known. We also discussed how it is possible in such models
to treat the fine-tuning problem in an alternative way. We have shown that an epoch of accelerated expansion appears
in a natural way in the family of such models
selected by requiring that their corresponding point like Lagrangian
admits a Noether symmetry. In the non minimally-coupled scalar tensor theory
of gravity, it is possible to perform an appropriate conformal
transformation and to move from the Jordan picture to the standard
Einstein one, but then matter becomes coupled to the scalar field. We
explored both descriptions and also considered the neutrino
mass varying model as a possible example of non minimally-coupled
scalar tensor theory.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig22.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg400.gif) |
Figure 22:
The growth index f in different cosmological
models.
The thick dashed red line corresponds to our non minimally-coupled model. The blue thin dashed curve corresponds to the standard  CDM model with CDM model with
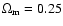 ,
and the
black solid line corresponds to another quintessence
model with an exponential potential (described in Demianski et al. 2005). ,
and the
black solid line corresponds to another quintessence
model with an exponential potential (described in Demianski et al. 2005). |
| Open with DEXTER |
Table 2:
The basic cosmological parameters derived from our model
are compared with observational data.
It turns out that the imposed requirement of a Noether
symmetry is quite restrictive, so we obtained a family of models
that is fully specified by 3 parameters: a parameter s that
determines the strength of the non-minimal coupling and the
potential of the scalar field, H0 as the Hubble constant, and a
parameter V0 that determines the scale of the potential. To
determine the values of these parameters, we compared predictions of
our model with several independent observational data. The results
of this parameter determination procedure are presented in Table 2.
We see that with our average value of s= - 1.46 the scale factor,
for small t, is changing as
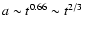 ,
and for
large t, as
,
and for
large t, as
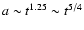 while
while
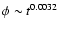 and
and
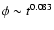 in corresponding asymptotic
regimes. The potential V decays to zero for large t, after
reaching a maximum value (see Fig. 23). Similarly,
the effective gravitational coupling
in corresponding asymptotic
regimes. The potential V decays to zero for large t, after
reaching a maximum value (see Fig. 23). Similarly,
the effective gravitational coupling
 decreases for large t, until it becomes zero for
decreases for large t, until it becomes zero for
 (we have a sort of asymptotic freedom at
(we have a sort of asymptotic freedom at
 ). It turns out that in our model the
observational constraints on the variation of the effective
gravitational constant are respected. Actually a new analysis of the
Big Bang Nucleosynthesis (Copi et al. 2004) restricts the variations in G to
). It turns out that in our model the
observational constraints on the variation of the effective
gravitational constant are respected. Actually a new analysis of the
Big Bang Nucleosynthesis (Copi et al. 2004) restricts the variations in G to
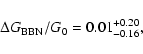 |
(98) |
at a  confidence level, where
confidence level, where
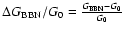 ,
and
,
and
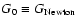 .
The
combined analysis of the new 4He and WMAP data implies that
.
The
combined analysis of the new 4He and WMAP data implies that
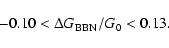 |
(99) |
A recent analysis of the secular variation of the period of
nonradial pulsations of the white dwarf G117-B15A
shows (Benvenuto et al. 2004) that
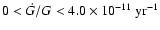 at 2
at 2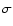 ,
which is of the same order of magnitude as
previous independent bounds (see also Biesiada & Malec 2004). With our unit
of time this becomes
,
which is of the same order of magnitude as
previous independent bounds (see also Biesiada & Malec 2004). With our unit
of time this becomes
 ,
where
,
where
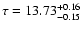 as given by the WMAP team (Spergel et al. 2006).
as given by the WMAP team (Spergel et al. 2006).
Initially, for small t, the matter energy density is higher than the energy
density of the scalar field. In Table 2 we present results of our analysis, and they
show that predictions of our model are fully compatible with the
recent observational data. Comparing results of this paper with
our previous analysis of minimally coupled scalar field models
(see Paper I), we conclude that the present-day observational
data connected with the post recombination evolution of the
universe can be fitted by several different models of
quintessence. More data on high-redshift supernovae of type Ia
and GRBs are needed, as is more information on the early
phase of structure formation in order to place stronger
restrictions on the allowed type of dark energy.
Acknowledgements
This work was supported in part by the grant of Polish Ministry of
Science and Higher Education 1-P03D-014-26, and by INFN Na12. The
authors are very grateful to Professor Djorgovski for providing the
data that we used in Sect. 3.1.1, and to Professors Verde and Simon,
for providing the data used in Sect. 3.2.2. Of course we take full
responsibility for the fitting procedure.
- Accetta, F. S.,
Zoller, D. J., & Turner, M. S. 1985, Phys. Rev. D, 31,
3064 [NASA ADS] [CrossRef]
- Acquaviva, V.,
Baccigalupi, C., Leach, S. M., Liddle, A. R., & Perrotta, F.
2005, Phys. Rev. D, 71, 104025 [NASA ADS] [CrossRef]
(In the text)
- Allen, S. W.,
Schmidt, R. W., & Fabian, A. C. 2002, MNRAS, 334, L11 [NASA ADS] [CrossRef]
(In the text)
- Allen, S. W., Schmidt,
R. W., Ebelling, H., Fabian, A. C., & van Speybroeck, L.
2004, MNRAS, 353, 457 [NASA ADS] [CrossRef]
- Amendola, L. 1999, Phys.Rev.
D, 60, 043501 [NASA ADS]
(In the text)
- Amendola, L.,
Gasperini, M., & Piazza, F. 2004, JCAP, 9, 014 [NASA ADS]
- Astier, P., Guy, J.,
Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Benvenuto, O. G.,
Garcia-Berro, E., & Isern, J. 2004, Phys. Rev. D, 69,
082002 [NASA ADS] [CrossRef]
(In the text)
- Bertotti, B., Iess,
L., & Tortora, P. 2003, Nature, 425, 374 [NASA ADS] [CrossRef]
- Bi, X.-J., Gu,
P., Wang, X., & Zhang, X. 2004, Phys. Rev. D, 69, 113007 [NASA ADS] [CrossRef]
- Biesiada, M., & Malec,
B. 2004, MNRAS, 350, 644 [NASA ADS] [CrossRef]
(In the text)
- Birkinshaw, M. 1999, Phys.
Rep., 310, 97 [NASA ADS] [CrossRef]
(In the text)
- Bloom, J. S., Frail,
D. A., & Kulkarni, S. R. 2003, ApJ, 594, 674 [NASA ADS] [CrossRef]
- Bonamente, M.,
Joy, M., La Roque, S., et al. 2005
[arXiv:astro-ph/0512349]
(In the text)
- Brookfield, A. W., van
de Bruck, C., Mota, D. F., & Tocchini-Valentini, D. 2006a,
Phys. Rev. Lett., 96, 061301 [NASA ADS] [CrossRef]
- Brookfield, A. W., van
de Bruck, C., Mota, D. F., & Tocchini-Valentini, D. 2006b,
Phys. Rev. D, 73, 083515 [NASA ADS] [CrossRef]
- Boisseau, B.,
Esposito-Farese, G., Polarski, D., & Starobinsky, A. A. 2000,
Phys. Rev. Lett., 85, 2236 [NASA ADS] [CrossRef]
- Caldwell, R. R., Dave, R., &
Steinhardt, P. J. 1998, Phys. Rev. Lett., 80, 1582 [NASA ADS] [CrossRef]
(In the text)
- Caldwell, R. R.,
Kamionkowski, M., & Weinberg, N. N. 2003, Phys. Rev. Lett., 91,
071301 [NASA ADS] [CrossRef]
- Capozziello, S., de Ritis,
R., Rubano, C., & Scudellaro, P. 1996, Riv. Nuovo Cimento, 19,
4
- Capozziello, S., de
Ritis, R., & Marino, A. A. 1997, Class. Quant. Grav., 14,
3243 [NASA ADS] [CrossRef]
- Cavaliere, A.,
& Fusco-Femiano, R. 1976, 49, 137
- Cavaliere,
A., & Fusco-Femiano, R. 1978, A&A, 70, 677 [NASA ADS]
- Clifton, T., Mota, D.
F., & Barrow, J. D. 2005, MNRAS, 358, 601 [NASA ADS] [CrossRef]
- Copi, C. J., Davis, A. N.,
& Krauss, L. M. 2004, Phys. Rev. Lett., 92, 171301 [NASA ADS] [CrossRef]
(In the text)
- Crooks, J. L., &
Frampton, P. H. 2006, Phys. Rev. D, 73, 123512 [NASA ADS] [CrossRef]
- Cyburt, R. H., Fields, B.
D., Olive, K. A., & Skillman, E. 2005, Astropart. Phys., 23,
313 [NASA ADS] [CrossRef]
- Dai, Z. G., Liang, E. W.,
& Xu, D. 2004, ApJ, 612 L101
(In the text)
- Daly, R. A., &
Djorgovski, S. G. 2004, ApJ, 612, 652 [NASA ADS] [CrossRef]
(In the text)
- Daly, R., & Djorgovski,
S. G., 2005 [arXiv:astro-ph/0512576]
(In the text)
- Das, S., Corasaniti, P.,
& Khoury, J. 2006, Phys. Rev. D, 73, 083509 [NASA ADS] [CrossRef]
(In the text)
- De La Macorra,
A., Melchiorri, A., Serra, P., & Bean, R. 2007, Astroparticle
Physics, 27, 406 [NASA ADS] [CrossRef]
(In the text)
- Demianski, M., de Ritis, R.,
Marmo, G., Platania, G., & Stornaoiolo, C. 1991, Phys. Rev. D,
44, 3136 [NASA ADS] [CrossRef]
- Demianski, M., de Ritis, R.,
Marino, A. A., & Piedipalumbo, E. 2003, A&A, 411, 33 [NASA ADS] [CrossRef] [EDP Sciences]
- Demianski, M., Piedipalumbo,
E., Rubano, C., & Tortora, C. 2005, A&A, 431, 27 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Demianski, M., Piedipalumbo,
E., Rubano, C., & Tortora, C. 2006, A&A, 454, 55 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- de Ritis, R., Marino, A.
A., Rubano, C., & Scudellaro, P. 2000, Phys. Rev. D, 62,
043506 [NASA ADS] [CrossRef]
(In the text)
- Damour, T., &
Esposito-Farese, G. 1993, Phys. Rev. Lett., 70, 2220 [NASA ADS] [CrossRef]
(In the text)
- Eke, V., Navarro, J. F.,
& Frenk, C. S. 1998, ApJ, 503, 569 [NASA ADS] [CrossRef]
(In the text)
- Elliott, S. R., &
Engel, J. 2004, J.Phys. G, 30, R 183
(In the text)
- Ellis, J., Lahanas, A. B.,
Nanopoulos, D. V., & Tamvakis, K. 1984, Phys. Lett. B, 134,
429 [NASA ADS] [CrossRef]
-
Esposito Farese, G. 2004, AIP Conf. Proc., 736, 35 [NASA ADS]
(In the text)
- Faraoni, V. 2000,
Phys. Rev. D, 62, 023504 [NASA ADS] [CrossRef]
- Fardon, R., Nelson, A.
E., & Weiner, N. 2004, JCAP 0410:005
(In the text)
- Frail, D. A., &
Kulkarni, S. R. 2003, ApJ, 594, 674 [NASA ADS] [CrossRef]
(In the text)
- Friedman, A. S., &
Bloom J. S. 2005, ApJ, 627, 1 [NASA ADS] [CrossRef]
- Garcia-Bellido, J.
1997, Phys. Rev. D, 55, 4603 [NASA ADS] [CrossRef]
- Gaztañaga, E.,
Garcia-Berro, E., Isern, J., Bravo, E., & Dominguez 2001, Phys.
Rev. D, 1
- Ghirlanda, G.,
Ghisellini, G., & Lazzati, D. 2004, ApJ, 616, 331 [NASA ADS] [CrossRef]
- Hannestad, S.
2005, Phys. Rev. Lett., 95, 221301 [NASA ADS] [CrossRef]
(In the text)
- Hu, W. 2005, Phys. Rev. D, 71,
047301 [NASA ADS] [CrossRef]
- Jimenez, R., Verde, L.,
Treu, T., & Stern, D. 2003, ApJ, 593, 622 [NASA ADS] [CrossRef]
(In the text)
- Kaplan, D. B., Nelson,
A. E., & Weiner, N. 2004, Phys. Rev. Lett., 93, 091801 [NASA ADS] [CrossRef]
- Klapdor-Kleingrothaus, H.
V. 2006, talk at SNOW, 2nd Scandinavian Neutrino Workshop
(Stockholm, Sweden)
(In the text)
- Klapdor-Kleingrothaus, H.
V., Krivosheina, I. V., Dietz, A., & Chkvorets, O. 2004, Phys.
Lett. B, 586, 198 [NASA ADS] [CrossRef]
(In the text)
- Komatsu, E.,
& Seljak, U. 2001, MNRAS, 327, 1353 [NASA ADS] [CrossRef]
- Lahav, O., Bridle, S. L.,
Percival, W. J., & the 2dFGRS Team 2002, MNRAS, 333, 961 [NASA ADS] [CrossRef]
(In the text)
- La Roque,
S., Bonamente, M., Joy, M., et al. 2006, ApJ, 652, 917 [NASA ADS] [CrossRef]
- Lesgourgues, J., &
Pastor, S. 2006, Phys. Rep., 429, 307 [NASA ADS] [CrossRef]
(In the text)
- Lima, J. A. S.,
Cunha, J. V., & Alcaniz, J. S. 2003, Phys. Rev., D, 68,
023510
- Marino, A. A., & de
Ritis, R. 2001, Phys. Rev. D, 64, 083509 [NASA ADS] [CrossRef]
(In the text)
- Masiero, A., Pietroni, M.,
& Rosati, P. 2000, Phys. Rev. D, 61, 023504 [NASA ADS] [CrossRef]
- Mohr, J., Mathiesen,
B., & Evrard, A. 1999, ApJ, 517, 627 [NASA ADS] [CrossRef]
- Peebles, P. J. E.,
& Ratra, B. 1988, Astrophys. J. Lett., 325, L17 [NASA ADS] [CrossRef]
- Perlmutter, S., Gabi, S.,
Goldhaber, G., et al. 1997, ApJ, 483, 565 [NASA ADS] [CrossRef]
- Rasia, E., Tormen, G.,
& Moscardini, L. 2004, MNRAS, 351, 237 [NASA ADS] [CrossRef]
- Reese, E., Carlstrom, J.
E., Joy, M., et al. 2002, ApJ, 581, 53 [NASA ADS] [CrossRef]
(In the text)
- Riazuelo, A., & Uzan,
J.-P. 2002, Phys. Rev. D, 66, 023525 [NASA ADS] [CrossRef]
- Riess, A. G. 2000,
PASP, 112, 1284 [NASA ADS] [CrossRef]
- Riess, A. G.,
Filippenko, A. V., Challis, P., et al. 1998, AJ, 116,
1009 [NASA ADS] [CrossRef]
- Riess, A. G.,
Strolger, L.-G., Tonry, J., et al. 2004, ApJ, 607, 665 [NASA ADS] [CrossRef]
- Riess, A. G.,
Strolger, L.-G., Casertano, S., et al. 2007
[arXiv:astro-ph/0611572]
(In the text)
- Rubano, C., &
Scudellaro, P. 2002, Gen. Rel. Grav., 34, 307 [CrossRef]
- Rubano, C., Scudellaro,
P., Piedipalumbo, E., Capozziello, S., & Capone, M. 2004, Phys.
Rev. D, 69, 103510 [NASA ADS] [CrossRef]
- Saini, T. D.,
Padmanabhan, T., & Bridle, S. 2003, MNRAS, 343, 533 [NASA ADS] [CrossRef]
- Sanyal, A. K., & Modak,
B. 2001, Class. Q. Grav. 18, 3767
- Sanyal, A. K., Rubano,
C., & Piedipalumbo, E. 2003, Gen. Rel. Grav., 35, 1617 [NASA ADS] [CrossRef]
- Sarazin, C. L. 1988,
X-Ray Emission from Cluster of Galaxies (Cambridge: Cambridge Univ.
Press)
- Schaefer, B. E.
2003, ApJ, 583, L67 [NASA ADS] [CrossRef]
(In the text)
- Schimd, C., Uzan,
J. P., & Riazuelo, A. 2005, Phys. Rev. D, 71, 083512 [NASA ADS] [CrossRef]
(In the text)
- Schmidt, B. P.,
Suntzeff, N. B., Phillips, M. M., et al. 1998, ApJ, 507,
46 [NASA ADS] [CrossRef]
- Shapiro, I. I. 1993,
in General Relativity and Gravitation 12, ed. N. Ashby,
et al., Cambridge University Press
- Shapiro, S. S., Davis, J.
L., Lebach, D. E., & Gregory, J. S. 2004, Phys. Rev. Lett., 92,
121101 [NASA ADS] [CrossRef]
- Shaw, D. J., &
Barrow, J. D. 2005, Phys. Lett. B, 639, 596 [NASA ADS]
- Simon, J., Jimenez, R.,
& Verde, L. 2005, Phys. Rev. D, 71, 123001 [NASA ADS] [CrossRef]
(In the text)
- Spergel, D. N., Bean,
R., Dorè, O., et al. 2006, ApJ, sumitted
- Steinhardt, P. J.,
Wang, L., & Zlatev, I. 1999, Phys. Rev. D, 59, 123504 [NASA ADS] [CrossRef]
- Tonry, J. L., Schmidt, B.
P., Barris, B., et al. 2003, ApJ, 594, 1 [NASA ADS] [CrossRef]
- Torres, D. F. 2002, Phys.
Rev. D, 66, 043522 [NASA ADS] [CrossRef]
- Urena-Lopez, L. A., &
Matos, T. 2000, Phys. Rev. D, 62, 081302 [NASA ADS] [CrossRef]
- Uzan, J. P. 1999, Phys.
Rev. D, 59, 123510 [NASA ADS] [CrossRef]
(In the text)
- Uzan, J. Ph. 2003, Rev. Mod.
Phys., 75, 403 [NASA ADS] [CrossRef]
- Verde, L., Kamionkowski, M.,
Mohr, J. J., & Benson, A. J. 2001, MNRAS, 321, L7 [NASA ADS] [CrossRef]
(In the text)
- Vikman, A. 2005, Phys. Rev.
D, 71, 023515 [NASA ADS] [CrossRef]
- Wang, L., Caldwell, R.
R., Ostriker, J. P., & Steinhardt, P. J. 2000, ApJ, 530,
17 [NASA ADS] [CrossRef]
- Weinberg, S.
1989, Rev. Mod. Phys., 61, 1 [NASA ADS] [CrossRef]
- Will, C. M. 1993, Theory
and Experiments in Gravitational Physics (Cambridge: Cambridge
Univ. Press)
(In the text)
- Williams, J. G., Newhall, X.
X., Dickey, J. O., et al. 1996, Phys. Rev. D, 53, 6730 [NASA ADS] [CrossRef]
- WMAP data at
http://lambda.gsfc.nasa.gov
(In the text)
- Zee, F. 1979, Phys. Rev.
Lett., 42, 417 [NASA ADS] [CrossRef]
- Zeldovich, Ya. B. 1967,
Pis'ma Zh. Eksp. Teor. Fiz., 6, 883 [NASA ADS] (1967, JETP Lett. 6, 316)
Copyright ESO 2008
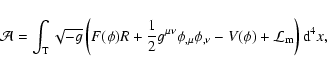
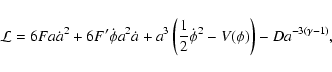
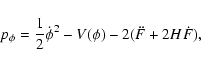
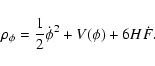
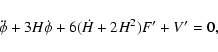
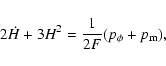
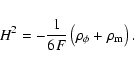
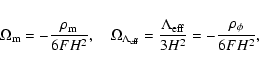
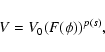
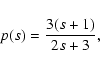
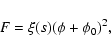
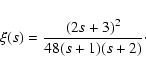
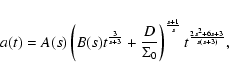
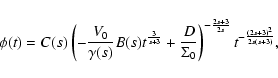
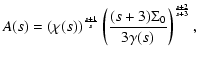
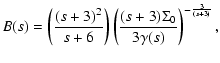
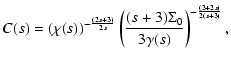
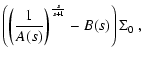

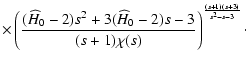
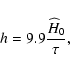
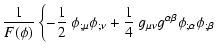
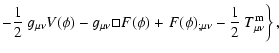
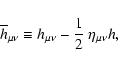
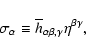
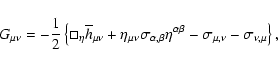
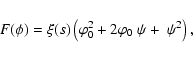
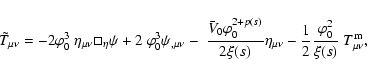
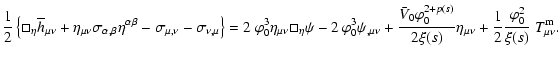
![$\displaystyle \left[\varphi_0^{2}\frac{1-16 \xi(s)}{2\xi(s)(1-12~\xi(s))}\right]\frac{M}{r}$](/articles/aa/full/2008/14/aa7045-06/img168.gif)
![$\displaystyle -\left[{M~\varphi_0^{2}\over 1-12\xi(s)}\frac{\bar{V}_0 (p(s)-4)(p(s)-1)}{1-2~\xi(s)
}\right]r$](/articles/aa/full/2008/14/aa7045-06/img169.gif)
![$\displaystyle - 4\pi \left[\frac{ \bar{V}_0\varphi_0^{2+p(s)}}{\xi(s)}+\frac{ 2...
...i_0^{4}}{2 (p(s)-1)}~\frac{\bar{V}_0 (p(s)-4)(p(s)-1)}{1-2~\xi(s) }\right ]r^2,$](/articles/aa/full/2008/14/aa7045-06/img170.gif)
![$\displaystyle \delta_{ij}\left\{\left[\varphi_0^{2}\frac{1-8 \xi(s)}{2\xi(s)(1-12~\xi(s))}\right]\frac{M}{r} \right.$](/articles/aa/full/2008/14/aa7045-06/img171.gif)
![$\displaystyle +\left.\left[{M~\varphi_0^{2}\over 1-12\xi(s)}\frac{\bar{V}_0 (p(s)-4)(p(s)-1)}{1-2~\xi(s)
}\right]r \right.$](/articles/aa/full/2008/14/aa7045-06/img172.gif)
![$\displaystyle + \! \left. 4\pi \left[\frac{
\bar{V}_0\varphi_0^{2+p(s)}}{\xi(s)...
...)}\frac{\bar{V}_0 (p(s)\!-\!4)(p(s)\!-\!1)}{1\!-\!2~\xi(s)
}\right]r^2\right\},$](/articles/aa/full/2008/14/aa7045-06/img173.gif)
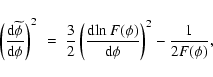
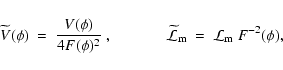
![\begin{displaymath}
\widetilde{{\cal A}}~=
~\int{\sqrt{-\widetilde{g}}\left[\wid...
...lde{\phi})+
\widetilde{{\cal L}}_{\rm m}\right]{\rm d}^{4}x} .
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img177.gif)
![\begin{displaymath}
\gamma^{\rm PPN}-1~=~-\frac{F'(\phi)^2}{F(\phi)+2[F'(\phi)]^2}~=-~\frac{4\xi(s)}{1+8\xi(s)} ,
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img182.gif)
![\begin{displaymath}\beta^{\rm PPN}-1~=~\frac{F(\phi){\cdot}
F'(\phi)}{F(\phi)+3[F'(\phi)]^2}\frac{{\rm d}\gamma^{\rm PPN}}{{\rm d}\phi}~=0 .
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img183.gif)
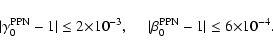
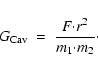
![$\displaystyle -\frac{1}{2F(\phi)}\left[1+\frac{[2F'(\phi)]^2}{4F(\phi)+3[2F'(\phi)]^2}\right]~$](/articles/aa/full/2008/14/aa7045-06/img196.gif)
![$\displaystyle -\frac{1}{2\xi(s)\phi^2}\left[\frac{1+16\xi(s)}{1+12\xi(s)}\right]~
=~G_{\rm eff}~\left[\frac{1+16\xi(s)}{1+12\xi(s)}\right],$](/articles/aa/full/2008/14/aa7045-06/img197.gif)
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig7.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg198.gif)
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig8.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg201.gif)
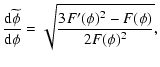
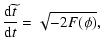
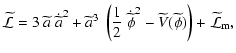
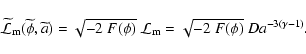
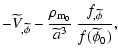
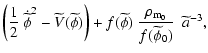
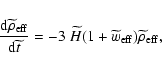
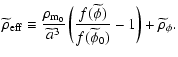
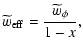
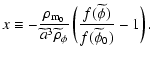
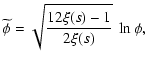
![$\displaystyle \Bigg\{2 C(s) s (s+3)
t^{-\frac{2s^2+6s+9}{2(s+3)s}}
\left[\left(...
...1}}-B(s)-\frac{V_0
B(s) t^{\frac{3}{s+3}} }{\gamma(s)}\right]^{1-\frac{3}{2 s}}$](/articles/aa/full/2008/14/aa7045-06/img237.gif)
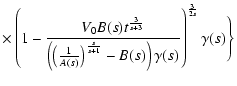
![$\displaystyle \times { _2F_1\left[\frac{-2 s^2-6 s-9}{6
s},1+\frac{3}{2s};\frac...
...t)^{\frac{s}{s+1}}-B(s)\right]
\gamma(s)}\right]\over \left(2 s^2+6
s+9\right)}$](/articles/aa/full/2008/14/aa7045-06/img239.gif)
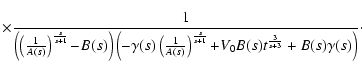
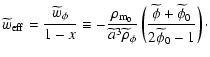
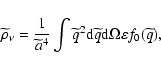
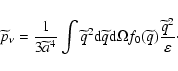
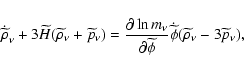
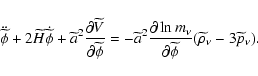
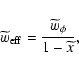
![\begin{displaymath}\widetilde{x}=-\frac{\widetilde{\rho}_{\nu0}}{\widetilde{a}^3...
...m_\nu(\widetilde{\phi})}{m_\nu(\widetilde{\phi}_0)}-
1\right].
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img278.gif)
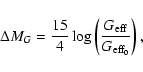
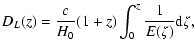
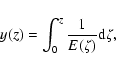
![\begin{displaymath}\chi^2(s, {\widehat H}_0) = \frac{1}{N - 3} \sum_{i = 1}^{N}{...
...(z_i; \alpha_1, {\widehat H}_0) - y_i}{\sigma_i} \right
]^2} ,
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img295.gif)
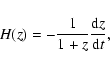
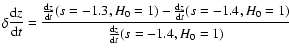 ,
and the blue line shows
,
and the blue line shows
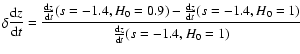 .
.
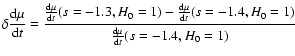 ,
and the
blue line shows
,
and the
blue line shows
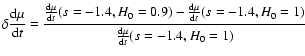 .
.
![\begin{displaymath}\chi^2(s, {\widehat H}_0) = \frac{1}{N - 3} \sum_{i = 1}^{N}{...
...ac{H(z_i; s, {\widehat H}_0) - H_i}{\sigma_i} \right ]^2}\cdot
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img305.gif)
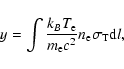
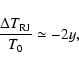
![\begin{displaymath}n_{\rm e}(r) = n_{\rm e0} \cdot
\left[f\left( 1+\frac{r^2}{r_...
...+\frac{r^2}{r_{\rm c2}^2} \right)^{-\frac{3\beta}{2}} \right].
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img318.gif)
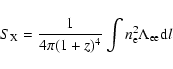
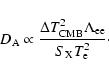
![$\displaystyle \chi^2(s, {\widehat H}_0) = \frac{1}{N - 3} \sum_{i =
1}^{N}\left[ \frac{(D_{\rm A}(z_i; s, {\widehat H}_0)-D_i) }{\sigma_i}
\right]^2\cdot$](/articles/aa/full/2008/14/aa7045-06/img336.gif)
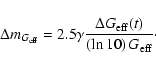
![\begin{displaymath}f_{\rm gas}(z) = \frac{b \Omega_b}{(1 + 0.19 \sqrt{h}) \Omega...
...{\rm A}^{\rm SCDM}(z)}{D_{\rm A}^{\rm mod}(z)} \right ]^{1.5},
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img354.gif)
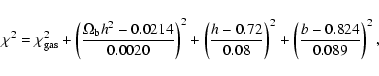
![\begin{displaymath}\chi_{\rm gas}^2 = \sum_{i = 1}^{N_{\rm gas}}{\left [ \frac{f...
...0) - f_{\rm gas}^{\rm obs}(z_i)}{\sigma_{\rm gi}} \right
]^2}.
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img361.gif)
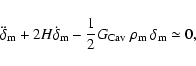
![\begin{displaymath}G_{\rm Cav}=
~-\frac{1}{2\xi(s)\phi^2}\left[\frac{1+16\xi(s)}{1+12\xi(s)}\right]\cdot
\end{displaymath}](/articles/aa/full/2008/14/aa7045-06/img379.gif)
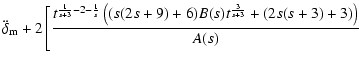
![$\displaystyle \left.\times \left(\left(\frac{1}{A(s)}\right)^{\frac{s}{s+1}}-B(...
...ac{3}{s+3}}-1\right)
B(s)\right)^{-1-\frac{1}{s}}\right]~{\dot \delta_{\rm m}}~$](/articles/aa/full/2008/14/aa7045-06/img382.gif)
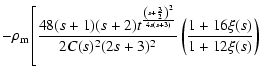
![$\displaystyle \times\left.
\small\left(\left(\frac{1}{A(s)}\right)^{\frac{s}{s+...
...3}{s+3}}}{2
s+3}-1\right)\right)^{2+\frac{3}{s}}\right] \delta_{\rm m}\simeq
0.$](/articles/aa/full/2008/14/aa7045-06/img384.gif)