| |
Figure 1:
Diagram of |
| Open with DEXTER | |
In the text
| |
Figure 2:
Behavior of the coupling factor |
| Open with DEXTER | |
In the text
| |
Figure 3:
Plot of
|
| Open with DEXTER | |
In the text
| |
Figure 4:
|
| Open with DEXTER | |
In the text
| |
Figure 5:
Rate of change in the equation of state as measured by
|
| Open with DEXTER | |
In the text
| |
Figure 6:
Plot of
|
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig7.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg198.gif) |
Figure 7:
Current limits on the PPN parameters restrict the range of the parameter s.
We see that the constraint on
|
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=5cm,clip]{7045fig8.eps} \end{figure}](/articles/aa/full/2008/14/aa7045-06/Timg201.gif) |
Figure 8:
Behavior of the Brans-Dicke parameter
|
| Open with DEXTER | |
In the text
| |
Figure 9:
Time evolution of the transformed scalar field
|
| Open with DEXTER | |
In the text
| |
Figure 10:
Evolution with the redshift of
|
| Open with DEXTER | |
In the text
| |
Figure 11:
Plot of
|
| Open with DEXTER | |
In the text
| |
Figure 12:
Redshift dependence of the second derivative of the scale
factor. The transition from a decelerating to an
accelerating expansion occurs close to |
| Open with DEXTER | |
In the text
| |
Figure 13:
Observational data of the SNIa sample compiled by Riess et al. (2007)
fitted to our model. The solid curve is the best fit curve, compared with a standard |
| Open with DEXTER | |
In the text
| |
Figure 14:
Updated Daly & Djorgovski database (Daly & Djorgovski 2005)
fitted to our model. The solid curve is the best fit curve with
|
| Open with DEXTER | |
In the text
| |
Figure 15:
The sensitivity of the
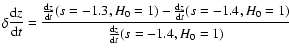 ,
and the blue line shows ,
and the blue line shows
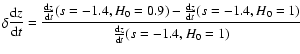 . .
|
| Open with DEXTER | |
In the text
| |
Figure 16:
The sensitivity of the
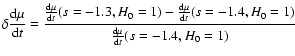 ,
and the
blue line shows ,
and the
blue line shows
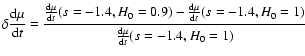 . .
|
| Open with DEXTER | |
In the text
| |
Figure 17:
The best-fit curve of the measured values of H(z) corresponding to
|
| Open with DEXTER | |
In the text
| |
Figure 18:
The best-fit curve to the H(z) data for our nmc model (dark blue line) and for the quintessence QCDM
fitted to the new released WMAP- three years + SNLS data
(WMAP New Three Year Results 2006)
|
| Open with DEXTER | |
In the text
| |
Figure 19:
Observational SZE data fitted to our model with
the best-fit values
|
| Open with DEXTER | |
In the text
| |
Figure 20:
Observational Hubble diagram for the recent SNIa sample
compiled by Riess et al. (2006) (empty lozenges), and the GRBs
data by () (empty boxes) fitted to our model. The
solid curve is the best-fit curve with,
|
| Open with DEXTER | |
In the text
| |
Figure 21:
The best-fit curve to the
|
| Open with DEXTER | |
In the text
| |
Figure 22:
The growth index f in different cosmological
models.
The thick dashed red line corresponds to our non minimally-coupled model. The blue thin dashed curve corresponds to the standard |
| Open with DEXTER | |
In the text
| |
Figure 23: The potential V as a function of the redshift z. |
| Open with DEXTER | |
In the text