A&A 481, 117-122 (2008)
DOI: 10.1051/0004-6361:20078906

Broad Ly$\alpha $ emission from supernova remnants in young galaxies[*]

K. Heng1,2 - R. A. Sunyaev1,3


1 - Max Planck Institut für Astrophysik, Karl-Schwarzschild-Stra$\beta $e 1, 85740 Garching, Germany
2 - Max Planck Institut für extraterrestrische Physik, Giessenbachstra$\beta $e, 85478 Garching, Germany
3 - Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32, 117997 Moscow, Russia

Received 23 October 2007 / Accepted 18 December 2007

Abstract
Context. Charge transfer (or exchange) reactions between hydrogen atoms and protons in collisionless shocks of supernova remnants (SNRs) are a natural way of producing broad Balmer, Lyman, and other lines of hydrogen.
Aims. We wish to quantify the importance of shock-induced, non-thermal hydrogen emission from SNRs in young galaxies.
Methods. We present a method estimating the luminosity of broad ($\sim$1000 km s-1) Ly$\alpha $, Ly$\beta $, Ly$\gamma $, H$\beta $ and P$\alpha $ lines, as well as the broad and narrow luminosities of the two-photon (2$\gamma $) continuum, from existing measurements of the H$\alpha $ flux. We consider cases of $\beta=0.1$ and 1, where $\beta \equiv T_{\rm e}/T_{\rm p}$ is the ratio of electron-to-proton temperatures. We examine a modest sample of 8 proximate, Balmer-dominated SNRs from our Galaxy and the Large Magellanic Cloud. The expected broad Ly$\alpha $ luminosity per object is at most $\sim$1036 erg s-1. The 2$\gamma $ continuum luminosities are comparable to the broad H$\alpha $ and Ly$\alpha $ ones. We restrict our analysis to homogenous and static media.
Results. Differences in the Ly$\alpha $/H$\alpha $ and Ly$\beta $/H$\alpha $ luminosity ratios between the $\beta=0.1$ and 1 cases are factors $\sim$2 for shock velocities $1000 \lesssim v_{\rm s} \lesssim 4000$ km s-1, thereby providing a direct and unique way to measure $\beta $. In principle, broad, ``non-radiative'' Ly$\alpha $ from SNRs in young galaxies can be directly observed in the optical range of wavelengths. However, by taking the different rates between core collapse and thermonuclear supernovae into consideration, as well as the duration we expect to observe such Ly$\alpha $ emission from SNRs, we expect their contribution to the total Ly$\alpha $ luminosity from $z \sim 3$ to 5 galaxies to be negligibly small ($\sim$0.001%), compared to the radiative shock mechanism described by Shull & Silk (1979). Although broad, non-thermal Ly$\alpha $ emission has never been observed, these photons are produced in SNRs. Hence, the non-radiative Ly$\alpha $ luminosity is a part of the intrinsic Ly$\alpha $ spectrum of young galaxies.

Key words: ISM: supernova remnants - atomic processes - radiation mechanisms: general - galaxies: general

1 Introduction

Observations of galaxies at high redshifts have revealed a broad class of Ly$\alpha $-emitting galaxies at $z \sim 3$ to 5 (e.g., Tapken et al. 2007). The Ly$\alpha $ emission from these objects is reaching us as light in the visible spectral band, enabling their study using large, ground-based optical telescopes, which in turn permits detailed spectroscopic studies of these galaxies. Observations of quasars at $z \sim 6$ (e.g., Fan et al. 2006) have revealed heavy elemental abundances exceeding solar values. We know that at least some of the galaxies at $z \sim 3$ to 5 have high abundances of heavy elements, facilitating the formation of dust. In homogenous and static media, the dust particles impede the escape of Ly$\alpha $ emission from gas-rich galaxies, because of the small mean free paths of the photons, low temperatures of the gas, and ultimately high probabilities of absorption. In clumpy media, dust can enhance the escape of Ly$\alpha $ photons relative to the continuum (Neufeld 1991; Hansen & Oh 2006). Broadening of Ly$\alpha $ lines due to multiple scatterings is a slow process requiring a long diffusion time (though velocity fields in the interstellar medium may broaden the Ly$\alpha $ lines and reduce the diffusion time). Hence, there is special interest in the physical processes that are able to naturally produce extremely broad wings in Ly$\alpha $ lines, which may permit the photons to leave the host galaxy without requiring many scatterings (but see Sect. 5).

Among obvious mechanisms is the one at work in the unique massive binary SS433 (for a recent review, see Fabrika 2004), with strongly blue- and redshifted H$\alpha $ and H$\beta $ lines result from the cooling and recombination of hydrogen in the baryon-dominated, precessing jet moving with velocity $\sim$0.26c. Such objects are very rare - SS433 is the only such example in our Galaxy. More well-known Galactic sources of H$\alpha $emission with broad line wings are the supernova remnants (SNRs) of type Ia, emitting because of charge transfer (or ``charge exchange'') reactions between hydrogen atoms and protons in the blast wave penetrating the low-density ($\sim$1 cm-3), ambient gas. The widths of the H$\alpha $ lines correspond to Doppler broadening with velocities up to $\sim$5000 km s-1. The same process should produce not only H$\alpha $ emission, but also photons in the Lyman series of hydrogen. Recently, some of these SNRs have been observed in Ly$\beta $using the FUSE spacecraft (Korreck et al. 2004; Ghavamian et al. 2007b, hereafter G07).

Knowledge of the cross sections of charge transfers to excited levels and excitation of the fast-moving hydrogen atoms permit us to find simple formulae relating the luminosities of SNRs in the broad H$\alpha $ and Ly$\alpha $ lines. The Ly$\alpha $ line should have a similar spectral distribution to the observed H$\alpha $ one in the broad wings, because the optical depth of the SNR for broad photons is negligibly small and the optical depth for coherent scattering (in the distant Lorentzian wings) in interstellar gas is low.

Table 1: H$\alpha $ & Ly$\beta $ observations of SNRs.

We compiled the existing data for core collapse and thermonuclear SNRs, including SNR 1987A (where the reverse shock is bright in the broad H$\alpha $ line), and present their theoretically expected broad Ly$\alpha $ and Ly$\beta $ luminosities. For two objects, we present their expected broad Ly$\gamma $, H$\beta $, and P$\alpha $ luminosities. Taking into account the supernova (SN) rates, the luminosities of the SNRs in H$\alpha $ and the duration of their active phase (for the charge transfer mechanism described), we find that - even without discussing the cosmological evolution of the SN rates - the expected broad Ly$\alpha $ is several orders of magnitude lower than the estimate of Shull & Silk (1979), who treated fully radiative SNRs with low metallicities and velocities (20 to 120 km s-1). We come to the conclusion that the contribution of both core collapse and thermonuclear SNRs to the Ly$\alpha $ luminosity of young galaxies is negligibly small. In Sect. 2, we gather a modest sample of 8 Galactic and Large Magellanic Cloud (LMC) remnants and use them as a template for estimating the expected Ly$\alpha $, Ly$\beta $, Ly$\gamma $, H$\beta $, and P$\alpha $ production. In Sect. 3, we compute the Ly$\alpha $/H$\alpha $, Ly$\alpha $/Ly$\beta $, Ly$\beta $/H$\alpha $, Ly$\gamma $/H$\alpha $, H$\beta $/H$\alpha $, and P$\alpha $/H$\alpha $ luminosity ratios. We present our results in Sect. 4 and discuss their implications in Sect. 5.

  
2 Galactic and LMC remnants

SNRs are the result of the interaction of SN ejecta with ambient matter. The nature of the interaction can be approximately categorized into several stages (Truelove & McKee 1999, hereafter TM99, and references therein): the ejecta-dominated (ED) or freely-streaming stage, the Sedov-Taylor (ST) or self-similar stage, the pressure-driven snowplow (PDS) stage, and a possible momentum-conserving snowplow stage (Cioffi et al. 1988). Many of the well-studied, young SNRs like Kepler, Tycho, and SN 1006 are intermediate between the ED and ST stages. This has been corroborated by the numerical studies of TM99, who show that there is no sharp transition between the two stages. The transition from the ED to ST stage occurs on a timescale $t_{\rm {ST}} \sim t_{\rm {ch}}$, with the characteristic timescale being

 \begin{displaymath}t_{\rm {ch}} = t_{\rm {ch},0} ~m^{5/6}_{\rm {ej}} E^{-1/2}_{51} n^{-1/3}_0, \end{displaymath} (1)

where $M_{\rm {ej}} = m_{\rm {ej}}~M_{\odot}$ is the mass of the ejecta, E = E51 1051 erg the energy of the supernova explosion, and n0 the density of the ambient medium (in cm-3). The coefficient in Eq. (1) is $t_{\rm {ch},0}= 423$ yrs (TM99). If one makes the argument that $M_{\rm {ej}}$ (with density $\rho = 1.4~m_{\rm {H}} n_0$) of mass is swept up in a time $t_{\rm {ch}}$, one instead gets $t_{\rm {ch},0}=186$ yrs. The PDS stage occurs at

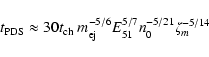\begin{displaymath}t_{\rm {PDS}} \approx 30 t_{\rm {ch}} ~m^{-5/6}_{\rm {ej}} E^{5/7}_{51} n^{-5/21}_0 \zeta_m^{-5/14} \end{displaymath} (2)

after the explosion (Cioffi et al. 1988; TM99), where $\zeta_m$ is a dimensionless metallicity correction factor. More precise estimates for $t_{\rm {ST}}$ and $t_{\rm {PDS}}$ are dependent upon the spatial density distributions of both the ejecta and the ambient matter.

In the ED and ST stages, the emission from some SNRs is ``non-radiative'', meaning the timescale for thermal, radiative losses from the interacting gases is much longer than $t_{\rm {ch}}$. When the blast wave of the SNR slams into ambient gas consisting predominantly of hydrogen atoms, it emits in Balmer and Lyman lines consisting of a broad ($\sim$1000 km s-1) and a narrow ($\sim$10 km s-1) component (Chevalier & Raymond 1978; Bychkov & Lebedev 1979; Chevalier et al. 1980; Heng & McCray 2007, hereafter HM07; Heng et al. 2007, hereafter H07; G07; and references therein). These objects are known as ``Balmer-dominated'' SNRs. Positive detections of the line components are so far only from Galactic and LMC SNRs. Even though narrow Ly$\alpha $ emission is produced, it is not seen due to interstellar absorption, and broad Ly$\alpha $ should be observed[*]. Non-thermal H$\alpha $ and Ly$\alpha $ emission has not been observed in studies of local starburst galaxies (e.g., Kunth et al. 2003).

The narrow Balmer and Lyman lines are produced when the fast-moving ejecta directly excite stationary hydrogen atoms in the surrounding material. The broad lines are produced when the post-shock protons and atoms engage in charge transfer reactions, creating a population of post-shock atoms in broad velocity distributions known as ``broad neutrals'' (HM07; H07). In the frame of the observer, these broad neutrals move at a velocity $v_{\rm {B}} \lesssim 3v_{\rm s}/4$, where $v_{\rm s}$ is the shock velocity (of the blast wave). For $v_{\rm s} \gtrsim 500$ km s-1, the broad neutrals can produce Ly$\alpha $ that is blue or redshifted out of resonance with the stationary atoms, thereby providing an escape route for the photons. The ratio of broad-to-narrow H$\alpha $ (and Ly$\alpha $) emission is a function of the shock velocity (HM07; H07); it also depends on factors like the pre-shock neutral density and the degree to which the temperatures of the electrons and ions are equilibrated. The contribution from the broad H$\alpha $ line dominates when the shock velocity is $\lesssim$3000 km s-1 and when the narrow H$\alpha $ line assumes Case A conditions (HM07). Existing observations of H$\alpha $ and Ly$\beta $ emission from 8 Balmer-dominated SNRs are catalogued in Table 1. At least 5 of these SNRs are believed to have resulted from type Ia explosions. Only SNR 1987A has a clear core collapse origin, and it is the youngest SNR in the sample.

To convert H$\alpha $ line fluxes to broad Ly$\alpha $ luminosities, we use

 \begin{displaymath}L_{\rm {Ly}\alpha} = 4 \pi d^2 F_{\rm {H}\alpha} ~\frac{\Re_{\rm bn}}{1+\Re_{\rm bn}} ~\Gamma_{\rm {Ly}\alpha/\rm {H}\alpha}, \end{displaymath} (3)

where d is the distance to the SNR and $\Re_{\rm bn} \sim 1$ is the observed ratio of broad to narrow H$\alpha $ emission. The quantity $\Gamma _{\rm {Ly}\alpha /\rm {H}\alpha }$ is the ratio of Ly$\alpha $ to H$\alpha $ luminosities (see Sect. 3). For SNRs in the LMC, we adopt d=50 kpc. In the case of the LMC remnant 0509-67.5, $\Re_{\rm bn}$ is unavailable, so we quote an upper limit. If several values for the H$\alpha $ flux are given, we simply choose the brightest one (e.g., different emission knots of Kepler's SNR). For SNR 1987A, we take the observed value of $\Re_{\rm bn} \sim 1$ (Heng et al. 2006), as opposed to the theoretically calculated one ($\sim$0.1; HM07). We use the measured H$\alpha $ flux to obtain an estimate for the broad Ly$\alpha $ luminosity, as the measured Ly$\alpha $ flux is subjected to resonant scattering. The Cygnus Loop is excluded from our sample due to its low shock velocity of $\sim$250 km s-1. In using Eq. (3), we note that the measured H$\alpha $and Ly$\beta $ fluxes are mostly from limb-brightened portions of the SNRs. Assuming spherical remnants, the intensities from these parts are brightened by factors ${\sim}(R/l_{\rm a})^{1/2}$ (Chevalier & Raymond 1978; H07), where $R \sim 1$ pc is the typical radius of the SNR and $l_{\rm a} \sim 10^{15}$ cm is the length scale for atomic interactions (assuming density $\sim$1 cm-3 and velocity $\gtrsim$1000 km s-1). Hence, the luminosity inferred might be overestimated by a factor $\sim$50.

  
3 The Ly $\alpha $/Ly$\beta $ and Ly$\alpha $/H$\alpha $ ratios


  \begin{figure} \par\includegraphics[width=9cm,clip]{8906fig1.eps} \end{figure} Figure 1: Luminosity ratios of Ly$\alpha $ to H$\alpha $, Ly$\alpha $ to Ly$\beta $, and Ly$\beta $ to H$\alpha $, denoted by $\Gamma _{\rm {Ly}\alpha /\rm {H}\alpha }$, $\Gamma _{\rm {Ly}\alpha /\rm {Ly}\beta }$, and $\Gamma _{\rm {Ly}\beta /\rm {H}\alpha }$, respectively, as a function of the shock velocity, $v_{\rm s}$.
Open with DEXTER

The ratio of Ly$\alpha $ to H$\alpha $ luminosities (Fig. 1) is computed using the methods developed by HM07:

 \begin{displaymath}\Gamma_{\rm {Ly}\alpha/\rm {H}\alpha}\left(nl,n^\prime l^\pri... ...T^*,n^\prime l^\prime} \right) + R_{T^*_0,n^\prime l^\prime}}, \end{displaymath} (4)

where $\epsilon = P_{T_0}/P_I$. The quantity PT0 is the probability of pre-shock atoms (found in a beam, i.e., at one velocity) engaging in charge transfer reactions with ions (thereby creating broad neutrals), while PI is the probability of the broad neutrals being ionized by both electrons and ions. Physically, broad H$\alpha $ emission is produced in two ways: charge transfer of the pre-shock atoms to excited states of broad neutrals (with a rate coefficient, in cm3 s-1, of RT*0,nl); creation of broad neutrals in the ground state, followed by excitation (RE,nl) and/or charge transfers between them and ions to excited states ( RT*,nl). Hence, $\epsilon$ is a measure of how efficient the first contribution is compared to the second one. At low shock velocities ( $v_{\rm s} \lesssim 1000$ km s-1), $\epsilon \gtrsim 3$ - charge transfer to the ground state is the dominant process, and it is efficient creating broad neutrals that subsequently get excited. We emphasize that Eq. (4) is only valid in the case of optically-thin plasmas.

For Ly$\alpha $, we consider charge transfers (with protons) and excitations (by electrons and protons) to the sub-levels 2p, 3s, and 3d. For H$\alpha $, we consider the same processes, but for the sub-levels 3s, 3p, and 3d. Hence, we compute $\Gamma_{\rm {Ly}\alpha/\rm {H}\alpha}(nl,n^\prime l^\prime)$ for $nl=2{\rm p}+3{\rm s}+3{\rm d}$ and $n^\prime l^\prime=3{\rm s}+3{\rm d}+ B_{3{\rm p},2{\rm s}} 3{\rm p}$, where the factor of $B_{\rm 3p,2s}=0.1183$ is the fraction of radiative decays from 3p that result in H$\alpha $, with the remainder going to Ly$\beta $. For $\Gamma_{\rm {Ly}\alpha/\rm {Ly}\beta}(nl,n^\prime l^\prime)$, we consider instead $n^\prime l^\prime=(1-B_{3{\rm p},2{\rm s}})3{\rm p}$. Cascade contributions from higher levels are $\lesssim$$5\%$ effects. For example, contributions to H$\alpha $ from n=4 are at most ${\sim}(3/4)^3 B_{4{\rm s,3p}} B_{\rm 3p,2s} \approx 2\%$; other contributions from 4p, 4d, and 4f are at the ${\lesssim}1\%$ level.


  \begin{figure} \par\includegraphics[width=9cm,clip]{8906fig2.eps}\end{figure} Figure 2: Luminosity ratios of Ly$\gamma $ to H$\alpha $, H$\beta $ to H$\alpha $, and P$\alpha $ to H$\alpha $, denoted by $\Gamma _{\rm {Ly}\gamma /\rm {H}\alpha }$, $\Gamma _{\rm {H}\beta /\rm {H}\alpha }$, and $\Gamma _{\rm {P}\alpha /\rm {H}\alpha }$, respectively, as a function of the shock velocity, $v_{\rm s}$. Only charge transfers to excited states are considered in these ratios, so they should be used with caution; we use only the luminosity ratios for $v_{\rm s} \gtrsim 5000$ km s-1 (see text).
Open with DEXTER

One can calculate the luminosity ratios for Ly$\gamma $/H$\alpha $, H$\beta $/H$\alpha $, and P$\alpha $/H$\alpha $ as well. However, the cross sections for impact excitation of hydrogen atoms by protons to the sub-levels 4s, 4p, 4d, and 4f are unavailable at the time of writing[*]. The cross sections for charge transfers to these excited states, however, are available. At $v_{\rm s} \gtrsim 5000$ km s-1, $\epsilon \lesssim 0.5$, and we may obtain luminosity ratios for Ly$\gamma $/H$\alpha $, H$\beta $/H$\alpha $, and P$\alpha $/H$\alpha $ to within a factor of 2 (Fig. 2). A list of the relevant radiative decay fractions, $B_{nl,n^\prime l^\prime}$, is given in Table 3 (see Appendix A for details). In principle, if the charge transfer and excitation cross sections are known to higher levels in the relevant velocity range, one can calculate the luminosity ratios for other lines in the Balmer, Lyman, Paschen, and other series of hydrogen.

We use the atomic cross sections of Balança, Lin & Feautrier (1998), Barnett et al. (1990), Belkíc et al. (1992), Harel et al. (1998), & Janev & Smith (1993), as well as those found in the NIST Electron-Impact Cross-Section Database. Details concerning the cross sections are given in Appendix B, where we provide fitting functions to them. We consider a pure hydrogen gas and include charge transfer, excitation, and ionization events between hydrogen atoms, electrons, and protons. We employ the thin-shock approximation, such that the relative velocity between atoms and ions is $3v_{\rm s}/4$, which has been shown by H07 to be an excellent approximation. At the shock velocities considered, $500 \lesssim v_{\rm s} \lesssim 10~000$ km s-1, the significance of impact excitation by electrons is comparable to that by protons and cannot be neglected. We do not consider broad emission from within the shock front (see Appendix C).

  
4 Results

The luminosity ratios $\Gamma _{\rm {Ly}\alpha /\rm {H}\alpha }$, $\Gamma _{\rm {Ly}\alpha /\rm {Ly}\beta }$, and $\Gamma _{\rm {Ly}\beta /\rm {H}\alpha }$ are shown in Fig. 1. In the shock velocity range $1000 \lesssim v_{\rm s} \lesssim 4000$ km s-1, the differences in $\Gamma _{\rm {Ly}\alpha /\rm {H}\alpha }$ and $\Gamma _{\rm {Ly}\beta /\rm {H}\alpha }$ between the $\beta=0.1$ and 1 cases are factors $\sim$2 and are due to the sensitivity to temperature of impact excitation and ionization of hydrogen atoms by electrons. This may present a direct and unique opportunity to measure $\beta $. We emphasize that our calculations are only valid for the broad lines; the narrow lines have optical depths $0 \le \tau \le 1$ and Lyman line trapping is a non-negligible effect (Ghavamian et al. 2001, 2002). For example, narrow Ly$\beta $photons may be converted into narrow H$\alpha $ photons and a two-photon (2$\gamma $) continuum. In addition, narrow Ly$\alpha $ cannot propagate easily through the interstellar gas.


  \begin{figure} \par\includegraphics[width=9cm,clip]{8906fig3.eps} \end{figure} Figure 3: Left: Expected Ly$\alpha $ luminosities, $L_{\rm {Ly}\alpha }$, from the SNR sample as a function of the shock velocity, $v_{\rm s}$. Right: $L_{\rm {Ly}\alpha }$ plotted versus the age of the SNR.
Open with DEXTER

We used the data in Table 1 to compute the expected luminosity of Ly$\alpha $, $L_{\rm {Ly}\alpha }$ (Fig. 3). In estimating a range for $L_{\rm {Ly}\alpha }$, we only considered the observational error bars in $F_{\rm {H}\alpha}$ (if available) and allowed for a generous range in temperature equilibration between electrons and protons, $0.1 \le \beta \le 1$, where $\beta = T_{\rm e}/T_{\rm p}$. Hence, the displayed error bars for $L_{\rm {Ly}\alpha }$ are not formal ones. We are aware of the recent work by Ghavamian et al. (2007b), who show that there is an empirical correlation between $\beta $ and $v_{\rm s}$ - namely, $\beta=1$ for $v_{\rm s} \lesssim 400$ km s-1 and $\beta \propto v^{-2}_{\rm s}$ for $v_{\rm s} \gtrsim 400$ km s-1. For the LMC remnants detected in Ly$\beta $ by G07, we computed the range in $L_{\rm {Ly}\alpha }$ by considering both the H$\alpha $ and Ly$\beta $fluxes. We note that the computed $(2.96 \pm 0.05) \times 10^{35}$ erg s-1value for broad Ly$\alpha $ in SNR 1987A is comparable to the ${\sim}10^{36}$ erg s-1 figure predicted by Michael et al. (2003). Note that the condition $L_{\rm {L}\beta}/L_{\rm {H}\alpha} \ge \lambda_{\rm {H}\alpha}/\lambda_{\rm {L}\beta} \approx 6.4$ is not true in general. This is because the cross section for charge transfers to the level 3p falls below that of 3s at a relative velocity $\sim$2000 km s-1 (Fig. B.2).

Table 2: Predicted broad Ly$\alpha $, Ly$\beta $, Ly$\gamma $, H$\beta $, P$\alpha $, and broad/narrow two-photon luminosities (erg s-1).

In Table 2, we make some predictions for the Ly$\beta $, Ly$\gamma $, H$\beta $, and P$\alpha $ luminosities. It is puzzling that the theoretically expected Ly$\beta $ luminosities are about 10 to 20 times higher than those inferred from the observations of G07. In other words, the observed H$\alpha $ fluxes in the LMC SNRs are comparable to the observed Ly$\beta $ ones. We are not certain why this is the case, but note that Ly$\beta $ is more susceptible to absorption by interstellar dust than H$\alpha $ and suspect this effect plays at least some part in the discrepancy. Moreover, the H$\alpha $ and Ly$\beta $ observations were taken at different epochs (Tuohy et al. 1982 versus Ghavamian et al. 2007b). As described in Sect. 3, we are only able to provide rough predictions for Ly$\gamma $, H$\beta $, and P$\alpha $, and only in the cases of 0509-67.5 and SNR 1987A, as these SNRs have shock velocities $\gtrsim$5000 km s-1.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{8906fig4.eps} \end{figure} Figure 4: Luminosity ratios of the 2$\gamma $ continuum to H$\alpha $, $\Gamma _{2\gamma /\rm {H}\alpha }$. Only charge transfers and excitations to the 2s level are considered (see text).
Open with DEXTER

We can make some estimates for the expected 2$\gamma $ continuum as well, which is produced in the ${\rm 2s} \rightarrow {\rm 1s}$ transition. In the case of an optically-thin plasma, the ${\rm 2s} \rightarrow {\rm 2p}$ transition is negligible as collisions are unimportant. In Table 2, we make conservative predictions for the 2$\gamma $ continuum luminosity from both broad and narrow atoms, but consider only charge transfers and excitations to the 2s level. Additional contributions from n=3 range from ${\sim}(2/3)^3 B_{3{\rm p},{\rm 2s}} \approx 4\%$ (Case A) to ${\sim}(2/3)^3 \approx 30\%$ (Case B); those from n=4 are $\ll$$1\%$. We only wish to make the point that $L_{2\gamma}$ is comparable to $L_{\rm {Ly}\alpha }$ and $L_{\rm {H}\alpha}$, so the 2$\gamma $transitions are a potentially observable source of continuum. In the case of Galactic and LMC SNRs, the Galaxy Evolution Explorer (GALEX) should be able to measure the low-frequency wing of 2$\gamma $decay, using its 135-175 and 175-280 nm channels. By comparing H$\alpha $ and 2$\gamma $ emission, it will be possible to estimate emission directly from the SNR shock due to broad Ly$\alpha $ (and the contribution of narrow Ly$\alpha $ that cannot reach us). This is an additional, unique source of information on the detailed physical processes in shocks.

Several sources of uncertainty can affect the predicted luminosities. These include uncertainties in the age of the SNR, $t_{\rm {age}}$, the distance to it, d, the measured non-radiative component of the H$\alpha $ flux, the temperature equilibration between electrons and ions, and the atomic cross sections used. Uncertainties in the cross sections are typically $\sim$10%. For charge transfer to excited states, the uncertainty can be as much as 30% (Janev 2007, private communication). The predicted luminosities have not been corrected for reddening by dust.

  
5 Discussion

SNR 1987A is a unique example of a Balmer-dominated SNR. By virtue of adiabatic expansion cooling, the SN ejecta comprises mostly neutral hydrogen and rushes out at velocities $\gtrsim$12 000 km s-1(Michael et al. 2003; Heng et al. 2006). The non-radiative H$\alpha $and Ly$\alpha $ result from the interaction of the ejecta with the reverse shock and not the blast wave (Heng 2007). As SNR 1987A has a type II origin, it is possible to produce Balmer and Lyman lines via this mechanism, which is obviously not possible with type Ia's. Smith et al. (2005) predict that the H$\alpha $ and Ly$\alpha $emission from the reverse shock of SNR 1987A is shortlived ($\sim$2012 to 2014) and will be extinguished by the increasing flux of extreme ultraviolet (EUV) and X-ray photons traveling into the pre-shock region and ionizing the atoms - pre-ionization. This is marginal evidence that broad Ly$\alpha $ from SNRs of a core collapse origin will be shortlived, i.e., $\lesssim$100 years. In general, for this scenario to work, some interaction of the blast wave with the ambient material is needed, but if it is too strong the pre-shock gas becomes ionized (Chevalier 2007, private communication).

To further investigate the viability of the short-lived, non-radiative Ly$\alpha $ hypothesis, we examined the sample of optically identified SNRs by Matonick & Fesen (1997), who studied an ensemble of SNR samples from 12 different galaxies, including the Small Magellanic Cloud (SMC), LMC, M31, and M33, with distances up to 7 Mpc. In galaxies like NGC 2403, M81 and M101, the SNRs are associated with starforming regions and most of them probably have a Type Ib/c origin. In most cases, the measured H$\alpha $ flux is ${\sim}10^{-15}$ erg cm-2 s-1 and the inferred luminosity is ${\sim}10^{36}$ erg s-1. Since Matonick & Fesen (1997) did not provide H$\alpha $ line profiles, it is impossible to estimate the proportion of the H$\alpha $ emission that is non-radiative. Furthermore, their selection criterion is based on picking out objects with [S  II]/H $\alpha \ge 0.45$, which will not detect SNRs with predominantly non-radiative H$\alpha $ emission.

Shull & Silk (1979) computed the temporally-averaged Ly$\alpha $ luminosity from radiative shocks of a population of type II SNRs, assuming low metallicities, to be

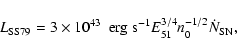\begin{displaymath}L_{\rm {SS79}} = 3 \times 10^{43}~\mbox{ erg~s}^{-1} E^{3/4}_{51} n^{-1/2}_0 \dot{N}_{\rm {SN}}, \end{displaymath} (5)

where $\dot{N}_{\rm {SN}}$ is the number of supernovae (SNe) a year. They considered SNRs in both the ST and the PDS stages, and $v_{\rm s} = 20$ to 120 km s-1. Charlot & Fall (1993) point out that the numerical coefficient in the preceding equation is about 40% lower if one assumes solar metallicity.

Table 3: Radiative decay fractions.

A very conservative upper limit on the broad Ly$\alpha $ from the Matonick & Fesen (1997) samples can be obtained if one generously allows for all of the H$\alpha $ to be broad, for the shock velocities to be low ($\sim$500 km s-1) such that $\Gamma_{\rm {Ly}\alpha/\rm {H}\alpha} \sim 100$, and for the non-radiative emission to last ${\sim}10^4$ years. Even in this very unlikely scenario, $L_{\rm {Ly}\alpha} \sim 10^{42}$ erg s-1 is only about $0.1 L_{\rm {SS79}}$. Hence, our charge transfer mechanism is not energetically competitive. There is the possibility a SNR can produce both radiative and non-radiative components of H$\alpha $. Well-known examples are Kepler (Fesen et al. 1989; Blair et al. 1991) and RCW 86 (Long & Blair 1990; Smith 1997). There is also the possibility that the non-radiative emission from the SNR is inhibited. For example, Foster (2005) observed and studied the Galactic SNR 3C 434.1 ( $t_{\rm {age}} \approx 25~000$ yr; $d = 4.5 \pm 0.9$ kpc; possible Type Ib/c), which formed inside the eastern portion of a pre-existing stellar-wind bubble of interior density $\sim$0.1 cm-3. Strong H$\alpha $ emission ( $6.1~\pm~~0.4~ \times 10^{36}$ erg s-1) is measured from the eastern side that is believed to be from a radiative shock. Being farther away from the western wall of the bubble, the shock on the western side is essentially still in free expansion and produces no measurable, non-radiative H$\alpha $.

Our SNR sample and the considerations of SNR 1987A lead us to believe that if the short-lived emission contribution from type Ib/c and type II SNRs in young galaxies exists, it has a luminosity of

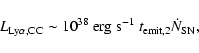\begin{displaymath}L_{\rm {Ly}\alpha,\rm {CC}} \sim 10^{38} \mbox{ erg s}^{-1} ~t_{\rm {emit},2} \dot{N}_{\rm {SN}}, \end{displaymath} (6)

where $t_{\rm {emit}} = t_{\rm {emit},2} 100$ years is the length of time we expect core collapse SNRs to produce shock-induced Ly$\alpha $emission. On the other hand, thermonuclear SNRs are expected to have $t_{\rm {emit}} = t_{\rm {emit},4} 10^4$ years  $\sim t_{\rm {PDS}}$. However, they are also believed to be much scarcer at high redshifts. For example, Dahlen et al. 2004 estimate that only 5% to 7% of available progenitors explode as type Ia SNRs. Therefore, the expected luminosity is

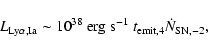\begin{displaymath}L_{\rm {Ly}\alpha,\rm {Ia}} \sim 10^{38} \mbox{ erg s}^{-1} ~t_{\rm {emit},4} \dot{N}_{\rm {SN},-2}, \end{displaymath} (7)

where $\dot{N}_{\rm {SN},-2}$ is the number of SN per year in units of 0.01. We conclude that, for both core collapse and thermonuclear SNRs, the expected luminosity from broad Ly$\alpha $ only has a ${\sim}0.001\%$effect, compared to the mechanism of Shull & Silk (1979). Ly$\alpha $line luminosities from $z \sim 3$ to 5 galaxies have been observationally determined to be ${\sim}10^{42}$ to 1043 erg s-1 (e.g., Saito et al. 2007), in general agreement with theoretical expectations. In addition, the lifetime of an emitting atom is approximately the length of time corresponding to one atomic length scale, and is only $t_{\rm mfp} \sim l_{\rm a}/v_{\rm s} \sim 10^7 n^{-1}_0 v^{-1}_{s,8}$ s, where $v_{s,8} = v_{\rm s}/1000$ km s-1 (H07).

We have restricted our analysis to homogeneous and static media. Though broad, non-thermal Ly$\alpha $ emission has never been observed, these photons are produced in SNRs, so the non-radiative Ly$\alpha $ luminosity is a part of the intrinsic Ly$\alpha $ spectrum of young galaxies. The optical depth for a broad photon in the line wings is (Verhamme et al. 2006)

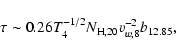\begin{displaymath}\tau \sim 0.26 T^{-1/2}_4 N_{{\rm H},20} v^{-2}_{w,8} b_{12.85}, \end{displaymath} (8)

where T = 104 T4 K and $N_{\rm H} = N_{{\rm H},20} 10^{20}$ cm-2 are the temperature and obscuring hydrogen column density of the medium, respectively. The turbulent velocity in the interstellar medium is b = 12.85 b12.85 km s-1 (Verhamme et al. 2006), while $v_{\rm w} = 1000 v_{\rm w,8}$ km s-1 is the velocity of the emitting atom in the line wings. Multiple scattering is important for $\tau \gtrsim 0.3$ (Chevalier 1986) and any realistic treatment of non-thermal Ly$\alpha $ lines in a young galaxy has to include radiative transfer effects, which we have neglected in our analysis.

Acknowledgements
K.H. is grateful to: Ratko Janev, C. D. Lin, and Fernando Martín for invaluable advice regarding atomic cross sections; Dick McCray, Roger Chevalier, Rob Fesen, Bob Kirshner, and Bryan Gaensler for engaging discussions; Christian Balança for providing atomic cross sections in an electronic form; John Raymond and Mike Shull for helpful suggestions following their careful reading of the manuscript. He acknowledges the Max Planck Institutes for Astrophysics (MPA) and Extraterrestrial Physics (MPE) for their generous support and kind hospitality during the months of June to October 2007, where he was a visiting postdoctoral scientist. He is indebted to the tranquil Bavarian countryside for necessary moments of academic solitude, and to his wife, Stefanie, for her steadfast support.

References

 

  
Online Material

  
Appendix A: Ratio of Einstein A-coefficients

To compute the rate coefficients for Ly$\alpha $, Ly$\beta $, Ly$\gamma $, H$\alpha $, H$\beta $ and P$\alpha $, one needs to calculate the ratio of Einstein A-coefficients. The Einstein A-coefficient for hydrogen, $A_{nl,n^\prime l^\prime}$, is the radiative decay rate (s-1) from the levels nl to $n^\prime l^\prime$. The radiative decay fraction is

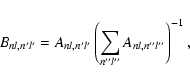\begin{displaymath}B_{nl,n^\prime l^\prime} = A_{nl,n^\prime l^\prime} \left (\s... ...ime}} A_{nl,n^{\prime \prime} l^{\prime \prime}} \right)^{-1}, \end{displaymath} (A.1)

where the sum is over all transitions $nl \rightarrow n^{\prime \prime} l^{\prime \prime}$ permitted by the electric dipole selection rule, $l^{\prime \prime} = l \pm 1$. A list of the relevant radiative decay fractions is found in Table 3. For example, to compute $\Gamma_{\rm {H}\beta/\rm {H}\alpha}(nl,n^\prime l^\prime)$, we need to consider $nl = B_{\rm 4s,2p} 4s + B_{\rm 4p,2s} 4{\rm p} + B_{\rm 4d,2s} 4{ \rm d}$. Our computed value of B3p,2s = 0.1183 agrees closely with the 0.1184 value quoted by Martín (1999).

The Einstein A-coefficients are proportional to the square of the magnitude of the radial integrals, $\vert R^{n^\prime l^\prime}_{nl} \vert^2$. (See Appendix A2 of HM07 for details on how to calculate them analytically.) As a check, we have compared our computed values of $\vert R^{n^\prime l^\prime}_{nl} \vert^2$ to the ones tabulated by Green et al. (1957), and find they agree.

  
Appendix B: Atomic cross-sections

Cross sections for interactions between protons and hydrogen atoms (charge transfer and excitation) to the sub-levels 3s, 3p and 3d are computed in Balança et al. (1998) and kindly provided to us by C. Balança (2007, priv. comm.). We note that these calculations utilize a two-center atomic-orbital (TCAO) close-coupling method with an asymmetric (TCAO-A) basis set of 26 states, so as to avoid the spurious numerical oscillations caused by using a traditional, symmetric set (TCAO-S). We fit these cross sections, as well as those from Belkíc et al. (1992), Harel et al. (1998) and the NIST Electron-Impact Cross Section Database using the function:

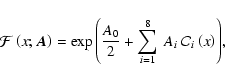\begin{displaymath}{\cal F}\left(x;\vec{A}\right) = \exp{\left(\frac{A_0}{2} + \sum^{8}_{i=1} ~A_i ~{\cal C}_i\left(x\right)\right)}, \end{displaymath} (B.1)

where the coefficients $\vec{A}=A_i$ for $0 \le i \le 8$ are the fitting parameters. The quantities ${\cal C}_i$ are the Chebyshev orthogonal polynomials:
$\displaystyle {\cal C}_1\left(x\right) = x,$     (B.2)
$\displaystyle {\cal C}_2\left(x\right) = 2x^2 - 1,$     (B.3)
$\displaystyle {\cal C}_3\left(x\right) = 4x^3 - 3x,$     (B.4)
$\displaystyle {\cal C}_4\left(x\right) = 8\left(x^4 - x^2 \right) + 1,$     (B.5)
$\displaystyle {\cal C}_5\left(x\right) = 16x^5 - 20x^3 + 5x,$     (B.6)
$\displaystyle {\cal C}_6\left(x\right) = 32x^6 - 48x^4 + 18x^2 - 1,$     (B.7)
$\displaystyle {\cal C}_7\left(x\right) = 64x^7 - 112x^5 + 56x^3 - 7x,$     (B.8)
$\displaystyle {\cal C}_8\left(x\right) = 128x^8 - 256x^6 + 160x^4 - 32x^2 + 1.$     (B.9)

The fitting variable x is defined as

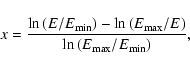\begin{displaymath}x= \frac{ \ln{\left(E/E_{\rm {min}}\right)} - \ln{\left(E_{\r... ...}}/E\right)} }{\ln{\left(E_{\rm {max}}/E_{\rm {min}}\right)}}, \end{displaymath} (B.11)

where E is the relative energy between the collidants; $E_{\rm {min}}$ and $E_{\rm {max}}$ are the respective minimum and maximum energies to which the data are available. We use the Levenberg-Marquardt algorithm, which combines the steepest descent and inverse-Hessian function fitting methods, as implemented in IDL. The fits are sensitive to the initial values of the parameters fed to the algorithm; we use the values of the fit parameters for $\sigma_{\rm {T,p},2s}$ in Barnett et al. (1990) as a guide. In providing ``measurement errors'' to our fitting algorithm, we assume a fiducial error of 10%. Selected cross sections are shown in Figs. B.1-B.5, while the fitting coefficients are presented in Table B.1.


  \begin{figure} \par\includegraphics[width=8cm,clip]{8906fig5.eps}\end{figure} Figure B.1: Cross sections for charge transfers between hydrogen atoms and protons, to the sub-levels 2s and 2p, taken from Belkíc et al. (1992) and Harel et al. (1998). Also shown are the fitting functions of Barnett et al. (1990), denoted by ``B90''.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{8906fig6.eps}\end{figure} Figure B.2: Cross sections for charge transfers between hydrogen atoms and protons, to the sub-levels 3s, 3p, and 3d, taken from Belkíc et al. (1992) and Harel et al. (1998). Shown for comparison are the calculations of Balança et al. (1998), denoted by ``BLF98''.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{8906fig7.eps}\end{figure} Figure B.3: Cross sections for charge transfers between hydrogen atoms and protons, to the sub-levels 4s, 4p, 4d, and 4f, taken from Belkíc et al. (1992) and Harel et al. (1998).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{8906fig8.eps}\end{figure} Figure B.4: Cross sections for impact excitation of hydrogen atoms by protons, from the two-center atomic-orbital (TCAO) close-coupling calculations of Balança et al. (1998). Shown are the fits to the TCAO-A calculations.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{8906fig9.eps}\end{figure} Figure B.5: Cross sections for impact excitation of hydrogen atoms by electrons, to the sub-levels 2p and 3p, from the NIST Electron-Impact Cross Section Database.
Open with DEXTER

Table B.1: Fitting parameters for various cross sections.

  
Appendix C: Broad emission from within the shock front?

We have considered only the case of hydrogen atoms crossing the shock front (in the frame of the front) and interacting with protons. In this appendix, we examine the possibility of Ly$\alpha $ being created within the shock front. The width of the shock front in collisional shocks is on the order of an atomic mean free path, $l_{\rm {mfp}}$, assuming a pure hydrogen gas. Zel'dovich & Raizer (1966) have shown that for weak shocks, the collisional shock width is

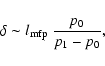\begin{displaymath}\delta \sim l_{\rm {mfp}} ~\frac{p_0}{p_1-p_0}, \end{displaymath} (C.1)

where p0 and p1 are the pre- and post-shock fluid pressures, both in the case of a viscous shock with no heat conduction and for a heat-conducting shock with no viscosity. When the change in pressure across the shock front is comparable to the magnitude of the pre-shock pressure, $\delta \sim l_{\rm {mfp}}$ (see also Landau & Lifshitz 1963). Even in the limit of infinite Mach number, Sakurai (1957) finds that $\delta/l_{\rm {mfp}} = 1.42$.

The question is: how robust is the assumption of shocks in Balmer-dominated SNRs being collisionless? This occurs when the electron and proton gyroradii - $r_{\rm e}$ and $r_{\rm p}$, respectively - are much smaller than $l_{\rm {mfp}}$. The typical value of the magnetic fields in SNRs is B = B-4 10-4 G. For example, Strom & Duin (1973) find $3 \times 10^{-4}$ and $5 \times 10^{-4}$ G for Tycho and Cas A, respectively. The electron gyroradius is

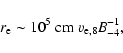\begin{displaymath}r_{\rm e} \sim 10^5 \mbox{ cm} ~v_{{\rm e},8} B^{-1}_{-4}, \end{displaymath} (C.2)

where $v_{\rm e,8} = v/1000$ km s-1 is the velocity of the electron. For protons, we have $r_{\rm p} \sim 10^8$ cm vp,8/B-4. It follows that the transition from collisionless to collisional shock occurs when the gyroradii ${\sim}l_{\rm {mfp}}$, or when the density of particles is $n_{\rm e} \gtrsim 10^{10} v^{-1}_{\rm e,8} \sigma^{-1}_{\rm a,-15} B_{-4}$ cm-3 and $n_{\rm p} \gtrsim 10^7 v^{-1}_{\rm p,8} \sigma^{-1}_{\rm a,-15} B_{-4}$ cm-3, where $\sigma_{\rm a} = \sigma_{\rm a,-15} 10^{-15}$ cm-2 is the typical value of the cross section for atomic interactions (charge transfer and ionization; see HM07 and H07). These densities are much higher than typical values for the interstellar medium ($\sim$1 cm-3) or even for molecular clouds ($\sim$100 to 1000 cm-3).

About $\exp{(-l_{\rm s}/l_{\rm {mfp}})}$ of the hydrogen atoms cross the shock front without being ionized, where $l_{\rm s}$ is the width of the shock. In collisional shocks, $l_{\rm s} \sim \delta$. In collisionless shocks, $l_{\rm s} \sim r_{\rm e}$, $l_{\rm s}/l_{\rm {mfp}} \ll 1$ and virtually all of the atoms pass through. We thus conclude that broad Ly$\alpha $ is probably not produced in a significant amount within the shock front, consistent with the findings of H07.


Copyright ESO 2008