A&A 481, 239-246 (2008)
DOI: 10.1051/0004-6361:20078689
B. K. Carter - R. Erdélyi
Solar Physics & Space Plasma Research Centre (SP2RC), Dept. of Applied Mathematics, The University of Sheffield, Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK
Received 17 September 2007 / Accepted 14 January 2008
Abstract
Aims. We study kink waves in a magnetic flux tube modelled as a straight core surrounded by a magnetically twisted annulus, both embedded in a straight ambient external field, and derive the dispersion relation for this configuration.
Methods. The existence and behaviour of the kink modes are examined with specific attention to the effect that the addition of magnetic twist has on phase speeds and periods. Analytic expansions to the short and long wavelength approximations are also considered.
Results. The magnetic twist is found to introduce of an infinite set of body modes into solutions of the dispersion relation not present in the untwisted case. Moreover, for the kink modes, the width of interval of this infinite set, generally found to occupy phase speeds around the annulus' longitudinal Alfvén speed, increases for longer wavelengths. Two surface modes are also present in the solution, one at each surface: the internal and the external edges of the annulus. The magnetic twist is found to increase or decrease the phase speeds of these surface modes that are depending on the ratio of internal and external Alfvén speeds in the flux tube.
Conclusions. The magnetic twist of the annulus region of a flux tube is found to have a marked effect on the phase speeds of occurring modes. A straight annulus layer increased (or decreased) the periods of the surface modes for a tube modelled as a density (magnetic) enhancement. The addition of twist reduces the periods of the modes in both cases.
Key words: magnetohydrodynamics (MHD) - waves - Sun: oscillations - Sun: magnetic fields
Oscillations of magnetic tubes in the form of a magnetic core and
shell have been investigated in detail by, amongst others,
Carter & Erdélyi (2007,2004), Mikhalyaev & Solov'ev (2005,2004), and Erdélyi & Carter (2006).
These works extended the much studied model of a single straight
magnetic tube embedded in a straight external magnetic field put
forward by Edwin & Roberts (1983) to a co-axial double flux tube consisting of
a core and shell region each with distinct magnetic field. In the
single tube case, for a slender flux tube, one may define two
characteristic speeds of propagation. These are the subsonic,
sub-Alfvénic tube speed ![]() given by
given by
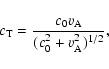
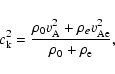
For the core-shell type flux tube model without a magnetic twist,
Mikhalyaev & Solov'ev (2005, hereafter MS05) and Carter & Erdélyi (2007) found that there
are twice as many surface modes as for the single tube case and
moreover that the modes have different properties. MS05 showed the
slow modes in the thin tube occur for all azimuthal wave numbers m while the fast modes exist only for m>0. For coronal
conditions, i.e.
![]() ,
the two slow modes are trapped in
the tube - one by the core, the other by the shell. The fast modes
are also trapped by the core and the shell provided the shell
Alfvén speed lies between the Alfvén speeds in the core
and external regions, e.g.
,
the two slow modes are trapped in
the tube - one by the core, the other by the shell. The fast modes
are also trapped by the core and the shell provided the shell
Alfvén speed lies between the Alfvén speeds in the core
and external regions, e.g.
![]() .
(In this paper
we shall use the subscripts i, 0 and e to denote quantities
corresponding
to the core, shell and external regions, respectively).
.
(In this paper
we shall use the subscripts i, 0 and e to denote quantities
corresponding
to the core, shell and external regions, respectively).
Carter & Erdélyi (2007) investigate, for the incompressible non-twisted case,
the effect of the shell width on the periods of propagating waves
for both the sausage and kink modes of oscillation. They find that
for typical photospheric parameters (
![]()
![]()
![]() )
the periods of the modes are decreased by the
existence of an annulus layer whereas periods are increased in the
case of a dense tube (
)
the periods of the modes are decreased by the
existence of an annulus layer whereas periods are increased in the
case of a dense tube (
![]() ).
).
A natural
extension of these previous works is that of the addition of
magnetic twist. A uniformly twisted magnetic tube embedded in a
straight magnetic environment was studied for an incompressible
plasma by Erdélyi & Fedun (2006); Bennett et al. (1999); Erdélyi & Fedun (2007). Some new features arising
due to the introduction of twist were found. Most prominent was
the existence of an infinite set of body modes which is absent in
the incompressible straight field case and is centered around the
internal Alfvén speed,
![]() ,
for the sausage modes and in
shorter wavelengths for the kink modes. Another aspect was the
coupling of the degenerated magneto-acoustic mode to the
Alfvén mode even in linear
theory of the incompressible limit.
,
for the sausage modes and in
shorter wavelengths for the kink modes. Another aspect was the
coupling of the degenerated magneto-acoustic mode to the
Alfvén mode even in linear
theory of the incompressible limit.
Erdélyi & Carter (2006) further extended the studies of MHD waves in a
twisted flux tube by considering a magnetically twisted shell
geometry. Specific modes of propagation and associated phase
speeds were studied for a magnetic configuration in which a
uniform twist is applied to the shell region. Only the more
tractable sausage modes were considered. By introducing a magnetic
twist to the shell it was found that, where there were only
surface modes before, there now existed an infinite set of body
modes which increased in width as the strength of the twist was
increased. It was also found that the phase speeds of the surface
modes were changed significantly (up to 5![]() )
by increasing
the twist just a
small amount.
)
by increasing
the twist just a
small amount.
In this paper, intended as a natural extension to Erdélyi & Carter (2006), we analyse a similar magnetic shell structure for the kink modes, with specific attention given to the modes of oscillation present and to the effect of the applied twist on wave periods of kink oscillations.
We investigate kink mode propagation in a magnetic tube consisting of a straight magnetic core and twisted magnetic annulus, or shell, embedded in a straight magnetic ambient external environment. We apply the general dispersion relation, as found by Erdélyi & Carter (2006), to two applicable situations in the solar atmosphere: (i) to a tube as a magnetic enhancement with a weak magnetic environment and (ii) to a tube defined by a density enhancement. For further insight into behaviour of the kink modes, long and short wavelength approximations are considered.
Since the kink modes, in general, are highly incompressible the limit of incompressibility is of great interest, not just for wave studies in the deeper part of the solar atmosphere (e.g. where the plasma-beta is high) but can also be directly applicable from the lower solar atmosphere to the corona.
For observational motivation supporting the study of MHD wave oscillations in magnetic waveguides see, for example, reviews by Aschwanden (2004), Banerjee et al. (2007), Nakariakov & Verwichte (2005). These reviews give insight into the current state-of-the-art of solar magneto-seismology, a rapidly emerging field of solar physics, with several more references to specific MHD waves and oscillations observed in the magnetised and highly structured solar atmosphere. As a specific example, Kukhianidze et al. (2006), Zaqarashvili et al. (2007) recently discovered Doppler oscillations in spicules in the lower atmosphere with estimated periods ranging between 20 and 110 s. They attributed these motions to kink waves in a region in which motions are approximated by incompressibility.
It is useful to note here that by Fourier analysing the linear MHD
equations like e
![]() and by taking m=1 (kink modes only)
we are considering a non-axisymmetric mode of oscillation. The
torsional Alfvén mode, being axisymmetric, is now removed from
the system and hence will not interact with modes present in the
analysis of this paper (see e.g. Erdélyi & Fedun 2007).
and by taking m=1 (kink modes only)
we are considering a non-axisymmetric mode of oscillation. The
torsional Alfvén mode, being axisymmetric, is now removed from
the system and hence will not interact with modes present in the
analysis of this paper (see e.g. Erdélyi & Fedun 2007).
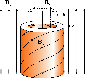 |
Figure 1: Configuration of the magnetic tube consisting of a twisted magnetic annulus and straight core embedded in an ambient straight external magnetic field. |
| Open with DEXTER | |
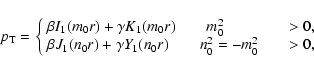 |
(5) |
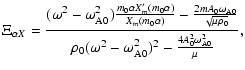 |
Let us assume that the tube is distinct to its environment due to
a magnetic enhancement and that it has otherwise uniform density
throughout (
![]() ,
,
![]() )
so that the Alfvén speeds for each region satisfy
the rendering
)
so that the Alfvén speeds for each region satisfy
the rendering
![]() .
These
conditions may be applicable to subsurface or lower solar
atmosphere up to the chromosphere and, since we consider kink
modes only, incompressibility will, of course, less restrict a
wider direct application even in the higher solar atmosphere.
Further, we shall consider only weak twists i.e.
.
These
conditions may be applicable to subsurface or lower solar
atmosphere up to the chromosphere and, since we consider kink
modes only, incompressibility will, of course, less restrict a
wider direct application even in the higher solar atmosphere.
Further, we shall consider only weak twists i.e.
![]() .
.
![\begin{figure}
\par\resizebox{9cm}{6cm}
{\includegraphics[100,377][567,700]{8689fig2.ps}}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg56.gif) |
Figure 2:
Plot of solutions to
Eqs. (6a,b) for typical
photospheric parameters (
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{6cm}{\includegraphics[100,377][567,700]{8689fig3.ps}}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg57.gif) |
Figure 3: Same as Fig. 2 but for a magnetic twist of 0.5. |
| Open with DEXTER | |
Figures 2 and 3 show,
for a twist,
![]() ,
of 0.1 and 0.5, the dispersion
curves for Eqs. (6a,b) for
the m=1 (kink) modes for a fixed annulus width (the emphasis
here is on the effect of the applied magnetic twist) so that
a/R=0.8. As in the case of sausage waves (Erdélyi & Carter 2006), there
exists an infinite set of body modes that broadens as twist is
increased. The envelope separating body and surface modes (
,
of 0.1 and 0.5, the dispersion
curves for Eqs. (6a,b) for
the m=1 (kink) modes for a fixed annulus width (the emphasis
here is on the effect of the applied magnetic twist) so that
a/R=0.8. As in the case of sausage waves (Erdélyi & Carter 2006), there
exists an infinite set of body modes that broadens as twist is
increased. The envelope separating body and surface modes (
![]() ,
indicated by the dashed lines) is not, anymore,
symmetrical about
,
indicated by the dashed lines) is not, anymore,
symmetrical about
![]() but stretches to larger phase speeds as
kza decreases. The set of body modes follows this trend; the
phase speeds of modes becoming increasingly larger as wavelength
increases indicating strong dispersion. The two surface modes,
given by the solid curves in
Figs. 2 and 3, are
trapped, as in the untwisted case (MS05; Carter & Erdélyi 2007), one by
the core, the other by the annulus, and they propagate with phase
speeds in the proximity of
but stretches to larger phase speeds as
kza decreases. The set of body modes follows this trend; the
phase speeds of modes becoming increasingly larger as wavelength
increases indicating strong dispersion. The two surface modes,
given by the solid curves in
Figs. 2 and 3, are
trapped, as in the untwisted case (MS05; Carter & Erdélyi 2007), one by
the core, the other by the annulus, and they propagate with phase
speeds in the proximity of
![]() and
and
![]() ,
respectively,
the latter showing somewhat more dispersion. For larger twists,
the separating envelope (the dashed curves separating the region
where body modes exist and the region where we find surface modes
only) expands meaning that the surface waves are only solutions
for shorter wavelengths. The surface modes do not appear to change
behaviour into body modes directly across the m0=0 separating
envelope as with the single twisted tube (as in Bennett et al. 1999)
and so it would seem that the twisted annulus configuration acts
to cause a ``splitting'' of the hybrid modes.
,
respectively,
the latter showing somewhat more dispersion. For larger twists,
the separating envelope (the dashed curves separating the region
where body modes exist and the region where we find surface modes
only) expands meaning that the surface waves are only solutions
for shorter wavelengths. The surface modes do not appear to change
behaviour into body modes directly across the m0=0 separating
envelope as with the single twisted tube (as in Bennett et al. 1999)
and so it would seem that the twisted annulus configuration acts
to cause a ``splitting'' of the hybrid modes.
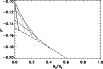 |
Figure 4:
Plot, for photospheric parameters, of the relative
difference, P*, between the period, P, of the surface mode
with phase speed approximately
|
| Open with DEXTER | |
 |
Figure 5:
Same as Fig. 4 but for the
core-shell model surface mode with phase speed approximately
|
| Open with DEXTER | |
Let us now investigate the effect of a twisted annulus on wave
periods. Figures 4 and 5 show
the relative changes in surface mode periods compared to an
incompressible straight magnetic monolithic tube (as
in Edwin & Roberts 1983) for different degrees of twist. In plots throughout
the paper we use the relative period difference, P*, between
the period, P, of the surface mode in question and the period,
![]() ,
of the straight, single monolithic tube with a certain
given internal
Alfvén speed where P* = (
,
of the straight, single monolithic tube with a certain
given internal
Alfvén speed where P* = (
![]() )/
)/
![]() .
.
Figure 4 shows the relative difference,
P*, between the period, P, of the surface mode at r=a shown
in Figs. 2 and 3 as
the upper of the two surface modes and the period,
![]() ,
of
the straight, single monolithic tube with internal Alfvén
speed taken as equal to the core Alfvén speed,
,
of
the straight, single monolithic tube with internal Alfvén
speed taken as equal to the core Alfvén speed,
![]() ,
in
the core-shell model. The introduction of a straight annulus layer
originally decreased the periods of the mode and it is found that
the application of twist to the configuration further reduces
these periods. The percentage change in phase speed due to the
twist from the single straight tube is much greater for longer
wavelengths. For
kza = 0.5 a 10
,
in
the core-shell model. The introduction of a straight annulus layer
originally decreased the periods of the mode and it is found that
the application of twist to the configuration further reduces
these periods. The percentage change in phase speed due to the
twist from the single straight tube is much greater for longer
wavelengths. For
kza = 0.5 a 10![]() difference due to the
annulus is increased to 16
difference due to the
annulus is increased to 16![]() by a twist,
by a twist,
![]() ,
of
just 0.05 whereas a twist an order of magnitude larger, of over 0.5, is necessary for a similar increase when kza =4. The
value of P* when there is no twist (when
,
of
just 0.05 whereas a twist an order of magnitude larger, of over 0.5, is necessary for a similar increase when kza =4. The
value of P* when there is no twist (when
![]() )
does
not change linearly with kza, instead there is a maximum value
that occurs between kza=0.5 and kza=2 which is discussed in
Carter & Erdélyi (2007) (see Sect. 2.4.1 and Fig. 6).
)
does
not change linearly with kza, instead there is a maximum value
that occurs between kza=0.5 and kza=2 which is discussed in
Carter & Erdélyi (2007) (see Sect. 2.4.1 and Fig. 6).
A similar effect is found for the other surface mode at r=R,
with a phase speed in the vicinity of
![]() ,
compared with a
single tube with inner Alfvén speed
,
compared with a
single tube with inner Alfvén speed
![]() (see
Fig. 5). Here we find that single tube
to straight annulus period differences of 4, 11 and 13
(see
Fig. 5). Here we find that single tube
to straight annulus period differences of 4, 11 and 13![]() ,
for example, are increased to 7, 16 and 18
,
for example, are increased to 7, 16 and 18![]() for an
applied twist of 0.2 for ka=4, 1 and 0.5, respectively.
for an
applied twist of 0.2 for ka=4, 1 and 0.5, respectively.
![\begin{figure}
\par\resizebox{9cm}{6cm}{\includegraphics[100,377][567,700]{8689fig6.ps}}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg65.gif) |
Figure 6:
Plot of the solution to the dispersion relation
Eqs. (6a,b) for parameters
approximating a dense tube (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8689fig7.ps}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg66.gif) |
Figure 7: Same as Fig. 6 but for a magnetic twist of 0.5. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8689fig8.ps}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg67.gif) |
Figure 8: Same as Fig. 4 but for parameters appropriate for a dense tube. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8689fig9.ps}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg68.gif) |
Figure 9: Same as Fig. 5 but for parameters appropriate for a dense tube. |
| Open with DEXTER | |
Figure 8 is the relative change in period
for the surface mode at the inner boundary, r=a, (the mode at
![]() in
Figs. 8 and 9)
with single tube inner Alfvén speed equal to the core
Alfvén speed in the annulus model and
Fig. 9 is for the other surface mode at
r=R (with phase speed around
in
Figs. 8 and 9)
with single tube inner Alfvén speed equal to the core
Alfvén speed in the annulus model and
Fig. 9 is for the other surface mode at
r=R (with phase speed around
![]() )
compared to the single
tube with internal Alfvén speed equal to the annulus'
Alfvén speed. In both cases the addition of the uniform twist
reduces the period of the mode, countering the increase in period
found to occur due to the annulus region. Since the two effects on
period seem to work against each other, this may be harder to
observationally justify. By studying the intersection of the
plotted lines of P* with the y-axis (when twist = 0) in
Fig. 8 we conclude that, for the
straight annulus, the period of the surface mode, compared to the
period of the mode for the single tube, is increased by just up to
3
)
compared to the single
tube with internal Alfvén speed equal to the annulus'
Alfvén speed. In both cases the addition of the uniform twist
reduces the period of the mode, countering the increase in period
found to occur due to the annulus region. Since the two effects on
period seem to work against each other, this may be harder to
observationally justify. By studying the intersection of the
plotted lines of P* with the y-axis (when twist = 0) in
Fig. 8 we conclude that, for the
straight annulus, the period of the surface mode, compared to the
period of the mode for the single tube, is increased by just up to
3![]() .
A uniform twist applied to the annulus region reduces
this effect and the phase speed of the mode is
reduced to up to 10
.
A uniform twist applied to the annulus region reduces
this effect and the phase speed of the mode is
reduced to up to 10![]() below that of the single tube.
below that of the single tube.
Figure 9 shows the difference between the
period, P, of the other surface mode at the external surface,
r=R, with phase speed close to
![]() and the straight tube
period,
and the straight tube
period,
![]() .
This mode, apparent from
Figs. 6 and 7, does
not exist for longer wavelengths unless the twist is particularly
small which makes the analysis on the mode less conclusive. The
general trend, however, is still clear. While the annulus layer
acts to increase the periods of the modes (in comparison to the
single tube periods) the addition of twist counters this and for a
twist,
.
This mode, apparent from
Figs. 6 and 7, does
not exist for longer wavelengths unless the twist is particularly
small which makes the analysis on the mode less conclusive. The
general trend, however, is still clear. While the annulus layer
acts to increase the periods of the modes (in comparison to the
single tube periods) the addition of twist counters this and for a
twist,
![]() ,
of around 0.3 the periods are
approximately equal to those of the straight tube with neither
twist nor annulus.
,
of around 0.3 the periods are
approximately equal to those of the straight tube with neither
twist nor annulus.
It is known that the existence of twist to a flux tube gives rise
to a current sheet at the boundaries which introduces a factor of
instability (Dungey & Loughhead 1954; Roberts 1956) and the kink (m=1) mode is the
most unstable. In the analysis of this paper we assume that the
applied twist is sufficiently weak that the modes studied remain
stable. It is not our intention in this paper to make a rigorous
analytical study of stability aspects of the current
configuration. It is possible, however, by setting
![]() in the dispersion relation Eqs. (6a,b), to
numerically plot the curves of marginal stability. These are shown
in Fig. 10 where we plot the
dimensionless wavenumber kza as a function of dimensionless
pitch kzp where
in the dispersion relation Eqs. (6a,b), to
numerically plot the curves of marginal stability. These are shown
in Fig. 10 where we plot the
dimensionless wavenumber kza as a function of dimensionless
pitch kzp where
![]() .
Modes found to occur below
these marginal stability curves are stable whilst modes above are
unstable. Figure 10 shows that the addition
of a straight core region to a twisted tube has a stabilising
effect on the system. The left hand plot is for the case of a
single twisted tube (Bennett et al. 1999) and the right hand plot shows
the stability curves for the current configuration for two
different relative core widths.
.
Modes found to occur below
these marginal stability curves are stable whilst modes above are
unstable. Figure 10 shows that the addition
of a straight core region to a twisted tube has a stabilising
effect on the system. The left hand plot is for the case of a
single twisted tube (Bennett et al. 1999) and the right hand plot shows
the stability curves for the current configuration for two
different relative core widths.
![\begin{figure}
\par\resizebox{9cm}{7cm}{\includegraphics[100,377][567,700]{8689fi10.ps}}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg70.gif) |
Figure 10:
Curves of marginal stability (
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{6cm}{\includegraphics[100,377][567,700]{8689fi11.ps}}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg76.gif) |
Figure 11:
Plot of the solutions to Eq. (11)
of the body kink modes in the long wavelength approximation for
typical photospheric parameters (
|
| Open with DEXTER | |
When studying the body modes (
-m02=n02>0) it is first useful
to note that for
![]() we find that
we find that
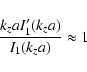 |
(9) |
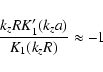 |
(10) |
![\begin{figure}
\par\resizebox{9cm}{6cm}{\includegraphics[100,377][567,700]{8689fi12.ps}}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg83.gif) |
Figure 12:
Same as Fig. 11 but for
parameters modelling a dense tube (
|
| Open with DEXTER | |
For the case of small twist (
![]() )
we are
able to simplify Eq. (11) and reduce the
approximate dispersion relation to
)
we are
able to simplify Eq. (11) and reduce the
approximate dispersion relation to
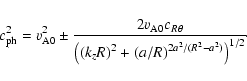 |
(13) |
It can be shown, see e.g. Spruit (1982) or Edwin & Roberts (1983) that, for an
incompressible plasma,
| (14) |
For
![]() let us first consider the body waves. Since
let us first consider the body waves. Since
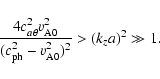 |
(16) |
When studying the surface modes we first notice that for the short
wavelength approximation (
![]() ), since
Eq. (15) holds, that
), since
Eq. (15) holds, that
![]() is also
true (this is for any
is also
true (this is for any
![]() and provided
and provided
![]() ). Expanding the Bessel functions I1(z),
I1'(z), K1(z) and K1'(z) for
). Expanding the Bessel functions I1(z),
I1'(z), K1(z) and K1'(z) for ![]() we are able, for
we are able, for
![]() ,
to reduce the dispersion relation
Eq. (6a) to
,
to reduce the dispersion relation
Eq. (6a) to
Solutions to Eq. (17) are plotted for parameters approximating a photospheric tube with different values of twist in Figs. 13. The plots indicate a relatively non-dispersive nature of the modes for large kza which is also apparent in the full dispersion plots (Figs. 2 and 3).
In the thin annulus limit,
![]() ,
and by noting that,
for short wavelengths, m0a and m0R can be approximated by
,
and by noting that,
for short wavelengths, m0a and m0R can be approximated by
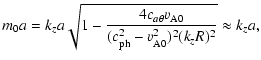 |
|||
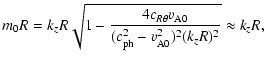 |
it is possible to further reduce Eq. (17) to a
quadratic one in
![]() yielding
yielding
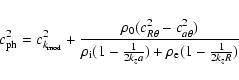 |
(18) |
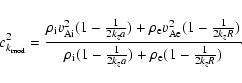 |
(19) |
![\begin{figure}
\par\resizebox{9cm}{6cm}{\includegraphics[100,377][567,700]{8689fi13.ps}}
\end{figure}](/articles/aa/full/2008/13/aa8689-07/Timg108.gif) |
Figure 13:
Plot of solutions to Eq. (17), the
short wavelength approximation for the surface kink modes, for
typical photospheric parameters (
|
| Open with DEXTER | |
The general dispersion relation (Eqs. (6a,b)) is now
studied for the m=1 (i.e. kink) modes. Numerical solutions to this
dispersion relation show, as in the m=0 sausage mode case, an
infinite set of body modes occurring due to the introduction of
magnetic twist. In the sausage mode case this set is found to be
symmetrical about the longitudinal component of Alfvén speed in
the twisted annulus region,
![]() .
The set of kink body modes,
however, is not symmetrical, the twist is found to increase the
phase speeds of the modes proportional to 1/kza so that they
approach infinity at longer wavelengths. For shorter wavelengths the
body modes do in fact approach
.
The set of kink body modes,
however, is not symmetrical, the twist is found to increase the
phase speeds of the modes proportional to 1/kza so that they
approach infinity at longer wavelengths. For shorter wavelengths the
body modes do in fact approach
![]() from above as
from above as
![]() .
.
Two surface modes exist for the twisted shell configuration, one due
to each surface (at r=a and r=R), where one mode is trapped by
the inner tube, the other by the annulus itself. Two characteristic
speeds arise for this configuration, the inner surface kink speed,
![]() and the external surface kink speed,
and the external surface kink speed,
![]() given by
given by
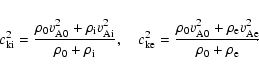 |
(20) |
For a physical condition perhaps closer to the one in the solar
photosphere (when the core Alfvén speed is greater than in the
annulus and external regions due to an enhancement of the magnetic
field) we find that the twist strengthens the effect of the straight
annulus alone (see Carter & Erdélyi 2007; Mikhalyaev & Solov'ev 2005). A straight annulus, i.e.
when twist,
![]() ,
decreases the periods of the inner
surface mode by between 10 and 15
,
decreases the periods of the inner
surface mode by between 10 and 15![]() (depending on the value
of kza). This decrease is extended, by a twist of less than
0.5, to between 16 and 19
(depending on the value
of kza). This decrease is extended, by a twist of less than
0.5, to between 16 and 19![]() (see
Fig. 4). A similar result was found for
the outer (r=R) surface mode - an initial reduction of
4-13
(see
Fig. 4). A similar result was found for
the outer (r=R) surface mode - an initial reduction of
4-13![]() is increased to a reduction of 17-19
is increased to a reduction of 17-19![]() for a
magnetic twist of 0.2.
for a
magnetic twist of 0.2.
For parameters approximating a dense tube (constant magnetic field
strength but higher density within the tube) the effect of a twisted
magnetic annulus on the oscillation periods was quite different.
While the annulus layer (without twist) increased the periods of the
mode, when twist was applied it acted to decrease the periods. For
the surface mode at r=a, an initial increase (for an
annulus with no twist) of 0-5![]() is reduced to a deficit by
the addition of a magnetic twist: a decrease in period of
2-12
is reduced to a deficit by
the addition of a magnetic twist: a decrease in period of
2-12![]() is seen for a twist of 0.5. The same trend arose for
the mode at the outer (r=R) surface with a twist of around 0.3reducing an increase of 5-18
is seen for a twist of 0.5. The same trend arose for
the mode at the outer (r=R) surface with a twist of around 0.3reducing an increase of 5-18![]() (with no twist) to zero,
essentially negating the effect of the annulus.
(with no twist) to zero,
essentially negating the effect of the annulus.
This study has given a first insight into the effect of magnetic twist in an annulus region on the phase speeds and periods of propagating kink modes in a magnetically twisted shell. It is hoped that this work can provide additional information that can be used in the study of, specifically, lower atmospheric kink oscillations such as those observed recently by Zaqarashvili et al. (2007); Kukhianidze et al. (2006). Future work could include a twist in the core region, multiple shells or the extension to the fully compressible case.
Acknowledgements
The authors thank M. Ruderman and N. Venkov for a number of useful discussions. RE acknowledges M. Kéray for patient encouragement. The authors are also grateful to NSF, Hungary (OTKA, Ref. No. K67746) and to The University of Sheffield (White Rose Consortium) for the financial support they received.