A&A 481, 141-147 (2008)
DOI: 10.1051/0004-6361:20077543
SMA observations of young disks: separating envelope, disk, and stellar masses in class I YSOs
D. Lommen1 - J. K. Jørgensen2,3 - E. F. van Dishoeck1 - A. Crapsi1,4
1 - Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
2 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
3 - Argelander-Institut für Astronomie, University of Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
4 - Observatorio Astronómico Nacional (IGN), Alfonso XII, 3, 28014 Madrid, Spain
Received 26 March 2007 / Accepted 14 January 2008
Abstract
Context. Young stars are born with envelopes, which in the early stages obscure the central (proto)star and circumstellar disk. In the Class I stage, the disks are still young, but the envelopes are largely dispersed. This makes the Class I sources ideal targets for studies of the early stages of disks.
Aims. We aim to determine the masses of the envelopes, disks, and central stars of young stellar objects (YSOs) in the Class I stage.
Methods. We observed the embedded Class I objects IRS 63 and Elias 29 in the 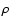 Ophiuchi star-forming region with the Submillimeter Array (SMA) at 1.1 mm.
Ophiuchi star-forming region with the Submillimeter Array (SMA) at 1.1 mm.
Results. IRS 63 and Elias 29 are both clearly detected in the continuum, with peak fluxes of 459 and 47 mJy/beam, respectively. The continuum emission toward Elias 29 is clearly resolved, whereas IRS 63 is consistent with a point source down to a scale of 3
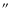 (400 AU). The SMA data are combined with single-dish data, and both disk masses of 0.055 and
(400 AU). The SMA data are combined with single-dish data, and both disk masses of 0.055 and 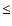 0.007
0.007  and envelope masses of 0.058 and
and envelope masses of 0.058 and 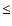 0.058
0.058  are empirically determined for IRS 63 and Elias 29, respectively. The disk+envelope systems are modelled with the axisymmetric radiative-transfer code RADMC, yielding disk and envelope masses that differ from the empirical results by factors of a few. HCO+ J = 3-2 is detected toward both sources, HCN J = 3-2 is not. The HCO+ position-velocity diagrams are indicative of Keplerian rotation and allow an estimate of the mass of the central stars. For a fiducial inclination of 30
are empirically determined for IRS 63 and Elias 29, respectively. The disk+envelope systems are modelled with the axisymmetric radiative-transfer code RADMC, yielding disk and envelope masses that differ from the empirical results by factors of a few. HCO+ J = 3-2 is detected toward both sources, HCN J = 3-2 is not. The HCO+ position-velocity diagrams are indicative of Keplerian rotation and allow an estimate of the mass of the central stars. For a fiducial inclination of 30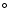 ,
we find stellar masses of
,
we find stellar masses of
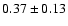 for IRS 63 and
for IRS 63 and
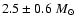 for Elias 29.
for Elias 29.
Conclusions. The sensitivity and spatial resolution of the SMA at 1.1 mm allow a good separation of the disks around Class I YSOs from their circumstellar envelopes and environments, and the spectral resolution makes it possible to resolve their dynamical structure and estimate the masses of the central stars. The ratios of the envelope and disk masses
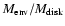 are found to be 0.2 for IRS 63 and 6 for Elias 29. This is lower than the values for Class 0 sources, which have
are found to be 0.2 for IRS 63 and 6 for Elias 29. This is lower than the values for Class 0 sources, which have
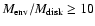 ,
suggesting that this ratio is a tracer of the evolutionary stage of a YSO.
,
suggesting that this ratio is a tracer of the evolutionary stage of a YSO.
Key words: circumstellar matter -
stars: formation - stars: individual: IRS 63 - stars: individual: Elias 29
1 Introduction
Low- and intermediate-mass stars are formed from the gravitational collapse of molecular cloud cores. In the earliest stages, the
newly-formed protostar remains embedded in the remnants of this core, a cold envelope of dust and gas, which is gradually accreted by the young star
(e.g., Shu 1977). Due to
the angular momentum initially present in the core, most of the envelope material does not fall directly onto the central protostar but is piled-up in a
circumstellar disk (e.g., Terebey et al. 1984). Understanding this interplay between star, disk, and envelope is crucial in order to be
able to relate the initial conditions of star formation such as the mass of the protostellar core to the end-product - namely the properties of the
young star, and the mass and thus potential of the disk for forming planets. Some of the key questions include: Where does most of the mass reside at a given time? Will all the mass that is seen in prestellar cores or in the envelopes around deeply embedded sources end up in the star, or will a large fraction be dispersed from the system? How do the masses of the circumstellar envelope, the disk, and that of the central star evolve over time, and how long does it take for the circumstellar matter to be accreted onto the star?
Young stellar objects (YSOs) are usually classified according to their slopes in the infrared (IR) wavelength regime. Originally, the LW classification (Lada 1987; Lada & Wilking 1984) ran from the embedded Class I, via the optically visible Class II or classical T Tauri stars, to the Class III spectral energy distributions of post-T Tauri stars. Later, the Class 0 stage was added to this classification (see, e.g., André et al. 1993), where the Class 0 sources are distinguished from the Class I sources through their high relative luminosity at submillimetre (submm) wavelengths.
This classification roughly reflects
the evolutionary stage of the YSOs under consideration. The most deeply embedded
Class 0 sources are thought to evolve through the Class I stage while
dissipating their circumstellar envelopes. Eventually they become optically visible as pre-main sequence T Tauri stars with circumstellar disks.
The Class 0 and Class II YSOs have been studied quite extensively with high-resolution (sub)millimetre
interferometers (e.g., Andrews & Williams 2007; Jørgensen et al. 2007, and references therein). Studies of deeply embedded Class 0 YSOs have shown that
circumstellar disks are formed early (Harvey et al. 2003; Jørgensen et al. 2004), but in these systems,
it is difficult to separate the emission from the disk from that of the envelope.
The Class I sources, in which a large part of the original circumstellar envelopes has been dissipated, are ideal to study young disks in
YSOs. Interferometric studies of Class I objects have so far been largely limited
to studies at around 3 mm (e.g., Hogerheijde et al. 1998; Looney et al. 2000; Ohashi et al. 1997; Hogerheijde et al. 1997).
The Submillimeter Array (SMA) allows observations around 1 mm, where the thermal dust continuum emission is an order of magnitude stronger
than at 3 mm. Also at these shorter wavelengths it is possible to detect the higher rotational transitions of the molecules that trace the dense
gas in the disks and inner envelopes of the young systems, rather than lower-density extended envelope emission.
We here present SMA observations of two Class I objects that appear to be in an evolutionary stage
where the kinematics of the circumstellar material are no longer dominated by infall. IRS 63 (WLY 2-63,
GWAYL 4) and Elias 29 (Elia 2-29, WLY 1-7) are located in the 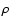 Ophiuchi cloud, taken to be at a
distance
Ophiuchi cloud, taken to be at a
distance
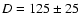 pc (de Geus et al. 1989). Spitzer photometry from the ``Cores to Disks'' Legacy program (Evans et al. 2003) was used to
determine the source's infrared colours and their bolometric luminosities and temperatures. IRS 63 and Elias 29 have similar bolometric
temperatures,
pc (de Geus et al. 1989). Spitzer photometry from the ``Cores to Disks'' Legacy program (Evans et al. 2003) was used to
determine the source's infrared colours and their bolometric luminosities and temperatures. IRS 63 and Elias 29 have similar bolometric
temperatures,
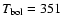 K and 391 K, respectively, which places them in the LW Class I regime. The bolometric luminosities were
calculated to be
K and 391 K, respectively, which places them in the LW Class I regime. The bolometric luminosities were
calculated to be
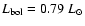 for IRS 63 and 13.6
for IRS 63 and 13.6 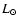 for Elias 29. According to their infrared slopes of
for Elias 29. According to their infrared slopes of
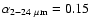 and 0.42, IRS 63 is the slightly more evolved, falling into the ``flat-spectrum'' class that separates the Class I
from the Class II sources (Greene et al. 1994).
The values for
and 0.42, IRS 63 is the slightly more evolved, falling into the ``flat-spectrum'' class that separates the Class I
from the Class II sources (Greene et al. 1994).
The values for
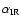 quoted here are from un-dereddened observations.
Correction for the extinction toward the
quoted here are from un-dereddened observations.
Correction for the extinction toward the 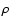 Ophiuchi star-forming region (e.g., Flaherty et al. 2007)
would result in lower values for
Ophiuchi star-forming region (e.g., Flaherty et al. 2007)
would result in lower values for
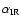 ;
in other words, the sources may be slightly more evolved than the raw values of
;
in other words, the sources may be slightly more evolved than the raw values of
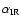 suggest.
In terms of environment, the two sources are quite each other's opposites. The SCUBA 850
suggest.
In terms of environment, the two sources are quite each other's opposites. The SCUBA 850 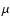 m map (Johnstone et al. 2004) from the
COMPLETE survey (Ridge et al. 2006) shows that IRS 63 is an isolated compact source. Elias 29, on the other hand, is located in a dense ridge of
molecular material, which contains several more YSOs. It is likely that these YSOs were formed from condensations in this molecular ridge.
m map (Johnstone et al. 2004) from the
COMPLETE survey (Ridge et al. 2006) shows that IRS 63 is an isolated compact source. Elias 29, on the other hand, is located in a dense ridge of
molecular material, which contains several more YSOs. It is likely that these YSOs were formed from condensations in this molecular ridge.
We present the masses of all main components of Class I YSOs, i.e., the central star, the disk, and the envelope, for the first time.
IRS 63 and Elias 29 are the
first two sources in a larger survey of Class I objects studied with the SMA at 1.1 mm. These observations complement the survey of Class 0 sources in the
PROSAC programme (Jørgensen et al. 2007) and will allow us to trace the similarities and differences of these evolving protostars.
The results of the complete campaign will be presented in a
future paper. In Sect. 2, the observations are presented, and the results and implications are discussed in
Sects. 3 and 4. We summarise the main conclusions in Sect. 5.
2 Observations
IRS 63 and Elias 29 were observed with the SMA![[*]](/icons/foot_motif.gif) (Ho et al. 2004) on 15 and 17 May 2006, respectively. Weather conditions were good on 15 May, with zenith optical depths at 225 GHz
(Ho et al. 2004) on 15 and 17 May 2006, respectively. Weather conditions were good on 15 May, with zenith optical depths at 225 GHz
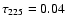 -0.06 (as measured by a tipping radiometer operated by the Caltech Submillimeter Observatory). Conditions were slightly worse
on 17 May, with
-0.06 (as measured by a tipping radiometer operated by the Caltech Submillimeter Observatory). Conditions were slightly worse
on 17 May, with
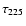 starting at 0.16, falling to 0.1 during
the first half of the night. Physical baselines ranged from 11.6 to 62.0 m, and the resulting projected baselines ranged from 5.9 to 63.8 k
starting at 0.16, falling to 0.1 during
the first half of the night. Physical baselines ranged from 11.6 to 62.0 m, and the resulting projected baselines ranged from 5.9 to 63.8 k ,
yielding a resolution of about
,
yielding a resolution of about
 (natural weighting). The correlator was configured to observe the lines of HCO+ J = 3-2 and HCN J = 3-2 together with the continuum emission at 268 and 278 GHz.
The line data were taken with 512 channels of 0.2 MHz width each, resulting in a velocity resolution of 0.23 km s-1.
(natural weighting). The correlator was configured to observe the lines of HCO+ J = 3-2 and HCN J = 3-2 together with the continuum emission at 268 and 278 GHz.
The line data were taken with 512 channels of 0.2 MHz width each, resulting in a velocity resolution of 0.23 km s-1.
Calibration was done using the MIR package (Qi 2005), and imaging was done using the MIRIAD package (Sault et al. 1995). The quasars
QSO B1622-297 and QSO B1514-241 served as gain calibrators, and the absolute fluxes were calibrated on Uranus. The absolute flux
calibration is estimated to have an uncertainty of 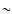 20%.
The passbands were calibrated on Callisto and the quasar QSO B1253-055 (3C 279).
20%.
The passbands were calibrated on Callisto and the quasar QSO B1253-055 (3C 279).
3 Results
The basic results of the observations are shown in Fig. 1 and summarised in Table 1.
Table 1:
Results of SMA observations at 1.1 mm.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7543fig1.eps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg38.gif) |
Figure 1:
SMA images of the 1.1 mm continuum ( top panels) and integrated HCO+ 3-2 ( bottom panels) emission. Contours are drawn at 2, 4, 8, 16, 32, and 64 times the respective rms noise levels, with the rms being about 6 mJy bm-1 for the continuum and about 65 mJy bm-1 for the line data. Negative contours are dashed. The positional offsets are with
respect to the coordinates of the observational phase centre. The dashed lines indicate how the position-velocity diagrams (Fig. 7) are directed. |
| Open with DEXTER |
3.1 Continuum data
Both sources are clearly detected in the continuum at 1.1 mm.
Point-source and Gaussian fits were done in the (u, v) plane to determine the peak and integrated fluxes, respectively.
A continuum peak flux of 459 mJy bm-1 and an integrated flux of 474 mJy were found for IRS 63, at a position which
agrees with the 2MASS K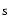 -band position within
-band position within
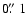 .
IRS 63 was also observed with the SMA by Andrews & Williams (2007) at higher resolution at
1.3 mm. Their interferometer flux for IRS 63, to which they refer as L1709 B
.
IRS 63 was also observed with the SMA by Andrews & Williams (2007) at higher resolution at
1.3 mm. Their interferometer flux for IRS 63, to which they refer as L1709 B![[*]](/icons/foot_motif.gif) , is consistent with the value here and a mm slope
, is consistent with the value here and a mm slope
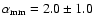 .
The data of Elias 29 are best fitted by two sources. The brightest of the two agrees with the 2MASS
.
The data of Elias 29 are best fitted by two sources. The brightest of the two agrees with the 2MASS 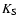 -band position
of Elias 29 within
-band position
of Elias 29 within
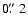 ,
whereas the other source is offset by 3
,
whereas the other source is offset by 3
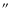 .
The second peak is attributed to an enhancement in
the ridge, from which Elias 29 likely formed, and is designated by ``Ridge'' in Table 1. Elias 29 and the ridge
component yield continuum peak fluxes of 47 and 31 mJy bm-1, and integrated fluxes of 72 and 28 mJy, respectively.
.
The second peak is attributed to an enhancement in
the ridge, from which Elias 29 likely formed, and is designated by ``Ridge'' in Table 1. Elias 29 and the ridge
component yield continuum peak fluxes of 47 and 31 mJy bm-1, and integrated fluxes of 72 and 28 mJy, respectively.
Plots of the visibility amplitudes as functions of projected baseline for
IRS 63 and Elias 29 are shown in Fig. 2. Elias 29 shows
a steeply rising flux toward the shortest baselines, indicating that an envelope is present around this source. The emission toward IRS 63 does not change appreciably with
baseline length, indicating that this source is unresolved up to
baselines of 60 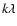 ,
or down to physical scales of about
400 AU.
,
or down to physical scales of about
400 AU.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7543fig2.eps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg45.gif) |
Figure 2:
Continuum amplitude as a function of projected baseline for IRS 63 ( left panel) and Elias 29 ( right panel). The data points give the amplitude per bin, where the data are binned in annuli according to (u, v) distance. The error bars show the statistical 1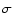 errors, most often smaller than the data points, and the dotted lines give the expected amplitude for zero signal, i.e., the anticipated amplitude in the absence of source emission. The half-open circles at zero (u, v) distance give the zero-spacing 1.1 mm flux, interpolated between 850
errors, most often smaller than the data points, and the dotted lines give the expected amplitude for zero signal, i.e., the anticipated amplitude in the absence of source emission. The half-open circles at zero (u, v) distance give the zero-spacing 1.1 mm flux, interpolated between 850 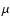 m and 1.25 mm single-dish fluxes (André & Montmerle 1994; Ridge et al. 2006; Johnstone et al. 2004, see text). m and 1.25 mm single-dish fluxes (André & Montmerle 1994; Ridge et al. 2006; Johnstone et al. 2004, see text). |
| Open with DEXTER |
Figure 2 also shows the estimated single-dish flux at 1.1 mm. For this, the ``mapped'' fluxes from André & Montmerle (1994) at 1.25 mm were combined with newly determined 850 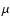 m fluxes (SCUBA maps from the COMPLETE survey, Ridge et al. 2006; Johnstone et al. 2004). The SEDs are assumed to have a
m fluxes (SCUBA maps from the COMPLETE survey, Ridge et al. 2006; Johnstone et al. 2004). The SEDs are assumed to have a
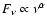 dependence in this wavelength range, and are interpolated to the 1.1 mm wavelength at which the SMA observations were conducted. Fluxes of 355 and 780 mJy are found for Elias 29 and IRS 63, respectively, with an estimated uncertainty of 25%. These fluxes are significantly larger than the interferometer fluxes and
indicate that extended emission is present around the compact components picked up with the SMA. This extended emission may be due to a circumstellar envelope, or to surrounding or intervening interstellar clouds, since the ``mapped'' regions of
André & Montmerle (1994) are rather large, 40
dependence in this wavelength range, and are interpolated to the 1.1 mm wavelength at which the SMA observations were conducted. Fluxes of 355 and 780 mJy are found for Elias 29 and IRS 63, respectively, with an estimated uncertainty of 25%. These fluxes are significantly larger than the interferometer fluxes and
indicate that extended emission is present around the compact components picked up with the SMA. This extended emission may be due to a circumstellar envelope, or to surrounding or intervening interstellar clouds, since the ``mapped'' regions of
André & Montmerle (1994) are rather large, 40
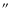 for Elias 29 and 60
for Elias 29 and 60
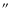 for IRS 63.
for IRS 63.
3.2 Line data
HCO+ J = 3-2 is detected toward both sources, whereas HCN J = 3-2 is not. Elias 29 appears to be about ten times as strong in HCO+ J = 3-2 integrated emission as IRS 63 (see Table 1). The emission toward IRS 63 is compact, coincident with the continuum peak, and shows a velocity gradient in the north-south
direction, see Fig. 3.
The integrated emission in the direction of Elias 29 is more extended and can be
fitted with two elliptical Gaussians, as is shown in the left panel of Fig. 4. The centre position of the
smaller Gaussian coincides with the continuum peak, as well as with
the infrared position, and is attributed
to Elias 29 itself. The second Gaussian has a very elongated shape, offset from the infrared source, and is attributed to a density enhancement in
the nearby ridge.
The right panel of Fig. 4 shows the HCO+ J = 3-2 spectra toward the continuum positions of Elias 29 and IRS 63, binned to 0.9 km s-1.
The HCO+ J = 3-2 emission toward IRS 63 appears to be centred at
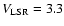 km s-1.
km s-1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7543fig3.eps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg47.gif) |
Figure 3:
First-moment map of IRS 63. Contours are drawn at 2, 4, and 8 times the RMS of 67 mJy bm-1. The positional offsets are with respect to the coordinates of the observational phase centre, and the cross indicates the continuum position of IRS 63 from a point-source fit
in the (u, v) plane, see Table 1. A colour version of this figure can be obtained from the electronic version of the paper. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7543fig4.ps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg48.gif) |
Figure 4:
Left panel: HCO+ J = 3-2 integrated emission toward Elias 29. The grayscale is linear from 0.2 to 1.2 Jy bm-1. The emission is fitted with two Gaussians, the one in the north-south direction tracing the emission due to Elias 29, and the other, larger one tracing emission from a density enhancement in the ridge. Right panel: spectral lines, integrated over
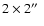 regions, centred on the continuum positions of Elias 29, of the ridge (shifted by +4 Jy bm-1), and of IRS 63 (shifted by -4 Jy bm-1), and binned to 0.9 km s-1. The HCO+ J = 3-2 emission toward IRS 63 appears to be centred at regions, centred on the continuum positions of Elias 29, of the ridge (shifted by +4 Jy bm-1), and of IRS 63 (shifted by -4 Jy bm-1), and binned to 0.9 km s-1. The HCO+ J = 3-2 emission toward IRS 63 appears to be centred at
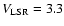 km s-1. km s-1. |
| Open with DEXTER |
4 Discussion and interpretations
4.1 Envelope and disk masses
The basic data as presented in the previous section are used to determine the masses of the disks and the envelopes in the systems, both empirically
(Sect. 4.1.1) and through detailed radiative-transer modelling (Sect. 4.1.2). The differences between the two
methods and the over-all conclusions are discussed in Sect. 4.1.3.
4.1.1 Empirical results
A first-order estimate
of the disk and envelope masses can be obtained by assuming that the continuum flux of the envelope is resolved out
by the interferometer on the longest baselines (Fig. 2).
Hence, the emission on the longest baselines is solely due to the disk, whereas the single-dish flux comes from the disk and envelope combined.
Assuming that the disk and the envelope are isothermal and the dust emission is optically thin, the disk mass is given by
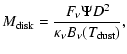 |
|
|
(1) |
where 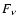 is the flux at frequency
is the flux at frequency 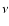 on the longest baselines,
on the longest baselines, 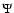 is the gas-to-dust ratio,
is the gas-to-dust ratio,
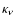 is the dust opacity at
is the dust opacity at 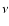 ,
and
,
and
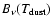 is the emission from a black body at
is the emission from a black body at
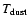 .
Using fiducial values for all these parameters -
.
Using fiducial values for all these parameters -
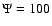 ,
,
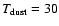 K, and
K, and
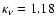 cm2 g-1 (``OH5''
coagulated dust with icy mantles, found in the fifth column of Table 1 of Ossenkopf & Henning 1994, interpolated to the observed frequency
cm2 g-1 (``OH5''
coagulated dust with icy mantles, found in the fifth column of Table 1 of Ossenkopf & Henning 1994, interpolated to the observed frequency
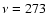 GHz) - disk masses of 0.055
GHz) - disk masses of 0.055  and 0.007
and 0.007  are found for IRS 63 and Elias 29, respectively.
Using the opacity law as quoted by Beckwith et al. (1990),
are found for IRS 63 and Elias 29, respectively.
Using the opacity law as quoted by Beckwith et al. (1990),
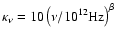 ,
and taking
,
and taking 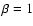 ,
a dust opacity at 273 GHz of
,
a dust opacity at 273 GHz of
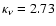 cm2 g-1
is found, and the disk masses decrease to
0.024
cm2 g-1
is found, and the disk masses decrease to
0.024  for IRS 63 and 0.003
for IRS 63 and 0.003  for Elias 29
for Elias 29![[*]](/icons/foot_motif.gif) .
Note that this method of estimating the disk mass is only valid when the disk is unresolved by the observations.
If the disk were clearly resolved, the flux on the longest baselines would not include the emission from the outer disk, but only that from
smaller radii, unresolved by those baselines. Due to its closeness, the enhancement in the ridge near Elias 29 may
contribute to its flux, even on the longest baselines of
.
Note that this method of estimating the disk mass is only valid when the disk is unresolved by the observations.
If the disk were clearly resolved, the flux on the longest baselines would not include the emission from the outer disk, but only that from
smaller radii, unresolved by those baselines. Due to its closeness, the enhancement in the ridge near Elias 29 may
contribute to its flux, even on the longest baselines of 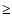 50 k
50 k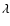 or scales <
or scales <
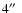 .
However, in the estimate of the flux on the longest baselines (Table 1), the ridge component was fitted simultaneously with Elias 29,
and hence its contribution to the derived disk mass is expected to be minimal.
.
However, in the estimate of the flux on the longest baselines (Table 1), the ridge component was fitted simultaneously with Elias 29,
and hence its contribution to the derived disk mass is expected to be minimal.
In a similar fashion the envelope masses in the systems can be found. First, the contributions from the envelopes to the 1.1 mm single-dish
fluxes are determined by subtracting the fluxes at baselines 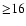 k
k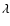 (see Table 1) from the single-dish fluxes as found
in Sect. 3. The envelope masses are then found by using Eq. (1), with the temperatures of the envelopes taken
to be 20 K. For an optically thin envelope around stars with luminosities of 0.79 and 13.6
(see Table 1) from the single-dish fluxes as found
in Sect. 3. The envelope masses are then found by using Eq. (1), with the temperatures of the envelopes taken
to be 20 K. For an optically thin envelope around stars with luminosities of 0.79 and 13.6 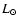 applicable to IRS 63 and Elias 29, a temperature of 17-29 K
is expected at a radius of 940 AU corresponding to the size of the JCMT single-dish beam (from, e.g., Eq. (2) of Chandler & Richer 2000, taking the opacity index
applicable to IRS 63 and Elias 29, a temperature of 17-29 K
is expected at a radius of 940 AU corresponding to the size of the JCMT single-dish beam (from, e.g., Eq. (2) of Chandler & Richer 2000, taking the opacity index
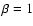 ). This yields an envelope mass
). This yields an envelope mass
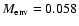
 for IRS 63 within a 30
for IRS 63 within a 30
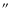 radius, where the
contribution from the envelope to the total 1.1 mm flux is 38%. Coincidentally, also for Elias 29 an envelope
mass
radius, where the
contribution from the envelope to the total 1.1 mm flux is 38%. Coincidentally, also for Elias 29 an envelope
mass
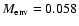
 ,
within a 20
,
within a 20
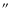 radius, is found. However, in this system
the contribution from the envelope to the total 1.1 mm flux is 84%. As for the disk mass, also the envelope mass found for Elias 29 should be taken as an upper limit because of the closeness of the ridge enhancement. Note, however, that it is unlikely that the bulk of the continuum emission is due to this enhancement, because of the coincidence of the continuum peak with the infrared source and also with the single-dish submillimetre positions. Using the opacities of Beckwith et al. (1990) will lower all masses by a factor of about 2.
radius, is found. However, in this system
the contribution from the envelope to the total 1.1 mm flux is 84%. As for the disk mass, also the envelope mass found for Elias 29 should be taken as an upper limit because of the closeness of the ridge enhancement. Note, however, that it is unlikely that the bulk of the continuum emission is due to this enhancement, because of the coincidence of the continuum peak with the infrared source and also with the single-dish submillimetre positions. Using the opacities of Beckwith et al. (1990) will lower all masses by a factor of about 2.
4.1.2 Modelling
To provide more physical grounding to the values for
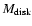 and
and
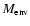 estimated in the previous section, a radiative transfer code was used to fit simultaneously the millimetre interferometry and the spectral energy distributions. IRS 63 and Elias 29 were modelled with a new version of the programme RADMC (e.g., Dullemond & Dominik 2004). RADMC is an axisymmetric Monte-Carlo code for dust continuum radiative transfer in circumstellar disks and envelopes in which the
stellar photons are traced in three dimensions. The code is based on the method of Bjorkman & Wood (2001).
estimated in the previous section, a radiative transfer code was used to fit simultaneously the millimetre interferometry and the spectral energy distributions. IRS 63 and Elias 29 were modelled with a new version of the programme RADMC (e.g., Dullemond & Dominik 2004). RADMC is an axisymmetric Monte-Carlo code for dust continuum radiative transfer in circumstellar disks and envelopes in which the
stellar photons are traced in three dimensions. The code is based on the method of Bjorkman & Wood (2001).
The density structure of the disk is given by (see Crapsi et al. 2008)
![$\displaystyle \rho_{\rm disk}(r, \theta) = \frac{\Sigma_0(r/R_0)^{-1}}{\sqrt(2\...
...(r)}\exp \left( - \frac{1}{2}\left[\frac{r \cos(\theta)}{H(r)}\right]^2\right),$](/articles/aa/full/2008/13/aa7543-07/img68.gif) |
|
|
(2) |
where r is the radial distance from the central star and 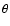 is the angle from the axis of symmetry. The inner radius was fixed to 0.1 AU for IRS 63, and to
0.25 AU for Elias 29, to account for the higher luminosity of the star. At these radii, the temperature is of the order of the dust sublimation temperature.
Note that the exact sublimation temperature, and hence the disk inner radius, depends on the exact dust species and local density. The vertical scale height of the disk
is given by
is the angle from the axis of symmetry. The inner radius was fixed to 0.1 AU for IRS 63, and to
0.25 AU for Elias 29, to account for the higher luminosity of the star. At these radii, the temperature is of the order of the dust sublimation temperature.
Note that the exact sublimation temperature, and hence the disk inner radius, depends on the exact dust species and local density. The vertical scale height of the disk
is given by
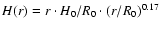 ,
where R0 was left free to vary, and H0/R0 was arbitrarily fixed to 0.17.
Chiang & Goldreich (1997) find
,
where R0 was left free to vary, and H0/R0 was arbitrarily fixed to 0.17.
Chiang & Goldreich (1997) find
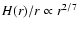 .
However, that estimate is based on grey opacities and constant surface density, and somewhat smaller
flaring is usually more realistic. Hence, we chose
.
However, that estimate is based on grey opacities and constant surface density, and somewhat smaller
flaring is usually more realistic. Hence, we chose
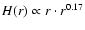 .
.
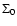 was scaled to the disk mass, which was also left as a free parameter.
The envelope density follows the equation for a rotating, infalling model (Ulrich 1976; Crapsi et al. 2008)
was scaled to the disk mass, which was also left as a free parameter.
The envelope density follows the equation for a rotating, infalling model (Ulrich 1976; Crapsi et al. 2008)
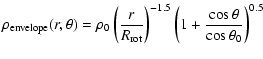 |
|
|
|
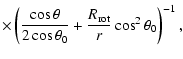 |
|
|
(3) |
where 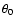 is the solution of the parabolic motion of an infalling particle,
is the solution of the parabolic motion of an infalling particle,
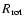 is the centrifugal radius of the envelope, and
is the centrifugal radius of the envelope, and
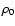 is the density in the equatorial plane at
is the density in the equatorial plane at
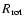 .
.
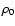 was scaled to accomodate the total envelope mass, and
was scaled to accomodate the total envelope mass, and
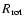 ,
which can have a significant influence on the amplitude as a function of baseline length,
was left free to vary. The outer radius of the envelope was fixed to 10 000 AU, where the temperature is similar to that of the ambient interstellar cloud.
The parameters, as summarised in Table 2, give the best-fit models by eye; a full
,
which can have a significant influence on the amplitude as a function of baseline length,
was left free to vary. The outer radius of the envelope was fixed to 10 000 AU, where the temperature is similar to that of the ambient interstellar cloud.
The parameters, as summarised in Table 2, give the best-fit models by eye; a full 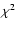 minimization is not warranted by the relatively low resolution and S/N of the data. Our models do not have outflow cavities in the envelopes. Note that the actual physical structure of the envelope (centrifugal radius, outflow cavities, etc.) may considerably affect the mid-IR SED and thus the derived inclination from the
models (e.g., Whitney et al. 2003; Jørgensen et al. 2005).
minimization is not warranted by the relatively low resolution and S/N of the data. Our models do not have outflow cavities in the envelopes. Note that the actual physical structure of the envelope (centrifugal radius, outflow cavities, etc.) may considerably affect the mid-IR SED and thus the derived inclination from the
models (e.g., Whitney et al. 2003; Jørgensen et al. 2005).
Table 2:
Model parameters for IRS 63 and Elias 29.
Two different dust species are used in these models, ``hot''
dust where the temperature is higher than 90 K, and ``cold'' dust where the temperature is below 90 K.
The opacities used are ``OH2''
(coagulated dust without ice mantles, Ossenkopf & Henning 1994) for the hot dust, and ``OH5'' (coagulated dust with thin ice mantles) for the cold
dust. The central stars were represented by sources with luminosities of 0.79 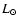 for IRS 63 and 13.6
for IRS 63 and 13.6 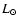 for Elias 29, which were
taken to be equal to the bolometric luminosities of the sources, and the temperature structures in the disks and envelopes were then calculated by
propagating the stellar photons through the systems.
for Elias 29, which were
taken to be equal to the bolometric luminosities of the sources, and the temperature structures in the disks and envelopes were then calculated by
propagating the stellar photons through the systems.
The results of the modelling are shown in Fig. 5.
A model with only a 0.055  disk reproduces the amplitude as a function of baseline quite well for IRS 63, but fails to
produce enough single-dish flux. A 0.35
disk reproduces the amplitude as a function of baseline quite well for IRS 63, but fails to
produce enough single-dish flux. A 0.35  envelope-only model, on the other hand, produces enough single-dish flux in the (sub)mm regime,
but falls off
too quickly toward longer baselines.
To allow for a comparison with the empirical model (Sect. 4.1.1) the envelope mass was defined as the mass, present within the single-dish
aperture (i.e., a 30
envelope-only model, on the other hand, produces enough single-dish flux in the (sub)mm regime,
but falls off
too quickly toward longer baselines.
To allow for a comparison with the empirical model (Sect. 4.1.1) the envelope mass was defined as the mass, present within the single-dish
aperture (i.e., a 30
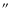 radius for IRS 63 and a 20
radius for IRS 63 and a 20
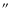 radius for Elias 29), and not contained in the disk.
A model with both a disk and an envelope is necessary to explain the observations of IRS 63, and the best model
consists of a disk of 0.13
radius for Elias 29), and not contained in the disk.
A model with both a disk and an envelope is necessary to explain the observations of IRS 63, and the best model
consists of a disk of 0.13  and an envelope of 0.022
and an envelope of 0.022  .
This model also fits the observed IRS 63 SED well, if a foreground
extinction of
.
This model also fits the observed IRS 63 SED well, if a foreground
extinction of
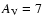 mag is assumed, see Fig. 6.
The region in which IRS 63 is located has a very high
mag is assumed, see Fig. 6.
The region in which IRS 63 is located has a very high 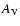 of about 24 mag as found in extinction maps produced by the Spitzer
``Cores to Disks'' Legacy program (Evans et al. 2007,2003). These maps measure the large scale (
of about 24 mag as found in extinction maps produced by the Spitzer
``Cores to Disks'' Legacy program (Evans et al. 2007,2003). These maps measure the large scale (
 )
cloud extinction on
the basis of background stars, and therefore includes an extra contribution besides envelope extinction.
)
cloud extinction on
the basis of background stars, and therefore includes an extra contribution besides envelope extinction.
The amplitude as a function of baseline for Elias 29 is best explained by a 0.004  disk and a 0.025
disk and a 0.025  envelope. For this source,
no further attempt to model the SED was made, because the close presence of the ridge enhancement makes a model that is axisymmetric on scales
larger than several 100 AU unapplicable.
envelope. For this source,
no further attempt to model the SED was made, because the close presence of the ridge enhancement makes a model that is axisymmetric on scales
larger than several 100 AU unapplicable.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7543fig5.eps} \end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg87.gif) |
Figure 5:
Continuum amplitude as a function of projected baseline for IRS 63 ( left panel) and Elias 29 ( right panel), with models overplotted. The dashed lines show models, consisting of an envelope only. They fit the single-dish (sub)mm data well, but fall off too fast to longer projected baselines. The dash-dotted lines are from disk-only models. They fit the interferometric data well, but do not have enough flux on the shortest baselines. The solid lines are for the models that provide a good fit to the SED and to the spatial information provided by the interferometric observations. The dotted lines indicate the expected amplitude for zero signal. |
| Open with DEXTER |
4.1.3 Discussion
Even though the disk and envelope masses derived from the empirical and detailed model results differ by up to a factor of a few, we are confident
that they are accurate within this range. For example, a significantly larger disk in the IRS 63 model would show a very steep fall-off in
the amplitude as a function of baseline length, which is not observed (Fig. 5). Likewise, an envelope significantly more massive than 0.022  found
for IRS 63 would obscure the central star so much that the near- and mid-IR flux would be severly underestimated (Fig. 6). In the further discussion, we
will use the disk and envelope masses as found by the detailed modelling, but note that the overall conclusions do not change if the empirical results are used.
found
for IRS 63 would obscure the central star so much that the near- and mid-IR flux would be severly underestimated (Fig. 6). In the further discussion, we
will use the disk and envelope masses as found by the detailed modelling, but note that the overall conclusions do not change if the empirical results are used.
The envelope masses of IRS 63 and Elias 29 are in the same range as those presented by, e.g.,
Hogerheijde et al. (1997) for a sample of embedded Class I sources in the Taurus-Auriga star-forming region. However, the envelope masses
of the deeply embedded Class 0 objects are found to be considerably higher, 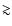 1
1  (Young et al. 2003; Hatchell et al. 2007; Jørgensen et al. 2002; Shirley et al. 2002).
While some fraction of sources may simply originate from lower mass cores, it is clear that all Class 0 objects must pass through a stage with
(Young et al. 2003; Hatchell et al. 2007; Jørgensen et al. 2002; Shirley et al. 2002).
While some fraction of sources may simply originate from lower mass cores, it is clear that all Class 0 objects must pass through a stage with
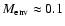
 on their way to the pre-main sequence stage. A larger sample is needed to address the question
whether the mass that was initially present in the envelope will first accumulate in the disk, or whether it will pass through the disk and onto the
star directly, leaving the disk in a steady state through the entire Class I stage.
on their way to the pre-main sequence stage. A larger sample is needed to address the question
whether the mass that was initially present in the envelope will first accumulate in the disk, or whether it will pass through the disk and onto the
star directly, leaving the disk in a steady state through the entire Class I stage.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7543fig6.eps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg90.gif) |
Figure 6:
Spectral energy distribution of IRS 63 using the model parameters of Table 2 extincted by
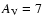 mag (solid line). The dashed line shows the model star, which has a luminosity of 0.79 mag (solid line). The dashed line shows the model star, which has a luminosity of 0.79 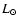 ,
and is represented by a black-body with a temperature of 3000 K.
Overplotted are JHKL photometry (Haisch et al. 2002), MIPS 24 and 70 ,
and is represented by a black-body with a temperature of 3000 K.
Overplotted are JHKL photometry (Haisch et al. 2002), MIPS 24 and 70 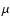 m fluxes
(c2d m fluxes
(c2d![[*]](/icons/foot_motif.gif) ), JCMT 850 ), JCMT 850 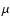 m 60 m 60
 integrated flux (COMPLETE), SMA 1.10 mm peak flux (this work; square), and IRAM 1.25 mm 60
integrated flux (COMPLETE), SMA 1.10 mm peak flux (this work; square), and IRAM 1.25 mm 60
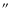 integrated flux (André & Montmerle 1994).
integrated flux (André & Montmerle 1994). |
| Open with DEXTER |
An interesting quantity for these YSOs is the ratio
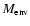 /
/
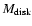 ,
as this may be a direct measure for their evolutionary stage.
The values for the two objects under consideration here - 0.2 for IRS 63 and 6 for Elias 29 -
are quite different, although the value for Elias 29 is rather uncertain
due to the contribution of the ridge enhancement to the continuum emission.
From these simple arguments, Elias 29 is the less evolved, rather like the deeply embedded Class 0 sources in the PROSAC sample (Jørgensen et al. 2007), which show
,
as this may be a direct measure for their evolutionary stage.
The values for the two objects under consideration here - 0.2 for IRS 63 and 6 for Elias 29 -
are quite different, although the value for Elias 29 is rather uncertain
due to the contribution of the ridge enhancement to the continuum emission.
From these simple arguments, Elias 29 is the less evolved, rather like the deeply embedded Class 0 sources in the PROSAC sample (Jørgensen et al. 2007), which show
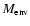 /
/
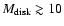 .
IRS 63, on the other hand, is well on its way toward the optically visible Class II or T Tauri stage,
which have
.
IRS 63, on the other hand, is well on its way toward the optically visible Class II or T Tauri stage,
which have
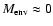 .
This confirms the notion that the Lada classification is primarily a phenomenological one, not necessarily representing the actual physical stage the YSO is in
(see, e.g., Crapsi et al. 2008).
.
This confirms the notion that the Lada classification is primarily a phenomenological one, not necessarily representing the actual physical stage the YSO is in
(see, e.g., Crapsi et al. 2008).
4.2 Keplerian rotation and stellar masses
Both IRS 63 and Elias 29 show a velocity gradient in the HCO+ emission, which is interpreted as the rotation of a circumstellar disk.
The mass of the central object can be estimated from position-velocity diagrams along
the major axis of the disk, as indicated in Fig. 1.
An elliptical Gaussian was fitted to each channel in the HCO+ data in the (u, v) plane, using the MIRIAD task uvfit. This yielded a best-fit
position per channel with corresponding uncertainties in right ascension and declination, and consequently a
declination offset from the phase centre in the physical plane. Note that the fitting was carried out in the (u, v) plane, so as not to be hindered by
artefacts that may arise in the deconvolution process. Position-velocity diagrams were created by plotting the declination offset as a function of velocity
channel, where only coordinates with an uncertainty in the declination of less than
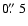 were taken into account. Subsequently, the signatures of Keplerian
rotation around a point source were fitted to the position-velocity diagrams
(Fig. 7). In the fitting process, the values for
were taken into account. Subsequently, the signatures of Keplerian
rotation around a point source were fitted to the position-velocity diagrams
(Fig. 7). In the fitting process, the values for
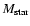 (the mass of the central object), the central velocity of the
system with respect to the local rest frame, and the declination offset from the source to the phase centre were varied, and a global minimum
(the mass of the central object), the central velocity of the
system with respect to the local rest frame, and the declination offset from the source to the phase centre were varied, and a global minimum 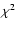 was determined.
was determined.
Assuming a Keplerian disk seen edge-on (
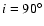 ), a central mass of
), a central mass of
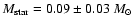 is found for IRS 63.
The exact inclination of IRS 63 is hard to determine due to the high extinction in the region. However, an inclination larger than
is found for IRS 63.
The exact inclination of IRS 63 is hard to determine due to the high extinction in the region. However, an inclination larger than
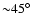 can be ruled out
because of the source's brightness at 3-5
can be ruled out
because of the source's brightness at 3-5 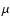 m (Pontoppidan et al. 2003).
Assuming an inclination of 30
m (Pontoppidan et al. 2003).
Assuming an inclination of 30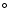 ,
and taking
into account the
,
and taking
into account the 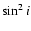 dependence, the mass of the
central object increases to
dependence, the mass of the
central object increases to
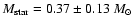 .
For Elias 29, the points attributed to the emission from the dense ridge (Fig. 7) were disregarded in the fitting
procedure.
A lower limit to the central mass of
.
For Elias 29, the points attributed to the emission from the dense ridge (Fig. 7) were disregarded in the fitting
procedure.
A lower limit to the central mass of
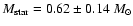 is found, under the assumption
is found, under the assumption
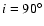 .
The flatness of the SED limits the inclination of this source to
.
The flatness of the SED limits the inclination of this source to
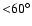 (Boogert et al. 2002). A fully face-on orientation,
on the other hand, is unlikely, given the presence of low surface brightness scattered K-band light (Zinnecker et al. 1988). An inclination
(Boogert et al. 2002). A fully face-on orientation,
on the other hand, is unlikely, given the presence of low surface brightness scattered K-band light (Zinnecker et al. 1988). An inclination
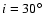 yields a mass for the central source of
yields a mass for the central source of
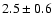
 .
With such a high mass, the central star is likely to emerge as a Herbig Ae/Be star, once the surrounding envelope is dissipated.
.
With such a high mass, the central star is likely to emerge as a Herbig Ae/Be star, once the surrounding envelope is dissipated.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7543fig7.eps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg102.gif) |
Figure 7:
Velocity of the HCO+ J = 3-2 line as a function of the declination offset from the phase centre for IRS 63 ( upper panel) and Elias 29 ( lower panel). The solid lines show the results from 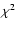 fits to the data, yielding central masses of 0.37
fits to the data, yielding central masses of 0.37  (IRS 63) and 2.5
(IRS 63) and 2.5  (Elias 29) for inclinations of 30
(Elias 29) for inclinations of 30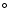 ;
the dashed lines show formal 99% confidence intervals. Points attributed to the emission from the dense ridge are indicated and are not included in the fit. The declination offsets are different for the two panels. ;
the dashed lines show formal 99% confidence intervals. Points attributed to the emission from the dense ridge are indicated and are not included in the fit. The declination offsets are different for the two panels. |
| Open with DEXTER |
It is interesting to compare the inferred masses to those inferred for optically visible pre-main sequence stars. With a stellar mass of 0.37  and a
stellar luminosity of 0.79
and a
stellar luminosity of 0.79 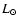 ,
IRS 63 would be found to have an age of about
,
IRS 63 would be found to have an age of about
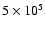 yr, when compared to evolutionary tracks of classical and weak-lined T Tauri stars in the
yr, when compared to evolutionary tracks of classical and weak-lined T Tauri stars in the
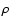 Ophiuchi cloud (D'Antona & Mazzitelli 1997; Wilking et al. 2005). A similar age would be found for Elias 29 (e.g., Palla & Stahler 1993).
Ophiuchi cloud (D'Antona & Mazzitelli 1997; Wilking et al. 2005). A similar age would be found for Elias 29 (e.g., Palla & Stahler 1993).
5 Conclusions
We used the SMA to observe the Class I YSOs Elias 29 and IRS 63 at 1.1 mm. The main results are as follows.
- Both sources are detected in the continuum and in the HCO+ J = 3-2 line, but not in the HCN J = 3-2 line. The HCO+ emission toward IRS 63 is compact and associated with the YSO, whereas a significant part of the molecular emission in the direction of Elias 29 is due to an enhancement in the ridge from which Elias 29 formed.
- Assuming that the continuum emission toward the sources is optically thin, and that any circumstellar envelope is resolved out by the interferometer on the longest baselines, we find empirical disk masses of 0.055 for IRS 63 and
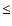 0.007
0.007  for Elias 29.
By comparing our interferometer data with single-dish observations, envelope masses of 0.058
for Elias 29.
By comparing our interferometer data with single-dish observations, envelope masses of 0.058  are derived for both sources, within 30
are derived for both sources, within 30
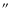 radius for IRS 63 and 20
radius for IRS 63 and 20
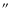 radius for Elias 29, where the value for Elias 29 should be treated as
an upper limit because of the presence of the ridge enhancement.
radius for Elias 29, where the value for Elias 29 should be treated as
an upper limit because of the presence of the ridge enhancement.
- Using a radiative-transfer code to create SEDs and amplitude vs. (u, v)-distance plots for different combinations of disk and
envelope masses, we find disk masses of 0.13
 for IRS 63 and 0.004
for IRS 63 and 0.004  for Elias 29, and envelope masses
of 0.022
for Elias 29, and envelope masses
of 0.022  and 0.025
and 0.025  .
.
- The modelling results yield rather different ratios of
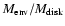 :
0.2 for IRS 63 and 6 for Elias 29,
with uncertainties of a factor of a few.
From this it is concluded that IRS 63 is well on its way to become an optically visible Class II source, rather than an embedded Class I source. Elias 29, on
the other hand, is more like the deeply embedded Class 0 sources.
:
0.2 for IRS 63 and 6 for Elias 29,
with uncertainties of a factor of a few.
From this it is concluded that IRS 63 is well on its way to become an optically visible Class II source, rather than an embedded Class I source. Elias 29, on
the other hand, is more like the deeply embedded Class 0 sources.
- Velocity gradients in the HCO+ J = 3-2 emission are interpreted as signs of Keplerian rotation, and indicate central masses
of
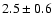
 for Elias 29 and
for Elias 29 and
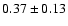
 for IRS 63, for inclinations of 30
for IRS 63, for inclinations of 30 .
These masses correspond to ages of
a few 105 yr.
.
These masses correspond to ages of
a few 105 yr.
With a larger set of sources treated in a similar manner as is presented for IRS 63 and Elias 29 here, it will be possible to
constrain models for the evolution of the envelope, disk, and stellar masses through this important stage of YSOs.
Acknowledgements
We would like to thank the anonymous referee for a very constructive report, which greatly improved the paper.
Demerese Salter and Doug Johnstone are thanked for providing us with data from JCMT SCUBA observations. The discussions with the members of the
Leiden ``AstroChem'' group were very useful.
We are grateful to Kees Dullemond for
providing us with the most recent version of the RADMC package. Partial support for this work was provided by a Netherlands Research School For
Astronomy network 2 grant, and by a Netherlands Organisation for Scientific Research Spinoza grant.
- André, P.,
& Montmerle, T. 1994, ApJ, 420, 837 [NASA ADS] [CrossRef]
- André, P.,
Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef]
(In the text)
- Andrews,
S. M., & Williams, J. P. 2007, ApJ, 659, 705 [NASA ADS] [CrossRef]
- Beckwith,
S. V. W., Sargent, A. I., Chini, R. S., &
Guesten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef]
(In the text)
- Benson,
P. J., & Myers, P. C. 1989, ApJS, 71, 89 [NASA ADS] [CrossRef]
- Bjorkman,
J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef]
(In the text)
- Boogert,
A. C. A., Hogerheijde, M. R., Ceccarelli, C.,
et al. 2002, ApJ, 570, 708 [NASA ADS] [CrossRef]
(In the text)
- Chandler,
C. J., & Richer, J. S. 2000, ApJ, 530, 851 [NASA ADS] [CrossRef]
(In the text)
- Chiang,
E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef]
(In the text)
- Crapsi, A.,
van Dishoeck, E. F., Hogerheijde, M. R., Pontoppidan,
K. M., & Dullemond, C. P. 2008, A&A, in
press.
(In the text)
- D'Antona,
F., & Mazzitelli, I. 1997, Mem. Soc. Astron. Ital., 68,
807 [NASA ADS]
- de Geus,
E. J., de Zeeuw, P. T., & Lub, J. 1989, A&A, 216,
44 [NASA ADS]
(In the text)
-
Dullemond, C. P., & Dominik, C. 2004, A&A, 417,
159 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Evans,
N. J., Allen, L. E., Blake, G. A., et al. 2003,
PASP, 115, 965 [NASA ADS] [CrossRef]
(In the text)
- Evans, II,
N. J., Harvey, P. M., Dunham, M. M., et al.
2007, Delivery of Data from the c2d Legacy Project: IRAC and MIPS,
Pasadena, SSC
- Flaherty,
K. M., Pipher, J. L., Megeath, S. T., et al.
2007, ApJ, 663, 1069 [NASA ADS] [CrossRef]
(In the text)
- Greene,
T. P., Wilking, B. A., Andre, P., Young, E. T.,
& Lada, C. J. 1994, ApJ, 434, 614 [NASA ADS] [CrossRef]
(In the text)
- Haisch, Jr.,
K. E., Barsony, M., Greene, T. P., & Ressler,
M. E. 2002, AJ, 124, 2841 [NASA ADS] [CrossRef]
(In the text)
- Harvey,
D. W. A., Wilner, D. J., Myers, P. C., &
Tafalla, M. 2003, ApJ, 596, 383 [NASA ADS] [CrossRef]
- Hatchell,
J., Fuller, G. A., Richer, J. S., Harries, T. J.,
& Ladd, E. F. 2007, A&A, 468, 1009 [NASA ADS] [CrossRef] [EDP Sciences]
- Ho,
P. T. P., Moran, J. M., & Lo, K. Y. 2004,
ApJ, 616, L1 [NASA ADS] [CrossRef]
(In the text)
-
Hogerheijde, M. R., van Dishoeck, E. F., Blake,
G. A., & van Langevelde, H. J. 1997, ApJ, 489,
293 [NASA ADS] [CrossRef]
-
Hogerheijde, M. R., van Dishoeck, E. F., Blake,
G. A., & van Langevelde, H. J. 1998, ApJ, 502,
315 [NASA ADS] [CrossRef]
-
Johnstone, D., Di Francesco, J., & Kirk, H. 2004, ApJ, 611,
L45 [NASA ADS] [CrossRef]
(In the text)
-
Jørgensen, J. K., Schöier, F. L., & van
Dishoeck, E. F. 2002, A&A, 389, 908 [NASA ADS] [CrossRef] [EDP Sciences]
-
Jørgensen, J. K., Hogerheijde, M. R., van Dishoeck,
E. F., Blake, G. A., & Schöier, F. L. 2004,
A&A, 413, 993 [NASA ADS] [CrossRef] [EDP Sciences]
-
Jørgensen, J. K., Bourke, T. L., Myers, P. C.,
et al. 2005, ApJ, 632, 973 [NASA ADS] [CrossRef]
-
Jørgensen, J. K., Bourke, T. L., Myers, P. C.,
et al. 2007, ApJ, 659, 479 [NASA ADS] [CrossRef]
- Lada, C. J.
1987, in Star Forming Regions, ed. M. Peimbert, &
J. Jugaku, IAU Symp., 115, 1
- Lada, C. J.,
& Wilking, B. A. 1984, ApJ, 287, 610 [NASA ADS] [CrossRef]
- Looney,
L. W., Mundy, L. G., & Welch, W. J. 2000, ApJ,
529, 477 [NASA ADS] [CrossRef]
- Ohashi, N.,
Hayashi, M., Ho, P. T. P., & Momose, M. 1997, ApJ,
475, 211 [NASA ADS] [CrossRef]
-
Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS]
(In the text)
- Palla, F.,
& Stahler, S. W. 1993, ApJ, 418, 414 [NASA ADS] [CrossRef]
(In the text)
-
Pontoppidan, K. M., Fraser, H. J., Dartois, E.,
et al. 2003, A&A, 408, 981 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Qi, C. 2005, The MIR
Cookbook, The Submillimeter Array / Harvard-Smithsonian Center for
Astrophysics http://cfa-www.harvard.edu/~cqi/mircook.html
(In the text)
- Ridge,
N. A., Di Francesco, J., Kirk, H., et al. 2006, AJ, 131,
2921 [NASA ADS] [CrossRef]
(In the text)
- Sault,
R. J., Teuben, P. J., & Wright, M. C. H.
1995, in Astronomical Data Analysis Software and Systems IV, ASP
Conf. Ser., 77, 433
(In the text)
- Shirley,
Y. L., Evans, II, N. J., & Rawlings,
J. M. C. 2002, ApJ, 575, 337 [NASA ADS] [CrossRef]
- Ulrich,
R. K. 1976, ApJ, 210, 377 [NASA ADS] [CrossRef]
- Whitney,
B. A., Wood, K., Bjorkman, J. E., & Wolff, M. J.
2003, ApJ, 591, 1049 [NASA ADS] [CrossRef]
- Wilking,
B. A., Meyer, M. R., Robinson, J. G., & Greene,
T. P. 2005, AJ, 130, 1733 [NASA ADS] [CrossRef]
- Young,
C. H., Shirley, Y. L., Evans, II, N. J., &
Rawlings, J. M. C. 2003, ApJS, 145, 111 [NASA ADS] [CrossRef]
-
Zinnecker, H., Perrier, C., & Chelli, A. 1988, in Proc.
NOAO-ESO Conference on High-Resolution Imaging by Interferometry:
Ground-Based Interferometry at Visible and Infrared Wavelengths,
ed. F. Merkle
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7543fig1.eps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg38.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7543fig3.eps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg47.gif)
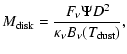
![$\displaystyle \rho_{\rm disk}(r, \theta) = \frac{\Sigma_0(r/R_0)^{-1}}{\sqrt(2\...
...(r)}\exp \left( - \frac{1}{2}\left[\frac{r \cos(\theta)}{H(r)}\right]^2\right),$](/articles/aa/full/2008/13/aa7543-07/img68.gif)
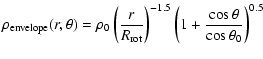
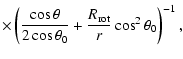
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7543fig6.eps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{7543fig7.eps}\end{figure}](/articles/aa/full/2008/13/aa7543-07/Timg102.gif)