A&A 480, 589-597 (2008)
DOI: 10.1051/0004-6361:20079214
J. E. Baldwin1 - P. J. Warner1 - C. D. Mackay2
1 - Cavendish Laboratory, Madingley Rd, Cambridge CB3 0HE, UK
2 -
Institute of Astronomy, Madingley Rd, Cambridge CB3 0HE, UK
Received 7 December 2007 / Accepted 22 December 2007
Abstract
Aims. We investigate the properties of astronomical images made by combining the best images selected from a sequence of short-exposure frames (Lucky Imaging); we assess the match between modelling and observation and discover what variations in seeing occur on very short timescales.
Methods. Numerical simulations of a random phase-changing screen passing across a telescope aperture with ideal optics are used to determine the expected point spread function and isoplanatic properties for a range of seeing conditions for comparison with observations.
Results. All the model images comprise a diffraction-limited core with Strehl ratios from 0.05-0.5 and an underlying broad disk. The isoplanatic patch sizes are large and coherence times long. The observations are a close match to the models in most respects. Large variations in seeing occur on temporal scales as short as 0.2 s and spatial scales as small as 1 m.
Key words: atmospheric effects - techniques: high angular resolution
We have used the term Lucky Imaging in several earlier papers (Baldwin et al. 2001; Tubbs et al. 2002; Mackay et al. 2003; Law et al. 2006) to describe the technique of improving angular resolution in astronomical images by combining images with the best Strehl ratios selected from a sequence of short-exposure frames using recentring on the brightest speckle. This follows the original usage by Fried (1978) applied to the selection of the single best image from a sequence. Law et al. (2006) presented observations made with the 2.5 m Nordic Optical Telescope (NOT) at wavelengths close to 800 nm giving a quantitative assessment of the improved resolution obtained in practice. The main conclusions were:
Numerical simulations of stellar images observed through a random phase screen were adopted for this discussion. They provide images which can be analysed in exactly the same way as the observational data and they allow estimation of observational parameters which are difficult to extract using the analytic methods employed in many investigations of seeing.
The simulations were made to match the circumstances of the observations made
with the 2.5 m Nordic Optical Telescope, mostly with a 20% bandwidth at
wavelengths near 800 nm, under seeing conditions ranging from 0.4-1.2 arcsec. Their application is much wider since the properties of the
images are determined by the ratio, D/r0, of the telescope aperture D to
the Fried seeing parameter r0. For instance, they would apply equally to a
4 m aperture at 1.3 ![]() m and an 8 m aperture at 2.2
m and an 8 m aperture at 2.2 ![]() m under similar
seeing conditions. It is likely that a similarly wide bandwidth will be
necessary at most wavelengths to allow the use of faint reference stars. We
therefore present the results as a function of D/r0 in Sect. 3 and convert
them to the NOT parameters for comparison with the observations in Sect. 4.
The range of values of D/r0 in these simulations and observations is
approximately 6-18. This range was already identified by earlier authors
(Hecquet & Coupinot 1984) as being one in which significant
improvements in angular resolution could be achieved by selection and
recentring of images.
m under similar
seeing conditions. It is likely that a similarly wide bandwidth will be
necessary at most wavelengths to allow the use of faint reference stars. We
therefore present the results as a function of D/r0 in Sect. 3 and convert
them to the NOT parameters for comparison with the observations in Sect. 4.
The range of values of D/r0 in these simulations and observations is
approximately 6-18. This range was already identified by earlier authors
(Hecquet & Coupinot 1984) as being one in which significant
improvements in angular resolution could be achieved by selection and
recentring of images.
A 2-dimensional random phase screen was generated within a
![]() pixel array, based on the code developed by Buscher (1988). For each
screen the amplitude a(k) for each cosine and sine component of spatial
frequency k were chosen as independent Gaussian random variables with zero
mean and variance
pixel array, based on the code developed by Buscher (1988). For each
screen the amplitude a(k) for each cosine and sine component of spatial
frequency k were chosen as independent Gaussian random variables with zero
mean and variance
![]() .
The diameter,
D, of the telescope aperture was chosen to be 56 pixels. Then, in the
comparison with the NOT observations, the largest scale of turbulence in the
simulation is
.
The diameter,
D, of the telescope aperture was chosen to be 56 pixels. Then, in the
comparison with the NOT observations, the largest scale of turbulence in the
simulation is ![]() 100 m and the smallest
100 m and the smallest ![]() 0.09 m. The consequent
truncations of the Kolmogorov spectrum have no significant effect on the
results. The largest scales provide only tip-tilt variation of phase across the
2.5 m aperture and are therefore removed in the shift-and-add process. 100 m
is, in any case, as large as the outer scale of turbulence believed to exist
for most sites. The power missing at the shortest scales is too small to
affect the results except for seeing poorer than we have used in these
simulations. We have not explored the effects of alternative slopes in the
power spectrum of turbulence but draw attention in Sects. 3.1 and 4 to
observational aspects of short-exposure images which reveal it.
0.09 m. The consequent
truncations of the Kolmogorov spectrum have no significant effect on the
results. The largest scales provide only tip-tilt variation of phase across the
2.5 m aperture and are therefore removed in the shift-and-add process. 100 m
is, in any case, as large as the outer scale of turbulence believed to exist
for most sites. The power missing at the shortest scales is too small to
affect the results except for seeing poorer than we have used in these
simulations. We have not explored the effects of alternative slopes in the
power spectrum of turbulence but draw attention in Sects. 3.1 and 4 to
observational aspects of short-exposure images which reveal it.
Images of stars were generated by taking a
![]() sub-array centred
on the telescope aperture with unit amplitude and the corresponding phases
within the aperture and zero amplitude outside. The square of the Fourier
transform of this 2-dimensional array gives one instantaneous image. Several
checks were made on the overall normalisation of the process, first by
averaging the images from a large number of phase screens, confirming that the
expected seeing disk was generated. Other checks were provided by the
tilt-corrected mean phase variance over the telescope aperture discussed in
Sect. 3.1. It was to allow these comparisons that the effect of
secondary
mirror blockage was not included in the simulations; for most telescopes the
effects are small. Two additions to the model were made to meet the
circumstances of the observations and their analysis as closely as possible.
Images simulating a
sub-array centred
on the telescope aperture with unit amplitude and the corresponding phases
within the aperture and zero amplitude outside. The square of the Fourier
transform of this 2-dimensional array gives one instantaneous image. Several
checks were made on the overall normalisation of the process, first by
averaging the images from a large number of phase screens, confirming that the
expected seeing disk was generated. Other checks were provided by the
tilt-corrected mean phase variance over the telescope aperture discussed in
Sect. 3.1. It was to allow these comparisons that the effect of
secondary
mirror blockage was not included in the simulations; for most telescopes the
effects are small. Two additions to the model were made to meet the
circumstances of the observations and their analysis as closely as possible.
Images simulating a ![]() optical bandwidth were constructed by calculating
the image for 11 uniformly spaced wavelengths,
optical bandwidth were constructed by calculating
the image for 11 uniformly spaced wavelengths, ![]() ,
across the band, the
phases in the screen being scaled as
,
across the band, the
phases in the screen being scaled as
![]() .
Since the angular scale of
the images on the sky is proportional to
.
Since the angular scale of
the images on the sky is proportional to ![]() ,
averaging of the images
also required linear interpolation of each image to a standard angular scale.
The second feature was to move the aperture across the screen from the lower
left to the upper right corner to create a sequence of 664 successive
instantaneous images corresponding to a ``frozen'' turbulent screen carried by
the wind crossing the telescope aperture. Comparisons could then be made with
temporal and isoplanatic aspects of the observations. The spatial interval
between successive images corresponded to shifts of 0.07575D, or 0.187 m for
the NOT comparison, which is adequate sampling for all aspects of the analysis.
,
averaging of the images
also required linear interpolation of each image to a standard angular scale.
The second feature was to move the aperture across the screen from the lower
left to the upper right corner to create a sequence of 664 successive
instantaneous images corresponding to a ``frozen'' turbulent screen carried by
the wind crossing the telescope aperture. Comparisons could then be made with
temporal and isoplanatic aspects of the observations. The spatial interval
between successive images corresponded to shifts of 0.07575D, or 0.187 m for
the NOT comparison, which is adequate sampling for all aspects of the analysis.
![\begin{figure}
\par\includegraphics[width = 6cm,clip]{9214f1a.eps}\par\includegraphics[width = 6cm,clip]{9214f1b.eps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg15.gif) |
Figure 1: a) One instantaneous image; D/r0 = 8.3, Strehl ratio 0.16. b) Average of best 10% of images; D/r0 = 8.3, Strehl ratio 0.19. |
| Open with DEXTER | |
This procedure was repeated for a number, typically 8, of different phase screens for each value of D/r0. The residual statistical fluctuations in the results presented here due to the finite number of frames are small but may account for some of the differences between the curves in Figs. 6 and 7.
Figure 1a shows a typical short-exposure image for
D/r0 = 8.3. It
has a Strehl ratio of 0.16. 10![]() of the images in this sequence have higher
Strehl ratios. The image formed by shift-and-add on these 10
of the images in this sequence have higher
Strehl ratios. The image formed by shift-and-add on these 10![]() is shown in
Fig. 1b. Much of the speckle is averaged out in this image which
corresponds to the analysis of about 10 s of data for the NOT parameters.
is shown in
Fig. 1b. Much of the speckle is averaged out in this image which
corresponds to the analysis of about 10 s of data for the NOT parameters.
Each image in a sequence of 664 was analysed initially to give a list of parameters including the shifts in position of the peak pixel and the centroid relative to their undeviated values, the Strehl ratio and the full widths enclosing 30, 50 and 70% of the flux. Images selected by their Strehl ratios could then be combined using shift-and-add to give resulting images with a range of percentages of selection. The radial distribution of flux in each combined image was obtained by integration in narrow annuli centred on the peak pixel of the image. The mean radial profiles for a range of percentage selection for D/r0 = 8.3 and for a range of D/r0 for 10% selection are shown in Fig. 2, all the curves being plotted on the same intensity scale to allow direct comparison of the Strehl ratios of the images. In each case the main features are a central peak corresponding to the ideal diffraction-limited response of the aperture D superimposed on a much broader feature whose dimensions are roughly similar to those of the normal seeing disk. In these respects the images resemble those seen in analysis of observations with the NOT (see Fig. 4 of Law et al. (2006) and Sect. 3.3 of this paper). As noted in the earlier paper, they are also similar to those seen in partially corrected images using adaptive optics. Figure 3 summarises the results obtained for the Strehl ratios of images for a wide range of D/r0 and percentage selection.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f2a.ps}\par\vspace*{2mm}
\includegraphics[angle=-90,width=8cm,clip]{9214f2b.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg16.gif) |
Figure 2: Mean radial profiles of images a) D/r0 = 8.3; 1, 10, 100% selection. b) D/r0 = 5, 6.5, 8.3, 12.5, 16.7; 10% selection. The intensity scale has been normalised so that the peak value for each profile is the Strehl ratio of that image. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f3.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg17.gif) |
Figure 3:
Strehl ratios for a range of D/r0 and |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f4a.ps}\par\vspace*{2mm}
\includegraphics[angle=-90,width=8cm,clip]{9214f4b.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg18.gif) |
Figure 4: a) Full line: histogram of tilt-corrected phase variances for 10 000 independent phase screens. Dashed line: theoretical distribution for Zernike modes Z4 - Z10 + 0.04 (to represent all higher modes). b) Phase variances and Strehl ratios for a sequence of frames with D/r0 = 8.3. |
| Open with DEXTER | |
We now examine some of the properties of the phase fluctuations which are
responsible for the variations of the Strehl ratios. The distribution of the
tilt-corrected phase variance,
![]() ,
across the aperture
for 10 000 independent phase screens in these simulations is shown in
Fig. 4a. Its mean value is
0.133(D/r0)5/3. This is in good
agreement with the coefficient of 0.134 given by Noll (1976). The value
here is expected to be marginally smaller because of the truncation of the
model turbulent spectrum at small and large scales but in any case the
agreement is within the expected statistical error. The highest Strehl ratios
on the plot in Fig. 3 are a good fit to the approximate formula
,
across the aperture
for 10 000 independent phase screens in these simulations is shown in
Fig. 4a. Its mean value is
0.133(D/r0)5/3. This is in good
agreement with the coefficient of 0.134 given by Noll (1976). The value
here is expected to be marginally smaller because of the truncation of the
model turbulent spectrum at small and large scales but in any case the
agreement is within the expected statistical error. The highest Strehl ratios
on the plot in Fig. 3 are a good fit to the approximate formula
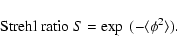 |
(1) |
It is of interest to examine the contributions to the wide spread of values
displayed in Fig. 4a. The mean for the whole histogram is
0.133(D/r0)5/3. The corresponding coefficient for the first three Zernike
modes after tip-tilt correction, (Z4 - Z6), is 0.069, and 0.094 if the
first seven modes, (
Z4 - Z10), are included (Noll 1976). All the
higher modes contribute a mean of only 0.04 to the total. The amplitudes of the
Zernike modes are Gaussian random variables and for any such variable x with
variance ![]() ,
the probability distribution of x2 has a mean value of
,
the probability distribution of x2 has a mean value of
![]() and a variance
and a variance ![]() .
Hence the high order modes make an
extremely small contribution (1.5%) to the spread of phase variance, whilst
90% is provided by the modes (Z4 - Z6). The dotted histogram shows the
effect of calculating the full probability distribution for the Zernike terms
(Z4 - Z10) and taking a delta function at 0.04 to represent the
probability distribution of all the higher terms.
.
Hence the high order modes make an
extremely small contribution (1.5%) to the spread of phase variance, whilst
90% is provided by the modes (Z4 - Z6). The dotted histogram shows the
effect of calculating the full probability distribution for the Zernike terms
(Z4 - Z10) and taking a delta function at 0.04 to represent the
probability distribution of all the higher terms.
Important consequences of this are that the mean value of 0.04 (D/r0)5/3of the phase variance for the higher order terms is the lower limit to the phase variance histogram and hence sets an upper limit to the Strehl ratio of the images. Variations in the distribution of power between the higher modes will alter the speckle pattern in the outer parts of images but exert almost no influence on variations in the Strehl ratios and hence no influence on the selection of Lucky images. The few lowest order Zernike modes determine a large correlation length for the Strehl ratios as the screen is moved past the telescope aperture, resulting in large isoplanatic patch sizes (Sect. 3.2) and correspondingly long correlation times (Sect. 3.3).
An example of the Strehl ratios of a set of instantaneous images and their associated tilt-corrected phase variances for D/r0 = 8.3 is shown in Fig. 4b. As expected, the highest Strehl ratios correspond to the smallest residual phase variances across the aperture and there is a general decrease in Strehl ratio with increasing phase variance; but some of the higher Strehl ratios are associated with images in which the phase variance is large. These are examples of a behaviour which, in the extreme case of a square wave phase variation of one wavelength peak-to-peak amplitude, would give a Strehl ratio of unity. It illustrates that the images obtained by selection for Strehl ratio in Lucky Imaging are not identical to those obtained by selection for residual phase variance; nor will they be identical to those given by partially-corrected adaptive optics in which the aim has been to minimise the residual phase variance.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f5a.ps}\par\vspace*{2mm}
\includegraphics[angle=-90,width=8cm,clip]{9214f5b.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg23.gif) |
Figure 5:
Mean radial profiles of images a)
|
| Open with DEXTER | |
The outer parts of the radial profiles can be seen best in the logarithmic
plots, Figs. 5a and b, with the same percentage
selection and D/r0 parameters as in Fig. 2. A profile for a
conventional long-exposure image is included for comparison. A feature of all
the profiles is the constant slope of the curves close to -11/3 in the
outermost parts. It can be understood in terms of a simplified one-dimensional
model. For a sinusoidal spatial variation of phase, ![]() ,
in the screen
,
in the screen
| (2) |
| |
= | (3) | |
| = | (4) |
| (5) |
For small spatial frequencies, ![]() may be >1 radian, say n radians.
The scattered beams lie as before at
may be >1 radian, say n radians.
The scattered beams lie as before at
![]() ,
and also
its harmonics out to
,
and also
its harmonics out to
![]() but falling very rapidly
in amplitude at larger angles. The small spatial frequencies thus make no
direct contribution to the distribution of intensity at large angles. There are
in addition some cross-product terms between the large and small spatial
frequencies, kl and ks, giving contributions at angles
but falling very rapidly
in amplitude at larger angles. The small spatial frequencies thus make no
direct contribution to the distribution of intensity at large angles. There are
in addition some cross-product terms between the large and small spatial
frequencies, kl and ks, giving contributions at angles
| (6) |
The discussion up to this point has emphasized the properties of the reference
star images. The key issue for the use of Lucky imaging as a generally
applicable technique is whether target objects lie within the region of
isoplanatism of the reference star. For a single frozen screen moved relative
to the telescope aperture, the sequence of images can be interpreted either as
a time sequence for any chosen wind speed (Sect. 3.3) or to analyse the
isoplanatic behaviour of the model. As discussed above, the image of the star
chosen as the reference object is analysed by choosing the percentage of frames
to be included, checking whether a particular frame should be included and, if
so, adding its contribution to the combined image with its measured positional
shifts. A star displaced from the centre of the field by an angle ![]() will be seen by the telescope through a patch of the screen displaced by a
distance
will be seen by the telescope through a patch of the screen displaced by a
distance ![]() ,
where h is the assumed height of the screen. Thus, to
construct the expected image at an angle
,
where h is the assumed height of the screen. Thus, to
construct the expected image at an angle ![]() from the reference star,
images are taken from the sequence displaced by
from the reference star,
images are taken from the sequence displaced by ![]() from each of the
selected reference star images and combined as before but using the same
positional shifts as are used for the reference star. The net effect of these
changes is that the images of stars at a distance from the reference have lower
Strehl ratios, falling progressively with distance. Figures 6a and b show these reductions for several values of D/r0 and for
three differing percentages of selection. The Strehl ratios fall by a factor of
two relative to the value at the centre of the field for a displacement of the
screen
from each of the
selected reference star images and combined as before but using the same
positional shifts as are used for the reference star. The net effect of these
changes is that the images of stars at a distance from the reference have lower
Strehl ratios, falling progressively with distance. Figures 6a and b show these reductions for several values of D/r0 and for
three differing percentages of selection. The Strehl ratios fall by a factor of
two relative to the value at the centre of the field for a displacement of the
screen
![]() and a corresponding angular radius
and a corresponding angular radius
![]() .
The effect is only weakly dependent on the percentage
selection of images or on the ratio D/r0 over the range of values considered
here, some of the differences between the curves being due to statistical
fluctuations from the finite simulations. The independence of seeing is
expected following the discussion in Sect. 3.1 where it was shown that the
spatial scale of variations in Strehl ratios arises from the relative weights
of the lowest Zernike modes and hence depends only on the aperture size D and
not on the seeing. It will therefore also be independent of wavelength.
.
The effect is only weakly dependent on the percentage
selection of images or on the ratio D/r0 over the range of values considered
here, some of the differences between the curves being due to statistical
fluctuations from the finite simulations. The independence of seeing is
expected following the discussion in Sect. 3.1 where it was shown that the
spatial scale of variations in Strehl ratios arises from the relative weights
of the lowest Zernike modes and hence depends only on the aperture size D and
not on the seeing. It will therefore also be independent of wavelength.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f6a.ps}\par\vspace*{2mm}
\includegraphics[angle=-90,width=8cm,clip]{9214f6b.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg40.gif) |
Figure 6:
Isoplanatic effect of decrease in Strehl ratio as a function of shift
in the screen a)
|
| Open with DEXTER | |
This is of practical importance, since small changes in the seeing during an observing run will not affect the factors, as a function of radius, needed to correct the image intensities to a uniform scale over the whole field. If the field of view is very large, so that several reference stars are available, the same analysis will apply for each of these stars giving the same isoplanatic response with radius from that star even though different frames from the sequence are being selected for each reference object.
The atmospheric fluctuations are not in general confined to a layer at a single
height. The shape of the curves in Fig. 6 will be affected by the
range of values of h present but no overall qualitative change in
isoplanaticity is expected, since the same argument regarding the correlation
scale applies for all the layers. This conclusion may appear to conflict with
the results of Roddier et al. (1982) in their analysis of the
isoplanatic patch size in speckle interferometry. They obtain an isoplanatic
angular size ![]() D/h for a single thin turbulent layer but
D/h for a single thin turbulent layer but ![]()
![]() for a thick layer of thickness
for a thick layer of thickness ![]() .
The difference arises from their
assumption of a large value of D/r0 in their application. The Lucky Imaging
case, where D/r0 is small, differs by the image being dominated by a single
bright speckle in all the cases considered where selection by Strehl ratio is
employed (see Fig. 2).
.
The difference arises from their
assumption of a large value of D/r0 in their application. The Lucky Imaging
case, where D/r0 is small, differs by the image being dominated by a single
bright speckle in all the cases considered where selection by Strehl ratio is
employed (see Fig. 2).
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f7.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg43.gif) |
Figure 7: Autocorrelation function of Strehl ratios as a function of shift of the screen for D/r0= 5,8.3,12.5. |
| Open with DEXTER | |
An important factor in Lucky observations is the choice of exposure time for
each frame. For good sensitivity it must be as long as possible without
incurring blurring of the images. The simulations used for the isoplanatic
patch in Sect. 3.2 give a direct measure of this, since a shift in the screen
corresponds to a time interval for any given wind speed. So the effect of a
finite integration time on the Strehl ratio of the best images can be deduced
by smoothing the curve in Fig. 6 over the appropriate interval.
Averaging over a shift of the screen of
![]() gives an
acceptably small reduction in Strehl ratio of
gives an
acceptably small reduction in Strehl ratio of ![]() ,
the reduction increasing
roughly as the square of the integration time for longer integrations. For the
NOT observations this corresponds to an integration time of 75 ms for an
assumed wind speed of 10 m s-1. It corresponds well with those found to be
satisfactory in practice.
,
the reduction increasing
roughly as the square of the integration time for longer integrations. For the
NOT observations this corresponds to an integration time of 75 ms for an
assumed wind speed of 10 m s-1. It corresponds well with those found to be
satisfactory in practice.
A measure of the wind speed V can be obtained straightforwardly from the time
variation of the Strehl ratios. Figure 7 shows the autocorrelation
function of the Strehl ratios of a sequence of images for three values of
D/r0 as a function of the distance moved by the screen. The autocorrelation
function is independent of the seeing, for the same reasons as discussed for
isoplanatism. It falls to 0.5 for values of displacement of about
![]() and a corresponding time interval
and a corresponding time interval
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f8a.ps}\par\vspace*{2mm}
\includegraphics[angle=-90,width=8cm,clip]{9214f8b.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg48.gif) |
Figure 8: a) Radial profiles of a star in M15 and simulated image for the same seeing conditions. b) Logarithmic plot with line of slope -11/3 added for comparison purposes. |
| Open with DEXTER | |
The results of Sect. 3 can be scaled to the NOT observations using the
appropriate value for D/r0. For 0.6 arcsec seeing at 820 nm,
r0 = 0.30 m
giving
D/r0 = 8.3 for the 2.5 m NOT aperture. Data taken under these
conditions are compared with the theoretical profiles from the simulations in
Fig. 8. The simulations were made with a pixel scale of 7.2 mas,
whilst the actual observations were made with 40 mas pixels on a star separated
from the reference by 2 arcsec and with an exposure time of 85 ms. The pixel
size affects both the precision of centring the reference star and blurs the
profile of the target star. Photon noise in the reference star response must
also be considered but is not significant in this example. These factors have
been taken into account in generating the curve for
D/r0 = 8.3, which is the
best estimate of what would be expected in practice. The observed radial
profile differs in having a broader central peak and a correspondingly lower
Strehl ratio. However, the total flux in the central peak is the same to within
15![]() in the two cases. The reason for the broadening of the peak is unknown,
but the effect is typical of all the data taken in 2003 and 2004 on the NOT. A
possible reason is that it is due to residual errors in the mirror figure which
are too large to be corrected fully by atmospheric fluctuations. It would not
be suprising given that the specification for the primary mirror at the time of
construction was that 80 percent of the energy should lie within a circle of 0.4 arcsec diameter. We note however that some of the data in the original
Lucky observations in 2001 (Baldwin et al. 2001) did give a central
peak in the image which was very close to the diffraction limit. The outer part
of the radial profile (Fig. 8), corresponding to spatial scales
in the turbulence
in the two cases. The reason for the broadening of the peak is unknown,
but the effect is typical of all the data taken in 2003 and 2004 on the NOT. A
possible reason is that it is due to residual errors in the mirror figure which
are too large to be corrected fully by atmospheric fluctuations. It would not
be suprising given that the specification for the primary mirror at the time of
construction was that 80 percent of the energy should lie within a circle of 0.4 arcsec diameter. We note however that some of the data in the original
Lucky observations in 2001 (Baldwin et al. 2001) did give a central
peak in the image which was very close to the diffraction limit. The outer part
of the radial profile (Fig. 8), corresponding to spatial scales
in the turbulence ![]() (D/4), or 0.6 m for the NOT, matches those of the
simulations very closely and confirms that the actual slope of the turbulence
power spectrum was close to -11/3. A comparison of the rms motions of the image
centroid with those in the simulations showed that this slope was maintained at
least up to spatial scales as large as 2.5 m.
(D/4), or 0.6 m for the NOT, matches those of the
simulations very closely and confirms that the actual slope of the turbulence
power spectrum was close to -11/3. A comparison of the rms motions of the image
centroid with those in the simulations showed that this slope was maintained at
least up to spatial scales as large as 2.5 m.
As discussed in Sect. 3.2, comparison of the isoplanatic patch simulations with the observational data provides a direct estimate of the effective height of the turbulent layer. Values of 17-30 arcsec radius were found by Law et al. (2006) in the NOT observations. With D = 2.5 m these give heights for the layer ranging from 5-10 km. We have no independent evidence of the height of the turbulence during NOT observations but these values lie well within the range commonly measured, suggesting that this technique is a useful addition to existing methods of measuring atmospheric parameters.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f9.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg50.gif) |
Figure 9: Autocorrelation function of Strehl ratios: D/r0 = 8.3model with V = 11 m s-1 compared with M15 data. |
| Open with DEXTER | |
An example of the autocorrelation function of the Strehl ratios for one sequence of NOT data is shown in Fig. 9 together with the corresponding curve from simulations scaled to fit, giving a wind speed of 11 m s-1.
The overall conclusion of this comparison of the observations and simulations is that the observed Lucky Imaging behaviour is entirely consistent with assuming a constant value of the seeing parameters and the expected statistical variations within that constraint. It does not exclude the possibility that there are intervals when the mean seeing is poorer, since images from those periods would not be chosen in the selection process.The data provide useful evidence on the effective height and wind speed in the turbulent layer.
The separate question of whether short-period variations in seeing are present
in the data requires a measure of the seeing on a short timescale which is
unaffected by the natural fluctuations in a random screen for a constant value
of the seeing. We assume in this discussion that ``the seeing'' can be
represented by a single quantity, such as r0 or the FWHM of a long exposure
image. It is evident from the previous analysis that some quantities are poor
indicators of the mean seeing in a single short-exposure image. For instance, a
very wide range of Strehl ratios arise from a single value of the seeing,
making the Strehl ratio of a single frame unreliable as a measure of the
seeing. The standard measure of full width to half maximum is also of no value
for a single exposure since it will be simply that of the brightest speckle,
close to the diffraction-limited value. A more useful quantity can be
identified by looking at the integral profile of the images.
Figure 10 shows the integral of the flux within a given radius for
the images in Figs. 2a and 5a for
D/r0 = 8.3and 1, 10 and 100![]() selection. As the percentage of enclosed flux is
increased, the three curves show a progressively smaller scatter in fractional
radius indicating that the best values (
selection. As the percentage of enclosed flux is
increased, the three curves show a progressively smaller scatter in fractional
radius indicating that the best values (![]() selection) differ least from the
mean (
selection) differ least from the
mean (![]() selection). This is a direct consequence of the convergence of
the curves in Fig. 5a at large radii, which imply that the
fraction of the flux not enclosed will be almost independent of the percentage
selection. It suggests that the radius enclosing the largest possible fraction
of the flux will give the most consistent estimate of the seeing from a single
instantaneous image. In practice this has to be balanced against the difficulty
in measuring the very low brightness outer parts of the image against a noisy
and perhaps uneven background. For the NOT data taken with LuckyCam, which has
exceptionally low noise and good baseline stability, the full width enclosing
selection). This is a direct consequence of the convergence of
the curves in Fig. 5a at large radii, which imply that the
fraction of the flux not enclosed will be almost independent of the percentage
selection. It suggests that the radius enclosing the largest possible fraction
of the flux will give the most consistent estimate of the seeing from a single
instantaneous image. In practice this has to be balanced against the difficulty
in measuring the very low brightness outer parts of the image against a noisy
and perhaps uneven background. For the NOT data taken with LuckyCam, which has
exceptionally low noise and good baseline stability, the full width enclosing
![]() of the flux (fw70pcef) was found to be a good compromise.
of the flux (fw70pcef) was found to be a good compromise.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f10.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg53.gif) |
Figure 10:
Integral of flux in image within radius r.
D/r0 =8.3;
1, 10 and 100 |
| Open with DEXTER | |
Histograms of this quantity for single instantaneous frames in the simulations
show good discrimination of the seeing for each of the values of D/r0. Their
means and rms scatter are listed in Table 1, the ratio of the scatter in the
estimates to the mean being about 0.1. Note that the values of fw70pcef are
typically a factor of about
![]() larger than
larger than
![]() ,
the FWHM
of a conventional image. If the instrumental constraints do not allow such a
low brightness level in the image to be used, a lower value of the percentage
enclosed flux, say 50% or 30%, can be used but with some loss in
discrimination of the seeing value. For 30% enclosed flux, the ratio of
rms scatter to the mean increases to about 0.2.
,
the FWHM
of a conventional image. If the instrumental constraints do not allow such a
low brightness level in the image to be used, a lower value of the percentage
enclosed flux, say 50% or 30%, can be used but with some loss in
discrimination of the seeing value. For 30% enclosed flux, the ratio of
rms scatter to the mean increases to about 0.2.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9214f11a.ps}\par\vspace*{2mm}
\includegraphics[angle=-90,width=8cm,clip]{9214f11b.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg56.gif) |
Figure 11: fw70pcef for a sequence of images a) model data with D/r0 = 8.3, V=10.5 m s-1. b) Observations of a star in M15. |
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[angle=-90,width=8.2cm,clip]{921...
...vspace*{2mm}
\includegraphics[angle=-90,width=8cm,clip]{9214f12b.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg57.gif) |
Figure 12: fw70pcef a) from a long run in 2005. b) showing large and rapid variations from a run in 2004. |
| Open with DEXTER | |
Table 1:
Full width 70![]() enclosed flux
enclosed flux
![]() .
.
A plot of a sequence of values of fw70pcef from the simulations with D/r0 = 8.3 scaled to the NOT parameters with a velocity of the screen of 10.5 m s-1 are compared with the same quantity for the best seeing conditions from the NOT observing run in 2003 in Fig. 11. The two plots are extremely similar in both the amplitude and temporal character of the fast fluctuations, showing that the modelling accurately reflects the actual behaviour of the atmospheric fluctuations. There are in addition some slower variations in the mean seeing in the NOT data on timescales of 5-15 s.
Figure 12a shows a longer sequence of data from 2005 with variations
by a factor of ![]()
![]() on time scales between 10 s and 400 s (note
the change of scale on both axes). These are similar to those discussed by
Wilson et al. (1999) for the William Herschel Telescope situated
about 400 m
from the NOT. More extreme fluctuations are displayed in Fig. 12b,
variations in seeing by a factor
on time scales between 10 s and 400 s (note
the change of scale on both axes). These are similar to those discussed by
Wilson et al. (1999) for the William Herschel Telescope situated
about 400 m
from the NOT. More extreme fluctuations are displayed in Fig. 12b,
variations in seeing by a factor ![]() occurring on timescales as short as
0.2 s.
occurring on timescales as short as
0.2 s.
It raises the question of just how short the transitions can be in the simulations. To test this a mosaic was constructed from two of the phase screens used earlier having D/r0 = 8.3 and 16.7. It comprised alternating stripes of width 1.6 D from each of the screens with sharp transitions between the stripes. This arrangement is physically unrealistic, giving large discontinuities in phase across the boundaries in some cases, but it represents the limiting case of a seeing change by a factor of two. The behaviour of the quantity fw70pcef as the boundary crosses the aperture is notably smooth. 16 transitions were averaged to reduce the rapid fluctuations in fw70pcef of the type seen in Fig. 11 and the result is plotted in Fig. 13. The main features are well fitted by an approximate model also shown in which the value of fw70pcef is a weighted mean of the two end states, the weights being proportional to the areas of the aperture occupied by each of the two seeing regimes.
A comparison of the simulation with the sharpest transitions in the data requires a knowledge of the effective speed of the screen, derived as discussed in Sect. 3.3 from the autocorrelation function of the sequence of Strehl ratios. That measurement requires a period of constant seeing to avoid the shape of the auto-correlation function being dominated by those seeing changes. NOT data from a run in 2004 (Fig. 14a) shows a period of good and fairly constant seeing followed by a rapid increase in fw70pcef from 0.95 to 1.6 arcsec in about 0.2 s. The variance of the image motion also increases sharply at this point, showing that the change in seeing occurs over a wide range of spatial frequencies. The wind speed derived from the first period was 11 m s-1 and this was used to scale the simulation of a step increase in seeing to the NOT parameters. The close agreement with the observations (Fig. 14b) indicates that the change in mean seeing must have been spatially extremely sharp, certainly within a distance of 1 m. This argument depends on the assumption that the motion of the region of poor seeing is travelling at the same speed. If it were in a separate layer travelling at a higher speed, say 20 m s-1, then the constraint on the spatial extent of the transition would be relaxed to about 2 m. However, this possibility would require an even greater contrast between the good and poor seeing in that layer, and seems somewhat unlikely.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{9214f13.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg60.gif) |
Figure 13: Change of fw70pcef as step function in seeing crosses the aperture. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{9214f14a.ps}\par\vspace*{2mm}
\includegraphics[angle=-90,width=8.2cm,clip]{9214f14b.ps}\end{figure}](/articles/aa/full/2008/11/aa9214-07/Timg61.gif) |
Figure 14: a) Rapid changes in fw70pcef for a run in 2004. b) Comparison of change in fw70pcef with simulation of step change (see text). |
| Open with DEXTER | |
On some occasions, variable quality of seeing at the NOT is reported to be associated with wind directions from the E and SE blowing air directly from the caldera. The NOT weather station records for the 2004 observing run show surface wind speeds of 5-10 m s-1 in directions between NW and NE, so there is no reason to suspect a local cause for the extreme variations in seeing presented here.
The seeing variations displayed in Figs. 11 and 12a, b were chosen from a very large dataset to be representative of the variations experienced in each of the separate observing runs in 2003, 2005 and 2004 respectively. The range extended from barely perceptible changes occurring over periods of minutes to changes by a factor of 3 or more on timescales down to 0.2 s and included all intermediate types. Figure 12b is of particular interest. The average seeing would be described as moderate yet the periods of good seeing are excellent, with fw70pcef of 0.65 arcsec, equivalent to 0.5 arcsec FWHM of a conventional image. It illustrates how Lucky Imaging can take full advantage of such conditions.
We do not know whether this seeing behaviour is typical of all sites and emphasize the need for appropriate seeing measurements to be made. It represents a significant departure from the model of seeing commonly assumed and would have implications for other high resolution techniques such as Adaptive Optics and Long Baseline Interferometry. For Adaptive Optics the mean seeing conditions may vary significantly on scales smaller than the aperture being corrected, raising difficulties in the optimisation of the modes and timescales for correction. For Long Baseline Interferometry the main effect would be to increase the range of tilt-corrected phase variance across the individual telescope apertures, resulting in a greater probability of very low fringe visibilities. This would make it more difficult to lock the fringe phase, especially in cases where several short baselines are used to enable long integrations on a long baseline.
Numerical simulations of the process of Lucky Imaging have been carried out using random phase screens with a Kolmogorov spectrum of turbulence passing across a telescope aperture with ideal optics. Lucky images made by selection and superposition using shift-and-add for a range of 5-16 in D/r0 all have the same characteristics:
The observations show clear evidence of variations in the mean seeing by
factors up to ![]() on time-scales from several minutes down to periods as
short as 0.2 s and spatial scales of 1 m.
on time-scales from several minutes down to periods as
short as 0.2 s and spatial scales of 1 m.
Acknowledgements
We thank David Buscher for his original random screen code and Paul Alexander and Dave Green for extensive and generous help and advice. The Nordic Optical Telescope is operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway and Sweden in the Spanish Observatorio del Roque de los Muchachos of the Institute de Astrophfisica de Canarias.