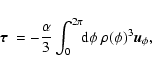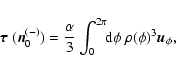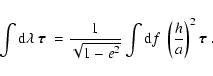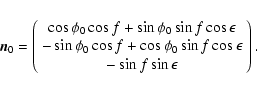A&A 480, 1-3 (2008)
DOI: 10.1051/0004-6361:20078389
Vanishing torque from radiation pressure
(Research Note)
D. Nesvorný1,2 -
D. Vokrouhlický1,3
1 - Department of Space Studies, Southwest Research Institute,
1050 Walnut St., Suite 300, Boulder, Colorado 80302, USA
2 -
Observatório Nacional, R. Gal. José Cristino 77,
20921-400 Rio de Janeiro, Brazil
3 -
Institute of Astronomy, Charles University,
V Holesovickách 2, 18000, Prague 8, Czech Republic
Received 31 July 2007 / Accepted 5 November 2007
Abstract
Context. Pioneering works on the effect of solar irradiation on the rotation of small objects in interplanetary space raised the possibility that the radiation pressure from solar photon absorption could modify the objects' spin states. Later numerical studies found that the torque from radiation pressure, when averaged over spin and orbital periods, vanished for all studied asteroid shape models.
Aims. We demonstrate that the average torque from radiation pressure vanishes for any surface shape deformation.
Methods. We have calculated the torque analytically. The main assumption of our calculation is that the object rotates around its principal axis of inertia.
Results. We show that the average torque vanishes for any surface shape deformation because the individual radiation-pressure contributions from configurations separated by 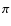 in orbital longitude cancel each other out.
in orbital longitude cancel each other out.
Conclusions. Unlike the thermal radiation and reflection of solar photons from surface, which can produce important effects over planetary timescales, the radiation pressure cannot change asteroid rotation.
Key words: minor planets, asteroids
The surface of an irregularly-shaped small object in the interplanetary
space is irradiated by sunlight. The torque produced by absorbed photons is
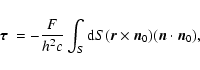 |
(1) |
where the integral is taken over the illuminated part of the surface. Here,
c is the speed of light, F=1378 W m-2 the solar flux
at distance 1 AU from the Sun, and h the heliocentric distance of the
object in AU. Vectors 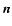 and
and 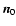 are unit vectors pointing
from surface element
are unit vectors pointing
from surface element 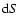 in normal and toward-the-Sun directions,
respectively. Vector
in normal and toward-the-Sun directions,
respectively. Vector 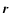 connects the center of mass of the object
to
connects the center of mass of the object
to 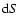 .
.
In addition to (1), two other torque components arise from the interaction
of the surface with solar radiation. These are produced by (i) reflected solar
photons and (ii) thermal photons departing from the surface heated by sunlight.
The total torque, called the YORP torque (after researchers Yarkovsky, O'Keefe,
Radzievskii, and Paddack; Rubincam 2000), can be obtained by adding torque
components together. The YORP effect has important applications in asteroid
spin dynamics (e.g., Vokrouhlický et al. 2003, 2007; Bottke et al. 2006).
We limit the analysis in this paper to the Keplerian orbital motion of a
small body around the Sun and its rotation around the principal axis of inertia.
The latter assumption is justified for km-sized and larger asteroids because
any excess in the rotational energy can be efficiently dissipated in their
interior (e.g., Sharma et al. 2005).
To study secular spin dynamics, it is convenient to average
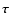 over the spin and orbit periods of the small object (Rubincam 2000). The mean torque,
over the spin and orbit periods of the small object (Rubincam 2000). The mean torque,
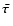 ,
is defined as
,
is defined as
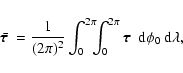 |
(2) |
where 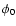 is the spin phase angle (see Sect. 2) and
is the spin phase angle (see Sect. 2) and 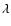 the mean
longitude of the small body presumed here to be orbiting around the Sun on a fixed orbit.
the mean
longitude of the small body presumed here to be orbiting around the Sun on a fixed orbit.
Early studies of the YORP effect discussed the possibility whether (2) can
produce changes in the spin state of a small object.
Modern numerical works have found that (2) vanished in every studied case,
including asteroids with known shape models and artificial objects (Rubincam 2000;
Vokrouhlický & Capek 2002). Here we calculate
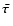 analytically. Our results imply that
analytically. Our results imply that
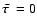 for any shape
deformation. Accordingly, the radiation pressure does not secularly affect principal
axis rotation.
for any shape
deformation. Accordingly, the radiation pressure does not secularly affect principal
axis rotation.
This note is organized as follows. In Sect. 2, we introduce useful reference
frames. In Sect. 3, we show that the instantaneous torque from the radiation
pressure only depends on the object's silhouette as seen from the Sun. Finally,
in Sect. 4, we demonstrate that the torque vanishes when it is averaged over
the orbital period.
We use several reference frames all with the origin at the center of mass of the small
object (Nesvorný & Vokrouhlický 2007). Figure 1 illustrates these frame
systems. The body frame,
Ox''y''z'', has the z'' axis fixed along the
object's spin axis (assumed here to coincide with the principal inertia axis) and
the x'' axis along its shortest axis of inertia. The rotating orbital frame,
Ox'y'z', has the z' axis pointing toward the normal of the
orbital plane and the x' axis pointing toward the Sun. The transformation of
a vector from the rotating orbital frame to the body frame is given by
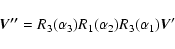 |
(3) |
with Euler angles
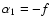 ,
,
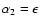 and
and
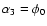 ,
where
,
where
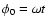 denotes the phase angle of the body's rotation with respect
to the inertial frame,
denotes the phase angle of the body's rotation with respect
to the inertial frame, 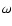 is the angular frequency of rotation,
is the angular frequency of rotation, 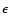 the obliquity, and f the true orbital longitude of the Sun. Symbols R1
and R3 in Eq. (3) are the usual rotation matrices that represent
the rotation of the reference system around the (generic) x and z axes, respectively.
the obliquity, and f the true orbital longitude of the Sun. Symbols R1
and R3 in Eq. (3) are the usual rotation matrices that represent
the rotation of the reference system around the (generic) x and z axes, respectively.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{f1.eps} \end{figure}](/articles/aa/full/2008/10/aa8389-07/Timg20.gif) |
Figure 1:
The illustration of various reference frames used in this
study. Oxyz, Ox'y'z', and
Ox''y''z'' denote the solar, rotating
orbital, and body frames, respectively. See Sect. 2 for the definition
of these reference systems. The body frame has been obtained from the rotating
orbital frame via three rotations indicated here (Eq. (3)). |
| Open with DEXTER |
Our third reference system is the frame with the z axis pointing toward
the Sun and the x axis pointing toward the normal of the orbital frame. We
call this reference system the solar frame. This frame rotates
in an inertial system with the angular speed given by the orbital motion of
the small body around the Sun. The transformation of any vector 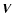 from the solar frame to the rotating orbital frame is
from the solar frame to the rotating orbital frame is
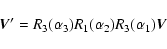 |
(4) |
with Euler angles
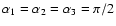 .
The colatitude and
longitude in the solar frame is denoted by
.
The colatitude and
longitude in the solar frame is denoted by 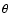 and
and 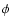 .
.
We calculate Eq. (1) in the solar frame where
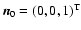 with index T denoting the transposed vector. Because
with index T denoting the transposed vector. Because
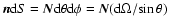 ,
Eq. (1) can be written as
,
Eq. (1) can be written as
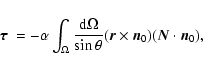 |
(5) |
where
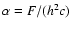 ,
,
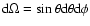 ,
,
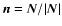 ,
,
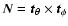 ,
and where
,
and where
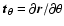 and
and
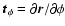 are
tangential vectors. The integration over solid angle
are
tangential vectors. The integration over solid angle 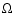 goes over the
illuminated part of the surface. Assuming
goes over the
illuminated part of the surface. Assuming
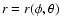 ,
which is appropriate
for all shapes except the ones for which radial ray
,
which is appropriate
for all shapes except the ones for which radial ray
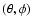 can intersect
the surface in more than one point, it can be easily shown that
can intersect
the surface in more than one point, it can be easily shown that
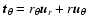 and
and
 ,
where
,
where
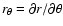 and
and
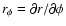 .
The vectors
.
The vectors 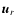 ,
,
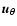 ,
and
,
and
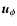 used above were
defined as
used above were
defined as
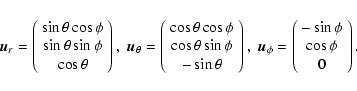 |
(6) |
They form an orthonormal triad (i.e.,
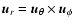 ,
etc.). Using these vectors the expression for
,
etc.). Using these vectors the expression for 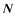 reads as
reads as
![\begin{displaymath}%
\vec{N} =
r\left[ r \sin \theta~ \vec{u}_r - r_\theta \sin \theta~ \vec{u}_\theta - r_\phi~
\vec{u}_\phi \right];
\end{displaymath}](/articles/aa/full/2008/10/aa8389-07/img48.gif) |
(7) |
therefore,
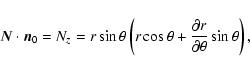 |
(8) |
where Nz is the z-component of 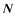 in the solar frame. We also have in the
solar frame that
in the solar frame. We also have in the
solar frame that
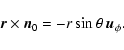 |
(9) |
Now, substituting the above expressions into (5), we find that
The above integral over  needs to be taken over the illuminated part
of the surface. The illuminated part of the surface of an ideally spherical object
is its whole hemisphere facing the Sun. In such an idealized case, the integral over
needs to be taken over the illuminated part
of the surface. The illuminated part of the surface of an ideally spherical object
is its whole hemisphere facing the Sun. In such an idealized case, the integral over
 would go from 0 to
would go from 0 to 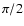 .
For a general surface deformation for which
shadowing of surface elements can occur, the integral over
.
For a general surface deformation for which
shadowing of surface elements can occur, the integral over 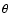 can be written as
can be written as
![\begin{displaymath}%
\int {\rm d}\theta {\partial \over \partial \theta} (r^3 \s...
...left[ r^3 \sin^3 \theta \right]_{\theta_{1,j}}^{\theta_{2,j}},
\end{displaymath}](/articles/aa/full/2008/10/aa8389-07/img56.gif) |
(11) |
where
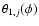 ,
and
,
and
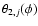 denote the latitude limits of
illuminated segments stretching along the body's meridian (with constant
denote the latitude limits of
illuminated segments stretching along the body's meridian (with constant 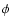 ).
Given the illumination geometry in the solar frame, we note that
).
Given the illumination geometry in the solar frame, we note that
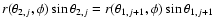 for
all j. Therefore, although in general discontinuous in
for
all j. Therefore, although in general discontinuous in 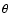 ,
Eq. (11) is
continuous in
,
Eq. (11) is
continuous in
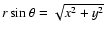 ,
where x and y are the Cartesian
coordinates in the solar frame. Equation (10) can be reduced to
,
where x and y are the Cartesian
coordinates in the solar frame. Equation (10) can be reduced to
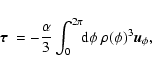 |
(12) |
where
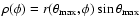 with
with
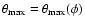 denoting the value of
denoting the value of 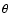 at the terminator.
at the terminator.
The meaning of (12) is clear: the instantaneous torque from the radiation
pressure only depends on the silhouette that the irregular object presents to the
Sun (Rubincam 2000). It is straightforward to show that the same result also holds
for a more general case of surface deformation where radial ray
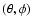 is allowed to intersect the surface at more than one point.
is allowed to intersect the surface at more than one point.
Until now we have assumed that the object is illuminated with
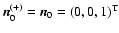 in the solar frame. If, instead, the object is illuminated from the opposite
direction, i.e. with
in the solar frame. If, instead, the object is illuminated from the opposite
direction, i.e. with
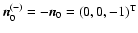 ,
the silhouette
of the object and therefore also the magnitude of the torque would be the same. It is easy to show,
moreover, that the instantaneous torque vector produced with
,
the silhouette
of the object and therefore also the magnitude of the torque would be the same. It is easy to show,
moreover, that the instantaneous torque vector produced with
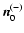 goes in the opposite direction to the one obtained with
goes in the opposite direction to the one obtained with
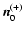 ;
i.e.,
;
i.e.,
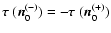 .
This last statement stems from the following. With
.
This last statement stems from the following. With
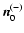 ,
Eq. (10)
remains the same except for the integration domain that now spans over the opposite
hemisphere of the object than before; the integration path in
,
Eq. (10)
remains the same except for the integration domain that now spans over the opposite
hemisphere of the object than before; the integration path in 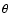 must be changed
accordingly. We obtain
must be changed
accordingly. We obtain
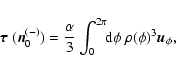 |
(13) |
as claimed above.
To determine average torque (2), we need to transform the torque vector from the
solar frame to the body frame and average it over 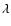 and
and 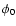 .
We note that the
integration over
.
We note that the
integration over 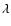 can be simplified by introducing true longitude f as the new
integration variable:
can be simplified by introducing true longitude f as the new
integration variable:
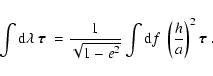 |
(14) |
The dependence on h then conveniently cancels out from (14) because
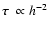 according to (1).
We therefore find that the stronger torques produced by sunlight at the perihelion are
compensated for by the shorter time interval that an asteroid spends near perihelion.
according to (1).
We therefore find that the stronger torques produced by sunlight at the perihelion are
compensated for by the shorter time interval that an asteroid spends near perihelion.
In the body frame, the object presents different silhouettes to the Sun
depending on the Sun's location. With the help of transformation rules (3)
and (4), we can transform the vector  from the solar frame,
where
from the solar frame,
where
 ,
to the body frame, where
,
to the body frame, where
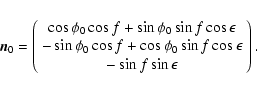 |
(15) |
In the course of its spin and orbital motion, the object shows different
sides of its figure to the Sun. Yet, it is clear that its silhouettes as seen from the Sun are the same for 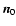 and
and
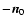 .
This reversal of the Sun's direction in the body frame is achieved when f is substituted
by
.
This reversal of the Sun's direction in the body frame is achieved when f is substituted
by 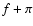 in (15). According to the results in the
previous section, the instantaneous torque vectors for
in (15). According to the results in the
previous section, the instantaneous torque vectors for
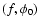 and
and
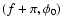 then cancel when added together. Therefore, the integral
over
then cancel when added together. Therefore, the integral
over 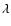 in (2) vanishes. We conclude that
in (2) vanishes. We conclude that
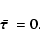 |
(16) |
Our result implies that the average torque from the radiation pressure vanishes
for any surface shape deformation. This represents an important generalization
from the previous analytical results (e.g., Breiter et al. 2007) and shows that the
radiation pressure effects cannot change asteroid rotation.
According to (12), the radiation pressure can only apply a tiny and variable
instantaneous torque to the rotating body. The physical importance of this effect
is negligible in the present studies of asteroidal dynamics. Still, in principle,
the varying radiation pressure torques could cause small periodical changes in an
asteroid's spin state. It is even possible, in the absence of efficient dissipation
of the excess spin energy, that these variable torques could produce slight deviations
of the spin vector from the principal axis. Our assumption of principal axis rotation
must be relaxed to make theoretical investigations into such matters possible.
Acknowledgements
The funding for this work was provided by NASA's Planetary Geology and Geophysics
program, and by CNPq. The work of D.V. was supported by the Grant Agency of the
Czech Republic (grant 205/05/2737). We thank Miroslav Broz for Fig. 1.
- Bottke, W. F.,
Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D.
2006, ARA&A, 34, 157
(In the text)
- Breiter, S., Michalska,
H., Vokrouhlický, D., & Borczyk, W. 2007, A&A, 471,
345 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Nesvorný, D.,
& Vokrouhlický, D. 2007, AJ, 134, 1750 [NASA ADS] [CrossRef]
(In the text)
- Rubincam, D. P. 2000,
Icarus, 148, 2 [NASA ADS] [CrossRef]
(In the text)
- Sharma, I., Burns, J.
A., & Hui, C.-Y. 2005, MNRAS, 359, 79 [NASA ADS] [CrossRef]
(In the text)
- Vokrouhlický,
D., & Capek, D. 2002, Icarus, 159, 449 [NASA ADS] [CrossRef]
(In the text)
- Vokrouhlický,
D., Nesvorný, D., & Bottke, W. F. 2003, Nature, 425,
147 [NASA ADS] [CrossRef]
(In the text)
- Vokrouhlický,
D., Breiter, S., Nesvorný, D., & Bottke, W. F. 2007,
Icarus, in press
(In the text)
Copyright ESO 2008
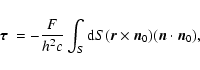
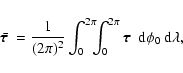
![\begin{figure}
\par\includegraphics[width=7cm,clip]{f1.eps} \end{figure}](/articles/aa/full/2008/10/aa8389-07/Timg20.gif)
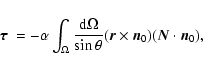
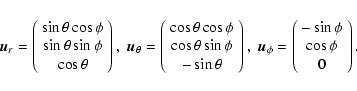
![\begin{displaymath}%
\vec{N} =
r\left[ r \sin \theta~ \vec{u}_r - r_\theta \sin \theta~ \vec{u}_\theta - r_\phi~
\vec{u}_\phi \right];
\end{displaymath}](/articles/aa/full/2008/10/aa8389-07/img48.gif)
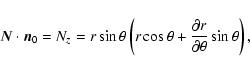
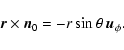
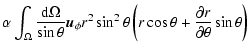
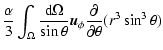
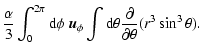
![\begin{displaymath}%
\int {\rm d}\theta {\partial \over \partial \theta} (r^3 \s...
...left[ r^3 \sin^3 \theta \right]_{\theta_{1,j}}^{\theta_{2,j}},
\end{displaymath}](/articles/aa/full/2008/10/aa8389-07/img56.gif)