A&A 480, 27-33 (2008)
DOI: 10.1051/0004-6361:20077562
A. Bonanno1,2 - V. Urpin1,3
1 - INAF - Osservatorio Astrofisico di Catania,
via S. Sofia 78, 95123 Catania, Italy
2 - INFN, Sezione di Catania, via S. Sofia 72,
95123 Catania, Italy
3 - A.F. Ioffe Institute of Physics and Technology and
Isaac Newton Institute of Chile, Branch in St. Petersburg,
194021 St. Petersburg, Russia
Received 28 March 2007 / Accepted 5 December 2007
Abstract
Context. Observations of protostellar disks indicate the presence of the magnetic field of thermal (or superthermal) strength. In such a strong magnetic field, many MHD instabilities responsible for turbulent transport of the angular momentum are suppressed.
Aims. We consider the shear-driven instability that can occur in protostellar disks even if the field is superthermal.
Methods. This instability is caused by the combined influence of shear and compressibility in a magnetized gas and can be an efficient mechanism to generate turbulence in disks.
Results. The typical growth time is of the order of several rotation periods.
Key words: accretion, accretion disks - magnetohydrodynamics (MHD) - instabilities - turbulence - stars: formation
Protostellar disks require sufficiently strong turbulence to enhance the efficiency of angular momentum transport. The origin of turbulence is often attributed to hydrodynamic and hydromagnetic instabilities that can arise in differentially-rotating, stratified gaseous disks. One of the candidates is magnetorotational instability (MRI), which can operate in a conductive flow if the angular velocity decreases with the cylindrical radius and the magnetic field is not strong (Velikhov 1959). The MRI has been studied in depth in the case of stellar and accretion disk conditions (see, e.g., Fricke 1969; Safronov 1969; Acheson 1978, 1979; Balbus & Hawley 1991; Kaisig et al. 1992; Kumar et al. 1994; Zhang et al. 1994). Simulations of the MRI in disks (Hawley et al. 1995; Matsumoto & Tajima 1995; Brandenburg et al. 1995; Torkelsson et al. 1996; Arlt & Rüdiger 2001) show the turbulence generated can significantly enhance the angular momentum transport.
Most likely, however, the number of instabilities that can arise in astrophysical disks is quite large. An analysis of MHD modes in stratified accretion disks demonstrates a wide variety of instabilities even in the case of simple magnetic geometry (Keppens et al. 2002). Therefore, the current point of view on the origin of turbulence in disks is likely highly simplified. Even pure, hydrodynamic origin of turbulence cannot be excluded (see Urpin 2003; Arlt & Urpin 2004; Dubrulle et al. 2005) despite the most efficient local linear hydrodynamic instabilities advocated to date are not sufficiently efficient. Global instabilities, such as the baroclinic-like instability of Klahr & Bodenheimer (2003), are sensitive to boundary conditions (Johnson & Gammie 2006) and, therefore, are unlikely to drive turbulence in disks. Note, however, that such factors as fast radiative cooling, high thermal diffusion, and large radial temperature gradients can strengthen the baroclinic feedback and make the baroclinic instability more efficient (Petersen et al. 2007). Astrophysical disks are stratified and stratification can change stability properties of shear flows, providing either a stabilizing or destabilizing effect, depending on details of the disk structure. Recently, Dubrulle et al. (2005) have considered one of the possible ``strato-rotational'' instabilities arising in the presence of both differential rotation and stable stratification. However, Brandenburg & Rüdiger (2005) demonstrated that the growth rate of this instability decreases with an increasing Reynolds number, rendering the instability less relevant for astrophysical applications. Note also that convection can drive turbulence in disks with unstable stratification, but it induces inward turbulent transport of the angular momentum instead of the required outward one (see, e.g., Stone & Balbus 1996).
As it has been argued by Lesur & Longaretti (2005),
nonlinear hydrodynamic instability that often occurs in linearly-stable
flows at sufficiently large Reynolds numbers is likely inefficient in
disks even for the most optimistic extrapolations of numerical data.
At least, the subcritical transition to
hydrodynamic turbulence cannot occur in quasi-Keplerian flows at Reynolds
numbers up to ![]() 106 (Ji et al. 2006). Of course, Reynolds numbers are much
higher in real disks; nevertheless it seems that there is little room for
nonlinear instability.
106 (Ji et al. 2006). Of course, Reynolds numbers are much
higher in real disks; nevertheless it seems that there is little room for
nonlinear instability.
The stability properties of protostellar disks are much different from those of accretion disks. The magnetic Reynolds number is likely not very large in cold- and dense-protostellar disks because of a low electrical conductivity, and so the field cannot be treated as ``frozen'' into the gas (Gammie 1996). The effect of Ohmic dissipation on the MRI has been considered in the linear (Jin 1996) and nonlinear regimes (Sano et al. 1998; Drecker et al. 2000). Fleming & Stone (2003) and Turner et al. (2006) treated turbulent mixing caused by the MRI in protostellar disks, taking into account magnetic diffusivity. They found that the midplane is shielded from cosmic rays, and that MRI does not occur even under the most favorable conditions. Nevertheless, turbulence can mix a fraction of the weakly-conducting surface material into the interior, providing some coupling of the midplane gas to the magnetic field. As a result, weak stresses can appear in the disk midplane.
As first pointed out by Wardle (1999), poorly conducting protostellar disks can be strongly magnetized if electrons are the main charge carriers. Therefore, transport must be anisotropic with substantially different properties along and across the magnetic field. In strongly magnetized gas the Hall component provides the main contribution to the resistivity tensor, which produces the electric field perpendicular to both the magnetic and electric current. The stability analysis by Wardle (1999) shows that the Hall effect can provide either stabilizing or destabilizing influences depending on the direction of the field. Balbus & Terquem (2001) have conducted a more general study of the role of the Hall term on MRI. They found that the Hall effect qualitatively changes the stability properties of protostellar disks and can lead to instability even if the angular velocity increases outward. These authors, however, did not take into account the effect of gravity that is crucial for disks. Urpin & Rüdiger (2005) considered MRI under the combined influence of the Hall effect and gravity, and also derived also the criteria of several other instabilities that can occur in protostellar disks. Sano & Stone (2002) investigated the effect of the Hall term on the evolution of the MRI in weakly-ionized disks using local axisymmetric simulations. These authors concluded the properties of the MRI depend essentially on the direction of the magnetic field as it is anticipated from the dispersion equation in a linear stability analysis. Salmeron & Wardle (2005) have also considered the properties of the MRI modified by the Hall effect. These authors argued that the MRI is active in protoplanetary disks over a wide range of field strengths and fluid conditions. The Hall conductivity results in a faster growth of perturbations and extends the region of instability. Recently, Livertz et al. (2007) and Shtemler et al. (2007) have considered the Hall MRI in a non-axisymmetric case. This type of instability is proposed as a viable mechanism for the azimuthal fragmentation of the protoplanetary disks and planet formation. The non-axisymmetric instability is caused by the combined effect of the radial stratification and Hall electric field. Note that the MRI and its modifications can be completely suppressed if the magnetic field is sufficiently strong (see Urpin 1996; Kitchatinov & Rüdiger 1997).
If rotation is cylindrical and
![]() ,
where
,
where ![]() is the
angular velocity and s is the cylindrical radius, the critical magnetic
field that suppresses the MRI is given approximately by the condition
is the
angular velocity and s is the cylindrical radius, the critical magnetic
field that suppresses the MRI is given approximately by the condition
![]() where
where
![]() is the Alfvén velocity. Since
is the Alfvén velocity. Since
![]() in the standard disk,
where
in the standard disk,
where ![]() is the sound speed, we find that the MRI is suppressed if the
magnetic field is superthermal,
is the sound speed, we find that the MRI is suppressed if the
magnetic field is superthermal,
![]() .
Recent measurements
(Hutawarakorn & Cohen 1999, 2005; Donati et al. 2005) indicate that the
magnetic field can be strong in protostellar disks. This particularly
concerns the innermost regions where the field strength reaches
.
Recent measurements
(Hutawarakorn & Cohen 1999, 2005; Donati et al. 2005) indicate that the
magnetic field can be strong in protostellar disks. This particularly
concerns the innermost regions where the field strength reaches ![]() 1 kG
at the radius
1 kG
at the radius ![]() 0.05 AU (Donati et al. 2005). The field configuration
includes the azimuthal component whose direction agrees with
the radial field sheared by the disk differential rotation. The
derived ratio of the azimuthal and radial fields in the surface layers is
0.05 AU (Donati et al. 2005). The field configuration
includes the azimuthal component whose direction agrees with
the radial field sheared by the disk differential rotation. The
derived ratio of the azimuthal and radial fields in the surface layers is
![]() 0.5. Note that the azimuthal component can be substantially stronger
than the radial one in the disk interiors because dynamo theories
(such as the
0.5. Note that the azimuthal component can be substantially stronger
than the radial one in the disk interiors because dynamo theories
(such as the
![]() dynamo) usually predict that the generated
field should have a strong toroidal component. According to estimates by
Donati et al. (2005), the equipartition field strength with roughly equal
thermal and magnetic pressures should be
dynamo) usually predict that the generated
field should have a strong toroidal component. According to estimates by
Donati et al. (2005), the equipartition field strength with roughly equal
thermal and magnetic pressures should be ![]() 103 Gauss at the radius
103 Gauss at the radius ![]() 0.05 AU in protostellar disks. This indicates the detected field is approximately of
the thermal or even superthermal strength and can substantially
modify or even suppress the MRI.
0.05 AU in protostellar disks. This indicates the detected field is approximately of
the thermal or even superthermal strength and can substantially
modify or even suppress the MRI.
Recently, Bonanno & Urpin (2006, 2007) have argued that a compressible, differentially-rotating flow is unstable if the magnetic field has a non-vanishing, radial component. A remarkable feature of this shear-driven instability is that it can arise even if the magnetic field is superthermal. Bonanno & Urpin (2006, 2007) have considered the instability in the case of a highly conductive plasma when the magnetic diffusivity plays no role. However, the instability can also arise in weakly-ionized protostellar disks where the magnetic field has a radial component detected in observations (Donati et al. 2005). The effect of a finite diffusivity can be important for the onset of instability and for the properties of generated turbulence, particularly near the the mid-plane where conductivity is extremely low. In this paper, we consider the shear-driven instability in the conditions of protostellar disks and show that the conditions of instability in weakly and highly ionized plasmas differ substantially. Nevertheless, the shear-driven instability can manifest itself even in weakly-ionized protostellar disks.
The paper is organized as follows. In Sect. 2, we consider the basic equations governing instability in compressible dissipative fluids and we then derive the dispersion relation. In Sect. 3, we derive the criteria of instability and discuss conditions under which instability can occur in protostellar disks. The growth rate of instability is calculated in Sect. 4. Finally, in Sect. 5, we discuss the results obtained.
The electrical conductivity is low in protostellar disks- and
the magnetic field cannot be considered as ``frozen'' into the gas. The
magnetic diffusivity is given by
![]() where
where ![]() and
and ![]() are the mass and number density of
electrons, respectively, and
are the mass and number density of
electrons, respectively, and ![]() is their relaxation time (see, e.g.,
Spitzer 1978). In protostellar disks,
is their relaxation time (see, e.g.,
Spitzer 1978). In protostellar disks, ![]() is determined by the scattering
of electrons on neutrals, then
is determined by the scattering
of electrons on neutrals, then
![]() where
where
![]() is the average product of the cross-section and
velocity, and n is the number density of neutrals. Using the fitting
expression for
is the average product of the cross-section and
velocity, and n is the number density of neutrals. Using the fitting
expression for
![]() obtained by Draine et al. (1983),
we have
obtained by Draine et al. (1983),
we have
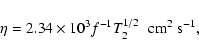 |
(1) |
The magnetic diffusivity can be anisotropic in some regions of protostellar
disks (Wardle 1999) because the electron gas is magnetized despite a low
temperature. The effect of the magnetic field on transport properties is
usually characterized by the magnetization parameter
![]() ,
where
,
where
![]() is the gyrofrequency of electrons
(see, e.g., Spitzer 1978). Again, using the fitting formula by Draine et al.
(1983), we can estimate the magnetization parameter as
is the gyrofrequency of electrons
(see, e.g., Spitzer 1978). Again, using the fitting formula by Draine et al.
(1983), we can estimate the magnetization parameter as
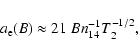 |
(2) |
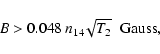 |
(3) |
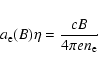 |
(4) |
| (5) |
| (6) |
| (7) |
![$\displaystyle %
\dot{\vec{B}} - \nabla \times (\vec{v} \times \vec{B})
+ \frac{...
...ec{B}) \times \vec{B} \right]
+ \eta \nabla \times (\nabla \times \vec{B}) = 0,$](/articles/aa/full/2008/10/aa7562-07/img40.gif) |
(8) |
| (9) |
The basic state on which the stability analysis is performed is assumed to
be quasi-stationary with the angular velocity
![]() and
and
![]() .
We assume hydrostatic equilibrium for
basic state:
.
We assume hydrostatic equilibrium for
basic state:
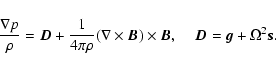 |
(10) |
![$\displaystyle %
[\nabla \times (\vec{v} \times \vec{B})]_{\varphi} =
\! \left\{...
...\!
\right\}_{\varphi}
+ \eta [\nabla \times (\nabla \times \vec{B})]_{\varphi}.$](/articles/aa/full/2008/10/aa7562-07/img50.gif) |
(11) |
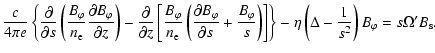 |
(12) |
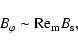 |
(13) |
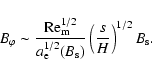 |
(14) |
We consider the stability of axisymmetric short-wavelength perturbations.
Small perturbations will be indicated by subscript 1, while unperturbed
quantities will have no subscript. The linearized momentum equation is:
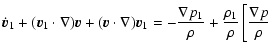 |
|||
![$\displaystyle \left. -\frac{1}{4 \pi \rho} (\nabla \times \vec{B}) \times \vec{B} \right]
+ \frac{1}{4 \pi \rho} (\nabla \times \vec{B}_{1}) \times \vec{B}$](/articles/aa/full/2008/10/aa7562-07/img61.gif) |
|||
| (15) |
| (16) |
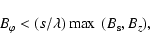 |
(17) |
Following similar transformations with the remaining Eqs. (6)-(9), we
arrived at the linearized equations needed for stability analysis. We consider
perturbations with the space-time
dependence ![]()
![]() ,
where
,
where
![]() is the wavevector. Then, the linearized
MHD-equations read with accuracy in the lowest order in
is the wavevector. Then, the linearized
MHD-equations read with accuracy in the lowest order in ![]() :
:
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
The dispersion equation, corresponding to Eqs. (18)-(22) is rather complex in
the general case. Therefore, we consider only a particular case when the
wavevector is perpendicular to the magnetic field,
![]() .
After some algebra, Eqs. (18)-(22) can be combined into a sixth-order
dispersion relation,
.
After some algebra, Eqs. (18)-(22) can be combined into a sixth-order
dispersion relation,
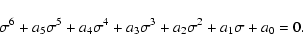 |
(23) |
In the non-dissipative, incompressible, limit when the sound speed ![]() is
very large, Eq. (23) reduces to the dispersion relation for the inertial
waves,
is
very large, Eq. (23) reduces to the dispersion relation for the inertial
waves,
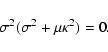 |
(24) |
In non-dissipative limit,
![]() ,
Eq. (23) recovers the
dispersion relation derived by Bonanno & Urpin (2006) for perturbations
with
,
Eq. (23) recovers the
dispersion relation derived by Bonanno & Urpin (2006) for perturbations
with
![]() ,
,
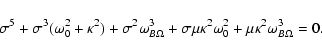 |
(25) |
Equation (23) can be simplified in many cases of interest if we take into account
that, likely, the s-component of the magnetic field in disks is greater
than the z-component,
![]() .
For perturbations with
.
For perturbations with
![]() ,
we have
,
we have
![]() .
Then,
.
Then,
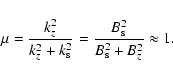 |
(26) |
| (27) |
| (28) |
The Hurwitz theorem states that an equation of the fourth order,
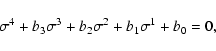 |
(29) |
| (30) | |||
| b3 b2 - b1 < 0, | (31) | ||
| b1 (b3 b2 - b1) - b32 b0 <0, | (32) |
| (33) | |||
| (34) |
![\begin{displaymath}%
\delta \frac{H s \Omega'}{c_{\rm A}} > \frac{\eta}{c_{\rm A...
...ft[
\frac{2 \eta^2}{c_{\rm A}^2 H^2} (kH)^4 + (kH)^2 \right].
\end{displaymath}](/articles/aa/full/2008/10/aa7562-07/img119.gif) |
(35) |
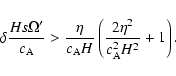 |
(36) |
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{7562fig1.ps}\end{figure}](/articles/aa/full/2008/10/aa7562-07/Timg135.gif) |
Figure 1:
The region of parameters where the instability can occur in
accordance with Eq. (32) for different values |
| Open with DEXTER | |
By analogy, we can also transform condition (34). The minimal unstable
rotation shear corresponds again to the maximal possible wavelength. Again,
the maximum wavelength can be estimated from the condition ![]() .
For
such wavevectors, Eq. (36) can be transformed into:
.
For
such wavevectors, Eq. (36) can be transformed into:
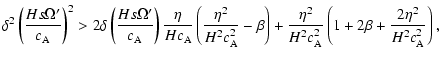 |
(37) |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{7562fig2.ps}\end{figure}](/articles/aa/full/2008/10/aa7562-07/Timg139.gif) |
Figure 2:
The region of parameters where instability can occur in
accordance with Eq. (33). The values of
|
| Open with DEXTER | |
In Fig. 2, we show the region of parameters where the instability can occur
in accordance with Eq. (37). Inequality (37) is quadratic in
![]() and can be satisfied if this parameter is larger/smaller
than the largest/smallest root of the corresponding quadratic equation.
Therefore, for a given combination of
and can be satisfied if this parameter is larger/smaller
than the largest/smallest root of the corresponding quadratic equation.
Therefore, for a given combination of ![]() and
and ![]() ,
the regions of instability lie
above the upper line and below the lower line.
,
the regions of instability lie
above the upper line and below the lower line.
To calculate the instability growth rate, it is convenient to
introduce dimensionless quantities,
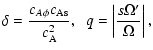 |
| (38) |
![\begin{figure}
\par\includegraphics[width=7.9cm]{7562fig3.ps}\end{figure}](/articles/aa/full/2008/10/aa7562-07/Timg145.gif) |
Figure 3:
The dependence of the growth rate on x=kH for the Keplerian
disk, with q=3/2 and
|
| Open with DEXTER | |
In Fig. 3, we plot the dependence of the growth rate on x for the
Keplerian disk with q=3/2 and
![]() and for several values of the
parameter
and for several values of the
parameter ![]() .
In all cases, the growth rate decreases monotonically with
decreasing wavelength
.
In all cases, the growth rate decreases monotonically with
decreasing wavelength
![]() because ohmic dissipation is
more efficient for perturbations with a shorter wavelength.
For any ratio of the magnetic and gas pressures, the instability does not
occur if kH > 12. If the magnetic pressure is greater than the gas
pressure (
because ohmic dissipation is
more efficient for perturbations with a shorter wavelength.
For any ratio of the magnetic and gas pressures, the instability does not
occur if kH > 12. If the magnetic pressure is greater than the gas
pressure (![]() ), the growth rate can reach relatively large values
), the growth rate can reach relatively large values
![]() .
This corresponds to the growth time only 3-4 times longer than the rotation period. The magnetorotational instability
cannot arise in such a strong magnetic field no matter how large is the
electrical conductivity of gas. Even if
.
This corresponds to the growth time only 3-4 times longer than the rotation period. The magnetorotational instability
cannot arise in such a strong magnetic field no matter how large is the
electrical conductivity of gas. Even if ![]() is not perpendicular
to
is not perpendicular
to ![]() ,
the MRI can occur only if the magnetic field and
wavevector satisfy the condition
,
the MRI can occur only if the magnetic field and
wavevector satisfy the condition
![]() .
Assuming
that
.
Assuming
that
![]() ,
we can transform this inequality approximately
into
,
we can transform this inequality approximately
into
![]() .
Since
.
Since
![]() in
the Keplerian disk, we find that MRI arises if
in
the Keplerian disk, we find that MRI arises if
![]() .
In the
case
.
In the
case ![]() ,
this condition never applies and the MRI is suppressed.
On the contrary, the shear-driven instability turns out to be rather efficient
in such a strong field.
,
this condition never applies and the MRI is suppressed.
On the contrary, the shear-driven instability turns out to be rather efficient
in such a strong field.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{7562fig4.ps}\end{figure}](/articles/aa/full/2008/10/aa7562-07/Timg155.gif) |
Figure 4:
The same as in Fig. 3 but for a non-Keplerian disk with q=1 and
|
| Open with DEXTER | |
In Fig. 4, we plot the same dependence, but for the non-Keplerian disk with
q=1 and
![]() .
The other parameters are same. Qualitatively,
the dependences are very similar to those shown in Fig. 3. The instability
grows faster in the disk with larger
.
The other parameters are same. Qualitatively,
the dependences are very similar to those shown in Fig. 3. The instability
grows faster in the disk with larger ![]() ,
which seems to be a general
feature of the shear-driven instability. However, the growth rate is typically
smaller for a non-Keplerian disk. The range of unstable wavevectors is
limited approximately by kH < 10. Note that the half-thickness H is
essentially larger in a non-Keplerian disk than in the Keplerian one.
,
which seems to be a general
feature of the shear-driven instability. However, the growth rate is typically
smaller for a non-Keplerian disk. The range of unstable wavevectors is
limited approximately by kH < 10. Note that the half-thickness H is
essentially larger in a non-Keplerian disk than in the Keplerian one.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{7562fig5.ps}\end{figure}](/articles/aa/full/2008/10/aa7562-07/Timg156.gif) |
Figure 5:
The dependence of the growth rate on |
| Open with DEXTER | |
The dependence of the growth rate on
![]() is shown in Fig. 5 for the disk with q=3/2 and
is shown in Fig. 5 for the disk with q=3/2 and
![]() .
At a given wavelength,
the growth rate increases with
.
At a given wavelength,
the growth rate increases with ![]() slowly approaching a saturation
value that depends on q. The saturation growth rate is
slowly approaching a saturation
value that depends on q. The saturation growth rate is ![]()
![]() and
and
![]() for q=5 and 10, respectively. This correspond to the
growth time of about
for q=5 and 10, respectively. This correspond to the
growth time of about ![]() 3 and
3 and ![]() 6 rotation periods. The dependence
of the shear-driven instability on the magnetic field is unusual,
at least, in the domain of parameters because usually a strong
magnetic field tends to suppress other types of instability.
Figure 6 shows the dependence of the growth rate on the parameter
6 rotation periods. The dependence
of the shear-driven instability on the magnetic field is unusual,
at least, in the domain of parameters because usually a strong
magnetic field tends to suppress other types of instability.
Figure 6 shows the dependence of the growth rate on the parameter ![]() ,
which
is approximately equal to the inverse magnetic Reynolds
number,
,
which
is approximately equal to the inverse magnetic Reynolds
number,
![]() .
Therefore, higher values of
.
Therefore, higher values of ![]() correspond to a higher dissipation rate, and the instability should be
suppressed at large
correspond to a higher dissipation rate, and the instability should be
suppressed at large ![]() .
Indeed, the growth rate goes to 0 if
.
Indeed, the growth rate goes to 0 if
![]() ,
depending on the wavelength. Hence, one can expect that the
shear-driven instability occurs even in disks with a relatively small
magnetic Reynolds number
,
depending on the wavelength. Hence, one can expect that the
shear-driven instability occurs even in disks with a relatively small
magnetic Reynolds number ![]() 100.
100.
![\begin{figure}
\par\includegraphics[width=8.25cm,clip]{7562fig6.ps}\end{figure}](/articles/aa/full/2008/10/aa7562-07/Timg163.gif) |
Figure 6:
The dependence of the growth rate on |
| Open with DEXTER | |
We have considered the new instability that can arise in protostellar
disks under the combined influence of the magnetic field, differential
rotation, and compressibility. To illustrate the main qualitative features
of the instability, we analyzed a particular case of perturbations with the
wavevector ![]() perpendicular to the magnetic field
perpendicular to the magnetic field ![]() .
In this
case, the standard MRI does not occur because its growth rate is
.
In this
case, the standard MRI does not occur because its growth rate is ![]()
![]() .
The considered instability is related
to shear and compressibility of a magnetized gas. In the incompressible
limit (
.
The considered instability is related
to shear and compressibility of a magnetized gas. In the incompressible
limit (
![]() )
we have, from Eq. (27),
)
we have, from Eq. (27),
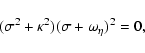 |
(39) |
The magnetic field is likely thermal or superthermal in protostellar disks
(see Donati et al. 2005). The considered instability can arise even in a
very strong magnetic field when the MRI is suppressed completely, It is
known that the MRI does not occur if the magnetic field satisfies the
condition
![]() .
The shear-driven
instability can operate even if the field is stronger than
.
The shear-driven
instability can operate even if the field is stronger than
![]() .
The
growth time of instability is still rather short (several rotation periods)
in the gas where the magnetic pressure is greater than the thermal pressure.
.
The
growth time of instability is still rather short (several rotation periods)
in the gas where the magnetic pressure is greater than the thermal pressure.
The criteria for the considered instability can be satisfied in
protostellar disks. Likely, all disks have both radial and azimuthal magnetic
fields. These magnetic fields are found in observations, as well as in
numerical simulations. Superthermal magnetic fields do not suppress the
instability crucial in cold protostellar disks. The instability can arise even in
a low conductive gas where the magnetic Reynolds number associated with
rotation is relatively small, Re
![]() .
.
Our paper considers only a local axisymmetric instability. Most likely, the same mechanism of instability will efficiently destabilize perturbations with the wavelength comparable to the disk scale height. Dissipative effects are less important for these perturbations, and the unstable modes can grow even faster. A global instability caused by a combined influence of differential rotation and compressibility will be considered elsewhere. The turbulence that could be generated by the considered instability can be strongly anisotropic in the (s,z)-plane because both the criteria and growth rate are sensitive to the direction of the wave vector. The generated turbulence, however, might be efficient in the radial transport of angular momentum in strongly magnetized protostellar disks.
Acknowledgements
This research project has been supported by a Marie Curie Transfer of Knowledge Fellowship of the European Community's Sixth Framework Programme under contract number MTKD-CT-002995. VU thanks also INAF-Osservatorio Astrofisico di Catania for hospitality.