A&A 479, L45-L49 (2008)
DOI: 10.1051/0004-6361:20079130
LETTER TO THE EDITOR
M. Montalto1,2 - A. Riffeser2 - U. Hopp1,2 - S. Wilke2 - G. Carraro3
1 - Max-Planck-Institute for Extraterrestrial Physics, Giessenbachstr., 85741
Garching b. Muenchen, Germany
2 -
Universitaets-Sternwarte der
Ludwig-Maximilians-Universitaet, Scheinerstr.1, 81679 Muenchen, Germany
3 -
ESO, Santiago
Received 22 November 2007 / Accepted 7 January 2008
Abstract
Context. On October 24, 2007 the periodic comet 17P/Holmes underwent an astonishing outburst that increased its apparent total brightness from magnitude ![]() up to
up to ![]() in roughly two days. In this contribution we report on Wendelstein 0.8 m telescope (WST) photometric observations of the early evolution stages of the outburst.
in roughly two days. In this contribution we report on Wendelstein 0.8 m telescope (WST) photometric observations of the early evolution stages of the outburst.
Aims. We studied the evolution of the structure morphology and its kinematic and provide an estimate of the ejected dust mass.
Methods. We analyzed 126 images of the comet in the BVRI photometric bands spread between October 26, 2007 and November 20, 2007. The bright comet core appeared to be separated from a quickly expanding dust cloud in all the data, and the bulk of the cloud was contained in the field of view of our instrument during the days soon after the outburst, allowing precise estimates both of the separation velocities of the two luminous baricenters and of the expansion velocity of the dust cloud. The ejected dust mass was derived on the basis of differential photometry on background stars occulted by the moving cloud.
Results. The two cores were moving apart from each other at a relative, projected constant velocity of
![]() arcsec/day (
arcsec/day (
![]() km s-1). In the inner regions of the dust cloud we observed a linear increase in size at a mean constant velocity of
km s-1). In the inner regions of the dust cloud we observed a linear increase in size at a mean constant velocity of
![]() arcsec/day (
arcsec/day (
![]() km s-1). Evidence of a radial velocity gradient in the expanding cloud was also found. Our estimate for the expanding coma's mass was approximately
10-2-1 comet's mass, implying a significant disintegration event.
km s-1). Evidence of a radial velocity gradient in the expanding cloud was also found. Our estimate for the expanding coma's mass was approximately
10-2-1 comet's mass, implying a significant disintegration event.
Conclusions. We interpret our observations in the context of an explosive scenario that was more probably triggered by some internal instability processes rather than by an impact with an asteroidal body. Due to the peculiar characteristics of this event, further observations and investigations are necessary to bring the nature of the physical processes that determined it to light.
Key words: comets: individual: 17P/Holmes - solar system: general
The periodic comet 17P/Holmes was discovered on
November 6, 1892 by
E. Holmes in London, during an outstanding brightness increase,
followed by another similar event on January 16, 1893.
When discovered by Mr. Holmes, the comet
was around 5 months past perihelion
(T = June 13).
On October 24, 2007, around 6 months after the last perihelion passage (T = May 4, 2007), the comet
underwent a phenomenon similar to
those observed more than one hundred years
ago. The heliocentric distance of
the object at the time of the two major
events was around
![]() = 2.39 AU in 1892 and
= 2.39 AU in 1892 and
![]() = 2.44 AU in 2007,
and the orbital inclination remained
substantially unaltered during this
period (
= 2.44 AU in 2007,
and the orbital inclination remained
substantially unaltered during this
period (
![]() ).
This Letter is structured in the following way. In
Sect. 2, we present the observations
and the data reduction method. In Sect. 3,
we discuss the morphological evolution of the expanding
structure. In Sect. 4, we calculate the separation
velocities between the comet and the center of the dust cloud,
as well as the expansion velocity of the cloud.
In Sect. 5, we estimate the ejected dust mass.
Finally in Sect. 6, we sum up our results.
).
This Letter is structured in the following way. In
Sect. 2, we present the observations
and the data reduction method. In Sect. 3,
we discuss the morphological evolution of the expanding
structure. In Sect. 4, we calculate the separation
velocities between the comet and the center of the dust cloud,
as well as the expansion velocity of the cloud.
In Sect. 5, we estimate the ejected dust mass.
Finally in Sect. 6, we sum up our results.
Table 1: Number of images of 17P/Holmes taken during the different observing nights in the BVRI filters.
During night 28, the photometric conditions were both good and stable
over the whole night, and we thus acquired some images of the
Landolt standard field PG0918
in all our filters.
We obtained 2 images in the B, V, R bands and 4 images in the I band.
These data were
reduced in exactly the same manner as the scientific
observations (see also Sect. 5). The magnitudes
of the standard stars were reported to 1 airmass
and 1 arcsec and finally calibrated to the Landolt
photometric system, thanks to the Stetson Photometric
Standard Fields![]() data of PG0918. We found a total of 26 common stars
between our catalog and the one provided by Stetson,
and obtained the following calibration equation for the R band
against the V-R color:
data of PG0918. We found a total of 26 common stars
between our catalog and the one provided by Stetson,
and obtained the following calibration equation for the R band
against the V-R color:
To show the evolution of the morphological structure of the object, we selected one representative image in the R band for each night in our dataset. These images were scaled to the same exposure time, airmass, and intensity range, in order to properly sample the surface brightness of the coma in the whole dataset. The lowest intensity level was chosen close to the lowest counts we got on the last image of our dataset, while the highest was chosen close to the coma's peak intensity of the image taken on October 28, 2007. We did not process the image acquired on October 26, 2007 in this way, because it was too noisy. The images were then normalized to the lowest intensity level. Finally, we displayed the images codified on a logarithmic color scale, as shown in Fig. 1. We overplotted the isophote intensities levels to each panel to highlight the structure of the inner part of the cloud.
The most interesting feature in Fig. 1 is the presence of two bright cores (the comet core being towards the upper left side). These two cores were increasingly separating during the observing period and appeared elongated towards each other, indicating an exchange of mass. Moreover, the expansion of the global structure is evident from the sequence of images. We also displayed the intensity value of the closest isophote to the cloud's center and of the adjacent one in the outwards direction. The exact values given by the isophotes depend on the adopted number of isophotes in each panel, which also determines the intensity step between them. We set the number of isophotes to approximately provide the same sampling of the inner regions of the cloud. Thus, the quoted numbers must be considered as indicative of the relative surface brightnesses of the cloud on the different nights. The intensity of the innermost isophote of night 2007 Oct. 28 was around 2 orders of magnitude larger with respect to the correpondent isophote's intensity of night 2007 Nov. 20, and the intensity step between the isophotes was also 1order of magnitude larger in the first case with respect to the second. We emphasize that there is no way to significantly change these conclusions by adopting different isophotal mapping criteria, as we accurately verified. Actually, both these results are the consequence of the rapid expansion of the dust cloud, which determines a steady decrease in its surface brightness, and a more homogeneous light distribution in the more evolved and less concentrated phases.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{9130fig1.eps} %
\end{figure}](/articles/aa/full/2008/09/aa9130-07/Timg18.gif) |
Figure 1:
Snapshot of R band images acquired during each night of our
observing run, showing the evolution of
comet 17P/Holmes' morphological structure.
Each image has been scaled to the
same exposure time, airmass, and intensity range
and
displayed on a logarithmic color scale, codified by the bottom
color bar. The top 6 images are zoomed inside the inner
regions of the object and have a field of view of
|
| Open with DEXTER | |
In this section we derive the separation velocity of the two bright
baricenters and the dust cloud's expansion velocity. The
comet's center appeared in all our images as a point-like source, so
the peak's position was derived with a Gaussian fitting algorithm,
as for stellar objects. The light distribution of the dust cloud was
extended over a much larger area and was not Gaussian overall, but we found
that the inner part could be always represented by a Gaussian.
We thus fit a bidimensional
Gaussian using the light distributions along the x and y axis. An initial
guess for the centroid was provided with a maximum finding algorithm run
in a small region around the peak (![]() 30 arcsec). Then a least-square
fit provided the refined position for the centroid
and the
30 arcsec). Then a least-square
fit provided the refined position for the centroid
and the ![]() and
and ![]() of the
fitting Gaussians. In Fig. 2 (left panel)
we plotted the two bright cores' projected distances against the Julian date
(JD) of the observations. The correction for the Earth's
variable distance has been taken into account, although it is negligible.
We obtained a uniform increasing separation with a mean velocity of
of the
fitting Gaussians. In Fig. 2 (left panel)
we plotted the two bright cores' projected distances against the Julian date
(JD) of the observations. The correction for the Earth's
variable distance has been taken into account, although it is negligible.
We obtained a uniform increasing separation with a mean velocity of
![]() arcsec/day (
arcsec/day (
![]() km s-1).
The uncertainties are dominated by the errors in the diffuse
cloud centroids. In the right panel of Fig. 2,
we report the
km s-1).
The uncertainties are dominated by the errors in the diffuse
cloud centroids. In the right panel of Fig. 2,
we report the ![]() of the diffuse clouds (actually the mean of the
of the diffuse clouds (actually the mean of the
![]() and
and ![]() )
as a function of the JD.
We did not include the last two nights in this figure,
because the cloud was too expanded.
Two images acquired on night 2007 Nov. 2 in the R band were also excluded because
of the large offset of the cloud's centroid with respect to the
image's center. The errorbars in this figure were calculated as the
difference of the
)
as a function of the JD.
We did not include the last two nights in this figure,
because the cloud was too expanded.
Two images acquired on night 2007 Nov. 2 in the R band were also excluded because
of the large offset of the cloud's centroid with respect to the
image's center. The errorbars in this figure were calculated as the
difference of the ![]() along the x and y axes.
The different colors in the figure codify observations
obtained in the different photometric bands. Also in this case
we observed a linear increase in size with a mean velocity of
along the x and y axes.
The different colors in the figure codify observations
obtained in the different photometric bands. Also in this case
we observed a linear increase in size with a mean velocity of
![]() arcsec/day (
arcsec/day (
![]() km s-1). Repeating
the calculation separately for the different
bands gave the results in Table 2.
These mean values and their errors
were obtained using a weighted least-square algorithm.
The different bands allow exploration of the different layers of the expanding
cloud, more external in the B and deeper in the redder
bands. Thus, this result can be interpreted as evidence of a
radial velocity gradient in the expanding cloud. For each couple of
adiacent bands, we considered the ratio between the
difference of the expansion velocities reported in Table 2
and the difference in the correspondent
km s-1). Repeating
the calculation separately for the different
bands gave the results in Table 2.
These mean values and their errors
were obtained using a weighted least-square algorithm.
The different bands allow exploration of the different layers of the expanding
cloud, more external in the B and deeper in the redder
bands. Thus, this result can be interpreted as evidence of a
radial velocity gradient in the expanding cloud. For each couple of
adiacent bands, we considered the ratio between the
difference of the expansion velocities reported in Table 2
and the difference in the correspondent ![]() values given by the
least-square fitting
models for the night 2007 Nov. 2, for which we obtained the largest separation among
the expanding shells. Taking the mean of these values, we obtained an estimate
of the radial velocity gradient during that night equal to
values given by the
least-square fitting
models for the night 2007 Nov. 2, for which we obtained the largest separation among
the expanding shells. Taking the mean of these values, we obtained an estimate
of the radial velocity gradient during that night equal to
![]() ,
which means an increase of
around 0.3 cm/s every km going from the center to the surface of
the coma.
,
which means an increase of
around 0.3 cm/s every km going from the center to the surface of
the coma.
| |
Figure 2:
Left: angular projected distance between the
centroid of the two bright baricenters, for all the images in our
dataset, against the |
| Open with DEXTER | |
The formation of spherical expanding envelopes around the cometary
nucleus of 17P/Holmes was observed for both the events
in November 1892 and January 1893.
Bobrovnikoff (1943) compared the observations
by different authors between 16 and 22 January 1893,
deriving a uniform expansion velocity of
![]() km s-1,
similar to what we found here.
The sudden brightness variations, the formation of
spherical dust envelopes with similar kinematic properties, the
correspondence in the orbital phase at the instant of the major outbursts
noted in Sect. 1, point towards a common mechanism
at the base of the observed phenomena. Moreover, the distance from the
ecliptic plane was around 0.8 AU in both cases.
Given that, although it cannot be completely excluded,
it seems unlikely that
the above-mentioned explosive mechanism was triggered by an asteroidal impact,
making it more probably an internal instability process.
km s-1,
similar to what we found here.
The sudden brightness variations, the formation of
spherical dust envelopes with similar kinematic properties, the
correspondence in the orbital phase at the instant of the major outbursts
noted in Sect. 1, point towards a common mechanism
at the base of the observed phenomena. Moreover, the distance from the
ecliptic plane was around 0.8 AU in both cases.
Given that, although it cannot be completely excluded,
it seems unlikely that
the above-mentioned explosive mechanism was triggered by an asteroidal impact,
making it more probably an internal instability process.
Table 2: The derived expansion velocities in arcsec/day along with their uncertainties for the expanding dust cloud in the different bands. In parenthesis we report the corresponding values in km s-1.
In the following we provide an estimate of the ejected dust mass during the
outburst, through the extinction produced by the dust cloud on the
surrounding background stars. We selected two well-exposed,
seeing images taken on October 28, 2007 in the R filter.
These images had the largest time
separation (2 h) in the whole dataset, among equal filter images
acquired during the same observing night.
Thus, they provided the largest apparent
motion of the cloud on the sky plane. At the same time, this
temporal difference is small enough to avoid the expansion of the
cloud changing the extinction map significantly,
thereby allowing a homogeneous comparison
of the two images. Finally, day 28 was close
enough to the outburst to allow the dust cloud to fit well inside our field of
view.
We performed PSF fitting photometry with
DAOPHOT/ALLSTAR (Stetson 1987) and rejected
all the stars with ![]() and
any absolute sharp values bigger than 1.
These parameters and selection criteria allowed those objects to be excluded
for which
a reliable fit of the stellar model could not be performed, because close
to saturation, or close to bad pixels, and to reject non-stellar sources
such as cosmic rays, background galaxies, or
spikes of saturated stars.
The sky background in these images was estimated locally around each star
in an annular region comprised 1.5 and 3.5 arcsec from the stars'
centroids. This region was selected after performing different tests looking
for the best subtraction of the analyzed stars. The modal value of the pixel
counts inside the selected annular region was considered as the estimate of
the sky background. The photometry was extracted in a circular
region centered on the stars' centroids with radius equal to 1.3 arcsec, which
corresponded to the seeing value in both images. The derived magnitudes
were then reported to 1 airmass and 1 s of exposure time for both the
images. We then considered all the common
objects with a radial distance from the center of the comet
>25 arcsec and with radial distance from the center
of the cloud <3 arcmin in both the images.
The inner limit was needed to avoid the
photometry of the stars being biased by the luminous core of the comet. The
outer limit was chosen to avoid detector border effects,
accounting for the position of the center of the cloud in both the images.
At the end, we obtained a catalog of
20 stars spread inside the analyzed region of the cloud;
see Fig. 3.
and
any absolute sharp values bigger than 1.
These parameters and selection criteria allowed those objects to be excluded
for which
a reliable fit of the stellar model could not be performed, because close
to saturation, or close to bad pixels, and to reject non-stellar sources
such as cosmic rays, background galaxies, or
spikes of saturated stars.
The sky background in these images was estimated locally around each star
in an annular region comprised 1.5 and 3.5 arcsec from the stars'
centroids. This region was selected after performing different tests looking
for the best subtraction of the analyzed stars. The modal value of the pixel
counts inside the selected annular region was considered as the estimate of
the sky background. The photometry was extracted in a circular
region centered on the stars' centroids with radius equal to 1.3 arcsec, which
corresponded to the seeing value in both images. The derived magnitudes
were then reported to 1 airmass and 1 s of exposure time for both the
images. We then considered all the common
objects with a radial distance from the center of the comet
>25 arcsec and with radial distance from the center
of the cloud <3 arcmin in both the images.
The inner limit was needed to avoid the
photometry of the stars being biased by the luminous core of the comet. The
outer limit was chosen to avoid detector border effects,
accounting for the position of the center of the cloud in both the images.
At the end, we obtained a catalog of
20 stars spread inside the analyzed region of the cloud;
see Fig. 3.
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{9130fg3a.eps}\hspace*{2mm}...
...} \includegraphics[width=6.5cm,clip]{9130fg3c.eps}\hspace*{1cm}}
%
\end{figure}](/articles/aa/full/2008/09/aa9130-07/Timg31.gif) |
Figure 3:
Top: spatial distribution of the 20 background stars
used in Sect. 5 to probe the differential
extinction produced by the coma, for the two images acquired on
October 28, 2007. The image on the left was taken 2 h before
the right one.
The selected stars are
indicated by white circles. The associated numeration
corresponds to the one in the lower panel,
allowing each star to be related to the correspondent
measured differential extinction.
Bright sources were saturated
(black regions), as well as was the center of the cometary nucleus.
The black lines indicate the distances, referred to in
Sect. 5 as r1 and r2, of
one star with respect to the
estimated coma's centers.
Bottom: the correlation between the differential extinctions in
the R band ( |
| Open with DEXTER | |
To demonstrate the radial dependence of the
extinction from the center of the cloud,
we assumed a uniform and homogeneous,
spherically symmetric mass distribution.
Thus, because r is the position
of one star with respect to the cloud's center,
we can express the optical depth of
the cloud at the distance r as
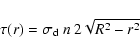 |
(1) |
![\begin{displaymath}\Delta A = m_1~-~m_2~=~-2.5~\log\left(\frac{I_1}{I_2}\right)=...
...1^2}}}{{\rm e}^{-\sigma_{\rm d}~n~2~\sqrt{R^2-r_2^2}}}\right],
\end{displaymath}](/articles/aa/full/2008/09/aa9130-07/img36.gif) |
(2) |
| |
= | ||
| = | (3) |
| (4) |
The most important assumptions of the model
are the dust cloud's spherical geometry and the homogeneous and uniform
mass distribution. The geometry of the
cloud was well-constrained by the observations
and the analysis presented in the previous
sections. As for the second hypothesis, it
allowed expression of the optical depth in a straightforward and
convenient way, as shown in Eq. (1), and
ultimately implies the linear dependence
of the observed differential extinctions on the geometrical
factor x. A strong deviation from that assumption
would imply a strong deviation from the linear model prediction,
which is not observed (Fig. 3).
The scatter in that relation
(![]() 0.06 mag) is greater than
the scatter derived from the calibration of
the Landolt standard field discussed in Sect. 2 (
0.06 mag) is greater than
the scatter derived from the calibration of
the Landolt standard field discussed in Sect. 2 (![]() 0.02 mag).
Otherwise, in the science
images, the surface brightness of the coma determined a background around 10 times larger than in the Landolt images, which explains the factor of 3 increase in the scatter.
The radial velocity gradient of the expanding material
discussed in Sect. 4 points away from the uniform mass
distribution hypothesis. Otherwise, as
shown in the right panel of Fig. 2, during
night 28 the expanding shells were certainly more concentrated
than in the later evolved phases
since closer that night to the outburst.
In conclusion, it is reasonable to believe that, on the chosen night, the
material was not far from being uniformly distributed and homogeneously mixed,
and we considered this hypothesis as a good
approximation of the structural properties of the observed coma.
Therefore, the dominant factor that explains the observations is related to
the cloud's geometrical structure, in the sense that the observed differential
extinctions were determined by the variable quantity of mass over the cloud's
different line of sights probed by the background stars (directly implied by its
spherical structure). This is demonstrated overall by the observed linear dependence
of the differential extinction on the geometrical factor x and by the
positive value of the
0.02 mag).
Otherwise, in the science
images, the surface brightness of the coma determined a background around 10 times larger than in the Landolt images, which explains the factor of 3 increase in the scatter.
The radial velocity gradient of the expanding material
discussed in Sect. 4 points away from the uniform mass
distribution hypothesis. Otherwise, as
shown in the right panel of Fig. 2, during
night 28 the expanding shells were certainly more concentrated
than in the later evolved phases
since closer that night to the outburst.
In conclusion, it is reasonable to believe that, on the chosen night, the
material was not far from being uniformly distributed and homogeneously mixed,
and we considered this hypothesis as a good
approximation of the structural properties of the observed coma.
Therefore, the dominant factor that explains the observations is related to
the cloud's geometrical structure, in the sense that the observed differential
extinctions were determined by the variable quantity of mass over the cloud's
different line of sights probed by the background stars (directly implied by its
spherical structure). This is demonstrated overall by the observed linear dependence
of the differential extinction on the geometrical factor x and by the
positive value of the ![]() coefficient, also predicted by the model.
coefficient, also predicted by the model.
To derive the coma's mass, we considered
spherical dust grains with a mean density ![]() (
(
![]() )
and a ``typical'' dimension
)
and a ``typical'' dimension ![]() (and thus mass
(and thus mass
![]() ).
Thanks to the definition of the
).
Thanks to the definition of the ![]() parameter in Eq. (3),
the mass of the cloud M can be expressed through the
formula
parameter in Eq. (3),
the mass of the cloud M can be expressed through the
formula
| M | = | 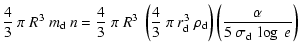 |
|
| = | (5) |
There are different factors that could affect our results.
Dust grains in cometary ejecta typically span a range of
different dimensions and optical properties (see e.g. Lisse et al. 2007; Tozzi et al. 2007). Both the assumption on the uniform and homogeneous mass
distribution and the lack of specific observations able to constrain the dust
population characteristics for this particular object together justify our simplified
approach to summarizing the cloud's grain content, assuming a ``typical'' grain
dimension and the corresponding geometrical cross-section.
Another possible drawback in our coma's mass estimate
regards the pre-outburst activity of the comet.
During the most recent observations
of the comet obtained before the outburst (Snodgrass et al. 2006), the object
appeared to be inactive, although the heliocentric distance at that time
was ![]() 4.66 AU, whereas at the outburst it was
4.66 AU, whereas at the outburst it was ![]() 2.44 AU.
Moreover, it seems probable that the explosive event described in this
work largely overcame the common activity of the comet. Finally, the stars used
to probe the differential
extinction produced by the coma (Fig. 3), were
well-distributed inside the coma, avoiding the region close
to the comet's nucleus, and thus more closely reflecting the contribution to the
differential extinction of the material coming directly from the explosion.
2.44 AU.
Moreover, it seems probable that the explosive event described in this
work largely overcame the common activity of the comet. Finally, the stars used
to probe the differential
extinction produced by the coma (Fig. 3), were
well-distributed inside the coma, avoiding the region close
to the comet's nucleus, and thus more closely reflecting the contribution to the
differential extinction of the material coming directly from the explosion.
Despite these approximations, the result presented in Eq. (5), has the advantage to enlight the dependence among the total mass of the cloud, the cloud's geometrical, composition properties and the observed differential extinctions, and of providing an estimate for the expanding coma's mass that points towards a consistent disintegration phenomenon, as suggested by the large outburst event.
In this Letter we analyzed the early phases of the 2007 October 24 outburst
comet 17P/Holmes. We acquired BVRIphotometric images at the Wendelstein 0.8 m telescope
between October 26, 2007 and November 20, 2007. We observed a spherically
symmetric dust cloud moving
away from the comet nucleus with a mean projected constant velocity of
![]() arcsec/day (
arcsec/day (
![]() km s-1), while the
dust cloud was expanding with a mean constant velocity
of
km s-1), while the
dust cloud was expanding with a mean constant velocity
of
![]() arcsec/day (
arcsec/day (
![]() km s-1).
These results agree with those
obtained during past outbursts of this comet.
Evidence of a gradient in the expansion velocity of the dust cloud was also
found with the velocity increasing towards the external regions. Finally,
performing differential photometry on background stars occulted
by the moving cloud, and assuming a uniform and homogeneous spherical
mass distribution, we derived a value of
1012-1014 kg for the coma's mass, around
10-2-1 of the comet's mass.
We interpreted our observations in the context of an explosive event,
probably caused by some internal instability processes rather than by an
asteroidal body's impact.
Various mechanisms have been proposed in the past
to explain the comets' splitting, involving tidal, thermal,
and rotational forces (Sekanina 1997). These processes could
have played an important role in the event discussed here,
although some specific characteristics allow us to consider it as more peculiar.
For example, the separation velocities of the splitting components
are generally a few
km s-1).
These results agree with those
obtained during past outbursts of this comet.
Evidence of a gradient in the expansion velocity of the dust cloud was also
found with the velocity increasing towards the external regions. Finally,
performing differential photometry on background stars occulted
by the moving cloud, and assuming a uniform and homogeneous spherical
mass distribution, we derived a value of
1012-1014 kg for the coma's mass, around
10-2-1 of the comet's mass.
We interpreted our observations in the context of an explosive event,
probably caused by some internal instability processes rather than by an
asteroidal body's impact.
Various mechanisms have been proposed in the past
to explain the comets' splitting, involving tidal, thermal,
and rotational forces (Sekanina 1997). These processes could
have played an important role in the event discussed here,
although some specific characteristics allow us to consider it as more peculiar.
For example, the separation velocities of the splitting components
are generally a few ![]() ,
while in this case we found a projected
relative velocity around 2 orders of magnitude greater. The outburst itself
represents the largest apparent brightness increase ever observed for a comet.
In conclusion, we underline the importance of considering
other observational results in order to accurately characterize
this event and to provide a more insightful
view of its enigmatic and still not well-understood nature.
,
while in this case we found a projected
relative velocity around 2 orders of magnitude greater. The outburst itself
represents the largest apparent brightness increase ever observed for a comet.
In conclusion, we underline the importance of considering
other observational results in order to accurately characterize
this event and to provide a more insightful
view of its enigmatic and still not well-understood nature.
Acknowledgements
We warmly thank the anonymous Referee for the helpful comments and suggestions allowing significant improvement to this Letter.