A&A 479, 741-750 (2008)
DOI: 10.1051/0004-6361:20078687
Structural parameters of 11 faint Galactic globular clusters derived with 2MASS
C. Bonatto - E. Bica
Universidade Federal do Rio Grande do Sul, Departamento de Astronomia
CP 15051, RS, Porto Alegre 91501-970, Brazil
Received 17 September 2007 / Accepted 7 November 2007
Abstract
Context. Structural parameters and the total 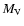 magnitude are important properties for the characterisation of individual globular clusters. With the growth in statistics, especially of the intrinsically faint objects, the collective properties of the Galactic globular cluster system will be better defined, leading to a deeper understanding of the Galaxy formation processes.
magnitude are important properties for the characterisation of individual globular clusters. With the growth in statistics, especially of the intrinsically faint objects, the collective properties of the Galactic globular cluster system will be better defined, leading to a deeper understanding of the Galaxy formation processes.
Aims. We determine the structural parameters of 11 faint Galactic globular clusters that, in most cases, had not been previously studied in this context: IC 1257, Lyngå 7, Terzan 4, Terzan 10, BH 176, ESO 452-SC11, ESO 280-SC08, 2MASS-GC01, 2MASS-GC02, GLIMPSE-C01, and AL 3. They are projected not far from the central region of the Galaxy. Field-star contamination is significant in the colour-magnitude diagrams. Half of the sample has an absorption
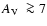 ,
in some cases reaching
,
in some cases reaching
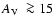 .
.
Methods. Stellar radial number-density and surface-brightness profiles were built with 2MASS photometry that, for the present clusters, corresponds to giant-branch stars. Field-star decontamination is essential for clusters in dense fields, so an algorithm that we had previously developed for open clusters in rich fields was employed to better define cluster sequences. With decontaminated photometry we also computed the total 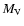 of four such globular clusters, using M 4 as a template. King-like functions were fitted to the radial profiles, from which the core, half-light, half-star count, and tidal radii were derived, together with the concentration parameter. The derived parameters were then compared to equivalent ones available in the literature for other Galactic globular clusters.
of four such globular clusters, using M 4 as a template. King-like functions were fitted to the radial profiles, from which the core, half-light, half-star count, and tidal radii were derived, together with the concentration parameter. The derived parameters were then compared to equivalent ones available in the literature for other Galactic globular clusters.
Results. Compared to massive globular clusters, those in the present sample have smaller tidal and larger core radii for a given Galactocentric distance, which is consistent with rather loose structures. Globular cluster radii derived from number-density and surface-brightness profiles have similar values. The present magnitude estimates are
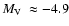 (ESO 280-SC08),
(ESO 280-SC08),
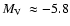 (2MASS-GC01), and
(2MASS-GC01), and
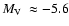 (2MASS-GC02). We also estimate
(2MASS-GC02). We also estimate
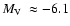 for GLIMPSE-C01, which is somewhat less luminous than previously given. The density profiles of Tz 4 and 2MASS-GC01 show evidence of post-core collapse clusters.
for GLIMPSE-C01, which is somewhat less luminous than previously given. The density profiles of Tz 4 and 2MASS-GC01 show evidence of post-core collapse clusters.
Conclusions. The structural parameters and luminosity of most of the faint globular clusters dealt with in this paper are consistent with those of Palomar-like (low mass and loose structure) globular clusters. This work helps to improve the coverage of the globular cluster parameter space.
Key words: Galaxy: globular clusters: general
1 Introduction
Astrophysical parameters of globular clusters (GCs) are of strong interest because they can be
used to characterise GCs individually, eventually leading to a deeper understanding of their
properties as a class in the Galaxy. From a broad perspective, such parameters may provide important
clues to the investigation of the formation and evolution processes of the GC system of the Galaxy
and elsewhere, e.g. Harris (1996, and the 2003 update![[*]](/icons/foot_motif.gif) - hereafter H03), Mackey & van den Bergh (2005), and Bica et al. (2006b). From the observational perspective, the depth of
this kind of analysis directly depends on the statistical completeness of the sample, especially in
the faint-GC tail, and on the reliability of the derived parameters.
- hereafter H03), Mackey & van den Bergh (2005), and Bica et al. (2006b). From the observational perspective, the depth of
this kind of analysis directly depends on the statistical completeness of the sample, especially in
the faint-GC tail, and on the reliability of the derived parameters.
In general terms, the standard picture of the GC structure assumes an isothermal central region
and a tidally truncated outer region, usually described by a roughly spherical symmetry (e.g.
Binney & Merrifield 1998). In this context, the structure of most GCs is approximated well by a rather
dense core and a sparse halo, but with a broad range in concentration. The most commonly used
structural parameters are the core (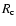 ), half-light (
), half-light (
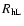 ), and tidal radii (
), and tidal radii (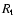 ), along with the
concentration parameter
), along with the
concentration parameter
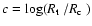 ,
related to the isothermal sphere, single-mass model
introduced by King (1962) to fit the surface brightness profiles (SBPs) of Galactic GCs.
,
related to the isothermal sphere, single-mass model
introduced by King (1962) to fit the surface brightness profiles (SBPs) of Galactic GCs.
As they age, GCs are continually harassed by external processes, such as tidal stress and dynamical
friction (from the Galactic bulge and disk and from giant molecular clouds), and by internal ones, such as
mass loss by stellar evolution, mass segregation, and low-mass star evaporation (e.g. Khalisi et al. 2007;
Lamers et al. 2005; Gnedin & Ostriker 1997). Over a Hubble time, these effects tend to lower the cluster mass,
which may accelerate the core-collapse phase for some clusters (Djorgovski & Meylan 1994, and references therein).
As a dramatic end result, low-mass clusters may be completely disintegrated over the course of a few disruption
time scales (
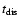 ). Observational evidence for the dependence of
). Observational evidence for the dependence of
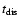 on cluster mass are given by,
e.g. Janes & Adler (1982), Wielen (1991), and Lamers et al. (2005). The last group of authors find
on cluster mass are given by,
e.g. Janes & Adler (1982), Wielen (1991), and Lamers et al. (2005). The last group of authors find
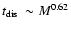 ,
which agrees with the N-body estimate of Baumgardt & Makino (2003) for the disruption time scale due to the Galactic
tidal field. Theoretically, the dependence of
,
which agrees with the N-body estimate of Baumgardt & Makino (2003) for the disruption time scale due to the Galactic
tidal field. Theoretically, the dependence of
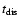 on cluster mass was investigated by, e.g.,
Spitzer (1958) and Gnedin & Ostriker (1997). Most of the above processes are related to the large-scale mass
distribution of the Galaxy. Thus, their strength should depend on Galactocentric distance, and they are
expected to be more effective for the less-massive clusters (e.g. Djorgovski & Meylan 1994; van den Bergh 1991;
Chernoff & Djorgovski 1989). Consequently, the distribution of structural parameters among the Galactic GC population,
as well as their dependence on Galactocentric distance, may also be related to the physical conditions
prevailing at the early formation phase (e.g. van den Bergh 1991).
on cluster mass was investigated by, e.g.,
Spitzer (1958) and Gnedin & Ostriker (1997). Most of the above processes are related to the large-scale mass
distribution of the Galaxy. Thus, their strength should depend on Galactocentric distance, and they are
expected to be more effective for the less-massive clusters (e.g. Djorgovski & Meylan 1994; van den Bergh 1991;
Chernoff & Djorgovski 1989). Consequently, the distribution of structural parameters among the Galactic GC population,
as well as their dependence on Galactocentric distance, may also be related to the physical conditions
prevailing at the early formation phase (e.g. van den Bergh 1991).
Considering all these arguments, it is natural to assume that the long-term (more than 10 Gyr, in most
cases) dynamical evolution of the collective GC population (as well as the individual GCs) may be reflected
in the statistical properties of their structural parameters. It is in this context that intrinsically faint
GCs play an important rôle, since they are more sensitive to the processes discussed above and have shorter
dynamical-evolution time scales than the massive ones.
In most cases, the SBPs of faint GCs may contain significant noise owing to the intrinsically-low surface
brightness outside the central region, and because of the random presence of relatively bright stars,
either from the field or cluster members. The same applies to the outer parts, where background starlight
is usually a major contributor, even in luminous GCs. Structural parameters measured in such SBPs would
certainly be affected to varying degrees. In such cases, the alternative is to work with stellar radial
density profiles (RDPs), in which only the projected number-density of stars is taken into account,
irrespective of the individual stellar brightness. RDPs are particularly appropriate for the outer parts,
provided that a statistically significant, and reasonably uniform, comparison field is available to tackle
the background contamination. Such wide fields are provided by 2MASS (e.g. Bonatto & Bica 2005; Bonatto & Bica 2007a).
However, the 2MASS photometric depth limit implies that the giant branch can be accessed in GCs more
distant than a few kpc from the Sun (Bonatto & Bica 2007b). Thus, it is necessary to take depth-limited effects
into account when considering such structural parameters in the context of absolute comparisons using parameters
obtained with deeper photometry. This issue was studied in Bonatto & Bica (2007b) by means of model GCs built
assuming different conditions, which allowed us to investigate relations among radii measured in RDPs and
SBPs, together with their dependence on photometric depth.
Trager et al. (1995) presented a catalogue of SBPs for 125 Galactic GCs with structural parameters derived
mostly with the King (1966) profile. Based mostly on the earlier work, H03 provide structural parameters
for 141 (of the total catalogued 150 at the time) GCs. Recently, Cohen et al. (2007) have used surface brightness
profiles in J, H, and 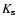 with 2MASS
with 2MASS![[*]](/icons/foot_motif.gif) photometry to derive core radii for 104 GCs, by means of fits of a power-law with a core function.
The 9 remaining GCs in H03 are faint and were not included in Cohen et al. (2007).
photometry to derive core radii for 104 GCs, by means of fits of a power-law with a core function.
The 9 remaining GCs in H03 are faint and were not included in Cohen et al. (2007).
The compilation of H03 contains 150 GCs but, as a consequence of recent deeper surveys, the number of known
GCs in the Galaxy has been increasing. For instance, Kobulnicky et al. (2005) discovered the far-IR GC GLIMPSE-C01.
Carraro (2005) identified Whiting 1 as a young halo GC. Two stellar systems detected with the Sloan
Digital Sky Survey (SDSS) in the outer halo, Willman 1 (SDSS J1049+5103) and SDSS J1257+3419, might
be GCs or dwarf galaxies (Willman et al. 2005; Sakamoto & Hasegawa 2006). Ortolani et al. (2006) identified AL 3 as a
new GC in the bulge with a blue horizontal branch. Next, Froebrich et al. (2007) found evidence that FSR 1735 is an
inner Galaxy GC, and Belokurov et al. (2007) found the faint halo GC SEGUE 1 using SDSS. More recently,
Koposov et al. (2007) have reported the discovery of two very-low luminosity halo GCs (Koposov 1 and 2) detected with
SDSS. The last three GCs are beyond the scope of the present paper because they are too distant and/or
exceedingly faint. Another object, FSR 0584, has recently been identified as a nearby Palomar-like halo GC or an
old open cluster (OC) by Bica et al. (2007). Finally, Bonatto et al. (2007) have identified FSR 1767 as a bulge-projected
(
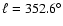 ,
,
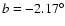 )
Palomar-like GC (
)
Palomar-like GC (
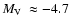 )
that appears to be the nearest one
(
)
that appears to be the nearest one
(
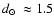 kpc) so far discovered. Fundamental parameters and updates to the GCs in H03 were provided
by Bica et al. (2006b), also available as a Vizier on-line
catalogue
kpc) so far discovered. Fundamental parameters and updates to the GCs in H03 were provided
by Bica et al. (2006b), also available as a Vizier on-line
catalogue![[*]](/icons/foot_motif.gif) .
.
The main goal of the present work is to derive structural parameters, using RDPs and SBPs built with 2MASS
star-counts and photometry, for the remaining 9 faint GCs in H03, which lack this kind of data. The targets
are IC 1257, Lyngå 7, Terzan 4, Terzan 10, BH 176, ESO 452-SC11, ESO 280-SC08, 2MASS-GC01, and
2MASS-GC02. We also include in the analyses the more recently discovered GCs GLIMPSE-C01 (Kobulnicky et al. 2005)
and AL 3 (Ortolani et al. 2006).
This paper is structured as follows. In Sect. 2 we present previous results on the
present GCs that are relevant for this work. In Sect. 3 we describe the 2MASS photometry,
including extraction and errors, build the near-infrared colour-magnitude diagrams (CMDs) for the
present GCs, briefly discuss the tools and algorithms employed to decontaminate the CMDs of field
stars, and estimate the absolute V magnitudes of ESO 280-SC06, 2MASS-GC01, 2MASS-GC02, and
GLIMPSE-C01. In Sect. 4 we build RDPs and SBPs and derive the core, half-light, half-star
count, and tidal radii, together with the concentration parameter for the present GC sample. In
Sect. 5 we discuss the potential effects of depth-limited photometry in the derivation of
structural parameters from radial profiles and compare such parameters with those of other globular
clusters in the Galaxy. Finally, concluding remarks are given in Sect. 6.
2 The faint GC sample
In the following we recall fundamental literature results for the present analyses.
This object was first classified as an OC (Lyngå 1987,
and references therein), but Harris et al. (1997) identified it as a GC using B, V, and I photometry.
They also determined the cluster reddening
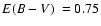 ,
distance from the Sun
,
distance from the Sun
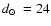 kpc,
and metallicity
kpc,
and metallicity
![$\mbox{$\rm [Fe/H]$ }=-1.7$](/articles/aa/full/2008/09/aa8687-07/img33.gif) .
Its absolute magnitude is
.
Its absolute magnitude is
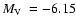 (H03).
(H03).
Lyngå (1964) discovered and classified Lyngå 7 as a Trumpler type
II 2 p OC, which was later reported in Alter et al. (1970). Ortolani et al. (1993) identified it as a GC with B, V, and I photometry and determined
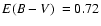 ,
,
![$\mbox{$\rm [Fe/H]$ }=-0.40$](/articles/aa/full/2008/09/aa8687-07/img36.gif) and
and
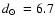 kpc. Tavarez & Friel (1995)
used moderate resolution spectroscopy to obtain a radial velocity
kpc. Tavarez & Friel (1995)
used moderate resolution spectroscopy to obtain a radial velocity
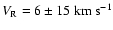 ,
,
![$\mbox{$\rm [Fe/H]$ }=-0.62$](/articles/aa/full/2008/09/aa8687-07/img39.gif) ,
,
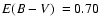 ,
and
,
and
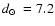 kpc. Based on 2MASS photometry, Sarajedini (2004) derived
kpc. Based on 2MASS photometry, Sarajedini (2004) derived
![$\mbox{$\rm [Fe/H]$ }=-0.76$](/articles/aa/full/2008/09/aa8687-07/img42.gif) and
and
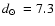 kpc by adopting
kpc by adopting
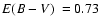 .
.
This GC was discovered by Terzan (1971). Based on V, I, and Gunn Z photometry, Ortolani et al. (1997) derived
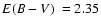 ,
,
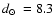 kpc and
kpc and
![$\mbox{$\rm [Fe/H]$ }=-2.0$](/articles/aa/full/2008/09/aa8687-07/img47.gif) .
Origlia & Rich (2004) obtained
.
Origlia & Rich (2004) obtained
![$\mbox{$\rm [Fe/H]$ }=-1.6$](/articles/aa/full/2008/09/aa8687-07/img48.gif) using high-dispersion spectroscopy. Ortolani et al. (2007)
derived
using high-dispersion spectroscopy. Ortolani et al. (2007)
derived
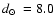 kpc from HST-NICMOS photometry. Its absolute magnitude is
kpc from HST-NICMOS photometry. Its absolute magnitude is
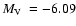 (H03).
(H03).
This is another GC discovered by Terzan (1971). Ortolani et al. (1997)
derived
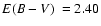 ,
,
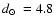 kpc, and
kpc, and
![$\mbox{$\rm [Fe/H]$ }=-1.0$](/articles/aa/full/2008/09/aa8687-07/img53.gif) from V, I, and Gunn Z photometry.
Its absolute magnitude is
from V, I, and Gunn Z photometry.
Its absolute magnitude is
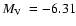 (H03).
(H03).
It was discovered by van den Bergh & Hagen (1975). Ortolani et al. (1995) obtained
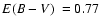 ,
,
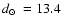 kpc, and a nearly solar metallicity by means of V and I photometry. They emphasise
that, owing to its low Galactic latitude and high metallicity, the nature of BH 176 as a metal-rich
GC or an old OC was not clear. Phelps & Schick (2003) obtained an age of 7 Gyr,
kpc, and a nearly solar metallicity by means of V and I photometry. They emphasise
that, owing to its low Galactic latitude and high metallicity, the nature of BH 176 as a metal-rich
GC or an old OC was not clear. Phelps & Schick (2003) obtained an age of 7 Gyr,
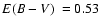 ,
,
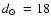 kpc,
and
kpc,
and
![$\mbox{$\rm [Fe/H]$ }=0.0$](/articles/aa/full/2008/09/aa8687-07/img59.gif) with V and I photometry. They point out that that the cluster might be an old
metal-rich OC or a young metal-rich GC. Another possibility is that BH 176 is associated with an
accreted galaxy event now related to the Galactic anticentre stellar structure or the Monoceros
Ring (Frinchaboy 2006). H03 provides the absolute magnitude
with V and I photometry. They point out that that the cluster might be an old
metal-rich OC or a young metal-rich GC. Another possibility is that BH 176 is associated with an
accreted galaxy event now related to the Galactic anticentre stellar structure or the Monoceros
Ring (Frinchaboy 2006). H03 provides the absolute magnitude
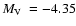 .
.
It was discovered and classified as a GC by Lauberts (1981).
Bica et al. (1999) confirmed it as a GC and determined
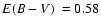 ,
,
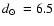 kpc, and
kpc, and
![$\mbox{$\rm [Fe/H]$ }=-1.5$](/articles/aa/full/2008/09/aa8687-07/img63.gif) from V and I photometry. Using V and I photometry Cornish et al. (2006) found
from V and I photometry. Using V and I photometry Cornish et al. (2006) found
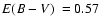 ,
,
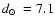 kpc,
and
kpc,
and
![$\mbox{$\rm [Fe/H]$ }=-1.15$](/articles/aa/full/2008/09/aa8687-07/img66.gif) .
ESO 452-SC11 is intrinsically faint, with
.
ESO 452-SC11 is intrinsically faint, with
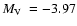 (H03).
(H03).
Lauberts (1982) reported and classified ESO 280-SC06 as an
OC. Ortolani et al. (2000) identify it as a GC, and also obtained
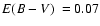 ,
,
![$\mbox{$\rm [Fe/H]$ }=-1.8$](/articles/aa/full/2008/09/aa8687-07/img69.gif) ,
and
,
and
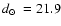 kpc from V and I photometry.
kpc from V and I photometry.
The infrared 2MASS-GC01 was discovered by Hurt et al. (2000).
Ivanov et al. (2000) obtained
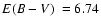 and
and
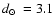 kpc from NTT near IR photometry.
Ivanov & Borissova (2002) obtained
kpc from NTT near IR photometry.
Ivanov & Borissova (2002) obtained
![$\mbox{$\rm [Fe/H]$ }=-1.19$](/articles/aa/full/2008/09/aa8687-07/img73.gif) from 2MASS photometry.
from 2MASS photometry.
The infrared GC 2MASS-GC02 was discovered by Hurt et al. (2000).
Ivanov et al. (2000) obtained
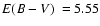 ,
,
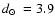 kpc, and
kpc, and
![$\mbox{$\rm [Fe/H]$ }=-0.66$](/articles/aa/full/2008/09/aa8687-07/img76.gif) from NTT near IR-photometry.
from NTT near IR-photometry.
The infrared GC GLIMPSE-C01 was discovered by Kobulnicky et al. (2005),
who obtained a kinematic distance of 3.1-5.2 kpc,
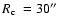 ,
and
,
and
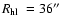 and estimated a total magnitude
and estimated a total magnitude
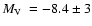 .
Ivanov et al. (2005) derived
.
Ivanov et al. (2005) derived
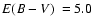 ,
,
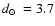 kpc
and
kpc
and
![$\mbox{$\rm [Fe/H]$ }=-1.61$](/articles/aa/full/2008/09/aa8687-07/img82.gif) from NTT near IR photometry. They also obtained the structural parameters
from NTT near IR photometry. They also obtained the structural parameters
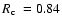 pc (
pc (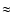
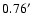 )
and
)
and
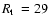 pc (
pc (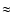
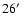 ), which we compare
with the present values (Sect. 4). These cluster radii (especially the tidal) were
estimated by extrapolation, since they worked with NTT/Sofi photometry that covers an area of
), which we compare
with the present values (Sect. 4). These cluster radii (especially the tidal) were
estimated by extrapolation, since they worked with NTT/Sofi photometry that covers an area of
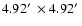 (
(
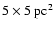 ), which does not reach the tidal
radius.
), which does not reach the tidal
radius.
This cluster was discovered by Andrews & Lindsay (1967) and also catalogued as
BH 261 by van den Bergh & Hagen (1975). In these studies it was classified as an OC. Ortolani et al. (2006) identify it
as a GC with B, V, and I photometry and derive
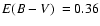 ,
,
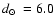 kpc,
kpc,
![$\mbox{$\rm [Fe/H]$ }=-1.3$](/articles/aa/full/2008/09/aa8687-07/img92.gif) ,
a half-density
radius
,
a half-density
radius
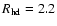 pc, and
pc, and
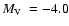 .
.
Table 1 summarises the fundamental data for the sample GCs. It also contains absolute
magnitude estimates derived in this work (Sect. 3.4) for some GCs that lacked this
information. For GLIMPSE-C01 we include an additional row that gives our estimate of 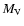 .
.
Table 1:
Fundamental parameters in the literature and 2MASS extraction radius.
3 2MASS photometry and CMD analytical tools
In recent years we have developed a series of tools to statistically disentangle field and cluster stars that
have been applied to objects in a wide variety of environmental conditions. They are based on wide-field
2MASS photometry and essentially deal with CMDs and stellar RDPs. As a result, CMDs containing more enhanced
cluster sequences, and RDPs with a significant contrast with the background were obtained, which in turn,
allowed us to derive more constrained cluster fundamental and structural parameters. For instance, nearby OCs
were analysed in detail like NGC 3960 and M 52 (Bonatto & Bica 2006), and NGC 4755 (Bonatto et al. 2006b), embedded
clusters like NGC 6611 (Bonatto et al. 2006a), and relatively distant OCs like BH 63 (Bica et al. 2006a). These
tools are explained in Bonatto & Bica (2007a), where we studied relatively distant OCs in heavily contaminated fields
towards the bulge and/or low-disk directions.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig1.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg116.gif) |
Figure 1:
2MASS CMDs extracted from the
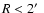 region of GLIMPSE-C01. Top panels: observed
photometry with the colours
region of GLIMPSE-C01. Top panels: observed
photometry with the colours
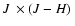 ( left) and
( left) and
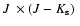 ( right). Middle: equal-area
comparison field showing that the dominant contamination, in this case, arises from disk stars.
Bottom panels: field star decontaminated CMDs. The colour-magnitude filter used to isolate probable
cluster stars (Sect. 3.3) is shown as a shaded region.
( right). Middle: equal-area
comparison field showing that the dominant contamination, in this case, arises from disk stars.
Bottom panels: field star decontaminated CMDs. The colour-magnitude filter used to isolate probable
cluster stars (Sect. 3.3) is shown as a shaded region. |
| Open with DEXTER |
With respect to cluster structure, most of our analysis is based on large-scale radial profiles, which are
fundamental to derive structural parameters of star clusters, the tidal radius in particular. Such profiles
can be obtained using the uniform, all-sky photometric coverage provided by 2MASS (e.g. Bonatto & Bica 2007a,2005).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig3.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg118.gif) |
Figure 3:
Decontaminated
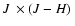 CMDs of the remaining GCs. The colour-magnitude filters
are shown as a shaded region.
CMDs of the remaining GCs. The colour-magnitude filters
are shown as a shaded region. |
| Open with DEXTER |
3.1 2MASS extractions
The present faint GCs were analysed with J, H, and 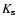 2MASS photometry extracted in circular
fields of radius
2MASS photometry extracted in circular
fields of radius
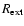 (Table 1) centred on the coordinates of the objects (Table 1)
using VizieR
(Table 1) centred on the coordinates of the objects (Table 1)
using VizieR![[*]](/icons/foot_motif.gif) . Our experience with
OC analysis (e.g. Bonatto & Bica 2007a, and references therein) shows that, as long as no other populous
cluster is present in the field and differential absorption is not prohibitive, wide extraction
areas can provide the required stellar statistics, in terms of magnitude and colours, for a consistent
field-star decontamination (Sect. 3.2). Working with wide comparison fields also results in stellar
radial profiles with more enhanced contrast with the background (Sect. 4).
. Our experience with
OC analysis (e.g. Bonatto & Bica 2007a, and references therein) shows that, as long as no other populous
cluster is present in the field and differential absorption is not prohibitive, wide extraction
areas can provide the required stellar statistics, in terms of magnitude and colours, for a consistent
field-star decontamination (Sect. 3.2). Working with wide comparison fields also results in stellar
radial profiles with more enhanced contrast with the background (Sect. 4).
Based on our experience with the analysis of clusters in crowded field directions using 2MASS photometry
(Bonatto & Bica 2007a, and references therein), the upper limit for the J, H, and 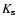 photometric
uncertainties in the 2MASS extractions was adopted as 0.5 mag. This condition represents a compromise
between statistically significant star counts and photometric quality. Note that about
photometric
uncertainties in the 2MASS extractions was adopted as 0.5 mag. This condition represents a compromise
between statistically significant star counts and photometric quality. Note that about
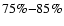 of the
extracted stars have errors smaller than 0.06 mag in the three 2MASS bands. A typical distribution of 2MASS
errors as a function of magnitude, for clusters at approximately the same central directions as the present
GCs, can be found in Bonatto & Bica (2007a). The relatively small size of error bars, propagated to the colours, can
be appreciated in the actual CMDs of the present sample GCs shown in Figs. 1-3.
of the
extracted stars have errors smaller than 0.06 mag in the three 2MASS bands. A typical distribution of 2MASS
errors as a function of magnitude, for clusters at approximately the same central directions as the present
GCs, can be found in Bonatto & Bica (2007a). The relatively small size of error bars, propagated to the colours, can
be appreciated in the actual CMDs of the present sample GCs shown in Figs. 1-3.
We illustrate as CMD analyses GLIMPSE-C01 (Fig. 1) and Lyngå 7 (Fig. 2), which
are projected 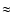
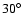 from the direction of the centre (Table 1). 2MASS
from the direction of the centre (Table 1). 2MASS
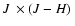 and
and
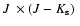 CMDs extracted from a central (
CMDs extracted from a central (
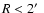 )
region of both GCs (top panels) can be
contrasted with the respective equal-area CMDs extracted from the comparison field (middle panels). It is
clear that the main contaminant are disk stars in both cases, with some contribution from bulge stars.
)
region of both GCs (top panels) can be
contrasted with the respective equal-area CMDs extracted from the comparison field (middle panels). It is
clear that the main contaminant are disk stars in both cases, with some contribution from bulge stars.
3.2 Field-star decontamination
To disentangle the intrinsic CMD morphology from the field, we apply the statistical decontamination
algorithm described in Bonatto & Bica (2007a). It measures the relative number-densities of candidate cluster and
field stars in small cubic CMD cells with axes corresponding to the magnitude J and the colours (J-H) and
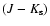 (considering also the
(considering also the 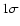 uncertainties in the 2MASS bands). These colours provide
the maximum discrimination among CMD sequences for star clusters of different ages (e.g. Bonatto et al. 2004).
uncertainties in the 2MASS bands). These colours provide
the maximum discrimination among CMD sequences for star clusters of different ages (e.g. Bonatto et al. 2004).
Basically, the algorithm (i) divides the full range of magnitude and colours of a CMD into a
3D grid, (ii) computes the expected number-density of field stars in each cell based on the number
of comparison field stars with magnitude and colours compatible with those in the cell, and (iii)
subtracts the expected number of field stars from each cell. Typical cell dimensions
are
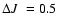 ,
and
,
and
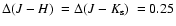 ,
which are large enough to allow sufficient star-count
statistics in individual cells and small enough to preserve the morphology of the CMD evolutionary
sequences. As comparison field we use the region within the respective tidal (Table 2) and
extraction (Table 1) radii to obtain representative background statistics.
,
which are large enough to allow sufficient star-count
statistics in individual cells and small enough to preserve the morphology of the CMD evolutionary
sequences. As comparison field we use the region within the respective tidal (Table 2) and
extraction (Table 1) radii to obtain representative background statistics.
The algorithm is applied for 3 different grid specifications in each dimension to minimise potential
artifacts introduced by the choice of parameters, thus resulting in 27 different outputs. The average
number of probable cluster stars
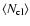 is computed from these outputs. Typical standard
deviations of
is computed from these outputs. Typical standard
deviations of
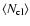 are at the
are at the 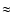
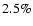 level. The final field star-decontaminated
CMD contains the
level. The final field star-decontaminated
CMD contains the
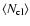 stars with the highest number frequencies. Stars that remain after
the decontamination are in cells where the stellar density presents a clear excess over the
field. Consequently, they have a significant probability of being cluster members. More details on the
algorithm, including discussions on subtraction efficiency and limitations, are given in Bonatto & Bica (2007a).
stars with the highest number frequencies. Stars that remain after
the decontamination are in cells where the stellar density presents a clear excess over the
field. Consequently, they have a significant probability of being cluster members. More details on the
algorithm, including discussions on subtraction efficiency and limitations, are given in Bonatto & Bica (2007a).
The resulting decontaminated CMDs of GLIMPSE-C01 and Lyngå 7 are shown in the bottom panels of
Figs. 1 and 2. As expected, most of the disk component is removed, leaving a
sequence of stars that corresponds essentially to the giant branch.
For the sake of space, only the decontaminated
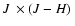 CMDs of the remaining GCs are shown
in Fig. 3. In all cases, the spatial region shown in the CMDs lies within the respective
half-star count radius (Table 2).
CMDs of the remaining GCs are shown
in Fig. 3. In all cases, the spatial region shown in the CMDs lies within the respective
half-star count radius (Table 2).
Differential absorption appears to be similar in each GC and in respective field extractions,
as indicated, for instance, by GLIMPSE-C01 (Fig. 1), which is affected by a high reddening
value. The similarity provides a consistent field subtraction, as suggested by the decontaminated
resulting giant branches in Fig. 3. Actually, differential absorption, when present, is more
critical for low-density star clusters (e.g. the open cluster NGC 6611, Bonatto et al. 2006a), especially
in the optical.
3.3 Colour-magnitude filters
Decontaminated CMDs present better-defined cluster sequences. Based on these sequences, more intrinsic
colour-magnitude filters can be designed to remove stars with colours compatible with those of the
foreground/background field, which in turn improves the cluster/background contrast. They are wide enough
to accommodate the colour distribution
of cluster CMD sequences, allowing for 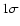 uncertainties. However, residual field stars with colours
similar to those of the cluster are expected to remain within the colour-magnitude filter. This residual
contamination is statistically evaluated by means of the comparison field. Colour-magnitude filter widths
should also account for formation or dynamical evolution-related effects, such as enhanced fractions of
binaries (and other multiple systems) towards the central parts of clusters, since such systems tend to
widen the sequences (e.g. Bonatto & Bica 2007a; Bonatto et al. 2005; Hurley & Tout 1998; Kerber et al. 2002).
uncertainties. However, residual field stars with colours
similar to those of the cluster are expected to remain within the colour-magnitude filter. This residual
contamination is statistically evaluated by means of the comparison field. Colour-magnitude filter widths
should also account for formation or dynamical evolution-related effects, such as enhanced fractions of
binaries (and other multiple systems) towards the central parts of clusters, since such systems tend to
widen the sequences (e.g. Bonatto & Bica 2007a; Bonatto et al. 2005; Hurley & Tout 1998; Kerber et al. 2002).
The colour-magnitude filters for the present GCs are shown in Figs. 1-3 as a
shaded region superimposed on the field-star decontaminated CMDs. In the present cases, they
basically isolate giant-branch stars. As a rule, the filters are wide enough to take all the relevant
stars into account in both colours. Thus, we only apply the method to the (J-H) colour.
Table 2:
Structural parameters derived from 2MASS data.
3.4 Absolute magnitude estimates
ESO 280-SC06, 2MASS-GC01, and 2MASS-GC02 lack absolute magnitudes, while the available estimate for
GLIMPSE-C01 has a large uncertainty (Table 1). Here, such values are estimated following a
similar method to the one used for the recently identified GC FSR 1767 (Bonatto et al. 2007). Basically,
we compare the number of giant stars in ESO 280-SC06, 2MASS-GC01, 2MASS-GC02, and GLIMPSE-C01 with
that in the nearby (
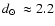 kpc), intermediate-metallicity (
kpc), intermediate-metallicity (
![$\mbox{$\rm [Fe/H]$ }=-1.2$](/articles/aa/full/2008/09/aa8687-07/img184.gif) )
and total absolute magnitude
)
and total absolute magnitude
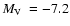 GC M 4 (H03, and references therein). In all cases, including M 4, the number of member
giant stars is computed from decontaminated 2MASS photometry (Sect. 3.2), considering
stars in the region from the cluster centre to the tidal radius.
GC M 4 (H03, and references therein). In all cases, including M 4, the number of member
giant stars is computed from decontaminated 2MASS photometry (Sect. 3.2), considering
stars in the region from the cluster centre to the tidal radius.
We assume that the decontaminated giants in ESO 280-SC06, 2MASS-GC01, 2MASS-GC02, and
GLIMPSE-C01 are roughly of the same spectral type as in M 4, and also that the luminosity of a
typical GC is dominated by the number of giants. Thus, the total absolute magnitude of a given
GC can be estimated by scaling the total number of giants with that in M 4. We found
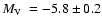 for 2MASS-GC01,
for 2MASS-GC01,
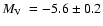 for 2MASS-GC02,
for 2MASS-GC02,
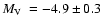 for ESO 280-SC06, and
for ESO 280-SC06, and
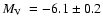 for GLIMPSE-C01. Our estimate puts GLIMPSE-C01
for GLIMPSE-C01. Our estimate puts GLIMPSE-C01 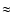 2 mag fainter than that of Kobulnicky et al. (2005),
but still within their uncertainty. As a caveat, we note that the uncertainties in
2 mag fainter than that of Kobulnicky et al. (2005),
but still within their uncertainty. As a caveat, we note that the uncertainties in 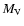 only reflect
the statistical Poisson fluctuation of the number of giants in the above GCs and M 4. They do not
take into account the individual spectral types or the presence of horizontal-branch stars (that are
clearly seen in the 2MASS CMD of the central region of M 4 - Bonatto et al. 2007). Thus, they should be
taken as lower limits on the actual uncertainties, especially in the case of ESO 280-SC06, which is
only reflect
the statistical Poisson fluctuation of the number of giants in the above GCs and M 4. They do not
take into account the individual spectral types or the presence of horizontal-branch stars (that are
clearly seen in the 2MASS CMD of the central region of M 4 - Bonatto et al. 2007). Thus, they should be
taken as lower limits on the actual uncertainties, especially in the case of ESO 280-SC06, which is
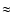 22 kpc distant from the Sun. The GCs 2MASS-GC01, 2MASS-GC02, and GLIMPSE-C01 are only
22 kpc distant from the Sun. The GCs 2MASS-GC01, 2MASS-GC02, and GLIMPSE-C01 are only
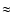 1 kpc more distant from the Sun than M 4.
1 kpc more distant from the Sun than M 4.
The resulting RDPs for the sample GCs (Sect. 4) follow the King-like profiles, which
suggests that star-count losses in the central regions are not significant. Similar analysis applied
to M 4 implies a loss of 2-3 giants only in the innermost region. Thus, the errors associated with
such effects are encompassed by the uncertainties quoted in Table 1 (Col. 7).
In any case, the present total 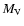 estimates of ESO 280-SC06, 2MASS-GC01, 2MASS-GC02, and GLIMPSE-C01
are consistent with the expected low-luminosity nature of these GCs (Sect. 5).
estimates of ESO 280-SC06, 2MASS-GC01, 2MASS-GC02, and GLIMPSE-C01
are consistent with the expected low-luminosity nature of these GCs (Sect. 5).
4 Structural parameters
Structural parameters are derived using both the stellar radial number-density and surface brightness
profiles, extracted from colour-magnitude filtered photometry (Sect. 3.3).
To avoid oversampling near the centre and undersampling at large radii, the profiles are built in
rings of increasing width with distance to the centre. The number and width of rings are adjusted
to produce profiles with adequate spatial resolution and as small as possible 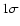 Poisson
errors. The residual background level of each RDP corresponds to the average number density of
colour-magnitude filtered stars measured in the comparison field. The R coordinate and respective
uncertainty in each ring correspond to the average position and standard deviation of the stars inside
the ring. The vertical error bars correspond to the
Poisson
errors. The residual background level of each RDP corresponds to the average number density of
colour-magnitude filtered stars measured in the comparison field. The R coordinate and respective
uncertainty in each ring correspond to the average position and standard deviation of the stars inside
the ring. The vertical error bars correspond to the 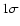 Poisson fluctuation of the star
counts in each ring. Obviously, the precision in the RDP level depends directly on the 2MASS resolution and
photometric limit. Stars fainter than
Poisson fluctuation of the star
counts in each ring. Obviously, the precision in the RDP level depends directly on the 2MASS resolution and
photometric limit. Stars fainter than
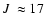 and/or those with projected companions close
enough to produce distorted images have been discarded by 2MASS.
and/or those with projected companions close
enough to produce distorted images have been discarded by 2MASS.
The SBPs in the 2MASS J band are built in a similar way to the RDPs. The average surface brightness measured
in the comparison field is subtracted from what is computed in each cluster ring. As a caveat we note
that the radial surface brightness is computed by summing the individual fluxes of all stars in each
ring that have been resolved by 2MASS. Thus, SBPs are essentially subject to the same technical
limitations as the RDPs. In this sense, the present SBPs are somewhat different (fainter) from the
classical ones built with aperture photometry.
By definition, RDPs represent star count densities, which do not take into account individual stellar
magnitudes or asymmetries in the spatial distribution of stellar spectral types. Consequently, depending
on the degree of large-scale mass segregation, RDP-derived parameters are expected to become larger than
their counterparts obtained from SBPs.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig4.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg191.gif) |
Figure 4:
Stellar RDPs (filled circles) in angular scale. Solid lines: best-fit King-like
profile (Eq. (1)). Horizontal shaded region: background level (
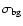 ). Gray
regions: ). Gray
regions: 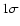 fit uncertainty range.
fit uncertainty range. |
| Open with DEXTER |
The resulting RDPs are displayed in Fig. 4, which also shows how the residual background
contamination varies in each case. Because 2MASS is magnitude-limited, the contrast with the background
level and error bars among the RDPs are different and depend on the relative richness, distance from
the Sun, and direction in the Galaxy of each GC. Nevertheless, most of the RDPs are well-defined with
relatively high cluster/background contrasts, except for AL 3, the most centrally projected GC of
the present sample.
We fit the SBPs with the empirical isothermal sphere, single-mass profile introduced by King (1962)
to describe the surface brightness profiles of globular clusters. To the RDPs, we applied the King-like
profile
![\begin{displaymath}
\sigma(R)=\sigma_{\rm bg}+\sigma_0\left[\frac{1}{\sqrt{1+(R/...
...})^2}} -
\frac{1}{\sqrt{1+(R_{\rm t}/R_{\rm c})^2)}}\right]^2,
\end{displaymath}](/articles/aa/full/2008/09/aa8687-07/img192.gif) |
(1) |
where
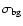 is the residual background density,
is the residual background density, 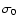 is the central number-density of
stars, and
is the central number-density of
stars, and 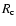 and
and 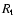 are the core and tidal radii. This function is similar to the King (1962)
profile. In recent years, more sophisticated models have been employed to fit SBPs of Galactic and
extra-Galactic GCs. The most often used are the single-mass, modified isothermal sphere of King (1966)
that is the basis of the Galactic GC parameters given by Trager et al. (1995) and H03, the modified isothermal
sphere of Wilson (1975), which assumes a pre-defined stellar distribution function (resulting in
more extended envelopes than King 1966), and the power law with a core of Elson et al. (1987) that has
been applied to massive young clusters especially in the Magellanic Clouds (e.g. Mackey & Gilmore 2003a-c).
Each function is characterised by different parameters that are somehow related to cluster structure.
However, considering that the 2MASS photometric range basically covers the giant branch in most of the
present GCs, and that RDP and SBP error bars are significant, we decided on the simplest model
(King 1962) as fit function.
are the core and tidal radii. This function is similar to the King (1962)
profile. In recent years, more sophisticated models have been employed to fit SBPs of Galactic and
extra-Galactic GCs. The most often used are the single-mass, modified isothermal sphere of King (1966)
that is the basis of the Galactic GC parameters given by Trager et al. (1995) and H03, the modified isothermal
sphere of Wilson (1975), which assumes a pre-defined stellar distribution function (resulting in
more extended envelopes than King 1966), and the power law with a core of Elson et al. (1987) that has
been applied to massive young clusters especially in the Magellanic Clouds (e.g. Mackey & Gilmore 2003a-c).
Each function is characterised by different parameters that are somehow related to cluster structure.
However, considering that the 2MASS photometric range basically covers the giant branch in most of the
present GCs, and that RDP and SBP error bars are significant, we decided on the simplest model
(King 1962) as fit function.
In all cases, the adopted King-like profile (Eq. (1)) represents the RDPs well along the full
radial scale (Fig. 4), within uncertainties. However, the innermost point in the RDPs of Tz 4
and 2MASS-GC01 presents a 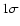 excess density over the fit, which might suggest post-core collapse.
GCs with that structure occur mostly in the bulge, but some halo GCs like NGC 6397 also have it (e.g.
Chernoff & Djorgovski 1989; Trager et al. 1995). Although to a lesser extent, the same occurs for ESO 452-SC 11.
Because the core radius results from the fit of Eq. (1) to the several radial points contained
in RDPs, the probable post-core collapse structure of Tz 4 and 2MASS-GC01 are not reflected in the
respective concentration parameters (Table 2 and Fig. 8).
excess density over the fit, which might suggest post-core collapse.
GCs with that structure occur mostly in the bulge, but some halo GCs like NGC 6397 also have it (e.g.
Chernoff & Djorgovski 1989; Trager et al. 1995). Although to a lesser extent, the same occurs for ESO 452-SC 11.
Because the core radius results from the fit of Eq. (1) to the several radial points contained
in RDPs, the probable post-core collapse structure of Tz 4 and 2MASS-GC01 are not reflected in the
respective concentration parameters (Table 2 and Fig. 8).
Two additional parameters are computed, the half-light radius (
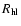 ), which can be used for comparisons
with previous works and the equivalent half-star count radius (
), which can be used for comparisons
with previous works and the equivalent half-star count radius (
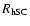 ). The half-light radius is derived
through direct integration of the background-subtracted SBPs, with no fit involved in the process. Derivation
of the distance from the centre which contains half of the background-subtracted cluster stars,
). The half-light radius is derived
through direct integration of the background-subtracted SBPs, with no fit involved in the process. Derivation
of the distance from the centre which contains half of the background-subtracted cluster stars,
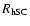 ,
follows
a similar procedure, where number densities are used instead of surface brightness.
Figure 5 displays the present RDPs in the usual, background-subtracted presentation
for GCs, which also shows the respective King-like fits and
,
follows
a similar procedure, where number densities are used instead of surface brightness.
Figure 5 displays the present RDPs in the usual, background-subtracted presentation
for GCs, which also shows the respective King-like fits and 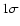 -fit uncertainties.
-fit uncertainties.
The RDP and SBP structural parameters that result from the above fits are given in Table 2,
in angular units, where we also provide the arcmin to parsec scale for each GC, based on the distances
from the Sun listed in Table 1.
Within uncertainties, both types of profiles produce similar parameters. This is confirmed in
Fig. 6, where RDP and SBP parameters (in absolute units) are compared. The agreement
is good for large radii, but fails for some GCs with small radii, especially the tidal one, where
RDP radii are larger than SBP ones. The best overall agreement occurs for the half-type radii, and
the approximate identity holds for about one order of magnitude in the radii scales (Sect. 5).
Some structural parameters, derived from SBPs, are available for GLIMPSE-C01 (Kobulnicky et al. 2005;
Ivanov et al. 2005). The present values of core and half-light radii (Table 2) are comparable
to those given in Kobulnicky et al. (2005) and a factor 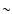 2 smaller than the core radius estimated
by Ivanov et al. (2005). The present tidal radius, on the other hand, is
2 smaller than the core radius estimated
by Ivanov et al. (2005). The present tidal radius, on the other hand, is 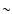 1/6 of that given by
Ivanov et al. (2005), which they estimated by extrapolation.
1/6 of that given by
Ivanov et al. (2005), which they estimated by extrapolation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig6.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg198.gif) |
Figure 6:
Comparison of cluster structural parameters derived from RDPs and SBPs. Identity is indicated by
the dashed line. GCs that lie at more than 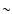 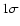 from the identity line are labelled. The
highest concentration level (panel d)) occurs for IC 1257, the most distant GC of the present sample, with
from the identity line are labelled. The
highest concentration level (panel d)) occurs for IC 1257, the most distant GC of the present sample, with
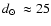 kpc and kpc and
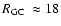 kpc. Absolute units are used. kpc. Absolute units are used. |
| Open with DEXTER |
5 Discussion
5.1 Photometric depth effects
The structural parameters dealt with in this paper were derived from RDPs and SBPs built with
depth-limited photometry that, for the present GCs, essentially correspond to the giant branch.
Potential effects on cluster radii introduced by this observational limitation should be taken
into account before comparing the parameters of present 11 faint GCs with those given in the
literature for the remaining GCs that, in general, have been obtained with deeper photometry.
This issue was investigated by Bonatto & Bica (2007b) by means of model star clusters of different
ages, structures, and mass functions, with a spatial distribution of stars assumed to follow a
pre-established analytical function. Model SBPs were built for the 2MASS J band. Cluster radii
were then measured in RDPs and SBPs extracted from data with different photometric depths,
varying from the giant branch to the low-main sequence. The main results drawn from the GC
models are:
- (i)
- Structural parameters derived from SBPs are essentially insensitive to
photometric depth.
- (ii)
- RDPs built with shallow photometry yield cluster radii underestimated with
respect to the values obtained with deep photometry. Tidal, half-star count, and core radii
are affected with increasing intensity for a given photometric depth. Tidal, half-star count,
and core radii underestimation factors are
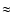
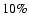 ,
,
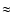
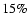 ,
and
,
and 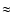
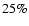 ,
respectively, for RDPs built essentially with giant-branch stars.
,
respectively, for RDPs built essentially with giant-branch stars.
- (iii)
- Profiles with photometry deeper than the turnoff have systematically larger
RDP radii than SBP ones, especially the core. In the deepest profiles, RDP to SBP radii ratios
are
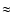 1.2 both for the tidal and half-type radii, and
1.2 both for the tidal and half-type radii, and 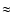 1.4 for the core radius.
1.4 for the core radius.
- (iv)
- Changes in RDP parameters with photometric depth result from a spatially variable
mass function.
Most of the above results are directly related to cluster dynamical evolution. Large-scale mass segregation
drives preferentially low-mass stars towards large radii (while evaporation pushes part of these
stars beyond the tidal radius, into the field), and high-mass stars towards the central parts of
clusters. If the stellar mass distribution can be described by a spatially variable mass function
flatter at the centre than in the halo, the resulting RDP radii should be larger than SBP ones.
The differences should be more noticeable in the core than the half and tidal radii, since the
core would contain, on average, stars more massive than the halo, and especially near the tidal
radius. Such differences, in addition, increase for profiles built with deeper photometry
(Bonatto & Bica 2007b).
It follows from the above that radial number-density and surface-brightness profiles built with
shallow photometry, as is the case of the present GCs, are expected to yield similar values for
the three types of cluster radii and that RDP radii are underestimated by the factors given in
(ii) above with respect to the intrinsic values. However, we note that the underestimation factors
for the present faint GCs are, in most cases, smaller than (or similar to) the 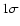 fit
uncertainties (Table 2). The similarity between the values of RDP and SBP radii effectively
occurs for most of the present faint-GC sample (Fig. 6), especially concerning the half-light
and half-star count radii.
fit
uncertainties (Table 2). The similarity between the values of RDP and SBP radii effectively
occurs for most of the present faint-GC sample (Fig. 6), especially concerning the half-light
and half-star count radii.
5.2 Comparison with GCs in H03
In Fig. 7 we compare our faint GCs with the GCs in H03 in terms of Galactic coordinates
(panels a and b), reddening E(B-V) (panel c), metallicity
![$\rm [Fe/H]$](/articles/aa/full/2008/09/aa8687-07/img99.gif) (panel d), and distance from the Sun
(panel e). The present GCs are projected not far from the bulge and close to the plane. Such
difficult directions, together with relatively high reddening values in the optical (GLIMPSE-C01,
2MASS-GC01, and 2MASS-GC02 have
(panel d), and distance from the Sun
(panel e). The present GCs are projected not far from the bulge and close to the plane. Such
difficult directions, together with relatively high reddening values in the optical (GLIMPSE-C01,
2MASS-GC01, and 2MASS-GC02 have 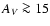 ), explain why the present GCs have so far been scarcely
studied. They have metallicities as low as
), explain why the present GCs have so far been scarcely
studied. They have metallicities as low as
![$\mbox{$\rm [Fe/H]$ }=-1.8$](/articles/aa/full/2008/09/aa8687-07/img69.gif) with a single case (BH 176) being metal-rich
(
with a single case (BH 176) being metal-rich
(
![$\mbox{$\rm [Fe/H]$ }=0.0$](/articles/aa/full/2008/09/aa8687-07/img59.gif) ), and
), and 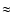
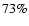 have metallicity lower than
have metallicity lower than
![$\mbox{$\rm [Fe/H]$ }=-1.0$](/articles/aa/full/2008/09/aa8687-07/img53.gif) .
The same fraction of GCs is
less than
.
The same fraction of GCs is
less than 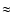 10 kpc distant from the Sun.
10 kpc distant from the Sun.
Further comparisons with the GCs in H03 are explored in Fig. 8. With respect to luminosity,
most of the GCs of the present sample are 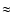 3 mag fainter than the
average luminosity of the H03 GC distribution, while at least 3 of them populate the faint-magnitude
tail (panel a). The exception perhaps is GLIMPSE-C01 with
3 mag fainter than the
average luminosity of the H03 GC distribution, while at least 3 of them populate the faint-magnitude
tail (panel a). The exception perhaps is GLIMPSE-C01 with
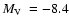 ,
but with
,
but with 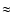 3 mag of
uncertainty (Kobulnicky et al. 2005). Our estimate gives
3 mag of
uncertainty (Kobulnicky et al. 2005). Our estimate gives
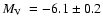 for GLIMPSE-C01, which is
consistent with a low-luminosity GC. About 73% of them are located within 5 kpc of the Galactic
centre (panel b), which implies that some are probably bulge GCs; the remaining GCs (IC 1257,
BH 176 and ESO 280-SC06) have Galactocentric distances compatible with the halo. The present
tidal radius distribution suggests a bias towards low values (panel c) with respect to H03,
while the half-star count radii are more evenly distributed (panel d). The core radii appear to
be distributed similarly to those in H03 (panel e). Consequently, the concentration parameters
(panel f) are biased towards GCs of loose structure. Loose structure, together with low-luminosity
(
for GLIMPSE-C01, which is
consistent with a low-luminosity GC. About 73% of them are located within 5 kpc of the Galactic
centre (panel b), which implies that some are probably bulge GCs; the remaining GCs (IC 1257,
BH 176 and ESO 280-SC06) have Galactocentric distances compatible with the halo. The present
tidal radius distribution suggests a bias towards low values (panel c) with respect to H03,
while the half-star count radii are more evenly distributed (panel d). The core radii appear to
be distributed similarly to those in H03 (panel e). Consequently, the concentration parameters
(panel f) are biased towards GCs of loose structure. Loose structure, together with low-luminosity
(
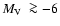 ), is typical of Palomar-like GCs, i.e. low-mass GCs that do not contain populous giant
branches (Bonatto et al. 2007, and references therein).
), is typical of Palomar-like GCs, i.e. low-mass GCs that do not contain populous giant
branches (Bonatto et al. 2007, and references therein).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig7.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg206.gif) |
Figure 7:
Astrophysical parameters of the present faint GCs (shaded histograms) compared to
the GCs in H03 (empty histograms). Inset of panel c): GCs with high reddening values. The
y-scale in panel d) was multiplied by 2 for clarity purposes. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig8.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg207.gif) |
Figure 8:
Same as Fig. 7, but including the structural parameters (panels c)- f)). In panel a) we
used
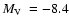 (Kobulnicky et al. 2005) for GLIMPSE-C01; our estimate is more compatible with a low-luminosity GC,
(Kobulnicky et al. 2005) for GLIMPSE-C01; our estimate is more compatible with a low-luminosity GC,
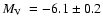 .
Post-core collapse GCs in H03 occupy the c=2.5 bin in panel f). The y-scale in panels a) and f) was multiplied by 2 for clarity purposes. .
Post-core collapse GCs in H03 occupy the c=2.5 bin in panel f). The y-scale in panels a) and f) was multiplied by 2 for clarity purposes. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig9.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg210.gif) |
Figure 9:
Dependence of cluster radii on Galactocentric distance. Empty circles: massive (
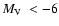 )
GCs in H03. Asterisks: Palomar-like ( )
GCs in H03. Asterisks: Palomar-like (
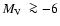 ) GCs from H03. Empty triangle: FSR 1767.
Filled triangles: present faint GCs. ) GCs from H03. Empty triangle: FSR 1767.
Filled triangles: present faint GCs. |
| Open with DEXTER |
5.3 Dependence on Galactocentric distance
Finally, in Fig. 9 we examine the dependence of cluster radii on Galactocentric distance.
GCs from H03 shown in this figure are separated according to luminosity, massive (
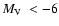 ), and
Palomar-like (
), and
Palomar-like (
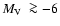 ) GCs. We also include for comparison the recently identified Palomar-like
GC FSR 1767 (Bonatto et al. 2007). Massive and Palomar-like GCs follow the well-known relation of
increasing cluster radii with Galactocentric distance (e.g. Mackey & van den Bergh 2005; Djorgovski & Meylan 1994).
However, compared to the massive GCs, the Palomar-like ones tend to have smaller tidal and larger
core radii than the massive ones for a given Galactocentric distance, especially for small
) GCs. We also include for comparison the recently identified Palomar-like
GC FSR 1767 (Bonatto et al. 2007). Massive and Palomar-like GCs follow the well-known relation of
increasing cluster radii with Galactocentric distance (e.g. Mackey & van den Bergh 2005; Djorgovski & Meylan 1994).
However, compared to the massive GCs, the Palomar-like ones tend to have smaller tidal and larger
core radii than the massive ones for a given Galactocentric distance, especially for small
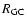 ,
which is consistent with their loose structures. The half-light radii distributions of both
types of GCs are very similar.
,
which is consistent with their loose structures. The half-light radii distributions of both
types of GCs are very similar.
Concerning the 11 faint GCs dealt with in this paper, the core and tidal radii distributions
with Galactocentric distance are similar to those of the Palomar-like GCs. We note that this
conclusion would only suffer minor changes in the case of correcting the measured radii for the
photometric depth effects discussed above (Sect. 5.1). The intrinsic (i.e. corrected)
core radii would be somewhat larger than the measured ones. To a lesser extent, the same applies
to the relation between depth-limited and intrinsic tidal radii, thus confirming the loose structure
of the present GCs.
Associated with the low luminosities (Table 1), the radii distributions with Galactocentric
distance imply that the present faint GCs share similar characteristics as the sample of Palomar-like
GCs present in H03.
6 Concluding remarks
Compilations of astrophysical parameters of globular (e.g. H03) and open (e.g. WEBDA![[*]](/icons/foot_motif.gif) ) clusters represent a fundamental step in the study of several aspects
related to the clusters themselves and the Galactic subsystems they belong to.
) clusters represent a fundamental step in the study of several aspects
related to the clusters themselves and the Galactic subsystems they belong to.
The majority of the GCs are rather populous and concentrated, which results in high contrast with
respect to the background/foreground stellar field. The bottom line is that such GCs can be fairly
easily observed in most regions of the Galaxy, from near the centre to the remote halo outskirts.
Thus, through the statistics of observables such as the age, metallicity, luminosity, dynamics, and
kinematics, GCs can be taken as excellent tracers of the formation history of the Galaxy. Obviously,
the same applies to extra-Galactic GCs and their host galaxies.
Faint globular clusters, in particular, are important because, compared to massive clusters, they
are more severely affected by the many Galaxy tidal effects and have shorter dynamical-evolution
time scales. Consequently, the distribution of their structural parameters throughout the Galaxy
may provide clues to the dynamical evolution of individual GCs and their system.
With the present work we derived structural parameters of 9 faint GCs listed in H03 and 2 others
recently identified, by means of stellar radial number-density and surface-brightness profiles.
These GCs either lacked such parameters or, in some cases, had first-order estimates based on CCD
observations covering fields smaller than the angular diameters of clusters. The profiles in the
present work were built with wide-field 2MASS photometry (J band). Because of the 2MASS depth-limit
and the distances of the present GCs, the resulting photometry essentially samples giant-branch stars.
In all cases, the radial profiles at least reached the respective tidal radius. We also estimated total 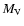 values, which were not available for ESO 280-SC06, 2MASS-GC01, and 2MASS-GC02, and provided an independent
values, which were not available for ESO 280-SC06, 2MASS-GC01, and 2MASS-GC02, and provided an independent 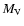 estimate for GLIMPSE-C01 (which resulted
estimate for GLIMPSE-C01 (which resulted 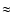 2 mag fainter than previously given), based on
the field-star decontaminated photometry of the giant stars, using M 4 as a template GC. Our estimates
are in the range
2 mag fainter than previously given), based on
the field-star decontaminated photometry of the giant stars, using M 4 as a template GC. Our estimates
are in the range
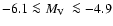 ,
which confirms them as low-luminosity GCs.
,
which confirms them as low-luminosity GCs.
The stellar radial profiles were fitted with King-like functions from which the core, half-star
count, half-light, and tidal radii, as well as the concentration parameter, were derived. Most of
the present objects turned out to be so-far neglected Palomar-like (low mass and loose structure)
GCs. The distributions of core and tidal radii with respect to Galactocentric distance are also
consistent with the Palomar-like nature.
Besides a better understanding of the individual structure of some faint globular clusters, this work
provides an improved coverage of the GC parameter space.
Acknowledgements
We thank the anonymous referee for helpful suggestions.
We acknowledge partial support from the Brazilian agency CNPq.
- Alter, G., Ruprecht,
J., & Vanysek, V. 1970, Catalog of Star Clusters and
Associations, second edition, ed. G. Alter, B. Balazs, & J.
Ruprecht (Budapest: Akademia Kiado)
(In the text)
- Andrews, A. D.,
& Lindsay, E. M. 1967, IrAJ, 8, 126 [NASA ADS]
(In the text)
- Baumgardt, H., &
Makino, J. 2003, MNRAS, 340, 227 [NASA ADS] [CrossRef]
(In the text)
- Belokurov,
V., Evans, N. W., Irwin, M. J., et al. 2007, ApJ, 658,
337 [NASA ADS] [CrossRef]
(In the text)
- van den Bergh, S., &
Hagen, G. L. 1975, AJ, 80, 11 [NASA ADS] [CrossRef]
(In the text)
- van den Bergh, S.
1991, ApJ, 375, 594 [NASA ADS] [CrossRef]
(In the text)
- Bica, E., Ortolani, S.,
& Barbuy, B. 1999, A&AS, 136, 363 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bica, E., Bonatto,
C., & Blumberg, R. 2006a, A&A, 460, 83 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bica, E., Bonatto, C.,
Barbuy, B., & Ortolani, S. 2006b, A&A, 450, 105 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bica, E., Bonatto, C.,
Ortolani, S., & Barbuy, B. 2007, A&A, 472, 483 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Binney, J.,
& Merrifield, M. 1998, in Galactic Astronomy (Princeton, NJ:
Princeton University Press), Princeton series in Astrophysics
(In the text)
- Bonatto, C.,
& Bica, E. 2005, A&A, 437, 483 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bonatto, C., & Bica,
E. 2006, A&A, 455, 931 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bonatto, C., & Bica,
E. 2007a, MNRAS, 377, 1301 [NASA ADS] [CrossRef]
(In the text)
- Bonatto, C., & Bica,
E. 2007b, A&A, submitted
(In the text)
- Bonatto, C.,
Bica, E., & Girardi, L. 2004, A&A, 415, 571 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bonatto, C., Bica, E.,
& Santos Jr., J. F. C. 2005, A&A, 433, 917 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bonatto, C., Santos, J.
F. C., Jr., & Bica, E. 2006a, A&A, 445, 567 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bonatto, C., Bica, E.,
Ortolani, S., & Barbuy, B. 2006b, A&A, 453, 121 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bonatto, C., Bica,
E., Ortolani, S., & Barbuy, B. 2007, MNRAS, 381, L45 [NASA ADS]
(In the text)
- Carraro, G. 2005,
ApJ, 621, L61 [NASA ADS] [CrossRef]
(In the text)
- Chernoff, D., &
Djorgovski, S. 1989, ApJ, 339, 904 [NASA ADS] [CrossRef]
(In the text)
- Cohen, J. G., Hsieh,
S., Stanimir, M., et al. 2007, AJ, 133, 99 [NASA ADS] [CrossRef]
(In the text)
- Cornish, A. S.
M., Phelps, R. L., Briley, M. M., & Friel, E. D. 2006, AJ, 131,
2543 [NASA ADS] [CrossRef]
(In the text)
- Djorgovski, S., &
Meylan, G. 1994, AJ, 108, 1292 [NASA ADS] [CrossRef]
(In the text)
- Elson, R. A. W., Fall, S.
M., & Freeman, K. C. 1987, ApJ, 323, 54 [NASA ADS] [CrossRef]
(In the text)
- Frinchaboy, P. M.
2006, in Globular Clusters - Guides to Galaxies, ESO/Springer Conf.
Proc., ed. T. Richtler, & S. Larsen, in press
[arXiv:astro-ph/0604133]
(In the text)
- Froebrich, D., Meusinger,
H., & Scholz, A. 2007, MNRAS, 377, L54 [NASA ADS]
(In the text)
- Gnedin, O. Y., &
Otriker, J. P. 1997, ApJ, 474, 223 [NASA ADS] [CrossRef]
(In the text)
- Harris, W. E. 1996,
AJ, 112, 1487 [NASA ADS] [CrossRef]
- Harris, W. E., Phelps, R. L.,
Madore, B. F., et al. 1997, AJ, 113, 688 [NASA ADS] [CrossRef]
(In the text)
- Hurley, J., & Tout, A.
A. 1998, MNRAS, 300, 977 [NASA ADS] [CrossRef]
(In the text)
- Hurt, R. L., Jarrett,
T. H., Kirkpatrick, J. D., et al. 2000, AJ, 120, 1876 [NASA ADS] [CrossRef]
(In the text)
- Ivanov, V. D.,
& Borissova, J. 2002, A&A, 390, 937 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Ivanov, V. D.,
Borissova, J., & Vanzi, L. 2000, A&A, 362, L1 [NASA ADS]
(In the text)
- Ivanov, V. D., Kurtev,
R., & Borissova, J. 2005, A&A, 442, 195 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Janes, K., & Adler, D.
1982, ApJ, 49, 425 [NASA ADS] [CrossRef]
(In the text)
- Kerber, L. O.,
Santiago, B. X., Castro, R., & Valls-Gabaud, D. 2002, A&A,
390, 121 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Khalisi, E.,
Amaro-Seoane, P., & Spurzem, R. 2007, MNRAS, 374, 703 [NASA ADS] [CrossRef]
(In the text)
- King, I. 1962, AJ,
67, 471 [NASA ADS] [CrossRef]
(In the text)
- King, I. R. 1966, AJ,
71, 64 [NASA ADS] [CrossRef]
(In the text)
- Kobulnicky, H. A.,
Monson, A. J., Bickalew, B. A., et al. 2005, AJ, 129, 239 [NASA ADS] [CrossRef]
(In the text)
- Koposov, S., de
Jong, J. T. A., Belokurov, V., et al. 2007, ApJ, 669, 337 [NASA ADS] [CrossRef]
(In the text)
- Lamers, H. J. G. L.
M., Gieles, M., Bastian, N., et al. 2005, A&A, 441,
117 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Lauberts, A.
1982, in ESO/Uppsala survey of the ESO(B) atlas, European Southern
Observatory (ESO), Garching
(In the text)
- Lauberts, A.,
Holmberg, E. B., Schuster, H. E., & West, R. M. 1981, A&AS,
43, 307 [NASA ADS]
(In the text)
- Lyngå, G., in Studies of
the Milky Way from Centaurus to Norma. II. Open clusters, Lund
Medd. Astron. Obs. Ser. II, No. 140
(In the text)
- Lyngå, G. 1987, in
Catalogue of Open Cluster Data, Lund Observatory
(In the text)
- Mackey, A. D., &
Gilmore, G. F. 2003a, MNRAS, 338, 85 [NASA ADS] [CrossRef]
- Mackey, A. D., &
Gilmore, G. F. 2003b, MNRAS, 338, 120 [NASA ADS] [CrossRef]
- Mackey, A. D., &
Gilmore, G. F. 2003c, MNRAS, 340, 175 [NASA ADS] [CrossRef]
- Mackey, A. D., &
van den Bergh, S. 2005, MNRAS, 360, 631 [NASA ADS] [CrossRef]
(In the text)
- Origlia, L.,
& Rich, R. M. 2004, AJ, 127, 3422 [NASA ADS] [CrossRef]
(In the text)
- Ortolani, S., Bica, E.
& Barbuy, B. 1993, A&A, 273, 415 [NASA ADS]
(In the text)
- Ortolani, S., Bica, E.,
& Barbuy, B. 1995, A&A, 300, 726 [NASA ADS]
(In the text)
- Ortolani, S., Bica, E.,
& Barbuy, B. 1997, A&AS, 126, 319 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Ortolani, S., Bica, E.,
& Barbuy, B. 2000, A&A, 361, L57 [NASA ADS]
(In the text)
- Ortolani, S., Bica, E.,
& Barbuy, B. 2006, ApJ, 646, L115 [NASA ADS] [CrossRef]
(In the text)
- Ortolani, S., Barbuy,
B., Bica, E., Zoccali, M., & Renzini, A. 2007, A&A, 470,
1043 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Phelps, R. L., &
Schick, M. 2003, AJ, 126, 265 [NASA ADS] [CrossRef]
(In the text)
- Sakamoto, T.,
& Hasegawa, T. 2006, ApJ, 653, L29 [NASA ADS] [CrossRef]
(In the text)
- Sarajedini, A. 2004,
AJ, 128, 1228 [NASA ADS] [CrossRef]
(In the text)
- Spitzer, L. 1958,
ApJ 127, 17
(In the text)
- Tavarez, M.,
& Friel, E. 1995, AJ, 110, 223 [NASA ADS] [CrossRef]
(In the text)
- Terzan, A. 1971,
A&A, 15, 336 [NASA ADS]
(In the text)
- Trager, S., King, I. R.,
& Djorgovski, S. 1995, AJ, 109, 218 [NASA ADS] [CrossRef]
(In the text)
- Wielen, R. 1991, in
The Formation and Evolution of Star Clusters, ed. K. Janes, ASP
Conf. Ser., 13, San Francisco, CA, 343
(In the text)
- Willman, B.,
Blanton, M. R., West, A. A., et al. 2005, AJ, 129, 2692 [NASA ADS] [CrossRef]
(In the text)
- Wilson, C. P. 1975,
AJ, 80, 175 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig1.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg116.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig2.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg117.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig3.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg118.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig4.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg191.gif)
![\begin{displaymath}
\sigma(R)=\sigma_{\rm bg}+\sigma_0\left[\frac{1}{\sqrt{1+(R/...
...})^2}} -
\frac{1}{\sqrt{1+(R_{\rm t}/R_{\rm c})^2)}}\right]^2,
\end{displaymath}](/articles/aa/full/2008/09/aa8687-07/img192.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig5.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg194.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig6.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg198.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig7.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg206.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig8.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg207.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig9.eps}\end{figure}](/articles/aa/full/2008/09/aa8687-07/Timg210.gif)