A&A 479, 641-654 (2008)
DOI: 10.1051/0004-6361:20078435
The impact of Galactic synchrotron emission
on CMB anisotropy measurements
I. Angular power spectrum analysis of total intensity
all-sky surveys
L. La Porta1 -
C. Burigana2,3 -
W. Reich1 -
P. Reich1
1 - Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121 Bonn, Germany
2 -
INAF - IASF Bologna,
via P. Gobetti 101, 40129 Bologna, Italy
3 -
Dipartimento di Fisica,
Universita' degli Studi di Ferrara,
via Saragat 1, 44100 Ferrara, Italy
Received 7 August 2007 / Accepted 7 November 2007
Abstract
Context. Galactic foreground emission fluctuations are a limiting factor for precise cosmic microwave background (CMB) anisotropy measurements.
Aims. We intend to improve current estimates of the influence of Galactic synchrotron emission on the analysis of CMB anisotropies.
Methods. We perform an angular power spectrum analysis (APS) of all-sky total intensity maps at 408 MHz and 1420 MHz, which are dominated by synchrotron emission out of the Galactic plane. We subtract the brighter sources from the maps, which turns out to be essential for the results obtained. We study the APS as a function of Galactic latitude by considering various cuts and as a function of sky position by dividing the sky into patches of 
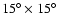 in size.
in size.
Results. The APS of the Galactic radio diffuse synchrotron emission is best fitted by a power law,
 ,
with
,
with
![$\alpha \in [-3.0,-2.6]$](/articles/aa/full/2008/09/aa8435-07/img43.gif) ,
where the lower values of
,
where the lower values of 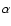 typically correspond to the higher latitudes. Nevertheless, the analysis of the patches reveals that strong local variations exist. A good correlation is found between the APS normalized amplitude,
typically correspond to the higher latitudes. Nevertheless, the analysis of the patches reveals that strong local variations exist. A good correlation is found between the APS normalized amplitude,
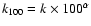 ,
at 408 MHz and 1420 MHz. The mean APS for
,
at 408 MHz and 1420 MHz. The mean APS for
![$\ell \in [20,40]$](/articles/aa/full/2008/09/aa8435-07/img46.gif) is used to determine the mean spectral index between 408 MHz and 1420 MHz,
is used to determine the mean spectral index between 408 MHz and 1420 MHz,
![$\beta_{(0.408-1.4)~~{\rm GHz}} \in [-3.2,-2.9]$](/articles/aa/full/2008/09/aa8435-07/img47.gif) (
(
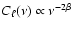 ), which is then adopted to extrapolate the synchrotron APS results to the microwave range.
), which is then adopted to extrapolate the synchrotron APS results to the microwave range.
Conclusions. We use the 408 MHz and 1420 MHz APS results to predict the Galactic synchrotron emission fluctuations at frequencies above 20 GHz. A simple extrapolation to 23 GHz of the synchrotron emission APS found at these radio frequencies does not explain all the power in the WMAP synchrotron component even at middle/high Galactic latitudes. This suggests a significant microwave contribution (of about 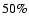 of the signal) by other components such as free-free or spinning dust emission. The comparison between the extrapolated synchrotron APS and the CMB APS shows that a mask excluding the regions with
of the signal) by other components such as free-free or spinning dust emission. The comparison between the extrapolated synchrotron APS and the CMB APS shows that a mask excluding the regions with
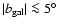 would reduce the foreground fluctuations to about half of the cosmological ones at 70 GHz even at the lowest multipoles. The main implications of our analysis for the cosmological exploitation of microwave temperature anisotropy maps are discussed.
would reduce the foreground fluctuations to about half of the cosmological ones at 70 GHz even at the lowest multipoles. The main implications of our analysis for the cosmological exploitation of microwave temperature anisotropy maps are discussed.
Key words: Galaxy: general - radiation mechanisms: non-thermal - methods: statistical -
cosmic microwave background
The possibility to study the primordial phases of our
Universe and its properties and evolution through CMB anisotropies
relies on our capability to precisely extract the cosmological signal
from observations (Tegmark et al. 2000).
Maps of the microwave sky include many
Galactic and extragalactic astrophysical contributions.
A correct recovery of the CMB anisotropy field requires
an accurate removal of those foreground signals from the
observed maps. Current knowledge of the foreground components
permits one to retrieve the bulk of the cosmological
information encoded in the CMB anisotropy, and, in particular,
its angular power spectrum (APS).
Nevertheless, a deeper understanding of the foregrounds is
crucial to settle important cosmological
issues, which arose from the
WMAP![[*]](/icons/foot_motif.gif) results
(Naselsky et al. 2006; Naselsky & Verkhodanov 2006; Chiang et al. 2007)
and could potentially be addressed by the forthcoming
P LANCK
results
(Naselsky et al. 2006; Naselsky & Verkhodanov 2006; Chiang et al. 2007)
and could potentially be addressed by the forthcoming
P LANCK![[*]](/icons/foot_motif.gif) mission (Tauber 2004).
Moreover, it would enable a precise reconstruction of the
individual foreground components and therefore
a complete astrophysical exploitation of the satellite data.
mission (Tauber 2004).
Moreover, it would enable a precise reconstruction of the
individual foreground components and therefore
a complete astrophysical exploitation of the satellite data.
Galactic synchrotron emission is the major source of
contamination at frequencies below 50 GHz
for intermediate and large angular scales,
as recently confirmed by the impressive WMAP results
(Bennett et al. 2003; Hinshaw et al. 2007).
Synchrotron radiation (Rybicki & Lightman 1979) arises
from cosmic ray electrons gyrating in the magnetic field
of our Galaxy.
The energy spectrum and the density of the cosmic ray electrons
as well as the magnetic field strength vary across the Galaxy,
therefore the observed synchrotron emission will depend
on the frequency and on the region of the sky.
Radio observations at
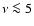 GHz provide
the clearest picture of the Galactic synchrotron morphology,
since at these frequencies the diffuse non-thermal radiation
clearly dominates over all other emission components
outside the Galactic plane.
In the past, the 408 MHz all-sky map (Haslam et al. 1982)
has extensively been used as a template for the
Galactic synchrotron emission in foreground separation attempts
(e.g. Bouchet & Gispert 1999; Bennett et al. 2003).
In addition, that map as well as other less suited
surveys have been exploited to find an appropriate
parametrization of the synchrotron emission APS to be
i) extrapolated to the microwave range for estimating the
contamination of CMB anisotropies at different angular scales
(Giardino et al. 2001; Baccigalupi et al. 2001)
and
ii) used to set priors in foreground separation applications
(Bouchet & Gispert 1999; Bouchet et al. 1999; Tegmark & Efstathiou 1996).
The outcome of these analyses is that the APS of the
synchrotron emission computed over large portions of the sky
can be modelled
by a power law, i.e.
GHz provide
the clearest picture of the Galactic synchrotron morphology,
since at these frequencies the diffuse non-thermal radiation
clearly dominates over all other emission components
outside the Galactic plane.
In the past, the 408 MHz all-sky map (Haslam et al. 1982)
has extensively been used as a template for the
Galactic synchrotron emission in foreground separation attempts
(e.g. Bouchet & Gispert 1999; Bennett et al. 2003).
In addition, that map as well as other less suited
surveys have been exploited to find an appropriate
parametrization of the synchrotron emission APS to be
i) extrapolated to the microwave range for estimating the
contamination of CMB anisotropies at different angular scales
(Giardino et al. 2001; Baccigalupi et al. 2001)
and
ii) used to set priors in foreground separation applications
(Bouchet & Gispert 1999; Bouchet et al. 1999; Tegmark & Efstathiou 1996).
The outcome of these analyses is that the APS of the
synchrotron emission computed over large portions of the sky
can be modelled
by a power law, i.e.
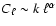 (
(
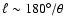 ), with a spectral
index
), with a spectral
index
![$\alpha \sim [-3,-2.5]$](/articles/aa/full/2008/09/aa8435-07/img54.gif) for
for
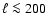 ,
corresponding
to angular scales
,
corresponding
to angular scales
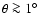 .
Clearly, such a general result is just a first step as it
does not describe the complexity of the synchrotron emission APS,
whose parameters are expected to change with frequency
and with sky direction.
.
Clearly, such a general result is just a first step as it
does not describe the complexity of the synchrotron emission APS,
whose parameters are expected to change with frequency
and with sky direction.
We have carried out a detailed analysis of all-sky radio
maps and improved on previous attempts by providing an
accurate characterization of the synchrotron
emission APS.
The results obtained for the new 1.4 GHz polarization
all-sky survey (Reich et al., in prep.) will be
reported in a forthcoming companion paper.
The analysis presented in this paper focuses on
the synchrotron emission APS in total intensity.
A substantial improvement was possible by using
a new all-sky map at 1.42 GHz (Reich et al., in prep.),
which has a higher angular resolution and better sensitivity,
in addition to the all-sky map at 408 MHz.
These maps are currently the best suited data
for studying the Galactic synchrotron emission
at largest angular scales.
A more detailed description of some technical aspects related to this work
can be found in La Porta (2007).
We extensively used the
HEALPix![[*]](/icons/foot_motif.gif) software package (Górski et al. 2005).
HEALPix (Hierarchical Equal Area
isoLatitude Pixelization) is a curvilinear partition of
the sphere optimized for fast spherical harmonics
transforms and angular power spectrum estimation.
The latter task is performed by the facility Anafast.
We also made use of the data reduction package
based on the NOD2-software (Haslam 1974).
software package (Górski et al. 2005).
HEALPix (Hierarchical Equal Area
isoLatitude Pixelization) is a curvilinear partition of
the sphere optimized for fast spherical harmonics
transforms and angular power spectrum estimation.
The latter task is performed by the facility Anafast.
We also made use of the data reduction package
based on the NOD2-software (Haslam 1974).
The paper is organized as follows.
Section 2 describes the characteristics of the 408 MHz
and 1.42 GHz total intensity surveys, their projection
onto HEALPix maps and noise considerations.
In Sect. 3 the Galactic radio emission APS
over large areas is examined, which reveals
the necessity of a discrete source subtraction
for a correct evaluation of the diffuse synchrotron APS.
The two all-sky maps are decomposed into a map of the
diffuse component and a map of discrete sources.
Their angular power spectra are derived and discussed.
The results obtained by fitting the angular power
spectra of the diffuse component maps are presented.
In Sect. 4 the radio survey angular power spectra
are extrapolated to the microwave range for a
comparison with the WMAP 3-yr results.
Sect. 5 is dedicated to a local analysis of the radio map APS.
We summarize our results and conclusions in Sect. 6.
The present analysis focuses on the APS of the
Galactic synchrotron emission at radio frequencies.
However, the 23 GHz synchrotron component obtained
by Hinshaw et al. (2007)
using the WMAP 3-yr data has also been
considered to some extent and will be further
discussed in Sect. 4.
The 408 MHz map (Haslam et al. 1982) was produced by merging
different datasets obtained with large parabolic reflector
telescopes (Jodrell Bank 76 m,
Effelsberg 100 m and Parkes 64 m telescopes -
see Fig. 1 of Haslam et al. 1982), using a similar
observing strategy and the same calibration procedure.
The final map is characterized by an angular resolution of
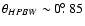 and a
and a
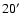 pixel rms-noise
of about 670 mK.
The version used in the present analysis was corrected
for a zero level problem concerning the portion of the sky observed
from Jodrell Bank (Reich & Reich 1988).
pixel rms-noise
of about 670 mK.
The version used in the present analysis was corrected
for a zero level problem concerning the portion of the sky observed
from Jodrell Bank (Reich & Reich 1988).
The total intensity map at 1420 MHz has been obtained by combining a northern and
a southern sky survey (Reich et al., in preparation).
Both surveys are on an absolute temperature scale and zero level
by using low resolution sky horn measurements (Testori et al. 2001).
This includes a correction for far-side lobe contamination
for single-dish telescopes.
Receiving systems were used, which provide total intensities unaffected by
linear polarization.
The northern sky survey
was observed with the Stockert 25-m telescope and
extends in declination from
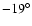 to
to
 (Reich 1982; Reich & Reich 1986).
The southern sky survey was carried out with the Villa Elisa 30-m telescope
in Argentina and covers the latitude range
(Reich 1982; Reich & Reich 1986).
The southern sky survey was carried out with the Villa Elisa 30-m telescope
in Argentina and covers the latitude range
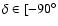 to
to
![$-10^{\circ}]$](/articles/aa/full/2008/09/aa8435-07/img62.gif) (Reich et al. 2001).
Both have an angular resolution
(Reich et al. 2001).
Both have an angular resolution
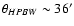 and overlap for latitudes in the range [
and overlap for latitudes in the range [
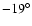 ,
,
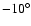 ].
The resulting map has a
].
The resulting map has a
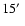 pixel rms-noise of
pixel rms-noise of 
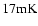 .
The original maps are provided
as equidistant cylindrical (ECP) maps.
For the present analysis these maps have been projected
into the HEALPix (Górski et al. 2005)
pixelization scheme adopted by the WMAP and
P LANCK Consortia.
For this purpose a simple regridding algorithm has been implemented,
which is described in detail by La Porta et al. (2005).
The reliability of the projection provided by this simple
approach has been verified by successfully performing forward
and backward transformations between the two tessellation
schemes.
The produced HEALPix maps have a pixel size
of
.
The original maps are provided
as equidistant cylindrical (ECP) maps.
For the present analysis these maps have been projected
into the HEALPix (Górski et al. 2005)
pixelization scheme adopted by the WMAP and
P LANCK Consortia.
For this purpose a simple regridding algorithm has been implemented,
which is described in detail by La Porta et al. (2005).
The reliability of the projection provided by this simple
approach has been verified by successfully performing forward
and backward transformations between the two tessellation
schemes.
The produced HEALPix maps have a pixel size
of  7' (the number of pixels for an all-sky map
is
7' (the number of pixels for an all-sky map
is
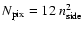 ;
here we used
;
here we used
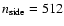 ).
).
The authors of the radio maps have estimated the rms-noise
directly on the ECP maps
by calculating the standard deviation of
low emission regions.
Going from a Cartesian representation of the sphere to the
HEALP IX scheme, the rms-noise per pixel should theoretically decrease
toward the polar caps, according to the formula:
where N is the number of the ECP pixels corresponding to each
HEALPix pixel at a fixed latitude. Such a relation
holds under the hypothesis that the noise is Gaussian
and uncorrelated among the pixels. Both these assumptions
are not necessarily satisfied in the examined surveys,
in primis because the pixel size is about half the angular resolution.
Furthermore, the rms-noise quoted for the 408 MHz and 1420 MHz surveys
quantifies the temperature fluctuations per pixel, which is
due not only to the
receiver white noise, but also to the
contribution of unresolved sources
and of residual systematics effects (as ``scanning strategy effects''),
that could not be fully eliminated in the data
reduction procedure.
The overall rms-noise in the HEALPix maps
is therefore probably higher than the guess determined
in this way, thus making this formula suitable for
deriving a lower limit.
With this formula we constructed
a map of rms-noise at both frequencies.
The rms-noise per pixel decreases for increasing latitude
and varies between  10 mK and
10 mK and  18.7 mK at 1420 MHz and
18.7 mK at 1420 MHz and  0.5 K and
0.5 K and  0.7 K at 408 MHz.
Due to varying integration times,
the rms-noise is not constant over the ECP map,
but it is expected to diminish toward the celestial poles.
Also taking this effect into account, while applying
the above formula, the derived estimate
decreases at most by a factor
0.7 K at 408 MHz.
Due to varying integration times,
the rms-noise is not constant over the ECP map,
but it is expected to diminish toward the celestial poles.
Also taking this effect into account, while applying
the above formula, the derived estimate
decreases at most by a factor  2.
This way we obtain an optimistic lower limit for the rms-noise
in the HEALPix maps.
The corresponding APS is computed as:
2.
This way we obtain an optimistic lower limit for the rms-noise
in the HEALPix maps.
The corresponding APS is computed as:
where 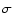 is the mean value of the rms-noise
in the considered area and
is the mean value of the rms-noise
in the considered area and
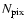 is the total
number of pixels in the HEALPix map.
A generous upper limit for the noise APS is provided instead by
the high multipole tail of the APS.
This way we have bracketed the noise APS for each
considered sky region.
is the total
number of pixels in the HEALPix map.
A generous upper limit for the noise APS is provided instead by
the high multipole tail of the APS.
This way we have bracketed the noise APS for each
considered sky region.
The HEALPix maps produced at 408 MHz and 1420 MHz contain precise
statistical information only for angular scales that are:
- -
- larger than the beam,
i.e. for
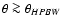 ,
therefore the maximum multipole
relevant in the APS analysis of these surveys is
,
therefore the maximum multipole
relevant in the APS analysis of these surveys is
![$\ell_{\rm max} \sim 180^{\circ}/\theta_{HPBW}[^{\circ}]$](/articles/aa/full/2008/09/aa8435-07/img74.gif) ;
;
- -
- smaller than the maximum angular extent of the considered
area,
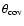 ,
so that the coverage sets the minimum
multipole. A safe choice is
,
so that the coverage sets the minimum
multipole. A safe choice is
![$\ell_{\rm min} \sim 5 \times 180^{\circ}/\theta_{\rm cov}[^{\circ}]$](/articles/aa/full/2008/09/aa8435-07/img76.gif) .
.
To investigate the dependence of the synchrotron emission APS parameters
on latitude, the Galactic plane has been ``cut off'' from the maps at
different latitudes by setting to zero pixels with
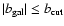 ,
where
,
where
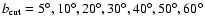 .
At the same time,
this approach preserves the largest possible coverage,
important to keep the widest range of statistically significant multipoles.
We also considered ``asymmetric cuts'', i.e. regions
with
.
At the same time,
this approach preserves the largest possible coverage,
important to keep the widest range of statistically significant multipoles.
We also considered ``asymmetric cuts'', i.e. regions
with
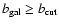 (northern cuts)
and
(northern cuts)
and
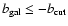 (southern cuts),
thus taking into account the difference
between the two Galactic hemispheres.
In fact, the northern hemisphere contains a large and bright feature of
the radio sky, i.e. the North Polar Spur (NPS), which is
widely believed to be
an old supernova remnant in the Solar System
vicinity (Salter 1983; Egger & Aschenbach 1995).
(southern cuts),
thus taking into account the difference
between the two Galactic hemispheres.
In fact, the northern hemisphere contains a large and bright feature of
the radio sky, i.e. the North Polar Spur (NPS), which is
widely believed to be
an old supernova remnant in the Solar System
vicinity (Salter 1983; Egger & Aschenbach 1995).
We computed the corresponding APS by using the facility
Anafast of the HEALPix package and renormalized
it to account for the incomplete sky coverage.
The angular power spectra derived for
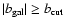 with
with
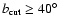 are shown in Fig. 1, as representative examples.
All the recovered angular power spectra
flatten towards higher multipoles.
Such a behaviour of the APS might be due to noise,
systematic effects (``stripes''), discrete sources or might be an
intrinsic characteristic of the synchrotron emission
fluctuation field.
Instrumental white noise can be discarded because its APS should be
constant, whereas after the flattening the angular power spectra
decrease with
are shown in Fig. 1, as representative examples.
All the recovered angular power spectra
flatten towards higher multipoles.
Such a behaviour of the APS might be due to noise,
systematic effects (``stripes''), discrete sources or might be an
intrinsic characteristic of the synchrotron emission
fluctuation field.
Instrumental white noise can be discarded because its APS should be
constant, whereas after the flattening the angular power spectra
decrease with 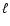 as
in the presence of beam smoothing.
``Stripes'' are systematic baseline
distortions in the telescope's scanning direction
and are mainly due to the limited stability of the
receiving system and to the influence of weather conditions.
They could also be cancelled from the list of possible
causes from the comparison with a destriped version
of the 408 MHz map
(Platania et al. 2003).
The cut-off APS of the two versions of the 408 MHz map
present only marginal differences at intermediate multipoles
(see Fig. 2).
as
in the presence of beam smoothing.
``Stripes'' are systematic baseline
distortions in the telescope's scanning direction
and are mainly due to the limited stability of the
receiving system and to the influence of weather conditions.
They could also be cancelled from the list of possible
causes from the comparison with a destriped version
of the 408 MHz map
(Platania et al. 2003).
The cut-off APS of the two versions of the 408 MHz map
present only marginal differences at intermediate multipoles
(see Fig. 2).
![\begin{figure}
\par\includegraphics[height=8.8cm,width=4.7cm,angle=90,clip]{8435f01.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg84.gif) |
Figure 1:
Angular power spectra of the Galactic plane cut-offs
(
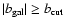 )
at radio frequencies.
Each line refers to a certain )
at radio frequencies.
Each line refers to a certain
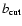 ( from the bottom: black
( from the bottom: black
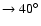 ,
fuchsia ,
fuchsia
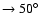 ,
green ,
green
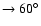 ). ).
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.2cm,height=8.5cm,angle=90,clip]{8435f02.ps}\end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg85.gif) |
Figure 2:
Comparison between the cut-off angular power spectra of the original
(fuchsia lines at the top) and destriped (blue) version of the 408 MHz map.
The cut-off angular power spectra of the difference map are also shown
(green lines at the bottom). |
| Open with DEXTER |
3.1 Discrete source subtraction
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=4.5cm,angle=90]{84...
...ncludegraphics[width=4.5cm,angle=90]{8435f03b.ps}\\
\end{tabular} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg86.gif) |
Figure 3:
Mollweide projection of the HEALPix maps produced
at 408 MHz ( top) and 1420 MHz ( bottom)
by subtracting the discrete sources.
The maps are in Galactic coordinates.
The center of the maps is
l = 0 , b = 0.
The Galactic longitude increases
toward the left up to
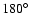 . .
|
| Open with DEXTER |
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=2.3cm,angle=90,cl...
... &
\includegraphics[width=3cm,clip]{8435f04f.ps}\\
\end{tabular} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg87.gif) |
Figure 4:
HEALPix maps of the Galactic plane cut-offs
extracted from the 1.4 GHz all-sky map after DS subtraction.
A mollweide projection is displayed for the cuts with
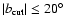 and a gnomonic view (centered on a
Galactic pole)
for those with
and a gnomonic view (centered on a
Galactic pole)
for those with
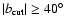 . .
|
| Open with DEXTER |
Beside diffuse emission, a large number of discrete sources (DSs)
are visible in the radio maps. A DS subtraction has been done
by performing a 2-dimensional Gaussian fitting that
also provides an estimate of the diffuse
background, which is approximated by a tilted plane.
Such an estimate has been used to fill the pixels originally
corresponding to the subtracted DSs.
Where the background emission shows strong gradients
the source fitting is more difficult.
Consequently, the flux limit above which all discrete
sources most likely have been subtracted is different close to the
plane and far out of it.
Namely, for
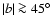 all the sources with
peak flux above
all the sources with
peak flux above  0.8 Jy (respec.
0.8 Jy (respec.  6.4 Jy)
have been subtracted from the 1420 MHz (respec. 408 MHz),
whereas for
6.4 Jy)
have been subtracted from the 1420 MHz (respec. 408 MHz),
whereas for
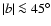 such a
source detection threshold
is
such a
source detection threshold
is  4.6 Jy (respec.
4.6 Jy (respec.  63.8 Jy).
All discrete sources that could be reasonably fitted by
a Gaussian profile have been eliminated and two new maps have been
generated at 408 MHz and at 1420 MHz (Fig. 3).
63.8 Jy).
All discrete sources that could be reasonably fitted by
a Gaussian profile have been eliminated and two new maps have been
generated at 408 MHz and at 1420 MHz (Fig. 3).
The subtracted DSs (see Burigana et al. 2006, for
a map) are mostly point sources,
except for some rather extended objects, as
for instance the radiogalaxy Centaurus A,
appearing in the original radio maps right of the
Galactic center at
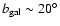 .
Such extended objects are among the brighter subtracted DSs and concentrate
along or in the proximity of the Galactic plane.
They are mainly Galactic sources, i.e. HII-regions
or supernova remnants.
On the contrary, the DSs subtracted at medium and high latitudes
are nearly all extragalactic sources.
.
Such extended objects are among the brighter subtracted DSs and concentrate
along or in the proximity of the Galactic plane.
They are mainly Galactic sources, i.e. HII-regions
or supernova remnants.
On the contrary, the DSs subtracted at medium and high latitudes
are nearly all extragalactic sources.
The maps of some Galactic plane cut-offs at 1420 MHz (respec. 408 MHz)
after DS subtraction are shown in
Fig. 4 (respec. Fig. 5).
The maps are displayed adopting different scales, in order
to emphasize the relative importance of the various components.
Note that ``scanning strategy effects'' are clearly visible
in the southern sky at high latitude in the map at 408 MHz.
As discussed above,
the angular power spectra of the destriped and original
versions of the Haslam map do not exhibit significant differences,
thus implying that ``stripes'' are not
an issue for the APS analysis at 1420 MHz.
Figure 6 (respec. Fig. 7)
shows the APS of the Galactic plane cut-offs at 1420 MHz (respec. 408 MHz)
for the original map, for the DS-subtracted map and
for the map of subtracted DSs.
The APS of the DS maps almost perfectly matches the flat
part of the original map APS at large 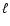 .
This result
identifies DSs as the reason for the flattening of
the original APS and also confirms that the major contribution
from source contamination has been eliminated in the
DS-subtracted maps.
At high latitude the APS of the Galactic fluctuation
field is dominated by the DS contribution
for
.
This result
identifies DSs as the reason for the flattening of
the original APS and also confirms that the major contribution
from source contamination has been eliminated in the
DS-subtracted maps.
At high latitude the APS of the Galactic fluctuation
field is dominated by the DS contribution
for
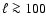 ,
which is due to the enhanced
relative contribution of the DSs respect to the weak diffuse
background emission.
,
which is due to the enhanced
relative contribution of the DSs respect to the weak diffuse
background emission.
![\begin{figure}
\par\includegraphics[width=5.2cm,height=8.8cm,angle=90,clip]{8435f06.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg93.gif) |
Figure 6:
APS of some Galactic plane cut-off for the 1420 MHz maps:
(from the top in each panel)
original (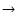 fuchsia), after discrete source subtraction (
fuchsia), after discrete source subtraction (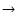 blue)
and DSs only (
blue)
and DSs only (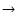 green).
green). |
| Open with DEXTER |
Figure 8 shows
the APS of the various cuts for the DS map at 1420 MHz.
Note that for all the southern cuts and for the northern cuts
with
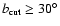 the DS angular power spectra
are rather flat up to
the DS angular power spectra
are rather flat up to
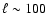 and then
decrease as for a beam smoothing.
On the contrary, for the northern cut at
and then
decrease as for a beam smoothing.
On the contrary, for the northern cut at
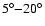 the DS angular power spectra present a power law behaviour
at lower multipoles, that implies the existence of significant
fluctuations also at the larger angular scales, as expected
in presence of relatively extended discrete structures.
The DS APS of the cut at
the DS angular power spectra present a power law behaviour
at lower multipoles, that implies the existence of significant
fluctuations also at the larger angular scales, as expected
in presence of relatively extended discrete structures.
The DS APS of the cut at
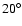 is superimposed
on that of the cut at
is superimposed
on that of the cut at
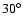 for
for
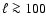 ,
whereas it exhibits a power law behaviour at lower multipoles.
The difference between the angular power spectra of the northern cuts
at
,
whereas it exhibits a power law behaviour at lower multipoles.
The difference between the angular power spectra of the northern cuts
at
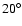 and
and
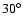 is then due to the DSs located in
the portion of the sky characterized by
is then due to the DSs located in
the portion of the sky characterized by
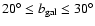 ,
which includes Centaurus A,
thus explaining the power law behaviour of the APS at the
lower multipoles.
The same situation was found at 408 MHz.
,
which includes Centaurus A,
thus explaining the power law behaviour of the APS at the
lower multipoles.
The same situation was found at 408 MHz.
![\begin{figure}
\par\includegraphics[width=4cm,height=8.5cm,angle=90,clip]{8435f08.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg103.gif) |
Figure 8:
Angular power spectra of the northern (
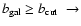 left panel) and southern (
left panel) and southern (
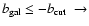 right)
cuts for the map of discrete sources at 1420 MHz.
Color legend (see online version):
black (dotted)
right)
cuts for the map of discrete sources at 1420 MHz.
Color legend (see online version):
black (dotted)
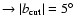 ,
black ,
black
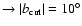 ,
green ,
green
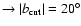 ,
red ,
red
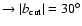 ,
dark blue ,
dark blue
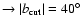 ,
fuchsia ,
fuchsia
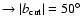 ,
light blue ,
light blue
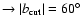 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[height=8.5cm,angle=90,clip]{8435f09.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg104.gif) |
Figure 9:
Comparison between the APS of the cuts for the DS-subtracted map
at 1420 MHz.
The left (respec. right) panels display the angular power spectra
of the northern (respec. southern) cuts.
First (respec. second) row panels:
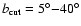 (respec.
(respec.
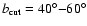 ).
Color legend (see online version):
black dotted ).
Color legend (see online version):
black dotted
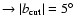 ,
black ,
black
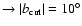 ,
green ,
green
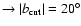 ,
red ,
red
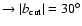 ,
dark blue ,
dark blue
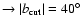 ,
fuchsia ,
fuchsia
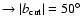 ,
dark green ,
dark green
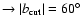 . .
|
| Open with DEXTER |
The angular power spectra of the maps after source subtraction
approximately follow a power law, as expected for the diffuse
Galactic synchrotron emission.
For
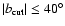 the angular power spectra of
all symmetric (
the angular power spectra of
all symmetric (
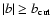 )
and
asymmetric (
)
and
asymmetric (
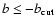 ,
,
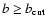 )
Galactic cuts
are very similar to each other and appear progressively shifted
downward (see top panels of Fig. 9).
This result reflects the fact that the Galactic
diffuse emission becomes weaker for increasing latitude.
The angular power spectra of the symmetric cuts
with
)
Galactic cuts
are very similar to each other and appear progressively shifted
downward (see top panels of Fig. 9).
This result reflects the fact that the Galactic
diffuse emission becomes weaker for increasing latitude.
The angular power spectra of the symmetric cuts
with
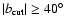 are superimposed.
The same result holds for the angular power
spectra of the northern cuts, whereas in the southern hemisphere
the APS amplitude decreases for increasing
are superimposed.
The same result holds for the angular power
spectra of the northern cuts, whereas in the southern hemisphere
the APS amplitude decreases for increasing
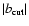 .
This discrepancy leads to the conclusion that the angular
power spectra of the symmetric cuts with
.
This discrepancy leads to the conclusion that the angular
power spectra of the symmetric cuts with
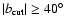 are mainly influenced by the northern hemisphere.
Indeed, the angular power spectra of the northern
cuts at
are mainly influenced by the northern hemisphere.
Indeed, the angular power spectra of the northern
cuts at
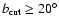 have amplitudes
larger than those of the southern cuts at both frequencies.
As an example, Fig. 10 shows the
comparison between the angular power spectra of the
northern and the southern cuts at 1420 MHz.
The angular power spectra of the two Galactic hemispheres
can reasonably be expected to be similar for the Galactic diffuse
synchrotron emission, while they turn out to be different in
amplitude and to some extent (mostly at smaller scales)
in shape. That difference results from the combination of two effects.
In the southern sky, the angular power spectra of the DS-subtracted maps
tend to flatten at
have amplitudes
larger than those of the southern cuts at both frequencies.
As an example, Fig. 10 shows the
comparison between the angular power spectra of the
northern and the southern cuts at 1420 MHz.
The angular power spectra of the two Galactic hemispheres
can reasonably be expected to be similar for the Galactic diffuse
synchrotron emission, while they turn out to be different in
amplitude and to some extent (mostly at smaller scales)
in shape. That difference results from the combination of two effects.
In the southern sky, the angular power spectra of the DS-subtracted maps
tend to flatten at
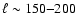 due to the presence
of unsubtracted sources, whose relative contribution to the fluctuation
field increases because of the low background signal.
In the northern hemisphere, the Galactic diffuse synchrotron
emission is strongly influenced by the radiation of the NPS.
due to the presence
of unsubtracted sources, whose relative contribution to the fluctuation
field increases because of the low background signal.
In the northern hemisphere, the Galactic diffuse synchrotron
emission is strongly influenced by the radiation of the NPS.
![\begin{figure}
\par\includegraphics[width=3.8cm,height=8.6cm,angle=90,clip]{8435f10.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg112.gif) |
Figure 10:
Comparison between the angular power spectra of the northern
(
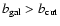 , ,
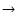 blue - upper lines) and
southern (
blue - upper lines) and
southern (
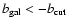
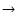 red - lower)
cuts for the DS-subtracted map at 1420 MHz.
red - lower)
cuts for the DS-subtracted map at 1420 MHz.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.7cm,height=8.8cm,angle=90,clip]{8435f11.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg113.gif) |
Figure 11:
Angular power spectra of the northern ( top panels)
and southern cuts ( bottom) for the DS-subtracted map at 1420 MHz
together with the best fit curves obtained. The individual contributions
of synchrotron emission (blue lines) and of sources (green lines)
are also plotted (smoothed by the beam).
|
| Open with DEXTER |
3.3 Fit of the APS after source subtraction
The radio maps after source subtraction include
two astrophysical components:
the Galactic diffuse emission and the
(mainly) extragalactic source contribution, which
are convolved with the telescope beam and
contaminated by the instrument noise, that
can be approximately treated as white noise.
We therefore express the corresponding APS as
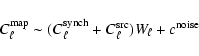 |
(1) |
where
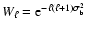 is the window function of the symmetric and Gaussian
beam
is the window function of the symmetric and Gaussian
beam![[*]](/icons/foot_motif.gif) ,
with
,
with
![$\sigma_{\rm b}=\theta_{HPBW}[rad]/\sqrt{8{\rm ln}2}$](/articles/aa/full/2008/09/aa8435-07/img117.gif) .
The synchrotron emission APS is empirically modelled
as
.
The synchrotron emission APS is empirically modelled
as
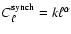 .
We note that such an empirical choice qualitatively can be explained by
magnetohydrodynamic turbulence arguments
(Cho & Lazarian 2003; Chepurnov 1998; Cho & Lazarian 2002).
The contribution of the unsubtracted DSs is approximated
by a constant term, according to the formalism of Poisson
fluctuations from extragalactic point sources (Franceschini et al. 1989).
The contribution of fluctuations due to source clustering
is expected to be negligible with respect to the Poisson term
at the source detection threshold achieved in our
maps (Toffolatti et al. 1998).
.
We note that such an empirical choice qualitatively can be explained by
magnetohydrodynamic turbulence arguments
(Cho & Lazarian 2003; Chepurnov 1998; Cho & Lazarian 2002).
The contribution of the unsubtracted DSs is approximated
by a constant term, according to the formalism of Poisson
fluctuations from extragalactic point sources (Franceschini et al. 1989).
The contribution of fluctuations due to source clustering
is expected to be negligible with respect to the Poisson term
at the source detection threshold achieved in our
maps (Toffolatti et al. 1998).
Table 1:
Best fit parameters obtained by modelling
the angular power spectra of the northern and southern
cuts at 1420 MHz according to Eq. (1).
In order to derive the range of variability of the synchrotron
emission amplitude and slope, two extreme
cases have been considered (see Appendix C of La Porta 2007
for
details).
The flattest synchrotron APS compatible with the data
is found by neglecting
the source term in Eq. (1)
and the steepest one is recovered by assuming a
null noise contribution
and maximizing the source term.
We performed a least-square fit to the APS by exploring the
parameter space on adaptive grids![[*]](/icons/foot_motif.gif) .
The uncertainties on the best fit parameters are
derived as the difference with those obtained in
the two extreme cases.
Figures 11 and 12
show the angular power spectra and the best fit curves
corresponding to the best model at the two frequencies,
while Tables 1 and 2
list the obtained parameters and their uncertainties.
For the synchrotron term, we quote the value of the normalized
amplitude
.
The uncertainties on the best fit parameters are
derived as the difference with those obtained in
the two extreme cases.
Figures 11 and 12
show the angular power spectra and the best fit curves
corresponding to the best model at the two frequencies,
while Tables 1 and 2
list the obtained parameters and their uncertainties.
For the synchrotron term, we quote the value of the normalized
amplitude
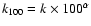 ,
which
corresponds to a physical quantity.
In fact,
,
which
corresponds to a physical quantity.
In fact,
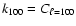 ,
thus implying that
the normalized amplitude gives the mean temperature
fluctuations at angular scales of
,
thus implying that
the normalized amplitude gives the mean temperature
fluctuations at angular scales of 
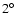 .
Figure 13 shows the best
fit parameters of the synchrotron APS as a function of the
Galactic latitude. The normalized amplitude, k100,
is maximum when the considered cut includes the lower
latitudes, where the Galactic radio emission peaks.
In particular, at 408 MHz (respec. at 1420 MHz)
.
Figure 13 shows the best
fit parameters of the synchrotron APS as a function of the
Galactic latitude. The normalized amplitude, k100,
is maximum when the considered cut includes the lower
latitudes, where the Galactic radio emission peaks.
In particular, at 408 MHz (respec. at 1420 MHz)
![$k_{100} \in [488,6527]\;{\rm mK}^2$](/articles/aa/full/2008/09/aa8435-07/img194.gif) (respec.
(respec.
![$[0.21,4.57]\;{\rm mK}^2$](/articles/aa/full/2008/09/aa8435-07/img195.gif) )
for the northern cuts and
)
for the northern cuts and
![$k_{100} \in [138,6734]\;{\rm mK}^2$](/articles/aa/full/2008/09/aa8435-07/img196.gif) (respec.
(respec.
![$[0.03,4.00]\;{\rm mK}^2$](/articles/aa/full/2008/09/aa8435-07/img197.gif) )
for the southern cuts.
The mean error on k100 is of
)
for the southern cuts.
The mean error on k100 is of

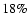 for the cuts at the lower
latitude (
for the cuts at the lower
latitude (
![$\vert b_{\rm cut}\vert \in [5^{\circ},30^{\circ}]$](/articles/aa/full/2008/09/aa8435-07/img199.gif) )
and of
)
and of 
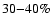 for the others. The
uncertainty is larger for the cuts at higher
latitude due to the reduced multipole range suitable
for the fitting procedure.
The slope of the synchrotron APS for the northern cuts
varies in the interval
for the others. The
uncertainty is larger for the cuts at higher
latitude due to the reduced multipole range suitable
for the fitting procedure.
The slope of the synchrotron APS for the northern cuts
varies in the interval  [-3.0,-2.8] at 408 MHz and
[-3.0,-2.8] at 408 MHz and  [-3.0,-2.7] at 1420 MHz, while in the southern cuts
[-3.0,-2.7] at 1420 MHz, while in the southern cuts
![$\alpha \sim [-2.9,-2.6]$](/articles/aa/full/2008/09/aa8435-07/img201.gif) and
and
![$\alpha \sim [-3.0,-2.7]$](/articles/aa/full/2008/09/aa8435-07/img202.gif) ,
respectively. The errors
on
,
respectively. The errors
on 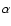 are on average
are on average 
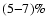 for
for
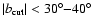 and
typically increase to
and
typically increase to 
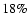 for cuts at higher
latitude.
for cuts at higher
latitude.
At both frequencies there is no evidence of a
systematic dependence of the synchrotron
emission APS slope on latitude
(see Fig. 13).
Table 2:
As in Table 1 but at 408 MHz.
![\begin{figure}
\par\mbox{\includegraphics[width=4.2cm,height=4.4cm,clip]{8435f13...
...m}
\includegraphics[width=4.2cm,height=4.4cm,clip]{8435f13b.ps} }
\end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg261.gif) |
Figure 13:
Best-fit parameters obtained for the Galactic radio synchrotron emission APS
against Galactic latitude. |
| Open with DEXTER |
The source term
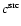 increases
for decreasing latitude, as expected given that the
source subtraction is less complete below
increases
for decreasing latitude, as expected given that the
source subtraction is less complete below 
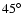 .
From extragalactic source counts at 1.4 GHz in total intensity
(Prandoni et al. 2001), the expected source contribution is
.
From extragalactic source counts at 1.4 GHz in total intensity
(Prandoni et al. 2001), the expected source contribution is
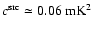 for flux densities below
for flux densities below  1 Jy
(
1 Jy
(
![$c^{\rm src}\simeq [0.03{-}0.3] {\rm ~mK}^2$](/articles/aa/full/2008/09/aa8435-07/img264.gif) including
the quoted
including
the quoted 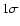 errors and also considering
the effect of the finite sampling) and
errors and also considering
the effect of the finite sampling) and
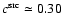 mK2 (
mK2 (
![$c^{\rm src}\simeq [0.15{-}1.50]$](/articles/aa/full/2008/09/aa8435-07/img267.gif) mK2 )
for flux densities below
mK2 )
for flux densities below  5 Jy.
At 408 MHz the available source counts (Jamrozy 2004)
lead to
5 Jy.
At 408 MHz the available source counts (Jamrozy 2004)
lead to
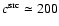 mK2 for
flux densities below
mK2 for
flux densities below  6.4 Jy
(
6.4 Jy
(
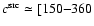 mK2) and
mK2) and
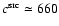 mK2 for flux densities below
mK2 for flux densities below  64 Jy
(
64 Jy
(
![$c^{\rm src}\simeq [260{-}1150]~{\rm mK}^2$](/articles/aa/full/2008/09/aa8435-07/img271.gif) ).
The values resulting from the fits are consistent with the
above estimates.
).
The values resulting from the fits are consistent with the
above estimates.
4 Extrapolation to the microwave range
In this section we extrapolate the results obtained
from the analysis of the 408 MHz and 1420 MHz surveys
over large areas to the microwave range, in order to
make a direct comparison with the WMAP 3-yr results.
The main objective of the WMAP mission was the
realization of a CMB anisotropy total intensity map
and the estimation of the corresponding APS.
By-products of the mission are maps of the foregrounds
contaminating the cosmological signal at
the five frequencies observed by
the satellite (
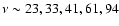 GHz), i.e.
the microwave emission from the Milky Way, characterized
by diffuse (dust, free-free, synchrotron)
and discrete (e.g., H II regions, SNRs) components,
and from extragalactic sources.
The maps were worked out (Hinshaw et al. 2007) by using
templates of the various astrophysical components,
constructed by exploiting ancillary data.
Then a pixel-by-pixel (MEM based) fit of all the maps
(see Bennett et al. 2003, for a description of the method),
i.e. templates and WMAP frequency maps after subtraction
of the CMB anisotropy field,
was performed posing some priors on the
spectral behaviour of the foregrounds.
GHz), i.e.
the microwave emission from the Milky Way, characterized
by diffuse (dust, free-free, synchrotron)
and discrete (e.g., H II regions, SNRs) components,
and from extragalactic sources.
The maps were worked out (Hinshaw et al. 2007) by using
templates of the various astrophysical components,
constructed by exploiting ancillary data.
Then a pixel-by-pixel (MEM based) fit of all the maps
(see Bennett et al. 2003, for a description of the method),
i.e. templates and WMAP frequency maps after subtraction
of the CMB anisotropy field,
was performed posing some priors on the
spectral behaviour of the foregrounds.
4.1 Comparison with the WMAP K-band synchrotron component
The 23 GHz (K-band) synchrotron map by Hinshaw et al. (2007)
is considered in this section for a comparison
with the 408 MHz and 1420 MHz data.
It is evident that such a map provides a picture of the global
non-thermal emission observed by the satellite at 23 GHz, rather
than the Galactic synchrotron component only. Several
extragalactic sources are clearly recognizable.
Furthermore, as pointed out by Hinshaw et al. (2007),
the diffuse non-thermal emission is concentrated at low
latitudes and appears remarkably well correlated with the
dust component![[*]](/icons/foot_motif.gif) .
This might suggest the presence at 23 GHz
of anomalous dust emission, as due for example to spinning
dust grains (Draine & Lazarian 1998). In fact, most dusty active star-forming
regions are localized along the Galactic plane.
This hypothesis seems further
supported by the joint analysis of the WMAP maps
(1-yr release) and the Green Bank Galactic Plane
Survey by Finkbeiner (2004).
De Oliveira-Costa et al. (2004) estimated the fluctuations
expected at 10 GHz and 15 GHz for the foreground component traced
by the K-MEM synchrotron map by Bennett et al. (2003) (1-yr
results), by cross-correlating the latter with the
Tenerife 10 GHz and 15 GHz CMB maps and all the WMAP CMB maps.
They found values one order of magnitude below what is expected
for the synchrotron emission and
concluded that the K-MEM synchrotron component
by Bennett et al. (2003) is dominated by anomalous dust
emission even at
.
This might suggest the presence at 23 GHz
of anomalous dust emission, as due for example to spinning
dust grains (Draine & Lazarian 1998). In fact, most dusty active star-forming
regions are localized along the Galactic plane.
This hypothesis seems further
supported by the joint analysis of the WMAP maps
(1-yr release) and the Green Bank Galactic Plane
Survey by Finkbeiner (2004).
De Oliveira-Costa et al. (2004) estimated the fluctuations
expected at 10 GHz and 15 GHz for the foreground component traced
by the K-MEM synchrotron map by Bennett et al. (2003) (1-yr
results), by cross-correlating the latter with the
Tenerife 10 GHz and 15 GHz CMB maps and all the WMAP CMB maps.
They found values one order of magnitude below what is expected
for the synchrotron emission and
concluded that the K-MEM synchrotron component
by Bennett et al. (2003) is dominated by anomalous dust
emission even at
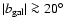 .
Hildebrandt et al. (2007) also found evidence for
anomalous microwave emission at high Galactic latitudes
by cross-correlating the COSMOSOMAS 11 GHz observations
with the WMAP K- and Ka-band map.
The same conclusion also was reached by Davies et al. (2006),
who cross-correlated the WMAP 1-yr map with foreground templates
in a dozen small patches located at medium and high latitude.
However, the origin of the spatial correlation
found at WMAP frequencies between synchrotron
and dust emission is still a matter of debate.
Bennett et al. (2003) claim that
the observed correlation is
the result of a spatially varying synchrotron
spectral index, which significantly alters the
morphology of the synchrotron emission with frequency.
Hinshaw et al. (2007) affirm that the issue is
left open also by the WMAP 3-yr results and that
high quality and large coverage surveys at
.
Hildebrandt et al. (2007) also found evidence for
anomalous microwave emission at high Galactic latitudes
by cross-correlating the COSMOSOMAS 11 GHz observations
with the WMAP K- and Ka-band map.
The same conclusion also was reached by Davies et al. (2006),
who cross-correlated the WMAP 1-yr map with foreground templates
in a dozen small patches located at medium and high latitude.
However, the origin of the spatial correlation
found at WMAP frequencies between synchrotron
and dust emission is still a matter of debate.
Bennett et al. (2003) claim that
the observed correlation is
the result of a spatially varying synchrotron
spectral index, which significantly alters the
morphology of the synchrotron emission with frequency.
Hinshaw et al. (2007) affirm that the issue is
left open also by the WMAP 3-yr results and that
high quality and large coverage surveys at
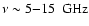 are needed
for a decisive test of both the above discussed
explanations of the synchrotron-dust correlation.
are needed
for a decisive test of both the above discussed
explanations of the synchrotron-dust correlation.
The separation of the free-free and synchrotron
emission in low latitude regions is also very uncertain.
On one hand, the 408 MHz map used as a template of the non-thermal
emission contains a non-negligible contribution (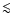
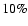 )
of
free-free at lower latitudes (Dickinson et al. 2003; Paladini et al. 2005).
On the other hand, the H
)
of
free-free at lower latitudes (Dickinson et al. 2003; Paladini et al. 2005).
On the other hand, the H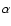 map used as
template for the free-free emission (Finkbeiner 2003)
cannot be properly corrected for dust extinction
for
map used as
template for the free-free emission (Finkbeiner 2003)
cannot be properly corrected for dust extinction
for
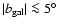 ,
thus potentially leading
to an underestimation of the expected
thermal emission at 23 GHz.
The situation in the vicinity of the Galactic plane
is extremely complicated and remains unclear.
,
thus potentially leading
to an underestimation of the expected
thermal emission at 23 GHz.
The situation in the vicinity of the Galactic plane
is extremely complicated and remains unclear.
The extrapolation of the angular power
spectra derived at 408 MHz and 1420 MHz
to the microwave range is a delicate issue.
The astrophysical components contributing to
the fluctuation field APS of the radio
surveys scale with frequency in a different way.
For the Galactic radio emission between 408 MHz and 1420 MHz
Reich et al. (2004) compiled a map of the
spectral index 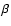 (
(
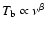 )
that
reveals a complex structure, due to superposition
of the spectral behaviour of the map components
(synchrotron emission, sources, free-free).
The situation is further complicated by
a possible but not well known
steepening of the diffuse synchrotron emission
power spectrum above 10 GHz, due to the steepening
of the cosmic ray electron energy spectrum
(Banday & Wolfendale 1991; Strong et al. 2007; Banday & Wolfendale 1990).
Last but not least, the fact that the astrophysical
components of the map scale with frequency in a different way
may imply a change in the overall
APS shape, since the relative weight of the
foreground contribution to the APS could
vary significantly.
)
that
reveals a complex structure, due to superposition
of the spectral behaviour of the map components
(synchrotron emission, sources, free-free).
The situation is further complicated by
a possible but not well known
steepening of the diffuse synchrotron emission
power spectrum above 10 GHz, due to the steepening
of the cosmic ray electron energy spectrum
(Banday & Wolfendale 1991; Strong et al. 2007; Banday & Wolfendale 1990).
Last but not least, the fact that the astrophysical
components of the map scale with frequency in a different way
may imply a change in the overall
APS shape, since the relative weight of the
foreground contribution to the APS could
vary significantly.
Given the complexity of the open issues discussed above,
the following analysis merely aims to verify the consistency
between the information about the non-thermal radiation
APS coming from the 408 MHz and 1420 MHz data and
from the 23 GHz WMAP data.
We focused on what happens at medium and high
Galactic latitudes, since the problems in interpreting the Galactic
emission are more complicated close to the plane.
![\begin{figure}
\par\includegraphics[width=6.3cm,height=8.7cm,angle=90,clip]{8435f14.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg283.gif) |
Figure 14:
Angular power spectra of the DS-subtracted radio maps
(green 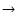 408 MHz, fuchsia
408 MHz, fuchsia 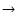 1420 MHz) extrapolated
to 23 GHz for a direct comparison with those of the WMAP 3-yr
DS-subtracted synchrotron component (blue).
The radio angular power spectra have been smoothed to
1420 MHz) extrapolated
to 23 GHz for a direct comparison with those of the WMAP 3-yr
DS-subtracted synchrotron component (blue).
The radio angular power spectra have been smoothed to 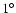 to match the angular resolution of the 23 GHz map.
The frequency spectral indices
adopted in the extrapolation are
to match the angular resolution of the 23 GHz map.
The frequency spectral indices
adopted in the extrapolation are
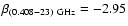 and
and
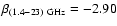 for the northern cut and
for the northern cut and
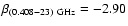 and
and
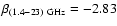 for the southern one.
for the southern one. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.4cm,height=8cm,angle=90,clip]{8435f15.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg285.gif) |
Figure 15:
Mean angular power spectra,
![$\langle C_{\ell}(\nu)\rangle_{\ell\in[20,40]}$](/articles/aa/full/2008/09/aa8435-07/img284.gif) ,
of
high latitude cuts ( ,
of
high latitude cuts (
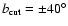 )
against frequency.
The straight line defined by the mean APS of the two lower frequencies
is also plotted. )
against frequency.
The straight line defined by the mean APS of the two lower frequencies
is also plotted.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=9cm,height=13cm,angle=90,clip]{8435f16.ps}\end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg286.gif) |
Figure 16:
Comparison between the CMB APS retrieved by Hinshaw et al. (2007)
and the synchrotron angular power spectra derived for some cuts of the
1420 MHz map (from Table 1 and Fig. 11),
extrapolated to 30 GHz and 70 GHz with a spectral index of -2.9.
Color legend (see online version):
blue (upper straight lines) 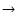
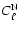 (northern cut),
red (lower)
(northern cut),
red (lower) 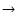
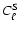 (southern cut).
The left panels also display the APS for the all-sky (black line)
extrapolated as above.
The empty square in the top right panel marks the upper limit
on synchrotron contamination inferred from COBE-DMR observations
(Kogut et al. 1996).
(southern cut).
The left panels also display the APS for the all-sky (black line)
extrapolated as above.
The empty square in the top right panel marks the upper limit
on synchrotron contamination inferred from COBE-DMR observations
(Kogut et al. 1996).
|
| Open with DEXTER |
We first carried out a source subtraction on the 23 GHz
map at intermediate and high latitudes (
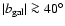 ),
similar to that performed on the radio surveys.
The comparison of the map of subtracted sources with
the mask of sources produced by the WMAP team
shows that most (
),
similar to that performed on the radio surveys.
The comparison of the map of subtracted sources with
the mask of sources produced by the WMAP team
shows that most (
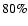 )
of the objects have been
identified
and subtracted.
We have derived and compared the APS of the
original, source-subtracted and source map at 23 GHz
for some northern and southern cuts. Namely, we considered
)
of the objects have been
identified
and subtracted.
We have derived and compared the APS of the
original, source-subtracted and source map at 23 GHz
for some northern and southern cuts. Namely, we considered
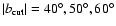 and
verified that
and
verified that
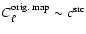 over
the significant multipole range (i.e.
over
the significant multipole range (i.e.
 ). This means that in
the 23 GHz map the source contribution dominates the high latitude cut
APS at all angular scales. In Fig. 14
we show the APS of the 23 GHz map after source
subtraction for the asymmetric cuts with
). This means that in
the 23 GHz map the source contribution dominates the high latitude cut
APS at all angular scales. In Fig. 14
we show the APS of the 23 GHz map after source
subtraction for the asymmetric cuts with
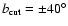 .
For comparison, we also display the extrapolated radio APS
(from Tables 1 and 2), derived as
.
For comparison, we also display the extrapolated radio APS
(from Tables 1 and 2), derived as
where
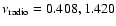 GHz. The frequency spectral
index
GHz. The frequency spectral
index 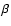 is chosen case by case as the value that
brings the radio APS to overlay the WMAP one
at the lower multipoles (the exact values are reported
in the figure caption).
The extrapolated angular power spectra
are very similar to each other, but
steeper than those of WMAP. Furthermore,
the frequency spectral indices needed in the extrapolation
suggest the existence of a steeper spectral behaviour
between 408 MHz and 23 GHz than between 1420 MHz and 23 GHz.
For the Galactic diffuse synchrotron emission we would
expect instead
is chosen case by case as the value that
brings the radio APS to overlay the WMAP one
at the lower multipoles (the exact values are reported
in the figure caption).
The extrapolated angular power spectra
are very similar to each other, but
steeper than those of WMAP. Furthermore,
the frequency spectral indices needed in the extrapolation
suggest the existence of a steeper spectral behaviour
between 408 MHz and 23 GHz than between 1420 MHz and 23 GHz.
For the Galactic diffuse synchrotron emission we would
expect instead
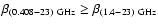 because of the possible steepening of the cosmic ray
energy spectrum.
In order to obtain a more quantitative estimate of
the mean spectral index between the lower frequencies
and 23 GHz, we used the mean value of the APS
of the source-subtracted maps for
because of the possible steepening of the cosmic ray
energy spectrum.
In order to obtain a more quantitative estimate of
the mean spectral index between the lower frequencies
and 23 GHz, we used the mean value of the APS
of the source-subtracted maps for
![$\ell \in [20,40]$](/articles/aa/full/2008/09/aa8435-07/img46.gif) .
In fact, in this range the APS is dominated
by the diffuse synchrotron emission, whereas at higher
multipoles the APS could still be influenced by the
contribution of unsubtracted sources.
Figure 15 shows the mean APS as a function
of frequency for the cuts with
.
In fact, in this range the APS is dominated
by the diffuse synchrotron emission, whereas at higher
multipoles the APS could still be influenced by the
contribution of unsubtracted sources.
Figure 15 shows the mean APS as a function
of frequency for the cuts with
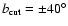 .
The spectral index
.
The spectral index 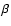 is obtained as
is obtained as
For the northern cut we found
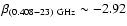 and
and
 .
For the southern cuts,
.
For the southern cuts,
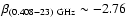 and
and
 .
These values of
.
These values of 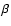 have a typical uncertainty
of a few percent according to the
choice of the multipole range adopted to compute
the mean value of the APS. However, it turns out that
have a typical uncertainty
of a few percent according to the
choice of the multipole range adopted to compute
the mean value of the APS. However, it turns out that
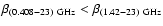 for all reasonable choices of the multipole range.
One possible explanation for such a result is that
the 23 GHz map includes one or more astrophysical components
beside synchrotron emission. On the one hand, the 23 GHz
map could still include some Galactic free-free emission,
residual from the component separation. Another and likely
more relevant candidate is Galactic spinning dust emission.
A rough estimate of the excess signal in the 23 GHz
map can be obtained by extrapolating
the radio results to 23 GHz, as shown in Fig. 15.
The observed and extrapolated mean APS differ by a
factor of
for all reasonable choices of the multipole range.
One possible explanation for such a result is that
the 23 GHz map includes one or more astrophysical components
beside synchrotron emission. On the one hand, the 23 GHz
map could still include some Galactic free-free emission,
residual from the component separation. Another and likely
more relevant candidate is Galactic spinning dust emission.
A rough estimate of the excess signal in the 23 GHz
map can be obtained by extrapolating
the radio results to 23 GHz, as shown in Fig. 15.
The observed and extrapolated mean APS differ by a
factor of  2.5 in the northern cut
and
2.5 in the northern cut
and  8.4 in the southern cut. Thus, they differ by
factors of
8.4 in the southern cut. Thus, they differ by
factors of  1.6 and
1.6 and  2.9 respectively
in terms of signal in the map. We repeated this
calculation by computing the mean APS over other
reasonable intervals of multipoles and found in this way
that the uncertainty for the given values of the excess
signal is about 20%.
The difference between the observed and extrapolated
values of the mean APS is smaller in the northern
hemisphere, which is likely due to the compensatory
contribution of the NPS.
2.9 respectively
in terms of signal in the map. We repeated this
calculation by computing the mean APS over other
reasonable intervals of multipoles and found in this way
that the uncertainty for the given values of the excess
signal is about 20%.
The difference between the observed and extrapolated
values of the mean APS is smaller in the northern
hemisphere, which is likely due to the compensatory
contribution of the NPS.
Table 3:
Frequency spectral index of the Galactic synchrotron
fluctuations between 408 MHz and 1420 MHz
derived from the APS.
Finally, we find that the angular power spectra
of the northern and southern sky are almost superimposed
at 23 GHz for
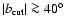 .
This can be interpreted as the combination of two effects.
The synchrotron emission of the NPS has a steeper frequency
spectrum than the average one (Reich & Reich 1988)
and the contribution of emission processes
other than synchrotron may be significant
at 23 GHz. Therefore, the relative importance of the NPS with
respect to the overall diffuse background diminishes from
408 MHz and 1420 MHz to microwave frequencies.
.
This can be interpreted as the combination of two effects.
The synchrotron emission of the NPS has a steeper frequency
spectrum than the average one (Reich & Reich 1988)
and the contribution of emission processes
other than synchrotron may be significant
at 23 GHz. Therefore, the relative importance of the NPS with
respect to the overall diffuse background diminishes from
408 MHz and 1420 MHz to microwave frequencies.
It is a standard practice to estimate the foreground
contamination of CMB anisotropies by means of the
corresponding APS, which is usually extrapolated
from the frequency range where the foreground component
is best observed. For the Galactic synchrotron emission
a constant spectral index in the interval  [-2.5,-3.0]
is commonly adopted, as suggested by the spectral
behaviour of the Galactic diffuse emission at radio frequencies.
We instead derive the spectral index directly from the
results of our APS analysis, thus identifying a proper
value for each cut considered.
As in the previous section, we compute the mean value
of the APS at 408 MHz and at 1420 MHz over the lower
multipoles (
[-2.5,-3.0]
is commonly adopted, as suggested by the spectral
behaviour of the Galactic diffuse emission at radio frequencies.
We instead derive the spectral index directly from the
results of our APS analysis, thus identifying a proper
value for each cut considered.
As in the previous section, we compute the mean value
of the APS at 408 MHz and at 1420 MHz over the lower
multipoles (
![$\ell \in [20,40]$](/articles/aa/full/2008/09/aa8435-07/img46.gif) )
and perform a linear
extrapolation based on the two points.
We prefer to work with the APS of the source-subtracted
map rather than with the synchrotron power law
derived by fitting it, since the former provides us with
a value that exclusively depends on observed data.
Our results are reported in Table 3.
The obtained spectral indices vary by a few percent
for a different choice of the multipole range
used to calculate the mean APS.
Figure 16 shows the CMB APS recovered by WMAP
(Hinshaw et al. 2007), together with the synchrotron APS derived from the 1420 MHz survey, extrapolated
to 30 GHz and 70 GHz (corresponding to the lowest
and the highest P LANCK-LFI channels). We display
the results obtained for four coverage cases
(
)
and perform a linear
extrapolation based on the two points.
We prefer to work with the APS of the source-subtracted
map rather than with the synchrotron power law
derived by fitting it, since the former provides us with
a value that exclusively depends on observed data.
Our results are reported in Table 3.
The obtained spectral indices vary by a few percent
for a different choice of the multipole range
used to calculate the mean APS.
Figure 16 shows the CMB APS recovered by WMAP
(Hinshaw et al. 2007), together with the synchrotron APS derived from the 1420 MHz survey, extrapolated
to 30 GHz and 70 GHz (corresponding to the lowest
and the highest P LANCK-LFI channels). We display
the results obtained for four coverage cases
(
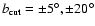 ).
For comparison, we also extrapolated as above
the APS directly extracted from the map
for the region at
).
For comparison, we also extrapolated as above
the APS directly extracted from the map
for the region at
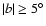 and for the all-sky.
The foreground dominates over the CMB at 30 GHz for a wide multipole range
if a mask excluding the Galactic plane is not applied.
The frequency spectrum of free-free emission,
relevant at low latitudes, is flatter than
that of the synchrotron emission. Thus, the
extrapolated APS provides a lower limit to the overall
Galactic foreground, even neglecting dust emission.
and for the all-sky.
The foreground dominates over the CMB at 30 GHz for a wide multipole range
if a mask excluding the Galactic plane is not applied.
The frequency spectrum of free-free emission,
relevant at low latitudes, is flatter than
that of the synchrotron emission. Thus, the
extrapolated APS provides a lower limit to the overall
Galactic foreground, even neglecting dust emission.
The analysis of the low-frequency maps shows that the
APS amplitude of the northern Galactic hemisphere is
strongly influenced by the presence of the NPS.
Consequently, the results obtained at 1420 MHz
for the northern cuts constitute a conservative
upper limit for the Galactic diffuse synchrotron
emission and can be used together with those
of the southern cuts to bracket the synchrotron
APS at microwave frequencies.
At 30 GHz, a severe contamination is expected from the
synchrotron emission up to
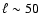 for
an almost complete sky coverage (
for
an almost complete sky coverage (
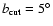 ).
A mask excluding the region with
).
A mask excluding the region with
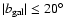 reduces the expected synchrotron signal to about half of
the CMB anisotropies for
reduces the expected synchrotron signal to about half of
the CMB anisotropies for
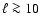 ,
whereas
for lower multipoles the two are comparable.
Kogut et al. (1996) examined the COBE-DMR
results at 31.5 GHz for
,
whereas
for lower multipoles the two are comparable.
Kogut et al. (1996) examined the COBE-DMR
results at 31.5 GHz for
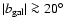 and derived an upper limit
of
and derived an upper limit
of 
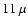 K on the temperature fluctuations
due to synchrotron emission on angular scales
of
K on the temperature fluctuations
due to synchrotron emission on angular scales
of 
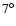 .
This value, marked in
Fig. 16 by an empty
square, is in good agreement with the extrapolated APS for
the northern cut at
.
This value, marked in
Fig. 16 by an empty
square, is in good agreement with the extrapolated APS for
the northern cut at
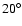 .
.
At 70 GHz, which is the most promising channel
for CMB anisotropy measurements
since
the overall foreground emission reaches a
minimum for
![$\nu \sim [60,80]$](/articles/aa/full/2008/09/aa8435-07/img318.gif) GHz
(Bennett et al. 2003), the contribution of the
Galactic synchrotron emission to the microwave sky
fluctuation field is small over the multipole
range explored in our analysis (
GHz
(Bennett et al. 2003), the contribution of the
Galactic synchrotron emission to the microwave sky
fluctuation field is small over the multipole
range explored in our analysis (
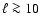 ).
The CMB anisotropies are larger than
the foreseen foreground fluctuations by a factor
).
The CMB anisotropies are larger than
the foreseen foreground fluctuations by a factor 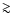 10 for a cut at
10 for a cut at 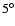 .
For
.
For
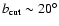 the foreground signal
further decreases by a factor
the foreground signal
further decreases by a factor  2.
The extrapolation of our results to
2.
The extrapolation of our results to
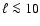 indicates that the cosmological signal should be a factor
indicates that the cosmological signal should be a factor 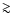 2 larger than the foreground at the
largest angular scales.
The precise recovery of the CMB APS for
2 larger than the foreground at the
largest angular scales.
The precise recovery of the CMB APS for
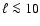 therefore remains a delicate issue, since the
foreground emission is a competitive signal.
However, we note that the APS extracted directly from the map
shows a certain flattening toward lowest multipoles, slightly
improving the situation with respect to the above
power law extrapolation.
therefore remains a delicate issue, since the
foreground emission is a competitive signal.
However, we note that the APS extracted directly from the map
shows a certain flattening toward lowest multipoles, slightly
improving the situation with respect to the above
power law extrapolation.
We have also carried out the analysis of the APS on patches
of roughly
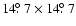 ,
in
order to describe the local variations of the Galactic
emission at 408 MHz and 1420 MHz.
Significant changes in the amplitude of the synchrotron APS with the considered portion of the sky are expected,
since the diffuse radio background gradually increases
toward the Galactic plane, where it reaches maximum intensity.
,
in
order to describe the local variations of the Galactic
emission at 408 MHz and 1420 MHz.
Significant changes in the amplitude of the synchrotron APS with the considered portion of the sky are expected,
since the diffuse radio background gradually increases
toward the Galactic plane, where it reaches maximum intensity.
These patches correspond to the pixels of an HEALPix map
at
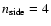 and allow the study of the angular power spectra
on the multipoles range
and allow the study of the angular power spectra
on the multipoles range  [60,200-300].
An angular size
[60,200-300].
An angular size
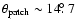 is a good compromise
between the wish to divide the sky in a large number of
areas and the need to preserve a relatively wide
interval of statistically relevant multipoles
(
is a good compromise
between the wish to divide the sky in a large number of
areas and the need to preserve a relatively wide
interval of statistically relevant multipoles
(
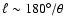 ).
We have computed the patch angular power spectra
for all the versions of the radio maps (original,
DS-subtracted and DSs only), both by using
the HEALPix facility Anafast and by integrating
the two point correlation function (see Appendix D
of La Porta 2007, for details).
Despite the differences found in individual cases,
on the average there is a good agreement between
the angular power spectra derived with the two methods
(in Fig. 17 some examples of bad,
fair and good cases are shown for the map at 1420 MHz
after DS subtraction).
).
We have computed the patch angular power spectra
for all the versions of the radio maps (original,
DS-subtracted and DSs only), both by using
the HEALPix facility Anafast and by integrating
the two point correlation function (see Appendix D
of La Porta 2007, for details).
Despite the differences found in individual cases,
on the average there is a good agreement between
the angular power spectra derived with the two methods
(in Fig. 17 some examples of bad,
fair and good cases are shown for the map at 1420 MHz
after DS subtraction).
The angular power spectra obtained by using Anafast
typically present more oscillations![[*]](/icons/foot_motif.gif) and tend to be slightly flatter than the correlation function
angular power spectra at
and tend to be slightly flatter than the correlation function
angular power spectra at
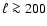 .
However,
the correlation function results are less reliable at higher
multipoles, where the choice of the window function might
have a non negligible influence.
Consequently, we exploited the Anafast
angular power spectra in the following analysis.
.
However,
the correlation function results are less reliable at higher
multipoles, where the choice of the window function might
have a non negligible influence.
Consequently, we exploited the Anafast
angular power spectra in the following analysis.
![\begin{figure}
\par\includegraphics[width=3.8cm,height=8.8cm,angle=90,clip]{8435f17.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg326.gif) |
Figure 17:
Comparison between the angular power spectra derived using
Anafast (fuchsia) and via integration of the correlation
function. Some examples of good ( left panel), fair and
poor ( right) agreement are shown for the
map at 1420 MHz after DSs subtraction.
|
| Open with DEXTER |
The patch angular power spectra for the map after DS subtraction
are fitted exactly as done in the case of the
Galactic cuts (see Sect. 3.3).
The maps of the obtained parameters are shown in
Figs. 18 and 19.
The results derived by using the best model are summarized
in Tables 4 and 5.
The estimated relative error of the synchrotron APS slope
averaged over the ensamble of patches is
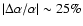 at 408 MHz and 22% at 1420 MHz.
The mean relative error of the normalized
amplitude, k100, is
at 408 MHz and 22% at 1420 MHz.
The mean relative error of the normalized
amplitude, k100, is 
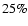 at 408 MHz
and
at 408 MHz
and 
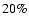 at 1420 MHz.
at 1420 MHz.
Table 4:
Characteristics of the synchrotron APS best fit parameters
derived in the local analysis of the 408 MHz map.
k1001 refers to
the patches covering about
the brightest half of the sky, which includes the Galactic plane and
the NPS.
k1002 correspond to the other half with weak
high latitude emission.
Table 5:
As in Table 4, but at 1420 MHz.
![\begin{figure}
\par\begin{tabular}{@{}ccc@{}}
Fit no SRC & Best Model & Fit no ...
...idth=3.9cm,height=5.9cm,angle=90]{8435f18j.ps} & \\
\end{tabular} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg338.gif) |
Figure 18:
Maps of the best fit parameters obtained by fitting the
angular power spectra of the local analysis patches at 1420 MHz.
The maps aligned along each row refer to the same parameter.
From the top,
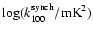 , ,
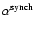 , ,
 and
and
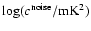 .
The first and third columns correspond to the extreme cases,
assuming respectively that the source contribution
or the noise contamination is negligible. .
The first and third columns correspond to the extreme cases,
assuming respectively that the source contribution
or the noise contamination is negligible.
|
| Open with DEXTER |
The most striking result is that at each frequency
the maps of the corresponding parameters, derived
by adopting the three different fitting models,
show a very similar morphology.
Such a resemblance proves that the parameter patterns
revealed by thelocal analysis are reliable,
despite the uncertainties in the obtained
parameter values.
The slope of the synchrotron APS does not show a
systematic dependence on Galactic latitude, in agreement
with the findings of Sect. 3.3.
The normalized amplitude of the synchrotron APS, k100, peaks
close to the Galactic plane, which reflects the
observed morphology.
A good correlation is found between the
normalized amplitude of the synchrotron APS
at 408 MHz and 1420 MHz,
which is defined by
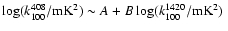 ,
where
,
where
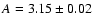 and
and
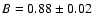 (see Fig. 20).
We note that
(see Fig. 20).
We note that
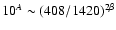 with
with
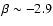 ,
in agreement with the results
of Table 3.
,
in agreement with the results
of Table 3.
The contribution of sources reaches a maximum in
the vicinity of the Galactic plane,
mainly because a less complete source subtraction was possible for
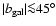 than at higher
latitudes (see Sect. 3.1).
The obtained source terms are in fair agreement with
the values estimated by using source counts.
This comparison is particularly significant
at 1420 MHz, where such estimates are more reliable.
We summarize the results obtained in this case in
Table 6.
than at higher
latitudes (see Sect. 3.1).
The obtained source terms are in fair agreement with
the values estimated by using source counts.
This comparison is particularly significant
at 1420 MHz, where such estimates are more reliable.
We summarize the results obtained in this case in
Table 6.
The aim of our analysis is to improve our
understanding of the Galactic synchrotron
emission as a foreground for CMB dedicated experiments.
For this purpose, we carried out an unprecedented detailed
study of the Galactic radio emission, in terms of its
angular power spectrum (APS), using total intensity
all-sky maps at 408 MHz and 1420 MHz.
An accurate modeling of the synchrotron APS is missing
in the literature so far, but is urgently required for a more
precise and complete exploitation of the information
awaited from the P LANCK satellite.
It constitutes a precious input for component separation
activities, both for the realization of spatial templates
of the foreground and for the definition of priors on
its spatial and frequency dependence.
![\begin{figure}
\par\includegraphics[width=5cm,height=7.3cm,angle=90,clip]{8435f20.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg345.gif) |
Figure 20:
Correlation between the best fit values obtained
for the synchrotron emission APS
normalized amplitude (k100)
at 408 MHz and 1420 MHz.
|
| Open with DEXTER |
- 1.
- Being interested in the diffuse component of the
synchrotron emission, the brighter discrete sources (DS)
have been eliminated from the radio maps by
2-dimensional Gaussian fitting.
This approach is very flexible and also permits
the removal of extended structures.
- 2.
- The APS was computed
for both large areas and
small patches and several consistency tests were
used to check the reliability of the recovered
APS in the case of limited sky coverage (see Appendix B of
La Porta 2007).
The study of the APS for various cuts, i.e. of
regions with Galactic latitudes above or below a
certain value
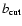 (
(
![$\vert b_{\rm cut}\vert \in [5^{\circ},60^{\circ}]$](/articles/aa/full/2008/09/aa8435-07/img346.gif) ),
allowed us to explore a possible dependence of
the mean properties of the Galactic synchrotron
emission on latitude, preserving at the same time
the largest possible coverage, which is important when
estimating the CMB APS because of the sampling variance.
Such cuts provided information for
),
allowed us to explore a possible dependence of
the mean properties of the Galactic synchrotron
emission on latitude, preserving at the same time
the largest possible coverage, which is important when
estimating the CMB APS because of the sampling variance.
Such cuts provided information for
![$\ell \in [\ell_{\rm min},\ell_{\rm max}]$](/articles/aa/full/2008/09/aa8435-07/img347.gif) ,
where
,
where
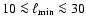 for increasing
for increasing
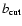 and
and
 at 408 MHz and 1420 MHz, respectively.
at 408 MHz and 1420 MHz, respectively.
The patches correspond to the pixels of an HEALPix map at
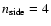 ,
which have an angular dimension of
,
which have an angular dimension of 
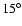 and permit us to investigate the local variations of the synchrotron APS for multipoles larger than
and permit us to investigate the local variations of the synchrotron APS for multipoles larger than  60.
60.
The derived angular power spectra were modelled in both cases
according to Eq. (1)
and a specific method was set up to find
the best least square fit on adaptive grids of the parameter
space and to evaluate the uncertanties on the retrieved
parameters (see Appendix C of La Porta 2007, for details).
- 3.
- An indirect cross-check of the fit result reliability
was provided in the case of the Galactic cuts
by the estimated source terms, which are consistent with the
expectations from extragalactic source counts
at both frequencies.
Nowadays, source counts at 1.4 GHz are well established down to
very low flux limits.
Table 6:
Characteristics of the source term derived in the local
analysis at 1420 MHz for
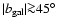 (
(
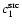 )
and
)
and
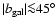 (
(
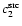 ).
).
It is remarkable that the source angular power spectra
obtained independently from source counts and from the
fit of the survey APS are in good agreement.
- 4.
- The slope of the synchrotron APS,
 ,
changes with
,
changes with
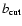 without showing a well-defined regular trend,
although it is found to be typically
steeper for
without showing a well-defined regular trend,
although it is found to be typically
steeper for
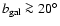 .
For the cuts,
.
For the cuts, 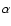 varies in the range
varies in the range
 [-3.0,-2.6] at both frequencies.
However, the analysis of the small patches gives evidence
that locally the synchrotron APS can be much flatter
for
[-3.0,-2.6] at both frequencies.
However, the analysis of the small patches gives evidence
that locally the synchrotron APS can be much flatter
for
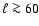 ,
reaching in some cases
values of
,
reaching in some cases
values of
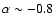 .
The normalized amplitude,
.
The normalized amplitude,
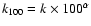 ,
gradually increases toward the Galactic plane,
following, as expected, the background radio
emission gradient.
A good correlation exists between the
results obtained for k100
at 408 MHz and 1420 MHz, for both cuts and patches.
This is expected, given that
the spectral properties of the electron density distribution
responsible for the Galactic diffuse non-thermal emission
should be the same in that frequency range
and further supports the reliability of
the obtained estimates of the synchrotron APS.
,
gradually increases toward the Galactic plane,
following, as expected, the background radio
emission gradient.
A good correlation exists between the
results obtained for k100
at 408 MHz and 1420 MHz, for both cuts and patches.
This is expected, given that
the spectral properties of the electron density distribution
responsible for the Galactic diffuse non-thermal emission
should be the same in that frequency range
and further supports the reliability of
the obtained estimates of the synchrotron APS.
- 5.
- The maps of k100 and
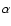 resulting
from the local analysis represent the starting point for the
simulation of small-scale fluctuation fields to be added to
the DS-subtracted maps to build phenomenological
templates of the Galactic synchrotron emission.
At present, an empirical approach is the most reliable
way to proceed in the realization of realistic templates
of the foreground, given the poor knowledge
of the Galactic magnetic field and of the cosmic ray
electron density distribution needed for a 3-dimensional
physical modelling.
resulting
from the local analysis represent the starting point for the
simulation of small-scale fluctuation fields to be added to
the DS-subtracted maps to build phenomenological
templates of the Galactic synchrotron emission.
At present, an empirical approach is the most reliable
way to proceed in the realization of realistic templates
of the foreground, given the poor knowledge
of the Galactic magnetic field and of the cosmic ray
electron density distribution needed for a 3-dimensional
physical modelling.
The issues (discussed in Sect. 4.1)
related to the K-band synchrotron component retrieved
by Hinshaw et al. (2007) are a clear example
of the difficulties encountered in the foreground separation
due to the lack of adequate priors and guess.
We performed a source subtraction on that map and produced a
map of the Galactic diffuse non-thermal emission
at 23 GHz to be compared with those at lower frequencies.
- 6.
- The extrapolation to 23 GHz of the APS
obtained at 408 MHz and 1420 MHz for higher latitude regions
(
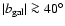 )
reveals that the
mean spectral index
(
)
reveals that the
mean spectral index
(
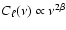 )
)
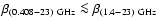 ,
which
is the opposite of what is expected for synchrotron emission.
We estimate the excess of the
signal in the 23 GHz map to be
,
which
is the opposite of what is expected for synchrotron emission.
We estimate the excess of the
signal in the 23 GHz map to be 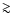
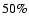 by using
the mean value of the APS at lower multipoles.
This result can be interpreted in terms of additional
contributions to the 23 GHz Galactic non-thermal emission,
which could be mainly due to anomalous dust.
by using
the mean value of the APS at lower multipoles.
This result can be interpreted in terms of additional
contributions to the 23 GHz Galactic non-thermal emission,
which could be mainly due to anomalous dust.
A direct application of the presented analysis is to
determine the level of contamination of the CMB anisotropies
due to the Galactic diffuse synchrotron emission
at different angular scales.
The conclusions reported below refer to the cuts,
which are more relevant for CMB measurements
because of the large coverage.
However, similar considerations could be
repeated using the results of the local analysis,
thus allowing the identification of the clearest
sky areas, which is essential for the success of
ground-based CMB experiments.
- 7.
- An important - although not unexpected - outcome
of the cut analysis is that
the amplitude of the APS for the northern hemisphere cuts
above

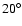 is raised
by the presence of the NPS.
Consequently, the results obtained separately for the
two Galactic hemispheres were used to bracket the APS
of the synchrotron emission.
is raised
by the presence of the NPS.
Consequently, the results obtained separately for the
two Galactic hemispheres were used to bracket the APS
of the synchrotron emission.
- 8.
- We used the APS results at 408 MHz and 1420 MHz to determine the frequency spectral index to be
adopted in the extrapolation to the microwave range
for each coverage case. In particular, we found that
![$\beta_{(0.408-1.4)~{\rm GHz}} \in [-3.2,-2.9]$](/articles/aa/full/2008/09/aa8435-07/img360.gif) with an
uncertainty of a few percent.
with an
uncertainty of a few percent.
- 9.
- The extrapolation to 30 GHz of the
synchrotron APS obtained at 1420 MHz
led to a signal in good agreement
with the upper limit fixed by COBE-DMR, thus
supporting the reliability of our results.
At this frequency the synchrotron emission
constitutes a severe contamination of
CMB anisotropies at the largest angular scales
(
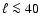 ). Nevertheless, a cut at
). Nevertheless, a cut at 
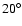 would reduce the synchrotron fluctuations to about
half the cosmological ones. The same holds
at
would reduce the synchrotron fluctuations to about
half the cosmological ones. The same holds
at
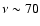 GHz for a cut at
GHz for a cut at 
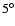 and
the situation further improves when excluding a larger
portion of the sky around the Galactic plane.
This implies that even though the current treatment of the
foregrounds does not permit an accurate removal of the
synchrotron emission, the latter does not prevent
the recovery of the bulk of the cosmological information
encoded in the CMB temperature APS.
and
the situation further improves when excluding a larger
portion of the sky around the Galactic plane.
This implies that even though the current treatment of the
foregrounds does not permit an accurate removal of the
synchrotron emission, the latter does not prevent
the recovery of the bulk of the cosmological information
encoded in the CMB temperature APS.
A deeper understanding of the foreground
is indispensable to settle other important issues
in the perspective of the forthcoming P LANCK
mission. P LANCK should achieve a sensitivity comparable
to the cosmic variance and its performance should
be limited mainly by foregrounds, thanks to the
extremely accurate control of all instrumental systematic
effects (Burigana et al. 2004; Mennella et al. 2004).
A first issue is the estimate of the CMB temperature-polarization APS, which carries information
about the reionization history and the tensor-to-scalar
ratio (see, e.g. Kogut 2003; Kogut et al. 2003, and
references therein). Possible foreground residual
contamination in the total intensity CMB anisotropy
map would affect fine analysis based on
the estimate of the cross-correlation APS,
also because the polarized component of the
cosmological signal is orders of magnitude lower.
Another issue is the evaluation of the Gaussianity
of the primordial fluctuations, which in the standard
inflationary paradigm![[*]](/icons/foot_motif.gif) generate the
structures observed in the Universe today.
Gaussianity tests are a powerful tool, complementary to
the tests exploiting the APS, which allow us
to probe the ``concordance''
model (Spergel et al. 2007)
and also to distinguish among inflationary
models (Bartolo et al. 2004).
The level of non-Gaussianity predicted
by the ``concordance'' model
cannot be detected by WMAP,
but in principle it should be observable with P LANCK.
Galactic foregrounds are non-Gaussian and anisotropic
and even low-level contamination in the maps
can produce detectable non-Gaussianities (see, e.g.
Naselsky et al. 2005), although they have minimal
effects on the estimated APS (Hinshaw et al. 2003).
Consequently, the foreground removal has to be
extremely accurate, so as not to limit P LANCK
in verifying this crucial
generate the
structures observed in the Universe today.
Gaussianity tests are a powerful tool, complementary to
the tests exploiting the APS, which allow us
to probe the ``concordance''
model (Spergel et al. 2007)
and also to distinguish among inflationary
models (Bartolo et al. 2004).
The level of non-Gaussianity predicted
by the ``concordance'' model
cannot be detected by WMAP,
but in principle it should be observable with P LANCK.
Galactic foregrounds are non-Gaussian and anisotropic
and even low-level contamination in the maps
can produce detectable non-Gaussianities (see, e.g.
Naselsky et al. 2005), although they have minimal
effects on the estimated APS (Hinshaw et al. 2003).
Consequently, the foreground removal has to be
extremely accurate, so as not to limit P LANCK
in verifying this crucial![[*]](/icons/foot_motif.gif) prediction.
prediction.
Acknowledgements
We are grateful to R. Wielebinski for a careful reading of the
original manuscript. We wish to thank G. De Zotti, L. Toffolatti
and R. Rebolo for helpful discussions.
L.L.P. warmly thanks R. Wielebinski and A. Zensus for
granting a post-doc fellowship.
C.B. acknowledge the support by
the ASI contract ``Planck LFI Activity of Phase E2''.
We are grateful to M. Genghini for technical support.
Some of the results in this paper have been derived
using the HEALPix (Górski et al. 2005) package.
The availability of the WMAP 3-yr maps is acknowledged.
We warmly thank the anonymous referee for useful comments.
- Alishahiha, M., Silverstein, E.,
& Tong, D. 2004, Phys. Rev., 70, 12
- Arfken,
G. B., & Weber, H. J., 2001, Mathematical Methods for
Physicists (Harcourt Academy Press), 893
-
Arkani-Hamed, N., Creminelli, P., Mukohyama, S., & Zaldarriaga,
M. 2004, JCAP, 4, 1 [NASA ADS]
-
Baccigalupi, C., Burigana, C., Perrotta, F., et al. 2001,
A&A, 372, 8 [NASA ADS] [CrossRef] [EDP Sciences]
- Banday,
A. J., & Wolfendale, A. W. 1990, MNRAS, 245,
182 [NASA ADS]
- Banday,
A. J., & Wolfendale, A. W. 1991, MNRAS, 252,
462 [NASA ADS]
- Bartolo, N.,
Komatsu, E., Matarrese, S., & Riotto, A. 2004, Phys. Rev.,
402, 103
(In the text)
- Bennett, C. L., Hill,
R. S., Hinshaw, G., et al. 2003, ApJS, 148, 97 [NASA ADS] [CrossRef]
-
Bouchet, F. R., & Gispert, R. 1999, NewA, 4, 443 [NASA ADS] [CrossRef]
- Bouchet,
F. R., Prunet, S., & Sethi, S. 1999, MNRAS, 302,
663 [NASA ADS] [CrossRef]
-
Burigana, C., Finelli, F., Salvaterra, R., et al. 2004,
MmSAI, 5, 415
- Burigana, C., La
Porta, L., Reich, P., & Reich, W. 2006, AN, 327, 491 [NASA ADS]
-
Chepurnov, A. V. 1998, A&AT, 17, 281 [NASA ADS]
-
Chiang, L.-Y., Coles, P., & Naselsky, P. D. 2007,
JCAP, 1, 21 [NASA ADS]
- Cho,
J., & Lazarian, A. 2002, ApJ, 575, L63 [NASA ADS] [CrossRef]
- Cho,
J., & Lazarian, A. 2003, NewAR, 47, 1143 [NASA ADS] [CrossRef]
- Davies,
R. D., Dickinson, C., Banday, A. J.,
et al. 2006, MNRAS, 370, 1125 [NASA ADS] [CrossRef]
(In the text)
-
De Oliveira-Costa, A, Tegmark, M., Davies, R. D.,
et al. 2004, ApJ, 606, L89 [NASA ADS] [CrossRef]
- Dickinson, C., Davies,
R. D., & Davis, R. J. 2003, MNRAS, 341, 369 [NASA ADS] [CrossRef]
-
Draine, B. T., & Lazarian, A. 1998, ApJ, 494,
L19 [NASA ADS] [CrossRef]
(In the text)
- Egger, R. J.,
& Aschenbach, B. 1995, A&A, 294, L25 [NASA ADS]
- Franceschini, A.,
Toffolatti, L., Danese, L., De Zotti, G. 1989, ApJ, 344,
35 [NASA ADS] [CrossRef]
(In the text)
-
Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef]
(In the text)
-
Finkbeiner, D. 2004, ApJ, 614, 186 [NASA ADS] [CrossRef]
-
Finkbeiner, D. P., Davis, M., & Schlegel,
D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef]
-
Giardino, G., Banday, A. J., Górski, K. M.,
et al. 2001, A&A, 371, 708 [NASA ADS] [CrossRef] [EDP Sciences]
-
Górski, K. M., Hivon, E., Banday, A. J.,
et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef]
(In the text)
- Haslam,
C. G. T. 1974, A&AS, 15, 333 [NASA ADS]
(In the text)
-
Haslam, C. G. T., Salter, C. J., Stoffel, H., &
Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS]
(In the text)
-
Hildebrandt, S. R., Rebolo, R., Rubiño-Martín,
J. A., et al. 2007, MNRAS, submitted
[arXiv:astro-ph/07061873]
(In the text)
-
Hinshaw, G., Spergel, D.N., Verde, L., et al. 2003, ApJS, 148,
135 [NASA ADS] [CrossRef]
(In the text)
- Hinshaw, G., Nolta, M. R.,
Bennett, C. L., et al. 2007, ApJS, 170, 288 [NASA ADS] [CrossRef]
-
James, F., & Roos, M. 1975, Comput. Phys. Comm., 10,
343 [NASA ADS] [CrossRef]
-
Jamrozy, M. 2004, A&A, 419, 63 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kogut, A. 2003, NewAR, 47,
977 [NASA ADS] [CrossRef]
-
Kogut, A., Banday, A. J., Bennett, C. L.,
et al. 1996, ApJ, 464, L5 [NASA ADS] [CrossRef]
(In the text)
- Kogut, A., Spergel, D. N., Barnes,
C., et al. 2003, ApJS, 148, 161 [NASA ADS] [CrossRef]
- La Porta,
L. 2007, Ph.D. Thesis, Bonn University, Germany
(In the text)
- La Porta, L.,
Reich, P., Burigana, C., & Reich, W. 2005, MPIfR-Memo,
1
(In the text)
- Linde,
A. 2005, NewAR, 49, 35 [NASA ADS] [CrossRef]
- Lyth,
D. H., & Riotto, A. A. 1999, Phys. Rep., 314,
1 [NASA ADS] [CrossRef]
- Lyth,
D. H., Ungarelli, C., & Wands, D. 2003, Phys. Rev.,
67, 2
- Mennella, A.,
Baccigalupi, C., Balbi, A., et al. 2004, Recent Research
Developments in Astronomy & Astrophysics, 2
[arXiv:astro-ph/0402528]
- Naselsky, P. D., &
Verkhodanov, O. V. 2006, MNRAS, submitted
[arXiv:astro-ph/0609409]
- Naselsky,
P. D., Chiang, L.-Y., Olesen, P., & Novikov,
I. D. 2005, Phys. Rev., 72, 063512
- Naselsky, P. D.,
Novikov, I. D., & Chiang, L.-Y. 2006, ApJ, 642,
617 [NASA ADS] [CrossRef]
-
Negrello, M., González-Nuevo, J., Magliocchetti, M.,
et al. 2005, MNRAS, 358, 896 [NASA ADS] [CrossRef]
-
Negrello, M., Magliocchetti, M., & De Zotti, G. 2006,
MNRAS, 368, 935 [NASA ADS] [CrossRef]
- Paladini,
R., De Zotti, G., Davies, R. D., & Giard, M. 2005,
MNRAS, 360, 1545 [NASA ADS] [CrossRef]
- Platania,
P., Burigana, C., Maino, D., et al. 2003, A&A, 410,
847 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Prandoni, I., Gregorini, L., Parma, P., et al. 2001, A&A,
365, 392 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Reich,
W. 1982, A&AS, 48, 219 [NASA ADS]
- Reich,
P., & Reich, W. 1986, A&AS, 63, 205 [NASA ADS]
-
Reich, P., & Reich, W. 1988, A&AS, 74, 7 [NASA ADS]
(In the text)
- Reich, P.,
Testori, J. C., & Reich, W. 2001, A&A, 376,
861 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Reich, P., Reich, W., &
Testori, J. C. 2004, Proceeding The Magnetized
Interstellar Medium, Antalya, Turkey, ed. B. Uyaniker, W. Reich,
& R. Wielebinski, (Katlenburg-Lindau: Copernicus GmbH), 63
(In the text)
- Rybicki,
G. B., & Lightman, A. P. 1979, Radiative
processes in astrophysics (New York: Wiley-Interscience)
(In the text)
- Salter,
C. J. 1983, BASI, 11, 1 [NASA ADS]
- Spergel, D. N., Bean, R.,
Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef]
(In the text)
- Strong,
A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007,
Annu. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef]
-
Tauber, J. 2004, AdSpR, 34, 91
(In the text)
- Tegmark, M., &
Efstathiou, G. 1996, MNRAS, 281, 1297 [NASA ADS]
- Tegmark, M.,
Eisenstein, D. J., Hu, W., & De Oliveira-Costa,
A. 2000, ApJ, 530, 133 [NASA ADS] [CrossRef]
(In the text)
- Toffolatti,
L., Argüeso Gómez, F., De Zotti, G., et al.
1998, MNRAS, 297, 117 [NASA ADS] [CrossRef]
(In the text)
-
Testori, J. C., Reich, P., Bava, J. A.,
et al. 2001, A&A, 368, 1123 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
Copyright ESO 2008
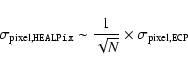
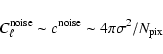
![\begin{figure}
\par\includegraphics[height=8.8cm,width=4.7cm,angle=90,clip]{8435f01.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg84.gif)
![\begin{figure}
\par\includegraphics[width=5.2cm,height=8.5cm,angle=90,clip]{8435f02.ps}\end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg85.gif)
![\begin{figure}
\par\begin{tabular}{c}
\includegraphics[width=4.5cm,angle=90]{84...
...ncludegraphics[width=4.5cm,angle=90]{8435f03b.ps}\\
\end{tabular} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg86.gif)
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=2.3cm,angle=90,cl...
... &
\includegraphics[width=3cm,clip]{8435f04f.ps}\\
\end{tabular} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg87.gif)
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[width=2.3cm,angle=90,cl...
... &
\includegraphics[width=3cm,clip]{8435f05f.ps}\\
\end{tabular} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=5.2cm,height=8.8cm,angle=90,clip]{8435f06.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=5.2cm,height=8.8cm,angle=90,clip]{8435f07.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg94.gif)
![\begin{figure}
\par\includegraphics[height=8.5cm,angle=90,clip]{8435f09.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=5.7cm,height=8.8cm,angle=90,clip]{8435f11.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg113.gif)
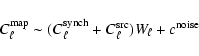
![\begin{figure}
\par\includegraphics[width=5.7cm,height=8.8cm,angle=90,clip]{8435f12.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg119.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=4.2cm,height=4.4cm,clip]{8435f13...
...m}
\includegraphics[width=4.2cm,height=4.4cm,clip]{8435f13b.ps} }
\end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg261.gif)
![\begin{figure}
\par\includegraphics[width=6.3cm,height=8.7cm,angle=90,clip]{8435f14.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg283.gif)
![\begin{figure}
\par\includegraphics[width=5.4cm,height=8cm,angle=90,clip]{8435f15.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg285.gif)
![\begin{figure}
\par\includegraphics[width=9cm,height=13cm,angle=90,clip]{8435f16.ps}\end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg286.gif)

![\begin{displaymath}\langle C_{\ell}(\nu_{1})\rangle _{\ell\in[20,40]}=\langle C_...
...}(\nu_{2})\rangle_{\ell\in[20,40]} (\nu_{1}/\nu_{2})^{2\beta} .\end{displaymath}](/articles/aa/full/2008/09/aa8435-07/img295.gif)
![\begin{figure}
\par\begin{tabular}{@{}ccc@{}}
Fit no SRC & Best Model & Fit no ...
...idth=3.9cm,height=5.9cm,angle=90]{8435f18j.ps} & \\
\end{tabular} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg338.gif)
![\begin{figure}
\begin{tabular}{@{}ccc@{}}
Fit no SRC & Best Model & Fit no Noi...
...th=3.8cm,height=5.8cm,angle=90]{8435f19j.ps} & \\
\end{tabular}
\end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg339.gif)
![\begin{figure}
\par\includegraphics[width=5cm,height=7.3cm,angle=90,clip]{8435f20.ps} \end{figure}](/articles/aa/full/2008/09/aa8435-07/Timg345.gif)