A&A 479, 347-353 (2008)
DOI: 10.1051/0004-6361:20078898
Mass limits for heavy neutrinos
E. Elfgren - S. Fredriksson
Department of Physics, Luleå University of Technology, 971 87 Luleå, Sweden
Received 22 October 2007 / Accepted 10 December 2007
Abstract
Context. Neutrinos heavier than
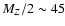 GeV are not excluded by particle physics data. Stable neutrinos heavier than this might contribute to the cosmic gamma ray background through annihilation in distant galaxies, as well as to the dark matter content of the universe.
GeV are not excluded by particle physics data. Stable neutrinos heavier than this might contribute to the cosmic gamma ray background through annihilation in distant galaxies, as well as to the dark matter content of the universe.
Aims. We calculate the evolution of the heavy neutrino density in the universe as a function of its mass, MN, and then the subsequent gamma ray spectrum from annihilation of distant 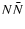 (from 0<z<5).
(from 0<z<5).
Methods. The evolution of the heavy neutrino density in the universe is calculated numerically. To obtain the enhancement due to structure formation in the universe, we approximate the distribution of N to be proportional to that of dark matter in the GalICS model. The calculated gamma ray spectrum is compared to the measured EGRET data.
Results. A conservative exclusion region for the heavy neutrino mass is 100 to 200 GeV, both from EGRET data and our re-evalutation of the Kamiokande data. The heavy neutrino contribution to dark matter is found to be at most 15%.
Key words: elementary particles - neutrinos - cosmology: dark matter - gamma rays: observations
The motivation for a fourth generation neutrino comes from the standard model of
particle physics. In fact, there is nothing in the standard model stating that there
should be exactly three generations of leptons (or of quarks, for that matter).
The present limits on the mass of a fourth generation of neutrinos are only
conclusive for
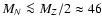 GeV (Yao et al. 2006, p. 35). This limit is obtained from measuring the invisible width of the Z0-peak in LEP,
which gives the number of light neutrino species, as
GeV (Yao et al. 2006, p. 35). This limit is obtained from measuring the invisible width of the Z0-peak in LEP,
which gives the number of light neutrino species, as
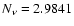
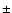 0.0083 (The LEP Collaborations 2001).
0.0083 (The LEP Collaborations 2001).
In Maltoni et al. (2000), a fourth generation of fermions is found to
be possible for
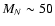 GeV, while heavier fermions are shown to be unlikely.
However, this constraint is only valid when there is a mixing between the generations
(Novikov et al. 2002); and since this is not necessarily true, we will not take it for certain.
GeV, while heavier fermions are shown to be unlikely.
However, this constraint is only valid when there is a mixing between the generations
(Novikov et al. 2002); and since this is not necessarily true, we will not take it for certain.
In the context of cosmology and astrophysics there are other contraints.
Light neutrinos, with 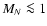 MeV, are relativistic when they decouple,
whereas heavier neutrinos are not. The light neutrinos must have
MeV, are relativistic when they decouple,
whereas heavier neutrinos are not. The light neutrinos must have
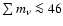 eV
in order for
eV
in order for
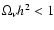 to be valid (Hannestad 2006b). For the dark matter (DM)
content calculated by Spergel et al. (2003), the bound is
to be valid (Hannestad 2006b). For the dark matter (DM)
content calculated by Spergel et al. (2003), the bound is
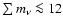 eV.
The number of light neutrino species are also constrained to
eV.
The number of light neutrino species are also constrained to
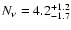 by
the cosmic microwave background (CMB), large scale structure (LSS),
and type Ia supernova (SNI-a) observations at 95% confidence (Hannestad 2006a).
by
the cosmic microwave background (CMB), large scale structure (LSS),
and type Ia supernova (SNI-a) observations at 95% confidence (Hannestad 2006a).
Neutrinos heavier than about 1 MeV, however, leave thermal equilibirum before
decoupling and therefore their number density drops dramatically,
see for example Dolgov & Zeldovich (1981). This will be discussed in more detail
in Sect. 2.
The most important astrophysical bound on heavy neutrinos comes from Kamiokande
(Mori et al. 1992) and this will be considered separately in the end.
In Fargion et al. (1995), it is found that the mass range
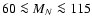 GeV
is excluded by heavy neutrino annihilation in the galactic halo.
However, according to Dolgov (2002, p. 57) this constraint is based on
an exaggerated value of the density enhancement in our galaxy.
Other works constraining the heavy neutrino mass include
Fargion et al. (1998,1999) and
Belotsky et al. (2004). There has also been a study of the gamma ray spectrum
of dark matter (DM) in general (Ando et al. 2007).
GeV
is excluded by heavy neutrino annihilation in the galactic halo.
However, according to Dolgov (2002, p. 57) this constraint is based on
an exaggerated value of the density enhancement in our galaxy.
Other works constraining the heavy neutrino mass include
Fargion et al. (1998,1999) and
Belotsky et al. (2004). There has also been a study of the gamma ray spectrum
of dark matter (DM) in general (Ando et al. 2007).
For an exhaustive review of modern neutrino cosmology, including current constraints
on heavy neutrinos, see Dolgov (2002). It is concluded that
there are no convincing limits on neutrinos in the mass range
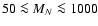 GeV.
A review of some cosmological implications of neutrino masses and mixing angles can be found in
Kainulainen & Olive (2003).
GeV.
A review of some cosmological implications of neutrino masses and mixing angles can be found in
Kainulainen & Olive (2003).
In this paper we consider a stable fourth-generation heavy neutrino with mass
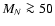 GeV
possessing the standard weak interaction. We assume that other particles of a fourth
generation are heavier and thus do not influence the calculations.
GeV
possessing the standard weak interaction. We assume that other particles of a fourth
generation are heavier and thus do not influence the calculations.
We assume a  CDM universe with
CDM universe with
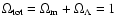 ,
where
,
where
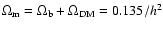 ,
,
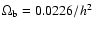 and
h = 0.71 (Spergel et al. 2003),
using WMAP data in combination with other CMB datasets and large-scale structure observations
(2dFGRS + Lyman
and
h = 0.71 (Spergel et al. 2003),
using WMAP data in combination with other CMB datasets and large-scale structure observations
(2dFGRS + Lyman  ).
Throughout the article we use natural units, so that the speed of light, Planck's reduced constant
and Boltzmann's constant equal unity,
).
Throughout the article we use natural units, so that the speed of light, Planck's reduced constant
and Boltzmann's constant equal unity,
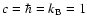 .
.
If heavy neutrinos (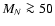 GeV) exist, they were created in the early universe.
They were in thermal equilibrium in the early stages of the hot big bang, but froze out
relatively early. After freeze-out, the annihilation of
GeV) exist, they were created in the early universe.
They were in thermal equilibrium in the early stages of the hot big bang, but froze out
relatively early. After freeze-out, the annihilation of 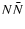 continued at an ever
decreasing rate until today.
Since those photons that were produced before the decoupling of photons
are lost in the CMB, only the subsequent
continued at an ever
decreasing rate until today.
Since those photons that were produced before the decoupling of photons
are lost in the CMB, only the subsequent 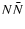 annihilations contribute to the photon background
as measured on earth.
annihilations contribute to the photon background
as measured on earth.
The photon intensity from 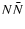 -annihilation
is affected by the number density of heavy neutrinos, nN,
whose mean density decreases as R-3, where R is the
expansion factor of the universe. However, in structures such as
galaxies the mean density will not change dramatically, and
since the number of such structures is growing with time, this
will compensate for the lower mean density.
Note that the photons are also
redshifted with a factor R due to their passage through space-time.
This also means that the closer annihilations will give photons
with higher energy than the farther ones.
-annihilation
is affected by the number density of heavy neutrinos, nN,
whose mean density decreases as R-3, where R is the
expansion factor of the universe. However, in structures such as
galaxies the mean density will not change dramatically, and
since the number of such structures is growing with time, this
will compensate for the lower mean density.
Note that the photons are also
redshifted with a factor R due to their passage through space-time.
This also means that the closer annihilations will give photons
with higher energy than the farther ones.
2 Evolution of neutrino density
Let us recapitulate the results of Dolgov & Zeldovich (1981).
The cosmic evolution of the number density,  ,
of a particle X can, in general,
be written as
,
of a particle X can, in general,
be written as
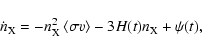 |
(1) |
where
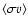 is the thermally averaged product of the mean velocity and total annihilation cross section for the particle, and
is the thermally averaged product of the mean velocity and total annihilation cross section for the particle, and
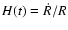 is the Hubble constant. The term
is the Hubble constant. The term
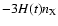 represents
the expansion of the universe, and the production term is
represents
the expansion of the universe, and the production term is
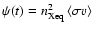 ,
where
,
where
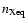 is the
equilibrium concentration of particle X.
is the
equilibrium concentration of particle X.
If we write
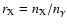 ,
Eq. (1) can be expressed as
,
Eq. (1) can be expressed as
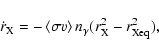 |
(2) |
where
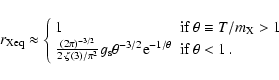 |
(3) |
Here
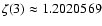 is the Riemann zeta function, T is the temperature,
is the Riemann zeta function, T is the temperature, 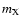 is the mass of particle X and
is the mass of particle X and 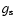 is the
number of spin states. For photons and electrons,
is the
number of spin states. For photons and electrons,
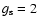 ,
while for massless
left-handed neutrinos,
,
while for massless
left-handed neutrinos,
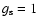 .
For reference,
.
For reference,
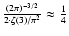 .
.
The value of the relative equilibrium concentration,
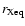 ,
is derived from
,
is derived from
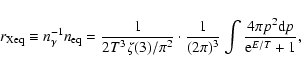 |
(4) |
where the expressions for 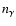 and
and
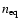 were taken from Dolgov (2002, Eq. (30)).
were taken from Dolgov (2002, Eq. (30)).
According to Dolgov & Zeldovich (1981, Eq. (2.9)), freeze-out (equilibrium destruction) occurs when
the rate of change of the equilibrium concentration due to the temperature decrease is
higher than the reaction rates, which means that
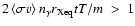 .
Until freeze-out, the relative particle density follows the equilibrium
density closely:
.
Until freeze-out, the relative particle density follows the equilibrium
density closely:
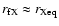 .
Hence, the relative density at the moment of freeze-out is
.
Hence, the relative density at the moment of freeze-out is
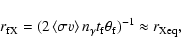 |
(5) |
where 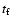 and
and
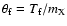 are the time and relative temperature at freeze-out.
are the time and relative temperature at freeze-out.
As the temperature decreases, the production term
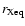 will drop exponentionally,
such that the relic concentration of X will be more or less independent of
will drop exponentionally,
such that the relic concentration of X will be more or less independent of
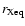 .
With this approximation (
.
With this approximation (
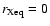 ), Eq. (2) can be solved for
), Eq. (2) can be solved for
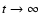 :
:
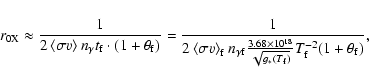 |
(6) |
where we have used
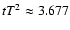
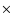
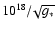 (Dolgov 2002, Eq. (37)), with
(Dolgov 2002, Eq. (37)), with
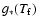 from
Kolb & Turner (1990, p. 65) being the number of relativistic species in thermal
contact with the photons. Furthermore,
from
Kolb & Turner (1990, p. 65) being the number of relativistic species in thermal
contact with the photons. Furthermore,
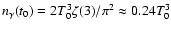 is the photon density today, where the photon temperature today is T0=2.725 K (Mather et al. 1999).
According to the standard model of particle physics,
g*=106.75 for
is the photon density today, where the photon temperature today is T0=2.725 K (Mather et al. 1999).
According to the standard model of particle physics,
g*=106.75 for 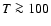 GeV
(
GeV
(
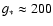 for supersymmetry models at yet higher temperatures).
If we assume that
for supersymmetry models at yet higher temperatures).
If we assume that
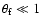 (which we will later show to be reasonable),
we obtain
(which we will later show to be reasonable),
we obtain
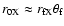 ,
which differs by a factor two from the result of Dolgov & Zeldovich (1981, Eq. (2.11)).
This is natural if they consider the density of
,
which differs by a factor two from the result of Dolgov & Zeldovich (1981, Eq. (2.11)).
This is natural if they consider the density of
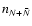 since our
since our 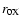 is valid for N and
is valid for N and 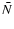 separately.
separately.
In order to take into account the increase in temperature due to entropy conservation
after freeze-out of particle X, we must take
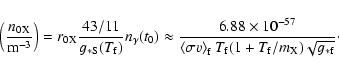 |
(7) |
(In fact
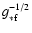 should be written
should be written
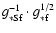 but for
but for
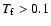 GeV,
GeV,
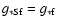 .)
.)
We now turn to the case of heavy neutrinos. Since we wish to avoid the lenghty calculations
of the cross sections of heavy neutrinos (Enqvist et al. 1989), we use Fargion et al. (1995, Fig. 1 and Eq. (4)# and solve for
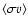 .
We assume that they use
.
We assume that they use
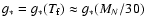 ,
but the exact value does not change the result in any significant way. The resulting
,
but the exact value does not change the result in any significant way. The resulting
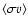 is presented in Fig. 1. The cross section drops from
is presented in Fig. 1. The cross section drops from
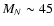 GeV, where the Z0 resonance peaks until the W+W- annihilation channel starts to dominate at
GeV, where the Z0 resonance peaks until the W+W- annihilation channel starts to dominate at
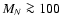 GeV.
GeV.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig1.eps}\end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg78.gif) |
Figure 1:
The cross section times the velocity (in m3/s) of heavy neutrino annihilation 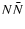 as a function of their mass (in GeV) at freeze-out,
as a function of their mass (in GeV) at freeze-out,
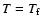 . . |
| Open with DEXTER |
According to Fargion et al. (1995), the cross sections of heavy neutrinos can be estimated using the annihilation channels
|
|
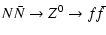 |
(8) |
| |
|
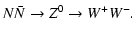 |
(9) |
There are several other possible annihilation channels for
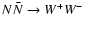 ,
like
,
like
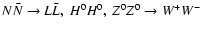 and also interference between
L and Z0, as well as between L and H0. However, in the limit
and also interference between
L and Z0, as well as between L and H0. However, in the limit
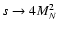 ,
which is valid for cosmological heavy neutrinos,
the dominant channel is through s-channel
,
which is valid for cosmological heavy neutrinos,
the dominant channel is through s-channel
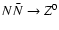 (Enqvist et al. 1989, p. 656).
Furthermore, the other annihilation products,
(Enqvist et al. 1989, p. 656).
Furthermore, the other annihilation products,
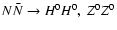 ,
are suppressed with respect to W+W--production (Enqvist et al. 1989, p. 651, 656). Hence, the above estimation of the
,
are suppressed with respect to W+W--production (Enqvist et al. 1989, p. 651, 656). Hence, the above estimation of the
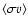 should be fairly accurate. If anything, it is slightly underestimated.
should be fairly accurate. If anything, it is slightly underestimated.
Using Eqs. (5) and (3), we can solve for
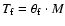 .
The result is presented in Fig. 2.
Note that although it looks like a straight line, it really is slightly curved.
We notice that
.
The result is presented in Fig. 2.
Note that although it looks like a straight line, it really is slightly curved.
We notice that
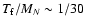 ,
which shows our
assumption
,
which shows our
assumption
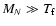 to be valid. This is also in agreement with previous
results, see e.g. Kolb & Turner (1990), where a value of
to be valid. This is also in agreement with previous
results, see e.g. Kolb & Turner (1990), where a value of
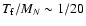 is quoted.
is quoted.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig2.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg90.gif) |
Figure 2:
The freeze-out temperature (in GeV
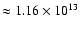 K)
of heavy neutrinos as a function of their mass (in GeV). K)
of heavy neutrinos as a function of their mass (in GeV). |
| Open with DEXTER |
We now return to Eq. (7) and apply it to the case of a heavy neutrino.
We plot the resulting relative relic neutrino density as a function of the mass MN in
Fig. 3 using
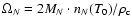 ,
where
,
where
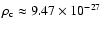 kg/m3 is the critical density
of the universe. The resulting heavy neutrino density is very similar to the one obtained by Fargion et al. (1995, Fig. 1).
The numerical simulation also shown in the figure will be the subject of the next section.
kg/m3 is the critical density
of the universe. The resulting heavy neutrino density is very similar to the one obtained by Fargion et al. (1995, Fig. 1).
The numerical simulation also shown in the figure will be the subject of the next section.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig3.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg93.gif) |
Figure 3:
The relic relative density of heavy neutrinos as a function of their mass (in GeV). |
| Open with DEXTER |
3 Numerical simulation of the neutrino density
For comparison, we evaluate the evolution of the heavy neutrino density numerically.
Equation (1) can be rewritten in terms of the temperature, T:
![\begin{displaymath}%
\frac{{\rm d}n}{{\rm d}T} = -\frac{{\rm d}t}{{\rm d}T} \lef...
...<\sigma v\right> \left(n(T)^2 - n_{\rm eq}(T)^2\right)\right],
\end{displaymath}](/articles/aa/full/2008/08/aa8898-07/img94.gif) |
(10) |
where
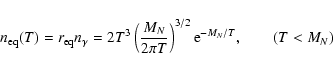 |
(11) |
and the relation between time and temperature is given by
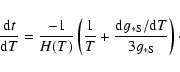 |
(12) |
Here the Hubble constant is
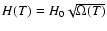 ,
where the total relative energy density of the universe is
,
where the total relative energy density of the universe is
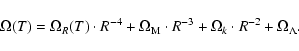 |
(13) |
The curvature term
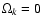 and the radiation density is
and the radiation density is
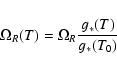 |
(14) |
due to the reheating as particles freeze out.
The reheating also means that
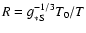 (Kolb & Turner 1990, p. 68).
The number of relativistic species
still in thermal contact with the photons,
(Kolb & Turner 1990, p. 68).
The number of relativistic species
still in thermal contact with the photons,
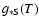 ,
is given in Coleman & Roos (2003, Fig. 1#.
For the critical region
0.15<T<0.30 GeV their Eqs. (8), (9) have been used to calculate
,
is given in Coleman & Roos (2003, Fig. 1#.
For the critical region
0.15<T<0.30 GeV their Eqs. (8), (9) have been used to calculate
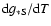 .
This updated value of
.
This updated value of
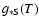 is needed to evaluate
is needed to evaluate
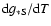 properly.
properly.
Using a fifth-order Runge-Kutta method with adaptive stepsize control, taken from Numerical Recipes
(Press et al. 1992, Ch. 16.2), we solve for n(T) in Eq. (10) using
the initial condition
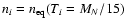 ,
which is well within the region of thermal
equilibrium for the heavy neutrinos. The resulting
relative relic neutrino density is presented in Fig. 3, where
,
which is well within the region of thermal
equilibrium for the heavy neutrinos. The resulting
relative relic neutrino density is presented in Fig. 3, where
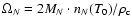 as before.
We notice that the peak of the curve is
as before.
We notice that the peak of the curve is
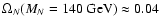 ,
which would
then account for
,
which would
then account for 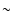 15% of the dark matter content of the universe.
15% of the dark matter content of the universe.
For comparison, we plot the number density of heavy neutrinos (in m-3) as a function of Tfor masses 50, 70, 90, 150, 500 and 1000 GeV in Fig. 4. As we can see, the transition
between thermal equilibirum density and completely decoupled neutrino density is not sharp.
This is one of the reasons for the difference between the analytical and the numerical relative density in Fig. 3.
Another reason for the difference is the inclusion of the change in
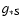 in the
evaluation of
in the
evaluation of
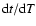 .
The evolution of
.
The evolution of
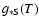 is the cause of the small ``knee'' in Fig. 4 seen at
is the cause of the small ``knee'' in Fig. 4 seen at 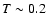 GeV (the reheating from
the quark-hadron transition). Furthermore, when electrons fall out of thermal equilibirum at
GeV (the reheating from
the quark-hadron transition). Furthermore, when electrons fall out of thermal equilibirum at 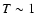 MeV there is another small knee, reducing again the heavy neutrino density somewhat.
MeV there is another small knee, reducing again the heavy neutrino density somewhat.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig4.eps}\end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg111.gif) |
Figure 4:
The number density of heavy neutrinos (in m-3) as a function of T for masses 50, 70, 90, 150, 500 and 1000 GeV (increasing from left to right in the upper right corner).
The dashed vertical lines represent the calculated value of 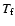 in Fig. 2.
Below T=0.01 GeV, the curves evolve as
in Fig. 2.
Below T=0.01 GeV, the curves evolve as
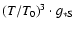 . . |
| Open with DEXTER |
4 Dark matter simulations
In Sect. 3, we calculated the mean density of neutrinos in the
universe as a function of redshift and the mass of the heavy neutrinos.
However, the neutrino annihilation rate, and thus the intensity from
their gamma spectrum, is proportional to the square of the neutrino density.
This means that inhomogeneities in the universe will tend to enhance the
gamma ray signal.
In this section we describe how we calculate the inhomogeneities as a
function of space and time, assuming only gravitational interaction
between the dark matter consisting of heavy neutrinos and other DM particles.
The clumping factor (also known as the boost factor) can then be used to calculate the actual intensity
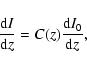 |
(15) |
where
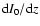 is the intensity contribution from redshift slice
is the intensity contribution from redshift slice 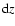 for a homogeneous universe and C(z) is the enhancement due to the clumping at redshift z.
for a homogeneous universe and C(z) is the enhancement due to the clumping at redshift z.
The clumping factor has been calculated in different settings before, ranging from
Berezinsky et al. (2006) for local clustering giving a clumping factor of 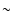 5to Diemand et al. (2005) for mini-halos giving a clumping factor of
two orders of magnitude.
For a discussion about the accuracy of approximating the enhancement with a single
clumping parameter, see Lavalle et al. (2007), though they focus on antiprotons.
5to Diemand et al. (2005) for mini-halos giving a clumping factor of
two orders of magnitude.
For a discussion about the accuracy of approximating the enhancement with a single
clumping parameter, see Lavalle et al. (2007), though they focus on antiprotons.
The spatial and temporal distribution of DM in the universe is calculated
with the GalICS program. The cosmological N-body simulation that we are referring to throughout this paper is done with the parallel tree-code developed by Ninin (1999).
The initial mass power
spectrum is taken to be a scale-free (
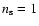 )
one,
evolved as predicted by Bardeen et al. (1986) and normalized to
the present-day abundance of rich clusters with
)
one,
evolved as predicted by Bardeen et al. (1986) and normalized to
the present-day abundance of rich clusters with 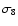 = 0.88
(Eke et al. 1996). The DM density field was calculated from z=35.59 to z=0, giving 100 ``snapshots'', spaced logarithmically in the expansion factor.
= 0.88
(Eke et al. 1996). The DM density field was calculated from z=35.59 to z=0, giving 100 ``snapshots'', spaced logarithmically in the expansion factor.
The basic principle of the simulations is to distribute a number of
DM particles N3 with mass
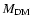 in a box of size L3.
Then, as time passes, the particles interact gravitationally, clumping together
and forming structures.
When there are at least 20 particles together, it is considered to be a DM halo.
It is supposed to be no other forces present than gravitation,
and the boundary conditions are assumed to be periodic.
in a box of size L3.
Then, as time passes, the particles interact gravitationally, clumping together
and forming structures.
When there are at least 20 particles together, it is considered to be a DM halo.
It is supposed to be no other forces present than gravitation,
and the boundary conditions are assumed to be periodic.
In the GalICS simulations the side of the box used was
L=100 h-1 Mpc, and the number of particles was set to 2563, which implies a
particle mass of 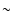 5.51
5.51 
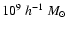 .
Furthermore, for the
simulation of DM, the cosmological parameters were set to
.
Furthermore, for the
simulation of DM, the cosmological parameters were set to
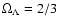 ,
,
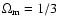 and h=2/3.
The simulations of the DM were done before the results from WMAP
were published, which
explains the difference between these parameters and the values
used elsewhere in this paper, as stated in the introduction.
Nevertheless, the difference is only a couple of percent and should not seriously
alter the results.
and h=2/3.
The simulations of the DM were done before the results from WMAP
were published, which
explains the difference between these parameters and the values
used elsewhere in this paper, as stated in the introduction.
Nevertheless, the difference is only a couple of percent and should not seriously
alter the results.
Between the initial halo formation at 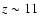 and the current
epoch in the universe, there are 72 snapshots. In each snapshot
a friend-of-friend algorithm was used to identify virialized groups of at least
20 DM particles.
For high resolutions, it is clear that the mass resolution
is insufficient. Fortunately, the first 20-particle DM clump appears at z=11.2, while
the bulk of the clumping comes from
and the current
epoch in the universe, there are 72 snapshots. In each snapshot
a friend-of-friend algorithm was used to identify virialized groups of at least
20 DM particles.
For high resolutions, it is clear that the mass resolution
is insufficient. Fortunately, the first 20-particle DM clump appears at z=11.2, while
the bulk of the clumping comes from 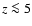 ,
where the lack of resolution is
no longer a problem.
,
where the lack of resolution is
no longer a problem.
In order to make a correct large-scale prediction of the distribution of the
DM, the size of the box would have to be of Hubble size, i.e., 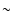 3000 h-1 Mpc.
However, for a given simulation time, increasing the size of the box and
maintaining the same number of particles would mean that we lose in mass
resolution, which is not acceptable if we want to reproduce a fairly realistic
scenario for the evolution of the universe.
3000 h-1 Mpc.
However, for a given simulation time, increasing the size of the box and
maintaining the same number of particles would mean that we lose in mass
resolution, which is not acceptable if we want to reproduce a fairly realistic
scenario for the evolution of the universe.
We will make the approximation that our single box, at different time-steps,
can represent the line of sight, and since we are only interested in the general
properties of the dark matter clumping, this approximation should be
acceptable.
GalICS is a hybrid model for hierarchical galaxy formation, combining
the outputs of large cosmological N-body simulations with simple, semi-analytic
recipes to describe the fate of the baryons within DM halos. The
simulations produce a detailed merging tree for the DM halos,
including complete knowledge of the statistical properties arising from the
gravitational forces.
The distribution of galaxies resulting from this GalICS simulation has been
compared with the 2dS (Colless et al. 2001) and the Sloan Digital Sky
Survey (Szapudi et al. 2001) and found to be realistic on the angular
scales of
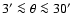 ,
see Blaizot et al. (2006).
The discrepancy in the spatial correlation function for other values of
,
see Blaizot et al. (2006).
The discrepancy in the spatial correlation function for other values of
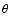 can be explained by the limits of the numerical simulation. Obviously,
any information on scales larger than the size of the box (
can be explained by the limits of the numerical simulation. Obviously,
any information on scales larger than the size of the box (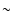 45') is not reliable.
The model has also proven to give sensible results for Lyman break galaxies at z=3(Blaizot et al. 2004).
It is also possible to model active galactic nuclei (Cattaneo et al. 2005).
45') is not reliable.
The model has also proven to give sensible results for Lyman break galaxies at z=3(Blaizot et al. 2004).
It is also possible to model active galactic nuclei (Cattaneo et al. 2005).
Since it is possible to reproduce reasonable
correlations from semi-analytic modelling of galaxy formation within
this simulation at z=0-3, we now attempt to do so also for somewhat higher redshifts.
We proceed to calculate the clumping factor C(z).
The inhomogeneities of the DM distribution can be calculated using the
relative clumping of dark matter halos:
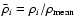 ,
where
,
where
 is the mean density of the dark matter in the universe
and
is the mean density of the dark matter in the universe
and 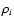 is the mean density of DM halo i.
is the mean density of DM halo i.
As matter contracts, the density increases, but since the gamma ray emitting volume
also decreases, the net effect is a linear enhancement from the quadratic dependence
on the density. This means that the DM halos will emit as:
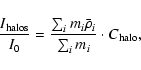 |
(16) |
where I0 is the intensity for a homogeneous universe and
the summation is done over all DM halos and thus
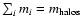 .
The factor
.
The factor
 accounts for the modification from the form and
properties of the halo itself. A simple conic DM distribution would give
accounts for the modification from the form and
properties of the halo itself. A simple conic DM distribution would give
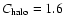 .
The more realistic distribution
.
The more realistic distribution
![$\rho(r)=\rho_0\cdot[(1+r)(1+r^2)]^{-1}$](/articles/aa/full/2008/08/aa8898-07/img132.gif) ,
where r is the radial coordinate relative to the halo radius, gives
,
where r is the radial coordinate relative to the halo radius, gives
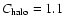 .
However, the radiation from within the denser part of the halo will also be
subject to more absorption, and so for the sake of simplicity we use
.
However, the radiation from within the denser part of the halo will also be
subject to more absorption, and so for the sake of simplicity we use
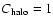 .
We notice that the average relative density over all the halos in the simulation
is fairly constant,
.
We notice that the average relative density over all the halos in the simulation
is fairly constant,
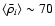 for z<5.
for z<5.
Simultaneously, the DM background (the DM particles that are not in halos) will decrease,
both in density by a factor
 and because of their decreasing fraction of the total mass in the box
and because of their decreasing fraction of the total mass in the box
 :
:
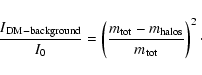 |
(17) |
This means that the total clumping factor is
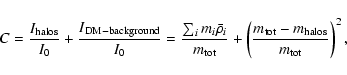 |
(18) |
where the second
term starts as unity whereafter it decreases and quickly becomes negligeable
with respect to the first
term, which starts at zero, but then rapidly increases.
The total clumping is plotted in Fig. 5 along with the competing
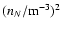 effect, as
well as the product, all as a function of the redshift z. The number density of heavy neutrinos
in the figure is taken for the mass MN=150 GeV.
We notice that the clumping enhancement remains
effect, as
well as the product, all as a function of the redshift z. The number density of heavy neutrinos
in the figure is taken for the mass MN=150 GeV.
We notice that the clumping enhancement remains 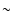 30 for z<1 and that the clumping is
30 for z<1 and that the clumping is
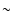 1 for z>5. This is mainly due to the proportion of mass within the halos
compared to the total DM mass. The clumping enhancement lies between
the two extreme values by Berezinsky et al. (2006) and Diemand et al. (2005) quoted above.
1 for z>5. This is mainly due to the proportion of mass within the halos
compared to the total DM mass. The clumping enhancement lies between
the two extreme values by Berezinsky et al. (2006) and Diemand et al. (2005) quoted above.
In fact, the clumping factor can be even higher if other halo shapes are assumed
with smaller radii (Ullio et al. 2002). The densities in the halos considered
in the present work have been evaluated at the virial radius.
We also point out that before the reionization, at 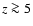 ,
there is absorption from neutral hydrogen in the interstellar medium (ISM), also known as the Gunn-Petersen effect (Gunn & Peterson 1965).
This means that photons from higher redshifts will be highly
attenuated. For z=5.3, the emission drops by roughly a factor of 10, and for
,
there is absorption from neutral hydrogen in the interstellar medium (ISM), also known as the Gunn-Petersen effect (Gunn & Peterson 1965).
This means that photons from higher redshifts will be highly
attenuated. For z=5.3, the emission drops by roughly a factor of 10, and for 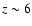 the opacity is
the opacity is
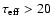 (Becker et al. 2001). Hence, any gamma ray signal
prior to this epoch would have been absorbed.
(Becker et al. 2001). Hence, any gamma ray signal
prior to this epoch would have been absorbed.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig5.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg144.gif) |
Figure 5:
The clumping factor (C, dotted line) compared to the competing effect of the
decreasing heavy neutrino number density squared (nN2, dashed line) for MN=150 GeV
and the product of the two (solid line). Different neutrino masses scale as in Fig. 4. |
| Open with DEXTER |
In order to evaluate the photon spectrum from 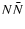 -collisions
we use PYTHIA version 6.410 (Sjöstrand et al. 2006). According to
Enqvist et al. (1989, Eq. (13))
the centre of mass energy squared is
-collisions
we use PYTHIA version 6.410 (Sjöstrand et al. 2006). According to
Enqvist et al. (1989, Eq. (13))
the centre of mass energy squared is
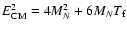 and
and
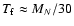 as estimated above.
as estimated above.
We generate 100,000 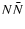 events for each mass
MN=50,60,...,1000 GeV
and calculate the photon spectrum and mean photon multiplicity and energy. We assume that
events for each mass
MN=50,60,...,1000 GeV
and calculate the photon spectrum and mean photon multiplicity and energy. We assume that
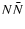 collisions at these energies and masses can be approximated by
collisions at these energies and masses can be approximated by
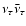 collisions at the same
collisions at the same
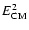 .
This is obviously not equivalent, but
.
This is obviously not equivalent, but
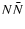 cannot be directly simulated in PYTHIA. Nevertheless, with the approximations
used in calculating
cannot be directly simulated in PYTHIA. Nevertheless, with the approximations
used in calculating
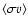 ,
the only difference between
,
the only difference between
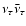 and
and 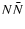 collisions (except in the cross section)
is the t-channel production of W+W- through
collisions (except in the cross section)
is the t-channel production of W+W- through 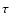 .
However, since
the heavy neutrinos are non-relativistic when they collide, the two Ws
will be produced back-to-back, which means that the inclusion of the t-channel
is unimportant.
.
However, since
the heavy neutrinos are non-relativistic when they collide, the two Ws
will be produced back-to-back, which means that the inclusion of the t-channel
is unimportant.
In order to verify this, we study the difference in the photon spectrum for
W decay at 0 and 90 degrees, and despite an increasing difference between
the two cases, even at MN=1000 GeV, the difference is not strong enough to change our conclusions.
The resulting photon distribution is presented in Fig. 6.
We note that the photon energies peak at
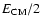 ,
which is natural
since the decaying particles can each have at most half of the centre of mass energy.
The curves continue to increase as
,
which is natural
since the decaying particles can each have at most half of the centre of mass energy.
The curves continue to increase as 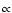 E-1 as E decreases further.
Note that the noise in the curves for lower E is due to lacking statistics for these
rare events, but it does not affect the outcome of the calculations.
We also calculate the mean photon energy and find it to be
E-1 as E decreases further.
Note that the noise in the curves for lower E is due to lacking statistics for these
rare events, but it does not affect the outcome of the calculations.
We also calculate the mean photon energy and find it to be
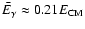 for all masses.
The curve is normalized such that the integral over
for all masses.
The curve is normalized such that the integral over
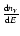 is unity.
The average number of photons,
is unity.
The average number of photons, 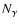 ,
produced for an
,
produced for an 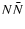 -collision is shown in Fig. 7. The sharp rise in the curve at
-collision is shown in Fig. 7. The sharp rise in the curve at
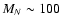 GeV is due to the jets from the emerging W+W--production.
GeV is due to the jets from the emerging W+W--production.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{8898fig6.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg157.gif) |
Figure 6:
The relative energy distributions of photons from 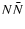 -collisions for
heavy neutrino masses MN= 50, 70, 90, 150, 500, 1000 GeV. -collisions for
heavy neutrino masses MN= 50, 70, 90, 150, 500, 1000 GeV.
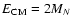 is the centre of mass energy.
is the centre of mass energy. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig7.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg158.gif) |
Figure 7:
The average number of photons produced for an 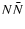 -collision as a function of
heavy neutrino mass MN in GeV. -collision as a function of
heavy neutrino mass MN in GeV. |
| Open with DEXTER |
The 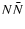 -collisions from the reionization at
-collisions from the reionization at 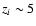 until today
give an integrated, somewhat redshifted, gamma spectrum for a heavy neutrino
with a given mass:
until today
give an integrated, somewhat redshifted, gamma spectrum for a heavy neutrino
with a given mass:
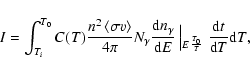 |
(19) |
where C(T) is the clumping factor in Fig. 5 and
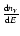 is the photon distribution in Fig. 6.
T0=2.725 K is the temperature of the CMB today and Ti is the reionization temperature,
which we set to
is the photon distribution in Fig. 6.
T0=2.725 K is the temperature of the CMB today and Ti is the reionization temperature,
which we set to
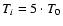 .
.
The resulting E2I is presented in Fig. 8. When we compare the calculated heavy neutrino signal with data from EGRET (Sreekumar et al. 1998), we see that only neutrino masses around
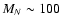 or 200 GeV
would be detectable, and then only as a small bump in the data around
or 200 GeV
would be detectable, and then only as a small bump in the data around
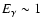 GeV.
For intermediary neutrino masses, the signal would exceed the observed gamma ray data.
In Fig. 9, the peak intensity for the different heavy
neutrino masses is plotted, as well as EGRET data for the corresponding energy with error bars.
The data represent the observed diffuse emission at high latitudes (
GeV.
For intermediary neutrino masses, the signal would exceed the observed gamma ray data.
In Fig. 9, the peak intensity for the different heavy
neutrino masses is plotted, as well as EGRET data for the corresponding energy with error bars.
The data represent the observed diffuse emission at high latitudes (
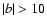 degrees),
where first the known point sources were removed and then the diffuse emission in our galaxy was subtracted.
degrees),
where first the known point sources were removed and then the diffuse emission in our galaxy was subtracted.
We have also compared the height of the curves, both with and without clumping,
and the integrated difference is roughly a factor of 30.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig8.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg164.gif) |
Figure 8:
Cosmic gamma radiation from photons produced in 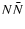 -collisions
as a function of photon energy for neutrino masses
MN=50, 70, 100, 140, 200, 500, 1000 GeV.
The dotted line represents MN=50 GeV
and the dot-dashed MN=1 TeV. The solid lines are the masses in between. The circles represent data from EGRET (Sreekumar et al. 1998),
with error bar, as derived for extragalactic sources. -collisions
as a function of photon energy for neutrino masses
MN=50, 70, 100, 140, 200, 500, 1000 GeV.
The dotted line represents MN=50 GeV
and the dot-dashed MN=1 TeV. The solid lines are the masses in between. The circles represent data from EGRET (Sreekumar et al. 1998),
with error bar, as derived for extragalactic sources. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig9.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg165.gif) |
Figure 9:
Maximum cosmic gamma radiation from photons produced in 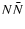 -collisions
as a function of neutrino mass (in GeV). The marked region is excluded since -collisions
as a function of neutrino mass (in GeV). The marked region is excluded since
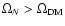 within. The data (with error bars) are taken at the energy corresponding to the maximum in Fig. 8.
within. The data (with error bars) are taken at the energy corresponding to the maximum in Fig. 8.
|
| Open with DEXTER |
7 Discussion and conclusions
The numerical calculation of the evolution of the heavy neutrino number density
indicates that in the mass region
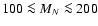 ,
the cosmological neutrinos would
give a cosmic ray signal that exceeds the measurements by the EGRET telescope (Sreekumar et al. 1998).
Note that the clumping factor for these limits is rather conservative.
In Ullio et al. (2002), this factor is much larger, which would also
produce a stronger limit on the heavy neutrino mass.
,
the cosmological neutrinos would
give a cosmic ray signal that exceeds the measurements by the EGRET telescope (Sreekumar et al. 1998).
Note that the clumping factor for these limits is rather conservative.
In Ullio et al. (2002), this factor is much larger, which would also
produce a stronger limit on the heavy neutrino mass.
We can also compare our neutrino density with the results from the Kamiokande collaboration
(Mori et al. 1992). We scale the neutrino signal in their Fig. 2 to
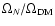 ,
where we use h0=0.71,
,
where we use h0=0.71,
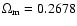 and
and
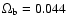 .
This is shown in Fig. 10, where we compare our numerical results for the relic neutrino density to the observed muon flux in the Kamiokande detector.
This gives an exclusion region of
.
This is shown in Fig. 10, where we compare our numerical results for the relic neutrino density to the observed muon flux in the Kamiokande detector.
This gives an exclusion region of
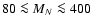 GeV.
Our analytical results, which are comparable to the traditional
relic neutrino densities, is about a factor two lower, giving an exclusion region of
GeV.
Our analytical results, which are comparable to the traditional
relic neutrino densities, is about a factor two lower, giving an exclusion region of
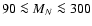 GeV. The model that gives these limits (Gould 1987) is rather
complicated and not verified experimentally, so these results cannot be taken strictly.
Note also that in the three-year WMAP analysis (Spergel et al. 2007), the value of
GeV. The model that gives these limits (Gould 1987) is rather
complicated and not verified experimentally, so these results cannot be taken strictly.
Note also that in the three-year WMAP analysis (Spergel et al. 2007), the value of
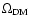 depends on which other data the WMAP data are combined with. For WMAP+CFHTLS
depends on which other data the WMAP data are combined with. For WMAP+CFHTLS
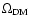 can be as high as 0.279 and for WMAP+CBI+VSA it can be as low as 0.155.
The higher of these possibilities would give an exclusion region of
can be as high as 0.279 and for WMAP+CBI+VSA it can be as low as 0.155.
The higher of these possibilities would give an exclusion region of
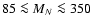 GeV.
The lower boundary value would give an exclusion region of
GeV.
The lower boundary value would give an exclusion region of
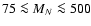 GeV.
A conservative limit based on the Kamiokande data gives the exclusion region
GeV.
A conservative limit based on the Kamiokande data gives the exclusion region
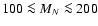 GeV.
GeV.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig10.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg175.gif) |
Figure 10:
Predicted signal from enhanced 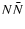 annihilation in the earth and the sun
compared to the measured signal in the Kamiokande.
On the y-axis: the number of muons (per 100 m2 year) produced by muon neutrinos resulting from heavy neutrino collisions in the sun and the earth, as evaluated by Mori et al. (1992), but scaled to our
annihilation in the earth and the sun
compared to the measured signal in the Kamiokande.
On the y-axis: the number of muons (per 100 m2 year) produced by muon neutrinos resulting from heavy neutrino collisions in the sun and the earth, as evaluated by Mori et al. (1992), but scaled to our
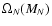 .
On the x-axis: the heavy neutrino mass in GeV. .
On the x-axis: the heavy neutrino mass in GeV. |
| Open with DEXTER |
If a heavy neutrino exists with a mass
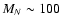 GeV or
GeV or
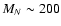 GeV
it would give a small bump in the data at
GeV
it would give a small bump in the data at
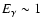 GeV.
Currently the data points are too far apart and the error bars too large to neither exclude
nor confirm the eventual existence of such a heavy neutrino.
Most of this part of the gamma ray spectrum is usually attributed to blazars,
which have the right spectral index,
GeV.
Currently the data points are too far apart and the error bars too large to neither exclude
nor confirm the eventual existence of such a heavy neutrino.
Most of this part of the gamma ray spectrum is usually attributed to blazars,
which have the right spectral index, 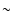 2 (Mukherjee et al. 1997).
2 (Mukherjee et al. 1997).
We note that there could be an enhancement in the signal due to the higher DM densities
within galaxies compared to the mean density in the halos. On the other hand, from within
galaxies there will also be an attenuation due to neutral hydrogen, thus reducing
the enhancement. There will also be a certain degree of extinction of the signal
due to neutral hydrogen along the line of sight, but even if we assume complete extinction
above z=4 the resulting spectrum decreases with only about 20%.
We are also aware of the ongoing debate concerning the antiprotons - whether or not the
DM interpretation of the EGRET gamma excess is compatible with antiproton measurements
(Bergström et al. 2006; de Boer et al. 2006).
We note the argument by de Boer that antiprotons are sensitive to electromagnetic fields,
and hence their flux need not be directly related to that of the photons, even if they
too were produced by 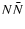 annihilation.
annihilation.
In the advent of the Large Hadron Collider, we also point out that there may be a possibility
to detect the existence of a heavy neutrino indirectly through the invisible Higgs boson
decay into heavy neutrinos (Belotsky et al. 2003).
It will of course be interesting to see the results of the gamma ray large area space telescope (GLAST). It has a field of view about twice as wide (more than 2.5 steradians),
and sensitivity about 50 times that of EGRET at 100 MeV and even more at higher
energies. Its two-year limit for source detection in an all-sky survey is 1.6 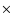 10-9 photons cm-2 s-1 (at energies >100 MeV). It will be able to locate sources
to positional accuracies of 30 arcsec to 5 arcmin.
The precision of this instrument could well be enough to detect a heavy neutrino signal
in the form of a small bump at
10-9 photons cm-2 s-1 (at energies >100 MeV). It will be able to locate sources
to positional accuracies of 30 arcsec to 5 arcmin.
The precision of this instrument could well be enough to detect a heavy neutrino signal
in the form of a small bump at 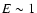 GeV in the gamma spectrum,
if a heavy neutrino with mass
GeV in the gamma spectrum,
if a heavy neutrino with mass 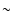 100 or 200 GeV would exist.
100 or 200 GeV would exist.
There are also some other possible consequences of heavy neutrinos that may be worth investigating.
The DM simulations could be used to estimate the spatial correlations that the gamma rays would have
and to calculate a power spectrum for the heavy neutrinos. This could be interesting at least for masses
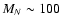 GeV and
GeV and
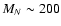 GeV. The annihilation of the heavy neutrinos could also help to explain the reionization of the universe.
Another possible interesting application of heavy neutrinos would be the
large look-back time they provide (Silk & Stodolsky 2006), with a decoupling temperature of
GeV. The annihilation of the heavy neutrinos could also help to explain the reionization of the universe.
Another possible interesting application of heavy neutrinos would be the
large look-back time they provide (Silk & Stodolsky 2006), with a decoupling temperature of 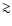 1013 K (Enqvist et al. 1989).
1013 K (Enqvist et al. 1989).
Acknowledgements
E.E. would like to express his gratitude to Konstantine Belotsky,
Lars Bergström, Michael Bradley, Alexander Dolgov,
Kari Enqvist, Kimmo Kainulainen and Torbjörn Sjöstrand
for useful discussions and helpful comments and explanations.
We are both grateful to the GalICS group, who has provided the complete dark
matter simulations and finally to the Swedish National Graduate School
in Space Technology for financial contributions.
- Ando, S., Komatsu, E.,
Narumoto, T., & Totani, T. 2007, Phys. Rev. D, 75,
063519 [NASA ADS] [CrossRef]
(In the text)
- Bardeen, J. M.,
Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ,
304, 15 [CrossRef]
(In the text)
- Becker, R. H.,
Fan, X., White, R. L., et al. 2001, AJ, 122, 2850 [NASA ADS] [CrossRef]
(In the text)
- Belotsky, K., Fargion,
D., Khlopov, M., Konoplich, R., & Shibaev, K. 2003,
Phys. Rev. D, 68, 054027 [NASA ADS] [CrossRef]
(In the text)
- Belotsky, K., Fargion,
D., Khlopov, M., & Konoplich, R. V. 2004,
[arXiv:hep-ph/0411093]
(In the text)
- Berezinsky, V.,
Dokuchaev, V., & Eroshenko, Y. 2006, Phys. Rev. D,
73, 063504 [NASA ADS] [CrossRef]
(In the text)
- Bergström, L.,
Edsjö, J., Gustafsson, M., & Salati, P. 2006, J. Cosmology
Astropart. Phys., 5, 6 [NASA ADS] [CrossRef]
- Blaizot, J.,
Guiderdoni, B., Devriendt, J. E. G., et al. 2004,
MNRAS, 352, 571 [NASA ADS] [CrossRef]
(In the text)
- Blaizot, J., Szapudi,
I., Colombi, S., et al. 2006, MNRAS, 369, 1009 [NASA ADS] [CrossRef]
(In the text)
- Cattaneo, A., Blaizot,
J., Devriendt, J., & Guiderdoni, B. 2005, MNRAS, 364, 407 [NASA ADS]
(In the text)
- Coleman, T. S.,
& Roos, M. 2003, Phys. Rev. D, 68, 027702 [NASA ADS] [CrossRef]
(In the text)
- Colless, M., Dalton,
G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [NASA ADS] [CrossRef]
(In the text)
- de Boer, W., Gebauer,
I., Sander, C., Weber, M., & Zhukov, V. 2006,
[arXiv:astro-ph/0612462]
- Diemand, J., Moore,
B., & Stadel, J. 2005, Nature, 433, 389 [NASA ADS] [CrossRef]
(In the text)
- Dolgov, A. D.
2002, Phys. Rep., 370, 333 [NASA ADS] [CrossRef]
(In the text)
-
Dolgov, A. D., & Zeldovich, Y. B. 1981, Rev. Mod.
Phys., 53, 1 [NASA ADS] [CrossRef]
(In the text)
- Eke, V. R., Cole,
S., & Frenk, C. S. 1996, MNRAS, 282, 263 [NASA ADS]
(In the text)
- Enqvist, K.,
Kainulainen, K., & Maalampi, J. 1989, Nucl. Phys. B, 317,
647 [NASA ADS] [CrossRef]
(In the text)
-
Fargion, D., Khlopov, M. Y., Konoplich, R. V., &
Mignani, R. 1995, Phys. Rev. D, 52, 1828 [NASA ADS] [CrossRef]
(In the text)
- Fargion, D., Khlopov,
M. Y., Konoplich, R. V., & Mignani, R. 1998, Sov. J.
Exp. Theor. Phys. Lett., 68, 685 [NASA ADS] [CrossRef]
- Fargion, D.,
Konoplich, R., Grossi, M., & Khlopov, M. 1999,
[arXiv:astro-ph/9902327]
- Gould, A. 1987, ApJ,
321, 571 [NASA ADS] [CrossRef]
(In the text)
- Gunn, J. E.,
& Peterson, B. A. 1965, ApJ, 142, 1633 [NASA ADS] [CrossRef]
(In the text)
- Hannestad, S. 2006a,
J. Cosmol. Astro-Part. Phys., 1, 1 [NASA ADS] [CrossRef]
(In the text)
- Hannestad, S. 2006b,
Progress Part. Nucl. Phys., 57, 309 [NASA ADS] [CrossRef]
(In the text)
- Kainulainen, K., &
Olive, K. A. 2003, in Neutrino Mass, ed. G. Altarelli
& K. Winter, 53
(In the text)
- Kolb, E., &
Turner, M. 1990, The Early Universe (Oxford: Westview Press), xlii
+ 547
(In the text)
- Lavalle, J., Pochon,
J., Salati, P., & Taillet, R. 2007, A&A, 462, 827 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Maltoni, M., Novikov,
V. A., Okun, L. B., Rozanov, A. N., & Vysotsky,
M. I. 2000, Phys. Lett. B, 476, 107 [NASA ADS] [CrossRef]
(In the text)
- Mather, J. C.,
Fixsen, D. J., Shafer, R. A., Mosier, C., &
Wilkinson, D. T. 1999, ApJ, 512, 511 [NASA ADS] [CrossRef]
(In the text)
- Mori, M., Hikasa, K.,
Nojiri, M. M., et al. 1992, Phys. Lett. B, 289, 463 [NASA ADS] [CrossRef]
(In the text)
- Mukherjee, R.,
Bertsch, D. L., Bloom, S. D., et al. 1997, ApJ, 490,
116 [NASA ADS] [CrossRef]
(In the text)
- Ninin, S. 1999, Ph.D. Thesis,
Université Paris 11
(In the text)
-
Novikov, V. A., Okun, L. B., Rozanov, A. N., &
Vysotsky, M. I. 2002, Phys. Lett. B, 529, 111 [NASA ADS] [CrossRef]
(In the text)
- Press, W. H., Teukolsky,
S. A., Vetterling, W. T., & Flannery, B. P.
1992, Numerical Recipes in C: The Art of Scientific Computing
(New York, NY, USA: Cambridge University Press)
(In the text)
- Silk, J., &
Stodolsky, L. 2006, Phys. Lett. B, 639, 14 [NASA ADS] [CrossRef]
(In the text)
- Sjöstrand, T.,
Mrenna, S., & Skands, P. 2006, J. High Energy Phys., 5, 26 [NASA ADS] [CrossRef]
(In the text)
- Spergel, D. N.,
Verde, L., Peiris, H. V., et al. 2003, ApJS, 148,
175 [NASA ADS] [CrossRef]
(In the text)
- Spergel, D. N.,
Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef]
(In the text)
- Sreekumar, P.,
Bertsch, D. L., Dingus, B. L., et al. 1998, ApJ,
494, 523 [NASA ADS] [CrossRef]
(In the text)
- Szapudi, I., Bond,
J. R., Colombi, S., et al. 2001, in Mining the Sky: Proc.
of the MPA/ESO/MPE Workshop, ed. A. Banday, S. Zaroubi, &
M. Bartelmann, 249
(In the text)
- The LEP Collaborations
2001, [arXiv:hep-ex/0112021]
(In the text)
- Ullio, P.,
Bergström, L., Edsjö, J., & Lacey, C. 2002,
Phys. Rev. D, 66, 123502 [NASA ADS] [CrossRef]
(In the text)
- Yao, W.-M., Amsler,
C., Asner, D., et al. 2006, J. Phys. G Nucl. Phys., 33, 1 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
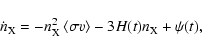
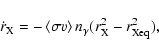
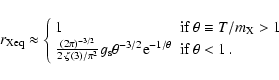
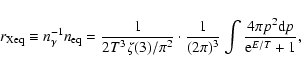
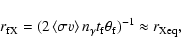
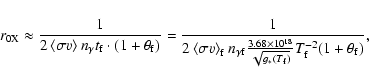
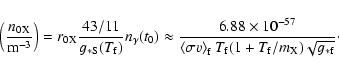
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig1.eps}\end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg78.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig2.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig3.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg93.gif)
![\begin{displaymath}%
\frac{{\rm d}n}{{\rm d}T} = -\frac{{\rm d}t}{{\rm d}T} \lef...
...<\sigma v\right> \left(n(T)^2 - n_{\rm eq}(T)^2\right)\right],
\end{displaymath}](/articles/aa/full/2008/08/aa8898-07/img94.gif)
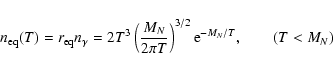
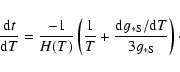
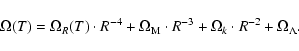
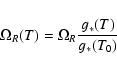
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig4.eps}\end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg111.gif)
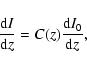
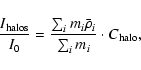
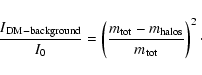
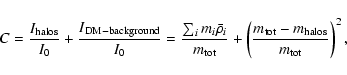
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig5.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg144.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{8898fig6.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg157.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig7.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg158.gif)
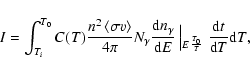
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig8.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg164.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig9.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg165.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{8898fig10.eps} \end{figure}](/articles/aa/full/2008/08/aa8898-07/Timg175.gif)