A&A 479, 377-388 (2008)
DOI: 10.1051/0004-6361:20078491
E. Lindt-Krieg1,2 - A. Eckart1,3 - R. Neri2 - M. Krips4 - J.-U. Pott1,5 - S. García-Burillo6 - F. Combes7
1 - Universität zu Köln, 1.Physikalisches Institut, Zülpicher Strasse 77, 50937 Köln, Germany
2 -
Institut de Radio-Astronomie Millimétrique (IRAM), 300 rue de la Piscine, 38406 St. Martin-d'Hères, France
3 -
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
4 -
Smithsonian Astrophysical Observatory (SAO), Submillimeter Array (SMA)645, North A'Ohoku Place, 96720 Hilo, USA
5 -
W.M. Keck Observatory, 65-1120 Mamalahoa Hwy, Kamuela, HI 96743, USA
6 -
Observatorio Astronómico Nacional (OAN), Alfonso XII, 3, 28014 Madrid, Spain
7 -
Observatoire de Paris, LERMA, 61 Av. de l'Observatoire, 75014 Paris, France
Received 16 August 2007 / Accepted 29 October 2007
Abstract
Within the frame of the NUclei of GAlaxies (NUGA) project, we have determined
the distribution and kinematics of the molecular gas within the central kpc
with high spatial resolution (100-150 pc), for a sample
of active galaxies. The goal is to study the gas-fueling mechanisms in AGN.
We present interferometric observations of 12CO(1-0) and 12CO(2-1) line emission
from the Seyfert 2 galaxy NGC 6574, obtained with the IRAM Plateau de Bure Interferometer (PdBI).
These data have been combined with 30 m mapping data in these lines to correct for the flux
resolved by the interferometer. At an angular resolution of 0.7
![]() (
(![]() 110 pc), the 12CO(2-1)
emission is resolved into an inner disk with a radius of 300 pc.
110 pc), the 12CO(2-1)
emission is resolved into an inner disk with a radius of 300 pc.
The molecular gas in NGC 6574 is primarily distributed in four components: nucleus, bar,
spiral arms - winding up into a pseudo-ring - and an extended
underlying disk component. For the overall galaxy host, we find a 12CO(2-1) to
12CO(1-0) line ratio of ![]() 0.3 indicative of cold or sub-thermally excited gas.
For the nucleus, this ratio is close to unity, indicating emission from dense and warm
molecular gas. Modeling the gas kinematics with elliptical orbits shows that the
molecular gas in the differentially rotating disk of NGC 6574 is strongly influenced
by the presence of a stellar bar. The nuclear component shows an extension toward
the southeast that may be an indication of the lopsidedness of the nuclear gas distribution.
0.3 indicative of cold or sub-thermally excited gas.
For the nucleus, this ratio is close to unity, indicating emission from dense and warm
molecular gas. Modeling the gas kinematics with elliptical orbits shows that the
molecular gas in the differentially rotating disk of NGC 6574 is strongly influenced
by the presence of a stellar bar. The nuclear component shows an extension toward
the southeast that may be an indication of the lopsidedness of the nuclear gas distribution.
We computed the gravity torques exerted from the stellar bar on the gas, deriving the gravitational potential from near-infrared images, and weighting the torques by the CO distribution. We find negative torques for the gas inside the ring, since the gas aligned with the bar has a slight advance phase shift, leading the bar. This means that gas is flowing in towards the center, at least down to 400 pc in radius, which can explain the observed high nuclear gas concentration. This concentration corresponds to a possible inner Lindblad resonance of the bar, according to the measured rotation curve. The gas has been piling up in this location quite recently, since no startburst has been observed yet.
Key words: galaxies: individual: NGC 6574 - galaxies: active - galaxies: kinematics and dynamics
The study of interstellar gas in the nuclei of galaxies is a fundamental for
understanding nuclear activity through fueling the active galactic nuclei (AGN)
and their relation to circum-nuclear star formation.
Some studies claim that pure gaseous density waves (spirals, bars, warps, or lopsided
instabilities) may be driving gas inflow towards the AGN
(Heller ![]() Shlosman 1994; Elmegreen et al. 1998; Regan
Shlosman 1994; Elmegreen et al. 1998; Regan ![]() Mulchaey 1999).
While such dynamical perturbations are responsible for the infall of gas on large scales,
the processes responsible for removing angular momentum on small scales (sub-kpc)
have not been understood very well yet.
Mulchaey 1999).
While such dynamical perturbations are responsible for the infall of gas on large scales,
the processes responsible for removing angular momentum on small scales (sub-kpc)
have not been understood very well yet.
Different scenarios have been introduced trying to explain this phenomenon, such as nested bars (e.g., Friedli & Martinet 1993; spirals e.g., Martini & Pogge 1999) warped nuclear disks (Schinnerer et al. 2000a,b), and lopsidedness or m=1 instabilities (Kormendy & Bender 1999; García-Burillo et al. 2000). Most of the gas within the central kiloparsec of spiral galaxies is in the molecular phase, while the atomic gas is deficient there.
This makes CO lines the best tracers of nuclear gas dynamics in the nuclear interstellar medium.
High-resolution (1
![]() -2
-2
![]() )
maps of the molecular component in the centers of galaxies
are required to model these nuclei within the NUclei of GAlaxies (NUGA) project.
The NUGA project aims at establishing a high angular resolution (
)
maps of the molecular component in the centers of galaxies
are required to model these nuclei within the NUclei of GAlaxies (NUGA) project.
The NUGA project aims at establishing a high angular resolution (![]() 0.5
0.5
![]() -1
-1
![]() )
and high-sensitivity CO survey of twelve objects. It covers the whole sequence of activity types:
Seyfert 1, Seyfert 2, LINERs, and transition objects, and it comprises 12 objects as a core sample and a total of
about 30 objects as an extended sample. The survey is being carried out with the IRAM Plateau de Bure
mm-Interferometer (PdBI) in France, because
it offers the best combination of sensitivity and
resolution, both crucial for this project.
A more detailed description of the NUGA project is given in Paper I
by García-Burillo et al. (2003).
)
and high-sensitivity CO survey of twelve objects. It covers the whole sequence of activity types:
Seyfert 1, Seyfert 2, LINERs, and transition objects, and it comprises 12 objects as a core sample and a total of
about 30 objects as an extended sample. The survey is being carried out with the IRAM Plateau de Bure
mm-Interferometer (PdBI) in France, because
it offers the best combination of sensitivity and
resolution, both crucial for this project.
A more detailed description of the NUGA project is given in Paper I
by García-Burillo et al. (2003).
Previous surveys of molecular gas in active galaxies have been carried out by
other groups (Heckman et al. 1989; Meixner et al. 1990; Vila-Vilaro et al. 1998; Sakamoto et al. 1999a,b),
but have had insufficient spatial resolution (4-7
![]() )
to resolve the nuclear
disk structures, or else were limited to small samples (Tacconi et al. 1997; Baker 2003).
Besides case-by-case analyses and simulations of each object of the
sample (García-Burillo et al. 2003; Combes et al. 2004;
Krips et al. 2005; García-Burillo et al. 2005),
the collected data of the NUGA project also provides an initial statistical basis
for studying different mechanisms that may be responsible for gas flow toward the nuclei
or may account for further accretion inward.
)
to resolve the nuclear
disk structures, or else were limited to small samples (Tacconi et al. 1997; Baker 2003).
Besides case-by-case analyses and simulations of each object of the
sample (García-Burillo et al. 2003; Combes et al. 2004;
Krips et al. 2005; García-Burillo et al. 2005),
the collected data of the NUGA project also provides an initial statistical basis
for studying different mechanisms that may be responsible for gas flow toward the nuclei
or may account for further accretion inward.
This paper describes the distribution and dynamics of molecular gas in
NGC 6574, one of the galaxies belonging to the NUGA survey.
NGC 6574 is a Seyfert 2 galaxy of Hubble type SB(s)bc, at a distance of 33 Mpc.
This results in a spatial scale of ![]() 160 pc per arcsecond.
Its main characteristic is a symmetric structure with two spiral arms
to the north and south of the center, nested on a small bar within the central 8
160 pc per arcsecond.
Its main characteristic is a symmetric structure with two spiral arms
to the north and south of the center, nested on a small bar within the central 8
![]() .
Kotilainen et al. (2000) present high spatial-resolution, near-infrared broad-band JHK and
Br
.
Kotilainen et al. (2000) present high spatial-resolution, near-infrared broad-band JHK and
Br![]() 2.166
2.166 ![]() m and H2 1-0 S(1) 2.121
m and H2 1-0 S(1) 2.121 ![]() m emission line images of the circum nuclear star-formation ring.
The overall near-infrared and radio morphologies (see Laine et al. 2006) generally agree with each other.
The observed H2/Br
m emission line images of the circum nuclear star-formation ring.
The overall near-infrared and radio morphologies (see Laine et al. 2006) generally agree with each other.
The observed H2/Br![]() ratio indicates that the main excitation mechanism of the molecular gas is
UV radiation from hot young stars. Shocks are likely to contribute only in a few regions. To explain
the NIR data, Kotilainen et al. (2000) prefer the model of an instantaneous burst of star formation with an upper
mass cutoff of
ratio indicates that the main excitation mechanism of the molecular gas is
UV radiation from hot young stars. Shocks are likely to contribute only in a few regions. To explain
the NIR data, Kotilainen et al. (2000) prefer the model of an instantaneous burst of star formation with an upper
mass cutoff of
![]() occurring
occurring ![]() 6-7 Myr ago.
An analysis of the molecular gas distribution at an angular resolution of about 4
6-7 Myr ago.
An analysis of the molecular gas distribution at an angular resolution of about 4
![]() in the 12CO(1-0)
line is presented by Sakamoto et al. (1999a,b). They find a prominent CO peak of 1 kpc diameter at the center
of the galaxy on a smooth gas disk with two gas/dust lanes that extend about 2 kpc from the central peak
to east and west at a PA of
in the 12CO(1-0)
line is presented by Sakamoto et al. (1999a,b). They find a prominent CO peak of 1 kpc diameter at the center
of the galaxy on a smooth gas disk with two gas/dust lanes that extend about 2 kpc from the central peak
to east and west at a PA of ![]() 105
105![]() .
From the tips of this gaseous bar, spiral arms start
to form a ring-like structure.
.
From the tips of this gaseous bar, spiral arms start
to form a ring-like structure.
In this paper we analyze data obtained with the IRAM PdBI and the 30 m single-dish telescope in the
12CO(1-0) and 12CO(2-1) lines. The angular resolution we obtained in the combined data set is
about 2
![]() and 0.7
and 0.7
![]() .
We describe the molecular gas distribution and kinematics with
elliptical bar orbits, to account for the influence of the stellar bar potential
in the nucleus of NGC 6574.
In Sect. 2 we describe the CO observations and in
Sect. 3 we present the first results.
The kinematic model and its results are discussed in Sect. 4.
Gravity torques and the nature of gas flows are derived in Sect. 5,
while Sect. 6 concludes.
.
We describe the molecular gas distribution and kinematics with
elliptical bar orbits, to account for the influence of the stellar bar potential
in the nucleus of NGC 6574.
In Sect. 2 we describe the CO observations and in
Sect. 3 we present the first results.
The kinematic model and its results are discussed in Sect. 4.
Gravity torques and the nature of gas flows are derived in Sect. 5,
while Sect. 6 concludes.
In this section we present the 12CO observations with the IRAM 30 m single dish, with the IRAM PdBI, including the short-spacing correction.
We performed IRAM 30 m observations in a
![]() raster pattern with 10
raster pattern with 10
![]() spacing
in August 2005, in order to add the short spacings
and to estimate the flux density filtered out by the interferometric observations.
We used 4 SIS receivers to observe simultaneously at the redshifted
frequencies of the 12CO(1-0) and the 12CO(2-1) lines, thereby assuming the LSR
velocity of NGC 6574 of 2282 km s-1. For each line, a 4 MHz channel filter bank was used with a velocity
resolution smoothed to about 10 km s-1 in order to improve the signal-to-noise ratios of the individual spectra.
The 4 MHz filter bank consists of nine units. Each unit has 256 channels which covers a total bandwidth of 1 GHz.
At 115 GHz and 230 GHz, the HPBW is 21.5
spacing
in August 2005, in order to add the short spacings
and to estimate the flux density filtered out by the interferometric observations.
We used 4 SIS receivers to observe simultaneously at the redshifted
frequencies of the 12CO(1-0) and the 12CO(2-1) lines, thereby assuming the LSR
velocity of NGC 6574 of 2282 km s-1. For each line, a 4 MHz channel filter bank was used with a velocity
resolution smoothed to about 10 km s-1 in order to improve the signal-to-noise ratios of the individual spectra.
The 4 MHz filter bank consists of nine units. Each unit has 256 channels which covers a total bandwidth of 1 GHz.
At 115 GHz and 230 GHz, the HPBW is 21.5
![]() and 10.75
and 10.75
![]() ,
respectively. The parameters for the two observing
runs are summarized in Table 1. We used the wobbler switch mode with a 6 s cycle and a throw of 240
,
respectively. The parameters for the two observing
runs are summarized in Table 1. We used the wobbler switch mode with a 6 s cycle and a throw of 240
![]() .
With the forward efficiency
.
With the forward efficiency
![]() ,
the main-beam efficiency is
,
the main-beam efficiency is
![]() at 115 GHz and 0.53 at 230 GHz. The typical system temperature varied between 200 and 450 K at both frequencies. The pointing
was checked regularly on continuum sources and the accuracy was consistent to 3
at 115 GHz and 0.53 at 230 GHz. The typical system temperature varied between 200 and 450 K at both frequencies. The pointing
was checked regularly on continuum sources and the accuracy was consistent to 3
![]() rms achieved by Greve et al. (1996).
The total bandwidth available was 512 MHz at 115 GHz and 230 GHz, corresponding to 1330 km s-1 and 666 km s-1,
respectively. The data reduction and analysis were done with the GILDAS package (e.g. Guilloteau & Lucas 2000).
For the short-spacing correction and further investigations, only the 4 MHz filter bank was used.
rms achieved by Greve et al. (1996).
The total bandwidth available was 512 MHz at 115 GHz and 230 GHz, corresponding to 1330 km s-1 and 666 km s-1,
respectively. The data reduction and analysis were done with the GILDAS package (e.g. Guilloteau & Lucas 2000).
For the short-spacing correction and further investigations, only the 4 MHz filter bank was used.
Table 1: Parameters of the observing run with IRAM 30 m single dish.
We observed the emission of the J=1-0 and J=2-1 lines of 12CO in a single
field centered at the radio position of the AGN
(i.e.,
![]() and
and
![]() )
in NGC 6574 with the IRAM Plateau de Bure interferometer (PdBI) in April 2002 (D configuration),
in November 2003 (C configuration) and February 2004 (A and C configurations). The six 15 m antennae were
equipped with dual-band SIS receivers. The spectral correlators were centered at 114.400 GHz and 228.798 GHz,
respectively, with three correlator units covering a total bandwidth of 400 MHz at each frequency. The difference between
LSR and heliocentric velocities is 12 km s-1, therefore the observations were centered on
)
in NGC 6574 with the IRAM Plateau de Bure interferometer (PdBI) in April 2002 (D configuration),
in November 2003 (C configuration) and February 2004 (A and C configurations). The six 15 m antennae were
equipped with dual-band SIS receivers. The spectral correlators were centered at 114.400 GHz and 228.798 GHz,
respectively, with three correlator units covering a total bandwidth of 400 MHz at each frequency. The difference between
LSR and heliocentric velocities is 12 km s-1, therefore the observations were centered on
![]() km s-1. The correlator was regularly calibrated by a noise source inserted in the IF system.
km s-1. The correlator was regularly calibrated by a noise source inserted in the IF system.
The bandpass calibrator was 3C 273 or MWC349, while the phase and amplitude calibration were performed on
the nearby quasars 1923+210 and 1749+096, depending on the data set. Flux densities were calibrated
relative to CRL618 and MWC349. The data were phase calibrated in the antenna-based mode. The frequencies were
centered on the redshifted 12CO(1-0) line in the USB at 3 mm and on the redshifted 12CO(2-1) line
in the LSB at 1 mm. For each line, the total bandwidth was 400 MHz and the spectral resolution 1.25 MHz.
The integration time for the central pointing amounts to ![]() 16 h on the source. The water vapor ranged
between 4 and 10 mm (i.e., opacities of
16 h on the source. The water vapor ranged
between 4 and 10 mm (i.e., opacities of ![]() 0.2-0.3) resulting in system temperatures of approximately 200-300 K on average.
0.2-0.3) resulting in system temperatures of approximately 200-300 K on average.
The flux densities of the primary calibrators were determined from IRAM measurements and taken as input for deriving the absolute flux density scales for our visibilities, estimated to be accurate to 10%. The parameters for the four observing runs are summarized in Table 2.
The data reduction and mapping was performed using the GILDAS software.
Data cubes with
![]() spatial pixels (0.25
spatial pixels (0.25
![]() /pixel) were created with velocity planes
separated by 5 km s-1 (for PdBI alone, and by 10 km s-1 for the short-spacing corrected data).
The cubes were cleaned with the Clark (1980) method for 12CO(1-0) data and with
MX for 12CO(2-1) data.
As synthesized clean beams we used a 2.48
/pixel) were created with velocity planes
separated by 5 km s-1 (for PdBI alone, and by 10 km s-1 for the short-spacing corrected data).
The cubes were cleaned with the Clark (1980) method for 12CO(1-0) data and with
MX for 12CO(2-1) data.
As synthesized clean beams we used a 2.48
![]() Gaussian
with
Gaussian
with
![]() at 3 mm and a 0.93
at 3 mm and a 0.93
![]() Gaussian
with
Gaussian
with
![]() at 1 mm. The rms noise levels in the cleaned maps (at 5 km s-1
velocity resolution) are 3 mJy/beam and 6 mJy/beam for the 12CO(1-0) and 12CO(2-1)
lines, respectively. No continuum emission was detected toward NGC 6574.
The maps were corrected for primary beam attenuation.
at 1 mm. The rms noise levels in the cleaned maps (at 5 km s-1
velocity resolution) are 3 mJy/beam and 6 mJy/beam for the 12CO(1-0) and 12CO(2-1)
lines, respectively. No continuum emission was detected toward NGC 6574.
The maps were corrected for primary beam attenuation.
Table 2: Parameters of the observing run with IRAM PdBI.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa8491fig1.eps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{aa8491fig2.eps}
\end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg41.gif) |
Figure 1: The 12CO(1-0) and 12CO(2-1) line intensity derived from the PdBI data set (red) and the combined PdBI+30 m data set (black). The spectra combine the information shown in the channel map in Fig. 2. The comparison shows the larger amount of extended emission for the 12CO(1-0) line that is resolved by the interferometer. Both sets of spectra also demonstrate the asymmetry in flux density between the red and blue shifted part of the spectrum. The red side of the spectrum is brighter mostly in its extended emission. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=17cm,clip]{aa8491fig3.eps}\end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg42.gif) |
Figure 2:
12CO(1-0) velocity-channel maps observed with the PdBI and corrected through short-spacing
by the 30 m single dish in the nucleus of NGC 6574.
The clean beam resulting from the observations is 2.48
|
| Open with DEXTER | |
Short spacings were included using the SHORT-SPACE task in the GILDAS software. To find the best
compromise between good angular resolution and complete restoration of the missing extended flux, the
weights attached to the 30 m and PdBI data were varied.
At the end, a factor of two was applied to the weights of the 30 m data enabling us to
recover more than 40% of the missing flux and to retain the angular resolution of 2.48
![]() at PA of 26
at PA of 26![]() for 12CO(1-0) emission and 0.93
for 12CO(1-0) emission and 0.93
![]() at PA of
12
at PA of
12![]() for 12CO(2-1) emission.
The combined data sets were written to visibility tables,
converted to maps using standard reduction procedures, and then deconvolved using the Clark algorithm.
The weights were adjusted to get the same mean weights in the single-dish data as in the interferometer
data in the u-v range of
for 12CO(2-1) emission.
The combined data sets were written to visibility tables,
converted to maps using standard reduction procedures, and then deconvolved using the Clark algorithm.
The weights were adjusted to get the same mean weights in the single-dish data as in the interferometer
data in the u-v range of
![]() to
to
![]() (D=15 m).
All figures presented in this paper are done with short-spacing corrected data.
(D=15 m).
All figures presented in this paper are done with short-spacing corrected data.
Table 3:
Line intensities and CO luminosities integrated
over the entire linewidth of the full
![]() km s-1
and the extent of the combined PdBI+30 m map after correcting corrected for primary beam
response (typical errors are of the order of 20%).
km s-1
and the extent of the combined PdBI+30 m map after correcting corrected for primary beam
response (typical errors are of the order of 20%).
The line intensities and CO luminosities integrated
over the entire linewidth of the full
![]() km s-1
extent of the combined PdBI+30 m map after correcting for primary beam
response are listed in Table 3.
Since these maps contain the entire galaxy, the corresponding
quantities give information on the overall molecular excitation in NGC 6574.
The difference between the integrated quantities for the 12CO(1-0)
line emission already indicate the presence of an extended disk
component that is resolved out by the interferometer (see Fig. 1).
km s-1
extent of the combined PdBI+30 m map after correcting for primary beam
response are listed in Table 3.
Since these maps contain the entire galaxy, the corresponding
quantities give information on the overall molecular excitation in NGC 6574.
The difference between the integrated quantities for the 12CO(1-0)
line emission already indicate the presence of an extended disk
component that is resolved out by the interferometer (see Fig. 1).
![\begin{figure}
\par {\includegraphics[width=16cm,clip]{aa8491fig4.eps} }
\end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg55.gif) |
Figure 3:
Primary beam corrected integrated intensity maps for the
12CO(1-0) ( left) and 12CO(2-1) ( right) line emission.
The straight lines at PA = 165 |
| Open with DEXTER | |
In this section we first describe the morphology of NGC 6574 and show its kinematics, then estimate the gas masses and related parameters.
Figure 2 shows the velocity-channel maps of the 12CO(1-0) line emission
in the central region of NGC 6574, with a velocity range of
410 km s-1 and a velocity resolution of 10 km s-1.
The typical ``butterfly'' structure visible in the iso-velocity maps in Fig. 5
is the signature of a spatially resolved rotating disk.
In the central 4
![]() -5
-5
![]() the location of the nuclear peak emission in
the 12CO emission also moves from the northern part of the channel
map at the velocity of -170 km s-1 to the southeast at
the velocity of 220 km s-1 with respect to the phase-tracking center of the map.
The displacement of the nuclear component as a function
of velocity shows that it is resolved, and it implies the rotation of the nuclear gas
around the very center of NGC 6574.
In the 12CO(1-0) integrated intensity map shown in Fig. 3 (left),
the molecular gas distribution reveals a regular ring-like structure,
with a mean
angular diameter of
the location of the nuclear peak emission in
the 12CO emission also moves from the northern part of the channel
map at the velocity of -170 km s-1 to the southeast at
the velocity of 220 km s-1 with respect to the phase-tracking center of the map.
The displacement of the nuclear component as a function
of velocity shows that it is resolved, and it implies the rotation of the nuclear gas
around the very center of NGC 6574.
In the 12CO(1-0) integrated intensity map shown in Fig. 3 (left),
the molecular gas distribution reveals a regular ring-like structure,
with a mean
angular diameter of ![]() 50
50
![]() and the peak of the emission in the central
4
and the peak of the emission in the central
4
![]() -5
-5
![]() .
The integrated map was produced by averaging the channel maps
over a total velocity width of 415 km s-1 (from -180 to 235 km s-1).
For the 12CO(1-0) emission, the ring consists of some molecular cloud
complexes that appear to be connected to each other.
They form the two spiral arms of NGC 6574 that start at a PA of
.
The integrated map was produced by averaging the channel maps
over a total velocity width of 415 km s-1 (from -180 to 235 km s-1).
For the 12CO(1-0) emission, the ring consists of some molecular cloud
complexes that appear to be connected to each other.
They form the two spiral arms of NGC 6574 that start at a PA of ![]() 100
100![]() and a projected radius of
and a projected radius of
![]() kpc (1.55 kpc deprojected with an inclination of 45
kpc (1.55 kpc deprojected with an inclination of 45![]() - see below),
near the end points of a prominent nuclear bar and extend out to radii of about
- see below),
near the end points of a prominent nuclear bar and extend out to radii of about ![]() kpc
towards the north and south, approximately along the major axis.
A comparison to NIR images (Kotilainen et al. 2000) reveals that the position of
the central, resolved CO source coincides to within less than 0.25
kpc
towards the north and south, approximately along the major axis.
A comparison to NIR images (Kotilainen et al. 2000) reveals that the position of
the central, resolved CO source coincides to within less than 0.25
![]() with that of the AGN.
From the 12CO(1-0) map in Fig. 3 (left) we estimate a gas bar PA of about
115
with that of the AGN.
From the 12CO(1-0) map in Fig. 3 (left) we estimate a gas bar PA of about
115
![]() ,
taking into account that the line emission on the western and
eastern sides of the bar appear to be displaced by about 1
,
taking into account that the line emission on the western and
eastern sides of the bar appear to be displaced by about 1
![]() -2
-2
![]() to the south and north, respectively.
Our value of 115
to the south and north, respectively.
Our value of 115![]() is in reasonably agreement with the value of 105
is in reasonably agreement with the value of 105![]() (towards the western tip of the bar and derived from a lower resolution map)
given by Sakamoto et al. (1999a,b). It also apparently agrees with the NIR maps presented
by Kotilainen et al. (2000).
The NIR stellar bar has a PA of 105
(towards the western tip of the bar and derived from a lower resolution map)
given by Sakamoto et al. (1999a,b). It also apparently agrees with the NIR maps presented
by Kotilainen et al. (2000).
The NIR stellar bar has a PA of 105![]() ,
which means that our
high-resolution CO maps are able to detect a slight advance phase shift between
the stellar and gas bars, the latter leading by about 10
,
which means that our
high-resolution CO maps are able to detect a slight advance phase shift between
the stellar and gas bars, the latter leading by about 10![]() .
Kotilainen et al. (2000) also interpret the elongation of the nuclear
component as a possible nuclear bar, with an orientation of
.
Kotilainen et al. (2000) also interpret the elongation of the nuclear
component as a possible nuclear bar, with an orientation of
![]() ,
however, this feature is not certain and could be due to projection
effects, as the PA of the major axis is 165
,
however, this feature is not certain and could be due to projection
effects, as the PA of the major axis is 165![]() .
The CO spiral arms, starting at the end of the bar,
mostly lie at the trailing edges of the nuclear bar.
This particular geometry may determine the feeding budget for the gas
in this region. The spiral arms and the central source are connected by a
molecular gas bridge - the small bar.
Contrary to 12CO(1-0), the 12CO(2-1) integrated emission is detected
mainly inside the central component within the radius of 4
.
The CO spiral arms, starting at the end of the bar,
mostly lie at the trailing edges of the nuclear bar.
This particular geometry may determine the feeding budget for the gas
in this region. The spiral arms and the central source are connected by a
molecular gas bridge - the small bar.
Contrary to 12CO(1-0), the 12CO(2-1) integrated emission is detected
mainly inside the central component within the radius of 4
![]() -6
-6
![]() ,
as shown
in Fig. 3 (right). The maximum of the emission is concentrated at the center as well.
While our 12CO(2-1) map lacks sensitivity outside the central 500 pc of the disk,
it does give a sharp image of the molecular gas distribution in the vicinity of the AGN.
Also the tips of the nuclear bar in the eastern and western parts of the galaxy
are indicated.
,
as shown
in Fig. 3 (right). The maximum of the emission is concentrated at the center as well.
While our 12CO(2-1) map lacks sensitivity outside the central 500 pc of the disk,
it does give a sharp image of the molecular gas distribution in the vicinity of the AGN.
Also the tips of the nuclear bar in the eastern and western parts of the galaxy
are indicated.
The kinematics of the molecular gas are dominated by its motion in a rotating disk.
In addition we see the influence of spiral arms and a bar potential.
Figure 4 shows the position-velocity (p-v) plot along the major
axis at
![]() and along the minor axis at
and along the minor axis at
![]() .
By comparing the 30 m and PdBI spectra extracted from the corresponding maps at the same positions,
we find that there is some excess extended emission
(as also suggested by Fig. 1),
especially in the southern part of NGC 6574.
Therefore both the PdBI and the 30 m data indicate that the molecular gas emission is asymmetric
with respect to
.
By comparing the 30 m and PdBI spectra extracted from the corresponding maps at the same positions,
we find that there is some excess extended emission
(as also suggested by Fig. 1),
especially in the southern part of NGC 6574.
Therefore both the PdBI and the 30 m data indicate that the molecular gas emission is asymmetric
with respect to
![]() ,
so the CO emission is preferentially redshifted
(see Fig. 1).
Our results agree well with the previous finding by Sakamoto et al. (1999a,b), which were
obtained at a lower resolution.
,
so the CO emission is preferentially redshifted
(see Fig. 1).
Our results agree well with the previous finding by Sakamoto et al. (1999a,b), which were
obtained at a lower resolution.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{aa8491fig5.eps}
\end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg62.gif) |
Figure 4:
Position-velocity diagrams of 12CO(1-0) and 12CO(2-1) along the major axis
at 165 |
| Open with DEXTER | |
The position velocity diagram along the major axis shows the rotation curve that still has to be
corrected for the inclination of the galactic disk.
For both lines of 12CO emission, the results are similar; however,
differences between them can be found in the central 2
![]() .
The p-v diagram of the 12CO(1-0) line resolves the disk and nuclear region of the galaxy.
There is some evidence of 12CO(2-1) line emission at the very central position, although
the diagram clearly shows that the emission at the systemic velocity is suppressed with respect to
the emission arising at 0.5
.
The p-v diagram of the 12CO(1-0) line resolves the disk and nuclear region of the galaxy.
There is some evidence of 12CO(2-1) line emission at the very central position, although
the diagram clearly shows that the emission at the systemic velocity is suppressed with respect to
the emission arising at 0.5
![]() to a 1
to a 1
![]() separation from the nucleus.
This expresses itself in
two emission clumps neighboring the central position and systemic velocity in the
12CO(1-0) p-v diagram. This could hint at the existence
of a small nuclear ring. The minor axis feature is a clear indication
of non circular motion, expected in a bar, supporting the nuclear
bar hypothesis.
In the 12CO(2-1) p-v diagram this contrast between the clumps is also visible on
the major axis and reduced on the
minor axis. However, the 12CO(2-1) map has less sensitivity, due to its increased
spatial resolution.
separation from the nucleus.
This expresses itself in
two emission clumps neighboring the central position and systemic velocity in the
12CO(1-0) p-v diagram. This could hint at the existence
of a small nuclear ring. The minor axis feature is a clear indication
of non circular motion, expected in a bar, supporting the nuclear
bar hypothesis.
In the 12CO(2-1) p-v diagram this contrast between the clumps is also visible on
the major axis and reduced on the
minor axis. However, the 12CO(2-1) map has less sensitivity, due to its increased
spatial resolution.
The distribution of the 12CO emission, as well as the iso-velocity maps, also indicates
a more complex molecular gas kinematics in the center of the galaxy.
The iso-velocity map of 12CO(1-0) and 12CO(2-1) line emission were made from maps at the full angular
resolution of 2.48
![]() and 0.93
and 0.93
![]() ,
respectively.
In both cases we used equally spaced velocity channels with a velocity range from -170 to 220 km s-1 (see Fig. 5) with the central channel centered on the systemic velocity.
The maps show the increase in velocities from north to south in both lines.
The iso-velocity lines of the central 10
,
respectively.
In both cases we used equally spaced velocity channels with a velocity range from -170 to 220 km s-1 (see Fig. 5) with the central channel centered on the systemic velocity.
The maps show the increase in velocities from north to south in both lines.
The iso-velocity lines of the central 10
![]() are parallel to each other but tilted
by about 20
are parallel to each other but tilted
by about 20![]() with respect to
those of the outer disk sections of NGC 6574. This is a clear indication of the presence of spiral arms
at the location of the bends between the iso-velocity contours and the influence of a barred potential
that expresses itself in an overall tilt of the velocity field with respect to that of the molecular disk.
While the 12CO(1-0) line shows the velocity field for the whole galaxy (disk + nucleus), the
12CO(2-1) line emission only allows us to derive the velocity field for the central 4
with respect to
those of the outer disk sections of NGC 6574. This is a clear indication of the presence of spiral arms
at the location of the bends between the iso-velocity contours and the influence of a barred potential
that expresses itself in an overall tilt of the velocity field with respect to that of the molecular disk.
While the 12CO(1-0) line shows the velocity field for the whole galaxy (disk + nucleus), the
12CO(2-1) line emission only allows us to derive the velocity field for the central 4
![]() region.
Here the overall orientation of the iso-velocity lines is similar to the 12CO(1-0) but shown at a higher
angular resolution - hence the influence of the barred potential is more pronounced.
region.
Here the overall orientation of the iso-velocity lines is similar to the 12CO(1-0) but shown at a higher
angular resolution - hence the influence of the barred potential is more pronounced.
![\begin{figure}
\par\includegraphics[angle=-0,width=17cm,clip]{aa8491fig6.eps} \end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg65.gif) |
Figure 5: Iso-velocity diagram of 12CO(1-0) ( left panel) and 12CO(2-1) emission ( right panel). The 12CO(2-1) emission is observed only in the central part (compare with left panel). The innermost solid contour line is at the systemic velocity and the velocity steps are 30 km s-1. |
| Open with DEXTER | |
The velocity-integrated 12CO(1-0) flux within the ![]() 50
50
![]() primary beam of the combined IRAM PdBI/30 m data
is used to estimate molecular hydrogen masses.
We use
primary beam of the combined IRAM PdBI/30 m data
is used to estimate molecular hydrogen masses.
We use
![]() [K km s
[K km s
![]() [Jy km s
[Jy km s
![]() Hz
Hz
![]() [
[
![]() ],
with the observing frequency
],
with the observing frequency ![]() and the beam size of the corresponding map
and the beam size of the corresponding map ![]() .
The column density of molecular hydrogen can be derived from
.
The column density of molecular hydrogen can be derived from
![]() by assuming the validity of an average
conversion factor
by assuming the validity of an average
conversion factor
![]() [cm-2 K km s-1]
(see e.g. Solomon & Barrett 1991):
[cm-2 K km s-1]
(see e.g. Solomon & Barrett 1991):
![\begin{displaymath}N({\rm H}_{2}) = X\left[\frac{{\rm cm^{-2}}}{{\rm K~km~s^{-1}}}\right] \cdot I'_{\rm CO}[{\rm K~km~s^{-1}}].
\end{displaymath}](/articles/aa/full/2008/08/aa8491-07/img73.gif) |
(1) |
![\begin{displaymath}M_{{\rm H}_{2}}[M_\odot] = 1.51 \times 10^{-14} \cdot N({\rm H}_{2})[{\rm cm^{-2}}]\cdot A[{\rm kpc^{2}}].
\end{displaymath}](/articles/aa/full/2008/08/aa8491-07/img75.gif) |
(2) |
![\begin{displaymath}M_{\rm gas}[M_\odot] =
1.36 \cdot (M_{{\rm H}_{2}}+M_{\rm H_{I}}),
\end{displaymath}](/articles/aa/full/2008/08/aa8491-07/img76.gif) |
(3) |
The total dynamical mass of NGC 6574 is derived from the virial theorem by using
the inclination-corrected circular velocity for a given radius via
![]() km s
km s
![]() [pc].
The error of the Keplerian dynamical mass due to the flatness
of the mass distribution is at most 30% for an exponential disk
(Binney & Tremaine 1987).
All results are summarized in Table 4, separated into
two components: the nucleus, which contains the flux of the inner 4
[pc].
The error of the Keplerian dynamical mass due to the flatness
of the mass distribution is at most 30% for an exponential disk
(Binney & Tremaine 1987).
All results are summarized in Table 4, separated into
two components: the nucleus, which contains the flux of the inner 4
![]() ,
and the disk, containing the residual flux within the 50
,
and the disk, containing the residual flux within the 50
![]() of the
integrated map.
This central source contains a molecular gas mass of
of the
integrated map.
This central source contains a molecular gas mass of ![]() 10
10
![]() .
Estimated from the kinematics revealed by the 12CO(1-0) line emission,
the total dynamical mass of NGC 6574 contained within a radius of about 15
.
Estimated from the kinematics revealed by the 12CO(1-0) line emission,
the total dynamical mass of NGC 6574 contained within a radius of about 15
![]() is
is
![]() .
The molecular gas contributes about 6% to the dynamical mass in the inner 6 kpc.
This is a typical value for a moderately gas-rich barred spiral.
.
The molecular gas contributes about 6% to the dynamical mass in the inner 6 kpc.
This is a typical value for a moderately gas-rich barred spiral.
Table 4: Results of IRAM PdBI and PdBI+30 m telescope.
Comparison of the two CO line maps, at the same resolution and with the same
spatial frequency sampling, can yield information about the excitation condition of the gas.
We studied the variation in the 12CO(2-1)/12CO(1-0) ratio in areas
with significant emission levels in both lines, i.e. in channels with velocities
from -180 to 220 km s-1.
Within the 20.5
![]() primary beam, the 12CO(2-1) map
was first smoothed to the spatial resolution of the 12CO(1-0) map to assure
that the two lines sample identical regions. The maps were then corrected for primary beam
attenuation.
We find a nuclear 12CO(2-1)/12CO(1-0) line ratio close to unity and an
off-nuclear ratio around 0.2.
primary beam, the 12CO(2-1) map
was first smoothed to the spatial resolution of the 12CO(1-0) map to assure
that the two lines sample identical regions. The maps were then corrected for primary beam
attenuation.
We find a nuclear 12CO(2-1)/12CO(1-0) line ratio close to unity and an
off-nuclear ratio around 0.2.
The values are also apparent from the maps in Fig. 3 (see caption).
The 12CO(2-1)/12CO(1-0)
ratio is best determined on the nucleus with a value close to unity.
The deconvolved source size in the J=2-1 line emission is ![]() arcsec.
This results in a 12CO(2-1) line flux of 55.7 Jy km s-1 in the 3 mm beam and a
12CO(2-1)/12CO(1-0) line ratio of
arcsec.
This results in a 12CO(2-1) line flux of 55.7 Jy km s-1 in the 3 mm beam and a
12CO(2-1)/12CO(1-0) line ratio of
![]() .
This ratio is typical of moderately
dense and warm (
.
This ratio is typical of moderately
dense and warm (
![]() cm-3,
cm-3,
![]() K),
optically thick molecular clouds if a small contribution from the cosmic microwave background
is taken into account as well (see Eckart et al. 1990; García-Burillo et al. 1993).
For the weak and extended line emission along the bar, we find an
off-nuclear 12CO(2-1)/12CO(1-0)
ratio of
K),
optically thick molecular clouds if a small contribution from the cosmic microwave background
is taken into account as well (see Eckart et al. 1990; García-Burillo et al. 1993).
For the weak and extended line emission along the bar, we find an
off-nuclear 12CO(2-1)/12CO(1-0)
ratio of
![]() .
This is indicative of a dominant contribution of cold (
.
This is indicative of a dominant contribution of cold (
![]() K)
or sub-thermally (
K)
or sub-thermally (
![]() cm-3) excited molecular gas.
cm-3) excited molecular gas.
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{aa8491fig7.eps}\end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg112.gif) |
Figure 6:
Integrated intensity map and position velocity diagram along the major axis for the
modeled 12CO(1-0) emission.
The dashed line at
|
| Open with DEXTER | |
It is interesting to compare our results achieved through observations
of 12CO(1-0) and 12CO(2-1) emission with observational results
at other wavelengths.
Laine et al. (2006) carried out 20 cm and 3.5 cm wavelength radio continuum observations with
the VLA and compare the results with the NIR data of
H2 and Br![]() from Kotilainen et al. (2000).
In the radio and NIR they find
a central point-like component and a circum-nuclear ring.
Both source components are
very consistent with our observations.
The ``jet'', which is represented as a connection between the nucleus
and the circumnuclear ring at 3.5 cm,
along the major axis of the galaxy, has no counterpart in our observations.
from Kotilainen et al. (2000).
In the radio and NIR they find
a central point-like component and a circum-nuclear ring.
Both source components are
very consistent with our observations.
The ``jet'', which is represented as a connection between the nucleus
and the circumnuclear ring at 3.5 cm,
along the major axis of the galaxy, has no counterpart in our observations.
In the following section we describe the model used to analyze the data obtained with the IRAM telescopes, then derive the rotation curve and the possible shape of the gaseous orbits.
The inner 200 pc of NGC 6574 show clear deviations from pure circular motions. To analyze the complex kinematics, we modeled the data with 3DRings similar to the approach of Krips et al. (2005), Pott et al. (2004), and Schinnerer et al. (2000b, see Appendix B therein). With 3DRings only fully symmetric structures can be modeled (i.e., no lopsidedness). The model subdivides the disk into many individual (circular or elliptical) orbits of molecular gas, which lie on the (possibly tilted) plane. With the 3DRings program we investigate the kinematical imprint of (warped) rotating gas.
We model non circular motions with 3DRings via elliptical orbits with changing position angles
characterizing gas motions in a bar. The inclination, position angle, and shape of the rotation curve
for the overall galaxy were held fixed. Each fitting process was started at large radii and
successively extended toward the center. In each case we tried several start setups that all converged
to similar (best) solutions with mean deviations from the data of less than about 10 km s-1 and 0.1 arcsec
for each radius and velocity in the p-v diagrams and 10![]() in the position angle of the
mapped structures.
The best decompositions were achieved using a systemic velocity of
in the position angle of the
mapped structures.
The best decompositions were achieved using a systemic velocity of
![]() km s-1 in agreement with the derived position velocity diagrams
shown in Fig. 4 (see also spectra and channel maps in Figs. 1 and 2).
The revised best-fit parameters were obtained by comparing the result with the observed
PdBI+30 m data and tuning the parameters until the match is optimal. We derived an inclination of
45
km s-1 in agreement with the derived position velocity diagrams
shown in Fig. 4 (see also spectra and channel maps in Figs. 1 and 2).
The revised best-fit parameters were obtained by comparing the result with the observed
PdBI+30 m data and tuning the parameters until the match is optimal. We derived an inclination of
45
![]() and position angle of 165
and position angle of 165
![]() for the galactic disc
in space. In Fig. 7 we show the intensity distribution and rotation curve
and in Fig. 8 the ellipticity
for the galactic disc
in space. In Fig. 7 we show the intensity distribution and rotation curve
and in Fig. 8 the ellipticity ![]() and the position angle of the elliptical
bar orbits as a function of radius that we used to model the 12CO(1-0) line emission data.
The position angle is counted from north to east with respect to the northern part of the
inclination axis. This is represented by the dashed line in Fig. 6.
and the position angle of the elliptical
bar orbits as a function of radius that we used to model the 12CO(1-0) line emission data.
The position angle is counted from north to east with respect to the northern part of the
inclination axis. This is represented by the dashed line in Fig. 6.
| |
Figure 7: Intensity distribution and rotation curve as a function of radius as used for modeling the 12CO(1-0) line emission data. |
| Open with DEXTER | |
As a result of the modeling we find:
| |
Figure 8:
The ellipticity |
| Open with DEXTER | |
We used the near-infrared images kindly made available by Reunanen.
The JHK images have been obtained by Kotilainen et al. (2000)
at UKIRT under 0.6-0.7
![]() seeing and a field of view of 70
seeing and a field of view of 70
![]() .
The H band image is superposed on the CO contours
in Fig. 9. There is a very good correspondence
between the NIR image and the CO(1-0) contours, indicating that
the molecular gas is well aligned along the bar
and nuclear bar in NGC 6574. However, a slight phase shift can be
noticed, with the gas on the leading side.
The nuclear bar is about 8
.
The H band image is superposed on the CO contours
in Fig. 9. There is a very good correspondence
between the NIR image and the CO(1-0) contours, indicating that
the molecular gas is well aligned along the bar
and nuclear bar in NGC 6574. However, a slight phase shift can be
noticed, with the gas on the leading side.
The nuclear bar is about 8
![]() (or 1.2 kpc) in diameter, while
the main bar is 20
(or 1.2 kpc) in diameter, while
the main bar is 20
![]() (or 3.2 kpc) in diameter.
(or 3.2 kpc) in diameter.
The color J-H image is also compared with the CO emission
in Fig. 10. It reveals a spiral structure emerging
of the main bar.
Also, the correlation with the CO distribution is evident.
The spiral arms in the CO emission wind up in a pseudo-ring,
conspicuous in H![]() (Gonzalez-Delgado et al. 1997) and in
Br
(Gonzalez-Delgado et al. 1997) and in
Br![]() (Kotilainen et al. 2000). This star-formation ring
is likely to correspond to the UHR resonance of the primary bar.
Indeed, in most studied galaxies, as shown by simulations and
confrontation with observations, the bar ends up near its UHR resonance.
(Kotilainen et al. 2000). This star-formation ring
is likely to correspond to the UHR resonance of the primary bar.
Indeed, in most studied galaxies, as shown by simulations and
confrontation with observations, the bar ends up near its UHR resonance.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa8491fig10.eps}\end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg120.gif) |
Figure 9:
CO(1-0) linear contours (1.7 to 17 by 1.7 Jy/beam)
superposed on the near-infrared H image,
from Kotilainen et al. (2000), in logarithmic levels.
The CO emission is aligned along the bar of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa8491fig11.eps}\end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg121.gif) |
Figure 10: CO(1-0) linear contours (1.7 to 17 by 1.7 Jy/beam) superposed on a color image in the near-infrared J-H, from Kotilainen et al. (2000), in logarithmic levels. The CO emission follows a spiral structure, which winds up in a pseudo ring. |
| Open with DEXTER | |
As described in previous papers (e.g. Garcia-Burillo et al. 2005), we assume that the NIR images can give us the best approximation for the total stellar mass distribution because it is less affected by dust extinction or by stellar population biases. We here recall the essential definitions and assumptions.
The H image was first deprojected according to the
angles
![]() and
and
![]() .
We did not deproject
the bulge separately, since we do not know its actual flattening, and the galaxy
- a late type (Sbc) - does not make a large contribution.
The image is, however, completed in the vertical
dimension by assuming an isothermal plane model with a constant scale height,
equal to
.
We did not deproject
the bulge separately, since we do not know its actual flattening, and the galaxy
- a late type (Sbc) - does not make a large contribution.
The image is, however, completed in the vertical
dimension by assuming an isothermal plane model with a constant scale height,
equal to ![]() 1/12th of the radial scale length of the image. The potential is
then derived by a Fourier transform method, assuming a constant mass-to-light (M/L) ratio.
The M/L value is selected to retrieve the observed CO rotation curve.
The axisymmetric part of the model, fitted by parametric functions,
is then derived to find
the proper frequencies, as shown in Fig. 11.
The rotation curve agrees within the uncertainties of the data
(Figs. 4)
with the rotation curve shown in Fig. 7,
which was derived while modeling the CO data alone.
1/12th of the radial scale length of the image. The potential is
then derived by a Fourier transform method, assuming a constant mass-to-light (M/L) ratio.
The M/L value is selected to retrieve the observed CO rotation curve.
The axisymmetric part of the model, fitted by parametric functions,
is then derived to find
the proper frequencies, as shown in Fig. 11.
The rotation curve agrees within the uncertainties of the data
(Figs. 4)
with the rotation curve shown in Fig. 7,
which was derived while modeling the CO data alone.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{aa8491fig12.ps}\end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg123.gif) |
Figure 11:
Rotation curve and derived frequencies |
| Open with DEXTER | |
For the non-axisymmetric part, the
potential
![]() is then decomposed in the different m-modes:
is then decomposed in the different m-modes:
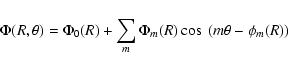
The strength of the m-Fourier component, Qm(R), is defined as
![]() ,
i.e. by the ratio between tangential
and radial forces (e.g. Combes & Sanders 1981).
The strength of the total non-axisymmetric perturbation is defined by
,
i.e. by the ratio between tangential
and radial forces (e.g. Combes & Sanders 1981).
The strength of the total non-axisymmetric perturbation is defined by
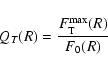
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{aa8491fig13.ps}\end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg131.gif) |
Figure 12:
Strengths (Q1, Q2, and total |
| Open with DEXTER | |
After having calculated the forces per unit mass (Fx and Fy) from the derivatives of
![]() on
each pixel, the torques per unit mass t(x,y) can be computed by
on
each pixel, the torques per unit mass t(x,y) can be computed by
To estimate the radial gas flow induced by the torques, we first computed the torque
per unit mass averaged over the azimuth, using
![]() as the actual weighting function, i.e.
as the actual weighting function, i.e.
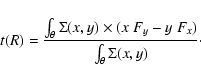
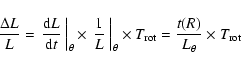
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa8491fig14.eps} \end{figure}](/articles/aa/full/2008/08/aa8491-07/Timg141.gif) |
Figure 13:
The CO(1-0) contours are overlaid onto the gravitational torque
map (
|
| Open with DEXTER | |
We show in Fig. 13 that the derived torques change sign following a characteristic 2D
butterfly pattern. The CO contours clearly reveal that the majority of the gas
at
![]() kpc is offset from the bar on the leading edge where the torques
are negative. The rotation sense in the galaxy is counterclockwise, and the spiral
structure is trailing.
Towards the center (r< 400 pc), however, the dominating torques are positive.
Indeed, the average value
of dL/L per rotation over 0-400 pc is -0.005, and over 400-1500 pc is 0.1.
kpc is offset from the bar on the leading edge where the torques
are negative. The rotation sense in the galaxy is counterclockwise, and the spiral
structure is trailing.
Towards the center (r< 400 pc), however, the dominating torques are positive.
Indeed, the average value
of dL/L per rotation over 0-400 pc is -0.005, and over 400-1500 pc is 0.1.
| |
Figure 14: The torque, or more precisely the fraction of the angular momentum transferred from/to the gas in one rotation dL/L, plotted for CO(1-0) ( left), and CO(2-1) ( right). The curve is noisier for the CO(2-1) line due to a lower sensitivity at 230 GHz. Both curves, however, show negative torques around 1 kpc radius (more precisely from 0.4 to 1.5 kpc for the CO(1-0)). |
| Open with DEXTER | |
The interpretation of these results can be done in the classical
scenario of angular momentum transfer in barred galaxies.
The main bar, 1.6 kpc in radius, ends in a pseudo-ring at its
ultra-harmonic resonance (UHR), where its pattern speed
equals
![]() .
According to Fig. 11,
we can then derive the probable pattern speed of
.
According to Fig. 11,
we can then derive the probable pattern speed of ![]() 60 km s-1 kpc-1.
Its co-rotation should then be around 2.8 kpc. Since the rotation
curve gradient is quite strong in the center, as revealed by the CO
kinematics, there must be an ILR in the circumnuclear region,
which might correspond to the high gas concentration there,
at r< 600 pc. The ILR is usually the site of high
gas concentration in a ring.
A suggestion of such a nuclear ring
has been given in Sect. 3, by
the two prominent concentrations of CO in the major axis p-v diagrams.
It is obvious that the CO emission is not peaked in the very
center, around systemic velocity, but corresponds to
an elongated nuclear ring, with highly
non-circular motions, at a radius of about 130 pc.
With the pattern speed of
60 km s-1 kpc-1.
Its co-rotation should then be around 2.8 kpc. Since the rotation
curve gradient is quite strong in the center, as revealed by the CO
kinematics, there must be an ILR in the circumnuclear region,
which might correspond to the high gas concentration there,
at r< 600 pc. The ILR is usually the site of high
gas concentration in a ring.
A suggestion of such a nuclear ring
has been given in Sect. 3, by
the two prominent concentrations of CO in the major axis p-v diagrams.
It is obvious that the CO emission is not peaked in the very
center, around systemic velocity, but corresponds to
an elongated nuclear ring, with highly
non-circular motions, at a radius of about 130 pc.
With the pattern speed of ![]() 60 km s-1 kpc-1, two ILR must exist,
as suggested by the rotation curve of Fig. 11. However, this indication is
only derived from the
60 km s-1 kpc-1, two ILR must exist,
as suggested by the rotation curve of Fig. 11. However, this indication is
only derived from the
![]() curve with the epicyclic
approximation, which is not valid for a strong bar.
The effective curve is lower, and the ILR
might be expected between 30 and 900 pc. Moreover, if a nuclear ring exists,
it is likely to be elongated, corresponding to the range of radii
usually found in numerical simulations.
In addition, the near infrared images give a hint of
a nuclear bar, but this is not certain. This nuclear bar is expected
from theory to decouple in such conditions, inside the nuclear ILR ring.
curve with the epicyclic
approximation, which is not valid for a strong bar.
The effective curve is lower, and the ILR
might be expected between 30 and 900 pc. Moreover, if a nuclear ring exists,
it is likely to be elongated, corresponding to the range of radii
usually found in numerical simulations.
In addition, the near infrared images give a hint of
a nuclear bar, but this is not certain. This nuclear bar is expected
from theory to decouple in such conditions, inside the nuclear ILR ring.
The gas flow towards the center is taken just in the act, at the present epoch.
The flow rate is not very high, due to a bar that is relatively weak
(see Fig. 12). But the gas flow already has a visible consequence:
a high concentration of molecular gas towards the center, which must be
recent, since the center is not the location of any starburst
(no peak in Br![]() or H
or H![]() ).
).
The maps presented here lack spatial resolution to determine
unambiguously whether the gas is stalled at the ILR of the
main bar, or if it could be still driven inwards due to a nuclear
bar. In either case, we conclude that we are seeing the gas inflow
fueling the center, which soon will feed the AGN nucleus.
A possibility is that the feeding is intermittent, since the gas flows
induced by gravity torques in the very center (r < 400 pc) have a
very short time scale of
![]() Myr.
Myr.
In this paper we present the analysis of subarcsec-resolution PdBI observations of molecular gas in the Seyfert 2 NGC 6574 with a short spacing correction derived from IRAM 30 m telescope observations. Our data complements the analysis made by Sakamoto et al. (1999a,b) for 12CO(1-0) observations and expands the analysis with observations of the 12CO(2-1) line emission. The successful descriptive modeling of the disk dynamics with elliptical bar orbits corroborates the hypothesis that the molecular gas is strongly influenced by the stellar bar-like potential located within a more extended molecular gas disk (Laine et al. 2006; Kotilainen et al. 2000).
Within the NUGA sample, a whide variety of morphologies and dynamics are observed (see introduction and e.g. García-Burillo et al. 2005). With the exception of a nuclear warp, NGC 6574 shows all of these attributes. But even a nuclear warp cannot be excluded as it only becomes apparent at the highest linear resolution (sub-100 pc), which can only be achieved for the closest nuclei (e.g. NGC 1068 and NGC 3227; e.g. Schinnerer et al. 2000a). In most cases, there is very little evidence that any of the observed features can be uniquely linked to the activity of the nucleus. In some cases (NGC 4826: García-Burillo et al. 2003; NGC 7217: Combes et al. 2004) the detailed analysis of the observed source properties even appear to rather inhibit than to support fueling of the nuclear region.
Contrary to the majority of NUGA galaxies studied so far, there is clear evidence in NGC 6574 of gas inflow on a very small scale, of a few hundred parsec, where we find CO emission down to our spatial resolution. The gas appears to accumulate at this central location, and the inflow must be recent, since there is still no nuclear starburst observed. The CO position-velocity diagrams reveal a hint of an elongated nuclear ring there, which would be the ILR of the main bar. Our resolution does not allow us to go further to determine whether the gas is stalled at this ILR ring or driven inwards to feed the AGN through a nuclear bar.
In either case, our result is consistent with the previous finding
that low-luminosity AGN
(the NUGA sample includes Seyferts and LINERs) do not require
any efficient fueling to sustain their luminosity (see e.g. Ho 2003).
It is also unclear which processes dominate the infall
of gas into the region with radii that are beyond our current angular
resolution i.e. linear scales of less than ![]() 100 pc.
Nuclear bars (Shlosman et al. 1989),
lopsidedness or m = 1 instabilities
(García-Burillo et al. 2000), and nuclear spiral density waves
(Englmaier & Shlosman 2000) provide processes that
enable the gas infall into the central
few parsecs.
In the case of NGC 6574, both the 12CO(1-0) and the 12CO(2-1)
integrated line-intensity maps consistently show evidence of
a weak extension toward the southeast. This may be interpreted as
indicating lopsidedness and may therefore be responsible for
transporting molecular gas into the central 100 pc.
If, however, none of the above-mentioned mechanisms are efficient,
then as an alternative, viscosity may support such a transport.
100 pc.
Nuclear bars (Shlosman et al. 1989),
lopsidedness or m = 1 instabilities
(García-Burillo et al. 2000), and nuclear spiral density waves
(Englmaier & Shlosman 2000) provide processes that
enable the gas infall into the central
few parsecs.
In the case of NGC 6574, both the 12CO(1-0) and the 12CO(2-1)
integrated line-intensity maps consistently show evidence of
a weak extension toward the southeast. This may be interpreted as
indicating lopsidedness and may therefore be responsible for
transporting molecular gas into the central 100 pc.
If, however, none of the above-mentioned mechanisms are efficient,
then as an alternative, viscosity may support such a transport.
How viscosity may be responsible for transporting gas toward the center of such disks has been shown by Duschl et al. (2000). The authors suggest that viscosity within these gaseous disks may provide an efficient AGN fueling mechanism. However, viscosity could also counteract low-gravity torques on the gas. García-Burillo et al. (2005) discuss the details of viscosity effects versus gravity torques to drive AGN fueling. The authors find that such a counteraction may occur if it acts on a nuclear ring of high gas-surface density contrast and a few 100 pc size. Whether only one of these mechanisms of different efficiency or a combination of them usually accounts for the gas infall is still unknown. García-Burillo et al. (2005) propose an evolutionary scenario in which gravity torques and viscosity act in concert to produce recurrent episodes of activity during the typical lifetime of any galaxy.
Alternatively, the timescales for fueling on the few 100 pc scale and the onset of activity are so different that both cannot be observed simultaneously (see e.g. Combes 2004). In that case detailed investigations of nuclear gas fueling that drives the AGN accretion and possibly the star formation process in the very center of the nuclear star cluster have to resort to studies of the molecular and atomic gas dynamics on size scales of less than 10 pc. This could become possible with the high sensitivity and angular resolution that will be provided by ALMA.
Acknowledgements
Part of this work was supported by the German Deutsche Forschungsgemeinschaft, DFG project number SFB 494. We thank the IRAM stuff from the Plateau de Bure and from Grenoble for carrying out the observations and help provided during the data reduction, especially to J. M. Winters.