A&A 479, L33-L36 (2008)
DOI: 10.1051/0004-6361:20077781
LETTER TO THE EDITOR
M. Gellert - G. Rüdiger - D. Elstner
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
Received 3 May 2007 / Accepted 22 December 2007
Abstract
Aims. We investigate the instability of toroidal magnetic fields resulting from the action of z-dependent differential rotation on a given axial field ![]() in a cylindrical enclosure where, in particular, the helicity of the resulting nonaxisymmetric flow is of interest. We probe the idea that helicity is related to the external field and the differential rotation as
in a cylindrical enclosure where, in particular, the helicity of the resulting nonaxisymmetric flow is of interest. We probe the idea that helicity is related to the external field and the differential rotation as
![]() .
.
Methods. We conduct isothermal magnetohydrodynamic simulations of a quasi-incompressible medium with finite viscosity and conductivity in a perfectly conducting container, and analyze both the kinematic and current helicity of the resulting field by regarding the nonaxisymmetric parts of the field as fluctuations.
Results. The observed instability leads to a nonaxisymmetric solution with dominating mode m=1. With the onset of instability, both kinematic and current helicity are produced which fulfill the suggested relation
![]() .
Obviously, differential rotation
.
Obviously, differential rotation
![]() only needs an axial field B0z to produce significant helicity. Any regular time-dependency of the helicity could not be found. The resulting axial
only needs an axial field B0z to produce significant helicity. Any regular time-dependency of the helicity could not be found. The resulting axial ![]() -effect
-effect
![]() is mainly due to the current helicity, the characteristic time scale between both the values is of the order of the rotation time. If the axial field is switched off, then the helicity and the
is mainly due to the current helicity, the characteristic time scale between both the values is of the order of the rotation time. If the axial field is switched off, then the helicity and the ![]() -effect disappear, and a dynamo is not observed.
-effect disappear, and a dynamo is not observed.
Key words: magnetohydrodynamics (MHD)
Helicity in rotating turbulence plays a basic role in dynamo theory for the generation of large-scale cosmic magnetic fields (Krause & Rädler 1980; Brandenburg & Subramanian 2005). Usually stratification of density or turbulence itself is needed to generate helicity. We demonstrate that, even without stratification, helicity can exist due to the common action of magnetic fields and differential rotation. Whereas differential rotation depending on latitude is well-known from observations of star spots, differential rotation (of the interior of stars) depending on the z-coordinate only, appears more rarely. It is predicted and observable, for instance, in the tachocline of the sun (Rüdiger & Kitchatinov 1997; Kitchatinov & Rüdiger 2005), and influences the internal rotation of massive stars (Maeder & Meynet 2003). It may open the possibility of studying nonaxisymmetric (large-scale) structures by shear-driven magnetohydrodynamic (MHD) instability of laminar flows (Braithwaite & Spruit 2004; Braithwaite 2006).
Differential rotation transforms poloidal field components into toroidal components, which due to the Tayler instability (TI), become unstable if a critical
amplitude is exceeded (Vandakurov 1972). Tayler (1973) showed that a magnetic field ![]() becomes unstable against nonaxisymmetric perturbations if
the condition
becomes unstable against nonaxisymmetric perturbations if
the condition
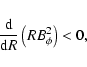 |
(1) |
Keeping in mind the pseudoscalar nature of helicity, a possible relation between helicity and both the external field and differential rotation would be
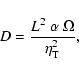 |
(5) |
In the following, the details of the model used are explained. Section 3 describes the onset of the TI in a cylindrical enclosure and
the resulting field structure. In Sect. 4, it is shown that - if the axial field is strong enough - the
numerical simulations are in good agreement with relation 4 in the case of z-dependent differential rotation, where it simplifies to
![]() and only a (strong enough) z-component B0z of the external field is needed. In
Sect. 5 we show that the generated helicity is connected with an
and only a (strong enough) z-component B0z of the external field is needed. In
Sect. 5 we show that the generated helicity is connected with an ![]() -effect, which is also proportional to the gradient of the
differential rotation.
-effect, which is also proportional to the gradient of the
differential rotation.
| |
Figure 1: The considered domain is a cylinder inside a box with Cartesian grid of side length 2.5 L and height L. The full set of equations is solved only in the cylindrical domain. |
| Open with DEXTER | |
We consider a differentially-rotating cylinder with radius L and height L embedded in a box with cartesian grid
of side length 2.5 L and height L (see Fig. 1). The cylinder radius is 20% less than the box side length, which appeared to be
a good compromise between wasted computing power in the corner regions and decreasing influence from the geometry of the box. We calculated
using the PENCIL code (Brandenburg & Dobler 2002), a high-order finite difference code (sixth order in space and third order in time). Inside the cylinder
domain, we solve both momentum and induction equations. Outside the cylinder, we kept the initial velocity to
sustain the differential rotation via this no-slip conditions on the rim of the cylinder. On the top and the bottom, we apply stress-free conditions
for the flow.
For the magnetic field, perfect conductor boundary conditions are applied on all box boundaries. Additionally,
in the region outside the cylinder, magnetic diffusivity ![]() is enhanced to a value ten times larger than inside the cylinder.
is enhanced to a value ten times larger than inside the cylinder.
To keep the system nearly incompressible with a code for compressible media, the value of
![]() is chosen in a way that the resulting maximum of the
(meridional) velocity never exceeds 16% of the speed of sound, which was set to
is chosen in a way that the resulting maximum of the
(meridional) velocity never exceeds 16% of the speed of sound, which was set to
![]() .
The initial density is set to
.
The initial density is set to
![]() ,
fluctuations
are of the order of 10-4. The spatial resolution is
,
fluctuations
are of the order of 10-4. The spatial resolution is
![]() .
Test runs with
.
Test runs with
![]() deliver only slight differences
with smoother fields.
deliver only slight differences
with smoother fields.
The initial magnetic field consists of the external time-independent homogeneous field
![]() applied only inside the cylinder. It is
twisted into a strong toroidal field by the differential rotation.
The strength of the generated field depends on B0z, varied between
B0z=0.01 and B0z=0.1, and the gradient of the differential rotation
applied only inside the cylinder. It is
twisted into a strong toroidal field by the differential rotation.
The strength of the generated field depends on B0z, varied between
B0z=0.01 and B0z=0.1, and the gradient of the differential rotation
![]() ,
where the latter was fixed to
,
where the latter was fixed to
![]() for all presented calculations. Based on the radius
(set to L = 1) and the velocity at z=1 (
for all presented calculations. Based on the radius
(set to L = 1) and the velocity at z=1 (
![]() ), and the viscosity (
), and the viscosity (![]() ), the Reynolds number has a value of
), the Reynolds number has a value of
![]() .
In the following text,
system rotation always refers to the rotation on top of the cylinder and time is given in units of rotation time. The magnetic Prandtl number
.
In the following text,
system rotation always refers to the rotation on top of the cylinder and time is given in units of rotation time. The magnetic Prandtl number ![]() is
varied between
is
varied between
![]() and
and
![]() with no qualitatively change of the instability. In the following analysis, we concentrate on
with no qualitatively change of the instability. In the following analysis, we concentrate on
![]() .
We choose a large Prandtl number to encourage dynamo action, although we observed no dynamo.
.
We choose a large Prandtl number to encourage dynamo action, although we observed no dynamo.
If ![]() becomes strong enough, the TI occurs and leads to a growing nonaxisymmetric field. The largest nonaxisymmetric
mode is m=1. By ``strong enough'' we mean that not only does the magnitude of
becomes strong enough, the TI occurs and leads to a growing nonaxisymmetric field. The largest nonaxisymmetric
mode is m=1. By ``strong enough'' we mean that not only does the magnitude of ![]() reach high enough values, but also a certain
threshold
reach high enough values, but also a certain
threshold
![]() (with
(with
![]() of the order of
of the order of ![]() )
needs to be crossed, which is different from the case of pure toroidal
fields (Tayler 1973; see Rüdiger et al. 2007). This means that an additional poloidal field component suppresses the instability. For
)
needs to be crossed, which is different from the case of pure toroidal
fields (Tayler 1973; see Rüdiger et al. 2007). This means that an additional poloidal field component suppresses the instability. For
![]() ,
the instability sets in at a Hartmann number of
,
the instability sets in at a Hartmann number of
![]() ,
where
,
where
![]() means the maximal value of the generated toroidal field
means the maximal value of the generated toroidal field ![]() .
To produce such a strong toroidal component an external field
.
To produce such a strong toroidal component an external field
![]() is needed.
The instability did not occur for
B0z > 0.08.
is needed.
The instability did not occur for
B0z > 0.08.
The nonaxisymmetric structures appear first near the axis in the lower part of the cylinder where velocity
magnitude is small, and grows to the steady state (Fig. 2). For BR and Bz, the m=1 mode becomes the largest one, in ![]() the axisymmetric mode remains dominant due to the permanently reproduced axisymmetric field. In the nonlinear regime, before the steady state is reached,
higher modes also appear. Nonetheless, their magnitudes stay below 10% of the
m=1 mode. One exception is the m=4 mode, caused by the box geometry. During the initial phase, this mode is already present and influences the magnetic
field outside the cylinder near the box boundaries. However, the field inside the cylinder is much less affected, and the m=4 mode does not seem to influence
the nature and onset of the instability at all. Additionally, during the growth phase of all other nonaxisymmetric modes, the m=4 remains nearly unchanged and
does not play an extraordinary role in the final state. Modes higher than m=4 are not plotted in Fig. 2.
the axisymmetric mode remains dominant due to the permanently reproduced axisymmetric field. In the nonlinear regime, before the steady state is reached,
higher modes also appear. Nonetheless, their magnitudes stay below 10% of the
m=1 mode. One exception is the m=4 mode, caused by the box geometry. During the initial phase, this mode is already present and influences the magnetic
field outside the cylinder near the box boundaries. However, the field inside the cylinder is much less affected, and the m=4 mode does not seem to influence
the nature and onset of the instability at all. Additionally, during the growth phase of all other nonaxisymmetric modes, the m=4 remains nearly unchanged and
does not play an extraordinary role in the final state. Modes higher than m=4 are not plotted in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7781fig2.eps}
\end{figure}](/articles/aa/full/2008/08/aa7781-07/Timg46.gif) |
Figure 2:
The power spectrum of the Fourier modes of |
| Open with DEXTER | |
The pattern of the m=1 mode (Fig. 3) possesses an azimuthal drift velocity relative to the system rotation. It rotates with 4.5 rotation periods of the cylinder, independent of the strength of the externally applied field. The TI in a Taylor-Couette system exhibits the same characteristics of the unstable mode (Rüdiger et al. 2007).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7781fig3.eps}\end{figure}](/articles/aa/full/2008/08/aa7781-07/Timg47.gif) |
Figure 3:
The m=1 pattern in the magnetic field |
| Open with DEXTER | |
To test the relation described by Eq. (4) in a simple setup, we restricted differential rotation to depend only on the z-direction![]() .
For this case, the helicity
.
For this case, the helicity ![]() should depend on the sign of
should depend on the sign of
![]() ,
but not on the sign of the external field and
scale with the squared value of the latter, i.e.
,
but not on the sign of the external field and
scale with the squared value of the latter, i.e.
![]() .
During the onset of the instability, the deviation of the flow structure from the original toroidal field is comparable
to that of the magnetic field. Also, here the mode m=1 is the largest nonaxisymmetric mode and the higher modes appear with less energy.
.
During the onset of the instability, the deviation of the flow structure from the original toroidal field is comparable
to that of the magnetic field. Also, here the mode m=1 is the largest nonaxisymmetric mode and the higher modes appear with less energy.
For the definition of fluctuations, we average velocity and magnetic field along the azimuthal direction, i.e.
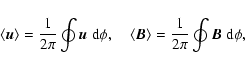 |
(7) |
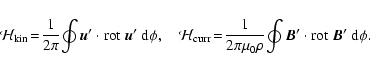 |
(8) |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{7781fig4.eps}\end{figure}](/articles/aa/full/2008/08/aa7781-07/Timg51.gif) |
Figure 4: The external field dependence on the energy of velocity and magnetic field fluctuations at R=0.5 averaged in vertical direction for 0.35<z<0.65. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{7781fig5.eps}\end{figure}](/articles/aa/full/2008/08/aa7781-07/Timg52.gif) |
Figure 5:
Kinematic helicity
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{7781fig6.eps}\end{figure}](/articles/aa/full/2008/08/aa7781-07/Timg53.gif) |
Figure 6:
Kinematic helicity
|
| Open with DEXTER | |
Equation (2) suggests that the changing sign of the helicities by changing the direction of
![]() will also
appear for the term
will also
appear for the term
![]() in the
in the ![]() -tensor responsible for the regeneration of the magnetic field. Indeed, calculating
-tensor responsible for the regeneration of the magnetic field. Indeed, calculating
![]() using the z-component of the electromotive force, gives values for
using the z-component of the electromotive force, gives values for
![]() with the same sign as
with the same sign as
![]() for z<0.65 (see Fig. 7).
Near the top boundary, the disturbances already discussed for the helicities change the values of
for z<0.65 (see Fig. 7).
Near the top boundary, the disturbances already discussed for the helicities change the values of
![]() dramatically to the opposite sign. We
excluded this region and took mean values of
dramatically to the opposite sign. We
excluded this region and took mean values of
![]() in the same range
0.35<z<0.65 used for the helicities and find coefficients between
in the same range
0.35<z<0.65 used for the helicities and find coefficients between
![]() for
B0z=0.04 and
for
B0z=0.04 and
![]() for
B0z=0.08. The correlation time derived from expression (2) using
both helicities,
for
B0z=0.08. The correlation time derived from expression (2) using
both helicities,
![]() ,
is of the order of the system rotation time. Note that
the
,
is of the order of the system rotation time. Note that
the ![]() -effect here is mainly due to the current helicity and the product
-effect here is mainly due to the current helicity and the product
![]() is
positive.
If the external field is switched off, all magnetic field modes decay in the investigated parameter region of low Reynolds numbers and magnetic Prandtl numbers
of the order of ten. The helicities drop down to zero nearly immediately. Despite the high magnetic Prandtl number, we do not observe any dynamo action,
as found in comparable geometry (Braithwaite 2006). Also, the reported cyclic behavior of the instability did not occur in our simulations.
is
positive.
If the external field is switched off, all magnetic field modes decay in the investigated parameter region of low Reynolds numbers and magnetic Prandtl numbers
of the order of ten. The helicities drop down to zero nearly immediately. Despite the high magnetic Prandtl number, we do not observe any dynamo action,
as found in comparable geometry (Braithwaite 2006). Also, the reported cyclic behavior of the instability did not occur in our simulations.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7781fig7.eps}\end{figure}](/articles/aa/full/2008/08/aa7781-07/Timg59.gif) |
Figure 7:
Coefficient of the |
| Open with DEXTER | |
We have demonstrated how the instability of toroidal magnetic fields leads to helicity generation in the nonaxisymmetric parts of a flow without density
stratification. The suggested relation between helicity, external field, and differential rotation,
![]() ,
is rather well fulfilled in the case of z-dependent differential rotation. Both the kinematic helicity and current helicity depend on the squared
value of the z-component of the external magnetic field B0z, and scale linearly with the gradient of the differential rotation. Also, the magnetically
dominated
,
is rather well fulfilled in the case of z-dependent differential rotation. Both the kinematic helicity and current helicity depend on the squared
value of the z-component of the external magnetic field B0z, and scale linearly with the gradient of the differential rotation. Also, the magnetically
dominated ![]() -effect depends on the direction of
-effect depends on the direction of
![]() ,
that is
,
that is
![]() holds the same sign as
holds the same sign as
![]() .
.
The realized model is too simple to estimate consequences of an ![]() -effect based on this new kind of helicity production for environments without
density stratification and possibly for new dynamo models. In a next step, therefore, we would like to check the relation (4) when differential rotation depending
on the distance from the rotation axis is present as well. With an appropriate flow it becomes
-effect based on this new kind of helicity production for environments without
density stratification and possibly for new dynamo models. In a next step, therefore, we would like to check the relation (4) when differential rotation depending
on the distance from the rotation axis is present as well. With an appropriate flow it becomes
![]() .
In this case, helicity generation should be observable only if both components
of the external field are unequal to zero. The problem with this constellation is the changing sign of the product of both field components in one hemisphere
in the simplest configuration, a dipole-like field.
.
In this case, helicity generation should be observable only if both components
of the external field are unequal to zero. The problem with this constellation is the changing sign of the product of both field components in one hemisphere
in the simplest configuration, a dipole-like field.