A&A 479, 365-376 (2008)
DOI: 10.1051/0004-6361:20077597
A possible interpretation of the Seyfert-like component in
3C 273 X-ray spectrum
P. Pietrini1 - G. Torricelli-Ciamponi2
1 -
Dipartimento di Astronomia e Scienza dello Spazio, Largo E. Fermi 2,
50125 Firenze, Italy
2 -
INAF, Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
Received 3 April 2007 / Accepted 29 October 2007
Abstract
Context. Recent studies of the X-ray spectrum of the quasar 3C 273, analyzing both BeppoSAX data and XMM-Newton data, have shown that, depending on the state of the source, Seyfert-like spectral features, including a significant soft excess, can be detected superimposed on the generally overwhelming beamed non-thermal emission (``jet'' component).
Aims. In order to explain the Seyfert-like component and the soft excess suggested by the X-ray spectrum analysis, we apply to 3C 273 a recently developed model for non-thermal emission of X-rays from AGN disk coronae, originally intended for the explanation of Seyfert type X-ray emission.
Methods. We perform an analysis of BeppoSAX data at different epochs, fitting the spectrum with a composition of a beamed ``jet'' component and our coronal model with a reflected component and an iron emission line.
Results. We obtained reasonable fits of BeppoSAX spectra at different epochs by changing the relative weight of our emission model and of the jet power-law component. We find that in all these cases the low energy (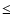 2 keV) part of the X-ray spectrum is accounted for by our Seyfert-like model; we also verify the existence of a positive correlation between the Seyfert-like component 2-10 keV flux and the 0.2-2 keV flux of the so-called soft excess.
2 keV) part of the X-ray spectrum is accounted for by our Seyfert-like model; we also verify the existence of a positive correlation between the Seyfert-like component 2-10 keV flux and the 0.2-2 keV flux of the so-called soft excess.
Conclusions. The results outlined above confirm the plausibility of our non-thermal flare-like coronal model as a possible interpretation of Seyfert-like emission in AGNs. We can conclude that the interpretation of the Seyfert-like component in terms of our non-thermal corona model is offering, as a natural result, a description of the soft excess origin, which is still the subject of lively debate.
Key words: radiation mechanisms: non-thermal - X-rays: galaxies -
galaxies: nuclei - galaxies: active - quasars: individual: 3C 273
3C 273 is a bright nearby (z= 0.158) quasar, widely observed and well studied at all wavelengths
from radio to  -rays, showing a radio morphology characterized by a relativistic
collimated (superluminal) jet originating from a central core.
Indeed, its radio and
-rays, showing a radio morphology characterized by a relativistic
collimated (superluminal) jet originating from a central core.
Indeed, its radio and  -ray properties led some authors (see, for instance, McHardy et al.
1999; Donato et al. 2005, and references therein; Paltani et al. 1998) to classify
this source as a ``blazar'', although 3C 273 does not share all of the typical properties of this last
class in other energy bands (McHardy et al. 1999, 2007; Deluit et al. 2006;
Chernyakova et al. 2007).
From the radio observations' point of view, 3C 273 is usually
(see Grandi et al. 2006; Ghisellini et al. 1998)
classified as an FSRQ (Flat Spectrum
Radio Quasar), which is a sub-class of blazar-like objects
(see, e.g., Falcone et al. 2004; Ghisellini et al. 1998). The properties of FSRQs'
X-ray spectra as observed by BeppoSAX have been analyzed by Giommi et al. (2002) and by
Grandi et al. (2006) (see Sect. 3.2).
Von Montigny et al. (1997) state that 3C 273 can be considered a ``borderline''
object and dub it a ``mini-blazar'', following Impey et al. (1989).
In general, a ``safe'' classification of this object could probably be a
radio loud quasar with several ``blazar-like'' properties, possibly, as stated by Georganopoulos et al.
(2006), due to the fact that
the relativistic jet is at a low angle with the line of sight, but not as small as that of better
aligned ``bona fide'' blazars, given that a strong Big Blue Bump is present in the optical portion of the
spectrum.
A comprehensive review of the various aspects of this
source has been presented by Courvoisier (1998)
and an exhaustive database (updated to November 2005) of its emission at different
wavelengths is available (see Türler et al. 1999).
The complexity of both time dependence and shape of its spectrum suggests
that 3C 273 emission is due to the contribution of several physical mechanisms at
work in different parts of the source. In fact, the optical-UV range of the spectrum, exhibiting a Big Blue
Bump (as well as strong emission lines), may indicate the contribution
of a thermal-type emission typically attributed to an
accretion disk (see for instance von Montigny et al. 1997; Kriss et al.
1999; Impey et al. 1989) while the X-ray portion of the spectrum,
which we are interested
in, is generally interpreted as mainly due to beamed non-thermal emission produced by
a jet that was first discovered in the radio domain and has been observed down
to a fraction of pc scale thanks to the VLBA (Savolainen et al. 2006).
The corresponding jet structure on a much larger scale
(i.e., on the Kpc - few tens of Kpc scale) has been recently observed also
in the optical (Jester et al. 2001) and in the X-ray (Röser et al. 2001; Sambruna et al. 2001; Marshall et al. 2001; Jester et al. 2006) domain.
-ray properties led some authors (see, for instance, McHardy et al.
1999; Donato et al. 2005, and references therein; Paltani et al. 1998) to classify
this source as a ``blazar'', although 3C 273 does not share all of the typical properties of this last
class in other energy bands (McHardy et al. 1999, 2007; Deluit et al. 2006;
Chernyakova et al. 2007).
From the radio observations' point of view, 3C 273 is usually
(see Grandi et al. 2006; Ghisellini et al. 1998)
classified as an FSRQ (Flat Spectrum
Radio Quasar), which is a sub-class of blazar-like objects
(see, e.g., Falcone et al. 2004; Ghisellini et al. 1998). The properties of FSRQs'
X-ray spectra as observed by BeppoSAX have been analyzed by Giommi et al. (2002) and by
Grandi et al. (2006) (see Sect. 3.2).
Von Montigny et al. (1997) state that 3C 273 can be considered a ``borderline''
object and dub it a ``mini-blazar'', following Impey et al. (1989).
In general, a ``safe'' classification of this object could probably be a
radio loud quasar with several ``blazar-like'' properties, possibly, as stated by Georganopoulos et al.
(2006), due to the fact that
the relativistic jet is at a low angle with the line of sight, but not as small as that of better
aligned ``bona fide'' blazars, given that a strong Big Blue Bump is present in the optical portion of the
spectrum.
A comprehensive review of the various aspects of this
source has been presented by Courvoisier (1998)
and an exhaustive database (updated to November 2005) of its emission at different
wavelengths is available (see Türler et al. 1999).
The complexity of both time dependence and shape of its spectrum suggests
that 3C 273 emission is due to the contribution of several physical mechanisms at
work in different parts of the source. In fact, the optical-UV range of the spectrum, exhibiting a Big Blue
Bump (as well as strong emission lines), may indicate the contribution
of a thermal-type emission typically attributed to an
accretion disk (see for instance von Montigny et al. 1997; Kriss et al.
1999; Impey et al. 1989) while the X-ray portion of the spectrum,
which we are interested
in, is generally interpreted as mainly due to beamed non-thermal emission produced by
a jet that was first discovered in the radio domain and has been observed down
to a fraction of pc scale thanks to the VLBA (Savolainen et al. 2006).
The corresponding jet structure on a much larger scale
(i.e., on the Kpc - few tens of Kpc scale) has been recently observed also
in the optical (Jester et al. 2001) and in the X-ray (Röser et al. 2001; Sambruna et al. 2001; Marshall et al. 2001; Jester et al. 2006) domain.
Indeed, X-ray broad-band spectra taken with different instruments have proven to be
more complex than the ``simple'' non-thermal jet emission interpretation.
The presence of a soft excess at energies below 1 keV was shown for the first time
by EXOSAT observations (Turner et al. 1985), and
it was confirmed by
other X-ray satellites, such as GINGA (Turner et al. 1990) and ROSAT
(Leach et al. 1995). ASCA
observations of 3C 273 also unambiguously indicated the existence of a variable soft excess below
1.5 keV (Cappi & Matsuoka 1997; Cappi et al. 1998),
as well as some indication of a fluorescence
iron line. More recently, this same source has been observed by RXTE (from 1996 to 2000, see
Kataoka et al. 2002), by BeppoSAX (see Haardt et al. 1998,
analyzing 1997 observation runs;
Grandi et al. 1997, dealing with the first 1996 observation;
and Grandi & Palumbo 2004, hereafter G&P, discussing
the ensemble of 3C 273 observations, since 1996, up to 2001), and by XMM-Newton (see Page et al.
2004) and INTEGRAL (Chernyakova et al. 2007).
All of these more recent observations, together with the previous ones as far as the soft
excess presence is concerned, pointed to the existence in the broad band X-ray spectra
of ``Seyfert-like'' components (more or less detectable, depending on
the specific epoch of observation), in addition to the usually non-thermal
jet power-law one. Therefore, a more composite general description of the spectrum itself
seems to be required.
In particular, Haardt et al. (1998), together with Cappi et al. (1998),
were the first to suggest that a
coronal/Seyfert-like emission component is also present; the original idea of these authors was that this
Seyfert-like component, generally ``underlying'' the beamed non-thermal jet component, should be
more evident during ``low'' source states (i.e., global low flux level states; Cappi et al. (1998)
give a quantitative estimate of ``low'' flux level as
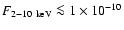 erg cm-2 s-1).
Based on these conclusions, Haardt et al. (1998) analysed the X-ray spectra observed by
BeppoSAX on January 1997, proposing a model in which a constant (in time) Seyfert-like component is
superimposed onto a non-thermal beamed jet power-law one; in those authors' view, this latter component
is, on the contrary,
variable in time, so that the Seyfert-like contribution is detectable at epochs in which the jet
component turns out to be at a low flux level.
This viewpoint was revised by the RXTE data analysis of Kataoka et al. (2002), who conclude
that there is an occasional superposition of a Seyfert-like
emission on the beamed one, but this is
not correlated with the flux level.
erg cm-2 s-1).
Based on these conclusions, Haardt et al. (1998) analysed the X-ray spectra observed by
BeppoSAX on January 1997, proposing a model in which a constant (in time) Seyfert-like component is
superimposed onto a non-thermal beamed jet power-law one; in those authors' view, this latter component
is, on the contrary,
variable in time, so that the Seyfert-like contribution is detectable at epochs in which the jet
component turns out to be at a low flux level.
This viewpoint was revised by the RXTE data analysis of Kataoka et al. (2002), who conclude
that there is an occasional superposition of a Seyfert-like
emission on the beamed one, but this is
not correlated with the flux level.
The power of multi-epoch broad band BeppoSAX data has been fully exploited by
G&P, who reexamined and widely developed the idea of a superposition of different
contributions in the X-ray spectrum,
decoupling the Seyfert-like and the beamed
components in the X-ray spectra of six Beppo-SAX observations of 3C 273 from 1996
to 2001. In the G&P ``physical'' model the jet emission is represented by a power-law,
while the non-beamed component consists of
a black body (accounting for the soft excess) and a cutoff
power-law (with a reflected component and an Fe line) representing the Seyfert-like emission.
These authors' conclusion is that long-term 3C 273 spectral variations
can be interpreted in terms of flux ratio modifications of the three ``physical'' components and it
relies on the possibility of analysing
the various observations of 3C 273 taken by
BeppoSAX instruments at different epochs. Fitting the data at different
epochs shows a different relative importance of the three main ``physical'' components
that they distinguish in their representation of the X-ray spectrum. In particular,
and contrary to previous ideas, this shows that
spectral variations, such as the relevance of the Seyfert-like spectral features with respect to the
non-thermal ``jet'' component, are not correlated with the total
2-10 keV flux (or luminosity) variations; in particular,
the appearance of a significant Seyfert-like component is not correlated with ``low''
total flux states of the source, as previously suggested.
In their picture the black body component
is essential to account for the soft excess present both in the time averaged spectrum and
in the spectra relative to each single epoch of observation.
While the presence of a soft excess in X-ray observed spectra is proven,
from the point of view of the physical interpretation,
its origin is at present not clear. Page et al. (2004) present a detailed
study of possible soft excess natures suggesting that it originates
from the Comptonization of disk photons by a second ``hot'' (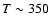 eV) population
of thermal electrons. However, their
analysis, while favoring Comptonization models, is not conclusive.
eV) population
of thermal electrons. However, their
analysis, while favoring Comptonization models, is not conclusive.
The above considerations prompted us to investigate whether the model we proposed
for coronal emission in Seyfert galaxies (Torricelli et al. 2005, hereafter
Paper I) could account
for the non-beamed component of 3C 273 spectra. Since the application of our model to NGC 5548
has shown that it can explain the soft excess in that source with no
need for an extra component, the aim of this paper is not only to test whether our
coronal model (with a reflected component and an Fe line) plus the jet power-law emission
could produce good fits of 3C 273 BeppoSAX data, but also to give a possible interpretation
of the observed soft excess.
In Sect. 2 the model, developed in Paper I, is briefly described. The fit with BeppoSAX
observations is developed in Sect. 3; Sect. 4 is devoted to a comparison of
our results with other authors and our conclusions are presented in Sect. 5.
3C 273 is a very bright quasar, and its overall
SED (Spectral Energy Distribution) shows some of the typical general traits of this vast class of objects,
as well as some characteristics that are more specific to blazar-like sources (see Sect. 1).
Indeed, most of its emission is interpreted as originating from non-thermal
mechanisms and specifically from a beamed relativistic jet pointing in a direction rather close to the line of sight
(see for example McHardy et al. 2007).
It is not our intention to discuss here the jet emission models.
On the contrary, we are interested in trying to
apply our model of X-ray emission from a non-thermal coronal structure surrounding the accretion disk, in
order to explain the X-ray spectral components that cannot simply be explained as ``jet-emission''.
This model was
presented and discussed in Paper I, where the model itself was intended to explain X-rays from Seyfert 1
AGNs; here we extend the application of our model to the more complex case of a quasar source
like 3C 273.
We want to show that our model can provide an explanation for the
Seyfert-like components that have been identified recently in the composite X-ray spectrum of 3C 273,
briefly discussed in the previous section,
as superimposed onto the beamed jet X-ray radiation.
For an appropriate application of our model, it is essential to identify the radiation component that can be
reliably considered as an input of soft ``seed'' photons for our model reprocessing mechanism in the coronal blobs
in order to produce the X-ray emission. In the following we briefly discuss the motivations of our choice for the
case of 3C 273.
An outline of the model applied to this source is then given in Sect. 2.2.
A decomposition into a beamed component and a non-beamed one analogous to the one
suggested by the X-ray data
has been studied in the past in the optical energy range.
We summarize in the following the discussion of the results regarding this issue.
The discrimination and separation of the beamed jet component and Seyfert-like thermal
component in this frequency range (optical-UV) is crucial to our coronal model
applied to the present composite source 3C 273, because we need to identify with certainty
the spectral component that, in our framework, can be considered as the soft ``seed'' spectrum
produced by the accretion disk and illuminating our active corona, that we consider to be composed of ``loops''/blobs
in which relativistic non-thermally distributed electrons interact with the soft ``seed'' photons
by inverse Compton process, producing the coronal component of the X-ray spectrum (see Paper I, and further on
in this section).
In Impey et al.
(1989) the results of two years of optical photometry and polarization measurements
are reported. The low polarization level (confirmed by the more recent observations of
Valtaoja et al. 1991) supports the Impey et al.
(1989) conclusion that
``3C 273 harbors a weak continuum component having all
the characteristic properties of a blazar ... diluted by light typical of a normal
low-polarization quasar''. These authors also report that the measured polarization increases toward
longer wavelengths thus allowing a separation between the jet and the Seyfert-like component.
A possible decomposition of thermal and beamed components is shown in Fig. 10 of Impey et al.
(1989);
for this particular case, which corresponds to the 1984 ``flare'' (here generically meaning an abrupt increase of
intensity),
the curves describing the two components intersect at around
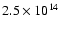 Hz:
for higher frequencies
the emission is essentially the thermal blue bump emission, whereas for lower frequencies
the beamed jet emission represents the dominant contribution. The
idea that for
Hz:
for higher frequencies
the emission is essentially the thermal blue bump emission, whereas for lower frequencies
the beamed jet emission represents the dominant contribution. The
idea that for
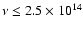 Hz the beamed component overwhelms
the thermal one is confirmed from March 1999 IR and X-ray observations
discussed by McHardy et al. (2007), who find a correlation between
the K-band (
Hz the beamed component overwhelms
the thermal one is confirmed from March 1999 IR and X-ray observations
discussed by McHardy et al. (2007), who find a correlation between
the K-band (
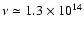 Hz) emission
and the 2-10 keV flux during a ``flare''. Hence, the general scenario that
can be inferred is
that, when the source is ``flaring'', the emission below
a value of frequency which is around the one corresponding to
Hz) emission
and the 2-10 keV flux during a ``flare''. Hence, the general scenario that
can be inferred is
that, when the source is ``flaring'', the emission below
a value of frequency which is around the one corresponding to
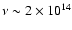 Hz
is essentially due to the non-thermal jet component.
Hz
is essentially due to the non-thermal jet component.
The situation is different in June 2004,
which was a quiescent period for 3C 273. In fact, the analysis of
Türler et al. (2006), reporting multi-wavelength observations of the source,
points out (see their Fig. 3) that
the observed optical-UV radiation, i.e. the emission for
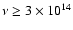 Hz, does not
significantly differ from the known average intensity level,
(that is, it is not decreased with respect to the average level itself),
while for longer wavelengths the
weakness of the jet component allows the appearance of the otherwise usually underlying IR thermal emission.
Türler et al. (2006) model this thermal IR radiation with three dust emission
components located far from the central corona we are dealing with.
This seems to suggest a framework (somewhat similarly to the Seyfert 1 sources' case), in which
the thermal component of the IR radiation can be mostly interpreted as coming from dusty
regions of the nucleus external to and (much) farther away than the inner portion of the disk
producing the Big Blue Bump and actively illuminating the surrounding coronal region.
Hz, does not
significantly differ from the known average intensity level,
(that is, it is not decreased with respect to the average level itself),
while for longer wavelengths the
weakness of the jet component allows the appearance of the otherwise usually underlying IR thermal emission.
Türler et al. (2006) model this thermal IR radiation with three dust emission
components located far from the central corona we are dealing with.
This seems to suggest a framework (somewhat similarly to the Seyfert 1 sources' case), in which
the thermal component of the IR radiation can be mostly interpreted as coming from dusty
regions of the nucleus external to and (much) farther away than the inner portion of the disk
producing the Big Blue Bump and actively illuminating the surrounding coronal region.
Moreover, from the combination of the above described inferences, namely
those of
- (1)
- Impey et al. (1989), supported by the further analysis of McHardy et al. (2007),
(i.e., beamed jet
dominating below
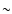
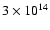 Hz, whereas the Big Blue Bump component prominent above that frequency
in the optical-UV range) on the one hand,
and of
Hz, whereas the Big Blue Bump component prominent above that frequency
in the optical-UV range) on the one hand,
and of
- (2)
- Türler et al. (2006) (i.e., intensity level of the observed optical-UV nearly unchanged
even when the jet component is particularly weak) on the other,
we can conclude that above
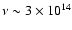 Hz the Big Blue Bump component substantially dominates the observed
optical-UV emission.
As a consequence, we believe it reasonable to proceed much in the same way as
followed in Paper I for the case of NGC 5548, and we can use the observations in
the optical-UV range as a direct estimate of the BBB component
that we consider as the input soft spectrum illuminating our model coronal region from the outside.
Hz the Big Blue Bump component substantially dominates the observed
optical-UV emission.
As a consequence, we believe it reasonable to proceed much in the same way as
followed in Paper I for the case of NGC 5548, and we can use the observations in
the optical-UV range as a direct estimate of the BBB component
that we consider as the input soft spectrum illuminating our model coronal region from the outside.
The beamed radiation from the non-thermal jet,
although clearly significant at low energies (where ``low'' means energies that could be upscattered
into the X-ray range by a population of relativistic electrons characterized by physical parameters
within the intervals typically resulting from our modeling, such as sub-millimetric to IR)
is by no means considered as a source of ``seed'' photons for our active loop relativistic electrons.
We do not want to discuss
a complex structural and geometrical model for 3C 273 as a
quasar, but it can be considered as plausible that the strongly beamed jet radiation does
not directly illuminate
the individual (flaring) X-ray emitting loops of our coronal structure.
Here we just give an outline of the model, which is fully described in Paper I.
The model developed in Paper I for an AGN non-thermal corona
supposes that the emission in the X-ray energy range is due to a population of relativistic
electrons streaming along magnetic field lines, upscattering lower energy ``seed''
photons by the inverse Compton mechanism. This corona is
solar-like and hence constituted of magnetic loops whose stretching and twisting
induces reconnection among magnetic lines of forces thus
transferring kinetic energy from the
disk motion to the AGN corona through magnetic
reconnection itself (which is usually invoked as the origin of
electron acceleration). In this context, in each of the active loops the electron distribution, injected
at time t0,
evolves in time owing to the emitted synchrotron and
inverse Compton radiation. We refer to Paper I for further details.
Following Paper I, the emission observed in the X-ray is
inverse Compton radiation from relativistic electrons on two different types
of seed photons, that is: i) the optical-UV-EUV
photons
most probably originating from the (central black hole) accretion-disk,
and ii) the photons produced locally, i.e. in each active loop,
by the same
population of relativistic electrons, due to the synchrotron mechanism (see Paper I).
The details of the physical processes defining our model spectrum are described in Paper I, but
the two types of ``seed'' photons for the inverse
Compton mechanism mentioned above deserve a little more attention.
We identify the first type of ``seed'' photons with the observed optical-UV-EUV Big Blue Bump,
and we consider the energy distribution of these photons as
determined by observations and thus given in the literature.
Since there are not optical-EUV observations simultaneous with BeppoSAX
data, we represent the spectral energy distribution of these ``soft'' photons with a curve that
is an average of the observations taken at different epochs.
In Fig. 1 the continuous line shows the adopted
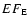 spectral distribution (for this first type of ``seed'' photon) and the
extension of the bars takes into account
both the flux ranges observed at a specific energy
at different times and the
errors affecting each observation.
The data are from von Montigny et al. (1997);
Kriss et al. (1999), and from the 3C 273 database cited by Türler et al. (1999).
At longer wavelengths (namely for
spectral distribution (for this first type of ``seed'' photon) and the
extension of the bars takes into account
both the flux ranges observed at a specific energy
at different times and the
errors affecting each observation.
The data are from von Montigny et al. (1997);
Kriss et al. (1999), and from the 3C 273 database cited by Türler et al. (1999).
At longer wavelengths (namely for
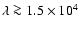 Å), as explained before, the thermal emission
comes from the dust located at larger distances (see Table 2 of Türler et al. 2006);
hence the related photons are geometrically diluted
and their number is negligible for the reprocessing.
For this reason our choice was to model the thermal seed spectrum in this energy range extrapolating
the observed optical emission towards longer wavelengths with
a power-law decreasing with increasing wavelength.
In this spectral region the contribution of this first type of seed photon is negligible
with respect to that of the second type of seed photon that we account for and shall discuss in the following
paragraph.
The spectral flux
Å), as explained before, the thermal emission
comes from the dust located at larger distances (see Table 2 of Türler et al. 2006);
hence the related photons are geometrically diluted
and their number is negligible for the reprocessing.
For this reason our choice was to model the thermal seed spectrum in this energy range extrapolating
the observed optical emission towards longer wavelengths with
a power-law decreasing with increasing wavelength.
In this spectral region the contribution of this first type of seed photon is negligible
with respect to that of the second type of seed photon that we account for and shall discuss in the following
paragraph.
The spectral flux 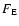 corresponding to the continuous line of Fig. 1
has been used to compute the corresponding spectral luminosity
corresponding to the continuous line of Fig. 1
has been used to compute the corresponding spectral luminosity
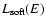 ,
as appearing in Eq. (8)
of Paper I, required for the calculation of
the inverse Compton luminosity,
,
as appearing in Eq. (8)
of Paper I, required for the calculation of
the inverse Compton luminosity,
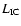 ,
as well as in the computation
of the electron distribution temporal evolution (see Sect. 2 of Paper I).
For this computation a distance of
,
as well as in the computation
of the electron distribution temporal evolution (see Sect. 2 of Paper I).
For this computation a distance of
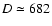 Mpc
(derived from
Mpc
(derived from
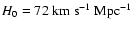 ,
q0 = 0.5 and z = 0.158)
has been assumed.
,
q0 = 0.5 and z = 0.158)
has been assumed.
As for the second type of
soft ``seed'' photons that are reprocessed, i.e. those locally produced by the synchrotron
mechanism in each magnetic loop, their spectral distribution and intensity depend
on the local intensity of the
magnetic field and on the relativistic electron distribution,
evolving in time
due to both synchrotron and inverse Compton losses; therefore, a consistent calculation must be performed
whenever the resulting inverse Compton spectrum is evaluated. However, for the ranges of parameter values
(specifically values of magnetic field intensity in the active loop, B,
and of
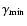 and
and
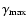 ,
defining the energy range for the electron
distribution at the time of injection,
where
,
defining the energy range for the electron
distribution at the time of injection,
where
 ))
that give a meaningful fit of the observed X-ray spectra,
it turns out that the resulting synchrotron component
typically peaks in the sub-millimetre range
and it is well below the level of the
radio-IR radiation of the observed spectrum.
Nonetheless, its contribution as a seed photon source can be quite significant, since the synchrotron photons
are produced by the relativistic electron population within the loop itself and they are seen by
this same relativistic electron population (as a scattering agent)
as non-diluted by geometric factors (see Paper I for more discussion of this issue).
In Paper I we have indicated the computed time-dependent synchrotron
spectral luminosity of each single active loop as
))
that give a meaningful fit of the observed X-ray spectra,
it turns out that the resulting synchrotron component
typically peaks in the sub-millimetre range
and it is well below the level of the
radio-IR radiation of the observed spectrum.
Nonetheless, its contribution as a seed photon source can be quite significant, since the synchrotron photons
are produced by the relativistic electron population within the loop itself and they are seen by
this same relativistic electron population (as a scattering agent)
as non-diluted by geometric factors (see Paper I for more discussion of this issue).
In Paper I we have indicated the computed time-dependent synchrotron
spectral luminosity of each single active loop as
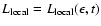 ,
where
,
where 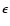 is the (soft) photon energy; this
spectral luminosity is explicitly given by Eq. (10) of Paper I.
is the (soft) photon energy; this
spectral luminosity is explicitly given by Eq. (10) of Paper I.
Having now defined our ``seed'' photon sources, the resulting inverse Compton emission
expected from our model is determined as the sum of the contributions from all the loops that are actively
flaring, and therefore emitting by an inverse Compton mechanism, in the coronal region at a given time; this resulting
emission can be computed following the relationships
derived and shown in Paper I.
As explained in Paper I (Sect. 4.2),
because of the relativistic electron distribution evolution,
the inverse Compton emission of each flare evolves
on time scales shorter than the integration time for data acquisition in the X-ray
domain. For this reason we can assume that
the observed spectrum is due to the superposition of the
temporal mean of several single flares and that we can reproduce this fact
averaging in time our model emission (see the deduction
of the spectral luminosity
 in Paper I).
The dashed curve in Fig. 1 shows an example of the
result of our model,
in Paper I).
The dashed curve in Fig. 1 shows an example of the
result of our model,
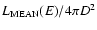 ,
for a specific set of parameters,
namely those used to reproduce the X-ray BeppoSAX observations of June 2000 (see
next section).
,
for a specific set of parameters,
namely those used to reproduce the X-ray BeppoSAX observations of June 2000 (see
next section).
 |
Figure 1:
The continuous line shows
the adopted optical-EUV spectrum for 3C 273. This curve
represents
a continuous fit to the observations taken
at different epochs and shown as bars in the figure
(see the text for details).
The dashed curve shows the mean spectrum obtained from the IC
reprocessing of the soft spectrum with an electron distribution
characterized by
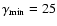 , ,
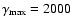 ,
s=3and ,
s=3and
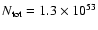 electrons.
This model is the one used to fit the June 2000 data. electrons.
This model is the one used to fit the June 2000 data. |
| Open with DEXTER |
As outlined in the introduction the aim of this paper
is to test whether our coronal model, successfully applied
to the Seyfert 1 source NGC 5548 in Paper I, can be applied to fit BeppoSAX data of 3C 273. This idea relies
on the results of the analysis of G&P. These authors, developing previous analyses of
3C 273 X-ray observations (see Sect. 1), conclude
that the 3C 273 spectrum can be interpreted as
the sum of different superimposed components,
whose relative importance depends on the epoch of BeppoSAX observation.
We propose here
a physical interpretation of the component described by G&P as ``Seyfert-like'', supposing that this
component can be accounted for by our coronal model, which is also directly responsible for
the production of the soft portion of the X-ray spectrum, and entirely responsible for the
observed ``soft excess''.
Hence, in this analysis
we want to check whether 3C 273 observations can be reproduced by a combination of
a jet power-law
spectrum and our coronal model (plus an iron line and a reflection component due to reprocessing
of our model emission by
the cold accretion disk) without
the addition of an ad hoc soft excess component.
To this purpose we attempt a fit of BeppoSAX observations from 1998 to 2001.
BeppoSAX observed 3C 273 at six different epochs,
in July 1996, in January 1997 (this is a composite observation, made of four
different data acquisition
sets, from January 13 to January 22, but in general these data are summed up in the analysis), in 1998, in
January 2000, in June 2000, and in June 2001. Our choice of analyzing in detail only the last four
observations is motivated as follows; first, the data sets of years 1996 and 1997 have been
studied more than once in other papers (see G&P for both and Grandi et al. 1997;
Orr et al. 1998;
for 1996 observation; as well as Haardt et al. 1998, concerning 1997 data).
Secondly, both G&P's recent analysis and previous studies show that BeppoSAX
observations of 3C 273 in 1996 and 1997 can be well reproduced
by models in which the jet is by far the dominant component (see the relative
importance of the normalization factors
 and
and
 in
Table 3 of G&P).
in
Table 3 of G&P).
For those BeppoSAX observations of 3C 273 in which G&P find
that the ``Seyfert-like'' features
are more prominent, namely those referring to the epochs 1998, January 2000, June 2000
and 2001, we propose and test against BeppoSAX data the following configuration.
The observed X-ray spectrum originates as the superposition of
a coronal emission
component (our model as described in Sect. 2) reprocessed by the cold
disk, thus giving rise to a reflected component and to an iron emission line,
plus a non-thermal jet-like emission described by a power-law component.
The resulting emission is absorbed by cold Galactic gas with hydrogen column density
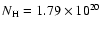 cm-2 (Dickey & Lockman 1990).
cm-2 (Dickey & Lockman 1990).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f2up.ps}}\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f2lo.ps}}
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg37.gif) |
Figure 2:
BeppoSAX spectrum of 3C 273 as observed in 1998. Upper panel:
the observed spectral energy distribution,
 ,
drawn in green, is modeled by
the combination of different components (all of which
absorbed by a cold Galactic absorber characterized by a column density ,
drawn in green, is modeled by
the combination of different components (all of which
absorbed by a cold Galactic absorber characterized by a column density
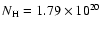 cm-2):
a coronal component (in red), represented by our Seyfert-like model, a reflection component
(in blue), due to its reprocessing,
an iron K cm-2):
a coronal component (in red), represented by our Seyfert-like model, a reflection component
(in blue), due to its reprocessing,
an iron K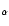 line (in green), and a beamed-jet power-law component (in light blue).
Lower panel: we show the corresponding data counts, along with the data/model ratio.
line (in green), and a beamed-jet power-law component (in light blue).
Lower panel: we show the corresponding data counts, along with the data/model ratio. |
| Open with DEXTER |
In order to obtain good fits we tried
different coronal configurations, changing the magnetic field
intensity, B, the number of the flaring regions within the coronal region, q,
the minimum value of the relativistic electron energy in
the electron energy distribution at injection,
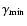 ,
and the total number of
relativistic electrons
,
and the total number of
relativistic electrons
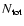 in the corona. All these parameters contribute to modify the spectral energy distribution
of the resulting emission and a change of value for any of them
significantly influences
the outcome of the spectral calculation defining our proposed X-ray ``primary'' (i.e., not yet reprocessed)
coronal model spectrum,
thus modifying the quality of the resulting fit.
In particular, variations in the magnetic field
mainly affect the spectral slope of the primary coronal component especially in the 2-20 keV energy range, while
changes in q and
in the corona. All these parameters contribute to modify the spectral energy distribution
of the resulting emission and a change of value for any of them
significantly influences
the outcome of the spectral calculation defining our proposed X-ray ``primary'' (i.e., not yet reprocessed)
coronal model spectrum,
thus modifying the quality of the resulting fit.
In particular, variations in the magnetic field
mainly affect the spectral slope of the primary coronal component especially in the 2-20 keV energy range, while
changes in q and
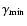 values modify the low energy part
(0.1-1 keV) of the spectrum, so that increasing q and/or decreasing
values modify the low energy part
(0.1-1 keV) of the spectrum, so that increasing q and/or decreasing
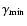 leads to an increase
of the soft X-ray emission with respect to the rest of the X-ray spectral range, thus
mimicking a ``soft excess'' increase.
Even
leads to an increase
of the soft X-ray emission with respect to the rest of the X-ray spectral range, thus
mimicking a ``soft excess'' increase.
Even
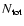 is not a simple normalization parameter for the emitted spectrum;
an increase in
is not a simple normalization parameter for the emitted spectrum;
an increase in
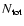 not only implies an increase in the inverse Compton flux but
also a change in its spectral shape because of the enhanced
synchrotron and inverse Compton losses that the electrons undergo.
not only implies an increase in the inverse Compton flux but
also a change in its spectral shape because of the enhanced
synchrotron and inverse Compton losses that the electrons undergo.
The definition of a model spectrum requires the specification of other parameters, whose values, however, here
are kept constant and the same for all of
the four models considered to fit the different observations, since they do not significantly influence
the spectrum shape in the energy range we are interested in or because their values
have been chosen following externally dictated physical conditions.
More specifically, these are
two parameters defining the electron energy distribution at injection, namely the
the spectral index of the distribution, s, whose value is chosen as s=3, and the upper
limit of the electron energy
range, which is set as
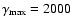 ,
together with two more parameters
characterizing the coronal structure,
that is the number density of the thermal material in each coronal loop/blob,
,
together with two more parameters
characterizing the coronal structure,
that is the number density of the thermal material in each coronal loop/blob,
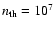 cm-3, and the overall extension of the coronal region,
cm-3, and the overall extension of the coronal region,
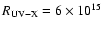 cm.
The values of s and
cm.
The values of s and
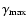 have been chosen in
a reasonable physical range within which their values modify the coronal spectrum only
in an energy range where the coronal emission is negligible with
respect to the jet emission, namely for very high energies,
have been chosen in
a reasonable physical range within which their values modify the coronal spectrum only
in an energy range where the coronal emission is negligible with
respect to the jet emission, namely for very high energies, 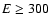 keV. As for the values
of
keV. As for the values
of
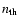 and
and
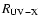 they have been chosen
on the basis of the following considerations.
they have been chosen
on the basis of the following considerations.
The size of the coronal region, can be
expressed in units of the Schwarschild radius,
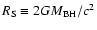 ,
once an estimate of the
mass of the central black hole of the source is defined. To this purpose, we take into
account the range of values
recently evaluated by Paltani & Türler (2005), namely
,
once an estimate of the
mass of the central black hole of the source is defined. To this purpose, we take into
account the range of values
recently evaluated by Paltani & Türler (2005), namely
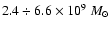 ,
corresponding to
,
corresponding to
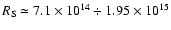 cm. With
this range for the Schwarzschild radius, the value we have chosen above for the coronal region size
corresponds to
cm. With
this range for the Schwarzschild radius, the value we have chosen above for the coronal region size
corresponds to
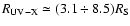 ,
which is consistent
with theoretical estimates demanding a coronal dimension
,
which is consistent
with theoretical estimates demanding a coronal dimension 
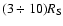 (see the discussion in
Sect. 2 of Paper I). Different values of
(see the discussion in
Sect. 2 of Paper I). Different values of
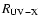 in the allowed range
have been tested and we refer to the conclusions of the present work for more details and references.
The choice of the
the number density value for the coronal thermal material is
related to the coronal characteristic size. In fact,
for
in the allowed range
have been tested and we refer to the conclusions of the present work for more details and references.
The choice of the
the number density value for the coronal thermal material is
related to the coronal characteristic size. In fact,
for
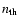 (whose value does not change
the spectrum shape at all within the ranges of coronal parameters that are physically
meaningful for an AGN coronal structure context) the essential physical requirement is that the upper
limit derived from the condition of small optical
depth to scattering on the thermal component electrons, i.e.,
(whose value does not change
the spectrum shape at all within the ranges of coronal parameters that are physically
meaningful for an AGN coronal structure context) the essential physical requirement is that the upper
limit derived from the condition of small optical
depth to scattering on the thermal component electrons, i.e.,
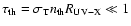 ,
is fulfilled
in order to neglect any thermal Comptonization distortion of the X-ray spectrum; for the value for
,
is fulfilled
in order to neglect any thermal Comptonization distortion of the X-ray spectrum; for the value for
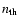 that we have chosen and specified above, this condition is satisfied.
that we have chosen and specified above, this condition is satisfied.
Given that in our model the emission is due to an ensemble of individual active loops located in
the coronal region
whose overall linear size is defined by
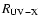 ,
we have to specify the fraction of the
total volume,
,
we have to specify the fraction of the
total volume, 
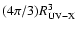 ,
of the coronal region corresponding to active loops,
i.e. the fraction of effectively X-ray emitting volume,
which is here fixed to w= 1/10 for all the fits executed;
this implies that we can identify the representative linear size of each single emitting loop as
,
of the coronal region corresponding to active loops,
i.e. the fraction of effectively X-ray emitting volume,
which is here fixed to w= 1/10 for all the fits executed;
this implies that we can identify the representative linear size of each single emitting loop as
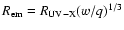 (see
Paper I, Sect. 4.3).
Also, in the present application we have chosen to fix both the spectral index of the jet power-law
photon distribution (
(see
Paper I, Sect. 4.3).
Also, in the present application we have chosen to fix both the spectral index of the jet power-law
photon distribution (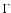 )
and the source inclination angle (i), which appears in the PEXRAV
routine (for the reflection component definition),
to the same
values used by G&P in their analysis (namely
)
and the source inclination angle (i), which appears in the PEXRAV
routine (for the reflection component definition),
to the same
values used by G&P in their analysis (namely
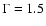 and
and
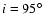 ). We recall (see
Paper I, Sect. 5.1)
that we make consistent use of the PEXRAV routine to evaluate the reflection component
by using as the required primary
power-law spectrum a cut-off power-law approximation of our computed model spectrum obtained by recursively
fitting the model spectrum itself in the range
). We recall (see
Paper I, Sect. 5.1)
that we make consistent use of the PEXRAV routine to evaluate the reflection component
by using as the required primary
power-law spectrum a cut-off power-law approximation of our computed model spectrum obtained by recursively
fitting the model spectrum itself in the range 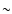 2-100 keV.
2-100 keV.
![\begin{figure}
\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f3up.ps}}\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f3lo.ps}}
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg55.gif) |
Figure 3:
BeppoSAX spectrum of 3C 273 for January year 2000. See Fig. 2
for an explanation. |
| Open with DEXTER |
![\begin{figure}
\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f4up.ps}}\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f4lo.ps}}
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg56.gif) |
Figure 4:
BeppoSAX spectrum of 3C 273 for June 2000. See Fig. 2
for an explanation. |
| Open with DEXTER |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f5up.ps}}\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f5lo.ps}}
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg57.gif) |
Figure 5:
BeppoSAX spectrum of 3C 273 for the year 2001. See Fig. 2
for explication. |
| Open with DEXTER |
The results of this analysis are shown in Figs. 2-5
and the relative parameter values for the four different fits are shown in Table 1,
together with the evaluated resulting fluxes, that we shall
discuss in the next subsection.
It seems beyond this analysis to derive a detailed
picture of the
geometrical and physical properties of the 3C 273 corona from the study of the temporal variations of
the observed X-ray emission as we model it.
We can only observe that B,
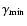 and
and
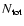 values do not change or change by a very
small amount relative to their absolute value
from one epoch to the other for the first three observations analyzed here; for these same three data sets
our best fit is obtained without changing q, the number of individual flaring regions within the corona, as well.
The case for the 2001 observation, the last one by BeppoSAX, looks different, since our best fit is, in this case,
obtained with a model for the primary coronal spectrum computed for values of B and
values do not change or change by a very
small amount relative to their absolute value
from one epoch to the other for the first three observations analyzed here; for these same three data sets
our best fit is obtained without changing q, the number of individual flaring regions within the corona, as well.
The case for the 2001 observation, the last one by BeppoSAX, looks different, since our best fit is, in this case,
obtained with a model for the primary coronal spectrum computed for values of B and
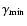 at least
that are clearly non-negligibly different from the corresponding values for the previous observations' fits;
moreover, for the year 2001, the geometrical configuration of the flaring corona also appears to
change significantly with respect to the cases of the first three observations, due to a considerable
difference in the number of flaring regions, q, required to obtain a good overall fit (see Table 1);
indeed, the highest number of flaring regions turns out to be associated with the maximum value
of the coronal emitted flux
at least
that are clearly non-negligibly different from the corresponding values for the previous observations' fits;
moreover, for the year 2001, the geometrical configuration of the flaring corona also appears to
change significantly with respect to the cases of the first three observations, due to a considerable
difference in the number of flaring regions, q, required to obtain a good overall fit (see Table 1);
indeed, the highest number of flaring regions turns out to be associated with the maximum value
of the coronal emitted flux
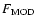 (2-10 keV) (which is the one for the case of 2001)
among those derived from the best fit of the various
observations that we analyzed.
(2-10 keV) (which is the one for the case of 2001)
among those derived from the best fit of the various
observations that we analyzed.
As is apparent from Figs. 2-5,
our model of a flaring corona,
in terms of loop-like localized non-thermal emission, can indeed account for the
flux required, in addition to a jet-like power-law component, to obtain a reasonably good fit of the observations.
Table 1:
Results of the application of our model to
3C 273 BeppoSAX data at different epochs. The magnetic field is
expressed in Gauss and
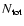 in units of 1053 electrons.
The normalization factor for the redshifted power-law representing the jet component,
in units of 1053 electrons.
The normalization factor for the redshifted power-law representing the jet component,
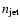 is in units of 10-3 photons cm-2 s-1 keV-1.
Jet and corona relative intensities are described by
their respective flux values,
in units of 10-11 erg s-1 cm-2 (see the text
for details).
is in units of 10-3 photons cm-2 s-1 keV-1.
Jet and corona relative intensities are described by
their respective flux values,
in units of 10-11 erg s-1 cm-2 (see the text
for details).
Moreover, and possibly even more important, Figs. 2-5 well show that our model
is capable of reproducing the observed soft excess entirely,
without any additional specific component required.
This capability of our model
had been verified in Paper I, where we had made use of this emission model to fit the BeppoSAX X-ray spectrum of
a ``bona fide'' Seyfert, NGC 5548, and it represents a most relevant and distinguishing feature of the emission
mechanism we have proposed for the Seyfert-like component of the X-ray spectral distribution of
the source under examination.
Indeed, the present successful application to a more complex source like the quasar 3C 273, whose spectrum is the result of the
superposition of more than one primary emission mechanism, confirms
the interest of our proposed mechanism for X-ray emission from an active corona surrounding the accretion disk of an AGN.
The main reason for this ability to provide an explanation of the observed soft-X-rays is that in our model scenario
the reprocessing of seed photons (via inverse Compton) includes, in addition
to disk photons, the syncrothron photons originating ``locally'' (i.e., in each active loop) from the same population of
relativistic electrons (see Sect. 2 and Paper I).
The importance of
the soft-X-rays component produced in
our model with respect to the other X-ray ranges (in other words, the ``level'' of the ``soft excess'' as
reproduced by our model) can be more or less pronounced, depending on the choice of the model parameters and on the
specific shape of the input soft
disk spectrum, so that our model may be able to explain also AGN spectra in which no strong soft excess is observed.
Indeed, ROSAT observations of a significant sample of Seyfert 1 AGNs show that 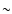 90% of the sources
do possess a soft excess to some level (see Piro et al. 1997; Walter & Fink 1993).
90% of the sources
do possess a soft excess to some level (see Piro et al. 1997; Walter & Fink 1993).
Figures 2-5 show that
the BeppoSAX spectrum of 2001, fitted in our framework, represents the most ``extreme''
case
in terms of relative contribution
of a beamed-jet component and Seyfert-like coronal component, described by our model: in fact, in the fit of
Fig. 5, referring to this specific epoch of observation, there is a clear dominance of the coronal component over the jet one, together with
a contribution of the reprocessed components (reflection and iron line), which is, consistently, more relevant
than in any other BeppoSAX observation that we have fitted.
In order to give a better evaluation of the relative importance
of the different components of our spectral representation and to compare
our results with those of G&P, for each of the observed spectra that we have fitted,
we have derived the flux values
in the range 2-10 keV for our coronal model alone (i.e., without the reprocessed
reflection component), for the
jet component alone and for the
the overall X-ray radiation detected by
BeppoSAX, thus including the contributions
to the flux in the 2-10 keV range
due to the various components we have used to fit the spectrum
(our coronal model, the reflection component arising from its
reprocessing, the iron line, and the beamed jet power-law); we indicate these fluxes as
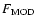 (2-10 keV),
(2-10 keV),
 (2-10 keV) and
(2-10 keV) and
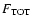 (2-10 keV), respectively.
We have also evaluated
(2-10 keV), respectively.
We have also evaluated
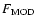 (0.2-2 keV), the contribution to the
soft X-ray flux due to our coronal model component.
The values of
(0.2-2 keV), the contribution to the
soft X-ray flux due to our coronal model component.
The values of
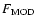 (0.2-2 keV) shown in Table 1 are the ``observed'' ones,
that is they are obtained as absorbed by the Galactic cold absorber component
(with
(0.2-2 keV) shown in Table 1 are the ``observed'' ones,
that is they are obtained as absorbed by the Galactic cold absorber component
(with
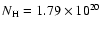 cm-2 fixed and constant for all the fits)
on the line of sight to 3C 273 (Dickey & Lockman 1990).
Of course, here
cm-2 fixed and constant for all the fits)
on the line of sight to 3C 273 (Dickey & Lockman 1990).
Of course, here
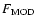 (0.2-2 keV)
represents the whole contribution to the ``soft'' range 0.2-2 keV due to our coronal emission model and not
only the so-called ``soft excess''.
(0.2-2 keV)
represents the whole contribution to the ``soft'' range 0.2-2 keV due to our coronal emission model and not
only the so-called ``soft excess''.
![\begin{figure}
\par\mbox{\includegraphics[width=2.5in]{7597f6le.ps}\hspace{0.60in}
\includegraphics[width=2.5in]{7597f6ri.ps} }\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg89.gif) |
Figure 6:
Left panel: the soft X-ray flux of our model versus the ``hard'' (2-10 keV) one is
shown for each performed fit identified by the observation number as defined in Table 1.
The expected correlation is clearly shown. Right panel: the beamed jet component
flux versus our model (2-10 keV) flux does not show any correlation. |
| Open with DEXTER |
The flux values derived as described above
are given in Table 1.
We can now compare our results with those of G&P. Given the different
representation of the Seyfert-like component in the two cases, a quantitative and direct comparison
of parameters would be out of place; in fact, in our scenario the coronal emission has a spectral shape
that is more complex than a simple power-law, as it is represented in G&P framework, and, as a consequence,
its importance cannot be parameterized by the value of its photon spectral flux at 1 keV
(
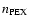 for G&P, as shown in their Table 3); in addition, in our model, no additional and separated
soft excess component is required. Therefore we have no direct comparison for the values of the flux
in the soft excess component
for G&P, as shown in their Table 3); in addition, in our model, no additional and separated
soft excess component is required. Therefore we have no direct comparison for the values of the flux
in the soft excess component
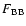 (0.2-2 keV) shown by G&P (which is represented by a black-body
spectral component, to be superimposed on the Seyfert-like component), but we can only compare the
behaviour of this
quantity changing from observation to observation with the trend shown by our analogous
(0.2-2 keV) shown by G&P (which is represented by a black-body
spectral component, to be superimposed on the Seyfert-like component), but we can only compare the
behaviour of this
quantity changing from observation to observation with the trend shown by our analogous
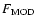 (0.2-2 keV),
whose meaning we have explained above.
However, it is possible to check the qualitative accordance
between the two analyses and a positive result would support the interpretation
of this source's X-ray emission
as a combination of Seyfert-like and Blazar-like features.
To this purpose, the relative flux values that we have determined and are shown in Table 1 can be used as a
measure of the strength of the corona and jet components in the various observations.
(0.2-2 keV),
whose meaning we have explained above.
However, it is possible to check the qualitative accordance
between the two analyses and a positive result would support the interpretation
of this source's X-ray emission
as a combination of Seyfert-like and Blazar-like features.
To this purpose, the relative flux values that we have determined and are shown in Table 1 can be used as a
measure of the strength of the corona and jet components in the various observations.
The behaviour of
the quantities
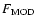 (0.2-2 keV),
(0.2-2 keV),
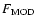 (2-10 keV),
(2-10 keV),
 (2-10 keV), from our fit in the sequence of
observations from 1998 to 2001,
is the same as that of the corresponding parameters in the G&P representation (namely,
(2-10 keV), from our fit in the sequence of
observations from 1998 to 2001,
is the same as that of the corresponding parameters in the G&P representation (namely,
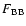 ,
,
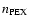 ,
,
 ), shown in Table 3 of G&P; in particular, as already mentioned, BeppoSAX
spectrum of year 2001 is the one in which the contribution of the Seyfert-like component
(i.e. our coronal model component) is most significant, as in the G&P analysis.
Secondly, the left panel of Fig. 6, representing
), shown in Table 3 of G&P; in particular, as already mentioned, BeppoSAX
spectrum of year 2001 is the one in which the contribution of the Seyfert-like component
(i.e. our coronal model component) is most significant, as in the G&P analysis.
Secondly, the left panel of Fig. 6, representing
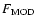 (0.2-2 keV)
versus
(0.2-2 keV)
versus
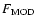 (2-10 keV) for the four
observations we fitted with our model, clearly shows that there is a positive correlation between
our coronal model fluxes in the two energy ranges, from our best fits of the data in the
various epochs. This is
in accordance with G&P Fig. 1A, where the authors show the 0.2-2 keV flux in the black-body component that
they use to represent the soft excess versus their Seyfert-like power-law flux in the range 2-10 keV, with a positive
correlation as well.
In our framework this positive
correlation is intrinsic to the model of the coronal emission and it is easily explained,
since the observed soft excess is entirely modeled by
the low-energy portion of the coronal model spectrum itself.
(2-10 keV) for the four
observations we fitted with our model, clearly shows that there is a positive correlation between
our coronal model fluxes in the two energy ranges, from our best fits of the data in the
various epochs. This is
in accordance with G&P Fig. 1A, where the authors show the 0.2-2 keV flux in the black-body component that
they use to represent the soft excess versus their Seyfert-like power-law flux in the range 2-10 keV, with a positive
correlation as well.
In our framework this positive
correlation is intrinsic to the model of the coronal emission and it is easily explained,
since the observed soft excess is entirely modeled by
the low-energy portion of the coronal model spectrum itself.
Also, in the right panel of Fig. 6
we see the similarity of our results
to those of G&P (Fig. 1B), confirming the lack of correlation of the variations of the coronal model
flux and the jet flux, both evaluated in
the energy range 2-10 keV, when changing the epoch of observation.
Therefore, the soft and hard fluxes of the Seyfert-like component do vary together (i.e., with a positive correlation),
but the jet component does not.
This is not surprising, as G&P also mentioned, because we
interpret the origin of the fluxes of the two components as physically uncorrelated (although both the related
physical mechanisms are at work in the inner regions of the quasar),
since
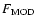 (2-10 keV)
originates from the active corona surrounding the inner accretion disk, whereas
(2-10 keV)
originates from the active corona surrounding the inner accretion disk, whereas
 (2-10 keV) is attributed to
the emission from an entirely different population of high energy electrons that are relativistically beamed
at a small angle to the line of sight in a ``jet''-like configuration.
(2-10 keV) is attributed to
the emission from an entirely different population of high energy electrons that are relativistically beamed
at a small angle to the line of sight in a ``jet''-like configuration.
Besides Fig. 6, we have plotted the various fluxes evaluated for the different observations (see Table 1)
to illustrate better the qualitative agreement, mentioned above, with the G&P results in analyzing the relative
variations of the spectral components with time, i.e. from epoch to epoch of observation.
Again in agreement with G&P analysis (see their Fig. 3C), no correlation is found between
the soft-X-ray emission level (here quantified by
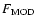 (0.2-2 keV)) and the variations of the total flux of the source in the
``hard'' range 2-10 keV, as can be seen from
the left panel of Fig. 7. This is a property that was known already from ROSAT observations (variations of
fluxes in the energy ranges
[0.1-0.3 keV] and [1.5-2.4 keV] uncorrelated, see Leach et al. 1995), and
further confirmed by the Kataoka et al. (2002) RXTE data analysis, concluding that the soft excess appearance was
``occasional'' and uncorrelated with the total flux changes.
As it is easy to understand, given the tight correlation of Fig. 6, a similar behaviour is
shown in the center panel of Fig. 7, where we plot the ``hard'' flux of the
model (
(0.2-2 keV)) and the variations of the total flux of the source in the
``hard'' range 2-10 keV, as can be seen from
the left panel of Fig. 7. This is a property that was known already from ROSAT observations (variations of
fluxes in the energy ranges
[0.1-0.3 keV] and [1.5-2.4 keV] uncorrelated, see Leach et al. 1995), and
further confirmed by the Kataoka et al. (2002) RXTE data analysis, concluding that the soft excess appearance was
``occasional'' and uncorrelated with the total flux changes.
As it is easy to understand, given the tight correlation of Fig. 6, a similar behaviour is
shown in the center panel of Fig. 7, where we plot the ``hard'' flux of the
model (
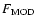 (2-10 keV)) with respect to the corresponding total flux,
(2-10 keV)) with respect to the corresponding total flux,
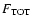 (2-10 keV).
(2-10 keV).
![\begin{figure}
\par\mbox{\includegraphics[width=1.8in]{7597f7le.ps}\hspace{0.5in...
...e.ps}\hspace{0.5in}
\includegraphics[width=1.8in]{7597f7ri.ps} }
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg91.gif) |
Figure 7:
The flux values shown are those given in Table 1
and identified by their respective observation number.
No correlation is present, for the data we have analysed, between the soft coronal component
and the total emission ( left panel), the coronal component and the total
emission ( central panel), the beamed jet component and the total emission ( right panel). |
| Open with DEXTER |
An indication of the lack of definite correlation between jet dominance and total flux of the source comes
from the right panel of Fig. 7. A conclusion similar to the one of G&P can be therefore drawn
as well:
the appearance and relevance of the Seyfert-like component is not strictly related to so-called ``low'' states
of the jet or of the source in general. A word of caution, however, is in order, since we only applied our model
to the four observations that appeared most promising from the point of view of the coronal model relevance,
thus we have only four points in our plots.
All the results described above refer to fits in which we have kept the slope of the power-law describing the
jet-component fixed to the same value chosen by G&P in their analysis, namely, for the photon spectral index,
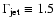 .
For each of the four BeppoSAX observations considered, we have analyzed the spectra
also leaving
.
For each of the four BeppoSAX observations considered, we have analyzed the spectra
also leaving
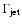 free to vary. We do not show the details of this analysis, but we summarize
the main results here. For four observations, we obtain best fits with essentially the same level of
quality, in terms of
free to vary. We do not show the details of this analysis, but we summarize
the main results here. For four observations, we obtain best fits with essentially the same level of
quality, in terms of
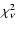 values (actually even better in two cases). Apart from the case for the
January 2000 spectrum, which is best fitted with a slightly larger contribution of the Seyfert-model component and
correspondingly a slightly lower
values (actually even better in two cases). Apart from the case for the
January 2000 spectrum, which is best fitted with a slightly larger contribution of the Seyfert-model component and
correspondingly a slightly lower
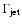 value (
value ( 1.45),
in general the best fit is obtained with
a more prominent jet, with a slightly flatter photon spectrum (i.e.,
1.45),
in general the best fit is obtained with
a more prominent jet, with a slightly flatter photon spectrum (i.e.,
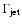 larger than the ``standard''
1.5 value, at most 1.67, obtained for the 2001 data), with the extreme case represented
by the 1998 spectrum, in which the jet component represents the dominant
contribution for energies higher than
larger than the ``standard''
1.5 value, at most 1.67, obtained for the 2001 data), with the extreme case represented
by the 1998 spectrum, in which the jet component represents the dominant
contribution for energies higher than  3 keV (see Fig. 2 for comparison).
3 keV (see Fig. 2 for comparison).
We do not discuss here the reasons for or the physical meaning of a change in time of the photon spectral index
for the beamed jet component of the X-ray spectrum.
Rather, we compare our range of resulting spectral index for the
power-law spectral component representing the beamed jet radiation with the values deduced from the
analysis of BeppoSAX observations of sources dominated by the beamed jet emission, i.e. real blazars.
In fact, from the catalog of the X-ray spectra of blazar sources observed by BeppoSAX presented by
Giommi et al. (2002), a rather wide variety of spectral slopes is obtained, in particular
isolating the sub-class of BL Lac objects; however, when restricting the analysis to the
other sub-class of FSRQs, to which
3C 273 belongs from the radio point of view (Grandi et al. 2006), the range
of photon spectral index turns out to be narrowed
to
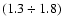 ,
with a distribution that is strongly peaked around 1.5-1.6, according to
Giommi et al. (2002). Further analysis of radio loud AGN BeppoSAX X-ray spectra has been presented
by Grandi et al. (2006); among their sample these authors isolate the properties of
FSRQs, generally showing a featureless continuum between 0.1 and 200 keV (except, of course, for the case for 3C 273,
included in their sample) with a
photon spectral index between 1.34 and 1.78 (apart from one object), but again with typical values around
1.5-1.6.
Finally, Fiocchi & Grandi (2004)
have estimated the ``average'' photon spectral index for X-ray spectra of FSRQs as observed by BeppoSAX
to be
,
with a distribution that is strongly peaked around 1.5-1.6, according to
Giommi et al. (2002). Further analysis of radio loud AGN BeppoSAX X-ray spectra has been presented
by Grandi et al. (2006); among their sample these authors isolate the properties of
FSRQs, generally showing a featureless continuum between 0.1 and 200 keV (except, of course, for the case for 3C 273,
included in their sample) with a
photon spectral index between 1.34 and 1.78 (apart from one object), but again with typical values around
1.5-1.6.
Finally, Fiocchi & Grandi (2004)
have estimated the ``average'' photon spectral index for X-ray spectra of FSRQs as observed by BeppoSAX
to be
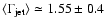 .
This is the reason why G&P had chosen to freeze the
beamed jet component spectral index to the value 1.5 in their analysis of 3C 273 X-ray spectra, and it is
also why we followed their choice.
Even when leaving the beamed jet component spectral index free to vary,
in our fits we always obtain values between 1.45 and 1.67 for
.
This is the reason why G&P had chosen to freeze the
beamed jet component spectral index to the value 1.5 in their analysis of 3C 273 X-ray spectra, and it is
also why we followed their choice.
Even when leaving the beamed jet component spectral index free to vary,
in our fits we always obtain values between 1.45 and 1.67 for
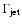 ,
which turn out to be
in accordance with the observed range for FSRQ sources.
,
which turn out to be
in accordance with the observed range for FSRQ sources.
We can then check whether the spectral shape of the Seyfert-like component as defined by
our coronal model also matches the average, typical spectral properties of Seyfert 1s X-ray spectra, in
particular as observed by BeppoSAX. In Paper I, we presented our analysis of the descriptive capability of our
coronal model with respect to some general observed properties of Seyfert 1s X-ray spectra and we refer to that
(see Sect. 6 of Paper I) for details.
One property of our best fit model coronal spectra for the present case can be easily tested against the
typical analogue of the Seyfert 1 class; this is the characteristic spectral slope in the range of 2-10 keV,
which is the range less affected by reprocessing components and, therefore, the range in which
the shape of the primary coronal spectrum can be more easily inferred from observations (see Paper I discussion).
We can easily estimate a representative spectral index
 for each of our best-fit model coronal
spectra, by fitting their shape in the above mentioned range 2-10 keV with a simple power-law so as
to evaluate their ``local'' slope in terms of
for each of our best-fit model coronal
spectra, by fitting their shape in the above mentioned range 2-10 keV with a simple power-law so as
to evaluate their ``local'' slope in terms of
 (where the flux is
(where the flux is
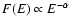 ).
The result of this exercise is that for our best fit models it is
).
The result of this exercise is that for our best fit models it is
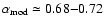 .
This then can be compared with the typical
Seyfert 1 spectral index
.
This then can be compared with the typical
Seyfert 1 spectral index 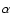 as inferred from
BeppoSAX 2-10 keV observations.
Indeed, Seyfert 1s have been deeply analyzed by several
authors and they all agree on the definition of a range for the spectral index
as inferred from
BeppoSAX 2-10 keV observations.
Indeed, Seyfert 1s have been deeply analyzed by several
authors and they all agree on the definition of a range for the spectral index 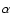 of the primary
spectrum (in flux) between 2 and 10 keV, which turns out to be
of the primary
spectrum (in flux) between 2 and 10 keV, which turns out to be
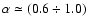 (see Bianchi et al.
2004; Perola et al. 2002; Matt 2001). The
usually considered ``canonical'' value for the spectral index
(see Bianchi et al.
2004; Perola et al. 2002; Matt 2001). The
usually considered ``canonical'' value for the spectral index
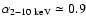 (see for instance
Nandra & Pounds 1994; Nandra et al. 1997; Zdziarski et al. 2000) appears from the
analysis of BeppoSAX spectra only when dealing with an ``average'' spectrum, that is a spectrum obtained from
the addition of the count spectra of individual sources, subsequently fitted as a whole (see
Malizia et al. 2003; Deluit & Courvoisier 2003).
Considering the discussion above, we can conclude that the range of spectral slope evaluated
from the analysis of our best fit coronal
models representing the Seyfert-like component of 3C 273 X-ray spectrum does indeed fall within the typical
Seyfert 1 range of values as inferred from BeppoSAx observations; this implies that our model spectra are indeed
representative of a ``typical'' Seyfert source behavior.
(see for instance
Nandra & Pounds 1994; Nandra et al. 1997; Zdziarski et al. 2000) appears from the
analysis of BeppoSAX spectra only when dealing with an ``average'' spectrum, that is a spectrum obtained from
the addition of the count spectra of individual sources, subsequently fitted as a whole (see
Malizia et al. 2003; Deluit & Courvoisier 2003).
Considering the discussion above, we can conclude that the range of spectral slope evaluated
from the analysis of our best fit coronal
models representing the Seyfert-like component of 3C 273 X-ray spectrum does indeed fall within the typical
Seyfert 1 range of values as inferred from BeppoSAx observations; this implies that our model spectra are indeed
representative of a ``typical'' Seyfert source behavior.
In summary, we have shown that in our composite fits the two main components of the spectrum do indeed
correspond to parameters, at least as far as spectral slope is concerned, that belong to the ranges
accepted as typical and characterizing separately each of the two components themselves, as inferred from
observations of ``pure'' Seyfert 1s, on one hand, and of ``pure'' FSRQ blazars, on the other.
This result clearly supports the validity of the construction for 3C 273, and of our coronal model
as well.
Even when the contribution to the spectrum
determined by our model for the Seyfert-like component is less relevant, the soft-X-ray portion of the spectrum itself
is still well fitted and the ``soft excess'' is still completely explained by the coronal emission, independently
of its level of importance in the other spectral regions. This result is strong support
for our physical model of the Seyfert-like component of the spectrum.
At least for the quasar source 3C 273,
the observed X-ray spectrum is the result of the superposition of both a non-thermal beamed jet component and a
Seyfert-like component, which, separately taken, have properties that characterize them as representative
of the typical X-ray spectrum of pure Seyfert 1s or pure FSRQ blazars respectively.
Both these components are variable in time and they do vary independently, because of their
entirely different origin, possibly with the ``jet'' component overwhelming or dominating most of the time.
However, depending on the overall state of the source itself, the Seyfert-like component that we interpret
as the X-ray emission from an active corona made of several ``loops'' (described in Sect. 2) can be
significant and distinguishable from the underlying beamed jet component, so that a fit properly including both
of them can somewhat quantify their relative importance. In the case of 3C 273, observed several
times by BeppoSAX, the years from 1998 to 2001 correspond to a period in which the coronal activity was
observable above the jet contribution. To strengthen this interpretation, we refer to the work of Foschini et al. (2006); the authors analyzed the X-ray spectra of a sample of 15 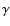 -ray loud
AGN observed by XMM-Newton, including 3C 273, during the years 2000-2004. From their analysis of 3C 273,
Foschini et al. (2006) conclude that there is indeed a ``softening'' of the X-ray spectrum, corresponding to
a trend of an increase of the Seyfert-like component
with respect to the jet one during the period of observation examined.
On the contrary, somewhat different conclusions have been drawn from the analysis of further XMM and INTEGRAL observations
of 3C 273, from 2003 to 2005, by Chernyakova et al. (2007); these last authors also recognize
the ``softening'' of the 3C 273 X-ray spectrum in the period of observations they study, but they assert that ``sophisticated''
models including disk reflection and a soft excess component described by a black-body do not give better fits
than a simpler model composed of two power-laws. On the basis of this result, they conclude that they do not reveal
the presence of a Seyfert-like component; however, they also add that more complex physical models have to be
devised to account for the spectral evolution of this source and explain it.
This necessity for more complex and more physical models for the description of the Seyfert-like features possibly present
in the X-ray spectrum is the same conclusion drawn by Page et al. (2004) in their attempt to
identify a physical representation for the soft excess of the source under examination, starting with the analysis of
XMM-Newton observations from 2000 to 2003. Page et al. (2004) propose a Comptonization
model for the X-ray emission, in
which the disk photons are upscattered in energy by two populations of ``hot'' electrons at two different temperatures;
the ``cooler'' population would give rise to the soft excess above a power-law emission resulting from Comptonization
by the second, ``hotter'', electron population. However, notwithstanding the capability of this model to give a reasonable
fit of the various observations of the soft excess as taken singly, when considering the variability
behaviour of the soft excess parameters,
these same authors recognize that there is an inconsistency with what would be expected from a simple and direct
interpretation of their proposed model (see Page et al. 2004), thus leading them to invoke more complex
explanations.
-ray loud
AGN observed by XMM-Newton, including 3C 273, during the years 2000-2004. From their analysis of 3C 273,
Foschini et al. (2006) conclude that there is indeed a ``softening'' of the X-ray spectrum, corresponding to
a trend of an increase of the Seyfert-like component
with respect to the jet one during the period of observation examined.
On the contrary, somewhat different conclusions have been drawn from the analysis of further XMM and INTEGRAL observations
of 3C 273, from 2003 to 2005, by Chernyakova et al. (2007); these last authors also recognize
the ``softening'' of the 3C 273 X-ray spectrum in the period of observations they study, but they assert that ``sophisticated''
models including disk reflection and a soft excess component described by a black-body do not give better fits
than a simpler model composed of two power-laws. On the basis of this result, they conclude that they do not reveal
the presence of a Seyfert-like component; however, they also add that more complex physical models have to be
devised to account for the spectral evolution of this source and explain it.
This necessity for more complex and more physical models for the description of the Seyfert-like features possibly present
in the X-ray spectrum is the same conclusion drawn by Page et al. (2004) in their attempt to
identify a physical representation for the soft excess of the source under examination, starting with the analysis of
XMM-Newton observations from 2000 to 2003. Page et al. (2004) propose a Comptonization
model for the X-ray emission, in
which the disk photons are upscattered in energy by two populations of ``hot'' electrons at two different temperatures;
the ``cooler'' population would give rise to the soft excess above a power-law emission resulting from Comptonization
by the second, ``hotter'', electron population. However, notwithstanding the capability of this model to give a reasonable
fit of the various observations of the soft excess as taken singly, when considering the variability
behaviour of the soft excess parameters,
these same authors recognize that there is an inconsistency with what would be expected from a simple and direct
interpretation of their proposed model (see Page et al. 2004), thus leading them to invoke more complex
explanations.
In the light of this last consideration, the results of Foschini et al. (2006) and of
Chernyakova et al. (2007), mentioned above, could be interpreted as
only apparently contradictory; the contradiction might be caused by the general use of ``phenomenological''
and uncorrelated emission components added in a fit of the observed spectra, instead of a more appropriate
and physical description of the Seyfert-like component, including a consistently computed soft-X-ray emission, such
as our attempt could be considered.
We have described our application of a physical model for the emission of X-ray radiation
from an active coronal region, surrounding the accretion disk of the central black hole in an AGN, in order to explain
the so called ``Seyfert-like'' features in the X-ray spectrum of the quasar 3C 273. The presence of this component
superimposed on the non-thermal beamed jet component, usually invoked for the physical description of the emission of
this source (sometimes qualified also as a Blazar), has been proposed several times by different authors,
analyzing 3C 273 X-ray spectra as observed by a number of X-ray satellites (see Sect. 1 for details),
in discussions of the soft excess.
The G&P analysis of BeppoSAX data, taken at different epochs between 1996 and 2001,
confirmed this idea.
In a previous paper (Paper I) we gave a model for a non-thermal active accretion disk corona in order to
account for the X-ray emission in Seyfert-like AGNs. In our framework, the X-ray emission is inverse Compton
radiation produced in the interaction of populations of relativistic non-thermal electrons, impulsively injected at the top
of (magnetically) active loops, with ``soft'' seed photons both coming from the underlying accretion disk and radiated
``locally'', i.e. within each loop, by the same local population of relativistic electrons, by the synchrotron mechanism.
The emitted radiation is intrinsically non-stationary and the resulting X-ray primary spectrum is obtained as the appropriate
temporal average of the sum of the contributions by all the individual active loops, whose ensemble we define as the
``active corona''. We refer the reader to Paper I for the details of the mechanism.
In Paper I, this model was successfully tested against the BeppoSAX observations of the Seyfert
nucleus of NGC 5548, and its predictions
were compared with a few general properties of the X-ray spectrum of Seyfert 1 AGNs as a class, obtaining an
agreement.
We applied our model of active X-ray emitting coronae to the case for the radio-loud
quasar 3C 273, whose X-ray spectral complexity requires a contribution from a Seyfert-like component, but whose
inferred physical properties as an AGN are quite different from those of a typical Seyfert 1.
For example, the central
black hole mass is estimated to be much larger than that of the Seyfert 1 AGNs. Paltani & Türler
(2005) have determined a range for 3C 273
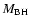 between
between
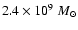 and
and
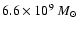 ,
to be compared with the estimate for NGC 5548,
,
to be compared with the estimate for NGC 5548,
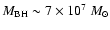 (see, for example,
Peterson et al. 2004, and Paper I).
The model is flexible and physically sound, because the description
of a source such as 3C 273 requires a different scaling of quantities and parameters characterizing the coronal
model itself.
(see, for example,
Peterson et al. 2004, and Paper I).
The model is flexible and physically sound, because the description
of a source such as 3C 273 requires a different scaling of quantities and parameters characterizing the coronal
model itself.
As discussed in the previous section, we are able to fit each of the four chosen BeppoSAX
observations (from 1998 to 2001), describing the X-ray spectrum as the superposition of a beamed jet component
represented by a power-law and a component defined by our model primary spectrum, together with an appropriate
reflection component and a Gaussian iron line. We can confirm and reproduce the trends inferred by G&P (2004),
although those authors adopted a representation of the Seyfert-like component including a simple power-law
for the primary X-rays,
the corresponding reflection, an iron line, and
a superimposed black-body component to separately account for the soft excess.
Similarly to the case of NGC 5548 (on a different scale, as mentioned above) studied in
Paper I, our model spectrum is, in each of observations analyzed, capable of accounting for
the observed ``soft excess'' entirely and with
no need for an extra component.
This result
offers a consistent explanation for the origin of the soft X-ray emission within our scenario.
We give a qualitative
overview of the consistency tests in the different ranges of physical parameters that
we adopt for the proper scaling of our proposed mechanism to such a powerful source as the quasar 3C 273.
a) Inverse Compton and synchrotron losses for the
relativistic electron population injected in each loop
for the present case (as well as for a typical Seyfert 1) by far dominate the evolution of the electron
energy distribution, thus allowing us to neglect collisional losses and derive the analytic solution for the time
evolution of the distribution itself (see Sect. 2.1 of Paper I).
b) With the adopted value for the thermal material number density in the coronal region, thermal Comptonization
effects, as well as ``recoil'' effects on the spectrum are still negligible,
given that the optical depth to scattering of the
thermal material component turns out to be still  1 (see Sect. 3.1), even though the characteristic global
extension of the coronal region,
1 (see Sect. 3.1), even though the characteristic global
extension of the coronal region,
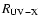 ,
here is much larger than in the Seyfert 1 application case.
,
here is much larger than in the Seyfert 1 application case.
c) As already mentioned in Sect. 3, when considering the very large values of black hole mass estimated for 3C 273
(Paltani & Türler 2005), the value we have chosen for the size of the coronal region,
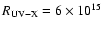 cm, expressed in units of the corresponding Schwarzschild radius,
is in the range
cm, expressed in units of the corresponding Schwarzschild radius,
is in the range
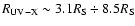 .
Referring to the discussion in Sect. 2 of Paper I, whose conclusion is that
various theoretical estimates (Miller & Stone 2000; Liu et al. 2002)
agree on a range
.
Referring to the discussion in Sect. 2 of Paper I, whose conclusion is that
various theoretical estimates (Miller & Stone 2000; Liu et al. 2002)
agree on a range 
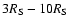 for the active corona extension above the disk, this seems to indicate
that, when scaling the coronal size with respect to the relevant physical parameter (i.e., the black hole mass in this
context), the models that do fit 3C 273 X-ray observations correspond to a coronal region of the appropriate proportions,
given the mass of the black hole.
for the active corona extension above the disk, this seems to indicate
that, when scaling the coronal size with respect to the relevant physical parameter (i.e., the black hole mass in this
context), the models that do fit 3C 273 X-ray observations correspond to a coronal region of the appropriate proportions,
given the mass of the black hole.
This is important, since the size of the coronal region
turns out to be crucial
in order to reproduce the intensity level and the shape of the observed soft portion of the X-ray spectrum.
A smaller corona would not have been able to emit enough soft X-ray radiation to reproduce the 3C 273 BeppoSAX spectra
shown in Sect. 3, although the corresponding decrease in ``hard'' coronal flux might have been compensated by a
suitable increase of the jet component. This is a clear indication of the general importance of the soft region of the spectrum
as for the definition of the proper description of X-ray emission in general and especially for our coronal model, which
intrinsically produces the soft component itself along with the hard one. In other words, we can say that, in the
framework of a description of the Seyfert-like X-ray emission given by our coronal model,
the presence of a soft X-ray excess can
be interpreted as the presence of a significant active corona, and, moreover, its level of intensity somewhat defines the
appropriate coronal size for our model.
In order to
properly fit the spectra of
very different AGNs, such as 3C 273 and NGC 5548 (Paper I), we have to choose coronal sizes that
appropriately scale, because of the very different black hole masses, in accordance with theoretical expectations and
estimates (Miller & Stone 2000; Liu et al. 2002)
for the dimension of a possible coronal structure. This agreement gives further support
to our proposed scenario.
d) The extent of the coronal region can be also related to the possibility of
reproducing the observed time scale variability.
It is not our intention to attempt a variability study and
this would not be possible on the basis of the the data sets
we analyse. The following brief discussion only aims to illustrate
the fact that our coronal structure, as defined
by the fitting of BeppoSAX data, would not be
inconsistent with observational variability constraints.
Different
authors report the observed time variability of 3C 273 flux,
integrated in the energy range 2.5-20 keV (Kataoka et al. 2002)
or 3-20 keV (McHardy et al. 2007; Chernyakova et al. 2007).
In this energy range the relative contributions of jet and coronal components can be different,
depending on the epoch, but the coronal component can be quite significant
(as seen in the previous sections); as a consequence, the requirements implied by the observed variability
time-scales should, in principle, apply to both the jet and the coronal contribution, since, at the present
stage, it is not possible to disentangle unambiguously their respective role in variability.
Hence, for our model,
we verify that the coronal size can be compatible with the temporal variability;
this is the case for the coronal model we propose.
If a flare would take place in only
one loop of our corona, we would expect the global emission to change by a fraction 1/qin a time
 .
Hence, within our model we might obtain variations of
.
Hence, within our model we might obtain variations of  5% in the Seyfert-like
component
flux on time-scales down to
5% in the Seyfert-like
component
flux on time-scales down to
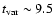 hours for observation epochs 1998, January and June 2000
and variations of
hours for observation epochs 1998, January and June 2000
and variations of  2.5% in the Seyfert-like
component
flux on time-scales down to
2.5% in the Seyfert-like
component
flux on time-scales down to
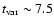 h for the observation of 2001.
The X-ray observations mentioned above (Chernyakova et al. 2007; McHardy et al. 2007;
Kataoka et al. 2002) agree that no variability is detectable on
time scales shorter than some hours. Besides this lower limit for flux variability detection,
the evidence of a
significant flare-like variability of the observed flux is apparent from those
analyses.
The most accurate temporal study of this issue is the one of Kataoka et al. (2002),
referring exactly to the same period of the observations we are dealing with. From the power spectrum analysis,
these authors derive
a variability time scale for individual flares of
h for the observation of 2001.
The X-ray observations mentioned above (Chernyakova et al. 2007; McHardy et al. 2007;
Kataoka et al. 2002) agree that no variability is detectable on
time scales shorter than some hours. Besides this lower limit for flux variability detection,
the evidence of a
significant flare-like variability of the observed flux is apparent from those
analyses.
The most accurate temporal study of this issue is the one of Kataoka et al. (2002),
referring exactly to the same period of the observations we are dealing with. From the power spectrum analysis,
these authors derive
a variability time scale for individual flares of  3 days.
Hence, the lower limits for variability time scales derived above for
our model can be consistent with the observations mentioned above.
3 days.
Hence, the lower limits for variability time scales derived above for
our model can be consistent with the observations mentioned above.
e) Our model is based on a single scattering inverse Compton mechanism. As a consequence, we have to verify
that, with the typical best fit parameters, the condition ensuring that the
second order scattering
probability is effectively negligible is fulfilled. This condition is that the optical depth to
non-thermal relativistic electron scattering is very small, i.e.,
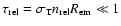 ,
where
,
where
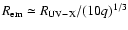 is the representative linear size of each individual emitting loop
and
is the representative linear size of each individual emitting loop
and
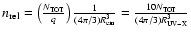 .
For the cases listed in Table 1 the
largest value we obtain is the one related to the model for the January 2000 observation which gives
.
For the cases listed in Table 1 the
largest value we obtain is the one related to the model for the January 2000 observation which gives
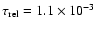 ,
fulfilling the condition above.
,
fulfilling the condition above.
f) We also estimate the local compactness
(see Guilbert et al. 1983; Svensson 1987, 1990) for
the individual emitting loops contributing to the X-ray emission in our model.
The compactness parameter, which is related to the optical depth to photon-photon pair production, when gamma-ray photons
at energies above the threshold for the process (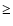 511 MeV) are present, is actually a measure of the
importance of pair production effects on the spectrum. For our model
to be fully consistent, we require that its value for each loop,
511 MeV) are present, is actually a measure of the
importance of pair production effects on the spectrum. For our model
to be fully consistent, we require that its value for each loop,
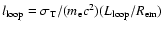 ,
is below the critical limit for
pair production to become significant, since we have not included the effects of this process in our computations.
The relevant value of the luminosity in the present case is of course the luminosity emitted because of our model mechanism
in each individual loop,
,
is below the critical limit for
pair production to become significant, since we have not included the effects of this process in our computations.
The relevant value of the luminosity in the present case is of course the luminosity emitted because of our model mechanism
in each individual loop,
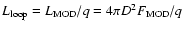 ,
where q is the number of active loops
at any given time
and the condition for negligibility of pair production effects on the spectrum is that
,
where q is the number of active loops
at any given time
and the condition for negligibility of pair production effects on the spectrum is that
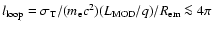 (see Svensson 1990).
The proper evaluation of the relevant luminosity is clearly crucial to the correct estimate of the
compactness.
(see Svensson 1990).
The proper evaluation of the relevant luminosity is clearly crucial to the correct estimate of the
compactness.
The photon-photon pair production process is a threshold process,
requiring that the product of the two interacting photons' energies,
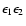 ,
fulfills the condition
,
fulfills the condition
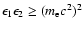 ,
which is intuitive since the minimum energy of each of the
two particles created (e+ and e-) must be their rest energy.
Whenever the spectrum of the emission extends beyond the
electron rest mass energy
,
which is intuitive since the minimum energy of each of the
two particles created (e+ and e-) must be their rest energy.
Whenever the spectrum of the emission extends beyond the
electron rest mass energy
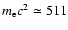 keV, in the
keV, in the 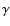 -ray range, the compactness to the pair production
process must be evaluated. Moreover, a photon of energy
-ray range, the compactness to the pair production
process must be evaluated. Moreover, a photon of energy
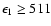 keV can only produce a pair by interacting
with another photon of energy
keV can only produce a pair by interacting
with another photon of energy
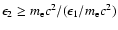 ,
i.e., the larger the energy of the
first
,
i.e., the larger the energy of the
first  -ray photon (beyond 511 keV), the ``softer'' the second photon involved in the interaction can be (that is,
the lower its energy can be).
As a consequence,
the identification of the (
-ray photon (beyond 511 keV), the ``softer'' the second photon involved in the interaction can be (that is,
the lower its energy can be).
As a consequence,
the identification of the ( -ray) energy beyond which our model emission
becomes negligible, that is, the ``highest'' energy for our potentially pair creating
-ray) energy beyond which our model emission
becomes negligible, that is, the ``highest'' energy for our potentially pair creating 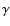 -ray photons,
strightforwadly determines the minimum energy of the ``soft'' interacting photon possibly involved in the process, which is
also the lower limit,
-ray photons,
strightforwadly determines the minimum energy of the ``soft'' interacting photon possibly involved in the process, which is
also the lower limit,
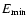 ,
of the energy range of the relevant luminosity for
the compactness evaluation,
,
of the energy range of the relevant luminosity for
the compactness evaluation,
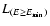 (erg/s).
For the typical parameters we have used to compute the best fit models for the BeppoSAX observations analyzed here,
the number density of high energy photons produced in our models is typically
negligible for energies above
(erg/s).
For the typical parameters we have used to compute the best fit models for the BeppoSAX observations analyzed here,
the number density of high energy photons produced in our models is typically
negligible for energies above
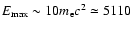 keV; thus the appropriate estimate for
keV; thus the appropriate estimate for
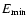 in our problem is given by the condition
in our problem is given by the condition
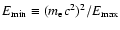 ,
which gives
,
which gives
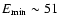 keV.
Our estimate of the relevant luminosity is therefore
keV.
Our estimate of the relevant luminosity is therefore
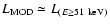 ;
for the January
2000 data fit, we have
;
for the January
2000 data fit, we have
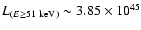 erg/s, and the corresponding value for
the individual loop compactness is
erg/s, and the corresponding value for
the individual loop compactness is
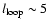 ,
which is below the limiting value
,
which is below the limiting value  cited above
(Svensson 1990), and, as a consequence, supports the consistency of our treatment, in which pair-production
effects on the spectrum have been neglected.
cited above
(Svensson 1990), and, as a consequence, supports the consistency of our treatment, in which pair-production
effects on the spectrum have been neglected.
In conclusion, all the considerations above support our model as physically consistent
even when applied to a context different
to that of a typical Seyfert 1.
Our model can provide a natural explanation of the
observed soft excess with no need for an extra component since the emission
in the soft X-ray range is intrinsic to the model itself. More than that,
the observed soft X-ray flux can be reproduced only for a value of the size of the coronal structure
which turns out to be in very good agreement with the theoretically expected scaling of the coronal
dimension in terms of the Schwarzschild radius.
Far from being a definite answer for this problem, our attempt to model the
the Seyfert-like component of the X-ray emission of AGNs with a coronal structure composed
of an ensemble of active loops
emitting radiation from the soft-X-ray to the hard band,
giving a natural explanation of
the soft excess measured,
can be considered as a step in the required direction.
Acknowledgements
This work was partly supported by the Italian Ministry for University
and Research.
- Bianchi, S.,
Matt, G., Balestra, I., Guainazzi, M., & Perola, G. C. 2004,
A&A, 422, 65 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Cappi, M., &
Matsuoka, M. 1996, in the X-Ray Imaging and Spectroscopy of Cosmic
Hot Plasmas, Proceedings of an International Symposium on X-ray
Astronomy ASCA Third Anniversary, Waseda University, Tokyo, ed. F.
Makino, & K. Mitsuda, 275
(In the text)
- Cappi, M., Matsuoka,
M., Otani, C., & Leighly, K. M. 1998, PASJ, 50, 213 [NASA ADS]
(In the text)
- Chernyakova, M.,
Neronov, A., Courvoisier, T. J.-L., et al. 2007, A&A, 465,
147 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Courvoisier, T. J.-L.
1998, A&ARv, 9, 1 [NASA ADS]
(In the text)
- Deluit, S., &
Courvoisier, T. J.-L. 2003, A&A, 399, 77 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Deluit, S.,
Stuhlinger, M., & Staubert, R. 2006, Adv.SS, 38, 1393
(In the text)
- Dickey, J. M.,
& Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef]
(In the text)
- Donato, D.,
Sambruna, R. M., & Gliozzi, M. 2005, A&A, 433, 1163 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Falcone, A. D.,
Bond, I. H., Boyle, P. J., et al. 2004, ApJ, 613, 710 [NASA ADS] [CrossRef]
(In the text)
- Fiocchi, M.,
& Grandi, P. 2004, Nucl. Phys. B, 132, 177
(In the text)
- Foschini, L.,
Ghisellini, G., Raiteri, C. M., et al. 2006, A&A, 453, 829 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Georganopoulos, M.,
Perlman, E. S., Kazanas, D., & McEnery, J. 2006, ApJ, 653,
L5 [NASA ADS] [CrossRef]
(In the text)
- Ghisellini, G.,
Celotti, A.,Fossati, G., et al. 1998, MNRAS, 301, 451 [NASA ADS] [CrossRef]
(In the text)
- Giommi, P.,
Capalbi, M., Fiocchi, M., et al. 2002, in Blazar Astrophysics with
BeppoSAX and Other Observatories, Proceedings of the international
workshop, ASI Science Data Center, ESA-ESRIN, ed. P. Giommi, E.
Massaro, & G. Palumbo, 63
(In the text)
- Grandi, P., &
Palumbo, G. G. C. 2004, Science, 306, 998 [NASA ADS] [CrossRef] (G&P)
(In the text)
- Grandi, P.,
Guainazzi, M., Mineo, T., et al. 1997, A&A, 325, L17 [NASA ADS]
(In the text)
- Grandi, P.,
Malaguti, G., & Fiocchi, M. 2006, ApJ, 642, 113 [NASA ADS] [CrossRef]
(In the text)
- Guilbert, P. W.,
Fabian, A. C., & Rees, M. J. 1983, MNRAS, 205,593
(In the text)
- Haardt, F., Fossati,
G., Grandi, P., et al. 1998, A&A, 340, 35 [NASA ADS]
(In the text)
- Impey, C. D., Malkan, M.
A., & Tapia, A. 1989, ApJ, 347, 96 [NASA ADS] [CrossRef]
(In the text)
- Jester, S.,
Röser, H.-J., Meisenheimer, K., Perley, R., & Conway, R.
2001, A&A, 373, 447 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Jester, S., Harris,
D. E., Marshall, H. L., & Meisenheimer, K. 2006, ApJ, 648,
900 [NASA ADS] [CrossRef]
(In the text)
- Kataoka, J.,
Tanihata, C., Kawai, N., et al. 2002, MNRAS, 336, 932 [NASA ADS] [CrossRef]
(In the text)
- Kriss, G. A., Davidsen, A.
F., Zheng, W., & Lee, G. 1999, ApJ, 527, 683 [NASA ADS] [CrossRef]
(In the text)
- Leach, C. M., McHardy, I.
M., & Papadakis, I. E. 1995, MNRAS, 272, 221 [NASA ADS]
(In the text)
- Liu, B. F., Mineshige,
S., & Shibata, K. 2002, ApJ, 572, L173 [NASA ADS] [CrossRef]
(In the text)
- Malizia, A.,
Bassani, L., Capalbi, M., et al. 2003, A&A, 406, 105 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Marshall, H. L., Harris, D.
E., Grimes, J. P., et al. 2001, ApJ, 549, L167 [NASA ADS] [CrossRef]
(In the text)
- Matt, G. 2001, in X-Ray
Astronomy: Stellar Endpoints, AGN, and the Diffuse X-Ray
Background, ed. N. E. White, G. Magaluti, & G. Palumbo (New
York: AIP), AIP Conf. Proc., 599, 209
(In the text)
- McHardy, I., Lawson,
A., Newsam, A., et al. 1999, MNRAS, 310, 571 [NASA ADS] [CrossRef]
(In the text)
- McHardy, I., Lawson,
A., Newsam, A., et al. 2007, MNRAS, 375, 1521 [NASA ADS] [CrossRef]
(In the text)
- Miller, K. A., &
Stone, J. M. 2000, ApJ, 534, 398 [NASA ADS] [CrossRef]
(In the text)
- Nandra, K., &
Pounds, K. A. 1994, MNRAS, 268, 405 [NASA ADS]
(In the text)
- Nandra, K., George,
I. M., Mushotzley, R. F., Turner, T. J., & Yaqoob, T. 1997,
ApJ, 477, 602 [NASA ADS] [CrossRef]
(In the text)
- Orr, A., Yaqoob, T.,
& Parmar, A. N. 1998, A&A, 337, 685 [NASA ADS]
(In the text)
- Page, K. L. Turner, M.
J. L., Done, C., et al. 2004, MNRAS, 349, 57 [NASA ADS] [CrossRef]
(In the text)
- Paltani, S.,
& Türler, M. 2005, A&A, 435, 811 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Paltani, S.,
Courvoisier, T. J.-L., & Walter, R. 1998, A&A, 340, 47 [NASA ADS]
(In the text)
- Perola, G. C.,
Matt, G., Cappi, M., et al. 2002, A&A, 389, 802 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Peterson, B.
M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef]
(In the text)
- Piro, L., Matt, G.,
& Ricci, R. 1997, A&AS, 126, 525 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Röser, H.-J.,
Meisenheimer, K., Neumann, M., Conway, R. G., & Perley, R. A.
2001, A&A, 360, 99 [NASA ADS]
(In the text)
- Sambruna, R., Urry, C.,
Megan Tavecchio, F., et al. 2001, ApJ, 549, L161 [NASA ADS] [CrossRef]
(In the text)
- Savolainen, T., Wiik, K.,
Valtaoja, E., & Tornikoski, M. 2006, A&A, 46, 71 [NASA ADS] [CrossRef]
(In the text)
- Svensson, R.
1987, MNRAS, 227, 403 [NASA ADS]
(In the text)
- Svensson, R.
1990, in NATO ASI Series, Series C-Vol.305, Physical Processes in
Hot Cosmic Plasmas, ed. W. Brinkmann, A. C. Fabian, & F.
Giovannelli (Dordrecht: Kluwer), 357
(In the text)
- Torricelli-Ciamponi, G.,
Pietrini, P., & Orr, A. 2005, A&A, 438, 55 [NASA ADS] [CrossRef] [EDP Sciences], Paper I
(In the text)
- Türler, M.,
Paltani, S., Courvoisier, T. J.-L., et al. 1999, A&AS, 134,
89 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Türler, M.,
Chernyakova, M., Courvoisier, T. J.-L., et al. 2006, A&A, 451,
L1 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Turner, M. J. L.,
Courvoisier, T., Staubert, R., Molteni, D., & Trumper, J. 1985,
SSRv, 40, 623 [NASA ADS]
(In the text)
- Turner, M. J. L.,
Williams, O. R., Courvoisier, T. J. L., et al. 1990, MNRAS, 244,
310 [NASA ADS]
(In the text)
- von Montigny, C.,
Aller, H., Aller, M., et al. 1997, ApJ, 483, 161 [NASA ADS] [CrossRef]
(In the text)
- Valtaoja, L., Valtaoja,
E., Shakhovskoy, N. M., et al. 1991, AJ, 102, 1946 [NASA ADS] [CrossRef]
(In the text)
- Walter, R., &
Fink, H. H. 1993, A&A, 274, 105 [NASA ADS]
(In the text)
- Wamsteker, W.,
Rodriguez-Pascual, P., Wills Beverley, J., et al. 1990, ApJ, 354,
446 [NASA ADS] [CrossRef]
- Zdziarski, A. A.,
Poutanen, J., & Johnson, W. N. 2000, ApJ, 542, 703 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008

![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f2up.ps}}\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f2lo.ps}}
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg37.gif)
![\begin{figure}
\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f3up.ps}}\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f3lo.ps}}
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg55.gif)
![\begin{figure}
\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f4up.ps}}\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f4lo.ps}}
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg56.gif)
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f5up.ps}}\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90]{7597f5lo.ps}}
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg57.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=2.5in]{7597f6le.ps}\hspace{0.60in}
\includegraphics[width=2.5in]{7597f6ri.ps} }\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg89.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=1.8in]{7597f7le.ps}\hspace{0.5in...
...e.ps}\hspace{0.5in}
\includegraphics[width=1.8in]{7597f7ri.ps} }
\end{figure}](/articles/aa/full/2008/08/aa7597-07/Timg91.gif)