A&A 479, 9-25 (2008)
DOI: 10.1051/0004-6361:20078522
L. Fu1,2 - E. Semboloni1,3 - H. Hoekstra4,![]() - M. Kilbinger1,3 - L. van Waerbeke5 - I. Tereno1,3 - Y. Mellier1 - C. Heymans1,5 - J. Coupon1 - K. Benabed1 - J. Benjamin5 - E. Bertin1 -
O. Doré6 - M. J. Hudson7 - O. Ilbert8,9 -
R. Maoli1,10 - C. Marmo1 - H. J. McCracken1 -
B. Ménard6
- M. Kilbinger1,3 - L. van Waerbeke5 - I. Tereno1,3 - Y. Mellier1 - C. Heymans1,5 - J. Coupon1 - K. Benabed1 - J. Benjamin5 - E. Bertin1 -
O. Doré6 - M. J. Hudson7 - O. Ilbert8,9 -
R. Maoli1,10 - C. Marmo1 - H. J. McCracken1 -
B. Ménard6
1 - Institut d'Astrophysique de Paris, UMR7095 CNRS,
Université Pierre & Marie Curie, 98 bis boulevard Arago, 75014 Paris,
France
2 - Shanghai Normal University, 100 Guilin RD, Shanghai 200234, PR China
3 - Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
4 - Department of Physics and Astronomy, University of Victoria, Victoria,
B.C. V8P 5C2, Canada
5 - University of British Columbia, Department of Physics and Astronomy, 6224
Agricultural Road, Vancouver, B.C. V6T 1Z1, Canada
6 - Canadian Institute for Theoretical Astrophysics, University of Toronto
60 St. George Street Toronto, Ontario, M5S 3H8, Canada
7 - Department of Physics and Astronomy, University of Waterloo, Waterloo ON N2L 3G1,
Canada
8 - Laboratoire d'Astrophysique de Marseille, UMR 6110 CNRS-Université de Provence, BP 8, 13376 Marseille Cedex 12, France
9 - Institute for Astronomy, 2680 Woodlawn Drive, Honolulu, HI
96822-1897, USA
10 - Department of Physics, University La Sapienza, Pl. A. Moro 2, 00185 Roma, Italy
Received 21 August 2007 / Accepted 27 November 2007
Abstract
Aims. We present an exploration of weak lensing by large-scale structure in the linear regime, using the third-year (T0003) CFHTLS Wide data release. Our results place tight constraints on the scaling of the amplitude of the matter power spectrum ![]() with the matter density
with the matter density
![]() .
.
Methods. Spanning 57 square degrees to
![]() over three independent fields, the unprecedented contiguous area of this survey permits high signal-to-noise measurements of two-point shear statistics from 1 arcmin to 4 degrees. Understanding systematic errors in our analysis is vital in interpreting the results. We therefore demonstrate the percent-level accuracy of our method using STEP simulations, an E/B-mode decomposition of the data, and the star-galaxy cross correlation function. We also present a thorough analysis of the galaxy redshift distribution using redshift data from the CFHTLS T0003 Deep fields that probe the same spatial regions as the Wide fields.
over three independent fields, the unprecedented contiguous area of this survey permits high signal-to-noise measurements of two-point shear statistics from 1 arcmin to 4 degrees. Understanding systematic errors in our analysis is vital in interpreting the results. We therefore demonstrate the percent-level accuracy of our method using STEP simulations, an E/B-mode decomposition of the data, and the star-galaxy cross correlation function. We also present a thorough analysis of the galaxy redshift distribution using redshift data from the CFHTLS T0003 Deep fields that probe the same spatial regions as the Wide fields.
Results. We find
![]()
![]() 0.043 using the aperture-mass statistic for the full range of angular scales for an assumed flat cosmology, in excellent agreement with WMAP3 constraints. The largest physical scale probed by our analysis is 85 Mpc, assuming a mean redshift of lenses of 0.5 and a
0.043 using the aperture-mass statistic for the full range of angular scales for an assumed flat cosmology, in excellent agreement with WMAP3 constraints. The largest physical scale probed by our analysis is 85 Mpc, assuming a mean redshift of lenses of 0.5 and a ![]() CDM cosmology. This allows for the first time to constrain cosmology using only cosmic shear measurements in the linear regime. Using only angular scales
CDM cosmology. This allows for the first time to constrain cosmology using only cosmic shear measurements in the linear regime. Using only angular scales
![]() arcmin, we find
arcmin, we find
![]()
![]() 0.084, which agree with the results from our full analysis. Combining our results with data from WMAP3, we find
0.084, which agree with the results from our full analysis. Combining our results with data from WMAP3, we find
![]()
![]() 0.019 and
0.019 and
![]()
![]() 0.029.
0.029.
Key words: gravitational lensing - cosmological parameters - cosmology: observations - large-scale structure of Universe
A primary scientific goal of the Canada-France-Hawaii Telescope Legacy
Survey (CFHTLS![]() )
is the exploration of the properties of the dark matter power spectrum
and its evolution with redshift using weak gravitational lensing. The
weak lensing signal manifests itself in a modification of the apparent
galaxy ellipticity induced by the cumulative weak gravitational shear
effects of large-scale structure (hereafter cosmic shear). The
statistical properties of the distortion field, as a function of
angular scale, reflect the properties of the Universe and of the dark
matter power spectrum projected along the line of sight (see
reviews from Munshi et al. 2006; Refregier 2003; Van Waerbeke & Mellier 2003; Bartelmann & Schneider 2001).
)
is the exploration of the properties of the dark matter power spectrum
and its evolution with redshift using weak gravitational lensing. The
weak lensing signal manifests itself in a modification of the apparent
galaxy ellipticity induced by the cumulative weak gravitational shear
effects of large-scale structure (hereafter cosmic shear). The
statistical properties of the distortion field, as a function of
angular scale, reflect the properties of the Universe and of the dark
matter power spectrum projected along the line of sight (see
reviews from Munshi et al. 2006; Refregier 2003; Van Waerbeke & Mellier 2003; Bartelmann & Schneider 2001).
The CFHTLS Deep and Wide surveys have been designed to maximise the scientific reward of the CFHT M EGAP RIME/M EGAC AM instrument and in particular to produce a high-quality cosmic shear survey. The Deep and Wide surveys provide image quality, depth and survey size optimised for weak lensing studies as well as ( u*,g',r',i',z') colours over the whole field to get photometric redshifts (Ilbert et al. 2006). Both depth and field of view have been increased by roughly one order of magnitude as compared to the first-generation of weak lensing surveys, like the Red Cluster Sequence (RCS, Hoekstra et al. 2002a) and VIRMOS-D ESCART (Van Waerbeke et al. 2005,2001,2002,2000) surveys that were carried out at CFHT.
The first CFHTLS cosmic shear results were analysed by Semboloni et al. (2006)
and Hoekstra et al. (2006) who demonstrated that M EGAP RIME/M EGAC AM
provides excellent quality data for weak lensing studies. Despite the
optical distortion of the MegaPrime Wide field corrector, after
correction, no significant B-modes, nor any obvious critical
systematic residuals that may affect the weak lensing signal at the
percent level, were found. The shear statistics as a function of
angular scale were in good agreement with the theoretical predictions
of the most popular cosmological models, and Semboloni et al. (2006) showed
that the amplitude of shear signal convincingly increased with depth,
as expected from its sensitivity to redshift. These early CFHTLS
cosmic shear data were used by Semboloni et al. (2006) and Hoekstra et al. (2006) to
derive constraints on
![]() -
-![]() and by Schimd et al. (2007) to explore some physical models of dark energy. The results
were consistent with the past CFHT weak lensing surveys but their
precision was still limited by the small sky coverage of the early
CFHTLS data and by the poor knowledge of the redshift distribution of
sources. Benjamin et al. (2007, hereafter B07) overcame these limitations
by using the early CFHTLS Wide data together with the Red Cluster
Sequence survey, VIRMOS-D ESCART and the Garching-Bonn Deep
Survey (GaBoDS, Hetterscheidt et al. 2007) weak lensing surveys, and
the photometric redshifts of the joint CFHTLS-VIMOS VLT Deep Survey
(VVDS) analysis (Ilbert et al. 2006). They then derived much more
reliable and accurate
and by Schimd et al. (2007) to explore some physical models of dark energy. The results
were consistent with the past CFHT weak lensing surveys but their
precision was still limited by the small sky coverage of the early
CFHTLS data and by the poor knowledge of the redshift distribution of
sources. Benjamin et al. (2007, hereafter B07) overcame these limitations
by using the early CFHTLS Wide data together with the Red Cluster
Sequence survey, VIRMOS-D ESCART and the Garching-Bonn Deep
Survey (GaBoDS, Hetterscheidt et al. 2007) weak lensing surveys, and
the photometric redshifts of the joint CFHTLS-VIMOS VLT Deep Survey
(VVDS) analysis (Ilbert et al. 2006). They then derived much more
reliable and accurate
![]() -
-![]() constraint, lowering
the upper limits on
constraint, lowering
the upper limits on ![]() to be fully consistent with Spergel et al. (2007).
to be fully consistent with Spergel et al. (2007).
The early CFHTLS weak lensing analysis, the joint B07 and the recent
Cosmic Evolution Survey studies (COSMOS, Massey et al. 2007b) explore
only small scale lensing. Their cosmological interpretation is
therefore sensitive to the non-linear evolution of the dark matter
power spectrum and several other physical and systematic effects that
primarily contaminate the lensing signal at small scales. The most
serious are the high contribution of non-Gaussianity to the error
budget (Semboloni et al. 2007) and the signal contamination on scales below
![]() 20 arcmin by the shear-shape correlation
(Heymans et al. 2006b; Hirata & Seljak 2004) and by the intrinsic ellipticity
correlation (Heymans & Heavens 2003; King & Schneider 2002).
20 arcmin by the shear-shape correlation
(Heymans et al. 2006b; Hirata & Seljak 2004) and by the intrinsic ellipticity
correlation (Heymans & Heavens 2003; King & Schneider 2002).
The CFHTLS Wide survey has been designed to probe angular scales up to 8 degrees (the largest scale explored by all Wide fields). The exploration of angular scales beyond one degree is technically challenging due to the decreasing amplitude of the lensing signal. Systematics in this unexplored territory are also still poorly understood or unknown. However, they depend on the large-scale accuracy and stability of field-to-field astrometric, photometric and Point Spread Function (PSF) calibrations, and thus there is a need for data homogeneity when analysing galaxy pairs separated by more than the one-degree M EGAC AM field of view.
The third release CFHTLS T0003 circumvents these issues: the T0003 Wide data explore angular scales up to 8 degrees, that is more than one order of magnitude larger than the largest non-linear angular scales. It covers a total field of view slightly smaller than B07, but with the great advantage of forming a single homogeneous sample and of being easily calibrated using the CFHTLS-VVDS photometric redshifts of Ilbert et al. (2006) that are also derived from the T0003 release.
This work presents a weak lensing analysis of the CFHTLS T0003
i'-band Wide survey. It extends the previous analysis of the CFHTLS
Wide to angular scales up to 230 arcmin (about 85 Mpc, assuming
![]() and h=0.72, a flat Universe and a mean lens
redshift of 0.5). Its sky coverage is 57 square degrees, that is
nearly two times larger than early CFHTLS data and about 35% of the
final CFHTLS wide sky coverage. Furthermore, it includes a new
uncorrelated field, W2, providing a better estimate of the
field-to-field variance. The shear measurement pipeline is calibrated
and its performance is evaluated using simulated images produced by
the Shear TEsting Programme (STEP, Massey et al. 2007b; Heymans et al. 2006a). The signal
error budget includes non-Gaussian corrections to the cosmic variance,
using the fitting formulae proposed by Semboloni et al. (2007). The effective
redshift distribution of sources is determined from the CFHTLS T0003
Deep survey and calibrated using the VVDS (Ilbert et al. 2006).
and h=0.72, a flat Universe and a mean lens
redshift of 0.5). Its sky coverage is 57 square degrees, that is
nearly two times larger than early CFHTLS data and about 35% of the
final CFHTLS wide sky coverage. Furthermore, it includes a new
uncorrelated field, W2, providing a better estimate of the
field-to-field variance. The shear measurement pipeline is calibrated
and its performance is evaluated using simulated images produced by
the Shear TEsting Programme (STEP, Massey et al. 2007b; Heymans et al. 2006a). The signal
error budget includes non-Gaussian corrections to the cosmic variance,
using the fitting formulae proposed by Semboloni et al. (2007). The effective
redshift distribution of sources is determined from the CFHTLS T0003
Deep survey and calibrated using the VVDS (Ilbert et al. 2006).
The paper is organized as follows: in Sect. 2 we give a description of the data set, including the image stacking procedure used in this work. In Sect. 3 we describe the production of weak lensing catalogues. After a brief review of the theoretical background, we present the two-point shear results, together with the sky curvature correction needed at large angular scales in Sect. 4. The redshift distribution is discussed in Sect. 5. In Sect. 6 we show the cosmological parameter estimates, discuss the constraints from linear scales and compare to other data sets. In Sect. 7 we discuss the contamination to our weak lensing measurement from shear-shape correlations. Finally, we summarise and give our conclusions in Sect. 8.
The Canada-France-Hawaii Telescope Legacy Survey (CFHTLS) is a 5-year
project set up jointly by the Canadian and French agencies. The Deep
and Wide observations are all carried out in service mode by the CFHT
operation staff using the M EGAP RIME/M EGAC AM instrument mounted
at the prime focus of the telescope. The M EGAC AM camera is
composed of an array of 9 ![]() 4 CCDs (2048
4 CCDs (2048 ![]() 4612 pixels
each). The pixel size at M EGAP RIME focus is
4612 pixels
each). The pixel size at M EGAP RIME focus is
![]() ,
so
that M EGAC AM comprises a compact field of view of
,
so
that M EGAC AM comprises a compact field of view of ![]()
![]()
![]() (Boulade et al. 2003).
(Boulade et al. 2003).
Details on the Deep and Wide fields have been introduced in Semboloni et al. (2006) and Hoekstra et al. (2006), respectively. After completion the W1, W2
and W3 Wide fields will be composed of 8 ![]() 9, 7
9, 7 ![]() 7,
7
7,
7 ![]() 7 different M EGAC AM pointing positions,
respectively
7 different M EGAC AM pointing positions,
respectively![]() . Each centre position is separated by its
nearest neighbour fields by about one degree. For each field, a
sequence of 7
. Each centre position is separated by its
nearest neighbour fields by about one degree. For each field, a
sequence of 7 ![]() 620-s i'-band exposures, separated by a
small dither, is taken. The dithering pattern is encompassed within a
3'
620-s i'-band exposures, separated by a
small dither, is taken. The dithering pattern is encompassed within a
3' ![]() 4' box. Hence, neighboring pointings overlap in right
ascension by a minimum of two and a maximum of three arc minutes,
whereas the overlap in declination is bounded between three and four
arc minutes. The overlapping regions are used for the
pointing-to-pointing internal astrometric calibration and
flux-rescaling processes.
4' box. Hence, neighboring pointings overlap in right
ascension by a minimum of two and a maximum of three arc minutes,
whereas the overlap in declination is bounded between three and four
arc minutes. The overlapping regions are used for the
pointing-to-pointing internal astrometric calibration and
flux-rescaling processes.
The CFHTLS Wide T0003 release is produced from all M EGAC AM
CFHTLS images obtained between June 1st, 2003 and September 5th, 2005,
that passed both the CFHT and initial Terapix validation
processes. Each individual raw image has been pre-processed
(bias/dark/fringe subtractions and flatfielding), CCD-to-CCD
flux-rescaled and photometrically calibrated at CFHT using the Elixir
pipeline (Magnier & Cuillandre 2004). The Elixir products are archived at CADC
and then transferred to the Terapix data centre for further higher
level processing and the production of the CFHTLS
releases![]() .
.
In this paper we use the i'-band pointings from the T0003 release, but we introduce a more severe image selection in order to optimise and homogenise the depth and the image quality over the whole field used for weak lensing studies. Each i'-band image must fulfil the following second-level criteria before entering into the calibration and stacking processes:
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{8522f1a.ps}\vspace*{3mm}
...
...1b.ps}\vspace*{3mm}
\includegraphics[width=8.1cm,clip]{8522f1c.ps} \end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg41.gif) |
Figure 1: Sky coverage of the W1, W2 and W3 fields used in this work. Each CCD is drawn as a small rectangle and each M EGAC AM field is a squared mosaic of 36 rectangles. The small white holes are regions with missing data. |
| Open with DEXTER | |
The input stack images used in this work are produced using the same
Terapix procedures and software tools as the T0003 CFHTLS release.
Terapix first generates individual weight map images and individual
primary catalogues. It then proceeds to astrometric calibration, M EGAC AM field-to-field photometric rescaling, image re-centering,
image resampling, image warping and, finally, image stacking. Both a
co-added image and its weight map are produced, as well as an ASCII DS9 readable mask file and a series of quality control meta-data. A
description of these processing steps and software tools can be found
on the Terapix web site![]() as
well as on the Terapix release document (Mellier et al. 2005). All
T0003 configuration files, parameter lists and processing command
lines are archived at CADC. Only i'-band images are considered in
this work since other filters cover a much smaller field of view, with
a large scatter in sky coverage and depth between each filter.
as
well as on the Terapix release document (Mellier et al. 2005). All
T0003 configuration files, parameter lists and processing command
lines are archived at CADC. Only i'-band images are considered in
this work since other filters cover a much smaller field of view, with
a large scatter in sky coverage and depth between each filter.
All fields are astrometrically calibrated and flux-rescaled using
SCAMP![]() (Bertin 2006,2005a). The astrometric reference catalogue is
USNO-B1, which is sufficiently accurate for the external astrometric
precision needed for this work. Internal astrometry and M EGAC AM
pointing-to-pointing flux rescaling is done by identifying common
objects located in each overlap area. The image re-centering,
resampling and stacking are produced by SWarp
(Bertin 2006,2005a). The astrometric reference catalogue is
USNO-B1, which is sufficiently accurate for the external astrometric
precision needed for this work. Internal astrometry and M EGAC AM
pointing-to-pointing flux rescaling is done by identifying common
objects located in each overlap area. The image re-centering,
resampling and stacking are produced by SWarp![]() (Bertin 2005b), using the same
configuration and image processing parameters as those discussed by
McCracken et al. (2003). All stacked images have a pixel size of
(Bertin 2005b), using the same
configuration and image processing parameters as those discussed by
McCracken et al. (2003). All stacked images have a pixel size of
![]() .
.
The astrometric calibration was performed for each pointing
individually. For each pointing, only exposures located inside a
circle of radius of 1.5 degrees were selected. This circle encompasses
all images at the centre field position together with all exposures
located around, at the 8 nearest neighbour centre positions. We
experienced that selecting images located beyond this radius did not
improve the accuracy and stability of the astrometric solution, and
sometimes would have even degraded it. The 8 nearest neighbour fields
provide enough common stars in overlap regions to stabilise the
solutions at the boundary of each field. The internal rms error
estimates of the astrometric calibration derived from the common
objects of nearest neighbour fields is
![]()
![]()
![]() for both M EGAC AM directions, where the uncertainty denotes the
mean field-to-field scatter. The external rms error is totally
dominated by the USNO-B1 internal error, which is
for both M EGAC AM directions, where the uncertainty denotes the
mean field-to-field scatter. The external rms error is totally
dominated by the USNO-B1 internal error, which is
![]() in
both directions.
in
both directions.
In contrast, each stack does not use nearest neighbour images, but
only composes together a sequence of exposures having a small dither
with respect to a centre field. Each stack is produced by SWarp,
using the weighted median value of each pixel and a Lanczos3
interpolation kernel. All output images have 19354 ![]() 19354 pixels
of
19354 pixels
of
![]() ,
with North-East orientation along the X and Y pixel coordinates. For all images we use a tangent projection and the
Equatorial J2000.0 astrometric coordinate system.
,
with North-East orientation along the X and Y pixel coordinates. For all images we use a tangent projection and the
Equatorial J2000.0 astrometric coordinate system.
The reference photometric zero-point has been derived by CFHT using
standard Landoldt calibration fields (Landoldt 1992), but all
catalogues produced prior to weak lensing analysis have a default
zero point magnitude set to 30.0. The magnitude system is instrumental
AB. An inspection of stellar colour-colour diagrams of each field
observed in 5 bands shows that the field-to-field scatter in the
overlapping regions is 0.03 mag. Comparison of SDSS and CFHTLS common
stars shows that the i'-band photometry agrees within 0.01-0.02 mag rms![]() . However, only 10 W3 and 2 W1 fields have common objects with SDSS, so similar external
quality assessments cannot be done for all Wide pointings.
. However, only 10 W3 and 2 W1 fields have common objects with SDSS, so similar external
quality assessments cannot be done for all Wide pointings.
The mask files produced at image processing consist on a set of polygons defined for each pointing in WCS coordinates. They mask the periphery of each M EGAC AM field of view and all halos and saturated spikes produced by bright stars. In order to avoid contamination by halos or diffusion from very luminous objects, all bright stars located up to a radius of 45 arcmin from the centre position are automatically masked. The size of polygons is scaled to their apparent magnitude provided in the USNO-B1 catalogue.
The masks are then tuned by adding or modifying polygons from a visual inspection of each stacked image. This step is necessary to clean all images from non-stellar contamination or stellar defects that were missed by the automatic masking process. This includes big halos produced by extremely bright stars, nearby galaxies or any features that may produce a diffuse light component with sufficiently steep gradient to contaminate the second moments of a galaxy's surface brightness profile which is used to derive its ellipticity. Regions with low signal-to-noise ratio are also masked. In particular, the imprints of gaps between CCDs as well as the boundary of each field are discarded and masked systematically. They are revealed by low-noise strips with a typical rectangular shape that draws the border of each detector. Finally, meteorite, asteroid and aeroplane tracks that may still remain in the stacks are masked as well. The size of each polygon is generally significantly larger than the visual size of the defect it masks. Using this conservative masking process, the final effective sky coverage of the 57 selected Wide fields drops to 34.2 deg2, roughly 60% of the total field.
Our shear measurement pipeline was optimised and calibrated using the STEP1 and STEP2 simulations from Heymans et al. (2006a) and Massey et al. (2007b). See Appendix A for a description of both our pipeline and the STEP simulations. Table A.1 lists the optimised parameter values of our pipeline.
The lensing catalogue is generated by the IMCAT software
(Kaiser et al. 1995). The size of each object is defined by the aperture
radius parameter ![]() given by the IMCAT peak finding
algorithm. The significance detection threshold, as defined by the
IMCAT parameter
given by the IMCAT peak finding
algorithm. The significance detection threshold, as defined by the
IMCAT parameter ![]() ,
is set to
,
is set to ![]() (i.e. above the
rms noise). This value was set according to the STEP tests in order to
maximise the number of objects detected while still keeping the bias
on the shear components negligible. The catalogue is then filtered to
remove objects with radius smaller than the seeing or larger than 6.75 pixels (about 1.3 arcsec). Pairs with angular separation smaller
than 10 pixels (
(i.e. above the
rms noise). This value was set according to the STEP tests in order to
maximise the number of objects detected while still keeping the bias
on the shear components negligible. The catalogue is then filtered to
remove objects with radius smaller than the seeing or larger than 6.75 pixels (about 1.3 arcsec). Pairs with angular separation smaller
than 10 pixels (
![]() )
are also discarded in order to avoid
contamination from overlapping isophotes.
)
are also discarded in order to avoid
contamination from overlapping isophotes.
The magnitude of each object is derived by computing its flux within
an aperture radius of
![]() .
Only objects with IMCAT
magnitude
.
Only objects with IMCAT
magnitude
![]() are kept into the final
analysis catalogue. Beyond this limit, the sample completeness drops
significantly below 50%, most objects are too noisy and their shapes
are no longer reliable for the precision needed for weak lensing
studies. The final catalogue based on the T0003 release of CFHTLS W1,
W2 and W3 fields contains roughly two million galaxies. Due to the
different weighting applied during the sample selection, the effective
number of galaxies used for the weak lensing analysis is 1.7 million,
spread over the effective area of 34.2 deg2. It corresponds to a
galaxy number density of 13.3 gal/arcmin2. The shapes of these
galaxies are quantified by measuring their ellipticities.
are kept into the final
analysis catalogue. Beyond this limit, the sample completeness drops
significantly below 50%, most objects are too noisy and their shapes
are no longer reliable for the precision needed for weak lensing
studies. The final catalogue based on the T0003 release of CFHTLS W1,
W2 and W3 fields contains roughly two million galaxies. Due to the
different weighting applied during the sample selection, the effective
number of galaxies used for the weak lensing analysis is 1.7 million,
spread over the effective area of 34.2 deg2. It corresponds to a
galaxy number density of 13.3 gal/arcmin2. The shapes of these
galaxies are quantified by measuring their ellipticities.
The ellipticities of galaxies are corrected from the PSF produced by telescope, detector, optical and atmospheric effects, using the Kaiser, Squires and Broadhurst method (Kaiser et al. 1995; Luppino & Kaiser 1997; Hoekstra et al. 1998), hereafter KSB+. Our implementation of KSB+ is based on the one used in Heymans et al. 2006a; Van Waerbeke et al. 2002,2001,2005,2000. We calibrated it and modified its input parameters after a new series of optimisations made with the STEP simulations. The results are presented in Appendix A. The version used in this work recovers shear with an underestimation of only 1% to 3% on the simulated images.
The PSF is measured at the stellar positions. After identifying the
stars in the images and assuming the PSF changes smoothly across the
field, the KSB-quantities known at the stellar positions can be
estimated at the galaxies positions by using a polynomial fit. The
typical pattern of the PSF anisotropy across one ![]() field shows
a significant variation across the whole camera (Fig. 2)
which suggests the need to perform the fit in each CCD
separately. Each CCD covers 7
field shows
a significant variation across the whole camera (Fig. 2)
which suggests the need to perform the fit in each CCD
separately. Each CCD covers 7 ![]()
![]() and
contains an average of 43 stars, which allows an accurate mapping of
the PSF with a second order polynomial function.
and
contains an average of 43 stars, which allows an accurate mapping of
the PSF with a second order polynomial function.
A weight, w, is assigned to the ellipticity components of each
galaxy and used in the shear measurement (see Eq. (10)). We use
the Hoekstra et al. (2002b) weighting scheme
The shape of the weighting as function of the magnitude is shown in Fig. 3. It decreases for fainter magnitudes since the error on the ellipticity increases when the signal-to-noise ratio decreases.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{8522f2.ps}\end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg58.gif) |
Figure 2:
The pattern of the PSF anisotropy in an example pointing
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=6cm,width=6.5cm,clip]{8522f3.ps}\end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg59.gif) |
Figure 3: The average galaxy weight (with arbitrary normalisation) as a function of i'AB in the range of [21.5; 24.5]. |
| Open with DEXTER | |
The cosmic shear power spectrum is identical to the lensing
convergence power spectrum, ![]() ,
which is a projection of the
dark matter power spectrum,
,
which is a projection of the
dark matter power spectrum,
![]() ,
along the line of sight
(see for example Bartelmann & Schneider 2001):
,
along the line of sight
(see for example Bartelmann & Schneider 2001):
The convergence power spectrum can be derived from the two-point shear
correlation functions. In particular, the ![]() correlation
functions relate to the power spectrum according to
correlation
functions relate to the power spectrum according to
Other two-point functions of the shear field may be derived from
![]() ,
such as the top-hat filtered variance of the shear and
the variance of the aperture-mass, in circular apertures
(Schneider et al. 2002b). Respectively,
,
such as the top-hat filtered variance of the shear and
the variance of the aperture-mass, in circular apertures
(Schneider et al. 2002b). Respectively,
All second-order statistics are different filtered versions of the convergence power spectrum. Therefore they probe different properties of the same power spectrum.
The cosmological shear field is (to first order) curl-free and is
called an E-type field. It is useful to decompose the observed shear
signal into E (non-rotational) and B (rotational) components. A
detection of non-zero B-modes indicates a non-gravitational
contribution to the shear field, which reveals a likely systematic
contamination to the lensing signal. Crittenden et al. (2002) and Pen et al. (2002) derived an analogous decomposition for the shear
correlations, which is also used in this work:
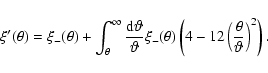 |
(9) |
The shear correlations are computed as follows:
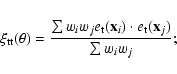
We correlate galaxies which are up to more than seven degrees apart. At such large angles the curvature of the sky is no longer negligible. To avoid a potential bias due to projections we calculate distances and angles in spherical co-ordinates as follows.
The distance d between two objects at right ascension and
declination
![]() ,
computed along the
great-circle connecting the 2 objects is given by
,
computed along the
great-circle connecting the 2 objects is given by
We compared the shear statistics computed using spherical
co-ordinates and using the following simple projection: Cartesian
co-ordinates (X, Y) of a galaxy with right ascension ![]() and
declination
and
declination ![]() are defined by
are defined by
![]() and
and
![]() ,
where
,
where
![]() is the declination of the field
centre. The relative error is on the order of a couple of percent on
average. On larger scales, where the shear signal is small, this
relative error can be much higher. Therefore, throughout this paper we
take the sky curvature into account by calculating the shear
statistics in spherical co-ordinates.
is the declination of the field
centre. The relative error is on the order of a couple of percent on
average. On larger scales, where the shear signal is small, this
relative error can be much higher. Therefore, throughout this paper we
take the sky curvature into account by calculating the shear
statistics in spherical co-ordinates.
![\begin{figure}
\par\hspace*{0.5mm}\includegraphics[height=7.3cm,width=6.4cm,angl...
...cludegraphics[height=7.35cm,width=6.4cm,angle=-90,clip]{8522f4c.ps} \end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg99.gif) |
Figure 4:
Two-point statistics from the combined 57 pointings. The
error bars of the E-mode include statistical noise added in
quadrature to the non-Gaussian cosmic variance. Only
statistical uncertainty contributes to the error budget for the
B-mode. Red filled points show the E-mode, black open points
the B-mode. The enlargements in each panel show the signal in
the angular range
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{8522f5.ps}\end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg100.gif) |
Figure 5:
The top-hat E-mode shear signals of W1 up to
|
| Open with DEXTER | |
The shear correlation functions ![]() are computed in narrow bins.
We use angular separations in the range between a conservative lower
limit of 3 arcsec and a maximum separation
are computed in narrow bins.
We use angular separations in the range between a conservative lower
limit of 3 arcsec and a maximum separation
![]() where the number of pairs per bin becomes very small. For each field,
the number of pairs per bin shows a similar ``top-hat'' behavior: a
very steep increase from
where the number of pairs per bin becomes very small. For each field,
the number of pairs per bin shows a similar ``top-hat'' behavior: a
very steep increase from
![]() followed by a roughly constant
value up to a
followed by a roughly constant
value up to a
![]() where it starts a very steep
decrease to zero. This separation
where it starts a very steep
decrease to zero. This separation
![]() is
is
![]() for W1,
for W1,
![]() for W2, and
for W2, and
![]() for W3.
for W3.
From the two-point shear correlation functions we calculate the shear
top-hat variance and the aperture-mass dispersion up to a radius of
![]() which is half of the largest separation
which is half of the largest separation
![]() ,
according to Eqs. (4) and (5).
,
according to Eqs. (4) and (5).
The missing information for
![]() and
and
![]() on scales larger than
on scales larger than
![]() is accounted for by adding theoretical predictions
of these off-sets to the data using a fiducial cosmological model.
Alternatively, we may set the B-modes of the shear correlation
function and top-hat variance to zero on the angular scales where we
measure zero aperture-mass dispersion B-modes. We checked that both
methods produce very similar and small off-set values and thus this
procedure does not bias the cosmological interpretation towards the
fiducial model used. Furthermore, our cosmological estimates are made
using the aperture-mass dispersion and are free of this small
arbitrariness.
is accounted for by adding theoretical predictions
of these off-sets to the data using a fiducial cosmological model.
Alternatively, we may set the B-modes of the shear correlation
function and top-hat variance to zero on the angular scales where we
measure zero aperture-mass dispersion B-modes. We checked that both
methods produce very similar and small off-set values and thus this
procedure does not bias the cosmological interpretation towards the
fiducial model used. Furthermore, our cosmological estimates are made
using the aperture-mass dispersion and are free of this small
arbitrariness.
The three statistics are plotted in Fig. 4 and the corresponding values and errors are provided in Tables B.1, B.2 in Appendix B. It is worth noting that this is the first time that a cosmic shear signal has been measured down to i'AB=24.5, beyond scales of one degree. Notice also that the independent measurements of the shear statistics made in the three individual fields W1, W2, W3 are statistically consistent at all scales. This is illustrated by Fig. 5, where the three measurements of top-hat dispersion are shown.
In Fig. 4 the error bars of the E-modes include statistical noise and cosmic variance calibrated for non-Gaussianity, while the error for the B-modes only includes statistical uncertainty. We find a clear E-mode signal and a B-mode which is consistent with zero throughout the explored range of angular scales, except between 50 and 130 arcmin where there is a small but significant feature in all three second-order functions. This bump of the B-mode peaks at about 60-80 arcmin which are the side and diagonal sizes of a Megacam field. We therefore guess it is due to a correlation in PSF residuals on the scale of the camera. In Sect. 6 we show that our cosmological results are not biased by this level of residual systematics on this range of angular scales.
On very large scales (120'-230') we find a very small B-mode,
much smaller than both the E-mode amplitude and cosmic variance, but
which is not always within ![]() of a zero detection. Notice
that the errors on the B-mode shown in Fig. 4 are
theoretical (statistical) and not estimated from the data, which
would include systematics (for example error contributions may arise
from the incomplete PSF correction). Moreover, the signal-to-noise
with the present CFHTLS Wide data is so high, even for B-modes, that
subtle effects may dominate the very small Poissonian error,
particularly on large scales where there are a significant number of
galaxy pairs.
of a zero detection. Notice
that the errors on the B-mode shown in Fig. 4 are
theoretical (statistical) and not estimated from the data, which
would include systematics (for example error contributions may arise
from the incomplete PSF correction). Moreover, the signal-to-noise
with the present CFHTLS Wide data is so high, even for B-modes, that
subtle effects may dominate the very small Poissonian error,
particularly on large scales where there are a significant number of
galaxy pairs.
The field-to-field variation of the B-modes is a possible way to
assess these effects on the error buget. We tried to measure this
by splitting the 3 Wide fields into 11 blocks of 2 ![]() 2 deg2 each, which allows to calculate the B-modes on scales up to
60 arcmin in each block. We obtained B-modes with amplitude very
similar to Fig. 4 but the field-to-field scatter is
larger than the plotted error bars and reaches a factor of 2 at 60'. This is an interesting indication that we are likely underestimating the error on B-modes, even though it is not a
precise measurement due to the small number of independant fields.
A thorough analysis of this noise contribution needs many more
field and is left to a future analysis of the CFHTLS four year data.
2 deg2 each, which allows to calculate the B-modes on scales up to
60 arcmin in each block. We obtained B-modes with amplitude very
similar to Fig. 4 but the field-to-field scatter is
larger than the plotted error bars and reaches a factor of 2 at 60'. This is an interesting indication that we are likely underestimating the error on B-modes, even though it is not a
precise measurement due to the small number of independant fields.
A thorough analysis of this noise contribution needs many more
field and is left to a future analysis of the CFHTLS four year data.
We cross-checked the shear measurement by using an independent analysis on the same data sets. This analysis was done with another version of KSB+ that has been tested with the STEP1+2 simulations (``HH'' in Massey et al. 2007b; Heymans et al. 2006a). Hereafter, we refer to our analysis as ``Pipeline I'' and to the ``HH'' results as ``Pipeline II''.
The left panel of Fig. 6 shows the shear estimated for each galaxy by each of the pipelines. The results are in good agreement for ellipticity values per component between -0.6 and 0.6. For ellipticities outside this range the dispersion between the pipelines is larger and a trend for an underestimation of the shear from Pipeline I with respect to Pipeline II can be seen. Note however that the pipelines are not optimised for large ellipticities, since the STEP simulation galaxies have ellipticities that are smaller than 0.1.
![\begin{figure}
\par\includegraphics[width=7.5cm,height=7.5cm]{8522f6a.ps}\includegraphics[width=8.cm,height=7.5cm, bb = 80 50 370 300]{8522f6b.ps}\end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg108.gif) |
Figure 6: Left panel: binned scatter plot of the shear estimates (one component) using the two pipelines. Dark colours show highest density of points. The bin size is 0.05 in e1. Right panel: the aperture-mass variance from W1, W2 and W3 measured with the two pipelines up to scale 210 arcmin, using only objects which are detected in both pipelines. For clarity of the comparison, the error bars only show the statistical errors, but the cosmological analysis of this work includes the whole error budget (see text). These error bars are larger than the one of Fig. 4 because number of common objects are smaller the full catalogue. Note that the large negative B-mode on small scales is not present in the full catalogue, see Fig. 4. |
| Open with DEXTER | |
We then compare the two-point functions using the aperture-mass
variance. We choose this statistic because angular scales are less
correlated than for the top-hat dispersion. Moreover, it does not have
any ambiguity related to a non-local E/B decomposition. The values of
![]() are calculated from the two pipelines using only
objects detected by both pipelines. Because the pipelines have
different selection criteria the common objects are only two-thirds of
the whole sample. Each object is assigned a weight which is the
product of its weights in each of the two pipelines. The largest
radius explored in the comparison is 210 arcmin. As can be seen
in Fig. 6 (right panel), the E- and B-modes of the two
pipelines are remarkably similar. The differences are within the
are calculated from the two pipelines using only
objects detected by both pipelines. Because the pipelines have
different selection criteria the common objects are only two-thirds of
the whole sample. Each object is assigned a weight which is the
product of its weights in each of the two pipelines. The largest
radius explored in the comparison is 210 arcmin. As can be seen
in Fig. 6 (right panel), the E- and B-modes of the two
pipelines are remarkably similar. The differences are within the
![]() errors on all angular scales. The small B-mode bump
appears in both results at 60-80 arcmin, as in
Fig. 4. It also drops to nearly zero at all scales beyond
120 arcmin for both pipelines. The bias between the two pipelines at
large ellipticities, seen in the left panel of Fig. 6 is
not visible here. The reason is that the large ellipticity galaxies
represent less than 4% of the sample. Furthermore these galaxies are
typically downweighted; large ellipticities are difficult to measure,
resulting of a larger error on the ellipticity measurement, and the
shear polarisability increases with ellipticities. They have
consequently a lower weight according to Eq. (1).
errors on all angular scales. The small B-mode bump
appears in both results at 60-80 arcmin, as in
Fig. 4. It also drops to nearly zero at all scales beyond
120 arcmin for both pipelines. The bias between the two pipelines at
large ellipticities, seen in the left panel of Fig. 6 is
not visible here. The reason is that the large ellipticity galaxies
represent less than 4% of the sample. Furthermore these galaxies are
typically downweighted; large ellipticities are difficult to measure,
resulting of a larger error on the ellipticity measurement, and the
shear polarisability increases with ellipticities. They have
consequently a lower weight according to Eq. (1).
These results are not expected to be identical to the aperture
mass dispersion computed with the whole sample, shown in
Fig. 4, because the number of objects in the two samples is
different. They are however similar, except for the large B-modes on
scales smaller than
![]() ,
which are detected by both pipelines
on the smaller sample. Since both analyses use KSB, these B-modes may
be due to similar residuals of the PSF correction, but we cannot rule
out an intrinsic B-mode contribution. Whatever the origin we only use
angular scales larger than
,
which are detected by both pipelines
on the smaller sample. Since both analyses use KSB, these B-modes may
be due to similar residuals of the PSF correction, but we cannot rule
out an intrinsic B-mode contribution. Whatever the origin we only use
angular scales larger than
![]() for the cosmological parameter
constraints (see also Sect. 4.1) in order to avoid any
contamination.
for the cosmological parameter
constraints (see also Sect. 4.1) in order to avoid any
contamination.
The most common and problematic source of contamination of the lensing
signal is the imperfect PSF anisotropy correction. The angular
dependence of any PSF systematic residual may be checked by computing
the correlation between the corrected galaxy and uncorrected stellar
ellipticities. Following Bacon et al. (2003) we normalise this
quantity by the star-star uncorrected ellipticity correlation in order
to assess its amplitude
The calibration of the source redshift distribution in the the CFHTLS Wide fields cannot be calculated from the Wide photometric data since only a few fields have already been observed in 5 bands. However, the CFHTLS Deep fields overlap, or are located very close to, the Wide fields. One can therefore use the photometric redshifts derived for the CFHTLS Deep data (Ilbert et al. 2006) as a representative sample of the Wide galaxy population, in particular for W1 that covers the D1 field.
The Ilbert et al. (2006) catalogue samples photometric redshifts of more
than 500 000 objects in the four CFHTLS Deep fields![]() , with an
i'AB limiting magnitude much fainter than that of the Wide
survey, covering the range
, with an
i'AB limiting magnitude much fainter than that of the Wide
survey, covering the range
![]() .
It has been calibrated
with spectroscopic redshifts obtained by the VVDS Survey in the CFHTLS
Deep D1 field (Le Fèvre et al. 2005). In this photometric redshift catalogue
318 776 galaxies have a magnitude matching the range used in the Wide
survey, i.e.
.
It has been calibrated
with spectroscopic redshifts obtained by the VVDS Survey in the CFHTLS
Deep D1 field (Le Fèvre et al. 2005). In this photometric redshift catalogue
318 776 galaxies have a magnitude matching the range used in the Wide
survey, i.e.
![]() .
This sub-sample is used
to build up our redshift distribution.
.
This sub-sample is used
to build up our redshift distribution.
For each object in Ilbert et al. (2006), the released photometric redshift
catalogue provides the maximum likelihood redshift ![]() and
error estimates such as the left and right 1
and
error estimates such as the left and right 1![]() error. In order
to estimate the redshift distribution we build a normalised Gaussian
probability distribution for each galaxy, with mean
error. In order
to estimate the redshift distribution we build a normalised Gaussian
probability distribution for each galaxy, with mean ![]() and
dispersion given by the mean of the left and right error. We then draw
a redshift z randomly and repeat the procedure 1000 times. The
variance of these 1000 randomizations is considered into the final
error budget.
and
dispersion given by the mean of the left and right error. We then draw
a redshift z randomly and repeat the procedure 1000 times. The
variance of these 1000 randomizations is considered into the final
error budget.
![\begin{figure}
\par\includegraphics[height=6.35cm,width=7.15cm,clip]{8522f7.ps}\end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg115.gif) |
Figure 7:
The cross-correlation function
|
| Open with DEXTER | |
To take into account the different selection functions between the
Deep parent sample and the Wide catalogue used in this work, each
galaxy is weighted according to the ratio of the Wide to Deep galaxy
number density, see Fig. 8. In addition, we
include the weak lensing weight (Fig. 3) to match the
redshift distribution to the weighted galaxy population selected for
weak lensing. The redshift distribution is built up with all
photometric redshifts in the range
![]() .
.
The errors on the histogram have several contributions. First, the
uncertainty in the photometric redshifts is estimated from the
variance of the 1000 randomizations from the CFHTLS Wide redshift
histogram constructed in Sect. 5.1. Second, Poisson noise,
![]() is added as
is added as ![]() ,
where n is the number of
galaxies per redshift bin. Third, we need to include sample variance,
,
where n is the number of
galaxies per redshift bin. Third, we need to include sample variance,
![]() ,
since we estimate the redshift distribution from a
reference catalogue. The sample variance is given as a function of
Poisson noise and redshift for various survey areas in Van Waerbeke et al. (2006). We use the
,
since we estimate the redshift distribution from a
reference catalogue. The sample variance is given as a function of
Poisson noise and redshift for various survey areas in Van Waerbeke et al. (2006). We use the
![]() ratio of a one
square degree survey, corrected for our bin size. We further rescale
it according to the weak-lensing selection function, since this
reduces the total number of galaxies, on which the ratio depends, as
ratio of a one
square degree survey, corrected for our bin size. We further rescale
it according to the weak-lensing selection function, since this
reduces the total number of galaxies, on which the ratio depends, as
![]() .
Note that we do
not divide the ratio by
.
Note that we do
not divide the ratio by ![]() to account for having four
independent Deep fields, since the Poisson error is calculated for the
sum of the four fields.
to account for having four
independent Deep fields, since the Poisson error is calculated for the
sum of the four fields.
With the large number of galaxies in our sample and the high accuracy
reached by the photometric redshifts at ![]() ,
the sample
variance is the dominating contribution to the error budget. Poisson
noise and redshift uncertainties only contribute
,
the sample
variance is the dominating contribution to the error budget. Poisson
noise and redshift uncertainties only contribute ![]()
![]() at z=1but become dominant for z>3 where the number of galaxies is very
low. As a cross-check, we have calculated the field-to-field variance
of the four Deep photometric redshift catalogues. The result is
consistent with the sample variance obtained by Van Waerbeke et al. (2006), using
numerical simulations.
at z=1but become dominant for z>3 where the number of galaxies is very
low. As a cross-check, we have calculated the field-to-field variance
of the four Deep photometric redshift catalogues. The result is
consistent with the sample variance obtained by Van Waerbeke et al. (2006), using
numerical simulations.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{8522f8.ps} \end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg125.gif) |
Figure 8: Magnitude distributions for the Deep (solid line) and Wide (dotted). We use the ratio Wide/Deep for the rescaling of our redshift distribution. The Wide effective number density takes into account all weak lensing selection criteria and has been multiplied by their corresponding weights (Fig. 3). |
| Open with DEXTER | |
A histogram of the sources redshifts is shown in
Fig. 9, where the error bars include redshift
uncertainty, Poisson noise and sample variance. Although sample
variance is taken into account, the histogram shows a significant
bump at redshift ![]() .
We cannot exclude the possibility that
this small peak might be partly a real feature resulting from the
joint spectroscopic, photometric and weak lensing selection functions
of our galaxy sample. It is however more likely to be an artifact
due to systematic photometric redshift misidentifications arising
from degeneracies that exist between the optical spectral energy
distributions of galaxies with z<0.2 and z>1.5. The recent
analysis of the spatial correlation of populations in different
photo-z bins (Van Waerbeke et al. 2007, in prep.) confirms that more than 50%
of galaxies in the peak are most probably at redshift
.
We cannot exclude the possibility that
this small peak might be partly a real feature resulting from the
joint spectroscopic, photometric and weak lensing selection functions
of our galaxy sample. It is however more likely to be an artifact
due to systematic photometric redshift misidentifications arising
from degeneracies that exist between the optical spectral energy
distributions of galaxies with z<0.2 and z>1.5. The recent
analysis of the spatial correlation of populations in different
photo-z bins (Van Waerbeke et al. 2007, in prep.) confirms that more than 50%
of galaxies in the peak are most probably at redshift ![]() .
.
We do not have a reliable estimate of the histogram bin-to-bin
correlation. Indeed, the off-diagonal sample variance was not
calculated in the numerical simulation analysis of Van Waerbeke et al. (2006),
and a field-to-field estimate using the four Deep fields is too
noisy to be of practical and reliable use. Thus, in order not to
propagate systematics present in the histogram into the cosmological
constraints it is preferable to use a fitting function to the
redshift distribution in the cosmological parameters estimation. For
this we consider all galaxies in the range
![]() and fit the redshift distribution with the following
function,
and fit the redshift distribution with the following
function,
This function provides a better fit to the main peak and the tail of
the distribution as compared to the power-law function used in
B07. The distribution shown in Fig. 9 corresponds to the
best-fit parameters listed in Table 1. As expected, the
peak at ![]() is no longer present. It is worth mentioning that,
although the histogram shows a significant fluctuation with respect to
the best-fit model at redshift
is no longer present. It is worth mentioning that,
although the histogram shows a significant fluctuation with respect to
the best-fit model at redshift ![]() ,
the mean redshift derived
from the best-fit distribution is within 1% of the mean value of the
histogram.
,
the mean redshift derived
from the best-fit distribution is within 1% of the mean value of the
histogram.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{8522f9.ps} \end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg130.gif) |
Figure 9: Final normalised redshift distribution. Galaxies are selected in the range [0; 4], and the best-fit is given for function given in Eq. (14). Note that the fit is only performed in the interval [0; 2.5]. |
| Open with DEXTER | |
Table 1:
Results of the fit to the redshift distribution
![]() ,
using Eq. (14). The
,
using Eq. (14). The ![]() error bars of
three parameters are shown as well.
error bars of
three parameters are shown as well.
![]() is the mean,
is the mean, ![]() the median redshift.
the median redshift.
The covariance matrices for the shear two-point correlation functions are calculated using the expressions of Schneider et al. (2002a), valid for a Gaussian shear field. They consist of a statistical noise term, a cosmic variance term and a mixed term. To account for possible residual systematics in the shear signal, we add the measured B-mode at a given angular scale quadratically to the corresponding diagonal element of the covariance.
The first three terms are calculated using a Monte Carlo method applied to the measured galaxy positions and their weight similar to the bootstrapping defined in Sect. 5. In that way the survey geometry, boundary effects and the non-uniform, discrete galaxy distribution are taken into account (Kilbinger & Schneider 2004). Furthermore, this method allows to compute a statistical noise that not only includes the shape noise of the two-point functions estimators but also takes into account Poisson or shot noise.
The non-Gaussianity of the shear field on small scales is considered
by applying a correction to the cosmic variance term using the
calibration formula of Semboloni et al. (2007). The parameters for the model
shear correlation function are
![]() and
and
![]() ,
using the Smith et al. (2003, hereafter S03) non-linear
prescription. The redshift distribution is the best-fit of the n(z) data (see Sect. 5). For the non-Gaussian calibration a mean redshift of 0.95 was assumed.
,
using the Smith et al. (2003, hereafter S03) non-linear
prescription. The redshift distribution is the best-fit of the n(z) data (see Sect. 5). For the non-Gaussian calibration a mean redshift of 0.95 was assumed.
The top-hat variance, the aperture-mass statistic and the
E-/B-correlation functions are functions of both ![]() and
and ![]() (Eqs. (4)-(8)). Therefore, their covariance matrices
depend on the full covariance of the combined data vector (
(Eqs. (4)-(8)). Therefore, their covariance matrices
depend on the full covariance of the combined data vector (
![]() ). However, we use only C++, the covariance of
). However, we use only C++, the covariance of ![]() ,
since the non-Gaussian calibration to the cosmic variance was derived
for this quantity (Semboloni et al. 2007). We divide the Poisson term of
C++ by two, which compensates for the additional information of
,
since the non-Gaussian calibration to the cosmic variance was derived
for this quantity (Semboloni et al. 2007). We divide the Poisson term of
C++ by two, which compensates for the additional information of
![]() .
The other terms contributing to the total covariance
(mixed, Gaussian and non-Gaussian cosmic variance) do not depend on
the number of galaxy pairs per bin. Therefore, they are not affected
by not taking into account the Poisson-noise contribution from
.
The other terms contributing to the total covariance
(mixed, Gaussian and non-Gaussian cosmic variance) do not depend on
the number of galaxy pairs per bin. Therefore, they are not affected
by not taking into account the Poisson-noise contribution from ![]() and thus they are unchanged.
and thus they are unchanged.
![\begin{figure}
\par\mbox{\includegraphics[width=8.3cm,clip]{8522f10a.ps} \includegraphics[width=8.3cm,clip]{8522f10b.ps} }
\end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg140.gif) |
Figure 10:
Left panel: likelihood contours ( |
| Open with DEXTER | |
The theoretical model that we fit to the data is a flat ![]() CDM cosmology with scale-free, adiabatic and Gaussian primordial
perturbations. The transfer function is the ``shape fit'' from
Eisenstein & Hu (1998) which takes into account baryonic suppression; we use a
fixed
CDM cosmology with scale-free, adiabatic and Gaussian primordial
perturbations. The transfer function is the ``shape fit'' from
Eisenstein & Hu (1998) which takes into account baryonic suppression; we use a
fixed
![]() .
The non-linear evolution of the power
spectrum is approximated with the fitting formula of S03.
.
The non-linear evolution of the power
spectrum is approximated with the fitting formula of S03.
The assumption of scale-invariance is not crucial for our results.
Indeed, marginalization over the primordial spectral index stretches
the confidence regions mainly along the
![]() -
-![]() degeneracy direction. The obtained normalisation for a given
degeneracy direction. The obtained normalisation for a given
![]() or the
or the
![]() -
-![]() relation remains
unchanged.
relation remains
unchanged.
We calculate the log-likelihood on a grid of 6-dimensional parameter
space: three cosmological parameters
![]() and three parameters of the redshift distribution (a, b, c).
and three parameters of the redshift distribution (a, b, c).
The Gaussian lensing log-likelihood is
The grid intervals are [0.1;1] for
![]() ,
[0.4;1.4] for
,
[0.4;1.4] for
![]() and [0.6;0.8] for the Hubble parameter h. The
redshift parameters values are taken inside of their
and [0.6;0.8] for the Hubble parameter h. The
redshift parameters values are taken inside of their ![]() range:
[0.53; 0.69] for a,
[6.90; 10.2] for b and
[0.49; 0.77] for
c. Translated into extreme
range:
[0.53; 0.69] for a,
[6.90; 10.2] for b and
[0.49; 0.77] for
c. Translated into extreme
![]() values, this
corresponds to an exploration range of
[0.71;1.02]. Since the
three redshift parameters are correlated, the grid includes models
that should be rejected by the redshift likelihood alone. For this
reason we multiply the likelihood, Eq. (15), by a prior
given by the likelihood of the redshift distribution estimation,
values, this
corresponds to an exploration range of
[0.71;1.02]. Since the
three redshift parameters are correlated, the grid includes models
that should be rejected by the redshift likelihood alone. For this
reason we multiply the likelihood, Eq. (15), by a prior
given by the likelihood of the redshift distribution estimation,
The left panel of Fig. 10 shows the
marginalised 2D-likelihood contours for
![]() and
and
![]() using the n(z) of Table 1. A fit to the degeneracy direction
yields
using the n(z) of Table 1. A fit to the degeneracy direction
yields
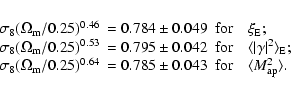
Because of the large connected area of the CFHTLS Wide, we are able to
obtain interesting cosmological constraints by using large scales
only. Although the error bars increase when small scales are not taken
into account, the sensitivity to several systematic effects is
strongly reduced. The deviation from the linear prediction of the
shear top-hat dispersion is 20% at a scale of
![]() ,
for the
redshift range probed by the Wide survey. The non-linear to linear
ratio of
,
for the
redshift range probed by the Wide survey. The non-linear to linear
ratio of
![]() is 3 at
is 3 at
![]() and 1.5 at
and 1.5 at
![]() ,
respectively. Our signal on large scales is therefore in
the linear regime and the resulting constraints do not depend on the
details of the non-linear modeling. In particular, we are not
sensitive to the difference between PD96 and S03 as can be seen in
Fig. 11. Other systematics which might bias the results
on small scales are baryonic effects
(e.g. Zhan & Knox 2004), intrinsic alignment and, maybe
most important, shear-shape correlations. All these effects are not
yet well understood as they depend on structure formation on small
scales and the relationship between galaxies and dark matter. In
particular, the shear-shape correlation leads to an underestimation of
,
respectively. Our signal on large scales is therefore in
the linear regime and the resulting constraints do not depend on the
details of the non-linear modeling. In particular, we are not
sensitive to the difference between PD96 and S03 as can be seen in
Fig. 11. Other systematics which might bias the results
on small scales are baryonic effects
(e.g. Zhan & Knox 2004), intrinsic alignment and, maybe
most important, shear-shape correlations. All these effects are not
yet well understood as they depend on structure formation on small
scales and the relationship between galaxies and dark matter. In
particular, the shear-shape correlation leads to an underestimation of
![]() (Hirata & Seljak 2004; Hirata et al. 2007). On scales larger than about
(Hirata & Seljak 2004; Hirata et al. 2007). On scales larger than about
![]() the shear field is Gaussian. The non-Gaussian calibration
of the covariance matrix is not needed and also the Gaussian
assumption of the likelihood is justified. These two factors will
yield more accurate error estimates on the cosmological parameters.
the shear field is Gaussian. The non-Gaussian calibration
of the covariance matrix is not needed and also the Gaussian
assumption of the likelihood is justified. These two factors will
yield more accurate error estimates on the cosmological parameters.
In the right panel of Fig. 10 the results
for small and large scales are shown. By using only small scales we
obtain tighter constraints than by using only large scales, as the
signal-to-noise ratio is higher. Using the aperture-mass dispersion,
the constraints derived from the three angular ranges are in
very good agreement, with all mean values within ![]() :
:
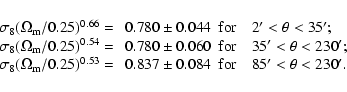
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8522f11.ps} \end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg155.gif) |
Figure 11:
The best-fit |
| Open with DEXTER | |
We checked that these constraints are not sensitive to possible
systematics on angular scales between 50 and 130 arc minutes, where
the B-mode shows a significant bump. We fit cosmological parameters
using scales with
![]() plus
plus
![]() ,
and
found the same results for
,
and
found the same results for
![]() and
and ![]() .
On the
other hand, fitting only the affected scales,
.
On the
other hand, fitting only the affected scales,
![]() ,
we get
,
we get
![]()
![]() 0.063 for
0.063 for
![]() ,
which
is consistent with the results from other scales.
,
which
is consistent with the results from other scales.
![\begin{figure}
\par\resizebox{18cm}{!}{
\includegraphics{8522f12a.ps}
\includegraphics[scale=1.325]{8522f12b.ps}
} \end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg160.gif) |
Figure 12:
Left panel: comparison (
|
| Open with DEXTER | |
Our results on cosmological parameters are in very good agreement with
the most recent cosmic shear analysis which combined the first CFHTLS
Wide data release, the RCS, the VIRMOS-D ESCART and the GaBoDS
surveys (the ``100 square degree survey'', B07). In order to compare
the two results we construct a new Wide n(z) histogram that has a
consistent redshift distribution. Following B07, we only use CFHTLS
Deep galaxies with a photometric redshift maximum peak probability in
the range [0.2;1.5]. We fit an exponential function proposed by
Baugh & Efstathiou (1993) and Van Waerbeke et al. (2002) in the same z-range.
The mean redshift
![]() matches the one in B07.
The left panel of Fig. 12 shows an excellent
agreement between the two results. The comparatively smaller sky
coverage of our survey is compensated by its larger range of angular
scales. It is also interesting to notice that our results are in
excellent agreement with the CTIO survey
(Jarvis et al. 2006,2003).
matches the one in B07.
The left panel of Fig. 12 shows an excellent
agreement between the two results. The comparatively smaller sky
coverage of our survey is compensated by its larger range of angular
scales. It is also interesting to notice that our results are in
excellent agreement with the CTIO survey
(Jarvis et al. 2006,2003).
Next, we compare our results for
![]() and
and ![]() with
the Wilkinson Microwave Anisotropy Probe 3-year constraints
(WMAP3, Spergel et al. 2007). We combine our likelihood with a CMB one
computed for a flat
with
the Wilkinson Microwave Anisotropy Probe 3-year constraints
(WMAP3, Spergel et al. 2007). We combine our likelihood with a CMB one
computed for a flat ![]() CDM cosmology using WMAP3 data only
including temperature (TT), temperature-polarisation (TE) and
polarisation (EE) modes. The combination of the two data sets leads to
remarkably smaller confidence levels as compared to individual
ones. In particular, as shown in the right panel of
Fig. 12, the combination of CFHTLS using the
aperture-mass variance and WMAP3 breaks the severe
CDM cosmology using WMAP3 data only
including temperature (TT), temperature-polarisation (TE) and
polarisation (EE) modes. The combination of the two data sets leads to
remarkably smaller confidence levels as compared to individual
ones. In particular, as shown in the right panel of
Fig. 12, the combination of CFHTLS using the
aperture-mass variance and WMAP3 breaks the severe
![]() -
-![]() degeneracy. This translates into a reduction of the
region allowed with 95
degeneracy. This translates into a reduction of the
region allowed with 95![]() confidence level by a factor of 3.15 as
compared to WMAP3 only. The marginalised constraints for each
parameter are shown in Table 2. This corresponds to a
relative accuracy of
confidence level by a factor of 3.15 as
compared to WMAP3 only. The marginalised constraints for each
parameter are shown in Table 2. This corresponds to a
relative accuracy of ![]() in
in
![]() and
and ![]() in
in
![]() ,
improving the WMAP3 constraints of Spergel et al. (2007,
Table 5) by a factor of 1.82 and 1.77 respectively. The
combinations of CFHTLS and WMAP3 using the shear correlation function
and top-hat shear variance show consistent results for
,
improving the WMAP3 constraints of Spergel et al. (2007,
Table 5) by a factor of 1.82 and 1.77 respectively. The
combinations of CFHTLS and WMAP3 using the shear correlation function
and top-hat shear variance show consistent results for
![]() and
and ![]() as listed in Table 2.
as listed in Table 2.
Table 2:
The combined constraints from CFHTLS and WMAP3 for
![]() and
and ![]() .
.
In view of the weak lensing signal we found on large scales, we
combine the WMAP3 data with the CFHTLS beyond one degree only, and
examine the cosmological constraints derived from the linear
regime. We look at the constraints on
![]() and
and ![]() by separating the large angular scales (
by separating the large angular scales (
![]() -
-
![]() )
from the whole sample, which is listed in Table 2. They
are shown in Fig. 13. One can see that the large
angular scales alone have a significant contribution to the total
constraint, although the survey only covers 57 deg2. It is then
realistic to predict from this figure that weak lensing surveys may
soon be able to explore cosmological models using linear theory only,
similar to CMB physics of primary anisotropies. This is very
promising for future surveys with sky coverage much larger
than CFHTLS Wide at the same depth. Equivalent constraints from the
linear structures, similar to the ones shown in
Fig. 13 will then be narrower by a factor of at
least 10.
)
from the whole sample, which is listed in Table 2. They
are shown in Fig. 13. One can see that the large
angular scales alone have a significant contribution to the total
constraint, although the survey only covers 57 deg2. It is then
realistic to predict from this figure that weak lensing surveys may
soon be able to explore cosmological models using linear theory only,
similar to CMB physics of primary anisotropies. This is very
promising for future surveys with sky coverage much larger
than CFHTLS Wide at the same depth. Equivalent constraints from the
linear structures, similar to the ones shown in
Fig. 13 will then be narrower by a factor of at
least 10.
Our joint analysis with WMAP3 data is in full agreement with
similar studies presented in Spergel et al. (2007), using several other
data sets. Our estimate for the matter density also coincides with
the result derived by Astier et al. (2006) based on their SNIa light curves
only, for a flat ![]() CDM Universe. The comparison with clusters
of galaxies is, in contrast, less conclusive. Cluster observations
estimate a broad range of
CDM Universe. The comparison with clusters
of galaxies is, in contrast, less conclusive. Cluster observations
estimate a broad range of ![]() values, with some being fully
consistent with our results
Gladders et al. (2007), (see also Hetterscheidt et al. 2007, for a compilation
of results), while a recent analysis of simulations argue for higher values
(Yepes et al. 2007; Evrard et al. 2007). The trends for a high value of
values, with some being fully
consistent with our results
Gladders et al. (2007), (see also Hetterscheidt et al. 2007, for a compilation
of results), while a recent analysis of simulations argue for higher values
(Yepes et al. 2007; Evrard et al. 2007). The trends for a high value of ![]() are
also derived from analyses of the Lyman-alpha forest (see Slosar et al. 2007, and
reference therein).
are
also derived from analyses of the Lyman-alpha forest (see Slosar et al. 2007, and
reference therein).
The gravitational lensing signal may be contaminated by the
intrinsic alignment and by the gravitational shear and intrinsic
ellipticity (or shear-shape) correlations. We do not consider the
first term since it would be negligible due to a broad redshift
distribution of our sample. On the other hand,
Mandelbaum et al. (2006) and Hirata et al. (2007) pointed out that
the shear-shape anti-correlation may bias the estimate of
![]() by 1 to
by 1 to ![]() for a
for a
![]() survey on
angular scales that we have explored in this work. It is therefore
important to estimate its amplitude and to which extent it may
spoil our cosmological constraints.
survey on
angular scales that we have explored in this work. It is therefore
important to estimate its amplitude and to which extent it may
spoil our cosmological constraints.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{8522f13.ps} \end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg179.gif) |
Figure 13:
Comparison (
|
| Open with DEXTER | |
We attempt a rather simple analysis of the shear-shape correlation
(GI) contribution to the shear signal. We use the following simple
model for the GI correlation function
![]() ,
which is
motivated by numerical simulations (Heymans et al. 2006b)
,
which is
motivated by numerical simulations (Heymans et al. 2006b)
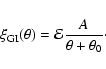 |
(17) |
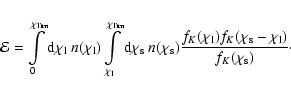
![\begin{figure}
\par\includegraphics[height=7.3cm,width=7.5cm,clip]{8522f14.ps} \end{figure}](/articles/aa/full/2008/07/aa8522-07/Timg186.gif) |
Figure 14:
The measured
|
| Open with DEXTER | |
We perform a combined likelihood analysis using the six cosmological
parameters as described in Sect. 6.2 and the GI amplitude A. The sum
![]() is fitted to the data. Since
the 7D-likelihood analysis is very time-consuming, we use the
marginalised 2
is fitted to the data. Since
the 7D-likelihood analysis is very time-consuming, we use the
marginalised 2![]() likelihood-region from the pure lensing
analysis (Sect. 6.3) as a flat prior and do not consider
models outside this region. The marginalised result on A is
consistent with zero. We find for the amplitude A in units of
[10-7 h/Mpc arcmin],
likelihood-region from the pure lensing
analysis (Sect. 6.3) as a flat prior and do not consider
models outside this region. The marginalised result on A is
consistent with zero. We find for the amplitude A in units of
[10-7 h/Mpc arcmin],
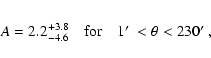
Although the confidence region for the constrained GI amplitude is
large it favours positive correlations, whereas from theory we would
expect the GI signal to be negative (Hirata & Seljak 2004). As a
consistency check we used a cosmology prior given by the marginalised
![]() likelihood region from a pure lensing analysis of the large
scale results with
likelihood region from a pure lensing analysis of the large
scale results with
![]() arcmin. The model
arcmin. The model
![]() is then fitted on scales with
is then fitted on scales with
![]() arcmin. The resulting marginalised likelihood for A favours
negative GI models but is still consistent with zero. This ansatz
gives a high weight to the large-scale cosmic shear signal, and any
systematics still present will influence the result. The large scale
increase in the measured star-galaxy cross correlation shown in
Fig. 7 highlights this concern. As we cannot currently
distinguish between GI and other possible systematic effects we can
only conclude from our simple analysis that we find no evidence for a
non-zero GI signal.
arcmin. The resulting marginalised likelihood for A favours
negative GI models but is still consistent with zero. This ansatz
gives a high weight to the large-scale cosmic shear signal, and any
systematics still present will influence the result. The large scale
increase in the measured star-galaxy cross correlation shown in
Fig. 7 highlights this concern. As we cannot currently
distinguish between GI and other possible systematic effects we can
only conclude from our simple analysis that we find no evidence for a
non-zero GI signal.
If our galaxy sample is strongly dominated by high-redshift spiral
galaxies, then the GI signal may be considerably weakened, as one can
anticipate from the morphological analysis of Mandelbaum et al. (2006). We do not have enough colour data to explore in
detail the spectral/morphological types of the galaxies used in this
work. However, Zucca et al. (2006) pointed out that about 80% of the VVDS
spectroscopic galaxy sample up to
![]() is composed of
spiral-like galaxies. It is then possible that the fraction of spirals
is much higher than elliptical galaxies in the population we are
sampling with cosmic shear. If so, it would reduce the contamination
to a very small effective contribution (Heymans et al. 2006b). A more
detailed investigation of the shear-shape analysis using photometric
redshifts and spectrophotometric information of galaxies is therefore
needed and will be discussed in a forthcoming paper.
is composed of
spiral-like galaxies. It is then possible that the fraction of spirals
is much higher than elliptical galaxies in the population we are
sampling with cosmic shear. If so, it would reduce the contamination
to a very small effective contribution (Heymans et al. 2006b). A more
detailed investigation of the shear-shape analysis using photometric
redshifts and spectrophotometric information of galaxies is therefore
needed and will be discussed in a forthcoming paper.
We have presented the weak lensing analysis of the CFHTLS T0003 Wide data. The survey covers 57 deg2, about two times the size of the previous analysis by Hoekstra et al. (2006), and includes a new independent field W2.
The galaxy shape measurements of a homogeneous sample of two million galaxies down to i'AB=24.5 have been validated using the STEP1 and STEP2 simulations (Massey et al. 2007b; Heymans et al. 2006a). The top-hat shear variance, aperture-mass dispersion and the two-point shear correlation functions show a significant signal, with no galaxy-star correlations, from 1 arcmin up to 4 degrees. The B-mode is consistent with zero on most of these angular scales. It shows, however, a statistically significant feature in the range 50-130 arcmin, of unknown origin. We have verified that this feature does not influence the cosmological results.
The two-point statistics show all expected properties of a cosmic
shear signal up to angular scales 10 times larger than the largest
non-linear scales of the survey. Hence, for the first time the cosmic
shear signal can be explored with enough confidence to physical scales
of about 85 Mpc assuming lenses at z=0.5, for a flat Universe with
h=0.72 and
![]() .
This is by far the widest scale
ever probed by weak lensing at that depth.
.
This is by far the widest scale
ever probed by weak lensing at that depth.
The weak lensing Wide data and the photometric redshifts sample of
Ilbert et al. (2006) are both part of the CFHTLS T0003 release and cover
common fields. The redshift distribution of the Wide data can
therefore be calibrated using these photometric redshifts, assuming
with a high confidence level that the two galaxy populations are
similar. Taking into account the selection criteria of the weak
lensing sample, we find a mean redshift of
![]() and a description of the redshift distribution in excellent agreement
with B07.
and a description of the redshift distribution in excellent agreement
with B07.
Using this redshift distribution, an exploration of constraints on
![]() -
-![]() has been carried out within the angular
range
has been carried out within the angular
range
![]() .
The marginalised result on
.
The marginalised result on
![]() -
-![]() derived from the aperture-mass variance
derived from the aperture-mass variance
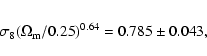
There is a clear trend towards a lower ![]() as compared to
Semboloni et al. (2006) and Hoekstra et al. (2006). This is a result of the less accurate
redshift distributions used in these analyses which were estimated
from the Hubble Deep Field photometric redshift sample. This is well
confirmed when we combine our predictions on
as compared to
Semboloni et al. (2006) and Hoekstra et al. (2006). This is a result of the less accurate
redshift distributions used in these analyses which were estimated
from the Hubble Deep Field photometric redshift sample. This is well
confirmed when we combine our predictions on
![]() and
and
![]() with WMAP3 of Spergel et al. (2007), shown in the right panel
of Fig. 12. There is a striking difference with
respect to the early comparison done by Spergel et al. (2007), using the
CFHTLS T0001 results. The
with WMAP3 of Spergel et al. (2007), shown in the right panel
of Fig. 12. There is a striking difference with
respect to the early comparison done by Spergel et al. (2007), using the
CFHTLS T0001 results. The ![]() tension is no longer visible; in
contrast, there is a large overlap between the two data sets. The
joint CFHTLS-WMAP3 likelihood analysis then leads to tight
marginalised constraints on
tension is no longer visible; in
contrast, there is a large overlap between the two data sets. The
joint CFHTLS-WMAP3 likelihood analysis then leads to tight
marginalised constraints on
![]() and
and ![]() ,
,
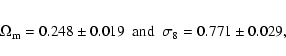
Considering the potential nuisances of systematic effects related to
non-linear scales, we split the sample into three ranges of angular
scales: the ``highly non-linear'' (
![]() ), the
``intermediate'' (
), the
``intermediate'' (
![]() )
and the ``linear''
(
)
and the ``linear''
(
![]() )
scales. The analysis of the
three sub-samples do not reveal significant differences between each
regime (see Fig. 10, right panel). The
results are also stable to changes in the lower angular scales
increasing from 2' to 4'. This shows that the CFHTLS Wide cosmic
shear survey is not yet dominated by uncertainties related to our poor
knowledge of astrophysical systematics at small scales. Finally, we
find that excluding scales with a significant B-mode (
)
scales. The analysis of the
three sub-samples do not reveal significant differences between each
regime (see Fig. 10, right panel). The
results are also stable to changes in the lower angular scales
increasing from 2' to 4'. This shows that the CFHTLS Wide cosmic
shear survey is not yet dominated by uncertainties related to our poor
knowledge of astrophysical systematics at small scales. Finally, we
find that excluding scales with a significant B-mode (
![]() )
from the analysis does not change our results. The
constraints on
)
from the analysis does not change our results. The
constraints on
![]() are therefore insensitive to the
level of residual systematics in our data. All these tests strengthen
the confidence and reliability of our results.
are therefore insensitive to the
level of residual systematics in our data. All these tests strengthen
the confidence and reliability of our results.
The very large range of angular scales explored by the CFHTLS Wide opens a new window to cosmic shear surveys. It enables for the first time a comparison of cosmic shear and WMAP3 signals using only linear scales. The constraints shown in Fig. 13 demonstrate that there is still great predictive power from the linear regime only. Future weak lensing surveys which cover areas significantly larger than the CFHTLS will be able to pin down a much narrower region in parameter space. Thus, it will be possible to obtain cosmological parameters to percent-level accuracy and below from combining CMB and weak lensing using linear theory.
Finally, the impact of the contamination by the shear-shape
correlation on cosmic shear surveys like CFHTLS is still unclear. We
find its amplitude to be very low and compatible with zero at all
scales we explored.
The low amplitude derived from
Hirata et al. (2007), using a survey shallower than the CFHTLS Wide,
had already suggested that it should be a small effect and a
difficult-to-detect signal in the CFHTLS-Wide,
in particular if our galaxy sample is dominated by high-redshift
spiral galaxies (Zucca et al. 2006). At present, we can measure
![]() to a precision of about
to a precision of about ![]() and so this bias is still
reasonably low. With future work, however, this bias may
become the main source of error.
and so this bias is still
reasonably low. With future work, however, this bias may
become the main source of error.
The CFHTLS is still in progress and the next release will include more sky coverage and also a new field, W4. In this work, we only use the wide i'-band data together with the photometric redshift from the Deep T0003 u*,g',r',i',z'. The next step is therefore a more detailed analysis of multi-colour data sets. A better check of systematics will be possible by cross-correlating the lensing signal obtained independently in indifferent filters. The larger CFHTLS Wide sample with u*,g',r',i',z' will also improve tomographic studies and will provide a photometric redshift to each individual galaxy. We will then be in the position to better control contaminations by intrinsic alignment and the shear-shape (GI) correlations (Bridle & King 2007) and to move towards a full tomographic exploration of the CFHTLS Deep and Wide surveys together.
Acknowledgements
We warmly thank the CFHT, Terapix and CADC staff for their assistance and the considerable work they do to produce the CFHTLS data, and the VVDS consortium for providing the galaxy spectroscopic sample in the CFHTLS fields. This work has made use of the VizieR catalogue access tool, CDS, Strasbourg, France. We thank R. Massey and the STEP collaboration for producing the STEP simulations used in this analysis, and Caltech, the University of British Columbia and JPL for their support to STEP. We thank F. Bernardeau, T. Erben, B. Fort, M. Hetterscheidt, H. Hildebrandt, C. Schimd, P. Schneider, T. Schrabback-Krahe, U. Seljak, C. Shu, J.-P. Uzan for useful discussions. LF thanks the ``European Association for Research in Astronomy'' training site (EARA) and the European Commission Programme for the Marie Curie Doctoral Fellowship MEST-CT-2004-504604. E.S. aknowledges the support from the Alexander von Humboldt Foundation. J.C., L.F., M.K. and Y.M. thank the CNRS-Institut National des Sciences de l'Univers (INSU) and the French Programme National de Cosmologie (PNC) for their support to the CFHTLS cosmic shear program. I.T. and Y.M. acknowledge the support of the European Commission Programme 6th framework, Marie Curie Training and Research Network ``DUEL'', contract number MRTN-CT-2006-036133. IT thanks the Deutsche Forschungsgemeinschaft under the project SCHN 342/8-1 and the Priority Programme 1177. MK is supported by the CNRS ANR ``ECOSSTAT'', contract number ANR-05-BLAN-0283-04. LVW, HH and MH are supported by the Natural Sciences and Engineering Research Council (NSERC), the Canadian Institute for Advanced Research (CIAR) and the Canadian Foundation for Innovation (CFI). CH acknowledges the support of the European Commission Programme 6th framework, Marie Curie Outgoing International Fellowship, contract number M01F-CT-2006021891.
One of the crucial issues for weak lensing studies is the reliability
of galaxy shape measurement and the control of systematics. The
detection and measurement of weak lensing is a technical
challenge. Weak distortion induced by gravitational lensing in the
observed shapes of galaxy images is only ![]()
![]() ,
much smaller than
the typical intrinsic ellipticity dispersion
,
much smaller than
the typical intrinsic ellipticity dispersion ![]()
![]() .
To further
complicate the situation the observed shape of the galaxies is
affected by the PSF. The Shear TEsting Programme
.
To further
complicate the situation the observed shape of the galaxies is
affected by the PSF. The Shear TEsting Programme![]() (Massey et al. 2007b; Heymans et al. 2006a),
hereafter STEP, is a collaborative project aiming to calibrate and
improve weak lensing methods using realistic Wide field simulated
images. The first and second generation of STEP simulations
(hereafter STEP1 and STEP2) are designed for a ground-based survey.
In order to check the reliability of the shear measurement used in
this analysis, we calibrated the pipeline using all data sets from
STEP1 and STEP2.
(Massey et al. 2007b; Heymans et al. 2006a),
hereafter STEP, is a collaborative project aiming to calibrate and
improve weak lensing methods using realistic Wide field simulated
images. The first and second generation of STEP simulations
(hereafter STEP1 and STEP2) are designed for a ground-based survey.
In order to check the reliability of the shear measurement used in
this analysis, we calibrated the pipeline using all data sets from
STEP1 and STEP2.
STEP1 simulations contain relatively simple galaxy morphologies
generated using the SkyMaker software![]() . Five constant shears,
. Five constant shears,
![]() [0.0, 0.005, 0.01, 0.05, 0.1], are applied
to the galaxies, while the second component
[0.0, 0.005, 0.01, 0.05, 0.1], are applied
to the galaxies, while the second component
![]() is
always set to zero. Finally, galaxy and stellar point sources are
convolved with six different constant PSFs which attempt to reproduce
PSF shapes, that are typical of ground-based observations. In this
way 30 sets of images, differing in PSF type and/or shear strength are
produced. Each set is composed of 64 images. The sky noise is
spatially uncorrelated.
is
always set to zero. Finally, galaxy and stellar point sources are
convolved with six different constant PSFs which attempt to reproduce
PSF shapes, that are typical of ground-based observations. In this
way 30 sets of images, differing in PSF type and/or shear strength are
produced. Each set is composed of 64 images. The sky noise is
spatially uncorrelated.
Table A.1: Summary of the shear measurement pipeline.
STEP2 simulations contain complex galaxy morphologies produced using a
shapelet simulation package (Massey et al. 2004). Six sets of 64 images
with random constant input shears are convolved each with a different
optical PSF. The six PSFs are chosen to span a range of realistic
ground-based observing conditions. For each image, a twin image is
produced, in which galaxies are rotated by ![]() before applying the
same shear and the same PSF. Combining the shear analysis on rotated
and non-rotated images demonstrates the pure measurement bias, since
the noise due to the scatter in a galaxies' intrinsic morphology is
removed. The model of the sky noise is also more complex than the one
adopted to generate STEP1 simulations. It is in fact a correlated
noise which aims to reproduce the noise of the drizzling process.
before applying the
same shear and the same PSF. Combining the shear analysis on rotated
and non-rotated images demonstrates the pure measurement bias, since
the noise due to the scatter in a galaxies' intrinsic morphology is
removed. The model of the sky noise is also more complex than the one
adopted to generate STEP1 simulations. It is in fact a correlated
noise which aims to reproduce the noise of the drizzling process.
Our pipeline is an application of the KSB+ method. The observed galaxy
shape is modeled as a convolution of the sheared galaxy with the PSF,
which in turn is modeled as a circular profile convolved with a small
anisotropy. Assuming the mean of the intrinsic ellipticity
distribution of galaxies to be zero and the PSF anisotropy to be
small, the first-order of the shear, ![]() ,
can be computed from
the observed ellipticities of galaxies,
,
can be computed from
the observed ellipticities of galaxies,
![]() as follows:
as follows:
We compute the stellar quantities,
![]() ,
,
![]() and
and ![]() ,
with the same filter function
,
with the same filter function
![]() in order to keep the calibration free
of extra bias. Following Hoekstra et al. (1998) and the STEP results
(Massey et al. 2007b; Heymans et al. 2006a), for each galaxy we compute all quantities,
including those estimated from the stars, using a filter scale
in order to keep the calibration free
of extra bias. Following Hoekstra et al. (1998) and the STEP results
(Massey et al. 2007b; Heymans et al. 2006a), for each galaxy we compute all quantities,
including those estimated from the stars, using a filter scale
![]() as given by IMCAT.
as given by IMCAT.
We did not apply the same PSF anisotropy correction to small and large
objects. Using the STEP1 and STEP2 simulated catalogues we found that
the measurement of moments from small objects can be significantly
improved and are more robust by first resampling the intensity of
light in each pixel. Each image is oversampled by a factor of two and
interpolated using a nearest neighbour interpolation kernel, prior to
measure shapes of objects. The interpolation works very well for
objects with a size close to the star size and does not produce any
detectable extra bias. However, it fails and may even degrade the
signal as the object size increases. STEP simulations show the
transition arises when object size exceeds 1.2![]() seeing.
seeing.
We approximate ![]() by half of its trace,
by half of its trace,
![]() .
Since individual
.
Since individual
![]() are
noisy, we derive their values from a fit as function of some galaxy
properties. As described in Heymans et al. (2006a) and Massey et al. (2007b), the shear
bias parameter m often depends on object sizes,
are
noisy, we derive their values from a fit as function of some galaxy
properties. As described in Heymans et al. (2006a) and Massey et al. (2007b), the shear
bias parameter m often depends on object sizes, ![]() ,
and
magnitudes mag. We therefore fit
,
and
magnitudes mag. We therefore fit
![]() in the
in the
![]() -mag plane using a polynomial that only depends on these two
parameters. The
-mag plane using a polynomial that only depends on these two
parameters. The
![]() -dependence on mag is more
scattered than that on
-dependence on mag is more
scattered than that on ![]() ,
so we choose a function that gives more
weight on
,
so we choose a function that gives more
weight on ![]() :
:
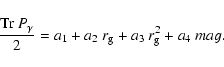 |
(A.2) |
Applying the pipeline to the STEP simulations, we quantify the STEP
results using the fit defined in Heymans et al. (2006a) and Massey et al. (2007b), which
expresses the difference between measured and input shear through a
linear relation:
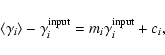 |
(A.3) |
These results show the residual bias is well constrained and
reasonably low for our purposes. In fact, the shape measurement bias
is much lower than the total error affecting the cosmological
parameter estimation. It should also be noticed that the STEP1
simulations have characteristics much more similar to the Wide data
than STEP2 simulations. In particular, the structure of the noise and
the PSF types adopted to generate the STEP1 simulations are very close
to the ones of our data. For this reason the effective bias in the
CFHTLS Wide shear catalogue is expected to be about ![]() .
.
The data vectors and ![]() error bars plotted in Fig. 4,
for the various shear two-point functions are listed in
Tables B.1, B.2.
error bars plotted in Fig. 4,
for the various shear two-point functions are listed in
Tables B.1, B.2.
Table B.1:
Values of the shear correlation function and the shear
top-hat variance, as function of scale ![]() in arcmin. The
errors include statistical errors and non-Gaussian-calibrated cosmic
variance for the E-mode, while only statistical uncertainty contributes to the error of the B-mode.
in arcmin. The
errors include statistical errors and non-Gaussian-calibrated cosmic
variance for the E-mode, while only statistical uncertainty contributes to the error of the B-mode.
Table B.2:
Values of the the aperture-mass variance, as function of
scale ![]() in arcmin.
in arcmin.