A&A 478, 675-684 (2008)
DOI: 10.1051/0004-6361:20078605

Time variation of the fine structure constant in the early universe and the Bekenstein model

M. E. Mosquera1,[*] - C. G. Scóccola1,2,[*] - S. J. Landau3,[*] - H. Vucetich1


1 - Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque, cp 1900 La Plata, Argentina
2 - Instituto de Astrofísica La Plata
3 - Departamento de Física, FCEyN, Universidad de Buenos Aires, Ciudad Universitaria - Pab. 1, 1428 Buenos Aires, Argentina

Received 3 September 2007 / Accepted 4 November 2007

Abstract
Aims. We calculate the bounds on the variation in the fine structure constant at the time of primordial nucleosynthesis and at the time of neutral hydrogen formation. We used these bounds and other bounds from the late universe to test the Bekenstein model.
Methods. We modified the Kawano code, CAMB, and CosmoMC to include the possible variation in the fine structure constant. We used observational primordial abundances of $\ensuremath{{\rm D}} $, $\ensuremath{\null^4{\rm He}} $, and $\ensuremath{\null^7{\rm Li}} $, recent data from the cosmic microwave background, and the 2dFGRS power spectrum, to obtain bounds on the variation in ${\alpha }$. We calculated a piecewise solution to the scalar field equation of the Bekenstein model in two different regimes: i) matter and radiation, ii) matter and cosmological constant. We match both solutions with the appropriate boundary conditions. We performed a statistical analysis, using the bounds obtained from the early universe and other bounds from the late universe to constrain the free parameters of the model.
Results. Results are consistent with no variation in ${\alpha }$ for the early universe. Limits on ${\alpha }$ are inconsistent with the scale length of the theory l being larger than the Planck scale.
Conclusions. In order to fit all observational and experimental data, the assumption $l>L_{\rm p}$ implied in Bekenstein's model has to be relaxed.

Key words: early Universe - cosmology: theory - cosmic microwave background

   
1 Introduction

Studying the time variation of fundamental constants has been an active field of theoretical and experimental research ever since the large number hypothesis (LNH) was proposed by Dirac (1937). The effective predictive power of the LNH induced a large number of research papers and suggested new sources of variation. Among them, the attempt to unify all fundamental interactions resulted in the development of multidimensional theories, like string-derived field theories (Damour et al. 2002a; Maeda 1988; Damour et al. 2002b; Wu & Wang 1986; Damour & Polyakov 1994; Barr & Mohapatra 1988), related brane-world theories (Brax et al. 2003; Youm 2001b,a; Palma et al. 2003), and Kaluza-Klein theories (Overduin & Wesson 1997; Gleiser & Taylor 1985; Kaluza 1921; Weinberg 1983; Klein 1926), where the gauge coupling constants may vary over cosmological time scales.

Following a different path of research, Bekenstein (1982) proposed a theoretical framework for studying the fine structure constant variability based on general assumptions: covariance, gauge invariance, causality, and time-reversal invariance of electromagnetism, as well as the idea that the Planck-Wheeler length $\left( 10^{-33}~{\rm cm} \right)$ is the shortest scale allowable in any theory. It is well known that bounds from the weak equivalence principle require $l<L_{\rm p}$. However, in this paper we are going to analyze data from cosmological time-scales rather than planetary scales that are relevant to probing the validity of the weak equivalence principle. The model was improved by Barrow et al. (2002) using the main assumption that cold dark matter has magnetic fields dominating its electric fields. Moreover, a super symmetric generalization of this model was performed by Olive & Pospelov (2002), allowing additional couplings between the scalar field and both a dark matter candidate and the cosmological constant. Chamoun et al. (2001) generalized the model to study the time variation in the strong coupling constant.

Different versions of the theories mentioned above predict different time behaviors of the gauge coupling constants. Thus, bounds obtained from astronomical and geophysical data are important tools for testing the validity of these theories. In unifying schemes like the ones described above, the variation in each gauge coupling constant is related to the others. In this paper, we limit ourselves to studing the variation in the fine structure constant (${\alpha }$).

The experimental research can be grouped into astronomical and local methods. The latter include: (i) geophysical methods, such as the natural nuclear reactor that operated about 1.8 $\times$ 109 years ago in Oklo, Gabon; (ii) the analysis of natural long-lived ${\beta }$decayers in geological minerals and meteorites; and (iii) laboratory measurements, such as comparisons of rates between clocks with different atomic numbers. The astronomical methods are based mainly in the analysis of spectra from high-redshift quasar absorption systems. Although most of the previously mentioned experimental data gave null results, evidence of time variation in the fine structure constant was reported recently from high-redshift quasar absorption systems (Murphy et al. 2001c; Webb et al. 2001,1999; Levshakov et al. 2007; Murphy et al. 2001b,2003). However, other recent independent analyses of similar data (Bahcall et al. 2004; Srianand et al. 2004; Quast et al. 2004; Martínez Fiorenzano et al. 2003) found no variation at all.

Bounds on the variation in ${\alpha }$ in the early universe can be obtained using data from the cosmic microwave background (CMB) radiation and from the abundances of light elements. Although these bounds are not as stringent as those mentioned above, they are important because they refer to a different cosmological epoch. Finally, other bounds at redshift higher than 30 could be obtained from the 21 cm signal once it could be measured (Khatri & Wandelt 2007). In this paper, we carefully analyze the time variation of ${\alpha }$ in the early universe. First, we used the available abundances of $\ensuremath{{\rm D}} $, $\ensuremath{\null^4{\rm He}} $, and $\ensuremath{\null^7{\rm Li}} $ and the latest data from the CMB to put bounds on the variation of ${\alpha }$ in the early universe without assuming any theoretical model. Then, we used these bounds and others from astronomical and geophysical data to test Bekenstein theory.

In Sect. 2 we use the abundances of the light elements to put bounds on $\frac{\Delta \alpha}{\alpha_0}$, where $\alpha_0$ is the present value of ${\alpha }$, allowing the baryon-to-photon density  $\eta _{\rm B}$ to vary. We also calculate the time variation of ${\alpha }$keeping $\eta _{\rm B}$ fixed to the WMAP estimation. In Sect. 3 we use the three-year WMAP, other CMB experiments, and the power spectrum of the 2dFGRS to put bounds on the variation in ${\alpha }$ during recombination, also allowing other cosmological parameters to vary. In Sects. 4-6 we describe the astronomical and local data from the late universe. In Sect. 7 we describe Bekenstein model for ${\alpha }$ variations and obtain solutions for the early and late universe. In Sect. 8 we show our results. Finally, in Sect. 9 we discuss the results and summarize our conclusions.

   
2 Bounds from BBN

Big Bang nucleosynthesis (BBN) is one of the most important tools for studying the early universe. The model is simple and has only one free parameter, the baryon-to-photon ratio  $\eta _{\rm B}$, which can be determined by comparing theoretical calculations and observations of the abundances of light elements. On the other hand, data from the CMB provide an independent method for determining $\eta _{\rm B}$ (Spergel et al. 2003; Sanchez et al. 2006; Spergel et al. 2006). Considering the baryon density from WMAP results, the predicted abundances are very consistent with the observed $\ensuremath{{\rm D}} $ but not with all $\ensuremath{\null^4{\rm He}} $ and $\ensuremath{\null^7{\rm Li}} $. Such a discrepancy is usually ascribed to unreported systematic errors in the observations of $\ensuremath{\null^4{\rm He}} $ and $\ensuremath{\null^7{\rm Li}} $. However, if the systematic errors of $\ensuremath{\null^4{\rm He}} $ and $\ensuremath{\null^7{\rm Li}} $ are correctly estimated, we may gain insight into new physics beyond the minimal BBN model. Dmitriev et al. (2004) consider the variation in the deuterium binding energy to solve the discrepancy between $\ensuremath{{\rm D}} $, $\ensuremath{\null^4{\rm He}} $, and $\ensuremath{\null^7{\rm Li}} $ abundances.

In this section we focus on the possibility that the fine structure constant may be different from its present value during BBN. The dependence of the primordial abundances on the fine structure constant has been evaluated by Bergström et al. (1999) and improved by Nollett & Lopez (2002). Semi-analytical analyses have been performed by some of us in earlier works (Landau et al. 2006; Chamoun et al. 2007). Ichikawa & Kawasaki (2002) study the effects of the variation of fundamental constants on BBN in the context of a dilaton superstring model. In a subsequent work, they study the primordial abundances of light elements when the fine structure constant and the cosmic expansion rate take non-standard values (Ichikawa & Kawasaki 2004). Müller et al. (2004) calculate the primordial abundances as a function of the Planck mass, fine structure constant, Higgs vacuum expectation value, electron mass, nucleon decay time, deuterium binding energy, and neutron-proton mass difference and study the dependence of the last three quantities as functions of the fundamental coupling and masses. Coc et al. (2007) set constraints on the variation in the neutron lifetime and neutron-proton mass difference using the primordial abundance of $^4{\rm He}$. Then, they translate these constraints into bounds on the time variation of the Yukawa couplings and the fine structure constant. Cyburt et al. (2005) study the number of relativistic species at the time of BBN and the variations in fundamental constants ${\alpha }$ and GN and set bounds on these quantities using the primordial abundances and the results of WMAP for  $\eta _{\rm B}$.

In this work, we modified the numerical code of Kawano (Kawano 1992,1988) in order to allow ${\alpha }$ to vary. In addition to the dependences on ${\alpha }$ discussed by other authors, we also included the dependence of the light nuclei masses on ${\alpha }$ (Landau et al. 2006). The code was also updated with the reaction rates reported by Bergström et al. (1999). We considered available observational data on $\ensuremath{{\rm D}} $, $\ensuremath{\null^4{\rm He}} $, and $\ensuremath{\null^7{\rm Li}} $. For $\ensuremath{{\rm D}} $ we considered the values reported by Pettini & Bowen (2001), O'Meara et al. (2001), Kirkman et al. (2003), Burles & Tytler (1998a), Burles & Tytler (1998b), Crighton et al. (2004), O'Meara et al. (2006), and Oliveira et al. (2006). For $\ensuremath{\null^7{\rm Li}} $ we considered the results from Ryan et al. (2000), Bonifacio et al. (1997), Bonifacio & Molaro (1997), Bonifacio et al (2002), Asplund et al. (2006), Boesgaard et al. (2005), and Bonifacio et al. (2007).

The $\ensuremath{\null^4{\rm He}} $ available observations can be summarized in the results reported by Peimbert et al. (2007), Izotov et al. (2007), and Olive & Skillman (2004). The reported values of $\ensuremath{\null^4{\rm He}} $ depend on the adopted set of $\rm {He} I $emissivities. In fact, Izotov et al. (2007) report two values, one calculated with old atomic data (Benjamin et al. 2002) and the other with new atomic data (Porter et al. 2005), while Peimbert et al. (2007) use the new values. We consider the results calculated using new atomic data. Olive & Skillman (2004) reanalyze the values of Izotov & Thuan (1998) and Peimbert et al. (2000) for the primordial abundance of $^4{\rm He}$. They examined some sources of systematic uncertainties and conclude that the observational determination of primordial helium abundance is limited by systematics errors. We considered the data of Peimbert et al. (2007) and Izotov et al. (2007) in our analysis. In Table 1 we show the theoretical predictions of the abundances in the standard model (without the variation in ${\alpha }$) with $\eta _{\rm B}$ fixed to the WMAP estimate.

Table 1: Theoretical abundances in the standard model.

To check the consistency of the data, we followed the analysis of Yao et al. (2006) for the data set considered in this work. We find that the ideogram method plots are not Gaussian-like, suggesting the existence of unmodeled systematic errors. We take them into account by increasing the standard deviation by a factor S. The values of S are 2.10, 1.40, and 1.90 for $\ensuremath{{\rm D}} $, $\ensuremath{\null^4{\rm He}} $, and $\ensuremath{\null^7{\rm Li}} $, respectively. A scaling of errors was also suggested by Olive & Skillman (2004).

We computed the light nuclei abundances and performed a statistical analysis to obtain the best-fit values for the parameters, for two different cases:

Even though the WMAP data are able to constrain the baryon density with good accuracy, there is still some degeneracy between the parameters involved in the statistical analysis. For this reason, we allowed the joint variation in baryon density and the fine structure constant to obtain an independent estimation for  $\eta _{\rm B}$.

2.1 Variation in ${\alpha }$ and ${\eta _B}$

In this case, we computed the light nuclei abundances for different values of $\eta _{\rm B}$ and $\frac{\Delta \alpha}{\alpha_0}$ and performed a statistical analysis to obtain the best-fit values for these parameters. As pointed out by several authors (Cyburt 2004; Ichikawa & Kawasaki 2004; Cuoco et al. 2004; Coc et al. 2004; Ichikawa & Kawasaki 2002), there is no good fit for the whole data set even for $\frac{\Delta \alpha}{\alpha_0} \neq 0$. However, reasonable fits can be found by excluding one group of data at a time (see Table 2).

Table 2: Best-fit parameter values and $1\sigma $ errors for the BBN constraints on $\frac{\Delta \alpha}{\alpha_0}$ and $\eta _{\rm B}$ (in units of 10-10).

For $\ensuremath{{\rm D}} + \ensuremath{\null^4{\rm He}} $, the value of $\eta _{\rm B}$ coincides with WMAP estimation and there is no variation in ${\alpha }$ within $3\sigma $. On the other hand, the other groups of data, favor values far from WMAP estimation, and the result for $\ensuremath{{\rm D}} + \ensuremath{\null^7{\rm Li}} $ is consistent with variation in ${\alpha }$ within $6\sigma$. In Figs. 1-3 the confidence contours and 1-dimensional likelihoods are shown, considering the available data of $\ensuremath{\null^4{\rm He}} + \ensuremath{\null^7{\rm Li}} $, $\ensuremath{{\rm D}} + \ensuremath{\null^7{\rm Li}} $, and $\ensuremath{{\rm D}} + \ensuremath{\null^4{\rm He}} $, respectively.


  \begin{figure} \par\includegraphics[width=6.6cm,clip]{8605fig1.ps}\end{figure} Figure 1: $1\sigma $, $2\sigma $, and $3\sigma $ likelihood contours for $\frac{\Delta \alpha}{\alpha_0}$ vs. $\eta _{\rm B}$ (in units of 10-10) and 1-dimensional likelihood using the data of $\ensuremath{\null^4{\rm He}} + \ensuremath{\null^7{\rm Li}} $.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.4cm,clip]{8605fig2.ps}\end{figure} Figure 2: $1\sigma $, $2\sigma $, and $3\sigma $ likelihood contours for $\frac{\Delta \alpha}{\alpha_0}$ vs. $\eta _{\rm B}$ (in units of 10-10) and 1-dimensional likelihood using the data of $\ensuremath{{\rm D}} + \ensuremath{\null^7{\rm Li}} $.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.6cm,clip]{8605fig3.ps}\end{figure} Figure 3: $1\sigma $, $2\sigma $, and $3\sigma $ likelihood contours for $\frac{\Delta \alpha}{\alpha_0}$ vs. $\eta _{\rm B}$ (in units of 10-10) and 1-dimensional likelihood using the data of $\ensuremath{{\rm D}} + \ensuremath{\null^4{\rm He}} $.
Open with DEXTER

2.2 Variation in ${\alpha }$ with ${\eta _B}$ fixed

Once again, we compute the light nuclei abundances for different values of $\frac{\Delta \alpha}{\alpha_0}$, keeping $\eta _{\rm B}$ fixed to the WMAP estimation (Spergel et al. 2006), and perform a statistical analysis in order to obtain the best-fit value for $\frac{\Delta \alpha}{\alpha_0}$. As pointed out in the previous section, there is no good fit for the whole data set and for $\ensuremath{\null^4{\rm He}} + \ensuremath{\null^7{\rm Li}} $, even for $\frac{\Delta \alpha}{\alpha_0} \neq 0$ (see Table 3).

For $\ensuremath{{\rm D}} + \ensuremath{\null^7{\rm Li}} $, the result is consistent with variation in ${\alpha }$within $6\sigma$; meanwhile, for $\ensuremath{{\rm D}} + \ensuremath{\null^4{\rm He}} $, there is no variation in ${\alpha }$ within $3\sigma $. In Figs. 4 and 5 the 1-dimensional likelihood is shown, considering the available data of $\ensuremath{{\rm D}} + \ensuremath{\null^7{\rm Li}} $ and $\ensuremath{{\rm D}} + \ensuremath{\null^4{\rm He}} $, respectively. To test Bekenstein model, we consider the results obtained using $\ensuremath{{\rm D}} + \ensuremath{\null^4{\rm He}} $ in this section. It is worth mentioning that, if we do not consider $\ensuremath{\null^7{\rm Li}} $ data, the results with and without varying $\eta _{\rm B}$ are the same.

Table 3: Best-fit parameter values and $1\sigma $ errors for the BBN constraints on $\frac{\Delta \alpha}{\alpha_0}$.


  \begin{figure} \par\includegraphics[angle=-90,width=7cm,clip]{8605fig4.ps}\end{figure} Figure 4: One-dimensional likelihood of $\frac{\Delta \alpha}{\alpha_0}$ using the data of $\ensuremath{{\rm D}} + \ensuremath{\null^7{\rm Li}} $.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=7cm,clip]{8605fig5.ps}\end{figure} Figure 5: One-dimensional likelihood of $\frac{\Delta \alpha}{\alpha_0}$ using the data of $\ensuremath{{\rm D}} + \ensuremath{\null^4{\rm He}} $.
Open with DEXTER

   
3 Bounds from CMB

Cosmic microwave background radiation provides valuable information about the physical conditions of the universe just before the decoupling of matter and radiation, and it allows their estimation thanks to its dependence upon cosmological parameters. Any change in the value of the fine structure constant affects the physics during recombination, mainly the redshift of this epoch, due to a shift in the energy levels and, in particular, the binding energy of hydrogen. The Thompson scattering cross section is also changed for all particles, since it is proportional to $\alpha^2$; therefore, the CMB power spectrum is modified by a change in the relative amplitudes of the Doppler peaks and shifts in their positions. On the other hand, changes in the cosmological parameters produce similar effects. Previous analysis of the CMB data including a possible variation in ${\alpha }$ have been performed by Martins et al. (2002), Rocha et al. (2003), and Ichikawa et al. (2006). In this paper, we use the WMAP 3-year temperature and temperature-polarization power spectrum (Spergel et al. 2006) and other CMB experiments, such as CBI (Readhead et al. 2004), ACBAR (Kuo et al. 2004), BOOMERANG (Jones et al. 2006; Piacentini et al. 2006), and the power spectrum of the 2dFGRS (Cole et al. 2005). We consider a spatially-flat cosmological model with adiabatic density fluctuations. The parameters of our model are

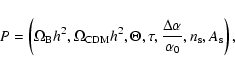\begin{displaymath}% P=\left(\Omega_{\rm B} h^2, \Omega_{\rm CDM} h^2, \Theta, \tau, \frac{\Delta \alpha}{\alpha_0}, n_{\rm s}, A_{\rm s}\right), \end{displaymath} (1)

where $\Omega_{\rm CDM} h^2$ is the dark matter density in units of the critical density, $\Theta$ gives the ratio of the comoving sound horizon at decoupling to the angular diameter distance to the surface of last scattering, $\tau$ is the reionization optical depth, $n_{\rm s}$the scalar spectral index, and $A_{\rm s}$ the amplitude of the density fluctuations.

We used a Markov-chain Monte Carlo method to explore the parameter space because the exploration of a multidimensional parameter space with a grid of points is computationally prohibitive. We used the publicly-available CosmoMC code of Lewis & Bridle (2002), which uses CAMB (Lewis et al. 2000) and RECFAST (Seager et al. 1999) to compute the CMB power spectra, and we modified them to include the possible variation in ${\alpha }$ at recombination. We ran eight different chains. We used the convergence criterion of Raftery & Lewis (1992) to stop the chains when R-1 < 0.003, which is more stringent than the usually adopted value. Results are shown in Table 4 and Fig. 6. Figure 6 shows a strong degeneracy between ${\alpha }$ and $\Theta$, which is directly related to H0, and also between ${\alpha }$ and $\Omega_{\rm B} h^2$. The values obtained for $\Omega_{\rm B} h^2$, h, $\Omega_{\rm CDM} h^2$, $\tau$, and $n_{\rm s}$ agree, within $1\sigma $, with the respective values obtained without including any variation in ${\alpha }$ by the WMAP team (Spergel et al. 2006). Our results are consistent within $2\sigma $ with no variation in ${\alpha }$ at recombination.

Table 4: Mean values and errors for the principal and derived parameters including ${\alpha }$ variation.


  \begin{figure} \par\includegraphics[width=14cm,clip]{8605fig6.eps}\end{figure} Figure 6: Marginalized posterior distributions obtained with CMB data, including the WMAP 3-year data release plus 2dFGRS power spectrum. The diagonal shows the posterior distributions for individual parameters, and the other panels show the 2D contours for pairs of parameters, marginalizing over the others.
Open with DEXTER

We also performed the analysis considering only CMB data. In that case, the strong degeneracy between ${\alpha }$ and H0 made the chains cover all the wide H0 prior, making it impossible to find reliable mean values and errors. Hence, we added a Gaussian prior to H0, which was obtained from the Hubble Space Telescope Key Project (Freedman et al. 2001), and chose the values of the mean and errors as those inferred from the closest objects in that paper, so we could neglect any possible difference between the value of ${\alpha }$ at that redshift and the present value. In this way, we post-processed the chains and found that the most stringent constraints were obtained in the first analysis (see Figs. 7 and 8).

   
4 Bounds from quasar absorption systems

Quasar absorption systems present ideal laboratories for searching for any temporal variation in the fine structure constant. Quasar spectra of high redshift show the absorption resonance lines of the alkaline ions like CIV, MgII, FeII, SiIV, and others. The relative magnitude of the fine splitting of the resonance lines of alkaline ions is proportional to $\alpha^2$. Several authors (Murphy et al. 2001c; Chand et al. 2005; Cowie & Songaila 1995; Martínez Fiorenzano et al. 2003; Varshalovich et al. 1996) have studied the SiIV doublet absorption lines systems at different redshifts ( 2.5 < z < 3.33), to put bounds on the variation in ${\alpha }$. Bahcall et al. (2004) used O III emission lines. Webb et al. (1999) and Murphy et al. (2003,2001b) compared transitions of different species with different masses and led to a single data consistent with time-varying fine structure constant for a range of redshifts ( 0.5 < z < 3.5). However, other recent independent analyses of similar data (Grupe et al. 2005; Srianand et al. 2004; Quast et al. 2004) have found no variation. Another method of testing cosmological variation in ${\alpha }$ was proposed by Levshakov et al. (2005) from pairs of Fe II lines observed in individual exposures from a high-resolution spectrograph. The authors found no variation in ${\alpha }$ at z=1.15 and z=1.839. However, a recent reanalysis of the spectrum of the quasar Q1101-264 has found variability within $1\sigma $ (Levshakov et al. 2007). We also consider in our analysis the bounds mentioned in Wolfe et al. (1976), Spinrad & McKee (1979), Cowie & Songaila (1995), and Tzanavaris et al. (2007), which were obtained by comparing the optical and radio redshifts. Furthermore, Murphy et al. (2001a) compare molecular and radio lines and obtain more stringent constraints. On the other hand, Darling (2004) reports bounds on the variation in ${\alpha }$ at z=0.2467 from the satellite 18 cm OH conjugate lines. Finally, Kanekar et al. (2005) compared the HI and OH main line absorption redshifts of the different components in the z=0.765 absorber and the z=0.685 lens toward B0218+357 to place stringent constraints on changes in $F= g_{\rm p} \left({\frac{\alpha^2}{\mu}}\right)^{1.57}$.

Since we want to compare the prediction of ${\alpha }$ evolution with cosmological time, we consider each individual measurement of the papers cited above and not the average value reported in each paper.


  \begin{figure} \par\includegraphics[width=6cm,clip]{8605fig7.eps}\end{figure} Figure 7: The $1\sigma $ and $2\sigma $ confidence level contours obtained with CMB data with and without data of the 2dFGRS power spectrum.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6cm,clip]{8605fig8.eps}\end{figure} Figure 8: The $1\sigma $ and $2\sigma $ confidence level contours obtained with CMB data with and without data of the 2dFGRS power spectrum.
Open with DEXTER

   
5 Bounds from geophysical data

5.1 The Oklo phenomenon

One of the most stringent limits on the time variation in the fine structure constant follows from the analysis of isotope ratios in the natural uranium fission reactor that operated 1.8 $\times$ 109 years ago at the present day site of the Oklo mine in Gabon, Africa. The proof of the past existence of a spontaneous chain reaction in the Oklo ore consists essentially of a substantial depletion of the uranium isotopic ratio  $^{235}{\rm U}/^{238}{\rm U}$with respect to the current standard value in terrestrial samples and a correlated peculiar distribution of some rare-earth isotopes. From an analysis of nuclear and geochemical data, the operating conditions of the reactor could be reconstructed and the thermal neutron capture cross sections of several nuclear species measured.

The high values of the thermal capture cross sections of $^{149}{\rm Sm}$, $^{155}{\rm Gd}$, and $^{157}{\rm Gd}$ are due to the existence of resonances in the thermal region. In the presence of such a resonance, the mono-energetic capture cross section is described well in the thermal region by the Breit-Wigner formula:

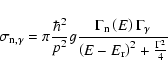\begin{displaymath}% \sigma_{{\rm n},\gamma}=\pi \frac{\hbar ^2}{p^2} g \frac{\G... ...gamma}}{{\left(E - E_{\rm r}\right)}^2 + \frac{\Gamma^2}{4}} \end{displaymath} (2)

where p is the momentum of the neutron, g a statistical factor depending upon the spins of the compound nucleus of the incident neutron and target nucleus, $\Gamma_{\gamma}$ is the radiative width, ${\Gamma}_{\rm n}\left(E\right)$ is the neutron partial width, ${\Gamma}$ is the total width. Thus, a shift in the lowest lying resonance level in $^{149}{\rm Sm}: \Delta = E_{\rm r}^{149{\rm (Oklo)}} -E_{\rm r}^{149{\rm (now)}}$ can be derived from a shift in the neutron capture cross section of the same nucleus (Damour & Dyson 1996; Fujii et al. 2000). The shift in the resonance energy can be translated (Damour & Dyson 1996) into bounds on a possible difference between the value of ${\alpha }$ during the Oklo phenomenon and its present value.

Various authors (Damour & Dyson 1996; Fujii et al. 2000; Lamoreaux & Torgerson 2004) have analyzed the Oklo data in order to put bounds on ${\alpha }$. Fujii et al. (2000) used samples of $^{149}{\rm Sm}$, $^{155}{\rm Gd}$, and $^{157}{\rm Gd}$ to reanalyze the bound on the resonance energy. They took the effect of contamination into account, assuming the same contamination parameter for all samples. Lamoreaux & Torgerson (2004) employ a more realistic spectrum than the commonly used Maxwell-Boltzmann to put the following bound on ${\alpha }$:

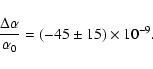\begin{displaymath}% \frac{\Delta \alpha}{\alpha_0} = (-45 \pm 15) \times 10^{-9}. \end{displaymath} (3)

This bound is very similar to the one found by Fujii et al. (2000) and therefore we are going to consider it when testing the Bekenstein model.

5.2 Long-lived ${\beta }$ decayers

The half-life of long-lived ${\beta }$ decayers such $^{187}\rm {Re}$ has been used by several authors to find bounds on the variation in ${\alpha }$. These nuclei have a very long half-life that has been determined either in laboratory measurements or by comparison with the age of meteorites. This last quantity can be measured from ${\alpha }$-decay radioactivity analysis. The most stringent bound on the variation in the half-life, $\lambda$, proceeds from the comparison of $^{187}\rm {Re}$ decay in the Solar System formation and the present (Olive et al. 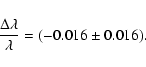2004):

\begin{displaymath}% \frac{\Delta \lambda}{\lambda} = (-0.016 \pm 0.016). \end{displaymath} (4)

Sisterna & Vucetich (1990) derived a relationship between the shift in the half-life of long-lived ${\beta }$ decayers and a possible variation between the values of the fundamental constants $\alpha, \Lambda _{\rm QCD}$, and $G_{\rm F}$ at the age of the meteorites and their values now. They used a phenomenological model in which the abundance of any unstable nucleus will obey the following decaying law:

\begin{displaymath}% N = N_0 \exp\left[-\left(\lambda t+ \dot \lambda t^2/2\right)\right]. \end{displaymath} (5)

In this paper, we only consider ${\alpha }$ variation and, therefore, the following equation holds:

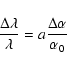\begin{displaymath}% \frac{\Delta \lambda}{\lambda} = a \frac{\Delta \alpha}{\alpha_0} \end{displaymath} (6)

where a=21600 for $^{187}\rm {Re}$.

   
6 Bounds from laboratory

The comparison of different atomic transition frequencies over time can be used to determine the present value of the temporal derivative of ${\alpha }$. Indeed, the most stringent limits on the variation in ${\alpha }$ are obtained using this method. The dependence of hyperfine transition frequencies with ${\alpha }$ can be expressed as

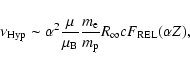\begin{displaymath}% \nu_{\rm Hyp} \sim \alpha^2 \frac{\mu}{\mu_{\rm B}}\frac{m_{\rm e}}{m_{\rm p}} R_{\infty} c F_{\rm REL}(\alpha Z), \end{displaymath} (7)

where $\mu$ is the nuclear magnetic moment, $\mu_{\rm B}$ the Bohr magneton, $R_{\infty}$ Rydberg's constant, $m_{\rm p}$ and $m_{\rm e}$ are the proton and electron mass, and $F_{\rm REL}$ is the relativistic contribution to the energy.

The comparison of rates between clocks based on hyperfine transitions in alkali atoms with different atomic number Zcan be used to set bounds on $\alpha^k \frac{\mu_{A_1}}{\mu_{A_2}}$where k depends on the frequencies measured and $\mu_{A_i}$ refers to the nuclear magnetic moment of each atom. The first three entries of Table 5 show the bounds on $\frac{\dot{\alpha}}{\alpha_0}$ obtained by comparing hyperfine transition frequencies in alkali atoms.

On the other hand, an optical transition frequency has a different dependence on ${\alpha }$:

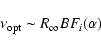\begin{displaymath}% \nu_{\rm opt} \sim R_{\infty} B F_i(\alpha) \end{displaymath} (8)

where B is a numerical constant assumed not to vary in time and $F_i(\alpha)$ is a dimensionless function of ${\alpha }$ that takes into account level shifts due to relativistic effects. The comparinson between an optical transition frequency and an hyperfine transition frequency can be used to set bound on $\alpha^k \frac{m_{\rm e}}{m_{\rm p}} \frac{\mu_{\rm A}}{\mu_{\rm B}}$.

Different authors (Bize et al. 2003; Fischer et al. 2004; Peik et al. 2004) have measured different optical transitions and set bounds on the variation in ${\alpha }$ using different methods. Fischer et al. (2004) have considered the joint variation in ${\alpha }$ and $\frac{\mu_{Cs}}{\mu_{\rm B}}$. We reanalyzed the data of Fischer et al. (2004), considering only the ${\alpha }$ variation, yielding the fifth entry of Table 5. On the other hand, Peik et al. (2004) measured an optical transition frequency in $^{171}{\rm Yb} $ with a cesium atomic clock. They performed a linear regression analysis using this result, together with other optical transition frequency measurements from Bize et al. (2003) and Fischer et al. (2004). We have already considered the other data; therefore, we reanalyzed the data, using only the comparison between Yb and Cs frequency, yielding the sixth entry in Table 5.

Table 5: The compared clocks, the value of $\frac{\dot{\alpha}}{\alpha_0}$, its corresponding error in units of $10^{-15}~{\rm yr}^{-1}$, the time interval for which the variation was measured, and the reference.

   
7 The model

In this section, we solve the equation of the scalar field, which drives the variation in ${\alpha }$ in the Bekenstein model. First, we obtain the analytical solution for the Friedmann-Robertson-Walker (FRW) equation for two different regimes and assure the continuity of the solution and its derivative. Unlike other works (Olive & Pospelov 2002; Barrow et al. 2002), we do not assume that the scalar field is connected with the dark matter field. We consider the weak field approximation, so only the electrostatic contribution to the scalar field equation is relevant. In this framework, the electric charge can be expressed in the form:

\begin{displaymath}% e=e_0 \epsilon(x^\mu) \end{displaymath} (9)

with $\epsilon$ a scalar field. The Lagrangian for a charged particle of rest mass m and charge $e_0 \epsilon$ is

 \begin{displaymath}% L=-m c \left(u^\mu u_\mu\right)^{1/2} + \frac{e_0 \epsilon}{c} u^\mu A_\mu \end{displaymath} (10)

where $u^\mu=\frac{{\rm d} x^\mu}{{\rm d}\tau}$, L a Lorentz invariant. After a gauge transformation, it changes only by a perfect derivative. Following Bekenstein (1982), we obtain the Lagrange equations for (10),

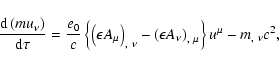\begin{displaymath}% \frac{{\rm d}\left(m u_\nu\right)}{{\rm d} \tau}=\frac{e_0}... ...t(\epsilon A_\nu\right)_{,~ \mu}\right\}u^\mu -m_{,~ \nu} c^2, \end{displaymath} (11)

and identify $F_{\mu\nu}$:

\begin{displaymath}% F_{\mu \nu} = \epsilon^{-1} \left[\left(\epsilon A_{\nu}\right),_{\mu} -\left(\epsilon A_{\mu}\right),_{\nu} \right]. \end{displaymath} (12)

Following Bekenstein (1982), the total action can be written as

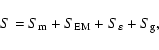\begin{displaymath}% S=S_{\rm m}+S_{\rm EM}+S_\varepsilon + S_{\rm g}, \end{displaymath} (13)

where

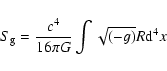\begin{displaymath}% S_{\rm g} = \frac{c^4}{16 \pi G} \int \sqrt{(-g)} R {\rm d}^4x \end{displaymath} (14)

belongs to the gravitational sector of the theory,

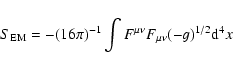\begin{displaymath}% S_{\rm EM}= -{\left(16 \pi\right)}^{-1} \int F^{\mu \nu} F_{\mu \nu} {(-g)}^{1/2} {\rm d}^4x \end{displaymath} (15)

is the electromagnetic action, and

\begin{displaymath}% S_{\rm m} = \sum_i \int \frac{1}{\gamma}\left[-m c^2 +(e_0 ... ...\mu}\right] \delta^3\left[x^i - x^i (\tau)\right] {\rm d}^4x \end{displaymath} (16)

is the matter action where the coupling between matter and the gauge field depends on the scalar field responsible for the variation in ${\alpha }$. The action of the scalar field can be expressed as

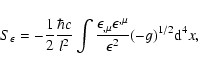\begin{displaymath}% S_\epsilon = -\frac{1}{2} \frac{\hbar c}{l^2} \int \frac{\e... ...on_{,\mu}\epsilon^{,\mu}}{\epsilon^2} {(-g)}^{1/2} {\rm d}^4x, \end{displaymath} (17)

where l is a scale length, which is introduced for dimensional reasons, and one of the assumption of this theoretical framework is $l>L_{\rm p}$. It will be shown (see Appendix A) that this condition implies violation of the weak equivalence principle. However, this requirement could be relaxed, due to string theory considerations (Antoniadis & Pioline 1999; Bachas 2000).

Varying the total action with respect to the gauge field, the modified Maxwell equations are obtained:

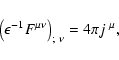\begin{displaymath}% \left(\epsilon^{-1} F^{\mu \nu}\right)_{;~ {\nu}} = 4 \pi j^{~\mu}, \end{displaymath} (18)

where

\begin{displaymath}% j^{~\mu} = \sum_i \frac{e_0}{c \gamma} u^{\mu} \frac{1}{\sqrt {-g}} \delta^3\left[x^i - x^i\left(\tau\right)\right], \end{displaymath} (19)

along with the equation of motion of the scalar field:

 \begin{displaymath}% \Box \ln \epsilon = \frac{l^2}{\hbar c} \left[ \epsilon \fr... ...l \epsilon} - \frac{1}{8 \pi} F^{\mu \nu} F_{\mu \nu} \right] \end{displaymath} (20)

where

\begin{displaymath}% \sigma = \sum _ i \frac{m c^2}{\gamma} \frac{1}{\sqrt {-g} }\delta^3\left[x^i - x^i\left(\tau\right)\right]. \end{displaymath} (21)

In an expanding Universe and evaluating the r.h.s. of Eq. (20) following Bekenstein (1982), the following expression can be obtained:
 
$\displaystyle % \partial_t \left(\frac{\partial_t{\epsilon}}{\epsilon} a^3(t)\right)= -a^3(t) \frac{l^2}{\hbar c}\zeta \rho_{\rm m} c^4$     (22)

where $\zeta=\frac{\rho_{\rm em}}{\rho_{\rm m}}$ is a dimensionless parameter that measures the fraction of mass in the form of Coulomb energy to the total matter density  $\rho_{\rm m}$. As suggested in Sandvik et al. (2002), we use $\zeta=10^{-4}$. Integrating Eq. (22), in an expanding universe and using $\rho_{\rm m}= \frac{ \Omega_{\rm m} \rho_{\rm c}}{a^3(t)}$, we obtain:
 
$\displaystyle % \frac{\partial_t{\epsilon}}{\epsilon} =-\frac{3}{8 \pi} \zeta \... ...p}}\right)^2 H_0^2 \Omega_{\rm m} \left(\frac{a_0}{a(t)}\right)^3 (t-t_{\rm c})$     (23)

where $t_{\rm c}$ is an integration constant and $\Omega_{\rm m}$ the total matter density in units of the critical density ( $\rho_{\rm c}$). In order to solve the above equation, we must first solve the Friedmann equation for the different regimes we are considering.

In a flat Friedman-Robertson-Walker (FRW) universe, the equation for the scale factor reads as

 
$\displaystyle % \left(\frac{\partial_t{a}}{a}\right)^2 = H_0^2 \left\{\Omega_{\... ...right)^3+\Omega_{\rm r} \left(\frac{a_0}{a(t)}\right)^4+\Omega_\Lambda \right\}$     (24)

with the initial condition $ a\left( 0\right)=0$, and satisfying $a\left(t_0\right)=a_0$=1. In the above equation, we assume that the scalar field contribution is negligible. Usually, this contribution is proportional to $\left(\frac{\partial_t \epsilon}{\epsilon}\right)^2$ and we expect the variation in ${\alpha }$ to be about 10-5.

The FRW equation has no analytical solution in terms of elementary functions when the radiation, matter, and cosmological constant are considered. We build a piecewise approximate solution by joining solutions obtained by conserving only some terms of the r.h.s of Eq. (24). We solve the FRW equation for two different cases: a) radiation and matter and b) matter and cosmological constant. In such a way, solution a) can be applied to nucleosynthesis and recombination of primordial hydrogen, whereas solution b) is proper for quasar absorption systems, geophysical data, and atomic clocks.

First, we integrate Eq. (24), considering only matter and radiation. To get an analytical expression for the scale factor as a function of time, we change the independent variable to conformal time $\eta$ as follows: $a_{\rm RM} {\rm d} \eta = {\rm d}t$. Defining $\xi = H_0 \eta$, we can write

 
$\displaystyle % a_{\rm RM}(\xi) =\frac{\xi^2 \Omega_{\rm m}}{4} + \xi \sqrt{\Omega_{\rm r}}.$     (25)

The time can be expressed as
 
$\displaystyle % H_o t(\xi)=\frac{\xi^3 \Omega_{\rm m}}{12} +\frac{\xi^2 \sqrt{\Omega_{\rm r}}}{2}\cdot$     (26)

Now, we solve Eq. (24) considering only the matter and cosmological constant and obtain:
 
$\displaystyle % a_{\rm MC}(t) = \left( \frac{\Omega_{\rm m}}{\Omega_\Lambda}\ri... ... +{\rm arcsh} \sqrt{\frac{\Omega_\Lambda}{\Omega_{\rm m}}}\right)\right]^{2/3}.$     (27)

The expansion factor must be a continuous and smooth function of time, and to match both solutions, the following conditions have to be fulfilled:


    $\displaystyle a_{\rm RM}(t_1) = a_{\rm MC}(t_1)$  
    $\displaystyle \frac{{\rm d} a_{\rm RM}}{{\rm d} t}(t_1) = \frac{{\rm d} a_{\rm MC}}{{\rm d} t}(t_1)$  

from where we obtain:
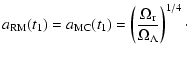$\displaystyle % a_{\rm RM}(t_1)=a_{\rm MC}(t_1)=\left(\frac{\Omega_{\rm r}}{\Omega_\Lambda}\right)^{1/4}\cdot$     (28)

In order to compare with astronomical and local bounds, we use the value of the cosmological parameters reported in Yao et al. (2006).

Now we can solve Eq. (23) using Eqs. (25) and (27). Using $\ln \frac{\epsilon (t)}{\epsilon (t_0)} \simeq \frac{1}{2} \frac{\Delta \alpha}{\alpha_0}$, we obtain the following expressions for the variation in ${\alpha }$ in the two different regimes. Defining $\lambda(\xi)=\xi \Omega_{\rm m} \ +4 \sqrt{\Omega_{\rm r}}$ for t<t1:

 
                         $\displaystyle % \frac{\Delta \alpha}{\alpha_0}$ = $\displaystyle -\frac{1}{\pi} \zeta \left(\frac{l}{L_{\rm p}}\right)^2 {\rm ln} ... ..._{\rm p}}\right)^2 {\rm ln} \left(\frac{\Omega_{\rm r}}{\Omega_\Lambda} \right)$  
    $\displaystyle +\frac{2}{\pi} \zeta \left(\frac{l}{L_{\rm p}}\right)^2 \sqrt{\Omega_{\rm r}} \left[\frac{1}{\lambda(\xi )} -\frac{1}{\lambda(\xi_1 )}\right]$  
    $\displaystyle -\frac{3}{4 \pi} \zeta \left(\frac{l}{L_{\rm p}}\right)^2 \frac{\... ...left\{\frac{1}{\xi}-\frac{1}{\xi_1}+\frac{\Omega_{\rm m}}{\lambda(\xi )}\right.$  
    $\displaystyle \left. -\frac{\Omega_{\rm m}}{\lambda(\xi_1 )} +\frac{ \Omega_{\r... ...}}{\rm ln}\left[\frac{\xi \lambda(\xi_1 )} {\xi_1 \lambda(\xi )}\right]\right\}$  
    $\displaystyle +\frac{1}{2\pi} \zeta \left(\frac{l}{L_{\rm p}}\right)^2 \sqrt{\O... ...m m}}\left(\frac{\Omega_{\rm r}} {\Omega_\Lambda}\right)^{3/4}}\right)} \right.$  
    $\displaystyle \left.-\frac{H_0\left(t_0-t_{\rm c}\right)}{{\rm th}\left({\rm arcsh} \sqrt{\frac{\Omega_\Lambda}{\Omega_{\rm m}}} \right)} \right\}\cdot$ (29)

Defining $\nu=H_0 t$, we can write for t>t1:
 
                              $\displaystyle % \frac{\Delta \alpha}{\alpha_0}$ = $\displaystyle \frac{1}{2\pi} \zeta \left(\frac{l}{L_{\rm p}}\right)^2 \sqrt{\Omega_\Lambda}$  
    $\displaystyle \times \left\{\frac{ \nu - \nu_{\rm c} }{{\rm th}\left(\frac{3}{2... ...left({\rm arcsh} \sqrt{\frac{\Omega_\Lambda}{\Omega_{\rm m}}} \right)} \right\}$  
    $\displaystyle -\frac{1}{3 \pi} \zeta \left(\frac{l}{L_{\rm p}}\right)^2 {\rm ln... ...\left(\frac{3}{2} \sqrt{\Omega_\Lambda} \left(\nu-\nu_0 \right) \right. \right.$  
    $\displaystyle \left. \left. + {\rm arcsh}\sqrt{\frac{\Omega_\Lambda}{\Omega_{\rm m}}} \right)\right].$ (30)

   
8 Results

8.1 The early universe

In Sect. 2, we used the primordial abundances of $\ensuremath{{\rm D}} $, $\ensuremath{\null^4{\rm He}} $, and $\ensuremath{\null^7{\rm Li}} $ to put bounds on the variation in ${\alpha }$ in the early universe. First, we performed a statistical analysis in order to check the consistency of each group of data and modified the observational errors accordingly. We have shown that all data could not be fitted at the same time, but reasonable fits can be found considering two groups of data at the time. We analyzed the cases where the baryon density is a free parameter and where it is fixed to the WMAP value. Tables and confidence contours are shown in Sect. 2. In all analyses described in Sect. 2 (with or without allowing $\eta _{\rm B}$ to vary), we find that, excluding the $\ensuremath{\null^7{\rm Li}} $ data, our results are consistent with WMAP estimation and no variation in ${\alpha }$.

In Sect. 3 we used the three-year WMAP data, together with other CMB experiments and the 2dFGRS power spectrum to put constraints on the variation in ${\alpha }$ during recombination. Tables and confidence contours are shown in Sect. 3.

We summarize our results for the variation in the fine structure constant in Table 6. Our results are consistent with no variation of the fine structure constant in the early Universe.

Table 6: Best-fit parameter values and $1\sigma $ errors for the BBN and CMB constraints on $\frac{\Delta \alpha}{\alpha_0}$.

8.2 The Bekenstein model

In this section we compare the Bekenstein model predictions obtained in Sect. 7 with the astronomical and geophysical data described in Sects. 4-6 and with the bounds on ${\alpha }$ from the early universe we have obtained in Sects. 2 and 3.

Fixing the time, Eqs. (29) or (30) gives the prediction for the ${\alpha }$ variation as a function of two free parameters: $\left(\frac{l}{L_{\rm p}}\right)^2$ and $\left(\frac{l}{L_{\rm P}}\right)^2 H_0 t_{\rm c} $. Therefore, we have N(number of data we are considering: 1 from Oklo, 1 from $^{187}\rm {Re}$, 6 from atomic clocks, 1 from BBN, 1 from CMB, 274 from QSO) conditional equations with two unknowns. We perform a $\chi^2$ test to obtain the best values of the free parameters of Bekenstein's theory. Our results are shown in Table 7.

Table 7: Best-fit parameter values and $1\sigma $ errors of the Bekenstein model.

We also performed the same statistical analysis discarding bounds of each group of data. In most of these cases, the results are similar to those considering all data. However, discarding the bound from nucleosynthesis changes the value of $\left(\frac{l}{L_{\rm P}}\right)^2 H_0 t_{\rm c} $ several orders of magnitude. Thus, the bound obtained from the primordial abundances of the light elements are crucial for fixing the value of $\left(\frac{l}{L_{\rm P}}\right)^2 H_0 t_{\rm c} $.

Our results show that the available limits on the ${\alpha }$ variation are inconsistent with the scale length of the theory l being larger than Planck scale.

   
9 Summary and discussion

In this paper, we have analyzed the variation in ${\alpha }$ in the early universe. We modified the Kawano code, CAMB, and CosmoMC in order to include the possible variation in ${\alpha }$. We used recent observational abundances of light elements to obtain bounds on $\frac{\Delta \alpha}{\alpha_0}$ at the time of primordial nucleosynthesis. We used recent data from the CMB and the 2dFGRS power spectrum to limit the variation in ${\alpha }$ at recombination. Results obtained in Sects. 2 and 3 are consistent with no variation in ${\alpha }$ during primordial nucleosynthesis and recombination of neutral hydrogen.

It is important to check that the values of the baryon density obtained using the light elements abundances (Sect. 2) are consistent with the respective value obtained using data from the CMB (Sect. 3). Using the relation $\eta_{\rm B} = 2.739$ $\times$ $10^{-8} \Omega_{\rm B} h^2$, we find that results are consistent within $1\sigma $.

We also used our results from the early universe and recent bounds from the late universe to test the Bekenstein model. We have improved the analysis of the Bekenstein model with respect to a previous work (Landau & Vucetich 2002) in various aspects: i) we obtained analytical expressions for the Bekenstein model that include the dependence on $t_{\rm c}$ (while other authors put $t_{\rm c}=0$) for the variation in ${\alpha }$ in two regimes: a) radiation and matter and b) matter and cosmological constant; ii) the whole data set is updated.

On the other hand, Eötvös-like experiments provide stringent constraints on the Bekenstein-model parameters. Constraints for $\frac{l}{L_{\rm P}}$ can be set using these kinds of experiments (see Appendix A). We obtain $\frac{l}{L_{\rm P}}<8.7$ $\times$ 10-3, which is one order of magnitude below the limits obtained in this paper using astronomical and geophysical data: $\frac{l}{L_{\rm P}}<6$ $\times$ 10-2. Nevertheless, the importance of our analysis lies in the fact that, while Eötvös-like experiments test planetary scales, in this paper we test different time scales, namely cosmological time scales.

The values obtained for the free parameters of the model disagree with the supposition that $l>L_{\rm p}$, implied in Bekenstein's framework. However, this requirement could be relaxed. Indeed, it should be noted that Bekenstein's framework is very similar to the dilatonic sector of string theory, and it has been pointed out that, in the context of string theories (Antoniadis & Pioline 1999; Bachas 2000) there is no need for a universal relation between the Planck and the string scales.

Acknowledgements
Support for this work was provided by Project G11/G071, UNLP, and PIP 5284 CONICET. The authors would like to thank Andrea Barral, Federico Bareilles, Alberto Camyayi, and Juan Veliz for technical and computational support. The authors would also like to thank Ariel Sanchez for support with CosmoMC. MEM wants to thank Sergio Iguri for the helpful discussions. CGS gives special thanks to Licia Verde and Nelson Padilla for useful discussions. SJL wants to thank Michael Murphy for useful discussions. The authors are grateful to Jacob Bekenstein for valuable advice.

   
Appendix A: Eötvös-like experiments

A general expression for the Eötvös parameter and recent calculations of the proton-neutron mass difference were performed by Chamoun & Vucetich (2002). From this work it follows that

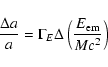\begin{displaymath}% \frac{\Delta a}{a}=\Gamma_E \Delta \left(\frac{E_{\rm em}}{Mc^2}\right) \end{displaymath} (A.1)

where a is the acceleration for different bodies falling freely in a gravitational field g, $E_{\rm em}$ the electromagnetic energy of the falling bodies, and M the nucleon mass at rest. A bound on $\Gamma_E$ was estimated in the same paper: $\left\vert \Gamma_E \right\vert<1.2$ $\times$ 10-9. Comparing this expression with Eq. (45) of Bekenstein (1982),

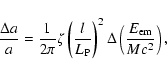\begin{displaymath}% \frac{\Delta a}{a}= \frac{1}{2\pi} \zeta \left(\frac{l}{L_{\rm P}}\right)^2 \Delta\left( \frac{E_{\rm em}}{Mc^2}\right), \end{displaymath} (A.2)

it follows that

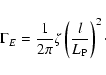\begin{displaymath}% \Gamma_E = \frac{1}{2\pi} \zeta \left(\frac{l}{L_{\rm P}}\right)^2\cdot \end{displaymath} (A.3)

We obtain $\frac{l}{L_{\rm P}}<8.7$ $\times$ 10-3.

References

 
Copyright ESO 2008