A&A 478, 823-842 (2008)
DOI: 10.1051/0004-6361:20077919
Bright OB stars in the Galaxy
IV. Stellar and wind parameters of early to late B supergiants
N. Markova1
- J. Puls2
1 - Institute of Astronomy,
National Astronomical Observatory,
Bulgarian Academy of Sciences,
PO Box 136, 4700 Smolyan, Bulgaria
2 - Universitäts-Sternwarte,
Scheinerstrasse 1, 81679 München, Germany
Received 21 May 2007 / Accepted 6 November 2007
Abstract
Context. B-type supergiants represent an important phase in the evolution of massive stars. Reliable estimates of their stellar and wind parameters, however, are scarce, especially at mid and late spectral subtypes.
Aims. We apply the NLTE atmosphere code FASTWIND to perform a spectroscopic study of a small sample of Galactic B-supergiants from B0 to B9. By means of the resulting data and incorporating additional datasets from alternative studies, we investigate the properties of OB-supergiants and compare our findings with theoretical predictions.
Methods. Stellar and wind parameters of our sample stars are determined by line profile fitting, based on synthetic profiles, a Fourier technique to investigate the individual contributions of stellar rotation and ``macro-turbulence'' and an adequate approach to determine the Si abundances in parallel with micro-turbulent velocities.
Results. Due to the combined effects of line- and wind-blanketing, the temperature scale of Galactic B-supergiants needs to be revised downward, by 10 to 20%, the latter value being appropriate for stronger winds. Compared to theoretical predictions, the wind properties of OB-supergiants indicate a number of discrepancies. In fair accordance with recent results, our sample indicates a gradual decrease in  over the bi-stability region, where the limits of this region are located at lower
over the bi-stability region, where the limits of this region are located at lower
 than those predicted. Introducing a distance-independent quantity Q' related to wind-strength, we show that this quantity is a well defined, monotonically increasing function of
than those predicted. Introducing a distance-independent quantity Q' related to wind-strength, we show that this quantity is a well defined, monotonically increasing function of
 outside this region. Inside and from hot to cool,
outside this region. Inside and from hot to cool,  changes by a factor (in between 0.4 and 2.5) which is much smaller than the predicted factor of 5.
changes by a factor (in between 0.4 and 2.5) which is much smaller than the predicted factor of 5.
Conclusions. The decrease in  over the bi-stability region is not over-compensated by an increase of
over the bi-stability region is not over-compensated by an increase of  , as frequently argued, provided that wind-clumping properties on both sides of this region do not differ substantially.
, as frequently argued, provided that wind-clumping properties on both sides of this region do not differ substantially.
Key words: stars: early-type - stars: supergiants - stars: fundamental parameters
- stars: mass-loss - stars: winds, outflows
Hot massive stars are key objects for studying and understanding many exciting
phenomena in the Universe such as re-ionisation and 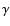 -ray bursters. Due
to their powerful stellar winds hot massive stars are important contributors
to the chemical and dynamical evolution of galaxies, and in the distant
Universe they dominate the integrated UV radiation in young galaxies.
-ray bursters. Due
to their powerful stellar winds hot massive stars are important contributors
to the chemical and dynamical evolution of galaxies, and in the distant
Universe they dominate the integrated UV radiation in young galaxies.
While the number of Galactic O and early B stars with reliably determined
stellar and wind parameters has progressively increased during the last few
years (e.g., Herrero et al. 2002; Bouret et al. 2005; Repolust et al. 2004; Crowther et al. 2006; Martins et al. 2005; Garcia & Bianchi 2004), mid and late B supergiants (SGs) are currently
under-represented in the sample of stars investigated so far. Given the fact
that B-SGs represent an important phase in the evolutionary sequence of
massive stars, any study aiming to increase our knowledge of these stars
would be highly valuable, since it would allow several important issues to
be addressed (see below).
Compared to O-type stars the B-SG spectra are more complicated due to a
larger variety of atomic species being visible, the most important among
which is Silicon, the main temperature indicator in the optical domain.
Thus, the reproduction of these spectra by methods of quantitative
spectroscopy is a real challenge for state-of-the art model atmosphere
codes, since it requires a good knowledge of the physics of these objects,
combined with accurate atomic data. In turn, any discrepancy that might
appear between computed and observed spectral features would help to
validate the physical assumptions underlying the model calculations as well
as the accuracy of the adopted atomic models and data.
Numerical simulations of the non-linear evolution of the line-driven flow
instability (for a review, see Owocki 1994), with various degrees of
approximation concerning the stabilising diffuse, scattered radiation field
(Owocki & Puls 1996,1999) as well as more recent simulations concentrating on
the outer wind regions (Runacres & Owocki 2002,2005), predict that hot star winds are
not smooth but structured, with clumping properties depending on the
distance to the stellar surface. However, recent observational studies of
clumping in O-SGs have revealed inconsistencies both between results
originating from different wind diagnostics, such as UV resonance lines,
H and the IR-/radio-excess (Puls et al. 2006; Fullerton et al. 2006), and between theoretical
predictions and observed constraints on the radial stratification of the
clumping factor (Puls et al. 2006; Bouret et al. 2005). In addition, there are
observational results which imply that clumping might depend on wind
density. Because of their dense winds, B-SGs might provide additional clues
to clarify these points.
and the IR-/radio-excess (Puls et al. 2006; Fullerton et al. 2006), and between theoretical
predictions and observed constraints on the radial stratification of the
clumping factor (Puls et al. 2006; Bouret et al. 2005). In addition, there are
observational results which imply that clumping might depend on wind
density. Because of their dense winds, B-SGs might provide additional clues
to clarify these points.
Due to their high luminosities, BA-SGs can be resolved and observed,
both photometrically and spectroscopically, even in rather distant,
extragalactic stellar systems (e.g., Bianchi & Efremova 2006; Bresolin et al. 2002; Urbaneja et al. 2003; Kudritzki et al. 1999). This fact makes them potential standard candles, allowing us to
determine distances by means of purely spectroscopic tools using the
wind-momentum luminosity relationship (WLR, Kudritzki et al. 1995). Even though
certain discrepancies between predicted and observed wind momenta of early
B0 to B3 subtypes have been revealed (Crowther et al. 2006), relevant
information about later subtypes is still missing.
During the last years, the quantitative analyses of spectra in the far-UV/UV
and optical domains (e.g.,
Herrero et al. 2002; Massey et al. 2004; Crowther et al. 2002; Repolust et al. 2004; Bianchi & Garcia 2002; Heap et al. 2006; Bouret et al. 2003) have
unambiguously shown that the inclusion of line-blocking and blanketing and
wind effects (if present) significantly modifies the temperature scale of
O-stars (for a recent calibration at solar metallicity, see
Markova et al. 2004; Martins et al. 2005). Regarding B-SGs, particularly of later
subtype, this issue has not been addressed so far, mostly due to lacking
 estimates.
estimates.
The main goal of this study is to test and to apply the potential of our
NLTE atmosphere code FASTWIND (Puls et al. 2005) to provide reliable estimates
of stellar and wind parameters of SGs with temperatures ranging from 30 to
11 kK. By means of these data and incorporating additional datasets from
alternative studies, we will try to resolve the questions outlined above.
In Sects. 2 and 3, we describe the stellar sample and the
underlying observational material used in this study. In Sect. 4 we outline
our procedure to determine the basic parameters of our targets, highlighting
some problems faced during this process. In Sect. 5 the effects of line
blocking/blanketing on the temperature scale of B-SGs at solar and SMC
metallicities will be addressed, and in Sect. 6 we investigate the wind
properties for Galactic B-SGs (augmented by O-and A-SG data), by comparison
with theoretical predictions. Particular emphasis will be given to the
behaviour of the mass-loss rate over the so-called bi-stability jump.
Section 7 gives our summary and implications for future work.
2 Observations and data reduction
High-quality optical spectra were collected for eight Galactic B-type
SGs of spectral types B0.5 to B9 using the Coudé spectrograph of
the NAO 2-m telescope of the Institute of Astronomy, Bulgarian Academy of
Sciences. The observations
were carried out using a BL632/14.7 grooves mm-1 grating in first
order, together with a PHOTOMETRICS CCD (1024  1024, 24
1024, 24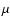 )
as a
detector
)
as a
detector![[*]](/icons/foot_motif.gif) .
This configuration produces spectra with a reciprocal dispersion of
.
This configuration produces spectra with a reciprocal dispersion of
 0.2 Å pixel-1 and an effective resolution of
0.2 Å pixel-1 and an effective resolution of
 2.0 pixels, resulting in a spectral resolution of
2.0 pixels, resulting in a spectral resolution of  15 000 at
H
15 000 at
H .
.
Table 1:
Galactic B-SGs studied in this work, together with
adopted photometric data. For multiple entries, see text.
The signal-to-noise (S/N) ratio, averaged over all spectral regions
referring to a given star, has typical values of 200 to 350, being
lower in the blue than in the red.
We observed the wavelength range between 4100 and 4900 Å, where most
of the strategic lines of H, He and Si ions are located, together with the
region around H .
Since our spectra sample about 200 Å, five settings
were used to cover the ranges of interest. These settings are as follows:
.
Since our spectra sample about 200 Å, five settings
were used to cover the ranges of interest. These settings are as follows:
- i)
- From 4110 to 4310 Å (covering Si II
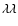 4128, 4131 , Si IV
4128, 4131 , Si IV 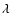 4116 and He II
4116 and He II 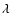 4200).
4200).
- ii)
- From 4315 to 4515 Å (He I
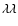 4387, 4471 and
H
4387, 4471 and
H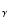 ).
).
- iii)
- From 4520 to 4720 Å (Si III
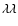 4553, 4568, 4575,
He I
4553, 4568, 4575,
He I 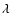 4713 and He II
4713 and He II
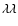 4541, 4686).
4541, 4686).
- iv)
- The region around H
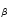 including
Si III
including
Si III
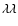 4813, 4820, 4829 and He I
4813, 4820, 4829 and He I 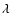 4922.
4922.
- v)
- The region around H
 including
He I
including
He I 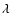 6678 and He II
6678 and He II
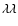 6527, 6683.
6527, 6683.
To minimise the effects of temporal spectral variability (if any), all
spectra referring to a given star were taken one after the other, with a time
interval between consecutive exposures of about half an hour. Thus, we
expect our results to be only sensitive to temporal variability of less than
2 h.
The spectra were reduced following standard procedures and using the
corresponding IRAF![[*]](/icons/foot_motif.gif) routines.
routines.
3 Sample stars
Table 1 lists our stellar sample, together with corresponding
spectral and photometric characteristics, as well as association/cluster
membership and distances, as adopted in the present study. For
hotter and intermediate temperature stars, spectral types and luminosity
classes (Col. 2) were taken from the compilation by Howarth et al. (1997),
while for the remainder, data from SIMBAD have been used.
Since HIPPARCOS based distances are no longer reliable in the distance
range considered here (e.g., de Zeeuw et al. 1999; Schröder et al. 2004), we have adopted
photometric distances collected from various sources in the literature
(Col. 4). In particular, for stars which are members of OB associations, we
drew mainly from Humphreys (1978) but also consulted the lists published
by Garmany & Stencel (1992) and by Barlow & Cohen (1977). In most cases, good agreement
between the three datasets was found, and only for Cyg OB3 did the distance
modulus provided by Humphreys turned out to be significantly larger than
that provided by Garmany & Stencel. In this latter case two entries for dare given in Table 1.
Apart from those stars belonging to the OB associations, there are two objects in
our sample which have been recognised as cluster members: HD 190603 and
HD 199478. The former was previously assigned as a member of Vul OB2
(e.g. Lennon et al. 1992), but this assignment has been questioned by
McErlean et al. (1999) who noted that there are three aggregates at approximately 1,
2 and 4 kpc in the direction of HD 190603. Since it is not obvious to which
of them (if any) this star belongs, they adopted a somewhat arbitrary
distance of 1.5 kpc. This value is very close to the estimate of 1.57 kpc
derived by Barlow & Cohen (1977), and it is this latter value which we will use in the
present study. However, in what follows we shall keep in mind that the
distance to HD 190603 is highly uncertain. For the second cluster member,
HD 199478, a distance modulus to its host cluster as used by Denizman & Hack (1988)
was adopted.
Visual magnitudes, V, and B-V colours (Cols. 5 and 6) have been taken
from the HIPPARCOS Main Catalogue (I/239). While for the majority of
sample stars the HIPPARCOS photometric data agree quite well (within
0.01 to 0.04 mag both in V and B-V) with those provided by SIMBAD,
for two of them (HD 190603 and HD 198478) significant differences
between the two sets of B-V values were found. In these latter cases two
entries for B-V are given, where the second one represents the mean
value averaged over all measurements listed in SIMBAD.
Absolute magnitudes, MV (Col. 8), were calculated using the standard
extinction law with R = 3.1 combined with intrinsic colours,
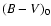 ,
from Fitzpatrick & Garmany (1990) (Col. 7) and distances, V and B-V magnitudes as
described above. For the two stars which do not belong to any
cluster/association (HD 185859 and HD 212593), absolute magnitudes
according to the calibration by Humphreys & McElroy (1984) have been adopted.
,
from Fitzpatrick & Garmany (1990) (Col. 7) and distances, V and B-V magnitudes as
described above. For the two stars which do not belong to any
cluster/association (HD 185859 and HD 212593), absolute magnitudes
according to the calibration by Humphreys & McElroy (1984) have been adopted.
For the majority of cases, the absolute magnitudes we derived, agree
within  0.3 mag with those provided by the Humphreys-McElroy
calibration. Thus, we adopted this value as a measure for the uncertainty in
MV for cluster members (HD 199478) and members of spatially more
concentrated OB associations (HD 198478 in Cyg OB7, see
Crowther et al. 2006). For other stars with known membership, a somewhat
larger error of
0.3 mag with those provided by the Humphreys-McElroy
calibration. Thus, we adopted this value as a measure for the uncertainty in
MV for cluster members (HD 199478) and members of spatially more
concentrated OB associations (HD 198478 in Cyg OB7, see
Crowther et al. 2006). For other stars with known membership, a somewhat
larger error of  0.4 mag was adopted to account for a possible spread in
distance within the host association. Finally, for HD 190603 and those two
stars with calibrated MV , we assumed a typical uncertainty of
0.4 mag was adopted to account for a possible spread in
distance within the host association. Finally, for HD 190603 and those two
stars with calibrated MV , we assumed a typical uncertainty of 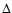 MV =
MV =  0.5 mag, representative for the spread in MV of OB stars within a
given spectral type (Crowther 2004)
0.5 mag, representative for the spread in MV of OB stars within a
given spectral type (Crowther 2004)![[*]](/icons/foot_motif.gif) .
.
4 Determination of stellar and wind parameters
The analysis presented here was performed with FASTWIND, which
produces spherically symmetric, NLTE, line-blanketed model atmospheres and
corresponding spectra for hot stars with winds. While detailed information
about the latest version used here can be found in Puls et al. (2005), we
highlight only those points which are important for our analysis of B
stars.
- (a)
- In addition to H and He, Silicon is used as an explicit element
(i.e., by means of a detailed model atom and using a comoving frame
transport for the bound-bound transitions). All other elements (e.g., C, N,
O, Fe, Ni etc.) are treated as background elements, where the major
difference (compared to the explicit ones) relates to the line transfer, which
is performed within the Sobolev approximation.
- (b)
- A detailed description of the Silicon atomic model can be found
in Trundle et al. (2004).
- (c)
- Since previous applications of FASTWIND have concentrated
on O and early B stars, we briefly note that correct
treatment of cooler stars requires sufficiently well described iron group
ions of stages II/III, whose lines are dominating the background
opacities for these objects. Details of the corresponding model atoms and
line-lists (from superstructure, Nussbaumer & Storey 1978; Eissner et al. 1974,
augmented by data from Kurucz 1992) can be found in
Pauldrach et al. (2001). In order to rule out important effects from still
missing data, we have constructed an alternative dataset which uses all
Fe/Ni II/III lines from the Kurucz line-list. Corresponding models
(in particular temperature structure and emergent fluxes) turned out to
remain almost unaffected by this alteration, so we are confident
that our original database is fairly complete, and can be used
for calculations roughly down to 10 kK.
- (d)
- A consistent temperature stratification utilising
a flux-correction method in the lower wind and the thermal balance of
electrons in the outer part is calculated, with a transition point between
the two approaches located roughly at a Rossland optical depth of
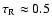 (in dependence of wind density).
(in dependence of wind density).
To allow for an initial assessment of the basic parameters, a coarse grid of
models was generated using this code (appropriate for the considered
targets). The grid involves 270 models covering the temperature range
between 12 and 30 kK (with increments of 2 kK) and including
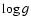 values from 1.6 to 3.4 (with increments of 0.2 dex). An extended
range of wind-densities, as combined in the optical depth invariant
Q (=
values from 1.6 to 3.4 (with increments of 0.2 dex). An extended
range of wind-densities, as combined in the optical depth invariant
Q (= /(
/(
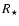 )1.5, cf. Puls et al. 1996)
has been accounted for as well, to allow for both thin and thick winds.
)1.5, cf. Puls et al. 1996)
has been accounted for as well, to allow for both thin and thick winds.
All models have been calculated assuming solar helium (
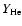 = 0.10,
with
= 0.10,
with
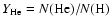 )
and Silicon abundance (log (Si/H)
= -4.45 by number
)
and Silicon abundance (log (Si/H)
= -4.45 by number![[*]](/icons/foot_motif.gif) , cf. Grevesse & Sauval 1998 and references
therein), and a micro-turbulent velocity,
, cf. Grevesse & Sauval 1998 and references
therein), and a micro-turbulent velocity,
 , of 15 km s
, of 15 km s for hotter
and 10 km s
for hotter
and 10 km s for cooler subtypes, with a border line at 20 kK.
for cooler subtypes, with a border line at 20 kK.
By means of this model grid, initial estimates on
 ,
, 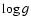 and
and  were obtained for each sample star. These estimates were subsequently used
to construct a smaller subgrid, specific for each target, to derive the
final, more exact values of the stellar and wind parameters (including
were obtained for each sample star. These estimates were subsequently used
to construct a smaller subgrid, specific for each target, to derive the
final, more exact values of the stellar and wind parameters (including
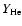 ,
log (Si/H) and
,
log (Si/H) and
 ).
).
To compare observed with synthetic profiles, radial velocities and
rotational speeds of all targets have to be known. We started our analysis
with radial velocities taken from the General Catalogue of Mean Radial
Velocities (III/213, Barbier-Brossat & Figon 2000). These values were then
modified to obtain better fits to the analysed absorption profiles. In doing
so we gave preference to Silicon rather than to helium or hydrogen lines
since the latter might be influenced by (asymmetrical) wind
absorption/emission. The finally adopted 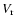 -values which provide the ``best''
fit to most of the Silicon lines are listed in Col. 3 of
Table 2. The accuracy of these estimates is typically
-values which provide the ``best''
fit to most of the Silicon lines are listed in Col. 3 of
Table 2. The accuracy of these estimates is typically  2 km s
2 km s .
.
Table 2:
Radial velocities (from Si), projected rotational velocities,
macro- and micro-turbulent velocities (all in km s ) and Si abundances, given
as log [N(Si)/N(H] + 12, of the sample stars
as determined in the present study. The number in brackets refers to the number
of lines used to derive
) and Si abundances, given
as log [N(Si)/N(H] + 12, of the sample stars
as determined in the present study. The number in brackets refers to the number
of lines used to derive 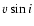 and
and
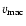 .
.
As a first guess for the projected rotational velocities of the sample
stars, 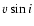 , we used values obtained by means of the spectral type -
, we used values obtained by means of the spectral type -
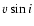 calibration for Galactic B-type SGs provided by
Abt et al. (2002). However, during the fitting procedure it was found
that
(i) these values provide poor agreement between observed and synthetic
profiles and (ii) an additional line-broadening agent must be introduced
to improve the quality of the fits. These findings are consistent with
similar results from earlier investigations claiming that absorption line
spectra of O-type stars and B-type SGs exhibit a significant amount of
broadening in excess to the rotational broadening (Rosenhald 1970; Howarth et al. 1997; Lennon et al. 1993; Conti & Ebbets 1977). Furthermore, although the physical mechanism responsible
for this additional line-broadening is still not understood
we shall follow Ryans et al. (2002) and refer to it as ``macro-turbulence''.
calibration for Galactic B-type SGs provided by
Abt et al. (2002). However, during the fitting procedure it was found
that
(i) these values provide poor agreement between observed and synthetic
profiles and (ii) an additional line-broadening agent must be introduced
to improve the quality of the fits. These findings are consistent with
similar results from earlier investigations claiming that absorption line
spectra of O-type stars and B-type SGs exhibit a significant amount of
broadening in excess to the rotational broadening (Rosenhald 1970; Howarth et al. 1997; Lennon et al. 1993; Conti & Ebbets 1977). Furthermore, although the physical mechanism responsible
for this additional line-broadening is still not understood
we shall follow Ryans et al. (2002) and refer to it as ``macro-turbulence''.
Since the effects of macro-turbulence are similar to those caused by axial
rotation, (i.e., they do not change the line strengths but ``only'' modify
the profile shapes) and since stellar rotation is a key parameter, such as
for
stellar evolution calculation (e.g., Meynet & Maeder 2000; Hirschi et al. 2005, and
references therein), it is particularly important to distinguish between the
individual contributions of these two processes.
There are at least two possibilities to approach this problem: either exploiting
the goodness of the fit between observed and synthetic profiles
(Ryans et al. 2002) or analysing the shape of the Fourier transforms (FT) of
absorption lines (Gray 1973,1975; Simon-Diaz & Herrero 2007). Since the second method
has been proven to provide better constraints (Dufton et al. 2006), we
followed this approach to separate and measure the relative magnitudes of
rotation and macro-turbulence.
The principal idea of the FT method relates to the fact that in Fourier
space the convolutions of the ``intrinsic line profile'' (which
includes the natural, thermal, collisional/Stark and
microturbulence broadening) with the instrumental, rotational and
macro-turbulent profiles, become simple products of the corresponding Fourier
components, thus allowing the contributions of the latter two processes to
be separated by simply dividing the Fourier components of the observed
profile by the components of the thermal and instrumental profile.
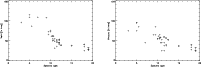 |
Figure 1:
Projected rotational ( left panel) and macro-turbulent ( right panel)
velocities of OB-SGs (spectral types refer to O-stars, i.e., 10
corresponds to B0 and 20 to A0). Data derived in the present study are
marked with diamonds while crosses refer to published data (Simon-Diaz & Herrero 2007; Dufton et al. 2006).
|
| Open with DEXTER |
The first minimum of the Fourier amplitudes of the obtained residual
transform will then fix the value of 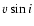 while the shape of the first
side-lobe of the same transform will constrain
while the shape of the first
side-lobe of the same transform will constrain
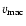 .
.
The major requirements to obtain reliable results from this method is the
presence of high quality spectra (high S/N ratio and high spectral
resolution) and to analyse only those lines which are free from strong
pressure broadening but are still strong enough to allow for reliable 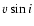 estimates.
estimates.
For the purpose of the present analysis, we have used the implementation of
the FT technique as developed by Simon-Diaz & Herrero (2007) (based on the original method
proposed by Gray 1973,1975) and applied it to a number of
preselected absorption lines fulfilling the above requirements. In
particular, for our sample of early B subtypes, the Si III multiplet
around 4553 Å but also lines of O II and N II were selected, whereas for
the rest the Si II doublet around 4130 Å and the Mg II line at
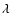 4481 were used instead.
4481 were used instead.
The obtained pairs of (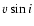 ,
,
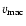 ), averaged over the measured lines,
were then used as input parameters for the fitting procedure and
subsequently modified to improve the fits
), averaged over the measured lines,
were then used as input parameters for the fitting procedure and
subsequently modified to improve the fits![[*]](/icons/foot_motif.gif) .
The finally adopted values of
.
The finally adopted values of 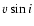 and
and
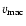 are listed in Cols. 4 and 5 of Table 2, respectively. Numbers in brackets refer to the
number of lines used for this analysis. The uncertainty of these estimates
is typically less than
are listed in Cols. 4 and 5 of Table 2, respectively. Numbers in brackets refer to the
number of lines used for this analysis. The uncertainty of these estimates
is typically less than  10 km s
10 km s ,
being largest for those stars
with a
relatively low rotational speed, due to the limitations given by the
resolution of our spectra (
,
being largest for those stars
with a
relatively low rotational speed, due to the limitations given by the
resolution of our spectra ( 35 km s
35 km s ).
Although the sample size is small, the
).
Although the sample size is small, the 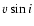 and
and
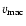 data listed in
Table 2 indicate that:
data listed in
Table 2 indicate that:
- in none of the sample stars is rotation alone able to reproduce the
observed line profiles (width and shape);
- both
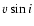 and
and
 decrease towards later subtypes (lower
decrease towards later subtypes (lower
 ), being about a factor of two lower at B9 than at B0.5;
), being about a factor of two lower at B9 than at B0.5;
- independent of spectral subtype, the size of the
macro-turbulent velocity is similar to the size of the
projected rotational velocity;
- also in all cases,
 is well beyond the speed of sound.
is well beyond the speed of sound.
Compared to similar data from other investigations for stars in common
(e.g. Rosenhald 1970; Howarth et al. 1997), our 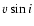 estimates are always
smaller, by up to 40%, which is understandable since these earlier
estimates refer to an interpretation in terms of rotational broadening
alone.
estimates are always
smaller, by up to 40%, which is understandable since these earlier
estimates refer to an interpretation in terms of rotational broadening
alone.
On the other hand, and within a given spectral subtype, our estimates of
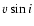 and
and
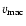 are consistent with those derived by Dufton et al. (2006)
and Simon-Diaz & Herrero (2007) (see Fig. 1).
From these data it is obvious that both
are consistent with those derived by Dufton et al. (2006)
and Simon-Diaz & Herrero (2007) (see Fig. 1).
From these data it is obvious that both 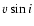 and
and
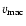 appear to
decrease (almost monotonically) in concert, when proceeding from early-O to
late B-types.
appear to
decrease (almost monotonically) in concert, when proceeding from early-O to
late B-types.
4.2 Effective temperatures,

For B-type stars the primary temperature diagnostic at optical
wavelengths is Silicon (McErlean et al. 1999; Trundle et al. 2004; Kilian et al. 1991; Becker & Butler 1990) which shows
strong lines from three ionisation stages through all the spectral types:
Si III/Si IV for earlier and Si II/Si III for later subtypes, with a
``short'' overlap at B1.5 - B2. To evaluate
 (and
(and 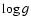 ), to a large
extent we employed the method of line profile fitting instead of using fit
diagrams (based on EWs), since in the latter case the corresponding
estimates rely on interpolations and furthermore do not account for the
profile shape. Note, however, that for certain tasks (namely the derivation
of the Si-abundance together with the micro-turbulent velocity), EW-methods
have been applied (see below).
), to a large
extent we employed the method of line profile fitting instead of using fit
diagrams (based on EWs), since in the latter case the corresponding
estimates rely on interpolations and furthermore do not account for the
profile shape. Note, however, that for certain tasks (namely the derivation
of the Si-abundance together with the micro-turbulent velocity), EW-methods
have been applied (see below).
In particular, to determine
 we used the Si II features at
we used the Si II features at
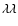 4129, 4131, the Si III features at
4129, 4131, the Si III features at
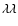 4553,
4568, 4575 and at
4553,
4568, 4575 and at
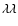 4813, 4819, 4828, with a preference on the
first triplet (see below) and the Si IV feature at
4813, 4819, 4828, with a preference on the
first triplet (see below) and the Si IV feature at
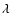 4116
4116![[*]](/icons/foot_motif.gif) . In addition, for stars
of spectral type B2 and earlier the helium ionisation balance was exploited
as an additional check on
. In addition, for stars
of spectral type B2 and earlier the helium ionisation balance was exploited
as an additional check on
 , involving He I transitions at
, involving He I transitions at
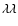 4471, 4713, 4387, 4922 and He II transitions at
4471, 4713, 4387, 4922 and He II transitions at
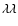 4200, 4541, 4686.
4200, 4541, 4686.
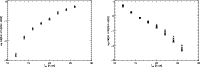 |
Figure 2:
Effects of micro-turbulence on the strength of Si IV 4116/Si III 4553
(left panel) and Si II 4128/Si III 4553 (right panel) equivalent width
ratios for B-type SGs.
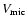 ranging from 4 to 18 km s
ranging from 4 to 18 km s ,
with increments of 4 km s ,
with increments of 4 km s . Triangles refer to the lowest value
of . Triangles refer to the lowest value
of
 ,
squares to the highest (see text). ,
squares to the highest (see text). |
| Open with DEXTER |
4.2.1 Micro-turbulent velocities and Si abundances
Though the introduction of a non-vanishing micro-turbulent velocity can
significantly improve the agreement between synthetical profiles and
observations (Smith & Howarth 1998; McErlean et al. 1998), it is still not completely clear whether
such a mechanism (operating on scales below the photon mean free
path) is really present or whether it is an artefact of some deficiency in
the present-day description of model atmospheres (e.g., Villamariz & Herrero 2000; McErlean et al. 1998, and references therein).
Since micro-turbulence can strongly affect the strength of helium and
metal lines, its inclusion into atmospheric models and profile functions
can significantly modify the derived stellar
abundances but also effective temperatures and surface gravities (the latter
two parameters mostly indirectly via its influence on line blanketing:
stronger
 implies more blocking/back-scattering, and thus lower
implies more blocking/back-scattering, and thus lower
 ).
).
Whereas Villamariz & Herrero (2000) showed the effects of
 to be relatively
small for O-type stars, for B-type stars this issue has only been
investigated for early B1-B2 giants (e.g., Vrancken et al. 2000) and a few,
specific BA supergiants (e.g. Przybilla et al. 2006; Urbaneja 2004). Here, we report on the
influence of micro-turbulence on the derived effective
temperatures
to be relatively
small for O-type stars, for B-type stars this issue has only been
investigated for early B1-B2 giants (e.g., Vrancken et al. 2000) and a few,
specific BA supergiants (e.g. Przybilla et al. 2006; Urbaneja 2004). Here, we report on the
influence of micro-turbulence on the derived effective
temperatures![[*]](/icons/foot_motif.gif) for the complete range of B-type SGs. For this purpose
we used a corresponding sub-grid of FASTWIND models with
for the complete range of B-type SGs. For this purpose
we used a corresponding sub-grid of FASTWIND models with
 ranging from 4 to 18 km s
ranging from 4 to 18 km s (with increments of 4 km s
(with increments of 4 km s ) and
) and 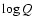 values
corresponding to the case of relatively weak winds. Based on these models we
studied the behaviour of the Si IV 4116/Si III 4553 and Si II 4128/Si III 4553 line
ratios and found these ratios to be almost insensitive to variations in
values
corresponding to the case of relatively weak winds. Based on these models we
studied the behaviour of the Si IV 4116/Si III 4553 and Si II 4128/Si III 4553 line
ratios and found these ratios to be almost insensitive to variations in
 (Fig. 2), except for the case of Si II/Si III beyond 18 kK
where differences of about 0.3 to 0.4 dex can be seen (and are to be expected,
due to the large difference in absolute line-strengths caused by strongly
different ionisation fractions). Within the temperature ranges of interest
(18
(Fig. 2), except for the case of Si II/Si III beyond 18 kK
where differences of about 0.3 to 0.4 dex can be seen (and are to be expected,
due to the large difference in absolute line-strengths caused by strongly
different ionisation fractions). Within the temperature ranges of interest
(18 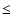

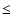 28 kK for Si IV/Si III and 12
28 kK for Si IV/Si III and 12 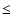

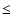 18 kK for Si II/Si III), however, the differences are relatively small, about
0.15 dex or less, resulting in temperature differences lower than 1000 K,
i.e., within the limits of the adopted uncertainties (see below).
18 kK for Si II/Si III), however, the differences are relatively small, about
0.15 dex or less, resulting in temperature differences lower than 1000 K,
i.e., within the limits of the adopted uncertainties (see below).
Based on these results, we relied on the following strategy to determine
 ,
,
 and Si abundances. As a first step, we used the FASTWIND model
grid as described previously (with
and Si abundances. As a first step, we used the FASTWIND model
grid as described previously (with
 =10 and 15 km s
=10 and 15 km s and ``solar'' Si
abundance) to put initial constraints on the stellar and wind parameters of
the sample stars. Then, by varying
and ``solar'' Si
abundance) to put initial constraints on the stellar and wind parameters of
the sample stars. Then, by varying
 (but also
(but also 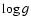 ,
,  and
velocity-field parameter
and
velocity-field parameter 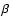 )
within the derived limits and by changing
)
within the derived limits and by changing
 within
within  5 km s
5 km s to obtain a satisfactory fit to most of the
strategic Silicon lines, we fixed
to obtain a satisfactory fit to most of the
strategic Silicon lines, we fixed
 /
/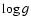 and derived rough estimates of
and derived rough estimates of
 .
Si abundances and final values for
.
Si abundances and final values for
 resulted from the following
procedure: for each sample star a grid of 20 FASTWIND models was calculated,
combining four abundances and five values of micro-turbulence (ranging from
10 to 20 km s
resulted from the following
procedure: for each sample star a grid of 20 FASTWIND models was calculated,
combining four abundances and five values of micro-turbulence (ranging from
10 to 20 km s or from 4 to 12 km s
or from 4 to 12 km s ,
to cover hot and cool stars,
respectively). By means of this grid, we determined those abundance ranges
which reproduce the observed individual EWs (within the corresponding
errors) of several previously selected Si lines from different ionisation
stages. Subsequently, we sorted out the value of
,
to cover hot and cool stars,
respectively). By means of this grid, we determined those abundance ranges
which reproduce the observed individual EWs (within the corresponding
errors) of several previously selected Si lines from different ionisation
stages. Subsequently, we sorted out the value of
 which provides the
best overlap between these ranges,
i.e., defines a unique abundance together
with appropriate errors (for more details, see e.g. Simon-Diaz et al. 2006; Urbaneja 2004 and
references therein).
which provides the
best overlap between these ranges,
i.e., defines a unique abundance together
with appropriate errors (for more details, see e.g. Simon-Diaz et al. 2006; Urbaneja 2004 and
references therein).
Our final results for
 were almost identical (within about
were almost identical (within about
 1 km s
1 km s ) to those derived from the ``best'' fit to Silicon. Similarly,
for all but one star, our final estimates for the Si abundance are
quite similar to the initially adopted ``solar'' one, within
) to those derived from the ``best'' fit to Silicon. Similarly,
for all but one star, our final estimates for the Si abundance are
quite similar to the initially adopted ``solar'' one, within
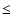
 0.1 dex, and only for HD 202850 an increase of 0.44 dex was
found.
Given that Si is not involved in CNO nuclear processing, the latter
result is difficult to interpret. On the one hand, fitting/analysis
problems are highly improbable, since no unusual results have been obtained
for the other late B-SG, HD 212593. Indeed, the overabundance is almost
``visible'' because the EWs of at least 2 of the 3 strategic Si lines are
significantly larger (by about 20 to 40%) in HD 202850 than in
HD 212593. On the other hand, the possibility that this star is metal
rich seems unlikely given its close proximity to our Sun. Another
possibility might be that HD 202850 is a Si star, though its magnetic
field does not seem particularly strong (but exceptions are still known,
e.g. V 828 Her B9sp, EE Dra B9, Bychkov et al. 2003). A detailed abundance
analysis may help to solve this puzzling feature.
0.1 dex, and only for HD 202850 an increase of 0.44 dex was
found.
Given that Si is not involved in CNO nuclear processing, the latter
result is difficult to interpret. On the one hand, fitting/analysis
problems are highly improbable, since no unusual results have been obtained
for the other late B-SG, HD 212593. Indeed, the overabundance is almost
``visible'' because the EWs of at least 2 of the 3 strategic Si lines are
significantly larger (by about 20 to 40%) in HD 202850 than in
HD 212593. On the other hand, the possibility that this star is metal
rich seems unlikely given its close proximity to our Sun. Another
possibility might be that HD 202850 is a Si star, though its magnetic
field does not seem particularly strong (but exceptions are still known,
e.g. V 828 Her B9sp, EE Dra B9, Bychkov et al. 2003). A detailed abundance
analysis may help to solve this puzzling feature.
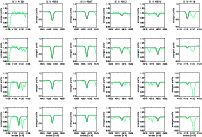 |
Figure 3:
Examples for the quality of our final (``best'') Silicon
line-profile fits. From top to bottom: HD 185859 (B0.5Ia), HD 190603
(B1.5Ia+), HD 206165 (B2Ib) and HD 198478 (B2.5Ia). Note the systematic
discrepancy between synthetic and observed profiles of the Si III lines at
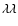 4813, 4819. 4813, 4819. |
| Open with DEXTER |
Finally, we have verified that our newly derived Si abundances (plus
 -values) do not affect the stellar parameters (which refer to the
initial abundances), by means of corresponding FASTWIND models. Though an
increase of 0.44 dex (the exceptional case of HD 202850)
makes the Si-lines stronger, this strengthening does not affect
the derived
-values) do not affect the stellar parameters (which refer to the
initial abundances), by means of corresponding FASTWIND models. Though an
increase of 0.44 dex (the exceptional case of HD 202850)
makes the Si-lines stronger, this strengthening does not affect
the derived
 ,
since the latter parameter depends on line ratios
from different ionisation stages, being thus almost independent of
abundance. In each case, however, the quality of the Silicon line-profile
fits has been improved, as expected.
,
since the latter parameter depends on line ratios
from different ionisation stages, being thus almost independent of
abundance. In each case, however, the quality of the Silicon line-profile
fits has been improved, as expected.
In Cols. 6 and 7 of Table 2 we present our final values for
 and Si abundance. The error of these estimates depends on the
accuracy of the measured equivalent widths (about 10%) and is typically
about
and Si abundance. The error of these estimates depends on the
accuracy of the measured equivalent widths (about 10%) and is typically
about  2 km s
2 km s and
and  0.15 dex for
0.15 dex for
 and the logarithmic Si
abundance, respectively. A closer inspection of these data indicates that
the micro-turbulent velocities of B-type SGs might be closely
related to spectral type (see also McErlean et al. 1999), being highest at
earlier (18 km s
and the logarithmic Si
abundance, respectively. A closer inspection of these data indicates that
the micro-turbulent velocities of B-type SGs might be closely
related to spectral type (see also McErlean et al. 1999), being highest at
earlier (18 km s at B0.5) and lowest at later B subtypes (7 km s
at B0.5) and lowest at later B subtypes (7 km s at B9).
Interestingly, the latter value is just a bit larger than the typical
values reported for A-SGs (3 to 8 km s
at B9).
Interestingly, the latter value is just a bit larger than the typical
values reported for A-SGs (3 to 8 km s , e.g., Venn 1995), thus
implying a possible decline in micro-turbulence towards even later spectral
types.
, e.g., Venn 1995), thus
implying a possible decline in micro-turbulence towards even later spectral
types.
4.2.2 Silicon line profiles fits - a closer inspection
During our fitting procedure, we encountered the problem that the strength
of the Si III multiplet near 4813 Å was systematically over-predicted
(see Fig. 3, for some illustrative examples). Though this
discrepancy is not very large (and vanishes if
 is modified within
(
is modified within
( 500 K), this discrepancy might point to some weaknesses in our model
assumptions or data. Significant difficulties in reproducing the strength of
Si III multiplets near 4553 and 4813 Å have also been encountered by
McErlean et al. (1999) and by Becker & Butler (1990). While in the former study both multiplets
were found to be weaker in their lowest-gravity models with
500 K), this discrepancy might point to some weaknesses in our model
assumptions or data. Significant difficulties in reproducing the strength of
Si III multiplets near 4553 and 4813 Å have also been encountered by
McErlean et al. (1999) and by Becker & Butler (1990). While in the former study both multiplets
were found to be weaker in their lowest-gravity models with
 beyond 22 500 K, in the latter study the second multiplet was overpredicted,
by a factor of about two.
beyond 22 500 K, in the latter study the second multiplet was overpredicted,
by a factor of about two.
The most plausible explanation for the problems encountered by
McErlean et al. (1999) (which are opposite to ours) is the neglect of
line-blocking/blanketing and wind effects in their NLTE model calculations,
as already suggested by the authors themselves.
The discrepancies reported by Becker & Butler (1990), on the other hand, are in
qualitative agreement to our findings, but
much more pronounced (a factor of two against 20 to 30%). Since both
studies use the same Si III model ion whilst we have updated the
oscillator strengths of the multiplet near 4553 Å(!) drawing from the
available atomic databases, we suggest that it is these improved oscillator
strengths in conjunction with modern stellar atmospheres which have reduced
the noted discrepancy.
Regardless of these improvements, the remaining discrepancy must have an
origin, and there are at least two possible explanations: (i) too small an
atomic model for Si III (cutoff effects) and/or (ii) radially stratified
micro-turbulent velocities (erroneous oscillator strengths cannot be
excluded, but are unlikely, since all atomic databases give similar
values).
The first possibility was discussed by Becker & Butler (1990) who concluded that this
defect cannot be the sole origin of their problem, since the required
corrections are too large and furthermore would affect the other term
populations in an adverse manner. Because the discrepancy found by us has
significantly decreased since then, the possibility of too small an
atomic model can no longer be ruled out though. Future work on improving the
complete Si atom will clarify this question.
In our analyses, we have used the same value of
 for all
lines in a given spectrum, i.e., assumed that this quantity does
not follow any kind of stratification throughout the atmosphere, whilst the
opposite might actually be true (e.g. Vrancken et al. 2000; McErlean et al. 1999; Trundle et al. 2004; Hunter et al. 2006; Trundle et al. 2002). If so, a micro-turbulent velocity being a factor of two
lower than inferred from the ``best'' fit to Si III 4553 and the Si II
doublet would be needed to reconcile calculated and observed strengths of
the 4813 Å multiplet. Such a number does not seem unlikely,
given the difference in line strengths, but clearly further investigations
are necessary (after improving upon the atomic model) to clarify this
possibility (see also Hunter et al. 2006 and references therein).
for all
lines in a given spectrum, i.e., assumed that this quantity does
not follow any kind of stratification throughout the atmosphere, whilst the
opposite might actually be true (e.g. Vrancken et al. 2000; McErlean et al. 1999; Trundle et al. 2004; Hunter et al. 2006; Trundle et al. 2002). If so, a micro-turbulent velocity being a factor of two
lower than inferred from the ``best'' fit to Si III 4553 and the Si II
doublet would be needed to reconcile calculated and observed strengths of
the 4813 Å multiplet. Such a number does not seem unlikely,
given the difference in line strengths, but clearly further investigations
are necessary (after improving upon the atomic model) to clarify this
possibility (see also Hunter et al. 2006 and references therein).
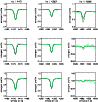 |
Figure 4:
Observed and synthetic helium line-profiles, calculated at the upper
(
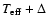
 : dashed) and lower ( : dashed) and lower (
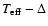
 : solid)
limit of the corresponding : solid)
limit of the corresponding
 determined from the ``best'' fits to
strategic Silicon lines. From top to bottom: HD 185859 (B0.5Ia),
HD 190603 (B1.5Ia+) and HD 206165 (B2Ib). determined from the ``best'' fits to
strategic Silicon lines. From top to bottom: HD 185859 (B0.5Ia),
HD 190603 (B1.5Ia+) and HD 206165 (B2Ib). |
| Open with DEXTER |
Considering the findings from above, we decided to follow Becker & Butler (1990)
and to give preference to the Si III multiplet near 4553 Å
throughout our analysis. Since this multiplet is observable over the whole B
star temperature range while the other (4813 Å) disappears at mid-B
subtypes, such a choice has the additional advantage of providing consistent
results for the complete sample, from B0 to B9.
Table 3:
Final results for our sample of Galactic B-SGs: Stellar and wind
parameters adopted (
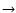 MV ) and derived using FASTWIND.
MV ) and derived using FASTWIND.
 in kK,
in kK,
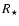 in
in 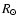 ,
, 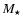 in
in 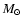 ,
,  in km s
in km s ,
,  in 10-6
in 10-6 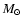 /yr.
/yr.
 (in cgs-units) denotes the modified wind-momentum rate.
High precision
(in cgs-units) denotes the modified wind-momentum rate.
High precision 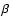 -values are given bold-faced. For non-tabulated errors, see text.
-values are given bold-faced. For non-tabulated errors, see text.
4.2.3 Helium line-profiles fits and helium abundance
As pointed out in the beginning of this section, for early-B subtypes,
the helium ionisation balance can be used to determine
 .
Consequently, for the three hottest stars in our sample we used
He I and He II lines to derive independent constraints on
.
Consequently, for the three hottest stars in our sample we used
He I and He II lines to derive independent constraints on
 ,
assuming
helium abundances as discussed below
,
assuming
helium abundances as discussed below![[*]](/icons/foot_motif.gif) .
Interestingly, in all these cases
satisfactory fits to the available strategic helium lines could be obtained
in parallel with Si IV and Si III (within the adopted uncertainties,
.
Interestingly, in all these cases
satisfactory fits to the available strategic helium lines could be obtained
in parallel with Si IV and Si III (within the adopted uncertainties,
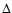
 =
=  500 K). This result is illustrated in
Fig. 4, where a comparison between observed and synthetic
helium profiles is shown, the latter being calculated at the upper and lower
limit of the
500 K). This result is illustrated in
Fig. 4, where a comparison between observed and synthetic
helium profiles is shown, the latter being calculated at the upper and lower
limit of the
 range derived from the Silicon ionisation balance. Our
finding contrasts Urbaneja (2004) who reported differences in the stellar
parameters beyond the typical uncertainties, if either Silicon or helium was
used independently.
range derived from the Silicon ionisation balance. Our
finding contrasts Urbaneja (2004) who reported differences in the stellar
parameters beyond the typical uncertainties, if either Silicon or helium was
used independently.
Whereas no obvious discrepancy between He I singlets and triplets (``He I
singlet problem'', Najarro et al. 2006, and references therein) has been seen
in stars of type B1.5 and earlier, we faced several problems when trying to
fit helium in parallel with Silicon in stars of mid and late subtypes (B2
and later)![[*]](/icons/foot_motif.gif) .
.
In particular, and at ``normal'' helium abundance (
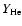 =
=
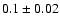 ), the
singlet line at
), the
singlet line at 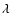 4387 is somewhat over-predicted for all stars in
this subgroup, except for the coolest one - HD 202850. At the same time,
the triplet transitions at
4387 is somewhat over-predicted for all stars in
this subgroup, except for the coolest one - HD 202850. At the same time,
the triplet transitions at
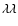 4471 and 4713 have been
under-predicted (HD 206165, B2 and HD 198478, B2.5), well reproduced
(HD 191243, B5 and HD 199478, B8) or over-predicted (HD 212593, B9).
Additionally, in half of these stars (HD 206165, HD 198478, and
HD 199478) the strength of the forbidden component of He I 4471 was
over-predicted, whereas in the other half this component was well
reproduced. In all cases, however, these discrepancies were not so large as
to prevent a globally satisfactory fit to the available He I lines in
parallel with Silicon. Examples illustrating these facts are shown in
Fig. 5. Again, there are at least two principle
possibilities to solve these problems: to adapt the He abundance or/and to
use different values of
4471 and 4713 have been
under-predicted (HD 206165, B2 and HD 198478, B2.5), well reproduced
(HD 191243, B5 and HD 199478, B8) or over-predicted (HD 212593, B9).
Additionally, in half of these stars (HD 206165, HD 198478, and
HD 199478) the strength of the forbidden component of He I 4471 was
over-predicted, whereas in the other half this component was well
reproduced. In all cases, however, these discrepancies were not so large as
to prevent a globally satisfactory fit to the available He I lines in
parallel with Silicon. Examples illustrating these facts are shown in
Fig. 5. Again, there are at least two principle
possibilities to solve these problems: to adapt the He abundance or/and to
use different values of
 , on the assumption that this parameter varies
as a function of atmospheric height (cf. Sect. 4.2.2).
, on the assumption that this parameter varies
as a function of atmospheric height (cf. Sect. 4.2.2).
For all sample stars a ``normal'' helium
abundance,
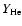 = 0.10, was adopted as a first guess. Subsequently, this
value has been adjusted (if necessary) to improve the helium line fits. For
the two hottest stars with well reproduced helium lines (and two ionisation
stages being present!), an error of only
= 0.10, was adopted as a first guess. Subsequently, this
value has been adjusted (if necessary) to improve the helium line fits. For
the two hottest stars with well reproduced helium lines (and two ionisation
stages being present!), an error of only  0.02 seems to be appropriate
because of the excellent fit quality. Among those, an overabundance in
helium (
0.02 seems to be appropriate
because of the excellent fit quality. Among those, an overabundance in
helium (
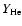 = 0.2) was found for the hypergiant HD 190603, which might
also be expected according to its evolutionary stage.
= 0.2) was found for the hypergiant HD 190603, which might
also be expected according to its evolutionary stage.
In mid and late B-type stars, on the other hand, the determination of
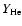 was more complicated, due to problems discussed above.
Particularly for stars where the discrepancies between synthetic and
observed triplet and singlet lines were opposite to each other, no
unique solution could be obtained by varying the helium abundance,
and we had to increase the corresponding error bars
(HD 206165 and HD 198478).
For HD 212593, on the other hand (where all available singlet and triplet
lines turned out to be over-predicted), a helium depletion by 30 to 40%
would be required to reconcile theory with observations.
was more complicated, due to problems discussed above.
Particularly for stars where the discrepancies between synthetic and
observed triplet and singlet lines were opposite to each other, no
unique solution could be obtained by varying the helium abundance,
and we had to increase the corresponding error bars
(HD 206165 and HD 198478).
For HD 212593, on the other hand (where all available singlet and triplet
lines turned out to be over-predicted), a helium depletion by 30 to 40%
would be required to reconcile theory with observations.
All derived values are summarised in Col. 8 of Table 3, but note
that alternative fits of similar quality are possible for those
cases where an overabundance/depletion in He has been indicated, namely by
using a solar helium content and
 being a factor of two larger/lower
than inferred from Silicon: due to the well known dichotomy between
abundance and micro-turbulence (if only one ionisation stage is present), a
unique solution is simply not possible, accounting for the capacity of the
diagnostic tools used here.
being a factor of two larger/lower
than inferred from Silicon: due to the well known dichotomy between
abundance and micro-turbulence (if only one ionisation stage is present), a
unique solution is simply not possible, accounting for the capacity of the
diagnostic tools used here.
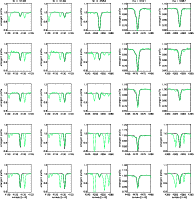 |
Figure 5:
Final (``best'') fits to Silicon and helium lines. From top to
bottom: HD 198478 (B2.5), HD 191243 (B5Ib), HD 199478 (B8ae),
HD 212593 (B9 Iab) and HD 202850 (B9 Iab). Note that the forbidden
component in the blue wing of He I  4471 is over-predicted in a
number of cases, and that the synthetic He I singlet at 4471 is over-predicted in a
number of cases, and that the synthetic He I singlet at  4387 is
systematically too strong. 4387 is
systematically too strong. |
| Open with DEXTER |
Column 4 of Table 3 lists all effective temperatures as
derived in the present study. As we have seen, these estimates are
influenced by several processes and estimates of other quantities, among
which are micro- and macro-turbulence, He and Si abundances, surface gravity
and mass-loss rate (where the latter two quantities are discussed in the
following). Nevertheless, we are quite confident that, to a large extent,
we have consistently and partly independently (regarding
 ,
,
 and Si
abundances) accounted for these influences. Thus, the errors in our
and Si
abundances) accounted for these influences. Thus, the errors in our
 estimates should be dominated by uncertainties in the fitting procedure,
amounting to about
estimates should be dominated by uncertainties in the fitting procedure,
amounting to about  500 K. Of course, these are differential errors
assuming that physics complies with all our assumptions, data and
approximations used within our atmosphere code.
500 K. Of course, these are differential errors
assuming that physics complies with all our assumptions, data and
approximations used within our atmosphere code.
Classically, the Balmer lines wings are used to determine the surface
gravity,  ,
where only higher members (H
,
where only higher members (H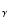 and H
and H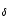 when
available) have been considered in the present investigation to prevent a
bias because of potential wind-emission effects in H
when
available) have been considered in the present investigation to prevent a
bias because of potential wind-emission effects in H and H
and H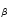 . Note
that due to stellar rotation the
. Note
that due to stellar rotation the 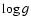 values derived from such
diagnostics are only effective values. To derive the true gravities,
values derived from such
diagnostics are only effective values. To derive the true gravities,
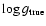 ,
required to calculate masses, one has to apply a centrifugal
correction (approximated by
,
required to calculate masses, one has to apply a centrifugal
correction (approximated by 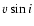 2/
2/ ), though for all
our sample stars this correction was found to be typically less than 0.03
dex.
), though for all
our sample stars this correction was found to be typically less than 0.03
dex.
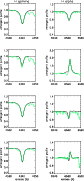 |
Figure 6:
Fit quality for H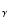 and H and H ,
for early
and mid subtypes. From top to bottom: HD 185859 (B0.5Ia), HD 190603
(B1.5Ia+), HD 206165 (B2Ib) and HD 198478 (B2.5). ,
for early
and mid subtypes. From top to bottom: HD 185859 (B0.5Ia), HD 190603
(B1.5Ia+), HD 206165 (B2Ib) and HD 198478 (B2.5). |
| Open with DEXTER |
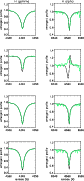 |
Figure 7:
As for Fig. 6, but for late B subtypes. From top to
bottom: HD 191243 (B5Ib), HD 199478 (B8ae), HD 212593 (B9Iab) and
HD 202850 (B9Iab). |
| Open with DEXTER |
Corresponding values for effective and corrected surface gravities are
listed in Cols. 5 and 6 of Table 3. The error of these
estimates was consistently adopted as  0.1 dex due to the rather good
quality of the fits and spectra (because of the small centrifugal
correction, corresponding errors can be neglected) except for HD 190603
and HD 199478 where an error of
0.1 dex due to the rather good
quality of the fits and spectra (because of the small centrifugal
correction, corresponding errors can be neglected) except for HD 190603
and HD 199478 where an error of  0.15 dex was derived instead. This
point is illustrated in Figs. 6 and 7 where our
final (``best'') fits to the observed H
0.15 dex was derived instead. This
point is illustrated in Figs. 6 and 7 where our
final (``best'') fits to the observed H profiles are shown. Note that
the relatively large discrepancies in the cores of HD 190603 and
HD 199478 might be a result of additional emission/absorption from
large-scale structures in their winds (Markova et al. 2007; Rivinius et al. 1997), which cannot be
reproduced by our models (see also Sect. 4.5 below). At least for
HD 190603, an alternative explanation in terms of too large a mass-loss
rate (clumping effects in H
profiles are shown. Note that
the relatively large discrepancies in the cores of HD 190603 and
HD 199478 might be a result of additional emission/absorption from
large-scale structures in their winds (Markova et al. 2007; Rivinius et al. 1997), which cannot be
reproduced by our models (see also Sect. 4.5 below). At least for
HD 190603, an alternative explanation in terms of too large a mass-loss
rate (clumping effects in H ) is possible as well.
) is possible as well.
The input radii used to calculate our model grid have been drawn from
evolutionary models. Of course, these radii are somewhat different
from the finally adopted ones (listed in Col. 7 of Table 3)
which have been derived following the procedure introduced by
Kudritzki (1980) (using the de-reddened absolute magnitudes from
Table 1 and the theoretical fluxes of our models).
With typical uncertainties of  500 K in our
500 K in our
 and of
and of  0.3
to 0.5 mag in MV , the error in the stellar radius is dominated by
the uncertainty in MV , and is of the order of
0.3
to 0.5 mag in MV , the error in the stellar radius is dominated by
the uncertainty in MV , and is of the order of  log
log 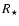 =
=
 0.06-0.10, i.e., less than 26% in
0.06-0.10, i.e., less than 26% in 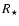 .
.
Luminosities have been calculated from the estimated effective temperatures and
stellar radii, while masses were inferred from the ``true'' surface
gravities. These estimates are given in Cols. 9 and 10 of
Table 3, respectively. The corresponding errors are
less then  0.21 dex in
0.21 dex in
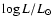 and
and  0.16
to 0.25 dex in log
0.16
to 0.25 dex in log 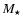 .
.
The spectroscopically estimated masses of our SG targets range from 7
to 53 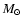
![[*]](/icons/foot_motif.gif) .
Compared to the evolutionary masses from Meynet & Maeder (2000) and apart from two
cases, our estimates are generally lower, by approximately 0.05 to 0.38 dex,
with larger differences for less luminous stars. While for some stars the
discrepancies are less than or comparable to the corresponding errors (e.g.,
HD 185859, HD 190603 first entry, HD206165), they are significant for
some others (mainly at lower luminosities) and might indicate a ``mass
discrepancy'', in common with previous findings
(Trundle & Lennon 2005; Crowther et al. 2006).
.
Compared to the evolutionary masses from Meynet & Maeder (2000) and apart from two
cases, our estimates are generally lower, by approximately 0.05 to 0.38 dex,
with larger differences for less luminous stars. While for some stars the
discrepancies are less than or comparable to the corresponding errors (e.g.,
HD 185859, HD 190603 first entry, HD206165), they are significant for
some others (mainly at lower luminosities) and might indicate a ``mass
discrepancy'', in common with previous findings
(Trundle & Lennon 2005; Crowther et al. 2006).
4.5 Wind parameters
For the four hotter stars in our sample,
individual terminal velocities are available in the literature, determined
from UV P Cygni profiles (Prinja et al. 1990; Howarth et al. 1997; Lamers et al. 1995). For these stars, we
adopted the estimates from Howarth et al. (1997). Interestingly, the initially
adopted value of 470 km s for
for  of HD 198478 did not provide a
satisfactory fit to H
of HD 198478 did not provide a
satisfactory fit to H ,
which in turn required a value of about
200 km s
,
which in turn required a value of about
200 km s .
This is at the lower limit of the ``allowed'' range, since the
photospheric escape velocity,
.
This is at the lower limit of the ``allowed'' range, since the
photospheric escape velocity,
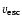 ,
is of the same order. Further
investigations, however, showed that at a different observational epoch the
H
,
is of the same order. Further
investigations, however, showed that at a different observational epoch the
H profile of HD 198478 indeed has extended to about 470 km s
profile of HD 198478 indeed has extended to about 470 km s (Crowther et al. 2006). Thus, for this object we considered a rather large
uncertainty, accounting for possible variations in
(Crowther et al. 2006). Thus, for this object we considered a rather large
uncertainty, accounting for possible variations in  .
.
Regarding the four cooler stars, on the other hand, we were forced to
estimate  by employing the spectral type - terminal velocity
calibration provided by Kudritzki & Puls (2000), since no literature values could be
found and since archival data do not show saturated P Cygni profiles which
could be used to determine
by employing the spectral type - terminal velocity
calibration provided by Kudritzki & Puls (2000), since no literature values could be
found and since archival data do not show saturated P Cygni profiles which
could be used to determine  . In all but one of these objects
(HD 191243, first entry), the calibrated
. In all but one of these objects
(HD 191243, first entry), the calibrated  -values were lower
than the corresponding escape velocities, and we adopted
-values were lower
than the corresponding escape velocities, and we adopted
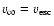 to
avoid this problem.
to
avoid this problem.
The set of  -values used in the present study is listed in Col. 11 of
Table 3. The error of these data is typically less than 100 km s
-values used in the present study is listed in Col. 11 of
Table 3. The error of these data is typically less than 100 km s (Prinja et al. 1990) except for the last four objects where an asymmetric error of
-25/+50% was assumed instead, allowing for a rather large insecurity
towards higher values.
(Prinja et al. 1990) except for the last four objects where an asymmetric error of
-25/+50% was assumed instead, allowing for a rather large insecurity
towards higher values.
In stars with denser winds (H in
emission)
in
emission) 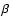 can be derived from H
can be derived from H with relatively high precision and
in parallel with the mass loss rate, due to the strong sensitivity of the H
with relatively high precision and
in parallel with the mass loss rate, due to the strong sensitivity of the H profile shape on this parameter (but see below). On the other hand, for
stars with thin winds (H
profile shape on this parameter (but see below). On the other hand, for
stars with thin winds (H in absorption) the determination of
in absorption) the determination of 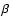 from
optical spectroscopy alone is (almost) impossible and a typical value of
from
optical spectroscopy alone is (almost) impossible and a typical value of
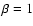 was consistently adopted, but lower and larger values have been
additionally used to constrain the errors. Note that for two of these stars
we actually found indications for values larger than
was consistently adopted, but lower and larger values have been
additionally used to constrain the errors. Note that for two of these stars
we actually found indications for values larger than 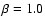 (explicitly stated in Table 3).
(explicitly stated in Table 3).
 ,
have been derived from fitting the
observed H
,
have been derived from fitting the
observed H profiles with model calculations. The obtained estimates are
listed in Col. 13 of Table 3. Corresponding errors, accumulated
from the uncertainties in Q
profiles with model calculations. The obtained estimates are
listed in Col. 13 of Table 3. Corresponding errors, accumulated
from the uncertainties in Q![[*]](/icons/foot_motif.gif) ,
, 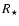 and
and
 , are typically less than
, are typically less than  0.16 dex for the three hotter stars in
our sample and less than
0.16 dex for the three hotter stars in
our sample and less than  0.26 dex for the rest, due to more insecure
values of
0.26 dex for the rest, due to more insecure
values of  and Q.
and Q.
The errors in Q itself have been determined from the fit-quality to H and from the uncertainty in
and from the uncertainty in 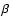 (for stars of thin winds), while the
contribution from the small errors in
(for stars of thin winds), while the
contribution from the small errors in
 have been neglected. Since we
assume an unclumped wind, the actual mass-loss rates of our sample
stars might, of course, be lower. In case of small-scale clumping, this
reduction would be inversely proportional to the square root of the
effective clumping factor being present in the H
have been neglected. Since we
assume an unclumped wind, the actual mass-loss rates of our sample
stars might, of course, be lower. In case of small-scale clumping, this
reduction would be inversely proportional to the square root of the
effective clumping factor being present in the H forming region (e.g.,
Puls et al. 2006 and references therein).
In Figs. 6 and 7 we present our final (``best'')
H
forming region (e.g.,
Puls et al. 2006 and references therein).
In Figs. 6 and 7 we present our final (``best'')
H fits for all sample stars. Apparent problems are:
fits for all sample stars. Apparent problems are:
- The P Cygni profile of H
 seen in HD 190603 (B1.5 Ia+) is not
well fitted. The model fails to reproduce the depth and the
width of the absorption trough. This (minor) discrepancy, however, has no
effect on the derived
seen in HD 190603 (B1.5 Ia+) is not
well fitted. The model fails to reproduce the depth and the
width of the absorption trough. This (minor) discrepancy, however, has no
effect on the derived  and
and 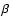 ,
because these parameters are mainly
determined by the emission peak and the red emission wing of the line which
are well reproduced.
,
because these parameters are mainly
determined by the emission peak and the red emission wing of the line which
are well reproduced.
- In two sample stars, HD 198478 and HD 199478, the observations
show H
 in emission whilst the models predict profiles of P Cygni-type. At
least for HD 198478, a satisfactory fit to the red wing and the emission
peak became possible, since the observed profile is symmetric with respect
to rest wavelength, thus allowing us to estimate
in emission whilst the models predict profiles of P Cygni-type. At
least for HD 198478, a satisfactory fit to the red wing and the emission
peak became possible, since the observed profile is symmetric with respect
to rest wavelength, thus allowing us to estimate  and
and  within our assumption of homogeneous and spherically
symmetric winds (see below).
For
within our assumption of homogeneous and spherically
symmetric winds (see below).
For  ,
we provide lower and upper limits in Table 3,
corresponding to the lower and upper limits of the adopted
,
we provide lower and upper limits in Table 3,
corresponding to the lower and upper limits of the adopted  (see also Sect. 6.1). For HD 199478, on the other hand,
(see also Sect. 6.1). For HD 199478, on the other hand,
 is more insecure due to the strong asymmetry in the profile
shape, leading to a larger range in possible mass loss rates and wind momenta.
is more insecure due to the strong asymmetry in the profile
shape, leading to a larger range in possible mass loss rates and wind momenta.
- The H
 profile of HD 202850, the coolest star in our sample,
is not well reproduced: the model predicts more absorption in the core
than is actually observed.
profile of HD 202850, the coolest star in our sample,
is not well reproduced: the model predicts more absorption in the core
than is actually observed.
The most likely reason for our failure to reproduce certain profile shapes
for stars with dense winds is our assumption of smooth and spherically
symmetric atmospheres. Besides the open question of small-scale clumping
(which can change the H morphology quite substantially
morphology quite substantially![[*]](/icons/foot_motif.gif) , cf.
Puls et al. 2006), the fact that in two of the four problematic cases
convincing evidence has been found for the presence of time-dependent
large-scale structure (HD 190603, Rivinius et al. 1997) or deviations from spherical
symmetry and homogeneity (HD 199478, Markova et al. 2007) seems to support
such a possibility. Note that similar problems in reproducing certain H
, cf.
Puls et al. 2006), the fact that in two of the four problematic cases
convincing evidence has been found for the presence of time-dependent
large-scale structure (HD 190603, Rivinius et al. 1997) or deviations from spherical
symmetry and homogeneity (HD 199478, Markova et al. 2007) seems to support
such a possibility. Note that similar problems in reproducing certain H profile shapes in B-SGs have been reported by Kudritzki et al. (1999, from here on
KPL99), Trundle et al. (2004), Crowther et al. (2006) and Lefever et al. (2007).
profile shapes in B-SGs have been reported by Kudritzki et al. (1999, from here on
KPL99), Trundle et al. (2004), Crowther et al. (2006) and Lefever et al. (2007).
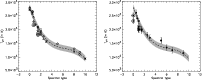 |
Figure 8:
Left: comparison of effective temperatures as derived in the
present study with data from similar investigations. Diamonds - our data;
triangles - data from Crowther et al. (2006); squares - Urbaneja (2004);
asterisks - Przybilla et al. (2006). Large circles mark the three
objects with strongest winds, which simultaneously show the largest
deviation in
 from the mean (all from the sample by Crowther et al.).
The dashed line represents a 3rd order polynomial fit to the data accounting
for the individual errors in from the mean (all from the sample by Crowther et al.).
The dashed line represents a 3rd order polynomial fit to the data accounting
for the individual errors in
 , and the grey-shaded area denotes the
corresponding standard deviation. Spectral types refer to B-stars (i.e.,
``-1'' corresponds to O9, and ``10'' to A0). Right: , and the grey-shaded area denotes the
corresponding standard deviation. Spectral types refer to B-stars (i.e.,
``-1'' corresponds to O9, and ``10'' to A0). Right:
 estimates for GROUP I stars from Lefever et al. (2007), as a function of
spectral type. The error bars correspond to
estimates for GROUP I stars from Lefever et al. (2007), as a function of
spectral type. The error bars correspond to  1000 K, and the dashed
line/shaded area refer to the fit on the left. Large circles mark
data points which deviate significantly from this regression (see text). 1000 K, and the dashed
line/shaded area refer to the fit on the left. Large circles mark
data points which deviate significantly from this regression (see text). |
| Open with DEXTER |
A comparison of present results with such from previous studies
(Barlow & Cohen 1977; Crowther et al. 2006) for three stars in common indicates that the
parameters derived by Crowther et al. (2006) for HD 190603 and HD 198478 are
similar to ours (accounting for the fact that higher
 and MV result
in larger
and MV result
in larger  and
and  ,
respectively, and vice versa). The mass-loss rates
from Barlow & Cohen (1977) (derived from the IR-excess!) for HD 198478 and
HD 202850, on the other hand, are significantly larger than ours and those
from Crowther et al., a problem already faced by Kudritzki et al. (1999) in a
similar (though more simplified) investigation. This might be either due to
certain inconsistencies in the different approaches, or might point to the
possibility that the IR-forming region of these stars is more heavily
clumped than the H
,
respectively, and vice versa). The mass-loss rates
from Barlow & Cohen (1977) (derived from the IR-excess!) for HD 198478 and
HD 202850, on the other hand, are significantly larger than ours and those
from Crowther et al., a problem already faced by Kudritzki et al. (1999) in a
similar (though more simplified) investigation. This might be either due to
certain inconsistencies in the different approaches, or might point to the
possibility that the IR-forming region of these stars is more heavily
clumped than the H forming one.
forming one.
5 The
 scale for B-SGs - comparison with other investigations
scale for B-SGs - comparison with other investigations
Besides the present study, two other investigations have determined the
effective temperatures of Galactic B-type SGs by methods
similar to ours, namely from Silicon and helium (when possible) ionisation
balances, employing state of the art techniques of quantitative spectroscopy
on top of high resolution spectra covering all strategic lines.
Crowther et al. (2006) have used the non-LTE, line blanketed code CMFGEN
(Hillier & Miller 1998) to determine
 of 24 supergiants (luminosity classes Ia,
Ib, Iab, Ia+) of spectral type B0-B3 with an accuracy of
of 24 supergiants (luminosity classes Ia,
Ib, Iab, Ia+) of spectral type B0-B3 with an accuracy of  1000 K,
while Urbaneja (2004) employed FASTWIND (as done here) and determined effective
temperatures of five early B (B2 and earlier) stars of luminosity classes
Ia/Ib with an (internal) accuracy of
1000 K,
while Urbaneja (2004) employed FASTWIND (as done here) and determined effective
temperatures of five early B (B2 and earlier) stars of luminosity classes
Ia/Ib with an (internal) accuracy of  500 K. In addition, Przybilla et al. (2006)
have recently published very precise temperatures (typical error of
500 K. In addition, Przybilla et al. (2006)
have recently published very precise temperatures (typical error of  200
K) of four BA SGs (among which one B8 and two A0 stars), again
derived by means of a line-blanketed non-LTE code, in this case in
plane-parallel geometry neglecting wind effects.
200
K) of four BA SGs (among which one B8 and two A0 stars), again
derived by means of a line-blanketed non-LTE code, in this case in
plane-parallel geometry neglecting wind effects.
Motivated by the good correspondence between data from FASTWIND
and CMFGEN (which has also been noted by Crowther et al. 2006), we plotted
the effective temperatures of all four investigations, as a function of
spectral type (left panel of Fig. 8). Overplotted (dashed
line) is a 3rd order polynomial regression to these data, accounting for the
individual errors in
 , as provided by the different investigations. The
grey-shaded area denotes the standard deviation of the regression.
Obviously, the correspondence between the different datasets is (more than)
satisfactory: for a given spectral subtype, the dispersion of the data does
not exceed
, as provided by the different investigations. The
grey-shaded area denotes the standard deviation of the regression.
Obviously, the correspondence between the different datasets is (more than)
satisfactory: for a given spectral subtype, the dispersion of the data does
not exceed  1000 K. There are only three stars (marked with large circles),
all from the sample of Crowther et al., which make an exception, showing
significantly lower temperatures: HD 190603, HD 152236 and HD 2905.
Given their strong P Cygni profiles seen in H
1000 K. There are only three stars (marked with large circles),
all from the sample of Crowther et al., which make an exception, showing
significantly lower temperatures: HD 190603, HD 152236 and HD 2905.
Given their strong P Cygni profiles seen in H and their high luminosities
- note that the first two stars are actually hypergiants - this result
should not be a surprise though (higher luminosity
and their high luminosities
- note that the first two stars are actually hypergiants - this result
should not be a surprise though (higher luminosity
 denser wind
denser wind
 stronger wind blanketing
stronger wind blanketing
 lower
lower
 ).
).
Very recently, Lefever et al. (2007) published a study with the goal to test
whether the variability of a sample of 28 periodically pulsating, Galactic
B-type SGs is compatible with opacity driven non-radial pulsations.
To this end, they analysed this sample plus 12 comparison objects, also by
means of FASTWIND, thus providing additional stellar and wind parameters of
such objects. In contrast to both our investigation and those mentioned
above, Lefever et al. could not use the Si (He) ionisation balance to
estimate
 , but had to rely on the analysis of one ionisation stage
alone, either Si II or Si III, plus two more He I lines
(
, but had to rely on the analysis of one ionisation stage
alone, either Si II or Si III, plus two more He I lines
(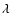 4471 and
4471 and 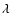 6678). The reason for doing so was the (very)
limited spectral coverage of their sample (though at very high resolution),
with only one representative Silicon ionisation stage observed per object.
6678). The reason for doing so was the (very)
limited spectral coverage of their sample (though at very high resolution),
with only one representative Silicon ionisation stage observed per object.
 |
Figure 9:
Differences between ``unblanketed'' and ``blanketed'' effective temperatures
for the combined sample (this work; Urbaneja 2004; Crowther et al. 2006;
Przybilla et al. 2006 and GROUP I objects from Lefever et al. 2007), as a
function of spectral type ( left panel) and as a function of 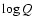 for
individual subtypes, B0 to B3 ( right panel). Unblanketed
for
individual subtypes, B0 to B3 ( right panel). Unblanketed
 are from
McErlean et al. (1999).
Left: Large circles denote the same objects as in
Fig. 8. The data point indicating a significant
negative temperature difference corresponds to the two B5 stars (at
same temperature) from the Lefever et al. sample.
Right: The size of the symbols corresponds to the size of the
peak emission seen in H are from
McErlean et al. (1999).
Left: Large circles denote the same objects as in
Fig. 8. The data point indicating a significant
negative temperature difference corresponds to the two B5 stars (at
same temperature) from the Lefever et al. sample.
Right: The size of the symbols corresponds to the size of the
peak emission seen in H . Filled circles mark data from CMFGEN, open
circles those from FASTWIND. . Filled circles mark data from CMFGEN, open
circles those from FASTWIND. |
| Open with DEXTER |
Given the problems we faced during our analysis (which only appeared
because we had a much larger number of lines at our disposal) and the fact
that Lefever et al. were not able to independently estimate Si
abundances and
 of their sample stars (as we have done here), the
results derived during this investigation are certainly prone to larger
error bars than those obtained by methods where all strategic lines
could be included (see Lefever et al. for more details).
of their sample stars (as we have done here), the
results derived during this investigation are certainly prone to larger
error bars than those obtained by methods where all strategic lines
could be included (see Lefever et al. for more details).
The right-hand panel of Fig. 8 displays their temperature
estimates for stars from the so-called GROUP I (most precise parameters),
overplotted by our regression from the left panel. The error bars
correspond to  1000 K quoted by the authors as a nominal error.
While most of their data are consistent (within their errors) with our
regression, there are also objects (marked again with large circles) which
deviate significantly.
1000 K quoted by the authors as a nominal error.
While most of their data are consistent (within their errors) with our
regression, there are also objects (marked again with large circles) which
deviate significantly.
Interestingly, all outliers situated below the regression are stars of early
subtypes (B0/B1), which furthermore show P Cygni profiles with relatively
strong emission components in H (except for HD 15043 which exhibits H
(except for HD 15043 which exhibits H in absorption), a situation that is quite similar to the one observed on the
left of this figure. (We return to this point in the next section.)
in absorption), a situation that is quite similar to the one observed on the
left of this figure. (We return to this point in the next section.)
On the other hand, there are two stars of B5-type with same
 , which lie
above the regression, i.e., seem to show ``overestimated'' temperatures. The
positions of these stars within the
, which lie
above the regression, i.e., seem to show ``overestimated'' temperatures. The
positions of these stars within the
 -spectral type plane have been
extensively discussed by Lefever et al. (2007) who suggested that the presence of
a radially stratified micro-turbulent velocity (as also discussed by us) or
a Si abundance being lower than adopted (solar) might explain the
overestimate (if so) of their temperatures. Note, however, that the
surface gravity of HD 108659 (=2.3), one of the Lefever et al. B5 targets,
seems to be somewhat large for a SG but appropriate for a bright
giant. Thus, it might still be that the ``overestimated'' temperature of
HD 108659 is a result of its misclassification as a SG whilst
actually it is a bright giant. This possibility, however, cannot be applied to
the other B5 target, HD 102997, which has
-spectral type plane have been
extensively discussed by Lefever et al. (2007) who suggested that the presence of
a radially stratified micro-turbulent velocity (as also discussed by us) or
a Si abundance being lower than adopted (solar) might explain the
overestimate (if so) of their temperatures. Note, however, that the
surface gravity of HD 108659 (=2.3), one of the Lefever et al. B5 targets,
seems to be somewhat large for a SG but appropriate for a bright
giant. Thus, it might still be that the ``overestimated'' temperature of
HD 108659 is a result of its misclassification as a SG whilst
actually it is a bright giant. This possibility, however, cannot be applied to
the other B5 target, HD 102997, which has 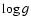 of 2.0 (and MV of -7.0),
i.e., is consistent with its classification as a supergiant.
of 2.0 (and MV of -7.0),
i.e., is consistent with its classification as a supergiant.
Interestingly, the surface gravity of ``our'' B5 star, HD 191243
(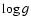 = 2.6), appears also to be larger than what is typical for a
supergiant of B5 subtype.
With a distance modulus of 2.2 kps (Humphreys 1978), the absolute
magnitude of HD 191243 would be more consistent with a supergiant
classification, but with d = 1.75 kpc (Garmany & Stencel 1992) a luminosity class II is more
appropriate. Thus, this star also seems to be misclassified
= 2.6), appears also to be larger than what is typical for a
supergiant of B5 subtype.
With a distance modulus of 2.2 kps (Humphreys 1978), the absolute
magnitude of HD 191243 would be more consistent with a supergiant
classification, but with d = 1.75 kpc (Garmany & Stencel 1992) a luminosity class II is more
appropriate. Thus, this star also seems to be misclassified![[*]](/icons/foot_motif.gif) .
.
5.2 Temperature revisions due to
line-blanketing and wind effects
In order to estimate now the effects of line-blocking/blanketing together
with wind effects in the B supergiant domain (as has been done previously
for the O-star domain, e.g., Markova et al. 2004; Repolust et al. 2004; Martins et al. 2005), we have
combined the different datasets as discussed above into one sample, keeping
in mind the encountered problems.
Figure 9, left panel, displays the differences between
``unblanketed'' and ``blanketed'' effective temperatures for this combined
sample, as a function of spectral type. The ``unblanketed'' temperatures
have been estimated using the
 -spectral type calibration provided by
McErlean et al. (1999), based on unblanketed, plane-parallel, NLTE model atmosphere
analyses. Objects enclosed by large circles are the same as in
Fig. 8, i.e., three from the analysis by Crowther et al.,
and seven from the sample by Lefever et al.
-spectral type calibration provided by
McErlean et al. (1999), based on unblanketed, plane-parallel, NLTE model atmosphere
analyses. Objects enclosed by large circles are the same as in
Fig. 8, i.e., three from the analysis by Crowther et al.,
and seven from the sample by Lefever et al.![[*]](/icons/foot_motif.gif) As to be expected and as noted by previous
authors on the basis of smaller samples (e.g.,
Lefever et al. 2007; Crowther et al. 2006), the ``blanketed'' temperatures of Galactic
B-SGs are systematically lower than the ``unblanketed'' ones. The
differences range from about zero to roughly 6000 K, with a tendency to
decrease towards later subtypes (see below for further discussion).
As to be expected and as noted by previous
authors on the basis of smaller samples (e.g.,
Lefever et al. 2007; Crowther et al. 2006), the ``blanketed'' temperatures of Galactic
B-SGs are systematically lower than the ``unblanketed'' ones. The
differences range from about zero to roughly 6000 K, with a tendency to
decrease towards later subtypes (see below for further discussion).
The most remarkable feature in Fig. 9 is the large dispersion
in 
 for stars of early subtypes, B0-B3. Since the largest
differences are seen for stars showing P Cygni profiles with a relatively
strong emission component in H
for stars of early subtypes, B0-B3. Since the largest
differences are seen for stars showing P Cygni profiles with a relatively
strong emission component in H , we suggest that most of this dispersion is
related to wind effects.
, we suggest that most of this dispersion is
related to wind effects.
To investigate this possibility, we have plotted the distribution of the
 -values of the B0-B3 object as a function of the
distant-invariant optical depth parameter
-values of the B0-B3 object as a function of the
distant-invariant optical depth parameter 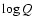 (cf.
Sect. 4). Since the H
(cf.
Sect. 4). Since the H emission strength does not depend on
Q alone but also on
emission strength does not depend on
Q alone but also on
 - for same Q-values cooler objects have more
emission due to lower ionisation - stars with individual subclasses were
studied separately to diminish this effect. The right-hand panel of
Fig. 9 illustrates our results, where the size of the circles
corresponds to the strength of the emission peak of the line. Filled
symbols mark data from CMFGEN, and open ones data from FASTWIND.
Inspection of these data indicates that objects with stronger H
- for same Q-values cooler objects have more
emission due to lower ionisation - stars with individual subclasses were
studied separately to diminish this effect. The right-hand panel of
Fig. 9 illustrates our results, where the size of the circles
corresponds to the strength of the emission peak of the line. Filled
symbols mark data from CMFGEN, and open ones data from FASTWIND.
Inspection of these data indicates that objects with stronger H emission
tend to show larger log Q-values and subsequently higher
emission
tend to show larger log Q-values and subsequently higher 
 -
a finding that is model independent. This tendency is particularly
evident in the case of B1 and B2 objects. On the other hand, there are at
least three objects which appear to deviate from this rule, but this might
still be due to the fact that the temperature dependence of Q has not been
completely removed (of course, uncertainties in
-
a finding that is model independent. This tendency is particularly
evident in the case of B1 and B2 objects. On the other hand, there are at
least three objects which appear to deviate from this rule, but this might
still be due to the fact that the temperature dependence of Q has not been
completely removed (of course, uncertainties in 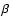 ,
,
 and
and 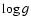 can
also contribute). All three stars (HD 89767, HD 94909
(both B0) and HD 154043 (B1)) are from the Lefever et al. sample
and do not exhibit strong H
can
also contribute). All three stars (HD 89767, HD 94909
(both B0) and HD 154043 (B1)) are from the Lefever et al. sample
and do not exhibit strong H emission but nevertheless the highest
emission but nevertheless the highest
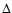
 among the individual subclasses.
among the individual subclasses.
In summary, we suggest that the dispersion in the derived effective
temperature scale of early B-SGs is physically real and originates from wind
effects. Moreover, there are three stars from the Lefever et al. GROUP
I sample (spectral types B0 to B1) whose temperatures seem to be
significantly underestimated, probably due to insufficient diagnostics. In
our follow-up analysis with respect to wind-properties, we will discard
these ``problematic'' objects to remain on the ``conservative'' side.
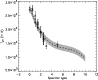 |
Figure 10:
Temperature scale for Galactic B-SG as derived in the present study
(dashed, see text), compared to
 estimates for similar stars in the SMC
(from Trundle et al. 2004 (diamonds) and Trundle & Lennon 2005 (triangles)).
The grey area denotes the standard deviation of the regression for Galactic
objects. Spectral types account for metallicity effects (from
Lennon 1997), see text. estimates for similar stars in the SMC
(from Trundle et al. 2004 (diamonds) and Trundle & Lennon 2005 (triangles)).
The grey area denotes the standard deviation of the regression for Galactic
objects. Spectral types account for metallicity effects (from
Lennon 1997), see text.
|
| Open with DEXTER |
Wanted to obtain an impression of the influence of
metallicity on the temperature scale for B-type SGs, by comparing Galactic
with SMC data. To this end, we derived a
 -spectral type calibration for
Galactic B-SGs on basis of the five datasets discussed above, discarding
only those (seven) objects from the Lefever et al. sample where the temperatures
might be particularly affected by strong winds or other uncertainties
(marked by large circles in Fig. 8, right). Accounting
for the errors in
-spectral type calibration for
Galactic B-SGs on basis of the five datasets discussed above, discarding
only those (seven) objects from the Lefever et al. sample where the temperatures
might be particularly affected by strong winds or other uncertainties
(marked by large circles in Fig. 8, right). Accounting
for the errors in
 ,
we obtain the following regression (for a
precision of three significant digits)
,
we obtain the following regression (for a
precision of three significant digits)
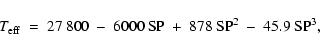 |
(1) |
where ``SP'' (0-9) gives the spectral type (from B0 to B9), and the
standard deviation is  1040 K. This regression was then compared to
1040 K. This regression was then compared to
 estimates obtained by Trundle et al. (2004) and Trundle & Lennon (2005) for
B-SGs in the SMC.
estimates obtained by Trundle et al. (2004) and Trundle & Lennon (2005) for
B-SGs in the SMC.
We decided to compare with these two studies only, because Trundle et
al. have used a similar (2004) or identical (2005) version of FASTWIND as
we did here, i.e., systematic, model dependent differences between different
datasets can be excluded and because the metallicity of the SMC is
significantly lower than in the Galaxy, so that metallicity dependent
effects should be maximised.
The outcome of our comparison is illustrated in
Fig. 10: In contrast to the O-star case (cf.
Massey et al. 2004,2005; Mokiem et al. 2006), the data for the SMC stars are,
within their errors, consistent with the temperature scale for their
Galactic counterparts. This result might be interpreted as an indication of
small or even negligible metallicity effects (both directly, via
line-blanketing, and indirectly, via weaker winds) in the temperature regime
of B-SGs, at least for metallicities in between solar and SMC (about
0.2 solar) values. Such an interpretation would somewhat contradict our
findings about the strong influence of line-blanketing in the
Galactic case (given that these effects should be lower in the SMC), but
might be misleading since Trundle et al. (2004, 2005) have used the spectral
classification from Lennon (1997), which already accounts for the lower
metallicity in the SMC. To check the influence of this re-classification, we
recovered the original (MK) spectral types of the SMC targets using data
provided by Lennon (1997, Table 2), and subsequently compared them to our
results for Galactic B-SGs. Unexpectedly, SMC objects still do not show any
systematic deviation from the Galactic scale but are, instead, distributed
quite randomly around the Galactic mean. Most plausibly, this outcome
results from the large uncertainty in spectral types as determined by
Azzopardi & Vigneau (1975)![[*]](/icons/foot_motif.gif) , such that metallicity effects cannot become apparent for
the SMC objects considered here. Nevertheless, we can also conclude that the
classification by Lennon (1997) has been done in a perfect way, namely
that Galactic and SMC stars of similar spectral type also have similar
physical parameters, as expected.
, such that metallicity effects cannot become apparent for
the SMC objects considered here. Nevertheless, we can also conclude that the
classification by Lennon (1997) has been done in a perfect way, namely
that Galactic and SMC stars of similar spectral type also have similar
physical parameters, as expected.
 |
Figure 11:
Left: WLR for Galactic
B-SGs, based on data from the combined sample: diamonds - our data;
triangles - data from Crowther et al. (2006); squares - data from Urbaneja (2004)
and plus signs - data from Lefever et al. (2007) (GROUP I, without the three
``problematic'' objects). The two pairs of symbols connected with dashed
lines correspond to the two entries for HD 190603 and HD 198478 as
listed in Table 2. For the latter object and for HD 199478, we
also provide error bars indicating the rather large uncertainty in their
wind-momenta. Specially marked objects are discussed in the text.
Right: wind-momenta of B-SGs from the left (diamonds and asterisks) are
compared with similar data for O-SGs (triangles). Filled diamonds indicate
B-type objects with
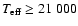 K, asterisks such with K, asterisks such with
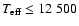 K and open diamonds B-types with temperatures in between
12 500 and 21 000 K. The high luminosity solution for HD 190603 is
indicated by a square. Overplotted are the early/mid B - (small plus-signs)
and A SG (large plus-signs) data derived by KPL99 and the theoretical
predictions from Vink et al. (2000) for Galactic SGs with
27 500 K and open diamonds B-types with temperatures in between
12 500 and 21 000 K. The high luminosity solution for HD 190603 is
indicated by a square. Overplotted are the early/mid B - (small plus-signs)
and A SG (large plus-signs) data derived by KPL99 and the theoretical
predictions from Vink et al. (2000) for Galactic SGs with
27 500 
  50 000 (dashed-dotted) and with
12 500
50 000 (dashed-dotted) and with
12 500 
 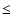 22 500 (dashed). Error bars provided in
the lower-right corner of each panel represent the typical errors in
22 500 (dashed). Error bars provided in
the lower-right corner of each panel represent the typical errors in
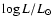 and
and
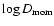 for data from our sample. Maximum errors in for data from our sample. Maximum errors in
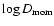 are about 50%
larger. are about 50%
larger.
|
| Open with DEXTER |
6 Wind-momentum luminosity relationship
6.1 Comparison with results from similar studies
Using the stellar and wind parameters, the modified wind momenta can be
calculated (Table 3, Col. 14), and the wind-momentum
luminosity diagram constructed. The results for the combined sample (to
improve the statistics, but without the ``problematic'' stars from the
Lefever et al. GROUP I sample) are shown on the left of Fig. 11. Data
from different sources are indicated by different symbols. For HD 190603
and HD 198478, both alternative entries (from Table 2) are
indicated and connected by a dashed line. Before we consider the global
behaviour, we first comment on few particular objects.
- The position of HD 190603 corresponding to B-V=0.540 (lower
luminosity) appears to be more consistent with the distribution of the
other data points than the alternative position with B-V=0.760.
In the following, we give more weight to the former solution.
- The positions of the two B5 stars suggested as being misclassified
(HD 191243 and HD 108659, large diamonds) fit well the global
trend of the data, implying that these bright giants do not behave differently
from supergiants.
- The minimum values for the wind momentum of HD 198478
(with
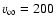 km s
km s ) deviate strongly from the global trend, whereas the
maximum ones (
) deviate strongly from the global trend, whereas the
maximum ones (
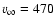 km s
km s ) are roughly consistent with this trend.
For our follow-up analysis, we discard this object because of the very
unclear situation.
) are roughly consistent with this trend.
For our follow-up analysis, we discard this object because of the very
unclear situation.
- HD 152236 (from the sample of Crowther et al., marked with a
large circle) is a hypergiant
with a very dense wind, for which the authors adopted
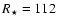
 ,
which makes this object the brightest one in the sample.
,
which makes this object the brightest one in the sample.
From the left of Fig. 11, we see that
the lower luminosity B-supergiants seem to follow a systematically lower
WLR than their higher luminosity counterparts, with a steep transition
between both regimes located in between
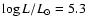 and
and
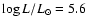 .
(Admittedly, most of the early type (high L) objects are Ia's, whereas the
later types concentrate around Iab's with few Ia/Ib's.)
This finding becomes even more apparent when the WLR is extended towards
higher luminosities by including Galactic O supergiants (from
Herrero et al. 2002; Markova et al. 2004; Repolust et al. 2004), as done on the right of the same
figure.
.
(Admittedly, most of the early type (high L) objects are Ia's, whereas the
later types concentrate around Iab's with few Ia/Ib's.)
This finding becomes even more apparent when the WLR is extended towards
higher luminosities by including Galactic O supergiants (from
Herrero et al. 2002; Markova et al. 2004; Repolust et al. 2004), as done on the right of the same
figure.
KPL99 were the first to point out that the offsets in the corresponding WLR
of OBA-supergiants depend on spectral type, being strongest for O-SGs,
decreasing from B0-B1 to B1.5-B3 and increasing again towards A
supergiants. While some of these results have been confirmed by recent
studies, others have not (Lefever et al. 2007; Crowther et al. 2006).
To investigate this issue in more detail and based on the large sample
available now, we have highlighted the early objects (B0-B1.5,
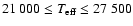 K) in the right-hand panel of
Fig. 11 using filled diamonds. (Very) Late objects with
K) in the right-hand panel of
Fig. 11 using filled diamonds. (Very) Late objects with
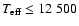 K have been indicated by asterisks, and intermediate temperature
objects by open diamonds. Triangles denote O-SGs. Additionally, the
theoretical predictions by Vink et al. (2000) are provided via dashed-dotted and
dashed lines, corresponding to the temperature regimes of O and B-supergiants,
respectively (from here on referred to as ``higher'' and ``lower''
temperature predictions). Indeed,
K have been indicated by asterisks, and intermediate temperature
objects by open diamonds. Triangles denote O-SGs. Additionally, the
theoretical predictions by Vink et al. (2000) are provided via dashed-dotted and
dashed lines, corresponding to the temperature regimes of O and B-supergiants,
respectively (from here on referred to as ``higher'' and ``lower''
temperature predictions). Indeed,
- O-SGs show the strongest wind momenta, determining a
different relationship than the majority of B-SGs (see below);
- the wind momenta of B0-B1.5 subtypes are larger than those
of B1.5-3, and both follow a different relationship. However, a direct
comparison with KPL99 reveals a large discrepancy for mid B1.5-B3 subtypes
(
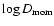 about 0.5 dex), while for B0-B1.5 subtypes their results
are consistent with those from our combined dataset;
about 0.5 dex), while for B0-B1.5 subtypes their results
are consistent with those from our combined dataset;
- late B4-B9 stars follow the same relationship as mid subtypes.
Thus, the only apparent disagreement with earlier
findings relates to the KPL99 mid-B types, previously pointed out by Crowther et al. (2006), and suggested to be a result of
line blocking/blanketing effects not accounted for in the KPL99
analysis![[*]](/icons/foot_motif.gif) . After a detailed
investigation of this issue for one proto-typical object from the KPL99
sample (HD 42087), we are convinced that the neglect of line
blocking/blanketing cannot solely account for such lower wind momenta. Other
effects must also contribute, e.g., overestimated
. After a detailed
investigation of this issue for one proto-typical object from the KPL99
sample (HD 42087), we are convinced that the neglect of line
blocking/blanketing cannot solely account for such lower wind momenta. Other
effects must also contribute, e.g., overestimated 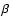 -values, though at
least the latter effect still leaves a considerable discrepancy.
-values, though at
least the latter effect still leaves a considerable discrepancy.
On the other hand, a direct comparison of the KPL99 A-supergiant dataset
(marked with large plus-signs on the right of Fig. 11) with data
from the combined sample shows that their wind momenta seem to be quite
similar to those of mid and late B subtypes. Further investigations based
on better statistics are required to clarify this issue.
According to the theoretical predictions by Vink et al. (2000), Galactic
supergiants with effective temperatures between 12 500 and 22 500 K
(spectral types B1 to B9) should follow a WLR different from that of hotter
stars (O-types and early B subtypes), with wind momenta being systematically
larger. From Fig. 11 (right), however, it is obvious that the
observed behaviour does not follow these predictions. Instead, the majority
of O-SGs (triangles - actually those with H in emission, see below)
follow the low-temperature predictions (dashed line), while most of the
early B0-B1.5 subtypes (filled diamonds) are consistent with the
high-temperature predictions (dashed-dotted), and later subtypes (from B2
on, open diamonds) lie below (!), by about 0.3 dex. Only few early B-types
are located in between both predictions or close to the low-temperature one.
in emission, see below)
follow the low-temperature predictions (dashed line), while most of the
early B0-B1.5 subtypes (filled diamonds) are consistent with the
high-temperature predictions (dashed-dotted), and later subtypes (from B2
on, open diamonds) lie below (!), by about 0.3 dex. Only few early B-types
are located in between both predictions or close to the low-temperature one.
The offset between both theoretical WLRs has been explained by
Vink et al. (2000) due to the increase in mass-loss rate at the
bi-stability jump (more lines from lower iron ionization stages available to
accelerate the wind), which is only partly compensated by a drop in terminal
velocity. The size of the jump in  ,
about a factor of five, was
determined requiring a drop in
,
about a factor of five, was
determined requiring a drop in  by a factor of two, as extracted from
earlier observations (Lamers et al. 1995).
by a factor of two, as extracted from
earlier observations (Lamers et al. 1995).
However, more recent investigations (Crowther et al. 2006; see also
Evans et al. 2004) have questioned the presence of such a ``jump'' in  ,
and argued in favour of a gradual decrease in
,
and argued in favour of a gradual decrease in  /
/
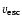 , from
, from  3.4
above 24 kK to
3.4
above 24 kK to  1.9 below 20 kK.
1.9 below 20 kK.
In the following, we comment on our findings regarding this problem
in some detail,
(i) because of the significant increase in data (also at lower
 ), (ii)
we will tackle the problem by a somewhat modified approach and
(iii) recently a new investigation of the bistability jump by means of radio
mass-loss rates has been published (Benaglia et al. 2007) which gives additional
impact and allows for further comparison/conclusions.
), (ii)
we will tackle the problem by a somewhat modified approach and
(iii) recently a new investigation of the bistability jump by means of radio
mass-loss rates has been published (Benaglia et al. 2007) which gives additional
impact and allows for further comparison/conclusions.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7919f12.ps}\end{figure}](/articles/aa/full/2008/06/aa7919-07/Timg115.gif) |
Figure 12:
Ratio of  / /
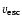 as a function of log as a function of log
 . Diamonds: combined
OBA-supergiant sample as in Fig. 11, right panel.
Asterisks/plus-signs refer to the early/mid B supergiants from the sample by
KPL99. Large diamonds again correspond to the potentially misclassified
B5-objects HD 191243 and HD 108659. The triangle denotes the hypergiant
HD 152236 and the three squares - the various positions of HD 53138 as
derived by Crowther et al. (2006), Lefever et al. (2007) and KPL99
(references ordered by increasing . Diamonds: combined
OBA-supergiant sample as in Fig. 11, right panel.
Asterisks/plus-signs refer to the early/mid B supergiants from the sample by
KPL99. Large diamonds again correspond to the potentially misclassified
B5-objects HD 191243 and HD 108659. The triangle denotes the hypergiant
HD 152236 and the three squares - the various positions of HD 53138 as
derived by Crowther et al. (2006), Lefever et al. (2007) and KPL99
(references ordered by increasing
 ). Individual errors extend
from 33% to 43%. See text. ). Individual errors extend
from 33% to 43%. See text. |
| Open with DEXTER |
First, let us define the ``position'' of the jump by means of the
 /
/
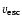 -ratios from the OBA-supergiant sample as defined in the previous
section (excluding the ``uncertain'' object HD 198478). In
Fig. 12, two temperature regimes with considerably different
values of such ratios have been identified, connected by a transition zone.
In the high temperature regime (
-ratios from the OBA-supergiant sample as defined in the previous
section (excluding the ``uncertain'' object HD 198478). In
Fig. 12, two temperature regimes with considerably different
values of such ratios have been identified, connected by a transition zone.
In the high temperature regime (
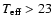 kK), our sample provides
kK), our sample provides
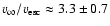 ,
whereas in the low temperature one
(
,
whereas in the low temperature one
(
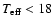 kK), we find
kK), we find
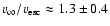 .
(Warning:
the latter estimate has to be considered cautiously, due to the large
uncertainties at the lower end where
.
(Warning:
the latter estimate has to be considered cautiously, due to the large
uncertainties at the lower end where
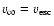 has been adopted for
few stars due to missing diagnostics.) Note that the individual errors
for
has been adopted for
few stars due to missing diagnostics.) Note that the individual errors
for
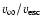 are fairly similar, of the order of 33% (for
are fairly similar, of the order of 33% (for
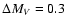 ,
,
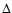
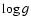 = 0.15 and
= 0.15 and
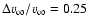 )
to 43% (in the most
pessimistic case
)
to 43% (in the most
pessimistic case
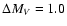 ), similar to the
corresponding Fig. 8 by Crowther et al.
), similar to the
corresponding Fig. 8 by Crowther et al.
In the transition zone, a variety of ratios are present, thus
supporting the findings discussed above. Obviously though, large ratios
typical for the high temperature region are no longer present from the
centre of the transition region on, so we can define a ``jump
temperature'' of

 20 000 K. Nevertheless, we have shifted the
border of the high-temperature regime to
20 000 K. Nevertheless, we have shifted the
border of the high-temperature regime to
 = 23 kK, since at least low
ratios are present until then (note the dashed vertical and horizontal lines
in Fig. 12). The low temperature border has been defined
analogously, as the coolest location with ratios >2 (dotted lines).
= 23 kK, since at least low
ratios are present until then (note the dashed vertical and horizontal lines
in Fig. 12). The low temperature border has been defined
analogously, as the coolest location with ratios >2 (dotted lines).
By comparing our (rather conservative) numbers with those from the
publications as cited above, we find a satisfactory agreement, both with
respect to the borders of the transition zone as well as with the average
ratios of  /
/
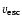 . In particular, our high temperature value is almost
identical to that derived by Crowther et al. (2006); Kudritzki & Puls 2000 provide
an average ratio of 2.65 for
. In particular, our high temperature value is almost
identical to that derived by Crowther et al. (2006); Kudritzki & Puls 2000 provide
an average ratio of 2.65 for
 > 21 kK), whereas in the low
temperature regime we are consistent with the latter investigation
(Kudritzki & Puls: 1.4). The somewhat larger value found by Crowther et
al. results from missing latest spectral subtypes.
> 21 kK), whereas in the low
temperature regime we are consistent with the latter investigation
(Kudritzki & Puls: 1.4). The somewhat larger value found by Crowther et
al. results from missing latest spectral subtypes.
Having defined the behaviour of  ,
we investigate
the behaviour of
,
we investigate
the behaviour of  , which is predicted to increase more strongly than
, which is predicted to increase more strongly than  decreases. As we have already seen from the WLR, this most probably is not the case for a statistically representative sample of ``normal''
B-SGs, but more definite statements become difficult for two
reasons. First, both the independent (
decreases. As we have already seen from the WLR, this most probably is not the case for a statistically representative sample of ``normal''
B-SGs, but more definite statements become difficult for two
reasons. First, both the independent (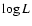 )
and the dependent (
)
and the dependent (
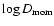 )
variable depend on
)
variable depend on 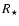 (remember, the fit quantity is not
(remember, the fit quantity is not  but Q),
which is problematic for Galactic objects. Second, the wind-momentum rate is
a function of L but not of
but Q),
which is problematic for Galactic objects. Second, the wind-momentum rate is
a function of L but not of
 alone, such that a division of different
regimes becomes difficult. To avoid these problems, let us firstly
recapitulate the derivation of the WLR, to see the differences compared to
our alternative approach formulated below.
alone, such that a division of different
regimes becomes difficult. To avoid these problems, let us firstly
recapitulate the derivation of the WLR, to see the differences compared to
our alternative approach formulated below.
From the scaling relations of line-driven wind theory, we have
where 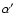 is the difference between the line force multipliers
is the difference between the line force multipliers
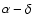 (corresponding to the slope of the line-strength distribution
function and the ionisation parameter; for details, see Puls et al. 2000),
k - the force-multiplier parameter proportional to the effective number of
driving lines and
(corresponding to the slope of the line-strength distribution
function and the ionisation parameter; for details, see Puls et al. 2000),
k - the force-multiplier parameter proportional to the effective number of
driving lines and 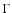 - the (distance independent!)
Eddington parameter. Note that the relation for
- the (distance independent!)
Eddington parameter. Note that the relation for  is
problematic because of its mass-dependence, and that
is
problematic because of its mass-dependence, and that  itself depends
on distance. By multiplying with
itself depends
on distance. By multiplying with  and (
and ( /
/ )1/2, we obtain
the well-known expression for the (modified) wind-momentum rate,
)1/2, we obtain
the well-known expression for the (modified) wind-momentum rate,
where we have explicitly included here those quantities which are dependent
on spectral type (and metallicity). Remember that this derivation assumes
the winds to be unclumped, and that
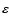 is small, which is true
at least for O-supergiants (Puls et al. 2000).
is small, which is true
at least for O-supergiants (Puls et al. 2000).
Investigating various possibilities, it turned out that the
(predicted) scaling relation for a quantity defined similarly as the
optical-depth invariant is particularly advantageous:
This relation for the distance independent quantity Q' becomes a
function of log
 and D0' alone if
and D0' alone if 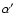 were exactly 2/3, i.e.,
under the same circumstances as the WLR. Obviously, this relation has all
the features we are interested in, and we will investigate the temperature
behaviour of
were exactly 2/3, i.e.,
under the same circumstances as the WLR. Obviously, this relation has all
the features we are interested in, and we will investigate the temperature
behaviour of  by plotting log Q' vs. log
by plotting log Q' vs. log
 . We believe that the
factor
. We believe that the
factor
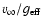 is a monotonic
function on both sides of and through the transition zone, as is also the
case for
is a monotonic
function on both sides of and through the transition zone, as is also the
case for
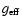 itself. Thus, the
itself. Thus, the
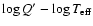 relation should
react only on differences in the effective number of driving lines and on
the different ratio
relation should
react only on differences in the effective number of driving lines and on
the different ratio  /
/
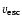 on both sides of the transition region.
on both sides of the transition region.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7919f13.ps}\end{figure}](/articles/aa/full/2008/06/aa7919-07/Timg146.gif) |
Figure 13:
Modified optical depth invariant, 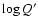 (Eq. (8), as a function of
log
(Eq. (8), as a function of
log
 . Symbols as in Fig. 12, with vertical bars indicating the
``transition'' region between 18 and 23 kK. Note that the mid B-type
supergiants from the KPL99 sample (plus-signs) deviate from the trend
displayed by the other objects. Regression for the complete sample
(excluding HD 53138, HD 152236 and the KPL99 B-supergiants) overplotted
in solid; dashed regression similar, but additionally excluding the objects
in the transition region (see text). . Symbols as in Fig. 12, with vertical bars indicating the
``transition'' region between 18 and 23 kK. Note that the mid B-type
supergiants from the KPL99 sample (plus-signs) deviate from the trend
displayed by the other objects. Regression for the complete sample
(excluding HD 53138, HD 152236 and the KPL99 B-supergiants) overplotted
in solid; dashed regression similar, but additionally excluding the objects
in the transition region (see text). |
| Open with DEXTER |
Figure 13 displays our final result. At first glance, there is almost
no difference between the relation on both sides of the ``jump'', whereas
inside the transition zone there is a large scatter, even if not accounting
for the (questionable) mid-B star data from KPL99.
Initially, we calculated the average slope of this relation by linear
regression, and then the corresponding slope by additionally excluding the
objects inside the transition region (dashed). Both regressions give similar
results, interpreted in terms of 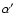 with values of 0.65 and 0.66 (!),
respectively
with values of 0.65 and 0.66 (!),
respectively![[*]](/icons/foot_motif.gif) , and with standard errors regarding
, and with standard errors regarding
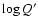 of
of 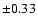 and
and 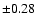 dex.
dex.
If the relations indeed were identical on both sides of the jump,
we would also have to conclude that the offset,
D0', is identical on both sides of the transition region. In this case,
the decrease in  /
/
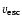 within the transition zone has to be more or
less exactly balanced by the same amount of a decrease in
within the transition zone has to be more or
less exactly balanced by the same amount of a decrease in
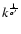 ,
i.e., both
,
i.e., both  and
and  are decreasing in parallel, in complete
contradiction to the prediction by Vink et al.
are decreasing in parallel, in complete
contradiction to the prediction by Vink et al.
A closer inspection of Fig. 13 (in combination with the
corresponding WLR of Fig. 11) implies an alternative
interpretation. At the hottest (high luminosity) end, we find the typical
division of supergiants with H in emission and absorption, where the
former display an offset of a factor 2-3 above the mean relation, a
fact which has been interpreted to be related to wind-clumping previously.
in emission and absorption, where the
former display an offset of a factor 2-3 above the mean relation, a
fact which has been interpreted to be related to wind-clumping previously.
Proceeding towards lower temperatures, the Q' relation becomes well
defined between roughly 31 kK and the hot side of the transition zone (in
contrast to the WLR, which shows more scatter, presumably due to uncertain
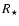 ). Inside the transition zone and also in the WLR around
). Inside the transition zone and also in the WLR around
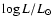
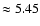 ,
a large scatter is present, followed by an apparent steep
decrease in
,
a large scatter is present, followed by an apparent steep
decrease in 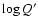 and wind-momentum rate, where the former is located
just at the ``jump temperature'' of 20 kK. Note that the mid-B type objects
of the KPL99 sample are located just in this region. From then on, Q'appears to remain almost constant until 14 kK, whereas the WLR is
rather flat between 5.1 <
and wind-momentum rate, where the former is located
just at the ``jump temperature'' of 20 kK. Note that the mid-B type objects
of the KPL99 sample are located just in this region. From then on, Q'appears to remain almost constant until 14 kK, whereas the WLR is
rather flat between 5.1 <
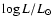 < 5.4, in agreement with the findings by
Benaglia et al. (2007, their Fig. 8). At the lowest temperatures/luminosities,
both Q' and the WLR decrease again, with a similar slope as in the hot
star domain. This offers a possibility of a discontinuous
behaviour, but, again, in contradiction to what is predicted.
< 5.4, in agreement with the findings by
Benaglia et al. (2007, their Fig. 8). At the lowest temperatures/luminosities,
both Q' and the WLR decrease again, with a similar slope as in the hot
star domain. This offers a possibility of a discontinuous
behaviour, but, again, in contradiction to what is predicted.
We now quantify the behaviour of the mass-loss rate in the low
temperature region (compared to the high temperature one), in a more
conservative manner than estimated above, by using both the 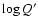 relation and the WLR. Accounting for the fact that the corresponding
slopes are rather similar on both sides of the transition zone, we define a
difference of offsets,
relation and the WLR. Accounting for the fact that the corresponding
slopes are rather similar on both sides of the transition zone, we define a
difference of offsets,
evaluated with respect to ``low'' minus ``high''. From the WLR, we have
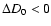 ,
whereas the Q' relation implies
,
whereas the Q' relation implies
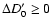 ,
to
be cautious. Thus, the change in
,
to
be cautious. Thus, the change in
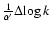 (which expresses the
difference in log
(which expresses the
difference in log  on both sides of the jump, cf. Eq. (2))
is constrained by
on both sides of the jump, cf. Eq. (2))
is constrained by
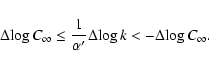 |
(13) |
To be cautious again, we note that
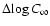 should lie in the
range log(1.9/2.4)-log(1.3/3.3) = -0.1--0.4, accounting
for the worst and the average situation (cf. Fig. 12).
should lie in the
range log(1.9/2.4)-log(1.3/3.3) = -0.1--0.4, accounting
for the worst and the average situation (cf. Fig. 12).
Thus, the scaling factors of mass-loss rates on both sides of the jump
(cool vs. hot) differ by
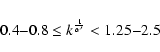 |
(14) |
i.e.,  either decreases in parallel with
either decreases in parallel with  /
/
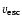 or increases marginally.
or increases marginally.
Before discussing the implications of these
findings, let us come back to the investigations by Benaglia et al. (2007) who
recently reported evidence of the possible presence of a local maximum in
the wind efficiency, 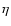 =
= 
 /(L/c), around 21 000 K, which
would be at least in qualitative agreement with theoretical
predictions. In Fig. 14, we compare the wind-efficiencies as
derived for our combined sample (from H
/(L/c), around 21 000 K, which
would be at least in qualitative agreement with theoretical
predictions. In Fig. 14, we compare the wind-efficiencies as
derived for our combined sample (from H ) to corresponding data from their
radio measurements (filled dots). The dashed line in the figure displays the
theoretical predictions, which, again, are based on the models by
Vink et al. (2000).
) to corresponding data from their
radio measurements (filled dots). The dashed line in the figure displays the
theoretical predictions, which, again, are based on the models by
Vink et al. (2000).
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7919f14.ps}\end{figure}](/articles/aa/full/2008/06/aa7919-07/Timg162.gif) |
Figure 14:
Wind-efficiency, 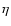 ,
as a function of ,
as a function of
 , for our combined
sample (symbols as in Fig. 12) and objects as analysed by
Benaglia et al. 2007 (filled dots, mass-loss rates from radio excess). Eight
objects in common have been discarded from the latter sample.
Overplotted (dashed) are their theoretical predictions, based on the models
by Vink et al. (2000). , for our combined
sample (symbols as in Fig. 12) and objects as analysed by
Benaglia et al. 2007 (filled dots, mass-loss rates from radio excess). Eight
objects in common have been discarded from the latter sample.
Overplotted (dashed) are their theoretical predictions, based on the models
by Vink et al. (2000). |
| Open with DEXTER |
There are eight stars in common with our sample for which we display the H results only, not to artificially increase the statistics. At least for
five of those, all of spectral type B0 to B2, a direct comparison of the H
results only, not to artificially increase the statistics. At least for
five of those, all of spectral type B0 to B2, a direct comparison of the H and radio results is possible, since same values of
and radio results is possible, since same values of
 ,
, 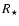 and
and  have been used to derive the corresponding wind efficiencies. In all but one
of these stars
have been used to derive the corresponding wind efficiencies. In all but one
of these stars![[*]](/icons/foot_motif.gif) , radio and optical mass-loss rates agree within
0.2 dex, which is comparable to the typical uncertainty of the optical data.
Translated to potential wind-clumping, this would mean that the outer and
inner wind-regions were affected by similar clumping
factors, in analogy to the findings for thin O-star winds
(Puls et al. 2006). From Fig. 14 now, several issues are apparent:
, radio and optical mass-loss rates agree within
0.2 dex, which is comparable to the typical uncertainty of the optical data.
Translated to potential wind-clumping, this would mean that the outer and
inner wind-regions were affected by similar clumping
factors, in analogy to the findings for thin O-star winds
(Puls et al. 2006). From Fig. 14 now, several issues are apparent:
- As for the wind-momenta and mass-loss rates, also the wind-efficiencies of
OB-supergiants do not behave as predicted, at least globally.
![[*]](/icons/foot_motif.gif) Instead, they follow a different trend (for
Instead, they follow a different trend (for
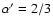 ,
one expects
,
one expects
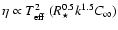 ,
i.e., a parabola with spectral type dependent offset), where, as we
have already seen, the offset at the cool side of the jump is much lower
than in the simulations by Vink et al. Actually, this is true for almost
the complete B-SGs domain (between 27 and 10 kK).
,
i.e., a parabola with spectral type dependent offset), where, as we
have already seen, the offset at the cool side of the jump is much lower
than in the simulations by Vink et al. Actually, this is true for almost
the complete B-SGs domain (between 27 and 10 kK).
- Similar as in the observed wind-momentum luminosity diagram
(Fig. 11, right panel), some of the O-supergiants do follow the
predictions, while others show wind-efficiencies which are larger by up to a
factor of two. Note that this result is supported by both H
 and radio diagnostics. If this discrepancy were interpreted in terms of
small-scale clumping, we would have to conclude that the winds of these
objects are moderately clumped, even at large distances from the stellar
surface.
and radio diagnostics. If this discrepancy were interpreted in terms of
small-scale clumping, we would have to conclude that the winds of these
objects are moderately clumped, even at large distances from the stellar
surface.
- Within the transition zone,
a large scatter towards higher values of
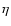 is observed, which, if not
due to systematic errors in the adopted parameters,
indeed might indicate the presence of a local maximum, thus supporting the
findings of Benaglia et al. (2007). From a careful investigation of the
distribution of stellar radii, terminal velocities and mass-loss rates, we
believe that this local bump does not seem to be
strongly biased by such uncertainties, but is instead due to a real increase
in
is observed, which, if not
due to systematic errors in the adopted parameters,
indeed might indicate the presence of a local maximum, thus supporting the
findings of Benaglia et al. (2007). From a careful investigation of the
distribution of stellar radii, terminal velocities and mass-loss rates, we
believe that this local bump does not seem to be
strongly biased by such uncertainties, but is instead due to a real increase
in  .
.
Regarding a comparison with theoretical models, the major conclusion to be
drawn from the previous section is as follows.
In addition to the well-known factor of two discrepancies for dense O-SG winds, the
most notable disagreement (discarding local effects within the transition
zone for the moment) is found in the low
 /low L B-SG domain, confirming
the analysis by Crowther et al. (2006). The predictions by Vink et al. clearly
require the decrease in
/low L B-SG domain, confirming
the analysis by Crowther et al. (2006). The predictions by Vink et al. clearly
require the decrease in  to be overcompensated by an increase in
to be overcompensated by an increase in
 throughout the complete mid/late B-star regime, whereas our analysis
has shown that this is not the case. At best,
throughout the complete mid/late B-star regime, whereas our analysis
has shown that this is not the case. At best,  increases by the same
amount as
increases by the same
amount as  decreases, though a reduction of
decreases, though a reduction of  seems to be more
likely, accounting for the fact that the upper limit in Eq. (14)
is a rather conservative estimate.
seems to be more
likely, accounting for the fact that the upper limit in Eq. (14)
is a rather conservative estimate.
Since the calculation of absolute mass-loss rates and wind-momenta is a
difficult task and depends on a number of uncertainties (see below), let us
firstly consider the possibility that at least the predictions regarding the
relative change in  (from hot to cool objects) are correct, and
that clumping affects this prediction only marginally.
(from hot to cool objects) are correct, and
that clumping affects this prediction only marginally.
In this case, the most simple explanation for the detected discrepancy is
that cooler objects are less clumped than hotter ones. Since Vink et al.
predict an increase in  of a factor of five, this would imply
that the clumping factors for hotter objects are
larger by factors of 4 (most optimistic case) to 156 (worst case) compared
to those of cooler ones
of a factor of five, this would imply
that the clumping factors for hotter objects are
larger by factors of 4 (most optimistic case) to 156 (worst case) compared
to those of cooler ones![[*]](/icons/foot_motif.gif) . Given our present knowledge (see
Fullerton et al. 2006; Puls et al. 2006, and references therein), this is not
impossible, but raises the question about the physical origin of such a
difference.
This hypothesis would also imply that all B-SG mass-loss rates are
overpredicted, though to a lesser extent for cooler subtypes.
. Given our present knowledge (see
Fullerton et al. 2006; Puls et al. 2006, and references therein), this is not
impossible, but raises the question about the physical origin of such a
difference.
This hypothesis would also imply that all B-SG mass-loss rates are
overpredicted, though to a lesser extent for cooler subtypes.
In the alternative, and maybe more reasonable scenario that the clumping
properties of OBA supergiants were not too different, we would have to
conclude that at least the low temperature predictions suffer from unknown
defects.
Note, however, that a potential ``failure'' of these predictions
does not invalidate the radiation driven wind theory itself. The actual
mass-loss rates depend on the effective number of driving lines, and, at
least in principle, this number should decrease towards lower
 ,
due to an increasing mismatch between the position of these lines and the
flux maximum (e.g., Puls et al. 2000). In Vink's models, it increases
instead because Fe III has many more lines than Fe IV, and because
these lines are distributed over a significant spectral range.
The absolute number of these lines and their strengths, however, depend on
details of the available data (not forgeting the elemental abundances,
Krticka & Kubat 2007), a consistent description of the
ionisation/excitation equilibrium and also on other, complicating effects
(e.g., the diffuse radiation field diminishing the line acceleration in the
lower wind, Owocki & Puls 1999, and the potential influence of microturbulence,
Lucy 2007), which makes quantitative predictions fairly
ambiguous. Moreover, if the winds were clumped, this would influence
the hydrodynamical simulations, due to a modified ionisation structure.
,
due to an increasing mismatch between the position of these lines and the
flux maximum (e.g., Puls et al. 2000). In Vink's models, it increases
instead because Fe III has many more lines than Fe IV, and because
these lines are distributed over a significant spectral range.
The absolute number of these lines and their strengths, however, depend on
details of the available data (not forgeting the elemental abundances,
Krticka & Kubat 2007), a consistent description of the
ionisation/excitation equilibrium and also on other, complicating effects
(e.g., the diffuse radiation field diminishing the line acceleration in the
lower wind, Owocki & Puls 1999, and the potential influence of microturbulence,
Lucy 2007), which makes quantitative predictions fairly
ambiguous. Moreover, if the winds were clumped, this would influence
the hydrodynamical simulations, due to a modified ionisation structure.
That there is an effect which is most probably related to the
principal bistability mechanism (Pauldrach & Puls 1990) remains undisputed, and is
evident from the more or less sudden decrease in  /
/
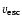 . Additionally,
there is a large probability that at least inside the transition zone a
``local'' increase of (
. Additionally,
there is a large probability that at least inside the transition zone a
``local'' increase of (
 ) is present, which would partly support
the arguments by Vink et al., though not on a global scale. Furthermore, the
scatter of Q' (and wind-momentum rate) turned out to be much larger
in the transition region than somewhere else. This might be explained by the
fact that hydrogen begins to recombine in the wind just in this region,
whereas the degree of recombination depends on a multitude of parameters,
thus leading to the observed variety of mass-loss rates and terminal
velocities. Finally, note that at least the observed hypergiant
seems to be consistent with the bistability scenario, which, after all, has
been originally ``invented'' for these kind of objects.
) is present, which would partly support
the arguments by Vink et al., though not on a global scale. Furthermore, the
scatter of Q' (and wind-momentum rate) turned out to be much larger
in the transition region than somewhere else. This might be explained by the
fact that hydrogen begins to recombine in the wind just in this region,
whereas the degree of recombination depends on a multitude of parameters,
thus leading to the observed variety of mass-loss rates and terminal
velocities. Finally, note that at least the observed hypergiant
seems to be consistent with the bistability scenario, which, after all, has
been originally ``invented'' for these kind of objects.
7 Summary and future work
In this study, we have presented a detailed investigation of the optical
spectra of a small sample of Galactic B supergiants, from B0 to B9. Stellar
and wind parameters have been obtained by employing the NLTE, unified model
atmosphere code FASTWIND (Puls et al. 2005), assuming unclumped winds.
The major findings of our analysis can be summarised as follows.
- 1.
- We confirm recent results (Ryans et al. 2002; Simon-Diaz & Herrero 2007; Dufton et al. 2006) of the
presence of a (symmetric) line-broadening mechanism in addition to stellar
rotation, denoted as ``macro-turbulence''. The derived values of
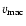 are
highly supersonic, decreasing from
are
highly supersonic, decreasing from 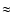 60 km s
60 km s at B0 to
at B0 to
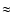 30 km s-1 at B9.
30 km s-1 at B9.
- 2.
- We determined the Si abundances of our sample stars
in parallel with their corresponding micro-turbulent velocities.
- (i)
- For all but one star, the estimated Si abundances were
consistent with the corresponding solar
value (within
 0.1 dex), in agreement with similar
studies (Gies & Lambert 1992; Przybilla et al. 2006; Rolleston et al. 2000; Urbaneja 2004). For HD 202850, on the other hand, an
overabundance of about 0.4 dex has been derived, suggesting that this late-B
supergiant might be a silicon star.
0.1 dex), in agreement with similar
studies (Gies & Lambert 1992; Przybilla et al. 2006; Rolleston et al. 2000; Urbaneja 2004). For HD 202850, on the other hand, an
overabundance of about 0.4 dex has been derived, suggesting that this late-B
supergiant might be a silicon star.
- (ii)
- The micro-turbulent velocities tend to decrease towards later B
subtypes, from 15 to 20 km s
 at B0 (similar to the situation in
O-supergiants) to 7 km s
at B0 (similar to the situation in
O-supergiants) to 7 km s at B9, which is also a typical value for
A-SGs.
at B9, which is also a typical value for
A-SGs.
- (iii)
- The effect of micro-turbulence on the derived
effective temperature was negligible as long as Si lines from
the two major ions are used to determine it.
- 3.
- Based on our
 estimates and incorporating data from similar
investigations (Lefever et al. 2007; Przybilla et al. 2006; Crowther et al. 2006; Urbaneja 2004), we confirm
previous results (e.g., Crowther et al. 2006)
on a 10% downwards revision of the effective temperature scale of
early B-SGs, required after incorporating the
effects of line blocking/blanketing. Furthermore, we suggest a similar
correction for mid and late subtypes. When strong
winds are present, this reduction can become a factor of two larger,
similar to the situation encountered in O-SGs (Crowther et al. 2002).
estimates and incorporating data from similar
investigations (Lefever et al. 2007; Przybilla et al. 2006; Crowther et al. 2006; Urbaneja 2004), we confirm
previous results (e.g., Crowther et al. 2006)
on a 10% downwards revision of the effective temperature scale of
early B-SGs, required after incorporating the
effects of line blocking/blanketing. Furthermore, we suggest a similar
correction for mid and late subtypes. When strong
winds are present, this reduction can become a factor of two larger,
similar to the situation encountered in O-SGs (Crowther et al. 2002).
- 4.
- To our surprise, a comparison with data from similar SMC objects
(Trundle & Lennon 2005; Trundle et al. 2004) did not reveal any systematic difference
between the two temperature scales. This result is interpreted as an
indication that the re-classification scheme as developed by
Lennon (1997) to account for lower metal line strengths in SMC
B-SGs also removes the effects of different degrees of line
blanketing.
- 5.
- Investigating the wind properties of a statistically significant sample
of supergiants
with
 between 10 and 45 kK, we identified a number of discrepancies
between theoretical predictions (Vink et al. 2000) and observations.
In fair accordance with recent results (Crowther et al. 2006; Evans et al. 2004), our sample
indicates a gradual decrease in
between 10 and 45 kK, we identified a number of discrepancies
between theoretical predictions (Vink et al. 2000) and observations.
In fair accordance with recent results (Crowther et al. 2006; Evans et al. 2004), our sample
indicates a gradual decrease in  in the bi-stability
(``transition'') region, which is located at lower temperatures than
predicted: 18 to 23 kK (present study) against 22.5 to 27 kK.
in the bi-stability
(``transition'') region, which is located at lower temperatures than
predicted: 18 to 23 kK (present study) against 22.5 to 27 kK.
By means of a newly defined, distance independent quantity,
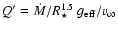 ,
we have investigated the behaviour of
,
we have investigated the behaviour of
 as a function of
as a function of
 . Whereas inside the transition zone a large
scatter is present (coupled with a potential local maximum in wind
efficiency around 21 kK), Q' remains a well defined function with low
scatter in the hot and cool temperature region outside the transition zone.
Combining the behaviour of Q' and the modified wind-momentum rate, the
change in
. Whereas inside the transition zone a large
scatter is present (coupled with a potential local maximum in wind
efficiency around 21 kK), Q' remains a well defined function with low
scatter in the hot and cool temperature region outside the transition zone.
Combining the behaviour of Q' and the modified wind-momentum rate, the
change in  over the bi-stability jump (from hot to cool) could be
constrained to lie within the factors 0.4 to 2.5, to be conservative. Thus,
over the bi-stability jump (from hot to cool) could be
constrained to lie within the factors 0.4 to 2.5, to be conservative. Thus,
 either decreases in parallel with
either decreases in parallel with  /
/
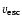 (more probable), or, at
most, the decrease in
(more probable), or, at
most, the decrease in  is just balanced by a corresponding increase in
is just balanced by a corresponding increase in
 (less probable). This finding contradicts the predictions by
Vink et al. (2000) that the decrease in
(less probable). This finding contradicts the predictions by
Vink et al. (2000) that the decrease in  should be over-compensated
by an increase in
should be over-compensated
by an increase in  , i.e., that the wind-momenta should increase over
the jump. Considering potential clumping effects, we have argued that
such effects will not change our basic result, unless hotter objects turn
out to be substantially more strongly clumped than cooler ones. In any case, at
least in the low temperature region present theoretical predictions for
, i.e., that the wind-momenta should increase over
the jump. Considering potential clumping effects, we have argued that
such effects will not change our basic result, unless hotter objects turn
out to be substantially more strongly clumped than cooler ones. In any case, at
least in the low temperature region present theoretical predictions for
 are too large!
are too large!
This finding is somewhat similar to the recent
``weak-wind problem'' for late O-dwarfs![[*]](/icons/foot_motif.gif) , though probably to a lesser extent.
Thus, it might be that our understanding of radiation driven winds is
not as complete as thought only a few years ago. Thus, it is of
extreme importance to continue the effort of constructing
sophisticated wind models, including the aforementioned effects
(wind-clumping, diffuse radiation field, micro-turbulence), both in terms of
stationary and time-dependent simulations. With respect to the objects of
the present study, a re-analysis of the ``peculiar'' mid-type B-supergiants
from the KPL99 sample is urgently required as well. Finally, let us (once
more) point to the unresolved problem of macro-turbulence, which implies the
presence of rather deep-seated, statistically distributed and highly
supersonic velocity fields. How can we explain such an effect within our
present-day atmospheric models of hot, massive stars?
, though probably to a lesser extent.
Thus, it might be that our understanding of radiation driven winds is
not as complete as thought only a few years ago. Thus, it is of
extreme importance to continue the effort of constructing
sophisticated wind models, including the aforementioned effects
(wind-clumping, diffuse radiation field, micro-turbulence), both in terms of
stationary and time-dependent simulations. With respect to the objects of
the present study, a re-analysis of the ``peculiar'' mid-type B-supergiants
from the KPL99 sample is urgently required as well. Finally, let us (once
more) point to the unresolved problem of macro-turbulence, which implies the
presence of rather deep-seated, statistically distributed and highly
supersonic velocity fields. How can we explain such an effect within our
present-day atmospheric models of hot, massive stars?
Acknowledgements
Many thanks to our anonymous referee for very
constructive suggestions on the original manuscript. We like to thank
Jorick Vink for providing us with his theoretical predictions for the
behaviour of wind-efficiency 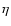 vs.
vs.
 . This investigation was
supported in part both by a NATO CLG No. PST/CLG 980007 and
by a Bulgarian NSF grand No. 1407/04. J.P. gratefully acknowledges
travel support by the Spanish MEC through project AYA2004-08271-CO2. The authors are gratful to the A&A editor in chief, Mr. Bertout, who made the publication of this article possible.
. This investigation was
supported in part both by a NATO CLG No. PST/CLG 980007 and
by a Bulgarian NSF grand No. 1407/04. J.P. gratefully acknowledges
travel support by the Spanish MEC through project AYA2004-08271-CO2. The authors are gratful to the A&A editor in chief, Mr. Bertout, who made the publication of this article possible.
- Abt, H. A., Levato,
H., & Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef]
(In the text)
- Asplund, M.,
Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances
as Records of Stellar Evolution and Nucleosynthesis, ed. T. G.
Barnes & F. N. Bash, ASP Conf. Ser., 336, 25
- Azzopardi, M., &
Vigneau, J. 1975, A&AS, 19, 271 [NASA ADS]
(In the text)
- Barbier-Brossat, & M.,
Figon, P. 2000, A&AS, 142, 217 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Barlow, M. J., &
Cohen, M. 1977, ApJ, 213, 737 [NASA ADS] [CrossRef]
(In the text)
- Becker, S. R., &
Butler, K. 1990, A&A, 235, 326 [NASA ADS]
- Benaglia, P.,
Vink, J. S., Marti, J., et al. 2007, A&A, 467,
1265 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bianchi, L., & Garcia,
M. 2002, ApJ, 581, 610 [NASA ADS] [CrossRef]
- Bianchi, L.,
& Efremova, B. V. 2006, AJ, 132, 378 [NASA ADS] [CrossRef]
- Bouret, J-C., Lanz,
T., & Hillier, D. J., et al. 2003, ApJ, 595,
1182 [NASA ADS] [CrossRef]
- Bouret, J-C., Lanz,
T., & Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences]
- Bresolin, F.,
Gieren, W., Kudritzki, R.-P., et al. 2002, ApJ, 567, 277 [NASA ADS] [CrossRef]
- Bychkov, V.D, Bychkova, &
L. V., Madej, L. 2003, A&A, 407, 631 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Conti, P. S., &
Ebets, D. 1977, ApJ, 213, 438 [NASA ADS] [CrossRef]
- Crowther, P.
2004, EAS 13, 1
(In the text)
- Crowther, P.,
Hillier, D. J., Evans, C. J., et al. 2002, ApJ, 579,
774 [NASA ADS] [CrossRef]
- Crowther,
P. A., Lennon, D. J., & Walborn, N. R. 2006,
A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences]
- de Koter, A.,
Heap, S. R., & Hubeny, I. 1998, ApJ, 509, 879 [NASA ADS] [CrossRef]
- Denizman, L., & Hack, M.
1988, A&AS, 75, 79 [NASA ADS]
(In the text)
- Dufton, P. L.,
Ryans, R. S. I., Simon-Diaz, S., et al. 2006,
A&A, 451, 603 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Eissner, W.,
Jones, M., & Nussbaumer, H. 1974, Comp. Phys. Comm., 8,
270 [NASA ADS] [CrossRef]
- Evans, C. J.,
Lennon, D. J., Trundle, C., et al. 2004, ApJ, 607,
451 [NASA ADS] [CrossRef]
(In the text)
- Fitzpatrick, E. L., &
Garmany, C. D. 1990, ApJ, 363, 119 [NASA ADS] [CrossRef]
(In the text)
- Fullerton, A., Massa,
D. L., & Prinja, R. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef]
- Garcia, M., & Bianchi,
L. 2004, ApJ, 606, 497 [NASA ADS] [CrossRef]
- Garmany, C. D., Stencel,
R. E. 1992, AAS, 94, 211 [NASA ADS]
(In the text)
- Gies, D. F., &
Lambert, D. L. 1992, ApJ, 387, 673 [NASA ADS] [CrossRef]
- Gray, D. F. 1973,
ApJ, 184, 461 [NASA ADS] [CrossRef]
- Gray, D. F. 1975,
ApJ, 202,148
- Grevesse, N., & Sauval,
A. J. 1998, SSRv, 85, 161 [NASA ADS] [CrossRef]
(In the text)
- Heap, S. R., Lanz,
T., & Hubeny, I. 2006, ApJ, 638, 409 [NASA ADS] [CrossRef]
- Herrero, A.,
Puls, J., & Najarro, F. 2002, A&A, 396, 946 [CrossRef]
- Hillier, D. J.,
& Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef]
(In the text)
- Hirschi, R., Meynet, G.,
& Maeder, A. 2005, A&A, 443, 581 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Howarth,
I. D., Siebert, K. W., Hussain, G. A. J.,
et al. 1997, MNRAS, 284, 265 [NASA ADS]
(In the text)
- Humphreys, R.
1978, ApJS, 38, 309 [NASA ADS] [CrossRef]
(In the text)
- Humphreys, R., & McElroy,
D. B. 1984, ApJ, 284, 565 [NASA ADS] [CrossRef]
(In the text)
- Hunter, I., Dufton, P.
L., Smartt, S. J., et al. 2007, A&A, 466, 277 [NASA ADS] [CrossRef] [EDP Sciences]
- Kilian, J.,
Becker, S. R., Gehren, T., Nissen, et al. 1991, A&A,
244, 419 [NASA ADS]
- Krticka, J., & Kubat,
J. 2004, A&A, 417, 1003 [NASA ADS] [CrossRef] [EDP Sciences]
- Krticka, J., & Kubat,
J. 2007, A&A, 464, L17 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kudritzki,
R.-P. 1980, A&A, 85, 174 [NASA ADS]
(In the text)
- Kudritzki, R.-P., &
Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] [CrossRef]
(In the text)
- Kudritzki, R.-P., Lennon,
D. J., & Puls, J. 1995, in Quantitative Spectroscopy of
Luminous Blue Stars in Distant Galaxies. ESO Astrophysics Symp.,
Science with the VLT, ed. J. R. Walsh & I. J.
Danziger (Heidelberg: Springer), 246
(In the text)
- Kudritzki, R.-P., Puls,
J., Lennon, D. J., et al. 1999, A&A, 350, 970 [NASA ADS]
(KPL99)
- Kurucz, R. L. 1992,
Rev. Mex. Astron. Astrof., 23, 45 [NASA ADS]
(In the text)
- Lamers,
H. J. G. M. L., Snow, T., & Lindholm,
D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef]
- Lefever, K., Puls,
J., & Aerts, C. 2007, A&A, 463, 1093 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Lennon, D. J.
1997, A&A, 317, 871 [NASA ADS]
(In the text)
- Lennon, D. J.,
Dufton, P.L, & Fitzsimmons, A. 1992, A&AS, 94, 569 [NASA ADS]
(In the text)
- Lennon, D. J.,
Dufton, P.L, & Fitzsimmons, A. 1993, A&AS, 97, 559 [NASA ADS]
- Lucy, L. B. 2007,
A&A, 468, 649 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Markova, N.,
Puls, J., Repolust,T., et al. 2003, A&A, 413, 693 [NASA ADS] [CrossRef]
- Markova, N., Prinja, R.,
Morrison, N., et al. 2007, in preparation
- Martins, F.,
Schaerer, D., Hillier, D. J., et al. 2004, A&A, 420,
1087 [NASA ADS] [CrossRef] [EDP Sciences]
- Martins, F.,
Schaerer, D., Hillier, D. J., et al. 2005, A&A, 441,
735 [NASA ADS] [CrossRef] [EDP Sciences]
- Massey, P.,
Bresolin, F., Kudritzki, R.-P., et al. 2004, ApJ, 608,
1001 [NASA ADS] [CrossRef]
- Massey, P., Puls,
P., Pauldrach, A. W. A., et al. 2005, ApJ, 627,
477 [NASA ADS] [CrossRef]
- McErlean, N. D.,
Lennon, D. J., & Dufton, P. L. 1998, A&A, 329,
613 [NASA ADS]
- McErlean, N. D.,
Lennon, D. J., & Dufton, P. L. 1999, A&A, 349,
553 [NASA ADS]
(In the text)
- Meynet, G., & Maeder,
A. 2000, A&A, 361,101
(In the text)
- Mokiem, M. R.,
de Koter, A., Evans, C. J., et al. 2006, A&A, 456,
1131 [NASA ADS] [CrossRef] [EDP Sciences]
- Najarro, F.,
Hillier, D. J., Puls, J., et al. 2006, A&A, 456,
659 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Nussbaumer,
H., & Storey, P. J. 1978, A&A, 64, 139 [NASA ADS]
- Owocki, S. P. 1994, in
Proc. of Isle-aux-Coudre Workshop Instability and Variability of
Hot-Star Winds, Astrophys. Space Sci., 221, 3
(In the text)
- Owocki, S. P., &
Puls, J. 1996, ApJ, 462, 894 [NASA ADS] [CrossRef]
- Owocki, S., & Puls, J.
1999, ApJ, 510, 355 [NASA ADS] [CrossRef]
- Pauldrach,
A. W. A., & Puls, J. 1990, A&A, 237, 409 [NASA ADS]
(In the text)
- Pauldrach,
A. W. A., Hoffmann, T. L., & Lennon, M. 2001,
A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Prinja, R. K., Barlow,
M. J., & Howarth, I. D. 1990, ApJ, 361, 607 [NASA ADS] [CrossRef]
- Przybilla, N., Butler,
K , Becker, S. R., et al. 2006, A&A, 445, 1099 [NASA ADS] [CrossRef] [EDP Sciences]
- Puls, J., Kudritzki,
R.-P., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS]
(In the text)
- Puls, J., Springmann,
U., & Lennon, M. 2000, A&AS, 141, 23 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Puls, J., Repolust, T.,
Hofmann, T., et al. 2003, IAUS, 212, 61 [NASA ADS]
- Puls, J., Urbaneja,
M. A., Venero, R. et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Puls, J., Markova, N,,
Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences]
- Repolust, T., Puls, J.,
& Herrero, A. 2004, A&A, 415, 349 [NASA ADS] [CrossRef] [EDP Sciences]
- Rivinius, T., Stahl, O.,
Wolf, B., et al. 1997, A&A, 318, 819 [NASA ADS]
- Rolleston,
W. R. J., Smartt, S. J., Dufton, P. L.,
et al. 2000, A&A, 363, 537 [NASA ADS]
- Rosenhald, J. D.
1970, ApJ, 159, 107 [NASA ADS] [CrossRef]
- Runacres, M. C., &
Owocki, S. P. 2002, A&A 381, 1015
- Runacres, M. C., &
Owocki, S. P. 2005, A&A, 429, 323 [NASA ADS] [CrossRef] [EDP Sciences]
- Ryans,
R. S. I., Dufton, P. L., Rolleston,
W. R. J., et al. 2002, MNRAS, 336, 577 [NASA ADS] [CrossRef]
(In the text)
- Santolaya-Rey,
A. E., Puls, J., & Herrero, A. 1997, A&A, 323,
488 [NASA ADS]
-
Schröder, S. E., Kaper, L., Lamers,
H. J. G. L. M., et al. 2004, A&A, 428,
149 [NASA ADS] [CrossRef] [EDP Sciences]
- Simon-Diaz, S., &
Herrero, A. 2007, A&A, 468, 1063 [NASA ADS] [CrossRef] [EDP Sciences]
- Simon-Diaz, S.,
Herrero, A., Esteban, C., et al. 2006, A&A, 448, 351 [NASA ADS] [CrossRef] [EDP Sciences]
- Smith, K. C., &
Howarth, I. D. 1998, MNRAS, 299, 1146 [NASA ADS] [CrossRef]
- Trundle, C.,
Dufton, P. L., Lennon, D. J., et al. 2002, A&A,
395, 519 [NASA ADS] [CrossRef] [EDP Sciences]
- Trundle, C.,
Lennon, D. J., Puls, J., et al. 2004, A&A, 417,
217 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Trundle, C.,
& Lennon, D. J. 2005, A&A, 434, 677 [NASA ADS] [CrossRef] [EDP Sciences]
- Venn K. A. 1995, ApJS,
99, 659 [NASA ADS] [CrossRef]
(In the text)
- Villamariz,
M. R., & Herrero, A. 2000, A&A, 357, 597 [NASA ADS]
- Vink, J. S., de
Koter, A., & Lamers, H. J. G. L. M. 2000,
A&A, 362, 295 [NASA ADS]
(In the text)
- Vrancken, M.,
Lennon, D. J., Dufton, et al. 2000, A&A, 358,
639 [NASA ADS]
(In the text)
- Urbaneja, M. A. 2004,
Ph.D. Thesis, University of La Laguna, Spain
- Urbaneja, M. A.,
Herrero, A., Bresolin, F., et al. 2003, ApJ, 584, L73 [NASA ADS] [CrossRef]
- de Zeeuw, P. T.,
Hoogerwerf, R., de Bruijne, J. H. J., et al. 1999,
AJ, 117, 354 [NASA ADS] [CrossRef]
Copyright ESO 2008










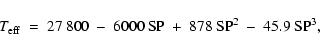

![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7919f12.ps}\end{figure}](/articles/aa/full/2008/06/aa7919-07/Timg115.gif)
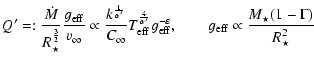
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7919f13.ps}\end{figure}](/articles/aa/full/2008/06/aa7919-07/Timg146.gif)
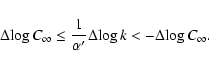
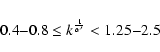
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7919f14.ps}\end{figure}](/articles/aa/full/2008/06/aa7919-07/Timg162.gif)