A&A 478, 443-452 (2008)
DOI: 10.1051/0004-6361:20078339
VLA and Effelsberg observations of the interstellar medium around the runaway star WR 124
S. Cichowolski1,2 - S. Pineault2 -
E. M. Arnal3,4 - C. E. Cappa3,4
1 - Instituto de Astronomía y Física del Espacio
(IAFE), CC67, Suc.28, 1428 Buenos Aires, Argentina
2 -
Département de Physique and Observatoire du Mont Mégantic, Université Laval,
Ste-Foy, Québec, G1K 7P4, Canada
3 -
Instituto Argentino de
Radioastronomía, C.C.5, 1894 Villa Elisa, Argentina
4 -
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de
La Plata, 1900 La Plata, Argentina
Received 23 July 2007 / Accepted 22 October 2007
Abstract
Aims. We present very large array (VLA) and Effelsberg radio continuum and 21 cm H I line observations of the interstellar medium (ISM) surrounding the runaway star WR 124 and the nebula M 1-67. The H I data have been used to investigate the effects that a star with a strong stellar wind and a high peculiar velocity has on the ISM.
Methods. The VLA 21 cm H I observations were combined with single-dish Effelsberg observations to produce a series of H I images sensitive to all angular scales from the VLA resolution limit (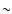
 )
up to the primary field of individual VLA antennae (FWHM = 36
)
up to the primary field of individual VLA antennae (FWHM = 36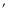 ). MSX and IRIS images were used to analyze the infrared emission around the star. Because the star is highly supersonic with respect to its local ISM, the observed H I distribution around the star is interpreted in terms of a simple bow shock model.
). MSX and IRIS images were used to analyze the infrared emission around the star. Because the star is highly supersonic with respect to its local ISM, the observed H I distribution around the star is interpreted in terms of a simple bow shock model.
Results. The analysis of the H I data reveals the presence of a cavity centered on the star at an LSR velocity of 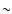 60
60
 ,
consistent with a distance estimate of 5 kpc for WR 124. A second H I cavity is observed located 10
,
consistent with a distance estimate of 5 kpc for WR 124. A second H I cavity is observed located 10 to the north of the stellar position, consistent with the direction of motion of WR 124. The VLA continuum image at 8.5 GHz shows a remarkable resemblance to the optical images. All available radio continuum data suggest a purely thermal spectrum for the nebula. The MSX and IRIS infrared data show a changing morphology with wavelength. The dust temperature deduced from the infrared luminosities is in agreement with previous observations of bow shocks.
to the north of the stellar position, consistent with the direction of motion of WR 124. The VLA continuum image at 8.5 GHz shows a remarkable resemblance to the optical images. All available radio continuum data suggest a purely thermal spectrum for the nebula. The MSX and IRIS infrared data show a changing morphology with wavelength. The dust temperature deduced from the infrared luminosities is in agreement with previous observations of bow shocks.
Key words: ISM: bubbles - ISM: individual objects: WR 124 - stars: Wolf-Rayet - ISM: H II regions
Massive stars have a prominent impact on their surrounding
interstellar medium (ISM), as testified by observations of H II regions, stellar wind bubbles, and supernova remnants. Analyzing and
modeling the interaction of massive stars with the ambient gas
provides a wealth of information on aspects such as the physical
processes at work in the interstellar gas and dust, the energetic
output of massive stars in the form of ionizing radiation and stellar
winds, and the large-scale dynamics of the ISM.
In this paper we analyze the ISM around the runaway star WR 124
( 209 BAC), classified as a Population I WN 8 star (van der Hucht 2001).
The nebula M 1-67 was discovered around the star by
Minkowski (1946) during an H
209 BAC), classified as a Population I WN 8 star (van der Hucht 2001).
The nebula M 1-67 was discovered around the star by
Minkowski (1946) during an H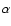 objective prism survey. He
suggested that M 1-67 might be a planetary nebula since the H
objective prism survey. He
suggested that M 1-67 might be a planetary nebula since the H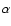 velocity is comparable to that of WR 124. The nebula was
later classified
as an H II region by Sharpless (Sh2-80, Sharpless 1959).
However, the presence of a WR star and the observed N-enhancement and
O-deficiency (Esteban et al. 1991) are typical of material ejected in
a previous evolutionary phase. These findings point to a progenitor
more massive than those usually associated with central stars of
planetary nebula. Consequently M 1-67 was then classified as a WR
ring nebula by these authors.
velocity is comparable to that of WR 124. The nebula was
later classified
as an H II region by Sharpless (Sh2-80, Sharpless 1959).
However, the presence of a WR star and the observed N-enhancement and
O-deficiency (Esteban et al. 1991) are typical of material ejected in
a previous evolutionary phase. These findings point to a progenitor
more massive than those usually associated with central stars of
planetary nebula. Consequently M 1-67 was then classified as a WR
ring nebula by these authors.
Crawford & Barlow (1991) also argued against a planetary nebula
interpretation. If M 1-67 were a planetary nebula, the distance
should be in the range 0.5 to 1.0 kpc (van der Hucht et al. 1985;
Bertola 1964). However, Crawford & Barlow (1991) showed that the
distance of M 1-67 must lie in the range 4-5 kpc. Thus M 1-67 is
likely a WR ring nebula.
Grosdidier et al. (1998) obtained an HST WFPC2 deep H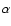 image of
M1-67 and noted that the nebulosity was very clumpy and did not show
an overall global shell structure. The velocity structure of the
nebula was investigated in complementary Fabry-Perot H
image of
M1-67 and noted that the nebulosity was very clumpy and did not show
an overall global shell structure. The velocity structure of the
nebula was investigated in complementary Fabry-Perot H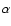 observations (Grosdidier et al. 2001) obtained at the
Canada-France-Hawaii Telescope. These authors concluded that a simple
thick shell by itself could not explain the observed multiple radial
velocities along the line of sight (LOS). Van der Sluys & Lamers (2003)
carried out various numerical simulations and showed that the
observational data of Grosdidier et al. (1998, 2001) were better
interpreted in terms of a bow shock model. Using a fully analytic
model describing the wind bow shock developed by Wilkin (1996), Van
der Sluys & Lamers (2003) concluded that the direction of motion of
the star with respect to its local ISM was within roughly
observations (Grosdidier et al. 2001) obtained at the
Canada-France-Hawaii Telescope. These authors concluded that a simple
thick shell by itself could not explain the observed multiple radial
velocities along the line of sight (LOS). Van der Sluys & Lamers (2003)
carried out various numerical simulations and showed that the
observational data of Grosdidier et al. (1998, 2001) were better
interpreted in terms of a bow shock model. Using a fully analytic
model describing the wind bow shock developed by Wilkin (1996), Van
der Sluys & Lamers (2003) concluded that the direction of motion of
the star with respect to its local ISM was within roughly
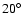 from the LOS to the star.
from the LOS to the star.
Distance estimates for WR 124 vary from 4.5 kpc (Pismis &
Recillas-Cruz 1979) to 6.5 kpc (Nugis & Lamers 2000). The star has a
terminal wind velocity of 710
 (van der Hucht 2001) and an upper
limit for the mass loss rate of
(van der Hucht 2001) and an upper
limit for the mass loss rate of
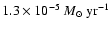 (Cappa et al. 2004). The stellar proper
motion is
(Cappa et al. 2004). The stellar proper
motion is
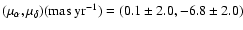 based on the Tycho-2 Catalogue (Hog et al. 2000)
and the catalogued heliocentric radial velocity is 194
based on the Tycho-2 Catalogue (Hog et al. 2000)
and the catalogued heliocentric radial velocity is 194 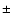 20
20
 (Wilson 1953).
(Wilson 1953).
In order to locate signs of the interaction between the stellar wind
and the ISM, we observed the radio continuum and the H I distribution around the star. We also made use of available infrared
data.
In particular the H I data are crucial in establishing
the large-scale (in arc-minutes) geometry around the star.
In order to image H I structures at all spatial frequencies,
the region near WR 124 was observed with both the VLA and the
Effelsberg radiotelescopes.
The Effelsberg data were obtained in August 1991. A 2
 region centered at the stellar position was
observed. Within this region, the observed points were sampled at
different spacings. The inner region, 1
region centered at the stellar position was
observed. Within this region, the observed points were sampled at
different spacings. The inner region, 1
 in
size, has a grid spacing of 5
in
size, has a grid spacing of 5 and is fully sampled, while outside
this region the spacing is 10
and is fully sampled, while outside
this region the spacing is 10 .
The HPBW and main-beam efficiency at
.
The HPBW and main-beam efficiency at
 21 cm are 9
21 cm are 9 and 0.72, respectively. The velocity
coverage is
and 0.72, respectively. The velocity
coverage is 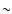 330
330
 and the velocity resolution 0.77
and the velocity resolution 0.77
 .
The rms noise level varies between 0.25 and 0.35 K in main-beam
brightness temperature units. This scale was derived from observations
of the IAU standard region S7 [(l, b) = (132
.
The rms noise level varies between 0.25 and 0.35 K in main-beam
brightness temperature units. This scale was derived from observations
of the IAU standard region S7 [(l, b) = (132
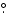 0, -1
0, -1
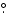 0)]
(Williams 1973). All profiles were corrected for stray radiation by
applying the procedure outlined by Kalberla et al.
(1980). The overall brightness temperature scale is accurate to
2%-3%.
0)]
(Williams 1973). All profiles were corrected for stray radiation by
applying the procedure outlined by Kalberla et al.
(1980). The overall brightness temperature scale is accurate to
2%-3%.
The central region was also observed with the VLA in the D-array on 25
May 1999. The instrumental parameters are summarized in Table
1. Using DRAO application software, the single dish and the
VLA data were then transformed to the u-v plane, filtered in a
complementary manner, and merged to provide an H I cube
containing 127 images. The final angular and velocity resolutions are
46
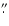 5
5  45
45
 5 at PA 16
5 at PA 16
 6 and 2.6
6 and 2.6
 ,
respectively.
,
respectively.
Radio continuum observations of M 1-67 at 8.5 GHz (3.6 cm) using the
VLA in its D-array configuration were carried out on 12 November
2001. The field of view is 5
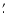 3 and the bandwidth is 50 MHz.
The on-source observing time was about 25 minutes to achieve a rms
noise of
3 and the bandwidth is 50 MHz.
The on-source observing time was about 25 minutes to achieve a rms
noise of  0.08 mJy beam-1. The observational parameters are
summarized in Table 1. The data were edited, calibrated in
both amplitude and phase and imaged following a standard procedure
using AIPS tasks. No short spacing information was added to the
interferometric image of M1-67 at 8.5 GHz.
0.08 mJy beam-1. The observational parameters are
summarized in Table 1. The data were edited, calibrated in
both amplitude and phase and imaged following a standard procedure
using AIPS tasks. No short spacing information was added to the
interferometric image of M1-67 at 8.5 GHz.
Table 1:
Observational parameters for VLA Data
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{8339fig1.eps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg33.gif) |
Figure 1:
Grey-scale images showing the H I gas distribution in
the velocity range 64.4 to 43.8
 observed with the VLA and the
100 m Effelsberg telescope. The position of WR 124 is indicated by a
star symbol. Velocity resolution is 2.6 observed with the VLA and the
100 m Effelsberg telescope. The position of WR 124 is indicated by a
star symbol. Velocity resolution is 2.6
 and the spatial
resolution is 46 and the spatial
resolution is 46
 5 5  45
45
 5 with a PA of
16 5 with a PA of
16
 6. The LSR velocity of each image is indicated in the top
left corner. Letters A and B indicate the cavities described in the
text. Contour levels with respect to the average over each image are
- 13, -8, -3, 0 and 5 K. Noise is 0.3 K or 1.05
mJy beam-1. 6. The LSR velocity of each image is indicated in the top
left corner. Letters A and B indicate the cavities described in the
text. Contour levels with respect to the average over each image are
- 13, -8, -3, 0 and 5 K. Noise is 0.3 K or 1.05
mJy beam-1. |
| Open with DEXTER |
Near and far infrared images of the WR 124 region were retrieved from
the Midcourse Space Experiment (MSX![[*]](/icons/foot_motif.gif) ) and IRIS
) and IRIS![[*]](/icons/foot_motif.gif) databases. MSX has carried out a
survey of the entire Galactic plane within the range
databases. MSX has carried out a
survey of the entire Galactic plane within the range 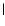 b
b 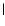
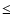 5
5 at six wavelengths from 4.2 to 21.3
at six wavelengths from 4.2 to 21.3
 m. For most of the Galactic plane work, four of these bands,
namely bands A (8.28
m. For most of the Galactic plane work, four of these bands,
namely bands A (8.28  m), C (12.1
m), C (12.1  m), D
(14.65
m), D
(14.65  m) and E (21.34
m) and E (21.34  m), are relevant. MSX
produced images with an angular resolution of 19
m), are relevant. MSX
produced images with an angular resolution of 19
 and an absolute
astrometric accuracy of 1
and an absolute
astrometric accuracy of 1
 9 (Egan et al. 1999; Price et al. 2001). The four MSX bandpasses are sensitive to different
emission processes. Bands A and C (as well as the
IRIS 12
9 (Egan et al. 1999; Price et al. 2001). The four MSX bandpasses are sensitive to different
emission processes. Bands A and C (as well as the
IRIS 12  m band) may contain contributions arising from both
fine-structure line emission and discrete PAH emission bands as
well as continuum emission from dust at
m band) may contain contributions arising from both
fine-structure line emission and discrete PAH emission bands as
well as continuum emission from dust at  400 K. The emission in
Bands C and E mainly arises from warm dust at
400 K. The emission in
Bands C and E mainly arises from warm dust at 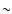 100 K, it may also be contaminated by a [S III] fine-structure line
emission at 18.71
100 K, it may also be contaminated by a [S III] fine-structure line
emission at 18.71  m (arising from H II regions of
intermediate excitation) and by a broad 22
m (arising from H II regions of
intermediate excitation) and by a broad 22  m emission feature
(Chan & Onaka 2000) (arising from dust in supernova remnants).
IRIS images (Miville-Deschênes & Lagache 2005) are a new
generation of IRAS images that benefit from a better zodiacal
light subtraction, calibration, zero levels compatible with
DIRBE and a better destriping. IRIS images have a lower angular
resolution, typically around 4
m emission feature
(Chan & Onaka 2000) (arising from dust in supernova remnants).
IRIS images (Miville-Deschênes & Lagache 2005) are a new
generation of IRAS images that benefit from a better zodiacal
light subtraction, calibration, zero levels compatible with
DIRBE and a better destriping. IRIS images have a lower angular
resolution, typically around 4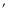 ,
than the IRAS ones.
,
than the IRAS ones.
To cover a large area towards WR 124, 1  1 deg2 MSX
and IRIS images centered at the optical position of WR 124
were downloaded from the archive node for scientific data sets from
NASA's infrared projects (IRSA1 site for short and the
IRIS web site2 ). The images were further processed using the
AIPS package. From an analysis of source-free regions located
close to WR 124, the noise level of the MSX A, C,
D and E bands were found to be 1.3, 19.2, 11.2 and 26.5
MJy sr-1, respectively.
1 deg2 MSX
and IRIS images centered at the optical position of WR 124
were downloaded from the archive node for scientific data sets from
NASA's infrared projects (IRSA1 site for short and the
IRIS web site2 ). The images were further processed using the
AIPS package. From an analysis of source-free regions located
close to WR 124, the noise level of the MSX A, C,
D and E bands were found to be 1.3, 19.2, 11.2 and 26.5
MJy sr-1, respectively.
3.1 H I distribution
The high-resolution fully sampled H I data cube provides a unique
opportunity to investigate the H I distribution around WR 124. We
inspected the entire H I cube, looking for signatures of the
interaction of the stellar wind with the ISM in a region close to the
stellar position. Since the work of van der Sluys & Lamers (2003)
suggests that the stellar motion with respect to its local ISM is
mostly along the LOS (receding), an H I deficiency
centered approximately at the position of the star is expected.
Indeed a structure possessing the characteristics expected for a star
with a strong wind (e.g., a relative minimum in the H I brightness
temperature distribution around the star surrounded by excess H I emission due to the swept-up gas) is observed in the velocity range
from about 54 to 64
 (LSR). The corresponding channel images are
shown in Fig. 1. In order to facilitate their display, the
images are shown with their mean level subtracted. At v =64.4
(LSR). The corresponding channel images are
shown in Fig. 1. In order to facilitate their display, the
images are shown with their mean level subtracted. At v =64.4
 the star is seen projected close to the center of a small H I depression (designated by the letter A) surrounded by weak H I emission. This minimum gets larger as we move towards lower
velocities, being better defined at 61.8
the star is seen projected close to the center of a small H I depression (designated by the letter A) surrounded by weak H I emission. This minimum gets larger as we move towards lower
velocities, being better defined at 61.8
 and barely visible at
54.1
and barely visible at
54.1
 .
.
In the velocity range from 56.7 to 51.5
 a strong and nearly
horizontal bar-like feature crosses the image near
a strong and nearly
horizontal bar-like feature crosses the image near
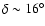 55
55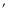 .
This structure probably distorts the northern part
of the H I depression. In Fig. 2 the distribution of the mean
brightness temperature averaged over the velocity range from 56.7 to
61.8
.
This structure probably distorts the northern part
of the H I depression. In Fig. 2 the distribution of the mean
brightness temperature averaged over the velocity range from 56.7 to
61.8
 is shown. A well-defined H I cavity near the
position of the star and the confusing presence of the bar-like
feature mentioned above are apparent.
is shown. A well-defined H I cavity near the
position of the star and the confusing presence of the bar-like
feature mentioned above are apparent.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{8339fig2.eps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg37.gif) |
Figure 2:
Average H I brightness temperature within the LSR
velocity interval 54.1 to 61.8
 .
Contour levels with respect to
the average over the image (28 K) are
-10, -6, -2, 0, 2 and 6 K. The cross indicates the position of WR 124. .
Contour levels with respect to
the average over the image (28 K) are
-10, -6, -2, 0, 2 and 6 K. The cross indicates the position of WR 124. |
| Open with DEXTER |
3.2 The ionized gas
Figure 3 shows the VLA radio continuum image at 3.6 cm and
the HST-WFPC2 H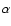 image of M 1-67 obtained by Grosdidier et al. (2001). The spatial extent of the emission at optical and radio
wavelengths is comparable. The radio image of M1-67 displays a clumpy
structure on a scale of a few arc seconds. No clear shell-like appearance
is obvious either in the optical or the radio image.
The flux density at 8.5 GHz is 205
image of M 1-67 obtained by Grosdidier et al. (2001). The spatial extent of the emission at optical and radio
wavelengths is comparable. The radio image of M1-67 displays a clumpy
structure on a scale of a few arc seconds. No clear shell-like appearance
is obvious either in the optical or the radio image.
The flux density at 8.5 GHz is 205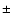 10 mJy.
10 mJy.
Previous radio images of M 1-67 include Westerbork observations by
Israel & Felli (1976) at 21 cm (HPBW  46
46
 )
and by Felli
& Perinotto (1979) at 6 cm (HPBW
)
and by Felli
& Perinotto (1979) at 6 cm (HPBW  11
11
 ). With the new high
sensitivity VLA image (Fig. 3a), the fainter outer regions
of M1-67 were detected, including the radio counterparts of the outer
areas observed in the optical range. Table 2 summarizes the
existing flux density determinations of M1-67. To derive the spectral
index we discarded flux density measurements with signal to noise
ratio lower than 3. A weighted least-square fit to the data yielded a
spectral index
). With the new high
sensitivity VLA image (Fig. 3a), the fainter outer regions
of M1-67 were detected, including the radio counterparts of the outer
areas observed in the optical range. Table 2 summarizes the
existing flux density determinations of M1-67. To derive the spectral
index we discarded flux density measurements with signal to noise
ratio lower than 3. A weighted least-square fit to the data yielded a
spectral index
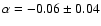 (
(
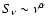 ). Within these errors, the radio flux densities are
consistent with a thermal spectrum. The large spread of values,
particularly around 5 GHz, may arise in : i) different
procedures used to remove the presence of background/foreground
emission, ii) observations with different sensitivity (those
with high rms noise will mask low level radio emission), and iii ) different absolute calibrations.
). Within these errors, the radio flux densities are
consistent with a thermal spectrum. The large spread of values,
particularly around 5 GHz, may arise in : i) different
procedures used to remove the presence of background/foreground
emission, ii) observations with different sensitivity (those
with high rms noise will mask low level radio emission), and iii ) different absolute calibrations.
In Fig. 4 the MSX emission in the range 8 to 21  m is shown. The infrared emission slightly departs from
circular symmetry in bands A and E, has an incomplete
shell morphology in band C, and is barely visible in band
D. The extent of the IR emission in band A is similar to the emission
observed in the H
m is shown. The infrared emission slightly departs from
circular symmetry in bands A and E, has an incomplete
shell morphology in band C, and is barely visible in band
D. The extent of the IR emission in band A is similar to the emission
observed in the H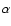 and 8.5 GHz radio continuum images. In all
bands WR 124 is slightly offset from the peak of emission. Based on
the measured flux densities quoted in Table 3 it is
clear that the grains responsible for the emission in the 60 and
100
and 8.5 GHz radio continuum images. In all
bands WR 124 is slightly offset from the peak of emission. Based on
the measured flux densities quoted in Table 3 it is
clear that the grains responsible for the emission in the 60 and
100  m IRIS images cannot be responsible for the emission
observed in the MSX bands. The lack of spatial correlation
between bands A and D may imply that the emission in band
A is dominated by fine-structure line emission and/or infrared
emission from PAH molecules. Detailed modeling beyond the scope of
this paper is needed to disentangle the main contributing agents.
m IRIS images cannot be responsible for the emission
observed in the MSX bands. The lack of spatial correlation
between bands A and D may imply that the emission in band
A is dominated by fine-structure line emission and/or infrared
emission from PAH molecules. Detailed modeling beyond the scope of
this paper is needed to disentangle the main contributing agents.
For a flat Galactic rotation model with
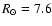 kpc
(Eisenhauer et al. 2005) and
kpc
(Eisenhauer et al. 2005) and
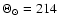
 (Kothes &
Dougherty 2007), the highest positive LSR radial velocity (i.e. the
velocity at the tangent point) permitted along the LOS (for
l = 50
(Kothes &
Dougherty 2007), the highest positive LSR radial velocity (i.e. the
velocity at the tangent point) permitted along the LOS (for
l = 50
 2) is about 50
2) is about 50
 .
The tangent point in this direction is
at a distance of about 5 kpc from the Sun. This means that strictly
speaking there should be no H I gas with velocities greater that 50
.
The tangent point in this direction is
at a distance of about 5 kpc from the Sun. This means that strictly
speaking there should be no H I gas with velocities greater that 50
 .
However, H I emission is observed up to 65
.
However, H I emission is observed up to 65
 .
Moreover, as
was described in Sect. 3.1, an H I cavity, named cavity
A, is observed near the stellar position in the LSR velocity range
from 64 to 54
.
Moreover, as
was described in Sect. 3.1, an H I cavity, named cavity
A, is observed near the stellar position in the LSR velocity range
from 64 to 54
 .
In order to reconcile the observed radial
velocity with the Galactic rotation model, we must allow the rotation
curve to have a small peculiar velocity in this direction. Assuming
for the tangent point a velocity of 65
.
In order to reconcile the observed radial
velocity with the Galactic rotation model, we must allow the rotation
curve to have a small peculiar velocity in this direction. Assuming
for the tangent point a velocity of 65
 ,
a kinematic distance of 5
kpc is inferred for cavity A. This H I distance is in good agreement
with previous distance determinations for the star (
,
a kinematic distance of 5
kpc is inferred for cavity A. This H I distance is in good agreement
with previous distance determinations for the star ( 5 kpc,
Pismis & Recillas-Cruz 1979; Nugis & Lamers 2000). Hereinafter a
distance of 5 kpc for both the star and the H I feature is adopted.
5 kpc,
Pismis & Recillas-Cruz 1979; Nugis & Lamers 2000). Hereinafter a
distance of 5 kpc for both the star and the H I feature is adopted.
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{8339fig3.ps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg42.gif) |
Figure 3:
a) Radio continuum image of M1-67 at 8.5 GHz with a
resolution of 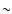 8 8
 .
The grey scale goes from 0 to 7 mJy beam-1
(dark grey). b) HST-WFPC2 H .
The grey scale goes from 0 to 7 mJy beam-1
(dark grey). b) HST-WFPC2 H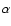 image of M 1-67 obtained
by Grosdidier et al. (2001). Resolution is
image of M 1-67 obtained
by Grosdidier et al. (2001). Resolution is 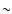 0 0
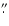 2. 2. |
| Open with DEXTER |
Given that WR 124 is seen projected on cavity A and both are likely
at the same distance from the Sun, we believe that cavity A is a
consequence of the stellar wind of WR 124. However, we can not
completely rule out the possibility that the spatial agreement between
cavity A and WR 124 arises from a chance coincidence. In order to
rule out a "by chance'' origin for cavity A, we have followed the
procedure described by Arnal (1992), who analyzed the H I distribution around several WR stars using Effelsberg data. Given the
difference between the Effelsberg and VLA beams (9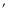 and
and 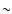 1
1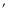 ,
respectively), the histograms given in his paper do not
apply. For this reason, we have used H I data obtained from the VLA
Galactic Plane Survey (VGPS, Stil et al. 2006) to reproduce his work.
We have chosen a region near WR 124 (49
,
respectively), the histograms given in his paper do not
apply. For this reason, we have used H I data obtained from the VLA
Galactic Plane Survey (VGPS, Stil et al. 2006) to reproduce his work.
We have chosen a region near WR 124 (49
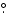 0
0  l
l 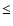 51
51
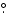 5, 0
5, 0
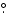 6
6 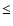 b
b 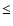 1
1
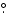 9 and
9 and
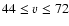
 )
where no massive stars or SNR are known to be present. In this case
any H I holes are just random structures and will be referred to as
random holes. Because of the turbulent nature of the H I on small
spatial scales, the images were first smoothed to a spatial resolution
of 2
)
where no massive stars or SNR are known to be present. In this case
any H I holes are just random structures and will be referred to as
random holes. Because of the turbulent nature of the H I on small
spatial scales, the images were first smoothed to a spatial resolution
of 2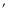 ,
i.e., about half the diameter of cavity A. Figure 5 shows two histograms, one corresponding to the area and the
other to the velocity extent of the observed random holes.
,
i.e., about half the diameter of cavity A. Figure 5 shows two histograms, one corresponding to the area and the
other to the velocity extent of the observed random holes.
Taken at face value, these histograms show that random H I holes peak
at an area of about 75 arcmin2 (equivalent to a diameter of about
10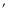 for a circular hole). These random holes also have a
relatively small velocity extent (peak near 5
for a circular hole). These random holes also have a
relatively small velocity extent (peak near 5
 )
compared to that
of cavity A. Using the two histograms to evaluate the probability that
cavity A has by chance the size and velocity extent observed, we
deduce a combined probability of about 0.01.
)
compared to that
of cavity A. Using the two histograms to evaluate the probability that
cavity A has by chance the size and velocity extent observed, we
deduce a combined probability of about 0.01.
The relatively small size of cavity A, compared to H I cavities
identified around other WR stars (Cappa et al. 2003), is of
significance and deserves further attention. The cavity radius at maximum
extent is only about 2
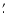 5 which, at a distance of 5 kpc,
corresponds to about 3.6 pc. For the sake of comparison, the radius
of a classical stellar wind bubble around a star at rest with respect
to the ISM is given by (Castor et al. 1975; Weaver et al. 1977)
5 which, at a distance of 5 kpc,
corresponds to about 3.6 pc. For the sake of comparison, the radius
of a classical stellar wind bubble around a star at rest with respect
to the ISM is given by (Castor et al. 1975; Weaver et al. 1977)
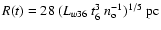 ,
where
,
where 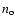 is the
undisturbed ISM number density,
is the
undisturbed ISM number density,
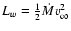 is the wind luminosity,
is the wind luminosity,
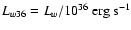 ,
t is the time over which the stellar wind has been acting upon the
surrounding ISM, and
,
t is the time over which the stellar wind has been acting upon the
surrounding ISM, and
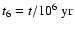 .
For any reasonable
value of the parameters, R(t) considerably exceeds the observed
radius of cavity A.
.
For any reasonable
value of the parameters, R(t) considerably exceeds the observed
radius of cavity A.
However, for a very fast hypersonically moving star such as WR 124,
the actual appearance of the ensuing structure is not described by the
symmetric structure characterized by the above equation for R(t).
Contrary to the standard theory of stellar wind bubbles, which
describes the evolution in time of the radius, and velocity of a closed
structure surrounding a massive star with a strong stellar wind, the
bow shock created by a supersonically moving star is a stationary
time-independent paraboloid structure (Wilkin 1996; Raga et al. 1997).
The scale of this bow shock depends not only on the wind velocity and
mass loss rate but also on the peculiar velocity of the star.
Furthermore the orientation of the bow shock symmetry axis is
determined by the direction of the relative velocity between the star
and its local ISM.
To assess the possible importance of the component of motion
of WR 124 on the sky, we use the value of inclination i given by van
der Sluys & Lamers (2003),
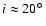 ,
and take 200
,
and take 200
 as
the approximate spatial velocity of WR 124 with respect to its local
ISM. The tangential component of velocity is thus
as
the approximate spatial velocity of WR 124 with respect to its local
ISM. The tangential component of velocity is thus
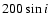

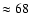
 ,
a significant number corresponding
to an approximate angular displacement on the sky (mostly towards
southern declination) of about 0
,
a significant number corresponding
to an approximate angular displacement on the sky (mostly towards
southern declination) of about 0
 8 t6. Based on this
qualitative argument, it is not justifiable to simply approximate the
motion of the star as mostly receding along the LOS and
some H I signature on the plane of the sky should be looked for.
8 t6. Based on this
qualitative argument, it is not justifiable to simply approximate the
motion of the star as mostly receding along the LOS and
some H I signature on the plane of the sky should be looked for.
Table 2:
Flux density estimates of M1-67.
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{8339fig4.ps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg71.gif) |
Figure 4:
MSX images towards WR 124 (star symbol). The lowest
contour level represents a noise level of 4.5 for band
A and 3
for band
A and 3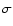 for the others bands. Low intensity regions are
indicated by light greys. Top left panel: 8.28
for the others bands. Low intensity regions are
indicated by light greys. Top left panel: 8.28  m (band
A) emission. The grey scale range is -2 to 35
MJy sr-1. The contour lines are 6, 10, 14, 18, 26, 34, 42 and
50 MJy sr-1. Top right panel: band C image
(12.1 m (band
A) emission. The grey scale range is -2 to 35
MJy sr-1. The contour lines are 6, 10, 14, 18, 26, 34, 42 and
50 MJy sr-1. Top right panel: band C image
(12.1  m). The grey scale spans -75 to 130 MJy sr-1. The
contour line is 57.7 MJy sr-1. Bottom left panel: band
D image at 14.65 m). The grey scale spans -75 to 130 MJy sr-1. The
contour line is 57.7 MJy sr-1. Bottom left panel: band
D image at 14.65  m. The grey scale range is -47 to 80
MJy sr-1. The contour line is 33.6 MJy sr-1. Bottom
right panel: band E image at 21.3 m. The grey scale range is -47 to 80
MJy sr-1. The contour line is 33.6 MJy sr-1. Bottom
right panel: band E image at 21.3  m. The grey scale
covers the range -130 to 260 MJy sr-1, contour lines are
79.5 and 159.0 MJy sr-1. m. The grey scale
covers the range -130 to 260 MJy sr-1, contour lines are
79.5 and 159.0 MJy sr-1. |
| Open with DEXTER |
The structure of interstellar bubbles (IB) created by the powerful
winds of massive stars has been well modeled (e.g. Castor et al. 1975;
Weaver et al. 1977). For a star at rest with respect to its ambient
interstellar gas, these models predict that the corresponding IB is
spherical in shape with the star projected near its center. However,
as the stellar spatial velocity increases, the idealized spherical
structure of the IB is distorted as compared to that formed by a low
velocity star (Weaver et al. 1977). If the stellar velocity becomes
supersonic, a bow shock structure develops. This structure is
axisymmetric along the direction of the stellar spatial velocity and
can be approximated by a paraboloid of revolution. An analytic
solution for its shape was derived by Wilkin (1996). In this model
the shape of the bow shock is determined by the balance between the
ram pressure of the wind, the ram pressure of the ambient medium in
the reference frame of the star, and the flow of momentum along the
surface of the bow shock. This model provides a simple and useful
description of the shape of the bow shock, the distribution of the
surface density and the gas velocity along its surface. The star is
assumed to move with a constant velocity
 relative to an
ISM of uniform density
relative to an
ISM of uniform density 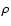 .
The isotropic stellar wind has mass
loss rate
.
The isotropic stellar wind has mass
loss rate 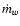 and constant terminal speed Vw, yielding a
paraboloid cometary structure with the stellar velocity vector as
symmetry axis. In this idealized model, the bow shock is at a
distance
and constant terminal speed Vw, yielding a
paraboloid cometary structure with the stellar velocity vector as
symmetry axis. In this idealized model, the bow shock is at a
distance 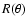 from the star, where
from the star, where
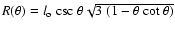 and
and 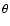 is the polar angle measured from the symmetry axis with the star at
the coordinate origin (see Fig. 6). The bow shock stand-off
distance (
is the polar angle measured from the symmetry axis with the star at
the coordinate origin (see Fig. 6). The bow shock stand-off
distance (
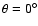 )
sets the length scale and is given by
)
sets the length scale and is given by
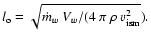 Although Wilkin's model uses a thin shell approximation,
several numerical simulations of bow shocks (Raga et al. 1997; Arthur
& Hoare 2006) have shown that this simple model traces relatively
well the average position of the bow shock. The main advantage of
using this simple model is that the number of variable parameters is
kept to a minimum, thus allowing one to focus on identifying dominant
effects rather than trying to precisely reproduce generally complex
observational data.
Although Wilkin's model uses a thin shell approximation,
several numerical simulations of bow shocks (Raga et al. 1997; Arthur
& Hoare 2006) have shown that this simple model traces relatively
well the average position of the bow shock. The main advantage of
using this simple model is that the number of variable parameters is
kept to a minimum, thus allowing one to focus on identifying dominant
effects rather than trying to precisely reproduce generally complex
observational data.
The tridimensional bow shock surface is obtained by rotating
Fig. 6 by 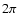 about the symmetry axis. The orientation is
given by specifying the inclination of the axis with respect to the
LOS (angle i) and the position of the projected
axis on the plane of the sky (position angle
about the symmetry axis. The orientation is
given by specifying the inclination of the axis with respect to the
LOS (angle i) and the position of the projected
axis on the plane of the sky (position angle 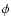 measured
counter-clockwise from north). For an image in equatorial
coordinates, the angles i and
measured
counter-clockwise from north). For an image in equatorial
coordinates, the angles i and 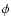 are related to the stellar
velocity by the relations
are related to the stellar
velocity by the relations
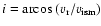 ,
,
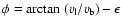 where
where
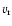 ,
,
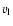 ,
,
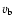 and
and
 are the radial
velocity, velocity in the longitude and latitude directions and total
stellar velocity with respect to the local ISM at the position of the
star, respectively. The angle
are the radial
velocity, velocity in the longitude and latitude directions and total
stellar velocity with respect to the local ISM at the position of the
star, respectively. The angle 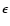 is the angle between a line
of constant declination and a line of constant Galactic latitude
measured counter-clockwise from the positive l axis. Detailed
transformation equations leading to i and
is the angle between a line
of constant declination and a line of constant Galactic latitude
measured counter-clockwise from the positive l axis. Detailed
transformation equations leading to i and 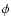 can be found in
van der Sluys & Lamers (2003) (note however that our definition of
can be found in
van der Sluys & Lamers (2003) (note however that our definition of
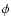 differs from theirs and that the sign of the
differs from theirs and that the sign of the 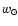 term
in their Eq. (19) must be reversed).
term
in their Eq. (19) must be reversed).
Table 3:
MSX and IRIS integrated flux densities.
As a consequence of the stellar velocity, the incoming ISM is shocked,
ionized and flows tangentially in a thin layer along the bow shock
surface (i.e., along the cone shown in Fig. 6; see also Fig. 1
of Wilkin 1996). Wilkin (1996) gives an analytic solution for the
velocity of the shocked gas at all points on the shell. It is unclear
whether the shocked matter can ever recombine to form a neutral H I layer and, if it does, where this takes place. One expects this to
happen significantly far downstream from the star, where the
tangential velocity has become negligible. The primary H I signature
of a bow shock is thus likely to be that of an elongated H I cavity
having a conical structure aligned with the projected direction of
motion of the star (i.e., the empty interior within the bow shock
surface). It is important to mention that in a realistic ISM,
the conical structure may be broken or distorted by the presence along
the same LOS of unrelated (with respect to the bow shock)
H I features.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{8339fig5.eps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg97.gif) |
Figure 5:
Histograms of the random H I holes area and velocity extent
identified in a region near the stellar position. The arrows indicate
the area and velocity extent observed for cavity A. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{8339fig6.eps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg98.gif) |
Figure 6:
Schematic side view representation of the geometry of the bow shock
model. The horizontal axis represents the symmetry axis of the bow
shock and 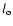 is the stand-off distance.
is the stand-off distance. |
| Open with DEXTER |
Keeping in mind van der Sluys & Lamers' (2003) estimate for the
approximate direction of the stellar velocity on the sky, we inspected
the H I distribution looking for signatures of a bow shock. Figure
1 shows that another H I minimum (indicated as B) is
observed at 56.7
 .
This H I depression is centered at
.
This H I depression is centered at
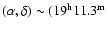 ,
17
,
17
 0), i.e.
0), i.e.  10
10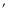 to the north of the stellar position and is present to
velocities about 46
to the north of the stellar position and is present to
velocities about 46
 .
This cavity is elongated in a general N-S
direction.
.
This cavity is elongated in a general N-S
direction.
The elongated large-scale horizontal
structure crossing the field near
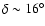 55
55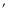 appears to be responsible for the fact that
cavities A and B appear separated and/or distorted, rather than forming
a smooth structure like that suggested by Fig. 6.
Within the bow shock picture, cavity A corresponds to the
approximate position of the apex, while cavity B
can be interpreted as corresponding to the rear part of the bow shock.
appears to be responsible for the fact that
cavities A and B appear separated and/or distorted, rather than forming
a smooth structure like that suggested by Fig. 6.
Within the bow shock picture, cavity A corresponds to the
approximate position of the apex, while cavity B
can be interpreted as corresponding to the rear part of the bow shock.
The positions of cavities A and B can be used to correctly orient the
structure shown in Fig. 6 so that it fits the H I data for
WR 124. This procedure consists of obtaining estimates of the angles
i and 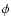 .
As mentioned before, van der Sluys and Lamers (2003),
using the Fabry-Perot H
.
As mentioned before, van der Sluys and Lamers (2003),
using the Fabry-Perot H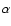 observations of Grosdidier et al. (2001), had obtained values of
observations of Grosdidier et al. (2001), had obtained values of
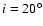 and
and
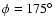 (our definition of
(our definition of 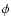 ). It is worth noting however,
that their results are based on optical observations of a region of
ionized gas covering only about
). It is worth noting however,
that their results are based on optical observations of a region of
ionized gas covering only about
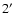 on the sky. In a sense,
the optical data only sample the exact region of the apex while our
neutral hydrogen images cover a much wider field of some
on the sky. In a sense,
the optical data only sample the exact region of the apex while our
neutral hydrogen images cover a much wider field of some
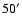 in diameter and sample the more global bow shock structure. As the
main goal is to find a general fit of the "large-scale'' H I data
(basically an absence of H I within a given volume) to a bow shock
model, we wish to establish the range of parameters allowed by the
observational data (essentially the proper motions). Using a radial
velocity of
in diameter and sample the more global bow shock structure. As the
main goal is to find a general fit of the "large-scale'' H I data
(basically an absence of H I within a given volume) to a bow shock
model, we wish to establish the range of parameters allowed by the
observational data (essentially the proper motions). Using a radial
velocity of
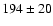
 (Wilson 1953), a proper motion
(
(Wilson 1953), a proper motion
(
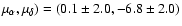 mas yr-1 (Tycho-2 Catalogue) and assuming a distance of
mas yr-1 (Tycho-2 Catalogue) and assuming a distance of 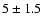 kpc, following van der Sluys & Lamers (2003) we obtain
kpc, following van der Sluys & Lamers (2003) we obtain
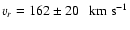 ,
,
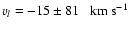 ,
,
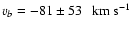 ,
and
,
and
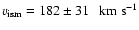 ,
from which we
deduce
,
from which we
deduce
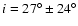 and
and
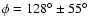 (
(
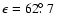 for WR 124). If instead
Hipparcos proper motions are used (
for WR 124). If instead
Hipparcos proper motions are used (
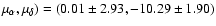 mas yr-1, we obtain
mas yr-1, we obtain
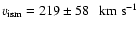 ,
,
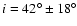 and
and
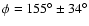 .
These
estimates, solely based on the observed radial velocity and proper
motions, suggest that the angles should lie in the approximate range
.
These
estimates, solely based on the observed radial velocity and proper
motions, suggest that the angles should lie in the approximate range
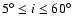 and
and
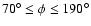 .
The stand-off distance, assuming a typical value of
1 cm-3 for the undisturbed ambient number density, is
.
The stand-off distance, assuming a typical value of
1 cm-3 for the undisturbed ambient number density, is
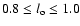 pc.
pc.
Taking into account the large allowed range for i and 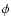 ,
mostly
as a consequence of the errors in the proper motions, we derive the
angles i and
,
mostly
as a consequence of the errors in the proper motions, we derive the
angles i and 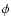 that best fit our H I observations. Under the
assumption that cavities A and B are part of the same bow shock
structure, the angles obtained are
that best fit our H I observations. Under the
assumption that cavities A and B are part of the same bow shock
structure, the angles obtained are
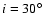 and
and
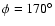 .
.
The corresponding 3D rotated structure for
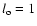 pc is presented
in the bottom right corner of Figs. 7a,b, where the observed H I distribution at v = 61.8and 54.1
pc is presented
in the bottom right corner of Figs. 7a,b, where the observed H I distribution at v = 61.8and 54.1
 is shown. As mentioned in Sect. 3.1, the
presence of a horizontal structure at
is shown. As mentioned in Sect. 3.1, the
presence of a horizontal structure at
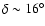 55
55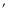 precludes the observation of the H I minima that would correspond to
intermediate parts of the paraboloid, hence giving the false
impression that cavities A and B are unrelated to each another.
Keeping in mind that a realistic inhomogeneous ambient ISM is likely
to result in significant deviations from the ideal model, the 3D bow
shock structure shown as an inset in Figs. 7a,b indicates that the bow shock model is consistent
with the H I observations. It is implicit to our interpretation of
the H I data that the observed holes (cavities A and B) arise as a
consequence of the hollow structure of a bow shock that is being
viewed from its rear part, along a LOS that makes a small angle with
respect to the symmetry axis of the parabolic shape defining an ideal
bow shock structure. This picture is also consistent with a scenario
where the ionization front generated by the Lyman continuum photons
emitted by WR 124 is trapped within the stellar wind shock. If this
were not the case, the H II region would be much larger than the bow
shock (Raga et al. 1997). In our scheme, the radio continuum, the
infrared, and the H
precludes the observation of the H I minima that would correspond to
intermediate parts of the paraboloid, hence giving the false
impression that cavities A and B are unrelated to each another.
Keeping in mind that a realistic inhomogeneous ambient ISM is likely
to result in significant deviations from the ideal model, the 3D bow
shock structure shown as an inset in Figs. 7a,b indicates that the bow shock model is consistent
with the H I observations. It is implicit to our interpretation of
the H I data that the observed holes (cavities A and B) arise as a
consequence of the hollow structure of a bow shock that is being
viewed from its rear part, along a LOS that makes a small angle with
respect to the symmetry axis of the parabolic shape defining an ideal
bow shock structure. This picture is also consistent with a scenario
where the ionization front generated by the Lyman continuum photons
emitted by WR 124 is trapped within the stellar wind shock. If this
were not the case, the H II region would be much larger than the bow
shock (Raga et al. 1997). In our scheme, the radio continuum, the
infrared, and the H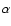 emission arise from a small region
circumscribed to the apex of the bow shock structure.
emission arise from a small region
circumscribed to the apex of the bow shock structure.
Along the same line of reasoning we can even go as far as to argue
that a much larger H I cavity than the one observed centered on
WR 124 would have been incompatible with the highly supersonic motion
of the star and the unavoidable formation of a bow shock structure.
Furthermore the existence of an H I deficiency in the general
direction from which the star is incoming, strengthens the probability
argument against chance coincidence. A simple probability argument
consists of estimating the combined probability that, simply by
chance, WR 124 is seen superposed on cavity A and that cavity B is
seen in a direction (as seen from the position of WR 124)
corresponding to the incoming direction of the star on the sky
(estimated on the basis of the size subtended by cavity B as seen from
WR 124). This simple argument yields a small combined probability of
less than 0.01.
Concerning the kinematics of the H I gas, it is important to
emphasize that the observed velocities are not expansion velocities
(as is the case for spherical bubbles). The difference in velocity
between cavity A and B can be explained in terms of the expected
velocity dispersion of the H I gas (4.2
 ,
Blitz & Spergel 1991)
as well as turbulent motions. Cavities A and B can be considered as
part of the same structure having a centroid velocity of
,
Blitz & Spergel 1991)
as well as turbulent motions. Cavities A and B can be considered as
part of the same structure having a centroid velocity of 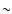 55
55
 .
.
![\begin{figure}
\par\includegraphics[width=14.4cm,clip]{8339fig7.eps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg122.gif) |
Figure 7:
a) H I emission distribution at v = 61.8, where
cavity A is best delineated. b) H I emission distribution at v
= 54.1
 ,
where cavity B is best delineated.
In both panels contour levels are -10, 0 and 5 K. The cross marks
the position of WR 124. The 3D bow shock structure for ,
where cavity B is best delineated.
In both panels contour levels are -10, 0 and 5 K. The cross marks
the position of WR 124. The 3D bow shock structure for
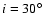 and
and
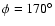 is shown in the bottom right corner.
is shown in the bottom right corner. |
| Open with DEXTER |
The fact that cavity B is not open to the north can be interpreted as
an indication that the bow shock cavity has begun to close behind the
star.
For
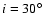 and
and
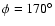 ,
the distance
traveled by the star from the northernmost part of cavity B is
D* = 23 pc. As a first rough approximation the cavity can be
assumed to close on a sound-crossing timescale. The sound speed
,
the distance
traveled by the star from the northernmost part of cavity B is
D* = 23 pc. As a first rough approximation the cavity can be
assumed to close on a sound-crossing timescale. The sound speed 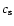 required for the cavity to close on the timescale it takes the star
to travel the distance D* is
required for the cavity to close on the timescale it takes the star
to travel the distance D* is
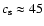
 .
This sound
speed corresponds to a gas temperature of
.
This sound
speed corresponds to a gas temperature of 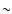
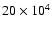 K,
consistent with what may be expected for hot stellar wind gas. From
the form
K,
consistent with what may be expected for hot stellar wind gas. From
the form 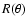 of the cavity, we can estimate the transverse
(i.e., perpendicular to the symmetry axis) dimension of the cavity
dt at the distance D*. We obtain
of the cavity, we can estimate the transverse
(i.e., perpendicular to the symmetry axis) dimension of the cavity
dt at the distance D*. We obtain
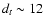 pc,
corresponding to an angular width of
pc,
corresponding to an angular width of
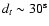 (or
8
(or
8
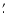 3) at 5 kpc. This value is in good agreement with the width of
the northernmost part of cavity B. The corresponding angle
3) at 5 kpc. This value is in good agreement with the width of
the northernmost part of cavity B. The corresponding angle 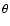 (see Fig. 6) is about
(see Fig. 6) is about
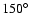 .
Although it is clear that
the model will break down at very large distances downstream, Raga et al. (1997) and Arthur & Hoare (2006) obtained the same angle in their
numerical simulations. In fact, Fig. 4 of Raga et al. (1997) and Fig. 22 of Arthur & Hoare (2006), show their
numerical solutions behave generally as expected by the analytical
model out to angles of about
.
Although it is clear that
the model will break down at very large distances downstream, Raga et al. (1997) and Arthur & Hoare (2006) obtained the same angle in their
numerical simulations. In fact, Fig. 4 of Raga et al. (1997) and Fig. 22 of Arthur & Hoare (2006), show their
numerical solutions behave generally as expected by the analytical
model out to angles of about
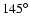 .
The simulation of Arthur
& Hoare (2006) shows a structure more open than the analytical model
and the shock at the apex more distant by about a factor of 1.5. The
simulation of Raga et al. (1997) was for a fast (100
.
The simulation of Arthur
& Hoare (2006) shows a structure more open than the analytical model
and the shock at the apex more distant by about a factor of 1.5. The
simulation of Raga et al. (1997) was for a fast (100
 )
star moving
in a low density medium (1 cm-3) whereas that of Arthur &
Hoare (2006) is more typical of cometary H II regions (low velocity
of 20
)
star moving
in a low density medium (1 cm-3) whereas that of Arthur &
Hoare (2006) is more typical of cometary H II regions (low velocity
of 20
 and high density of 6000 cm-3). These simulations
give us confidence that the use of Wilkin's analytical model is
justified.
and high density of 6000 cm-3). These simulations
give us confidence that the use of Wilkin's analytical model is
justified.
Finally it is encouraging that the fitting of a simple minded
bow shock model to the H I images ( 50
50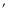 in diameter)
leads to values of i and
in diameter)
leads to values of i and 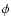 (
(
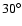 and
and
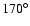 ,
respectively) which are in good agreement with the values
(
,
respectively) which are in good agreement with the values
(
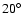 and
and
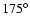 ,
based on our definition of
,
based on our definition of 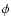 )
obtained by van der Sluys & Lamers (2003) using a completely
different database and involving the same simple model but on a
considerably smaller angular scale.
)
obtained by van der Sluys & Lamers (2003) using a completely
different database and involving the same simple model but on a
considerably smaller angular scale.
The physical parameters derived for the ionized gas in the nebula are
summarized in Table 4. The ionized mass Mi and
electron density 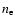 were obtained from the classical expressions
(Mezger & Henderson 1967) for a sphere of 55
were obtained from the classical expressions
(Mezger & Henderson 1967) for a sphere of 55
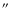 in radius (
in radius (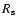 = 1.3 pc at 5 kpc) with uniform electron density
= 1.3 pc at 5 kpc) with uniform electron density 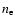 and an electron
temperature of 6200 K (Esteban et al. 1991). The adopted values
coincide with those by Grosdidier et al. (1998), although the
distances are slightly different. We give separate estimates
corresponding to different values of the volume filling factor
f. The case f = 1 is unrealistic as it is clear from
Fig. 3a that the plasma is quite clumpy. The bow shock
is not a uniformly filled sphere but is better modeled as a
hemispherical shell of radius
and an electron
temperature of 6200 K (Esteban et al. 1991). The adopted values
coincide with those by Grosdidier et al. (1998), although the
distances are slightly different. We give separate estimates
corresponding to different values of the volume filling factor
f. The case f = 1 is unrealistic as it is clear from
Fig. 3a that the plasma is quite clumpy. The bow shock
is not a uniformly filled sphere but is better modeled as a
hemispherical shell of radius 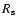 and thickness
and thickness
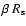 with
with
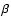 in the range 0.1 to 0.2. The hot plasma covers only 40 to 60%
of the volume of this hemispherical shell. The last two lines of
Table 4 give the values of
in the range 0.1 to 0.2. The hot plasma covers only 40 to 60%
of the volume of this hemispherical shell. The last two lines of
Table 4 give the values of 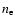 and Mi corresponding
to filling factors between 0.05 and 0.15. Our estimates of
and Mi corresponding
to filling factors between 0.05 and 0.15. Our estimates of 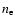 and
Mi for f = 0.05 are consistent with the values derived by
Grosdidier et al. (1998) on the basis of the HST H
and
Mi for f = 0.05 are consistent with the values derived by
Grosdidier et al. (1998) on the basis of the HST H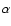 image
(Fig. 3b).
image
(Fig. 3b).
The small physical size of the continuum nebula suggests that it
corresponds to a limited region near the head of the bow shock where
the surface density and hence emissivity is maximum (e.g., Mac Low et al. 1991; Van Buren et al. 1990). The fact that the structure
observed at radio continuum, optical and infrared wavelengths does not
conform to the expected one (namely an arc-like structure on the plane
of the sky, see Fig. 1 of van Buren et al. 1990) has to do with the direction
of motion of WR 124, that is is almost along the LOS. Under these conditions, projection
effects render impossible
the detection of the classic arc-like geometry which would be produced
by a star mainly moving on the plane of the sky.
Table 4:
Main parameters derived from the radio
continuum data at 3.6 cm for an assumed distance d of 5 kpc.
It is also evident from Fig. 3a that the radio continuum
emission is highly irregular on scales probed by the VLA 3.6 cm
observations. The origin of these irregularities is uncertain. On
the basis of detailed abundance analysis (Esteban et al. 1991), the
ionized mass has been inferred to consist mostly of ejecta. The
ionized mass derived from the radio continuum data is consistent with
this conclusion. As mentioned by van der Sluys & Lamers (2003),
because the outbursts responsible for the nebula occur inside the bow
shock, the ejecta collide with it and are then dragged along the bow
shock surface, eventually adopting its velocity. Depending on the
relative momentum of the outburst and of the wind-ISM shock, the
outburst may adopt the geometry of the bow shock or, in an extreme
case, distort it severely. We see structures down to the
VLA resolution limit (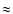 8
8
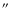 )
corresponding to a linear scale
)
corresponding to a linear scale
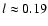 pc at a distance of 5 kpc. These structures could
correspond to irregularities of the bow shock surface (perhaps caused
by inhomogeneities in the ISM) or alternatively to irregularities in
the angular distribution of the stellar wind. The HST image of
Grosdidier et al. (2001) (Fig. 3b) shows that irregularities
are in fact present on scales much smaller than those probed by the
radio observations.
pc at a distance of 5 kpc. These structures could
correspond to irregularities of the bow shock surface (perhaps caused
by inhomogeneities in the ISM) or alternatively to irregularities in
the angular distribution of the stellar wind. The HST image of
Grosdidier et al. (2001) (Fig. 3b) shows that irregularities
are in fact present on scales much smaller than those probed by the
radio observations.
The data of Table 2 (see Sect. 3.2) are consistent
with a thermal spectrum, which is the norm for stellar wind
structures. However, a significant proportion of stellar wind objects
also exhibit non-thermal radio emission. A case of particular interest
is that of colliding-wind binaries (Eichler & Usov 1993) where the
non-thermal emission is shown to arise at the point of ram pressure
balance between the two stellar winds (Dougherty & Williams 2000;
Dougherty et al. 2005). One might then ask whether a non-thermal
component could be present in the WR 124 nebula. Such emission is
clearly negligible if one considers emission integrated over the
entire structure (Table 2). The apex of the bow shock
would seem the ideal place to look for non-thermal radio
emission. However, in order to look for possible spectral index
variations, a higher-resolution radio image would be needed at a
frequency sufficiently different from our own image.
Since the radio continuum image is free from extinction by dust, the
morphological agreement between the VLA and HST images suggests a
relatively low and rather uniform extinction across the nebula,
which in turn suggests that ionized gas and dust are well mixed, and/or the
presence of dust beyond the location of the ionized material. This
last suggestion is also consistent with the fact that we are observing
M1-67 through the major symmetry axis of the paraboloid.
As for dust emission, we integrate the energy distribution given in
Table 3 and obtain the infrared luminosity of the nebula
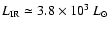 .
Under the assumption that
the 60 and 100
.
Under the assumption that
the 60 and 100  m emission is mostly due to radiatively heated
dust grains, by fitting a modified Planck function of the form
m emission is mostly due to radiatively heated
dust grains, by fitting a modified Planck function of the form
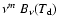 to the flux densities at 60 and 100
to the flux densities at 60 and 100  m, where
the first term accounts for the frequency dependence of the grain
emission, we derive a mean dust temperature
m, where
the first term accounts for the frequency dependence of the grain
emission, we derive a mean dust temperature
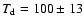 K
(for m=1) and
K
(for m=1) and
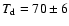 K (for m=2). The high
K (for m=2). The high 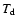 values merely reflect the fact that the observed feature is much
stronger at 60
values merely reflect the fact that the observed feature is much
stronger at 60  m than at 100
m than at 100  m, a behavior typical of bow
shocks (van Buren & McCray 1988).
m, a behavior typical of bow
shocks (van Buren & McCray 1988).
The high ( 200
200
 )
peculiar velocity of WR 124 implies the
presence of a strong shock, particularly at the apex of the bow shock.
This may lead to the selective (i.e., with respect to size)
destruction of dust grains (Whittet 2003, p. 288) and to the
collisional heating of the grains (Dwek 1987; Arendt 1989). Both
factors are likely to significantly affect the intensity (hence
morphology) and frequency dependence (dust temperature) of the
observed IR emission.
)
peculiar velocity of WR 124 implies the
presence of a strong shock, particularly at the apex of the bow shock.
This may lead to the selective (i.e., with respect to size)
destruction of dust grains (Whittet 2003, p. 288) and to the
collisional heating of the grains (Dwek 1987; Arendt 1989). Both
factors are likely to significantly affect the intensity (hence
morphology) and frequency dependence (dust temperature) of the
observed IR emission.
In this work we have presented new high resolution radio data in the
environs of WR 124. These data have allowed us to analyze the effects
of the interaction between the stellar wind and the ISM surrounding
WR 124.
The runaway nature of the star is fundamental in
interpreting and understanding the observations.
From the analysis of the H I distribution, two cavities (named cavity
A and cavity B) were identified as possibly related to the star. Both
cavities are observed at LSR velocities of about 55
 .
While
cavity A is observed with WR 124 projected inside it, cavity B is
located 10
.
While
cavity A is observed with WR 124 projected inside it, cavity B is
located 10 to the north of the stellar position. There is
convincing evidence that these two apparently disconnected H I cavities are in fact part of the same bow shock structure caused by
the star's supersonic motion.
to the north of the stellar position. There is
convincing evidence that these two apparently disconnected H I cavities are in fact part of the same bow shock structure caused by
the star's supersonic motion.
From the continuum data, the new radio image together with past data
obtained with a number of radio telescopes are consistent with a
purely thermal emission process, as is the case for the majority of
ring nebulae around massive stars (Cappa et al. 2003). Because of the
particular viewing geometry in the present case, the radio continuum
image represents essentially a snapshot picture of the ionized gas in
the immediate vicinity of the forward bow shock cone associated with
the supersonic motion of WR 124 through its local ISM. The radio
morphology has been shown to be extremely similar to the optical one,
suggesting that the ionized gas and the dust are well mixed and/or the
dust is located beyond the ionized material.
The dust temperature deduced from the 60  m and 100
m and 100  m images
(
m images
(
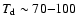 K) and the brighter 60
K) and the brighter 60  m emission are in
agreement with previous observations of bow shocks (van Buren &
McCray 1988). The MSX images show that the IR morphology changes
dramatically between different wavelengths. We interpret these results
as indicating that the physical conditions in bow shocks associated
with supersonically moving stars are significantly different from
those encountered in the standard stationary stellar wind shocks.
m emission are in
agreement with previous observations of bow shocks (van Buren &
McCray 1988). The MSX images show that the IR morphology changes
dramatically between different wavelengths. We interpret these results
as indicating that the physical conditions in bow shocks associated
with supersonically moving stars are significantly different from
those encountered in the standard stationary stellar wind shocks.
Acknowledgements
We thank W.M. Goss for helping us with the reduction of the H I VLA
data and for useful comments and suggestions in many phases of this
project. We thank Gilles Joncas for providing us with the HST image of
M1-67. The work of S.P. and S.C. was supported by the Natural
Sciences and Engineering Research Council of Canada and the Fonds
Québecois pour la Recherche sur les sciences de la Nature et la
Technologie. The National Radio Astronomy Observatory is a facility
of the National Science Foundation operated under cooperative
agreement by Associated Universities, Inc. This research was
partially supported by Facultad de Ciencias Astronómicas y
Geofísicas, Universidad Nacional de La Plata under project
11/G072, by the Agencia Nacional de Promoción Cienfífica y
Tecnológica (ANPCYT) under project PICT 14018/03, and by Consejo
Nacional de Investigaciones Científicas y Técnicas (CONICET) of
Argentina under projects PIP 2274 and 5886. We are grateful to the
referee, whose suggestions led to the improvement of this paper.
- Arendt, R. G.
1989, ApJS, 70, 181 [NASA ADS] [CrossRef]
(In the text)
- Arnal, E. M. 1992,
A&A, 254, 305 [NASA ADS]
(In the text)
- Arthur, S. J.,
& Hoare, M. G. 2006, ApJS, 165, 283 [NASA ADS] [CrossRef]
(In the text)
- Bertola, F.
1964, PASP, 76, 241 [NASA ADS] [CrossRef]
(In the text)
- Blitz, L., &
Spergel, D. N. 1991, ApJ, 370, 205 [NASA ADS] [CrossRef]
(In the text)
- Cappa, C. E.,
Arnal, E. M., Cichowolski, S., Goss, W. M., & Pineault, S.
2003, in A massive star odyssey: from main sequence to supernova,
ed. K. A. van der Hucht, A. Herrero, & C. Esteban (PASP), IAU
Symp., 212, 596
(In the text)
- Cappa, C. E.,
Goss, W. M., & van der Hucht, K. A. 2004, AJ, 127, 2885 [NASA ADS] [CrossRef]
(In the text)
- Castor, J.,
McCray, R., & Weaver, R. 1975, ApJ, 200, L107 [NASA ADS] [CrossRef]
(In the text)
- Chan, K. W., &
Onaka, T. 2000, ApJ, 533, L33 [NASA ADS] [CrossRef]
(In the text)
- Crawford,
I. A., & Barlow, M. J. 1991, A&A, 249, 518 [NASA ADS]
(In the text)
- Condon, C. C.,
& Kaplan D. L. 1998, ApJS, 117, 361 [NASA ADS] [CrossRef]
- Condon, J. J.,
Broderick, J. J., Seielstad, G. A., Douglas, K., & Gregory, P.
C. 1994, AJ, 107, 1829 [NASA ADS] [CrossRef]
- Dougherty,
S. M., & Williams, P. M. 2000, MNRAS, 319, 1005 [NASA ADS] [CrossRef]
(In the text)
- Dougherty,
S. M., Beasley, A. J., Claussen, M. J., Zauderer, B. A., &
Bolingbroke, N. J. 2005, ApJ, 623, 447 [NASA ADS] [CrossRef]
(In the text)
- Dwek, E. 1987, ApJ,
322, 812 [NASA ADS] [CrossRef]
(In the text)
- Egan, M. P., Price,
S. D., Moshir, M. M., Cohen, M., & Tedesco, E. 1999, The
Midcourse Space Experiment Point Source Catalog Version 1.2
Explanatory Guide. Air Force Research Laboratory Technical Report,
AFRL-VS-TR 1999-1522
(In the text)
- Eichler, D.,
& Usov, V. 1993, ApJ, 402, 271 [NASA ADS] [CrossRef]
(In the text)
- Eisenhauer, F., Genzel, R., Alexander,
T., et al. 2005, ApJ, 628, 246 [NASA ADS] [CrossRef]
(In the text)
- Esteban, C.,
Vilchez, J. M., Smith, L.J., & Manchado, A. 1991, A&A, 244,
205 [NASA ADS]
(In the text)
- Felli, M., &
Perinotto, M. 1979, A&A, 76, 69 [NASA ADS]
(In the text)
- Fürst, E.,
Reich, W., Reich, P., & Reif, K. 1990, AAS, 85, 805 [NASA ADS]
-
Grosdidier, Y., Moffat, A. F. J., Joncas, G., & Acker, A. 1998,
ApJ, 506, L127 [NASA ADS] [CrossRef]
(In the text)
-
Grosdidier, Y., Moffat, A. F. J., Blais-Ouellette, S., Joncas, G.,
& Acker, A. 2001, ApJ, 562, 753 [NASA ADS] [CrossRef]
(In the text)
- Hog, E., Fabricius,
C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS]
(In the text)
- Israel, F. P.,
& Felli, M. 1976, A&A, 50, 47 [NASA ADS]
(In the text)
- Kalberla,
P. M. W., Mebold, U., & Reich, W. 1980, A&A, 82, 275 [NASA ADS]
(In the text)
- Kothes, R.,
& Dougherty, S. M., 2007, A&A, 468, 993 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Mac Low, M.-M., Van
Buren, D., Wood, D. O. S., & Churchwell, E. 1991, ApJ, 369,
395 [NASA ADS] [CrossRef]
(In the text)
- Mezger, P. G.,
& Henderson, A. P. 1967, ApJ, 147, 471 [NASA ADS] [CrossRef]
(In the text)
-
Minkowski, R. 1946, PASP, 58, 305 [NASA ADS] [CrossRef]
(In the text)
-
Miville-Deschênes, M.A., & Lagache, G. 2005, ApJSS, 157,
302 [NASA ADS] [CrossRef]
(In the text)
- Nugis, T., &
Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS]
(In the text)
- Pismis, P.,
& Recillas-Cruz, E. 1979, Rev. Mex. Astron. Astrofis., 4,
271 [NASA ADS]
(In the text)
- Price, S. D.,
Egan, M. P., Carey, S., Mizuno, D., & Kuchar, T. 2001, AJ, 121,
2819 [NASA ADS] [CrossRef]
(In the text)
- Raga, A. C.,
Noriega-Crespo, A., Cantó, J., et al. 1997, RMxAA, 33, 73 [NASA ADS]
(In the text)
- Reich, W., Reich,
P., & Fürst, E. 1990, AAS, 83, 539 [NASA ADS]
-
Sharpless, S. 1959, ApJS, 4, 257 [NASA ADS] [CrossRef]
(In the text)
- Stil, J. M., Taylor,
A. R., Dickey, J. M., et al. 2006, AJ, 132, 1158 [NASA ADS] [CrossRef]
(In the text)
- Van Buren, D., &
McCray, R. 1988, ApJ, 329, L93 [NASA ADS] [CrossRef]
(In the text)
- Van Buren, D., Mac
Low, M.-M., Wood, D. O. S., & Churchwell, E. 1990, ApJ, 353,
570 [NASA ADS] [CrossRef]
(In the text)
- van der Hucht, K. A.,
Jurriens, T. A., Wesselius, P. R., et al. 1985, A&A, 145,
L13 [NASA ADS]
(In the text)
- van der Hucht, K. A.
2001, New Astron. Rev., 45, 135 [NASA ADS] [CrossRef]
(In the text)
- van der Sluys, M. V.,
& Lamers, H. J. G. L. M. 2003, A&A, 398, 181 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Weaver, R.,
McCray, R., Castor, J. I., Shapiro, P., & Moore, R. 1977, ApJ,
218, 377 [NASA ADS] [CrossRef]
(In the text)
- Whittet, D.
C. B. 2003, Dust in the galactic environment, 2nd Ed. (London: The
Institute of Physics)
(In the text)
- Wilkin, F. P.
1996, ApJ, 459, L31 [NASA ADS] [CrossRef]
(In the text)
- Williams, D.
R. W. 1973, A&AS, 8, 505 [NASA ADS]
(In the text)
- Wilson, R. E.
1953, General Catalogue of Stellar Radial Velocities, Carnegie
Inst. Washington D. C. Publ. 601
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{8339fig1.eps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{8339fig2.eps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg37.gif)
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{8339fig3.ps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{8339fig4.ps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{8339fig5.eps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg97.gif)
![\begin{figure}
\par\includegraphics[width=14.4cm,clip]{8339fig7.eps}\end{figure}](/articles/aa/full/2008/05/aa8339-07/Timg122.gif)