A&A 478, 553-558 (2008)
DOI: 10.1051/0004-6361:20078274

Energy flux of Alfvén waves in weakly ionized plasma

J. Vranjes1,2 - S. Poedts1 - B. P. Pandey3 - B. De Pontieu4


1 - Centrum voor Plasma-Astrofysica, Celestijnenlaan 200 B, 3001 Leuven, Belgium
2 - Faculté des Sciences Appliquées, avenue F.D. Roosevelt 50, 1050 Bruxelles, Belgium
3 - Department of Physics, Macquarie University, Sydney, NSW 2109, Australia
4 - Lockheed Martin Solar and Astrophysics Lab, 3251 Hanover St., Org. ADBS, Bldg. 252, Palo Alto, CA 94304 94304, USA

Received 13 July 2007 / Accepted 31 October 2007

Abstract
Context. The overshooting convective motions in the solar photosphere, resulting in the foot point motion of different magnetic structures in the solar atmosphere, are frequently proposed as the source for the excitation of Alfvén waves, which are assumed to propagate towards the chromosphere and corona resulting finally in the heating of these layers by the dissipation of this wave energy. However, the photosphere is a) very weakly ionized, and, b) the dynamics of the plasma particles in this region is heavily influenced by the plasma-neutral collisions.
Aims. The purpose of this work is to check the consequences of these two facts on the above scenario and their effects on the electromagnetic waves.
Methods. Standard plasma theory is used and the wave physics of the weakly ionized photosphere is discussed. The magnetization and the collision frequencies of the plasma constituents are quantitatively examined.
Results. It is shown that the ions and electrons in the photosphere are both un-magnetized; their collision frequency with neutrals is much larger than the gyro-frequency. This implies that eventual Alfvén-type electromagnetic perturbations must involve the neutrals as well. This has the following consequences: i) in the presence of perturbations, the whole fluid (plasma + neutrals) moves; ii) the Alfvén velocity includes the total (plasma + neutrals) density and is thus considerably smaller compared to the collision-less case; iii) the perturbed velocity of a unit volume, which now includes both plasma and neutrals, becomes much smaller compared to the ideal (collision-less) case; and iv) the corresponding wave energy flux for the given parameters becomes much smaller compared to the ideal case.
Conclusions. The wave energy flux through the photosphere becomes orders of magnitude smaller, compared to the ideal case, when the effects of partial ionization and collisions are consistently taken into account.

Key words: Sun: photosphere - Sun: oscillations

1 Introduction

In a weakly ionized but highly collisional medium, a propagating Alfvén wave also involves the motion of the neutrals that are present in the medium. This is due to the friction between charged particles and neutrals. The effect has been described in the literature, first by Tanenbaum & Mintzer (1962), Woods (1962), Jephcott & Stocker (1962), and in many subsequent works, e.g., Kulsrud & Pierce (1969), Pudritz (1990), Haerendel (1992), De Pontieu & Haerendel (1998), Watts & Hanna (2004). This fundamental result is valid for any weakly ionized plasma, including the plasma in the lower solar atmosphere.

The Alfvén wave has been a very popular tool in the scenarios and models dealing with the heating of upper solar atmosphere. A necessary ingredient in such models is an efficient and abundant source for the excitation of these waves, which acts permanently and generates waves throughout the solar atmosphere. Very frequently it is assumed that the omnipresent overshooting convective motions in the photosphere could serve for this purpose. The amount of thermal energy per unit volume in the solar corona is in fact extraordinarily small in comparison with the lower (and much colder) layers of the solar atmosphere. This is due to the rapidly decreasing density with altitude. On the other hand, the complete photosphere is covered by overshooting convective gas motions with typical velocities of about 0.5 km s-1, that may go up to 2 km s-1. The kinetic energy per cubic meter stored in this macroscopic motion of a mainly neutral gas exceeds for several orders of magnitude the internal energy density in the corona. Clearly, only a tiny fraction of the convective kinetic energy of the neutral gas would be sufficient to heat the higher layers to the given temperatures. Such a scenario is attractive in view of the fact that this macroscopic motion in the lower atmosphere is permanent and widespread throughout the solar surface. However, the photosphere is very weakly ionized and it is also a strongly collisional mixture of the tiny plasma component and the predominantly neutral (uncharged) gas.

Table 1: Collision frequencies (in Hz) and magnetization ratio of electrons and protons in the photosphere for two altitudes h (in km) and for the magnetic field B0=10-2 T.

The energy flux of the Alfvén waves is given by $m_{\rm i} n_{\rm i} v_{\rm i}^2 c_{\rm a}/2$, where $c_{\rm a}$ is the Alfvén velocity and $v_{\rm i}$ is the perturbed velocity of ions involved in the oscillations. Typically, in the estimate of the flux in the photosphere, this perturbed velocity taken is of the same order as the macroscopic convective motion mentioned above (Hollweg 1981).

In the present work, we focus on the physics involved in the propagation of the Alfvén wave in a weakly ionized plasma like the solar photosphere. Using simple and reliable physical arguments and widely accepted plasma theory, we discuss the flux of the Alfvén waves under these circumstances. It will be shown that, if we assume the existence of the necessary electromagnetic perturbations in such a weakly ionized medium, the energy flux of the waves is in fact much lower compared to what is usually expected from estimates based on ideal magnetohydrodynamics. This is due to the fact that the photospheric gas dynamics is heavily influenced by collisions. More precisely, in the presence of some accidental electromagnetic perturbations, which in the first step involve plasma species (electrons and ions) only, the neutral atoms respond to these electromagnetic perturbations due to the strong friction. This, and the fact that the ionization ratio is rather small (viz. of the order of 10-4), results in very small amplitudes of the perturbed velocity of the total plasma-gas fluid.

2 Physics of weakly ionized plasmas

We introduce here the collision frequencies between charged and uncharged particles $\nu_{j{\rm n}}=n_{\rm n0}\sigma_{j{\rm n}} v_{{\rm\scriptscriptstyle T}j}$ for $j= {\rm e, i}$, and the formulas (Spitzer 1962; Mitchner & Kruger 1973) for the Coulomb collisions between charged plasma particles:

\begin{eqnarray*}\nu_{\rm ee}+ \nu_{\rm ei}\! \simeq\! 2 \nu_{{\rm ei}}\! =\! \l... ...varepsilon_0)]^2 L_{\rm ei}/[3 (\kappa T_{\rm e})^{3/2}]\right], \end{eqnarray*}



\begin{eqnarray*}\nu_{\rm ii}= \left[4 n_{\rm i0} (\pi/m_{\rm i})^{1/2} [{\rm e}... ...varepsilon_0)]^2 L_{\rm ii}/[3 (\kappa T_{\rm i})^{3/2}]\right]. \end{eqnarray*}


All frequencies will be given in Hz and the Coulomb logarithm is given by $L_{\rm ei}=\log [12 \pi \varepsilon_0(\varepsilon_0/n_{\rm i0})^{1/2} (\kappa T_{\rm e})^{3/2}/({\rm e e}_{\rm i}^2)]$.

Several comments are noteworthy before continuing the derivation. Using the full quantum theory as well as the semi-classical approach, the elastic proton-hydrogen ($\rm H^++H$) collision cross section  $\sigma_{\rm in}$ is calculated by Krstic & Schultz (1999), and its integral value at 0.5 eV is about 1.8 $\times$ 10-18 m2 for the elastic scattering, and about 10-18 m2 for the momentum transfer. As for the electron-hydrogen ($\rm e^-+H$) collisions, the collision cross section  $\sigma_{\rm en}$ is also temperature dependent and the corresponding values can be found in the works of Bedersen & Kieffer (1971), and Zecca et al. (1996). At energies of 0.5 eV it is about 3.5 $\times$ 10-19 m2, so that for the elastic scattering we have $\sigma_{\rm in}/\sigma_{\rm en}\simeq 6$.

On the other hand, here we do not include the inelastic collisions that take place in a partially ionized plasma, like in the photosphere. It can be shown (Vranjes & Poedts 2006) that, in the photosphere, all ions in a unit volume are recombined many times per second. The three-body recombination (the process of the type  $\rm H^+ + e^- + e^-\rightarrow H + e^-$) is dominant in this region. At the altitude of h=500 km, the radiative recombination (the process described by ${\rm H^+ + e^-\rightarrow H} + h \nu$) and the three-body recombination are of the same order. At higher altitudes, the radiative recombination becomes the leading loss effect. At h=1000 km, it is by a factor 100 larger than the three-body recombination.

In addition, the charge exchange between the ionized and neutral hydrogen is frequent. The cross section (Krstic & Schultz 1999) for the proton-hydrogen charge exchange  $\sigma_{\rm ex}$ at the above given temperatures is about 5.6 $\times$ 10-19 m2, i.e., for hydrogen it is a large fraction ($\simeq$0.3) of the realistic elastic scattering cross section  $\sigma_{\rm in}$ given above. Note, however, that for some other gases, like He, Ne, and Ar, we have $\sigma_{\rm ex}> \sigma_{\rm in}$ (Raizer 1991), i.e., the charge exchange cross section exceeds the one for the elastic scattering. Consequently, due to the inelastic collisions and the charge exchange, neutrals/ions in the plasma spend a part of their time in the ionized/neutral state, respectively. As a result, the effective collision frequencies are expected to be even higher than the values that we shall use.

Using the data for a quiet Sun model (Vernazza et al. 1981), in Table 1 we summarize the values for the electron and proton elastic scattering collision frequencies at two altitudes (viz. h=0 km, and h=250 km) in the solar photosphere (see also Vranjes et al. 2007). Here, we have taken B0=10-2 T, the corresponding temperatures are respectively T=6420 K and T=4780 K, the electron number densities are n0=6.4 $\times$ 1019 m-3 and n0=2.7 $\times$ 1018 m-3, and the atomic hydrogen number densities are $n_{\rm n0}=1.17$ $\times$ 1023 m-3 and $n_{\rm n0}=2.3$ $\times$ 1022 m-3. We assume that the proton and electron number densities are equal. It is seen that both protons and electrons are un-magnetized. Note that in Table 1 the collision frequencies between the plasma species and neutrals are dominant for both electrons and ions, compared to the frequencies for Coulomb collisions between charged particles.

It is believed (Sen & White 1972; Priest 1987) that, due to the low temperature, the ions in the lower photosphere are in fact mainly metal ions. Sen & White (1972) have assumed that the mean mass of these metal ions is 35 au. In that case, due to the rather different masses of (metal) ions and neutral (hydrogen) atoms, in calculating the collision frequency it is appropriate to use a more accurate formula $\nu_{\rm mn}=n_{\rm n0}\sigma_{\rm mn} [m_{\rm n}/(m_{\rm m} + m_{\rm n})] [8 \kappa T_{\rm m}/(\pi \mu)]^{1/2}$, where the index m denotes the metal ion, n denotes the neutrals (hydrogen), and $\mu=m_{\rm m} m_{\rm n}/(m_{\rm m}+ m_{\rm n})$ is the reduced mass. The calculations may be inaccurate because the collision cross section  $\sigma_{\rm mn}$ is not known. As a guess, we take it as the value for protons multiplied by $m_{\rm m}/m_{\rm p}$. Taking the layer h=250 km, we find $\nu_{\rm mm}=6.4$ $\times$ 105 Hz, $\nu_{\rm mn} = 4$ $\times$ 108 Hz, and $\Omega_{\rm m}=2.7$ $\times$ 104 Hz. Comparing to protons from Table 1, the metal ions appear to be even less magnetized, i.e., $\Omega_{\rm m}/\nu_{\rm m} = 6.6$ $\times$ 10-5, where $\nu_{\rm m}=\nu_{\rm mm}+ \nu_{\rm mn}$. At h=0 km, we have $\nu_{\rm mm}=1.2$ $\times$ 107 Hz, $\nu_{\rm mn} = 2$ $\times$ 109 Hz, and $\Omega_{\rm m}/\nu_{\rm m}\simeq 1.3$ $\times$ 10-5. The mentioned uncertainty in determining $\sigma_{\rm mn}$ will clearly not substantially change the fact that the ions are un-magnetized.

3 Physical picture of Alfvén waves in a weakly ionized plasma

Following standard textbooks (e.g. Chen 1988), in the case of the shear Alfvén wave with $\vec B_0= B_0\vec e_z$, both ion and electron fluids oscillate in the direction of the perturbed magnetic field vector $\vec B_1=B_1 \vec e_y$. This is due to the $\vec E_1 \times \vec B_0$ drift, which separates neither charges nor masses, and the direction of the electric field is determined by the Faraday law. The wave is in fact sustained by the additional polarization drift $\vec v_{{\rm p}j}= (m_j/q_jB_0^2) \partial \vec E_1/\partial t$ and the consequent Lorentz force $j_x \vec e_x \times \vec B_0$, which is again in the y-direction and has a proper phase shift. Note that the polarization drift appears as a higher order term due to $\vert\partial/\partial t\vert\ll \Omega_{\rm i}$. It introduces the ion inertia effects and if it is neglected, then the Alfvén wave vanishes. The $\vec E\times \vec B$ term essentially describes the magnetic field frozen-in property of the plasma. The mode is fully described by the wave equation

 \begin{displaymath}% \nabla\times \nabla\times \vec E_1= \frac{\omega^2}{c^2} \vec E_1 + \frac{{\rm i} \omega}{\varepsilon_0 c^2} \vec j_1, \end{displaymath} (1)

the momentum equations for ions and electrons
 
$\displaystyle % m_{\rm i}n_{\rm i} \left[\frac{\partial \vec v_{\rm i}}{\partia... ..._{\rm n}) - m_{\rm i} n_{\rm i} \nu_{\rm ie} (\vec v_{\rm i} - \vec v_{\rm e}),$     (2)


 
$\displaystyle % m_{\rm e}n_{\rm e} \left[\frac{\partial \vec v_{\rm e}}{\partia... ..._{\rm n}) - m_{\rm e} n_{\rm e} \nu_{\rm ei} (\vec v_{\rm e} - \vec v_{\rm i}),$     (3)

and the corresponding equation for neutrals

 \begin{displaymath}% m_{\rm n}n_{\rm n} \left[\frac{\partial \vec v_{\rm n}}{\pa... ...m n} n_{\rm n}\nu_{\rm ne}(\vec v_{\rm n}\!-\!\vec v_{\rm e}). \end{displaymath} (4)

Usually, the viscosity may be omitted, and this is valid even for the neutrals. We note that the dynamic viscosity coefficient for the atomic hydrogen $\mu$for the layers h=0 and 250 km (with the temperatures T0=6420 K and T0=4780 K), can be taken (Vargaftik et al. 1996) as 6.5 $\times$ 10-5 Ns/m2 and 5.2 $\times$ 10-5 Ns/m2, respectively. The corresponding kinematic viscosity coefficient $\eta=\mu/(m_{\rm n}n_{\rm n})$ is 1.34 m2/s. The ratio  $\eta k^2/\nu_{\rm ni}$ for the wave-lengths of interest is very small and the viscosity effects appear negligible in spite of such a low ionization. Further, using the momentum conservation in the friction force terms yields $\nu_{\rm ni}=m_{\rm i} n_0 \nu_{\rm in}/(m_{\rm n} n_{\rm n0})$, and at h=250 km and for $m_{\rm i}=m_{\rm n}$ we obtain $\nu_{\rm ni}=3$ $\times$ 104 Hz. The thermal effects may also be omitted, as will be explained below.

In the absence of collisions, the response of a plasma to the magnetic and electric field perturbations is instantaneous, and a volume element of the plasma moves in the previously described manner. In such an ideal case, the energy flux of the Alfvén wave is given by

 \begin{displaymath}% F_{\rm id}=m_{\rm i} n_0 v_{\rm i}^2 c_{\rm a}/2. \end{displaymath} (5)

Here, $v_{\rm i}$ is the leading order $\vec E\times \vec B$ perturbed ion velocity. Its amplitude is given by $v_{\rm i}=E_1/B_0$. Using the Faraday law we have $E_1=\omega B_1/k$, hence $v_{\rm i}=c_{\rm a} B_1/B_0$. For the estimate only, we assume small perturbations of the magnetic field, viz. around $1 \%$ (a comment on larger perturbations will be given later on). For the parameters at h=250 km, this yields $c_{\rm a}=B_0/(\mu_0 n_{\rm i0} m_{\rm i})=1.3$ $\times$ 105 m/s. Consequently, the perturbed plasma (ion) velocity is $v_{\rm i}=10^{-2} c_{\rm a}=1.3$ $\times$ 103 m/s. The wave energy flux in the ideal case, and for $m_{\rm i}=m_{\rm p}$, becomes $F_{\rm id}=5.3$ $\times$ 102 J/(m2 s). Setting $m_{\rm i}=35 m_{\rm p}$ yields $F_{\rm id} \simeq 90$ J/(s m2).


  \begin{figure} \par\includegraphics[width=6.6cm,clip]{8274fig1.eps} \end{figure} Figure 1: Schematic presentation of the motion of a charged particle in non-magnetized plasma.
Open with DEXTER

Collisions may heavily alter the motion of the perturbed electron and ion fluids. The plasma response to the electromagnetic (Alfvén-type) perturbations in fully and weakly ionized plasmas is essentially different from various points of view. Here, we present some facts that should help in understanding the physics involved in the description of the Alfvén waves in the partially ionized plasmas, and in particular in the photosphere.

1.
From Eq. (2) we see that the ratio of the Lorentz and the friction forces (for predominant ion-neutral collisions and in the case of initially unperturbed neutrals), is $\Omega_{\rm i}/\nu_{\rm in}$. For the given photospheric plasma this is $\sim$1/103.

2.
The motion of an un-magnetized charged particle is depicted in Fig. 1. Arrows denote the tangential direction at the moment of collision when the particle switches to another gyro-orbit with a possibly different velocity (indicated by different gyro-radius). A collision occurs after a very tiny fraction (largely exaggerated here) of the gyro orbit has been traveled. According to the numbers from the Table 1, the particle trajectory along a gyro-orbit around one specific magnetic line is only about 1/103 part of the full circle. Hence, in the given case the path of the particle between two collisions is nearly a straight line, like in the case when the magnetic field is absent. In fact, the particle never makes a full rotation. The motion is similar in the fully ionized plasmas, however, there it is related to ion-ion collisions (i.e., viscosity, not to friction).

3.
Contrary to the case of fully ionized plasma where all particles in a volume element move together due to the given electric field while still colliding with each other, in the present case the collisions introduce a limitation. In the beginning only charged particles are supposed to move due to the applied electric field, while neutrals have a tendency to stay behind. If $\nu_{\rm in}\gg \Omega_{\rm i}, \omega$, each plasma particle collides many times within the theoretical gyro-rotation, or within the assumed wave oscillation.

4.
Contrary to the viscosity, which is of primary importance for short scale processes, the friction is more effective in the opposite limit, i.e., at smaller wave-numbers (and also at larger wave-periods) an ion is subject to larger number of collisions with neutrals within one oscillation period.
Below, we discuss the effects of collisions in detail. According to the presently widely accepted physical description of Alfvén waves in partially ionized plasmas (Kulsrud & Pierce 1969; Haerendel 1992; De Pontieu & Haerendel 1998; Pécseli & Engvold 2000), the effects of neutrals are the following: a) for a relatively small amount of neutrals (or for high frequency short wavelengths), the damping of the mode is proportional to the collision frequency $\nu_{\rm in}$, more collisions increases the friction (Kulsrud & Pierce 1969); and b) in a very weakly ionized plasma the collisions are numerous and the whole fluid moves together. In this case, the stronger the collisions the better locking of the gas-plasma fluid, and the damping of the wave (which is now proportional to $1/\nu_{\rm in}$) vanishes. The Alfvén velocity in such a mixture includes the total fluid density $m_{\rm i} n_{\rm i} + m_{\rm n} n_{\rm n}$. The dispersion equation of the Alfvén wave is, according to De Pontieu & Haerendel (1998):

\begin{eqnarray*}\frac{\omega}{k}=c_{\rm {\scriptscriptstyle A}}\left(1- {\rm i}... ...{[\mu_0 (m_{\rm i} n_{\rm i} + m_{\rm n} n_{\rm n})]^{1/2}}\cdot \end{eqnarray*}


Taking these statements as facts, here we suggest the following item to be added in order to complete the physical picture, thus c) the perturbed velocity of the gas-plasma mixture may be drastically reduced in a weakly ionized plasma (like the photosphere), and, consequently, the wave energy flux becomes very small.

To describe what happens in reality, we here assume the same magnitude of the magnetic field perturbation as in the ideal case discussed above, i.e., taking it as $1 \%$. Due to the perturbed magnetic field, there appears the electric field as described above, and the consequent ion motion in the same direction as the perturbed vector $\vec B_1$. We denote this perturbed $\vec E\times \vec B$-drift velocity of ions by $V_{\rm i}$. Note that this velocity is the same for electrons, and that we are speaking about fluid velocities. The relaxation velocity of neutrals and ions can be obtained from the following estimates (Milic 1970). Assume that in the starting moment the unit volume of the neutrals have a different velocity $V_{\rm n}$. In view of the huge difference in mass, we neglect electrons for simplicity. The collision frequency (see Table 1) is extraordinarily high, of the order of $\sim$109 Hz. Compare this with the theoretical gyro-frequency for ions $\Omega_{\rm i} \sim 10^{6}$ Hz. Knowing that the wave frequency must be much smaller, the frequency ordering that we have here is:

 \begin{displaymath}% \omega\ll \Omega_{\rm i}\ll \nu_{\rm i}. \end{displaymath} (6)

As a result, we can take the starting/maximal value of the ion velocity $V_{\rm i}$and estimate for the value it will take within the collisional time.

In view of the ordering (6), the time dependence of the velocities of the two fluids (ions and neutral) in relative motion, after the initial movement of the plasma due to electromagnetic perturbations has taken place (regardless of the origin of these perturbations), is determined mainly by the friction, and can be obtained from the following equations:

 \begin{displaymath}% \partial \vec v_{\rm n}/\partial t= \nu_{\rm ni} (\vec v_{\... ...i}/\partial t= \nu_{\rm in} (\vec v_{\rm n} - \vec v_{\rm i}). \end{displaymath} (7)

Simple combinations of these equations yield two integrals of motion:

\begin{eqnarray*}\nu_{\rm in} \vec v_{\rm n} \!+ \!\nu_{\rm ni} \vec v_{\rm i}\!... ...\! \vec V_{\rm i}\right) \exp~[-(\nu_{\rm in} + \nu_{\rm ni})t]. \end{eqnarray*}


This further yields

 \begin{displaymath}% \vec v_{\rm n}=\frac{\nu_{\rm in} \vec V_{\rm n} + \nu_{\rm... ...n}+ \nu_{\rm ni}} \cdot\exp~[-(\nu_{\rm in} + \nu_{\rm ni})t], \end{displaymath} (8)


 \begin{displaymath}% \vec v_{\rm i}=\frac{\nu_{\rm in} \vec V_{\rm n} + \nu_{\rm... ...n}+ \nu_{\rm ni}} \cdot\exp~[-(\nu_{\rm in} + \nu_{\rm ni})t]. \end{displaymath} (9)

It is seen that the two velocities relax very quickly towards the first term on the right-hand sides in these expressions. Taking $m_{\rm i}\sim m_{\rm n}$ and $\vec V_{\rm n}=0$, we obtain for the relaxed (common) velocity for both species

 \begin{displaymath}% v_{\rm c} = V_{\rm i}\frac{ \nu_{\rm ni}}{\nu_{\rm in} + \n... ...n_{\rm n0}}\simeq V_{\rm i} \frac{n_{\rm i0}}{n_{\rm n0}}\cdot \end{displaymath} (10)

Hence, if ions start to move due to the electromagnetic force caused by the wave, the strong friction will result in a common velocity, which i) is achieved very quickly, and ii) is much below the starting velocity of the ion fluid. This behavior is presented in Fig. 2 for the photospheric parameters at h=250 km.


  \begin{figure} \par\includegraphics[width=6.8cm,clip]{8274fig2.eps} \end{figure} Figure 2: Relaxation of the ion and neutral velocities (normalized to $v_{\rm c}=(\nu _{\rm in} V_{\rm n} + \nu _{\rm ni} V_{\rm i})/(\nu _{\rm in} + \nu _{\rm ni})$) due to collisions, for parameters appropriate for the solar photosphere. The initial velocities for neutrals and ions are respectively 0 and $1.3 \times 10^3$ m/s.
Open with DEXTER

Here, for the same perturbation of the magnetic field ($1 \%$), we have $v_{\rm c}=1.15$ $\times$ $10^{-4} V_{\rm i}=0.15$ m/s. Compare this to the velocity in the ideal case $V_{\rm i}=1.3$ $\times$ 103 m/s. Note also that both $V_{\rm i}$ and $v_{\rm c}$ are below/much below the sound velocity $c_{\rm s}=8.9$ $\times$ 103 m/s, respectively. Hence, neglecting the pressure (compressibility) effects is justified. Because $v_{\rm c}$ is so small, in Fig. 2 we normalize velocities to $v_{\rm c}$ and give the plot for $v_{\rm n}$ and $1/v_{\rm i}$. It is seen that the velocities of both neutrals and ions relax towards the same (normalized) value (=1) within a time interval that is many orders of magnitude shorter than the wave oscillation period. As a result, using (5), we have the flux in the weakly ionized plasma (for $m_{\rm i}=m_{\rm p}$) given by

 \begin{displaymath}% F=\frac{1}{2} (m_{\rm i} n_{\rm i} + m_{\rm n} n_{\rm n}) c... ...}}{m_{\rm i} n_{\rm i}+ m_{\rm n} n_{\rm n}}\right)^{3/2}\cdot \end{displaymath} (11)

For the given parameters in the photosphere this gives

 \begin{displaymath}% F\simeq 10^{-6}\cdot F_{\rm id}=5.3 \times 10^{-4} ~~{\rm J/( m^2s)}. \end{displaymath} (12)

It is seen that the actual flux is always small for any realistic amplitude of perturbations. For example, even taking exceptionally strong magnetic field perturbations, e.g. B1=B0, yields $F\simeq 5$ J/(m2s). Consequently, regardless of the physical mechanism for eventual excitation of the Alfvén waves in the photosphere, the expected amplitude of the perturbed velocity is of the order of 0.1 m/s, and the energy flux of the waves is about one million times smaller than the one obtained from the ideal models that assume a perfect coupling between the plasma and magnetic field (i.e., ignoring the effects of collisions between ions and neutrals, and the consequent weak magnetization of plasma species).

The estimated flux presented above is obtained for $m_{\rm i}=m_{\rm p}$. Taking the more realistic value $m_{\rm i}=35 m_{\rm p}$ (Sen & White 1972), we obtain only F=0.02 J/(m2 s). Assuming in addition a stronger magnetic perturbation of $10 \%$, we obtain F=2 J/(m2 s) and the common velocity amplitude $v_{\rm c}\simeq 9$ m/s. The actual flux may have larger values, e.g., due to stronger magnetic field perturbations, but the linear wave theory then becomes unapplicable.

Since the electromagnetic force still acts on the plasma volume in the time interval $ \nu_{\rm in}^{-1}$, after the initial movement of the plasma has taken place, one could claim that the flux may be higher. Yet, in view of the frequency ordering (6), which implies a difference of many orders of magnitude, the inclusion of this additional electromagnetic effect in Eq. (7) is insignificant. In fact, it is questionable and indeed unlikely that the ions can really achieve the assumed starting perturbed velocity  $\vec V_{\rm i}$ in the first place. This is because the assumed value for $\vec V_{\rm i}$ follows from the ideal case discussed above, with time and spatial scales determined by $\omega^{-1}$ and k-1, respectively, resulting in the characteristic velocity $c_{\rm a}$, while in the collisional case that we have here, these scales are determined by $ \nu_{\rm in}^{-1}$ and $\kappa_{\rm f}^{-1}$, where $\kappa_{\rm f}^{-1}=v_{\scriptscriptstyle{T}{\rm i}}/\nu_{\rm in}$ is the ion mean free path. Hence, the characteristic velocity that now appears instead of $c_{\rm a}$ is $v_{\scriptscriptstyle{T}{\rm i}}=(\kappa T_{\rm i}/m_{\rm i})^{1/2}$ and it is about 2 orders of magnitude lower than $c_{\rm a}$, and a realistic flux should be even smaller than the value obtained earlier. One could also argue that the case discussed above, $\vec V_{\rm n}=0$, may look the least favorable for the propagation of the wave because neutrals are initially usually in the state of motion. Clearly this does not change anything, because in this case, due to the strong collisions, the ions will nearly be in the same state of motion (see in the Sect. 4 below), while the ion velocity $\vec V_{\rm i}$ would still describe an access ion momentum obtained due to the electromagnetic perturbation, which neutrals initially do not take part in.

4 Discussion

Standard estimates of the wave energy flux through the solar photosphere assume a plasma velocity in the photosphere of the order of 1 km s-1. This implies two effects: that plasma particles move with the observed speed of the convective motion, and that the motion of plasma species involves the magnetic field perturbations due to frozen-in magnetic field effect. The first effect is only partly satisfied. If in the equilibrium neutrals move perpendicular to the magnetic field, say in the x-direction, the plasma particles will move also due to the friction effect. The induced velocities of ions and electrons can be calculated from Eqs. (2) and (3) reading

 \begin{displaymath}% \vec v_{{\rm i}\bot 0} = \alpha_{\rm i}\left( -\frac{\nu_{{... ...c{\nu_{{\rm in}}^2}{\Omega_{\rm i}^2} \vec v_{n\bot 0}\right), \end{displaymath} (13)

and
 
$\displaystyle % \vec v_{{\rm e}\bot 0} = \alpha_{\rm e}\left( \frac{\nu_{{\rm e... ...ac{\nu_{{\rm ei}} \nu_{\rm e}}{\Omega_{\rm e}^2} \vec v_{{\rm i}\bot 0}\right),$     (14)

where

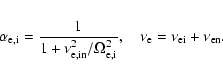
\begin{eqnarray*}\alpha_{\rm e, i}= \frac{1}{1+ \nu_{\rm e, in}^2/\Omega_{\rm e, i}^2}, \quad \nu_{\rm e}= \nu_{{\rm ei}} + \nu_{{\rm en}}. \end{eqnarray*}


The ion drag velocity (in the x-direction) and the drift component (in the y-direction) become, respectively,

 \begin{displaymath}% v_{\rm i0,~ drag}=v_{{\rm i}x0}=\frac{1}{1 + \Omega_{\rm i}^2/\nu_{{\rm in}}^2} v_{{\rm n}x0}, \end{displaymath} (15)

and

 \begin{displaymath}% v_{\rm i0, drift}=v_{{\rm i}y0}= -\frac{\nu_{{\rm in}}}{\Om... ...}^2}=-\frac{\Omega_{\rm i}}{\nu_{{\rm in}}} v_{\rm i0,~ drag}. \end{displaymath} (16)

The corresponding electron components are

 \begin{displaymath}% v_{\rm e0,~ drag}\!=\! v_{{\rm e}x0}\!=\!\alpha_{\rm e} v_{... ...\! \frac{\Omega_{\rm i}^2}{\nu_{\rm in}^2}\right)^{-1}\right], \end{displaymath} (17)

and

 \begin{displaymath}% v_{\rm e0,~ drift}=v_{{\rm e}y0}\!=\! \alpha_{\rm e} v_{{\r... ...frac{\Omega_{\rm i}^2}{\nu_{\rm in}^2}\right)^{-1}\right]\cdot \end{displaymath} (18)

The induced ion and electron velocities are not necessarily equal, implying the presence of equilibrium currents. For the same parameters used in Table 1 and taking the neutral velocity of 500 m/s, at h=250 km we have the drag and drift velocities for electrons 315 and 240 m/s, respectively. The ion drag velocity is almost equal to the neutral velocity. This is all due to the fact that the plasma particles are un-magnetized, $\Omega_{\rm i}/\nu_{\rm i}=3.6$ $\times$ 10-3, $\Omega_{\rm e}/\nu_{\rm e}=0.76$. However, due to the same reason the frozen-in condition is far from reality and the ion/electron motion perpendicular to the magnetic lines does not necessarily involve the appropriate movement of the magnetic lines. The actual motions develops as described in the previous section.

Table 2: Parameters of waves (wave-lengths $\lambda $ in km and frequencies in Hz) propagating through the chromosphere for two different altitudes h (in km).

In view of the item b) discussed in Sect. 3 (Kulsrud & Pierce 1969), such an upwards propagating wave is very weakly damped in the photosphere (the damping is proportional to $1/\nu_{\rm in})$. This holds provided that the wavelengths exceed a certain minimal value. However, it will in fact be more strongly damped in the upper layers, e.g., in the chromosphere where the amount of neutrals decreases but the damping is proportional to $\nu_{\rm in}$. For the chromosphere this can be directly demonstrated by solving the dispersion equation that follows from (1) where the perpendicular currents are calculated from Eqs. (2)-(4). The expressions are very lengthy and we shall not give them here.

As an example, assuming the wave propagating towards the chromosphere, the dispersion equation is solved for several wavelengths $\lambda $, with all collision frequencies included, at the altitude h=1065 km where (Vernazza et al. 1981) T=6040 K, $n_{\rm n0}=1.71$ $\times$ 1019 /m3, and n0= 9.35 $\times$ 1016 /m3, and at the altitude h=1990 km where T=7160 K, $n_{\rm n0}= 10^{17}$ /m3, and n0= 3.9 $\times$ 1016 /m3. The results are given in Table 2. It is seen that shorter wavelengths are more damped at lower altitudes. In the same time, longer wavelengths (i.e., those that are presumably better transmitted by the photosphere) are in fact more damped at higher altitudes. This mode behavior is in agreement with the model of Kulsrud & Pierce (1969). However, this trend certainly can not continue because neutrals vanish at still higher altitudes.

We stress that the equilibrium parameters change with the altitude and for the large wavelengths the model becomes violated. A numerical approach should give more reliable results. Such an approach could help explain how and where the Alfvén waves, that were recently detected in the chromosphere (De Pontieu et al. 2007), are generated.

Our analysis is based on the presence of a temperature minimum in which most of the plasma is neutral, which is predicted by hydrostatic models averaged in space and time, such as VAL and FAL. If flux tubes for some reason lack this temperature minimum, the analysis we present here may not be an accurate description of how Alfven waves are generated in the photosphere.

5 Conclusions

The physics of a multi-component weakly ionized plasma, like the one in the solar photosphere, is highly complex. Various aspects of this complexity have been pointed out in Sects. 2-4. For a temperature of about 0.5 eV, typical for the photosphere, there is a plethora of processes that take place and that are nontrivial to include in an analytical work like the one presented here. Among others, these include the elastic and inelastic collisions, the charge exchange being an important sort of the latter, which imply the creation and loss of plasma particles. Yet, in spite of that, some conclusions regarding the importance of the electromagnetic Alfvén-type perturbations in such weakly ionized environments can be made with some certainty. The important conclusion is that if we assume Alfvén-type waves generated around the temperature minimum, in fact their amplitudes are such that the wave energy flux is very small. The main reason for this is ion collisions, which are so frequent that ions almost do not feel the effects of the magnetic field. As seen from Fig. 1, in such an environment the ion motion is very similar to the Brownian motion of atoms and molecules in a gas. The physics presented here should be taken into account in the estimates of the role of the Alfvén waves generated in the solar photosphere in coronal heating scenarios. However, the solar photosphere is only a thin plasma layer and the parameters in the solar atmosphere change with the altitude and so does the physics of the Alfvén waves. Our analysis suggests that if these waves are generated below the chromosphere, they cannot probably be generated around the temperature minimum, but perhaps would have to come from lower down, i.e., below the surface where the plasma is again much more ionized and the ion-neutral collisions are not significant.

Acknowledgements
These results are obtained in the framework of the projects G.0304.07 (FWO-Vlaanderen), C 90203 (Prodex), GOA/2004/01 (K.U.Leuven), and the Interuniversity Attraction Poles Programme - Belgian State - Belgian Science Policy.

References

 
Copyright ESO 2008