A&A 478, L27-L30 (2008)
DOI: 10.1051/0004-6361:20078200
LETTER TO THE EDITOR
Is there a need and another way to measure the cosmic microwave
background temperature more accurately?
J. Chluba1 - R. A. Sunyaev1,2
1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1,
85741 Garching bei München, Germany
2 -
Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32,
117997 Moscow, Russia
Received 2 July 2007 / Accepted 4 December 2007
Abstract
The recombination history of the Universe depends exponentially on
the temperature, T0, of the cosmic microwave background. Therefore tiny
changes of T0 are expected to lead to significant changes in the
free electron fraction.
Here we show that even the current 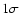 -uncertainty in the
value of T0 results in more than half a percent ambiguity in the
ionization history, and more than
-uncertainty in the
value of T0 results in more than half a percent ambiguity in the
ionization history, and more than 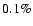 uncertainty in the TT and EE power spectra at small angular scales.
We discuss how the value of T0 affects the highly redshifted cosmological
hydrogen recombination spectrum and demonstrate that T0 could, in
principle, be measured by looking at the low frequency distortions of the
cosmic microwave background spectrum. For this no absolute measurements are
necessary, but sensitivities on the level of
uncertainty in the TT and EE power spectra at small angular scales.
We discuss how the value of T0 affects the highly redshifted cosmological
hydrogen recombination spectrum and demonstrate that T0 could, in
principle, be measured by looking at the low frequency distortions of the
cosmic microwave background spectrum. For this no absolute measurements are
necessary, but sensitivities on the level of  30 nK are required to
extract the quasi-periodic frequency-dependent signal with typical
30 nK are required to
extract the quasi-periodic frequency-dependent signal with typical
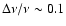 coming from cosmological recombination.
We also briefly mention the possibility of obtaining additional
information on the specific entropy of the Universe, and other cosmological
parameters.
coming from cosmological recombination.
We also briefly mention the possibility of obtaining additional
information on the specific entropy of the Universe, and other cosmological
parameters.
Key words: cosmology: cosmic microwave background - cosmology: theory - cosmology: cosmological parameters
1 Introduction
The recombination history of the Universe (Seager et al. 1999,2000; Peebles 1968; Zeldovich et al. 1968) depends exponentially on the exact value of
T0 (Sunyaev & Zeldovich 1970). Therefore one expects that tiny changes of T0lead to significant modifications of the ionization history.
The temperature of the cosmic microwave background (CMB) was measured with
tremendously high accuracy using the C OBE/F IRAS instrument:
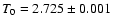 K (Fixsen & Mather 2002) or
K (Fixsen & Mather 2002) or
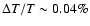 ,
where 1 mK is the
,
where 1 mK is the 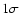 -error, or
-error, or
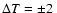 mK at
95% confidence (Mather et al. 1999).
This value is based on the results obtained with the C OBE/F IRAS and
the quoted uncertainties from other methods, e.g. by measuring the CMB
dipole anisotropy with the C OBE/D MR instrument:
mK at
95% confidence (Mather et al. 1999).
This value is based on the results obtained with the C OBE/F IRAS and
the quoted uncertainties from other methods, e.g. by measuring the CMB
dipole anisotropy with the C OBE/D MR instrument:
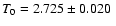 K (Kogut et al. 1996) or its slightly improved value
K (Kogut et al. 1996) or its slightly improved value
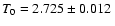 K (Mather et al. 1999), are much larger, yielding
K (Mather et al. 1999), are much larger, yielding
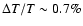 and
and
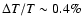 respectively. Also within the
C OBE/F IRAS instrument a systematic difference of
respectively. Also within the
C OBE/F IRAS instrument a systematic difference of
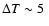 mK arose due
to readout current heating (Mather et al. 1999), which was only understood
later (Fixsen & Mather 2002; Fixsen et al. 1996; Mather et al. 1999). The main goal of the
present paper is to demonstrate that even changes of the order of a few mK
lead to percent-level corrections in the ionization history, and that in
principle there may be another indirect, but potentially accurate way
to measure the CMB monopole temperature using the cosmological
recombination spectrum coming from redshifts
mK arose due
to readout current heating (Mather et al. 1999), which was only understood
later (Fixsen & Mather 2002; Fixsen et al. 1996; Mather et al. 1999). The main goal of the
present paper is to demonstrate that even changes of the order of a few mK
lead to percent-level corrections in the ionization history, and that in
principle there may be another indirect, but potentially accurate way
to measure the CMB monopole temperature using the cosmological
recombination spectrum coming from redshifts
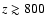 .
.
The impact of the uncertainty in the CMB monopole temperature on the
CMB angular power spectra was addressed well before the era of precision
cosmology (Hu et al. 1995) with the conclusion that the corresponding
theoretical error is below 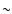
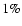 .
However, the great success in observations of the CMB temperature and
polarization anisotropies (Page et al. 2006; Hinshaw et al. 2006) renders this level of
uncertainty insufficient for the analysis and interpretation of future
CMB data, which will become available after the launch of the P LANCK
Surveyor
.
However, the great success in observations of the CMB temperature and
polarization anisotropies (Page et al. 2006; Hinshaw et al. 2006) renders this level of
uncertainty insufficient for the analysis and interpretation of future
CMB data, which will become available after the launch of the P LANCK
Surveyor![[*]](/icons/foot_motif.gif) , or with C MBPOL.
As explained in Seljak et al. (2003), the ultimate goal is to achieve
, or with C MBPOL.
As explained in Seljak et al. (2003), the ultimate goal is to achieve 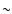
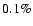 accuracy for the theoretical prediction of the CMB power spectra.
In particular when discussing the imprints of different inflationary
models on the power spectra, or when obtaining estimates of the key
cosmological parameters that reach sub-percent accuracy, this precision
becomes necessary.
accuracy for the theoretical prediction of the CMB power spectra.
In particular when discussing the imprints of different inflationary
models on the power spectra, or when obtaining estimates of the key
cosmological parameters that reach sub-percent accuracy, this precision
becomes necessary.
Currently, in this context the largest uncertainty is considered to be due to
our understanding of the epoch of cosmological recombination
(e.g. Seljak et al. 2003).
This fact has recently motived several studies on high precision computations
of the cosmological hydrogen (Chluba et al. 2007; Dubrovich & Grachev 2005; Chluba & Sunyaev 2006b; Kholupenko & Ivanchik 2006; Chluba & Sunyaev 2007a,b; Rubiño-Martín et al. 2006), and helium (Switzer & Hirata 2007b; Kholupenko et al. 2007; Hirata & Switzer 2007; Wong & Scott 2007; Rubino-Martin et al. 2007; Switzer & Hirata 2007a) recombination history.
All the discussed additional physical processes lead to 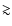
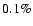 level
corrections of the ionization history, which also partially cancel each other.
The overall theoretical uncertainty in the CMB temperature and polarization
power spectra, in particular at large l, still exceeds the level of
level
corrections of the ionization history, which also partially cancel each other.
The overall theoretical uncertainty in the CMB temperature and polarization
power spectra, in particular at large l, still exceeds the level of 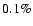 .
Here we show that the current
.
Here we show that the current 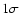 -error in the value of
T0 also yields more than
-error in the value of
T0 also yields more than 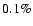 uncertainty in the TT and EEpower spectra.
uncertainty in the TT and EEpower spectra.
During the epoch of cosmological hydrogen recombination, roughly 5 photons are
emitted per recombined hydrogen atom (Chluba & Sunyaev 2006a). As realized earlier
(e.g. see Dubrovich & Grachev 2004; Burgin 2003; Bernshtein et al. 1977; Dubrovich & Stolyarov 1995; Kholupenko et al. 2005; Dubrovich 1975; Peebles 1968; Zeldovich et al. 1968), the amount of these
photons and their spectral distribution also depends on the parameters of the
Universe.
Here we demonstrate that for the cosmological recombination spectrum the
dependence on the CMB monopole temperature, T0, the total amount
of baryons,
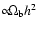 ,
and the abundance ratio of helium to
hydrogen,
,
and the abundance ratio of helium to
hydrogen, 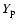 ,
are likely to be most important.
Basing our analysis on the code developed in Rubiño-Martín et al. (2006) and
Chluba et al. (2007), we illustrate that in principle, by measuring the
cosmological recombination spectrum in the decimeter spectral band, one should
be able to determine the value of T0.
Most importantly, for this no absolute measurements are necessary, but
sensitivities on the level of 30 nK are required to extract the
quasi-periodic signal with typical
,
are likely to be most important.
Basing our analysis on the code developed in Rubiño-Martín et al. (2006) and
Chluba et al. (2007), we illustrate that in principle, by measuring the
cosmological recombination spectrum in the decimeter spectral band, one should
be able to determine the value of T0.
Most importantly, for this no absolute measurements are necessary, but
sensitivities on the level of 30 nK are required to extract the
quasi-periodic signal with typical
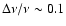 coming from
cosmological recombination.
For observations of the CMB angular fluctuations, a sensitivity level of
10 nK in principle can be achieved (Readhead 2007). However, here the
same signal is coming from every direction on the sky. Therefore one may use
wide-angle horns, so that one is dealing with a huge flux of
photons, carefully selecting regions on the sky that are cleanest with respect
to foreground signals.
coming from
cosmological recombination.
For observations of the CMB angular fluctuations, a sensitivity level of
10 nK in principle can be achieved (Readhead 2007). However, here the
same signal is coming from every direction on the sky. Therefore one may use
wide-angle horns, so that one is dealing with a huge flux of
photons, carefully selecting regions on the sky that are cleanest with respect
to foreground signals.
![\begin{figure}
\par\includegraphics[width=8.8cm]{eps/8200fig1.eps}
\end{figure}](/articles/aa/full/2008/05/aa8200-07/Timg25.gif) |
Figure 1:
Ambiguity in the ionization history due to uncertainty in the value
of T0. We changed
T0=2.725 K by 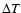 as labeled. All the other
parameters were not altered.
as labeled. All the other
parameters were not altered. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm]
{eps/8200fig2.eps}\\
\includegraphics[width=8.5cm]
{eps/8200fig3.eps}
\end{figure}](/articles/aa/full/2008/05/aa8200-07/Timg26.gif) |
Figure 2:
Ambiguity in the temperature ( top panel) and E-mode
polarization (lower panel) power spectra due to uncertainty in the value of
T0. We changed
T0=2.725 K by 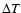 as labeled. All the other
parameters were not modified.
as labeled. All the other
parameters were not modified. |
| Open with DEXTER |
2 Effect on the free electron fraction and CMB power spectra
To study how the uncertainty in the value of T0 affects the ionization
history and CMB temperature and polarization power spectra, we used the
C MBEASY code (Doran 2005). We ran our computations for a flat
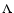 CDM cosmological concordance model
(Bennett et al. 2003)
with
T0=2.725 K,
CDM cosmological concordance model
(Bennett et al. 2003)
with
T0=2.725 K,
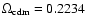 ,
,
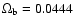 ,
h=0.71 and
,
h=0.71 and
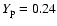 .
.
In Fig. 1 we show the uncertainty in the free electron fraction,
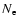 .
As expected, a slightly higher value of T0 delays recombination, while a
smaller value shifts the time of recombination towards higher redshifts.
Even for
.
As expected, a slightly higher value of T0 delays recombination, while a
smaller value shifts the time of recombination towards higher redshifts.
Even for
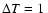 mK, the change in the ionization history exceeds half a
percent at
mK, the change in the ionization history exceeds half a
percent at 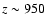 .
This shows that due to the exponential dependence of
.
This shows that due to the exponential dependence of
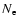 on T0 (Sunyaev & Zeldovich 1970) a tiny error of
on T0 (Sunyaev & Zeldovich 1970) a tiny error of
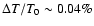 is amplified by more than one order of magnitude.
The maximal change in the free electron fraction roughly scales as
is amplified by more than one order of magnitude.
The maximal change in the free electron fraction roughly scales as
![$\Delta
N_{\rm e}/N_{\rm e}\approx 15~\Delta T/T_0\approx 0.55\% \times [\frac{\Delta
T}{1{\rm mK}}]$](/articles/aa/full/2008/05/aa8200-07/img35.gif) for
for
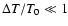 .
.
In Fig. 2 we show the corresponding uncertainty in the TT and
EE power spectra. At large scales, the positions of the first peaks are
slightly shifted, while at small scales (
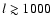 ), the actual
modifications due to photon diffusion (Silk 1968) dominate. For earlier
recombination (
), the actual
modifications due to photon diffusion (Silk 1968) dominate. For earlier
recombination (
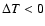 ), more power is left in the TT power-spectrum
at small scales. On the other hand the amplitude of the E-mode polarization
is lower, likely due to less scattering off moving electrons.
In both cases the uncertainty is several times smaller than for the ionization
history: even for
), more power is left in the TT power-spectrum
at small scales. On the other hand the amplitude of the E-mode polarization
is lower, likely due to less scattering off moving electrons.
In both cases the uncertainty is several times smaller than for the ionization
history: even for
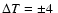 mK, where
mK, where
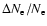 exceeds 2% close to its maximum, the power spectra are affected by less than
a percent at
exceeds 2% close to its maximum, the power spectra are affected by less than
a percent at
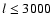 .
For the TT power spectrum one has
.
For the TT power spectrum one has
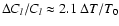 at
at 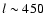 and
and
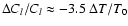 at
at
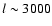 .
Similarly for the EE power spectrum one finds
.
Similarly for the EE power spectrum one finds
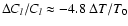 at
at 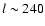 and
and
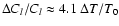 at
at
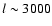 .
.
The relative change is growing towards larger l, but at
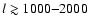 the signals connected with clusters of galaxies
(Sunyaev & Zeldovich 1972,1970; and e.g. Springel et al. 2001; Schäfer et al. 2006), weak lensing,
foregrounds, and (especially at high frequencies) S CUBA sources
(Haiman & Knox 2000) and starforming, merging, dusty galaxies (Righi et al. 2007)
will start to be more important.
Still, at
the signals connected with clusters of galaxies
(Sunyaev & Zeldovich 1972,1970; and e.g. Springel et al. 2001; Schäfer et al. 2006), weak lensing,
foregrounds, and (especially at high frequencies) S CUBA sources
(Haiman & Knox 2000) and starforming, merging, dusty galaxies (Righi et al. 2007)
will start to be more important.
Still, at
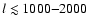 the multi-l comparison of the observed CMB
power spectra with the predicted theoretical mean model over a wide
range of angular scales makes the discussed changes potentially
important once systematic and statistical errors decrease with the
improvements achieved using future CMB experiments.
Furthermore, the effect under discussion has a similar order of magnitude as
the corrections due to previously neglected physical processes (see
Introduction), so it should be included in the list of mechanisms that lead to
small modifications in the ionization history and CMB power spectra.
the multi-l comparison of the observed CMB
power spectra with the predicted theoretical mean model over a wide
range of angular scales makes the discussed changes potentially
important once systematic and statistical errors decrease with the
improvements achieved using future CMB experiments.
Furthermore, the effect under discussion has a similar order of magnitude as
the corrections due to previously neglected physical processes (see
Introduction), so it should be included in the list of mechanisms that lead to
small modifications in the ionization history and CMB power spectra.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]
{eps/8200fig4.eps}
\end{figure}](/articles/aa/full/2008/05/aa8200-07/Timg51.gif) |
Figure 3:
Dependence of the bound-bound recombination spectrum on the value of
T0. We chose a large value for 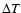 in order to illustrate the
effect. All the other cosmological parameters remained unchanged. The
results are based on computations including 50 shells for the hydrogen atom
(see Rubiño-Martín et al. 2006 and Chluba et al. 2007, for computational details).
The whole recombination spectrum is shifted along the frequency axis, but
the overall normalization is not affected.
in order to illustrate the
effect. All the other cosmological parameters remained unchanged. The
results are based on computations including 50 shells for the hydrogen atom
(see Rubiño-Martín et al. 2006 and Chluba et al. 2007, for computational details).
The whole recombination spectrum is shifted along the frequency axis, but
the overall normalization is not affected. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]
{eps/8200fig5.eps}\\
\includegraphics[width=8.7cm,clip]
{eps/8200fig6.eps}\end{figure}](/articles/aa/full/2008/05/aa8200-07/Timg52.gif) |
Figure 4:
Dependence of the bound-bound recombination spectrum on the number of
hydrogen nuclei,
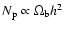 .
In the upper panel we
varied h, but fixed .
In the upper panel we
varied h, but fixed
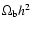 and
and
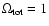 ,
while in
the lower panel we changed ,
while in
the lower panel we changed
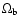 keeping h and
keeping h and
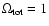 fixed.
All results are based on computations including 50 shells for the hydrogen
atom (see Rubiño-Martín et al. 2006 and Chluba et al. 2007, for computational
details).
fixed.
All results are based on computations including 50 shells for the hydrogen
atom (see Rubiño-Martín et al. 2006 and Chluba et al. 2007, for computational
details). |
| Open with DEXTER |
3 Dependence of the recombination spectrum on different cosmological parameters
In this section we illustrate the impact of different
cosmological parameters on the hydrogen recombination spectrum. We restrict
ourselves to the bound-bound emission spectrum and included 50 shells for the
hydrogen atom into our computations. A more rigorous investigation is in
preparation, however, the principle conclusions should not be affected.
In Fig. 3 we illustrate the dependence of the hydrogen
recombination spectrum on the value of T0.
The value of T0 mainly defines the time of recombination, and consequently
when most of the emission in each transition appears. This leads to a
dependence of the line positions on T0, but the total intensity in each
transition (especially at frequencies
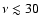 GHz) remains
practically the same. The fractional shift of the low frequency
spectral features along the frequency axis scales roughly as
GHz) remains
practically the same. The fractional shift of the low frequency
spectral features along the frequency axis scales roughly as
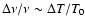 .
Hence
.
Hence
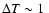 mK implies
mK implies
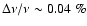 or
or
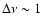 MHz at 2 GHz.
Since the maxima and minima of the line features due to the large duration of
recombination are rather broad (
MHz at 2 GHz.
Since the maxima and minima of the line features due to the large duration of
recombination are rather broad (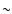
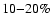 ), it is probably better to look
for these shifts close to the steep parts of the lines, where the derivatives
of the spectral distortion due to hydrogen recombination are largest.
It is also important to mention that the hydrogen recombination spectrum is
shifted as a whole, allowing to increase the significance of a
measurement by considering many spectral features at several frequencies.
), it is probably better to look
for these shifts close to the steep parts of the lines, where the derivatives
of the spectral distortion due to hydrogen recombination are largest.
It is also important to mention that the hydrogen recombination spectrum is
shifted as a whole, allowing to increase the significance of a
measurement by considering many spectral features at several frequencies.
The upper panel of Fig. 4 shows that at low frequencies the
cosmological hydrogen recombination spectrum is practically independent of the
value of h. Only the features due to the Lyman, Balmer, Paschen and
Brackett series are slightly modified.
This is connected to the fact that h affects the ratio of the atomic time
scales to the expansion time. Therefore changing h affects the escape rate
of photons in the Lyman-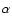 transition and the relative importance of
the 2s-1s transition. For transitions among highly excited states it is not
crucial via which channel the electrons finally reach the ground state of
hydrogen and hence the modifications of the recombination spectrum at low
frequencies due to changes of h are small.
Changes of
transition and the relative importance of
the 2s-1s transition. For transitions among highly excited states it is not
crucial via which channel the electrons finally reach the ground state of
hydrogen and hence the modifications of the recombination spectrum at low
frequencies due to changes of h are small.
Changes of
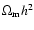 should affect the recombination spectrum for
the same reason.
should affect the recombination spectrum for
the same reason.
The lower panel in Fig. 4 illustrates the dependence of the
hydrogen recombination spectrum on
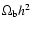 .
The total
number of photons released during hydrogen recombination is directly
related to the total number of hydrogen nuclei (e.g. Chluba & Sunyaev 2006a).
Therefore one expects that the overall normalization of the recombination
spectrum depends on the total number of baryons,
.
The total
number of photons released during hydrogen recombination is directly
related to the total number of hydrogen nuclei (e.g. Chluba & Sunyaev 2006a).
Therefore one expects that the overall normalization of the recombination
spectrum depends on the total number of baryons,
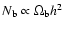 ,
and the helium to hydrogen abundance ratio,
,
and the helium to hydrogen abundance ratio,
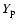 .
Varying
.
Varying
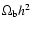 indeed leads to a change in the overall
amplitude
indeed leads to a change in the overall
amplitude
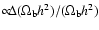 .
Similarly, changes of
.
Similarly, changes of 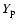 would affect the normalization of the
hydrogen recombination spectrum, however it is important to also
take the helium recombination spectrum into account.
Changing
would affect the normalization of the
hydrogen recombination spectrum, however it is important to also
take the helium recombination spectrum into account.
Changing 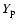 will affect the relative contribution of the helium to
the hydrogen recombination spectrum. Since the physics of helium
recombination is different than in the case of hydrogen (e.g. the spectrum
of neutral helium is more complicated; helium recombination occurs at
earlier times, when the medium was hotter;
will affect the relative contribution of the helium to
the hydrogen recombination spectrum. Since the physics of helium
recombination is different than in the case of hydrogen (e.g. the spectrum
of neutral helium is more complicated; helium recombination occurs at
earlier times, when the medium was hotter;
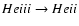 is more rapid, so the recombination
lines are narrower
is more rapid, so the recombination
lines are narrower![[*]](/icons/foot_motif.gif) ), one can
expect to find direct evidence of the presence of helium in the full
recombination spectrum. These might be used to quantify the total amount of
helium during the epoch of recombination, well before the first appearance
of stars.
), one can
expect to find direct evidence of the presence of helium in the full
recombination spectrum. These might be used to quantify the total amount of
helium during the epoch of recombination, well before the first appearance
of stars.
4 Discussion and conclusions
In Sect. 2 we have shown that the 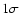 -error in
the exact value of T0 leads to more than half a percent ambiguity in the
recombination history, resulting in more than
-error in
the exact value of T0 leads to more than half a percent ambiguity in the
recombination history, resulting in more than 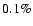 uncertainty in the TTand EE power spectra. In the analysis of future CMB data one can easily
include this additional source of uncertainty by considering the value
of T0 as a well-constrained free parameter.
uncertainty in the TTand EE power spectra. In the analysis of future CMB data one can easily
include this additional source of uncertainty by considering the value
of T0 as a well-constrained free parameter.
It is clear that at the 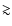
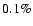 level, the uncertainties in the helium
abundance ratio,
level, the uncertainties in the helium
abundance ratio, 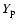 ,
and the effective number of neutrinos,
,
and the effective number of neutrinos,
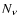 ,
should also be considered (e.g. Cyburt 2004; Steigman 2006; Olive & Steigman 1995; Hu et al. 1995). In particular the value of
,
should also be considered (e.g. Cyburt 2004; Steigman 2006; Olive & Steigman 1995; Hu et al. 1995). In particular the value of 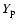 has a strong impact, directly affecting the peak of the Thomson
visibility function (Sunyaev & Zeldovich 1970) due to the dependence of the number
of hydrogen nuclei,
has a strong impact, directly affecting the peak of the Thomson
visibility function (Sunyaev & Zeldovich 1970) due to the dependence of the number
of hydrogen nuclei, 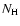 ,
for a fixed number of baryons, on the
helium abundance ratio (
,
for a fixed number of baryons, on the
helium abundance ratio (
![$N_{\rm H} \propto [1-Y_{\rm p}]$](/articles/aa/full/2008/05/aa8200-07/img67.gif) ).
It is important to mention that the effects connected with the angular
fluctuations of the CMB temperature (
).
It is important to mention that the effects connected with the angular
fluctuations of the CMB temperature (
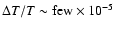 ), as observed with C OBE and W MAP, is expected to be one
order of magnitude smaller.
), as observed with C OBE and W MAP, is expected to be one
order of magnitude smaller.
In Sect. 3 we discussed the dependence of the cosmological
hydrogen recombination spectrum on different cosmological parameters. We have
illustrated that changes in the value of the CMB temperature, T0, lead to
an overall shift of the hydrogen recombination spectrum along the frequency
axis, leaving the total normalization practically unchanged. On the other hand
changes of the total amount of baryons, 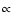
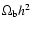 ,
mainly
affects the amplitude of the recombination signal.
This in principle should allow measurement of both parameters separately.
However, a more detailed analysis is required, also including the lines from
cosmological helium recombinations (Rubino-Martin et al. 2007), and the
free-bound and two-photon contributions.
In this way it may be possible to construct an accurate spectral
template, which can be used to disentangle the cosmological recombination
spectrum from other astrophysical sources.
,
mainly
affects the amplitude of the recombination signal.
This in principle should allow measurement of both parameters separately.
However, a more detailed analysis is required, also including the lines from
cosmological helium recombinations (Rubino-Martin et al. 2007), and the
free-bound and two-photon contributions.
In this way it may be possible to construct an accurate spectral
template, which can be used to disentangle the cosmological recombination
spectrum from other astrophysical sources.
In addition to the interesting potential of constraining cosmological
parameters (without suffering from limitations set by cosmic
variance), an observation of the radiation from the epoch of recombination
will yield the final proof that our theoretical understanding of how the
Universe became neutral is correct.
This aspect is particularly important when considering the possibility of
non-standard recombination scenarios (Bean et al. 2003,2007; Doroshkevich et al. 2003; Peebles et al. 2000), which would also affect the results obtained here.
Acknowledgements
The authors wish to thank E. E. Kholupenko for his comments
on the paper, and J. R. Bond, C. Hernández-Monteagudo,
J. A. Rubiño-Martín and B. D. Wandelt for useful discussions. We
are grateful for discussions on experimental possibilities with
J. E. Carlstrom, D. J. Fixsen, A. Kogut, M. Pospieszalski, A. Readhead,
E. J. Wollack and especially J. C. Mather.
- Bean, R.,
Melchiorri, A., & Silk, J. 2003, Phys. Rev. D, 68,
083501 [NASA ADS] [CrossRef]
- Bean, R.,
Melchiorri, A., & Silk, J. 2007, Phys. Rev. D, 75,
063505 [NASA ADS] [CrossRef]
- Bennett,
C. L., Halpern, M., Hinshaw, G., et al. 2003, ApJS, 148,
1 [NASA ADS] [CrossRef]
(In the text)
-
Bernshtein, I. N., Bernshtein, D. N., & Dubrovich,
V. K. 1977, SvA, 21, 409 [NASA ADS]
- Burgin,
M. S. 2003, Astron. Rep., 47, 709 [NASA ADS] [CrossRef]
- Chluba, J.,
& Sunyaev, R. A. 2006a, A&A, 458, L29 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Chluba, J.,
& Sunyaev, R. A. 2006b, A&A, 446, 39 [NASA ADS] [CrossRef] [EDP Sciences]
- Chluba, J.,
& Sunyaev, R. A. 2007a, A&A, 475, 109 [NASA ADS] [CrossRef] [EDP Sciences]
- Chluba, J.,
& Sunyaev, R. A. 2007b, ArXiv e-prints, 705
- Chluba, J.,
Rubiño-Martín, J. A., & Sunyaev, R. A.
2007, MNRAS, 374, 1310 [NASA ADS] [CrossRef]
- Cyburt,
R. H. 2004, Phys. Rev. D, 70, 023505 [NASA ADS] [CrossRef]
- Doran, M. 2005,
J. Cosmol. Astro-Part. Phys., 10, 11 [NASA ADS]
(In the text)
-
Doroshkevich, A. G., Naselsky, I. P., Naselsky,
P. D., & Novikov, I. D. 2003, ApJ, 586, 709 [NASA ADS] [CrossRef]
-
Dubrovich, V. K. 1975, SvA, 1, 196
-
Dubrovich, V. K., & Grachev, S. I. 2004, Astron.
Lett., 30, 657 [NASA ADS] [CrossRef]
-
Dubrovich, V. K., & Grachev, S. I. 2005, Astron.
Lett., 31, 359 [NASA ADS] [CrossRef]
-
Dubrovich, V. K., & Stolyarov, V. A. 1995, A&A,
302, 635 [NASA ADS]
- Fixsen,
D. J., & Mather, J. C. 2002, ApJ, 581, 817 [NASA ADS] [CrossRef]
(In the text)
- Fixsen,
D. J., Cheng, E. S., Gales, J. M., et al. 1996,
ApJ, 473, 576 [NASA ADS] [CrossRef]
- Haiman, Z.,
& Knox, L. 2000, ApJ, 530, 124 [NASA ADS] [CrossRef]
(In the text)
- Hinshaw, G.,
Nolta, M. R., Bennett, C. L., et al. 2006, ArXiv
Astrophysics e-prints
- Hirata, C. M., & Switzer,
E. R. 2007, ArXiv Astrophysics e-prints
- Hu, W., Scott, D.,
Sugiyama, N., & White, M. 1995, Phys. Rev. D, 52,
5498 [NASA ADS] [CrossRef]
(In the text)
- Kholupenko,
E. E., & Ivanchik, A. V. 2006, Astron. Lett., 32,
795 [NASA ADS] [CrossRef]
- Kholupenko,
E. E., Ivanchik, A. V., & Varshalovich, D. A.
2005, Gravitation Cosmol., 11, 161
- Kholupenko,
E. E., Ivanchik, A. V., & Varshalovich, D. A.
2007, MNRAS, 378, L39 [NASA ADS]
- Kogut, A.,
Banday, A. J., Bennett, C. L., et al. 1996, ApJ,
470, 653 [NASA ADS] [CrossRef]
(In the text)
- Mather,
J. C., Fixsen, D. J., Shafer, R. A., Mosier, C.,
& Wilkinson, D. T. 1999, ApJ, 512, 511 [NASA ADS] [CrossRef]
(In the text)
- Olive,
K. A., & Steigman, G. 1995, ApJS, 97, 49 [NASA ADS] [CrossRef]
- Page, L., Hinshaw,
G., Komatsu, E., et al. 2006, ArXiv Astrophysics e-prints
- Peebles,
P. J. E. 1968, ApJ, 153, 1 [NASA ADS] [CrossRef]
- Peebles,
P. J. E., Seager, S., & Hu, W. 2000, ApJ, 539,
L1 [NASA ADS] [CrossRef]
- Readhead, A.
2007, private communication
(In the text)
- Righi, M.,
Hernandez-Monteagudo, C., & Sunyaev, R. 2007, ArXiv e-prints,
707
(In the text)
-
Rubiño-Martín, J. A., Chluba, J., & Sunyaev,
R. A. 2006, MNRAS, 371, 1939 [NASA ADS] [CrossRef]
- Rubino-Martin,
J. A., Chluba, J., & Sunyaev, R. A. 2007, ArXiv
e-prints, 711
- Schäfer,
B. M., Pfrommer, C., Bartelmann, M., Springel, V., &
Hernquist, L. 2006, MNRAS, 370, 1309 [NASA ADS] [CrossRef]
(In the text)
-
Seager, S., Sasselov, D. D., & Scott, D. 1999, ApJ, 523,
L1 [NASA ADS] [CrossRef]
- Seager, S.,
Sasselov, D. D., & Scott, D. 2000, ApJS, 128, 407 [NASA ADS] [CrossRef]
- Seljak, U.,
Sugiyama, N., White, M., & Zaldarriaga, M. 2003,
Phys. Rev. D, 68, 083507 [NASA ADS] [CrossRef]
(In the text)
- Silk, J. 1968, ApJ,
151, 459 [NASA ADS] [CrossRef]
(In the text)
- Springel,
V., White, M., & Hernquist, L. 2001, ApJ, 549, 681 [NASA ADS] [CrossRef]
(In the text)
- Steigman,
G. 2006, J. Cosmol. Astro-Part. Phys., 10, 16 [NASA ADS] [CrossRef]
- Sunyaev,
R. A., & Zeldovich, Y. B. 1970, Ap&SS, 7, 3 [NASA ADS]
(In the text)
- Sunyaev,
R. A., & Zeldovich, Y. B. 1972, Comm. Astrophys.
Space Phys., 4, 173 [NASA ADS]
-
Switzer, E. R., & Hirata, C. M. 2007a, ArXiv
Astrophysics e-prints
- Switzer, E. R., &
Hirata, C. M. 2007b, ArXiv Astrophysics e-prints
- Wong, W. Y.,
& Scott, D. 2007, MNRAS, 375, 1441 [NASA ADS] [CrossRef]
- Zeldovich,
Y. B., Kurt, V. G., & Syunyaev, R. A. 1968, Zh.
Eksperim. Teoretich. Fiziki, 55, 278 [NASA ADS]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=8.8cm]{eps/8200fig1.eps}
\end{figure}](/articles/aa/full/2008/05/aa8200-07/Timg25.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm]
{eps/8200fig2.eps}\\
\includegraphics[width=8.5cm]
{eps/8200fig3.eps}
\end{figure}](/articles/aa/full/2008/05/aa8200-07/Timg26.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]
{eps/8200fig4.eps}
\end{figure}](/articles/aa/full/2008/05/aa8200-07/Timg51.gif)
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]
{eps/8200fig5.eps}\\
\includegraphics[width=8.7cm,clip]
{eps/8200fig6.eps}\end{figure}](/articles/aa/full/2008/05/aa8200-07/Timg52.gif)