A&A 478, L15-L18 (2008)
DOI: 10.1051/0004-6361:20078733
LETTER TO THE EDITOR
Particle-in-cell simulations of shocks and band splitting of type
II solar radio bursts
J. I. Sakai1 - M. Karlický2
1 - Laboratory for Plasma Astrophysics, Faculty of Engineering,
University of Toyama, 3190 Gofuku, Toyama 930-8555, Japan
2 - Astronomical Institute, Academy of Sciences of the Czech Republic, v.v.i.,
Fricova 298, 251 65 Ondrejov, Czech Republic
Received 25 September 2007 / Accepted 22 November 2007
Abstract
Aims. We investigate the emission process of electromagnetic waves from proton beams reflected by the front of a fast magnetosonic shock that propagates in a non-uniform density region, by changing the propagation angle with respect to a uniform magnetic field from  to
to 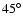 .
.
Methods. A two-dimensional, electromagnetic, relativistic particle-in-cell (PIC) code is used.
Results. Near the shock front, some protons are reflected and accelerated. The reflected protons can drag the background electrons to keep the charge neutrality, resulting in electron acceleration. Due to the accelerated electrons, the electrostatic waves (Z-modes in the oblique propagation) can be excited where the reflected protons are generated. It is found that for about 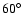 propagation, the extra-ordinary waves can be excited from the shock front with a double oscillating structure. These waves are excited both near the fundamental and second harmonic frequency region of the local plasma frequency. The second harmonic waves have a band splitting structure and the lower band is brighter than the upper band part. For
propagation, the extra-ordinary waves can be excited from the shock front with a double oscillating structure. These waves are excited both near the fundamental and second harmonic frequency region of the local plasma frequency. The second harmonic waves have a band splitting structure and the lower band is brighter than the upper band part. For 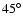 propagation, the fundamental frequency region has a band splitting structure.
propagation, the fundamental frequency region has a band splitting structure.
Key words: plasmas - radiation mechanisms: general - methods: numerical - Sun: radio radiation
It is commonly accepted that solar type II radio bursts are generated by fast
magnetosonic shocks travelling from the flare site through the solar corona
into the interplanetary space (Nelson & Melrose 1985). The basic spectral
properties of type II bursts are as follows (McLean 1980): they are observed
in the frequency range below 500 MHz; most of them appear in harmonic bands and
they are characterized by slow frequency drift from high to low frequencies at
less than 1 MHz s-1. Some bursts show a secondary doubling of the bands
called band splitting (
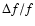
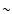 10
10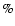 ,
where f is the
frequency, in each of the fundamental and harmonic bands).
,
where f is the
frequency, in each of the fundamental and harmonic bands).
Nelson & Robinson (1975) analyzed observations of harmonic split-band type II
bursts at 160 and 80 MHz or 80 and 43 MHz. They found that the lower frequency
component of split bands is observed earlier in time than the upper component.
In most cases the lower component was brighter than the upper one.
There are several ideas explaining this band splitting. McLean (1967)
interpret it in terms of the density structure along the shock. A variant of this
model was proposed by Uchida (1974). On the other hand,
Smerd et al. (1974) suggested that the two bands correspond to emission in front
of and behind the shock front. They showed that electron density jumps at a
shock with the shock Mach number in the 1.2-1.7 range are sufficient to explain
the observed band splitting.
Recently, Vrsnak et al. (2001, 2002, 2004) and Cho et al. (2007) have used this model to determine the Alfvén velocity and magnetic field
strength along the trajectory of coronal and interplanetary type II shocks.
They have found several arguments in favour of this model. Nevertheless,
details of the band-splitting process remain unknown.
Recently, Sakai et al. (2005) addressed the formation of shock waves driven by CME, the acceleration process of both protons and electrons and the emission mechanism of electromagnetic waves (solar type II bursts) from the shock front, by using a two-dimensional, fully relativistic particle-in-cell (PIC) simulation. They showed that for fast magnetosonic
shock waves with MA  2.0 and a propagation angle between
2.0 and a propagation angle between  and
and 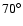 ,
protons near the shock front can be accelerated by the surfatron acceleration mechanism (Sagdeev & Shapiro 1973), while the emission of the
electromagnetic waves from the shock front was observed almost independently of the Alfvén Mach number and the propagation angles. They also found for perpendicular propagation that near the shock front, electron Bernstein waves are generated
and can be converted to electromagnetic waves (type II radio bursts) through direct linear mode conversion. It was also found from the oblique propagation that near the shock front, electrostatic Langmuir waves (Z-mode) are generated
and also can be converted to electromagnetic waves through direct linear mode conversion.
,
protons near the shock front can be accelerated by the surfatron acceleration mechanism (Sagdeev & Shapiro 1973), while the emission of the
electromagnetic waves from the shock front was observed almost independently of the Alfvén Mach number and the propagation angles. They also found for perpendicular propagation that near the shock front, electron Bernstein waves are generated
and can be converted to electromagnetic waves (type II radio bursts) through direct linear mode conversion. It was also found from the oblique propagation that near the shock front, electrostatic Langmuir waves (Z-mode) are generated
and also can be converted to electromagnetic waves through direct linear mode conversion.
In the present paper we extended the work of Sakai et al. (2005) by focusing on two aspects: first we used the real mass ratio
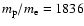 between proton and electron instead of
between proton and electron instead of
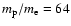 ,
secondly we considered fast magnetosonic shock propagation in an inhomogeneous background by changing the propagation angle with respect to a uniform magnetic field from
,
secondly we considered fast magnetosonic shock propagation in an inhomogeneous background by changing the propagation angle with respect to a uniform magnetic field from  to
to 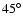 .
The first effect of the use of the real mass ratio results in the proper description of proton reflection at the shock front. Then the reflected protons are accelerated to form proton beam near the shock front. The second effect of the density inhomogeneity and oblique propagation introduce a new effect with a double structure in the shock for oblique propagation less
.
The first effect of the use of the real mass ratio results in the proper description of proton reflection at the shock front. Then the reflected protons are accelerated to form proton beam near the shock front. The second effect of the density inhomogeneity and oblique propagation introduce a new effect with a double structure in the shock for oblique propagation less 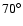 .
.
In Sect. 2 we present the simulation model and results. In Sect. 3 we summarize our results and discuss their applications to solar radio bursts.
We used a 2D3V, fully relativistic electromagnetic PIC code, modified from the
3D3V TRISTAN code (Buneman 1993).
The system size is
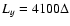 and
and
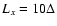 ,
where
,
where
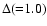 is the grid size. The free boundary condition in the y direction and the periodic boundary condition in the x direction are imposed on particles and fields. In the
left boundary, the average number of electron-ion pairs is 400 per cell and the density decreases linearly in the y-direction. The average density near the right boundary is 100 per cell. To excite a fast magnetosonic shock wave, the initial flow velocity vy=0.24c is applied
to the y-direction by the electric field Ez through
Ez=vyBx near the left boundary (see Sakai et al. 2005).
is the grid size. The free boundary condition in the y direction and the periodic boundary condition in the x direction are imposed on particles and fields. In the
left boundary, the average number of electron-ion pairs is 400 per cell and the density decreases linearly in the y-direction. The average density near the right boundary is 100 per cell. To excite a fast magnetosonic shock wave, the initial flow velocity vy=0.24c is applied
to the y-direction by the electric field Ez through
Ez=vyBx near the left boundary (see Sakai et al. 2005).
The parameters used in this simulation are as follows. The ratio of ion mass to the electron mass
is
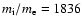 ,
the ratio of electron cyclotron frequency to the plasma frequency is about
,
the ratio of electron cyclotron frequency to the plasma frequency is about
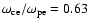 ,
plasma beta is
,
plasma beta is
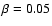 ,
skin depth is
,
skin depth is
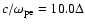 ,
electron
thermal velocity is
,
electron
thermal velocity is
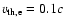 ,
electron Larmor radius is
,
electron Larmor radius is
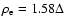 ,
ion Larmor radius is
,
ion Larmor radius is
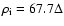 ,
and the simulation time step is
,
and the simulation time step is
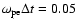 ,
respectively. The parameters
,
respectively. The parameters
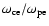 ,
,
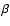 ,
,
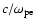 ,
,
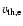 ,
,
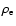 ,
and
,
and
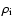 are calculated at the right edge where the density is 100 pairs per cell.
are calculated at the right edge where the density is 100 pairs per cell.
In this paper we present only the results of 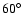 propagation. Figure 1 shows the time development of the fast magnetosonic shock wave at a later stage. As seen in Fig. 1a, an oscillating part appears behind the shock front. The oscillating part shows large amplitude magnetosonic waves that were never observed in the nearly perpendicular propagation between
propagation. Figure 1 shows the time development of the fast magnetosonic shock wave at a later stage. As seen in Fig. 1a, an oscillating part appears behind the shock front. The oscillating part shows large amplitude magnetosonic waves that were never observed in the nearly perpendicular propagation between  and
and 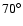 .
As time goes on, the leading shock front propagates faster than the wave behind the front, as seen in Figs. 1b,c. This double structure becomes distinct around
.
As time goes on, the leading shock front propagates faster than the wave behind the front, as seen in Figs. 1b,c. This double structure becomes distinct around 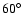 propagation, while for
propagation, while for 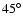 propagation the situation of the structure of the shock changes: the leading part becomes more oscillating with large amplitude waves, and behind the leading part there is non-oscillating part with small amplitude.
Figure 2 shows the time development of the proton phase-space (
propagation the situation of the structure of the shock changes: the leading part becomes more oscillating with large amplitude waves, and behind the leading part there is non-oscillating part with small amplitude.
Figure 2 shows the time development of the proton phase-space (
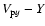 ). As seen in Fig. 2a, the reflected protons are accelerated by the shock. The Alfv
). As seen in Fig. 2a, the reflected protons are accelerated by the shock. The Alfv
 n Mach number
n Mach number 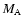 is about
is about
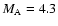 ,
which exceeds the critical Mach number (about 2.7) showing that a fraction of incoming protons are reflected from the shock front. In the two regions where the shock splits to double structures, some of the accelerated protons can be decelerated. The reason is that the decelerated protons accelerate electrons that can excite the longitudinal electric fields corresponding to the Z-modes. Recent papers by Sakai et al. (2007a,b) showed that when proton beams propagate in inhomogeneous plasmas, the background electrons are forced to move together to keep charge neutrality, resulting in the excitation of electrostatic waves. Figure 3 shows the time development of the electric field Ey. As seen in Fig. 3c, the electric field Ey near the leading shock front becomes stronger than that near the oscillating region behind the shock. This effect may play an important role in the production of band splitting that will be discussed later. Figure 4 shows the time development of the electron phase-space (
,
which exceeds the critical Mach number (about 2.7) showing that a fraction of incoming protons are reflected from the shock front. In the two regions where the shock splits to double structures, some of the accelerated protons can be decelerated. The reason is that the decelerated protons accelerate electrons that can excite the longitudinal electric fields corresponding to the Z-modes. Recent papers by Sakai et al. (2007a,b) showed that when proton beams propagate in inhomogeneous plasmas, the background electrons are forced to move together to keep charge neutrality, resulting in the excitation of electrostatic waves. Figure 3 shows the time development of the electric field Ey. As seen in Fig. 3c, the electric field Ey near the leading shock front becomes stronger than that near the oscillating region behind the shock. This effect may play an important role in the production of band splitting that will be discussed later. Figure 4 shows the time development of the electron phase-space (
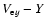 ). As seen from the figure. the electrons can be accelerated in both regions where the electric fields Ey are strongly excited.
). As seen from the figure. the electrons can be accelerated in both regions where the electric fields Ey are strongly excited.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8733f2.eps}\end{figure}](/articles/aa/full/2008/04/aa8733-07/Timg39.gif) |
Figure 2:
The proton phase space plots (
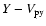 )
at (a) )
at (a)
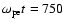 ,
(b) ,
(b)
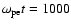 and (c)
and (c)
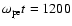 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8733f4.eps}\end{figure}](/articles/aa/full/2008/04/aa8733-07/Timg41.gif) |
Figure 4:
The electron phase space plots (
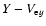 )
at a) )
at a)
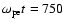 ,
b) ,
b)
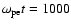 and c)
and c)
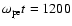 . . |
| Open with DEXTER |
Next we investigate the electromagnetic emission process from the shock region. Figure 5 shows the time development of the electric field Ez which corresponds to the electromagnetic waves of the extra-ordinary mode. From Fig. 5a we find some emission of electromagnetic waves that propagate faster than the shock front. This emission has similar characteristics to our previous simulation by Sakai et al. (2005). At the later time seen in Fig. 5c strong emission appears from the shock front that is seen in the range of
3500<Y<4000. To find the wave characteristics in this region, we performed a space-time Fourier transformation of Ey and Ez, where the data points are taken in the space of
3000<Y<4024 and in the time period of
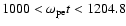 .
The result is shown in Fig. 6b. There occur two wave branches: one is a lower frequency branch corresponding to the proton beam mode and the other is a high frequency branch corresponding to extra-ordinary modes. The strongest excitation is around the local plasma frequency (about
.
The result is shown in Fig. 6b. There occur two wave branches: one is a lower frequency branch corresponding to the proton beam mode and the other is a high frequency branch corresponding to extra-ordinary modes. The strongest excitation is around the local plasma frequency (about
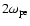 in Fig. 6b) and further strong excitation occurs around the harmonic of this plasma frequency (about
in Fig. 6b) and further strong excitation occurs around the harmonic of this plasma frequency (about
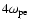 in Fig. 6b). The
in Fig. 6b). The
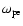 is defined by using the density at the right boundary. Therefore the local plasma frequency where the emission occurs is two times larger than the
is defined by using the density at the right boundary. Therefore the local plasma frequency where the emission occurs is two times larger than the
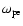 at the right boundary. It is remarkable that the harmonic band has band splitting and the lower band intensity is relatively stronger than the upper band intensity. This band splitting is only observed at late times. Figure 6a shows the wave dispersion relation of Ey. There are two branches: one is the lower branch corresponding to the proton beam mode and other is the upper frequency branch that corresponds to Z-modes. These Z-modes can be excited from the electrons accelerated by coupling with the proton beam. The Z-modes can be transformed to extra-ordinary waves through direct linear mode conversion by the background density inhomogeneity. The reason that the lower band branch near the harmonics becomes strong is related to the fact that the electric field Ey associated with the Z-mode near the leading part, which is excited in the lower density region, is stronger than the part behind the shock front as seen in Fig. 3c.
at the right boundary. It is remarkable that the harmonic band has band splitting and the lower band intensity is relatively stronger than the upper band intensity. This band splitting is only observed at late times. Figure 6a shows the wave dispersion relation of Ey. There are two branches: one is the lower branch corresponding to the proton beam mode and other is the upper frequency branch that corresponds to Z-modes. These Z-modes can be excited from the electrons accelerated by coupling with the proton beam. The Z-modes can be transformed to extra-ordinary waves through direct linear mode conversion by the background density inhomogeneity. The reason that the lower band branch near the harmonics becomes strong is related to the fact that the electric field Ey associated with the Z-mode near the leading part, which is excited in the lower density region, is stronger than the part behind the shock front as seen in Fig. 3c.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8733f6.eps}\end{figure}](/articles/aa/full/2008/04/aa8733-07/Timg47.gif) |
Figure 6:
a) The dispersion relation of Ey. b) The dispersion relation of Ez. |
| Open with DEXTER |
These band splittings can be observed in the 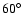 propagation, while in the
propagation, while in the 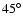 propagation the fundamental shows the band splitting in the electric field Ex. This means that the ordinary waves propagating with an angle of
propagation the fundamental shows the band splitting in the electric field Ex. This means that the ordinary waves propagating with an angle of 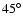 have band splitting in the fundamental band.
have band splitting in the fundamental band.
With a small transverse mesh points in the present simulations (a quasi-one dimensional situation), statements about the variation of emission with shock propagation are limited by the small range of k-B angles.
We investigated the emission of electromagnetic waves from proton beams reflected by the front of a fast magnetosonic shock that propagates in a non-uniform density region. For the shock propagation angles with respect to a uniform magnetic field from  to
to 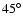 ,
some protons are reflected and accelerated near the shock front. The reflected protons can drag the background electrons to keep the charge neutrality, resulting in electron acceleration. Due to the accelerated electrons, the electrostatic waves corresponding to the Z-modes in the oblique propagation can be excited in the region where the reflected protons are generated. It was found that for about
,
some protons are reflected and accelerated near the shock front. The reflected protons can drag the background electrons to keep the charge neutrality, resulting in electron acceleration. Due to the accelerated electrons, the electrostatic waves corresponding to the Z-modes in the oblique propagation can be excited in the region where the reflected protons are generated. It was found that for about 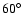 propagation, the extra-ordinary waves can be excited from the shock front with a double oscillating structure. This double oscillating shock structure was observed only in the present numerical experiment where the background density is non-uniform. This shock with a double oscillating structure can lead to the important result that the extra-ordinary waves are excited both near fundamental and second harmonic frequency region of the local plasma frequency. The second harmonic waves show band splitting and the lower band is brighter than the upper band. For
propagation, the extra-ordinary waves can be excited from the shock front with a double oscillating structure. This double oscillating shock structure was observed only in the present numerical experiment where the background density is non-uniform. This shock with a double oscillating structure can lead to the important result that the extra-ordinary waves are excited both near fundamental and second harmonic frequency region of the local plasma frequency. The second harmonic waves show band splitting and the lower band is brighter than the upper band. For 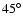 propagation, the fundamental frequency band shows band splitting.
propagation, the fundamental frequency band shows band splitting.
We compare the model of Smerd et al. (1974), which
is used for coronal diagnostics (see Vrsnak et al. 2001, 2002,
2004; Cho et al. 2007), with the present simulations. As
in the model of Smerd et al. (1974), in simulations there are two
regions with different plasma densities where the electromagnetic waves
forming the band-split spectrum are generated. But contrary to the model
of Smerd et al. (1974), where one region is in front of and a second one
behind the shock, in simulations both these regions are in the complex
structure of the shock. Moreover, we found the band-splitting at the
local plasma frequency for the propagation angle of 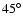 and
band-splitting of harmonic of the local plasma frequency for the angle of
and
band-splitting of harmonic of the local plasma frequency for the angle of
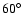 .
It complicates explanation of the simultaneous splitting
of both the fundamental and harmonic bands, except the radio emission is
generated simultaneously at two different parts of the shock where there
are appropriate propagation angles compard to the local magnetic field.
.
It complicates explanation of the simultaneous splitting
of both the fundamental and harmonic bands, except the radio emission is
generated simultaneously at two different parts of the shock where there
are appropriate propagation angles compard to the local magnetic field.
In a separate paper we will present details of the simulation results with different propagation angles.
Acknowledgements
The authors thank the anonymous referee for useful comments that improved our paper. J. I. Sakai thanks Dr. M. Karlický for his hospitality during stay at the Astronomical Institute. This work is supported by Grant IAA300030701 of the Academy of Sciences of the Czech Republic.
- Buneman, O. 1993, in
Computer Space Plasma Physics, Simulation Techniques and Software,
ed. H. Matsumoto, & Y. Omura (Tokyo: Terra Scientific), 67
(In the text)
- Cho, K. S., Lee,
J., Gary, D. E., Moon, Y. J., & Park, Y. D. 2007, ApJ, 665,
799 [NASA ADS] [CrossRef]
(In the text)
- McLean, D. J. 1967,
Proc. Astron. Soc. Austr., 1., 47
(In the text)
- McLean, D. J. 1980,
in Radio Physics of the Sun, ed. M. R. Kundu, & T. E. Gergely
(Dordrecht: Reidel), Proc. IAU Symp., 86, 223
(In the text)
-
Nelson, G. J., & Robinson, R. D. 1975, Proc. Astron. Soc.
Austr., 2, 370 [NASA ADS]
(In the text)
-
Nelson, G. J., & Melrose, D. B. 1985, in Solar Radiophysics,
ed. D. J. McLean, & M. R. Labrum (Cambridge, UK: Cambridge
University Press), 333
(In the text)
- Sagdeev, R. Z., &
Shapiro, V. D. 1973, JETP Lett., 17, 279 [NASA ADS]
(In the text)
- Sakai, J. I., &
Nagasugi, Y. 2007a, A&A, 470, 1117 [NASA ADS] [CrossRef] [EDP Sciences]
- Sakai, J. I., &
Nagasugi, Y. 2007b, A&A, 474, L33 [NASA ADS] [CrossRef] [EDP Sciences]
- Sakai, J. I., Mori, T.,
& Saito, S. 2005, A&A, 442, 687 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Smerd, S. F.,
Sheridan, K. V., & Stewart, R. T. 1974, in Coronal
Disturbances, ed. G. Newkirk (Dordrecht: Reidel), Proc. IAU Symp.,
57, 389
(In the text)
- Uchida, Y. 1974,
Sol. Phys., 39, 431 [NASA ADS] [CrossRef]
(In the text)
- Vrsnak, B., Aurass,
H., Magdalenic, J., & Gopalswamy, N. 2001, A&A, 377,
321 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Vrsnak, B.,
Magdalenic, J., Aurass, H., & Mann, G. 2002, A&A, 396,
673 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Vrsnak, B.,
Magdalenic, J., & Zlobec, P. 2004, A&A, 413, 753 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Wild, J. P.,
& Smerd, S. F. 1972, ARA&A, 10, 159 [NASA ADS] [CrossRef]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8733f1.eps}\end{figure}](/articles/aa/full/2008/04/aa8733-07/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8733f2.eps}\end{figure}](/articles/aa/full/2008/04/aa8733-07/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8733f3.eps}\end{figure}](/articles/aa/full/2008/04/aa8733-07/Timg40.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8733f4.eps}\end{figure}](/articles/aa/full/2008/04/aa8733-07/Timg41.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8733f5.eps}\end{figure}](/articles/aa/full/2008/04/aa8733-07/Timg46.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8733f6.eps}\end{figure}](/articles/aa/full/2008/04/aa8733-07/Timg47.gif)