A&A 477, L33-L36 (2008)
DOI: 10.1051/0004-6361:20078915
LETTER TO THE EDITOR
Y. Revaz1 - F. Combes1 - P. Salomé2
1 - LERMA, Observatoire de Paris, 61 Av. de l'Observatoire, 75014 Paris, France
2 -
Institut of Radio Astronomy (IRAM), Domaine Universitaire, 300 rue de la piscine, 38400 Saint-Martin d'Hères, France
Received 24 October 2007 / Accepted 20 November 2007
Abstract
Emission-lines in the form of filamentary structures is common in bright clusters characterized by short cooling times. In the Perseus cluster, cold molecular gas, tightly linked to the H![]() filaments, has been recently revealed by CO observations.
In order to understand the origin of these filamentary structures,
we have investigated the evolution of the hot ICM gas perturbed by the AGN central activity in a Perseus like cluster.
Using very-high resolution TreeSPH simulations combined with a multiphase model and a model of plasma bubbles, we have been able to follow the density and temperature evolution of the disturbed ICM gas around the bubbles.
Our simulations show that a fraction of the
filaments, has been recently revealed by CO observations.
In order to understand the origin of these filamentary structures,
we have investigated the evolution of the hot ICM gas perturbed by the AGN central activity in a Perseus like cluster.
Using very-high resolution TreeSPH simulations combined with a multiphase model and a model of plasma bubbles, we have been able to follow the density and temperature evolution of the disturbed ICM gas around the bubbles.
Our simulations show that a fraction of the
![]() gas present at the center of clusters is trapped and entrained
by the rising buoyant bubble to higher radius where the AGN heating is less efficient.
The radiative cooling makes it cool in a few tens of Myr below
gas present at the center of clusters is trapped and entrained
by the rising buoyant bubble to higher radius where the AGN heating is less efficient.
The radiative cooling makes it cool in a few tens of Myr below
![]() ,
forming cold filamentary structures in the wake and in the rim of the bubbles.
The predicted cold gas formed outside the cluster center is in agreement with the total CO mass and density profile of the observed molecular gas
as well as with the kinematics of the H
,
forming cold filamentary structures in the wake and in the rim of the bubbles.
The predicted cold gas formed outside the cluster center is in agreement with the total CO mass and density profile of the observed molecular gas
as well as with the kinematics of the H![]() filaments.
This scenario explains the H
filaments.
This scenario explains the H![]() and CO filaments observed in luminous clusters
without contradicting the observed lack of
and CO filaments observed in luminous clusters
without contradicting the observed lack of
![]() gas.
It also emphasizes that if the AGN feedback provides some heating (negative feedback) it also
perturbs the ICM, increasing its cooling (positive feedback).
gas.
It also emphasizes that if the AGN feedback provides some heating (negative feedback) it also
perturbs the ICM, increasing its cooling (positive feedback).
Key words: cooling flows
Cooling flows in clusters of galaxies has been a puzzling topic for more than 30 years (Fabian 1994; Peterson & Fabian 2006). While early models of X-ray clusters (Cowie & Binney 1977) applied to observations predict a large cold gas mass
accretion rate, the recent data from Chandra and XMM-Newton ruled out such large amounts of cooling (Peterson et al. 2003).
There are now numerous observations showing that the AGN activity may be a
clue to the cooling flow problem (Fabian et al. 2003b; McNamara & Nulsen 2007; McNamara et al. 2000; Fabian et al. 2000,2003a,2006; Owen et al. 2000; Blanton et al. 2003; Wise et al. 2006).
The emerging picture is that cooling flows are considerably reduced by the heating provided by the
AGN feedback (Churazov et al. 2001; Cattaneo & Teyssier 2007; Quilis et al. 2001; Omma et al. 2004; Omma & Binney 2004; Sijacki & Springel 2006; Brüggen & Kaiser 2001; Reynolds et al. 2002; Heinz et al. 2006; Böhringer et al. 2002).
The bulk of the ICM gas remains hot (![]()
![]() )
down to the cluster center, where it is accreted by the central black hole (Bondi accretion).
)
down to the cluster center, where it is accreted by the central black hole (Bondi accretion).
However, in this picture, it is difficult to understand the origin of
the observed cold neutral gas (Edge 2001; Salomé & Combes 2003; Salomé et al. 2006; Edge & Frayer 2003; Salomé & Combes 2004) and the filamentary H![]() structures (Conselice et al. 2001; Crawford et al. 2005).
The connection between radio source and cold CO gas (Salomé & Combes 2004) as well as the excess of optical/UV/IR light in clusters with central cooling time less than
structures (Conselice et al. 2001; Crawford et al. 2005).
The connection between radio source and cold CO gas (Salomé & Combes 2004) as well as the excess of optical/UV/IR light in clusters with central cooling time less than
![]() are signs of the link between the filaments, the cooling and the AGN activity.
Very deep Chandra observation of the Perseus cluster shows a clear correlation between the soft X-ray emission (between 0.5 and
are signs of the link between the filaments, the cooling and the AGN activity.
Very deep Chandra observation of the Perseus cluster shows a clear correlation between the soft X-ray emission (between 0.5 and
![]() )
and the optical filamentary H
)
and the optical filamentary H![]() structures (Fabian et al. 2006,2003b).
As the filaments cover a large range of cooling time within the hot gas, it is unlikely that they
form by direct cooling of the
structures (Fabian et al. 2006,2003b).
As the filaments cover a large range of cooling time within the hot gas, it is unlikely that they
form by direct cooling of the
![]() component. Moreover, the kinematics of the filament in H
component. Moreover, the kinematics of the filament in H![]() (Hatch et al. 2006) and soft X-rays (Fabian et al. 2006) matches the gas flow under a buoyantly rising bubble. This led Fabian et al. (2006,2003b) and Hatch et al. (2006) to propose that the filaments have been pulled out from a central reservoir of cold and warm gas by the action of radio plasma bubbles inflated by AGN jets.
(Hatch et al. 2006) and soft X-rays (Fabian et al. 2006) matches the gas flow under a buoyantly rising bubble. This led Fabian et al. (2006,2003b) and Hatch et al. (2006) to propose that the filaments have been pulled out from a central reservoir of cold and warm gas by the action of radio plasma bubbles inflated by AGN jets.
In this letter, without answering the question of the inner quenching of the cooling flow, we present a series of very high
resolution TreeSPH simulations of a Perseus type cluster including AGN feedback.
We show that buoyantly rising bubbles entrain a fraction of the
![]() central ICM gas
to much higher radius where it has time to cool and fall back to the cluster center, forming cold filamentary structures (T < 104).
central ICM gas
to much higher radius where it has time to cool and fall back to the cluster center, forming cold filamentary structures (T < 104).
We have constructed a cluster model in order to fit the Perseus data from Sanders et al. (2004).
The initial conditions are based on two components, a dark halo and a hot gas phase.
Both share the same ![]() -profile with
-profile with ![]() (pseudo-isothermal sphere), with a core radius of
(pseudo-isothermal sphere), with a core radius of
![]() and a central mass density of
and a central mass density of
![]()
![]()
![]() .
The gas represents
.
The gas represents ![]() of the total mass and is treated as self-gravitating in the fixed potential of the halo. Assuming a hydrogen mass fraction of 0.76, we found a central electron density of
of the total mass and is treated as self-gravitating in the fixed potential of the halo. Assuming a hydrogen mass fraction of 0.76, we found a central electron density of
![]() and a temperature of 2.85
and a temperature of 2.85 ![]()
![]() .
The model is truncated at a radius of
.
The model is truncated at a radius of
![]() ,
giving a total mass of 5.3
,
giving a total mass of 5.3 ![]()
![]() .
With these parameters, the mean cooling time at the center is about
.
With these parameters, the mean cooling time at the center is about
![]() .
.
Computing the interaction between the AGN and the hot ICM requires us to deal with a huge range of
temperatures, spanning from more than
![]() down to
down to
![]() .
This may be achieved
by assuming a multiphase behavior of the gas where hot and cold gas represents two distinct phases.
.
This may be achieved
by assuming a multiphase behavior of the gas where hot and cold gas represents two distinct phases.
The warm-hot gas phase (
![]() )
is modeled by an ideal gas with an adiabatic index of 5/3. The radiative cooling of the gas is computed from the normalized cooling function tabulated by Sutherland & Dopita (1993), assuming an abundance of one third solar (Sanders et al. 2004).
Hydrodynamical equations are integrated using the Lagrangian SPH technique.
)
is modeled by an ideal gas with an adiabatic index of 5/3. The radiative cooling of the gas is computed from the normalized cooling function tabulated by Sutherland & Dopita (1993), assuming an abundance of one third solar (Sanders et al. 2004).
Hydrodynamical equations are integrated using the Lagrangian SPH technique.
Below
![]() ,
instead of quenching the cooling, the gas is assumed to change phase, becoming
very cold and clumpy, as commonly observed in the ISM. In this phase, the semi-collisional nature of the gas is well modeled by the sticky particle technique widely used to compute
the behavior of the ISM in the disk of galaxies (Schwarz 1981; Bournaud & Combes 2002; Combes & Gerin 1985; Semelin & Combes 2002).
,
instead of quenching the cooling, the gas is assumed to change phase, becoming
very cold and clumpy, as commonly observed in the ISM. In this phase, the semi-collisional nature of the gas is well modeled by the sticky particle technique widely used to compute
the behavior of the ISM in the disk of galaxies (Schwarz 1981; Bournaud & Combes 2002; Combes & Gerin 1985; Semelin & Combes 2002).
We take into account the possibility of forming stars from the cold phase. This is computed following the standard process described in Katz et al. (1996) which simulates quite well a Schmidt law.
We also take into account supernova feedback by injecting energy in both thermal (![]() )
and kinetic (
)
and kinetic (![]() )
form,
assuming that
)
form,
assuming that
![]() are released for each solar mass formed.
are released for each solar mass formed.
We have modeled the AGN feedback by instantaneously generating bubbles of gas in the ICM.
This technique, which has already been used by several authors
(Churazov et al. 2001; Saxton et al. 2001; Sijacki et al. 2007; Gardini 2007; Sijacki & Springel 2006; Brüggen & Kaiser 2001),
does not consider the evolution of the jet at its origin that may be modeled by mass or energy injection (Cattaneo & Teyssier 2007; Quilis et al. 2001; Omma et al. 2004; Brüggen & Kaiser 2002; Brüggen et al. 2002; Omma & Binney 2004; Reynolds et al. 2002; Heinz et al. 2006; Dalla Vecchia et al. 2004; Brüggen 2003).
We have implemented a new bubble generator allowing us to control precisely the relative pressure, density and specific energy of the bubble with respect to the ambient gas. We have also taken into account the presence
of the puzzling cooler and denser gas forming a bright shell around the radio bubbles
(Fabian et al. 2003b; Nulsen et al. 2002; Blanton et al. 2001; McNamara & Nulsen 2007; McNamara et al. 2000; Fabian et al. 2000,2006; Blanton et al. 2003), asssuming that it is the result of ambient gas pushed out by the inflating bubble.
From these assumptions, we can generate bubbles with densities differing from the ambient gas,
without violating the total mass conservation.
In a given sphere of radius
![]() at a distance
at a distance
![]() from the cluster center,
the density
from the cluster center,
the density ![]() ,
mass mi, specific energy ui and pressure Pi of a particle i are modified as follows:
,
mass mi, specific energy ui and pressure Pi of a particle i are modified as follows:
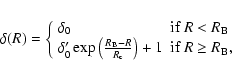 |
(2) |
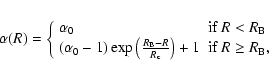 |
(3) |
Table 1: List of simulations and respective parameters. See Sect. 2 for the meaning of each parameter.
The models have been run using a modified version of the parallel TreeSPH code Gadget2 (Springel 2005) which conserves both energy and entropy. Additional physics have been included as described in paragraph 2.2 and 2.3.
In order to reach a very high resolution in the cluster central region (up to
![]() ),
we have constructed our model using a multi-resolution technique. The models are made out of 7 cells where two consecutive cells differ by their resolution only by a factor of two, ensuring
the stability of the integration of the motion equations. This technique allows us to compute the evolution of the bubbles within a central region of
),
we have constructed our model using a multi-resolution technique. The models are made out of 7 cells where two consecutive cells differ by their resolution only by a factor of two, ensuring
the stability of the integration of the motion equations. This technique allows us to compute the evolution of the bubbles within a central region of
![]() ,
reaching a mass resolution of 2.4
,
reaching a mass resolution of 2.4 ![]()
![]() and a spatial resolution of about
and a spatial resolution of about
![]() ,
appreciably better than previous works using similar Lagrangian codes.
The total number of particles is 6 041 002, equivalent to 33 554 432 particles
in a similar model where no multi-resolution technique is used.
,
appreciably better than previous works using similar Lagrangian codes.
The total number of particles is 6 041 002, equivalent to 33 554 432 particles
in a similar model where no multi-resolution technique is used.
In order to explore the effect of the bubbles on the ambient gas, we have run several simulations exploring all the parameters.
We have completed our study with a control run where no bubble is launched. This simulation is described in Appendix A.
Hereafter, we focus on a subset of 5 representative simulations.
For each simulation, the parameters are listed in Table 1. Bubbles are created at
![]() and are followed for
and are followed for
![]() .
.
Except for model 1, we have set
![]() (bubbles are in pressure equilibrium with the ambient gas). This choice is motivated by the work of Cattaneo & Teyssier (2007) showing that the bulk of the AGN feedback energy can be deposited at the center of the cluster in the form of thermal energy. Consequently, as we have not implemented central thermal feedback, our models are subject to the cooling catastrophe, occurring in the 10 central kpc.
(bubbles are in pressure equilibrium with the ambient gas). This choice is motivated by the work of Cattaneo & Teyssier (2007) showing that the bulk of the AGN feedback energy can be deposited at the center of the cluster in the form of thermal energy. Consequently, as we have not implemented central thermal feedback, our models are subject to the cooling catastrophe, occurring in the 10 central kpc.
The evolution of the bubbles for the 5 models is displayed in Fig. 1.
The first stage is very similar to previous
works. Once generated, the bubbles quickly start moving upwards, reaching velocities of between
50 and
![]() and forming typical atomic mushrooms.
However, contrary to Eulerian simulations, the latter phase does not show the formation of a torus.
The bubble is only weakly affected by hydrodynamic instabilities (see Agertz et al. 2006, for a complete discussion of the damping of Kelvin-Helmoltz and Rayleigh-Taylor instabilities in SPH codes) and dissolves only when reaching regions of similar specific entropy.
and forming typical atomic mushrooms.
However, contrary to Eulerian simulations, the latter phase does not show the formation of a torus.
The bubble is only weakly affected by hydrodynamic instabilities (see Agertz et al. 2006, for a complete discussion of the damping of Kelvin-Helmoltz and Rayleigh-Taylor instabilities in SPH codes) and dissolves only when reaching regions of similar specific entropy.
A common feature between the 5 simulations is the systematic formation of very cold gas in the wake of the bubbles, far from the cluster core![]() .
In a few Myrs, a substantial fraction of gas cools from the ambient ICM temperature (
.
In a few Myrs, a substantial fraction of gas cools from the ambient ICM temperature (
![]() )
down to
)
down to
![]() ,
with a small fraction of it reaching temperatures below
,
with a small fraction of it reaching temperatures below
![]() and forming a thin trunk (see Fig. 1).
The presence of cooler gas in the trunk of a buoyantly rising bubble already has been mentioned by
different authors (Churazov et al. 2001; Saxton et al. 2001; Gardini 2007; Brüggen & Kaiser 2001).
However, in all these simulations, the gas temperature never falls below 5
and forming a thin trunk (see Fig. 1).
The presence of cooler gas in the trunk of a buoyantly rising bubble already has been mentioned by
different authors (Churazov et al. 2001; Saxton et al. 2001; Gardini 2007; Brüggen & Kaiser 2001).
However, in all these simulations, the gas temperature never falls below 5 ![]()
![]() .
The high resolution obtained in our simulations reinforced by the Lagrangian technique enables us to resolve higher densities, critical for the correct estimation of the cooling time.
.
The high resolution obtained in our simulations reinforced by the Lagrangian technique enables us to resolve higher densities, critical for the correct estimation of the cooling time.
In our simulations, the filaments are formed by
![]() gas (observed in the central regions of the Perseus cluster (Fabian et al. 2006)) having short cooling time (between 400 and
gas (observed in the central regions of the Perseus cluster (Fabian et al. 2006)) having short cooling time (between 400 and
![]() )
at the time the bubble is formed.
In the case of large bubbles (models 1-3) this gas is situated below the bubble.
When smaller bubbles are created near the center (models 4, 5), gas with sufficiently short cooling times is also found above the bubble.
In both cases, this gas is trapped by the rising bubble and entrained outside the cooling cluster core where its sufficiently short cooling time allows it to cool quickly to very low temperatures. Figure 2 shows the evolution of particles becoming part of the filaments
(
)
at the time the bubble is formed.
In the case of large bubbles (models 1-3) this gas is situated below the bubble.
When smaller bubbles are created near the center (models 4, 5), gas with sufficiently short cooling times is also found above the bubble.
In both cases, this gas is trapped by the rising bubble and entrained outside the cooling cluster core where its sufficiently short cooling time allows it to cool quickly to very low temperatures. Figure 2 shows the evolution of particles becoming part of the filaments
(
![]() )
at
)
at
![]() for models 2 and 5 (See also Figs. B.1 and B.2 for the evolution of particles becoming part of the filaments at
for models 2 and 5 (See also Figs. B.1 and B.2 for the evolution of particles becoming part of the filaments at
![]() ). At the beginning of simulation 2, particles being in the filaments at
). At the beginning of simulation 2, particles being in the filaments at
![]() (resp.
(resp.
![]() )
are part of the bottom rim of the bubble at
a distance of between 20 and
)
are part of the bottom rim of the bubble at
a distance of between 20 and
![]() (resp. 30 and
(resp. 30 and
![]() )
of the center, with a temperature between 1 and
)
of the center, with a temperature between 1 and
![]() .
During the rising of the bubble, this gas is dragged up to
.
During the rising of the bubble, this gas is dragged up to
![]() (resp.
(resp.
![]() ).
The radiative cooling slowly decreases the gas temperature, which reaches
).
The radiative cooling slowly decreases the gas temperature, which reaches
![]() around
around
![]() .
At these temperatures, the gas is no longer supported by the pressure and falls towards the center while being compressed.
Its density is enhanced by a factor of 10 which substantially decreases its cooling time
.
At these temperatures, the gas is no longer supported by the pressure and falls towards the center while being compressed.
Its density is enhanced by a factor of 10 which substantially decreases its cooling time![]() . A very cold thin filament with a temperature below
. A very cold thin filament with a temperature below
![]() is then formed. The main difference of model 5 is that the bubble is formed at smaller radius.
Gas with a short enough cooling time (<
is then formed. The main difference of model 5 is that the bubble is formed at smaller radius.
Gas with a short enough cooling time (<
![]() )
is initially situated above the bubble.
As for the model 2, it is dragged at higher altitude (up to
)
is initially situated above the bubble.
As for the model 2, it is dragged at higher altitude (up to
![]() )
and crossed by the bubble, before reaching low temperatures and forming the cold observed filament.
)
and crossed by the bubble, before reaching low temperatures and forming the cold observed filament.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{8915fig1.ps} \end{figure}](/articles/aa/full/2008/03/aa8915-07/Timg70.gif) |
Figure 1:
Temperature map of the evolution of bubbles for models 1 ( top) to 5 ( bottom line). Colors represent the logarithm of the temperature between 104 and
|
| Open with DEXTER | |
| |
Figure 2:
Evolution of the gas around the bubble of model 2 ( top) and 5 ( bottom) that forms the cold filament (
|
| Open with DEXTER | |
While a more complete model, including thermal heat, visosity and turbulence will be needed in the future, in Appendix C we show that the CO gas observed in the Perseus cluster may be compatible with the production of cold gas by a dozen of bubble pairs similar to bubbles of model 5.
The kinematics of the cooling gas (with temperature less than
![]() along the filament is displayed in Fig. 3. The top of the filament is still entrained by the bubble and has positive velocities between 100 and
along the filament is displayed in Fig. 3. The top of the filament is still entrained by the bubble and has positive velocities between 100 and
![]() ,
while the bottom of the filament is falling towards the center with negative velocities. This result, showing that the filaments are stretching, is qualitatively in agreement with the observations of Hatch et al. (2006).
,
while the bottom of the filament is falling towards the center with negative velocities. This result, showing that the filaments are stretching, is qualitatively in agreement with the observations of Hatch et al. (2006).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.15cm,clip]{8915fig3.ps} \end{figure}](/articles/aa/full/2008/03/aa8915-07/Timg75.gif) |
Figure 3:
Velocity of gas in the filament of model 5 at
|
| Open with DEXTER | |
New very-high resolution SPH simulations of the Perseus cluster show
that the cold gas observed in H![]() and CO filaments outside the cluster core
is a natural product of the perturbations of the ICM by buoyantly rising bubbles.
During the rise of a bubble, a fraction of the low cooling time ambient ICM gas around the bubble
is entrained and cools at higher radius, forming cold gas below
and CO filaments outside the cluster core
is a natural product of the perturbations of the ICM by buoyantly rising bubbles.
During the rise of a bubble, a fraction of the low cooling time ambient ICM gas around the bubble
is entrained and cools at higher radius, forming cold gas below
![]() in the trunk of the bubble. The stretching of the filaments observed in H
in the trunk of the bubble. The stretching of the filaments observed in H![]() by Hatch et al. (2006) is qualitatively reproduced.
by Hatch et al. (2006) is qualitatively reproduced.
Because no central heating is taken into account, all our models are subject to the cooling catastrophe. Is the proposed scenario still valid in a model where the cooling flow is quenched by heating processes? The role of the heating source is to suppress the formation of gas with a temperature lower than
![]() ,
but
,
but
![]() gas will still be present in abundance in the cluster center (Fabian et al. 2006). As seen in Sect. 3.2, this is precisely this gas that is trapped by the bubbles and later forms the cold filaments. The heating at the origin of the cooling flow quenching will thus have only a very weak influence on the amount of cold gas formed.
In the new emerging picture of cooling flow, AGN feedback provides some heating
(negative feedback), but it is also responsible for a positive feedback, where ICM perturbations induce cold gas production. This is a step forward in the "cold feedback'' scenario (Soker et al. 2001; Pizzolato & Soker 2005) where the feedback takes place within a large region (
gas will still be present in abundance in the cluster center (Fabian et al. 2006). As seen in Sect. 3.2, this is precisely this gas that is trapped by the bubbles and later forms the cold filaments. The heating at the origin of the cooling flow quenching will thus have only a very weak influence on the amount of cold gas formed.
In the new emerging picture of cooling flow, AGN feedback provides some heating
(negative feedback), but it is also responsible for a positive feedback, where ICM perturbations induce cold gas production. This is a step forward in the "cold feedback'' scenario (Soker et al. 2001; Pizzolato & Soker 2005) where the feedback takes place within a large region (
![]() ).
).
Acknowledgements
We are grateful to the anonymous referee for interesting and helpful comments. This work has been supported by the Horizon project.
We present the result of the control simulation run without feedback.
Figure A.1 (the equivalent of Fig. 1) shows the temperature map
of the cluster.
The cooling catastrophe occurs after
![]() .
After
.
After
![]() ,
only the
central
,
only the
central
![]() have temperatures below
have temperatures below
![]() .
Figure A.3 shows the evolution
of the mean temperature profile of the cluster. The cluster core is defined as the region
where the temperature drops below
.
Figure A.3 shows the evolution
of the mean temperature profile of the cluster. The cluster core is defined as the region
where the temperature drops below
![]() .
.
Figure A.2 shows the cold gas surface density of the outlying regions (
![]() ).
Those values have been used to correct the equivalent values for models with bubble perturbation
presented in in Appendix C.
).
Those values have been used to correct the equivalent values for models with bubble perturbation
presented in in Appendix C.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{8915fig5.ps} \end{figure}](/articles/aa/full/2008/03/aa8915-07/Timg82.gif) |
Figure A.2:
Cold gas surface density as a function of radius for the control run,
at t=400 (green) and
|
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{8915fig6.ps} \end{figure}](/articles/aa/full/2008/03/aa8915-07/Timg85.gif) |
Figure A.3:
Evolution of the mean temperature profile of the reference model, corresponding to a purely cooling flow (black:
|
Figures B.1 and B.2 show the evolution and interaction with
the rising bubble of the gas of models 2 and 5, that ends in the filament at t=600 with a
temperature below
![]() .
.
In this appendix, we compute the amount of cold gas (
![]() )
formed outside the cluster core (
)
formed outside the cluster core (
![]() ), due to the uplift of the ambient ICM gas during the bubble rise and compare it with available CO observation of the Perseus cluster.
As no central heating is taken into account at the cluster center, a large amount of cold gas is naturally deposited within the central region (at a rate of about
), due to the uplift of the ambient ICM gas during the bubble rise and compare it with available CO observation of the Perseus cluster.
As no central heating is taken into account at the cluster center, a large amount of cold gas is naturally deposited within the central region (at a rate of about
![]() ). From the amount of gas found for each simulation,
we have then subtracted the equivalent value obtained from the control simulation (see Appendix A), where no bubbles
have been launched. This ensures that the cold gas observed for
). From the amount of gas found for each simulation,
we have then subtracted the equivalent value obtained from the control simulation (see Appendix A), where no bubbles
have been launched. This ensures that the cold gas observed for
![]() is only due to ICM perturbation by the rising bubbles.
is only due to ICM perturbation by the rising bubbles.
Figure C.1, compares the cold gas surface density of models 1-3 and 5![]() ,
at three different times, with the surface density of the cold gas deduced from the Salomé et al. (2006) data (dashed line). Clearly, all models fail to reproduce the amount of gas observed between 10 and
,
at three different times, with the surface density of the cold gas deduced from the Salomé et al. (2006) data (dashed line). Clearly, all models fail to reproduce the amount of gas observed between 10 and
![]() .
However, we have to recall that in those models, only two symmetric bubbles are responsible for the ICM cooling outside the cluster core.
In a more complete model, taking into account the recurrent or continuous activity
of the AGN will generate more bubbles, multiplying the production of cold gas by a dex.
It then means that models 1-3 probably over predict the cold gas, especially at a radius larger than
.
However, we have to recall that in those models, only two symmetric bubbles are responsible for the ICM cooling outside the cluster core.
In a more complete model, taking into account the recurrent or continuous activity
of the AGN will generate more bubbles, multiplying the production of cold gas by a dex.
It then means that models 1-3 probably over predict the cold gas, especially at a radius larger than
![]() .
However, the surface density profile of model 5 at t=400 and t=500 becomes remarkably similar to the Perseus observations.
This argumentation is supported by the direct comparison of cold gas in the HorseShoe region (Pos. 11 in Salomé et al. 2007). An amount of 0.9
.
However, the surface density profile of model 5 at t=400 and t=500 becomes remarkably similar to the Perseus observations.
This argumentation is supported by the direct comparison of cold gas in the HorseShoe region (Pos. 11 in Salomé et al. 2007). An amount of 0.9 ![]()
![]() has been estimated in this region, remarkably similar to the cold gas formed in the
rim of the bubbles of models 2-4, ranging between 0.5 and 10
has been estimated in this region, remarkably similar to the cold gas formed in the
rim of the bubbles of models 2-4, ranging between 0.5 and 10 ![]()
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{8915fig9.ps} \end{figure}](/articles/aa/full/2008/03/aa8915-07/Timg92.gif) |
Figure C.1:
Cold gas surface density as a function of radius for models 1-3, 5,
at t=300 (blue), t=400 (green) and
|
It is important to notice that a carefull comparison between the models and observations should also take into account the lifetime of the filaments with respect of the AGN duty cycle. Unfortunately, the lifetime of the filaments is difficult to predict because it depends on several physical processes like heat conduction (Nipoti & Binney 2004), viscosity or turbulence, not included in the present model.