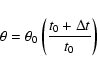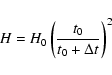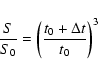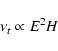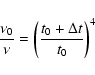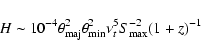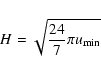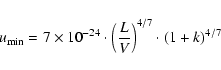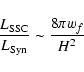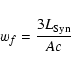A&A 477, 807-812 (2008)
DOI: 10.1051/0004-6361:20078098
Radio spectrum evolution and magnetic field
in extreme GPS radio sources
The case of RXJ1459+3337
M. Orienti1,2,3 -
D. Dallacasa2,3
1 - Instituto de Astrofisica de Canarias, 38200 La Laguna, Tenerife, Spain
2 -
Dipartimento di Astronomia, Università di Bologna, via Ranzani 1,
40127 Bologna, Italy
3 -
Istituto di Radioastronomia - INAF, via Gobetti 101, 40129 Bologna,
Italy
Received 15 June 2007 / Accepted 5 November 2007
Abstract
Aims. The knowledge of the properties of the youngest radio sources is very important in order to trace the earliest phase of the evolution of the radio emission. RXJ1459+3337, with its high turnover frequency (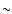 25 GHz) provides a unique opportunity to study this class of extreme objects.
25 GHz) provides a unique opportunity to study this class of extreme objects.
Methods. High-sensitivity multi-frequency VLA observations have been carried out to measure the flux-density with high accuracy, while multi-frequency VLBA observations were performed, aimed at determining the pc-scale structure. Archival ROSAT data have been used to infer the X-ray luminosity.
Results. The comparison between our new VLA data and those available in the literature shows a steady increment of the flux-density in the optically-thick part of the spectrum and a decrement of the turnover frequency. In the optically-thin regime, the source flux density has already started to decrease. Such a variability can be explained in terms of an adiabatically-expanding homogeneous radio component. The frequency range spanned by our VLBA observations, together with the resolution achieved, allows us to determine the source size and the turnover frequency, and then to derive the magnetic field directly from these observable quantities. The value obtained in this way is in good agreement with that computed assuming equipartition condition. A similar value is also obtained by comparing the radio and X-ray luminosities.
Key words: galaxies: active - galaxies: evolution - radio continuum:
general - magnetic fields - radiation mechanisms: non-thermal
The radio emission of extragalactic sources is synchrotron
radiation produced by relativistic electrons with a power-law energy
distribution. The relativistic electrons produce a power-law radio
spectrum which
reaches its maximum in
correspondence to the turnover frequency 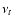 .
.
At frequencies below
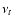 ,
the
spectrum turns over likely due to synchrotron self-absorption (Snellen
et al. 2000), although free-free absorption may also play a
role (Mutoh et al. 2002; Kameno et al. 2000).
,
the
spectrum turns over likely due to synchrotron self-absorption (Snellen
et al. 2000), although free-free absorption may also play a
role (Mutoh et al. 2002; Kameno et al. 2000).
The evolutionary models proposed to interpret the various stages of the
life-cycle of radio sources relate the typical spectral peak
of very small and then compact region with age.
In the evolutionary scenario, the peak of the spectrum
progressively moves toward lower frequencies as the radio source
expands/grows.
In this framework, GHz-peaked spectrum (GPS) and compact
steep-spectrum (CSS) radio sources, the former with
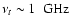 and the latter with
and the latter with
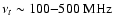 ,
are
considered to represent early stages in the individual radio source
evolution.
,
are
considered to represent early stages in the individual radio source
evolution.
The timescale of the spectral evolution in extremely young radio
sources is very short, of the order of a few tens of years
(Dallacasa 2003).
This implies that the ideal targets to investigate
how the radio spectrum evolves, and
that are the main mechanisms at work, must be sought among
sources with very high
turnover frequencies.
The existence of "extreme'' GPS sources with
turnover frequency above 10 GHz, termed "high frequency peakers''
(HFPs) by Dallacasa et al. (2000), is expected
from all the radio source evolutionary models.
Their detection is, however, quite difficult since they are
short-lived objects evolving into GPS and then CSS sources, and
to observational
limitations preventing their selection.
For a source to be recognized
as an extreme GPS object, the characteristic turnover frequency
must lie within
the frequency range sampled by large area surveys.
The frequencies of
the surveys currently available are not high enough to allow an
efficient selection of high-frequency peaking objects, since there is
insufficient information above 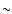 5 GHz.
5 GHz.
The radio source RXJ1459+3337 was one of the first objects to be
recognized as an "extreme'' GPS with the
turnover frequency at about 30 GHz and a peak flux density of
about 800 mJy as reported by Edge et al. (1996).
This object is associated with a quasar at
z = 0.6448. It was
detected by ROSAT (Brinkmann et al. 2000) and shows
an X-ray luminosity
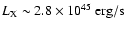 .
.
Multi-epoch VLA observations
indicate strong variability in the optically-thick part of its
radio spectrum. In particular, the flux-density variability at 5 GHz
(i.e. in the optically-thick regime) seems
to steadily increase.
Although flux-density variability is quite rare in GPS sources (O'Dea
1998), an increment of the flux density at frequencies below
 may be a consequence of the evolution of a synchrotron
self-absorbed spectrum in an expanding component.
may be a consequence of the evolution of a synchrotron
self-absorbed spectrum in an expanding component.
In this paper we present the results of
multi-frequency VLA and VLBA observations conducted in 2003 and 2005, respectively. In order to
identify the mechanisms at the basis of the spectral evolution we
combine the information on the physical conditions provided by
our new VLA data with that from archival data obtained in 1996
and 1999.
The frequency range sampled by
the new VLBA observations, together with their high-resolution,
allows us to compute the magnetic field by means of
observable quantities only, such as peak frequency, peak flux
density and the source size, as from the synchrotron theory
(Kellermann & Pauliny-Toth 1981; see also Sect. 4.2).
The comparison between this value with the
field strength obtained assuming equipartition provides important
information on the physical conditions of the radio source.
Throughout this paper, we assume the following cosmology:
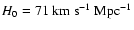 ,
,
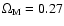 and
and
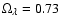 ,
in a flat Universe.
,
in a flat Universe.
Our target RXJ1459+3337
was observed with the VLA on September 12th 2003
at 8 independent frequencies (1.4, 1.7, 4.5, 4.9, 8.1, 8.4, 15.0 and 22.2 GHz) during the monitoring program of HFP candidates
(Dallacasa et al. 2000; Tinti et al. 2005),
the characteristics of the observations and the
data reduction are described in Orienti et al. (2007).
In VLA data the rms noise level on the image plane is not relevant
(always well below 1 mJy),
if compared to the main
uncertainty coming from the amplitude calibration errors, which are
within (1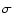 )
3% at 1.4, 1.7, 4.5, 5.0, 8.1 and 8.4 GHz, and 5%
at 15 and 22 GHz, and which are predominant in the case of relatively
strong radio sources such as RXJ1459+3337.
)
3% at 1.4, 1.7, 4.5, 5.0, 8.1 and 8.4 GHz, and 5%
at 15 and 22 GHz, and which are predominant in the case of relatively
strong radio sources such as RXJ1459+3337.
![\begin{figure}
\par\includegraphics[width=4.1cm,height=5cm,clip]{8098fg1a.eps}\h...
...ce*{4mm}
\includegraphics[width=4.1cm,height=5cm,clip]{8098fg1f.eps}\end{figure}](/articles/aa/full/2008/03/aa8098-07/Timg10.gif) |
Figure 1:
VLBA images of the source J1459+3337
at 1.7, 5, 8.4, 15, 22 and 43 GHz. On each image we give the following information on the plot
itself: a) peak flux density in mJy/beam;
b) first contour intensity (mJy/beam), which is generally
equal to 3 rms of the noise level;
contour levels increase by a factor of 2; c) the dynamic range
(the ratio of the peak brightness and 1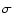 );
d) the restoring beam, plotted on the bottom left corner of each image. );
d) the restoring beam, plotted on the bottom left corner of each image. |
| Open with DEXTER |
VLBA observations of the radio source RXJ1459+3337 were carried
out on April 4th 2005 at 1.7, 5, 8.4, 15, 22 and 43 GHz, in
full polarization mode with a recording band-width of 32 MHz at 128
Mbps, for a total time of 10 hours.
The correlation was performed at the VLBA correlator in
Socorro and the data reduction was carried out with the NRAO AIPS package.
After the application of system temperature and antenna gain, the
amplitudes were checked using the data on 4C39.25 (J0927+3902).
The error on the absolute flux density scale is generally within
3%-10%, being worse at the highest frequencies.
The same source 4C39.25 was used to generate the bandpass
correction at each frequency.
However, at 43.2 GHz
a problem on the scan on the calibrator
precluded a good bandpass calibration.
Images of RXJ1459+3337
at each frequency were produced after a number of
phase-only self-calibration iterations (Fig. 1).
The source was found to
be marginally
resolved at all frequencies (Fig. 2).
The source flux densities at each frequency
have been measured on both VLBA and VLA images
in several ways, giving similar results, and the values
are reported in Table 1.
The VLBA flux-densities at each frequency are
consistent within <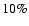 with those measured by the VLA, indicating the
lack of low-surface brightness features on the pc-scale.
with those measured by the VLA, indicating the
lack of low-surface brightness features on the pc-scale.
GPS radio sources are usually characterized by the lack of any
significant flux-density variability and they can be considered as the
least variable class of extragalactic radio sources (O'Dea
1998), with an average variation within 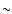 5% (Stanghellini et al. 2005). In the case of RXJ1459+3337, however,
a comparison between our new simultaneous multi-frequency VLA
observations
with those available from the literature has pinpointed a
substantial variability in the optically thick part of the spectrum.
5% (Stanghellini et al. 2005). In the case of RXJ1459+3337, however,
a comparison between our new simultaneous multi-frequency VLA
observations
with those available from the literature has pinpointed a
substantial variability in the optically thick part of the spectrum.
Figure 3 shows the light-curves of RXJ1459+3337 at
each frequency:
from these plots it seems that at 1.4 and 5 GHz, well below the turnover frequency, the flux density
has steadily increased, while
in the optically-thin regime (i.e. 22 GHz), the flux density has
decreased. Following the approach from Dallacasa
et al. (2000), we fit the simultaneous radio spectra with a
purely analytical function used to determine
the peak flux density Sm and the frequency 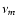 at which it occurs:
at which it occurs:
In this equation, the parameters a,b,c and d are
purely numeric, and do not provide any direct physical information.
Based on the results of the fit, we found that
the spectral peak has moved to lower
frequencies, from 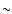
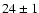 GHz in 1996 to
GHz in 1996 to 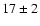 GHz in 1999 and to
GHz in 1999 and to
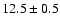 in 2003 (Fig. 4). The errors on these quantities were
calculated following the error propagation theory.
in 2003 (Fig. 4). The errors on these quantities were
calculated following the error propagation theory.
The decrement of the spectral peak together with the steady
increment of the flux-density in the optically-thick part of spectrum
suggest that the source is adiabatically expanding.
Despite the high resolution achieved by VLBA observations, the
radio source RXJ1459+3337 is only marginally resolved
even at 43 GHz.
Since the inferred source size is substantially smaller than the
VLBA beam
size at the highest frequency, our measurements are not sensitive to
small changes on the angular size and thus cannot confirm the
source expansion suggested by the spectrum evolution.
The strong variability in the optically thick part of the spectrum is
not common among sources peaking below 5 GHz (O'Dea 1998).
However, the timescale of evolution of extreme GPS sources
appears to be
quite short, of the order of a few tens of years.
In the context of
the youth scenario, such a result is not unexpected since
very young radio sources should evolve quite rapidly (Dallacasa
2003).
In the following discussion we investigate the physical conditions of
the radio emission and which mechanisms are involved in the evolution of
the radio spectrum.
As noted above,
the radio emission in extragalactic radio sources is due to
synchrotron radiation from relativistic particles with a power-law
energy distribution. However, in very small objects the observed radio spectrum
significantly departs from the power-law shape, turning over at
frequencies below the peak. Such a deviation is mostly explained in
terms of synchrotron self-absorption.
![\begin{figure}
\par\includegraphics[width=4.3cm,height=4.2cm,clip]{8098fg2.eps}
\end{figure}](/articles/aa/full/2008/03/aa8098-07/Timg17.gif) |
Figure 2:
Plot of amplitude vs. projected baseline length at 22 GHz. |
| Open with DEXTER |
The mechanism which plays the major role in the evolution of the
optically-thick part of the spectrum is the adiabatic expansion.
In this regime we have that
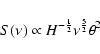 |
(1) |
(Kellermann & Pauliny-Toth 1981)
where S is the flux density at a given frequency 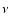 in the
optically-thick part of the spectrum, H is the magnetic field
and
in the
optically-thick part of the spectrum, H is the magnetic field
and 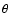 is the angular size of the emitting region.
As the radio source adiabatically expands, the opacity decreases, the
turnover frequency moves to lower frequencies and the flux
density increases at frequencies below the turnover frequency.
is the angular size of the emitting region.
As the radio source adiabatically expands, the opacity decreases, the
turnover frequency moves to lower frequencies and the flux
density increases at frequencies below the turnover frequency.
Is it possible to relate the flux-density variability observed in
RXJ1459+3337 to adiabatic expansions?
Table 1:
The VLA and VLBA flux densities of RXJ1459+3337.
![\begin{figure}
\par\includegraphics[width=5cm,height=5cm,clip]{8098fg3a.eps}\hsp...
...egraphics[width=5cm,height=5cm,clip]{8098fg3e.eps}\hspace*{2.5cm}}
\end{figure}](/articles/aa/full/2008/03/aa8098-07/Timg21.gif) |
Figure 3:
Light-curves of
RXJ1459+3337 at 1.4, 5, 8.4, 15 and 22 GHz.
In addition to the data points presented in this paper we include
those concerning the epochs 1986 (87GB, Gregory et al. 1996),
1991 (Neumann et al. 1994), 1993 (Laurent-Muehleisen et al. 1997), 1996 (Edge et al. 1996)
and 1999 (Dallacasa 2003). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6cm,height=6cm,clip]{8098fg4.eps}\end{figure}](/articles/aa/full/2008/03/aa8098-07/Timg22.gif) |
Figure 4:
The VLA radio spectrum of RXJ1459+3337 in 1996
( squares, Edge et al. 1996), in 1999 (
crosses, Dallacasa 2003), and in 2003 ( triangles,
these new data). |
| Open with DEXTER |
First of all, we assume that the radio emission is due to a
homogeneous component which is adiabatically expanding at a constant
rate:
where
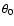 is the source angular size at the time
t0 and
is the source angular size at the time
t0 and 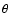 at the time
at the time
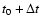 .
.
We also assume that the magnetic field is frozen in the plasma:
where H0 is the magnetic field at the time t0 and H the magnetic field at the time
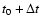 .
From Eq. (1) we find that:
.
From Eq. (1) we find that:
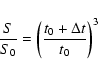 |
(2) |
where S0 and S are the flux densities measured at the same
frequency at the time t0 and
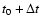 respectively.
respectively.
In the case of the 5 GHz light-curve, where enough data points are
available, we estimate the time of onset of radio emission by
fitting
the flux density measured at the different epochs
with the function
y = b + (x/a)
where
y = (S/S0)1/3,
x = t - t0, a the age
the radio emission had at epoch t0 and b a free parameter
which is almost equal to unity in our fits. As S0we consider the flux density measured at the oldest epoch
available (t0; i.e. 1986). From the best fit to the data we obtain
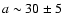 years, i.e. the birth of the radio emission should
have occurred in
years, i.e. the birth of the radio emission should
have occurred in
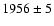 .
In the case of the 1.4 GHz light-curve, the availability of only 3 data points makes the determination of the age less accurate with
.
In the case of the 1.4 GHz light-curve, the availability of only 3 data points makes the determination of the age less accurate with
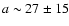 years, i.e. the radio emission should have started in
years, i.e. the radio emission should have started in
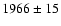 ,
in agreement with the 5 GHz determination.
We do not perform fits on the light-curves at higher
frequencies since they are affected by contamination due to the
flattening occurring near the spectral peak.
,
in agreement with the 5 GHz determination.
We do not perform fits on the light-curves at higher
frequencies since they are affected by contamination due to the
flattening occurring near the spectral peak.
As previously mentioned, adiabatic expansion also causes the spectral peak
to shift at lower frequencies. We know that the turnover frequency
is
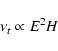 |
(3) |
where the energy of the relativistic particles is
defined as
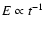 (Pacholczyk 1970). This implies that
(Pacholczyk 1970). This implies that
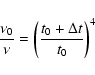 |
(4) |
where 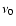 and
and 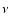 are the turnover frequency at the time t0 and
are the turnover frequency at the time t0 and
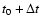 respectively.
respectively.
We estimate the epoch of the origin of radio emission by fitting the
frequency peak measured at the different epochs with the same function used
to fit the multi-epoch flux density. In this case,
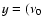 /
/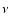 )1/4,
x= t - t0
and a the age the radio emission had at the epoch t0.
)1/4,
x= t - t0
and a the age the radio emission had at the epoch t0. 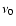 is
the peak frequency at the oldest epoch available (t0, in this case 1996).
From the best fit we find
is
the peak frequency at the oldest epoch available (t0, in this case 1996).
From the best fit we find
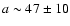 years, implying that the radio
emission originated at
years, implying that the radio
emission originated at 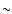
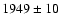 ,
still in agreement
with the values
obtained from the flux density increment, although with higher
uncertainties, since the fit has been performed on 3 data points only.
The good agreement on the determination of the source age
may indicate that the radio source is evolving
with the physical conditions predicted
by simple self-similar growth models, as previously assumed.
,
still in agreement
with the values
obtained from the flux density increment, although with higher
uncertainties, since the fit has been performed on 3 data points only.
The good agreement on the determination of the source age
may indicate that the radio source is evolving
with the physical conditions predicted
by simple self-similar growth models, as previously assumed.
Direct measurements of the magnetic field are very difficult to carry
out. The magnetic field H can be determined
from observable quantities, such as the turnover frequency 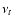 in GHz,
the peak flux density
in GHz,
the peak flux density
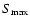 in Jy and the source angular sizes
in Jy and the source angular sizes
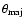 and
and
 in mas as
directly inferred from the observations.
In this case we have
in mas as
directly inferred from the observations.
In this case we have
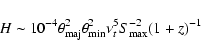 |
(5) |
(Kellermann & Pauliny-Toth 1981) where H is in Gauss.
From the fit to our new VLA data (see Sect. 2),
we obtained
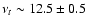 GHz and
GHz and
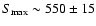 mJy.
In addition, by using the task JMFIT we measured a source angular size of
mJy.
In addition, by using the task JMFIT we measured a source angular size of
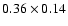 mas (
mas (
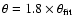 where
where
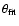 is the deconvolved full width at
half-maximum of a Gaussian brightness
distribution as used in the fitting procedure) on our best VLBA
image, namely that at 22 GHz, since the longest spacings at 43 GHz are poorly
sampled and with a rather high noise.
The resulting resolution at 43 GHz is therefore no better than
that at 22 GHz.
With these parameters we obtain
is the deconvolved full width at
half-maximum of a Gaussian brightness
distribution as used in the fitting procedure) on our best VLBA
image, namely that at 22 GHz, since the longest spacings at 43 GHz are poorly
sampled and with a rather high noise.
The resulting resolution at 43 GHz is therefore no better than
that at 22 GHz.
With these parameters we obtain
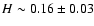 G.
G.
Another way to constrain the magnetic field is to assume that the radio
source is in equipartition conditions.
From the minimum energy conditions (Pacholczyk 1970),
the equipartition magnetic field is
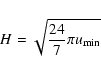 |
(6) |
where the minimum energy density
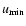 is
is
and L is the luminosity calculated at 22 GHz, i.e.
in the
optically-thin part of the spectrum, and V the volume of the radio
source in pc3.
For the calculation of V,
we assume that the radio emission has an ellipsoidal geometry and an
average optically thin spectral index of 0.7 (
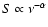 ).
Furthermore, proton and
electron energies are assumed to be equal (k=1), with a filling factor
of
unity (i.e. the source volume is fully and homogeneously filled by
relativistic plasma). From Eq. (6),
we calculate an equipartition magnetic field
).
Furthermore, proton and
electron energies are assumed to be equal (k=1), with a filling factor
of
unity (i.e. the source volume is fully and homogeneously filled by
relativistic plasma). From Eq. (6),
we calculate an equipartition magnetic field
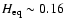 G, in very good agreement with the value directly derived
from the observed spectral quantities.
G, in very good agreement with the value directly derived
from the observed spectral quantities.
Since RXJ1459+3337 is also an X-ray source, we can try to constrain
the magnetic field by comparing the radio and X-ray luminosities, if we
assume that all the X-ray emission is due to Comptonization of the
electrons responsible for the synchrotron emission in the radio
band.
In this case we have:
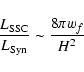 |
(7) |
(e.g. Singal 1986)
where
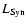 and
and
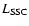 are the synchrotron and the
synchrotron self-Compton luminosity respectively and wf is the
radiation field, defined as
are the synchrotron and the
synchrotron self-Compton luminosity respectively and wf is the
radiation field, defined as
with A
the surface area of the synchrotron emission,
and c the
speed of light.
The ROSAT X-ray flux density of RXJ1459+3337 is
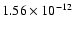 erg s-1 cm-2 (Brinkmann et al. 2000),
which corresponds to an X-ray
luminosity
erg s-1 cm-2 (Brinkmann et al. 2000),
which corresponds to an X-ray
luminosity
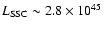 erg/s.
From the radio flux density we derive a synchrotron luminosity
erg/s.
From the radio flux density we derive a synchrotron luminosity
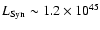 erg/s.
erg/s.
If in Eq. (7) we introduce these luminosities and the source
emitting area
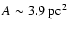 as derived
from VLBA images assuming an
ellipsoidal geometry (see above), we obtain a magnetic
field
as derived
from VLBA images assuming an
ellipsoidal geometry (see above), we obtain a magnetic
field
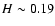 G, still in good agreement with the values derived
by the previous methods.
G, still in good agreement with the values derived
by the previous methods.
These results strongly suggest that the radio emitting plasma in such an
extreme object is consistent with the equipartition conditions.
We have presented new multi-frequency
VLBA and VLA observations of the radio source
RXJ1459+3337. Given the position of the spectral peak at
very high frequency,
this object is classified as an extreme
GPS radio source, also known as HFP.
By comparing our VLA observations with data from the literature spanning
about 17 years, we find that the flux-density in the
optically-thick part of the spectrum has been continuously increasing,
while the turnover frequency has been moving toward lower
frequencies.
Such a regular variability, although not common in GPS sources peaking below 5 GHz, can be described in the case the radio emission
originates from an adiabatically-expanding homogeneous component.
If in this context we compare either the flux-densities at the same frequency
measured at different times or the turnover frequencies,
we constrain the age of the radio emission, which is about
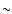
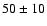 years.
years.
The resolution achieved by the VLBA observations, together with the
frequency range sampled, allowed us to "observe'' the
turnover frequency and to directly measure parameters, such
as the peak flux density and angular size of the source with great
accuracy.
In this
way we estimate the magnetic field to be
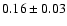 G
by means of observable
quantities only.
The consistency of this value with the field derived for a minimum
energy condition
strongly supports the idea that
such extreme objects, as RXJ1459+3337 may already be
in equipartition.
The availability of ROSAT X-ray observations allowed us to infer the
magnetic field by comparing radio and X-ray luminosities. Even in this
case, the value inferred for the magnetic field agrees with the
previous results.
G
by means of observable
quantities only.
The consistency of this value with the field derived for a minimum
energy condition
strongly supports the idea that
such extreme objects, as RXJ1459+3337 may already be
in equipartition.
The availability of ROSAT X-ray observations allowed us to infer the
magnetic field by comparing radio and X-ray luminosities. Even in this
case, the value inferred for the magnetic field agrees with the
previous results.
Acknowledgements
We thank the anonymous referee for carefully reading the manuscript
and valuable suggestions.
The VLA and VLBA are operated by the US National Radio Astronomy Observatory
which is a facility of the National Science Foundation operated under
a cooperative agreement by Associated University, Inc.
This work has
made use of the NASA/IPAC Extragalactic Database NED which is operated
by the JPL, California Institute of Technology, under contract with
the National Aeronautics and Space Administration.
- Becker, R. H.,
White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef]
- Brinkmann, W.,
Laurent-Muehleisen, S. H., Voges, W., et al. 2000, A&A, 356,
445 [NASA ADS]
(In the text)
- Dallacasa, D. 2003, PASA,
20, 79 [NASA ADS]
(In the text)
- Dallacasa, D.,
Stanghellini, C., Centonza, M., & Fanti, R. 2000, A&A, 363,
887 [NASA ADS]
(In the text)
- Edge, A. C., Jones, M.,
Saunders, R., Pooley, G., & Grainge, K. 1996, in Proceedings of
the Second Workshop on GPS and CSS Radio Sources, ed. I. A. G.
Snellen et al. (Leiden: Leiden Observatory), 208
(In the text)
- Gregory, P. C.,
Scott, W. K., Douglas, K., & Condon, J. J. 1996, ApJS, 103,
427 [NASA ADS] [CrossRef]
(In the text)
- Kameno, S.,
Horiuchi, S., Shen, Z.-Q., et al. 2000, PASJ, 52, 209 [NASA ADS]
(In the text)
- Kellermann, K. I., &
Pauliny-Toth, I. I. K. 1981, ARA&A, 19, 373 [NASA ADS] [CrossRef]
(In the text)
-
Laurent-Muehleisen, S. A., Kollgaard, R. I., Ryan, P. J., et al.
1997, A&AS, 122, 235 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Mutoh, M., Makoto,
I., Kameno, S., et al. 2002, PASJ, 54, 131 [NASA ADS]
(In the text)
- Neumann, M.,
Reich, W., Fuerst, E., et al. 1994, A&AS, 106, 303 [NASA ADS]
(In the text)
- O'Dea, C. P. 1998,
PASP, 110, 493 [NASA ADS] [CrossRef]
(In the text)
- Orienti, M., Dallacasa, D.,
& Stanghellini, C. 2007, A&A, 475, 813 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Pacholkczyk, A. G.
1970, Radio Astrophysics (San Francisco: Freeman & Co.)
(In the text)
- Polatidis, A. G., &
Conway, J. E. 2003, PASA, 20, 69 [NASA ADS]
- Singal, A. K. 1986,
A&A, 155, 242 [NASA ADS]
(In the text)
- Snellen, I. A. G.,
Schilizzi, R. T., Miley, G. K., et al. 2000, MNRAS, 319, 445 [NASA ADS] [CrossRef]
(In the text)
- Stanghellini, C., O'Dea, C.
P., Dallacasa, D., et al. 2005, A&A, 443, 891 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Tinti, S., Dallacasa, D.,
de Zotti, G., Celotti, A., & Stanghellini, C. 2005, A&A,
432, 31 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=4.1cm,height=5cm,clip]{8098fg1a.eps}\h...
...ce*{4mm}
\includegraphics[width=4.1cm,height=5cm,clip]{8098fg1f.eps}\end{figure}](/articles/aa/full/2008/03/aa8098-07/Timg10.gif)
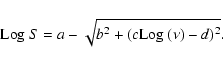
![\begin{figure}
\par\includegraphics[width=4.3cm,height=4.2cm,clip]{8098fg2.eps}
\end{figure}](/articles/aa/full/2008/03/aa8098-07/Timg17.gif)
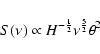
![\begin{figure}
\par\includegraphics[width=5cm,height=5cm,clip]{8098fg3a.eps}\hsp...
...egraphics[width=5cm,height=5cm,clip]{8098fg3e.eps}\hspace*{2.5cm}}
\end{figure}](/articles/aa/full/2008/03/aa8098-07/Timg21.gif)
![\begin{figure}
\par\includegraphics[width=6cm,height=6cm,clip]{8098fg4.eps}\end{figure}](/articles/aa/full/2008/03/aa8098-07/Timg22.gif)