A&A 477, 649-655 (2008)
DOI: 10.1051/0004-6361:20078266
M. Bárta1 - B. Vrsnak2 - M. Karlický1
1 - Astronomical Institute of the Academy of Sciences of the Czech Republic, 25165 Ondrejov, Czech Republic
2 -
Hvar Observatory, Faculty of Geodesy, Kaciceva 26, 10000 Zagreb, Croatia
Received 13 July 2007 / Accepted 28 September 2007
Abstract
Context. Moving blob-like features observed in the soft X-ray and EUV range above flare-loops are often interpreted as signatures of plasmoids formed by the current sheet tearing in the flare-associated reconnection process.
Aims. We investigate the evolution of the flare-associated current sheet numerically in order to analyse the kinematics and dynamics of plasmoids. The goal is to explain the broad diversity of kinematical properties of the plasmoid signatures recorded by various observational techniques.
Methods. We performed a 2-dimensional resistive-MHD numerical simulation of the reconnection starting from the Harris-type current sheet. After identifying the plasmoids, we followed their motion to determine basic kinematical parameters (velocity and acceleration), and we analysed the associated magnetic field topology.
Results. The simulation reveals a broad variety of the kinematical/dynamical properties of plasmoids - after formation, a plasmoid can move upward, downward, or can even change its direction of propagation. The highest velocities, in the range of the ambient Alfvén speed, are found in the case of upward propagating plasmoids. The acceleration is determined by the net magnetic field tension of the reconnected field lines. Downwardly propagating plasmoids achieve only a fraction of the ambient Alfvén speed. They strongly decelerate during the coalescence with low-lying flare-loops, when distinct energy-release peaks occur and loop system oscillations are excited.
Conclusions. The presented results explain, qualitatively and quantitatively, the broad spectrum of kinematical properties of various observational features attributed to the current-sheet plasmoids.
Key words: Sun: flares - Sun: corona - magnetohydrodynamics (MHD) - methods: numerical
The eruption of a coronal mass ejection (CME) is supposed to be associated with the formation of a large-scale vertical current sheet (CS) between the CME body and the solar surface: e.g., Lin (2004), Riley et al. (2007); for the observational aspect see, e.g., Vrsnak et al. (2002), Ko et al. (2003) Bemporad et al. (2006). The length of the CS increases in time due to the outward propagation of the CME, and when its length-to-width ratio becomes high enough, tearing instability sets in (Furth et al. 1963; Ugai 1987; for the observational aspect see Vrsnak et al. 2003). The X-type neutral line forms along the CS, becoming the heart of fast reconnection in the erupting magnetic field arcade. Reconnection results in a growing system of post-eruption loops, and if the reconnection-associated electric fields are strong enough to accelerate sufficient number of non-thermal particles (for various mechanisms of particle acceleration see, e.g., Aschwanden 2002), the loops become the site of a solar flare.
As the CS elongates, it is more and more likely that two (or more) X-lines form, and in between a plasmoid(s) is created (e.g., Schumacher & Kliem 1997). This is a common feature in 2-D numerical simulations of the two-ribbon flare reconnection (for 3-dimensional effects of the plasmoid formation and evolution, see Vrsnak 2003). Most often, such numerical studies are focused mainly on the coalescence of small-scale plasmoids to explain the fragmentation of the flare's energy release (Kliem et al. 2000; Shibata & Tanuma 2001), or on the upward ejected plasmoids, aiming to explain the CME process itself (see, e.g., Ugai 1992). However, we note that Forbes & Priest (1983) already recognised the downward-moving plasmoids.
The plasmoid concept is frequently used to interpret various observational phenomena from X-rays to radio waves. In the soft X-ray (SXR) range, upward-moving blobs of hot plasma are frequently observed (e.g., Shibata et al. 1995; Ohyama & Shibata 1998; Kundu et al. 2001; Kim et al. 2005, and references therein). White-light coronagraphic observations frequently reveal rising blob-like features in "rays'' formed in the wake of CMEs (Ko et al. 2003; Lin et al. 2005) or downward-moving structures in the region above the post-eruption loop system (Sheeley & Wang 2002; for a similar phenomenon observed in SXR and EUV see MacKenzie & Hudson 1999; McKenzie 2000; Raymond et al. 2003). Slowly drifting pulsating-structures sometimes observed in the microwave-wavelength dynamic spectra are often interpreted as a signature of upward or downward moving plasmoids (Kliem et al. 2000; Karlický 2004; Karlický & Bárta 2007; Ning et al. 2007).
In this paper we perform a detailed analysis of the kinematics of current-sheet plasmoids, employing numerical magnetohydrodynamical (MHD) simulations. In Sect. 2 we briefly describe the model and numerical procedure (details are provided in the Appendix; see also Bárta et al. 2007). In Sect. 3 we analyse the kinematics of plasmoids in various situations. The dynamics of the plasmoid motion is interpreted and discussed in Sect. 4, and the conclusions are drawn in Sect. 5.
The simulation is based on the standard set of 2-dimensional (2D) MHD equations, with the
resistivity dependent on the electric current density (see Appendix). The initial configuration is
a symmetric Harris-type CS coaligned with the y-axis, which is set in the middle of the 2D
rectangular computation domain (Fig. 1). We use dimensionless variables for convenience
throughout the simulation: the spatial coordinates x and y are expressed in units of the
initial CS width ![]() and time in units of the Alfvén transit time
and time in units of the Alfvén transit time
![]() ,
where
,
where
![]() is the asymptotic value
(
is the asymptotic value
(
![]() )
of the Alfvén speed at t=0 (see papers by Karlický 1988;
and Kliem et al. 2000, for details). In the following, we denote by v the velocity
normalised to the Alfvén velocity
)
of the Alfvén speed at t=0 (see papers by Karlický 1988;
and Kliem et al. 2000, for details). In the following, we denote by v the velocity
normalised to the Alfvén velocity
![]() ,
whereas by a we denote the dimensionless
acceleration, expressed in units of
,
whereas by a we denote the dimensionless
acceleration, expressed in units of
![]() ,
i.e.,
,
i.e.,
![]() .
The
ratio of specific heats is chosen to be
.
The
ratio of specific heats is chosen to be ![]() ,
and the initial asymptotic value of
plasma-to-magnetic pressure ratio is set to
,
and the initial asymptotic value of
plasma-to-magnetic pressure ratio is set to
![]() .
.
At t = 0, a limited area at the coordinate-system origin is perturbed by anomalous resistivity to
initiate reconnection. It results in plasma inflow from both sides of the CS, which leads to its
compression. As a consequence, around
![]() the dissipative region (an
X-type neutral point; hereinafter X-point) moves rapidly from the origin to a new location at
the dissipative region (an
X-type neutral point; hereinafter X-point) moves rapidly from the origin to a new location at
![]() (see also Karlický & Bárta 2006). This change of magnetic field
topology is associated with a distinct peak of dissipation power (see the bottom panel of Fig. 1;
for definition see Appendix). After this transient stage, a long period of quasi-stationary
Petschek-like regime of reconnection is established, lasting from
(see also Karlický & Bárta 2006). This change of magnetic field
topology is associated with a distinct peak of dissipation power (see the bottom panel of Fig. 1;
for definition see Appendix). After this transient stage, a long period of quasi-stationary
Petschek-like regime of reconnection is established, lasting from
![]() to
to
![]() (see the smooth part of the dissipation power profile at the bottom of Fig. 1).
During this period the newly formed loop system slowly grows (the X-point moves upward) as a
consequence of newly reconnected magnetic flux, being "rooted'' at the bottom boundary (
vx(x, 0)
= 0). This behaviour is consistent with general flare models, as well as with observations. The
final phase of the computation (
(see the smooth part of the dissipation power profile at the bottom of Fig. 1).
During this period the newly formed loop system slowly grows (the X-point moves upward) as a
consequence of newly reconnected magnetic flux, being "rooted'' at the bottom boundary (
vx(x, 0)
= 0). This behaviour is consistent with general flare models, as well as with observations. The
final phase of the computation (
![]() )
is highly intermittent, due to
formation of a number of plasmoids. The dissipation power shows numerous peaks, each caused either
by mutual coalescence of plasmoids or by coalescence of plasmoids with the underlying loop system
(see the bursting part of the dissipation power profile; for detailed discussion see Bárta et al. 2007).
)
is highly intermittent, due to
formation of a number of plasmoids. The dissipation power shows numerous peaks, each caused either
by mutual coalescence of plasmoids or by coalescence of plasmoids with the underlying loop system
(see the bursting part of the dissipation power profile; for detailed discussion see Bárta et al. 2007).
![\begin{figure}
\par\includegraphics[width=16cm,clip]{8266fig1.eps} \end{figure}](/articles/aa/full/2008/02/aa8266-07/Timg21.gif) |
Figure 1: The first three rows show an upward-moving plasmoid, downward-moving plasmoid, and a pair of upward-moving plamoids and their coalescence. Magnetic field lines are presented by dashed lines on the grayscale background representing the density; the field lines outlining the plasmoids are enhanced by bold lines (schematically presented in Fig. 7). The time profile of the dissipation power is presented in the bottom panel. |
| Open with DEXTER | |
In Fig. 2 the upward propagation of the plasmoid formed around
![]() at
at
![]() is presented (see also 1st row of Fig. 1). The accuracy of the measured
positions of the plasmoid centroid and its leading and following edge is
is presented (see also 1st row of Fig. 1). The accuracy of the measured
positions of the plasmoid centroid and its leading and following edge is
![]() .
The velocity estimates are based on
.
The velocity estimates are based on
![]() intervals, so the velocities
determined from two successive position measurements have an accuracy of
intervals, so the velocities
determined from two successive position measurements have an accuracy of
![]() .
.
As expected, the plasmoid velocity is close to the external Alfvén speed: the mean velocity of
the plasmoid estimated by the linear least-square fit equals
![]() (see
inset in Fig. 2). However, we note that the plasmoid centroid, in fact, does not move
uniformly but shows acceleration. The mean value estimated by using the 2nd degree polynomial
least-square fit equals
(see
inset in Fig. 2). However, we note that the plasmoid centroid, in fact, does not move
uniformly but shows acceleration. The mean value estimated by using the 2nd degree polynomial
least-square fit equals
![]() .
.
Beside upward-propagating plasmoids, our simulation reveals downward-moving plasmoids, too. In
Fig. 3 the downward propagation of the plasmoid formed at
![]() around
around
![]() (see 2nd row in Fig. 1) is presented. Obviously, the motion is more
complex than in the case of freely upward-propagating plasmoid: there is an acceleration phase,
followed by a phase of approximately constant velocity, and finally, strong deceleration occurs
before the plasmoid loses its identity in coalescence with the flare-loops.
(see 2nd row in Fig. 1) is presented. Obviously, the motion is more
complex than in the case of freely upward-propagating plasmoid: there is an acceleration phase,
followed by a phase of approximately constant velocity, and finally, strong deceleration occurs
before the plasmoid loses its identity in coalescence with the flare-loops.
The maximum velocity reached is
![]() .
The initial-phase acceleration is of
the order of
.
The initial-phase acceleration is of
the order of
![]() .
Strong deceleration begins after
the interaction with the low-lying flare loops has started. The interaction is revealed by
deformation of the X-point structure between the plasmoid and loops. The X-point transforms into a
small horizontal CS, characterised by an intense reverse current. The deceleration is especially
rapid at the frontal edge of the plasmoid; e.g., the X-point decelerates at
.
Strong deceleration begins after
the interaction with the low-lying flare loops has started. The interaction is revealed by
deformation of the X-point structure between the plasmoid and loops. The X-point transforms into a
small horizontal CS, characterised by an intense reverse current. The deceleration is especially
rapid at the frontal edge of the plasmoid; e.g., the X-point decelerates at
![]() .
On the other hand, the centroid decelerates at
.
On the other hand, the centroid decelerates at
![]() and such a non-uniform deceleration causes a deformation of the
plasmoid shape. The mean velocity over the distance from
and such a non-uniform deceleration causes a deformation of the
plasmoid shape. The mean velocity over the distance from
![]() to
to
![]() (t=1080-1150
(t=1080-1150
![]() )
equals
)
equals
![]() .
.
In Fig. 4 we present a complex propagation of the plasmoid formed at
![]() around
around
![]() .
The plasmoid initially moves upward at the velocity
.
The plasmoid initially moves upward at the velocity
![]() ,
showing a deceleration of
,
showing a deceleration of
![]() .
After achieving the
maximum height
.
After achieving the
maximum height
![]() ,
it starts to accelerate downwards at
,
it starts to accelerate downwards at
![]() and achieves the highest velocity of
and achieves the highest velocity of
![]() .
Finally, after the
onset of the interaction with low-lying flare loops, the plasmoid decelerates at
.
Finally, after the
onset of the interaction with low-lying flare loops, the plasmoid decelerates at
![]() ,
until it stops and loses its identity at
,
until it stops and loses its identity at
![]() .
The evolution of the reverse current formed in the interaction of the plasmoid and
flare-loops, and the associated plasmoid deceleration are qualitatively similar to that described
in Sect. 3.2. However, the deceleration is considerably weaker in this case.
.
The evolution of the reverse current formed in the interaction of the plasmoid and
flare-loops, and the associated plasmoid deceleration are qualitatively similar to that described
in Sect. 3.2. However, the deceleration is considerably weaker in this case.
In Fig. 5 we present kinematics of two plasmoids that coalesce above the flare loops.
Initially, both plasmoids move upward at
![]() .
The phase lasting from t=1500 to
1520
.
The phase lasting from t=1500 to
1520
![]() is characterised by the accelerated merging motion towards the X-point between
the plasmoids. The leading plasmoid decelerates by
is characterised by the accelerated merging motion towards the X-point between
the plasmoids. The leading plasmoid decelerates by
![]() and the
following one accelerates by
and the
following one accelerates by
![]() .
The X-point in between them moves
at approximately constant velocity of
.
The X-point in between them moves
at approximately constant velocity of
![]() .
.
During the coalescence phase, the X-line located between plasmoids transforms: the reconnection of
the magnetic field bounding the CS stops, because the merging motion of plasmoids reduces the
length-to-width ratio of the CS segment between them. After the plasmoids come close enough, the
secondary CS is induced between them. In this small CS (characterised by the reverse current), the
reconnection of the poloidal fields of plasmoids starts, driven by the attractive force of the
parallel currents flowing along the plasmoids. This phase lasts from t=1520 to 1530
![]() ,
during which the plasmoids lose their individuality. After
,
during which the plasmoids lose their individuality. After
![]() the newly
formed plasmoid continues to move upward at the velocity
the newly
formed plasmoid continues to move upward at the velocity
![]() .
After
.
After
![]() ,
a complex motion similar to what is shown in Fig. 4 is observed
(
,
a complex motion similar to what is shown in Fig. 4 is observed
(
![]() ), but characterised by a faster descending motion,
), but characterised by a faster descending motion,
![]() .
The final deceleration of the plasmoid is around
.
The final deceleration of the plasmoid is around
![]() .
.
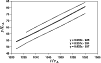 |
Figure 2:
Kinematics of the upward-propagating plasmoid formed at
|
| Open with DEXTER | |
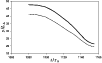 |
Figure 3:
Kinematics of the downward propagating plasmoid formed around
|
| Open with DEXTER | |
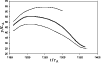 |
Figure 4:
Kinematics of the plasmoid formed around
|
| Open with DEXTER | |
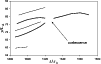 |
Figure 5:
Kinematics of a pair of plasmoids formed around
|
| Open with DEXTER | |
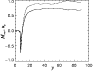 |
Figure 6:
The outflow speed uy (dashed line) and the magnetosonic Mach number
|
| Open with DEXTER | |
The presented analysis demonstrates that plasmoids show a broad variety of kinematical behaviours.
Bearing this in mind, it is instructive to check outflow velocities in the steady-state
reconnection regime (![]() 300-1000
300-1000
![]() ), representing a kind of the
referent velocity pattern. In Fig. 6 we show the plasma flow velocity uy(y) and the
corresponding magnetosonic Mach number
), representing a kind of the
referent velocity pattern. In Fig. 6 we show the plasma flow velocity uy(y) and the
corresponding magnetosonic Mach number
![]() ,
measured along the y-axis.
,
measured along the y-axis.
Inspecting Fig. 6, we find several differences between the upward and downward jets, which
are separated by the diffusion region centred around
![]() ,
where uy=0. The
upward jet consists of a flow-acceleration segment (
,
where uy=0. The
upward jet consists of a flow-acceleration segment (![]() 10-15
10-15 ![]() )
and the
constant-velocity segment (
)
and the
constant-velocity segment (
![]()
![]() )
characterised by the velocity
)
characterised by the velocity
![]() 0.9-1
0.9-1
![]() .
Such outflow velocities are consistent with the analytical
reconnection theory (see, e.g., Appendix in Aurass et al. 2002). On the other hand, the
downward jet, being squeezed between the diffusion region and the flare loops, consists of the
acceleration segment (
.
Such outflow velocities are consistent with the analytical
reconnection theory (see, e.g., Appendix in Aurass et al. 2002). On the other hand, the
downward jet, being squeezed between the diffusion region and the flare loops, consists of the
acceleration segment (![]() 10-8
10-8 ![]() )
and the deceleration segment
(
)
and the deceleration segment
(![]() 8-7
8-7 ![]() ). The velocity never exceeds 0.75
). The velocity never exceeds 0.75
![]() ,
so flow
velocities, similar to plasmoid velocities, tend to be higher in the upward than in the downward
jet.
,
so flow
velocities, similar to plasmoid velocities, tend to be higher in the upward than in the downward
jet.
It is interesting to note that, although the upward and downward outflow velocities are quite different, the maximum magnetosonic Mach numbers are relatively similar, ranging around 0.6 and 0.7 for the downward and upward jets, respectively. Thus, both jets are submagnetosonic and have comparable Mach numbers. Such an outcome differs from simulations performed by Forbes (1986) and Forbes & Malherbe (1991), where it was found that flow velocities in the upward and downward jets are comparable only if the upward jet is supermagnetosonic. According to these simulations, the downward outflow does not exist if the upward jet is submagnetosonic. It is quite likely that our reconnection regime is somewhere in between these two situations, but it should be also emphasised that the simulations differ in several physical and technical details (e.g., energy equation, numerical resistivity, etc.).
Finally, it should be noted that, for the ratio of specific heats ![]() ,
which we used in the
simulation, one would expect from the analytic theory that reconnection outflows are
supermagnetosonic already for
,
which we used in the
simulation, one would expect from the analytic theory that reconnection outflows are
supermagnetosonic already for ![]() (see, e.g., Eq. (39) of Forbes &
Malherbe 1991). In other words, according to the analytic theory, our jets should be
supermagnetosonic, since we used
(see, e.g., Eq. (39) of Forbes &
Malherbe 1991). In other words, according to the analytic theory, our jets should be
supermagnetosonic, since we used
![]() .
Such a discrepancy is inherent in comparisons of the
analytical and numerical results. For example, Forbes & Malherbe (1991) found that
outflows become supermagnetosonic for
.
Such a discrepancy is inherent in comparisons of the
analytical and numerical results. For example, Forbes & Malherbe (1991) found that
outflows become supermagnetosonic for ![]() ,
whereas one would expect the limiting value to
be
,
whereas one would expect the limiting value to
be ![]() ,
since they used
,
since they used
![]() .
A possible explanation might be related to the
numerical limitations of simulations; for example, after checking the spatial distribution of
.
A possible explanation might be related to the
numerical limitations of simulations; for example, after checking the spatial distribution of
![]() ,
we found that its value starts to be well above
,
we found that its value starts to be well above
![]() already at
0.1-0.2
already at
0.1-0.2 ![]() ,
upstream of the slow mode shocks.
,
upstream of the slow mode shocks.
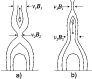 |
Figure 7: Schematics of the magnetic field pattern when the plasmoid moves: a) upward, b) downward (compare with Fig. 1). Horizontal arrows depict the magnetic-flux inflow rate at the diffusion region above (v1B1) and below (v2B2) the plasmoid. Vertical arrows indicate the direction of the plasmoid motion. |
| Open with DEXTER | |
The basic question that arises from the presented analysis is what conditions determine the direction of the plasmoid motion. Since the magnetic tension of the reconnected field lines is the primary driver of the plasma motion in the reconnection outflow jet (the "sling-shot effect''; see, e.g., Vrsnak & Skender 2005), we compare the magnetic field-line pattern in situations of upward and downward motion. In Fig. 7a we sketch the pattern we find in the case of upward-moving plasmoids (note the V-shape of field lines around the plasmoid, giving rise to the upward directed tension), whereas in Fig. 7b we show the pattern corresponding to downward moving plasmoids (the inverse V-shape of field lines results in downward-directed tension).
The primary parameter that governs the described shapes of field lines is the reconnection rate
![]() at X-points above and below the plasmoid. If
at X-points above and below the plasmoid. If
![]() is
higher at the X-point above the plasmoid than at the X-point below it, i.e., if the rate by which
the magnetic flux is reconnected in the upper diffusion region is higher than in lower one, the
field lines form a pattern like in Fig. 7b and the field line tension drags the plasmoid
downwards. If more field lines are reconnected in the lower diffusion region than in the upper one,
the resulting pattern is like in Fig. 7a and the plasmoid is expelled upwards.
is
higher at the X-point above the plasmoid than at the X-point below it, i.e., if the rate by which
the magnetic flux is reconnected in the upper diffusion region is higher than in lower one, the
field lines form a pattern like in Fig. 7b and the field line tension drags the plasmoid
downwards. If more field lines are reconnected in the lower diffusion region than in the upper one,
the resulting pattern is like in Fig. 7a and the plasmoid is expelled upwards.
Especially interesting are situations when the direction of motion changes (Fig. 4, as well
as Fig. 5 after the coalescence). Indeed, in these cases the topology of field lines changes
from that drawn in Fig. 7a into what is shown in Fig. 7b (e.g., around
![]() the pattern is like in Fig. 7a, and around
the pattern is like in Fig. 7a, and around
![]() the
pattern is like in Fig. 7b). Such a transformation implies a change in the reconnection rate
in both the upper and lower diffusion region; i.e., the magnetic flux inflow increases above the
plasmoid and decreases below it. In this respect, note that the rate at which magnetic flux flows
into the CS generally depends on the position, i.e., the y-coordinate; it fluctuates around the
steady-state conditions due to MHD waves created in the interaction of the downward directed
reconnection jet (and imbedded plasmoids) with the flare loops, as well as due to perturbations
left behind the previous upward and/or downward moving plasmoids.
the
pattern is like in Fig. 7b). Such a transformation implies a change in the reconnection rate
in both the upper and lower diffusion region; i.e., the magnetic flux inflow increases above the
plasmoid and decreases below it. In this respect, note that the rate at which magnetic flux flows
into the CS generally depends on the position, i.e., the y-coordinate; it fluctuates around the
steady-state conditions due to MHD waves created in the interaction of the downward directed
reconnection jet (and imbedded plasmoids) with the flare loops, as well as due to perturbations
left behind the previous upward and/or downward moving plasmoids.
The acceleration of the CS outflow, i.e., the existence of the fast outflow jets in the
reconnecting CS, is a consequence of the magnetic field tension of strongly bent reconnected field
lines. The equation of motion can be written in an approximate form:
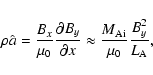 |
(1) |
The accelerations found in Sect. 3 are in the range
![]() -0.01
-0.01
![]() ;
i.e., they are somewhat smaller than
calculated, probably because the CS thickness at the plasmoid location is larger than
;
i.e., they are somewhat smaller than
calculated, probably because the CS thickness at the plasmoid location is larger than ![]() .
Taking the order of magnitude values
.
Taking the order of magnitude values
![]() km s-1 and
km s-1 and
![]() km (see
the Appendix for details), which is equivalent to
km (see
the Appendix for details), which is equivalent to
![]() s, this corresponds to
s, this corresponds to
![]() -10 km s-2. If we compare this order of magnitude estimate with
Kim et al. (2005), who measured in three SXR plasmoids a strong acceleration of about 2.5,
1.3, and 2 km s-2, we find that our result is consistent with the SXR observations if we
assume
-10 km s-2. If we compare this order of magnitude estimate with
Kim et al. (2005), who measured in three SXR plasmoids a strong acceleration of about 2.5,
1.3, and 2 km s-2, we find that our result is consistent with the SXR observations if we
assume
![]() km s-1, which is a reasonable value for the active region corona
(see, e.g., Vrsnak et al. 2004).
km s-1, which is a reasonable value for the active region corona
(see, e.g., Vrsnak et al. 2004).
Our simulation shows that plasmoids achieve a wide range of velocities, with an upper limit around
![]() .
This is consistent with the SXR observations that usually reveal velocities
from several tens to several hundred km s-1 (e.g., Shibata et al. 1995), rarely
exceeding 1000 km s-1 (Kim et al. 2005). Somewhat lower velocities are observed in
downflows (McKenzie & Hudson 1999; McKenzie 2000), as we also found in our
simulation.
.
This is consistent with the SXR observations that usually reveal velocities
from several tens to several hundred km s-1 (e.g., Shibata et al. 1995), rarely
exceeding 1000 km s-1 (Kim et al. 2005). Somewhat lower velocities are observed in
downflows (McKenzie & Hudson 1999; McKenzie 2000), as we also found in our
simulation.
In this respect, it is interesting to note that the blob-like features recorded by coronagraphs (Ko et al. 2003; Lin et al. 2005), presumably representing plasmoids at greater heights, show similar velocities but considerably weaker accelerations (below 100 m s-2; Ko et al. 2003) than SXR plasmoids. Lower accelerations are probably a consequence of a larger CS width and weaker ambient field at greater heights, resulting in a weaker tension. On the other hand, velocities are similar, since in the considered height range the Alfvén velocity does not change very much (Vrsnak et al. 2004). The downward propagating coronagraphic plasmoids again show a somewhat lower velocities, generally below 100 km s-1 (Sheeley & Wang 2002).
The deceleration of downward-directed plasmoids in the stage of coalescence with flare loops is especially important, since these intervals correspond to the most powerful energy-release episodes (Bárta et al. 2007). During the coalescence the "reverse'' current is induced, causing strong deceleration of the plasmoid: since the merging speed is higher than the diffusion velocity, the magnetic field piles up, which leads to the magnetic pressure increase between the flare-loops and the plasmoid. Due to the strong "collision'', the plasmoid and flare-loops get deformed. As a result, large amplitude waves are excited, propagating downward along outermost loops in the system. After the coalescence, eigenmode oscillations in the loop system develop (to be analysed in a separate paper).
Interactions of plasmoids with the flare loops, as well as plasmoid-plasmoid interactions, are also important from the point of view of the flare energetics. Each time the plasmoid-loop or the plasmoid-plasmoid coalescence occurs, we find a prominent sharp peak in the dissipation-power curve, as can be seen in the bottom panel of Fig. 1. It is interesting to note that the plasmoid-loop coalescence should have a distinct observational signature. Since the plasmoid interacts with the field lines that map the part of the flare ribbon that is already behind the frontal edge of the ribbon, the plasmoid-loop coalescence should be seen as re-brightening of certain parts of the flaring area. Such a phenomenon might be difficult to observe in chromospheric spectral lines, which are often burdened by saturation effects. On the other hand, it might explain re-brightenings of certain footpoint sources sometimes observed in hard X-rays (see, e.g., Miklenic et al. 2007).
The current-sheet tearing results in formation of plasmoids whose dynamics is determined by the
reconnection rate at the two associated X-points. If the reconnection rate is higher at the X-point
located below the plasmoid, the plasmoid moves upward since the net tension causes the upward
acceleration. If the reconnection is faster at the X-point above the plasmoid, it accelerates
downward. The accelerations are limited
![]() .
For the ambient
Alfvén velocity of the order of 1000 km s-1, the dimensionless reconnection rate
.
For the ambient
Alfvén velocity of the order of 1000 km s-1, the dimensionless reconnection rate
![]() ,
and the effective CS thickness of 1000 km (Shibata & Tanuma 2001; Lin et
al. 2007), the upper limit to the acceleration equals to a=10 km s-2. This upper
limit is consistent with the observed accelerations of upward-moving SXR plasmoids, which attain
values of several km s-2 (Kim et al. 2005).
,
and the effective CS thickness of 1000 km (Shibata & Tanuma 2001; Lin et
al. 2007), the upper limit to the acceleration equals to a=10 km s-2. This upper
limit is consistent with the observed accelerations of upward-moving SXR plasmoids, which attain
values of several km s-2 (Kim et al. 2005).
The upper limit to the plasmoid velocity found in our simulation for the upward propagating plasmoids is
consistent with the analytical-approach limit
![]() (see Appendix in Aurass et
al. 2002). It is also consistent with observations which do not show significant difference of the
plasmoid velocities in the heliocentric distance range R=2-10, where the Alfvén speed is in the range
300-600 km s-1 (see Fig. 3 in Vrsnak et al. 2004).
(see Appendix in Aurass et
al. 2002). It is also consistent with observations which do not show significant difference of the
plasmoid velocities in the heliocentric distance range R=2-10, where the Alfvén speed is in the range
300-600 km s-1 (see Fig. 3 in Vrsnak et al. 2004).
The downward-moving plasmoids are characterised by lower velocities (only a fraction of
![]() ), since they do not have enough time to accelerate to full speed. The acceleration is stopped
by the coalescence of the plasmoid and the low-lying flare loops. After the interaction starts, the
plasmoid experiences a strong deceleration as a result of the magnetic flux pile-up between the
plasmoid and the loops (the motion is faster than the reconnection velocity), so the mean velocity
of the downward-moving plasmoids is significantly lower than the Alfvén speed, which might
explain relatively low velocities of downward-moving features observed above the flare loops
(MacKenzie & Hudson 1999; McKenzie 2000) or post-eruption loops (Sheeley &
Wang 2002).
), since they do not have enough time to accelerate to full speed. The acceleration is stopped
by the coalescence of the plasmoid and the low-lying flare loops. After the interaction starts, the
plasmoid experiences a strong deceleration as a result of the magnetic flux pile-up between the
plasmoid and the loops (the motion is faster than the reconnection velocity), so the mean velocity
of the downward-moving plasmoids is significantly lower than the Alfvén speed, which might
explain relatively low velocities of downward-moving features observed above the flare loops
(MacKenzie & Hudson 1999; McKenzie 2000) or post-eruption loops (Sheeley &
Wang 2002).
Finally, we note that our simulation run lasts until
![]() .
Assuming the effective
Alfvén transit time
.
Assuming the effective
Alfvén transit time
![]() s, this corresponds to
s, this corresponds to ![]() 0.5 h. The
plasmoid-dominated phase starts after
0.5 h. The
plasmoid-dominated phase starts after
![]() ;
i.e., our simulation covered some
10 min of this phase, which apparently continues after the end of our run. In this stage, plasmoids
have been forming irregularly in 1-2 min intervals. Assuming the Alfvén velocity of
1000 km s-1, that would correspond to the spatial separation of the order of
;
i.e., our simulation covered some
10 min of this phase, which apparently continues after the end of our run. In this stage, plasmoids
have been forming irregularly in 1-2 min intervals. Assuming the Alfvén velocity of
1000 km s-1, that would correspond to the spatial separation of the order of
![]() 100 Mm. Bearing in mind that some plasmoids move downward, this implies a typical
separation between upward-moving plasmoids in the low corona of a few 100 Mm, crossing a certain
coronal level in several-minute intervals. Analogously, the downward-moving plasmoids and
consequent interactions with flare loops should be observed at a similar frequency.
100 Mm. Bearing in mind that some plasmoids move downward, this implies a typical
separation between upward-moving plasmoids in the low corona of a few 100 Mm, crossing a certain
coronal level in several-minute intervals. Analogously, the downward-moving plasmoids and
consequent interactions with flare loops should be observed at a similar frequency.
We describe the evolution of the magnetised plasma by the compressible resistive one-fluid MHD
equations
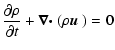 |
|||
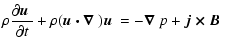 |
|||
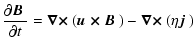 |
|||
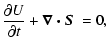 |
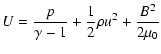 |
|||
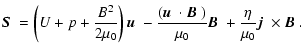 |
At the very beginning of the simulation, the system consists of the symmetric vertical Harris-type current sheet in the middle of the 2D rectangular computation domain. At t=0, a limited area surrounding the origin is perturbed by anomalous resistivity for a short time. Then the evolution is numerically simulated using the 2D Lax-Wendroff scheme with free boundary conditions on upper part and (due to the sheet symmetry) on both the left and right sides.
Symmetric (
Q(y)=Q(-y)) and anti-symmetric (
Q(y)=-Q(-y)) relations are respectively used for
quantities (Q)
![]() and uy, Bx at the bottom part of boundary. This choice
ensures a vertical magnetic field at the bottom boundary, and it is equivalent to a fixed boundary
simulating the presence of the dense solar photosphere.
and uy, Bx at the bottom part of boundary. This choice
ensures a vertical magnetic field at the bottom boundary, and it is equivalent to a fixed boundary
simulating the presence of the dense solar photosphere.
In order to have a simple quantitative measure of reconnection energetics we use the power
dissipated into the Joule heat,
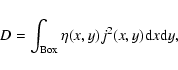
Acknowledgements
This research was supported by Grant IAA300030701 of the Academy of Sciences and grant 205/07/1100 of the Grant Agency of the Czech Republic. B.V. is grateful to the Astronomical Institute of the Academy of Sciences of the Czech Republic for sponsoring his stay at Ondrejov in 2006. B.V. also acknowledges the support of ISSI-Bern, who sponsored the project "Current Sheet Observations vs. Current Sheet Models'' (P.I. Dr. Giannina Poletto) and provided the organisation of team meetings that played a significant role in motivating this work. We would like to thank to Drs. Alessandro Bemporad, Jun Lin, and Giannina Poletto, as well as an unknown referee, whose comments and suggestions led to significant improvement of the paper.