A&A 477, 443-457 (2008)
DOI: 10.1051/0004-6361:20054773
R. Quast1 - D. Reimers2 - R. Baade2
1 - Brockmann Consult, GKSS-Forschungszentrum / GITZ, Max-Planck-Straße 2,
21502 Geesthacht, Germany
2 -
Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112,
21029 Hamburg, Germany
Received 24 December 2005 / Accepted 8 October 2007
Abstract
Aims. We examine the ionization, abundances, and differential dust depletion of metals, the kinematic structure, and the physical conditions in the molecular hydrogen-bearing sub-damped Ly ![]() system toward HE 0515-4414.
system toward HE 0515-4414.
Methods. We used the STIS and VLT UVES spectrographs to obtain high-resolution recordings of the damped Ly ![]() profile and numerous associated metal lines. Observed element abundances were corrected with respect to dust depletion effects.
profile and numerous associated metal lines. Observed element abundances were corrected with respect to dust depletion effects.
Results. The sub-damped Ly ![]() absorber at redshift z=1.15 is unusual in several aspects. The velocity interval of associated metal lines extends for 700 km s-1. In addition, saturated H I absorption is detected in the blue damping wing of the
absorber at redshift z=1.15 is unusual in several aspects. The velocity interval of associated metal lines extends for 700 km s-1. In addition, saturated H I absorption is detected in the blue damping wing of the
![]() cm-2 main component. The column density ratios of associated Al II, Al III, and Fe II lines indicate that the absorbing material is ionized. Nineteen of a total of 31 detected metal line components are formed within peripheral H II regions, while only 12 components are associated with the predominantly neutral main absorber. The bimodal velocity distribution of metal line components suggests two interacting absorbers. For the main absorber, the observed abundance ratios of refractory elements to Zn range from a Galactic warm disk
cm-2 main component. The column density ratios of associated Al II, Al III, and Fe II lines indicate that the absorbing material is ionized. Nineteen of a total of 31 detected metal line components are formed within peripheral H II regions, while only 12 components are associated with the predominantly neutral main absorber. The bimodal velocity distribution of metal line components suggests two interacting absorbers. For the main absorber, the observed abundance ratios of refractory elements to Zn range from a Galactic warm disk
![]()
![]() 0.06,
0.06,
![]()
![]() 0.05 to halo-like and essentially undepleted patterns. The dust-corrected metal abundances indicate a nucleosynthetic odd-even effect and might imply an anomalous depletion of Si relative to Fe for two components, but otherwise they do correspond to solar ratios. The intrinsic average metallicity is almost solar
0.05 to halo-like and essentially undepleted patterns. The dust-corrected metal abundances indicate a nucleosynthetic odd-even effect and might imply an anomalous depletion of Si relative to Fe for two components, but otherwise they do correspond to solar ratios. The intrinsic average metallicity is almost solar
![]()
![]() 0.19, whereas the uncorrected average is
0.19, whereas the uncorrected average is
![]()
![]() 0.04. The ion abundances in the periphery conform to solar element composition.
0.04. The ion abundances in the periphery conform to solar element composition.
Conclusions. The detection of H II, as well as the large variation in dust depletion for this sight line, raises the question whether in future studies of damped Ly ![]() systems ionization and depletion effects have to be considered in more detail. Ionization effects, for instance, may mimic an enrichment of
systems ionization and depletion effects have to be considered in more detail. Ionization effects, for instance, may mimic an enrichment of ![]() elements. An empirical recipe for detecting H II regions is provided.
elements. An empirical recipe for detecting H II regions is provided.
Key words: cosmology: observations - galaxies: abundances - galaxies: interactions - galaxies: intergalactic medium - galaxies: quasars: absorption lines - galaxies: quasars: individual: HE 0515-4414
The study of QSO absorption lines provides vital information on the
nucleosynthetic history of the universe by complementing the
compositional analysis of stars and interstellar space in local galaxies
with element abundances at higher redshift. In particular, interests are
focused on extragalactic structures termed damped Ly ![]() (DLA)
systems, essentially comprised of neutral hydrogen with column densities
(DLA)
systems, essentially comprised of neutral hydrogen with column densities
![]()
![]() 1020 atoms cm-2 (for a review
see Wolfe et al. 2005). Absorbers in the sub-DLA range with column
densities
1020 atoms cm-2 (for a review
see Wolfe et al. 2005). Absorbers in the sub-DLA range with column
densities
![]() atoms cm-2 might be mainly
neutral when the ionizing background is reduced
(Péroux et al. 2003,2002). The aim of these examinations is
to establish accurate element abundances for the aggregations of neutral
gas that are examples of interstellar environments in the high-redshift
universe. Since the measurement of metal column densities is
straightforward, the only problem is their correct interpretation.
atoms cm-2 might be mainly
neutral when the ionizing background is reduced
(Péroux et al. 2003,2002). The aim of these examinations is
to establish accurate element abundances for the aggregations of neutral
gas that are examples of interstellar environments in the high-redshift
universe. Since the measurement of metal column densities is
straightforward, the only problem is their correct interpretation.
The true nature of DLA systems is unknown and the underlying population, being constituted of hierarchical structures with different morphologies, chemical enrichment histories, and physical environments, is multifarious. The diversity is attested by the disparate values obtained for metal abundances at any given redshift.
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{dla_f1}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg20.gif) |
Figure 1: STIS Echelle order showing the sub-damped H I profile with redshift z=1.15. The solid curve indicates the optimized profile decomposition of the spectrum, while the dashed curves mark the damped profile. The blue damping wing is blended with further H I absorption which is associated with numerous metal lines (Fig. 2). The origin of the radial velocity axis corresponds to the redshift z=1.15080. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{dla_f2a}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg21.gif) |
Figure 2: Metal lines associated with the sub-damped profile shown in Fig. 1. The dashed and solid curves indicate the optimized profile decomposition and its instrumental convolution. Individual components are marked by vertical lines. Data represented by empty circles are ignored in the profile decomposition. Components 3, 16, and 17 possibly are unresolved blends (Quast et al. 2004a). This figure is continued in the Online Material. |
| Open with DEXTER | |
The metallicity of DLA systems is not correlated with their column density, however, there is an upper bound for distribution of column densities versus metallicity (Boissé et al. 1998). Though there are high column density DLA absorbers with high metallicity in the foreground of the star forming hosts of gamma-ray bursts (Watson et al. 2005), similar absorbers are not detected toward QSOs. The cosmic mean metallicity of DLA absorbers increases with cosmic time (Rao et al. 2005; Kulkarni et al. 2005; Prochaska et al. 2003), but is an order of magnitude lower than predicted by cosmic star formation history (see the discussion of the missing metals problem by Wolfe et al. 2005). The solution to this problem is a matter of debate. Conclusive evidence of enriched material ejected from DLA absorbers into the intergalactic medium or of active star formation restricted to compact regions is missing. The latter possibility is closely linked to the physical properties of the interstellar medium and its molecular content (Wolfe et al. 2003b,a). Molecular gas is uncommon in DLA absorbers. If found, the fraction of molecular hydrogen, usually between 10-6 and 10-2, is not correlated with the column density of atomic hydrogen (Ledoux et al. 2003). However, Petijean et al. (2006) have demonstrated that the presence of molecular hydrogen at high redshift is strongly correlated with the metallicity.
Since the spectroscopic analysis is restricted to the gaseous phase of the absorbing medium, observed element abundances are potentially distorted by dust removing atoms in varying amounts, depending on their affinity to the solid state. In particular high-metallicity and molecule-bearing absorbers are affected by dust (Ledoux et al. 2003; Petijean et al. 2002). Depletions are largely lower than in the Galactic halo, but increase with metallicity (Vladilo 2004). In practice, the observed element abundances are corrected ad hoc, using Galactic interstellar depletion patterns as reference (Vladilo 2002a,b). Another aspect of dust is the possibility that DLA absorbers may elude detection because the background QSOs are obscured (Fall & Pei 1993). The selection effects are complicated since obscurement is counteracted, but not compensated, by amplification due to gravitational lensing (Smette et al. 1997). The effect of dust is subject of several studies (Vladilo & Péroux 2005; Akerman et al. 2005; Quast et al. 2004b; Murphy & Liske 2004; Wild et al. 2005; Smette et al. 2005). A further difficulty are ionization effects. Examples of DLA-associated metal line components formed within mainly ionized material are given by Prochaska et al. (2002) and Dessauges-Zavadsky et al. (2006).
The column density distribution and kinematic structure of absorbers provide important constraints on hierarchical structuring (e.g. Nagamine et al. 2004; Cen et al. 2003) and immediate insight into the processes of galaxy formation (Wolfe & Prochaska 2000). The extended multicomponent velocity structure and characteristic asymmetry of DLA-associated metal lines is consistent with galaxy formation models in hierarchic cold dark matter cosmologies, and reproducible by the hydrodynamical simulation of rotation, random motion, infall, and merging of irregular protogalactic clumps hosted by collapsed dark matter halos (Haehnelt et al. 1998). The velocity structure of sub-DLA absorbers compares to that of the higher column density systems (Péroux et al. 2003), which is unexpected since semianalytic galaxy formation models (Maller et al. 2003,2001) predict markedly different kinematic properties. The absorption velocity intervals of both sub-DLA and DLA absorbers typically extend for 100 km s-1. More extended systems tend to higher metallicities and lower hydrogen column densities (Wolfe & Prochaska 1998). In particular the latter property is unexpected and difficult to interpret in terms of rotating disks models. The most extended systems, however, are probably due to interacting or merging galaxies (Richter et al. 2005; Petijean et al. 2002). Strong observational evidence for a correlation between DLA metallicity and absorption profile velocity spread, which probably is the consequence of a mass-metallicity relation, has recently been provided by Ledoux et al. (2006).
In this study we revisit the z=1.15 sub-DLA system toward HE 0515-4414 (de la Varga et al. 2000; Reimers et al. 1998). The main components of associated metal lines exhibit excited neutral carbon and molecular hydrogen (Quast et al. 2002; Reimers et al. 2003). Most outstanding, the absorption velocity interval extends for 700 km s-1. Based on refined spectroscopy, we examine the ionization, abundances, and differential dust depletion of metals as well as the kinematic structure, and physical conditions of this unusual absorption line system.
Ranging from the NUV to the end of the visual, the observations cover the sub-damped profile at 2615 Å (Fig. 1) and numerous associated metal lines (Fig. 2).
Table 1: Details of spectra obtained with UVES.
HE 0515-4414 was observed during ten nights between October 7, 2000 and January 3, 2001, using the UV-Visual Echelle Spectrograph (UVES) installed at the second VLT Unit Telescope (Kueyen). Thirteen exposures were made in the dichroic mode using standard settings for the central wavelengths of 3460/4370 Å in the blue, and 5800/8600 Å in the red (Table 1). The CCDs were read out in fast mode without binning. Individual exposure times were 3600 and 4500 s, under photometric to clear sky and seeing conditions ranging from 0.47 to 0.70 arcsec. The slit width was 0.8 arcsec providing a spectral resolution of about 55 000 in the blue and slightly less in the red. The raw data frames were reduced at the ESO Quality Control Garching using the UVES pipeline Data Reduction Software. Finally, the individual vacuum-barycentric corrected spectra were combined resulting in an effective signal-to-noise ratio per pixel of 90-140.
The UV-visual recordings were supplemented by spectra obtained with the
Space Telescope Imaging Spectrograph (STIS) during three orbits between
January 31 and February 1, 2000, ranging from 2300 to 3100 Å. The total
exposure time was 31 500 s, while the instrument was operating in the
medium resolution NUV mode (E230M) with the entrance aperture of
![]()
![]()
![]() providing a spectral resolution of about
30 000. The raw spectra were reduced at the Space Telescope Science
Institute using the STIS pipeline software completed by an additional
interorder background correction. The combined spectra show an effective
signal-to-noise ratio per pixel of 5-10.
providing a spectral resolution of about
30 000. The raw spectra were reduced at the Space Telescope Science
Institute using the STIS pipeline software completed by an additional
interorder background correction. The combined spectra show an effective
signal-to-noise ratio per pixel of 5-10.
There are several basically different techniques for the analysis of QSO absorption lines: the classical line profile decomposition, the apparent optical depth method (Savage & Sembach 1991), and Monte Carlo inversion (Levshakov et al. 2000). While the classical profile decomposition postulates discrete homogenous absorbers with Gaussian (i.e. thermal or microturbulent) particle velocity distributions, the apparent optical depth technique allows the very direct interpretation of observed spectra without the need to consider the velocity structure of spectral lines as long as the absorption is optically thin or sufficiently resolved. Otherwise, the apparent optical depth is not representative and additional operations are required to recover the correct column density (Jenkins 1996). The corrective procedure, however, is only approved for synthetic spectra with Gaussian velocity distributions underlying the individual components. Monte Carlo inversion considers random velocity and density fields along the sight line, but requires photoionization calculations to connect the random fields to the observed absorption that are too time-consuming for DLA systems.
Since we consider many blended or optically thick lines, we prefer the classical decomposition technique for the analysis and use the apparent optical depth method to supplement the diagnostics. Throughout the analysis we use the atomic data compiled by Morton (2003).
The general problem of line profile decomposition in QSO spectra and its solution by means of evolutionary forward modelling is described in detail by Quast et al. (2005). For the specific purpose of measuring accurate metal column densities we introduce several additional constraints:
The apparent optical depth method is only applied to the weaker
transitions of a given atomic or ionic species to avoid narrow
saturation. The spectra are normalized using the optimized continuum
approximation obtained from the line profile decomposition. The
normalized flux is averaged using a moving window of 10 km s-1. Low
apparent optical depths
![]() are clipped.
are clipped.
In this section we present the optimized profile decomposition and examine the ionization, chemical composition and dust content, kinematic structure, and physical conditions in the absorbing medium.
The optimized decomposition of the sub-damped Ly ![]() profile and
associated metal lines is depicted in Figs. 1-4.
The corresponding line parameters are listed in Tables 2
and 3. Since only the metal line components 20-31 are
associated with the sub-damped profile, components 1-19 and 20-31 are
termed peripheral and main components, respectively. Note that components 23 and 24 correspond to the neutral carbon and H2-bearing
components considered by Quast et al. (2002) and Reimers et al. (2003).
profile and
associated metal lines is depicted in Figs. 1-4.
The corresponding line parameters are listed in Tables 2
and 3. Since only the metal line components 20-31 are
associated with the sub-damped profile, components 1-19 and 20-31 are
termed peripheral and main components, respectively. Note that components 23 and 24 correspond to the neutral carbon and H2-bearing
components considered by Quast et al. (2002) and Reimers et al. (2003).
Table 2: Optimized decomposition of the sub-damped profile shown in Fig. 1. The listed numbers correspond to a straight continuum, for a curved continuum the errors increase. The origin of the radial velocity scale corresponds to the redshift z=1.15080. Note that the non-damped absorption does provide only little information. The line parameters are listed for completeness only.
![\begin{figure}
\par\includegraphics[width=14.25cm,clip]{dla_f3a}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg36.gif) |
Figure 3: Close-up of associated metal lines. Individual components are labeled by numbers 23-28. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.1cm,clip]{dla_f3b}
\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg37.gif) |
Figure 3:
continued. The shadings mark the main components of the
Mg I
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{dla_f4}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg38.gif) |
Figure 4: Associated Ca II lines ( left panel) compared with interstellar Ca II absorption in the Galactic halo along the same line-of-sight. |
| Open with DEXTER | |
The decomposition of the peripheral components is defined by the structure of Mg I, Mg II, Si II, and Fe II lines. Part of the Si II profile is ignored due to contamination by Lyman forest lines. The weakest components with 1011 metal ions cm-2 are indicated by the Mg II lines, whereas the components exceeding 1013 ions cm-2 are saturated for Mg II, but well defined for Fe II. Nonetheless, the decomposition is uncertain in detail, since components 3, 16, and 17 possibly are unresolved blends. The ambiguities, however, do not affect the chemical abundance analysis.
For some components the Fe II lines are narrower than those corresponding to lighter elements. The constraints on the decomposition of Fe II, however, are much stronger than those on the rest of lines. The evidence of thermal broadening is therefore not conclusive.
Table 3: Optimized decomposition of the metal lines shown in Figs. 2 and 3. This list is abridged for convenience, the complete table is available in the Online Material.
The decomposition of the main components is well constrained by the
structure of Mg I, Si II, Ca II and Fe II lines. The Mg II lines are saturated, with column densities exceeding 2 ![]() 1013 ions cm-2. The Al II line is ignored because it is blended with a lower-redshift Mg II system
at z=0.28
1013 ions cm-2. The Al II line is ignored because it is blended with a lower-redshift Mg II system
at z=0.28![]() .
Though the blended line ensemble can be disentangled, the optimized
column densities calculated for components 23 and 24 are not reliable
since the superimposed narrow Mg II absorption is saturated. The
Si II
.
Though the blended line ensemble can be disentangled, the optimized
column densities calculated for components 23 and 24 are not reliable
since the superimposed narrow Mg II absorption is saturated. The
Si II
![]() line is saturated for components 23 and 24,
but the optically thin Si II
line is saturated for components 23 and 24,
but the optically thin Si II
![]() absorption compensates
the lack of information. The red part of the Zn II
absorption compensates
the lack of information. The red part of the Zn II
![]() line is blended with the blue part of Mg I
line is blended with the blue part of Mg I
![]() ,
but due
to the distinct Mg I
,
but due
to the distinct Mg I
![]() absorption both ensembles can
be restored. Similarly, the red part of the Cr II
absorption both ensembles can
be restored. Similarly, the red part of the Cr II
![]() line is blended with the blue part of Zn II 2063, but
Cr II
line is blended with the blue part of Zn II 2063, but
Cr II
![]() and the blue part of
Zn II
and the blue part of
Zn II
![]() are unperturbed.
are unperturbed.
For the H2-bearing components 23 and 24 the broadening velocity is correlated with the ionization potential of the absorbing species as if the ionizing radiation was spatially fluctuating. The lines corresponding to species with lower first ionization potential than hydrogen (C I, Mg I and Ca II) are systematically less broadened than the Si II and Fe II lines, indicating different spatial origins. This systematic difference is well known from the study of Galactic molecular gas (Spitzer & Jenkins 1975, Fig. 2). Indeed, the detection of Si I, S I, and Fe I lines with low broadening velocities (Table 3) may indicate an embedded layer of cold neutral gas. Note that the Fe I absorption lines toward HE 0001-2340 that have recently been detected by D'Odorico (2007) also show an extremely low broadening parameter.
For most elements, the singly ionized state predominates in the neutral interstellar medium because the first ionization potential is lower, whereas the second is higher than the hydrogen ionization threshold. Exceptions to this rule are N, O, and Ar, where the first ionization potential exceeds the threshold, and Ca, where even the second ionization potential is lower. Since for interstellar abundance studies the total amount of an element is usually assumed to be equal to the amount existing in the predominant stage of ionization, substantial errors are made if the absorbing medium is a mixture of H I and H II regions.
Immediate evidence of ionized gas is provided by the detection of C IV lines (Fig. 2) and the presence of Si III and Si IV absorption (see Fig. 5 provided in the Online Material). Apparent column densities of up to 1013 cm-2 are found for all high-ions. Except for the broad C IV lines, the velocity structures of low- and high-ion profiles are similar, suggesting a common spatial origin. In particular for components 2-4 the apparent column densities of different Si ions compare, which indicates an H II region. The apparent optical depths of Si III and Si IV decreases for components 7-16, whereas the optical depth of Si II peaks at component 16. The optically thick absorption between components 19 and 20 of the Si III profile indicates ionization, but Si III absorption for this velocity interval is not confirmed by the rest of metal lines.
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{dla_f6}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg97.gif) |
Figure 6: Empirical diagram of ionization vs. apparent abundance of Al relative to Fe. Note that the peripheral and main components are well separated. |
| Open with DEXTER | |
Firm evidence of ionized gas is provided by the column density ratios
of Al II, Al III, and Fe II lines. For components 2-4,
6, 12, 16, and 18 the apparent abundance of Al relative to Fe is a factor
of 4-30 higher than expected for a neutral medium with solar chemical
composition (Fig. 6). The apparent enrichment of Al
cannot be explained by the presence of dust because the expected
depletion of Al into grains is typically an order of magnitude higher
than that of Fe (Spitzer & Jenkins 1975). On the other hand, Al is
produced with ![]() -elements which are known to experience a
nucleosynthetic history different from that of Fe. For instance, in
Galactic thick disk stars the abundance ratio of Al to Fe is found to be
enhanced by a factor of 2-4 relative to the solar value
(Prochaska et al. 2000). Nonetheless, the apparent enrichment of Al is
correlated with the column density ratio of Al III to Al II lines, indicating ionization rather than nucleosynthetic enrichment (Fig. 6).
-elements which are known to experience a
nucleosynthetic history different from that of Fe. For instance, in
Galactic thick disk stars the abundance ratio of Al to Fe is found to be
enhanced by a factor of 2-4 relative to the solar value
(Prochaska et al. 2000). Nonetheless, the apparent enrichment of Al is
correlated with the column density ratio of Al III to Al II lines, indicating ionization rather than nucleosynthetic enrichment (Fig. 6).
Further confidence is provided by photoionization simulations. For the
calculations we consider a plane-parallel slab of gas that is irradiated
by the cosmic UV background of QSOs and galaxies
(Madau et al. 1999)![]() . We further assume
a column density of 1016 hydrogen atoms cm-2 and solar chemical
composition. The photoionization models are defined by the total hydrogen
density
. We further assume
a column density of 1016 hydrogen atoms cm-2 and solar chemical
composition. The photoionization models are defined by the total hydrogen
density ![]() and the dimensionless ionization parameter
and the dimensionless ionization parameter
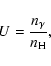 |
(1) |
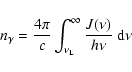 |
(2) |
In summary, there is conclusive evidence that the peripheral metal line components are formed within H II regions. An empirical method to identify a H II region when individual H I components are not detected is provided by Fig. 6.
The presence of ionized gas within the main absorber is not as evident as
for the periphery. The Si III profile is optically thick,
suggesting an apparent column density possibly exceeding 1013 ions cm-2 for components 20-28, but most of the absorption is due to
Lyman forest lines (see the preceding subsection). While the stronger
Si IV profile is blended into the Lyman forest, the weaker
Si IV profile may confirm the Si III absorption for
components 27-31. Conclusive evidence of ionized gas is provided by the
C IV and Al III lines. The velocity structure of the
C IV line, with an apparent column density of up to
2 ![]() 1012 ions cm-2, is weak and without noticeable
substructure in the domain of components 22-26, indicating that ionized
and neutral gas are not intermixed. In contrast, the Al III
profiles indicate a homogenous distribution of high- and low-ions for
components 23-25. The column density ratio of Al III to
Al II lines is less than 1/10 for all components
(Fig. 6).
1012 ions cm-2, is weak and without noticeable
substructure in the domain of components 22-26, indicating that ionized
and neutral gas are not intermixed. In contrast, the Al III
profiles indicate a homogenous distribution of high- and low-ions for
components 23-25. The column density ratio of Al III to
Al II lines is less than 1/10 for all components
(Fig. 6).
According to simple photoionization calculations an ionization of the molecular regions due to the cosmic UV background is ruled out (Fig. 8). However, some fractional ionization due to stellar sources is conceivable. The comparison with photoionization simulations considering both interstellar radiation and the formation of molecules and dust requires an accurate recording of H2 lines that is not available. Our simple attempts assuming Galactic environmental conditions have yielded inconsistent results, which reproduce the column density ratios of Fe I to Fe II and Si I to Si II as well as the relative population of neutral carbon fine-structure levels, but both overpredict the amount of molecular hydrogen and underpredict the strength of the Ca II absorption by more than one order of magnitude. Our calculations hence suggest that the radiation field and the density structure of the absorber are more complex. In fact, for component 23 the neutral species Fe I, Si I and S I have much lower broadening parameters than Fe II and Si II, which indicates that the different ionization stages are not formed in the same region. Photoionization calculations without modelling the density structure are therefore meaningless. Similar conclusions have been drawn by D'Odorico (2007) who failed to reproduce the observed Mg I to Mg II, Fe I to Fe II and Ca I to Ca II ratios in a metal line system toward HE 0001-2340.
Besides ionization and nucleosynthetic effects, the chemical composition
analysis of interstellar environments is hampered by dust grains removing
an unknown amount of atoms from the gaseous phase
(Savage & Sembach 1996; Spitzer & Jenkins 1975). The accepted
procedure to unravel these effects is to compare the abundance of
refractory and volatile elements X, Y for which the photospheric
abundance ratio (X/Y) is constant in stars over a wide range of
metallicities. In that case an observed deviation from the stellar ratios
is unlikely to have a nucleosynthetic origin. Even though the existence
of a stellar proxy for interstellar abundances is questionable
(Sofia & Meyer 2001) the Sun is used as a standard of reference for
the total, i.e. gas plus dust, interstellar composition. For given
observed column densities ![]() and
and ![]() the relative abundance of
elements X and Y is expressed as
the relative abundance of
elements X and Y is expressed as
| (3) |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{dla_f7}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg105.gif) |
Figure 7:
Photoionization simulations considering a plane-parallel slab
of gas with column density of 1016 hydrogen atoms cm-2 and
solar chemical composition. The abscissas mark the ionization parameter U and the total hydrogen density |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{dla_f8}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg106.gif) |
Figure 8:
The same as Fig. 7 but a plane parallel slab
with column density of 1020 hydrogen atoms cm-2 is considered.
Top: for a total hydrogen density of 10-1 particles cm-3 the cosmic
UV background corresponds to an ionization parameter of U=2 |
| Open with DEXTER | |
Since the peripheral components are formed within H II regions, the element abundances cannot be determined directly. The observed ion abundances, however, are supersolar and photoionization calculations conform with the idea that both absolute and relative metal abundances are solar (Fig. 7).
For the main components photoionization calculations suggest that the absorbing material is predominantly neutral and ionization effects are negligible, i.e. all elements are accurately represented by the predominant ions. For the chemical composition analysis and the proper unravelling of dust depletion and nucleosynthetic effects the detection of volatile elements is essential. The only volatile element detected in the predominant ionization stage with accurate column density measurements for several main components is Zn. For other volatile elements like N and O also detected in the predominant ionization stage, the absorption is saturated and largely blended with Lyman forest lines (Fig. 5). Even though the Zn II absorption is weak, the individual column densities are well defined because the positional and broadening parameters of the decomposed Zn II profiles are tied to those of the Fe II lines.
The apparent underabundance of Fe (and Si) relative to Zn cannot be the result of ionization effects caused by the cosmic UV background since these would mimic an enhanced abundance (Fig. 8). Therefore, the interpretation of the observed underabundance as evidence of depletion into dust grains cannot be questioned without admitting very unusual nucleosynthetic effects. On the other hand, if the observed underabundance of Fe (and Si) relative to Zn is the net result of dust depletion and ionization effects, the true depletion might be even stronger than illustrated in Fig. 9.
In summary, there is decisive evidence of Galaxy-like differential depletion of elements into dust grains, with a significant gradient from component to component as if the sight line is intersecting different interstellar environments comparable to the Galactic disk and halo. Another such example may be the DLA system toward the gravitationally lensed QSO HE 0512-3329, where different element abundances are detected along two lines of sight (Lopez et al. 2005). Further examples are given by Dessauges-Zavadsky et al. (2006).
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{dla_f9}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg108.gif) |
Figure 9: Gas-phase abundance ratios (relative to solar ratios) for the main components 23-28 compared with those in the Galactic interstellar medium (dotted line: warm halo gas; dashed line: warm disk gas; solid line: cold disk gas; Welty et al. 2001). If the volatile element Zn is undepleted, the abundance ratios reflect the differential depletion of chemical elements into dust grains. Note that Cr, Mn, Fe, and Ni are strongly depleted for the H2-bearing components 23 and 24, but essentially undepleted for component 28. |
| Open with DEXTER | |
For any interstellar environments i,j and constant sensitivity of the
chemical composition of dust to variations in the dust-to-metal ratio ![]() and the chemical composition of the medium, the fractions of the generic and reference elements X, Y contained in dust grains are related by
and the chemical composition of the medium, the fractions of the generic and reference elements X, Y contained in dust grains are related by
Equation (4) is capable of reproducing the Galactic
interstellar depletion patterns
![]() with a varying
dust-to-metal ratio
with a varying
dust-to-metal ratio
An explicit relation between observed and intrinsic absolute abundances
is obtained by using Eq. (4) to express the fraction of X contained in the gaseous phase of medium j:
Given the observed abundance ratios
![]() and an
educated guess of
and an
educated guess of
![]() ,
the dust-to-metal ratio
,
the dust-to-metal ratio ![]() is defined by Eq. (7). The rest of intrinsic abundance
ratios
is defined by Eq. (7). The rest of intrinsic abundance
ratios
![]() for elements
for elements
![]() implicitly follows
from
implicitly follows
from
Table 4:
Fractions of Fe contained in dust,
![]() ,
for the
main components 23-28 and different models. The results for models A and B do not depend on the exponent
,
for the
main components 23-28 and different models. The results for models A and B do not depend on the exponent
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{dla_f10}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg162.gif) |
Figure 10:
Dust-to-metal ratio |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{dla_f11}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg165.gif) |
Figure 11: Intrinsic abundance ratios (relative to solar ratios) for the main components 23-28. |
| Open with DEXTER | |
Table 5:
Cumulative dust-corrected column density of Fe contained in the
main absorber,
![]() (cm-2).
(cm-2).
Since only the total column density of hydrogen atoms contained in the
main absorber is known, Eq. (6) cannot be used to
calculate the intrinsic absolute abundances for individual components.
Nonetheless, by cumulating the individual dust-corrected column densities
![]() ,
we can calculate an
average intrinsic metallicity
,
we can calculate an
average intrinsic metallicity
![]() .
Inserting the
calculated fractions of Fe contained in dust (Table 5)
yields an almost solar intrinsic metallicity of
.
Inserting the
calculated fractions of Fe contained in dust (Table 5)
yields an almost solar intrinsic metallicity of
![]()
![]() 0.19. Assuming that the
observed H I absorption is only constituted by components 23-24,
the dust-to-metal ratio of
0.19. Assuming that the
observed H I absorption is only constituted by components 23-24,
the dust-to-metal ratio of ![]()
![]() 0.02 and the intrinsic
metallicity of
0.02 and the intrinsic
metallicity of
![]()
![]() 0.21 give an
average dust-to-gas ratio of
0.21 give an
average dust-to-gas ratio of
![]()
![]() 0.31.
0.31.
With an absorption velocity interval extending for 700 km s-1 the kinematic distribution of associated metal line components is quite unique. Only the z=1.97 DLA system toward QSO 0013-004 shows an even more extended spread (Petijean et al. 2002). The z=2.19 sub-DLA system toward HE 0001-2340 has a comparable neutral hydrogen column density, but a less extended absorption velocity interval of 400 km s-1 and much lower metallicity (Richter et al. 2005). Rotating disks models (Prochaska & Wolfe 1997) and simulations of merging protogalactic clumps (Haehnelt et al. 1998) do explain the characteristic kinematic features like asymmetric edge-leading line profiles, but fail to reproduce absorption intervals exceeding 250 km s-1. Large absorption intervals have therefore been associated with interacting or merging galaxies producing extended tidal filaments like the Antennae (e.g. Zhang et al. 2001; Wilson et al. 2000). Another viable scenario is a line-of-sight intercepting a cluster of galaxies. The kinematic distribution of metal line components associated with the present sub-DLA system (Fig. 2) indeed supports the idea that two different absorbers are involved.
The peripheral components show markedly different characteristics. For the velocity region from -560to -260 km -1 the average number density of components is about one component per 20 km s-1. The dominating substructure is edge-leading, but the remaining features appear randomly distributed. In contrast, the velocity region from -260 to -60 km s-1includes only four components, which are arranged in three isolated groups.
The main structure is characterized by the highest frequency of peaks, with an average of one peak every 15 km s-1. Two substructures may be recognized, both edge-leading for the less refractory elements like Mg and Si, but rather unordered otherwise.
Particularly instructive is the comparison of extragalactic Ca II absorption lines with those originating in the Galactic halo (Bowen 1991). First ignoring components 23 and 24, the redshifted and the Galactic line profiles are remarkably similar (Fig. 4), indicating that components 25-28 correspond to halo-like structures. Further developing this analogy, the narrow structures 23 and 24 not present in the absorption by the Galactic halo may be interpreted as signature of disk-like agglomeration, a picture which conforms with the observed depletion of elements into dust (Figs. 9, 10).
The physical conditions in DLA absorbers like the number density and kinetic temperature of hydrogen atoms and the local microwave and FUV radiation can be inferred from the diagnostics of fine-structure absorption lines (Silva & Viegas 2002; Bahcall & Wolf 1968). For the present absorber the analysis of excited C I lines associated with the H2 bearing components 23 and 24 provides an upper limit on the FUV input (Quast et al. 2002). The study of H2 lines predicts a radiation input exceeding the Galactic interstellar energy density by more than an order of magnitude and a number density greater than 100 hydrogen atoms cm-2 (Hirashita & Ferrara 2005; Reimers et al. 2003).
![\begin{figure}
\par\includegraphics[width=17cm,clip]{dla_f12}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg182.gif) |
Figure 12:
Physical conditions for the H2-bearing components 23 and 24
inferred from the observed population of C
|
| Open with DEXTER | |
Assuming an FUV input equal to the scaled generic Galactic radiation
field (Draine & Bertoldi 1996), but otherwise repeating the
statistical equilibrium calculations of Quast et al. (2002), we note
that both an intense radiation field and a number density exceeding 100 hydrogen atoms cm-2 only conform with the observed population of fine-structure levels, if the kinetic temperature is about
![]() K, which is different from the population
temperature of 80 K inferred from the lower rotational H2 levels
(Reimers et al. 2003). On the other hand, if the population of lower
and higher rotational H2 levels is in thermal equilibrium with
K, which is different from the population
temperature of 80 K inferred from the lower rotational H2 levels
(Reimers et al. 2003). On the other hand, if the population of lower
and higher rotational H2 levels is in thermal equilibrium with
![]() K, the number density of hydrogen atoms can only
exceed 60 cm-2 if the local and Galactic interstellar radiation
are comparable (Fig. 12). The present spectroscopy of H2 lines, however, is too inadequate to provide reliable results. Besides, the spatial distributions of carbon atoms and hydrogen molecules may not be identical, allowing different kinetic temperatures for both
constituents (Spitzer & Jenkins 1975). DLA systems where the population of lower and higher rotational H2 levels are not in thermal equilibrium and shielding effects are likely to play an
important role have been investigated by Noterdaeme et al. (2007a,b).
K, the number density of hydrogen atoms can only
exceed 60 cm-2 if the local and Galactic interstellar radiation
are comparable (Fig. 12). The present spectroscopy of H2 lines, however, is too inadequate to provide reliable results. Besides, the spatial distributions of carbon atoms and hydrogen molecules may not be identical, allowing different kinetic temperatures for both
constituents (Spitzer & Jenkins 1975). DLA systems where the population of lower and higher rotational H2 levels are not in thermal equilibrium and shielding effects are likely to play an
important role have been investigated by Noterdaeme et al. (2007a,b).
Based on high-resolution spectra obtained with STIS and the VLT UVES we have presented a reanalysis of the chemical composition, kinematic structure, and physical conditions of the H2-bearing sub-DLA system toward HE 0515-4414. The sub-damped system is unusual in several aspects:
Our analysis shows that sub-DLA systems can exhibit solar metallicities. If the highest-metallicity sub-DLA absorbers prove to be regular DLA absorbers having consumed large amounts of neutral hydrogen due to massive star formation, their detection is important. Modern surveys of DLA systems setting the cut-off below the traditional column density limit may provide interesting insights.
Acknowledgements
It is a pleasure to thank Francesco Haardt for providing us with machine readable lookup tables of the cosmic UV background. This research has been supported by the Verbundforschung of the BMBF/DLR under Grant No. 50 OR 9911 1 and by the DFG under Re 353/48.
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{dla_f2b}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg186.gif) |
Figure 2: continued. Note that the Al II profile is blended with an Mg II ensemble at redshift z=0.28. Blended parts of the C IV profiles are omitted for convenience. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{dla_f2c}
\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg187.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{dla_f5a}\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg188.gif) |
Figure 5: Associated metal lines recorded with the STIS spectrograph. The solid and dashed lines mark the observed flux and its standard deviation, respectively. Positions of associated metal lines found with UVES are indicated by vertical lines. Note that many lines are blended within the Lyman forest. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{dla_f5b}
\end{figure}](/articles/aa/full/2008/02/aa4773-05/Timg189.gif) |
Figure 5: continued. |
| Open with DEXTER | |
Table 3: Optimized decomposition of the metal lines shown in Figs. 2 and 3.