A&A 476, L33-L36 (2007)
DOI: 10.1051/0004-6361:20078371
LETTER TO THE EDITOR
R. Rezaei1 - O. Steiner1 - S. Wedemeyer-Böhm2 - R. Schlichenmaier1 - W. Schmidt1 - B. W. Lites3
1 - Kiepenheuer-Institut für Sonnenphysik,
Schöneckstrasse 6, 79104 Freiburg, Germany
2 -
Institute of Theoretical Astrophysics, PO Box 1029, Blindern,
0316 Oslo, Norway
3 -
High Altitude Observatory, NCAR, PO Box 3000, Boulder, CO 80307, USA
Received 27 July 2007 / Accepted 31 October 2007
Abstract
Aims. We study the structure of the magnetic elements in network-cell interiors.
Methods. A quiet Sun area close to the disc centre was observed with the spectro-polarimeter of the Solar Optical Telescope on board the Hinode space mission, which yielded the best spatial resolution ever achieved in polarimetric data of the Fe I 630 nm line pair. For comparison and interpretation, we synthesize a similar data set from a three-dimensional magneto-hydrodynamic simulation.
Results. We find several examples of magnetic elements, either roundish (tube) or elongated (sheet), which show a central area of negative Stokes-V area asymmetry framed or surrounded by a peripheral area with larger positive asymmetry. This pattern was predicted some eight years ago on the basis of numerical simulations. Here, we observationally confirm its existence for the first time.
Conclusions. We gather convincing evidence that this pattern of Stokes-V area asymmetry is caused by the funnel-shaped boundary of magnetic elements that separates the flux concentration from the weak-field environment. On this basis, we conclude that electric current sheets induced by such magnetic boundary layers are common in the photosphere.
Key words: Sun: photosphere - Sun: magnetic fields
With ever increasing polarimetric sensitivity and spatial resolution, it becomes now clear that even the most quiescent areas on the solar surface harbour ample amounts of magnetic flux. This flux becomes visible in small patches of field concentrations, called magnetic elements for short. While horizontal fields tend to occur near the edge of granules, the present investigation focusses on fields predominantly oriented in the vertical direction and mainly occurring in the intergranular space (Lites et al. 2007a,b). There, magnetic elements are often visible in G-band filtergrams as point-like objects. In more active regions, magnetic elements of extended size appear in the form of "crinkles'', "ribbon bands'', "flowers'', etc. (Berger et al. 2004), which show a sub-structure consisting of a dark central area surrounded by a striation of bright material and further outside by a downdraft of plasma (Langangen et al. 2007). While Doppler measurements of this downdraft are at the limit of spatial resolution with the best ground-based solar telescopes, spectro-polarimetric measurements have less spatial resolution due to image degradation by atmospheric seeing over the required long integration times.
Measurements with the spectro-polarimeter on board the Hinode satellite
have a superior spatial resolution of approximately
![]() thanks to
excellent pointing capabilities (Shimizu et al. 2007) and the absence of
seeing. Using Hinode data, we show examples of unipolar magnetic
elements of the network-cell interiors that possess a distinct
sub-structure, which is strikingly manifested in maps of the asymmetry of
spectral lines in the circularly polarized light - the Stokes-V area
asymmetry.
thanks to
excellent pointing capabilities (Shimizu et al. 2007) and the absence of
seeing. Using Hinode data, we show examples of unipolar magnetic
elements of the network-cell interiors that possess a distinct
sub-structure, which is strikingly manifested in maps of the asymmetry of
spectral lines in the circularly polarized light - the Stokes-V area
asymmetry.
The areas of the blue and the red lobes of Stokes-V profiles are identical when formed in a static atmosphere, but become asymmetric in the presence of gradients in the velocity and magnetic field strength (Solanki & Pahlke 1988; Illing et al. 1975; Landolfi & Landi degl'Innocenti 1996; Sanchez Almeida et al. 1989). Hence, the variation in the Stokes-V asymmetry across magnetic elements gives information on their magnetic field and plasma flow properties. Since this information is involved, we computed synthetic Stokes-Vprofiles of magnetic elements that occur in a three-dimensional simulation of magneto-convection and compare their asymmetry with the measured ones in order to understand their origin.
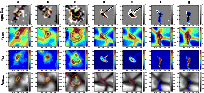 |
Figure 1:
Columns a)- c): observational data obtained
with the spectro-polarimeter of Hinode/SOT. Columns d) and f):
synthetic data from the 3D MHD simulation. Columns e) and g):
same as d) and f) but after application of the SOT-PSF to the
synthetic intensity maps. Rows from top to bottom: the
sign of the Stokes-V area asymmetry for the line Fe I 630.25 nm, where
black and white correspond to negative and positive, respectively, the
Fe I 630.15 nm line-wing velocity in km s-1,
|
| Open with DEXTER | |
The observations were carried out on 10 March, 2007 with the
spectro-polarimeter (SP) of the Solar Optical Telescope (SOT) on board of the Hinode
space satellite (Suematsu et al. 2007; Kosugi et al. 2007; Tsuneta et al. 2007). The four
Stokes profiles of the Fe I 630 nm line pair were recorded
in a quiet Sun area close to the disc centre. The integration time of 4.8 s led to
an rms noise level in the polarization signal of
![]() .
The data calibration for the SP is described in Ichimoto et al. (2007) and Tarbell (2006).
The field of view comprises an area of
.
The data calibration for the SP is described in Ichimoto et al. (2007) and Tarbell (2006).
The field of view comprises an area of
![]() with a spatial sampling of
with a spatial sampling of
![]() along the slit and
along the slit and
![]() in the scanning direction.
The spatial resolution of the resulting spectro-polarimetric maps is approximately
in the scanning direction.
The spatial resolution of the resulting spectro-polarimetric maps is approximately
![]() ,
and the spectral sampling is 2.15 pm. The rms continuum contrast at 630.0 nm is around 7.5%,
far above the 3% value typically observed from the ground at the same
wavelength (Rezaei et al. 2007; Khomenko et al. 2005).
This same data set served Lites et al. (2007a,b) in an investigation of
the horizontal magnetic fields in the quiet Sun.
,
and the spectral sampling is 2.15 pm. The rms continuum contrast at 630.0 nm is around 7.5%,
far above the 3% value typically observed from the ground at the same
wavelength (Rezaei et al. 2007; Khomenko et al. 2005).
This same data set served Lites et al. (2007a,b) in an investigation of
the horizontal magnetic fields in the quiet Sun.
The three-dimensional magnetohydrodynamic simulation comprises
an area of
![]() km
km![]() ,
corresponding to
,
corresponding to
![]() and spans a height range of 2 800 km
from the top layers of the convection zone to the middle chromosphere.
Details of the simulation, carried out with the CO
and spans a height range of 2 800 km
from the top layers of the convection zone to the middle chromosphere.
Details of the simulation, carried out with the CO
![]() BOLD code,
can be found in Schaffenberger et al. (2005,2006).
BOLD code,
can be found in Schaffenberger et al. (2005,2006).
Initially, a homogeneous vertical magnetic field with a strength of 1 mT was superposed on a model of relaxed thermal convection. After relaxation, fields of mixed polarity occur throughout the photosphere with an area-fractional imbalance typically of 3:1 for fields stronger than 1 mT. Similar polarity imbalances of even larger fields of view also occur in observational data (Lites 2002). Because of the periodic side boundaries and the conditions that the magnetic field must remain vertical at the top and bottom boundaries, the horizontally averaged vertical net magnetic-flux density remains 1 mT throughout the simulation. This value compares very well with the mean flux density of 1.12 mT reported by Lites et al. (2007a) for the Hinode data set. The mean absolute horizontal field strength is 2.5 mT in the upper photosphere of the simulation, 2.5 times the net vertical flux density. Lites et al. (2007a) report a ratio of 5.
The grid constant of the computational domain in the horizontal direction
is
![]() (1203 grid cells), three times
smaller than the spatial sampling of the Hinode SP data.
The simulation was advanced for 4400 s of real time. The results
presented here refer to the last 2400 s, well after the
initial relaxation phase.
Using the SIR code (Bellot Rubio 2003; Ruiz Cobo & del Toro Iniesta 1992), we
synthesized the Stokes profiles of the Fe I 630 nm line pair
from a large number of simulation snapshots with a spectral
sampling of 2 pm. Profiles were computed along vertical
lines-of-sight for each grid point. To the resulting intensity
maps, we additionally applied a theoretical point-spread function (PSF)
that models the spatial resolution capability of the SOT optics
(Wedemeyer-Böhm 2008).
(1203 grid cells), three times
smaller than the spatial sampling of the Hinode SP data.
The simulation was advanced for 4400 s of real time. The results
presented here refer to the last 2400 s, well after the
initial relaxation phase.
Using the SIR code (Bellot Rubio 2003; Ruiz Cobo & del Toro Iniesta 1992), we
synthesized the Stokes profiles of the Fe I 630 nm line pair
from a large number of simulation snapshots with a spectral
sampling of 2 pm. Profiles were computed along vertical
lines-of-sight for each grid point. To the resulting intensity
maps, we additionally applied a theoretical point-spread function (PSF)
that models the spatial resolution capability of the SOT optics
(Wedemeyer-Böhm 2008).
The line parameters extracted from both the calibrated Stokes data of the observation
and from the simulation include the area and amplitude asymmetry of Stokes-V ,
the line-core and line-wing velocities, and the total (signed) circular polarization
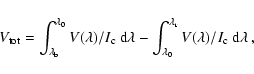 |
(1) |
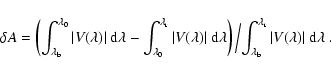 |
(2) |
The line-wing velocity of Fe I 630.15 nm, shown in the second row,
is obtained by averaging the Stokes-I
Doppler shift in the intensity interval 0.8-
![]() .
We set the convective blue shift of the line-core velocity in the quiet Sun to
-0.2 km s-1. Because of the low degree of polarization, the line-wing
velocity is not spoilt by magnetic influence.
.
We set the convective blue shift of the line-core velocity in the quiet Sun to
-0.2 km s-1. Because of the low degree of polarization, the line-wing
velocity is not spoilt by magnetic influence.
The third row displays
![]() ,
whose contours are shown in all the panels.
It is a linear measure of the magnetic flux density according
to Lites et al. (1999) and Lites et al. (2007b). From the fourth row, which
shows the continuum intensity at 630 nm, we see that the magnetic flux concentration occurs
mainly in the intergranular space.
,
whose contours are shown in all the panels.
It is a linear measure of the magnetic flux density according
to Lites et al. (1999) and Lites et al. (2007b). From the fourth row, which
shows the continuum intensity at 630 nm, we see that the magnetic flux concentration occurs
mainly in the intergranular space.
![\begin{figure}
\par\includegraphics[width=70mm]{8371fig2.eps}\end{figure}](/articles/aa/full/2007/48/aa8371-07/Timg27.gif) |
Figure 2:
Variation in |
| Open with DEXTER | |
Both the observation and the simulation show magnetic elements of either
sheet like or roundish shape, possessing the same striking pattern with regard
to the Stokes-V asymmetry: a central region with negative Stokes-V area
asymmetry is framed or surrounded by a narrow seam of pixels having positive area
asymmetry (Fig. 1, first row).
Plotting ![]() across a magnetic element, we find that
across a magnetic element, we find that
![]() is
typically larger in the periphery than in the central region of the magnetic flux
concentration. Representative cross sections that demonstrate this behaviour
are shown in Fig. 2 for both the observation and the simulation.
Along with
is
typically larger in the periphery than in the central region of the magnetic flux
concentration. Representative cross sections that demonstrate this behaviour
are shown in Fig. 2 for both the observation and the simulation.
Along with ![]() in the top right panel of Fig. 2,
Fig. 4 also gives the corresponding observed Stokes-V profiles.
Also from Fig. 1 we see that the magnetic elements are located
within and surrounded by a downdraft.
in the top right panel of Fig. 2,
Fig. 4 also gives the corresponding observed Stokes-V profiles.
Also from Fig. 1 we see that the magnetic elements are located
within and surrounded by a downdraft.
![\begin{figure}
\par\includegraphics[width=73mm]{8371fig3.eps}\end{figure}](/articles/aa/full/2007/48/aa8371-07/Timg30.gif) |
Figure 3:
Vertical cross section through the simulation box corresponding
to position
|
| Open with DEXTER | |
For gaining deeper insight, we now consider in Fig. 3 the vertical
cross section through the simulation snapshot shown in column d of
Fig. 1 for the position
![]() .
It displays the magnetic field
strength (colour-coded) together with the velocity field, projected on the vertical
plane (white arrows). The horizontally running curve indicates optical depth
.
It displays the magnetic field
strength (colour-coded) together with the velocity field, projected on the vertical
plane (white arrows). The horizontally running curve indicates optical depth
![]() .
A magnetic flux concentration
is forming in the downdraft and has reached a field strength of
0.13 T at
.
A magnetic flux concentration
is forming in the downdraft and has reached a field strength of
0.13 T at
![]() .
Close to the surface of optical
depth unity and through the photosphere, a relatively sharp,
funnel-shaped boundary separates the magnetic flux concentration from the
weak-field or field-free surroundings.
.
Close to the surface of optical
depth unity and through the photosphere, a relatively sharp,
funnel-shaped boundary separates the magnetic flux concentration from the
weak-field or field-free surroundings.
The inner vertical white lines indicate a
central part of the flux concentration (
880 < x < 1120 km), where
Stokes-V profiles have
![]() .
This is because their lines-of-sight
sample increasing field strength and increasing downflow velocity with increasing
continuum optical depth (Solanki & Pahlke 1988). This situation
changes drastically in the peripheral region
.
This is because their lines-of-sight
sample increasing field strength and increasing downflow velocity with increasing
continuum optical depth (Solanki & Pahlke 1988). This situation
changes drastically in the peripheral region
![]() km
and
km
and
![]() km (also indicated with white lines),
where
km (also indicated with white lines),
where
![]() .
Here, the
downflow speed still increases with optical depth; but because of the
funnel-shaped flux concentration, lines-of-sight traverse a magnetic
boundary layer, where the field strength rapidly drops
with increasing optical depth. The combination of increasing velocity
and decreasing field strength produces positive area asymmetry.
From this, we conclude that the narrow seam of positive area asymmetry
in the periphery of magnetic flux elements seen in the Hinode data is
a consequence of their well-defined boundary (or magnetopause)
that expands with height in a funnel-like manner.
.
Here, the
downflow speed still increases with optical depth; but because of the
funnel-shaped flux concentration, lines-of-sight traverse a magnetic
boundary layer, where the field strength rapidly drops
with increasing optical depth. The combination of increasing velocity
and decreasing field strength produces positive area asymmetry.
From this, we conclude that the narrow seam of positive area asymmetry
in the periphery of magnetic flux elements seen in the Hinode data is
a consequence of their well-defined boundary (or magnetopause)
that expands with height in a funnel-like manner.
| |
Figure 4:
Stokes-V profiles from the Hinode data across the magnetic element
of column b of Fig. 1.
|
| Open with DEXTER | |
As an immediate consequence of Ampère's law, this boundary carries an electric current sheet. The black contours in Fig. 3 indicate a current density of 0.5 A m-2, encircling higher values of up to 4.0 A m-2. This refers to the current component perpendicular to the section plane, which flows in the opposite direction on either side of the magnetic flux concentration.
If the magnetic flux concentration is inclined enough with respect to the
viewing direction, lines-of-sight
traverse the boundary layer on only one side of the flux concentration, which leads
to a one-sided seam of positive area asymmetry. This is almost the case
in Fig. 3 (and corresponding ![]() -panel of Fig. 1),
where the flux concentration is slightly inclined to the right making the
seam of positive
-panel of Fig. 1),
where the flux concentration is slightly inclined to the right making the
seam of positive ![]() to the left much narrower than that on the right side.
In fact, most magnetic elements in the field of view of the observation
show a one-sided pattern like in the upper right corner of the synthetic
to the left much narrower than that on the right side.
In fact, most magnetic elements in the field of view of the observation
show a one-sided pattern like in the upper right corner of the synthetic
![]() -map in Cols. d or e.
-map in Cols. d or e.
Because the mean magnetic flux density in the network cell interior is low, granular flow gathers only small amounts of flux so that only small and weak magnetic flux concentrations form (Steiner 2003). They form and disperse with the onset and cessation of intergranular downdrafts. Therefore we observe strong downflows associated with the magnetic elements considered in this work. Indeed, Grossmann-Doerth et al. (1996), Sigwarth et al. (1999), and Martínez Pillet et al. (1997) also observe mainly downflows associated with weak magnetic signals. In combination with increasing field strength, these downflows give rise to negative area asymmetry. Yet, the peripheral positive area asymmetry is larger (Fig. 2) and may partially balance or even outweigh the negative contribution when observing at a lower spatial resolution.
Langangen et al. (2007) finds that the downdraft velocity near the edges of magnetic elements is larger than in the central part. Here we find in both observations and simulation the maximum speed in the centre of the flux concentration. In the simulation this is because the magnetic element forms as a consequence of an intergranular downdraft, with peak velocity in the centre. This is different from the regime of a mature strong flux concentration for which simulations exhibit veritable downflow jets near their edges but not in the centre (Shelyag et al. 2007; Steiner et al. 1998). This regime might be more representative of the active region elements observed by Langangen et al. (2007).
Grossmann-Doerth et al. (1988,1989) and Solanki (1989) first pointed to the peripheral, canopy-like magnetopause of magnetic elements as the origin of the observed positive Stokes-V area asymmetry. Steiner (1999) found this effect at work in a two-dimensional MHD-simulation, but also found that the central region of the magnetic flux sheet tends to have negative values and that a delicate balance with the peripheral region exists in which the positive values may dominate and outweigh the negative ones. These findings have recently been confirmed in a three-dimensional environment by Shelyag et al. (2007). Bellot Rubio et al. (2000) came to a similar conclusion based on semi-empirical modelling. Leka & Steiner (2001) found a similar pattern in the Stokes-V area asymmetry in pores and magnetic knots. Here, for the first time, we find this pattern in observations of small-scale magnetic elements in the network cell interior.
Spectro-polarimetric data of a quiet Sun area close to the disc centre obtained with SOT on board Hinode were analysed. We find magnetic elements of either a roundish (tube) or an elongated (sheet) shape, which show Stokes-V profiles of negative area asymmetry in the centre, surrounded or framed by pixels of larger, positive area asymmetry. A comparison with results from 3D MHD-simulations suggests that this peculiar pattern in Stokes-V area asymmetry (first predicted by Steiner 1999) is due to the confined nature of the field in magnetic elements with a funnel-shaped boundary layer that gives rise to a steep gradient in field strength along the line of sight.
We also conclude that this kind of magnetic element
of the internetwork is accompanied by electric current sheets.
While these conclusions are evident from the comparison, we cannot
exclude the hypothesis that a suitable magnetic structuring on scales not
resolved by the present observation and simulation would lead to the observed
pattern in ![]() .
.
Acknowledgements
Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as the domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway). Part of this work was supported by the Deutsche Forschungsgemeinschaft (SCHM 1168/8-1).