A&A 476, 1365-1371 (2007)
DOI: 10.1051/0004-6361:20077939

The habitability of super-Earths in Gliese 581

W. von Bloh1 - C. Bounama1 - M. Cuntz2 - S. Franck1


1 - Potsdam Institute for Climate Impact Research, PO Box 60 12 03, 14412 Potsdam, Germany
2 - Department of Physics, University of Texas at Arlington, Box 19059, Arlington, TX 76019, USA

Received 24 May 2007 / Accepted 27 September 2007

Abstract
Aims. The planetary system around the M star Gliese 581 consists of a hot Neptune (Gl 581b) and two super-Earths (Gl 581c and Gl 581d). The habitability of this system with respect to the super-Earths is investigated following a concept that studies the long-term possibility of photosynthetic biomass production on a dynamically active planet.
Methods. A thermal evolution model for a super-Earth is used to calculate the sources and sinks of atmospheric carbon dioxide. The habitable zone is determined by the limits of photosynthetic life on the planetary surface. Models with different ratios of land / ocean coverage are investigated.
Results. The super-Earth Gl 581c is clearly outside the habitable zone, since it is too close to the star. In contrast, Gl 581d is a tidally locked habitable super-Earth near the outer edge of the habitable zone. Despite the adverse conditions on this planet, at least some primitive forms of life may be able to exist on its surface. Therefore, Gl 581d is an interesting target for the planned TPF/Darwin missions to search for biomarkers in planetary atmospheres.

Key words: stars: individual: Gl 581 - stars: planetary systems - astrobiology

1 Introduction

Planets have now been observed around more than 200 main-sequence stars. Based on the available observational techniques, most detected objects are giant (Jupiter-like) planets. Therefore, until very recently the existence and possible habitability of Earth-like planets in extrasolar planetary systems was highly speculative (von Bloh et al. 2003a,2007; Jones et al. 2006; Cuntz et al. 2003; Franck et al. 2003). Bonfils et al. (2005) reported the detection of a Neptune size planet around Gl 581, an M dwarf star at a distance of 6.26 pc with a mass of $0.31~M_{\odot}$ and a luminosity of 0.013 $L_{\odot}$. Very recently, Udry et al. (2007) announced the detection of two so called "super-Earth'' planets in this system, Gl 581c with a mass of 5.06 $M_\oplus$ with a semi-major axis of 0.073 AU, and Gl 581d with 8.3 $M_\oplus$ and 0.25 AU. Both mass estimates are minimum masses uncorrected for the inclination term $\sin i$, which is currently unknown.

According to Valencia et al. (2006), super-Earths are rocky planets from one to ten Earth masses with the same chemical and mineral composition as the Earth. In the following, we adopt the hypothesis that this is indeed the case, and consider for these planets our model previously developed for the Earth, using when appropriate scaling laws. This justifies the term super-Earth used here for these planets.

The main question is whether any of the two super-Earths around Gl 581 can harbour life, i.e., that any of the planets lies within the habitable zone (HZ). As a first approximation, Udry et al. (2007) computed an equilibrium surface temperature for Gl 581c of  $20~^{\circ}$C for an albedo of 0.5. They neglected, however, the likely greenhouse effect of the atmosphere. Typically, stellar HZs are defined as regions around the central star, where the physical conditions are favourable for liquid water to exist at the planet's surface for a period of time long enough for biological evolution to occur. Kasting et al. (1993) calculated the HZ boundaries for the luminosity and effective temperature of the present Sun as $R_{{\rm in}} = 0.82$ AU and $R_{{\rm out}} = 1.62$ AU. They defined the HZ of an Earth-like planet as the region where liquid water is present at the surface.

According to this definition, the inner boundary of the HZ is determined by the loss of water via photolysis and hydrogen escape. The outer boundary of the HZ is determined by the condensation of CO2 crystals out of the atmosphere that attenuate the incident sunlight by Rayleigh scattering. The critical CO2 partial pressure for the onset of this effect is about 5 to 6 bar. However, the cooling effect of CO2 clouds has been challenged by Forget & Pierrehumbert (1997). CO2 clouds have the additional effect of reflecting the outgoing thermal radiation back to the surface. The precise inner and outer limits of the climatic habitable zone are still unknown due to the limitations of the existing climate models. For the present Sun, the HZ is probably smaller than between 0.7 to 2 AU, but it is still impossible to give a better constraint, particularly for the outer boundary of the HZ. For limitations of the planetary habitability of M-type stars see Tarter et al. (2007).

The luminosity and age of the central star play important roles in the manifestation of habitability. The luminosity of Gl 581 can be obtained by (1) photometry (Udry et al. 2007; Bonfils et al. 2005), and (2) the application of the mass-radius relationship (Ribas 2006) together with the spectroscopically determined stellar effective temperature of $T_{\rm e} = 3480$ K (Bean et al. 2006). Both methods yield $L=0.013 \pm 0.002~L_\odot$. Bonfils et al. (2005) consider a stellar age of at least 2 Gyr.

In the following, we adopt a definition of the HZ previously used by Franck et al. (2000b,a). Here habitability at all times does not just depend on the parameters of the central star, but also on the properties of the planet. In particular, habitability is linked to the photosynthetic activity of the planet, which in turn depends on the planetary atmospheric CO2 concentration together with the presence of liquid water, and is thus strongly influenced by the planetary dynamics. We call this definition the photosynthesis-sustaining habitable zone, pHZ. In principle, this leads to additional spatial and temporal limitations of habitability, as the pHZ (defined for a specific type of planet) becomes narrower with time due to the persistent decrease of the planetary atmospheric CO2 concentration.

2 Estimating the habitability of a super-Earth

2.1 Definition of the photosynthesis-sustaining habitable zone

The climatic habitable zone at a given time for a star with luminosity L and effective temperature $T_{\rm e}$ different from the Sun can be calculated according to Jones et al. (2006) based on previous results by Kasting et al. (1993) as

 \begin{displaymath}R_{{\rm in}} = \left(\frac{L}{L_\odot\cdot S_{{\rm in}}(T_{\r... ...L}{L_\odot\cdot S_{{\rm out}}(T_{\rm e})}\right)^{\frac{1}{2}} \end{displaymath} (1)

with $S_{{\rm in}}(T_{\rm e})$, $S_{{\rm out}}(T_{\rm e})$ given as second order polynomials.

To assess the habitability of a terrestrial planet, an Earth-system model is applied to calculate the evolution of the temperature and atmospheric CO2 concentration. On Earth, the carbonate-silicate cycle is the crucial element for a long-term homeostasis under increasing solar luminosity. On geological time-scales, the deeper parts of the Earth are considerable sinks and sources of carbon.

  \begin{figure} \par\includegraphics[width=6cm,clip]{7939fig1.eps}\end{figure} Figure 1: Earth system box model. The arrows indicate the different forcing and feedback mechanisms. The bold arrows indicate negative feedback operating towards climate stabilization.
Open with DEXTER

Our numerical model couples the stellar luminosity L, the silicate-rock weathering rate $F_{{\rm wr}}$ and the global energy balance to obtain estimates of the partial pressure of atmospheric carbon dioxide $P_{{\rm CO}_2}$, the mean global surface temperature $T_{{\rm surf}}$, and the biological productivity $\Pi$ as a function of time t (Fig. 1). The main point is the persistent balance between the CO2 sink in the atmosphere-ocean system and the metamorphic (plate-tectonic) sources. This is expressed through the dimensionless quantities

 \begin{displaymath}f_{{\rm wr}}(t) \cdot f_A(t) = f_{{\rm sr}}(t), \end{displaymath} (2)

where $f_{{\rm wr}}(t) \equiv F_{{\rm wr}}(t)/F_{{\rm wr},0}$ is the weathering rate, $f_A(t) \equiv A_{\rm c}(t)/A_{{\rm c},0}$ is the continental area, and $f_{{\rm sr}}(t) \equiv S(t)/S_0$ is the areal spreading rate, which are all normalized by their present values of Earth. Equation (2) can be rearranged by introducing the geophysical forcing ratio, GFR (Volk 1987) as

 \begin{displaymath}f_{{\rm wr}}(T_{{\rm surf}},P_{{\rm CO}_2})=\frac{f_{{\rm sr}}}{f_A} \ =: \ {\rm GFR}(t) . \end{displaymath} (3)

Here we assume that the weathering rate depends only on the global surface temperature and the atmospheric CO2 concentration. For the investigation of a super-Earth under external forcing, we adopt a model planet with a prescribed continental area. The fraction of continental area relative to the total planetary surface fA is varied between 0.1 and 0.9.

The connection between the stellar parameters and the planetary climate can be formulated by using a radiation balance equation (Williams 1998)

 \begin{displaymath}\frac{L}{4\pi R^2} [1- a (T_{{\rm surf}}, P_{{\rm CO}_2})] = 4I_R (T_{{\rm surf}}, P_{{\rm CO}_2}), \end{displaymath} (4)

where a denotes the planetary albedo, IR the outgoing infrared flux, and R the distance from the central star. The Eqs. (3) and (4) constitute a set of two coupled equations with two unknowns,  $T_{{\rm surf}}$ and  $P_{{\rm CO}_2}$, if the parameterisation of the weathering rate, the luminosity, the distance to central star and the geophysical forcing ratio are specified. Therefore, a numerical solution can be attained in a straightforward manner.

The photosynthesis-sustaining HZ around Gl 581 is defined as the spatial domain of all distances R from the central star where the biological productivity is greater than zero, i.e.,

 \begin{displaymath}{{\rm pHZ}} \ := \ \{ R \mid \Pi (P_{{\rm CO}_2}(R,t), T_{{\rm surf}}(R,t))>0 \}. \end{displaymath} (5)

In our model, biological productivity is considered to be solely a function of the surface temperature and the CO2 partial pressure in the atmosphere. Our parameterisation yields maximum productivity at $T_{{\rm surf}} = 50~^{\circ}$C and zero productivity for $T_{{\rm surf}} \leq 0~^{\circ}$C or $T_{{\rm surf}} \geq 100~^{\circ}$C or $P_{{\rm CO}_2}\leq 10^{-5}$ bar (Franck et al. 2000a). The inner and outer boundaries of the pHZ do not depend on the detailed parameterisation of the biological productivity within the temperature and pressure tolerance window. Hyperthermophilic life forms can tolerate temperatures somewhat above $100~^{\circ}$C. However, these chemoautotrophic organisms are outside the scope of this study.

2.2 Silicate rock weathering

Weathering plays an important role in Earth's climate because it provides the main sink for atmospheric carbon dioxide. The overall chemical reactions for the weathering process are

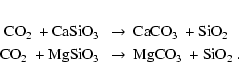
\begin{eqnarray*}\mbox{CO$_2$ }+ \mbox{CaSiO$_3$ } &\rightarrow & \mbox{CaCO$_3$... ...{MgSiO$_3$ } & \rightarrow & \mbox{MgCO$_3$ } + \mbox{SiO$_2$ }. \end{eqnarray*}


The total process of weathering embraces (1) the reaction of silicate minerals with carbon dioxide, (2) the transport of weathering products, and (3) the deposition of carbonate minerals in sediments. When combining all these effects, the normalized global mean weathering rate $f_{{\rm wr}}$ can be calculated as

 \begin{displaymath}f_{{\rm wr}} = {\left( \frac{a_{{\rm H}^+}}{a_{{\rm H}^+,0}}\... ... \frac{T_{{\rm surf}}-T_{{\rm surf},0}}{13.7~{\rm K}} \right), \end{displaymath} (6)

following Walker et al. (1981). Here the first factor reflects the role of the CO2 concentration in the soil, $P_{{\rm soil}}$, with $a_{{\rm H}^+}$ as the activity of ${\rm H}^+$ in fresh soil-water that depends on $P_{{\rm soil}}$ and the global mean surface temperature $T_{{\rm surf}}$. The quantities $a_{{\rm H}^+,0}$ and $T_{{\rm surf},0}$ are the present-day values for the ${\rm H}^+$activity and the surface temperature, respectively. The activity $a_{{\rm H}^+}$ is itself a function of the temperature and the CO2 concentration of the soil. The equilibrium constants for the chemical activities of the carbon and sulfur systems involved are taken from Stumm & Morgan (1981). Note that the sulfur content of the soil also contributes to the global weathering rate, but its influence does not depend on the temperature. It can be regarded as an overall weathering attribute that has to be taken into account for the estimation of the present-day value.

For any given weathering rate, the surface temperature and the CO2 concentration of the soil can be calculated in a self-consistent manner. $P_{{\rm soil}}$ is assumed to be linearly related to the terrestrial biological productivity $\Pi$ (see Volk 1987) and the atmospheric CO2 concentration $P_{{\rm CO}_2}$. Thus we have

 \begin{displaymath}\frac{P_{{\rm soil}}}{P_{{\rm soil},0}} = \frac{\Pi}{\Pi_0} \... ...soil},0}} \right) + \frac{P_{{\rm CO}_2}}{P_{{\rm soil},0}} , \end{displaymath} (7)

where $P_{{\rm soil},0}$, $\Pi_0$ and $P_{{\rm CO}_2,0}$ are again present-day values.

Since Earth is now harbouring complex life, the weathering rates might be lower on a planet without a complex biosphere. The parameterisation of biotic enhancement of weathering is based only on an increase of the CO2 concentration in the soil. This implies a rather weak functional dependence of the weathering rate on biological productivity. A ten-fold increase in soil CO2 concentration relative to the atmosphere only amounts to a 1.56 fold increase in the weathering rate due to the present biota. This is a significant underestimate, indicating that much of the observed biotic amplification of weathering is due to processes other than increased soil CO2 concentration. According to Schwartzman (1999) the total amplification due to complex land life is at least a factor of 10 and may exceed 100. To explore the effect of a stronger biological amplification of weathering a direct dependence (Lenton & von Bloh 2001) of weathering rate, $f_{{\rm wr}}$, on productivity of complex life (e.g. land plants), $\Pi_{{\rm complex}}$, with amplification factor, $\alpha_{{\rm bio}}$, can be included:

  \begin{displaymath}f'_{\rm {wr}}=\left(\left(1-\frac{1}{\alpha_{{\rm bio}}}\righ... ... complex},0}}+\frac{1}{\alpha_{{\rm bio}}}\right)f_{{\rm wr}}, \end{displaymath} (8)

where $\Pi_{{\rm complex,0}}$ is the productivity of the present biosphere. The aim of this calculation is to obtain the value for weathering for a planet without a complex biosphere. Therefore the weathering rate for an Earth with primitive life $f_{{\rm wr,primitive}}$( $\Pi_{{\rm complex}}\equiv 0$) is a factor of $\alpha_{{\rm bio}}$ lower than the weathering rate for a complex biosphere

 \begin{displaymath}f_{{\rm wr,primitive}}=\frac{1}{\alpha_{{\rm bio}}} f_{{\rm wr}}, \alpha_{{\rm bio}}>1. \end{displaymath} (9)

2.3 Thermal evolution model

Parameterised convection models are the simplest models for investigating the thermal evolution of terrestrial planets and satellites. They have been successfully applied to the evolution of Mercury, Venus, Earth, Mars, and the Moon (Sleep 2000; Stevenson et al. 1983). Franck & Bounama (1995) have investigated the thermal and volatile history of Earth and Venus in the framework of comparative planetology. The internal structure of massive terrestrial planets with one to ten Earth masses has been investigated by Valencia et al. (2006) to obtain scaling laws for total radius, mantle thickness, core size, and average density as a function of mass. Similar scaling laws were found for different compositions. We will use such scaling laws for mass-dependent properties of super-Earths and also mass-independent material properties given by Franck & Bounama (1995).

The thermal history and future of a super-Earth has to be determined to calculate the spreading rate for solving key Eq. (2). A parameterised model of whole mantle convection including the volatile exchange between the mantle and surface reservoirs (Franck & Bounama 1995; Franck 1998) is applied. Assuming conservation of energy, the average mantle temperature $T_{\rm m}$ can be obtained as

 \begin{displaymath}{4 \over 3} \pi \rho c (R_{\rm m}^3-R_{\rm c}^3) \frac{{\rm d... ...2 q_{\rm m} + {4 \over 3} \pi E(t) (R_{\rm m}^3-R_{\rm c}^3), \end{displaymath} (10)

where $\rho$ is the density, c is the specific heat at constant pressure, $q_{\rm m}$ is the heat flow from the mantle, E(t) is the energy production rate by decay of radiogenic heat sources in the mantle per unit volume, and $R_{\rm m}$ and $R_{\rm c}$ are the outer and inner radii of the mantle, respectively. The radiogenic heat source per unit volume is parameterised as

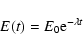\begin{displaymath}E(t)=E_0{\rm e}^{-\lambda t} \end{displaymath} (11)

where $\lambda$ is the decay constant of radiogenic heat and the constant E0is obtained from the present heat flux of $q_{\rm m}=0.07$ W m-2for an Earth-size planet at 4.6 Gyr.

The mantle heat flow is parameterised in terms of the Rayleigh number ${\rm Ra}$ as

 \begin{displaymath}q_{\rm m} = {k (T_{\rm m} - T_{{\rm surf}}) \over R_{\rm m} -... ...c}} \left({{\rm Ra} \over {\rm Ra}_{\rm {crit}}}\right)^\beta, \end{displaymath} (12)

with

 \begin{displaymath}{\rm Ra} = {g \alpha (T_{\rm m} - T_{{\rm surf}}) (R_{\rm m} - R_{\rm c})^3 \over \kappa \nu}, \end{displaymath} (13)

where k is the thermal conductivity, ${\rm Ra}_{\rm {crit}}$ is the critical value of ${\rm Ra}$ for the onset of convection, $\beta$ is an empirical constant, g is the gravitational acceleration, $\alpha$ is the coefficient of thermal expansion, $\kappa$ is the thermal diffusivity, and $\nu$ is the water-dependent kinematic viscosity. The viscosity $\nu$ can be calculated with the help of a water fugacity dependent mantle creep rate. It strongly depends on the evolution of the mass of mantle water, $M_{\rm w}$, and the mantle temperature, $T_{\rm m}$, i.e., $\nu\equiv\nu(T_{\rm m},M_{\rm w})$ and is parameterised according to Franck & Bounama (1995).

Table 1: Parameter values for the evolution model for mantle temperature and water.

The evolution of the mantle water can be described by a balance equation between the regassing flux $F_{{\rm reg}}$and outgassing flux $F_{{\rm out}}$ as
                     $\displaystyle \frac{{\rm d}M_{\rm w}}{{\rm d}t}$ = $\displaystyle F_{{\rm reg}}-F_{{\rm out}}$  
  = $\displaystyle f_{{\rm bas}}\rho_{{\rm bas}}d_{{\rm bas}}SR_{{\rm H_2O}}-\frac{M_{\rm w}} {\frac{4}{3}\pi(R_{\rm m}^3-R_{\rm c}^3)}d_{\rm m}f_{\rm w}S,$ (14)

where $f_{{\rm bas}}$ is the water content in the basalt layer, $\rho_{{\rm bas}}$ is the average density, $d_{{\rm bas}}$ is the average thickness of the basalt layer before subduction, S is the areal spreading rate, $d_{\rm m}$ is the melting generation depth and $f_{\rm w}$ is the outgasssing fraction of water. $R_{{\rm H_2O}}$ is the regassing ratio of water, i.e., the fraction of subducting water that actually enters the deep mantle. The regassing ratio depends linearly on the mean mantle temperature $T_{\rm m}$ that is derived from the thermal evolution model via

 \begin{displaymath}R_{{\rm H_2O}}(T_{\rm m})=R_{\rm T} \cdot\left(T_{\rm m}(0)-T_{\rm m}\right)+R_{{\rm H_2O},0}. \end{displaymath} (15)

The factor $R_{\rm T}$ is adjusted to get the correct modern amount of surface water (one ocean mass) for an Earth-size planet and  $R_{{\rm H_2O},0}$ is fixed at 0.001, i.e., the value is very low at the beginning of the planetary evolution because of the enhanced loss of volatiles resulting from back-arc volcanism at higher temperatures.

The areal spreading rate S is a function of the average mantle temperature $T_{\rm m}$, the surface temperature $T_{{\rm surf}}$, the heat flow from the mantle $q_{\rm m}$, and the area of ocean basins A0 (Turcotte & Schubert 1982), given as

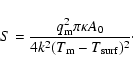\begin{displaymath}S = \frac{q_{\rm m}^2 \pi \kappa A_0}{4 k^2 (T_{\rm m} - T_{\rm surf})^2}\cdot \end{displaymath} (16)

In order to calculate the spreading rates for a planet with several Earth masses, the planetary parameters have to be adjusted. Therefore, we assume

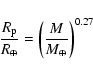\begin{displaymath}\frac{R_{\rm p}}{R_{\oplus}}= \left(\frac{M}{M_{\oplus}}\right)^{0.27} \end{displaymath} (17)

and where $R_{\rm p}$ is the planetary radius, see Valencia et al. (2006). The total radius, mantle thickness, core size and average density are all functions of mass, with subscript $\oplus$ denoting Earth values. The exponent of 0.27 has been obtained for super-Earths ( $M>1~M_\oplus$). The values of $R_{\rm m}$, $R_{\rm c}$, A0, the density of the planet, and the other planetary properties are scaled accordingly.

The CO2 concentration in the atmosphere $P_{{\rm CO}_2}$ is derived from the total mass of atmospheric carbon $C_{{\rm atm}}$ calculated from the balance between sources and sinks according to

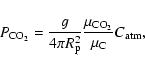\begin{displaymath}P_{{\rm CO}_2}=\frac{g}{4\pi R_{\rm p}^2}\frac{\mu_{{\rm CO}_2}}{\mu_{{\rm C}}}C_{{\rm atm}}, \end{displaymath} (18)

where $\mu_{{\rm CO}_2}$ and $\mu_{{\rm C}}$ are the molar weights of CO2 and C, respectively. The mass dependent pre-factor $g/R_{\rm p}^2$ scales with $M^{-0.08}\approx M^0$ and has therefore been neglected in our study.

In Table 1 we give a summary of the selected values for the parameters used in the thermal evolution model of the $5~M_\oplus$ and $8~M_\oplus$ super-Earth planets. For comparison, the values for an Earth-size planet are also shown. According to Valencia et al. (2007), we assume that a more massive planet is likely to convect in a plate tectonic regime similar to Earth. Thus, the more massive the planet is, the higher the Rayleigh number that controls convection, the thinner the top boundary layer (lithosphere), and the faster the convective velocities. In a first order approximation, we assume a fixed thickness of the basalt layer and melting depth corresponding to relatively low values. Furthermore, the initial amount of water $M_{\rm w}(0)$ scales linearly with the planetary mass. This might be an underestimate because more massive planets tend to accrete more volatiles.

The geophysical forcing ratios calculated from the thermal evolution model for a planet with one, five and eight Earth masses for a relative continental area of 0.3 are depicted in Fig. 2. It is obvious that the GFR increases with planetary mass and is at time zero about 1.8 times higher for $5~M_\oplus$ and 2.1 times higher for  $8~M_\oplus$ than for the Earth itself.

  \begin{figure} \par\includegraphics[width=6.7cm,clip]{7939fig2.eps}\end{figure} Figure 2: Geophysical forcing ratios (GFR) for a planet with $M=1~M_\oplus$ (solid line), $M=5~M_\oplus$ (dotted line) and $M=8~M_\oplus$(dash-dotted line) for a relative continental area of 0.3.
Open with DEXTER

2.4 Tidal locking

According to Peale (1977), the tidal locking radius $r_{\rm T}$ for a planet on a circular orbit can be estimated via

 \begin{displaymath}r_{\rm T}=0.027 \left( \frac{P_0t}{Q}\right)^{\frac{1}{6}}M_{{\rm star}}^{\frac{1}{3}} , \end{displaymath} (19)

where P0 is the original rotation period of the planet, t is the time, Q-1 is the dissipation function and $M_{{\rm star}}$ is the stellar mass (all quantities in cgs units). We assume analogously to Kasting et al. (1993) Q=100 and P0=13.5 h.

Planets inside the habitable zone of M stars are tidally locked. Due to tidal locking, a weaker intrinsic magnetic field is expected. Using simple scaling laws for the planetary magnetic dipole moment m, summarised by Grießmeier et al. (2005), we estimate values of about 0.5 $m_\oplus$ and 0.1 $m_\oplus$for Gl 581c and Gl 581d, respectively. The corresponding sizes of expected magnetospheres (compressed by coronal winds) can be quantified by the standoff distance $R_{\rm s}$ of the magnetopause (Khodachenko et al. 2007). The corresponding values for $R_{\rm s}$are on the order of several planetary radii. Thereby, the surfaces of the super-Earth planets Gl 581c and Gl 581d are expected to be protected from hot coronal winds.

For these estimates we assume that the super-Earths Gl 581c and Gl 581d have at least liquid outer cores. In contrast, according to Valencia et al. (2006), all super-Earth planets with masses higher than 1 $M_\oplus$ have completely solid cores for the preferred set of thermodynamic data. Nevertheless, using so-called high thermal parameters give warmer interiors and allow super-Earth planets to have a completely liquid core. This again points to a magnetospheric protection of super-Earth planetary atmospheres in Gl 581 from a dense flow of stellar plasma.

Furthermore, low mass stars have strong XUV irradiations during long time periods. Inside the habitable zone, such radiations can erode the atmosphere of an Earth-size planet and result in an additional limitation on the definition of habitability (Grießmeier et al. 2005). Another problem for the habitability of tidally locked planets is the freezing out of atmospheric volatiles on the dark side of the planet that makes the planets not habitable. Detailed investigations with the help of three-dimensional global circulation climate models, including the hydrological cycle, by Joshi et al. (1997) and Joshi (2003) showed that approximately 100 mbars of CO2 are sufficient to prevent atmospheric collapse. Therefore, super-Earth planets that generally are assumed to have more volatiles should not be restricted in their habitability by such effects. In case of an eccentric orbit of Gl 581d (e=0.2), the planet might be trapped in a m:n tidal locking (similar to Mercury in the Solar System), thus increasing its rotational period.

3 Results and discussion

The pHZ around Gl 581 for super-Earths with five and eight Earth masses has been calculated for L=0.011, 0.013, and $0.015~L_\odot$. The results for $5~M_\oplus$ are shown in Figs. 3a-c. The simulations have been carried out for a maximum CO2 pressure of 5 bar (light colours) and 10 bar (dark colours) neglecting the cooling effect of CO2 clouds. We assume that the maximum CO2 pressure of the atmosphere is not limited by the total amount of carbon on the planet. Sufficient amounts of carbon are assumed to be always available for building up a CO2 atmosphere of up to $P_{{\rm max}}=10$ bar. The biogenic enhancement factor of weathering  $\alpha_{{\rm bio}}$ has been set to one, i.e., a direct dependence of weathering on biological productivity according to Eq. (8) is neglected. Hence, the pHZ is calculated assuming a biotic enhancement of weathering similar to the modern biosphere on Earth. The tidal locking radius given by Eq. (19) is also shown. It is evident that both planets are well inside the tidal locking radius, assuming a stellar age of at least 2 Gyr (Bonfils et al. 2005). The inner boundary of the pHZ moves slightly outward, whereas the outer boundary decreases nonlinearly with age. Up to a critical age, the outer limit is constant and is determined by the maximum CO2 atmospheric pressure. Beyond this age, the outer boundary moves inward due to geodynamic effects. At this point the source of carbon released into the atmosphere is too low to prevent a freezing catastrophe.

The planet Gl 581c is clearly outside the habitable zone for all three luminosities. The luminosity of the central star would have to be as low as $L=0.0045~L_\odot$to yield habitable solutions for this planet. It should be pointed out that Gl 581c is closer to its parent star than Venus to the Sun, even with the stellar luminosity scaled accordingly. The results for Gl 581d are much more encouraging (Figs. 4a-c). In particular, for a maximum CO2concentration of 10 bar, the planet is inside the pHZ for $L\ge 0.0117~L_\odot$, a value consistent with the observed luminosity of Gl 581. Assuming an Earth-like fraction of continental area $a_{\rm c}=0.3$, this planet would be habitable for a duration of 5.75 Gyr. For a water world ( $a_{\rm c}=0.1$) the duration is extended to 9 Gyr, while for a land world ( $a_{\rm c}=0.9$) the duration is shortened to 0.3 Gyr.

Due to the tidal locking and the planet's position near the outer edge of the pHz, the appearance of complex life is rather unlikely on Gl 581d, i.e., $\Pi_{{\rm complex}}\equiv 0$. Life is adversely affected by low temperatures, small amounts of visible light, and insufficient shielding from intense flares. Thus, the simulations have been repeated with a parameterisation of weathering according to Eq. (8). The biogenic enhancement factor $\alpha_{{\rm bio}}$ has been set to 3.6 assuming that complex life amplifies weathering by this factor (von Bloh et al. 2003b). We find that the duration of habitability for primitive life is extended to 8.8 Gyr for $a_{\rm c}=0.3$. In general, higher values of $\alpha_{{\rm bio}}$ extend the life span of the biosphere (Lenton & von Bloh 2001; Franck et al. 2006). Incidentally, Tarter et al. (2007) argue that complex life might in principle be possible on planets around M stars.

Udry et al. (2007) determined the orbital eccentricity of Gl 581c and Gl 581d as $0.16 \pm 0.07$and $0.20 \pm 0.10$, respectively. Assuming an eccentric orbit does not affect the result that Gl 581c is outside the pHZ at all times; however, for Gl 581d, it would imply that it leaves and re-enters the pHZ during its orbital motion for any of the assumed model parameters (i.e., planetary climate model and stellar luminosity). But this would not thwart planetary habitability since a planet with a sufficiently dense atmosphere could harbour life even if its orbit is temporarily outside the HZ, see Williams & Pollard (2002).

However, it is noteworthy that the possible non-zero eccentricity values for the Gl 581 super-Earths are highly unlikely owing to the small number of radial-velocity measurements by Udry et al. (2007). As a small number of measurements always tends to render an overestimate in the deduced eccentricity, as well as a highly uncertain error bar (Butler et al. 2006), a circular orbit is strongly preferred in this case, as also done by Udry et al. (2007). In this case, the planetary orbit of Gl 581d is found to stay inside of the pHZ all the time for most of the considered planetary climate models and stellar luminosities.


  \begin{figure} \par\includegraphics[width=7cm,clip]{7939fig3.eps}\end{figure} Figure 3: The pHZ of Gl 581 for a super-Earth ( $M=5~M_\oplus$) with a relative continental area varied from 0.1 to 0.9 and a fixed stellar luminosity of  a)  $0.011~L_\odot$, b)  $0.013~L_\odot$, and  c)  $0.015~L_\odot$ as a function of planetary age. The light colours correspond to a maximum CO2 pressure of 5 bar, whereas the dark colours correspond to 10 bar. For comparison, the positions of Venus, Earth and Mars are shown scaled to the luminosity of Gl 581. The light grey shaded area denotes the HZ calculated from Eq. (1), while the dark shaded area corresponds to an extended outer limit following Mischna et al. (2000). The vertical bar at 2 Gyr denotes the range of distances due to the (possibly) eccentric orbit. The area below the solid black curve is affected by tidal locking.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{7939fig4.eps}\end{figure} Figure 4: The pHZ of Gl 581 for a super-Earth ( $M=8~M_\oplus$) with a relative continental area varied from 0.1 to 0.9 and a fixed stellar luminosity of  a)  $0.011~L_\odot$, b)  $0.013~L_\odot$, and  c)  $0.015~L_\odot$ as a function of planetary age. The light colours correspond to a maximum CO2 pressure of 5 bar, whereas the dark colours correspond to 10 bar. For comparison, the positions of Venus, Earth and Mars are shown scaled to the luminosity of Gl 581. The light grey shaded area denotes the HZ calculated from Eq. (1), while the dark shaded area corresponds to an extended outer limit following Mischna et al. (2000). The vertical bar at 2 Gyr denotes the range of distances due to the (possibly) eccentric orbit. The area below the solid black curve is affected by tidal locking.
Open with DEXTER

Table 2: Maximum outer limit $R_{\rm out}$ of the photosynthesis-sustaining habitable zone of Gl 581 for $L=0.013~L_\odot$ as a function of the maximum atmospheric CO2 pressure $P_{\rm max}$ for three different climate models.

The ultimate life span of a super-Earth is determined by the merging of the inner and outer pHZ boundaries and depends on the planetary mass. For a planet older than this ultimate life span, no habitability is found. An Earth-like planet with $1~M_\oplus$ and a relative continental area of 0.3 has an ultimate life span of 8.8 Gyr, while super-Earth planets with $5~M_\oplus$ and $8~M_\oplus$ have ultimate life spans of 11.1 Gyr and 11.9 Gyr, respectively. The critical age and ultimate life span is found to decrease with the relative continental area It is obvious that an almost completely ocean-covered planet ("water world'') has the highest likelihood of being habitable; see also previous models for 47 UMa by Franck et al. (2003). However, for an age of 2 Gyr, habitability for Gl 581d is not constraint by the outer edge of the pHZ for continental to total planetary surface ratios of less than 0.7. In the case of a biogenic enhancement factor $\alpha_{{\rm bio}}=3.6$ for complex life, habitability is maintained even for a land world with a continental to total planetary surface ratio of 0.9.

The simulations have been repeated for different maximum CO2 pressures $P_{\rm max}$ and three climate models (Table 2). For the climate model by Williams (1998), Gl 581d is habitable for $P_{\rm max}\geq 9$ bar, for a grey atmosphere model (Chamberlain 1980) no habitability can be found, while for the Budyko model (Budyko 1982) (climate sensitivity 4 K/2 $\times$ CO2) habitability is attained for $P_{\rm max}\ge 4$ bar.

A planet with eight Earth masses has more volatiles than an Earth size planet to build up such a dense atmosphere. This prevents the atmosphere from freezing out due to tidal locking. In case of an eccentric orbit of Gl 581d (e=0.2), the planet is habitable for the entire luminosity range considered in this study, even if the maximum CO2 pressure is assumed as low as 5 bar. In conclusion, one might expect that life may have originated on Gl 581d. The appearance of complex life, however, is unlikely due to the rather adverse environmental conditions. To get an ultimate answer to the profound question of life on Gl 581d, we have to await future space missions such as the TPF/Darwin. They will allow for the first time to attempt the detection of biomarkers (Grenfell et al. 2007) in the atmospheres of the two super-Earths around Gl 581.

References

 
Copyright ESO 2007