A&A 476, 359-368 (2007)
DOI: 10.1051/0004-6361:20078385
A. J. Díaz![]() - G. R. Donnelly - B. Roberts
- G. R. Donnelly - B. Roberts
Mathematical Institute, University of St Andrews, St Andrews, KY16 9SS, Scotland, UK
Received 31 July 2007 / Accepted 18 September 2007
Abstract
Aims. The role of longitudinal structuring of the surrounding corona on the modes of oscillation of a coronal magnetic flux tube was studied in Donnelly et al. (2006) for a piecewise uniform profile. Here we investigate whether a more realistic continuous exponential profile changes the conclusions drawn from that paper.
Methods. A partial differential equation is derived for the total pressure perturbation of the fast modes, which is then decomposed by separation of variables. The longitudinal part is solved numerically, obtaining a dispersion relation. These results are supported by an analytical investigation in terms of Bessel functions of purely imaginary order.
Results. Structure in the interior of the loop shifts the frequencies of the modes (and may trap higher harmonics), an effect which can be understood by taking an averaged profile with a suitable weight. Structure in the environment modifies only slightly the frequencies, but displaces the cutoff frequency. The shift due to the structure in the fundamental period is small, but the ratio between the periods of the fundamental mode and its harmonics can be used to probe the structure.
Conclusions. The results support our previous study in a more realistic, continuously varying profile and provide limits to the conclusions drawn in coronal seismology if an unstructured loop is used. Also, the ratio between the period of the fundamental kink (even) mode and its first (odd) harmonic is proven as an extra seismological tool for coronal loops.
Key words: Sun: oscillations - Sun: magnetic fields - Sun: corona
It is clear from the abundance of observations that fast magnetohydrodynamic (MHD) oscillations are a commonly occurring event for a coronal loop. As with any wave mode, oscillations of coronal loops carry information about the medium in which the wave propagates. If we understand the wave mode and its effect on the plasma as it propagates, we can extract the information the wave possesses about the plasma; this is known as coronal seismology (Nakariakov et al. 1999; Andries et al. 2005b; McEwan et al. 2006; Andries et al. 2005a; De Moortel et al. 2002; Roberts 1986; Nakariakov & Ofman 2001; Roberts et al. 1984).
In order to carry out coronal seismology, a good understanding of the oscillatory modes of a structure is necessary. Models generally consist of a straight cylindrical flux tube which is either infinitely long or line-tied (finite length) (Edwin & Roberts 1983; Roberts et al. 1984). When line-tying is considered it is also possible to study the effect of longitudinal structuring (Dymova & Ruderman 2006; Díaz et al. 2006; Donnelly et al. 2006; Erdélyi & Verth 2007; Andries et al. 2005b; McEwan et al. 2006; Andries et al. 2005a; Díaz et al. 2002,2004; Mendoza-Briceño et al. 2004; James 2003; Nakariakov & Ofman 2001; Nakariakov et al. 2000). In particular, in Donnelly et al. (2006) step functions are used to represent dense chromospheric layers both inside and outside the loop. However, the use of step functions is only a first approximation and, in an actual coronal loop, a continuously varying density profile is expected.
In this paper we consider continuous longitudinal density profiles, comparing our results with the uniform line-tied loop. We consider a loop of finite radius. An alternative approach is to use the thin tube approximation (Dymova & Ruderman 2006; Erdélyi & Verth 2007; McEwan et al. 2007). First we consider a loop with exponential behaviour along its full length, for which the influence of the loop radius as well as the level of structure between the loop apex and footpoint is studied. Secondly, a loop with uniform coronal region but with exponentially varying chromospheric regions close to the footpoints is considered.
We use the same mathematical method as in Donnelly et al. (2006), adapted to permit different longitudinal dependences in the density and Alfvén profiles. Since these profiles are continuous, a numerical approach may also be used to solve the resulting wave equations.
We consider a spatially structured static equilibrium of a cylindrically
symmetric line-tied coronal magnetic flux tube (lying parallel to the z axis)
of length 2 L and radius a. The equilibrium magnetic field
![]() is assumed to be uniform throughout the medium and is aligned with
the loop. The equilibrium density
is assumed to be uniform throughout the medium and is aligned with
the loop. The equilibrium density ![]() is structured both radially and
longitudinally. Gravitational effects are ignored.
is structured both radially and
longitudinally. Gravitational effects are ignored.
Small amplitude oscillations about this equilibrium are considered
in the limit of a zero ![]() plasma, in which wave propagation is dominated by magnetism and slow
waves are absent. The ideal adiabatic MHD equations
in cylindrical coordinates
plasma, in which wave propagation is dominated by magnetism and slow
waves are absent. The ideal adiabatic MHD equations
in cylindrical coordinates
![]() reduce to the
following system of coupled partial differential equations for a zero
reduce to the
following system of coupled partial differential equations for a zero ![]() plasma (Díaz et al. 2006,2002; Díaz 2004)
plasma (Díaz et al. 2006,2002; Díaz 2004)
We allow for a general longitudinal and transverse structuring in the form of step functions, the equilibrium plasma density profile taking the form
We consider trapped modes for which there is no propagation of energy towards or
away from the loop. This is achieved by imposing
![]() and
and
![]() as
as
![]() .
The loop is line-tied
with the footpoints fixed in the dense photosphere, where it is expected that
coronal perturbations carry such small energy that they are incapable of
perturbing the dense lower layers (Hood 1986): this leads to the line-tying boundary
condition
.
The loop is line-tied
with the footpoints fixed in the dense photosphere, where it is expected that
coronal perturbations carry such small energy that they are incapable of
perturbing the dense lower layers (Hood 1986): this leads to the line-tying boundary
condition
![]() .
In this model, we have interfaces over
which the equilibrium plasma properties jump discontinuously so we must know
how the perturbations behave across such surfaces. In the case where the
interface is parallel to the equilibrium field, the boundary conditions are
(Goedbloed 1983; Díaz et al. 2001; Díaz 2004)
.
In this model, we have interfaces over
which the equilibrium plasma properties jump discontinuously so we must know
how the perturbations behave across such surfaces. In the case where the
interface is parallel to the equilibrium field, the boundary conditions are
(Goedbloed 1983; Díaz et al. 2001; Díaz 2004)
We study oscillatory solutions to Eqs. (1) and (2).
Following Díaz et al. (2002), we assume a solution which is separable
in space and time, writing
Solving Eq. (8) for ![]() gives
gives
Equation (7) has solutions in the form
The dispersion relation for the trapped modes of oscillation of a line-tied
coronal loop with arbitrary longitudinal environmental structuring and step
functions in the radial coordinate is satisfied when the determinant of the
system of Eq. (18) vanishes. This condition describes the
sausage (m=0), kink (m=1) and fluting (![]() ) modes. An interesting
aspect of this general dispersion relation is that, due to the summation over all
harmonics, each mode is in general a combination of both surface and body
modes, whereas in a homogeneous tube these may be considered separately.
) modes. An interesting
aspect of this general dispersion relation is that, due to the summation over all
harmonics, each mode is in general a combination of both surface and body
modes, whereas in a homogeneous tube these may be considered separately.
The modes of oscillation of a uniform loop embedded in a uniform environment
are governed by the dispersion relation (see Edwin & Roberts 1983)
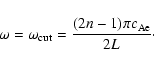 |
(22) |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{8385f1a.eps}\vspace*{3mm}
\includegraphics[width=6.9cm,clip]{8385f1b.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg75.gif) |
Figure 1:
Dispersion diagram plotting non-dimensional frequency
|
| Open with DEXTER | |
Figure 1 shows the dispersion diagram plotting non-dimensional
frequency
![]() against a/L for a uniform loop and
uniform environment, with (a)
against a/L for a uniform loop and
uniform environment, with (a)
![]() or (b)
or (b)
![]() .
This diagram is similar to the fast mode band of the coronal
case considered Edwin & Roberts (1983), with the fundamental kink mode the
only mode to propagate for all a/L. The kink mode has a phase speed
.
This diagram is similar to the fast mode band of the coronal
case considered Edwin & Roberts (1983), with the fundamental kink mode the
only mode to propagate for all a/L. The kink mode has a phase speed
![]() in the thin tube limit, with
in the thin tube limit, with
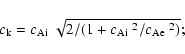 |
(23) |
Figure 1b shows an example of the dispersion diagram with higher density contrast between the interior and exterior, where both the first and second n families appear below the n=1 cutoff frequency. The first family, which also appears in Fig. 1a, has one extremum in the longitudinal direction while the second even family has three extrema in the longitudinal direction, so they represent different longitudinal harmonics. As there is no longitudinal structuring of the loop or the environment each family, with different longitudinal wavenumbers are decoupled; this permits the crossing of their dispersion curves.
We introduce longitudinal structure in the loop considering an exponential Alfvén
profile of the form
0pt
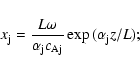 |
(27) |
Although the ordinary Bessel function has been extensively explored in the case of real orders the properties and methods of calculation of Bessel functions of purely imaginary order are not well known and the use of recurrence relations or integral representations is not straightforward (Dunster 1990). Accordingly, we find the use of numerical methods to solve the equation directly a more convenient approach for determining solutions of Eq. (26), although the solution in Eq. (29) provides a useful guide for understanding the properties of the solutions.
We may isolate the effect of loop structure. Previous studies in this area
have considered loop profiles using step functions (Díaz et al. 2004) to
approximate a coronal region above a dense chromospheric layer with a
homogeneous environment or profiles coming from other hydrodynamic equilibria
(Díaz et al. 2006; Andries et al. 2005b). Recently, continuous profiles have also been studied by
solving analytically and numerically the 1D equation that it is obtained in the thin-tube limit
(Dymova & Ruderman 2006; Erdélyi & Verth 2007; McEwan et al. 2007). We extend these models by approximating the
longitudinal density structure by a continuous exponential profile.
A density increase due to structure results in a decrease of the oscillation frequency (which may lead to trapping of more modes) but since the cutoff frequency depends purely on the
structure of the external medium, it remains at
![]() .
.
Figure 2a shows the dispersion diagram for the case
![]() .
The diagram is similar in structure to
that of Edwin & Roberts (1983) with only the fundamental kink mode propagating
for all values of a/L and all other modes reaching the cutoff frequency
where these modes become leaky. All modes are highly dispersive and sausage and
kink modes are distributed alternately; in the thin tube limit the frequency of
the fundamental kink mode is insensitive to a/L. Comparing
Fig. 2a with Fig. 1a, we see the
internal structure has resulted in a decrease in the frequency of each
mode. This is illustrated by the modification of the kink mode from
.
The diagram is similar in structure to
that of Edwin & Roberts (1983) with only the fundamental kink mode propagating
for all values of a/L and all other modes reaching the cutoff frequency
where these modes become leaky. All modes are highly dispersive and sausage and
kink modes are distributed alternately; in the thin tube limit the frequency of
the fundamental kink mode is insensitive to a/L. Comparing
Fig. 2a with Fig. 1a, we see the
internal structure has resulted in a decrease in the frequency of each
mode. This is illustrated by the modification of the kink mode from
![]() (Eq. (24)) in the uniform case to
(Eq. (24)) in the uniform case to
![]() as a result of the exponential structure.
as a result of the exponential structure.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{8385f2a.eps}\vspace*{3mm}
\includegraphics[width=6.9cm,clip]{8385f2b.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg99.gif) |
Figure 2:
Dispersion diagram plotting non-dimensional frequency
|
| Open with DEXTER | |
We also consider, in Fig. 2b, a density structure of
![]() = 8.
The structure of the dispersion diagram has now
significantly altered, with many more modes propagating in a given range
of a/L. Not only the fundamental kink mode but also its first harmonic
now propagate as trapped modes for all a/L (compare with
Fig. 1b); the frequency of the
fundamental mode has retained its insensitivity to a/L in the thin tube
limit but the first harmonic does not share this property; all other modes
reach the cutoff frequency. The structure of one sausage mode lying between
consecutive kink modes has now been broken as a result of many mode
interactions at avoided crossings (the spatial structure across an avoided
crossing will be discussed later) between like curves. Also, the presence of
avoided crossings seems to allow sausage and kink modes to cross, and so
have the same frequency for a specific loop dimension.
= 8.
The structure of the dispersion diagram has now
significantly altered, with many more modes propagating in a given range
of a/L. Not only the fundamental kink mode but also its first harmonic
now propagate as trapped modes for all a/L (compare with
Fig. 1b); the frequency of the
fundamental mode has retained its insensitivity to a/L in the thin tube
limit but the first harmonic does not share this property; all other modes
reach the cutoff frequency. The structure of one sausage mode lying between
consecutive kink modes has now been broken as a result of many mode
interactions at avoided crossings (the spatial structure across an avoided
crossing will be discussed later) between like curves. Also, the presence of
avoided crossings seems to allow sausage and kink modes to cross, and so
have the same frequency for a specific loop dimension.
The modifications in the frequency in Fig. 2 are
mainly due to an uniform scaling of the dispersion curves as seen in Fig. 3, where the dispersion curves of a uniform loop embedded in
a uniform environment with
![]() and the dispersion
curves of a structured loop with
and the dispersion
curves of a structured loop with
![]() embedded in a uniform
environment with
embedded in a uniform
environment with
![]() have been overlaid. This
scaling is related to the suggestion that the effect of the structure can be
approximated by an unstructured loop with the same weighted mean density,
weighted with the square of the fundamental eigenfunction (Andries et al. 2005b).
We can perform this calculation: in the exponentially structured model
(Eq. (25)), the internal weighted density
have been overlaid. This
scaling is related to the suggestion that the effect of the structure can be
approximated by an unstructured loop with the same weighted mean density,
weighted with the square of the fundamental eigenfunction (Andries et al. 2005b).
We can perform this calculation: in the exponentially structured model
(Eq. (25)), the internal weighted density
![]() is
given by
is
given by
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{8385f3.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg107.gif) |
Figure 3:
Dispersion diagram plotting
|
| Open with DEXTER | |
Another interesting point is how the actual crossings of the dispersion curves of the uniform loop correspond to the avoided crossings in the structured case. This suggests that for avoided crossings to occur in the structured loop the loop must have a large enough density enhancement so that a uniform loop of equivalent mass supports more than just the first family of modes below the cutoff frequency of the first family. As the oscillatory modes of a structured loop are a superposition of all families of the uniform loop, one family will generally be dominant; but at an avoided crossing the dominant family is changed, resulting in a change in spatial structure of the mode.
In conclusion, the uniform loop is a reasonable approximation to the structured loop provided an appropriate density is used. However, if loop parameters are determined from one point on the loop, especially an extreme point such as the apex or the footpoint, and the rest of the loop is assumed to be at the same value, this will give a poor representation, since some sort of averaging is necessary. If a higher accuracy is required, then the structured model should be employed rather than the uniform model, if the model is to capture all features such as modified frequencies and spatial structure of the eigenfunctions and interactions between modes at avoided crossings.
We next investigate the dependence of the oscillation frequency on the strength
of the structure. This is displayed in Fig. 4, showing dispersion
diagrams of the non-dimensional frequency as a function of the longitudinal
density contrast
![]() between the loop base and the loop apex.
We consider a thin tube, a/L=0.01, which is in line with the value used
by Nakariakov et al. (1999). In the uniform loop case
(
between the loop base and the loop apex.
We consider a thin tube, a/L=0.01, which is in line with the value used
by Nakariakov et al. (1999). In the uniform loop case
(
![]() )
and in the thin tube limit, only
the fundamental kink mode propagates as a trapped mode. For moderate levels of
structuring (
)
and in the thin tube limit, only
the fundamental kink mode propagates as a trapped mode. For moderate levels of
structuring (
![]() )
it is seen that the
frequency of the fundamental kink mode is strongly dependent on the density
structure, causing the frequency to decrease rapidly, this decrease becoming
slower as
)
it is seen that the
frequency of the fundamental kink mode is strongly dependent on the density
structure, causing the frequency to decrease rapidly, this decrease becoming
slower as
![]() becomes large.
becomes large.
Since the addition of density to the loop results in a reduction in oscillation frequency, eventually many of the kink harmonics (as well as the fundamental) will propagate as trapped modes in the thin tube limit. However, this is not the case for the sausage mode which never propagates as a trapped mode in the thin tube limit.
In Fig. 4, the results for the fundamental mode of a uniform loop - as determined by Eq. (24) with weighted averaged density given by Eq. (33) - have been overplotted to highlight that the average profile produces reasonably accurate results for the fundamental mode.
In order to isolate the effect of structure in the environment of a coronal loop we consider an exponentially structured environment surrounding a homogeneous loop, providing an extension of the study carried out in Donnelly et al. (2006). In this case the density of the environment increases towards the chromospheric-photospheric base and so can become denser than the loop. As the overall density of the environment has increased relative to the loop, the loop becomes a less efficient waveguide supporting fewer trapped modes. As noted in Donnelly et al. (2006), environmental structure reduces the cutoff frequency of the trapped modes, enhancing the leakage.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{8385f4.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg110.gif) |
Figure 4:
Dispersion diagram plotting as solid lines the non-dimensional
frequency
|
| Open with DEXTER | |
Figure 5 shows the dispersion diagram for a
homogeneous loop in a structured environment with
![]() or
or
![]() ,
with Fig. 1a
overplotted for comparison purposes.
The diagram shows similarities with that of the uniform loop in a uniform
environment, with the fundamental kink mode being the only mode to propagate for
all a/L; all other modes reach a uniform cutoff frequency beyond which
the modes become leaky.
All modes have a dispersive nature so their frequency is strongly dependent on
the loop radius or length. However, in the realistic thin tube region
(
a/L = 10-3-10-1), only the fundamental kink mode propagates
and then
,
with Fig. 1a
overplotted for comparison purposes.
The diagram shows similarities with that of the uniform loop in a uniform
environment, with the fundamental kink mode being the only mode to propagate for
all a/L; all other modes reach a uniform cutoff frequency beyond which
the modes become leaky.
All modes have a dispersive nature so their frequency is strongly dependent on
the loop radius or length. However, in the realistic thin tube region
(
a/L = 10-3-10-1), only the fundamental kink mode propagates
and then
![]() is insensitive to the loop radius.
Comparing the frequencies for structured environment with those of the
unstructured environment, we note that there is a significant reduction in the
cutoff frequency from
is insensitive to the loop radius.
Comparing the frequencies for structured environment with those of the
unstructured environment, we note that there is a significant reduction in the
cutoff frequency from
![]() for a uniform
environment to
for a uniform
environment to
![]() and
and
![]() for the exponential environments with
for the exponential environments with
![]() and
and
![]() ,
respectively. As a
result of the reduced cutoff frequency, the value of a/L for which
modes become leaky is increased. Another interesting point is that the
modification to the frequency in the range where
both sets of modes are trapped is relatively small, especially for larger
values of a/L. Notice also that the structure has resulted in a
reduction in the dispersive effect of a/L when compared with the
uniform environment.
,
respectively. As a
result of the reduced cutoff frequency, the value of a/L for which
modes become leaky is increased. Another interesting point is that the
modification to the frequency in the range where
both sets of modes are trapped is relatively small, especially for larger
values of a/L. Notice also that the structure has resulted in a
reduction in the dispersive effect of a/L when compared with the
uniform environment.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{8385f5.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg114.gif) |
Figure 5:
Dispersion diagram plotting
|
| Open with DEXTER | |
We conclude that environmental structure results in a small
modification to the oscillation frequency and a reduction in the dispersive
nature of the modes. The most significant alteration to the modes due to
environmental structure occurs in the cutoff frequency: adding density
results in a reduction in the cutoff frequency and so leakage is enhanced.
It should be noted that
density structuring with
![]() or 50 are modest compared
with a more realistic value of
or 50 are modest compared
with a more realistic value of
![]() ,
but trapped modes no
longer propagate for such high values.
,
but trapped modes no
longer propagate for such high values.
We next consider the influence of varying the
level of structuring in the environment to examine the effect on the
oscillation frequency and the cutoff frequency. We can see these effects
in Fig. 6. As previously noted, the external structure has little influence on the
oscillation frequency in the thin tube case,
but its main impact is on the cutoff frequency,
in that the addition of density to the environment in comparison
with the loop results in a reduction in the cutoff frequency as the loop
becomes a less efficient wave guide. In Fig. 6 we
can see a significant reduction in cutoff frequency, from a value of
![]() in the uniform case to a value of
in the uniform case to a value of
![]() for a structuring of
for a structuring of
![]() .
Notice the most rapid reduction in cutoff frequency
occurs as low levels of structuring are introduced,
.
Notice the most rapid reduction in cutoff frequency
occurs as low levels of structuring are introduced,
![]() ,
and the gradient becomes shallower as
,
and the gradient becomes shallower as
![]() becomes
larger. Another feature of the cutoff frequency is that it is independent of
the loop radius. As a result of
the reduction in the cutoff frequency, modes that have previously been
considered to propagate as a trapped mode, such as the fundamental kink mode in
the thin tube limit, are now seen to reach the cutoff frequency and become
leaky. Also in thicker loops, where many sausage and kink modes are expected to
propagate as trapped modes, for large enough environmental structuring (say
becomes
larger. Another feature of the cutoff frequency is that it is independent of
the loop radius. As a result of
the reduction in the cutoff frequency, modes that have previously been
considered to propagate as a trapped mode, such as the fundamental kink mode in
the thin tube limit, are now seen to reach the cutoff frequency and become
leaky. Also in thicker loops, where many sausage and kink modes are expected to
propagate as trapped modes, for large enough environmental structuring (say
![]() )
all modes become leaky.
)
all modes become leaky.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{8385f6.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg119.gif) |
Figure 6:
Dispersion diagram for a uniform loop in a exponentially structured
environment, plotting
|
| Open with DEXTER | |
Having seen separately the effects of structure in the loop or in the
environment, we now combine the effects of longitudinal
structure both inside and outside the loop, thus producing a more
realistic model for a coronal loop. We have seen that the main
influence of the internal structure is to modify the oscillation frequency
and the main influence of the external structure is in a
modification in the cutoff frequency. We consider a realistic density ratio in
the environment of
![]() between the coronal and
chromospheric-photospheric levels, and assume the photosphere to be uniform so
that
between the coronal and
chromospheric-photospheric levels, and assume the photosphere to be uniform so
that
![]() .
Although this may not always be accurate, we do not
expect significant changes due to variations in density in the
lower atmosphere, especially since the perturbations fall to zero at the
footpoints to satisfy the line tying condition. Hence, choosing again
.
Although this may not always be accurate, we do not
expect significant changes due to variations in density in the
lower atmosphere, especially since the perturbations fall to zero at the
footpoints to satisfy the line tying condition. Hence, choosing again
![]() results in
results in
![]() .
.
The dispersion diagram for this case is shown in Fig. 7 and is very similar in structure and appearance to the uniform loop and uniform environment: the fundamental kink mode propagating for all a/L and other modes reach the cutoff frequency. Also kink and sausage modes are again distributed alternately and there are no avoided crossings present. The most interesting aspects are seen most clearly when we make direct comparison between this case and the homogeneous loop and environment, where we have simply matched the densities at the loop apex. We see immediately that the fast mode bands for these two different coronal loop structures do not overlap. The structuring of the corona has reduced the dimensionless cutoff frequency to 1.4 (also see Fig. 6), which is below the lower limit of the frequency for the uniform loop and environment. Also the value of a/L for which modes reach the cutoff frequency has increased as a result of the reduction in the cutoff frequency. Previously, when we implemented such a large environmental structuring around a uniform loop, we found that the loop did not support any trapped modes. However, as noted earlier, the introduction of internal structure results in a modification to the oscillation frequency and in this case the loop again supports many trapped modes.
Therefore, we conclude exponential structuring of the form in Eq. (25) is an important factor for the cutoff frequency but more importantly for the oscillation frequency and period of the modes. If a uniform interior and exterior are used to approximate a structured loop, it is important that the parameters chosen for the uniform case reflect the overall structure along the loop rather than simply matching the densities at a single point (such as the apex or the footpoint). In fact the apex or the footpoints are inappropriate points to choose for a comparison, since they are most extreme in the model. A more effective method of representing the structured case by a uniform case is to match the total integrated densities in each of the appropriate regions.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{8385f7.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg120.gif) |
Figure 7:
Dispersion diagram plotting
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8385f8.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg121.gif) |
Figure 8:
Dispersion diagram plotting
|
| Open with DEXTER | |
Next we allow the external density structuring to vary, but retain the assumption
that the loop footpoint (![]() )
is uniform (so
)
is uniform (so
![]() ). The internal structure is modified appropriately.
For this case the loop always has a density enhancement over its environment. Figure 8 shows the dispersion diagrams plotting
non-dimensional frequency against
). The internal structure is modified appropriately.
For this case the loop always has a density enhancement over its environment. Figure 8 shows the dispersion diagrams plotting
non-dimensional frequency against
![]() .
The cutoff curve is identical to that of Fig. 6, since it is independent of the
internal structure and loop radius. We can see that in both cases modes remain
trapped for a larger range of density structuring compared with the case
displayed in Fig. 6. This is due to the modification
of the oscillation frequency as a result of the internal loop structure, where
we can see the fundamental kink mode remains trapped for all values of
structuring shown in Fig. 8 for the thin tube limit.
Therefore, in this case the effect of internal structuring in modifying the
oscillatory frequency is greater than the effect of the external structuring
in reducing the cutoff frequency.
.
The cutoff curve is identical to that of Fig. 6, since it is independent of the
internal structure and loop radius. We can see that in both cases modes remain
trapped for a larger range of density structuring compared with the case
displayed in Fig. 6. This is due to the modification
of the oscillation frequency as a result of the internal loop structure, where
we can see the fundamental kink mode remains trapped for all values of
structuring shown in Fig. 8 for the thin tube limit.
Therefore, in this case the effect of internal structuring in modifying the
oscillatory frequency is greater than the effect of the external structuring
in reducing the cutoff frequency.
In the previous section we took a step forward in that the density structuring
of the loop is continuous, whereas in Díaz et al. (2004) and Donnelly et al. (2006) step
functions were used to represent the longitudinal density profile changing from
the coronal to photospheric values. We consider a uniform
coronal region but allow an exponential density profile in the chromospheric
layers of thickness L-W near the footpoints.
Thus, the profile of the Alfvén speed is
If we select the density profile inside the loop consistent with
Eq. (34) and assume a uniform environment there is a modification in
the oscillation frequency but not the cutoff frequency.
However, the introduction of structuring across the chromospheric region results
in a slight correction to the frequency of the uniform loop.
We consider the impact of varying the chromospheric layer thickness (L-W)while holding the internal density ratio fixed at
![]() .
Figure 9 show
dispersion diagrams for this model. The case
W/L=0 corresponds to the exponential loop profile (Eq. (25)) considered
earlier and W/L=1 gives the uniform loop, so we will be able to observe the
evolution from the structured case to the uniform case. Figure 9 shows that only the fundamental kink mode is able to propagate as a trapped mode for all values of W/L, and its
frequency increases as we evolve from the exponential structure to the
uniform loop. Also, for smaller values of W/L we find the first and second
kink harmonics are trapped in the thin tube limit but are seen to reach the
cutoff frequency before the realistic range of values of
.
Figure 9 show
dispersion diagrams for this model. The case
W/L=0 corresponds to the exponential loop profile (Eq. (25)) considered
earlier and W/L=1 gives the uniform loop, so we will be able to observe the
evolution from the structured case to the uniform case. Figure 9 shows that only the fundamental kink mode is able to propagate as a trapped mode for all values of W/L, and its
frequency increases as we evolve from the exponential structure to the
uniform loop. Also, for smaller values of W/L we find the first and second
kink harmonics are trapped in the thin tube limit but are seen to reach the
cutoff frequency before the realistic range of values of
![]() .
Importantly, for a realistic range of chromospheric depth, the frequency
of the fundamental mode is insensitive to the chromospheric depth.
We conclude that loop structuring of the form (34) does not cause
significant changes to the frequency for realistic parameters (
W/L =0.8-1.0). In fact, it is reasonable to assume a uniform loop provided it is chosen
appropriately to match the structured loop at the apex.
.
Importantly, for a realistic range of chromospheric depth, the frequency
of the fundamental mode is insensitive to the chromospheric depth.
We conclude that loop structuring of the form (34) does not cause
significant changes to the frequency for realistic parameters (
W/L =0.8-1.0). In fact, it is reasonable to assume a uniform loop provided it is chosen
appropriately to match the structured loop at the apex.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8385f9.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg125.gif) |
Figure 9:
Dispersion diagram plotting
|
| Open with DEXTER | |
On the other hand, if we isolate the effect of structure of the form of
Eq. (34) in the environment by considering a uniform loop
we obtain a modification
to the cutoff frequency in this case, but only a small correction to the
oscillatory frequency.
Again we investigate the influence of the parameter W/L on the oscillation
and cutoff frequencies.
This is overplotted in Fig. 9 as a dotted line.
Only the fundamental kink mode propagates as a trapped mode, and even this mode
has a cutoff for
![]() (similar to Fig. 6). The
oscillation frequency of the fundamental kink mode shows only a slight
dependence on W/L, especially in the realistic range of
W/L=0.8-1.0.
(similar to Fig. 6). The
oscillation frequency of the fundamental kink mode shows only a slight
dependence on W/L, especially in the realistic range of
W/L=0.8-1.0.
So far we have explored the effects of structuring in density by looking
separately at its role in the loop interior or in the loop environment. In
reality, of course, the effects will arise in a combined way.
Structure is again taken to be of the form of Eq. (34), now applied
in both regions. In the environment, we choose
![]() ;
however, we assume a uniform
photospheric base, so
;
however, we assume a uniform
photospheric base, so
![]() .
The implication
of this is that the density structure of the loop across the chromosphere depth
is less than that of the environment.
The structuring results in a small correction to the oscillation
frequency, which is mainly due to the internal structure. However, the
reduction in the cutoff frequency is entirely a result of the external
structuring. Again, the uniform case provides an adequate representation of
this loop structure and would thus serve adequately for the purpose of coronal
seismology, but care should be taken in using modes close to the cutoff.
However, in this case the fundamental kink mode does not reach the cutoff
frequency in the thin tube case (Fig. 9, dot-dashed line). This is
due to the reduction in its frequency as a result of the internal structuring as
.
The implication
of this is that the density structure of the loop across the chromosphere depth
is less than that of the environment.
The structuring results in a small correction to the oscillation
frequency, which is mainly due to the internal structure. However, the
reduction in the cutoff frequency is entirely a result of the external
structuring. Again, the uniform case provides an adequate representation of
this loop structure and would thus serve adequately for the purpose of coronal
seismology, but care should be taken in using modes close to the cutoff.
However, in this case the fundamental kink mode does not reach the cutoff
frequency in the thin tube case (Fig. 9, dot-dashed line). This is
due to the reduction in its frequency as a result of the internal structuring as
![]() (such as in Fig. 8).
The frequency of all trapped modes in the realistic range
where
W/L=0.8-1.0 is found to be independent of W/L. This again points to
the fact that the uniform loop and uniform environment provides a robust model.
(such as in Fig. 8).
The frequency of all trapped modes in the realistic range
where
W/L=0.8-1.0 is found to be independent of W/L. This again points to
the fact that the uniform loop and uniform environment provides a robust model.
We can also explore the case in which the footpoint density
![]() becomes relatively large. In such a limit,
becomes relatively large. In such a limit,
![]() becomes large, and
the coefficients of the Bessel functions of imaginary order in
Eq. (35) become small. These functions have the property of having
an infinite number of oscillations as
becomes large, and
the coefficients of the Bessel functions of imaginary order in
Eq. (35) become small. These functions have the property of having
an infinite number of oscillations as
![]() (Dunster 1990), so
other modes would be able to propagate under that limit: those which a number of
small wiggles in the chromospheric regions (W<|z|<L). This type of solutions
have been described for the slow mode in Dymova & Ruderman (2006) and McEwan et al. (2006).
However, these solutions appear under the cutoff for extremely large
values of
(Dunster 1990), so
other modes would be able to propagate under that limit: those which a number of
small wiggles in the chromospheric regions (W<|z|<L). This type of solutions
have been described for the slow mode in Dymova & Ruderman (2006) and McEwan et al. (2006).
However, these solutions appear under the cutoff for extremely large
values of
![]() .
.
There is some observational evidence (Van Doorsselaere et al. 2007; Verwichte et al. 2004) that the period
ratio P1/n Pn between the period P1 of the fundamental kink mode and its harmonics with period Pn, ![]() deviates from unity in solar arcades.
Although there are only a few
detections of harmonics in coronal loops, the potential of this ratio for
coronal seismology has been studied theoretically (Andries et al. 2005a; McEwan et al. 2006,2007).
deviates from unity in solar arcades.
Although there are only a few
detections of harmonics in coronal loops, the potential of this ratio for
coronal seismology has been studied theoretically (Andries et al. 2005a; McEwan et al. 2006,2007).
In McEwan et al. (2006) various factors that cause the period ratio to
deviate from unity were discussed, and
it was found that the most important one was the effect of longitudinal
structure. Here we calculate the ratio P1/2 P2 for the
continuous exponential density profile of Sect. 4.1. The results are
shown in Fig. 10 for two values of
![]() ,
pointing
out that for values of
a/L < 10-1, the longitudinal structuring is
mainly responsible of the shift.
,
pointing
out that for values of
a/L < 10-1, the longitudinal structuring is
mainly responsible of the shift.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{8385f10.ps}\vspace*{4mm}
\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg132.gif) |
Figure 10:
P1/2P2 as a consequence of longitudinal structuring.
The density is exponentially stratified along the loop,
the solid line has a base density that is 8 times the density at the apex,
|
| Open with DEXTER | |
Therefore, it is interesting to take a fixed value of a/L and study the dependence of the ratio P1/2P2 as a function of the density contrast (Fig. 11). The result is a monotonically decreasing function. These results can be used in coronal seismology to estimate the scale height of the model (see McEwan et al. 2006).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8385f11.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg133.gif) |
Figure 11:
P1/(2P2) as a function of the density contrast
|
| Open with DEXTER | |
Using the results of Sect. 4.3, we could find a similar plot if an exponential density profile is considered in the embedding corona. We checked that the main effect is to modify the cutoff frequency, but for typical parameters the fundamental mode and its first harmonic do not reach it, and the frequency shift is mainly because of the internal structure. A plot very similar to Fig. 11 results.
On the other hand, the ratio P1/3P3 between the fundamental mode and its first even harmonic might also be of interest. In a homogeneous medium this ratio is unity, while in a coronal arcade it is no longer monotonically decreasing because of the appearance of avoided crossings between modes with the same symmetry (Donnelly et al. 2007). Avoided crossings are also present in the loop modes (Fig. 2b), so the P1/3P3 has extrema, shown in Fig. 12 for a coronal loop in a homogeneous corona (dashed line). However, in a coronal loop the first even harmonic becomes leaky for small values of a/L (Figs. 2a and 7), so it is less useful as a seismological tool, since the leaky modes are much harder to detect. We can see it in Fig. 12 (solid line), which shows that the mode becomes leaky further from the typical values of a/L for coronal loops. It is important to remark that the coronal structuring plays a relevant role in this ratio, since we can see in Fig. 2b that if the coronal structuring is not considered, then these harmonics may become trapped so P1/3P3 can be obtained for all the values of a/L, but this is a mathematical artifact due to that assumption of a homogeneous corona.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{8385f12.eps}\end{figure}](/articles/aa/full/2007/46/aa8385-07/Timg134.gif) |
Figure 12:
P1/(3P3) as a function of a/L for a structured loop
with
|
| Open with DEXTER | |
We have studied the effect of longitudinally structured density profiles in
either the loop interior, its exterior, or both. This extends the results in
Donnelly et al. (2006), where uniform layers were used. The first of these profiles was
was a purely exponential one and so the transition between the maximum density
at the loop footpoint and minimum at the apex is gradual, and therefore does not
reflect the more realistic rapid change from the photosphere to the corona over
the height of the chromosphere. For this profile the frequency of the
oscillation is strongly dependent on
![]() ,
the ratio of the loop apex density to density at the footpoints. This strong
dependence reflects the large addition of mass in the loop associated with the
exponential profile. Comparisons with a uniform loop show poor agreement in
frequency when the uniform loop parameters are chosen to match the apex of the
structured loop. However, a much better agreement is observed when a weighted
average for the density is used, as suggested by Andries et al. (2005b). When the
structure of the environment is included a modification in the cutoff frequency
arises; comparatively small changes in the oscillation frequency also occur,
when compared with the effect of internal structure. Drawing comparison with the
uniform loop in the case of the internal structure, good agreement is found when
the profiles of the structured and uniform environments are in mass balance.
,
the ratio of the loop apex density to density at the footpoints. This strong
dependence reflects the large addition of mass in the loop associated with the
exponential profile. Comparisons with a uniform loop show poor agreement in
frequency when the uniform loop parameters are chosen to match the apex of the
structured loop. However, a much better agreement is observed when a weighted
average for the density is used, as suggested by Andries et al. (2005b). When the
structure of the environment is included a modification in the cutoff frequency
arises; comparatively small changes in the oscillation frequency also occur,
when compared with the effect of internal structure. Drawing comparison with the
uniform loop in the case of the internal structure, good agreement is found when
the profiles of the structured and uniform environments are in mass balance.
The second density profile we considered was chosen to represent more accurately the rapid transition between the photosphere and the corona, extending the results for piecewise functions in Díaz et al. (2004) and Donnelly et al. (2006). In this profile a uniform coronal region of extent 2W is assumed to be grounded by an exponentially structured chromosphere. For this case there is excellent agreement between the uniform loop and structured loop which are matched at the apex. Other effects that appeared in previous piecewise works are also present here, namely, the avoided crossings between modes and the apparition of small extrema in the dense regions near the footpoints of the loop. Regarding the frequency of the fundamental modes of each family, these results demonstrate the robust nature of the Edwin & Roberts (1983) model and gives confidence to the results of coronal seismology (see, for example, Nakariakov & Ofman 2001) based on this model. Nonetheless, if observational data of sufficient accuracy were available, it should prove possible to probe structure effects through the use of more complex models such as that investigated here.
The ratio between different harmonics has also proven to contain valuable information about the structure, and it is ready to be used in coronal seismology. We have calculated the deviation from unity in P1/2P2, and these results were used in McEwan et al. (2006,2007) to estimate the loop scale height. Although choosing different equilibrium density profiles leads to some differences in this ratio (Dymova & Ruderman 2006), Fig. 10 gives a good diagnostic tool for a generic loop. On the other hand, the information of these ratios for higher harmonics might prove less useful, since these modes are leaky for typical values of a/L, and therefore harder to detect observationally.
In conclusion, the extension of this work for continuous density profiles
confirms that internal longitudinal structure shifts the phase speed of the
fundamental kink mode from
![]() in a way that can be explained by considering
a uniform loop with weighted averaged density, while external structure shifts
the cutoff frequency. For typical coronal parameters, the fundamental mode is
still able to propagate with its frequency shifted.
in a way that can be explained by considering
a uniform loop with weighted averaged density, while external structure shifts
the cutoff frequency. For typical coronal parameters, the fundamental mode is
still able to propagate with its frequency shifted.
Acknowledgements
The authors acknowledge financial support from PPARC. AJD also acknowledges financial support from the Spanish government Grant No. AYA2006-07637.