A&A 476, 263-277 (2007)
DOI: 10.1051/0004-6361:20078094
V. Guillet - G. Pineau des Forêts - A. P. Jones
Institut d'Astrophysique Spatiale, Université Paris Sud and CNRS (UMR 8617), 91405 Orsay, France
Received 15 June 2007 / Accepted 31 August 2007
Abstract
Aims. A new multi-fluid approach to the dust dynamics in transverse shocks in dense clouds is presented with the aim of modelling the dust processing in C- and J-type shocks.
Methods. We have augmented an existing steady-state shock code to include the effects of an MRN size distribution of grain cores with icy mantles. The dust charge distribution and its evolution is considered in detail and included in the ionization balance. The 2-D grain dynamics are determined, including the effects of grain inertia and charge fluctuations, paying particular attention to the gyration of the charged grains around the magnetic field lines and the feedback of the ionization state on grain dynamics.
Results. We find that the critical velocity for C shocks increases with the gas density but that it is only weakly dependent on a high abundance of PAHs and on the photodetachment of electrons by secondary photons induced by cosmic-rays. The detailed dust dynamics in C shocks is shown to comprise two distinct phases: 1) a short gyration phase followed by 2) a long term drift phase. In J shocks only the first gyration phase is present. In C shocks propagating through molecular clouds (![]() = 104 cm-3), large grains (
= 104 cm-3), large grains (![]() 100 Å) remain coupled to the magnetic field during the second phase. However, a high abundance of PAHs can lead to a shortage of electrons in the gas and the decoupling of large grains in the shock tail. Large grains are decoupled from the magnetic field all through the C shock in high density clouds (
100 Å) remain coupled to the magnetic field during the second phase. However, a high abundance of PAHs can lead to a shortage of electrons in the gas and the decoupling of large grains in the shock tail. Large grains are decoupled from the magnetic field all through the C shock in high density clouds (![]() = 106 cm-3). In all C shocks small grains (
= 106 cm-3). In all C shocks small grains (![]() 100 Å) remain strongly coupled to the magnetic field, whereas very small grains (
100 Å) remain strongly coupled to the magnetic field, whereas very small grains (![]() 100 Å) are subject to stochastic dynamics. As long as they are charged very small grains remain strongly coupled to the magnetic field but tend to couple to the neutral gas everytime they become neutral. We have investigated the effects of an electric field along the shock direction in C shocks and find that it does not significantly modify the relative velocities between grains. The derived grain dynamics can be used to study dust processing in C and J shocks in dense clouds through the effects of gas-grain and grain-grain collisions.
100 Å) are subject to stochastic dynamics. As long as they are charged very small grains remain strongly coupled to the magnetic field but tend to couple to the neutral gas everytime they become neutral. We have investigated the effects of an electric field along the shock direction in C shocks and find that it does not significantly modify the relative velocities between grains. The derived grain dynamics can be used to study dust processing in C and J shocks in dense clouds through the effects of gas-grain and grain-grain collisions.
Key words: shock waves - magnetohydrodynamics (MHD) - dust, extinction - ISM: clouds - ISM: jets and outflows - ISM: kinematics and dynamics
Interstellar shocks (see, for example, Draine & McKee 1993, for a review of this subject) are expected to form in the ISM in cloud-cloud collisions and when very energetic winds such as supernova explosions or jet emission from young stellar objects encounter and interact with the ambient ISM. Shocks propagate as supersonic pressure increases that accelerate, compress and heat the gas that they interact with.
The magnetic fields present in clouds allow the propagation of magnetosonic waves in the gas upstream of a shock. The nature of the shock is determined by comparing the shock speed with the velocity of propagation of the magnetosonic waves in the medium. The magnetosonic wave velocity depends on the intensity of the magnetic field transverse to the direction of propagation of the shock. On the one hand, if the pressure increase propagates faster than magnetosonic waves, as is the case for high shock velocities or weak transverse magnetic fields, the gas undergoes a J shock (J for "jump'') where all variables characterizing the flow are discontinuous at the shock front. On the other hand, for strong transverse magnetic fields or low shock velocities, magnetosonic waves can propagate faster than the shock front forming a magnetic precursor to the shock that informs the gas upstream of the arrival of the shock (Mullan 1971; Draine 1980). As the ionization fraction is very low in molecular clouds (
![]() )
the ionized and neutral fluids are decoupled by the magnetic precursor. The ionized fluid is accelerated and heated by the magnetic precursor whereas the neutral fluid is essentially unaffected by it. The resulting drift between the ionized and neutral fluids progressively heats and accelerates the neutral fluid, while at the same time radiative emission by H2 and other coolants cools the gas.
If the molecular coolants are not dissociated by the shock, the temperature of the gas can be low enough for the neutral gas to remain supersonic everywhere within the shock frame, i.e. the frame of reference where the shock is stationary. In this case there is no longer a shock front and a C-type shock results (C for "continuous''). If a sonic point is encountered where the supersonic gas becomes subsonic in the shock frame the transition should be discontinuous (J shock) but some authors also discuss the possibility of a continuous transition (C* shock, Chernoff 1987; Roberge & Draine 1990). Recently, the validity of this concept, where the magnetosonic velocity plays the role of a critical velocity for C shocks, has been put into question when dust grains are decoupled from the magnetic field (Ciolek et al. 2004, hereafter CRM04). This hypothesis awaits confirmation with the inclusion of radiative cooling and a full size distribution for the dust grains.
)
the ionized and neutral fluids are decoupled by the magnetic precursor. The ionized fluid is accelerated and heated by the magnetic precursor whereas the neutral fluid is essentially unaffected by it. The resulting drift between the ionized and neutral fluids progressively heats and accelerates the neutral fluid, while at the same time radiative emission by H2 and other coolants cools the gas.
If the molecular coolants are not dissociated by the shock, the temperature of the gas can be low enough for the neutral gas to remain supersonic everywhere within the shock frame, i.e. the frame of reference where the shock is stationary. In this case there is no longer a shock front and a C-type shock results (C for "continuous''). If a sonic point is encountered where the supersonic gas becomes subsonic in the shock frame the transition should be discontinuous (J shock) but some authors also discuss the possibility of a continuous transition (C* shock, Chernoff 1987; Roberge & Draine 1990). Recently, the validity of this concept, where the magnetosonic velocity plays the role of a critical velocity for C shocks, has been put into question when dust grains are decoupled from the magnetic field (Ciolek et al. 2004, hereafter CRM04). This hypothesis awaits confirmation with the inclusion of radiative cooling and a full size distribution for the dust grains.
In interstellar shocks the grains are subject to processes that can affect both the dust-to-gas mass ratio and the dust size distribution. Grain surfaces can be eroded by high velocity collisions with ions and atoms (Barlow 1978; Cowie 1978). Grains can be partially or completely vaporized by collision with another grain at velocities greater than ![]() 20 km s-1 (Tielens et al. 1994). The sputtering and vaporization of grains release the constituent atoms into the gas. Collisions between grains at velocities greater than a critical velocity of a few km s-1 can also shatter grains into fragments or craterize them (Borkowski & Dwek 1995; Jones et al. 1996, hereafter JTH96). Below some relative grain-grain velocity, which is dependent on the grain composition and size, and which is of the order 1 km s-1, the grains can stick together (Chokshi et al. 1993; Poppe & Blum 1997). The coagulation (shattering) process conserves the total dust mass but generally redistributes the dust size distribution towards larger (smaller) grains. The degree of shattering, coagulation, vaporization and sputtering in shocks is dependent on the relative velocities between the grains and a study of dust processing in shocks therefore necessitates a multi-fluid approach to the dust dynamics that takes account of the entire dust size spectrum.
20 km s-1 (Tielens et al. 1994). The sputtering and vaporization of grains release the constituent atoms into the gas. Collisions between grains at velocities greater than a critical velocity of a few km s-1 can also shatter grains into fragments or craterize them (Borkowski & Dwek 1995; Jones et al. 1996, hereafter JTH96). Below some relative grain-grain velocity, which is dependent on the grain composition and size, and which is of the order 1 km s-1, the grains can stick together (Chokshi et al. 1993; Poppe & Blum 1997). The coagulation (shattering) process conserves the total dust mass but generally redistributes the dust size distribution towards larger (smaller) grains. The degree of shattering, coagulation, vaporization and sputtering in shocks is dependent on the relative velocities between the grains and a study of dust processing in shocks therefore necessitates a multi-fluid approach to the dust dynamics that takes account of the entire dust size spectrum.
Previous studies of dust dynamics in C shocks in dense clouds focused on the impact of dust dynamics on the structure of C shocks. Earlier works modelled the dust size distribution by single-sized grains, whether for shocks with magnetic fields transverse to the direction of propagation of the shock (Draine 1980; Draine et al. 1983; Pilipp et al. 1990) or for oblique shocks with a rotating magnetic field (Pilipp & Hartquist 1994; Wardle 1998). Recently, Chapman & Wardle (2006) introduced a multi-fluid approach to the dust dynamics in their oblique shock code. Their conclusions, after Pilipp & Hartquist (1994), suggest that single-sized grain models tend to overestimate the impact of dust dynamics on the shock structure, compared to two-fluid or multi-fluid models including small grains. In all these studies grain inertia and the impact of charge fluctuations on the dust dynamics were ignored. Ciolek & Roberge (2002) developed a time-dependent code for transverse shocks where the dust grains are modelled as two fluids, one for large grains and one for small grains or PAHs, where they included grain inertia and grain charge fluctuations. This code was applied to the formation of the magnetic precursor in C shocks (CRM04).
The shock model that we use is that of Flower & Pineau des Forêts 2003 (hereafter FPdF03) which was designed to study steady-state transverse C and J shocks. The code has been augmented to allow for a study of the dust dynamics and processing while, in parallel, solving for the shock structure. The dust size distribution is modelled by size bins as per Jones et al. (1994, 1996). In this paper, we restrict our presentation to the modelling of dust charging and dynamics in shocks. The impact of dust processing on the dust size distribution and on the shock structure will be presented in a following paper. Here, we give particular attention to those aspects of the dust dynamics, already addressed in different contexts by other authors, that have or could have an impact on the processing of dust grains in shocks, i.e., the gyration of dust grains around magnetic field lines (Jones et al. 1994, 1996; Slavin et al. 2004), dust charging and the calculation of the ionization balance (Pilipp et al. 1990), charge fluctuations (Ciolek & Mouschovias 1993), the existence of electric field and electric forces (Pilipp et al. 1990; Ciolek & Mouschovias 1993; Wardle 1998).
Our paper is structured as follows. Section 2 presents the modelling of the dust size distribution as size bins and the charging processes as applied to the grains and PAHs. In Sect. 3 we compare our results for the dust charge distribution and ionization balance in molecular clouds with the results of previous modelling (FPdF03). Section 4 presents our new calculation of the critical velocity for C shocks, based on the work by CRM04, and developes our modelling of the grain dynamics for a variety of shock conditions. Within the perspective of modelling the dust processing in shocks, we show in Sect. 5 that the presence of an electric field in the direction of propagation of the shock, generated by non local electrical neutrality, has only a minor impact on the relative velocities between the different-sized dust grains, and can therefore be ignored in modelling the dust dynamics of relevance to dust processing. We also examine the dynamics of very small grains (![]() 100 Å), absent in the present model, but that we expect to be produced in great numbers by the shattering of large grains in grain-grain collisions.
100 Å), absent in the present model, but that we expect to be produced in great numbers by the shattering of large grains in grain-grain collisions.
We represent the dust size distribution in dense clouds by two independent, power-law size distributions of spherical silicate (
![]() = 3.3 g cm-3) and carbon (
= 3.3 g cm-3) and carbon (
![]() = 2.2 g cm-3) grain cores:
= 2.2 g cm-3) grain cores:
![]() for
a- < a < a+, where a is a grain radius.
For simplicity, we take identical values of
for
a- < a < a+, where a is a grain radius.
For simplicity, we take identical values of ![]() ,
a- and a+ for both the carbon and silicate distributions, though the code can be run with any values.
The dust size distributions are numerically modelled as discretised size bins as per Jones et al. (1994, 1996), in our work we use 8 size bins.
Here we focus on the silicate distribution (similar expressions exist for the carbon grains).
In molecular clouds the grain cores are probably larger than in the diffuse ISM because of the coagulation and accretion processes acting in denser environments (Cardelli et al. 1989). Adopting a dust size distribution based on Mathis et al. (1977, MRN) and characterized by a slope
,
a- and a+ for both the carbon and silicate distributions, though the code can be run with any values.
The dust size distributions are numerically modelled as discretised size bins as per Jones et al. (1994, 1996), in our work we use 8 size bins.
Here we focus on the silicate distribution (similar expressions exist for the carbon grains).
In molecular clouds the grain cores are probably larger than in the diffuse ISM because of the coagulation and accretion processes acting in denser environments (Cardelli et al. 1989). Adopting a dust size distribution based on Mathis et al. (1977, MRN) and characterized by a slope
![]() ,
we adapt the usual grain size limits to values more appropriate for dense clouds by choosing a- = 100 Å and a+ = 3000 Å as per FPdF03. See Appendix A for a description of our modelling of the grain core size distribution.
,
we adapt the usual grain size limits to values more appropriate for dense clouds by choosing a- = 100 Å and a+ = 3000 Å as per FPdF03. See Appendix A for a description of our modelling of the grain core size distribution.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.9cm,clip]{8094f1.ps}\par\includegraphics[angle=-90,width=7.9cm,clip]{8094f2.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg26.gif) |
Figure 1: a) Fraction of the silicate dust mass in each bin as a function of the average radius for that bin, with and without mantles. b) Same as a) for the fraction of the silicate grain number density in each bin. The mantle thickness is 147 Å for a pre-shock gas with no PAHs. The number density of the grains per unit volume is not modified by the accretion of mantles onto the grain cores. |
| Open with DEXTER | |
The low gas and dust temperatures in molecular clouds lead to the formation of icy mantles on the grain cores by the adsorption of gas phase species onto grain surfaces. The accreted species include H2O, CO and CO2 (see Table 2 of FPdF03 for a full list of the chemical species in the mantles in our model). The process of adsorption is counterbalanced by the desorption processes of sputtering, photodesorption, cosmic ray induced desorption and photoevaporation. At high gas temperatures, the sputtering of icy mantles by collisions with gas particles is the dominant erosion process. Mantle erosion can be accelerated by the presence of a high relative velocity between the grains and the gas. If this velocity is independent of grain radius, as it is when the dust grains are strongly coupled to the magnetic field, then the thickness of the icy mantles is independent of the grain core radius because the rates of accretion and erosion are proportional to the grain surface. We therefore consider that mantles of identical thickness cover all grains, independent of the grain size, in the pre-shock gas and elsewhere in the shock. Appendix B presents the method used to calculate the mantle thickness for a given size distribution of grain cores. Figure 1 presents the impact of the presence of icy mantles on the dust size distribution and we note that this is no longer a power-law when icy mantles cover the grain cores. When mantles are present, the smallest grains carry a significant fraction of the total dust mass, unlike an MRN size distribution. As expected, mantle accretion shifts the small grains to larger sizes proportionately more than it shifts the sizes of the larger grains. With a mantle 147 Å thick covering the grain cores (see Appendix B for a description of the numerical method for the calculation of mantle thickness in the pre-shock environment and in the shock), the total grain cross-section
![]() is 2.7 times larger than without mantles. This factor is increased to 3.1 for a 50-2500 Å core distribution.
is 2.7 times larger than without mantles. This factor is increased to 3.1 for a 50-2500 Å core distribution.
The presence of PAHs in molecular clouds is still a matter of debate because they could be accreted onto the grains or could be created by previous shocks. Their influence on the dust charge distribution being so important (FPdF03, Chapman & Wardle 2006) we include their presence in our modelling. We treat PAHs as per FPdF03, modelling them as a single type of molecule (circum-coronene,
![]() )
with a corresponding radius of 6.6 Å.
)
with a corresponding radius of 6.6 Å.
In molecular clouds the grains are primarly charged by the collisional attachment of free electrons and ions. The competition between the attachment of electrons and ions makes the grain charge fluctuate around an average value, resulting in a charge distribution.
Table 1:
Steady-state charge distribution model results for dense clouds: Col. (1) is our standard model and Col. (5) is taken from FPdF03 for comparaison with our results.
![]() (
(
![]() ,
,
![]() )
is the number density of negative (neutral, positive) grains per unit volume, summed over all grain size bins. Idem for PAHs.
The critical velocity
)
is the number density of negative (neutral, positive) grains per unit volume, summed over all grain size bins. Idem for PAHs.
The critical velocity
![]() can be computed either by assuming that only the charged grains are strongly coupled to the magnetic field, as in FPdF03, or by following Eq. (12) based on the work of CRM04.
can be computed either by assuming that only the charged grains are strongly coupled to the magnetic field, as in FPdF03, or by following Eq. (12) based on the work of CRM04.
Grain charging is critical for the study of dust processing in C shocks because it affects the coupling of the grains to the magnetic field and, thus, the relative velocity between grains.
Our model for grain charging is designed around our need to study dust processing in shocks where very small grain fragments (![]() 100 Å) are expected to be produced in great numbers by the shattering of large grains in grain-grain collisions (JTH96).
A significant fraction of these very small grains is neutral in C shocks, even in the hottest parts of the shock. Very small neutral grains tend to be coupled to the neutral gas (see Sect. 5) and may play an important role in the processing of charged grains which are coupled to the magnetic field. In order to determine the fraction of neutral grains, we therefore need to integrate the grain charge distribution (Ciolek & Roberge 2002, FPdF03).
The impact of the charge carried by the numerous small grain fragments on the density of free electrons in the gas is potentially important because C shocks remain very weakly ionized. A modification in the ionization state of the gas will in turn affect the charging, dynamics and processing of larger grains. Dust charging must therefore be determined as part of the calculation of the ionization balance (Pilipp et al. 1990; Ciolek & Roberge 2002, FPdF03).
100 Å) are expected to be produced in great numbers by the shattering of large grains in grain-grain collisions (JTH96).
A significant fraction of these very small grains is neutral in C shocks, even in the hottest parts of the shock. Very small neutral grains tend to be coupled to the neutral gas (see Sect. 5) and may play an important role in the processing of charged grains which are coupled to the magnetic field. In order to determine the fraction of neutral grains, we therefore need to integrate the grain charge distribution (Ciolek & Roberge 2002, FPdF03).
The impact of the charge carried by the numerous small grain fragments on the density of free electrons in the gas is potentially important because C shocks remain very weakly ionized. A modification in the ionization state of the gas will in turn affect the charging, dynamics and processing of larger grains. Dust charging must therefore be determined as part of the calculation of the ionization balance (Pilipp et al. 1990; Ciolek & Roberge 2002, FPdF03).
Our method for charge integration has two modes. Weakly charged grains (
![]() )
have their charge distribution integrated to determine the fraction of neutral grains. For highly charged grains (
)
have their charge distribution integrated to determine the fraction of neutral grains. For highly charged grains (![]() )
the probability for grains of this size to be neutral is close to zero. The integration of the whole charge distribution is then replaced by the integration of the average number of charges, which corresponds to the peak of the charge distribution. Switching between these two modes is managed automatically for each grain size without any noticeable effect on the charge and ionization state profiles (see Figs. 8 and 9, for example, and Appendix C for the details of charge integration).
)
the probability for grains of this size to be neutral is close to zero. The integration of the whole charge distribution is then replaced by the integration of the average number of charges, which corresponds to the peak of the charge distribution. Switching between these two modes is managed automatically for each grain size without any noticeable effect on the charge and ionization state profiles (see Figs. 8 and 9, for example, and Appendix C for the details of charge integration).
We consider a grain of radius a, cross-section ![]() and charge q = Ze (where e is the proton charge) embedded in a weakly ionized plasma composed of electrons with mass
and charge q = Ze (where e is the proton charge) embedded in a weakly ionized plasma composed of electrons with mass ![]() ,
density
,
density ![]() and temperature
and temperature ![]() and positive ions with charge +e and temperature
and positive ions with charge +e and temperature ![]() but with differing densities,
but with differing densities, ![]() ,
and masses,
,
and masses, ![]() .
We adopt the electron and ion attachment rates
.
We adopt the electron and ion attachment rates ![]() and
and ![]() defined by Eqs. (3.1), (3.3), (3.4) and (3.5) of Draine & Sutin (1987).
defined by Eqs. (3.1), (3.3), (3.4) and (3.5) of Draine & Sutin (1987).
In shocks the grains stream through the fluid formed by the ions and electrons, whether by their gyration around magnetic field lines or because of their weak coupling to the magnetic field (see Sect. 4). In the reference frame of the dust grains, the velocity distribution of the electrons (ions) is not a maxwellian of temperature ![]() (
(![]() )
as per Draine & Sutin (1987) but a velocity-shifted maxwellian of the same temperature (Shull 1978; Pilipp et al. 1990). The thermal velocity of the electrons in shocks is always much higher than the relative grain-electron velocity. However, the thermal velocity of ions is of the same order, or even lower, than the relative ion-grain velocity. The shift in the velocity distribution can therefore be neglected for electrons but not for ions.
We define
)
as per Draine & Sutin (1987) but a velocity-shifted maxwellian of the same temperature (Shull 1978; Pilipp et al. 1990). The thermal velocity of the electrons in shocks is always much higher than the relative grain-electron velocity. However, the thermal velocity of ions is of the same order, or even lower, than the relative ion-grain velocity. The shift in the velocity distribution can therefore be neglected for electrons but not for ions.
We define ![]() as the velocity of the grain and
as the velocity of the grain and
![]() as the velocity of the ions in the shock frame. Following Pineau des Forêts et al. (1986) we associate the velocity-shifted maxwellian of the ions in the reference frame of the grain with a maxwellian of effective ion-grain temperature
as the velocity of the ions in the shock frame. Following Pineau des Forêts et al. (1986) we associate the velocity-shifted maxwellian of the ions in the reference frame of the grain with a maxwellian of effective ion-grain temperature
![]() .
The expression for the "pseudo'' thermal velocity of the ions
.
The expression for the "pseudo'' thermal velocity of the ions
![]() for the effective ion-grain temperature
for the effective ion-grain temperature
![]() must correspond to the "real'' thermal velocity
must correspond to the "real'' thermal velocity
![]() of the ions when the grain follows the motion of the ions (i.e. when
of the ions when the grain follows the motion of the ions (i.e. when
![]() )
and tends towards the relative velocity
)
and tends towards the relative velocity
![]() of kinetic origin when the thermal velocity is negligible. The following expression for the effective ion-grain temperature
of kinetic origin when the thermal velocity is negligible. The following expression for the effective ion-grain temperature
![]() satisfies both criteria
satisfies both criteria
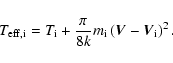 |
(3) |
Although the interstellar radiation field is attenuated by dust in the external layers of molecular clouds, there are ultraviolet photons in dark clouds due to cosmic-ray interactions. Most of the electrons produced by the cosmic-ray ionization of hydrogen are energetic enough to excite the Rydberg states of H2 which then fluoresce in the ultraviolet. For a cosmic ray ionization rate, ![]() ,
the rate per unit volume for fluorescence photons indirectly generated by cosmic-rays is
,
the rate per unit volume for fluorescence photons indirectly generated by cosmic-rays is
![]() (cm-3 s-1) if only
(cm-3 s-1) if only ![]() of secondary electrons can excite the Rydberg states of H2 (FPdF03), here
of secondary electrons can excite the Rydberg states of H2 (FPdF03), here
![]() is the proton density. Fluorescent photons are emitted with energies 7.1
is the proton density. Fluorescent photons are emitted with energies 7.1 ![]() 14.6 eV (Gredel et al. 1989, Fig. 1 therein). For simplicity, we here assume that all of the secondary photons have the same energy
14.6 eV (Gredel et al. 1989, Fig. 1 therein). For simplicity, we here assume that all of the secondary photons have the same energy ![]() = 10 eV. The secondary photons are absorbed by all grains, and PAHs if present (the absorption by molecules is negligible). The absorption is proportional to the dust cross-section
= 10 eV. The secondary photons are absorbed by all grains, and PAHs if present (the absorption by molecules is negligible). The absorption is proportional to the dust cross-section
![]() where a is the grain radius,
where a is the grain radius, ![]() is the geometrical cross-section of the grain and
is the geometrical cross-section of the grain and
![]() is the absorption efficiency factor for a photon of energy 10 eV. We consider the photoemission of valence band electrons from grains of charge Z and adopt the model of Weingartner & Draine (2001) for the dust material properties and for the photoemission yield Y(a,Z) as given by their Eq. (8).
In the FPdF03 model a grain has the following photoemission rate
is the absorption efficiency factor for a photon of energy 10 eV. We consider the photoemission of valence band electrons from grains of charge Z and adopt the model of Weingartner & Draine (2001) for the dust material properties and for the photoemission yield Y(a,Z) as given by their Eq. (8).
In the FPdF03 model a grain has the following photoemission rate
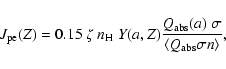 |
(4) |
Our numerical method for the calculation of the charge of dust grains is presented in Appendix C. The same charging processes, as for grains, are applied to PAHs but with constant rates and limited charge numbers -1, 0 or +1 (see FPdF03 Sect. 2.1 for further details on PAH charging).
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{8094f4.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg80.gif) |
Figure 2:
The grain charge probability, f(Z), as a function of the number of charges, Z, for silicate grains in a molecular cloud characterized by T = 10 K,
|
| Open with DEXTER | |
In our models we adopt typical molecular cloud densities (
![]() cm-3), gas temperatures and cosmic-ray ionization rate (
cm-3), gas temperatures and cosmic-ray ionization rate (
![]() s-1). For our standard model we take
s-1). For our standard model we take ![]() = 104 cm-3, T = 10 K and no PAHs. The fractional abundances of the elements in the grain cores are taken from Table 1 of FPdF03, equivalent to grain cores having 0.60% of gas mass. The abundances of the chemical species in the grain mantles are taken from Table 2 of FPdF03. Icy mantles represent 0.30% of gas mass, so that the dust totals 0.90% of gas mass. The resulting dust size distributions are presented in Fig. 1.
= 104 cm-3, T = 10 K and no PAHs. The fractional abundances of the elements in the grain cores are taken from Table 1 of FPdF03, equivalent to grain cores having 0.60% of gas mass. The abundances of the chemical species in the grain mantles are taken from Table 2 of FPdF03. Icy mantles represent 0.30% of gas mass, so that the dust totals 0.90% of gas mass. The resulting dust size distributions are presented in Fig. 1.
The FPdF03 shock code uses the integrator VODE to solve for the ionization state and chemical composition of the gas at a given temperature and density, with a chemical network including more than 130 chemical species and 900 chemical reactions occurring both in the gas phase and on the grain surfaces![]() . Mantle accretion is de-activated when solving for the steady-state conditions so as to prevent all gas species from accreting onto grains, we thus keep the mantle thickness constant during these integrations. The dust charge distribution for all dust bins is obtained self-consistently and requires integrating some 300 variables. The negative, neutral and positive PAHs (Z=-1,0,+1, respectively) are treated as chemical species. The electron density
. Mantle accretion is de-activated when solving for the steady-state conditions so as to prevent all gas species from accreting onto grains, we thus keep the mantle thickness constant during these integrations. The dust charge distribution for all dust bins is obtained self-consistently and requires integrating some 300 variables. The negative, neutral and positive PAHs (Z=-1,0,+1, respectively) are treated as chemical species. The electron density ![]() is determined from the local charge neutrality condition
is determined from the local charge neutrality condition
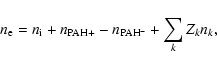 |
(5) |
The grain charge distribution in our standard molecular cloud model is presented in Fig. 2 for four grain sizes. The grain charge, Z, primarly varies between 0 and -1, with the exception of large grains where Z = -2 is not negligible. Clearly, limiting grain charges to -1, 0 +1 in quiescent molecular clouds is justified for most of the grains (FPdF03, CRM04). The influence of photodetachment by fluorescent, secondary UV photons is rather weak, unlike previous modelling by FPdF03. Our model, based on the Weingartner & Draine (2001) photoemission yields, gives low and nearly identical yields for neutral grains and grains with Z=-1. FPdF03 assumed higher yields, and a yield for the Z=-1 grains higher than that for neutral grains (see Sect. 2.2.2 of FPdF03). This shift resulted in a higher proportion of neutral grains in the earlier work.
When a high fractional abundance of PAHs is present in the gas (
![]() ,
equivalently 15% of the total carbon) a shortage of electrons (
,
equivalently 15% of the total carbon) a shortage of electrons (
![]() )
appears in the gas because the PAHs capture most of the free electrons. The decrease in the number of free electrons affects the balance between ion and electron attachment on grains. The resulting charge carried by the grains is reduced and the average grain charge is not centered around Z = -1 but around Z = 0.
)
appears in the gas because the PAHs capture most of the free electrons. The decrease in the number of free electrons affects the balance between ion and electron attachment on grains. The resulting charge carried by the grains is reduced and the average grain charge is not centered around Z = -1 but around Z = 0.
Table 1 presents the steady-state charge distribution for the assumed pre-shock conditions at densities of 104, 105 and 106 cm-3. In our pre-shock dust size distribution there are no grains with radii <![]() and so most grains are charged. The neutral grain fraction
and so most grains are charged. The neutral grain fraction
![]() is essentially independent of the cloud density when no PAHs are present (Cols. (1), (6) and (7),
is essentially independent of the cloud density when no PAHs are present (Cols. (1), (6) and (7),
![]() )
because the grain charge is a function of the ratio
)
because the grain charge is a function of the ratio
![]() (Draine & Sutin 1987) which remains close to unity in all environments as long as the grains and the PAHs do not carry a significant fraction of the electrons. The presence of a high abundance of PAHs (Col. (4)) leads to a shortage of electrons in the gas (
(Draine & Sutin 1987) which remains close to unity in all environments as long as the grains and the PAHs do not carry a significant fraction of the electrons. The presence of a high abundance of PAHs (Col. (4)) leads to a shortage of electrons in the gas (
![]() ), thereby reducing the abundance of negatively charged grains.
When the photoemission of electrons by secondary photons is included (Cols. (2) and (4)), the number of negatively charged grains naturally tends to diminish but this effect is far less important than in earlier models (Col. (5) as per FPdF03).
), thereby reducing the abundance of negatively charged grains.
When the photoemission of electrons by secondary photons is included (Cols. (2) and (4)), the number of negatively charged grains naturally tends to diminish but this effect is far less important than in earlier models (Col. (5) as per FPdF03).
The value of the magnetosonic speed separating the J and C shock domains,
![]() ,
depends on the intensity of the magnetic field, B, transverse to the direction of propagation of the shock and on the mass density of the particles strongly coupled to the magnetic field:
,
depends on the intensity of the magnetic field, B, transverse to the direction of propagation of the shock and on the mass density of the particles strongly coupled to the magnetic field:
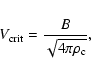 |
(6) |
| (7) |
In molecular clouds, the magnetic field intensity scales as
Whether a particular size of grain is coupled to the magnetic field or to the neutral gas is determined by the Hall factor, the ratio of the grain drag to grain gyration time-scales, i.e.,
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{8094f3.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg98.gif) |
Figure 3:
The Hall factor,
|
| Open with DEXTER | |
The friction or drag time-scale is defined as the time necessary for the grain to collide with a mass of gas equal to its own mass.
CRM04 undertook an extensive study of the conditions necessary for the propagation of a shock magnetic precursor. To calculate the magnetosonic speed they suggested adopting the criteria that only grains with
![]() participate in the propagation of magnetosonic waves. We adapt this criteria to our model by choosing a weight function in
participate in the propagation of magnetosonic waves. We adapt this criteria to our model by choosing a weight function in ![]() :
:
Table 1 compares the values for the magnetosonic speed, obtained using this method, for the pre-shock environments shown in Fig. 3. We also show the results for FPdF03, where
![]() was assumed to be the total mass of the charged grains. In FPdF03 the critical speed did not depend on the gas density but was sensitive to the presence of PAHs and secondary photons induced by cosmic-rays.
The CRM04 criterium leads to the opposite effect. In this case the critical velocity increases with the gas density, as expected from Fig. 3 where we see an increase in the decoupled grains (
was assumed to be the total mass of the charged grains. In FPdF03 the critical speed did not depend on the gas density but was sensitive to the presence of PAHs and secondary photons induced by cosmic-rays.
The CRM04 criterium leads to the opposite effect. In this case the critical velocity increases with the gas density, as expected from Fig. 3 where we see an increase in the decoupled grains (
![]() )
with increasing density, and is affected to a lesser extent by the presence of PAHs and secondary photons because of the smooth weight function we use (Eq. (12)). From here on we adopt the CRM04 method for the calculation of magnetosonic speed. The effect of secondary photons on the charge of dust grains only slightly increases the magnetosonic speed and will therefore be neglected in our shock modelling.
)
with increasing density, and is affected to a lesser extent by the presence of PAHs and secondary photons because of the smooth weight function we use (Eq. (12)). From here on we adopt the CRM04 method for the calculation of magnetosonic speed. The effect of secondary photons on the charge of dust grains only slightly increases the magnetosonic speed and will therefore be neglected in our shock modelling.
The model of Flower & Pineau des Forêts (2003) is specifically designed to study steady-state, transverse C and J shocks in dense or diffuse media. In a self-consistent way this code integrates numerous parameters, including: the velocity, temperature and density of the three magnetohydrodynamic (MHD) fluids (ions, electrons and neutral gas), the H2 level population and the abundances of a set of chemical species. This approach includes the presence of grains modelled by an MRN distribution and PAHs. Their charge state (limited to -1, 0, 1) is calculated. The charged grains are assumed to be coupled to the ions and the neutral grains to the neutral gas. The transfer of momentum and energy between gas and grains are taken into account in this approach. The form of the conservation equations can be found in Draine (1980).
In this work we have focused our attention on the detailed dust physics: grain charging and 2-D grain dynamics (size-dependent velocity profiles) for an MRN distribution modelled by size bins. The source terms in the conservation equations (e.g. momentum and energy equations) have now been updated to allow for the inclusion of grain charge, size and velocity calculated for each grain size bin. See Appendix D for a comparaison of our work with the earlier approach (FPdF03).
We assume steady-state, plane-parallel shocks (
![]() )
with velocity
)
with velocity ![]() .
As per FPdF03 the shock profiles are calculated in 1-D along z for the fluids.
We assume that the electrons and ions have distinct temperatures but the same velocity. Figure 4 shows the velocity and temperature profile for a 20 km s-1 C shock (pre-shock conditions: T = 10 K,
.
As per FPdF03 the shock profiles are calculated in 1-D along z for the fluids.
We assume that the electrons and ions have distinct temperatures but the same velocity. Figure 4 shows the velocity and temperature profile for a 20 km s-1 C shock (pre-shock conditions: T = 10 K,
![]() cm-3, B = 100
cm-3, B = 100 ![]() G and
G and
![]() s-1). The neutral velocity,
s-1). The neutral velocity, ![]() ,
and the ion velocity,
,
and the ion velocity, ![]() are presented in the shock frame.
The shock length is approximately 0.06 pc at a flow time of 3
are presented in the shock frame.
The shock length is approximately 0.06 pc at a flow time of 3 ![]() 104 yr.
104 yr.
![\begin{figure}
\par\hspace*{4mm}\includegraphics[angle=-90,width=7.5cm,clip]{809...
...e*{2mm}
\par\includegraphics[angle=-90,width=7.95cm,clip]{8094f6.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg123.gif) |
Figure 4:
Velocity and temperature profiles for a 20 km s-1 C shock propagating through our standard pre-shock conditions (T = 10 K,
|
| Open with DEXTER | |
The magnetic field lines remain transverse (i.e., along the x axis) to the shock propagation direction (z axis). Making the usual assumption that the magnetic field lines are frozen into the ion fluid, we find that the magnetic field intensity,
![]() ,
follows the ion compression
,
follows the ion compression
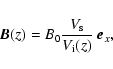 |
(13) |
The electric current in the z direction is zero everywhere in the shock because of the conservation of charge, i.e.,
From Eq. (15), we calculate the electron density
We propose a new multi-fluid approach to the dynamics of grains in steady-state shocks which allows us to study dust processing in shocks. Dust grains are not treated like MHD fluids but as test particles in the framework of a 3-fluid shock code (FPdF03). We integrate the dust charge distribution and include it in the calculation of the ionization balance. We adopt the Slavin et al. (2004) approach to dust dynamics to study the 2-D dynamics of grains as a function of size, giving particular attention to the gyration of grains around magnetic field lines and to grain decoupling from the magnetic field as induced by a shortage of electrons. The feedback from grain dynamics into the shock structure is included through the friction between the gas and grains.
Grain dynamical processes are primarly driven by a competition between the Lorentz force and the friction force exerted by the neutral gas but are also affected by grain charge fluctuations (Ciolek & Mouschovias 1993) and grain inertia.
Neutral grains can exist anywhere in a shock because of charge fluctuations. The lifetime of neutral grains of a given size,
![]() ,
is defined as the average time a grain remains neutral before an electron, ion or negative PAH attaches to it.
,
is defined as the average time a grain remains neutral before an electron, ion or negative PAH attaches to it.
In transverse shocks dust grains follow trajectories in the yz plane perpendicular to the magnetic field. Due to their large inertia, large grains dot not follow the motion of the ions in the precursor. Rather, they are launched with a velocity equal to that of the shock in the shock frame, and begin gyrating around the magnetic field lines (e.g. Slavin et al. 2004). This gyration phase, though short, can not be neglected in the study of dust processing as it results in high relative velocities between the grains which favour dust shattering.
The grain gyration damping time-scale,
![]() ,
defined as the average duration of the grain gyration phase, represents the time-scale for the transient grain dynamics before the grains behave as a fluid. It is equal to a few times the friction time-scale:
,
defined as the average duration of the grain gyration phase, represents the time-scale for the transient grain dynamics before the grains behave as a fluid. It is equal to a few times the friction time-scale:
![]() .
Small grains tend to undergo negligible gyration in dense clouds, while the gyration phase of larger grains can not be ignored in the study of dynamics for processing.
.
Small grains tend to undergo negligible gyration in dense clouds, while the gyration phase of larger grains can not be ignored in the study of dynamics for processing.
Although the integration of the neutral and ion velocities in our code is 1-D, we integrate the trajectories of the grains throughout the shock, considering that the shock is infinite in the direction parallel to the shock front (Slavin et al. 2004).
In the shock the grains undergo the Lorentz force and the friction force exerted by the neutrals. Applying the law of motion for a grain in a given bin k, the differential equation for the grain velocity in the shock frame is
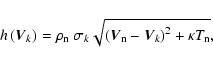 |
(19) |
Once gyration has disappeared the grains reach a velocity that is independent of the history of their dynamics and that depends only on the grain physical properties and the local shock conditions. Equation (6) of Wardle (1998) defines the general expression for this fluid velocity of the grains in C shocks. In our model the magnetic field is
![]() while the electric field
while the electric field ![]() has no component Ex along
has no component Ex along ![]() .
Adapting this equation to our context we find:
.
Adapting this equation to our context we find:
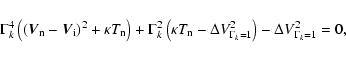 |
(22) |
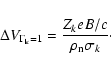 |
(23) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{8094f7.ps}\vspace*{2mm}
\includegraphics[angle=-90,width=8.1cm,clip]{8094f8.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg158.gif) |
Figure 5: a) Velocity profile, in the shock propagation direction, for various size grains for our standard shock model (see the Fig. 4 caption for details). b) Same as for a) but for the grain velocity component parallel to the shock front. |
| Open with DEXTER | |
Figure 5 shows the resulting profiles for the grain velocities in a C shock propagating through our standard pre-shock conditions (T = 10 K,
![]() cm-3,
cm-3,
![]() G,
G,
![]() s-1 and no PAHs). The shock length is approximately 0.06 pc, corresponding to a flow time of 3
s-1 and no PAHs). The shock length is approximately 0.06 pc, corresponding to a flow time of 3 ![]() 104 yr. In shocked molecular clouds the grain gyration phase is short with respect to the shock length because of the strong drag. During their gyration grains collide with each other at high relative velocities (of the order of the shock velocity). This phase will favour shattering in grain-grain collisions. This process modifies the dust size distribution, by increasing the number of small grains, and could be an important feedback mechanism onto the shock structure, this feedback will be examined in detail in a following paper.
Once the grain gyration has been damped, which happens in the early part of the precursor for the smallest grains of our dust size distribution, the grains remain coupled to the ions in the propagation direction of the shock (Fig. 5a) but not perpendicular to this direction (Fig. 5b) where a differential drift velocity remains throughout the shock. This differential drift velocity is induced by the gas drag in the presence of a magnetic field and is proportional to the grain radius for grains tightly coupled to the magnetic field (i.e. for
104 yr. In shocked molecular clouds the grain gyration phase is short with respect to the shock length because of the strong drag. During their gyration grains collide with each other at high relative velocities (of the order of the shock velocity). This phase will favour shattering in grain-grain collisions. This process modifies the dust size distribution, by increasing the number of small grains, and could be an important feedback mechanism onto the shock structure, this feedback will be examined in detail in a following paper.
Once the grain gyration has been damped, which happens in the early part of the precursor for the smallest grains of our dust size distribution, the grains remain coupled to the ions in the propagation direction of the shock (Fig. 5a) but not perpendicular to this direction (Fig. 5b) where a differential drift velocity remains throughout the shock. This differential drift velocity is induced by the gas drag in the presence of a magnetic field and is proportional to the grain radius for grains tightly coupled to the magnetic field (i.e. for
![]() ). For our standard shock the differential velocity is less than 1 km s-1 in the shock tail. Such conditions should favour the coagulation of grains at these low relative grain-grain velocities (e.g. Chokshi et al. 1993; Poppe & Blum 1997). This would only occur if the shock is old enough to have reached steady-state, for ages greater than the flow time of the steady-state C shock model (Chièze et al. 1998).
). For our standard shock the differential velocity is less than 1 km s-1 in the shock tail. Such conditions should favour the coagulation of grains at these low relative grain-grain velocities (e.g. Chokshi et al. 1993; Poppe & Blum 1997). This would only occur if the shock is old enough to have reached steady-state, for ages greater than the flow time of the steady-state C shock model (Chièze et al. 1998).
Figure 6 compares the time-scales for mantle erosion and for the damping of the grain gyration for our standard C shock model. The icy mantle is significantly eroded only after t = 400 yrs, i.e. after the end of the grain gyration phase. The gyration damping time-scale and that for mantle erosion both scale as
![]() and this should also be valid even at higher densities. This therefore justifies our inclusion of grain mantles in the study of the gyration phase in C shocks.
and this should also be valid even at higher densities. This therefore justifies our inclusion of grain mantles in the study of the gyration phase in C shocks.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{8094f9.eps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg161.gif) |
Figure 6: Evolution of the ice mantle thickness (left axis, Å) for our standard C shock compared with the evolution of grain gyration velocity and the ambipolar diffusion velocity (right axis, km s-1). Note that the gyration phase is over before ice mantles have been completely eroded. This is even more stringent for small grains which are the most affected by the presence of mantles (see Fig. 1). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{8094f10.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg162.gif) |
Figure 7: The grain trajectories in the shock reference frame for our standard pre-shock conditions. The grain drift in the direction parallel to the shock propagation direction due to gas drag means that large grains cover a distance which is significant compared to the shock length. |
| Open with DEXTER | |
The trajectory followed by dust grains (Fig. 7) in the shock reference frame is highly dependent on the grain radius. The drift velocity induced by gas drag is responsible for the motion of the grains parallel to the shock front, on length-scales comparable to the shock length. Our hypothesis of a homogenous shock front over such large scales may therefore be questionable. Grain gyration hardly appears in the trajectory because it does not last long and because it is dominated by the drift motion in the y and z direction.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{8094f11.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg163.gif) |
Figure 8: The evolution of the number of charges per grain, Z, through our standard shock. The grain charge is approximately proportional to the electron temperature and the grain radius. The small variations are due to the grain gyration or abrupt changes in the chemical composition of the ions. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{8094f12.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg164.gif) |
Figure 9:
The fractional abundance of free electrons, ions and electrons on grains in our standard shock. At this density (
|
| Open with DEXTER | |
Figure 8 presents the grain charge profile for our standard shock. The grain charge is basically proportional to the electron temperature and to the grain radius. The small variations are due to the grain gyration around the magnetic field lines which changes the ratio of the ion to electron attachment rates. Once the gyration has been damped the charge profile becomes smooth. The chemical evolution of the gas can also affect the grain charge (e.g. the abrupt changes in the grain charge at
![]()
![]() 1016 cm in Fig. 8). Figure 9 shows that grain charging, for our standard shock model, does not have much impact on the density of the free electrons.
1016 cm in Fig. 8). Figure 9 shows that grain charging, for our standard shock model, does not have much impact on the density of the free electrons.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{8094f13.ps}\vspa...
...space*{2mm}
\includegraphics[angle=-90,width=8.2cm,clip]{8094f15.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg166.gif) |
Figure 10:
a) and b) as for Fig. 5 but with a preshock proton density
|
| Open with DEXTER | |
Figures 10a,b show how the grain dynamics is significantly modified at high density (
![]() cm-3). Here the gas drag is much higher, than for the lower density case, and this affects both the damping of the grain gyration (
cm-3). Here the gas drag is much higher, than for the lower density case, and this affects both the damping of the grain gyration (
![]() )
and the degree of grain coupling to the magnetic field (
)
and the degree of grain coupling to the magnetic field (
![]() ).
Large grains do not even have the time to complete a single gyration before they follow a fluid.
The grains remain decoupled from the magnetic field throughout the shock in both the y and the z directions.This is the kind of dynamic obtained by Chapman & Wardle (2006) in the first multi-fluid study of dust dynamics in shocks in dense clouds. MHD models of dust dynamics ignoring grain inertia (e.g. Pilipp et al. 1990; Wardle 1998) are suitable for shocks in high density clouds where the grains can be considered as inertia-free.
As shown in Fig. 10c, the ionization balance in the shock is significantly affected by the dust charging (e.g. Pilipp et al. 1990). A shortage of electrons appears in the precursor and the grains can not be charged to the expected level, thus increasing the decoupling of the grains from the magnetic field.
Our assumption of local electro-neutrality is no longer valid at these high densities where the negatively charged grains are moving much faster than the ions and create a local positive charge. This issue is discussed in Sect. 5.1 where we present, following Pilipp et al. (1990), how we introduce into the dust dynamics the effect of an electric field Ez in the direction of propagation of the shock that is generated by the local electric charge.
).
Large grains do not even have the time to complete a single gyration before they follow a fluid.
The grains remain decoupled from the magnetic field throughout the shock in both the y and the z directions.This is the kind of dynamic obtained by Chapman & Wardle (2006) in the first multi-fluid study of dust dynamics in shocks in dense clouds. MHD models of dust dynamics ignoring grain inertia (e.g. Pilipp et al. 1990; Wardle 1998) are suitable for shocks in high density clouds where the grains can be considered as inertia-free.
As shown in Fig. 10c, the ionization balance in the shock is significantly affected by the dust charging (e.g. Pilipp et al. 1990). A shortage of electrons appears in the precursor and the grains can not be charged to the expected level, thus increasing the decoupling of the grains from the magnetic field.
Our assumption of local electro-neutrality is no longer valid at these high densities where the negatively charged grains are moving much faster than the ions and create a local positive charge. This issue is discussed in Sect. 5.1 where we present, following Pilipp et al. (1990), how we introduce into the dust dynamics the effect of an electric field Ez in the direction of propagation of the shock that is generated by the local electric charge.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{8094f16.ps}\vspa...
...space*{2mm}
\includegraphics[angle=-90,width=8.2cm,clip]{8094f18.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg168.gif) |
Figure 11:
As for Fig. 5 but with a PAH fractional abundance of
|
| Open with DEXTER | |
When we add PAHs to our standard model their presence can affect the ionization state in the shock as it does in the pre-shock gas (see Table 1). In our model the neutral PAHs are coupled to the neutral gas, the PAH cations to the ion fluid and the PAH anions to the electron fluid. Figures 11a,b presents the resulting grain velocity profile with a PAH fractional abundance of 10-6 added to our standard model. When comparing this figure with Fig. 5 we see that, at ![]() 900 yrs, the grains become decoupled from the magnetic field because of the loss of electrons from the gas, which is induced by the charging of PAHs in the shock tail (see Fig. 11c). In that part of the shock where the ambipolar diffusion is important, the negatively charged PAHs that follow the ion motion disappear because of electron detachment by energetic neutral species. In the shock tail, once the effect of ambipolar diffusion is small enough, the charged PAHs can no longer yield their attached electrons by collisions with the neutrals. This generates a shortage of free electrons in the gas and forces the grain charge towards zero. This loss of charge allows the frictional drag to decouple grains from the magnetic field. This effect is, however, small because negatively charged PAHs can also recombine with the grains. As the grains decouple their relative velocity with
900 yrs, the grains become decoupled from the magnetic field because of the loss of electrons from the gas, which is induced by the charging of PAHs in the shock tail (see Fig. 11c). In that part of the shock where the ambipolar diffusion is important, the negatively charged PAHs that follow the ion motion disappear because of electron detachment by energetic neutral species. In the shock tail, once the effect of ambipolar diffusion is small enough, the charged PAHs can no longer yield their attached electrons by collisions with the neutrals. This generates a shortage of free electrons in the gas and forces the grain charge towards zero. This loss of charge allows the frictional drag to decouple grains from the magnetic field. This effect is, however, small because negatively charged PAHs can also recombine with the grains. As the grains decouple their relative velocity with
![]() increases and so the rate of attachment of
increases and so the rate of attachment of
![]() onto grains increases. This tends to compensate for the shortage of electrons so that the grains do not completely decouple from the magnetic field. Under these conditions, of weak grains coupling to the magnetic field, the coagulation of grains is favoured because the relative velocities between grains is of the order of 1 km s-1. Without the recombination of negatively charged PAHs on grains, large grains would decouple from the magnetic field and acquire large velocities. In this case grain shattering, and not grain coagulation, would be favoured.
onto grains increases. This tends to compensate for the shortage of electrons so that the grains do not completely decouple from the magnetic field. Under these conditions, of weak grains coupling to the magnetic field, the coagulation of grains is favoured because the relative velocities between grains is of the order of 1 km s-1. Without the recombination of negatively charged PAHs on grains, large grains would decouple from the magnetic field and acquire large velocities. In this case grain shattering, and not grain coagulation, would be favoured.
The J shock structure is calculated according to Flower et al. (2003). In J shocks the velocity of the guiding centre for grain gyration is at any time equal to
![]() .
As per JTH96 we integrate the gyration velocity
.
As per JTH96 we integrate the gyration velocity
![]() of the grains around the magnetic field lines.
of the grains around the magnetic field lines.
When the magnetic field gradient is small enough, i.e. once the shock front is passed, the betatron effect accelerates the gyration of grains (Spitzer 1976). However, this effect is weak in dense clouds because of the large gas drag encountered (Draine et al. 1983): all the energy given by the magnetic field to the grains is taken almost immediatly by the gas through friction. We can therefore neglect betatron acceleration.
We use polar coordinates
![]() to integrate the gyration velocity of a grain of a given size through the shock (see Appendix C).
to integrate the gyration velocity of a grain of a given size through the shock (see Appendix C).
 |
(26) |
![\begin{figure}
\par\hspace*{5mm}\includegraphics[angle=-90,width=8.1cm,clip]{809...
...space*{2mm}
\includegraphics[angle=-90,width=7.5cm,clip]{8094f21.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg179.gif) |
Figure 12: a) The gas velocity and temperature profile for a J shock passing through our standard pre-shock conditions with a velocity of 30 km s-1. b) The grain velocity profile in the shock propagation direction. The shock front is not shown in this figure. c) The evolution of the grain gyration velocity (the absolute velocity of the grains relative to the ions). The damping of the grain gyration is caused by gas drag. The smaller grain gyrations are the first to be damped. |
| Open with DEXTER | |
Figure 12a presents the gas velocity and temperature profiles for a J shock propagating at a velocity of 30 km s-1 through our standard pre-shock conditions (T = 10 K, ![]() = 104 cm-3, B = 100
= 104 cm-3, B = 100 ![]() G and
G and ![]() = 10-17 s-1). The shock velocity, which is higher than the critical velocity for these pre-shock conditions (see Table 1), leads to the formation of a J shock. The evolution of the grain velocity in the shock direction (Fig. 12b) shows that grains only complete a few gyrations before being brought to rest with respect to the gas. The profile for the gyration velocity through the shock is very similar to that obtained by JTH96 for J shocks in the Warm Intercloud Medium, though its duration is much shorter due to the higher densities considered here.
= 10-17 s-1). The shock velocity, which is higher than the critical velocity for these pre-shock conditions (see Table 1), leads to the formation of a J shock. The evolution of the grain velocity in the shock direction (Fig. 12b) shows that grains only complete a few gyrations before being brought to rest with respect to the gas. The profile for the gyration velocity through the shock is very similar to that obtained by JTH96 for J shocks in the Warm Intercloud Medium, though its duration is much shorter due to the higher densities considered here.
Here we study in more detail two effects that are known to affect dust dynamics and that could have important consequences for our future study of dust processing in C shocks. Firstly, electric forces can modify the grain dynamics by forcing charged grains to remain coupled to the magnetic field. This was studied either by introducing an electric field in the shock propagation direction (Pilipp et al. 1990; Pilipp & Hartquist 1994; Wardle 1998; Chapman & Wardle 2006) or by modelling the electrostatic forces exerted between negatively charged grains and ions (Ciolek & Mouschovias 1993). Secondly, since the early studies of dust coupling in the context of ambipolar diffusion in pre-stellar cores (Elmegreen 1979; Nakano & Umebayashi 1980), grain charge fluctuations are known in some cases to decouple the neutral grains from the charged grains. This effect is not important for large grains in molecular clouds but is important for the very small grains. Within this perspective we verify and adapt the study of Ciolek & Mouschovias (1993) to our purposes.
In the framework of ambipolar diffusion in pre-stellar cores, Elmegreen (1979) suggested that grains with a Hall factor
![]() could still remain coupled to the magnetic field because of the electric forces exerted by ions on the negatively charged grains. Ciolek & Mouschovias (1993) further developped this idea. Pilipp et al. (1990), inspired by earlier studies on ambipolar diffusion (Nakano & Umebayashi 1980), studied the role of an electric field Ez in the direction of propagation of the shock in the modelling of C shocks at high densities.
could still remain coupled to the magnetic field because of the electric forces exerted by ions on the negatively charged grains. Ciolek & Mouschovias (1993) further developped this idea. Pilipp et al. (1990), inspired by earlier studies on ambipolar diffusion (Nakano & Umebayashi 1980), studied the role of an electric field Ez in the direction of propagation of the shock in the modelling of C shocks at high densities.
The role of electrical forces in the coupling of grains to the magnetic field is potentially important in the study of dust processing if it can affect the dynamics of large grains that contain the major part of dust mass. If the large grains can decouple from the magnetic field they will undergo strong shattering by collisions with the grains that remain coupled to the ions. However, if the large grains remain coupled to the magnetic field, because of electric forces, then the shattering and/or vaporization will be severely limited and coagulation will tend to be favoured.
As per Pilipp et al. (1990), we model the action of the electric forces through the existence of an electric field Ez in the shock propagation direction. In the shock grains move, on the average, somewhat faster than the ions, electrons and charged PAHs because of gas drag and they create a local electric charge
![]()
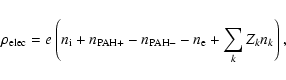 |
(29) |
Using the conservation of the charge flux through the shock (Eq. (15)), and Eqs. (25) and (A.13), we find an expression for the local charge density as a function of the dust properties alone:
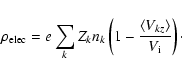 |
(30) |
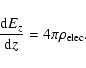 |
(31) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{8094f22.ps}\vspace*{2mm}
\includegraphics[angle=-90,width=8.2cm,clip]{8094f23.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg189.gif) |
Figure 13:
The velocity profiles for the same shock as in Fig. 10 but with the existence of an electric field Ez in the shock direction taken into account. The ions are now decoupled from the gas in the direction parallel to the shock front. The grain velocities along |
| Open with DEXTER | |
Figure 13 shows how the presence of an electric field Ez can affect the dust dynamics, as compared with Fig. 10 where local charge neutrality was assumed for the same shock and pre-shock conditions. The velocity profile along the z axis is little changed. The ions are decoupled from the gas, in the direction parallel to the shock, and move with an electric drift velocity cEz/B. Note that the shock length is not modified. The grain velocity profile in the direction parallel to the shock front has been shifted by ![]() cEz/B in the same manner. We can see that the electric field Ez is not able to recouple the larger grains to the magnetic field. This is a consequence of our modelling with an MRN distribution which includes numerous small grains which carry the major part of the electric charge of the grains. A small change in their velocity Vz, induced by a small electric field Ez, is enough to recover the local charge neutrality without affecting the dynamics of the large grains very much. This question remains open for other dust size distributions that do not present an overabundance of very small grains.
cEz/B in the same manner. We can see that the electric field Ez is not able to recouple the larger grains to the magnetic field. This is a consequence of our modelling with an MRN distribution which includes numerous small grains which carry the major part of the electric charge of the grains. A small change in their velocity Vz, induced by a small electric field Ez, is enough to recover the local charge neutrality without affecting the dynamics of the large grains very much. This question remains open for other dust size distributions that do not present an overabundance of very small grains.
The electric field Ez sensitively affects the grain velocities in the shock frame but has little effect on the relative velocities between the grains. With our multi-fluid approach there is little difference in the relative velocities between the grains when we compare our models with and without Ez. Our results for dust processing in C shocks should therefore not be very sensitive to the inclusion of an electric field Ez, unless it can affect the structure of the shock itself, which is not the case within the framework of our 3-fluid model for transverse shocks. See Appendix D for a discussion of the influence of dust dynamics on shock structure in our model. We can therefore neglect the electric field Ez in our modelling of the dust processing in transverse C shocks.
Grains smaller than 100 Å do not exist in our MRN pre-shock grain core distribution but will be produced in great numbers by the shattering of the large grains during their gyration phase. The fragments can in turn shatter or craterize other grains. They also increase the total dust cross-section but their contribution to the gas-grain friction is dependent on their degree of coupling to the magnetic field. Their dynamics must therefore be investigated because it is expected that small grain dynamics will be different from the dynamics of large grains due to their low inertia and their small cross-section. Whereas charge fluctuations do not have a major impact on the dynamics of the large grains, the influence of charge fluctuations on the dynamics of small grains can not be ignored (Ciolek & Mouschovias 1993).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{8094f24.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg191.gif) |
Figure 14:
The dynamics of four small charged test grains (10, 20, 40 and 80 Å) in our standard shock (see Fig. 5 for the characteristics of this shock). The grains are assumed to suddenly become neutral at a flow time |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{8094f25.ps}\end{figure}](/articles/aa/full/2007/46/aa8094-07/Timg192.gif) |
Figure 15: The average velocity V0z of neutral grains in the shock propagation direction, as given by Eq. (15) and adapted from Eq. (44) of Ciolek & Mouschovias (1993). The two vertical arrows delimit the domain of the shock presented in Fig. 14. The average velocity V0z is in good agreement with the integrated velocity of the grains Vz during their neutral phase presented in Fig. 14. |
| Open with DEXTER | |
As an example, we study the dynamics of small test grains in our standard shock (see Fig. 4 for the characteristics of the shock and the pre-shock gas).
As presented in Fig. 14, four small test grains (with radii of 10, 20, 40 and 80 Å) of charge Z= -1 are assumed to suddenly become neutral at the same position in the shock (corresponding to a flow time
![]() yrs) by recombination with an ion. Up until that point they are assumed to be strongly coupled to the magnetic field and to follow the ion motion. Once neutralized, we force these grains to stay neutral for a time that we take to be their neutral phase lifetime
yrs) by recombination with an ion. Up until that point they are assumed to be strongly coupled to the magnetic field and to follow the ion motion. Once neutralized, we force these grains to stay neutral for a time that we take to be their neutral phase lifetime ![]() at this point, as calculated by Eq. (17). Figure 14 presents the evolution of the instantaneous velocity, Vz, of grains in the shock direction, as calculated by the integration of the law of motion given by Eq. (18).
Once neutralized, at
at this point, as calculated by Eq. (17). Figure 14 presents the evolution of the instantaneous velocity, Vz, of grains in the shock direction, as calculated by the integration of the law of motion given by Eq. (18).
Once neutralized, at
![]() yrs, a 10 Å grain decouples from the magnetic field and quickly couples to the neutral fluid and then follows the motion of the neutrals for almost 40 years. At
yrs, a 10 Å grain decouples from the magnetic field and quickly couples to the neutral fluid and then follows the motion of the neutrals for almost 40 years. At
![]() years it becomes negatively charged by electron or ion attachment and starts to gyrate around magnetic field lines. The gyration is damped almost immediately by gas drag because of the small grain inertia. The situation is very different for a larger grain. A very short time (
years it becomes negatively charged by electron or ion attachment and starts to gyrate around magnetic field lines. The gyration is damped almost immediately by gas drag because of the small grain inertia. The situation is very different for a larger grain. A very short time (![]() 1 yr) after its neutralization, at
1 yr) after its neutralization, at
![]() yrs, a 80 Å grain becomes charged again. During its neutral phase this large grain does not have enough time to couple to the neutral fluid. Nevertheless, it has acquired via gas drag a small velocity that is now turned into a gyration velocity. It takes a few years for the gas to damp this gyration because of the greater inertia of this large grain.
The dynamics of very small neutral grains are therefore decoupled from the dynamics of very small charged grains which follow the ions.
yrs, a 80 Å grain becomes charged again. During its neutral phase this large grain does not have enough time to couple to the neutral fluid. Nevertheless, it has acquired via gas drag a small velocity that is now turned into a gyration velocity. It takes a few years for the gas to damp this gyration because of the greater inertia of this large grain.
The dynamics of very small neutral grains are therefore decoupled from the dynamics of very small charged grains which follow the ions.
If we neglect the damping of the gyration at the end of the neutral phase of each grain, which is truly negligible only for very small grains, the dynamics of each size of small grain can be modelled using two fluids, one for charged grains and one for neutral grains. Adopting Ciolek & Mouschovias Eq. (44) for the fluid velocity of the neutral grains, we combine the accelerated motion of the small neutral grains, as shown in Fig. 14, into a uniform motion of grains with an average velocity
The fact that the small neutral grains are not coupled to the ions can have a major impact on the dust processing in C shocks because they have an important velocity relative to the charged grains that remain coupled to the ion fluid. The small neutral grains might thus shatter small grains or craterize larger grains (the latter action being a progressive erosion rather than catastrophic shattering). This kind of erosional processing will result in grain fragmentation over long time-scales because the decoupling of the neutral grains from the charged grains is not limited to the precursor but is present throughout the shock, as long as the neutral and charged fluids are not recoupled.
Charge fluctuations also induce small relative velocities between ions and larger grains (here 80 Å) during their neutral and gyration damping phases. These small relative velocities should favour coagulation between large grains and the small charged grains that are strongly coupled to the magnetic field.
We present a new multi-fluid approach for dust dynamics in transverse C and J shocks in dense clouds, adapted to the perspective of our future study of dust processing. We model the dust size distribution by size bins containing grain cores covered by icy mantles. While calculating the shock structure, we determine the out-of-equilibrium charge distribution for each size of grain and incorporate its contribution into the ionization balance. The 2-D dust dynamics is properly integrated using the laws of motion, taking into account the grain inertia and the evolution of the grain cross-section due to the erosion/accretion of mantles.
In the pre-shock gas we find that grains with icy mantles have a cross-section a factor of three higher than the cross-section of the grain cores alone.
Adopting a weighting function to the Hall factor, ![]() ,
used to compute the fraction of dust mass in each bin that is coupled to the magnetic field, the critical velocity for C shocks is found to increase with the gas density and to be only weakly dependent on the presence of a high abundance of PAHs in the gas and on the photodetachement of electrons by secondary photons induced by cosmic-rays, unlike in the previous study (FPdF03).
,
used to compute the fraction of dust mass in each bin that is coupled to the magnetic field, the critical velocity for C shocks is found to increase with the gas density and to be only weakly dependent on the presence of a high abundance of PAHs in the gas and on the photodetachement of electrons by secondary photons induced by cosmic-rays, unlike in the previous study (FPdF03).
In C shocks propagating through dense clouds (
![]() cm-3) we find that the dust dynamics comprises two distinct phases: a very short transient phase where grains gyrate around magnetic field lines (resulting in high relative velocities between grains) followed by a long-term, inertia-free dynamics characterized by smaller relative velocities. In earlier studies of dust dynamics in C shocks in dense clouds the grain gyration phase was not taken into account. All grains have completed their gyration phase before a significant part of their mantles has been eroded. This justifies our inclusion of mantles onto grains in the determination of their dynamics.
cm-3) we find that the dust dynamics comprises two distinct phases: a very short transient phase where grains gyrate around magnetic field lines (resulting in high relative velocities between grains) followed by a long-term, inertia-free dynamics characterized by smaller relative velocities. In earlier studies of dust dynamics in C shocks in dense clouds the grain gyration phase was not taken into account. All grains have completed their gyration phase before a significant part of their mantles has been eroded. This justifies our inclusion of mantles onto grains in the determination of their dynamics.
In molecular clouds (
![]() cm-3), the gyration phase is significant. Once the gyration is damped, grains remain strongly coupled to the magnetic field. With a high abundance of PAHs the grains can become decoupled from the magnetic field in the shock tail where the attachment of electrons onto PAHs creates a shortage of free electrons in the gas. Negatively charged PAHs then become an important charge carrier and charge exchange between grains and negatively charged PAHs must be taken into account. This is important in calculating the charge carried by the grains in order to avoid ovestimating the decoupling of large grains.
cm-3), the gyration phase is significant. Once the gyration is damped, grains remain strongly coupled to the magnetic field. With a high abundance of PAHs the grains can become decoupled from the magnetic field in the shock tail where the attachment of electrons onto PAHs creates a shortage of free electrons in the gas. Negatively charged PAHs then become an important charge carrier and charge exchange between grains and negatively charged PAHs must be taken into account. This is important in calculating the charge carried by the grains in order to avoid ovestimating the decoupling of large grains.
In high density clouds (
![]() cm-3) and with no PAHs, the gyration phase is almost negligible due to higher gas drag. An electron shortage appears early in the precursor induced by the charging of the grains which carry a significant fraction of the free electrons. The high gas drag leads to a long-term decoupling of large grains from the magnetic field. However, small grains remain strongly coupled throughout the shock.
cm-3) and with no PAHs, the gyration phase is almost negligible due to higher gas drag. An electron shortage appears early in the precursor induced by the charging of the grains which carry a significant fraction of the free electrons. The high gas drag leads to a long-term decoupling of large grains from the magnetic field. However, small grains remain strongly coupled throughout the shock.
Very small grains (
![]() ), such as would be expected for the fragments of shattering in grain-grain collisions, may not be strongly coupled to the magnetic field in all environments because of charge fluctuations. When the lifetime of neutral grains is not negligible compared with the friction time-scale, very small grains follow stochastic dynamics where they tend to couple to the neutral fluid each time they become neutralized, otherwise following the motion of the ions. With our detailed grain dynamical modelling we confirm that the averaging approach to the dynamics of grains undergoing charge fluctuations adopted by Ciolek & Mouschovias (1993) is indeed valid. We model the impact of charge fluctuations on the dynamics of small grains by defining the average velocity of neutral grains and charged grains taken separately for each size of grain.
), such as would be expected for the fragments of shattering in grain-grain collisions, may not be strongly coupled to the magnetic field in all environments because of charge fluctuations. When the lifetime of neutral grains is not negligible compared with the friction time-scale, very small grains follow stochastic dynamics where they tend to couple to the neutral fluid each time they become neutralized, otherwise following the motion of the ions. With our detailed grain dynamical modelling we confirm that the averaging approach to the dynamics of grains undergoing charge fluctuations adopted by Ciolek & Mouschovias (1993) is indeed valid. We model the impact of charge fluctuations on the dynamics of small grains by defining the average velocity of neutral grains and charged grains taken separately for each size of grain.
The resulting shock structures integrating dust dynamics do not significantly differ from those obtained with our previous model where the charged dust grains were assumed to follow the ion motion. This conclusion remains valid even when large grains are strongly decoupled from the magnetic field, as for high densities. This is because the small grains (![]()
![]() )
are mainly responsible for the gas-grain coupling and remain coupled to the magnetic field throughout the shock as in our previous model.
)
are mainly responsible for the gas-grain coupling and remain coupled to the magnetic field throughout the shock as in our previous model.
The presence of an electric field Ez in the shock propagation direction, resulting from a local loss of charge neutrality induced by the decoupling of large grains from the magnetic field, affects the dynamics of grains very little when a full grain size distribution is used. The velocity of the grains in the shock direction is little modified because a very small change in the dynamics of smaller grains is enough to re-establish the local charge neutrality. The component of the grain velocity parallel to the shock is affected in the same way for all grains, thereby leaving the relative velocities approximately as before. Therefore, dust processing should not depend very much on the inclusion of the electric field Ez in the model, which we can therefore ignore.
Dust dynamics in J shocks only comprise a short gyration phase before the grains are brought to rest with respect to the gas. The high gyration velocity of the dust grains in the post-shock gas can lead to the efficient sputtering, vaporization and shattering of dust grains.
Our presented formalism will be applied, in a following paper, to the study of dust processing via gas-grain and grain-grain collisions in J and C shocks in dense clouds and to the feedback of dust processing on the shock structure.
Acknowledgements
We wish to thank the referee, Wayne Roberge, for his encouraging remarks and for his insightful comments that helped to improve the manuscript.
Our silicate and carbon dust size distributions are modelled using a range of size bins as per Jones et al. (1996). The bins are numbered with indice k running from 1 to
![]() .
The bin k contains all the grain cores with radius
ak- < a < ak+ (or in mass
mk- < m < mk+). In order to be given sufficient resolution for the smallest grain cores the bin limits follow a geometrical distribution in k
.
The bin k contains all the grain cores with radius
ak- < a < ak+ (or in mass
mk- < m < mk+). In order to be given sufficient resolution for the smallest grain cores the bin limits follow a geometrical distribution in k
 |
(A.1) |
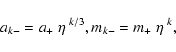 |
(A.2) |
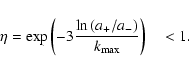 |
(A.3) |
Within each bin we assume a power law size distribution of index ![]() in mass and
in mass and ![]() in radius, defined by
in radius, defined by
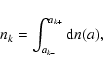 |
(A.9) |
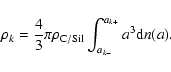 |
(A.10) |
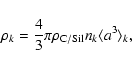 |
(A.11) |
| (A.15) |
| (A.16) |
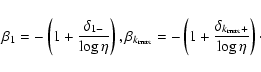 |
(A.19) |
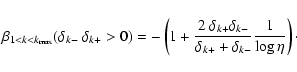 |
(A.20) |
However, if
![]() then the slope of the distribution changes sign around bin k. In this case we arbitrarily define the mass density index in bin k from the upper slope
then the slope of the distribution changes sign around bin k. In this case we arbitrarily define the mass density index in bin k from the upper slope
![]() :
:
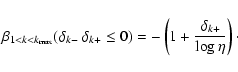 |
(A.21) |
In Sect. 2.1 we showed that all the grain cores are covered, at any position in the shock, by an icy mantle of identical thickness ![]() .
To calculate the mantle thickness, we follow an approach similar to Walmsley et al. (2004). The total volume of mantle material shared by all grains is obtained by subtracting the volume of the cores from the total grain volume and we then obtain the expression for the total mass density of the mantles:
.
To calculate the mantle thickness, we follow an approach similar to Walmsley et al. (2004). The total volume of mantle material shared by all grains is obtained by subtracting the volume of the cores from the total grain volume and we then obtain the expression for the total mass density of the mantles:
We now define new moments of order i (i = 0, 1, 2, 3) for the entire dust size distribution of grain cores
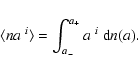 |
(B.2) |
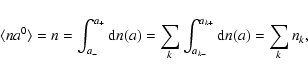 |
(B.3) |
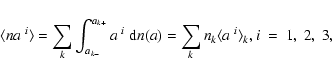 |
(B.4) |
| (B.6) |
Covering the "average'' grain cores by mantles of thickness ![]() the "average'' grain (core + mantle) for a given bin k has a radius, cross-section and mass given by:
the "average'' grain (core + mantle) for a given bin k has a radius, cross-section and mass given by:
| (B.7) |
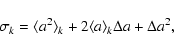 |
(B.8) |
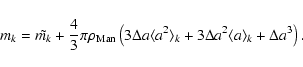 |
(B.9) |
Integrating the grain charge (Pilipp et al. 1990; Ciolek & Roberge 2002, FPdF03 ) allows the calculation of the ionization balance and the determination of the "out of equilibrium'' grain charge. It also allows us to calculate the grain charge when a shortage of electrons in the gas makes the use of fit formulas for grain charge impossible, a situation already encountered by Chapman & Wardle (2006) when PAHs were introduced into their model. Integrating the charge distribution is, furthermore, needed to determine the number density per unit volume of the neutral grains, which is necessary to model the impact of charge fluctuations on the dynamics of the grains and their processing (see Sect. 5.2).
Each bin k is associated with a dedicated charge grid [Zk-:Zk+] and associated with
Zk+- Zk-+1 "charged bins'' (k,Z), each with a core mass density ![]() ,
number density
,
number density
![]() ,
and flux of mass
,
and flux of mass
![]() .
When calculating the steady-state in the pre-shock gas at rest,
.
When calculating the steady-state in the pre-shock gas at rest,
![]() is set to 1 for all grains. For shocks integrated in cartesian coordinates,
is set to 1 for all grains. For shocks integrated in cartesian coordinates,
![]() (Eq. (34)) and
(Eq. (34)) and
![]() (Eq. (35)), whereas
(Eq. (35)), whereas
![]() for all grains when integrating in polar coordinates.
for all grains when integrating in polar coordinates.
The processes determining the charge distribution of the grains in bin k are modelled by a transfer of flux of grains between consecutive charge bins for the same bin k with the following rates:
From the charge distribution we can calculate the average charge Zk of grains in bin k
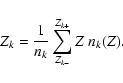 |
(C.2) |
The integration of the grain velocity vector ![]() in the shock frame in cartesian coordinates (Vy, Vz) is not always possible. Indeed, our integration variable is the position z in the shock, not the time t, so that the differential equation Eq. (20) is not defined whenever Vz crosses zero. If this happens for very short time-scales one can artificially impose Vz > 0 in that equation to allow the integration to continue, with only a minor change in the dynamics of grain. But if Vz < 0 over long time-scales, e.g. for all grains in J shocks or for large grains in some C shocks, one can use polar coordinates to integrate the gyration velocity vector
in the shock frame in cartesian coordinates (Vy, Vz) is not always possible. Indeed, our integration variable is the position z in the shock, not the time t, so that the differential equation Eq. (20) is not defined whenever Vz crosses zero. If this happens for very short time-scales one can artificially impose Vz > 0 in that equation to allow the integration to continue, with only a minor change in the dynamics of grain. But if Vz < 0 over long time-scales, e.g. for all grains in J shocks or for large grains in some C shocks, one can use polar coordinates to integrate the gyration velocity vector
 |
(C.4) |
We now present the expressions for the
![]() differential equation in polar coordinates valid for the integration of dust dynamics in C and J shocks. We define the gyration velocity vector
differential equation in polar coordinates valid for the integration of dust dynamics in C and J shocks. We define the gyration velocity vector
![]() in polar coordinates (
in polar coordinates (
![]() )
as
)
as
 |
(C.5) |
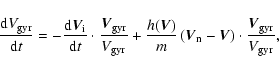 |
(C.7) |
| (C.9) |
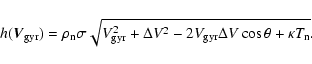 |
(C.10) |
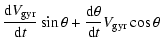 |
= | ||
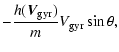 |
(C.11) |
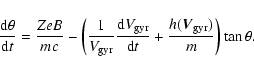 |
(C.12) |
Integration as a function of position z is obtained by dividing Eqs. (C.8) and (C.13) by
![]() .
The integration of the dust dynamics in polar coordinates is applicable for both J (
.
The integration of the dust dynamics in polar coordinates is applicable for both J (
![]() )
and C (
)
and C (
![]() )
shocks, with the restriction for C shocks that the grains must be strongly coupled to the magnetic field (
)
shocks, with the restriction for C shocks that the grains must be strongly coupled to the magnetic field (
![]() ). This condition is often satisfied in the circumstances where we must integrate in polar coordinates: i.e. shocks in molecular or diffuse clouds.
). This condition is often satisfied in the circumstances where we must integrate in polar coordinates: i.e. shocks in molecular or diffuse clouds.
Draine (1980) demonstrated that dust grains are more important than ions in coupling the momentum from the magnetic field to the neutrals in the hottest parts of transverse C shocks in clouds with low fractional ionization (
![]() ), assuming that dust grains are strongly coupled to the magnetic field (
), assuming that dust grains are strongly coupled to the magnetic field (
![]() ). Here we estimate the extent to which gas-grain coupling (and thus shock structure) is affected by the inclusion of a dust size distribution characterized by different Hall factors
). Here we estimate the extent to which gas-grain coupling (and thus shock structure) is affected by the inclusion of a dust size distribution characterized by different Hall factors ![]() (some of them larger than 1 as for high density clouds, see Fig. 10). We compare our results with our previous 3-fluid study (FPdF03) where the charged grains were all coupled to the magnetic field and followed the ion motion.
(some of them larger than 1 as for high density clouds, see Fig. 10). We compare our results with our previous 3-fluid study (FPdF03) where the charged grains were all coupled to the magnetic field and followed the ion motion.
Previous studies of dust dynamics in C shocks have concentrated on the impact of dust dynamics on the shock structure, especially the decoupling of large grains from the magnetic field lines, and found it important for oblique shocks (Pilipp & Hartquist 1994; Wardle 1998; Chapman & Wardle 2006): the out-of-plane drift of large grains following the magnetic field lines tends to increase the dissipation rate and therefore increase the peak temperature and reduce the shock thickness. This effect does not exist in the transverse shocks studied in the present paper where the dynamics of the grains is restricted to the plane transverse to the magnetic field direction. Chapman & Wardle (2006) presented the first multi-fluid study of dust dynamics in oblique shocks in order to determine how much the inclusion of a full dust size distribution (replacing the usual single-sized grain approximation) affects the rotation of the magnetic field throughout the shock. Within this framework they ignore the grain inertia as well as the grain contribution to the ionization balance but they do include the presence of an electric field Ez in the shock direction. They find that, once a full dust size distribution is introduced, the rotation of the magnetic field throughout the shock is far less important than in their previous model with single-sized grains, even in presence of a high PAH abundance favouring the decoupling of large grains. From the limited point of view of dust dynamics their results, when comparable, are in general agreement with ours.
Our study of transverse shocks reveals a small impact of the decoupling of large grains on the shock structure. At low densities (
![]() cm-3) the velocity and temperature profiles do not show any significant difference. The situation is little different at higher density. Figure D.1a,b compares the shock velocity and temperature profile for our model with those obtained with the FPdF03 shock model where charged dust grains are assumed to follow the ion motion. This comparison is for a C shock propagating at a velocity of 20 km s-1 in a cloud of density 106 cm-3: note that the shock is a little longer in our model (where the dust dynamics is integrated) than when the grains are assumed to follow ions. To emphasize the effect of dust, we show in Fig. D.1c the result for the same shock model with no dust.
cm-3) the velocity and temperature profiles do not show any significant difference. The situation is little different at higher density. Figure D.1a,b compares the shock velocity and temperature profile for our model with those obtained with the FPdF03 shock model where charged dust grains are assumed to follow the ion motion. This comparison is for a C shock propagating at a velocity of 20 km s-1 in a cloud of density 106 cm-3: note that the shock is a little longer in our model (where the dust dynamics is integrated) than when the grains are assumed to follow ions. To emphasize the effect of dust, we show in Fig. D.1c the result for the same shock model with no dust.
From Eq. (21) we can evaluate the coupling term between gas and grains
![]() in the shock direction which affects the shock length. Once the gyration is damped and when no electric field Ez is present, we get:
in the shock direction which affects the shock length. Once the gyration is damped and when no electric field Ez is present, we get:
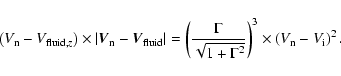 |
(D.1) |
The decoupling of large grains from the magnetic field therefore has little impact on the dynamics of transverse shocks. Our previous approach (FPdF03), with no electric field Ez and with the charged grains assumed to be strongly coupled the ions, is therefore satisfactory even at high densities where the large grains are in fact decoupled from the magnetic field. The situation will be different as soon as we consider dust processing, which will modify the dust size distribution and therefore the dust-gas coupling. This situation will be explored in a following paper.