A&A 476, 17-30 (2007)
DOI: 10.1051/0004-6361:20077988
C. R. Stark1 - D. A. Diver1 - A. A. da Costa2 - E. W. Laing1
1 - Dept. of Physics and Astronomy, University of Glasgow,
Glasgow G12 8QQ, Scotland, UK
2 - Secção de
Telecomunicações, DEEC/SPR, Instituto Superior Técnico,
1049-001 Lisboa, Portugal
Received 31 May 2007 / Accepted 30 September 2007
Abstract
Pulsar magnetospheres are composed of electron-positron plasmas characterised by broadband
electromagnetic emission, the source of which remains elusive. This paper investigates one possible emission mechanism in which electrostatic oscillations are coupled to propagating electromagnetic waves by the magnetic field inhomogeneity, thus creating a source of radiation in the pulsar magnetosphere. The full nonlinear equations in cylindrical geometry for a streaming cold electron-positron plasma are solved numerically, together with Maxwell's equations, using a Finite-Difference Time Domain method. Electrostatic oscillations are induced in a streaming plasma in the presence of a non-uniform magnetic field, and the resulting electromagnetic waves are modelled self-consistently. Also presented is the linear perturbation analysis of these model equations perturbed from a dynamical equilibrium in order to probe the fundamental modes present in the system. These simulations successfully exhibit the coupling mechanism
and the nonlinear interaction between electromagnetic waves and independent plasma oscillations, confirming the importance of coherent
plasma effects and collective plasma processes in the pulsar magnetosphere.
Key words: plasmas - radiation mechanisms: non-thermal - pulsars: general
Pulsar magnetospheres are composed of magnetised electron-positron
(pair) plasmas characterised by ultra strong magnetic fields and
broadband electromagnetic emission. Conventional modelling uses the
fact that the dominant Lorentz force produces a host of relativistic
charged particles, each of which radiates strongly and
stochastically, producing ![]() -ray photons. Such single-particle
models have been explored as possible radiation sources (da Costa & Kahn 1997), but have not been able to recover the highest
energy radiation observed.
-ray photons. Such single-particle
models have been explored as possible radiation sources (da Costa & Kahn 1997), but have not been able to recover the highest
energy radiation observed.
However this strict single particle approach, used in many pulsar models, doesn't exploit the properties of the pair plasma; it has been assumed that the magnitude of the pulsar electromagnetic fields dominate the influence of plasma effects. This is not the case since in the plasma rest frame local collective electric fields become significant when transformed into the rotating pulsar laboratory frame. Such fields are comparable with that of the dipolar low-frequency electromagnetic wave driving the magnetosphere (da Costa et al. 2001, hereafter referred as Paper I). Therefore the study of collective plasma processes is of the greatest importance for the dynamics of the magnetosphere, and the radiation mechanisms of pulsars.
Pair plasmas have gained considerable attention over the recent years due to their existence in a number of astrophysical environments such as pulsar magnetospheres. The various wave modes that exist in a pair plasma when the background is homogeneous has been extensively covered in the cold plasma regime (Stewart 1992,1993). Generation of magnetic fluctuations by field-aligned flows in plasmas (Shukla & Shukla 2007) shows a new range of instabilities relevant to strongly flowing constant-density plasmas; further instability studies in homogeneous pair plasmas have been undertaken by Marklund (Marklund et al. 2006), relevant to bursty systems; under certain simplifying conditions, pair-plasma waves can be described by the KdV equation (Verheest & Cattaert 2004). There are also studies of the plasma electromagnetic wave coupling from actual pair production (Bulanov et al. 2005). Our treatment will deal with a cold, free-streaming (but not field-aligned) anisotropic and inhomogeneous pair plasma, using the full nonlinear equations.
In cold non-relativistic plasma theory non-linear electrostatic oscillations in electron-positron plasmas develop a density instability in which the density of both species grows sharply at the edges of the oscillation site (Paper I). Folding thermodynamics into the system provides a possible mechanism for avoiding the onset of the instability, since pressure effects would oppose the density build up. Coupling the oscillation to an electromagnetic mode via an inhomogeneous background magnetic field would provide another means to avoid the onset of the instability. This would allow energy to be radiated away from the oscillation, quenching the density instability and giving a source of radiation in the pulsar magnetosphere. Ultimately thermodynamics will have to be incorporated into a more complete model but it would be advantageous to explore the coupling before relaxing the cold plasma approximation. Previous work has studied this mechanism in the quasi-linear regime (Diver et al. 2002, hereafter referred as Paper II) in which the background magnetic field was inhomogeneous but the plasma density was uniform. A fully consistent nonlinear treatment requires that both the density and magnetic field be inhomogeneous simultaneously.
This paper addresses the nonlinear generation of electromagnetic waves by large amplitude electrostatic oscillations, laying out the details of the equilibrium. The basic mathematical formulation of the electron-positron cold magnetoplasma and the mode coupling mechanism is described in Sect. 2. In Sect. 3 linear analysis of the equations perturbed from dynamical equilibrium is performed to gain an understanding of the modes present in the plasma. Section 4 describes the nonlinear numerical simulations, presenting and discussing the results.
where
![]() is the dimensionless
speed of light squared in the plasma. Note Poisson's
equation, Eq. (29), and the r component of the
Ampère-Maxwell equation, Eq. (30), are not both
required and have been included for completeness.
is the dimensionless
speed of light squared in the plasma. Note Poisson's
equation, Eq. (29), and the r component of the
Ampère-Maxwell equation, Eq. (30), are not both
required and have been included for completeness.
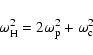 |
(33) |
Having an inhomogeneous magnetic field permeating the plasma requires the equilibrium to be non-uniform for the system to be self-consistent.
The nonlinear system of Eqs. (23)-(32) does not have a closed form analytical solution and must be solved numerically. Insight into the possible dynamical responses of the magnetised pair plasma can be obtained via linear analysis.
Linearise the full set of governing equations and look at large
values of ![]() .
In this regime
.
In this regime
![]() and
and
![]() const., as
const., as
![]() corresponding to a net motion of
the plasma in the radial direction only,
corresponding to a net motion of
the plasma in the radial direction only,
![]() .
To
be consistent with Eq. (40) requires that in the scale
length, R, of interest
.
To
be consistent with Eq. (40) requires that in the scale
length, R, of interest
![]() .
The governing equations
then become:
.
The governing equations
then become:
M and W are related to the confluent hypergeometric functions
![]() and
and
![]() as follows
as follows
| |
= | (60) | |
| = | (61) |
| |
= | ||
| (62) |
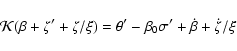 |
(71) |
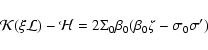 |
(72) |
| = | (74) | ||
| = | (75) |
![\begin{displaymath}\mathcal{K}[\mathcal{K}(\xi\mathcal{L})+\sigma_{0}\mathcal{L}]+\beta_{0}^{2}\xi(\mathcal{L}-2\Sigma_{0}\theta/\xi)=0.
\end{displaymath}](/articles/aa/full/2007/46/aa7988-07/img159.gif) |
(76) |
| |
= | ||
| (81) |
| |
= | 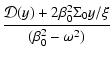 |
(85) |
| = | 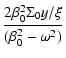 |
(86) |
| (89) |
| (90) |
| |
= | (91) | |
| (92) | |||
| (93) |
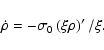 |
(99) |
| |
= | (100) | |
| = | (101) |
| |
= | ||
| = | |||
| = | (102) |
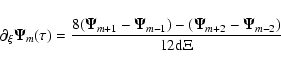 |
(103) |
| (104) | |
| (105) |
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7988fg1.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg254.gif) |
Figure 1:
Dynamical
equilibrium solutions for
|
| Open with DEXTER | |
The parameters
![]() ,
,
![]() and
and
![]() characterise the solution and infer the value of p consistent with
the system.
characterise the solution and infer the value of p consistent with
the system.
![]() is a key parameter (along with
is a key parameter (along with ![]() ,
the
initial values of
,
the
initial values of
![]() ,
,
![]() and
and ![]() )
since it defines the form of the solution while
)
since it defines the form of the solution while
![]() and
and
![]() merely scale it. Figure 1 shows
a typical example of a calculated equilibrium. In principle
merely scale it. Figure 1 shows
a typical example of a calculated equilibrium. In principle
![]() can be arbitrarily chosen to characterise the system,
for instance using a large value of
can be arbitrarily chosen to characterise the system,
for instance using a large value of
![]() to obtain a large
magnetic field inhomogeneity. Care has to be taken, however, since
the model described here is a non-relativistic one. Recall Eq. (13) for
to obtain a large
magnetic field inhomogeneity. Care has to be taken, however, since
the model described here is a non-relativistic one. Recall Eq. (13) for ![]() and define
Ur=ur/c and
Vr=vr/c. In the non-relativistic limit Ur,
and define
Ur=ur/c and
Vr=vr/c. In the non-relativistic limit Ur, ![]() ,
so
,
so
![]() hence
hence
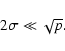 |
(110) |
Once the equilibrium has been defined the plasma is driven by an
initial charge density perturbation,
| = | ![$\displaystyle A_{0}
\sin\left[\pi\frac{\left(m-m_{0}+\varsigma\right)}{\varsigma}\right]$](/articles/aa/full/2007/46/aa7988-07/img269.gif) |
||
![$\displaystyle \times \exp\left[-\left(\lambda\frac{m-m_{0}}{\varsigma}\right)^{2}\right]$](/articles/aa/full/2007/46/aa7988-07/img270.gif) |
(112) |
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7988fg2.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg275.gif) |
Figure 2:
Spatial
and temporal evolution of |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7988fg3.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg276.gif) |
Figure 3:
Spatial
and temporal evolution of the radial electric field, |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7988fg4.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg277.gif) |
Figure 4:
Spatial
and temporal evolution of the axial magnetic field, |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7988fg5.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg278.gif) |
Figure 5:
Spatial
and temporal evolution of the azimuthal electric field, |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7988fg6.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg279.gif) |
Figure 6:
Spatial structure of the axial magnetic field, |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7988fg7.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg280.gif) |
Figure 7:
Spatial structure of the azimuthal electric field,
|
| Open with DEXTER | |
Table 1: Table of parameters for numerical simulations Figs. 1-7.
The set of parameters
![]() determine p and hence
the quantity
determine p and hence
the quantity
![]() ,
where the choice of
,
where the choice of
![]() and Ldefine the physical system to which the results apply. For the
solutions in Figs. 1-7 and using Table 1,
and Ldefine the physical system to which the results apply. For the
solutions in Figs. 1-7 and using Table 1,
![]() .
Following Paper I and assuming
that the required typical electron number densities for
.
Following Paper I and assuming
that the required typical electron number densities for ![]() -ray
radiation in the rest frame is
-ray
radiation in the rest frame is
![]() m-3, then
we have: ur0,
m-3, then
we have: ur0,
![]() m s-1;
m s-1;
![]() ,
,
![]() m s-1;
m s-1;
![]() V m-1;
V m-1;
![]() V m-1;
V m-1;
![]() T, where
T, where
![]() m. Translated into the laboratory frame in which the
pulsar rotates and assuming a typical Lorentz factor
m. Translated into the laboratory frame in which the
pulsar rotates and assuming a typical Lorentz factor
![]() gives
gives
![]() T.
T.
The relative emission efficiency of the mode coupling can be
characterised by the ratio
![]() .
This is quite
small but it is important to note that the coherent dynamical
response of the electrostatic oscillation cannot propagate in the
cold plasma context and hence it cannot be observed directly; only
the coherent, propagating electromagnetic response can be detected.
In contrast to single-particle radiation mechanisms the mode
coupling here generates a collective electromagnetic mode,
consistent with the background plasma conditions, from the coherent
plasma motion.
.
This is quite
small but it is important to note that the coherent dynamical
response of the electrostatic oscillation cannot propagate in the
cold plasma context and hence it cannot be observed directly; only
the coherent, propagating electromagnetic response can be detected.
In contrast to single-particle radiation mechanisms the mode
coupling here generates a collective electromagnetic mode,
consistent with the background plasma conditions, from the coherent
plasma motion.
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7988fg8.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg311.gif) |
Figure 8:
Dynamical equilibrium solutions for
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=7.7cm,clip]{7988fg9.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg312.gif) |
Figure 9:
Spatial and temporal evolution of |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=7.7cm,clip]{7988fg10.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg313.gif) |
Figure 10:
Spatial
and temporal evolution of the radial electric field, |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=7.7cm,clip]{7988fg11.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg314.gif) |
Figure 11:
Spatial
and temporal evolution of the axial magnetic field, |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=7.7cm,clip]{7988fg12.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg315.gif) |
Figure 12:
Spatial and temporal evolution of the azimuthal electric
field, |
| Open with DEXTER | |
As the generated mode propagates away from the oscillation site it will encounter regions of differing background density giving a corresponding variation in the plasma frequency, requiring a change in the wave amplitude to conserve energy. This is analogous to waves on a string with an impedance variation, but the plasma context introduces an extra feature: namely the interplay between the driving frequency of the wave and the local plasma frequency.
If the frequency of the wave is very large then the effect of the
plasma on the wave propagation becomes less significant. A wave
propagating towards smaller values of ![]() will encounter a gradual
increase in the background plasma density and will eventually be
partially reflected and absorbed when the frequency of the wave,
will encounter a gradual
increase in the background plasma density and will eventually be
partially reflected and absorbed when the frequency of the wave,
![]() falls below that of the local hybrid frequency,
falls below that of the local hybrid frequency,
![]() (Paper II). From Figs. 6-7
it is clear that the doppler shift is negligible, consistent with
our earlier linear analysis.
(Paper II). From Figs. 6-7
it is clear that the doppler shift is negligible, consistent with
our earlier linear analysis.
Figures 2-7 address small
perturbations (1%) to the equilibrium; finite amplitude effects
need larger perturbations. The nonlinearity of the mode coupling is
specifically exhibited in Figs. 9-16. For
these specific simulations the equilibrium, Fig. 8, was
calculated using the parameters from Table 2 with an
initial ![]() charge density perturbation. Over the initial charge
density perturbation the equilibrium values were:
charge density perturbation. Over the initial charge
density perturbation the equilibrium values were:
![]() ;
;
![]() ;
;
![]() and
and
![]() with
with
![]() .
In comparison to the
simulations discussed in Figs. 2-7 the ratio
.
In comparison to the
simulations discussed in Figs. 2-7 the ratio
![]() is much higher. Figures 13
and 14 clearly show the onset of the density
instability consistent with Paper I and its consequent effect on the
evolution of the electromagnetic wave it generates, Figs. 15-16. For these solutions again
setting
is much higher. Figures 13
and 14 clearly show the onset of the density
instability consistent with Paper I and its consequent effect on the
evolution of the electromagnetic wave it generates, Figs. 15-16. For these solutions again
setting
![]() m-3 in the plasma rest frame
yields: ur0,
m-3 in the plasma rest frame
yields: ur0,
![]() m s-1;
m s-1;
![]() ,
,
![]() m s-1;
m s-1;
![]() V m-1;
V m-1;
![]() V m-1;
V m-1;
![]() T, where
T, where
![]() m.
m.
![\begin{figure}
\par {\includegraphics[width=8.1cm,clip]{7988fg13.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg328.gif) |
Figure 13:
Spatial structure of |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.1cm,clip]{7988fg14.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg329.gif) |
Figure 14:
Spatial structure of |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7988fg15.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg330.gif) |
Figure 15:
Spatial structure of the azimuthal electric field,
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7988fg16.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg331.gif) |
Figure 16:
Spatial structure of the axial magnetic field, |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7988fg17.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg332.gif) |
Figure 17:
Variation of the azimuthal electric field |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.1cm,clip]{7988fg18.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg333.gif) |
Figure 18:
Variation of the phase and amplitude of the electric field
component, |
| Open with DEXTER | |
Increasing the amplitude (and therefore the energy content) of the initial density perturbation for a given background magnetic field gradient correspondingly increases the amplitude of the generated wave, and makes the wave profile more nonlinear, Figs. 17-19. Increasing the nonlinearity of the oscillation also affects its phase, consistent with the results of Paper I. Note that as the initial charge density perturbation is increased relative to the background plasma density the perturbed fluid velocities become relativistic. Relaxing the non-relativistic restrictions in future code developments will address this.
If the initial perturbation amplitude of the density oscillation is
kept constant and the background magnetic field gradient is varied,
the amplitude of the resulting EM wave increases nonlinearly as the
coupling strength
![]() is increased,
Fig. 20. Notice that as
is increased,
Fig. 20. Notice that as
![]() is increased the
resulting rate of increase in the EM amplitude begins to slow,
hinting perhaps at a maximum fraction of the electrostatic that may
be converted in this way.
is increased the
resulting rate of increase in the EM amplitude begins to slow,
hinting perhaps at a maximum fraction of the electrostatic that may
be converted in this way.
Table 2: Table of parameters for numerical simulations Figs. 8-16.
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7988fg19.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg340.gif) |
Figure 19:
Variation of the phase and amplitude of the electric field
component, |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.4cm,clip]{7988fg20.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg341.gif) |
Figure 20:
Variation of the azimuthal electric field |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.4cm,clip]{7988fg21.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg342.gif) |
Figure 21:
Plot
of axial magnetic field |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.4cm,clip]{7988fg22.eps} }
\end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg343.gif) |
Figure 22: Nonlinear response of plasma to EM wave interaction, when the outward directed injected EM wave has passed beyond the edge of the ES oscillation site. Plot shows the difference between the cases where the two EM waves are independently propagating, and when they interact nonlinearly. The solid line is the case where the ratio of the EM wave wavelength to the width of the density perturbation is unity. The dotted and dashed lines correspond to a ratio of 2 and 3 respectively. Note the EM wave amplitude is constant for all ratios. The residual nonlinear response consists of three main features: the reflected feature (left-hand side); the oscillation feature (centre); and a transmitted feature, corresponding to the injected EM wave (right-hand side). |
| Open with DEXTER | |
The physical origin of the reflected feature is due to two main phenomena: (1) the spatially and temporally varying refractive index of the electrostatic oscillation as the wave passes through it; and (2) the increased wave coupling, momentarily stimulated as the injected wave traverses the oscillation site. The structure and shape of the reflected feature depends strongly on these two factors. The central feature represents the increased wave coupling at the oscillation site due to the passage of the injected wave. The transmitted feature represents the influence of the interaction on the injected EM wave as it propagates away from the oscillation site.
The results of wavelength variation of the fixed-amplitude injected EM wave encountering a plasma oscillation of varying amplitude are presented in Figs. 23 and 24. These show that the maximum energy in the reflected feature occurs when the EM wavelength is not less than the width of the oscillation for smaller oscillation amplitudes, but this drifts to larger wavelengths as the oscillation becomes more nonlinear in character.
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7988fg23.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg344.gif) |
Figure 23: Plot of the magnetic energy of the resultant reflected feature as a function of the wavelength of the injected wave normalised to the width of the ES oscillation site. Note that the resultant is calculated by subtracting the full nonlinear calculation from the linear superposition of the two non-interacting cases (that is, the electrostatic oscillation alone, and the injected electromagnetic wave on its own). Notice that for a given density perturbation, the residual reflected feature is a strong function of wavelength of the injected EM wave peaking close to where the wavelength matches the ES site width. However, this peak response drifts with ES amplitude towards longer wavelengths, reflecting the essential nonlinearity of the coupling. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7988fg24.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg345.gif) |
Figure 24: Same as for Fig. 23. |
| Open with DEXTER | |
Figure 25 shows the results for the central feature, under similar conditions as for Figs. 23 and 24. There does not seem to be a peak in the response here, but instead a monotonic increase.
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7988fg25.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg346.gif) |
Figure 25: Plot of the amplitude of the central oscillating feature as a function of the wavelength of the injected EM wave normalised to the width of the ES oscillation site. |
| Open with DEXTER | |
Increasing the amplitude (but maintaining constant wavelength) of the injected wave also increases the local magnetic gradient at the oscillation site, and so we expect to see similar phenomena as in the variable wavelength case. The summary of these results is presented in Figs. 26 and 27, which show broadly similar behaviour to the earlier cases but with one notable difference: the reflected feature shows no maximum amplitude. It is clear that a maximum response is associated only with a resonance in scale-lengths, which is entirely reasonable.
![\begin{figure}
\par {\includegraphics[width=8.4cm,clip]{7988fg26.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg347.gif) |
Figure 26: Plot of the magnetic energy of the residual reflected feature as a function of the injected EM wave amplitude normalised to the to the value of the background magnetic gradient at the centre of the ES oscillation site. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.4cm,clip]{7988fg27.eps} } \end{figure}](/articles/aa/full/2007/46/aa7988-07/Timg348.gif) |
Figure 27: Plot of the amplitude of the central oscillating feature as a function of the amplitude of the injected EM wave normalised to the to the value of the background magnetic gradient at the centre of the ES oscillation site. |
| Open with DEXTER | |
In order to characterise the dynamical responses and small-amplitude modes of such a plasma, we have also presented a linear analysis as a preamble to a fully nonlinear treatment, and also to show continuity with earlier work.
The nonlinear numerical simulations have successfully confirmed the proposed coupling mechanism (Paper II) and displayed the nonlinear nature of the interaction between electromagnetic waves and independent electrostatic oscillations. These results open up a completely new way of describing pulsar radiation mechanisms. They offer the exciting possibility of interpreting sub-pulse structure in terms of local plasma densities and magnetic field gradients in terms of the nonlinear coupling and interactions of the waves and oscillations that are detailed here.
Such phenomena extend the usual pulsar electromagnetic field distribution, that is, the superposition of the underlying dipolar electromagnetic field of the star, plus the self-field of the flowing plasma (da Costa & Kahn 1982; Paper I).
Collective processes in the pulsar rest frame depend very strongly on the local plasma and field conditions, as we have shown, and so present a powerful diagnostic tool if such processes can be identified in the emission structure.
Future considerations include extending the cold plasma treatment to a kinetic one, in order that we can generalise from simple cold electrostatic oscillations to propagating electrostatic waves, such as Bernstein modes (Laing & Diver 2005; Keston et al. 2003). These modes could act as sources of electromagnetic radiation via the coupling mechanism, providing a rich spectrum of electromagnetic waves propagating in the magnetosphere. Such work is currently being considered by the authors.
Acknowledgements
We are gratefully acknowledge the support by PPARC for a studentship for C. R. Stark. The authors are grateful to the anonymous referees for constructive comments that greatly enhanced the presentation of this paper. We are also grateful for travel support from PPARC via Rolling grant PP/C00234/1.
Table A.1: Physical meaning of non-dimensionalised plasma quantities.
The quantity ![]() cannot equal zero since this would imply a
negative particle number density. As a result this requires that
cannot equal zero since this would imply a
negative particle number density. As a result this requires that
![]() in accordance with Eq. (B.6) and is
additionally consistent with having a non-zero magnetic field, Eq. (B.4), permeating the plasma. For
in accordance with Eq. (B.6) and is
additionally consistent with having a non-zero magnetic field, Eq. (B.4), permeating the plasma. For
![]() we must
also have
we must
also have ![]() to satisfy Eq. (B.3). These conditions
are in agreement with Eqs. (B.1), (B.2) and (B.5). In this regime the background plasma is uniform
and therefore the equilibrium magnetic field must be constant as
dictated by
Eq. (B.7). Note that no constraint is placed
on the behaviour of
to satisfy Eq. (B.3). These conditions
are in agreement with Eqs. (B.1), (B.2) and (B.5). In this regime the background plasma is uniform
and therefore the equilibrium magnetic field must be constant as
dictated by
Eq. (B.7). Note that no constraint is placed
on the behaviour of ![]() in this regime other than
in this regime other than
![]() .
.
| (B.8) |
![\begin{displaymath}\mathcal{D}(y)=\left[ \frac{(\xi y)'}{\xi}
\right]'+\frac{\om...
...Sigma_{0}/\xi-\beta_{0}^{2})}{p(\omega^{2}-\beta_{0}^{2})}y=0.
\end{displaymath}](/articles/aa/full/2007/46/aa7988-07/img165.gif) |
(B.10) |
| (B.11) |
 |
(B.12) |